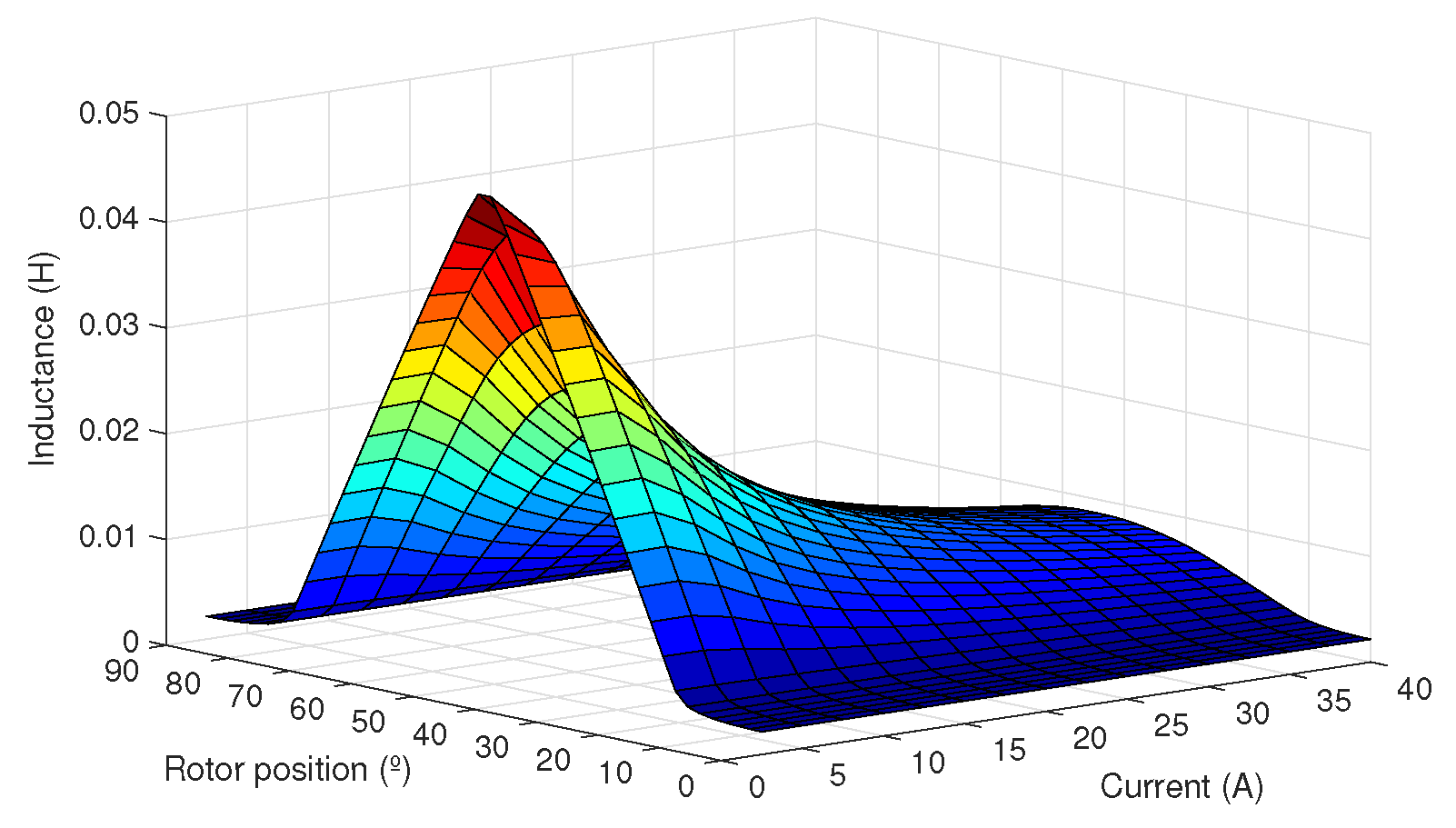
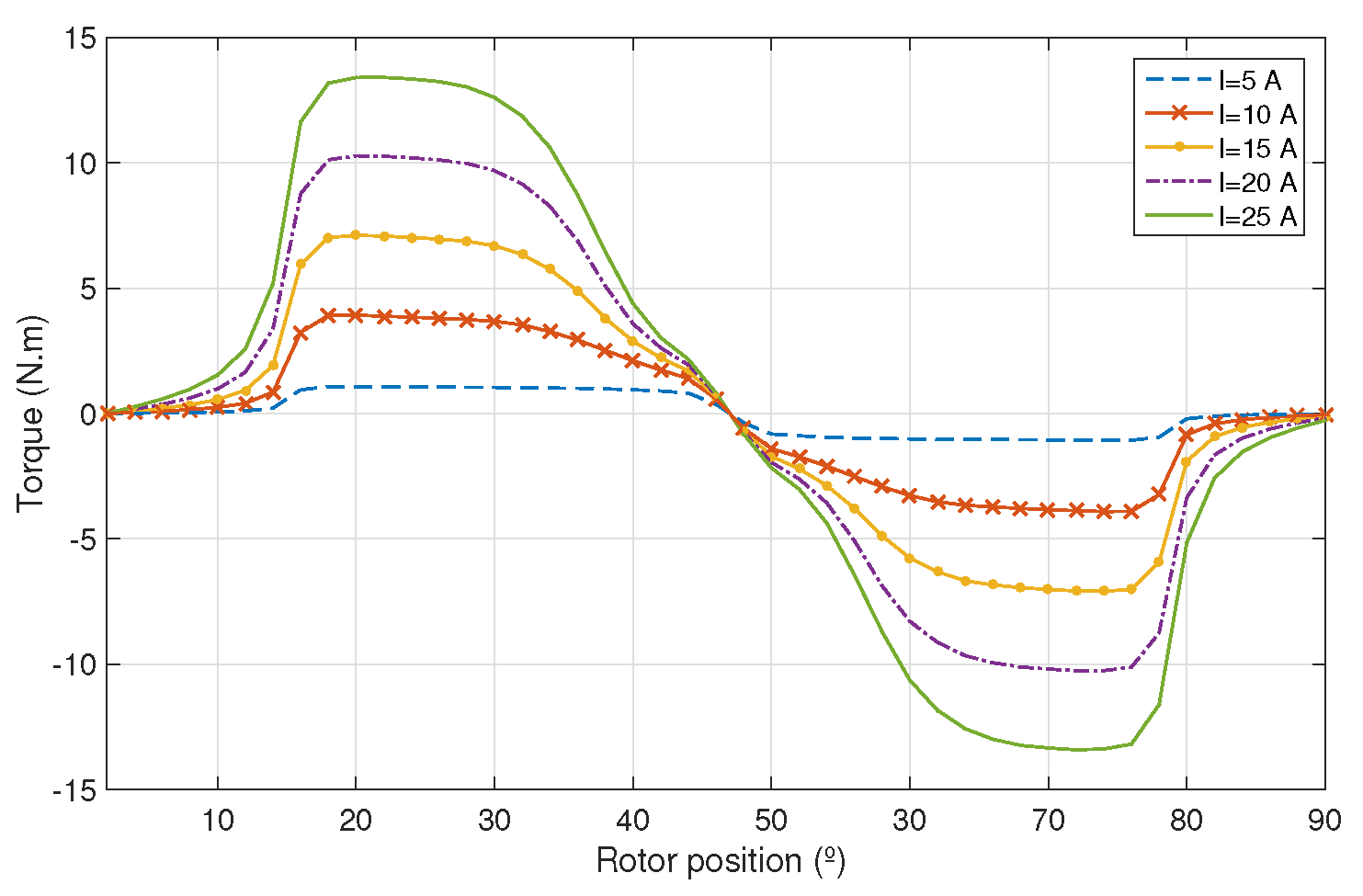
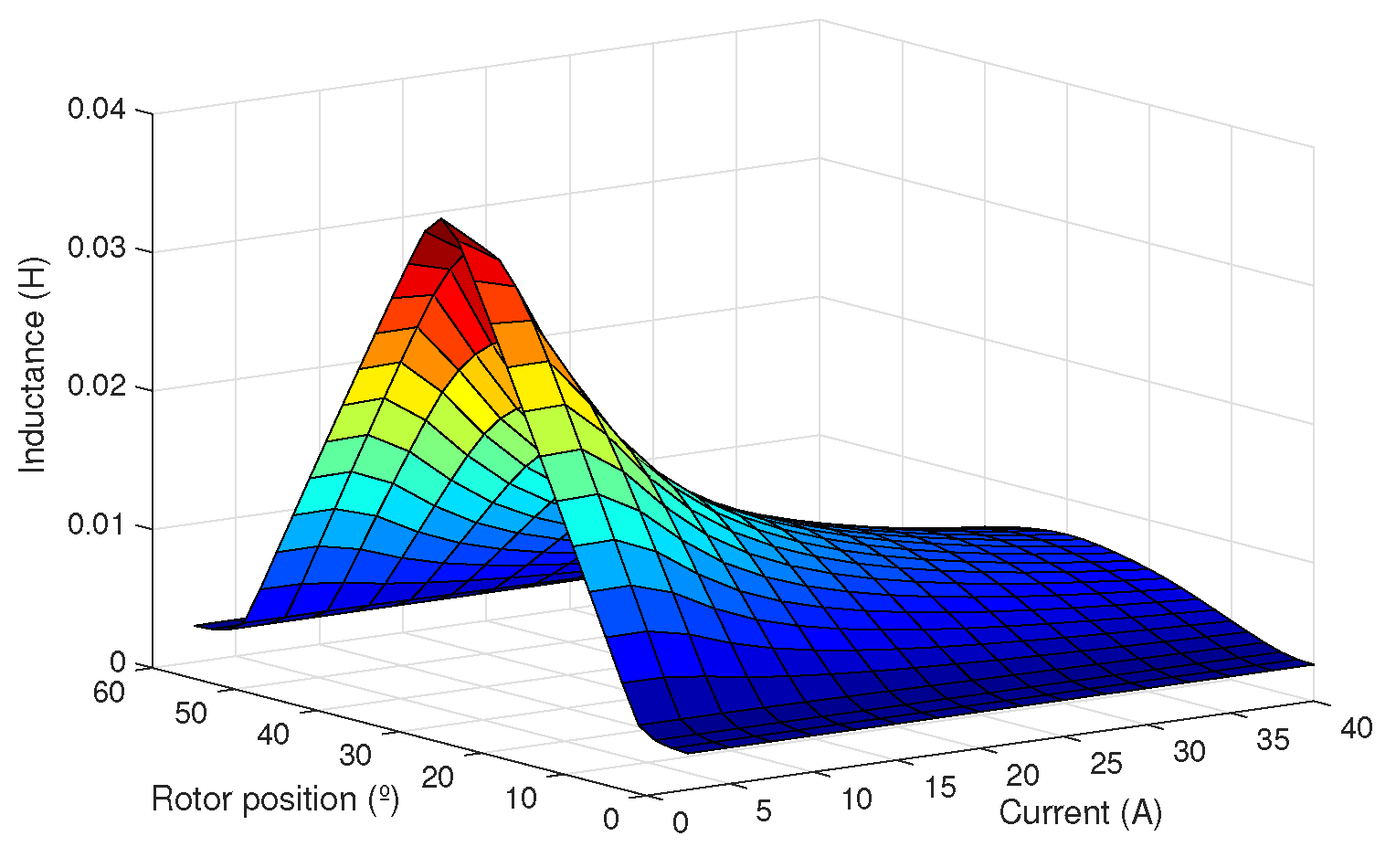
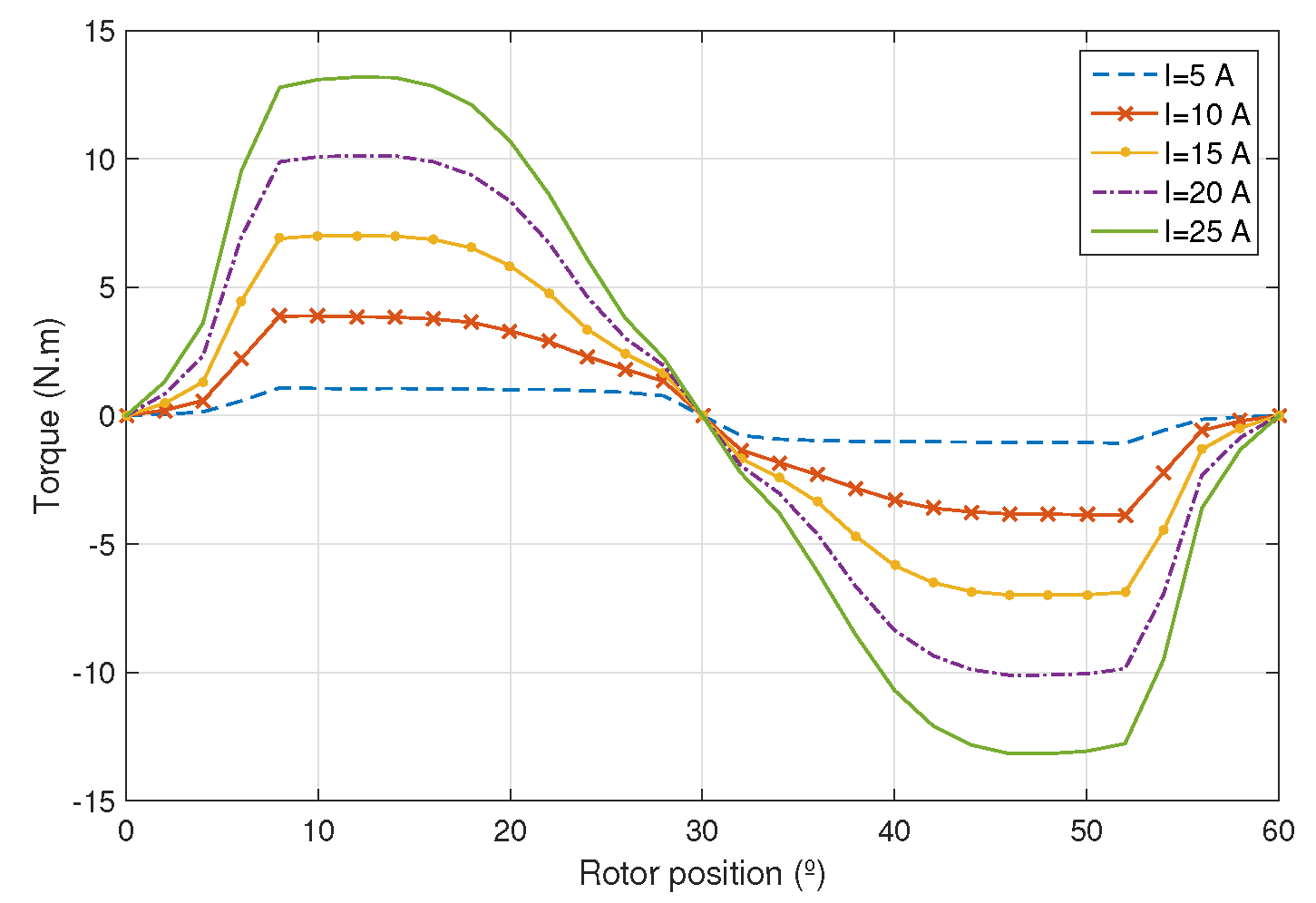
The general theory governing the design of an electrical machine includes studies in the fields of electromagnetism, arrangement of the windings, the magnetic circuit behavior, inductance and resistance of windings [
12]. The process of designing an electric machine takes into account all these studies and the empirical knowledge acquired over the years by designers and researchers. Designing a reluctance machine is not a very complicated task, but several factors must be taken into account during design, such as choosing appropriate values for flux density in the core, air gap, polar arcs. Bad choices can compromise the performance of the SRM final.
In the design of machines, there are a considerable number of free parameters. The task of finding an ideal solution becomes extremely complicated unless the number of these parameters is somewhat limited [
12]. Often, machine design includes the selection of table-based parameters that provide empirical data on asynchronous, synchronous, direct current and double-salient machines. These tables provide a range of empirically defined values of flux and current density, for example, for various machine types that can be applied in the preliminary design phase [
12]. This situation is repeated for SRM, and several of its parameters are selected in a range of values defined empirically by previous studies.
The SRM design is apparently similar to the design of traditional machines but diverges in several points due to the unique features of SRM. Some features, in fact, simplify the design, such as the absence of coils in the rotor, absence of brushes, empty space between the stator and rotor poles favor ventilation. However, other characteristics such as excessive saturation for some rotor positions, inductance nonlinearity, torque pulsation, negative torque production and the difficulty of modeling SRM make this a delicate process.
2.1. Revisit the Selection of SRM Dimensions
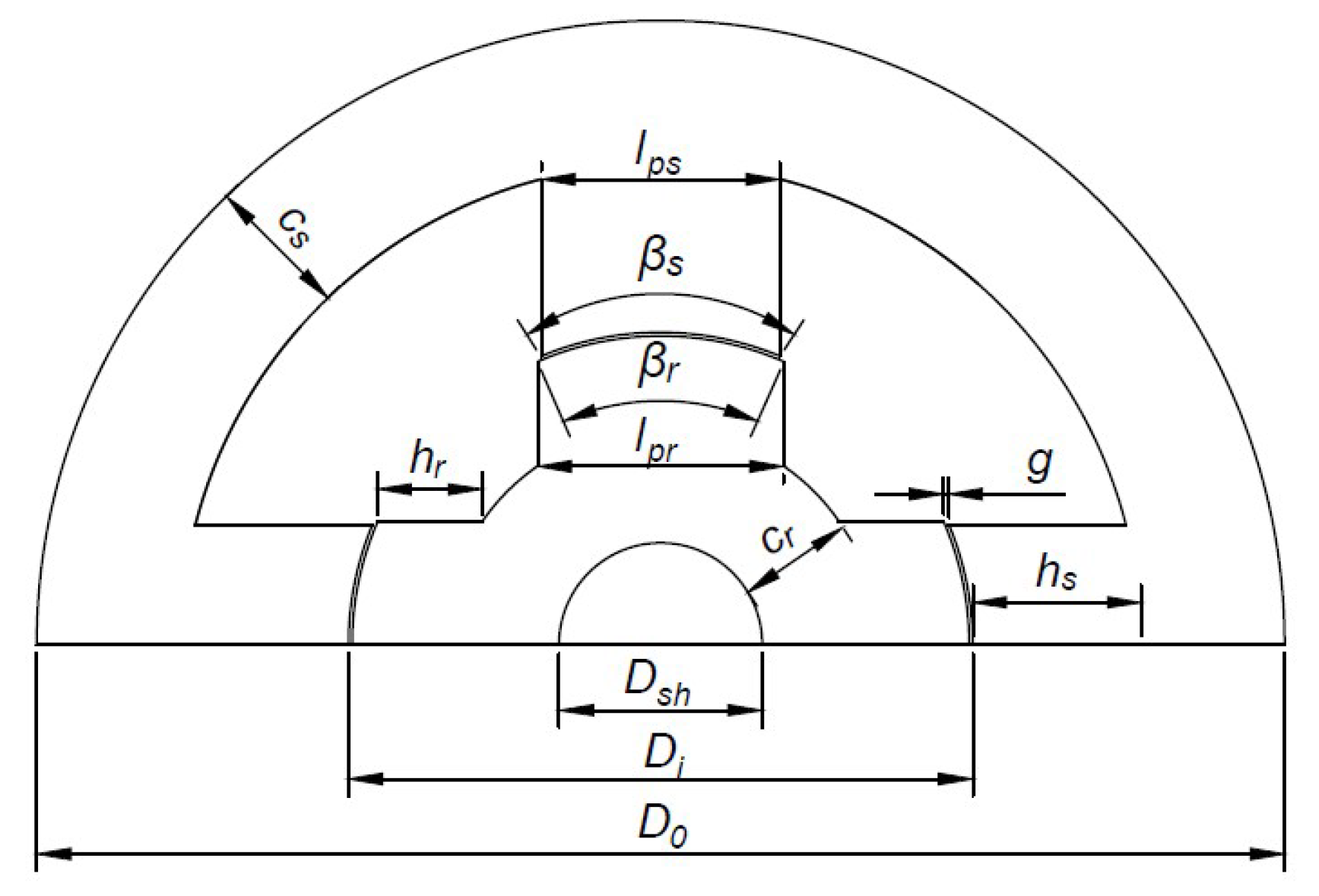
Figure 1 shows all the dimensions that must be determined for the construction of an SRM, where
is the polar arc of the stator;
is the polar arc of the rotor;
is the width of the stator pole;
is the width of the rotor pole;
is the stator yoke thickness;
is the rotor yoke thickness;
is the height of the stator pole;
is the height of the rotor pole;
is the diameter of the shaft;
is the inner diameter;
is the outer diameter;
g is the length of the air gap.
The starting point for designing a machine is to obtain the SRM power output equation, this process is presented by [
3] and from the output equation is determined the inner diameter of the machine.
where
is the power developed,
the relationship with the length of the core
L,
the efficiency,
the duty cycle,
a constant equal to
,
is the ratio between the inductance values in the misaligned and aligned position,
B the flux density,
is the specific electric loading and
the rotor speed in rpm.
The length of the core is determined as a multiple of the inner diameter, as shown in Equation (
2). The value of
is decided by the nature of the motor application and space limitation. For non-servo applications, the interval for
is given by Equation (
3), and for servo applications in Equation (
4).
The outer diameter, as well as the core length, is determined as a multiple of the inner diameter. Typically, the internal diameter is
a
times the value of the outer diameter [
1]. Equation (
5) shows this relationship.
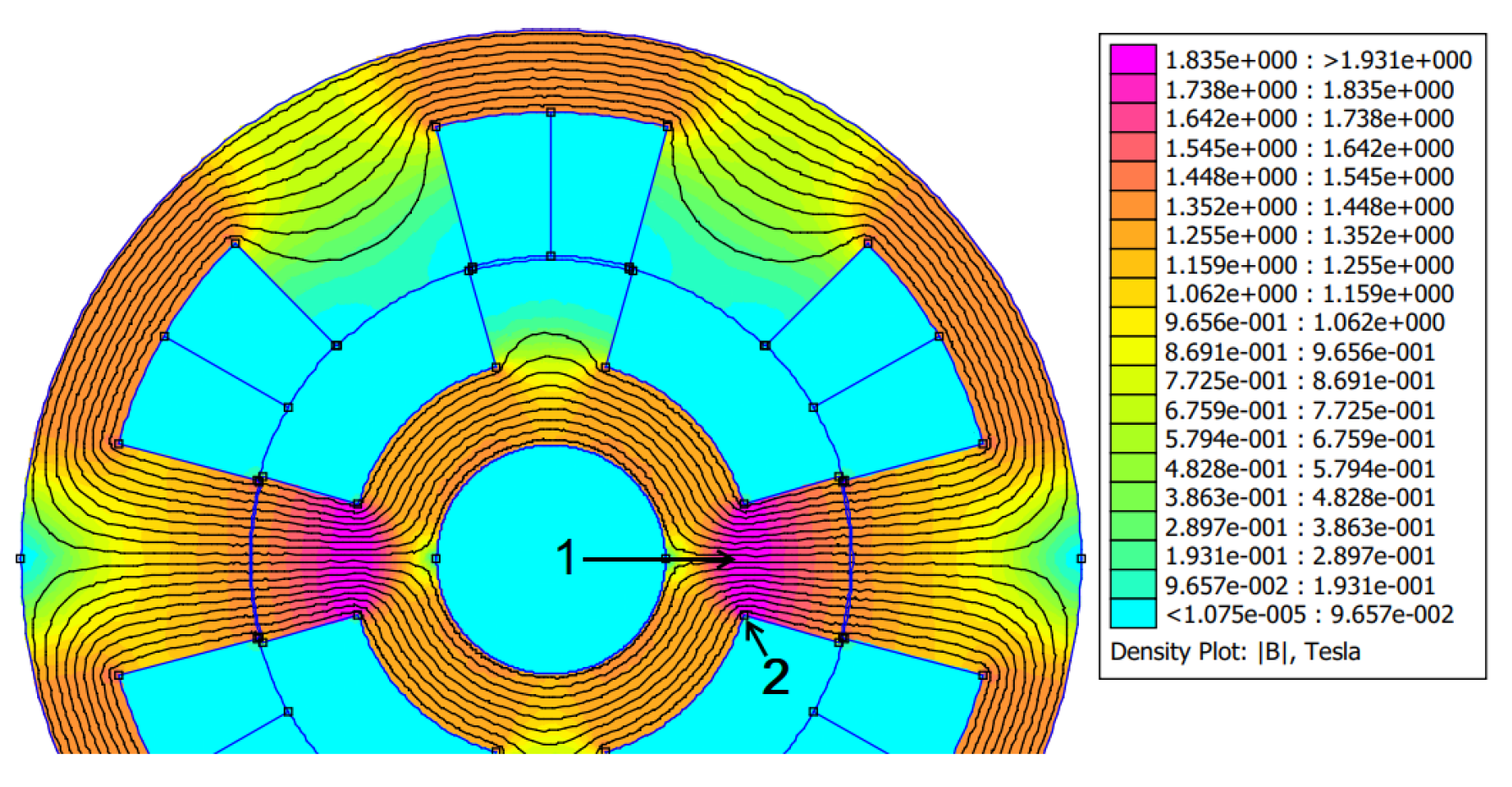
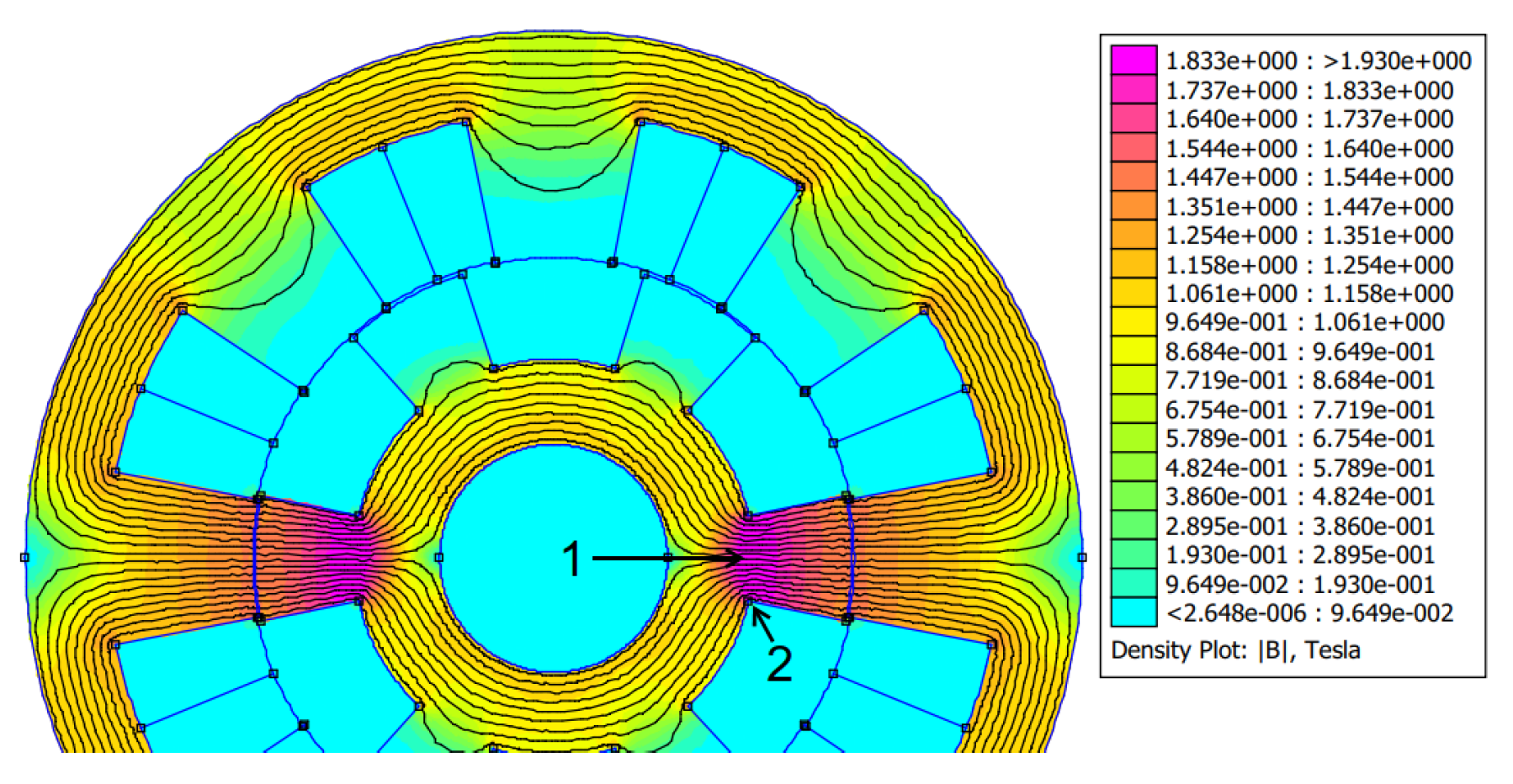
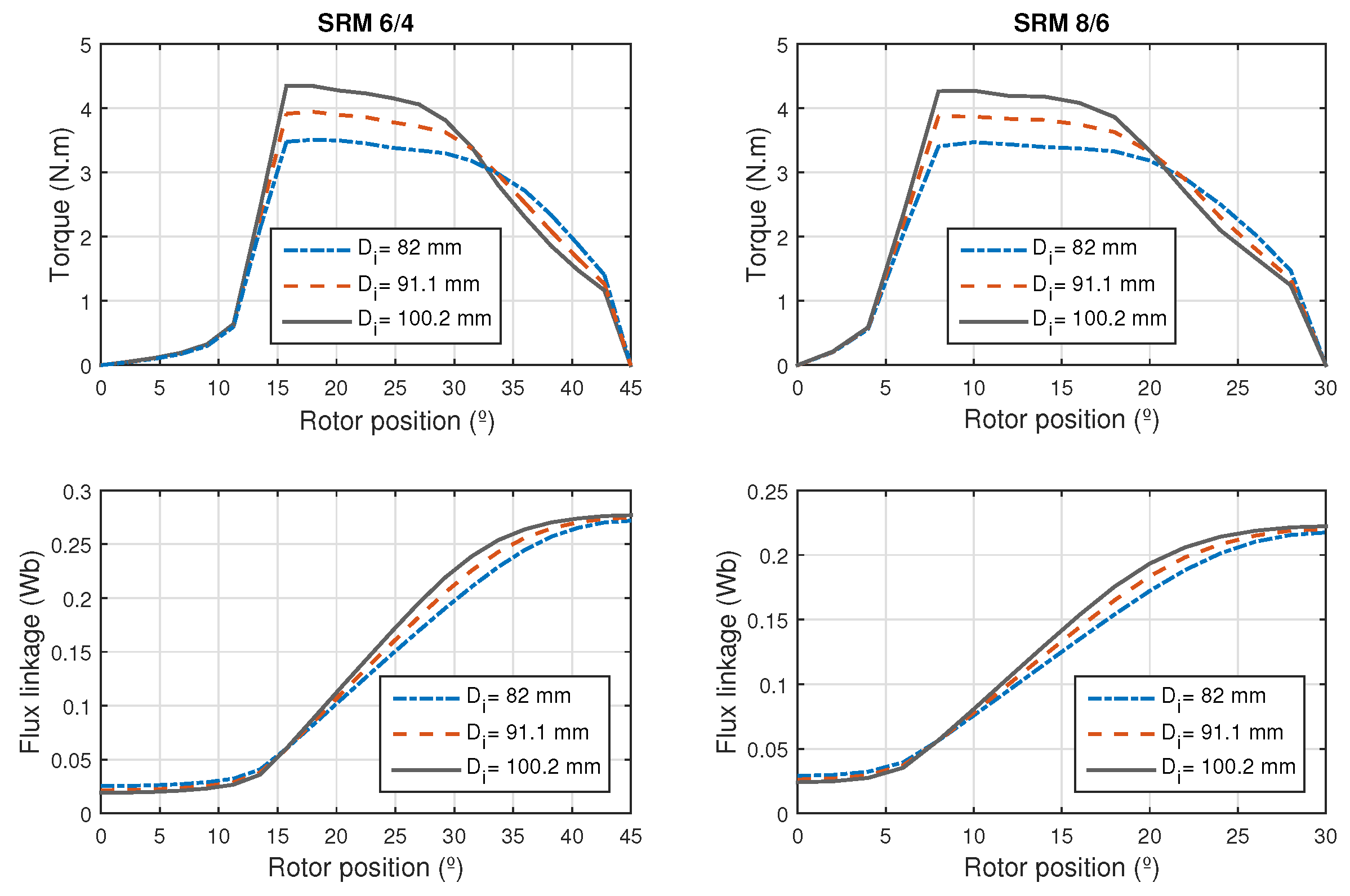
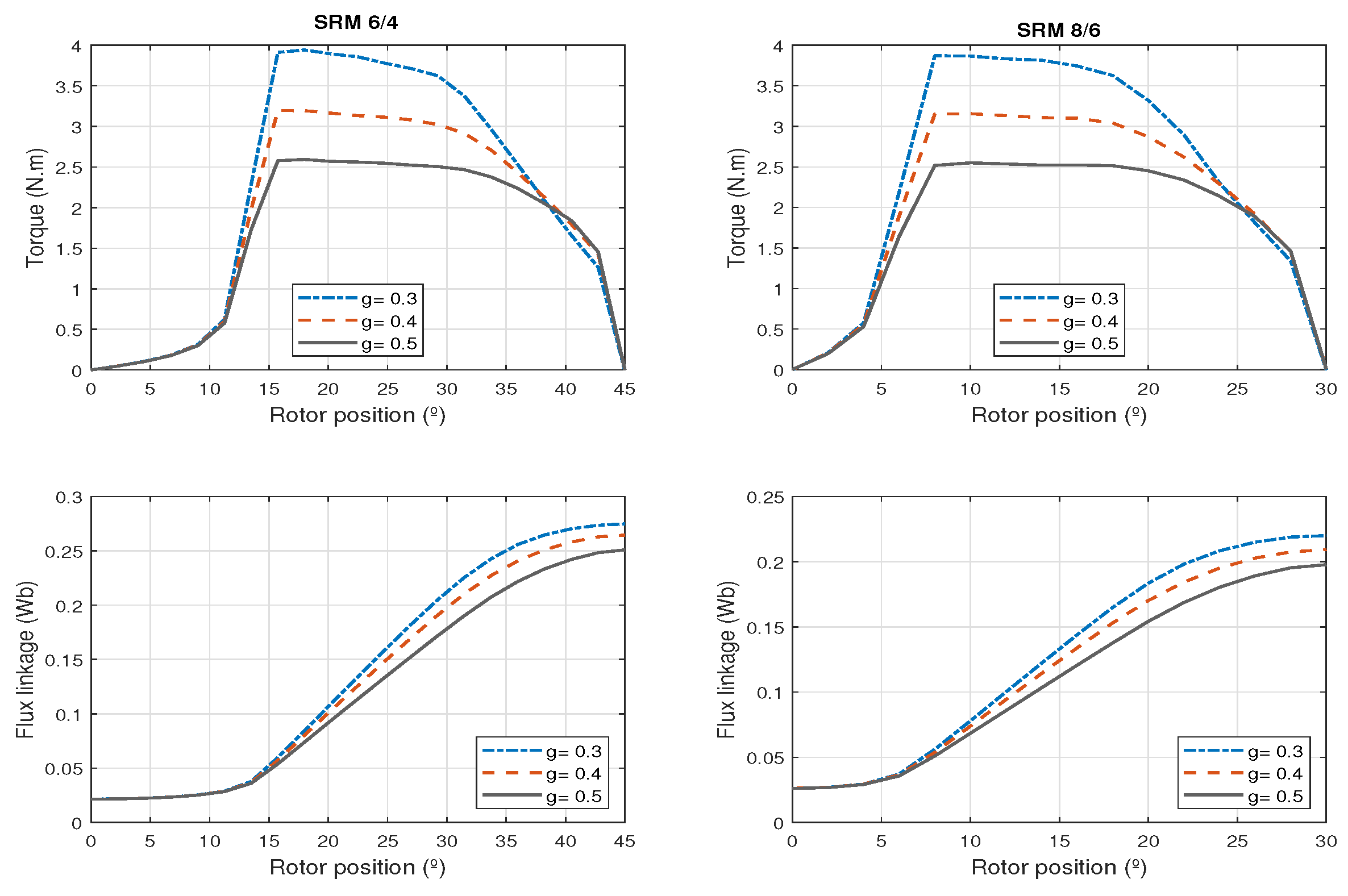
For switched reluctance machines, the air gap must be as small as possible to achieve a high average torque, high ratio between the inductance in the aligned and misaligned positions, with small rotor volumes. For [
3] the air gap value should be chosen according to the size of the machine, for small machines, with power less than 1.0 hp, the air gap should vary between
and
mm, and machines with power above
hp may have air gaps from
to
mm. For other authors, the air gap length should be selected to be about
to
of the rotor diameter [
12].
The width of rotor and stator poles are determined by the polar arcs and by the value of inner diameter. Thus, the stator and rotor pole widths may be computed respectively through Equations (
7) and (
8).
The stator yoke thickness should be large enough to support half the flux density passing through the stator pole. Therefore, the yoke thickness of the stator must be at least half the stator pole width. However, to improve robustness and minimize vibration and noise an additional factor should be considered. Thus, the value of the stator yoke thickness should be in the range:
It is recommended to choose values greater than the minimum for
. Already the rotor yoke does not need to be as thick as the stator yoke thickness and neither has to be equal to the minimum value, which is equal to the minimum value of the stator yoke thickness. The rotor yoke thickness in terms of the stator pole width can be set in the range given below:
Given the values of the outer and inner diameter and the stator yoke thickness, we can calculate the stator pole height value from Equation (
11).
The height of the rotor pole can be determined in the same way, and is defined by:
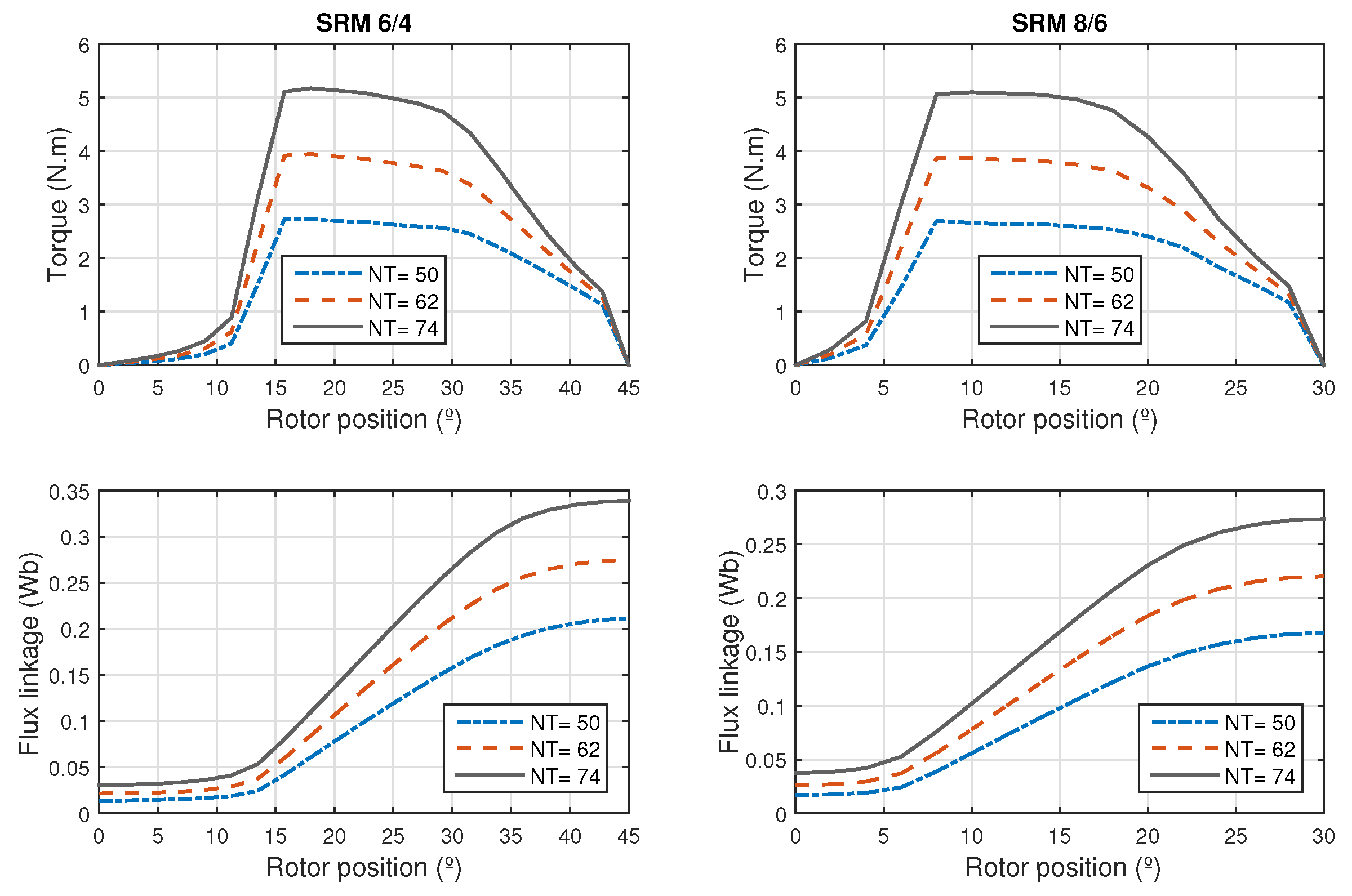
The number of turns (
) per phase of the SRM can be calculated in terms of the magnetic field strength in the air gap (
), the peak current (
) and the air gap length, see Equation (
13)
If
it is the maximum current density allowed in a coil and
q othe number of phases, the conductor section is calculated as:
The values of the polar arcs of the stator and the rotor are chosen to guarantee the proper starting of the machine and to shape the motor torque profile [
3]. These requirements are inserted into the SRM project by offering a lower and upper limit for the values of the polar arcs. In order to guarantee the proper starting of the machine and to prevent the occurrence of parasitic currents due to the magnetic flux dispersion effect, the rotor polar arc must be larger than the polar arc of the stator [
3,
13].
Krishnan in [
3] showed that the minimum value for polar arcs is set according to the number of poles of the machine by Equation (
16).
The angle between the corners of the adjacent rotor poles must be greater than the polar arc of the stator or there will be an overlap of the stator and rotor poles in the non-aligned position [
14]. This implies that the minimum inductance value will be greater, reducing the difference between the maximum and minimum values, which leads to a reduction in the torque value. This relation is presented in Equation (
17).
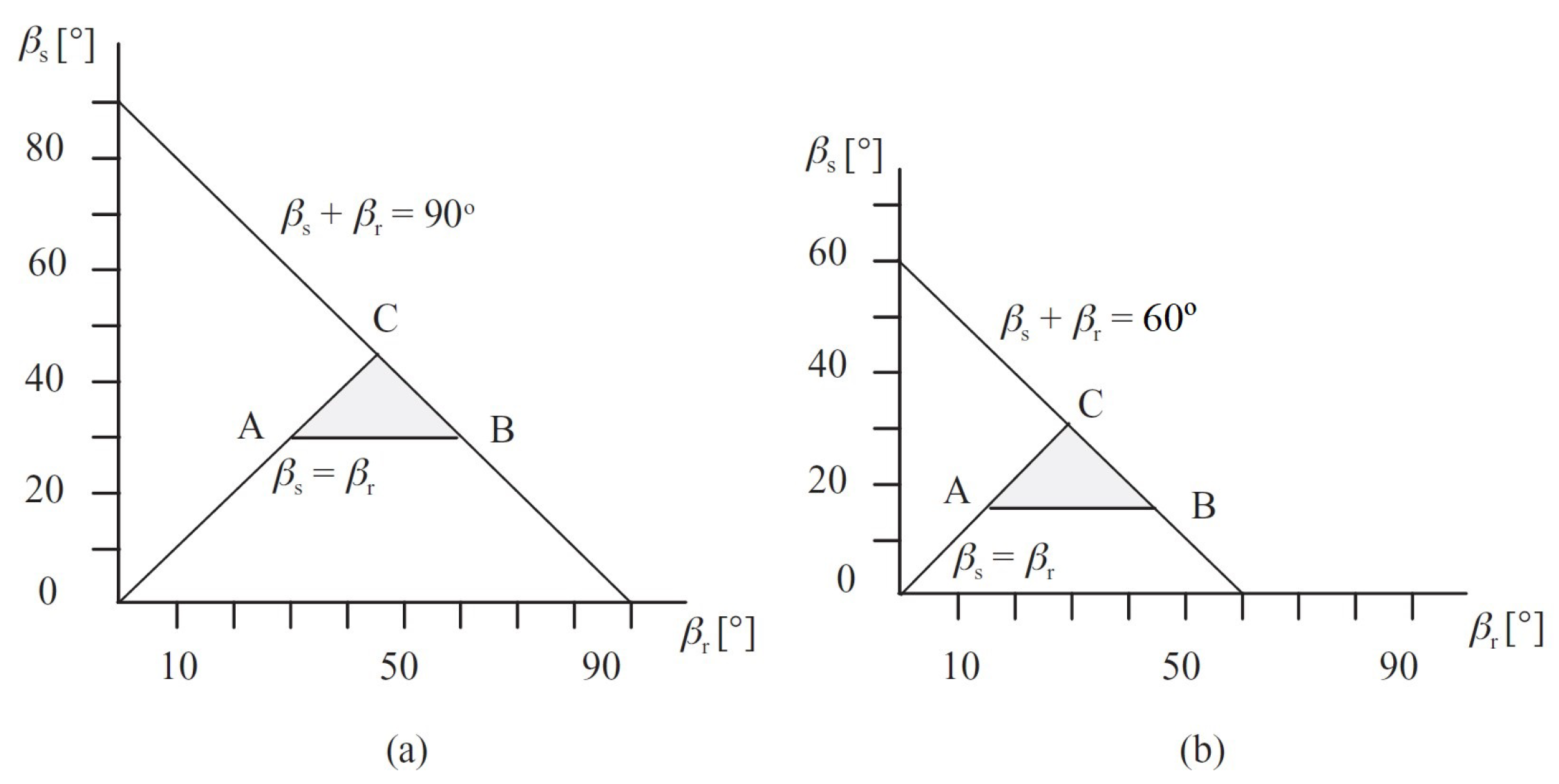
The conditions presented in Equations (
15)–(
17) can be represented graphically in a triangle of possibilities. It is necessary that the values of the polar arcs of the machine are in this triangle [
14].
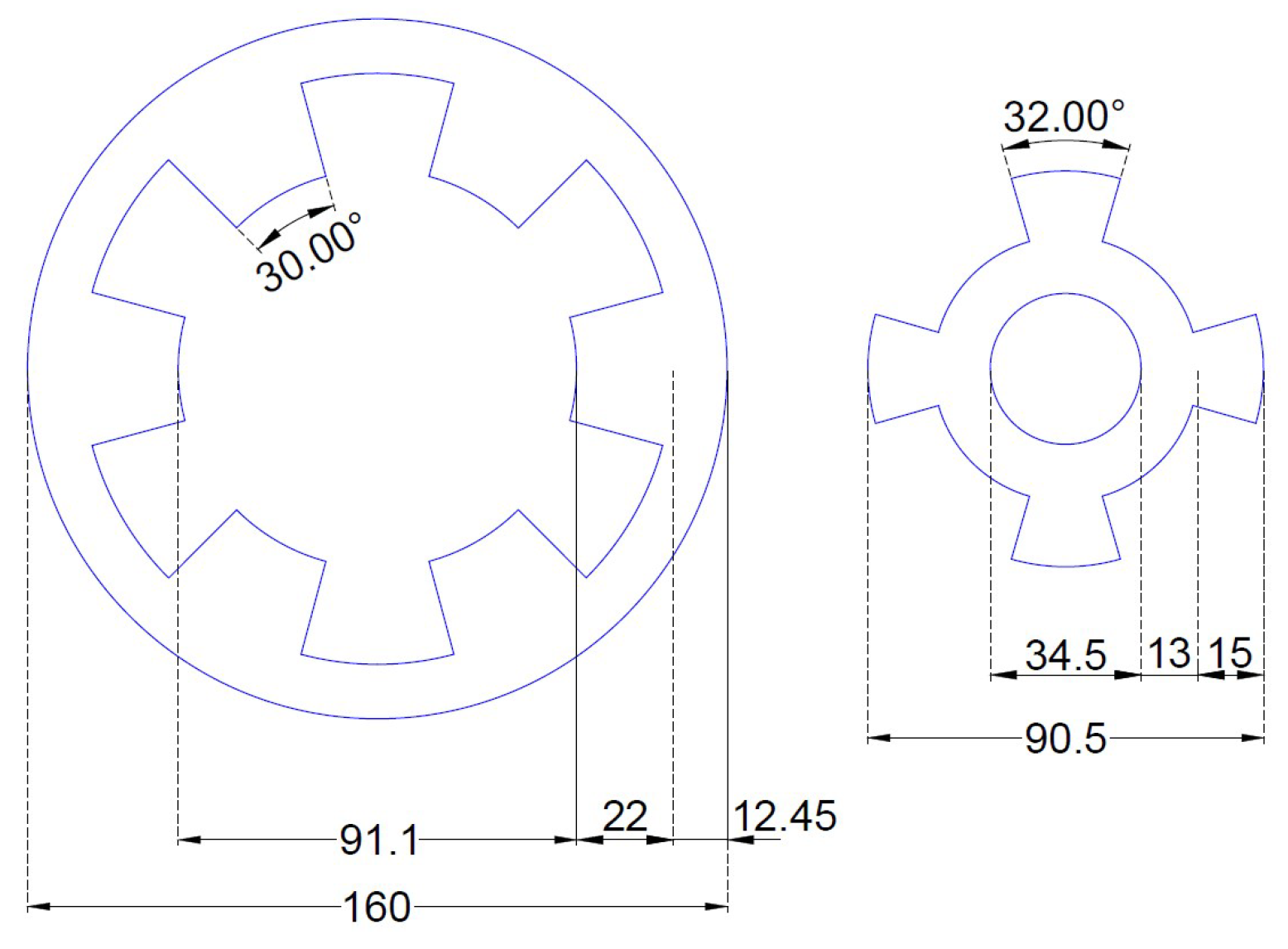
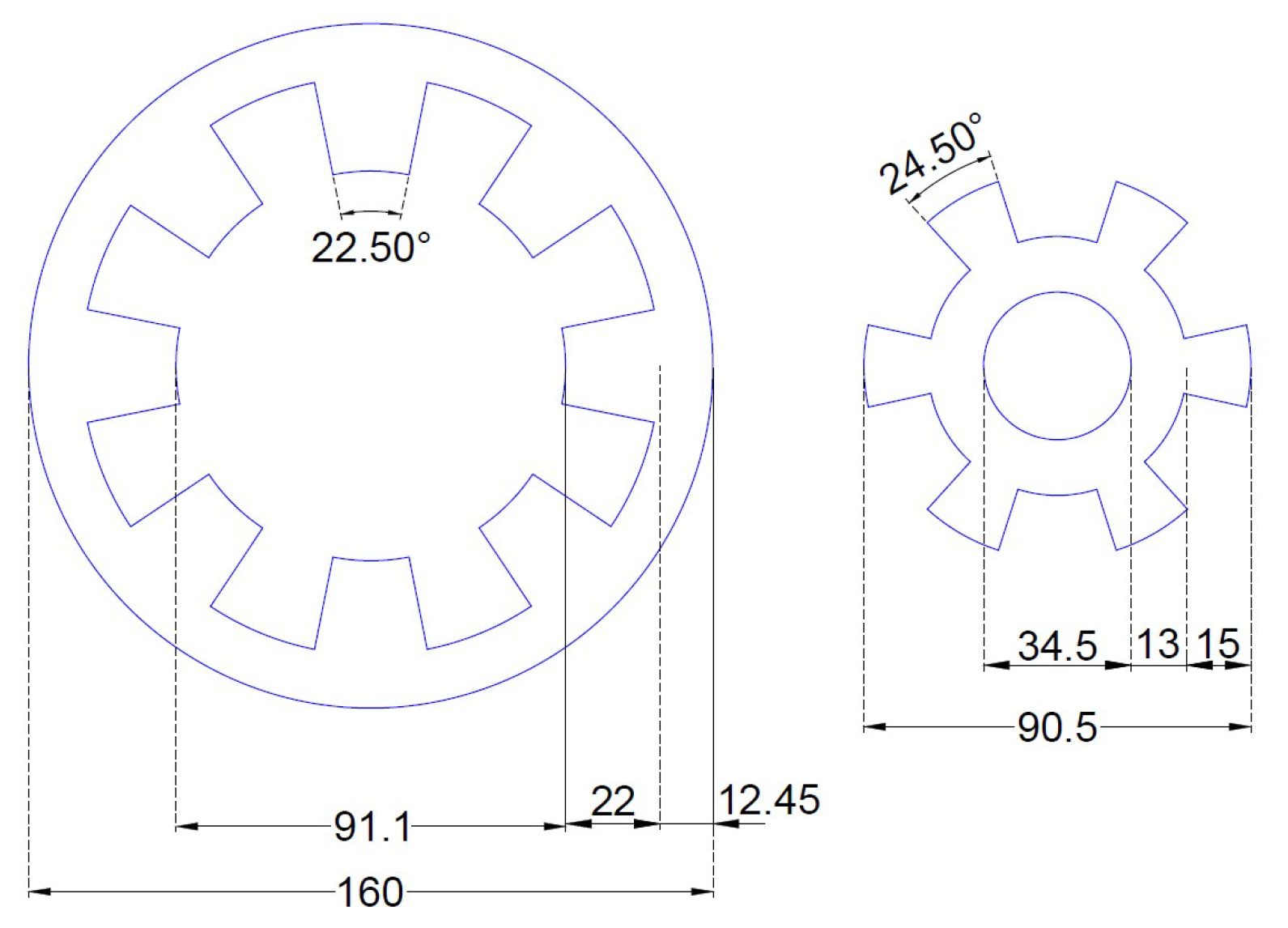
Figure 2 shows the triangle of possibilities for a SRM 6/4 and a SRM 8/6. For example, for a, SRM 8/6, if
so
.