On the Importance of Sleeve Flexibility in Passive Control of Critical Speeds of a Rotating Shaft Using Eccentric Sleeves †
Abstract
1. Introduction
2. Methodology
2.1. High Speed Test Facility
2.1.1. Test Shaft and Eccentric Sleeve
2.1.2. Instrumentation
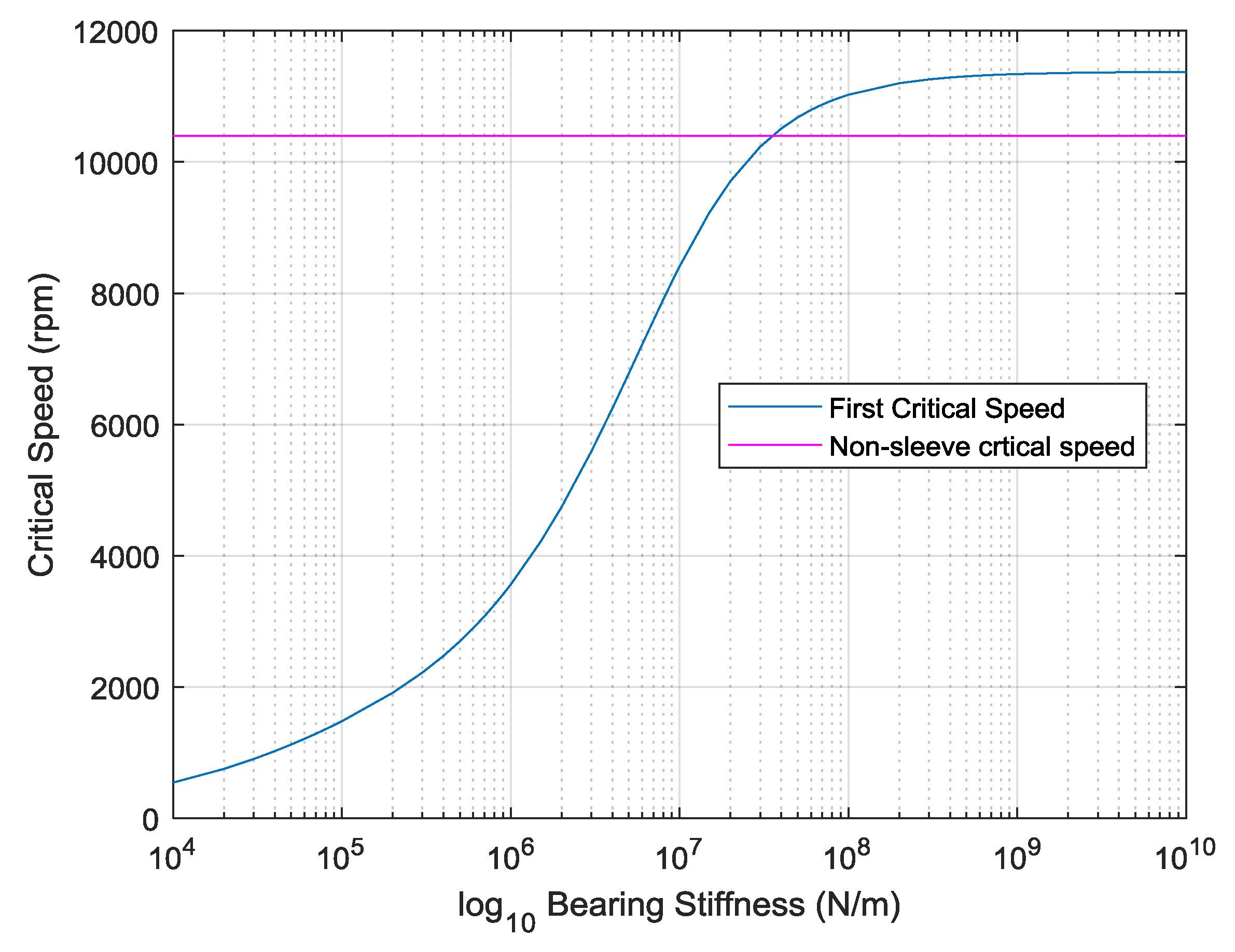
2.2. Finite Element Model Development
3. Results and Discussion
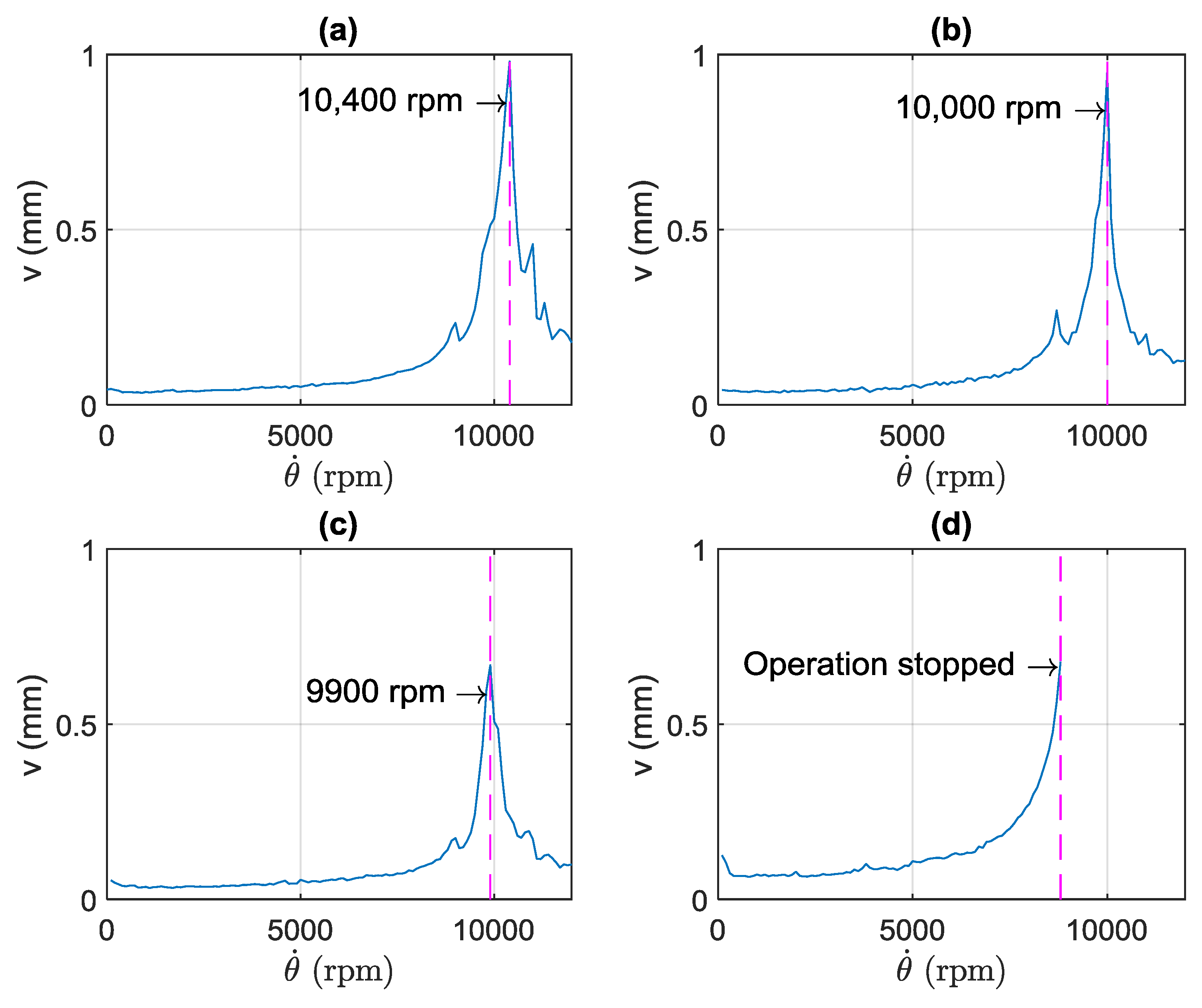
3.1. Experimental Results
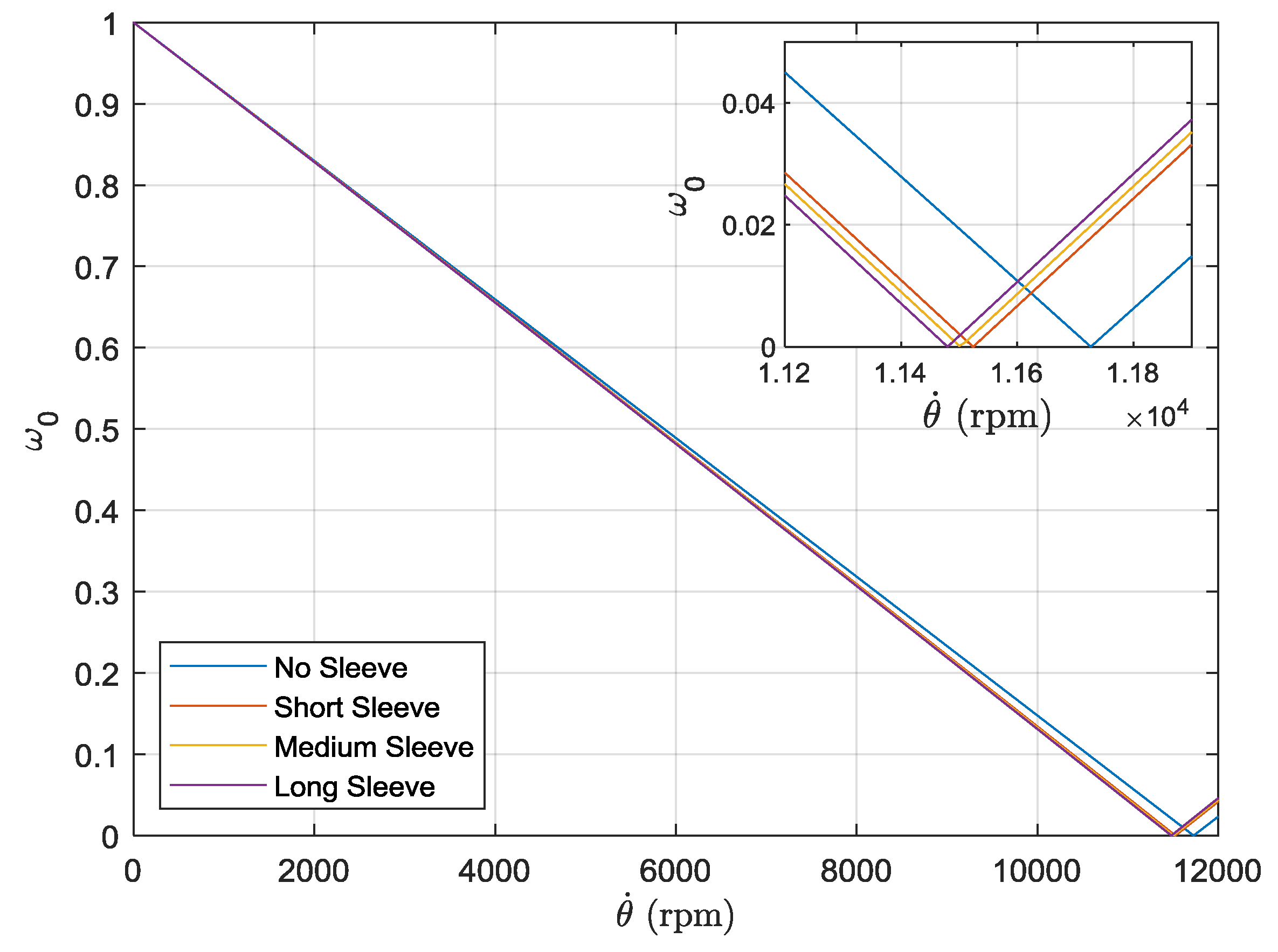
3.2. Numerical Results
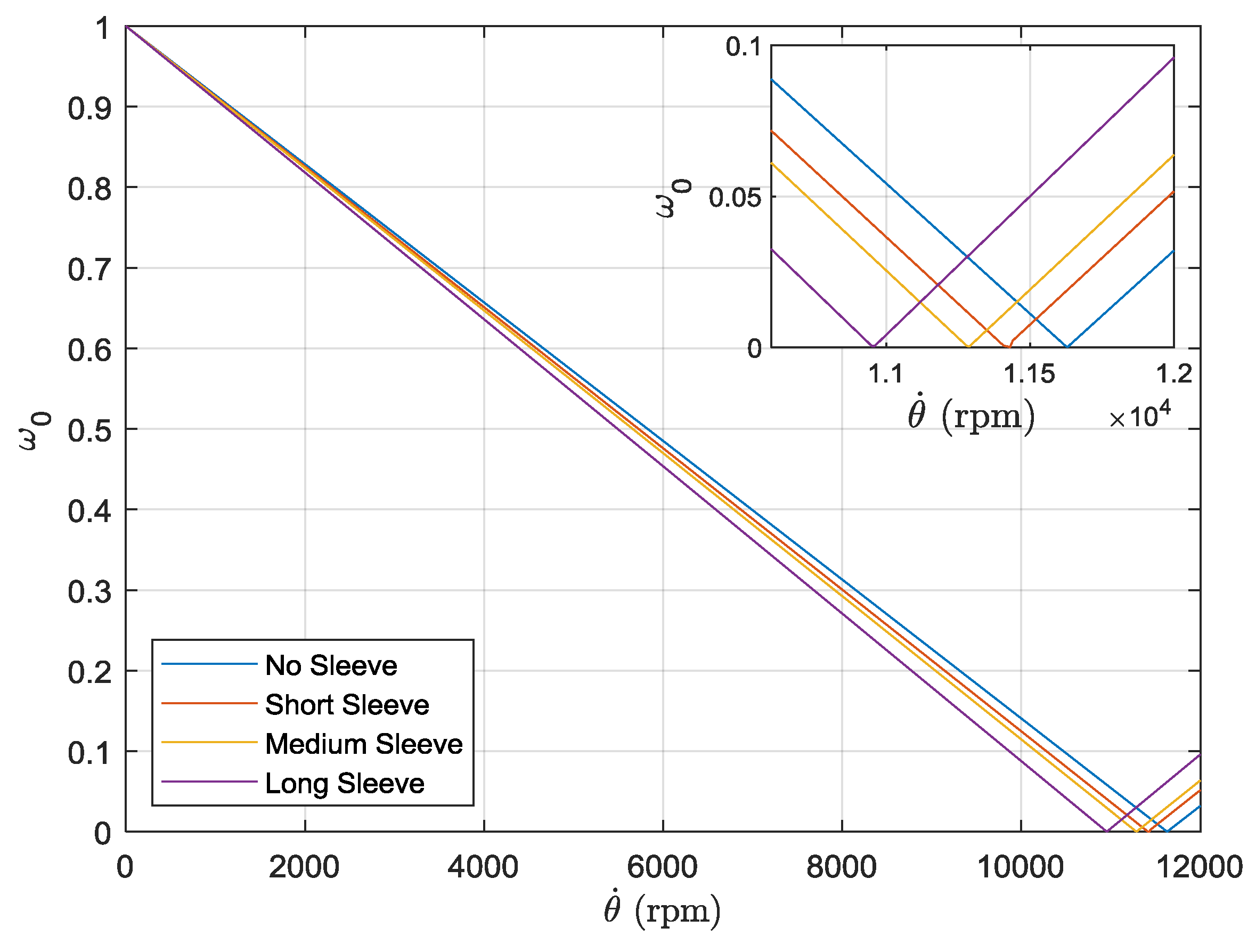
3.3. Modifications to the Finite Element Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Adams, M.L. Rotating Machinery Vibration, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Chuan, M.; Changsheng, Z. Unbalance Compensation for Active Magnetic Bearing Rotor System Using a Variable Step Size Real-Time Iterative Seeking Algorithm. IEEE Trans. Ind. Electron. 2018, 65, 4177–4186. [Google Scholar] [CrossRef]
- American Petroleum Institute. AQPI Standard 617—Special Purpose Couplings for Petroleum, Chemical and Gas Industry Services; American Petroleum Institute: Washington, DC, USA, 2017. [Google Scholar]
- Meeus, H.; Verrelst, B.; Moens, D.; Guillaume, P.; Lefeber, D. Experimental Study of the Shaft Penetration Factor on the Torsional Dynamic Response of a Drive Train. Machines 2018, 6, 31. [Google Scholar] [CrossRef]
- Lees, A.W.; Sinha, J.K.; Friswell, M.I. Model-based identification of rotating machines. Mech. Syst. Signal Process. 2009, 23, 1884–1893. [Google Scholar] [CrossRef]
- Sinha, J.K.; Lees, A.W.; Friswell, M.I. Estimating unbalance and misalignment of a flexible rotating machine from a single run-down. J. Sound Vib. 2004, 272, 967–989. [Google Scholar] [CrossRef]
- Sudhakar, G.N.D.S.; Sekhar, A.S. Identification of unbalance in a rotor bearing system. J. Sound Vib. 2011, 330, 2299–2313. [Google Scholar] [CrossRef]
- Yao, J.; Liu, L.; Yang, F.; Scarpa, F.; Gao, J. Identification and optimization of unbalance parameters in rotor-bearing systems. J. Sound Vib. 2018, 431, 54–69. [Google Scholar] [CrossRef]
- Morton, P.G. Modal balancing of flexible shafts without trial weights. IMechE Part C Mech. Eng. Sci. 1985, 199, 71–78. [Google Scholar] [CrossRef]
- Parkinson, A.G. Balancing of rotating machinery. IMechE Part C Mech. Eng. Sci. 1991, 205, 53–66. [Google Scholar] [CrossRef]
- Knowles, G.; Kirk, A.; Stewart, J.; Bickerton, R.; Bingham, C. Theoretical investigation into balancing high-speed flexible shafts, by the use of a novel compensating balancing sleeve. IMechE Part C 2014, 228, 2323–2336. [Google Scholar] [CrossRef]
- Kirk, A.J.; Griffiths, J.; Bingham, C.; Knowles, G.; Bickerton, R. Passive Control of Critical Speeds of a Rotating Shaft Using Eccentric Sleeves: Model Development. In Proceedings of the 2016 ASME Turbo Expo, Seoul, Korea, 13–17 June 2016; Volume 7A, p. V07AT32A034. [Google Scholar]
- Knowles, G.; Kirk, A.; Bingham, C.; Bickerton, R. Generalised analysis of compensating balancing sleeves with experimental results from a scaled industrial turbine coupling shaft. IMechE Part C 2017, 232, 3453–3468. [Google Scholar] [CrossRef]
- Elnady, M.E.; Sinha, J.K.; Oyadiji, S.O. Identification of Critical Speeds of Rotating Machines Using On-Shaft Wireless Vibration Measurement. J. Phys. Conf. Ser. 2012, 364, 012142. [Google Scholar] [CrossRef]
- Elnady, M.E.; Abdelbary, A.; Sinha, J.K.; Oyadiji, S.O. FE and Experimental Modeling of On-shaft Vibration Measurement. In Proceedings of the 15th International Conference on Aerospace Sciences & Aviation Technology, Cairo, Egypt, 28–30 May 2013. Paper: ASAT-15-168-ST. [Google Scholar]
- Vollen, A.; Komzsik, L. Computational Techniques of Rotor Dynamics with the Finite Element Model; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Tiwari, R.; Lees, A.; Friswell, M. Identification of dynamic bearing parameters: A review. Shock Vib. Dig. 2004, 36, 99–124. [Google Scholar] [CrossRef]

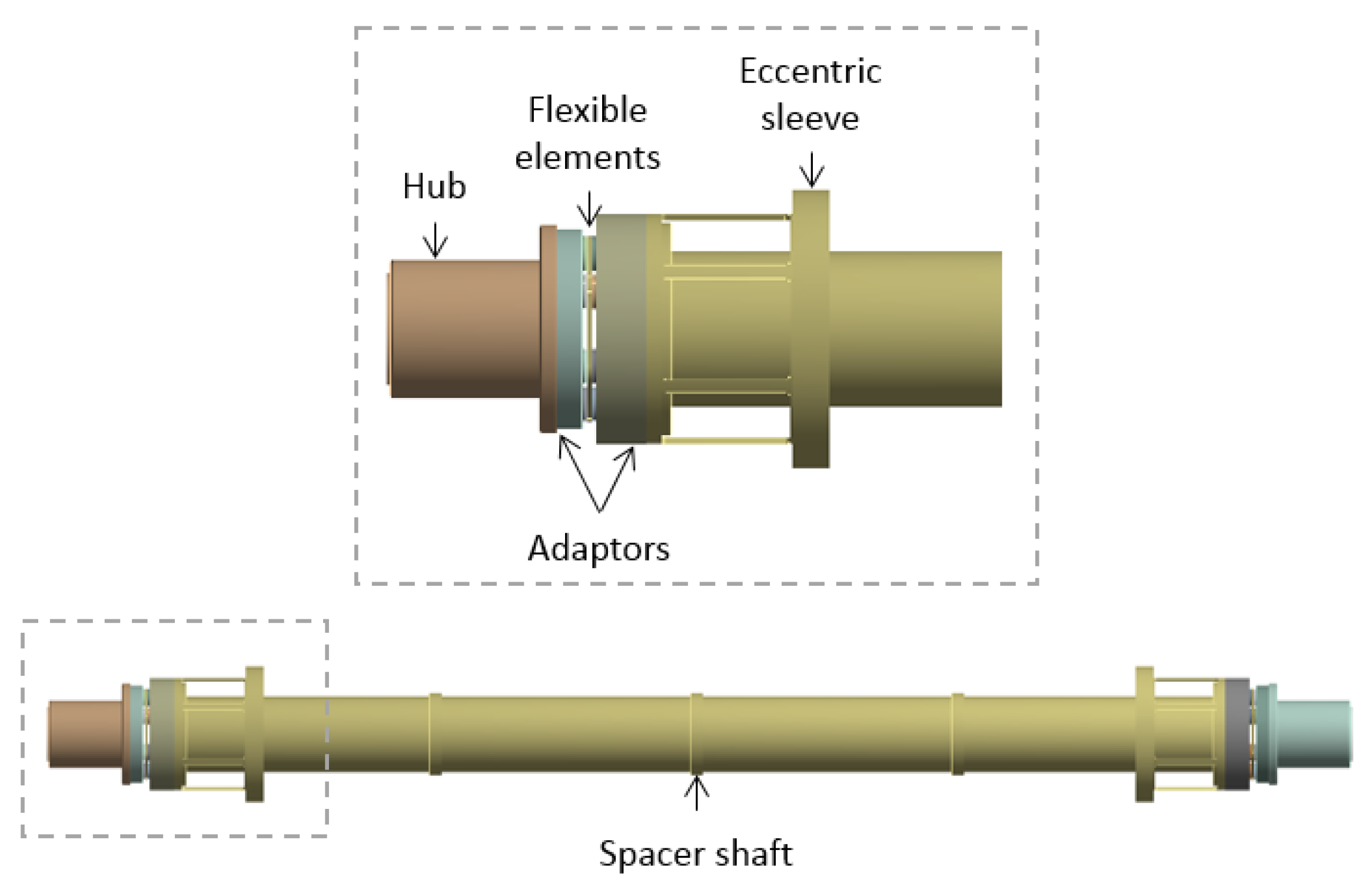





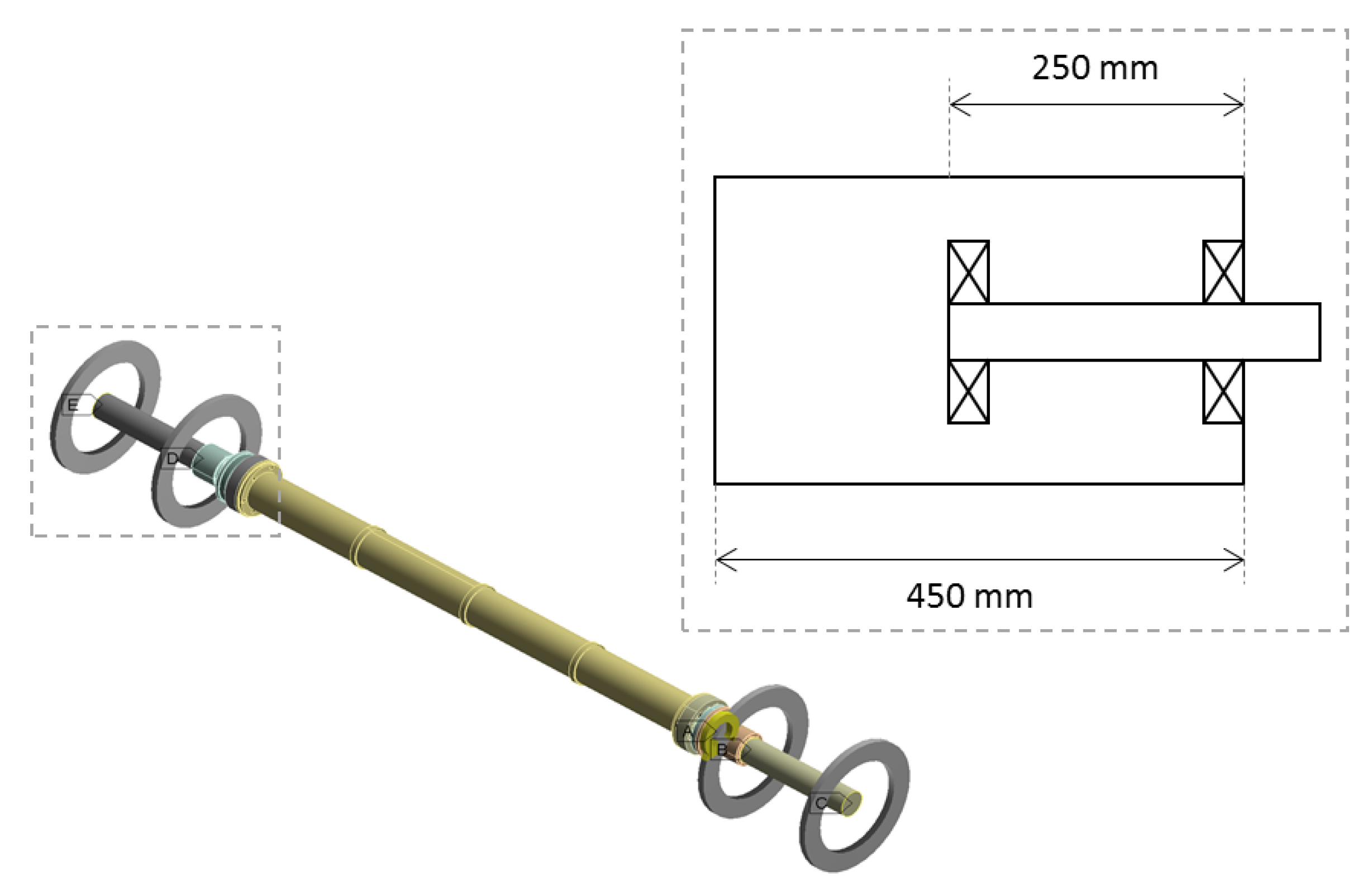
| Material | BS970 817M40T | AISI 301 Stainless | Grade 5 Titanium |
| Component(s) | Hub, Spacer, Sleeves | Flexible Elements | Adaptors |
| Modulus of Elasticity (GPa) | 205 | 195 | 114 |
| Poisson Ratio | 0.3 | 0.3 | 0.342 |
| Ultimate Tensile Strength (MPa) | 850 | 515 | 950 |
| Tensile Yield Strength (MPa) | 700 | 205 | 880 |
| Compressive Yield Strength (MPa) | 800 | 500 | 970 |
| Short | Medium | Long |
|---|---|---|
| 66 mm | 76 mm | 86 mm |
| No Sleeve | Short | Medium | Long | |
|---|---|---|---|---|
| Unbalance (g-mm) | 4.89 | 6.24 | 4.52 | 7.62 |
| No Sleeve | Short | Medium | Long | ||
|---|---|---|---|---|---|
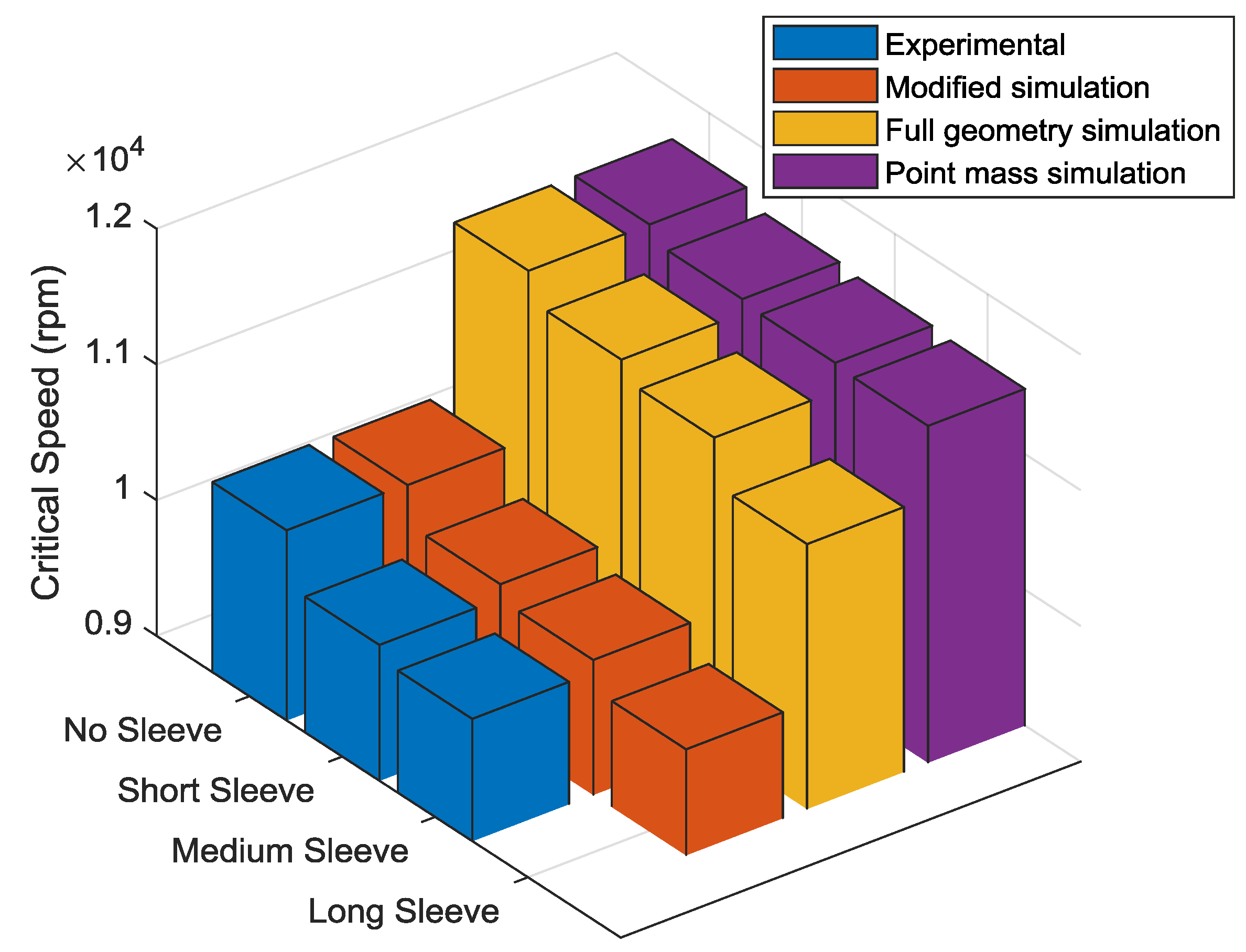
| Critical Speed (rpm) | Full Geometry Simulation | 11,630 | 11,420 | 11,290 | 10,950 |
| Point Mass Simulation | 11,525 | 11,500 | 11,480 | ||
| Experimental | 10,400 | 10,000 | 9900 | - | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kirk, A.; Griffiths, J. On the Importance of Sleeve Flexibility in Passive Control of Critical Speeds of a Rotating Shaft Using Eccentric Sleeves. Machines 2019, 7, 56. https://doi.org/10.3390/machines7030056
Kirk A, Griffiths J. On the Importance of Sleeve Flexibility in Passive Control of Critical Speeds of a Rotating Shaft Using Eccentric Sleeves. Machines. 2019; 7(3):56. https://doi.org/10.3390/machines7030056
Chicago/Turabian StyleKirk, Antony, and Jonathan Griffiths. 2019. "On the Importance of Sleeve Flexibility in Passive Control of Critical Speeds of a Rotating Shaft Using Eccentric Sleeves" Machines 7, no. 3: 56. https://doi.org/10.3390/machines7030056
APA StyleKirk, A., & Griffiths, J. (2019). On the Importance of Sleeve Flexibility in Passive Control of Critical Speeds of a Rotating Shaft Using Eccentric Sleeves. Machines, 7(3), 56. https://doi.org/10.3390/machines7030056





