Fluid–Structure Interaction Modeling Applied to Peristaltic Pump Flow Simulations
Abstract
1. Introduction
2. Geometry and Model
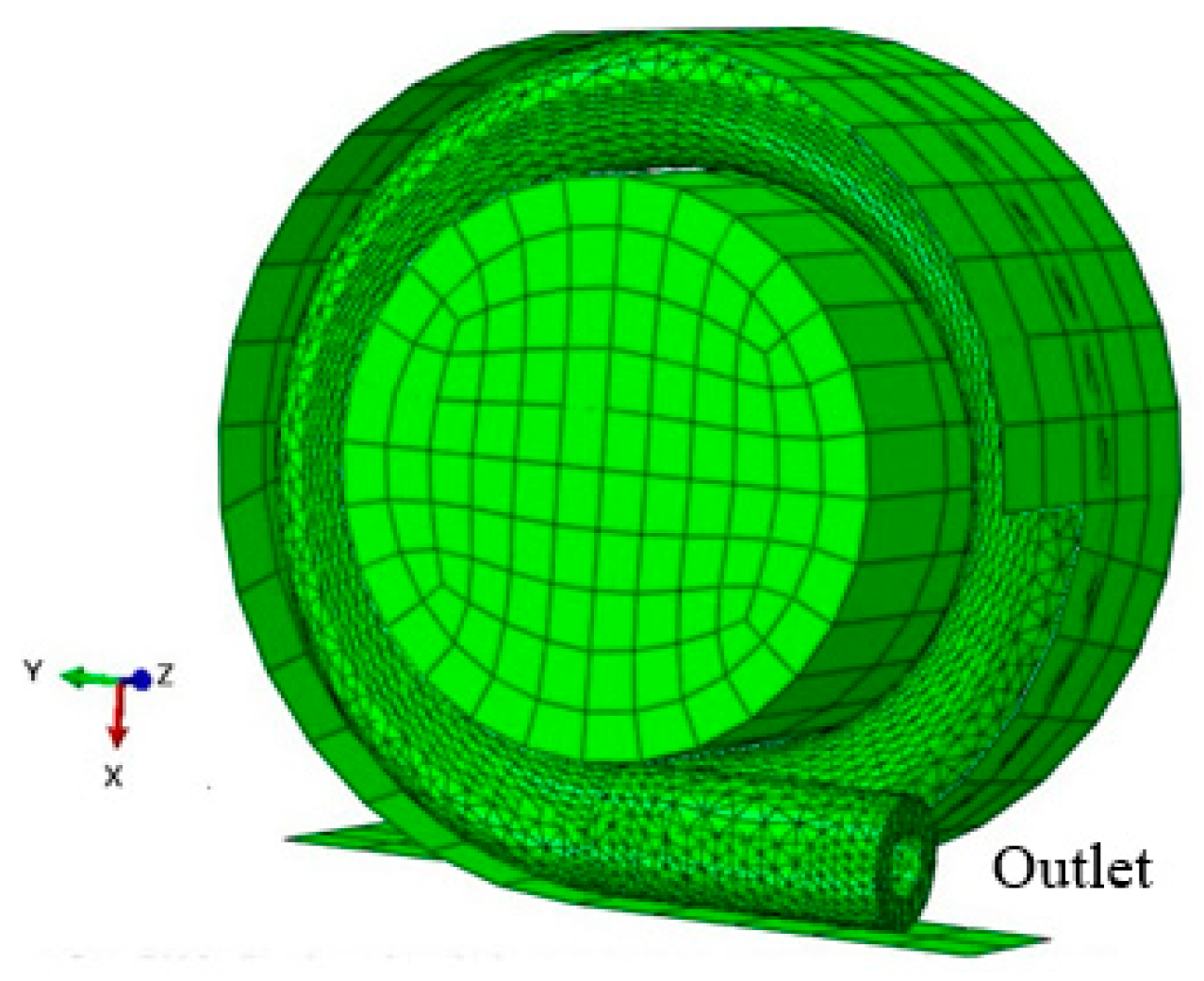
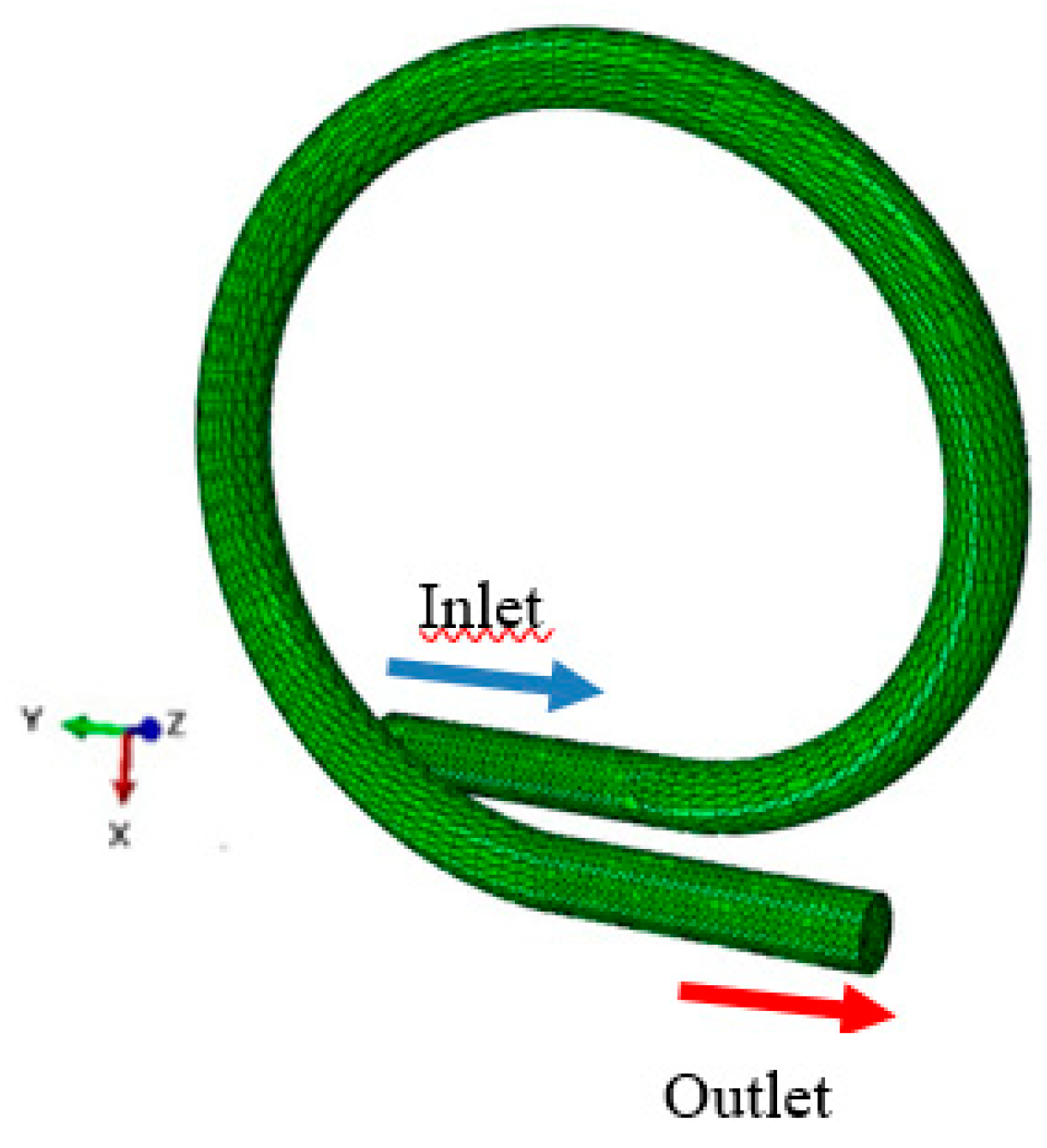
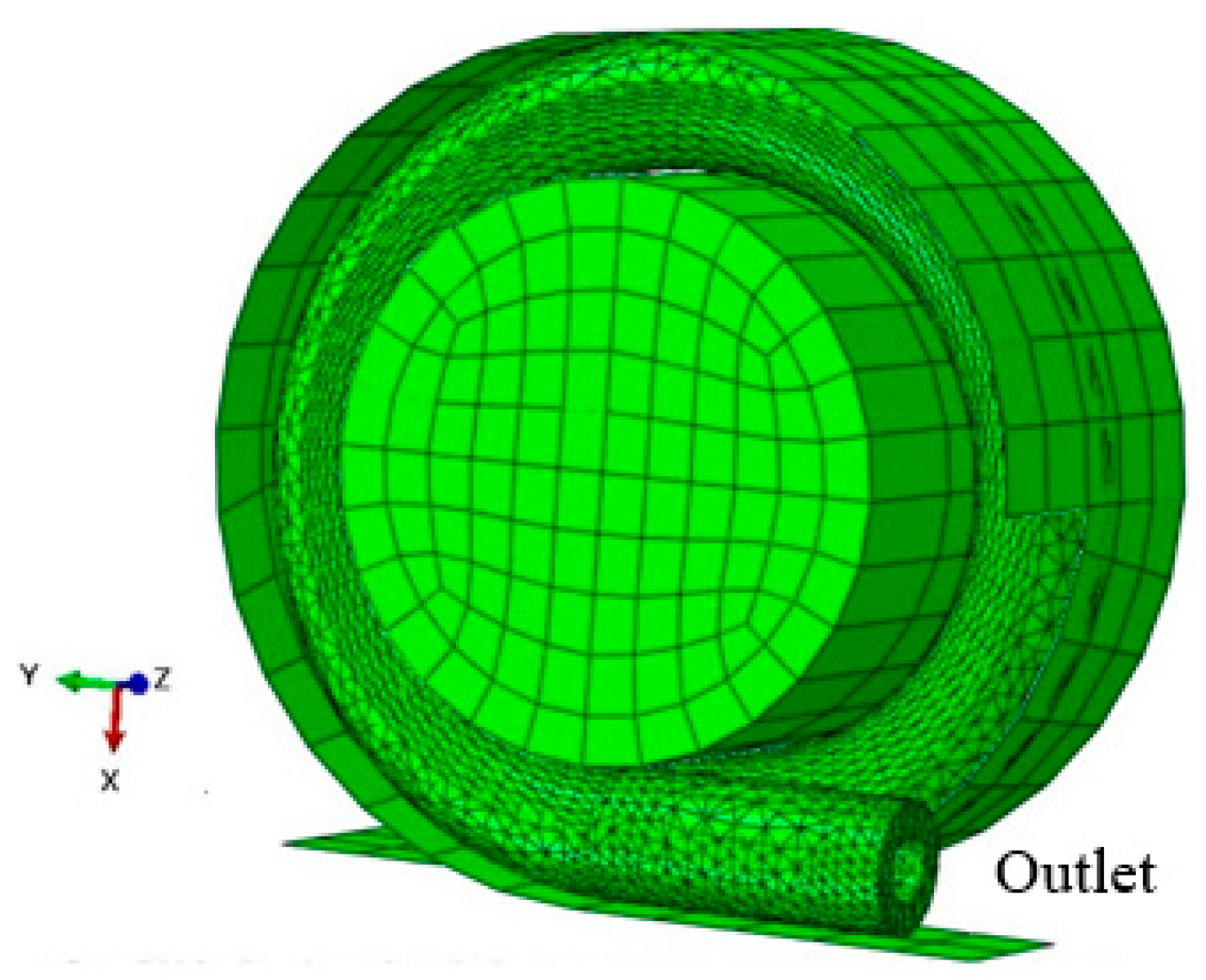
2.1. Model Geometry and Finite Element Mesh
2.2. Mathematical Model
- -
- For the fluid part: No-flux condition on the ends;
- -
- For the solid part: No-stress condition on the free surface.
2.3. Simulation Set-Up
3. Results and Discussion
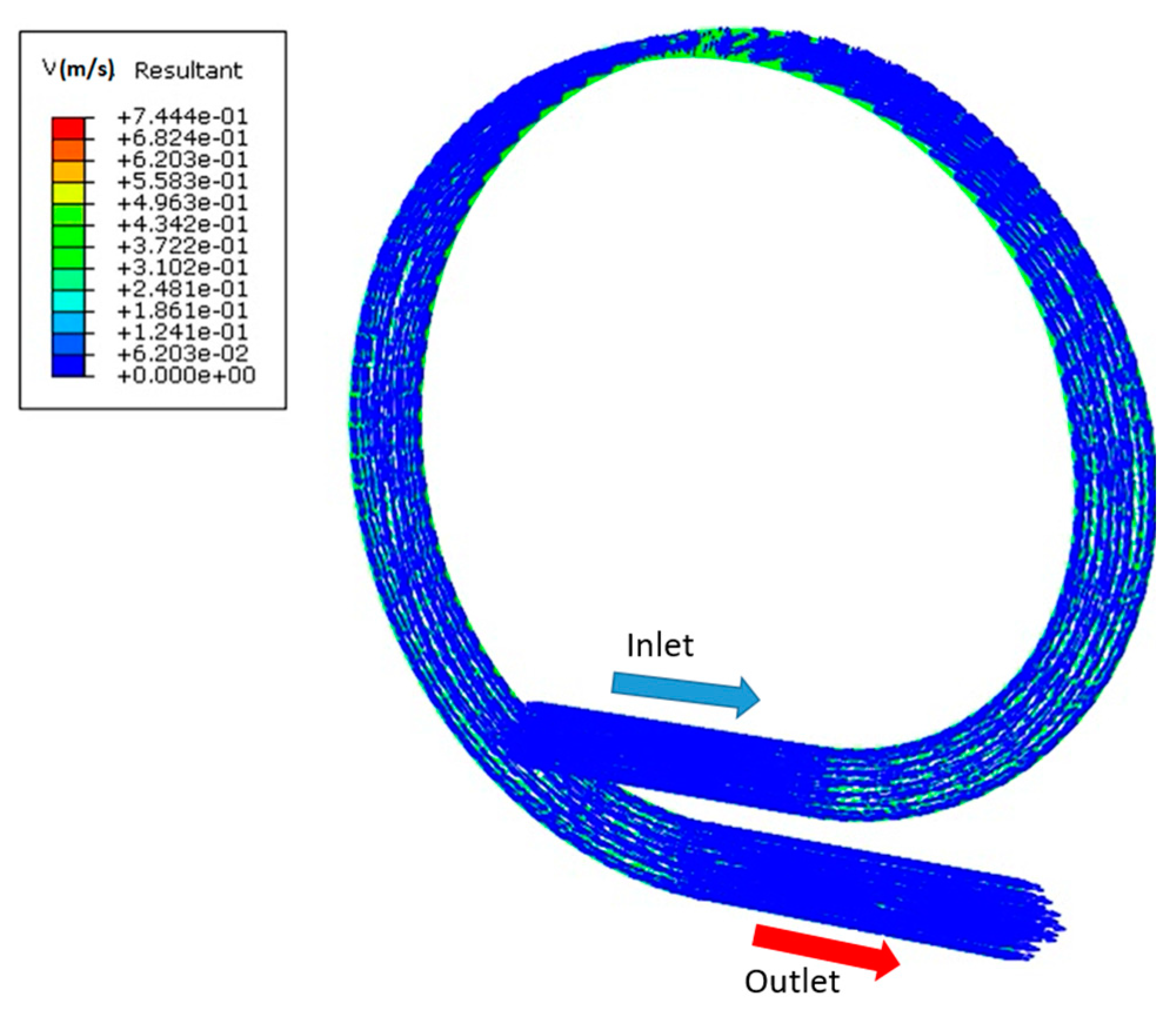
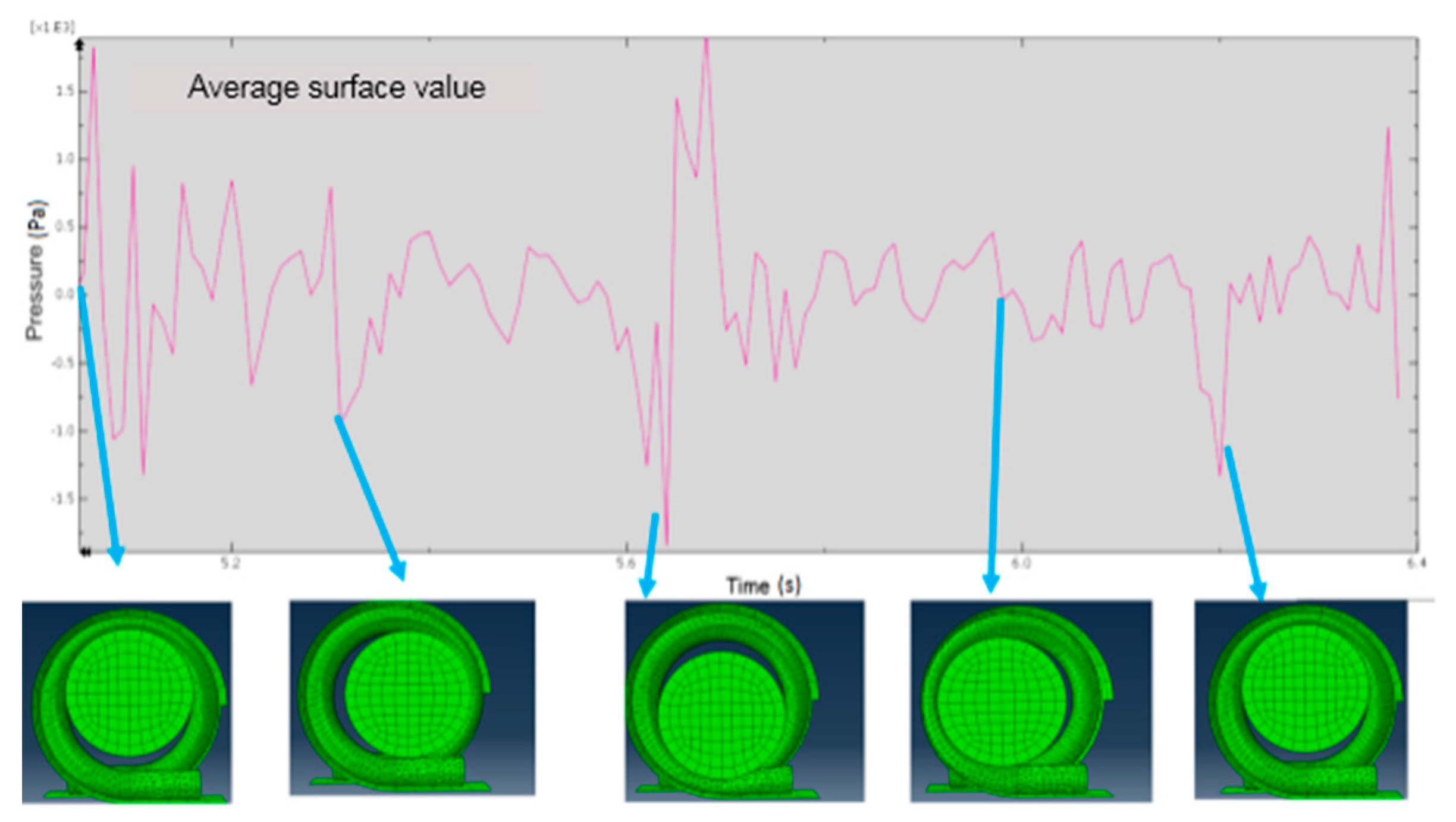
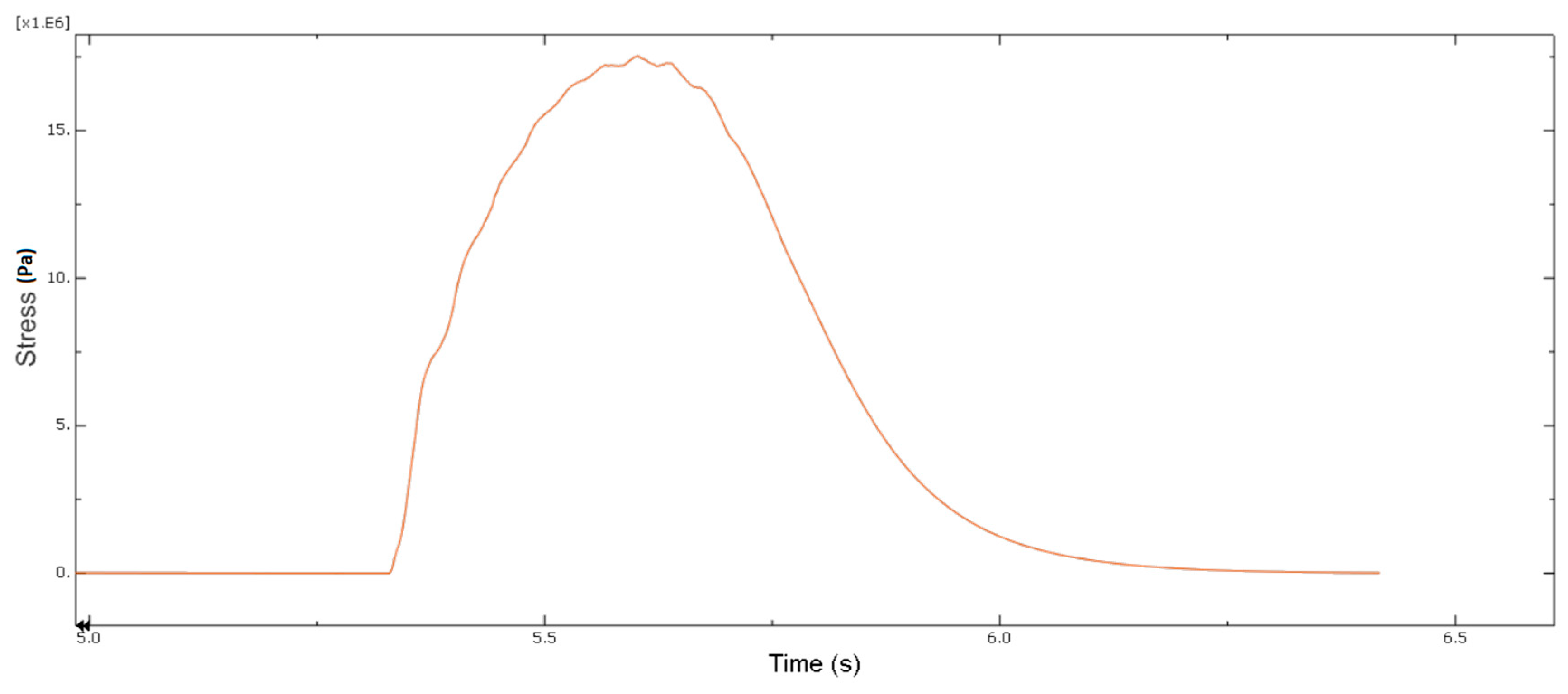
3.1. Numerical Simulation Tests
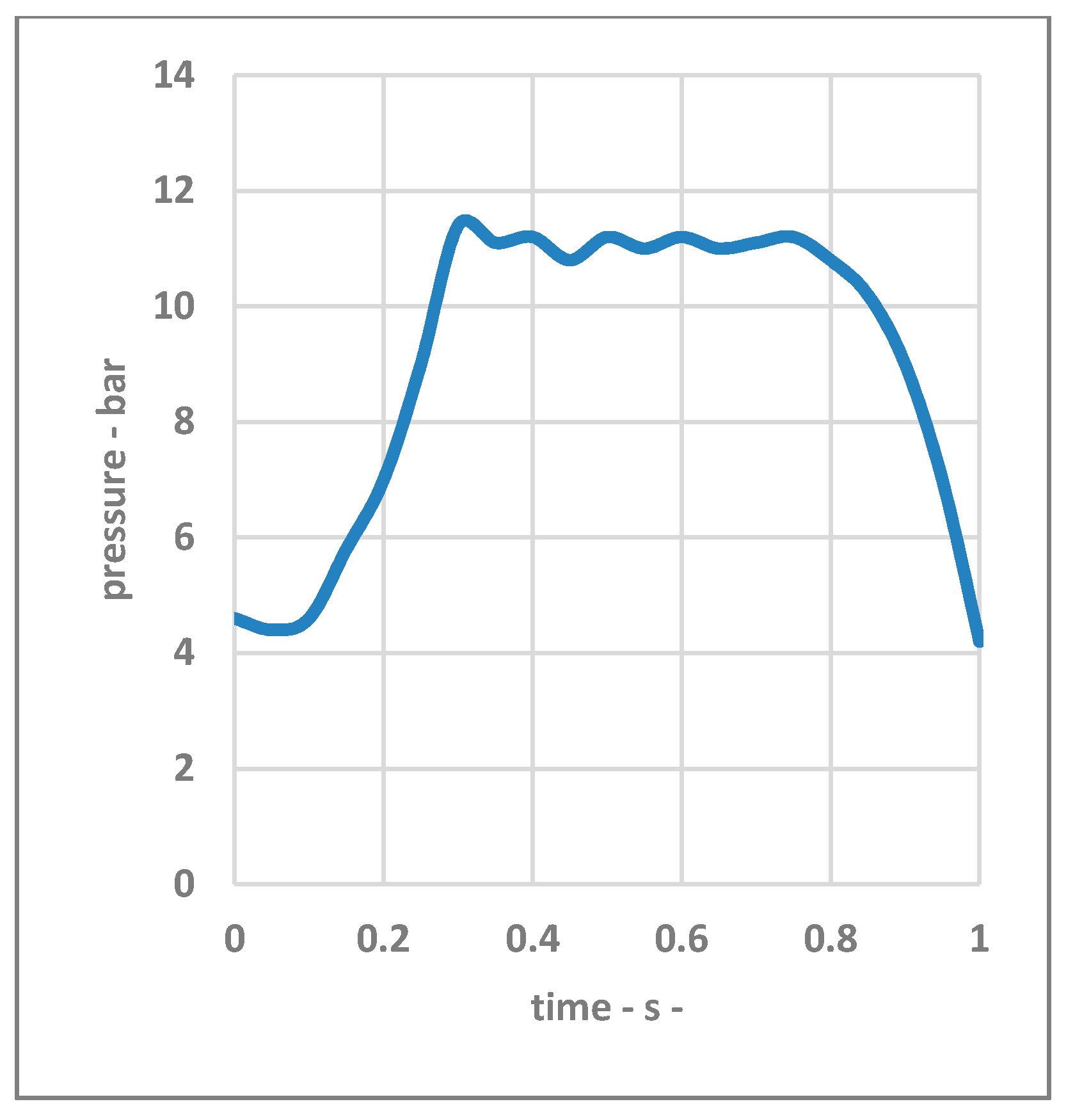
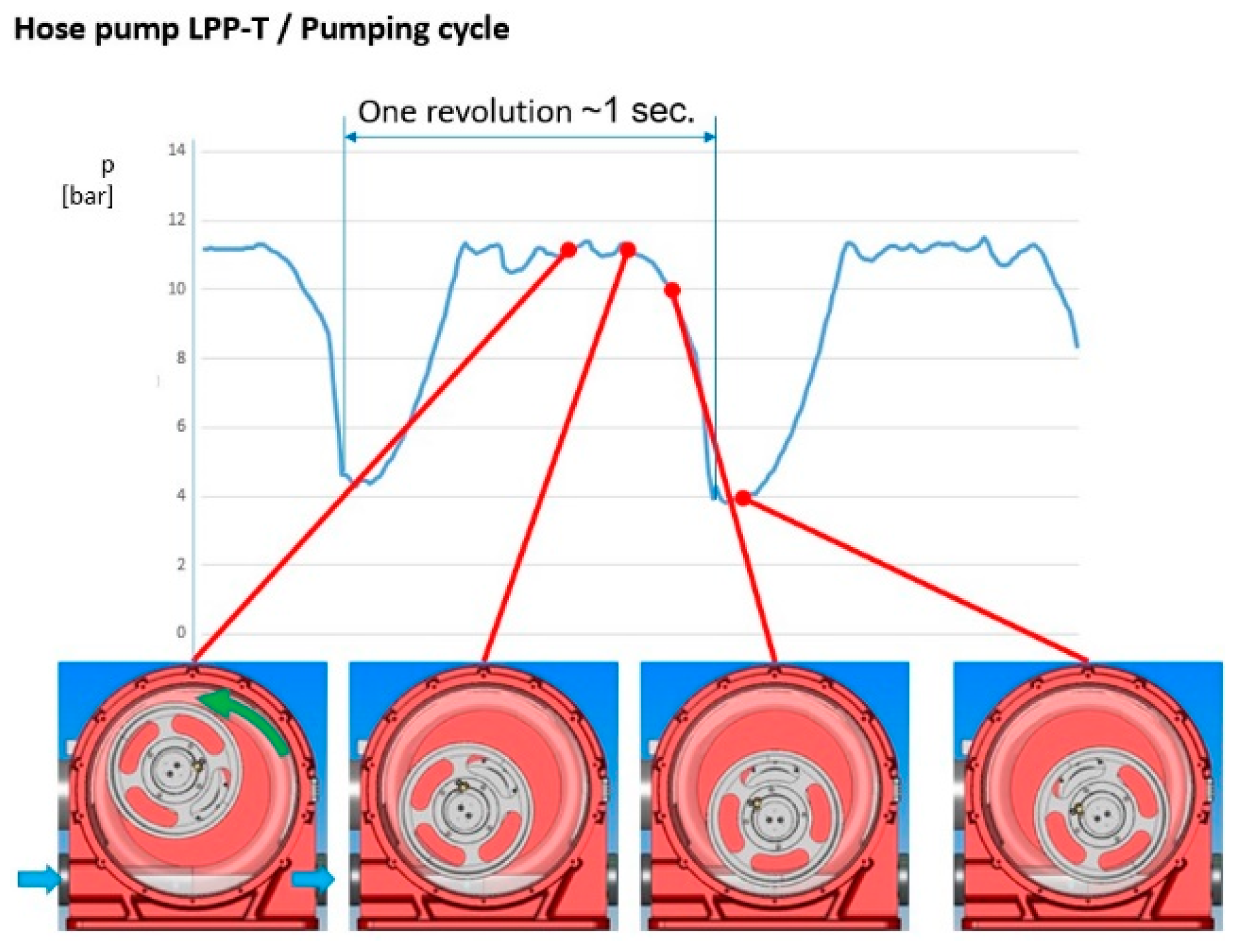
3.2. Experimental Tests
4. Discussion
- The absence of pressure counter in the model allowed a decrease in the pressure output. In the experimental case, there was a valve that generated pressure counter against the back flow.
- Different pipe material: The material parameter, as underlined in Equation (2), influences the fluid flow.
- The internal diameter when the roller squeezed the pipe was reduced by about 87%, (from 32 mm to 4 mm).
- -
- Dissipative friction effect between pipe and roller;
- -
- Roller as deformable material.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cammarata, A. A novel method to determine position and orientation errors in clearance-affected overconstrained mechanisms. Mech. Mach. Theory 2017, 118, 247–264. [Google Scholar] [CrossRef]
- Iannone, V.; De Simone, M.C.; Guida, D. Modeling of a DC Gear Motor for Feed-Forward Control Law Design for Unmanned Ground Vehicles. Actuators 2018, in press. [Google Scholar]
- Cammarata, A.; Angeles, J.; Sinatra, R. Kinetostatic and inertial conditioning of the McGill Schönflies-motion generator. Adv. Mech. Eng. 2010, 2, 186203. [Google Scholar] [CrossRef]
- De Simone, M.C.; Russo, S.; Rivera, Z.B.; Guida, D. Multibody Model of a UAV in Presence of Wind Fields. In Proceedings of the 2017 International Conference on Control, Artificial Intelligence, Robotics and Optimization (ICCAIRO 2017), Prague, Czech Republic, 20–22 May 2017; pp. 83–88. [Google Scholar]
- Cammarata, A. Unified formulation for the stiffness analysis of spatial mechanisms. Mech. Mach. Theory 2016, 105, 272–284. [Google Scholar] [CrossRef]
- De Simone, M.C.; Guida, D. Dry friction influence on structure dynamics. In Proceedings of the 5th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2015), Crete Island, Greece, 25–27 May 2015; pp. 4483–4491. [Google Scholar]
- Yazdanpanh-Ardakani, K.; Niroomand-Oscuii, H. New approach in modeling peristaltic transport of non-newtonian fluid. J. Mech. Med. Biol. 2013, 13, 1350052. [Google Scholar] [CrossRef]
- Quatrano, A.; De Simone, M.C.; Rivera, Z.B.; Guida, D. Development and implementation of a control system for a retrofitted CNC machine by using Arduino. FME Trans. 2017, 45, 565–571. [Google Scholar] [CrossRef]
- Cammarata, A.; Lacagnina, M.; Sinatra, R. Dynamic simulations of an airplane-shaped underwater towed vehicle marine. In Proceedings of the 5th International Conference on Computational Methods in Marine Engineering (MARINE 2013), Hamburg, Germany, 29–31 May 2013. [Google Scholar]
- Barbagallo, R.; Sequenzia, G.; Cammarata, A.; Oliveri, S.M. An integrated approach to design an innovative motorcycle rear suspension with eccentric mechanism. In Advances on Mechanics, Design Engineering and Manufacturing—Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2017; pp. 609–619. [Google Scholar]
- Pappalardo, C.M.; Guida, D. On the Lagrange multipliers of the intrinsic constraint equations of rigid multibody mechanical systems. Arch. Appl. Mech. 2018, 88, 419–451. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Guida, D. On the Computational Methods for the Dynamic Analysis of Rigid Multibody Mechanical Systems. Machines 2018, 6, 20. [Google Scholar] [CrossRef]
- Dasic, P. Determination of Reliability of Ceramic Cutting Tools on the basis of Comparative Analysis of Different Functions Distribution. Int. J. Qual. Reliab. Manag. 2001, 18, 431–443. [Google Scholar]
- Valencia, A.; Villanueva, M. Unsteady flow and mass transfer in models of stenotic arteries considering fluid-structure interaction. Int. Commun. Heat Mass Transf. 2006, 33, 966–975. [Google Scholar] [CrossRef]
- Reymond, P.; Crosetto, P.; Deparis, S.; Quarteroni, A.; Stergiopulos, N. Physiological simulation of blood flow in the aorta: Comparison of hemodynamic indices as predicted by 3-d fsi, 3-d rigid wall and 1-d models. Med. Eng. Phys. 2013, 35, 784–791. [Google Scholar] [CrossRef] [PubMed]
- Suito, H.; Takizawa, K.; Huynh, V.Q.; Sze, D.; Ueda, T. Fsi analysis of the blood flow and geometrical characteristics in the thoracic aorta. Comput. Mech. 2014, 54, 1035–1045. [Google Scholar] [CrossRef]
- Li, H.; Lin, K.; Shahmirzadi, D. Fsi simulations of pulse wave propagation in human abdominal aortic aneurysm: The effects of sac geometry and stiffness. Biomed. Eng. Comput. Biol. 2016, 7, 25–36. [Google Scholar] [CrossRef] [PubMed]
- Elabbasi, N.; Bergstrom, J.; Brown, S. Fluid-structure interaction analysis of a peristaltic pump. In Proceedings of the 2011 COMSOL Conference, Boston, MA, USA, 13–15 October 2011. [Google Scholar]
- Zhou, X.; Liang, X.M.; Zhao, G.; Su, Y.; Wang, Y. A new computational fluid dynamics method for in-depth investigation of flow dynamics in roller pump systems. Artif. Organs 2014, 38, E106–E117. [Google Scholar] [CrossRef] [PubMed]
- Pappalardo, C.M.; Guida, D. Use of the Adjoint Method in the Optimal Control Problem for the Mechanical Vibrations of Nonlinear Systems. Machines 2018, 6, 19. [Google Scholar] [CrossRef]
- De Simone, M.C.; Rivera, Z.B.; Guida, D. Obstacle avoidance system for unmanned ground vehicles by using ultrasonic sensors. Machines 2018, 6, 18. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Guida, D. Dynamic Analysis of Planar Rigid Multibody Systems modelled using Natural Absolute Coordinates. Appl. Comput. Mech. 2018, 12, 73–110. [Google Scholar] [CrossRef]
- De Simone, M.C.; Guida, D. Modal coupling in presence of dry friction. Machines 2018, 6, 8. [Google Scholar] [CrossRef]
- Zhai, Y.; Liu, L.; Lu, W.; Li, Y.; Yang, S.; Villecco, F. The application of disturbance observer to propulsion control of sub-mini underwater robot. In Proceedings of the Computational Science and Its Applications (ICCSA 2010), Fukuoka, Japan, 23–26 March 2010; pp. 590–598. [Google Scholar]
- Pappalardo, C.M.; Guida, D. Control of Nonlinear Vibrations using the Adjoint Method. Meccanica 2017, 52, 2503–2526. [Google Scholar] [CrossRef]
- De Simone, M.C.; Guida, D. On the development of a low-cost device for retrofitting tracked vehicles for autonomous navigation. In Proceedings of the 23rd Conference of the Italian Association of Theoretical and Applied Mechanics (AIMETA 2017), Salerno, Italy, 4–7 Spetember 2017; pp. 71–82. [Google Scholar]
- De Simone, M.C.; Guida, D. Control design for an under-actuated UAV model. FME Trans. 2018, 46, 443–452. [Google Scholar] [CrossRef]
- Barbagallo, R.; Sequenzia, G.; Oliveri, S.M.; Cammarata, A. Dynamics of a high-performance motorcycle by an advanced multibody/control co-simulation. Proc. Inst. Mech. Eng. Part K J. Multi Body Dyn. 2016, 230, 207–221. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Guida, D. System Identification Algorithm for Computing the Modal Parameters of Linear Mechanical Systems. Machines 2018, 6, 12. [Google Scholar] [CrossRef]
- Villecco, F. On the Evaluation of Errors in the Virtual Design of Mechanical Systems. Machines 2018, 6, 36. [Google Scholar] [CrossRef]
- Donea, J.; Huerta, A.; Ponthot, J.P.; Rodríguez-Ferran, A. Arbitrary Lagrangian_Eulerian Methods; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Balabel, A.; Dinkler, D. Turbulence models for fluid-structure interaction applications. Emir. J. Eng. Res. 2006, 11, 1–18. [Google Scholar]
- Barbagallo, R.; Sequenzia, G.; Cammarata, A.; Oliveri, S.M.; Fatuzzo, G. Redesign and multibody simulation of a motorcycle rear suspension with eccentric mechanism. Int. J. Interact. Des. Manuf. 2018, 12, 517–524. [Google Scholar] [CrossRef]
- De Simone, M.C.; Guida, D. Identification and control of a Unmanned Ground Vehicle by using Arduino. UPB Sci. Bull. Ser. D Mech. Eng. 2018, 80, 141–154. [Google Scholar]
- Cammarata, A.; Sequenzia, G.; Oliveri, S.M.; Fatuzzo, G. Modified chain algorithm to study planar compliant mechanisms. Int. J. Interact. Des. Manuf. 2016, 10, 191–201. [Google Scholar] [CrossRef]
- Cammarata, A. Optimized design of a large-workspace 2-DOF parallel robot for solar tracking systems. Mech. Mach. Theory 2015, 83, 175–186. [Google Scholar] [CrossRef]
- Chakraborty, D.; Prakash, J.R.; Friend, J.; Yeo, L. Fluid-structure interaction in deformable microchannels. Phys. Fluids 2012, 24, 102002. [Google Scholar] [CrossRef]
- Formato, A.; Guida, D.; Ianniello, D.; Villecco, F.; Lenza, T.L.; Pellegrino, A. Design of Delivery Valve for Hydraulic Pumps. Machines 2018, 6, 44. [Google Scholar] [CrossRef]
- Sequenzia, G.; Fatuzzo, G.; Oliveri, S.M.; Barbagallo, R. Interactive re-design of a novel variable geometry bicycle saddle to prevent neurological pathologies. Int. J. Interact. Des. Manuf. 2016, 10, 165–172. [Google Scholar] [CrossRef]
- Guida, D.; Pappalardo, C.M. Control Design of an Active Suspension System for a Quarter-Car Model with Hysteresis. J. Vib. Eng. Technol. 2015, 3, 277–299. [Google Scholar]
- Ghomshei, M.; Villecco, F.; Porkhial, S.; Pappalardo, M. Complexity in energy policy: A fuzzy logic methodology. In Proceedings of the Sixth International Conference on Fuzzy Systems and Knowledge Discovery (FSKD’09), Tianjin, China, 14–16 August 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 128–131. [Google Scholar]
- Pappalardo, C.M.; Guida, D. A time-domain system identification numerical procedure for obtaining linear dynamical models of multibody mechanical systems. Arch. Appl. Mech. 2018, 88, 1325–1347. [Google Scholar] [CrossRef]
- Naviglio, D.; Formato, A.; Scaglione, G.; Montesano, D.; Pellegrino, A.; Villecco, F.; Gallo, M. Study of the Grape Cryo-Maceration Process at Different Temperatures. Foods 2018, 7, 107. [Google Scholar] [CrossRef] [PubMed]
- Pappalardo, C.M. A Natural Absolute Coordinate Formulation for the Kinematic and Dynamic Analysis of Rigid Multibody Systems. Nonlinear Dyn. 2015, 81, 1841–1869. [Google Scholar] [CrossRef]
- Cammarata, A.; Lacagnina, M.; Sequenzia, G. Alternative elliptic integral solution to the beam deflection equations for the design of compliant mechanisms. Int. J. Interact. Des. Manuf. 2018, 13, 1–7. [Google Scholar] [CrossRef]
- Sena, P.; Attianese, P.; Pappalardo, M.; Villecco, F. FIDELITY: Fuzzy Inferential Diagnostic Engine for on-LIne supporT to phYsicians. In International Conference on Biomedical Engineering in Vietnam; Springer: Berlin Heidelberg, 2013. [Google Scholar]
- Cammarata, A.; Sinatra, R.; Maddio, P.D. A Two-Step Algorithm for the Dynamic Reduction of Flexible Mechanisms. In Proceedings of the 4th IFToMM Symposium on Mechanism Design for Robotics, Udine, Italy, 11–13 Sepember 2018; pp. 25–32. [Google Scholar]
- Muscat, M.; Cammarata, A.; Maddio, P.D.; Sinatra, R. Design and development of a towfish to monitor marine pollution. Eur. Mediter. J. Environ. Integr. 2018, 3, 11. [Google Scholar] [CrossRef]
- Cammarata, A.; Lacagnina, M.; Sinatra, R. Closed-form solutions for the inverse kinematics of the Agile Eye with constraint errors on the revolute joint axes. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Daejeon, Korea, 9–14 October 2016. [Google Scholar]
- Bergstrom, J.S. Mechanics of Solid Polymers: Theory and Computational Modeling; William Andrew: Norwich, NY, USA, 2015. [Google Scholar]



[kg/m3] | E [MPa] | [MPa] | [MPa−1] | [s−1] | [s] | |
|---|---|---|---|---|---|---|
| 970 | 37.9 | 0.48 | 127 | 48 | 0.4 | 0.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Formato, G.; Romano, R.; Formato, A.; Sorvari, J.; Koiranen, T.; Pellegrino, A.; Villecco, F. Fluid–Structure Interaction Modeling Applied to Peristaltic Pump Flow Simulations. Machines 2019, 7, 50. https://doi.org/10.3390/machines7030050
Formato G, Romano R, Formato A, Sorvari J, Koiranen T, Pellegrino A, Villecco F. Fluid–Structure Interaction Modeling Applied to Peristaltic Pump Flow Simulations. Machines. 2019; 7(3):50. https://doi.org/10.3390/machines7030050
Chicago/Turabian StyleFormato, Gaetano, Raffaele Romano, Andrea Formato, Joonas Sorvari, Tuomas Koiranen, Arcangelo Pellegrino, and Francesco Villecco. 2019. "Fluid–Structure Interaction Modeling Applied to Peristaltic Pump Flow Simulations" Machines 7, no. 3: 50. https://doi.org/10.3390/machines7030050
APA StyleFormato, G., Romano, R., Formato, A., Sorvari, J., Koiranen, T., Pellegrino, A., & Villecco, F. (2019). Fluid–Structure Interaction Modeling Applied to Peristaltic Pump Flow Simulations. Machines, 7(3), 50. https://doi.org/10.3390/machines7030050







