Integrated Fault Detection Framework for Classifying Rotating Machine Faults Using Frequency Domain Data Fusion and Artificial Neural Networks
Abstract
1. Introduction
2. Overview of Data Fusion for Faults Detection and Classification
3. Integrated Data Combination Approach
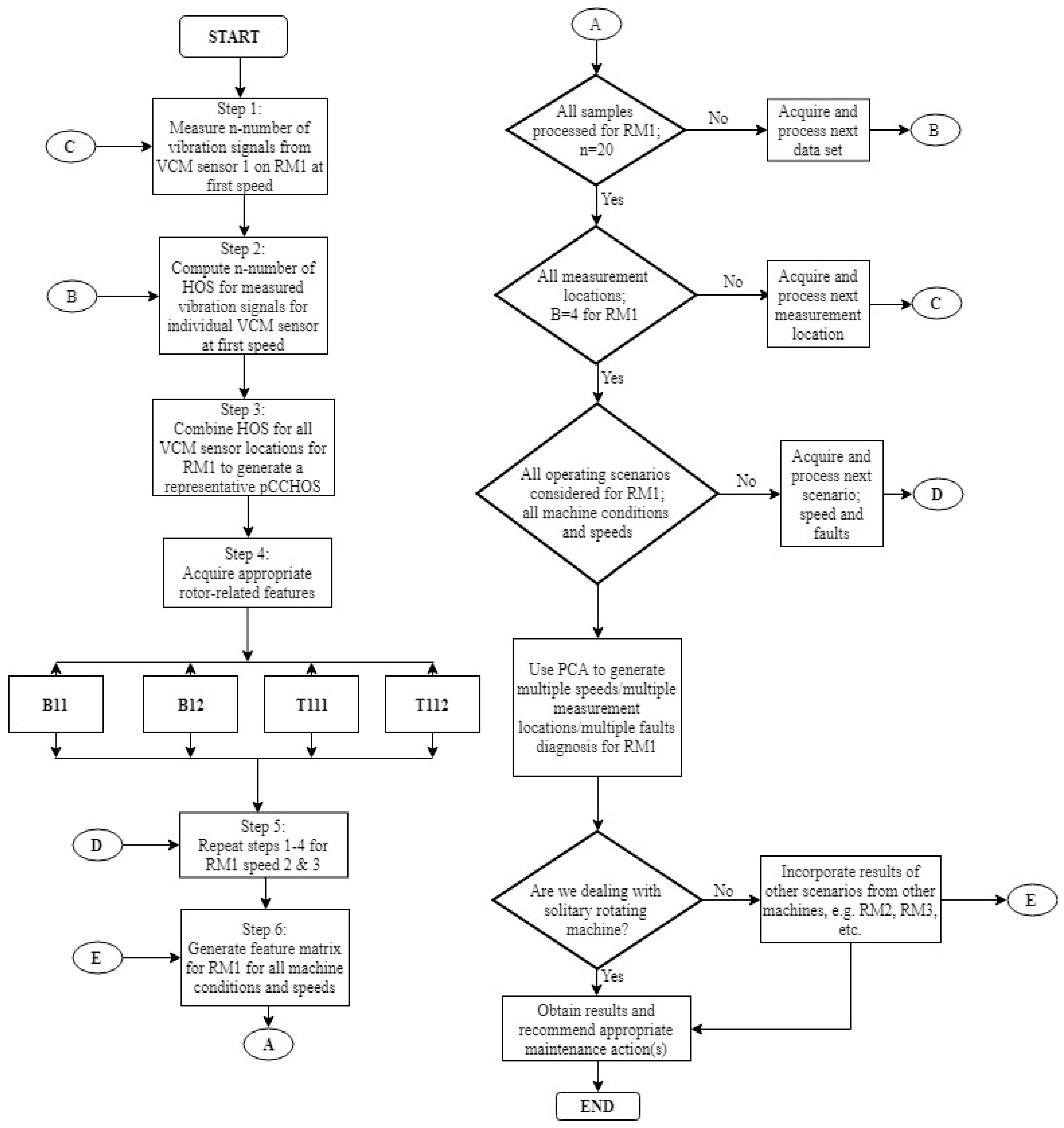
3.1. Stage 1: Sensor Level Data Fusion Using PCCB and pCCT
3.2. Stage 2: Feature Level Data Fusion Using ANN
4. Experimental Arrangement
5. Organisation of Measured Vibration Data
6. Observations and Discussions
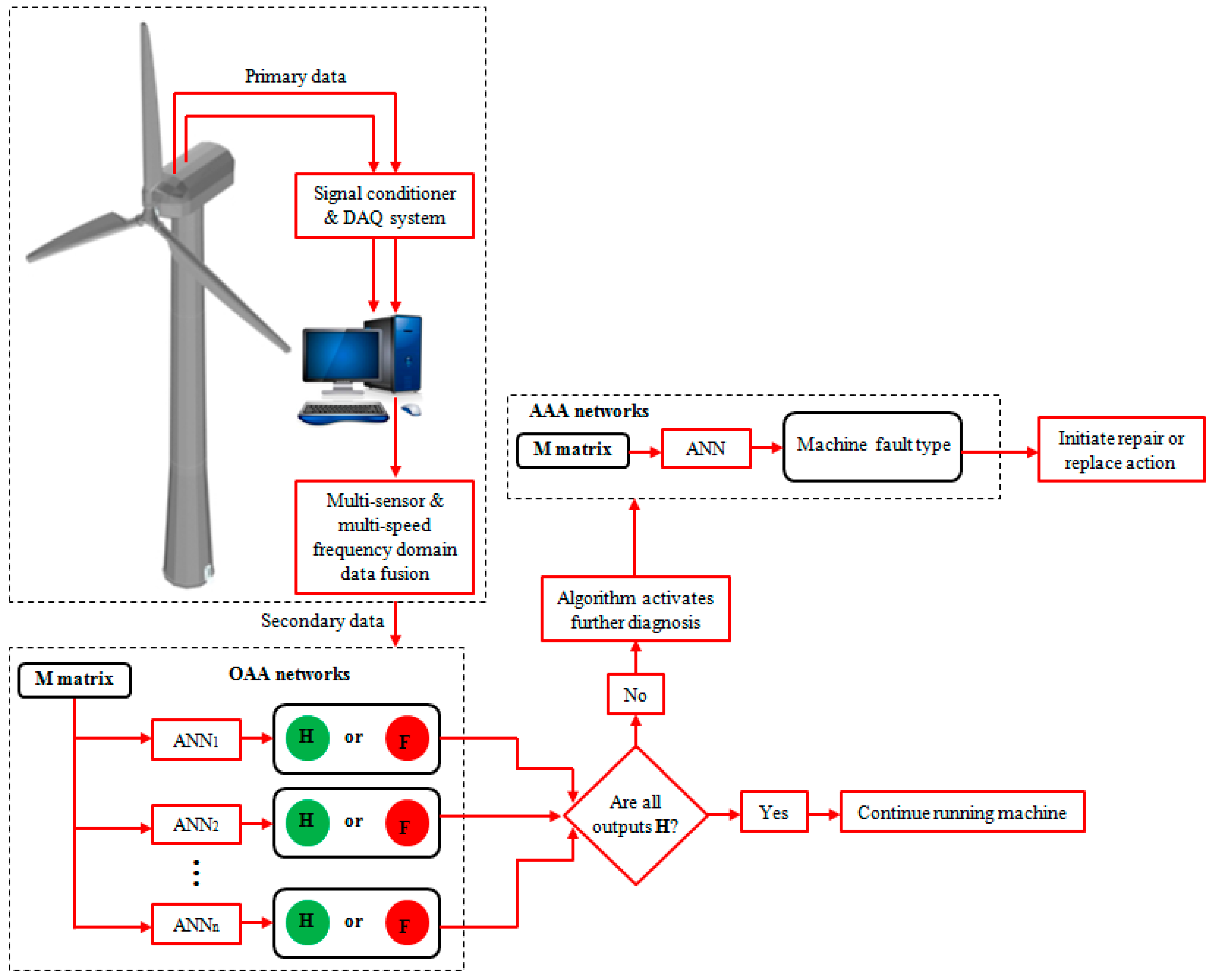
7. On-Site Operation of the Proposed Integrated Fault Detection Algorithm
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Deng, C.; Wu, J.; Wang, Y.; Xiong, Y. A corrective maintenance scheme for engineering equipment. Eng. Fail. Anal. 2014, 36, 269–283. [Google Scholar] [CrossRef]
- Karabay, S.; Uzman, I. Importance of early detection of maintenance problems in rotating machines in management of plants: Case studies from wire and tyre plants. Eng. Fail. Anal. 2009, 16, 212–224. [Google Scholar] [CrossRef]
- Ogaji, S.; Sampath, S.; Singh, R.; Probert, D. Novel approach for improving power-plant availability using advanced engine diagnostics. Appl. Energy 2002, 72, 389–407. [Google Scholar] [CrossRef]
- Eti, M.C.; Ogaji, S.O.; Probert, S.D. Development and implementation of preventive-maintenance practices in Nigerian industries. Appl. Energy 2006, 83, 1163–1179. [Google Scholar] [CrossRef]
- Haddad, G.; Sandborn, P.A.; Pecht, M.G. Using maintenance options to maximize the benefits of prognostics for wind farms. Wind Energy 2014, 17, 775–791. [Google Scholar] [CrossRef]
- Sampath, S.; Ogaji, S.; Singh, R.; Probert, D. Engine-fault diagnostics: An optimisation procedure. Appl. Energy 2002, 73, 47–70. [Google Scholar] [CrossRef]
- Yang, W.; Tavner, P.J.; Crabtree, C.J.; Feng, Y.; Qiu, Y. Wind turbine condition monitoring: Technical and commercial challenges. Wind Energy 2014, 17, 673–693. [Google Scholar] [CrossRef]
- Siegel, D.; Zhao, W.; Lapira, E.; AbuAli, M.; Lee, J. A comparative study on vibration-based condition monitoring algorithms for wind turbine drive trains. Wind Energy 2014, 17, 695–714. [Google Scholar] [CrossRef]
- Jardine, A.K.S.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Lee, J.; Wu, F.; Zhao, W.; Ghaffari, M.; Liao, L.; Siegel, D. Prognostics and health management design for machinery systems-Reviews, methodology and applications. Mech. Syst. Signal Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Heng, A.; Zhang, S.; Tan, A.C.C.; Mathew, J. Rotating machinery prognostics: State of the art, challenges and opportunities. Mech. Syst. Signal Process. 2009, 23, 724–739. [Google Scholar] [CrossRef]
- Lee, J.; Ni, J.; Djurdjanovic, D.; Qiu, H.; Liao, H. Intelligent prognostics tools and e-maintenance. Comput. Ind. 2006, 57, 476–489. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Nembhard, A.D.; Sinha, J.K. Experimental observations of rotor orbits analysis in rotating machines. In Proceedings of the 9th IFToMM International Conference on Rotor Dynamics (IFToMM ICORD 2014), Milan, Italy, 22–25 September 2014. [Google Scholar]
- Goldman, P.; Muszynska, A. Application of full spectrum to rotating machinery diagnosis. Orbit 1999, 20, 17–21. [Google Scholar]
- Patel, T.H.; Darpe, A.K. Experimental investigations on vibration response of misaligned rotors. Mech. Syst. Signal Process. 2009, 23, 2236–2252. [Google Scholar] [CrossRef]
- Patel, T.H.; Darpe, A.K. Vibration response of misaligned rotors. J. Sound Vib. 2009, 325, 609–628. [Google Scholar] [CrossRef]
- Fengqi, W.; Meng, G. Compound rub malfunctions feature extraction based on full-spectrum cascade analysis and SVM. Mech. Syst. Signal Process. 2006, 20, 2007–2021. [Google Scholar] [CrossRef]
- Collis, W.B.; White, P.R.; Hammond, J.K. Higher-order spectra: The bispectrum and trispectrum. Mech. Syst. Signal Process. 1998, 12, 375–394. [Google Scholar] [CrossRef]
- Fackrell, J.W.A.; White, P.R.; Hammond, J.K.; Pinnington, R.J.; Parsons, A.T. The interpretation of the bispectra of vibration signals-II: Experimental results and applications. Mech. Syst. Signal Process. 1995, 9, 267–274. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K. Combined bispectrum and trispectrum for faults diagnosis in rotating machines. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2014, 228, 419–428. [Google Scholar] [CrossRef]
- Sinha, J.K. Higher order spectra for crack and misalignment identification in the shaft of a rotating machine. Struct. Health Monit. 2007, 6, 325–334. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K. A comparison of signal processing tools: Higher order spectra versus higher order coherences. J. Vib. Eng. Technol. 2015, 3, 461–472. [Google Scholar]
- McCormick, A.C.; Nandi, A.K. Classification of rotating machine condition using artificial neural networks. Proc. Inst. Mech. Eng. Part C 1997, 211, 439–450. [Google Scholar] [CrossRef]
- McCormick, A.C.; Nandi, A.K. Real-time classification of rotating shaft loading conditions using artificial neural networks. IEEE Trans. Neural Netw. 1997, 8, 748–756. [Google Scholar] [CrossRef] [PubMed]
- Samanta, B. Gear fault detection using artificial neural networks and support vector machines with generic algorithms. Mech. Syst. Signal Process. 2004, 18, 625–644. [Google Scholar] [CrossRef]
- Burges, C.J.C. A tutorial on support vector machines for pattern recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Yuan, S.F.; Chu, F.L. Support vector machines-based faults diagnosis for turbo-pump rotor. Mech. Syst. Signal Process. 2006, 20, 939–952. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Y.; Zhu, Y. Intelligent faults diagnosis of rolling element bearing based on SVMs and fractal dimension. Mech. Syst. Signal Process. 2007, 21, 2012–2024. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K.; Nembhard, A.D. A novel faults diagnosis technique for enhancing maintenance and reliability of rotating machines. Struct. Health Monit. 2015, 14, 604–621. [Google Scholar] [CrossRef]
- Wasserman, P.D. Neural Computing: Theory and Practice; Van Nostrand Reinhold Co.: New York, NY, USA, 1989. [Google Scholar]
- Mandic, D.P.; Chambers, J. Recurrent Neural Networks for Prediction: Learning Algorithms, Architectures and Stability; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Peng, Y.; Qiao, W.; Qu, L.; Wang, J. Gearbox fault diagnosis using vibration and current information fusion. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–6. [Google Scholar]
- Cheng, F.; Peng, Y.; Qu, L.; Qiao, W. Current-based fault detection and identification for wind turbine drivetrain gearboxes. IEEE Trans. Ind. Appl. 2017, 53, 878–887. [Google Scholar] [CrossRef]
- Yang, B. Thermographic detection of fatigue damage of reactor pressure vessel (RPV) steels. J. Mater. Eng. Perform. 2003, 12, 345–353. [Google Scholar] [CrossRef]
- Avdelidis, N.P.; Almond, D.P. Transient thermography as a through skin imaging technique for aircraft assembly: Modelling and experimental results. Infrared Phys. Technol. 2004, 45, 103–114. [Google Scholar] [CrossRef]
- Moreton, G.; Yardley, E.D. The use of wear debris analysis to monitor gear transmissions underground. Condit. Monit. 1984, 84, 491–502. [Google Scholar]
- Peng, Z.; Kirk, T.B. Computer image analysis of wear particles in three-dimensions for machine condition monitoring. Wear 1998, 223, 157–166. [Google Scholar] [CrossRef]
- Hameed, Z.; Hong, Y.S.; Cho, Y.M.; Ahn, S.H.; Song, C.K. Condition monitoring and fault detection of wind turbines and related algorithms: A review. Renew. Sustain. Energy Rev. 2009, 13, 1–39. [Google Scholar] [CrossRef]
- Amirat, Y.; Benbouzid, M.E.H.; Al-Ahmar, E.; Bensaker, B.; Turri, S. A brief status on condition monitoring and fault diagnosis in wind energy conversion systems. Renew. Sustain. Energy Rev. 2009, 13, 2629–2636. [Google Scholar] [CrossRef]
- García Márquez, F.P.; Tobias, A.M.; Pinar Pérez, J.M.; Papaelias, M. Condition monitoring of wind turbines: Techniques and methods. Renew. Sustain. Energy Rev. 2012, 46, 169–178. [Google Scholar] [CrossRef]
- Hameed, Z.; Ahn, S.H.; Cho, Y.M. Practical aspects of a condition monitoring system for a wind turbine with emphasis on its design, system architecture, testing and installation. Renew. Sustain. Energy Rev. 2010, 35, 879–894. [Google Scholar] [CrossRef]
- Witty, A. New strategies for innovation in global health: A pharmaceutical industry perspective. Health Aff. 2011, 30, 118–126. [Google Scholar] [CrossRef] [PubMed]
- Hall, D.L.; Llinas, J. An introduction to multisensor data fusion. Proc. IEEE 1997, 85, 6–23. [Google Scholar] [CrossRef]
- Dempsey, P.J.; Sheng, S. Investigation of data fusion applied to health monitoring of wind turbine drivetrain components. Wind Energy 2013, 16, 479–489. [Google Scholar] [CrossRef]
- Liu, Q.C.; Wang, H.P. A case study on multisensor data fusion for imbalance diagnosis of rotating machinery. AI EDAM 2001, 15, 203–210. [Google Scholar] [CrossRef]
- Basir, O.; Yuan, X. Engine fault diagnosis based on multi-sensor information fusion using Dempster-Shafer evidence theory. Inf. Fusion 2007, 8, 379–386. [Google Scholar] [CrossRef]
- Niu, G.; Han, T.; Yang, B.S.; Tan, A.C.C. Multi-agent decision fusion for motor fault diagnosis. Mech. Syst. Signal Process. 2007, 21, 1285–1299. [Google Scholar] [CrossRef]
- Zhang, J. Improved on-line process fault diagnosis through information fusion in multiple neural networks. Comput. Chem. Eng. 2006, 30, 558–571. [Google Scholar] [CrossRef]
- Boutros, T.; Liang, M. Mechanical fault detection using fuzzy index fusion. Int. J. Mach. Tools Manuf. 2007, 47, 1702–1714. [Google Scholar] [CrossRef]
- Niu, G.; Yang, B.S.; Pecht, M. Development of an optimized condition-based maintenance system by data fusion and reliability-centered maintenance. Reliab. Eng. Syst. Saf. 2010, 95, 786–796. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K. Generic vibration-based faults identification approach for identical rotating machines installed on different foundations, VIRM 11-Vibrations in Rotating. Machinery 2016, 11, 499–510. [Google Scholar]
- Yunusa-Kaltungo, A.; Sinha, J.K. Sensitivity analysis of higher order coherent spectra in machine faults diagnosis. Struct. Health Monit. 2016, 15, 555–567. [Google Scholar] [CrossRef]
- Suryam, B.C.B.N.; Meher, K.K.; Sinha, J.K.; Rao, A.R. Coherence measurement for early contact detection between two components. J. Sound Vib. 2006, 290, 519–523. [Google Scholar] [CrossRef]
- Khan, Z.H.; Mohapatra, S.K.; Khodiar, P.K.; Ragu, K.S. Artificial neural network and medicine. Indian J. Physiol. Pharmacol. 1998, 42, 321–342. [Google Scholar] [PubMed]
- Amato, F.; López, A.; Peña-Méndez, E.M.; Vaňhara, P.; Hampl, A.; Havel, J. Artificial neural networks in medical diagnosis. J. Appl. Biomed. 2013, 11, 47–58. [Google Scholar] [CrossRef]
- Hashemi, A.; Pilevar, A.H.; Rafeh, R. Mass Detection in Lung CT Images Using Region Growing Segmentation and Decision Making Based on Fuzzy Inference System and Artificial Neural Network. Int. J. Image Gr. Signal Process. 2013, 5, 16. [Google Scholar] [CrossRef]
- Matulewicz, L.; Jansen, J.F.; Bokacheva, L.; Vargas, H.A.; Akin, O.; Fine, S.W.; Shukla-Dave, A.; Eastham, J.A.; Hricak, H.; Koutcher, J.A.; et al. Anatomic segmentation improves prostate cancer detection with artificial neural networks analysis of 1H magnetic resonance spectroscopic imaging. J. Magn. Reson. Imaging 2014, 40, 1414–1421. [Google Scholar] [CrossRef] [PubMed]
- Karaboga, D.; Gorkemli, B.; Ozturk, C.; Karaboga, N. A comprehensive survey: Artificial bee colony (ABC) algorithm and applications. Artif. Intell. Rev. 2014, 42, 21–57. [Google Scholar] [CrossRef]
- Ghiassi, M.; Skinner, J.; Zimbra, D. Twitter brand sentiment analysis: A hybrid system using n-gram analysis and dynamic artificial neural network. Expert Syst. Appl. 2013, 40, 6266–6282. [Google Scholar] [CrossRef]
- Yadav, A.K.; Malik, H.; Chandel, S.S. Selection of most relevant input parameters using WEKA for artificial neural network based solar radiation prediction models. Renew. Sustain. Energy Rev. 2014, 31, 509–519. [Google Scholar] [CrossRef]
- Yadav, A.K.; Chandel, S.S. Solar radiation prediction using Artificial Neural Network techniques: A review. Renew. Sustain. Energy Rev. 2014, 33, 772–781. [Google Scholar] [CrossRef]
- Conforti, M.; Pascale, S.; Robustelli, G.; Sdao, F. Evaluation of prediction capability of the artificial neural networks for mapping landslide susceptibility in the Turbolo River catchment (northern Calabria, Italy). Catena 2014, 113, 236–250. [Google Scholar] [CrossRef]
- Park, S.; Choi, C.; Kim, B.; Kim, J. Landslide susceptibility mapping using frequency ratio, analytic hierarchy process, logistic regression, and artificial neural network methods at the Inje area, Korea. Environ. Earth Sci. 2013, 68, 1443–1464. [Google Scholar] [CrossRef]
- Samanta, B.; Al-Balushi, K.R. Artificial neural network based fault diagnostics of rolling element bearings using time-domain features. Mech. Syst. Signal Process. 2003, 17, 317–328. [Google Scholar] [CrossRef]
- Saridakis, K.M.; Nikolakopoulos, P.G.; Papadopoulos, C.A.; Dentsoras, A.J. Identification of wear and misalignment on journal bearings using artificial neural networks. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2012, 226, 46–56. [Google Scholar] [CrossRef]
- Saravanan, N.; Siddabattuni, V.K.; Ramachandran, K.I. Fault diagnosis of spur bevel gear box using artificial neural network (ANN), and proximal support vector machine (PSVM). Appl. Soft Comput. 2010, 10, 344–360. [Google Scholar] [CrossRef]
- Sanz, J.; Perera, R.; Huerta, C. Fault diagnosis of rotating machinery based on auto-associative neural networks and wavelet transforms. J. Sound Vib. 2007, 302, 981–999. [Google Scholar] [CrossRef]
- Rafiee, J.; Arvani, F.; Harifi, A.; Sadeghi, M.H. Intelligent condition monitoring of a gearbox using artificial neural network. Mech. Syst. Signal Process. 2007, 21, 1746–1754. [Google Scholar] [CrossRef]
- Srinivas, H.K.; Srinivasan, K.S.; Umesh, K.N. Role of an artificial neural network and a wavelet transform for condition monitoring of the combined faults of unbalance and cracked rotors. Int. J. Acoust. Vib. 2010, 15, 121. [Google Scholar] [CrossRef]
- Walker, R.B.; Vayanat, R.; Perinpanayagam, S.; Jennions, I.K. Unbalance localization through machine nonlinearities using an artificial neural network approach. Mech. Mach. Theory 2014, 75, 54–66. [Google Scholar] [CrossRef]
- Woods, K.; Bowyer, K.W. Generating ROC curves for artificial neural networks. IEEE Trans. Med. Imaging 1997, 16, 329–337. [Google Scholar] [CrossRef] [PubMed]

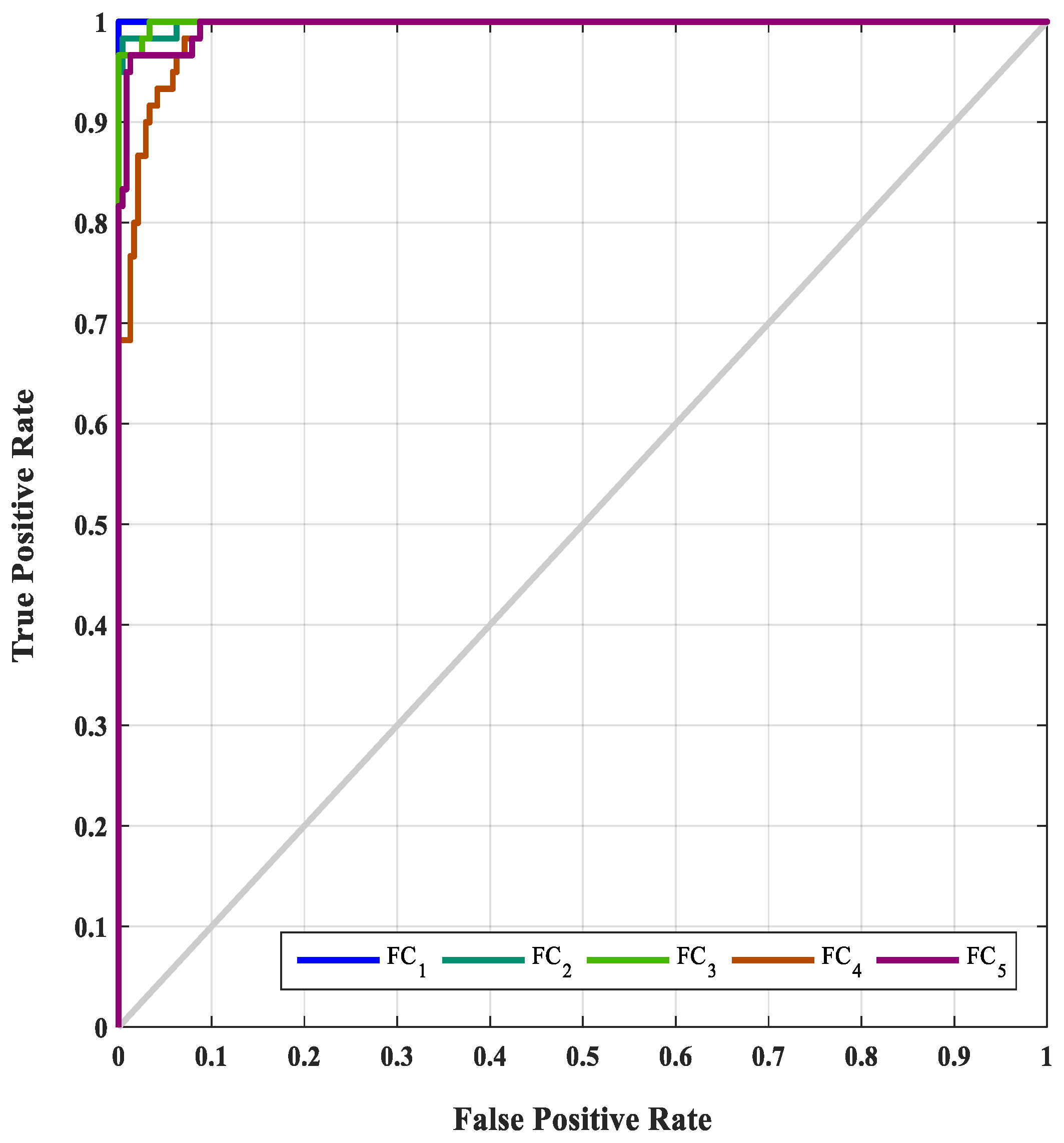
| Machine Condition | Abbreviation | Severity and Location |
|---|---|---|
| Healthy with residual misalignment | RC | Possible residual misalignment at couplings |
| Bent shaft | FC1 | 3.4 mm run-out was created at the centre of the 1000 mm long shaft |
| Shaft misalignment | FC2 | 0.4 mm mild steel shim beneath both sides of bearing 1 pedestal |
| Loose bearing | FC3 | Loose bearing 3 threaded bar nuts |
| Cracked shaft | FC4 | 4 mm (depth) × 0.25 mm (width) breathing crack on the 1000 mm long shaft, at 160 mm from bearing 1 (i.e., near electric motor) |
| Rubbing shaft | FC5 | Partial rub using 2 Perspex blades (top and bottom dead centres of the 1000 mm shaft), at 275 mm from bearing 1 (i.e., near electric motor) |
| Parameters | Properties | |||||
|---|---|---|---|---|---|---|
| ANN1 | ANN2 | ANN3 | ANN4 | ANN5 | ||
| Network Structure | 4–20–2 | 4–15–15–2 | 4–20–2 | 4–60–60–2 | 4–15–10–2 | |
| Fit (%) | Training | 100 | 99.6 | 100 | 99.7 | 100 |
| Validation | 100 | 99.4 | 100 | 99.7 | 100 | |
| Testing | 100 | 99.4 | 100 | 99 | 94.4 | |
| Sensitivity | 1 | 0.95 | 1 | 0.97 | 0.98 | |
| Specify | 1 | 1 | 1 | 0.97 | 1 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luwei, K.C.; Yunusa-Kaltungo, A.; Sha’aban, Y.A. Integrated Fault Detection Framework for Classifying Rotating Machine Faults Using Frequency Domain Data Fusion and Artificial Neural Networks. Machines 2018, 6, 59. https://doi.org/10.3390/machines6040059
Luwei KC, Yunusa-Kaltungo A, Sha’aban YA. Integrated Fault Detection Framework for Classifying Rotating Machine Faults Using Frequency Domain Data Fusion and Artificial Neural Networks. Machines. 2018; 6(4):59. https://doi.org/10.3390/machines6040059
Chicago/Turabian StyleLuwei, Kenisuomo C., Akilu Yunusa-Kaltungo, and Yusuf A. Sha’aban. 2018. "Integrated Fault Detection Framework for Classifying Rotating Machine Faults Using Frequency Domain Data Fusion and Artificial Neural Networks" Machines 6, no. 4: 59. https://doi.org/10.3390/machines6040059
APA StyleLuwei, K. C., Yunusa-Kaltungo, A., & Sha’aban, Y. A. (2018). Integrated Fault Detection Framework for Classifying Rotating Machine Faults Using Frequency Domain Data Fusion and Artificial Neural Networks. Machines, 6(4), 59. https://doi.org/10.3390/machines6040059






