Joint Mechanism That Mimics Elastic Characteristics in Human Running
Abstract
:1. Introduction
2. Joint Mechanism Mimicking the Joint Stiffness of a Human Leg
2.1. Requirements for a Joint Mechanism Based on Human Running
| Min. (Nm/rad) | Max. (Nm/rad) | |
|---|---|---|
| Knee | 300 | 600 |
| Ankle | 520 | 570 |
2.2. Design of a Joint Mechanism Mimicking the Joint Stiffness of a Human Leg
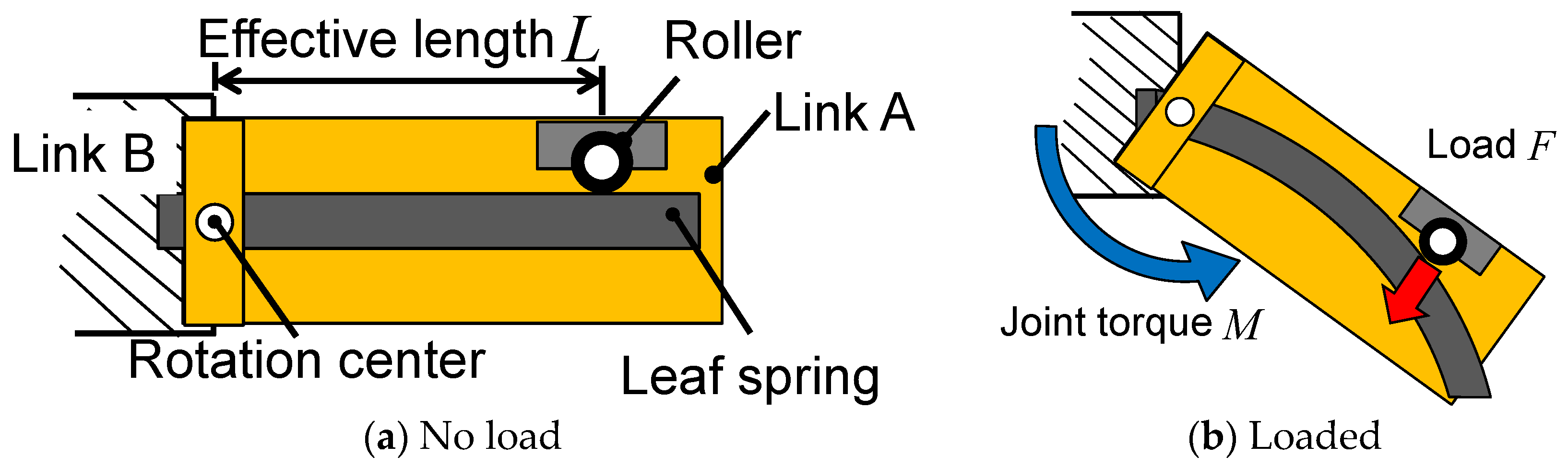
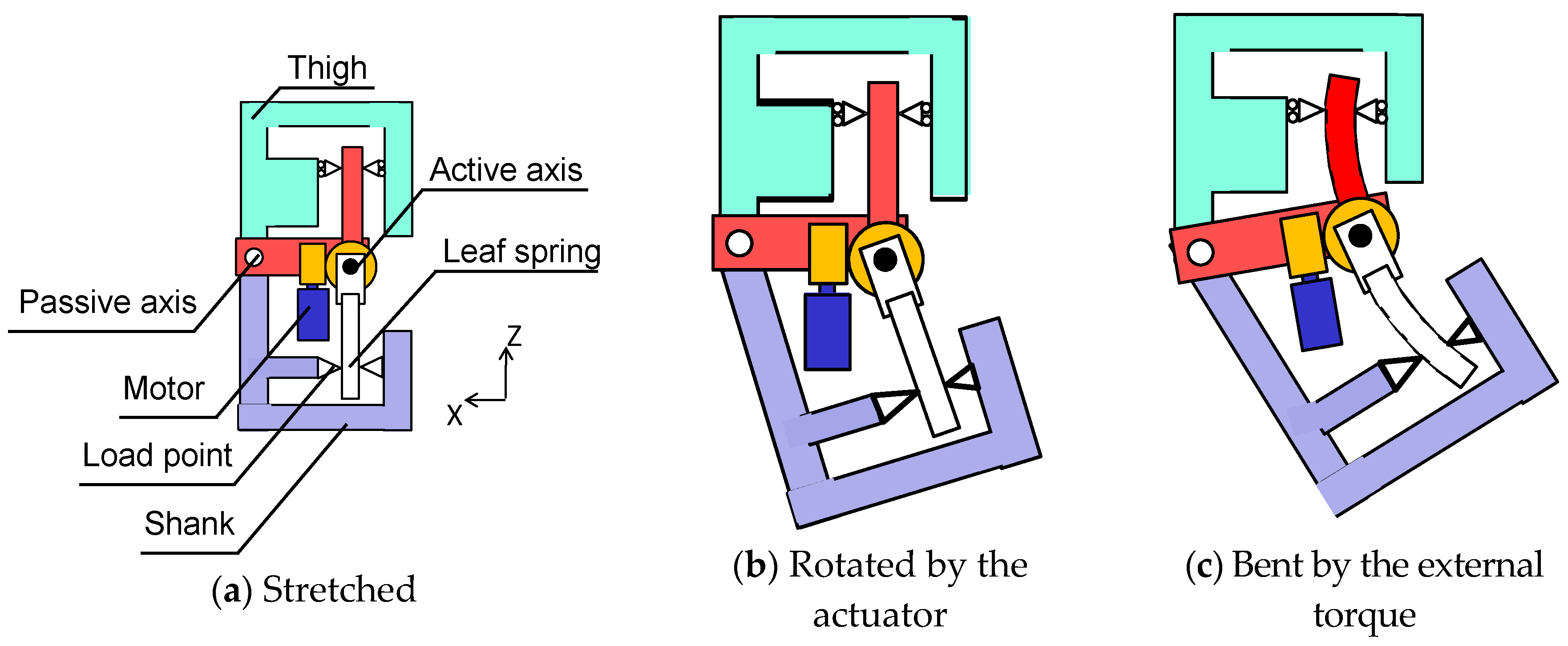
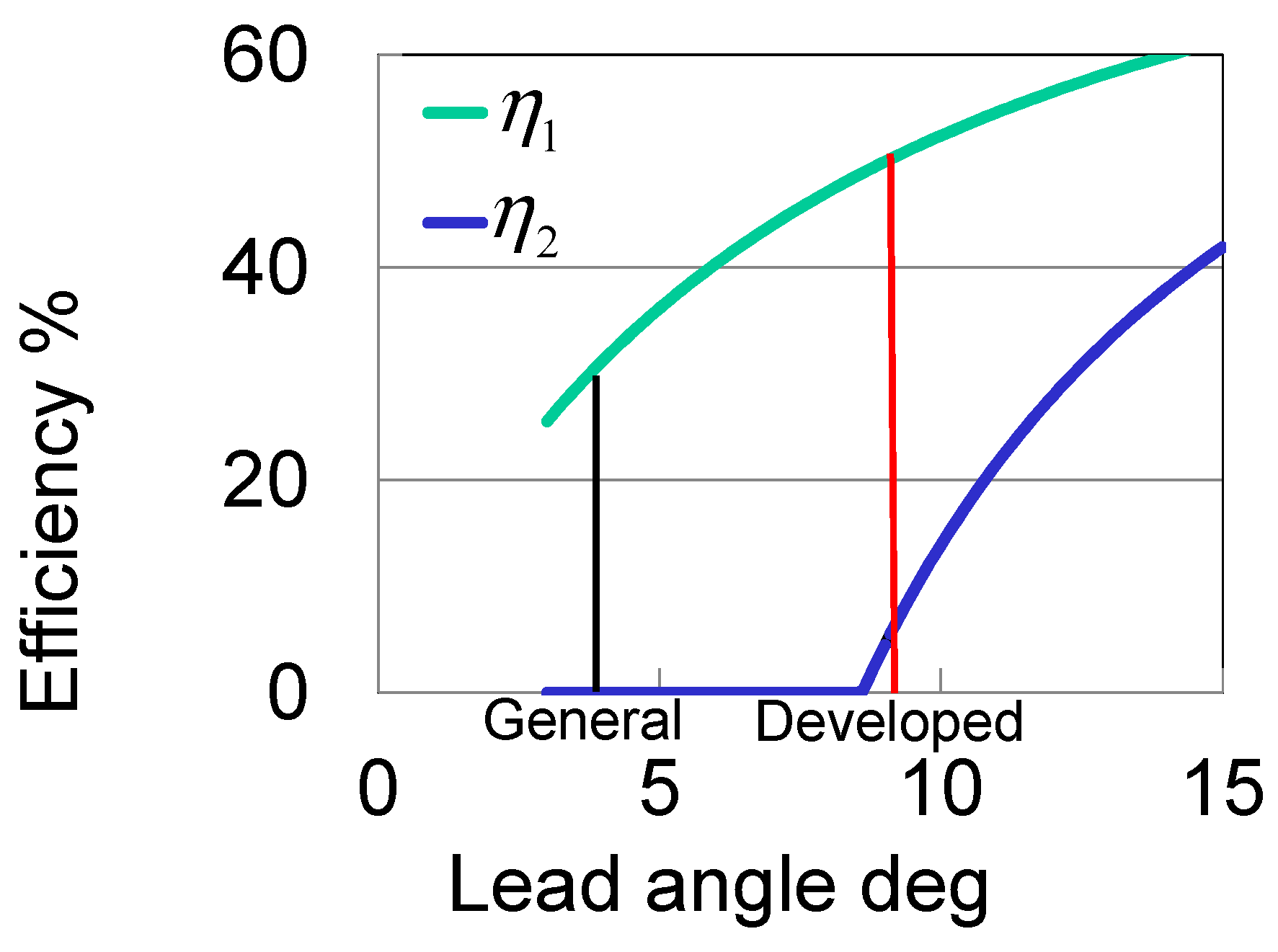
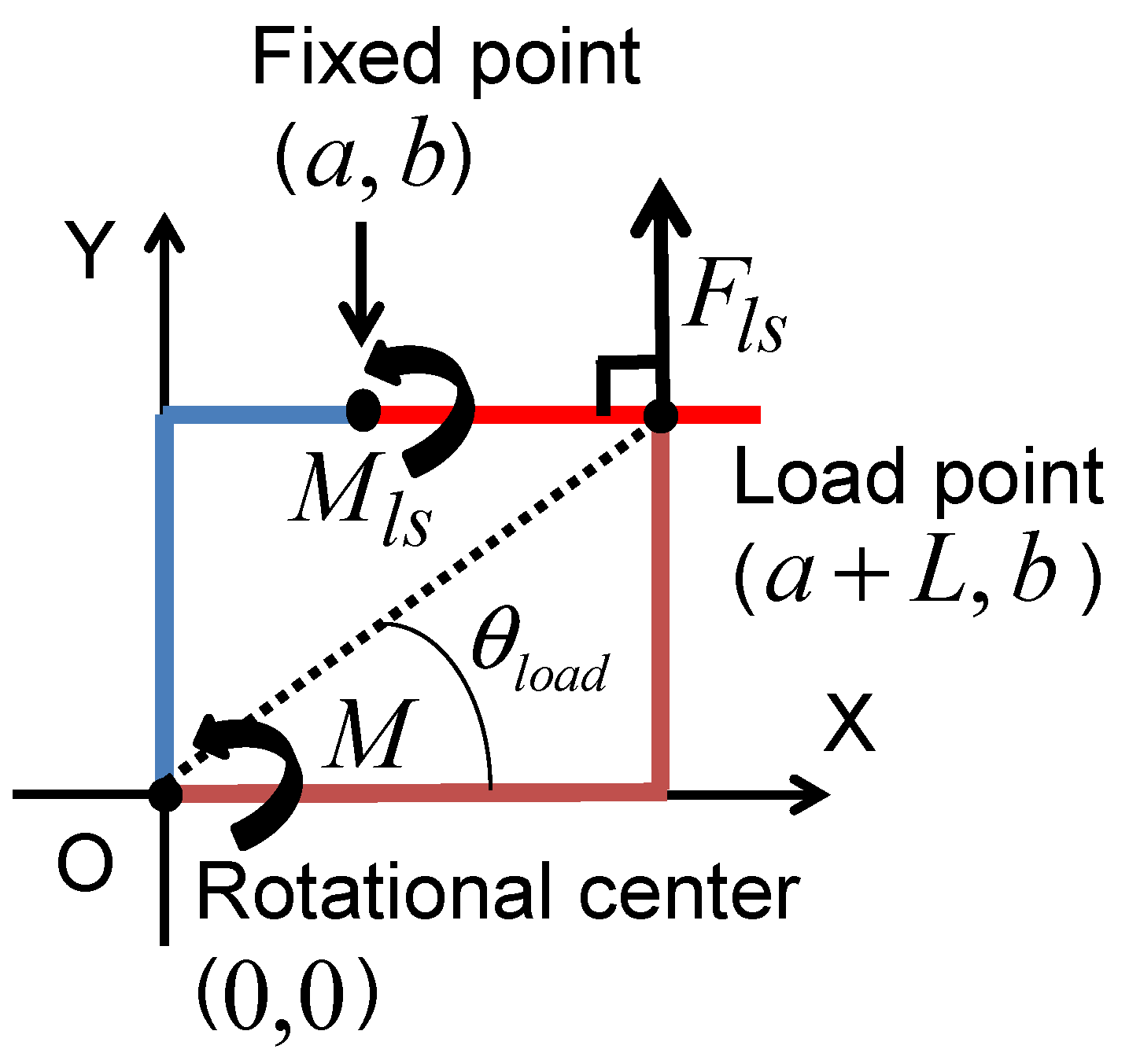
2.3. Joint Stiffness Equation Considering the Fixed Point
2.4. Laminated Leaf Spring Made of Carbon Fiber-Reinforced Plastic
| Material | Iron | CFRP |
|---|---|---|
| Size mm | 250 × 90 × 3.4 | 220 × 70 × 8.8 |
| Mass g | 600 | 200 |
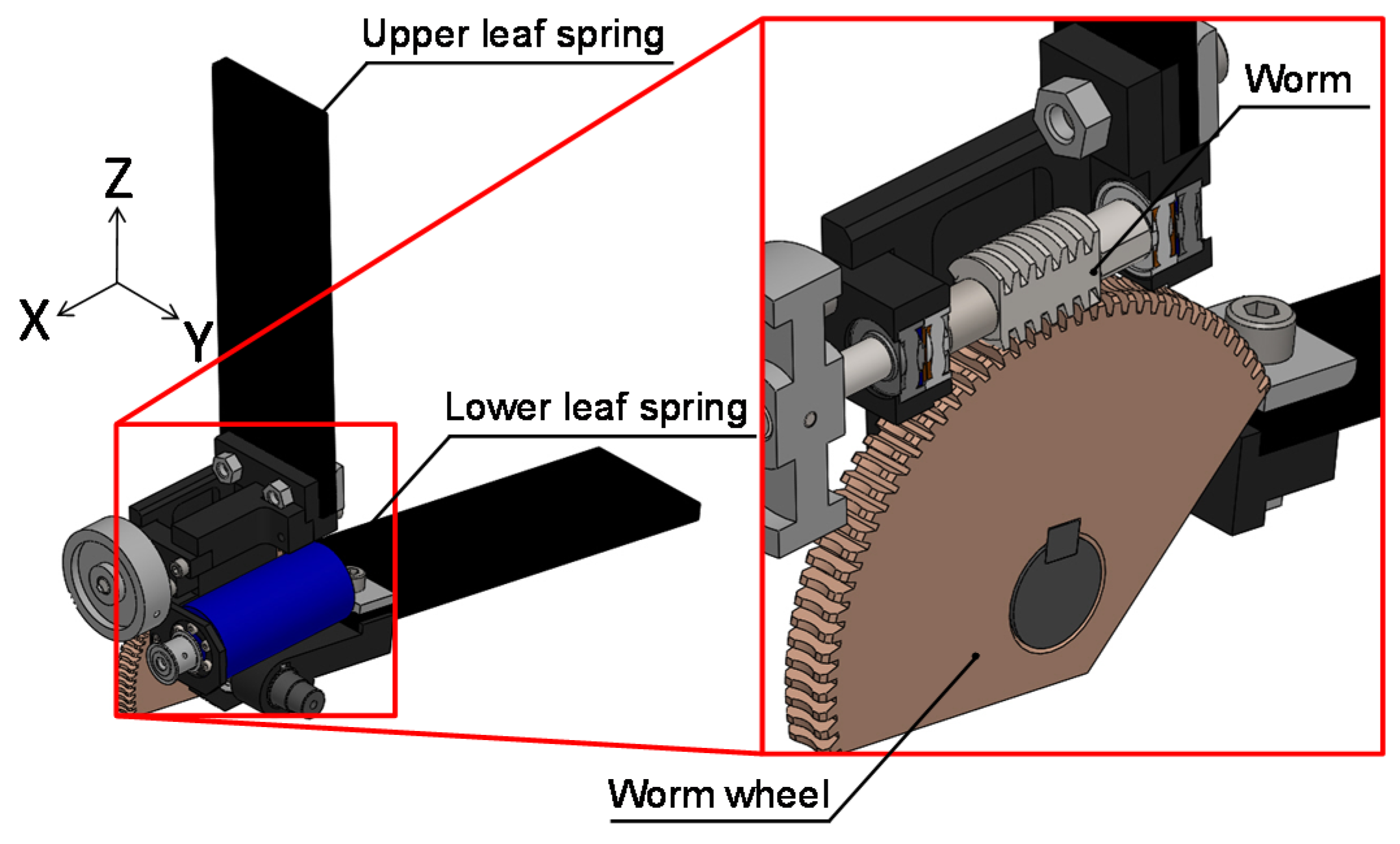
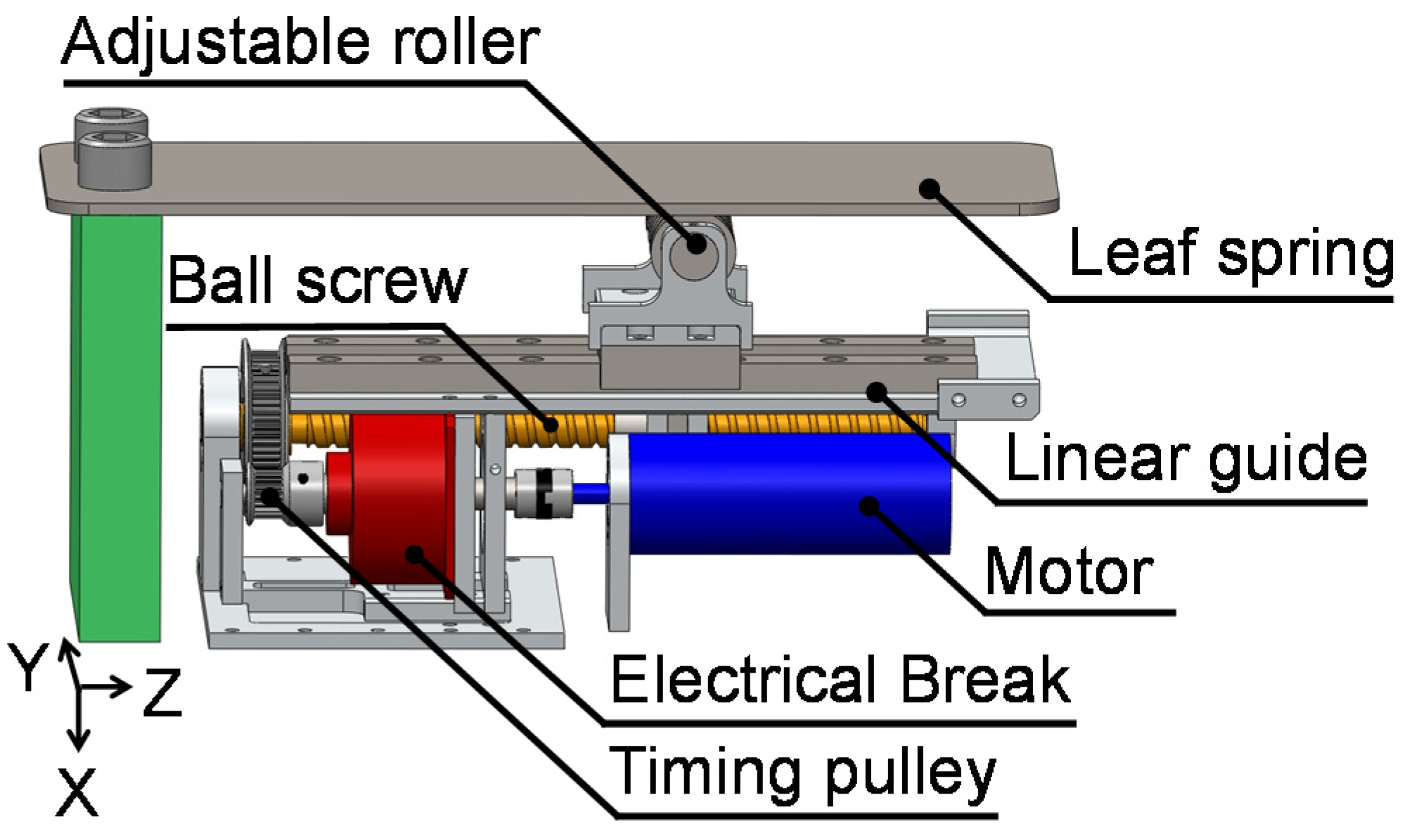
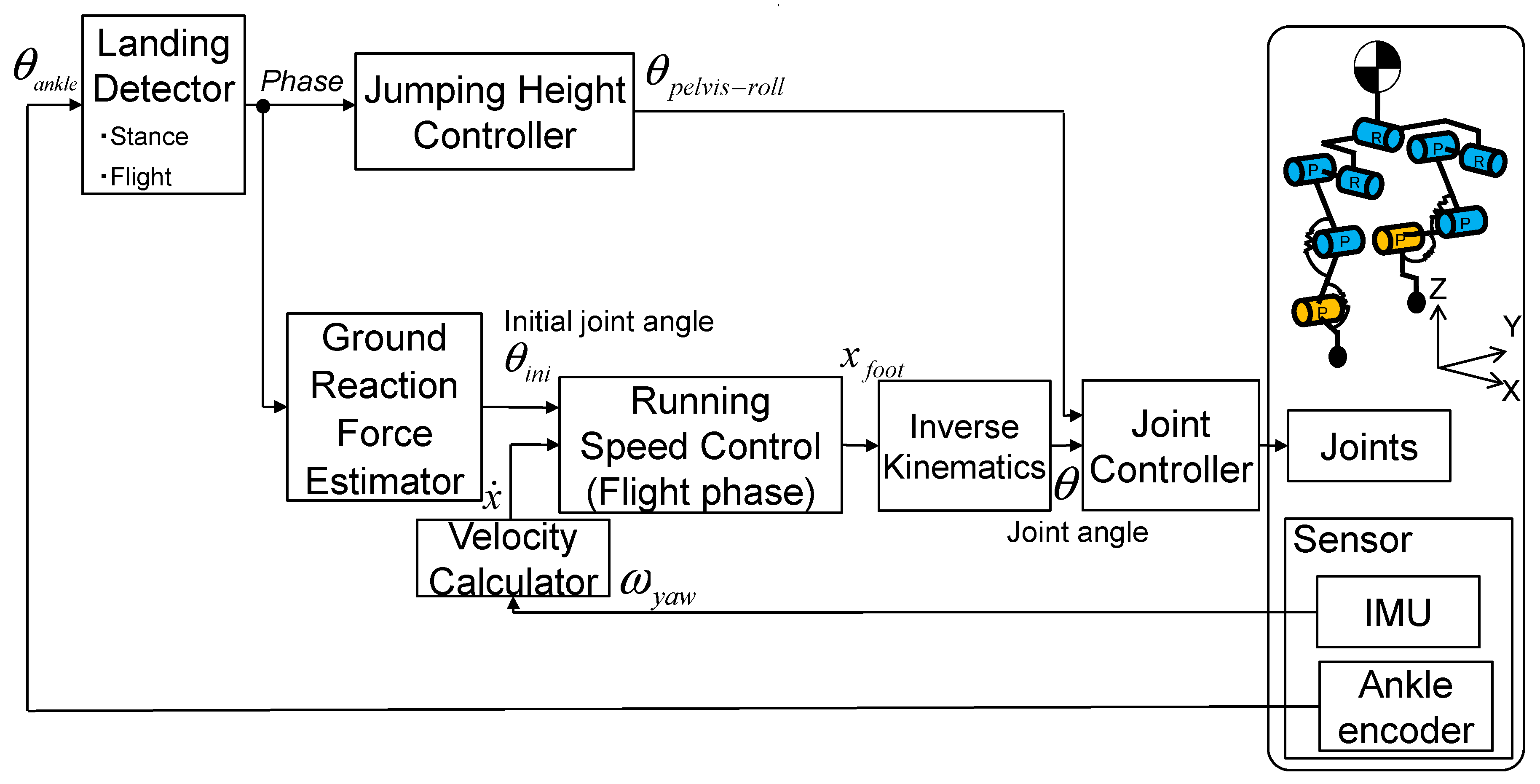
2.5. Implementation of the Joint Mechanism
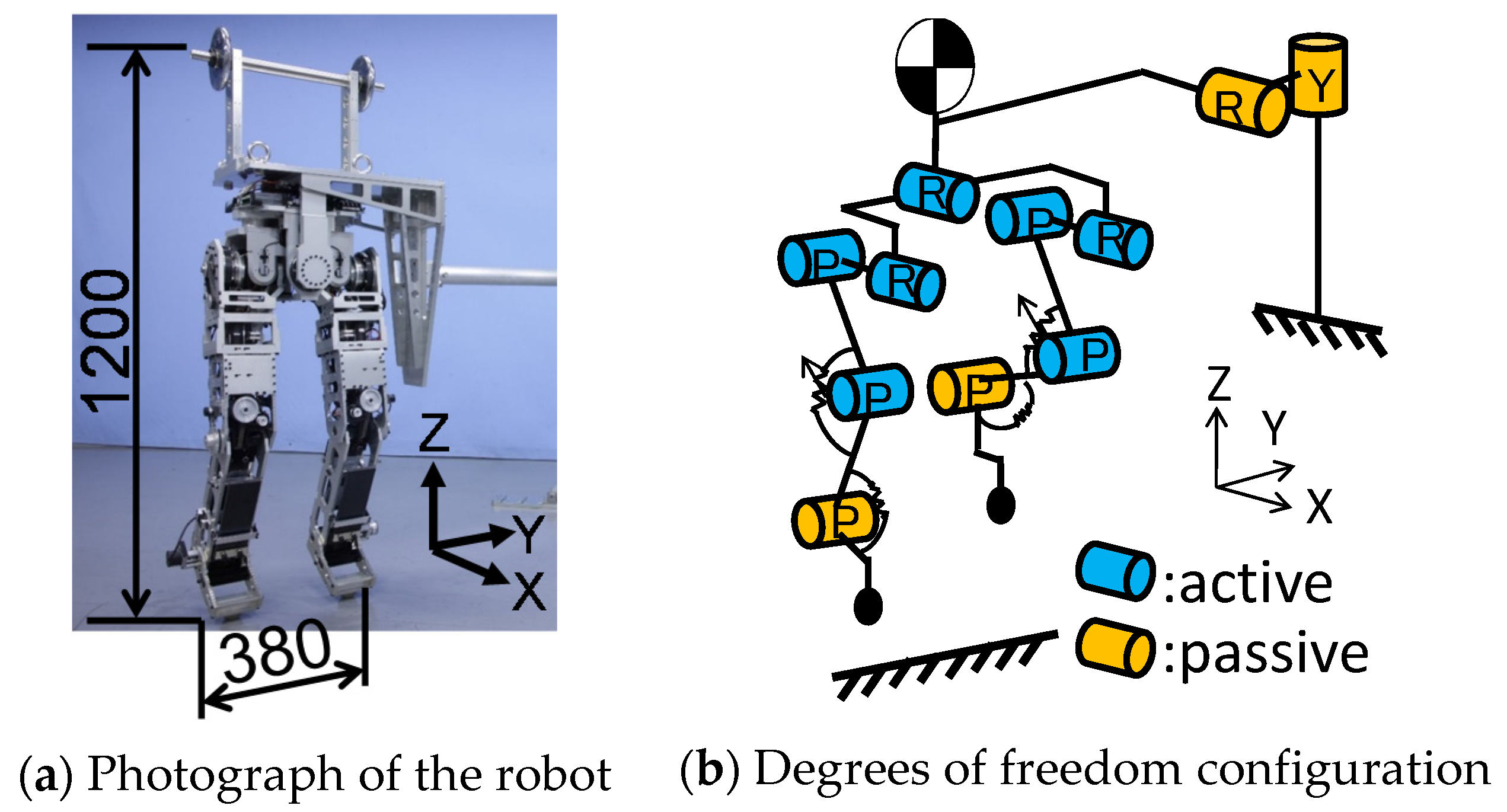
| Human [29] | Robot | |
|---|---|---|
| Distance between hip joints (mm) | 180 | 180 |
| Thigh length (mm) | 374 | 377 |
| Shank length (mm) | 339 | 339 |
| Foot length (mm) | 170 | 170 |
| Height of center of the mass (mm) | 786 | 691 |
| Moment of inertia (kg·m2) | 6.3 | 5.8 |
3. Experiments and Discussion
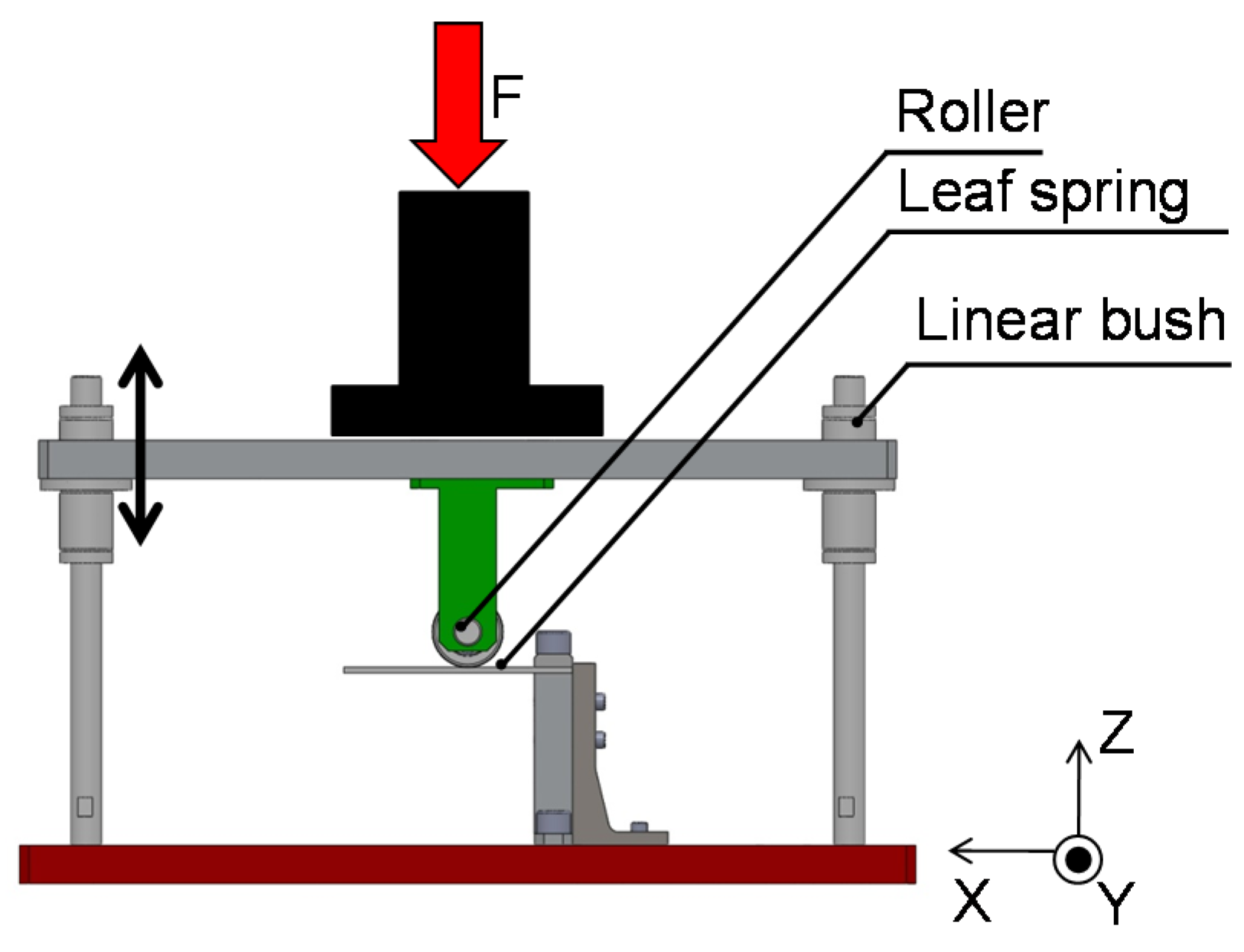
3.1. Verification of the CFRP-Laminated Leaf Spring
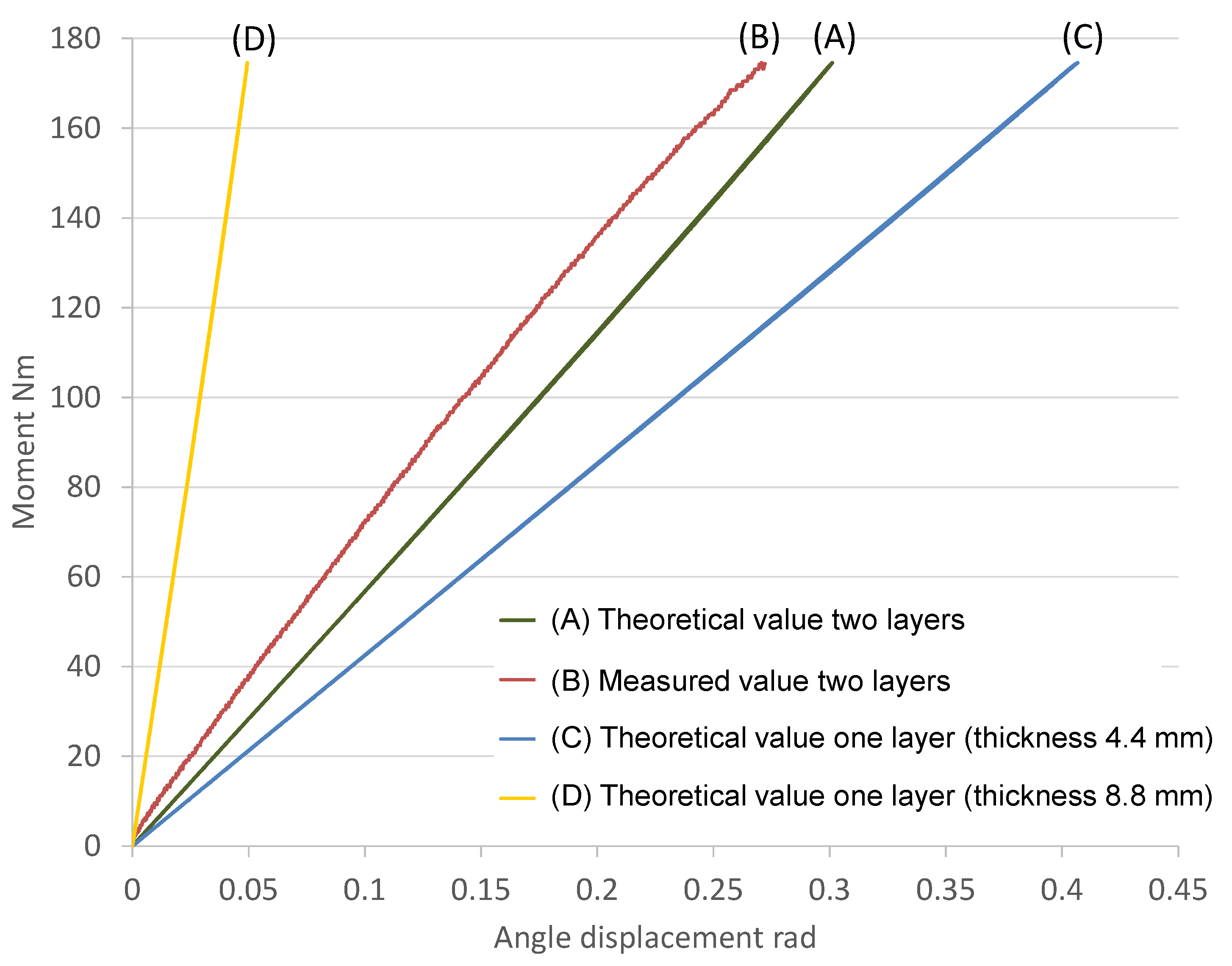
3.2. Verification of Joint Stiffness
| Min. (Nm/rad) | Max. (Nm/rad) | |
|---|---|---|
| Requirement for knee joint | 300 | 600 |
| Theoretical value | 230 | 690 |
| Measured value | 230 | 680 |
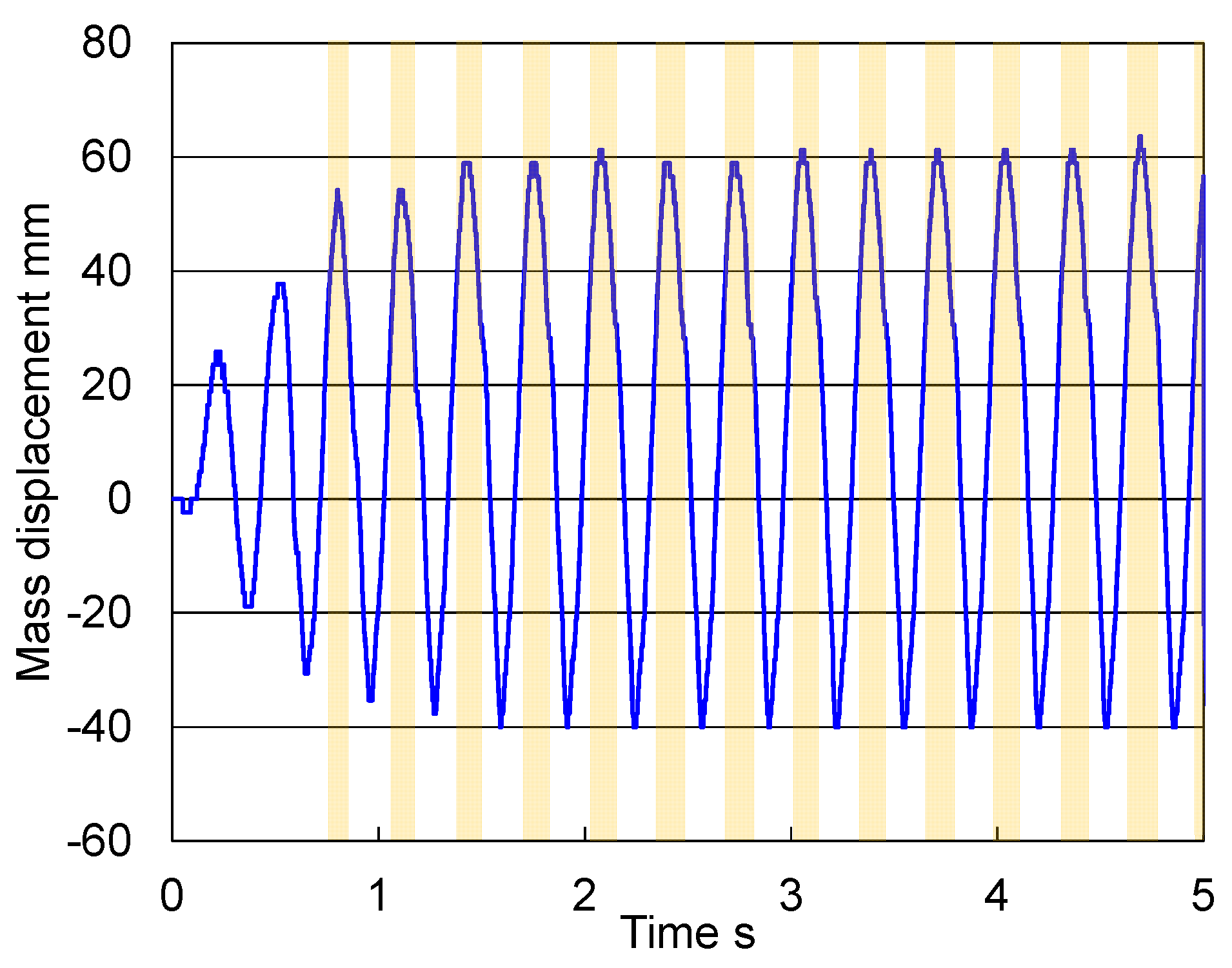
3.3. Hopping Experiment
| Parameter | |
|---|---|
| Whole mass (kg) | 60 |
| Running speed reference (m/s) | 0.2 |
| Pelvic oscillation amplitude (°) | 5 |
| Knee joint stiffness (Nm/rad) | 220 |
| Ankle joint stiffness (Nm/rad) | 520 |
| Natural period (s) | 0.3 |
| Hip angle of stance leg at landing (°) | 10 |
| Knee angle of stance leg at landing (°) | 40 |
| Ankle angle of stance leg at landing (°) | 90 |
| Hip angle of swing leg at landing (°) | 18 |
| Knee angle of swing leg at landing (°) | 75 |
| Ankle angle of swing leg at landing (°) | 90 |
| Specification | |
|---|---|
| Energy storage capacity (J) | 73 |
| Maximum torque (Nm) | 180 |
| Maximum power (W) | 1000 |
| Maximum deflection angle (rad) | 0.81 |
| Active movement range (rad) | 0–1.7 |
| Active movement angular velocity (rad/s) | 6.7 |

4. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ogura, Y.; Shimomura, K.; Kondo, H.; Morishima, A.; Okubo, T.; Momoki, S.; Lim, H.O.; Takanishi, A. Human-like Walking with Knee Stretched, Heel-contact and Toe-off Motion by a Humanoid Robot. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems 2006, Beijing, China, 9–15 October 2006; pp. 3976–3981.
- Hashimoto, K.; Hattori, K.; Otani, T.; Lim, H.O.; Takanishi, A. Foot Placement Modification for a Biped Humanoid Robot with Narrow Feet. Sci. World J. 2014, 2014, 259570. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, K.; Takezaki, Y.; Lim, H.O.; Takanishi, A. Walking Stabilization Based on Gait Analysis for Biped Humanoid Robot. Adv. Robot. 2013, 27, 541–551. [Google Scholar] [CrossRef]
- World Medical Association. Declaration of Helsinki; World Medical Association: Helsinki, Finland, 1964. [Google Scholar]
- Blickhan, R. The Spring-mass Model for Running and Hopping. J. Biomech. 1989, 22, 1217–1227. [Google Scholar] [CrossRef]
- McMahon, T.; Cheng, G. The Mechanics of Running: How does Stiffness Couple with Speed? J. Biomech. 1990, 23, 65–78. [Google Scholar] [CrossRef]
- Novacheck, T.F. The biomechanics of running. Gait Posture 1998, 7, 77–95. [Google Scholar] [CrossRef]
- Kuitunen, S.; Komi, P.V.; Kyrolainen, H. Knee and ankle joint stiffness in sprint running. Med. Sci. Sports Exerc. 2002, 34, 166–173. [Google Scholar] [CrossRef] [PubMed]
- Gunther, M.; Blickhan, R. Joint stiffness of the ankle and the knee in running. J. Biomech. 2002, 35, 1459–1474. [Google Scholar] [CrossRef]
- Ferber, R.; Davis, I.M.; Williams, D.S., III. Gender Differences in Lower Extremity Mechanics during Running. Clin. Biomech. 2003, 18, 350–357. [Google Scholar] [CrossRef]
- Chapman, A.E.; Caldwell, G.E. Factors determining changes in lower limb energy during swing in treadmill running. J. Biomech. 1983, 16, 69–77. [Google Scholar] [CrossRef]
- Otani, T.; Hashimoto, K.; Yahara, M.; Miyamae, S.; Isomichi, T.; Hanawa, S.; Sakaguchi, M.; Kawakami, Y.; Lim, H.; Takanishi, A. Utilization of Human-Like Pelvic Rotation for Running Robot. Front. Robot. 2015. [Google Scholar] [CrossRef]
- Hinrichs, N.R. Upper Extremity Function in Running. II: Angular Momentum Considerations. Int. J. Sport Biomech. 1987, 3, 242–263. [Google Scholar]
- Endo, T.; Miyashita, K.; Ogata, M. Kinetics factors of the lower limb joints decelerating running velocity in the last phase of 100 m race. Res. Phys. Educ. 2008, 53, 477–490. [Google Scholar] [CrossRef]
- Schache, G.A.; Blanch, D.P.; Dorn, W.T.; Brown, A.T.N.; Rosemond, D.; Pandy, G.M. Effect of Running Speed on Lower Limb Joint Kinetics. Med. Sci. Sports Exerc. 2011, 43, 1260–1271. [Google Scholar] [CrossRef] [PubMed]
- Dalleau, G.; Belli, A.; Bourdin, M.; Lacour, J.R. The Spring-Mass Model and the Energy Cost of Treadmill Running. Eur. J. Appl. Physiol. 1998, 77, 257–263. [Google Scholar] [CrossRef] [PubMed]
- Nagasaki, T.; Kajita, S.; Kaneko, K.; Yokoi, K.; Tanie, K. A Running Experiment of Humanoid Biped. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Sendai, Japan, 28 September–2 October 2004; pp. 136–141.
- Cho, B.K.; Park, S.S.; Oh, J.H. Controllers for running in the humanoid robot, HUBO. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots 2009, Paris, France, 7–10 December 2009; pp. 385–390.
- Takenaka, T.; Matsumoto, T.; Yoshiike, T.; Shirokura, S. Running Gait Generation for Biped Robot with Horizontal Force Limit. JRSJ 2011, 29, 93–100. [Google Scholar] [CrossRef]
- Tajima, R.; Honda, D.; Suga, K. Fast Running Experiments Involving a Humanoid Robot. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 1571–1576.
- Tamada, T.; Ikarashi, W.; Yoneyama, D.; Tanaka, K.; Yamakawa, Y.; Senoo, T.; Ishikawa, M. High Speed Bipedal Robot Running Using High Speed Visual Feedback. In Proceedings of the 14th IEEE-RAS International Conference on Humanoid Robots, Madrid, Spain, 18–20 November 2014; pp. 140–145.
- Niiyama, R.; Nishikawa, S.; Kuniyoshi, Y. Biomechanical Approach to Open-loop Bipedal Running with a Musculoskeletal Athlete Robot. Adv. Robot. 2012, 26, 383–398. [Google Scholar] [CrossRef]
- Grizzle, J.W.; Hurst, J.; Morris, B.; Park, H.W.; Sreenath, K. MABEL, a new robotic bipedal walker and runner. In Proceedings of the American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 2030–2036.
- Tsagarakis, N.G.; Laffranchi, M.; Vanderborght, B.; Caldwell, D.G. A compact soft actuator unit for small scale human friendly robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 4356–4362.
- Ugurlu, B.; Saglia, J.A.; Tsagarakis, N.G.; Caldwell, D.G. Hopping at the resonance frequency: A trajectory generation technique for bipedal robots with elastic joints. In Proceedings of the IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 1436–1443.
- Moro, F.L.; Tsagarakis, N.G.; Caldwell, D.G. Walking in the Resonance with the COMAN Robot with Trajectories based on Human Kinematic Motion Primitives (kMPs). Auton. Robots 2014, 36, 331–347. [Google Scholar] [CrossRef]
- Vu, H.Q.; Yu, X.; Iida, F.; Pfeifer, R. Improving energy efficiency of hopping locomotion by using a variable stiffness actuator. IEEE/ASME Trans. Mechatron. 2015. [Google Scholar] [CrossRef]
- Renjewski, D.; Seyfarth, A.; Manoonpong, P.; Wörgötter, F. The development of a biomechanical leg system and its neural control. In Proceedings of the 2009 International Conference on Robotics and Biomimetics, Guangxi, China, 19–23 December 2009; pp. 1894–1899.
- Grimmer, M. Powered Lower Limb Prostheses. Ph.D. Thesis, Technische Universitaet Darmstadt, Darmstadt, Germany, 2015. [Google Scholar]
- Yuan, K.; Zhu, J.; Wang, Q.; Wang, L. Finite-state control of powered below-knee prosthesis with ankle and toe. In Proceedings of the 18th IFAC World Congress, Milano, Italy, 28 August–2 September 2011; pp. 2865–2870.
- Waycaster, G.; Wu, S.K.; Xiangrong, S. Design and control of a pneumatic artificial muscle actuated above-knee prosthesis. J. Med. Devices 2011, 5. [Google Scholar] [CrossRef]
- Hitt, J.; Sugar, T.; Holgate, M.; Bellman, R. An active foot-ankle prosthesis with biomechanical energy regeneration. J. Med. Devices 2010, 4. [Google Scholar] [CrossRef]
- Morita, T.; Sugano, S. Development of 4-DOF manipulator using mechanical impedance adjuster. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; pp. 2902–2907.
- Merritt, H.E. Worm gear performance. Proc. Inst. Mech. Eng. 1982, 129, 127–194. [Google Scholar] [CrossRef]
- Kouchi, M.; Mochimaru, M. Human Dimension Database; AIST Digital Human Research Center: Tokyo, Japan, 2005. [Google Scholar]
- Ae, M.; Tang, H.; Yokoi, T. Estimation of inertia properties of the body segments in japanese athletes. Soc. Biomech. 1992, 11, 23–33. [Google Scholar]
- Otani, T.; Hashimoto, K.; Yahara, M.; Miyamae, S.; Isomichi, T.; Sakaguchi, M.; Kawakami, Y.; Lim, H.O.; Takanishi, A. Running with Lower-Body Robot That Mimics Joint Stiffness of Humans. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otani, T.; Hashimoto, K.; Isomichi, T.; Sakaguchi, M.; Kawakami, Y.; Lim, H.-O.; Takanishi, A. Joint Mechanism That Mimics Elastic Characteristics in Human Running. Machines 2016, 4, 5. https://doi.org/10.3390/machines4010005
Otani T, Hashimoto K, Isomichi T, Sakaguchi M, Kawakami Y, Lim H-O, Takanishi A. Joint Mechanism That Mimics Elastic Characteristics in Human Running. Machines. 2016; 4(1):5. https://doi.org/10.3390/machines4010005
Chicago/Turabian StyleOtani, Takuya, Kenji Hashimoto, Takaya Isomichi, Masanori Sakaguchi, Yasuo Kawakami, Hun-Ok Lim, and Atsuo Takanishi. 2016. "Joint Mechanism That Mimics Elastic Characteristics in Human Running" Machines 4, no. 1: 5. https://doi.org/10.3390/machines4010005
APA StyleOtani, T., Hashimoto, K., Isomichi, T., Sakaguchi, M., Kawakami, Y., Lim, H.-O., & Takanishi, A. (2016). Joint Mechanism That Mimics Elastic Characteristics in Human Running. Machines, 4(1), 5. https://doi.org/10.3390/machines4010005






