Magnetic Circuit Analysis and Design Optimized for Cost-Effectiveness of Surface-Inserted Rare Earth Consequent-Pole Permanent Magnet Machines
Abstract
1. Introduction
2. General Analytical Model of Cogging Torque
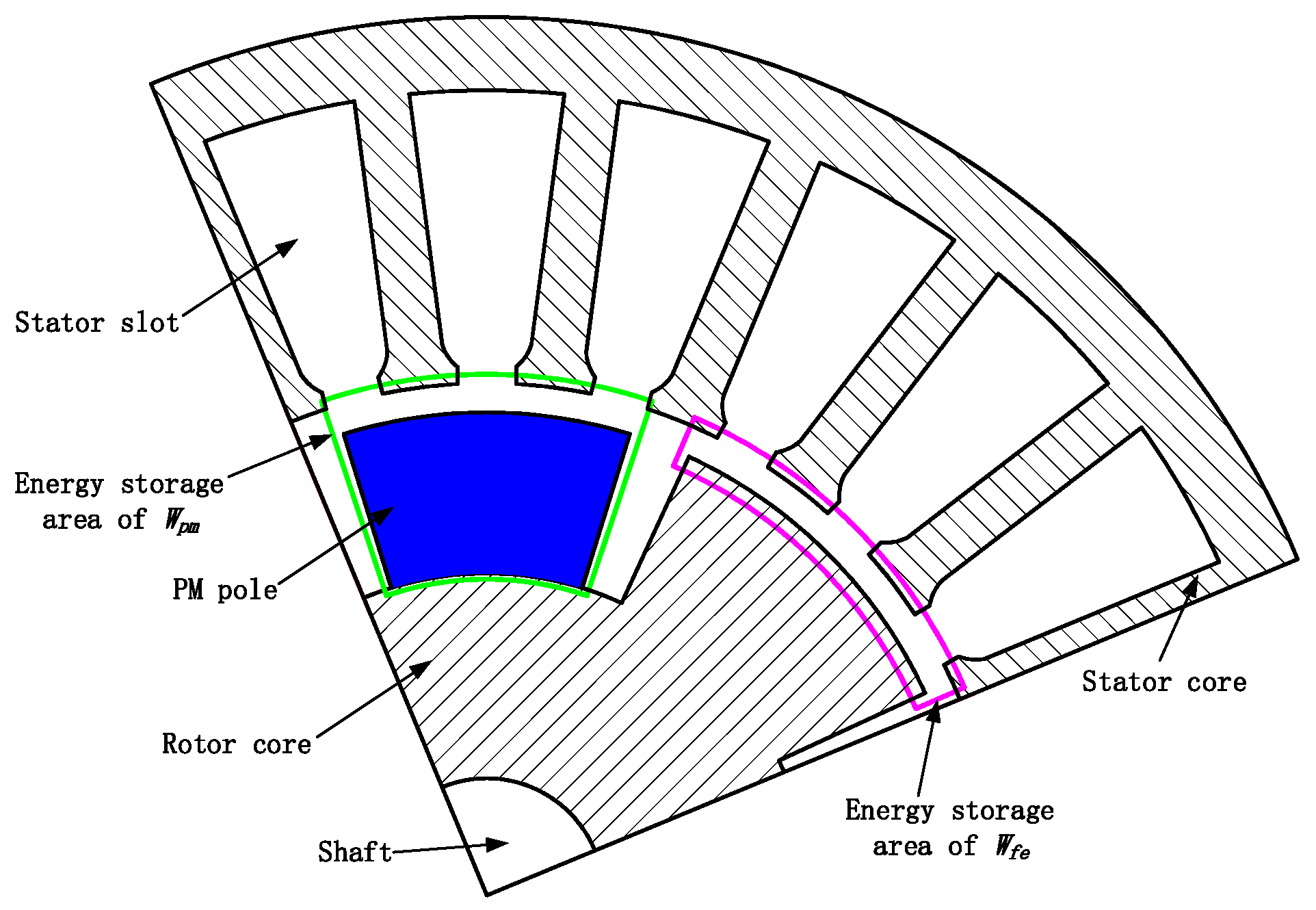
3. Analytical Model of Main Flux
4. Performance Analysis and Optimal Design
4.1. Sensitivity Analysis of Machine Parameters
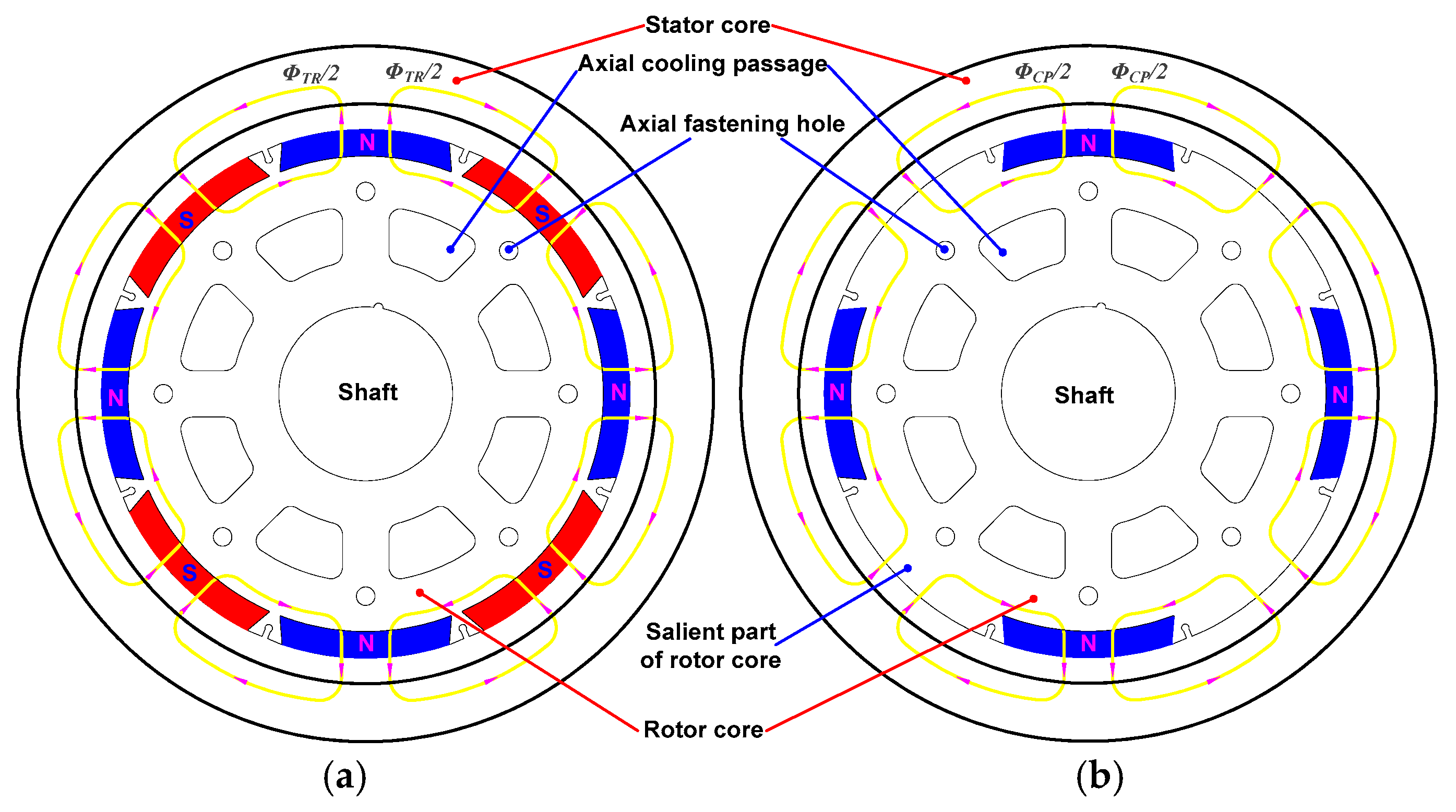
4.2. Direct Conversion of Conventional to CP Topologies
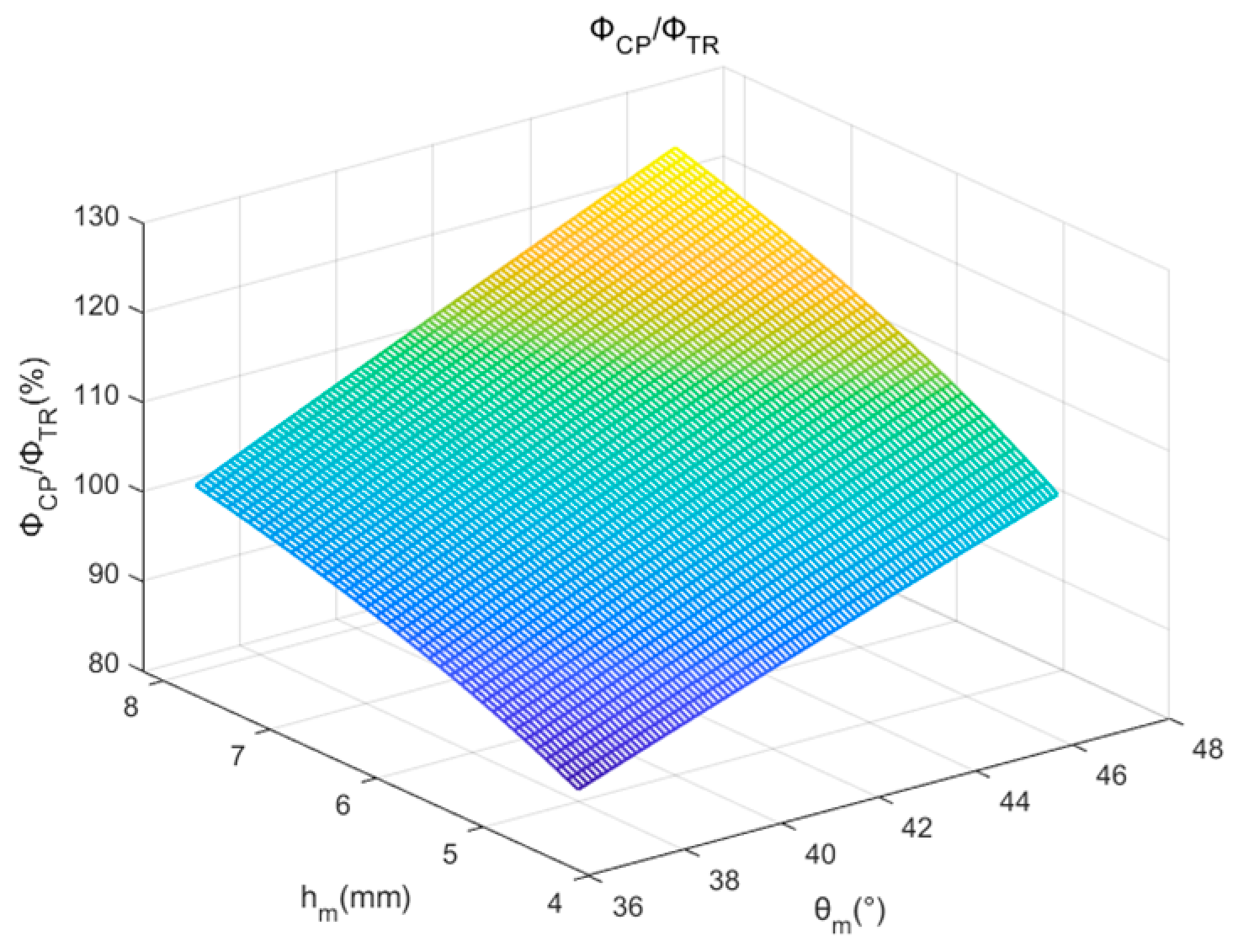
4.3. Performance-Oriented Optimization Targeting Total Flux Enhancement
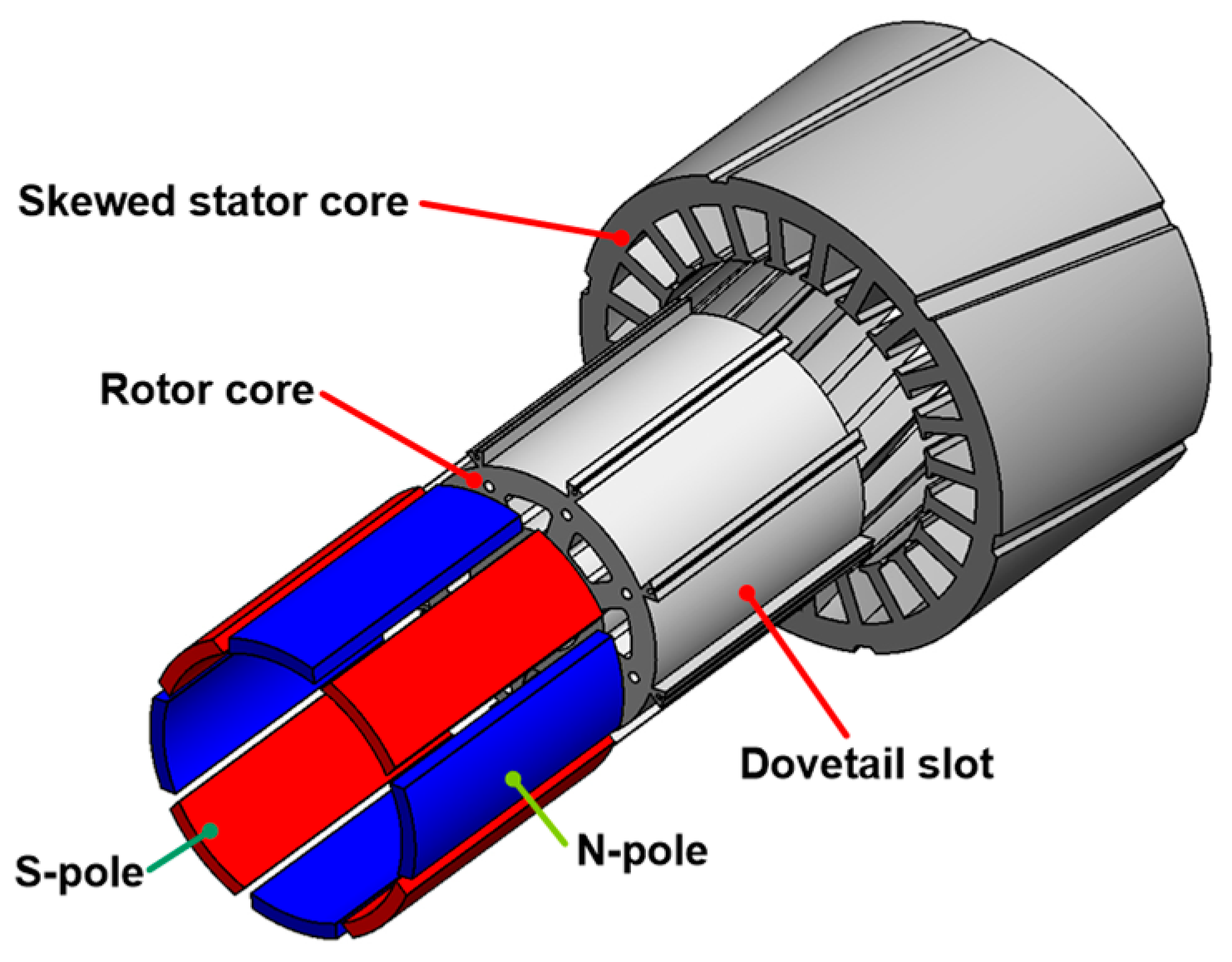
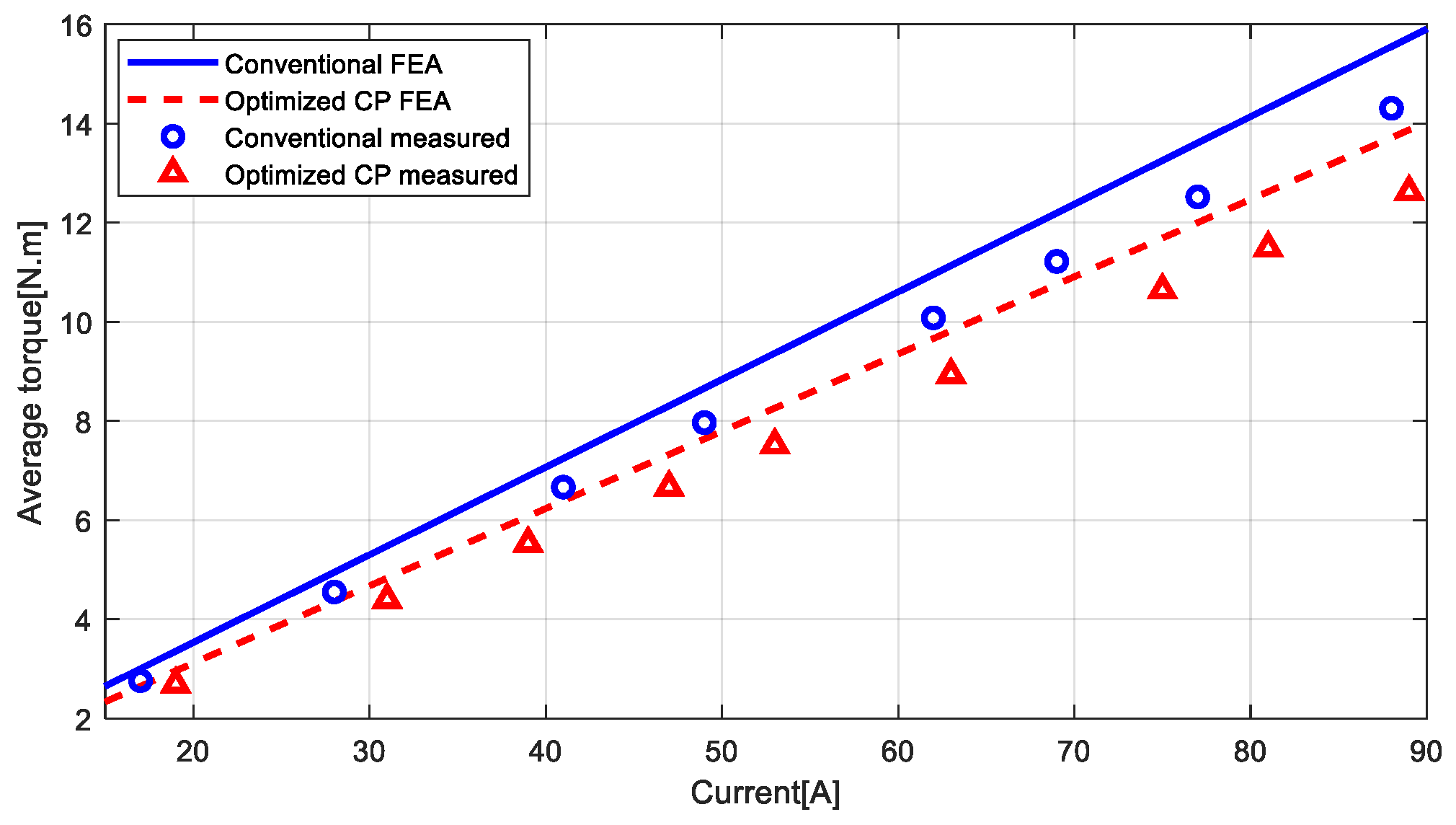
5. Experimental Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CPPM | Consequent-pole permanent magnet |
| CP | Consequent-pole |
| PM | Permanent magnet |
| REPM | Rare earth permanent magnet |
| NdFeB | Neodymium Iron Boron |
| SmCo | Samarium Cobalt |
| LCM | Least common multiple |
| EMF | Electromotive force |
References
- Li, Y.; Yang, H.; Lin, H.; Qin, L.; Lyu, S. Investigation of Double-Side Field Modulation Mechanism in Consequent-Pole PM Machines with Concentrated Windings. IEEE Trans. Energy Convers. 2021, 36, 1635–1648. [Google Scholar] [CrossRef]
- Hsieh, M.-F.; Chang, C.-Y.; Huynh, T.-A.; Dorrell, D.G. Design and Analysis of Consequent-Pole Permanent Magnet Vernier Motor with Cancellation of Even-Order Harmonics. IEEE Trans. Magn. 2023, 59, 8204406. [Google Scholar] [CrossRef]
- Wang, Z.; Dai, B.; Guo, Z.; Yang, J. Single-Loop Current-Constrained Speed Regulation for PMSM via a Switching Controller. IEEE Trans. Transp. Electrif. 2025, 11, 5974–5982. [Google Scholar] [CrossRef]
- Dai, B.; Wang, Z.; Zhao, J.; Li, S. Critical Current-Constrained Continuous Nonsingular Terminal Sliding Mode Control for PMSM Based on Control Barrier Function. IEEE Trans. Power Electron. 2025, 40, 15093–15103. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhu, Z.Q.; Liang, D.; Xu, H.; Zhou, Y.; Liu, H. Analysis and Reduction of Unipolar End Leakage Flux in Consequent-Pole PM Machines. IEEE Trans. Ind. Appl. 2025, 61, 196–208. [Google Scholar] [CrossRef]
- Dajaku, G. Comparison Study of Permanent Magnet Synchronous Machines with Consequent Pole and HUPM Rotor. IEEE Trans. Magn. 2022, 58, 8104110. [Google Scholar] [CrossRef]
- Kumar, R.; Um, D.Y.; Sjöberg, L.; Batra, T.; Atkinson, G. Electromagnetic Analysis and Comparative Study of Surface-Mounted and Consequent Pole Axial Flux Permanent Magnet Machines. IEEE Access 2024, 12, 188926–188939. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Q.; Ding, S.; Hang, J.; Li, W. Quantitative Evaluation of Torque Contributions of Multiple Working Harmonics on Halbach Array Consequent-Pole PM Machine. IEEE/ASME Trans. Mechatron. 2024, 29, 4572–4581. [Google Scholar] [CrossRef]
- Li, Y.; Yang, H.; Lin, H.; Zhao, Z. Comparative Study of Field Modulation Effects in Consequent-Pole PM Machines with Different Stator Slot Configurations. IEEE Trans. Magn. 2023, 59, 8103706. [Google Scholar] [CrossRef]
- Qi, J.; Zhu, Z.Q.; Yan, L.; Jewell, G.W.; Gan, C.; Ren, Y. Analytical Analysis of Cogging Torque in Permanent Magnet Machines with Unequal North and South Poles, with Particular Reference to Consequent Pole Machines. IEEE Trans. Energy Convers. 2023, 38, 1361–1375. [Google Scholar] [CrossRef]
- Chen, B.; Xiao, Y.; Shi, J.; Hu, Y.; Li, L.; Liu, M. Radial Force Characteristics of a Consequent-Pole Permanent Magnet Synchronous Motor. IEEE Trans. Ind. Appl. 2023, 59, 6664–6673. [Google Scholar] [CrossRef]
- Hosseinpour, A.; Abbas, A.; Sadegh, M.O.; Iqbal, A.; Flah, A.; Prokop, L. Optimal Structure to Maximize Torque per Volume for the Consequent-Pole PMSM and Investigating the Temperature Effect. IEEE Access 2024, 12, 108851–108862. [Google Scholar] [CrossRef]
- Li, F.; Wang, K.; Li, J.; Sun, H.Y. Electromagnetic Performance Analysis of Consequent-Pole PM Machine with Asymmetric Magnetic Pole. IEEE Trans. Magn. 2019, 55, 8103205. [Google Scholar] [CrossRef]
- Li, J.; Wang, K.; Zhang, H. Flux-Focusing Permanent Magnet Machines with Modular Consequent-Pole Rotor. IEEE Trans. Ind. Electron. 2020, 67, 3374–3385. [Google Scholar] [CrossRef]
- Xu, G.; Zhao, W.; Liu, G.; Zhai, F.; Chen, Q. Torque Performance Improvement of Consequent-Pole PM Motors with Hybrid Rotor Configuration. IEEE Trans. Transp. Electrif. 2021, 7, 1561–1572. [Google Scholar] [CrossRef]
- Jo, C.; Yun, I.; Hong, H.; Lee, J.; Kim, H. Asymmetric Design of Consequent Pole to Reduce Torque Ripple. IEEE Trans. Magn. 2024, 60, 8204905. [Google Scholar] [CrossRef]
- Qi, J.; Zhu, Z.Q.; Yan, L.; Jewell, G.W.; Gan, C.; Ren, Y. Suppression of Torque Ripple for Consequent Pole PM Machine by Asymmetric Pole Shaping Method. IEEE Trans. Ind. Appl. 2022, 58, 3545–3557. [Google Scholar] [CrossRef]
- Ullah, W.; Khan, F.; Hussain, S.; Alturise, F.; Yousuf, M.; Akbar, S. Consequences of Flux Gap on Intriguing Features of Modular Stator Inset Permanent Magnet Consequent Pole Synchronous Machine. IEEE Access 2022, 10, 49551–49565. [Google Scholar] [CrossRef]
- Hidaka, Y.; Takahashi, S.; Kondo, S.; Iezawa, M. Maintaining Average Torque and Suppressing Torque Ripple with T-Shaped Auxiliary Pole for Spoke Type Multi-Consequent-Pole Motor. IEEE Trans. Energy Convers. 2025, 40, 1400–1410. [Google Scholar] [CrossRef]
- Mitsuda, H.; Fukami, T.; Koyama, M.; Ito, K. Investigation of Flux-Modulating Consequent Pole Motors. IEEE Trans. Ind. Appl. 2023, 59, 1648–1658. [Google Scholar] [CrossRef]
- Zhou, H.; Tao, W.; Jiang, G.; Li, G.-J.; Liu, G. Reduction of Saturation and Unipolar Leakage Flux in Consequent-Pole PMV Machine. IEEE J. Emerging Sel. Top. Power Electron. 2022, 10, 1870–1880. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhu, Z.-Q.; Xu, H.; Yan, J.; Liang, D. Optimal Multi-Tooth Numbers for Vernier PM Synchronous Machines. IEEE Access 2024, 12, 89599–89612. [Google Scholar] [CrossRef]
- Zheng, Y.; Xiang, W.; Kang, M.; Wu, L.; Fang, Y. Analysis of Dual PM Vernier Machines with Different Consequent-Pole PM Topologies. IEEE Trans. Ind. Appl. 2023, 59, 1670–1677. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, Z.; Zhang, Z.; Wang, H. Comparative Analysis of Consequent-Pole PM Vernier Machines with Different Rotor Types. IEEE Trans. Transp. Electrif. 2024, 10, 450–461. [Google Scholar] [CrossRef]
- Liu, W.; Wang, J.; Lipo, T.A. A Consequent Pole Single Rotor Single Stator Vernier Design to Effectively Improve Torque Density of an Industrial PM Drive. IEEE Trans. Ind. Electron. 2023, 70, 255–264. [Google Scholar] [CrossRef]
- Ullah, W.; Khan, F.; Hussain, S.; Yousaf, M.; Akbar, S. Analytical Modeling and Optimization of Partitioned Permanent Magnet Consequent Pole Switched Flux Machine with Flux Barrier. IEEE Access 2022, 10, 123905–123919. [Google Scholar] [CrossRef]
- Ullah, W.; Khan, F.; Hussain, S.; Yousaf, M.; Akbar, S. Analytical Modeling of Novel High Thrust Force Density Segmented PM Consequent Pole Linear Flux Switching Machine. IEEE Access 2022, 10, 105887–105897. [Google Scholar] [CrossRef]
- Rehman, A.; Kim, B. Characteristics Analysis of Consequent-Pole Ferrite Magnet Vernier Machine Using Novel Equivalent Magnetic Circuit. IEEE J. Emerging Sel. Top. Power Electron. 2022, 10, 1823–1833. [Google Scholar] [CrossRef]
- Raza Siddiqi, M.; Humza, M.; Yazdan, T.; Hur, J.; Akbar, S. Cost-Effective Design of Dual Airgap Permanent Magnet Vernier Machine Having a Yokeless Consequent Pole Rotor. IEEE Access 2024, 12, 108224–108232. [Google Scholar] [CrossRef]
- Xu, L.; Li, Y.; Zhao, W.; Liu, G. Reduction of Unipolar Leakage Flux and Torque Ripple in Consequent-pole PM Vernier Machine. CES Trans. Electr. Mach. Syst. 2023, 7, 35–44. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Hua, H.; Pride, A.; Deodhar, R.; Sasaki, T. Analysis of unipolar leakage flux in series-hybrid permanent magnet Machines. In Proceedings of the 2017 IEEE International Magnetics Conference (INTERMAG), Dublin, Ireland, 24–28 April 2017; pp. 1–2. [Google Scholar]
- Li, F.; Wang, K.; Sun, H.Y.; Zhang, H.; Zhang, L. Quantitative Comparison between SPM Machine and Consequent Pole PM Machines with Different Rotor Topologies. In Proceedings of the 2019 IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 11–15 May 2019; pp. 127–134. [Google Scholar]
- Ge, X.; Zhu, Z.Q.; Li, J.; Chen, J. A Spoke-Type IPM Machine with Novel Alternate Airspace Barriers and Reduction of Unipolar Leakage Flux by Step-Staggered Rotor. IEEE Trans. Ind. Appl. 2016, 52, 4789–4797. [Google Scholar] [CrossRef]
- Wang, K.; Li, J.; Zhu, S.S.; Liu, C. Novel Hybrid-Pole Rotors for Consequent-Pole PM Machines Without Unipolar Leakage Flux. IEEE Trans. Ind. Electron. 2019, 66, 6811–6823. [Google Scholar] [CrossRef]
- Li, J.; Wang, K.; Li, F.; Zhu, S.S.; Liu, C. Elimination of Even-Order Harmonics and Unipolar Leakage Flux in Consequent-Pole PM Machines by Employing N-S-Iron–S-N-Iron Rotor. IEEE Trans. Ind. Electron. 2019, 66, 1736–1747. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhu, Z.Q.; Liang, D.; Zhou, Y.; Liu, H.; Chen, L. Analysis and Reduction of Unipolar End Leakage Flux in Consequent-pole Vernier and Fractional Slot PM Machines. In Proceedings of the 2023 IEEE International Electric Machines & Drives Conference (IEMDC), San Francisco, CA, USA, 15–18 May 2023; pp. 1–7. [Google Scholar]
- Xu, H.; Zhu, Z.Q.; Zheng, Y.; Zhou, Y.; Chen, L.; Yang, L. Investigation of Unipolar End Flux Leakage in Dual-PM Consequent-Pole Vernier Machines. IEEE Trans. Transp. Electrif. 2025, 11, 2939–2951. [Google Scholar] [CrossRef]



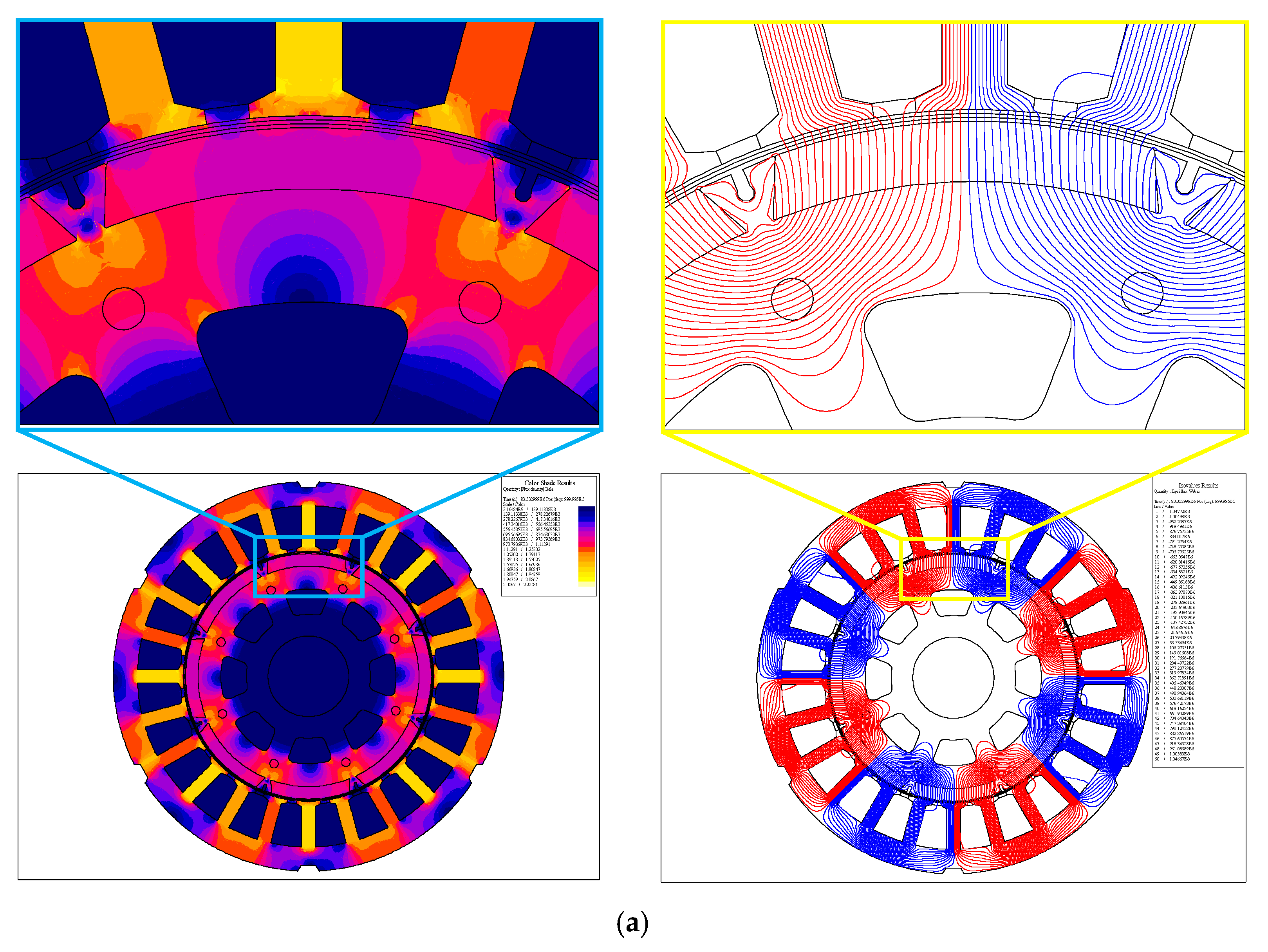

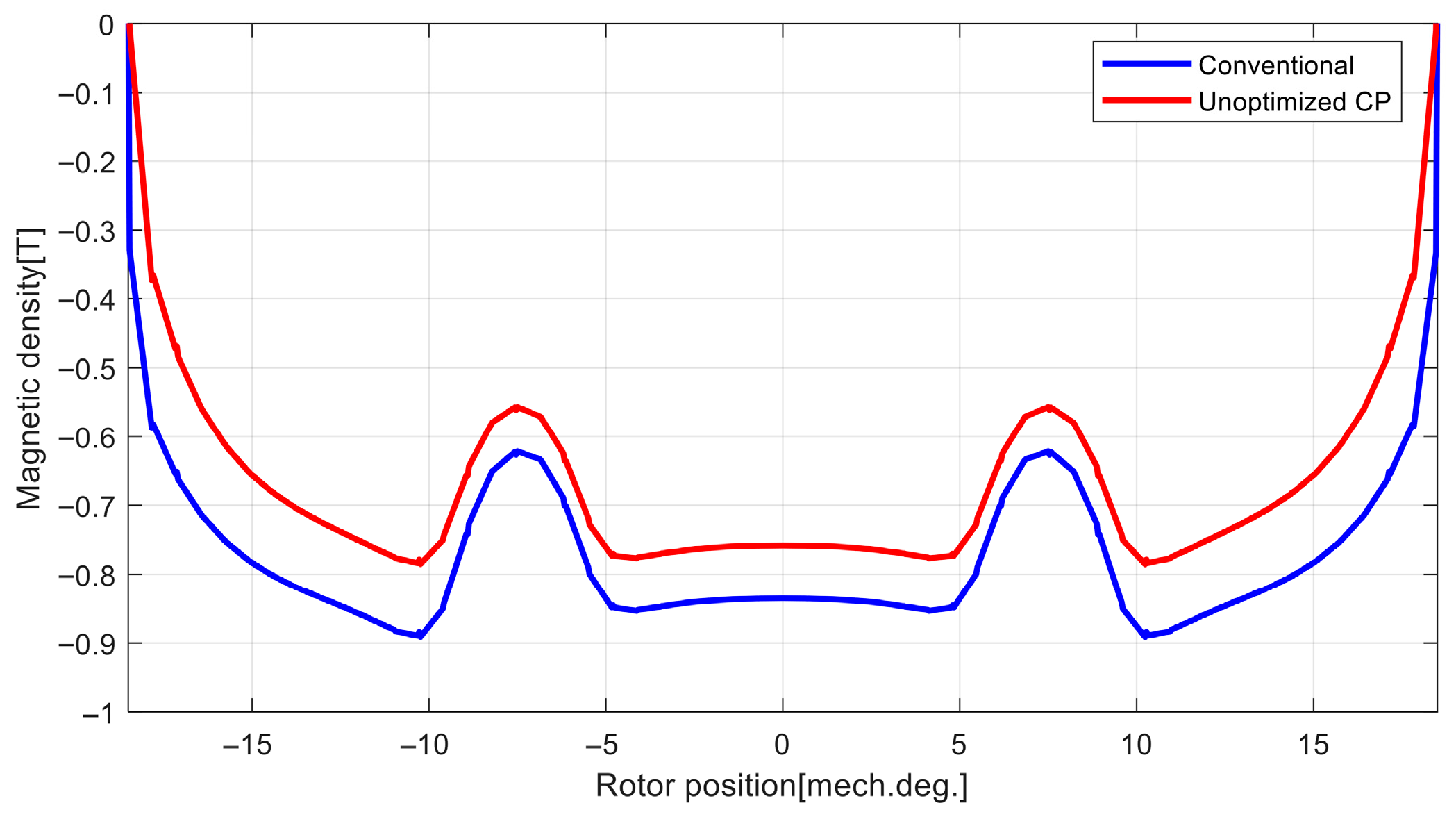
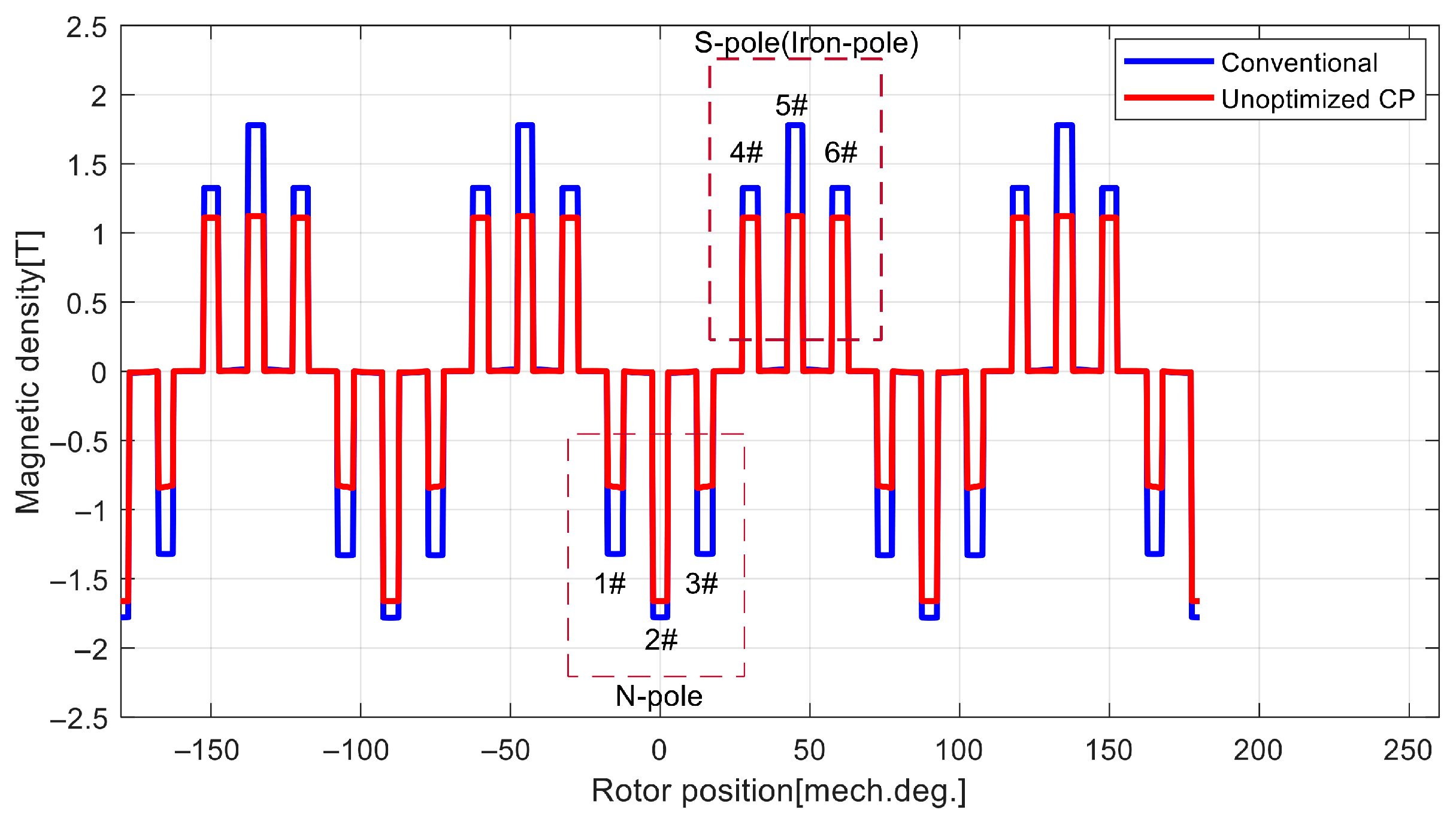

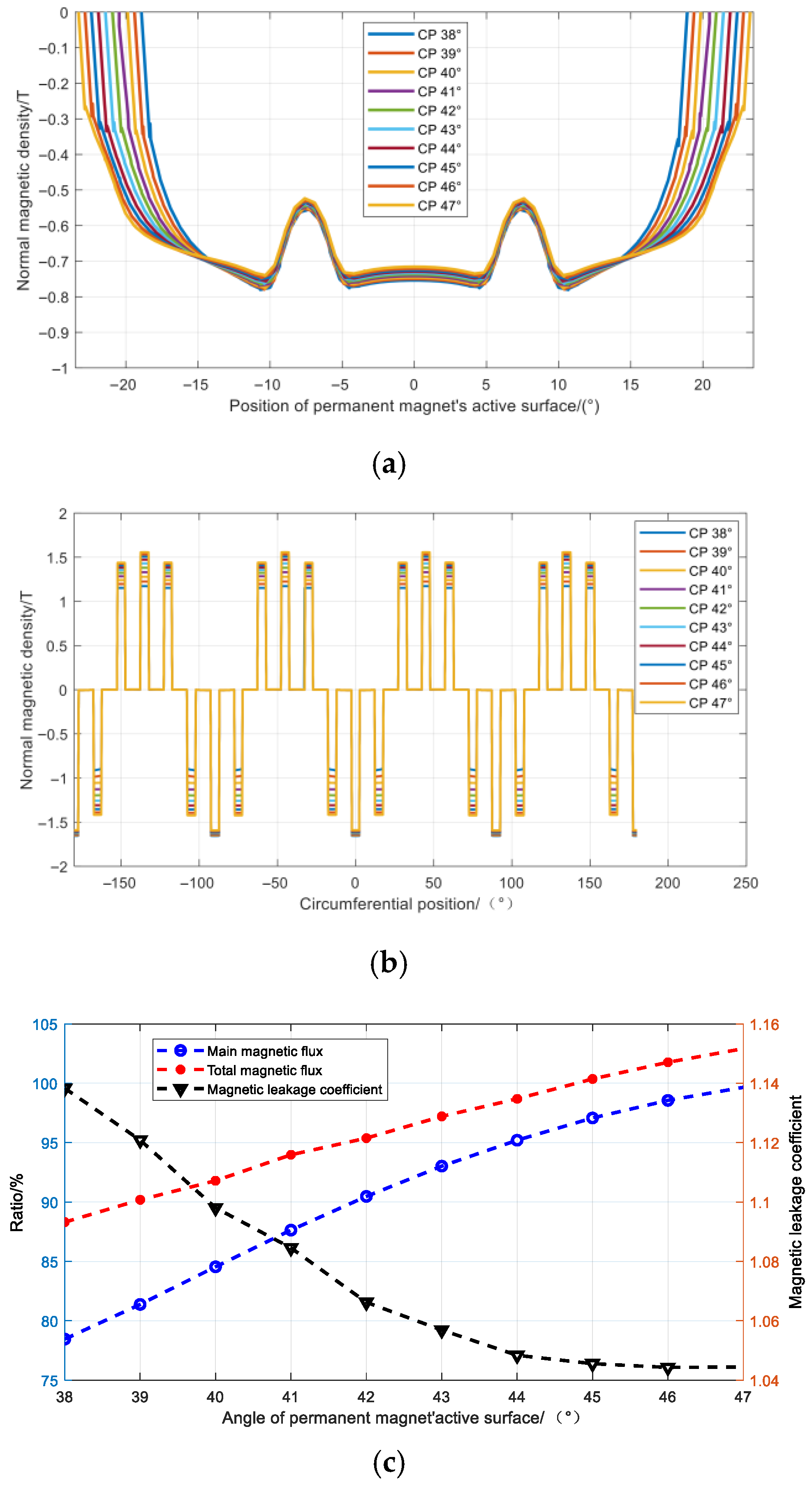
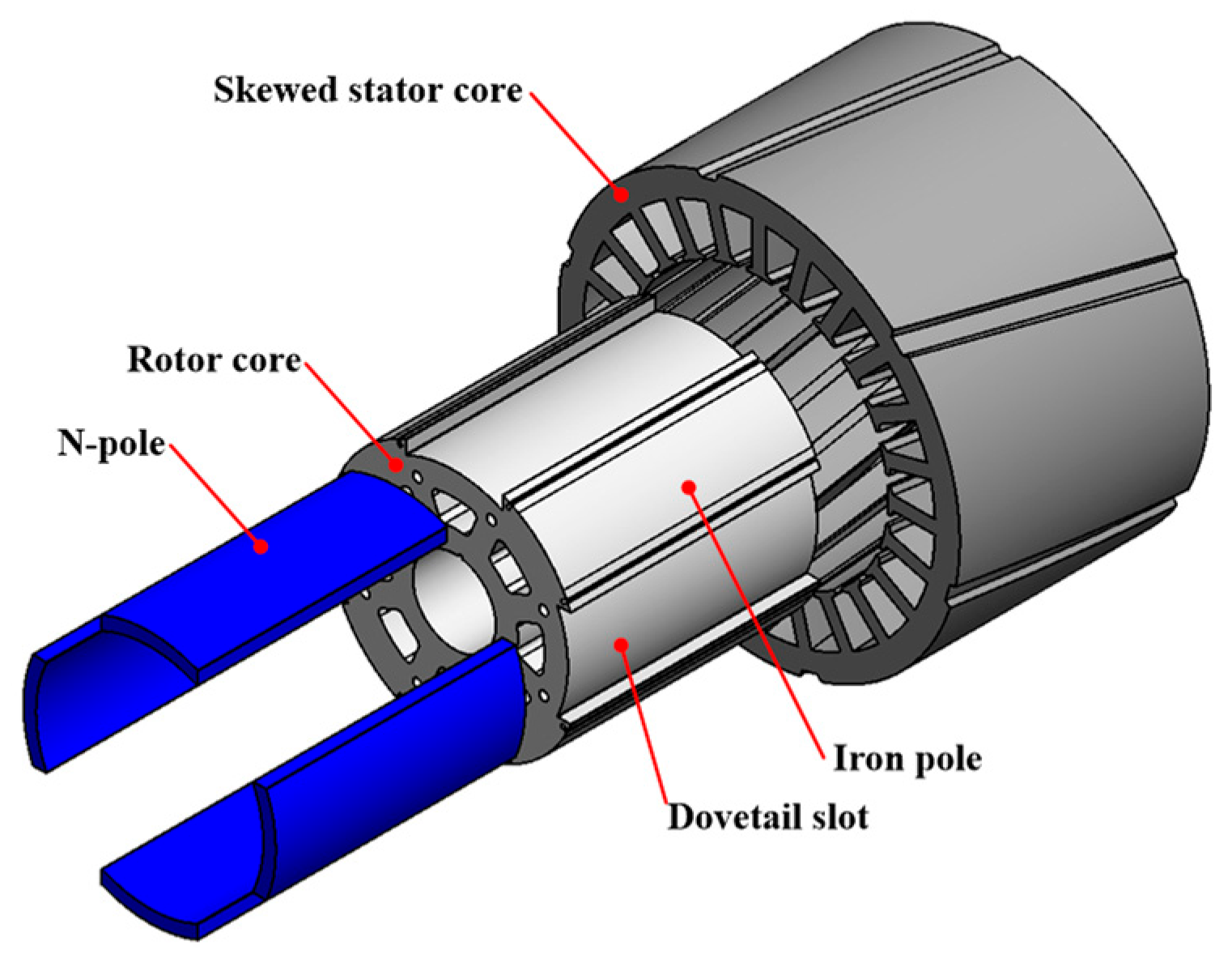

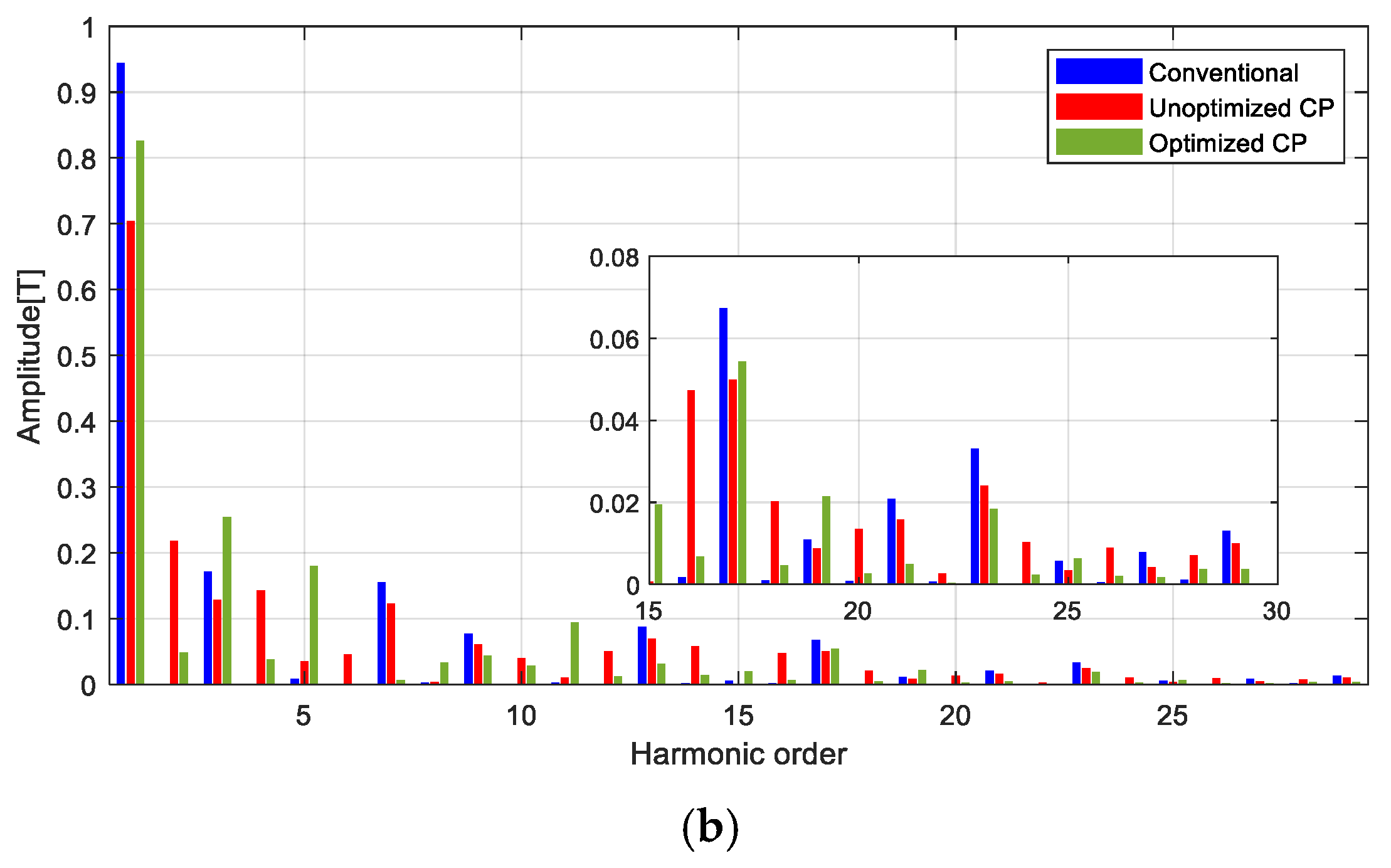
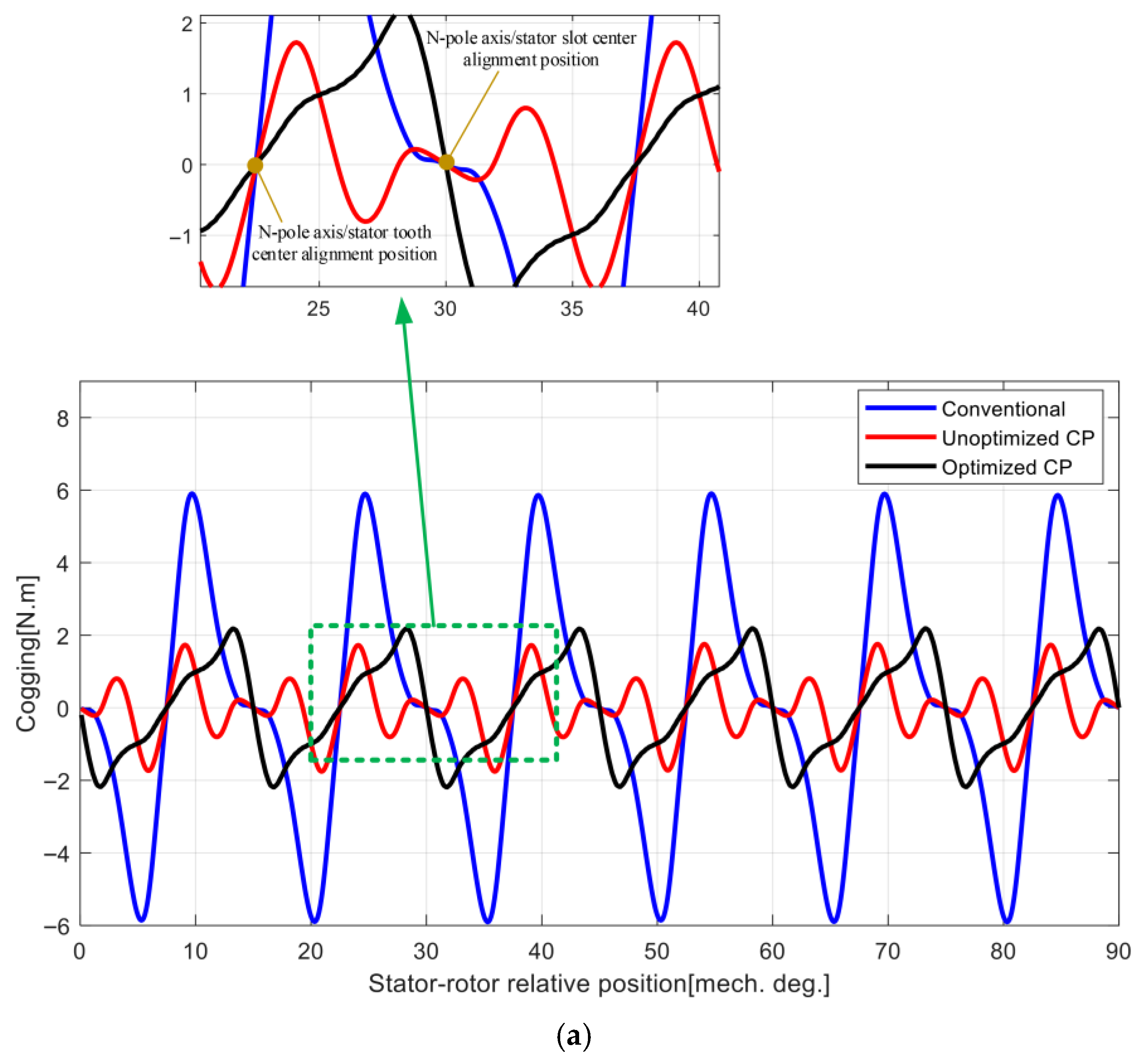
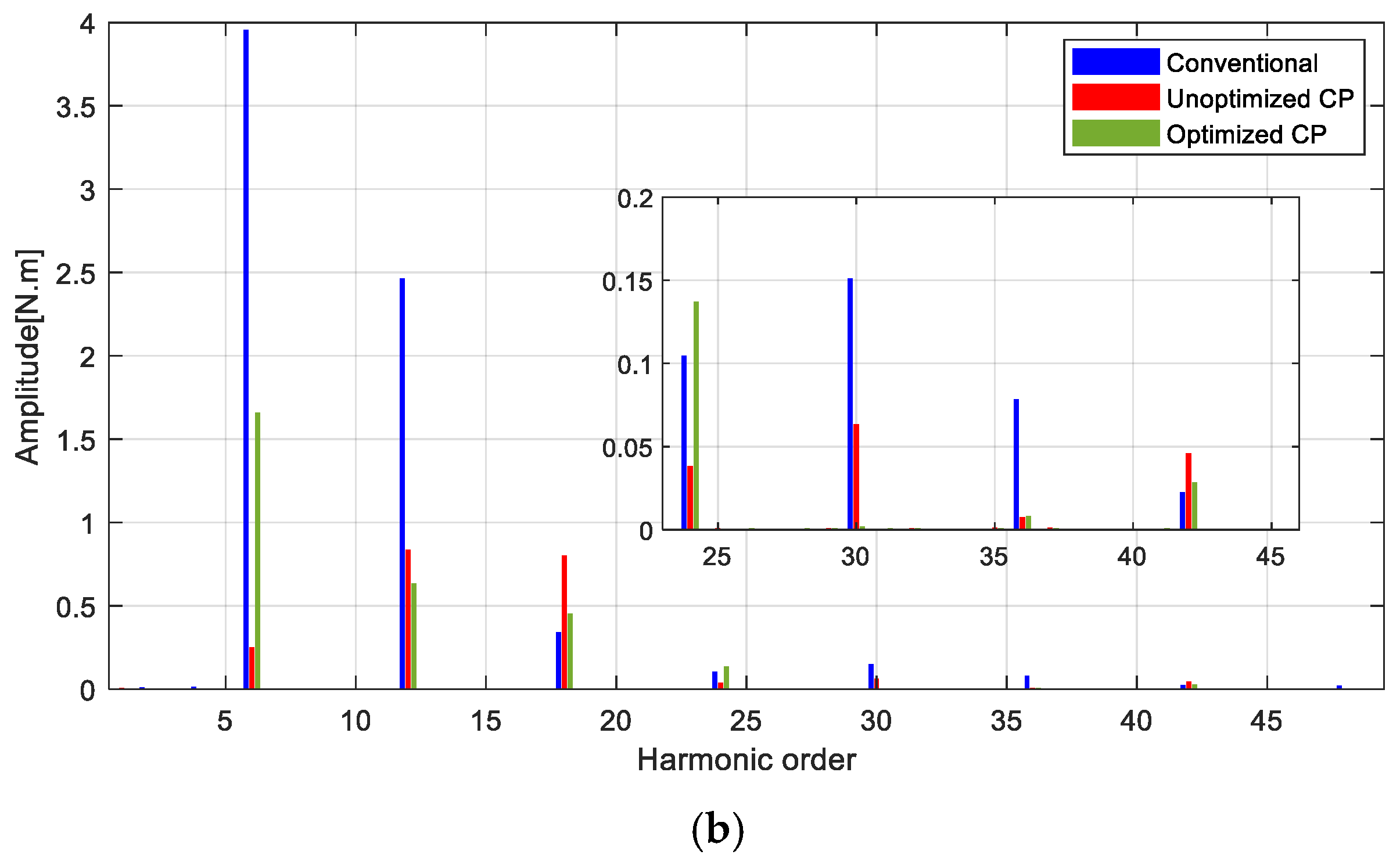




| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Number of stator slots | 24 | Active surface angle of PM/(°) | 37 |
| Number of rotor poles | 8 | Slot opening factor | 0.27 |
| Outer diameter of stator/mm | 145 | Number of series conductors per slot | 4 |
| Outer diameter of rotor/mm | 91.2 | Number of strands in parallel | 96 |
| Length of air gap/mm | 0.9 | Number of parallel paths | 1 |
| Thickness of PM/mm | 4.6 | Lamination steel grade | B50A600 |
| Stack length of iron core/mm | 90 | PM material grade | N35H |
| Number of Stator Teeth | 1# | 2# | 3# | 4# | 5# | 6# |
|---|---|---|---|---|---|---|
| Conventional | −1.330 T | −1.781 T | −1.330 T | 1.326 T | 1.778 T | 1.324 T |
| Unoptimized CP | −0.835 T | −1.662 T | −0.835 T | 1.110 T | 1.123 T | 1.110 T |
| Structure | PM Material (mm3) | Total Flux (Wb) | Main Flux (Wb) | Leakage Flux (Wb) | Leakage Coefficient |
|---|---|---|---|---|---|
| Conventional | 98,516 | 0.002048 | 0.002025 | 0.000023 | 1.0114 |
| Unoptimized CP | 49,258 | 0.001772 | 0.001523 | 0.000249 | 1.1638 |
| Parameter | Back-EMF Constant (V·Min·r−1) | Torque (N·m) | Torque Per Unit PM Volume (N·m·mm−3) |
|---|---|---|---|
| Conventional | 0.01889 | 14.14 | 1.435 × 10−4 |
| Unoptimized CP | 0.01482 | 11.18 | 2.270 × 10−4 |
| Parameter | Value |
|---|---|
| Volume of PM material (mm3) | 59,270 |
| Total flux (Wb) | 0.002055 |
| Main flux (Wb) | 0.001966 |
| Leakage flux (Wb) | 0.000089 |
| Leakage coefficient | 1.04555 |
| Back-EMF constant (V·min·r−1) | 0.01686 |
| Torque (N·m) | 12.47 |
| Torque per unit PM volume (N·m·mm−3) | 2.1039 × 10−4 |
| Material | Sintered NdFeB (kg) | Electrical Steel (kg) | Magnet Wire (kg) | Aluminum Alloy (kg) |
|---|---|---|---|---|
| Benchmark | 0.739 | 6.43 | 2.21 | 3.16 |
| Unoptimized CP | 0.445 | 7.08 | 2.21 | 3.16 |
| Material | Sintered NdFeB (CNY) | Electrical Steel (CNY) | Magnet Wire (CNY) | Aluminum Alloy (CNY) | Total (CNY) |
|---|---|---|---|---|---|
| Benchmark | 154.45 | 29.26 | 176.80 | 65.91 | 426.42 |
| Unoptimized CP | 93.00 | 32.21 | 176.80 | 65.91 | 367.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Saeed, M.S.; Fu, Z.; Liu, J.; Wu, X.; Wang, Q. Magnetic Circuit Analysis and Design Optimized for Cost-Effectiveness of Surface-Inserted Rare Earth Consequent-Pole Permanent Magnet Machines. Machines 2025, 13, 873. https://doi.org/10.3390/machines13090873
Wang L, Saeed MS, Fu Z, Liu J, Wu X, Wang Q. Magnetic Circuit Analysis and Design Optimized for Cost-Effectiveness of Surface-Inserted Rare Earth Consequent-Pole Permanent Magnet Machines. Machines. 2025; 13(9):873. https://doi.org/10.3390/machines13090873
Chicago/Turabian StyleWang, Li, Muhammad Saqlain Saeed, Zhaoyang Fu, Jinglin Liu, Xiqiao Wu, and Qi Wang. 2025. "Magnetic Circuit Analysis and Design Optimized for Cost-Effectiveness of Surface-Inserted Rare Earth Consequent-Pole Permanent Magnet Machines" Machines 13, no. 9: 873. https://doi.org/10.3390/machines13090873
APA StyleWang, L., Saeed, M. S., Fu, Z., Liu, J., Wu, X., & Wang, Q. (2025). Magnetic Circuit Analysis and Design Optimized for Cost-Effectiveness of Surface-Inserted Rare Earth Consequent-Pole Permanent Magnet Machines. Machines, 13(9), 873. https://doi.org/10.3390/machines13090873








