Remaining Secondary Voltage Mitigation in Multivector Model Predictive Control Schemes for Multiphase Electric Drives
Abstract
1. Introduction
- The inclusion of closed-loop regulation in the secondary subspaces improves current quality when the selected set of virtual vectors generates residual voltages in these planes. This control technique explicitly fills a gap in prior studies such as [36], where the contributions of these vectors to the plane were considered negligible.
- The capability of the proposed method to enhance drive performance is demonstrated both under regular operating conditions and in the presence of resistance dissymmetries.
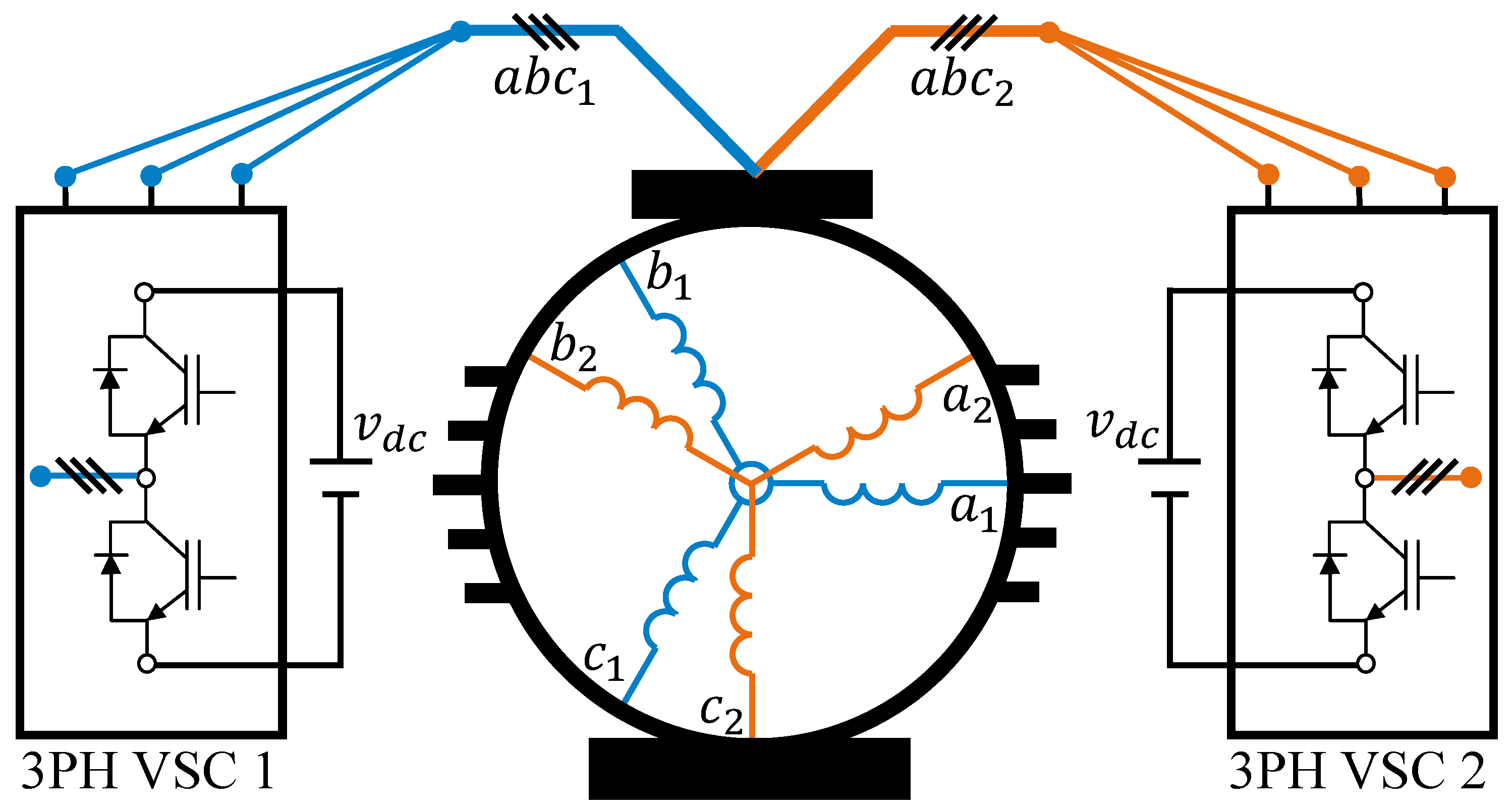
2. Six-Phase Induction Machine Topology
3. MPC Fundamentals
3.1. Standard MPC
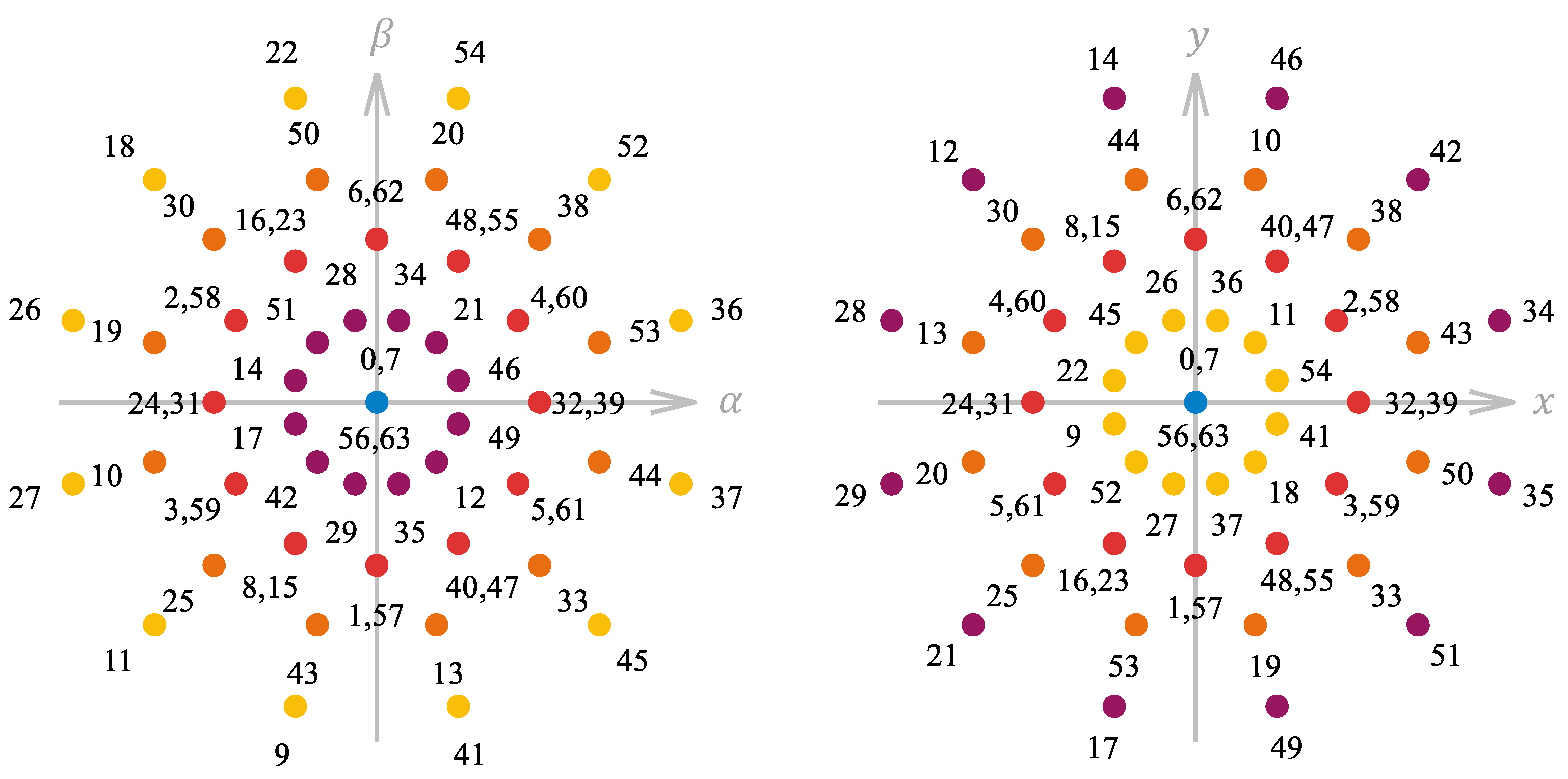
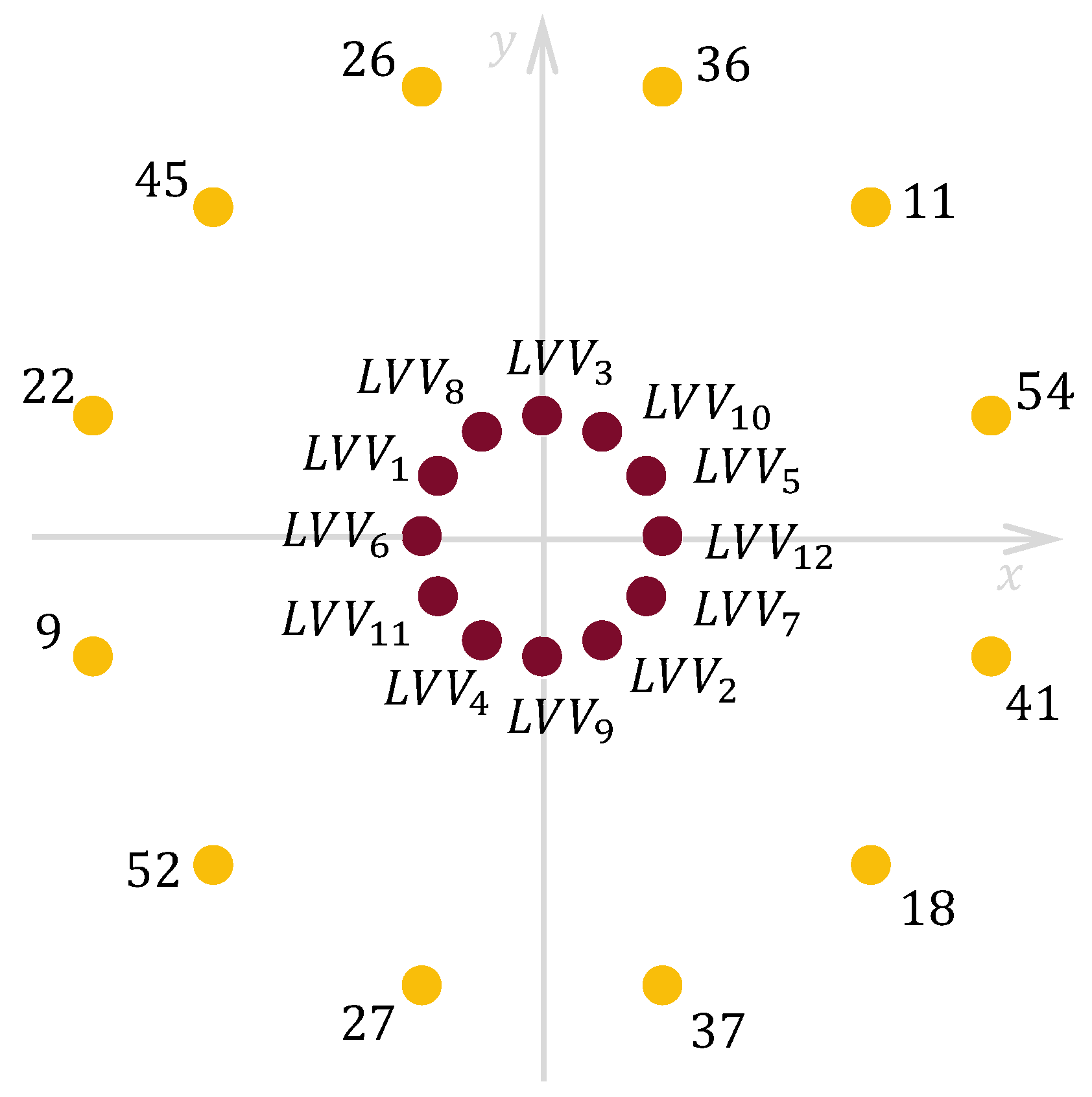
3.2. Multivector Schemes
4. The Effect of Secondary Current Control on the ED Performance
4.1. Open-Loop Control of the Currents
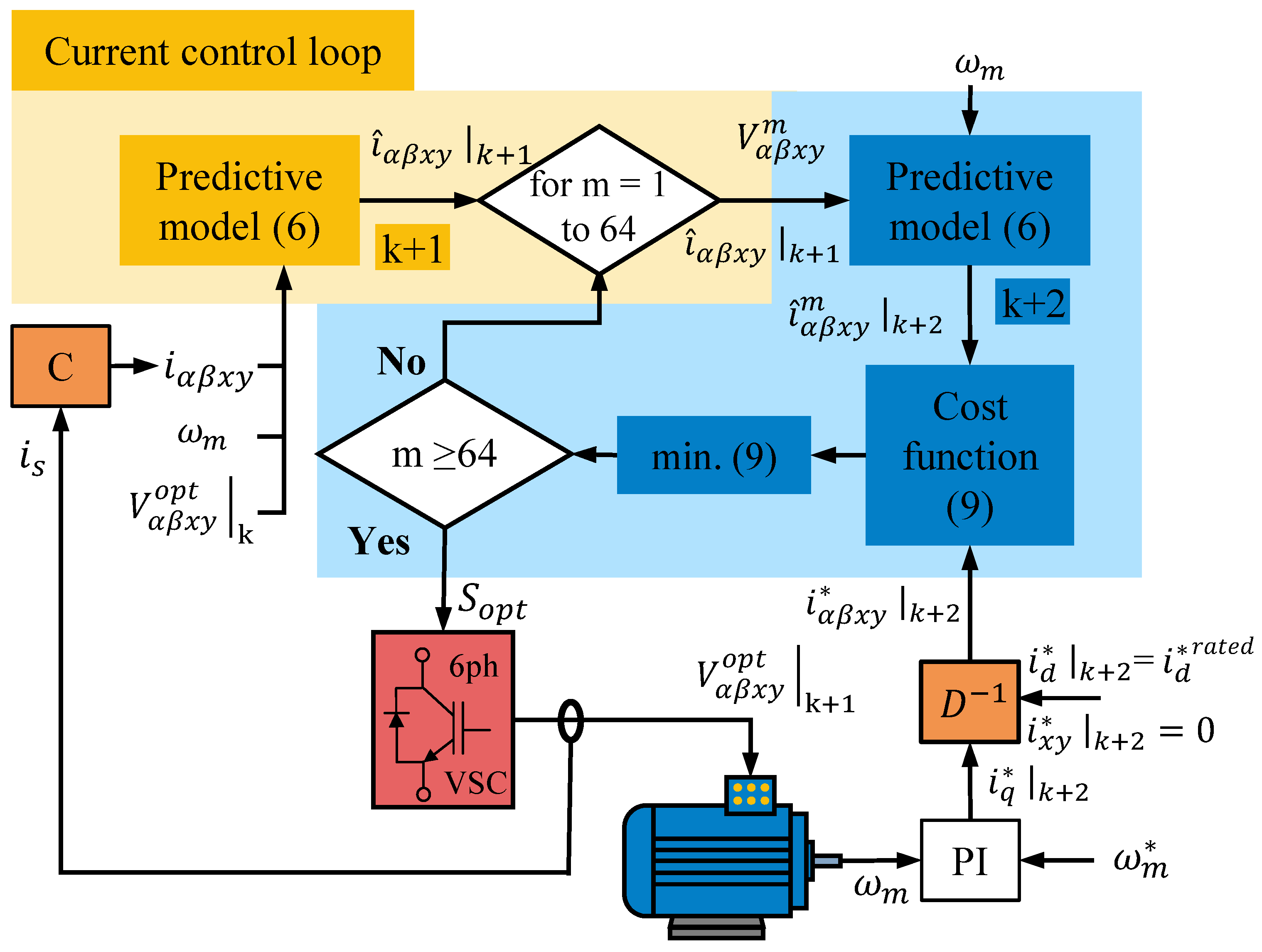
4.2. Proposed Control Scheme
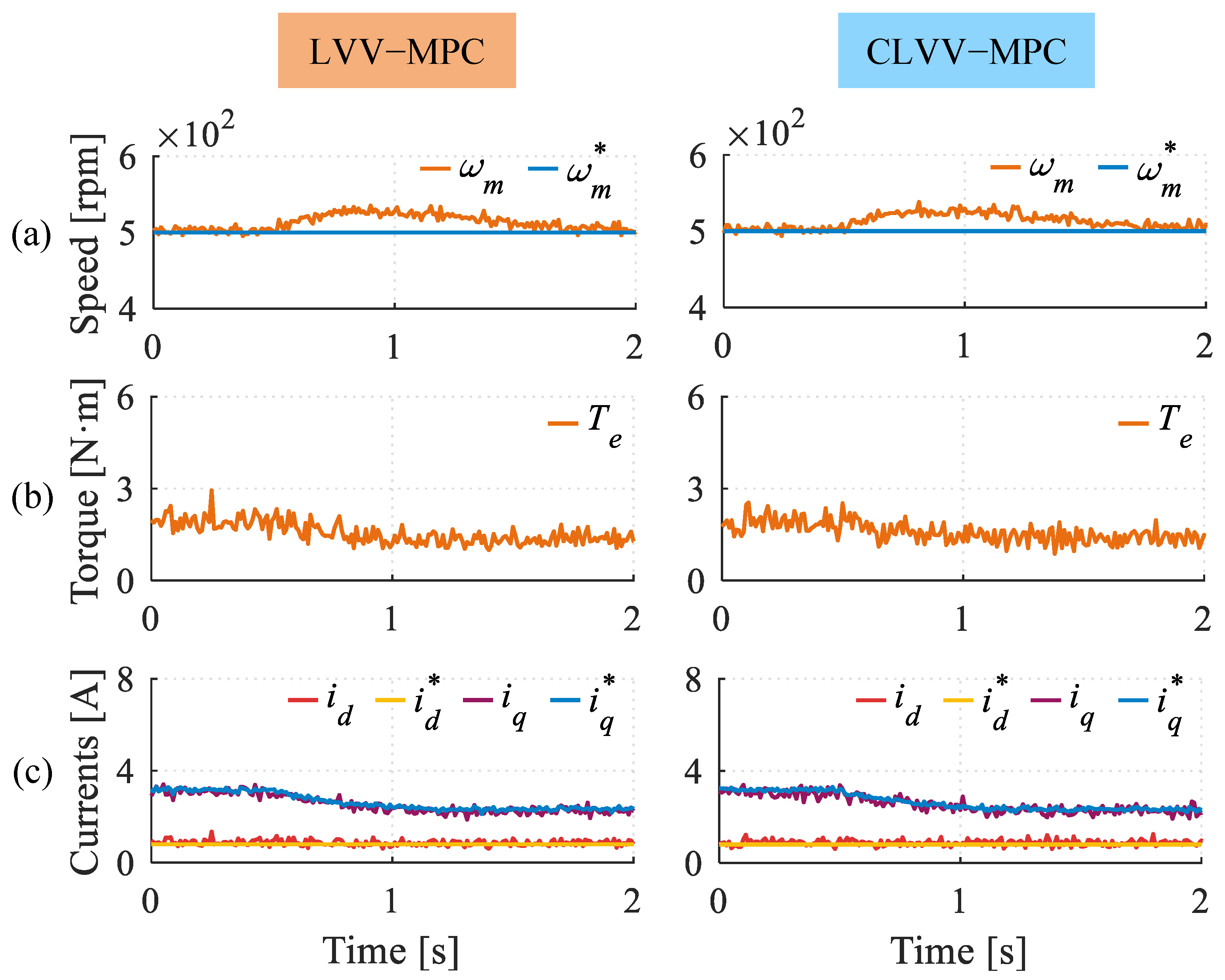
5. Experimental Results
5.1. Test Bench
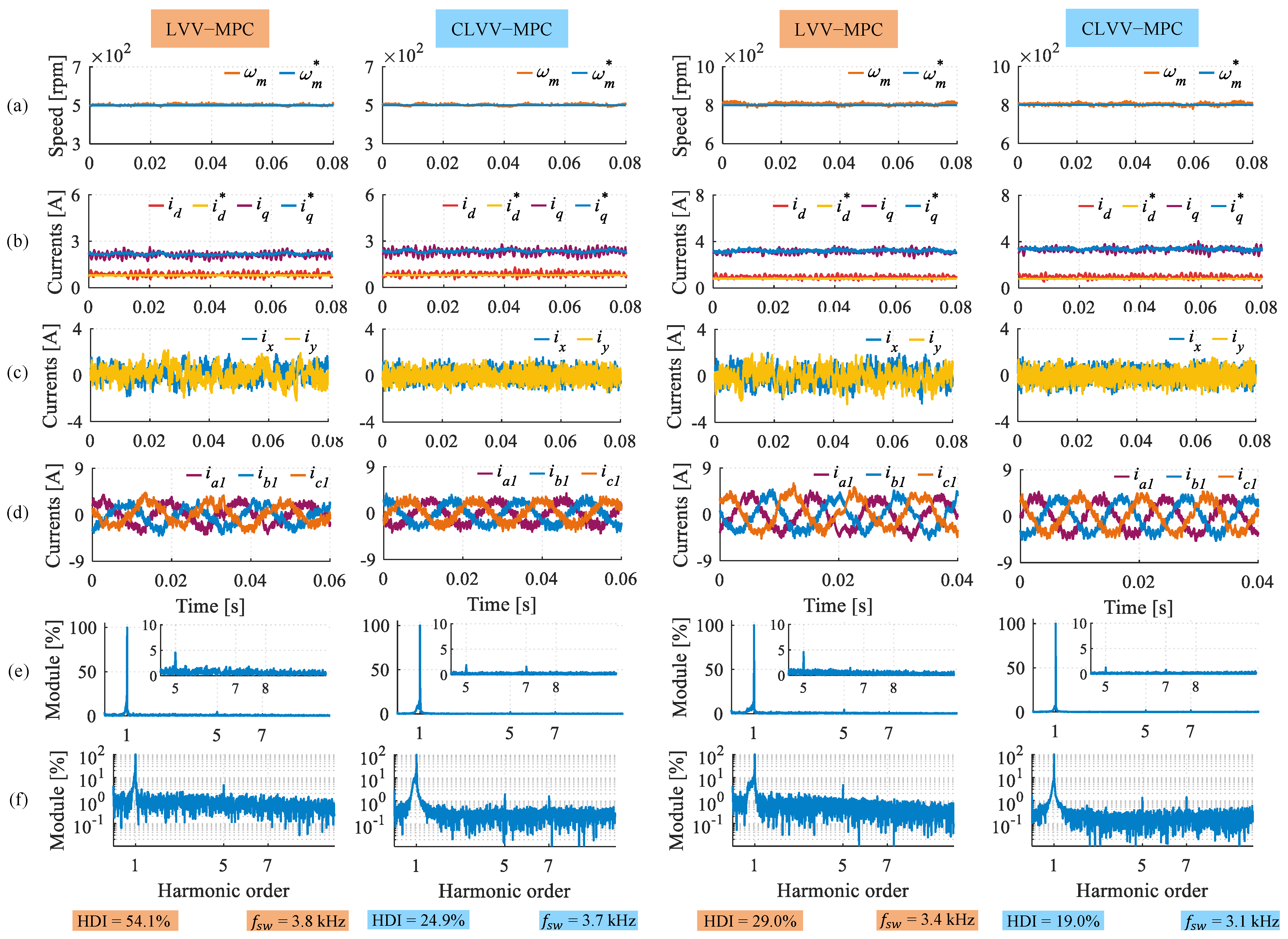
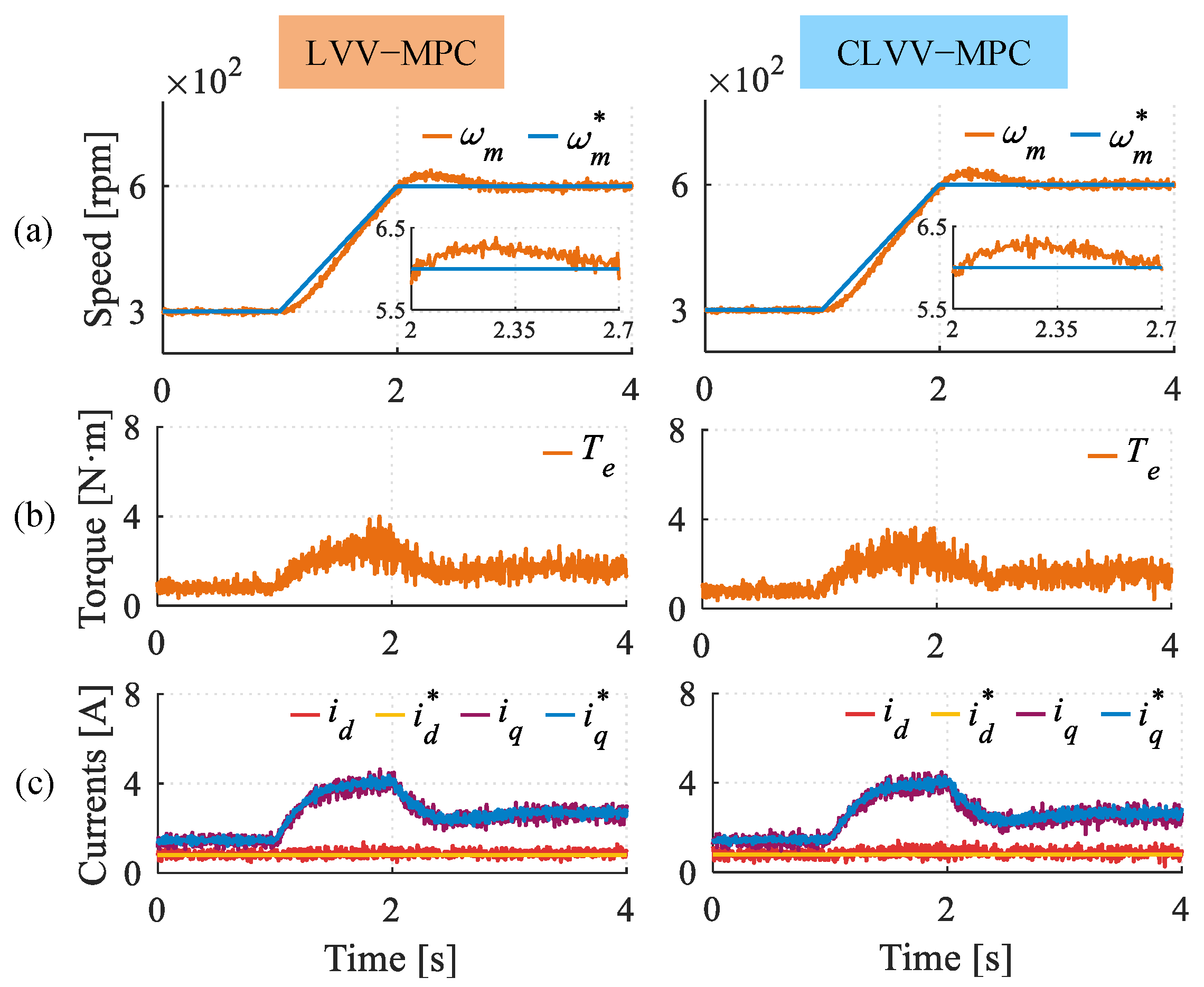
5.2. Comparative Evaluation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 6ph-IM | Six-phase induction machine. |
| CLVV-MPC | Closed-loop large virtual vector model predictive control. |
| CMV | Common-mode voltage vector. |
| ED | Electric drive. |
| FCS-MPC | Finite-control set model predictive control. |
| FFT | Fast Fourier transform. |
| FOC | Field-oriented control. |
| HDI | Harmonic distortion index. |
| THD | Total harmonic Distortion. |
| VSC | Voltage source converter. |
| VSD | Vector space decomposition. |
| VVV | Virtual voltage vector. |
References
- Frikha, M.A.; Croonen, J.; Deepak, K.; Benômar, Y.; El Baghdadi, M.; Hegazy, O. Multiphase Motors and Drive Systems for Electric Vehicle Powertrains: State of the Art Analysis and Future Trends. Energies 2023, 16, 768. [Google Scholar] [CrossRef]
- Mercedes AMG EQS 53. Available online: https://mercedes-benz-media.co.uk/releases/1618 (accessed on 16 September 2025).
- BMW iX M60. Available online: https://www.motortrend.com/news/2023-bmw-ix-m60-xdrive50-edrive-electric-motors-explained (accessed on 16 September 2025).
- Xue, Z.; Niu, S.; Chau, A.M.H.; Luo, Y.; Lin, H.; Li, X. Recent Advances in Multi-Phase Electric Drives Model Predictive Control in Renewable Energy Application: A State-of-the-Art Review. World Electr. Veh. J. 2023, 14, 44. [Google Scholar] [CrossRef]
- Andresen, B.; Birk, J. A high power density converter system for the Gamesa G10x 4,5 MW wind turbine. In Proceedings of the 2007 European Conference on Power Electronics and Applications, Aalborg, Denmark, 2–5 September 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Alvarez, P.; Satrústegui, M.; Elósegui, I.; Martinez-Iturralde, M. Review of High Power and High Voltage Electric Motors for Single-Aisle Regional Aircraft. IEEE Access 2022, 10, 112989–113004. [Google Scholar] [CrossRef]
- Zeroavia EPS. Available online: https://zeroavia.com/electric-propulsion/ (accessed on 16 September 2025).
- Levi, E.; Bojoi, R.; Profumo, F.; Toliyat, H.; Williamson, S. Multiphase induction motor drives—A technology status review. IET Electr. Power Appl. 2007, 1, 489–516. [Google Scholar] [CrossRef]
- Levi, E. Advances in Converter Control and Innovative Exploitation of Additional Degrees of Freedom for Multiphase Machines. IEEE Trans. Ind. Electron. 2016, 63, 433–448. [Google Scholar] [CrossRef]
- Yang, G.; Hussain, H.; Li, S.; Zhang, X.; Yang, J.; Lee, C.H.T. Design and Analysis of Universal Natural Fault-Tolerant SVPWM Strategy with Simplified Fault Diagnosis for Multiphase Motor Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 4340–4354. [Google Scholar] [CrossRef]
- Jung, E.; Yoo, H.; Sul, S.K.; Choi, H.S.; Choi, Y.Y. A Nine-Phase Permanent-Magnet Motor Drive System for an Ultrahigh-Speed Elevator. IEEE Trans. Ind. Appl. 2012, 48, 987–995. [Google Scholar] [CrossRef]
- Zhang, M.; Yuan, M.; Jiang, J. A Comprehensive Review of the Multiphase Motor Drive Topologies for High-Power Electric Vehicle: Current Status, Research Challenges, and Future Trends. IEEE Trans. Transp. Electrif. 2025, 11, 3631–3654. [Google Scholar] [CrossRef]
- Levi, E. Multiphase Electric Machines for Variable-Speed Applications. IEEE Trans. Ind. Electron. 2008, 55, 1893–1909. [Google Scholar] [CrossRef]
- Furmanik, M.; Gorel, L.; Konvičný, D.; Rafajdus, P. Comparative Study and Overview of Field-Oriented Control Techniques for Six-Phase PMSMs. Appl. Sci. 2021, 11, 7841. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Zheng, Z. A review of drive techniques for multiphase machines. CES Trans. Electr. Mach. Syst. 2018, 2, 243–251. [Google Scholar] [CrossRef]
- Bermúdez, M.; Barrero, F.; Martín, C.; Perales, M. Performance Analysis of Direct Torque Controllers in Five-Phase Electrical Drives. Appl. Sci. 2021, 11, 11964. [Google Scholar] [CrossRef]
- Rodriguez, J.; Garcia, C.; Mora, A.; Flores-Bahamonde, F.; Acuna, P.; Novak, M.; Zhang, Y.; Tarisciotti, L.; Davari, S.A.; Zhang, Z.; et al. Latest Advances of Model Predictive Control in Electrical Drives—Part I: Basic Concepts and Advanced Strategies. IEEE Trans. Power Electron. 2022, 37, 3927–3942. [Google Scholar] [CrossRef]
- Rodriguez, J.; Garcia, C.; Mora, A.; Davari, S.A.; Rodas, J.; Valencia, D.F.; Elmorshedy, M.; Wang, F.; Zuo, K.; Tarisciotti, L.; et al. Latest Advances of Model Predictive Control in Electrical Drives—Part II: Applications and Benchmarking with Classical Control Methods. IEEE Trans. Power Electron. 2022, 37, 5047–5061. [Google Scholar] [CrossRef]
- Singh, G.K.; Nam, K.; Lim, S.K. A simple indirect field-oriented control scheme for multiphase induction machine. IEEE Trans. Ind. Electron. 2005, 52, 1177–1184. [Google Scholar] [CrossRef]
- Che, H.S.; Levi, E.; Jones, M.; Hew, W.P.; Rahim, N.A. Current Control Methods for an Asymmetrical Six-Phase Induction Motor Drive. IEEE Trans. Power Electron. 2014, 29, 407–417. [Google Scholar] [CrossRef]
- Lopez, O.; Álvarez, J.; Malvar, J.; Yepes, A.G.; Vidal, A.; Baneira, F.; Pérez-Estévez, D.; Freijedo, F.D.; Doval-Gandoy, J. Space-Vector PWM with Common-Mode Voltage Elimination for Multiphase Drives. IEEE Trans. Power Electron. 2016, 31, 8151–8161. [Google Scholar] [CrossRef]
- Ayala, M.; Doval-Gandoy, J.; Rodas, J.; Gonzalez, O.; Gregor, R.; Rivera, M. A Novel Modulated Model Predictive Control Applied to Six-Phase Induction Motor Drives. IEEE Trans. Ind. Electron. 2021, 68, 3672–3682. [Google Scholar] [CrossRef]
- Aciego, J.J.; Gonzalez-Prieto, I.; Duran, M.J.; Gonzalez-Prieto, A.; Carrillo-Rios, J. Guiding the Selection of Multi-Vector Model Predictive Control Techniques for Multiphase Drives. Machines 2024, 12, 115. [Google Scholar] [CrossRef]
- Wang, W.; Fan, Y.; Chen, S.; Zhang, Q. Finite control set model predictive current control of a five-phase PMSM with virtual voltage vectors and adaptive control set. CES Trans. Electr. Mach. Syst. 2018, 2, 136–141. [Google Scholar] [CrossRef]
- da Paz, G.F.; Melo, V.F.M.B.; de Freitas, I.S.; de Sousa, R.P.R.; Salvadori, F. Virtual Vector Direct Torque Control for a Nine-Phase Induction Machine Drive System with Eight Active Voltage Vectors Emulating Virtual Voltage Vectors. IEEE Trans. Power Electron. 2024, 39, 9457–9469. [Google Scholar] [CrossRef]
- Rodas, J.; Gonzalez, O.; Maidana, P.; Medina, C.; Doval-Gandoy, J.; Norambuena, M.; Ayala, M.; Rodriguez, J. Sequential Model Predictive Torque Control for Six-Phase Machines Without Weighting Factors. IEEE Open J. Power Electron. 2025, 6, 802–810. [Google Scholar] [CrossRef]
- Huang, L.; Ji, J.; Zhao, W.; Tao, T.; Cui, J. Duty-Ratio-Based Direct Torque Control with Enhanced Harmonic Current Suppression for Dual-Three-Phase Permanent Magnet Motor. IEEE Trans. Power Electron. 2022, 37, 11098–11108. [Google Scholar] [CrossRef]
- Gonçalves, P.; Cruz, S.; Mendes, A. Finite Control Set Model Predictive Control of Six-Phase Asymmetrical Machines—An Overview. Energies 2019, 12, 4693. [Google Scholar] [CrossRef]
- Duran, M.J.; Gonzalez-Prieto, I.; Gonzalez-Prieto, A.; Aciego, J.J. The Evolution of Model Predictive Control in Multiphase Electric Drives: A Growing Field of Research. IEEE Ind. Electron. Mag. 2022, 16, 29–39. [Google Scholar] [CrossRef]
- Kouro, S.; Perez, M.A.; Rodriguez, J.; Llor, A.M.; Young, H.A. Model Predictive Control: MPC’s Role in the Evolution of Power Electron. IEEE Ind. Electron. Mag. 2015, 9, 8–21. [Google Scholar] [CrossRef]
- Arahal, M.; Satué, M.; Barrero, F. Multi-phase weighted stator current tracking using a hyper-plane partition of the control set. Control Eng. Pract. 2024, 153, 106114. [Google Scholar] [CrossRef]
- Ayala, M.; Doval-Gandoy, J.; Rodas, J.; Gonzalez, O.; Gregor, R. Current control designed with model based predictive control for six-phase motor drives. ISA Trans. 2020, 98, 496–504. [Google Scholar] [CrossRef] [PubMed]
- Arahal, M.R.; Satué, M.G.; Barrero, F.; Ortega, M.G. Adaptive Cost Function FCSMPC for 6-Phase IMs. Energies 2021, 14, 5222. [Google Scholar] [CrossRef]
- Abbaszadeh, A.; Khaburi, D.A.; Mahmoudi, H.; Rodríguez, J. Simplified model predictive control with variable weighting factor for current ripple reduction. IET Power Electron. 2017, 10, 1165–1174. [Google Scholar] [CrossRef]
- Bhowate, A.; Aware, M.; Sharma, S.; Tatte, Y. Predictive Torque Control for Five Phase Induction Motor Drive with Common Mode Voltage Reduction. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018-ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 1730–1735. [Google Scholar] [CrossRef]
- Durán, M.J.; Gonzalez-Prieto, I.; Gonzalez-Prieto, A. Large virtual voltage vectors for direct controllers in six-phase electric drives. Int. J. Electr. Power Energy Syst. 2021, 125, 106425. [Google Scholar] [CrossRef]
- Garcia-Entrambasaguas, P.; Zoric, I.; González-Prieto, I.; Duran, M.J.; Levi, E. Direct Torque and Predictive Control Strategies in Nine-Phase Electric Drives Using Virtual Voltage Vectors. IEEE Trans. Power Electron. 2019, 34, 12106–12119. [Google Scholar] [CrossRef]
- Gonzalez-Prieto, I.; Duran, M.J.; Aciego, J.J.; Martin, C.; Barrero, F. Model Predictive Control of Six-Phase Induction Motor Drives Using Virtual Voltage Vectors. IEEE Trans. Ind. Electron. 2018, 65, 27–37. [Google Scholar]
- González-Prieto, A.; González-Prieto, I.; Duran, M.J.; Aciego, J.J.; Salas-Biedma, P. Current Harmonic Mitigation Using a Multi-Vector Solution for MPC in Six-Phase Electric Drives. IEEE Access 2021, 9, 117761–117771. [Google Scholar] [CrossRef]
- Serra, J.; Bento, F.; Ma, A.J.M. Zero-Sequence Current Mitigation Using a Virtual Voltage Vector Solution for MPC in Symmetrical Six-Phase Electric Drives with Single-Star and Hexagon Winding Configurations. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 1601–1614. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, Y.; Ran, Y.; Wei, H.; Cui, J. Dual Three-Phase Permanent Magnet Multi-Plane Harmonic Closed-Loop Control. In Proceedings of the 2024 5th International Conference on Clean Energy and Electric Power Engineering (ICCEPE), Yangzhou, China, 9–11 August 2024; pp. 1068–1072. [Google Scholar] [CrossRef]
- Yan, L.; Zhang, X.; Yang, J.; Yang, G.; Deng, R. Synthetic Vectors-Based Predictive Control of Dual Three-Phase PMSMs for Current Harmonics Mitigation Considering Average Deception Effect. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 3103–3114. [Google Scholar] [CrossRef]
- Gonçalves, P.F.; Cruz, S.M.; Mendes, A.M. Bi-subspace predictive current control of six-phase PMSM drives based on virtual vectors with optimal amplitude. IET Electr. Power App. 2019, 13, 1672–1683. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, J.; Yan, S.; Xiong, Y.; Ma, Y.; Chen, H. Virtual Voltage Vector-Based Model Predictive Current Control for Five-Phase Induction Motor. Processes 2022, 10, 1925. [Google Scholar] [CrossRef]
- Yin, R.; Yang, J. Predictive current control for seven-phase induction motor based on the optimal operating time of four-dimensional vector. IET Electr. Power Appl. 2019, 13, 1684–1695. [Google Scholar] [CrossRef]
- Cui, J.; Kang, M.; Tao, T.; Zhao, W. Harmonics Suppression for Dual Three-Phase Permanent Magnet motor with Multi-Subspace Model Predictive Control. In Proceedings of the 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 12–14 May 2023; pp. 4364–4369. [Google Scholar]
- Aciego, J.J.; González Prieto, I.; Duran, M.J. Model Predictive Control of Six-Phase Induction Motor Drives Using Two Virtual Voltage Vectors. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 321–330. [Google Scholar] [CrossRef]
- Gonzalez, O.; Ayala, M.; Romero, C.; Delorme, L.; Rodas, J.; Gregor, R.; Gonzalez-Prieto, I.; Duran, M.J. Model Predictive Current Control of Six-Phase Induction Motor Drives Using Virtual Vectors and Space Vector Modulation. IEEE Trans. Power Electron. 2022, 37, 7617–7628. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, C. Elimination of Harmonic Currents Using a Reference Voltage Vector Based-Model Predictive Control for a Six-Phase PMSM Motor. IEEE Trans. Power Electron. 2019, 34, 6960–6972. [Google Scholar] [CrossRef]
- Pandit, J.K.; Aware, M.V.; Nemade, R.; Tatte, Y. Simplified Implementation of Synthetic Vectors for DTC of Asymmetric Six-Phase Induction Motor Drives. IEEE Trans. Ind. Appl. 2018, 54, 2306–2318. [Google Scholar] [CrossRef]
- Aciego, J.J.; González Prieto, I.; Duran, M.J.; Bermudez, M.; Salas-Biedma, P. Model Predictive Control Based on Dynamic Voltage Vectors for Six-Phase Induction Machines. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 2710–2722. [Google Scholar] [CrossRef]
- Zhao, Y.; Lipo, T. Space vector PWM control of dual three phase induction machine using vector space decomposition. In Proceedings of the 1994 IEEE Industry Applications Society Annual Meeting, Denver, CO, USA, 2–6 October 1994; Volume 1, pp. 742–749. [Google Scholar]
- Park, R.H. Two-reaction theory of synchronous machines generalized method of analysis—Part I. Trans. Am. Inst. Electr. Eng. 1929, 48, 716–727. [Google Scholar] [CrossRef]
- Karamanakos, P.; Liegmann, E.; Geyer, T.; Kennel, R. Model Predictive Control of Power Electronic Systems: Methods, Results, and Challenges. IEEE Open J. Ind. App. 2020, 1, 95–114. [Google Scholar] [CrossRef]
- Hadiouche, D.; Baghli, L.; Rezzoug, A. Space-vector PWM techniques for dual three-phase AC machine: Analysis, performance evaluation, and DSP implementation. IEEE Trans. Ind. Appl. 2006, 42, 1112–1122. [Google Scholar] [CrossRef]
- Yepes, A.G.; Riveros, J.A.; Doval-Gandoy, J.; Barrero, F.; Lopez, O.; Bogado, B.; Jones, M.; Levi, E. Parameter Identification of Multiphase Induction Machines with Distributed Windings—Part 1: Sinusoidal Excitation Methods. IEEE Trans. Energy Convers. 2012, 27, 1056–1066. [Google Scholar] [CrossRef]
- Riveros, J.A.; Yepes, A.G.; Barrero, F.; Doval-Gandoy, J.; Bogado, B.; Lopez, O.; Jones, M.; Levi, E. Parameter Identification of Multiphase Induction Machines with Distributed Windings—Part 2: Time-Domain Techniques. IEEE Trans. Energy Convers. 2012, 27, 1067–1077. [Google Scholar] [CrossRef]
- Yepes, A.G.; Doval-Gandoy, J.; Toliyat, H. Multifrequency Current Control for Multiphase Machines with Antiwindup, Distortion-Free Saturation and Full DC-Link Utilization. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 776–783. [Google Scholar]
- IEEE Std 519-2022 (Revision of IEEE Std 519-2014); IEEE Standard for Harmonic Control in Electric Power Systems. IEEE: Piscataway, NJ, USA, 2022; pp. 1–31. [CrossRef]
- Yepes, A.G.; Abdel-Azim, W.E.; Shawier, A.; Abdel-Majeed, M.S.; Che, H.S.; Abdel-Khalik, A.S.; Ahmed, S.; Doval-Gandoy, J. Online Control Strategy for Tolerating Resistance Asymmetry with Minimum Copper Loss in the Full Torque Range for Symmetrical Six-Phase AC Drives. IEEE Trans. Power Electron. 2023, 38, 151–164. [Google Scholar] [CrossRef]
- Hu, R.; Wang, J.; Mills, A.R.; Chong, E.; Sun, Z. Detection and Classification of Turn Fault and High Resistance Connection Fault in Permanent Magnet Machines Based on Zero Sequence Voltage. IEEE Trans. Power Electron. 2020, 35, 1922–1933. [Google Scholar] [CrossRef]
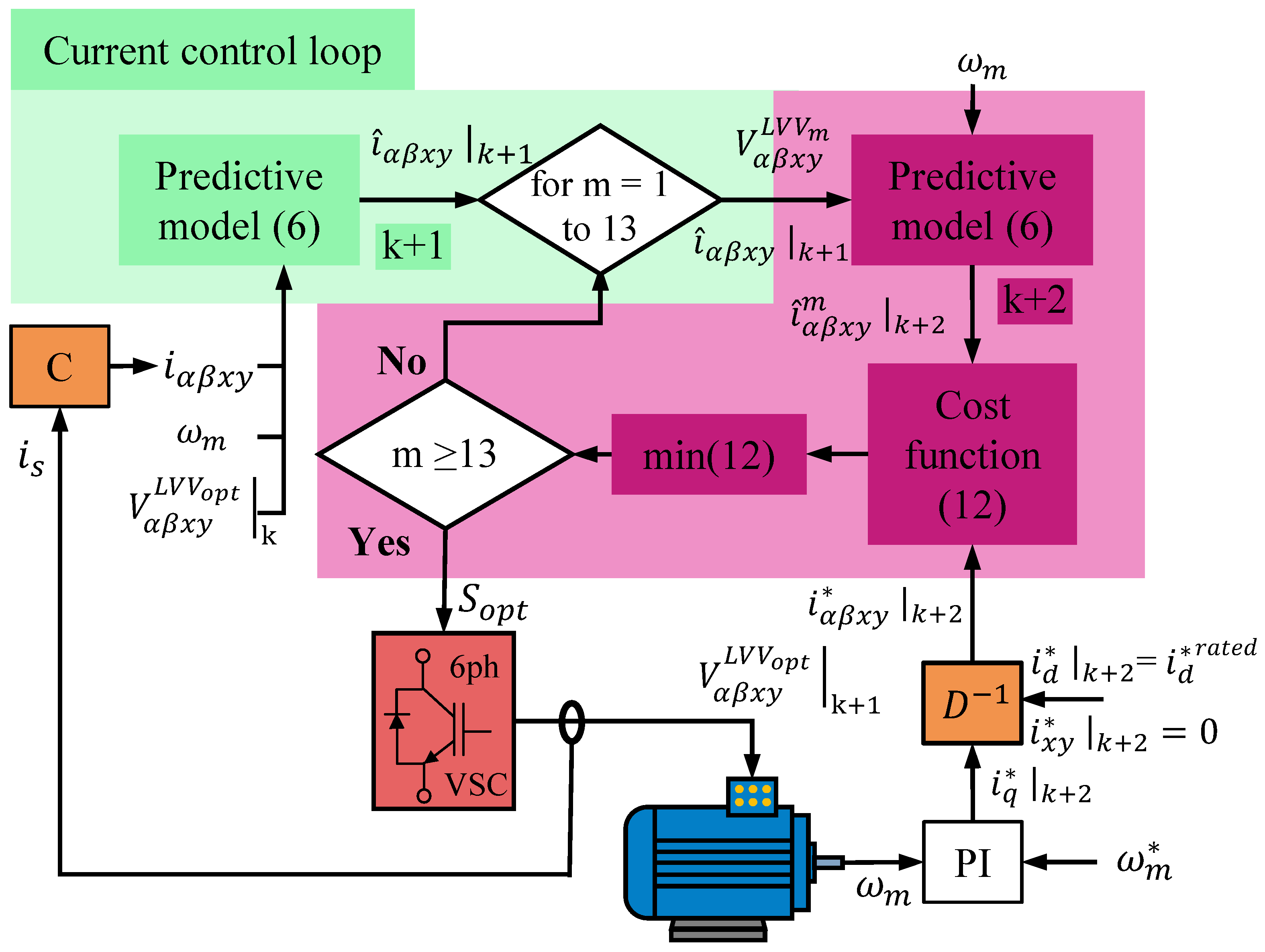
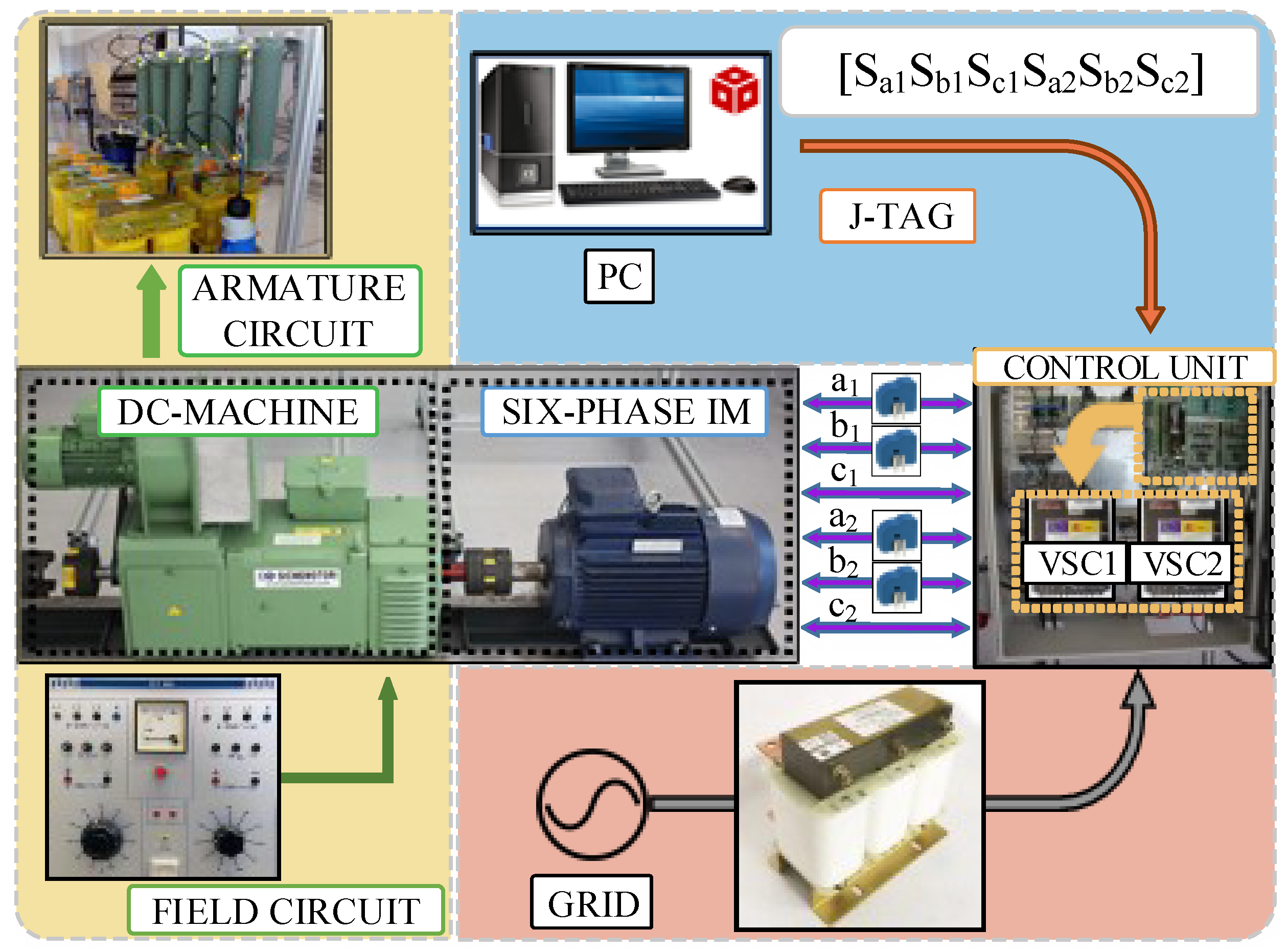

| Parameter | Description | Value |
|---|---|---|
| (V) | dc-link voltage | 325 |
| (A) | Peak current | 4.5 |
| (Ω) | Stator resistance | 4.19 |
| (Ω) | Rotor resistance | 3.2 |
| (mH) | Mutual inductance | 280 |
| (mH) | Stator leakage inductance | 4.2 |
| (mH) | Rotor leakage inductance | 55.1 |
| (s) | Sampling time | 100 |
| (A − 2) | WF employed in CLVV-MPC | 0.2 |
| Method | Metric | 500 rpm | 800 rpm |
|---|---|---|---|
| LVV-MPC | THD (%) | 35.2 | 24.9 |
| HDI (%) | 54.1 | 29.0 | |
| (kHz) | 3.8 | 3.4 | |
| CLVV-MPC | THD (%) | 24.2 | 17.5 |
| HDI (%) | 24.9 | 19.0 | |
| (kHz) | 3.7 | 3.1 |
| Method | Computational Cost (s) |
|---|---|
| LVV-MPC | 22 |
| CLVV-MPC | 27 |
| FCS-MPC | 67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrillo-Rios, J.; Aciego, J.J.; Gonzalez-Prieto, A.; Gonzalez-Prieto, I.; Duran, M.J.; Lara-Lopez, R. Remaining Secondary Voltage Mitigation in Multivector Model Predictive Control Schemes for Multiphase Electric Drives. Machines 2025, 13, 862. https://doi.org/10.3390/machines13090862
Carrillo-Rios J, Aciego JJ, Gonzalez-Prieto A, Gonzalez-Prieto I, Duran MJ, Lara-Lopez R. Remaining Secondary Voltage Mitigation in Multivector Model Predictive Control Schemes for Multiphase Electric Drives. Machines. 2025; 13(9):862. https://doi.org/10.3390/machines13090862
Chicago/Turabian StyleCarrillo-Rios, Juan, Juan Jose Aciego, Angel Gonzalez-Prieto, Ignacio Gonzalez-Prieto, Mario J. Duran, and Rafael Lara-Lopez. 2025. "Remaining Secondary Voltage Mitigation in Multivector Model Predictive Control Schemes for Multiphase Electric Drives" Machines 13, no. 9: 862. https://doi.org/10.3390/machines13090862
APA StyleCarrillo-Rios, J., Aciego, J. J., Gonzalez-Prieto, A., Gonzalez-Prieto, I., Duran, M. J., & Lara-Lopez, R. (2025). Remaining Secondary Voltage Mitigation in Multivector Model Predictive Control Schemes for Multiphase Electric Drives. Machines, 13(9), 862. https://doi.org/10.3390/machines13090862










