Ultra-Long, Minor-Diameter, Untethered Growing Continuum Robot via Tip Actuation and Steering
Abstract
1. Introduction
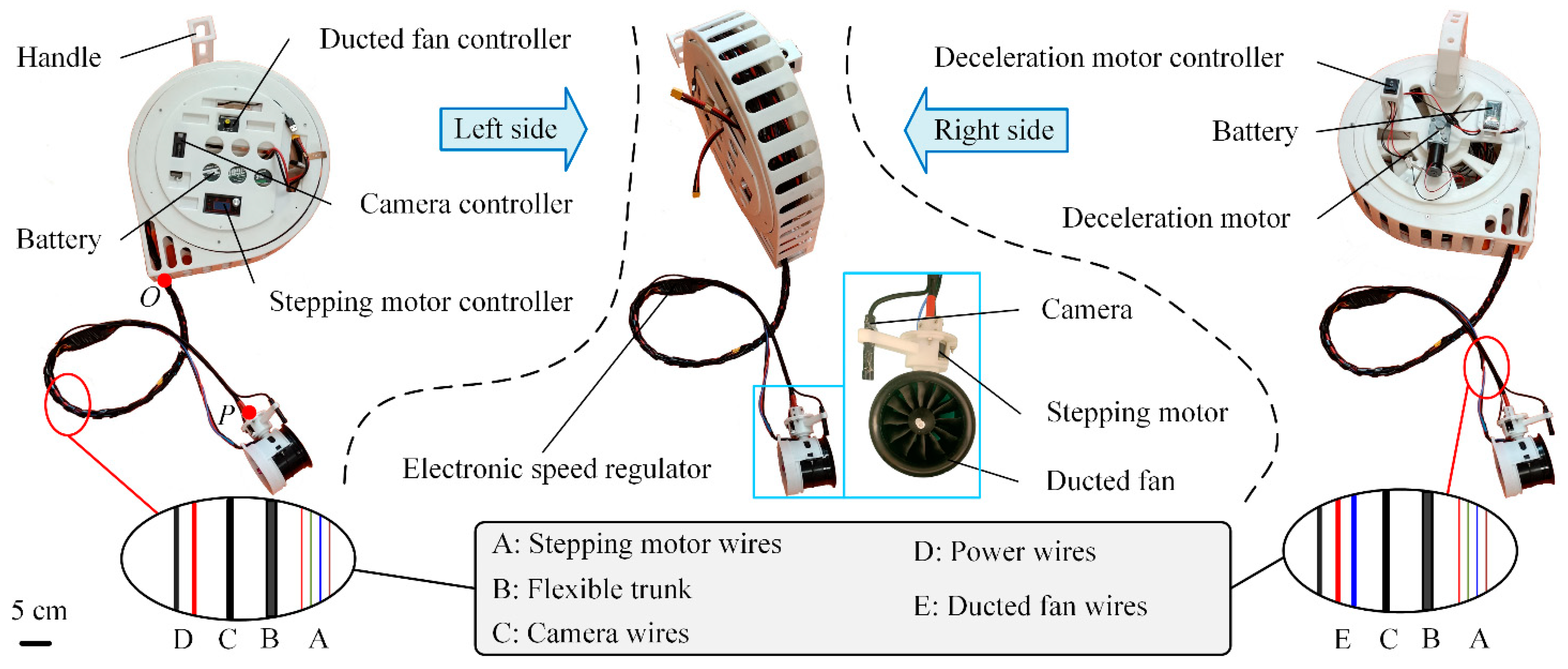
2. Design and Fabrication
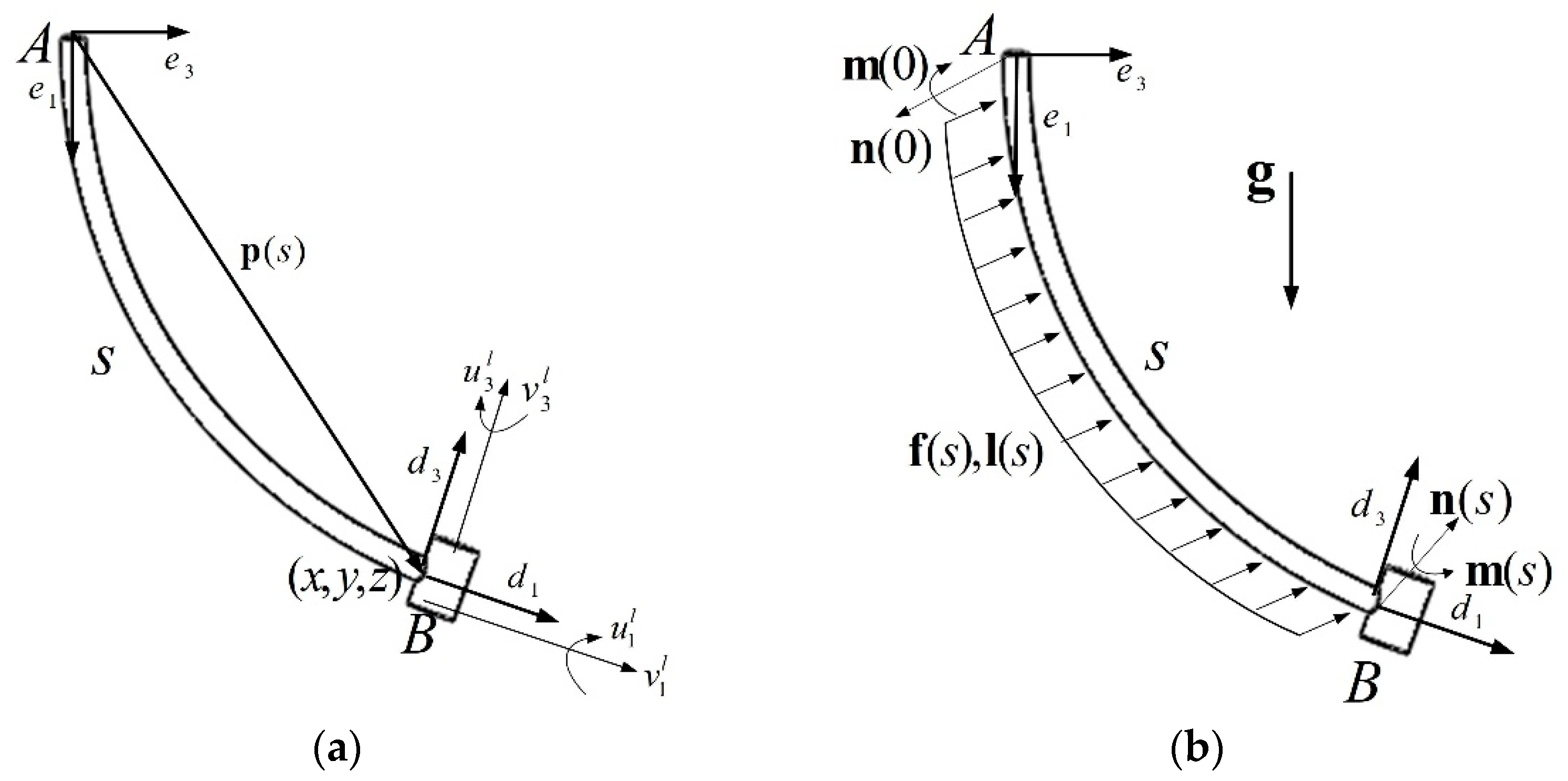
3. Modeling
4. Results and Discussion
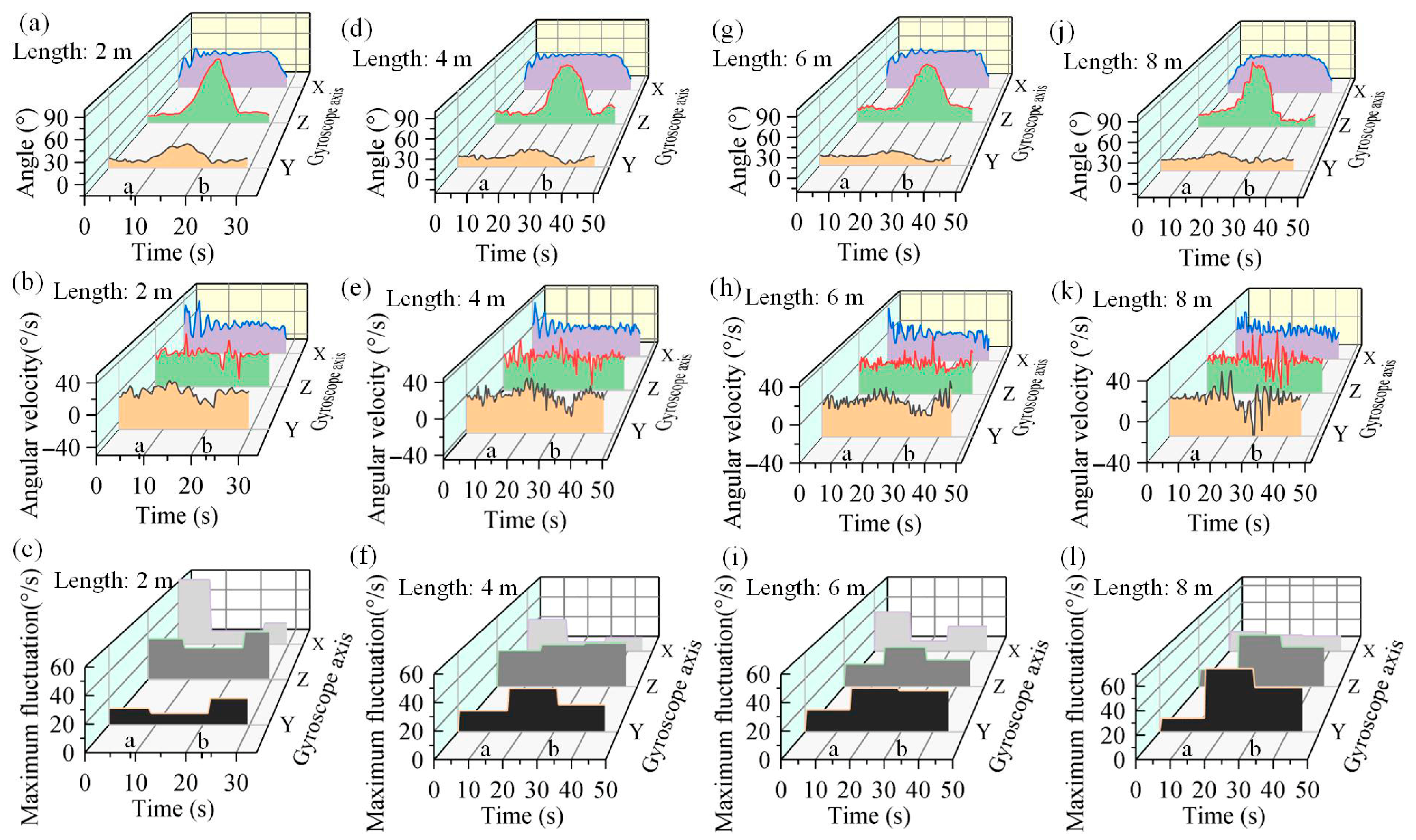
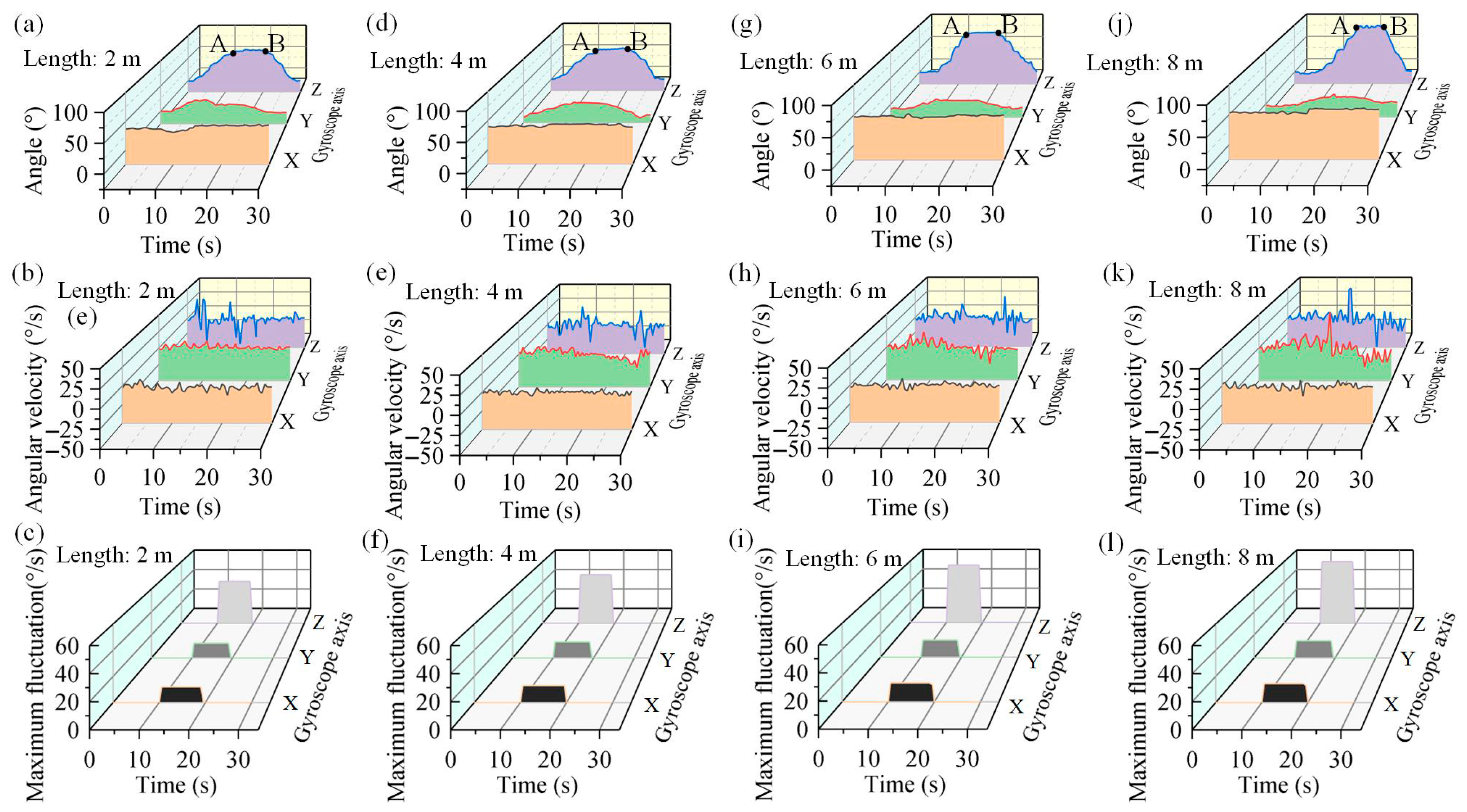
4.1. Manipulation Experiment
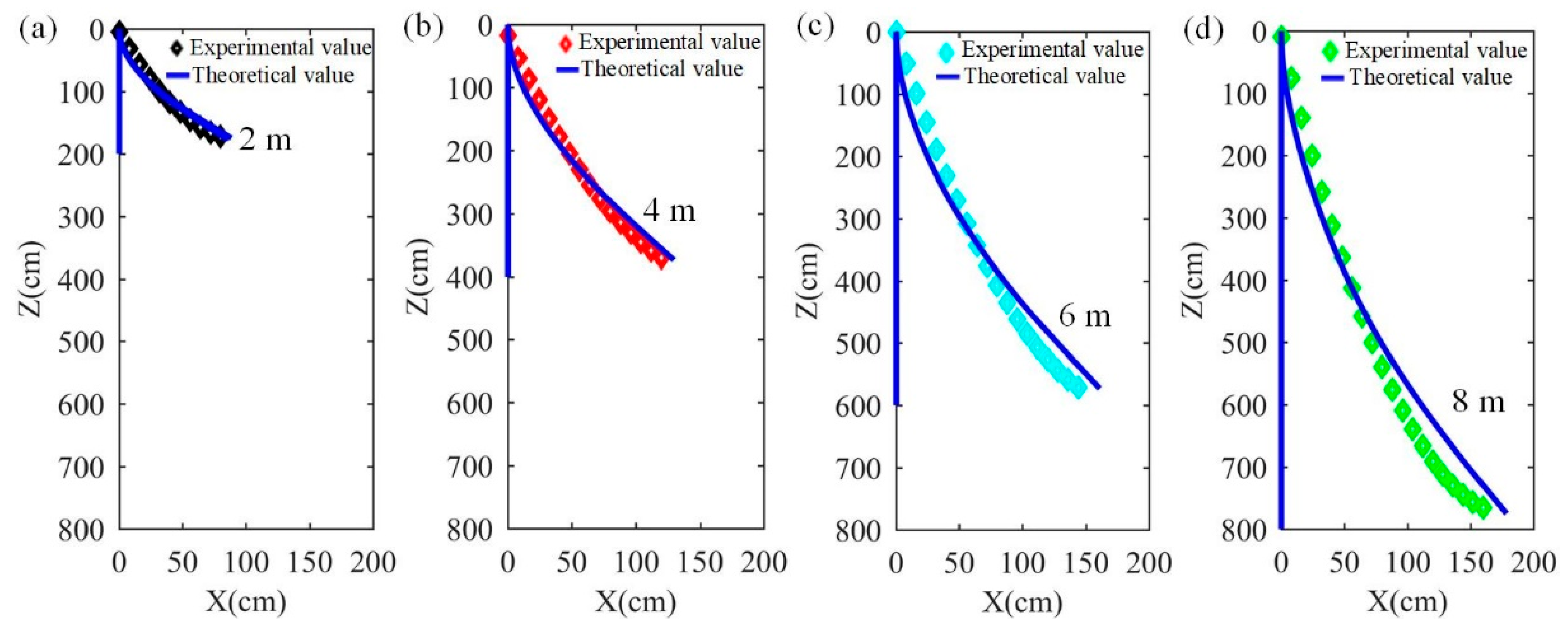
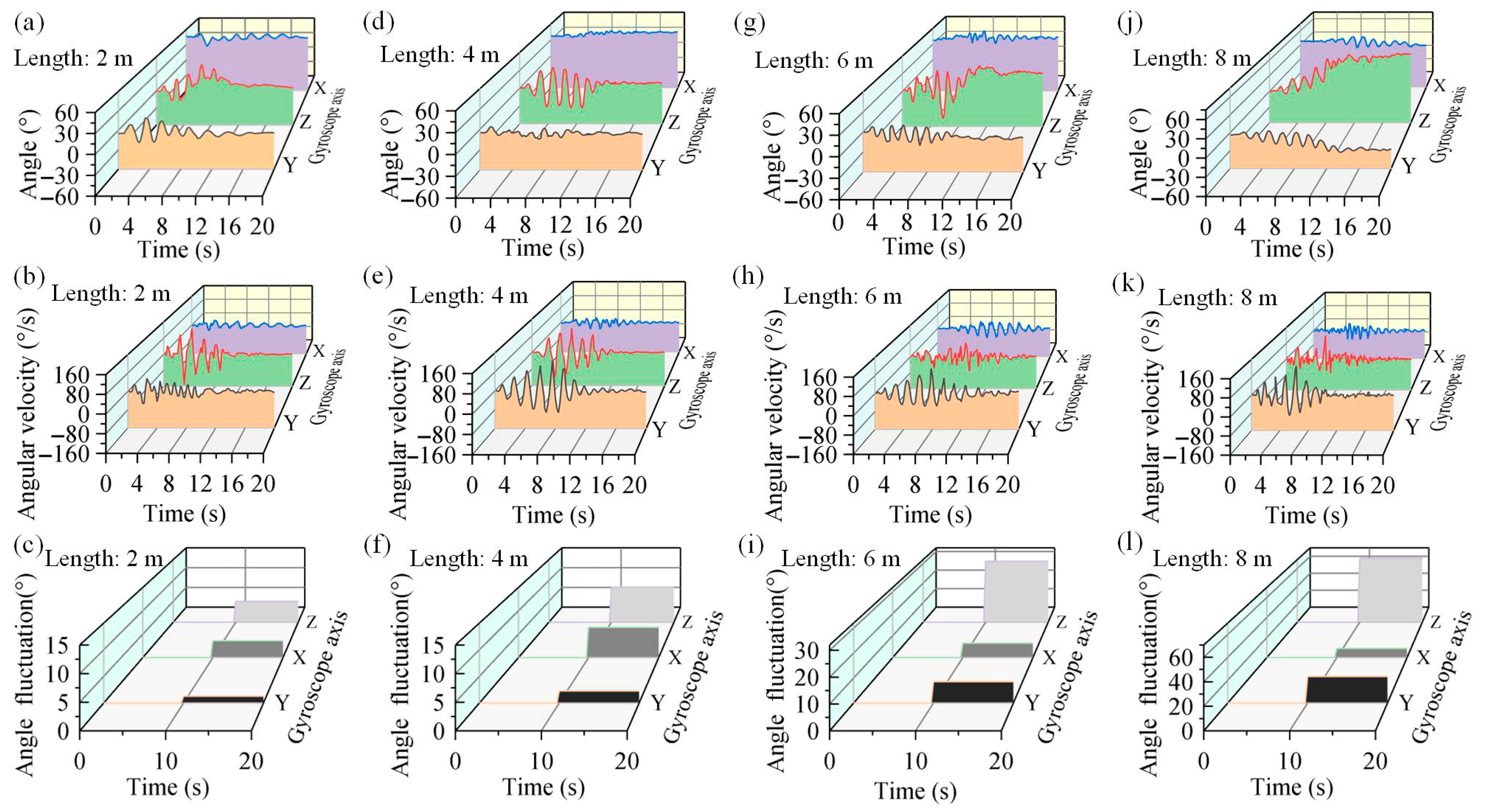
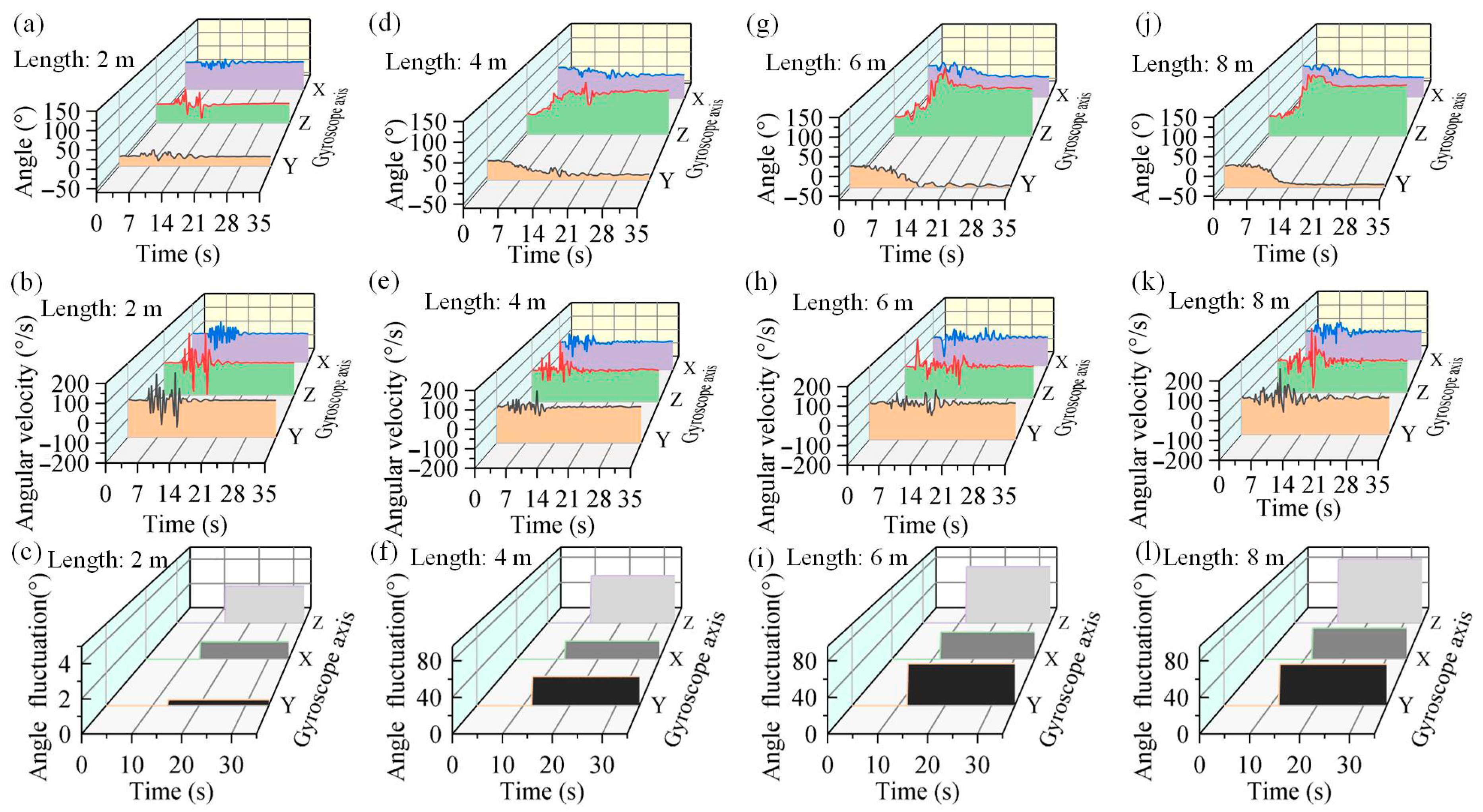
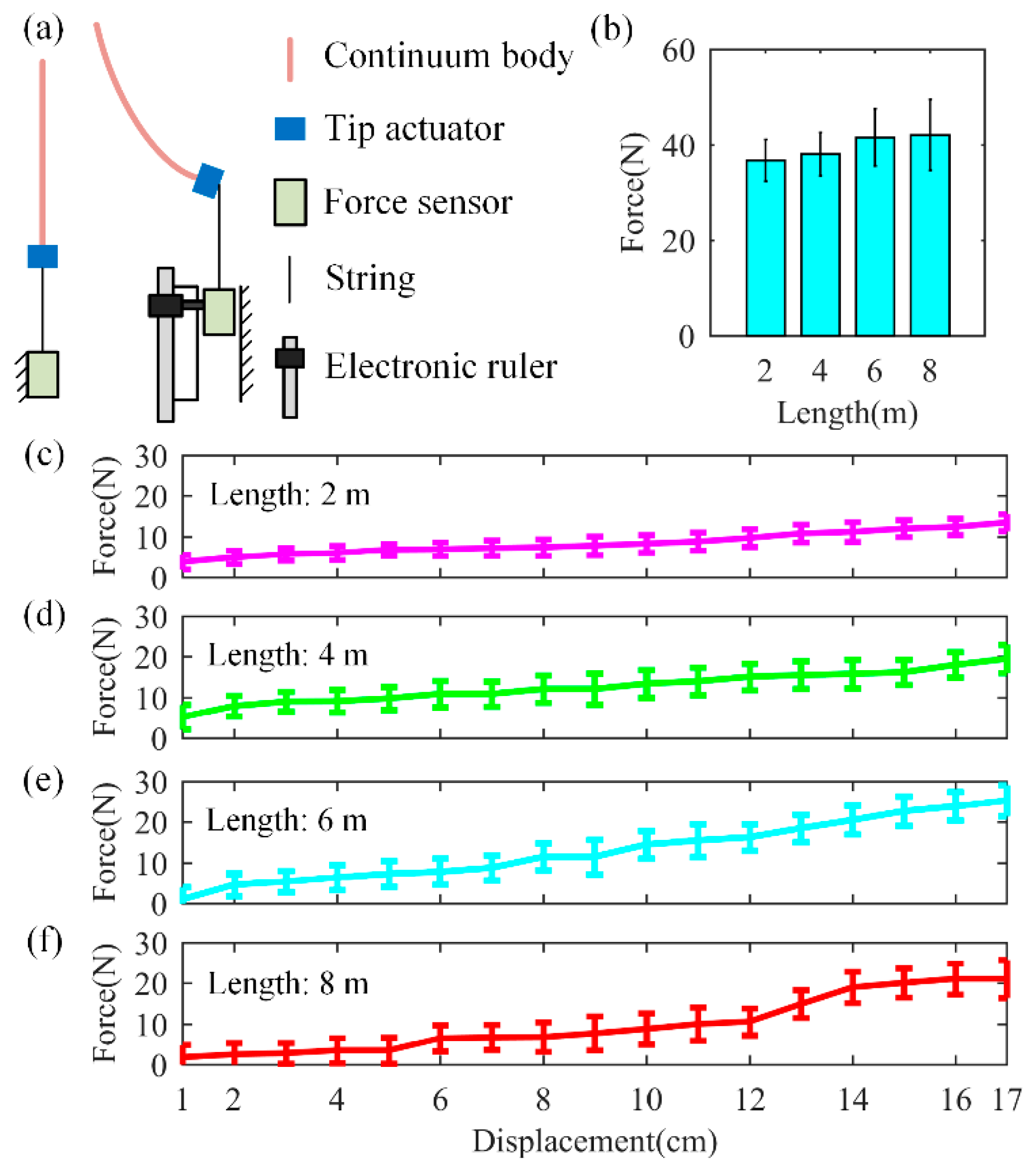
4.2. Motion Performance
4.3. Load Performance
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Russo, M.; Sadati, S.M.H.; Dong, X.; Mohammad, A.; Walker, I.D.; Bergeles, C.; Xu, K.; Axinte, D.A. Continuum robots: An overview. Adv. Intell. Syst. 2023, 5, 2200367. [Google Scholar] [CrossRef]
- Chen, G.; Tang, S.; Duan, X.; Wang, H. Design, modeling, and evaluation of parallel continuum robots: A survey. Sci. China Technol. Sci. 2024, 67, 673–695. [Google Scholar] [CrossRef]
- Wu, H.; Yu, J.; Pan, J.; Pei, X. A novel obstacle avoidance heuristic algorithm of continuum robot based on FABRIK. Sci. China Technol. Sci. 2022, 65, 2952–2966. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, H.; Cao, Y.; Cui, Y.; Zhang, L. Magnetically actuated continuum medical robots: A review. Adv. Intell. Syst. 2023, 5, 202200416. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, X.; Huang, Y.; Cao, L.; Liu, J. A review of soft manipulator research, applications, and opportunities. J. Field Robot. 2022, 39, 281–311. [Google Scholar] [CrossRef]
- Fang, Y.; Dong, X.; Mohammad, A.; Axinte, D. Design and control of a multiple-section continuum robot with a hybird sensing system. IEEE/ASME Trans. Mechatron. 2023, 28, 1522–1533. [Google Scholar] [CrossRef]
- Leibrandt, K.; da Cruz, L.; Bergeles, C. Designing robots for reachability and dexterity: Continuum surgical robots as a pretext application. IEEE Trans. Robot. 2023, 39, 2989–3007. [Google Scholar] [CrossRef]
- Nwafor, C.; Laurent, G.J.; Rabenorosoa, K. Miniature parallel continuum robot made of glass: Analysis, design, and proof-of-concept. IEEE/ASME Trans. Mechatron. 2023, 28, 2038–2046. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, L.; Yang, X.; Tan, R.; Lu, H.; Shen, Y. Millimeter-scale soft continuum robots for large-angle and high-precision manipulation by hybrid actuation. Adv. Intell. Syst. 2021, 3, 202000189. [Google Scholar] [CrossRef] [PubMed]
- Hyatt, P.; Kraus, D.; Sherrod, V.; Rupert, L.; Day, N.; Killpack, M.D. Configuration estimation for accurate position control of large-scale soft robots. IEEE/ASME Trans. Mechatron. 2019, 24, 88–99. [Google Scholar] [CrossRef]
- Li, X.; Sun, K.; Guo, C.; Liu, H. Modeling and experimental validation for a large-scale and ultralight inflatable robotic arm. IEEE/ASME Trans. Mechatron. 2022, 27, 418–429. [Google Scholar] [CrossRef]
- Li, X.; Sun, K.; Guo, C.; Liu, H. Hybrid adaptive disturbance rejection control for inflatable robotic arms. ISA Trans. 2022, 126, 617–628. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.D.; Asbeck, A.T. Design and characterization of a modular hybrid continuum robotic manipulator. IEEE/ASME Trans. Mechatron. 2020, 25, 2812–2823. [Google Scholar] [CrossRef]
- Zhang, Z.; Tang, S.; Fan, W.; Xun, Y.; Wang, H.; Chen, G. Design and analysis of hybrid-driven origami continuum robots with extensible and stiffness-tunable sections. Mech. Mach. Theory 2022, 169, 104607. [Google Scholar] [CrossRef]
- Lee, K.; Wang, Y.; Zheng, C. TWISTER hand: Underactuated robotic gripper inspired by origami twisted tower. IEEE Trans. Robot. 2020, 36, 488–500. [Google Scholar] [CrossRef]
- Santoso, J.; Onal, C.D. An origami continuum robot capable of precise motion through torsionally stiff body and smooth inverse kinematics. Soft Robot. 2021, 8, 371–386. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Wang, Z.; Jin, Y.; Chen, X.; Li, P.; Gan, Y.; Lin, S.; Chen, X. Hierarchical control of soft manipulators towards unstructured interactions. Int. J. Robot. Res. 2021, 40, 411–434. [Google Scholar] [CrossRef]
- Melancon, D.; Forte, A.E.; Kamp, L.M.; Gorissen, B.; Bertoldi, K. Inflatable origami: Multimodal deformation via multistability. Adv. Funct. Mater. 2022, 32, 202201891. [Google Scholar] [CrossRef]
- Kim, W.; Byun, J.; Kim, J.-K.; Choi, W.-Y.; Jakobsen, K.; Jakobsen, J.; Lee, D.-Y.; Cho, K.-J. Bioinspired dual-morphing stretchable origami. Sci. Robot. 2019, 4, eaay3493. [Google Scholar] [CrossRef]
- Oh, N.; Rodrigue, H. Toward the development of large-scale inflatable robotic arms using hot air welding. Soft Robot. 2023, 10, 88–96. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Palacio, J.M.; Monteiro, E.; Riwan, A.; Mechbal, N. A novel inflatable actuator based on simultaneous eversion retraction. Soft Robot. 2021, 8, 699–710. [Google Scholar] [CrossRef]
- Goswami, D.; Liu, S.; Pal, A.; Silva, L.G.; Martinez, R.V. 3D-architected soft machines with topologically encoded motion. Adv. Funct. Mater. 2019, 29, 201808713. [Google Scholar] [CrossRef]
- Rubio, A.P.; Fan, D.; Jenett, B.; Ferrandis, J.d.Á.; Tourlomousis, F.; Abdel-Rahman, A.; Preiss, D.; Zemánek, J.; Triantafyllou, M.; Gershenfeld, N. Modular morphing lattices for large-scale underwater continuum robotic structures. Soft Robot. 2023, 10, 724–736. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Hu, Y.; Li, Y.; Ma, K.; Wei, Y.; Yang, J.; Wu, Z.; Rajabi, H.; Peng, H.; Wu, J. Versatile like a seahorse tail: A bio-inspired programmable continuum robot for conformal grasping. Adv. Intell. Syst. 2022, 4, 202200263. [Google Scholar] [CrossRef]
- Maloisel, G.; Knoop, E.; Schumacher, C.; Bacher, M. Automated routing of muscle fibers for soft robots. IEEE Trans. Robot. 2021, 37, 996–1008. [Google Scholar] [CrossRef]
- Xing, Z.; Zhang, J.; McCoul, D.; Cui, Y.; Sun, L.; Zhao, J. A super-lightweight and soft manipulator driven by dielectric elastomers. Soft Robot. 2020, 7, 512–520. [Google Scholar] [CrossRef]
- Atia, M.G.B.; Mohammad, A.; Gameros, A.; Axinte, D.; Wright, I. Reconfigurable soft robots by building blocks. Adv. Sci. 2022, 9, e2203217. [Google Scholar] [CrossRef]
- Kim, Y.; Parada, G.A.; Liu, S.; Zhao, X. Ferromagnetic soft continuum robots. Sci. Robot. 2019, 4, eaax7329. [Google Scholar] [CrossRef]
- Lin, D.; Jiao, N.; Wang, Z.; Liu, L. A magnetic continuum robot with multi-mode control using opposite-magnetized magnets. IEEE Robot. Autom. Lett. 2021, 6, 2485–2492. [Google Scholar] [CrossRef]
- Blumenschein, L.H.; Coad, M.M.; Haggerty, D.A.; Okamura, A.M.; Hawkes, E.W. Design, modeling, control, and application of everting vine robots. Front. Robot. AI 2020, 7, 548266. [Google Scholar] [CrossRef]
- Talas, S.K.; Baydere, B.A.; Altinsoy, T.; Tutcu, C.; Samur, E. Design and development of a growing pneumatic soft robot. Soft Robot. 2020, 7, 521–533. [Google Scholar] [CrossRef] [PubMed]
- Coad, M.M.; Thomasson, R.P.; Blumenschein, L.H.; Usevitch, N.S.; Hawkes, E.W.; Okamura, A.M. Retraction of soft growing robots without buckling. IEEE Robot. Autom. Lett. 2020, 5, 2115–2122. [Google Scholar] [CrossRef]
- Blumenschein, L.H.; Koehler, M.; Usevitch, N.S.; Hawkes, E.W.; Rucker, D.C.; Okamura, A.M. Geometric solutions for general actuator routing on inflated-beam soft growing robots. IEEE Trans. Robot. 2022, 38, 1820–1840. [Google Scholar] [CrossRef]
- Greer, J.D.; Morimoto, T.K.; Okamura, A.M.; Hawkes, E.W. A soft, steerable continuum robot that grows via tip Extension. Soft Robot. 2019, 6, 95–108. [Google Scholar] [CrossRef]
- Satake, Y.; Takanishi, A.; Ishii, H. Novel growing robot with inflatable structure and heat-welding rotation mechanism. IEEE/ASME Trans. Mechatron. 2020, 25, 1869–1877. [Google Scholar] [CrossRef]
- Satake, Y.; Ishii, H. Pitch-up motion mechanism with heat welding by soft inflatable growing robot. IEEE Robot. Autom. Lett. 2022, 7, 5071–5078. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Y.; Zhang, G.; Zhou, D.; Li, L. A bioinspired soft robot combining the growth adaptability of vine plants with a coordinated control system. Research 2021, 2021, 9843859. [Google Scholar] [CrossRef]
- Coad, M.M.; Blumenschein, L.H.; Cutler, S.; Zepeda, J.A.R.; Naclerio, N.D.; El-Hussieny, H.; Mehmood, U.; Ryu, J.-H.; Hawkes, E.W.; Okamura, A.M. Vine robots: Design, teleoperation, and deployment for navigation and exploration. IEEE Robot. Autom. Mag. 2019, 27, 120–132. [Google Scholar] [CrossRef]
- Hawkes, E.W.; Blumenschein, L.H.; Greer, J.D.; Okamura, A.M. A soft robot that navigates its environment through growth. Sci. Robot. 2017, 2, eaan3028. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, T.; Ambe, Y.; Ando, H.; Konyo, M.; Tadakuma, K.; Maruyama, S.; Tadokoro, S. A mechanical approach to suppress the oscillation of a long continuum robot flying with water jets. IEEE Robot. Autom. Lett. 2019, 4, 4346–4353. [Google Scholar] [CrossRef]
- Li, S.; Awale, S.A.; Bacher, K.E.; Buchner, T.J.; Della Santina, C.; Wood, R.J.; Rus, D. Scaling up soft robotics: A meter-scale, modular, and reconfigurable soft robotic system. Soft Robot. 2022, 9, 324–336. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, P.; Lin, Z.; Zhou, L.; Li, H.; Basin, M.; Yao, J. Ultra-Long, Minor-Diameter, Untethered Growing Continuum Robot via Tip Actuation and Steering. Machines 2025, 13, 851. https://doi.org/10.3390/machines13090851
Zhou P, Lin Z, Zhou L, Li H, Basin M, Yao J. Ultra-Long, Minor-Diameter, Untethered Growing Continuum Robot via Tip Actuation and Steering. Machines. 2025; 13(9):851. https://doi.org/10.3390/machines13090851
Chicago/Turabian StyleZhou, Pan, Zhaoyi Lin, Lang Zhou, Haili Li, Michael Basin, and Jiantao Yao. 2025. "Ultra-Long, Minor-Diameter, Untethered Growing Continuum Robot via Tip Actuation and Steering" Machines 13, no. 9: 851. https://doi.org/10.3390/machines13090851
APA StyleZhou, P., Lin, Z., Zhou, L., Li, H., Basin, M., & Yao, J. (2025). Ultra-Long, Minor-Diameter, Untethered Growing Continuum Robot via Tip Actuation and Steering. Machines, 13(9), 851. https://doi.org/10.3390/machines13090851





