Second-Order Complex-Coefficient Flux Observer with Stator Resistance Estimation for Induction Motor Sensorless Drives
Abstract
1. Introduction
2. Model of Induction Motor
3. Proposed Flux Observer
3.1. Second-Order Complex-Coefficient Flux Observer
3.2. Stability Analysis
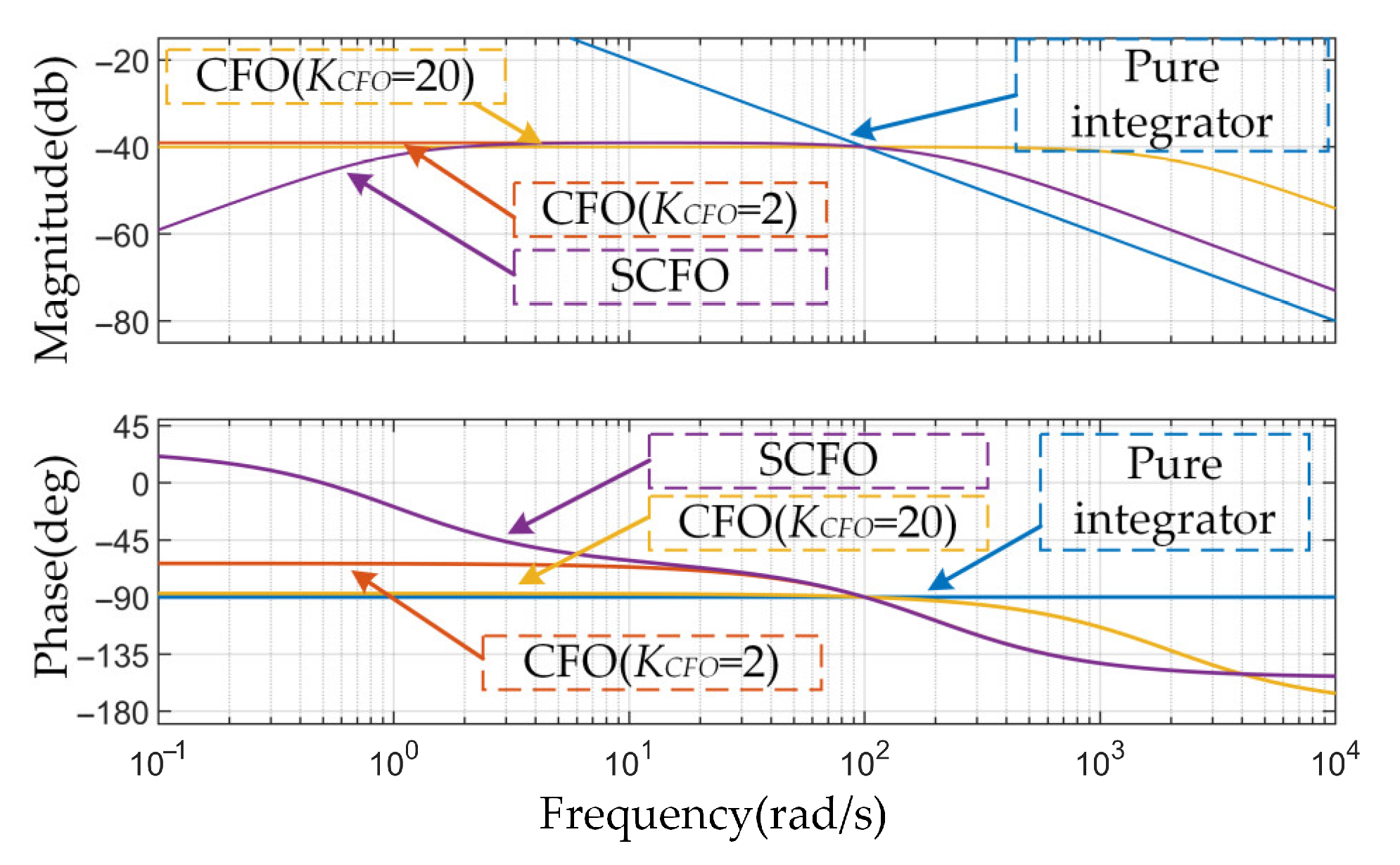
3.3. Performance Analysis
3.4. Discrete Implementation
3.5. Analysis of Parameter Perturbation on the SCFO
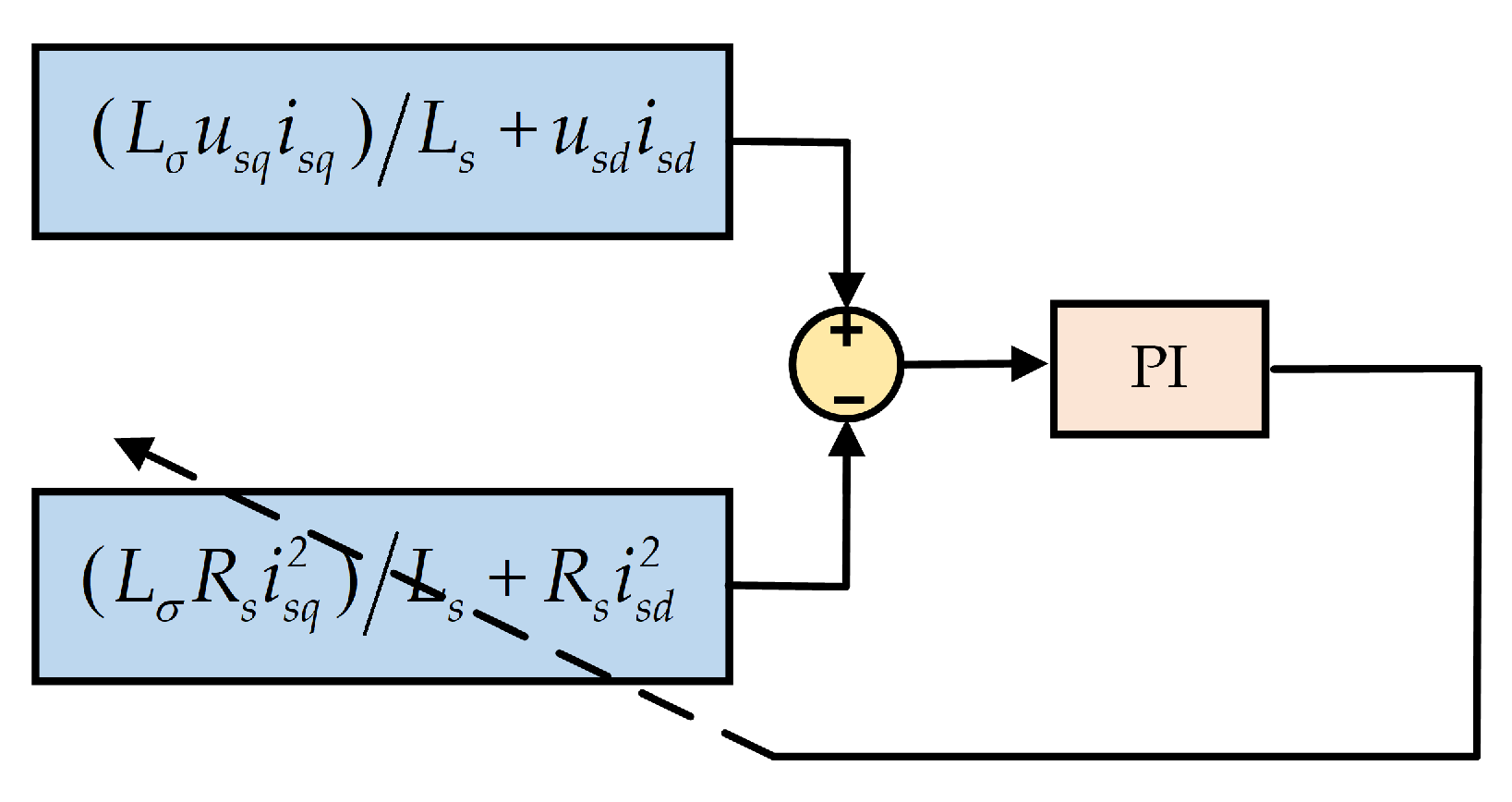
4. Proposed Stator Resistance Estimator
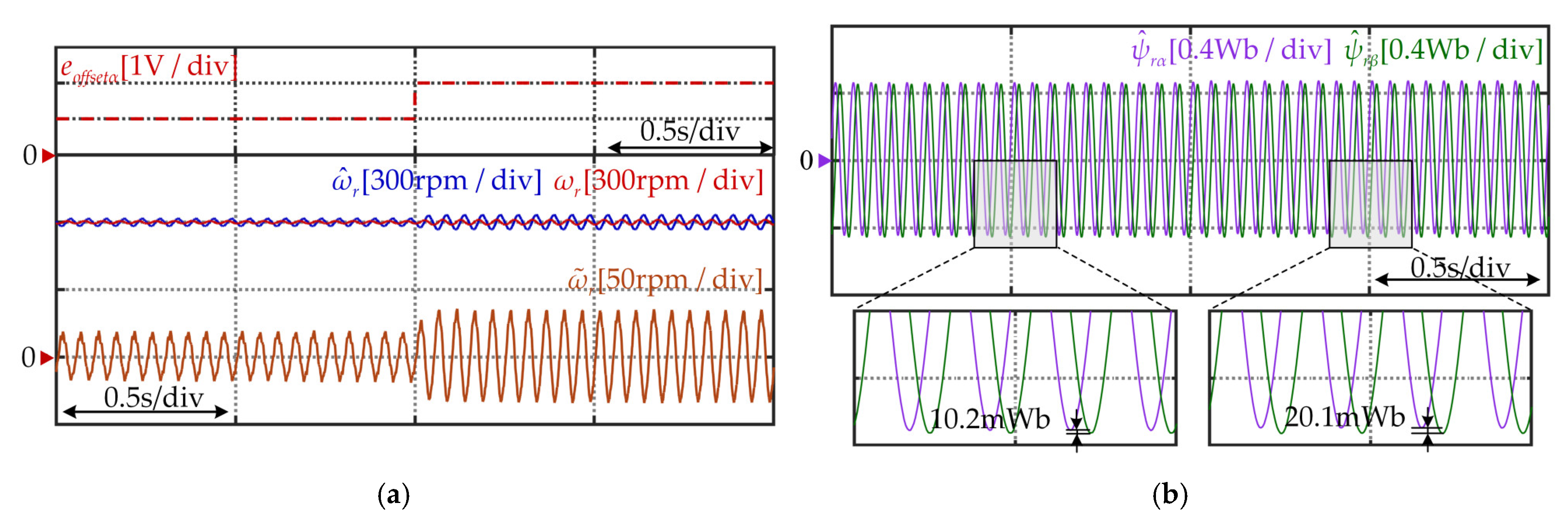
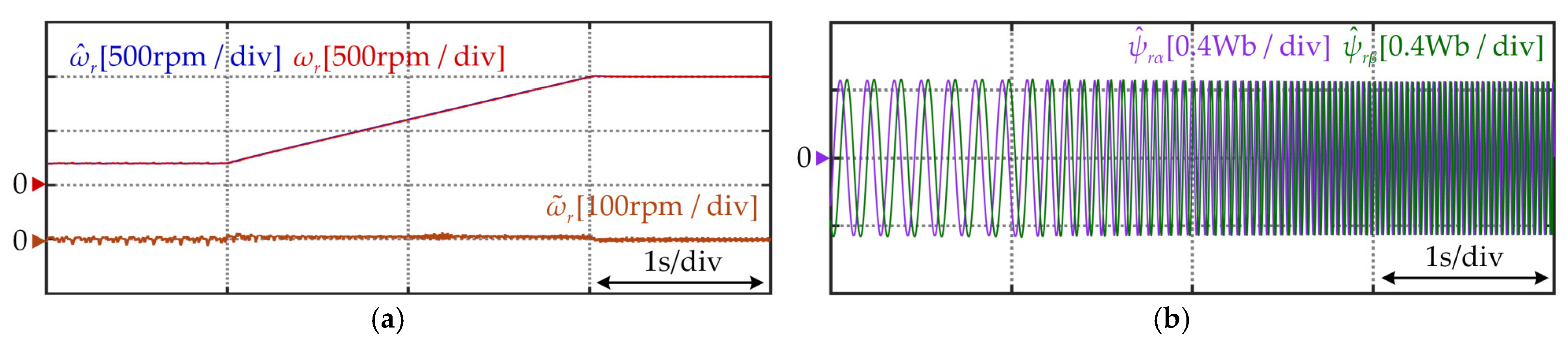
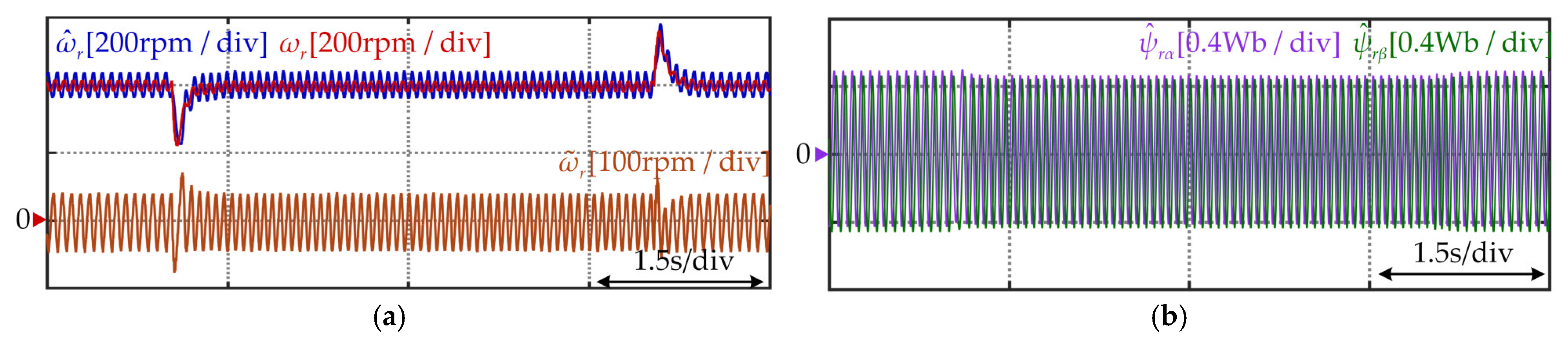
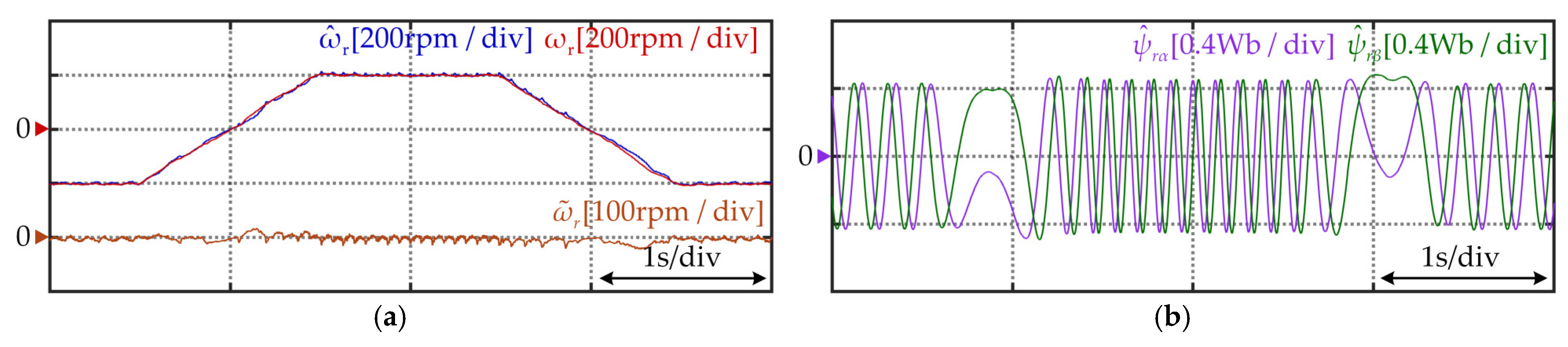
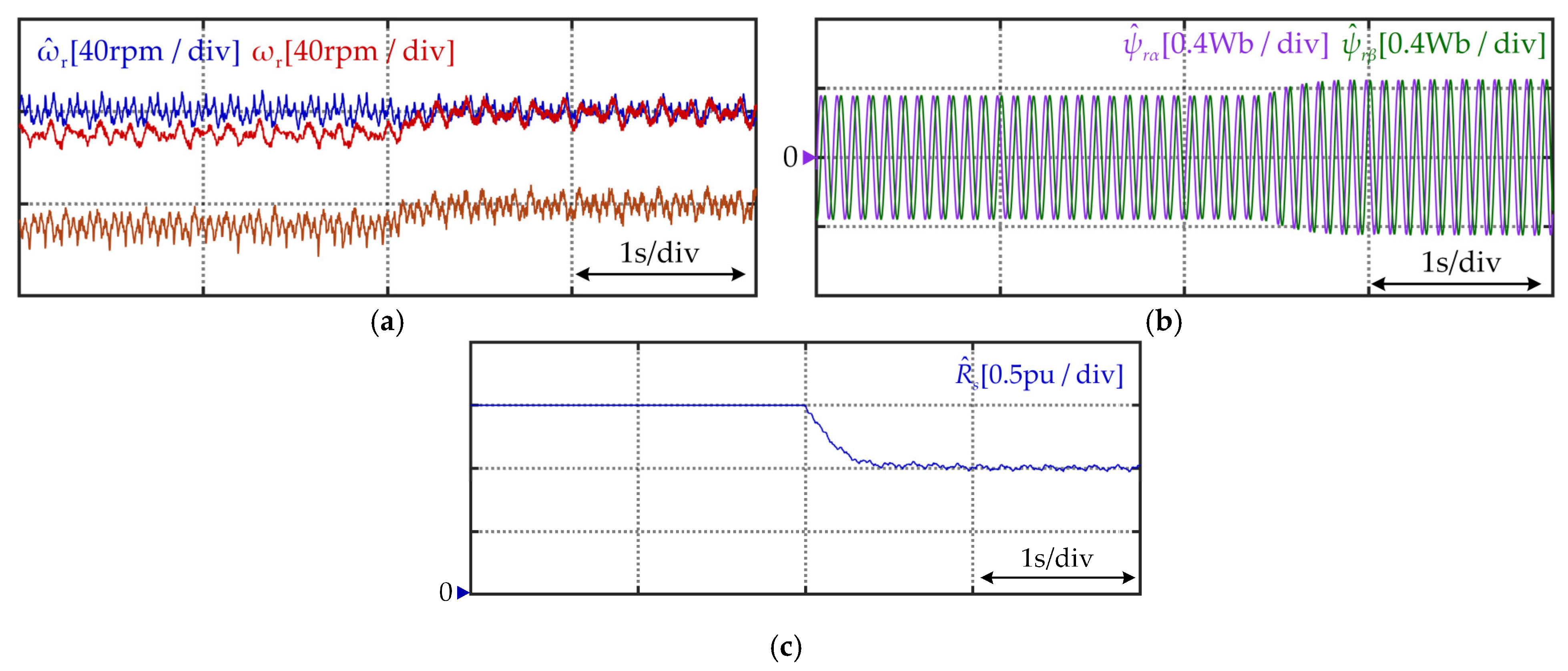
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Algorithm: SCFO | ||
| Input: | . | |
| Output: | . | |
| 1: | //Calculate back-EMF after DC offset compensation. | |
| 2: | ||
| 3: | ||
| 4: | //Calculate quadrature error. | |
| 5: | //update offset estimation for next iteration | |
| 6: | ||
| 7: | //Calculate rotor flux estimation. | |
| 8: | ||
| 9: | ||
References
- Chen, J.; Yuan, X.; Blaabjerg, F.; Lee, C.H.T. Overview of Fundamental Frequency Sensorless Algorithms for AC Motors: A Unified Perspective. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 915–931. [Google Scholar] [CrossRef]
- Reddy, C.U.; Prabhakar, K.K.; Singh, A.K.; Kumar, P. Speed Estimation Technique Using Modified Stator Current Error-Based MRAS for Direct Torque Controlled Induction Motor Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1223–1235. [Google Scholar] [CrossRef]
- Bıçak, A.; Gelen, A. Modified Super-Twisting Algorithm Based Model Reference Adaptive Observer for Sensorless Control of the Interior Permanent-Magnet Synchronous Motor in Electric Vehicles. Machines 2023, 11, 871. [Google Scholar] [CrossRef]
- Delorme, L.; Ayala, M.; Gonzalez, O.; Rodas, J.; Gregor, R.; Hernandez, J.C. SpeedSensorless Control for a Six-Phase Induction Machine Based on a Sliding Mode Observer. Machines 2025, 13, 639. [Google Scholar] [CrossRef]
- Tir, Z.T.; Kowalska, O.; Ahmed, H.; Houari, A. Adaptive High Gain Observer Based MRAS for Sensorless Induction Motor Drives. IEEE Trans. Ind. Electron. 2024, 71, 271–281. [Google Scholar] [CrossRef]
- Wang, H.; Yang, Y.; Ge, X.; Zuo, Y.; Yue, Y.; Li, S. PLL- and FLL-Based Speed Estimation Schemes for Speed-Sensorless Control of Induction Motor Drives: Review and New Attempts. IEEE Trans. Power Electron. 2022, 37, 3334–3356. [Google Scholar] [CrossRef]
- Wang, G.; Li, Z.; Zhang, G.; Yu, Y.; Xu, D. Quadrature PLL-Based High-Order Sliding-Mode Observer for IPMSM Sensorless Control with Online MTPA Control Strategy. IEEE Trans. Energy Convers. 2013, 28, 214–224. [Google Scholar] [CrossRef]
- Jiang, F.; Sun, S.; Liu, A.; Xu, Y.; Li, Z.; Liu, X.; Yang, K. Robustness Improvement of Model-Based Sensorless SPMSM Drivers Based on an Adaptive Extended State Observer and an Enhanced Quadrature PLL. IEEE Trans. Power Electron. 2021, 36, 4802–4814. [Google Scholar] [CrossRef]
- Lascu, C.; Boldea, I.; Blaabjerg, F. A modified direct torque control for induction motor sensorless drive. IEEE Trans. Ind. Appl. 2000, 36, 122–130. [Google Scholar] [CrossRef]
- Junggi, L.; Jinseok, H.; Kwanghee, N.; Ortega, R.; Praly, L.; Astolfi, A. Sensorless Control of Surface-Mount Permanent-Magnet Synchronous Motors Based on a Nonlinear Observer. IEEE Trans. Power Electron. 2010, 25, 290–297. [Google Scholar] [CrossRef]
- Holtz, J.; Juntao, Q. Drift- and parameter-compensated flux estimator for persistent zero-stator-frequency operation of sensorless-controlled induction motors. IEEE Trans. Ind. Appl. 2003, 39, 1052–1060. [Google Scholar] [CrossRef]
- Jo, G.-J.; Choi, J.-W. Rotor Flux Estimator Design with Offset Extractor for Sensorless-Driven Induction Motors. IEEE Trans. Power Electron. 2022, 37, 4497–4510. [Google Scholar] [CrossRef]
- Comanescu, M.; Xu, L. An improved flux observer based on PLL frequency estimator for sensorless vector control of induction motors. IEEE Trans. Ind. Electron. 2006, 53, 50–56. [Google Scholar] [CrossRef]
- Zhao, R.; Xin, Z.; Loh, P.C.; Blaabjerg, F. A Novel Flux Estimator Based on Multiple Second-Order Generalized Integrators and Frequency-Locked Loop for Induction Motor Drives. IEEE Trans. Power Electron. 2017, 32, 6286–6296. [Google Scholar] [CrossRef]
- Xu, W.; Jiang, Y.; Mu, C.; Blaabjerg, F. Improved Nonlinear Flux Observer-Based Second-Order SOIFO for PMSM Sensorless Control. IEEE Trans. Power Electron. 2019, 34, 565–579. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, W.; Mu, C.; Zhu, J.; Dian, R. An Improved Third-Order Generalized Integral Flux Observer for Sensorless Drive of PMSMs. IEEE Trans. Ind. Electron. 2019, 66, 9149–9160. [Google Scholar] [CrossRef]
- Zhang, Y.; Yin, Z.; Gao, F.; Liu, J. Research on Anti-DC Bias and High-Order Harmonics of a Fifth-Order Flux Observer for IPMSM Sensorless Drive. IEEE Trans. Ind. Electron. 2022, 69, 3393–3406. [Google Scholar] [CrossRef]
- He, W.; Wu, X.; Chen, J. Optimization Design of PMSM Sensorless Control Using Generalized Integrator. IEEE Trans. Ind. Electron. 2023, 71, 8625–8634. [Google Scholar] [CrossRef]
- Hinkkanen, M.; Luomi, J. Modified integrator for voltage model flux estimation of induction motors. IEEE Trans. Ind. Electron. 2003, 50, 818–820. [Google Scholar] [CrossRef]
- Stojic, D.; Milinkovic, M.; Veinovic, S.; Klasnic, I. Improved Stator Flux Estimator for Speed Sensorless Induction Motor Drives. IEEE Trans. Power Electron. 2015, 30, 2363–2371. [Google Scholar] [CrossRef]
- Vasic, V.; Vukosavic, S.N.; Levi, E. A stator resistance estimation scheme for speed sensorless rotor flux oriented induction motor drives. IEEE Trans. Energy Convers. 2003, 18, 476–483. [Google Scholar] [CrossRef]
- Chen, J.; Huang, J. Stable Simultaneous Stator and Rotor Resistances Identification for Speed Sensorless IM Drives: Review and New Results. IEEE Trans. Power Electron. 2018, 33, 8695–8709. [Google Scholar] [CrossRef]
- Luo, C.; Wang, B.; Yu, Y.; Chen, C.; Huo, Z.; Xu, D. Decoupled Stator Resistance Estimation for Speed-Sensorless Induction Motor Drives Considering Speed and Load Torque Variations. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1193–1207. [Google Scholar] [CrossRef]
- Zaky, M.S.; Khater, M.M.; Shokralla, S.S.; Yasin, H.A. Wide-Speed-Range Estimation with Online Parameter Identification Schemes of Sensorless Induction Motor Drives. IEEE Trans. Ind. Electron. 2009, 56, 1699–1707. [Google Scholar] [CrossRef]
- Zaky, M.S.; Metwaly, M.K. Sensorless Torque/Speed Control of Induction Motor Drives at Zero and Low Frequencies with Stator and Rotor Resistance Estimations. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1416–1429. [Google Scholar] [CrossRef]
- Zhao, L.; Huang, J.; Liu, H.; Li, B.; Kong, W. Second-Order Sliding-Mode Observer with Online Parameter Identification for Sensorless Induction Motor Drives. IEEE Trans. Ind. Electron. 2014, 61, 5280–5289. [Google Scholar] [CrossRef]
- Serra, F.M.; Dòria-Cerezo, A.; Bodson, M. A Multiple-Reference Complex-Based Controller for Power Converters. IEEE Trans. Power Electron. 2021, 36, 14466–14477. [Google Scholar] [CrossRef]
- Pellegrino, G.; Guglielmi, P.; Armando, E.; Bojoi, R.I. Self-Commissioning Algorithm for Inverter Nonlinearity Compensation in Sensorless Induction Motor Drives. IEEE Trans. Ind. Appl. 2010, 46, 1416–1424. [Google Scholar] [CrossRef]








| Flux Observer | Order | Addition Operation | Multiplication Operation | Offset Suppression |
|---|---|---|---|---|
| CFO | 1 | 6 | 8 | medium |
| SOGI | 2 | 8 | 12 | medium |
| TOGI | 3 | 12 | 16 | Good |
| SCFO | 2 | 10 | 12 | Good |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| rated speed | 1500 rpm | magnetizing inductance | 91 mH |
| rated voltage | 220 V | stator leakage inductance | 10 mH |
| rated current | 6.3 A | stator resistance | 1.21 Ω |
| pole pairs | 2 | rotor resistance | 0.74 Ω |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, K.; Song, B.; Tang, X.; Zhou, X. Second-Order Complex-Coefficient Flux Observer with Stator Resistance Estimation for Induction Motor Sensorless Drives. Machines 2025, 13, 845. https://doi.org/10.3390/machines13090845
Zhao K, Song B, Tang X, Zhou X. Second-Order Complex-Coefficient Flux Observer with Stator Resistance Estimation for Induction Motor Sensorless Drives. Machines. 2025; 13(9):845. https://doi.org/10.3390/machines13090845
Chicago/Turabian StyleZhao, Kun, Bao Song, Xiaoqi Tang, and Xiangdong Zhou. 2025. "Second-Order Complex-Coefficient Flux Observer with Stator Resistance Estimation for Induction Motor Sensorless Drives" Machines 13, no. 9: 845. https://doi.org/10.3390/machines13090845
APA StyleZhao, K., Song, B., Tang, X., & Zhou, X. (2025). Second-Order Complex-Coefficient Flux Observer with Stator Resistance Estimation for Induction Motor Sensorless Drives. Machines, 13(9), 845. https://doi.org/10.3390/machines13090845






