Abstract
This study investigates the nonlinear dynamics and control of an underactuated hybrid system consisting of a Duffing oscillator, a pendulum, and a piezoelectric energy harvester. A novel Piezoelectric Harvester Proportional–Derivative (PHPD) control scheme is introduced, which integrates the harvester’s electrical output directly into the feedback loop to achieve simultaneous vibration suppression and energy utilization. The nonlinear governing equations are derived and analyzed using the Multiple-Scale Perturbation Technique (MSPT) to obtain reduced-order dynamics. Bifurcation analysis is employed to identify stability boundaries and critical parameter transitions, while numerical simulations based on the fourth-order Runge–Kutta method validate the analytical predictions. Furthermore, frequency response curves (FRCs) and an ideal system are evaluated under multiple controller and system parameter configurations. Bifurcation classification is performed on the analyzed figure to detect various bifurcations within the system, along with the computation of the Largest Lyapunov Exponent (LLE). The results demonstrate that PHPD control significantly reduces vibration amplitude and accelerates convergence, offering a new pathway for energy-efficient, high-performance control in nonlinear electromechanical systems.
1. Introduction
To optimize overall system efficiency, a multidomain transudative energy architecture integrates heterogeneous power generation and storage technologies, such as photovoltaic (PV) arrays or a diesel generator, coupled with a Battery Energy Storage System (BESS). The BESS operates as both a bidirectional power interface and a dynamic energy buffer, enabling the capture and storage of surplus electrical energy from distributed generation units. Through intelligent energy management and state-of-charge (SoC) regulation, the BESS ensures seamless power dispatch, grid stability, and continuous load support, thereby mitigating intermittency and enhancing system reliability. The sensor nodes can be equipped with batteries, and they might become self-sufficient with the use of energy harvesters [1]. The authors of [2] offered a revolutionary vibration energy harvester design that expands the frequency range it can function in and generates several peaks in its frequency response. The harvester is made up of a magnetoelectric transducer connected to a cantilever with a spiral form and magnets at the tip. By use of magnetic coupling, the magnets and transducer are linked, enabling peak frequency adaptation and a decrease in the frequency difference between neighboring modes. The objective of energy harvesters for microelectromechanical systems (MEMSs) is to transform mechanical vibrations into electrical power. Multiple types of nonlinear piezoelectric energy harvesters, which employ the use of cantilever structures and magnetic interactions, were examined and evaluated in [3]. Equations governing magnetic force are obtained by using a magnetizing current procedure. Through numerical analysis, the authors of [4] investigated the dynamics of a suspended pendulum with a forced Duffing oscillator. A bifurcation assessment of the pendulum was also carried out. The goal was to evaluate recent advancements in this field in a distinctive manner by utilizing dynamic analysis, mathematical modeling, and creative computer simulations. In [5], the nonlinear stability of the framework was analyzed during the full motion of a 3DOF damper SP. The dampened motion of an SP, in which the anchored point travels on a circular trajectory, was analyzed in [6]. Ref. [7] showed how a piezoelectric device stands apart from an electromagnetic instrument in the impact it has on a nonlinearly damped SP with two degrees of freedom. As the name suggests, a proportional–derivative controller (PD controller) is a controller that incorporates a combination of a “proportional action” and a “derivative action.” Basically, a gain multiplies either the variable or its error from the desired value. A proportional action is proportionate to the variable controlled or its error (the difference between the desired value and the actual value of the controlled variable). An action that assumes the derivative of the variable being monitored is identified as a derivative action. A dissolved Jeffcott rotor’s oscillations are designed to be mitigated by the PD controller applying two pairs of poles [8]. By contrasting it with PD controllers, Yan et al. [9] enhanced the teleoperation cyber-physical system’s (TCPS) steady-state and dynamical characteristics. The proposed technique aims to use a PD controller under excited states with a simultaneous resonance situation to reduce the vibrations of the MFC laminated shell structure. A controller for parametric primary forces and a time-delayed PD controller were presented by Eissa et al. [10,11] to reduce vibrations of magnetically contained systems with cubic and quadratic nonlinear coefficients underneath parametric fundamental forces. Feedback signal gain and time delay execution are monitored for the best possible results and a consistent range of time delays for high-quality performance. Proportional (P), proportional–integral (PI), and proportional–integral–derivative (PID) controllers are the three types of controllers that are displayed. To control the torsional vibration characteristics of a dynamical mechanism, we used PID control. Once the effects of P and PI control are observed, the PID controller seeks to improve system stability. This type of control guarantees that the structure is free of unstable parts [12]. As demonstrated, for instance, in [13,14,15], the PD approach was created to increase the robustness of robotic system control. Specifically, a fully adaptive PD controller can change the control torque in response to the end-effector’s set-point control error in real-time position monitoring. For cases when the solutions concurrently rely on substantially disparate scales, the multiple-scale technique is required [16,17,18]. Internal resonances of the plate with melted forces have been detected in two and three degrees of freedom by Mousa et al. [19] and Sayed et al. [20], respectively. The stability and perturbation strategy of the composite laminated piezoelectric rectangular plate under synchronous transverse and in-plane excitations has been explored by Sayed and Mousa [21]. For minimizing the flexural and torsional vibrations of the plate, Ashour and Nayfeh [22] utilized a nonlinear controller as a vibration absorber that relies on saturation processes. To improve the saturation control’s effectiveness, the framework now includes a measurement of the excitation frequency. The system’s performance is evaluated using the Runge–Kutta fourth-order procedure. The scheduled frequency response curves of the studied structure are analyzed for influences, containing substantial coefficients, within the numerical data [23]. Ref. [24] determined how the controlled system is affected by the effective parameters. Several response curves for the overall structure that display the stable and unstable zones when the controller is off and on have been plotted using the frequency response equation that was generated. In [25,26], bifurcation diagrams and Poincaré maps are used to analyze the bifurcation and chaotic behaviors in a Duffing oscillator. It also looks at ways to manage chaotic dynamics. On the contrary, Ref. [27] examined the nonlinear dynamics in rotor systems with an emphasis on bifurcation phenomena and chaos. Transitions between periodic and chaotic regimes were analyzed using the Poincaré maps. The investigators examined a 2DOF framework with piezoelectric devices and feedback control in [28]. Feedback structures, bifurcation habits, and stability are offered to enhance performance and control. We investigate the Duffing oscillator’s chaotic and stable dynamics under sinusoidal activation [29]. The bifurcation, stability limits, and chaotic transitions in nonlinear oscillators are explored. A piezoelectric energy harvester combined with coupled damped oscillators is discussed in [30]. The stability analysis of a class of switched nonlinear systems with delay and fluctuation feedback is the main emphasis of [31,32]. In [33], the authors presented a generalized framework for analyzing small-time local controllability (STLC) of switched nonlinear systems (SNSs). By introducing high-order control variations and geometric interpretations of “bad” Lie brackets, they establish a unified STLC condition that extends and connects existing controllability results for switched and non-switched linear and nonlinear systems.
The main contribution of this paper is the development of a nonlinear control framework for vibration reduction in a two-degree-of-freedom (2DOF) mechanical oscillator equipped with a piezoelectric energy harvester. A Proportional–Derivative (PD) controller is designed to minimize the settling time and improve the dynamic stability of the system. The Duffing-type oscillator with an attached pendulum and piezoelectric element represents a highly nonlinear and underactuated system. To analyze the system’s behavior, a combination of the Multiple-Scale Perturbation Technique (MSPT) and bifurcation analysis is utilized. The effectiveness of the proposed control approach is verified through numerical simulations using the fourth-order Runge–Kutta method. The novelty of this work lies in the synergy between vibration reduction, settling time minimization, and nonlinear bifurcation control via a piezoelectric interface.
The remainder of the paper is structured as follows: Section 2 introduces an overview of the proposed dynamical framework. Section 3 investigates perturbation analysis and formulates the system’s equations of motion. Section 4 assesses the system’s stability under various conditions. Section 5 presents detailed observations and discussions on the behavior of the system. Section 6 verifies the model using the FRC with and without control. Section 7 provides a bifurcation classification of the nonlinear system. Section 8 compares the findings with previously published research to highlight the contribution of the present work. Finally, Section 9 concludes the paper and outlines future research directions.
2. Overview of the Framework
Figure 1a illustrates a hybrid system that incorporates a vibration absorber based on a pendulum. Figure 1b illustrates an automotive suspension system, which describes the main function of an automobile’s suspension system as maintaining stability by counteracting outside forces. The forces that potholes, bumps, and other road impediments apply to the car’s body are referred to as external forces in this context. The suspension also provides better handling by keeping the vehicle steady at high speeds and in curves, which is one of the most important applications of the system, as shown in Figure 1a.
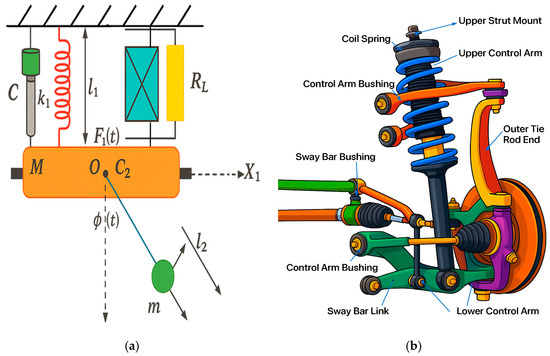
Figure 1.
(a) A visual representation model for the fundamental mechanism. (b) Suspension system in operation.
Below is a brief outline of its elements and purpose:
- A.
- The fundamental component of the mechanical base structure:
We provide a table that describes a piezoelectric or electromagnetic energy based on a coupled pendulum–oscillator system. The base mass is excited by an external force , causing it to oscillate . This motion induces the pendulum (, ) to swing . The pendulum’s movement is converted into electrical energy (Voltage ) through a transducer (not explicitly named but implied by ), which is dissipated over the load resistance . The elements , , and model the mechanical stiffness and damping of the system. All symbol descriptions and units can be illustrated in Table 1.

Table 1.
Complete table of symbols, their descriptions, and their typical International System of Units (SI units).
- B.
- Real-World Applications:
- Energy Harvesting in Infrastructure: Vibrations from passing cars or trains can be converted into electrical energy for sensors or structural health monitoring systems on bridges or railroads using comparable technologies.
- Vibration Reduction in Buildings: Pendulum-based TMDs can be incorporated into skyscrapers or buildings to generate electricity for embedded monitoring electronics and lessen swaying caused by wind or earthquakes.
- Industrial Machinery Monitoring: Such systems can power wireless sensor nodes used in predictive maintenance while also reducing vibrations in large machinery or rotating machinery.
- Autonomous Sensor Systems: They can be used in isolated or off-grid settings where changing the battery is not feasible. Sensors continue to operate continuously by harvesting vibration energy from the environment.
3. Motivation from Classical PH to PHPD (PH + PD)
The derivation of the equation system is concluded in Appendix B.
We added three distinct categories of controllers to the structure’s equations [25]:
It represents the many kinds of controls to reduce vibration. The control parameters are and .
First type: Piezoelectric Harvester Control (PH)
where: ,
Second type: Proportional–Derivative (PD)
The control parameters are presented as follows:
Third type: Piezoelectric Harvester Proportional–Derivative (PHPD)
where,
The flowchart diagram in Figure 2 summarizes the comparison between the different types of controllers:
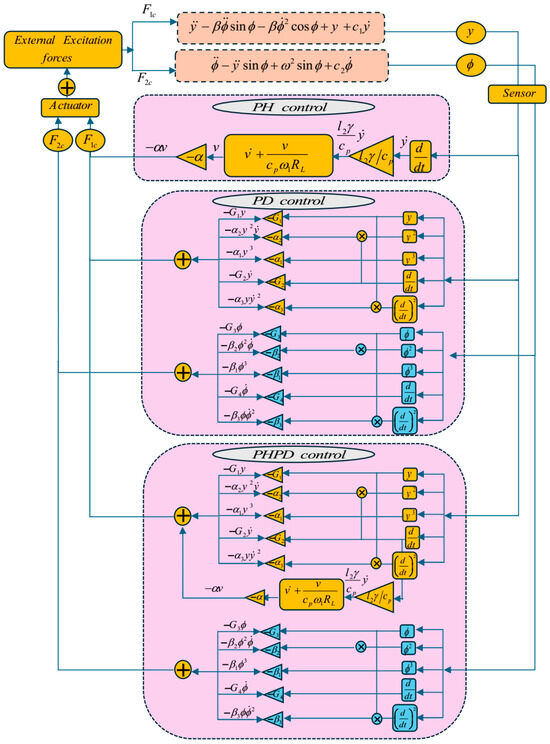
Figure 2.
The flowchart diagram for the main system with three different controllers.
Following the addition of PHPD controllers, the newly revised kinematics (1) and (2) motion corresponding to the hybrid system are expressed as follows:
It is believed that:
where and are minor perturbation components.
We should use the multiple-scale technique to obtain the third-order approximate estimate for Equations (5)–(7) to investigate the impacts of the PHPD controllers on the modified plate [16,17,18].
We obtain a response to (5)–(7) in the following manner:
where , , and . The derivatives have the following forms:
When Equations (8)–(11) are substituted into (5)–(7), we correlate the coefficients of powers and obtain the following:
The following are the most common solutions to Equations (12)–(14):
where and denote complex functions in .
We agree with the responses to each of the resulting equations, which are given as follows, by substituting (21)–(23) into (15)–(17). After neglecting the secular terms, we obtain the following:
Then, the first approximate solutions can be written as:
C.C. is the complex conjugate.
Substituting Equations (21)–(29) into (18)–(20) yields the following:
where, .
Consequently, the second-order approximate solutions, after neglecting the secular terms, are listed below:
From the obtained solutions of the equations, the resonance case can be considered as:
- (i)
- Primary resonance: or .
- (ii)
- Internal resonance: .
- (iii)
- Simultaneous resonance: internal and primary resonance.
This research considers the simultaneous resonance situation ( and ) to be the worst resonance case. In the next part, we will analyze and numerically examine the stability of this instance, respectively.
4. Assessment of Stability
4.1. Simultaneous Resonance Case
The improved model’s stability analysis will be examined in the event of simultaneous resonance.
The available detuning parameters are and .
Starting with the second approximations in (30)–(32) to obtain the solvability criteria, we insert (36) into secular and small-divisor terms to obtain the following:
From Equation (39), we can illustrate as:
where is the integration constant.
Using the polar formula to symbolize , we obtain the following:
where and signify the motion’s steady-state phases and amplitudes, respectively. The autonomous system equations are obtained by integrating the real and imaginary components of Equation (41) into Equations (37) and (38), respectively.
where, .
Then, we obtain the following:
4.2. Frequency Response Equations (FREs)
At , the model’s steady-state solution via PHPD controllers connected to the fixed points of (42)–(47) is obtained.
Then, FRE can be considered as:
4.3. Examination of Stability Adjacent to the Fixed Point
The following procedures are used to build the steady-state solution’s stability:
where and are perturbations expected to be minimal in comparison to and , which fulfills Equations (42)–(47). Use only the linear terms in and after replacing Equation (54) with Equations (42)–(47), along with the location. Then, we obtain the following:
The structure of the algebraic equation obtained in the subsequent matrix is as follows:
The right halves of Equations (55)–(58) can be utilized for defining the Jacobian matrix .
The following equation assumes the eigenvalues of :
denotes the coefficient found in Equation (58). Hence, (60) can be rewritten as follows:
where the coefficients of Equation (61) are , , , and , which are given in Appendix A. The solution of the system with PHPD is stable if the real branch of has a negative sign; if not, it is unstable. The next determinant D and all its primary minors must be positive for all the roots of Equation (61) to have negative real portions, according to the Routh–Hurwitz criterion [31].
5. Observations and Comments
This subsection describes the nonlinear dynamical framework that appeared in Figure 3 to describe Equations (1)–(3), which uses PH control. The MATLAB® R2023b computer program is then used to numerically simulate the associated PHPD control to select the optimal control, as seen in Figure 4. When the PHPD controllers are used, the vibration amplitudes for the primary system become 0.00025744 (), 5.10093 × 10−35 () as shown in Figure 4. This indicates that the vibrations are suppressed to about 99.67% () and 100% () of their value, with a time range of for and for . Hence, the components that are used for the modeling process are , , , , and at the initial conditions:
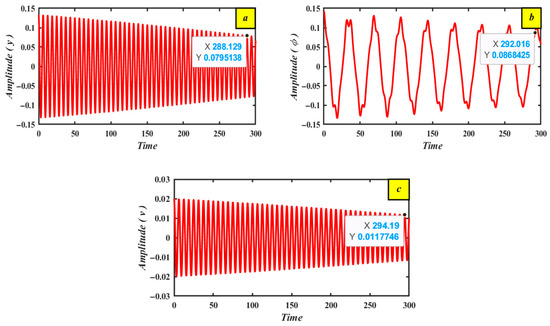
Figure 3.
Mechanisms of vibration amplitude with PH control (a) First system amplitude () (b) Second system amplitude () (c) Voltage amplitude ().
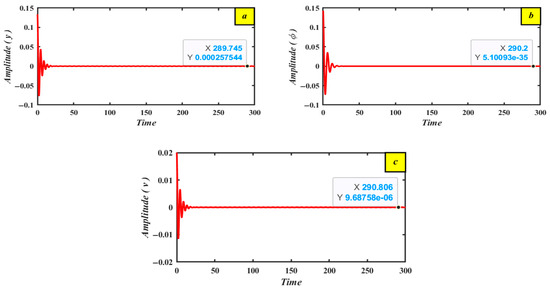
Figure 4.
The primary PHPD-controlled structure (a) First system amplitude () (b) Second system amplitude () (c) Voltage amplitude ().
By displaying their individual time histories, Figure 5 contrasts the perturbation techniques of Equations (42)–(47) with the computational simulation of Equations (5)–(7). The generalized coordinate’s amplitude modulation, as determined by the MSPT, is shown by the blue crossed lines. On the other hand, the mechanical system’s time history of oscillations as computed using the RK-4 technique with the PHPD controller is indicated by the red straight lines. The suggested method is validated by the strong agreement between the theoretical and computational results.
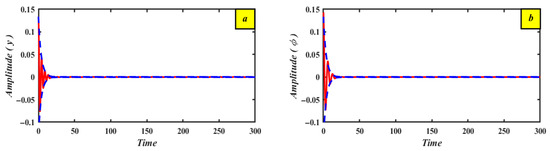
Figure 5.
Comparative analysis of numerical modeling (red) and perturbation assessment (blue) for the primary mechanism under PHPD control (a) First system amplitude () (b) Second system amplitude ().
The generated FRCs, which are shown in Figure 6 and Figure 7, provide a full description of the actions of the different coefficients of the controlled scheme that uses PHPD. Figure 6a–d show the collaboration between multiple parameters via the detuning parameter and the main system , while Figure 7a–e depict the behavior of the parameters with the detuning parameter and the system . Figure 6 and Figure 7 have just one peak with a stable region. After understanding the prior FRC, the amplitudes of the primary system () increase as increases, as seen in Figure 6a. Figure 6b illustrates how affects FRC. As the value of increases, the corresponding system curve falls. Figure 6c,d show the actions of and through and the primary system . Both and have a high amplitude for , with tiny values for both and , and subsequently, the amplitude decreases, with large values for both. Additionally, a dramatic drop in the amplitude of was noted for large values of .
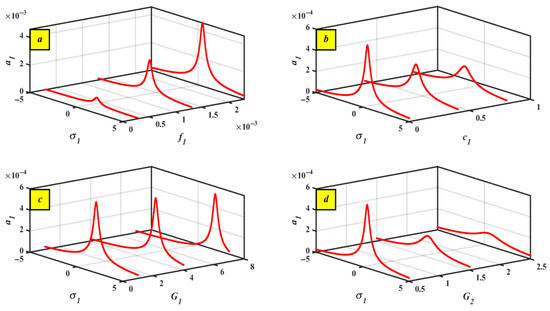
Figure 6.
Through the detuning parameter , the controlled structures interact with the primary mechanism (a) at different values of (b) at different values of (c) at different values of (d) at different values of .
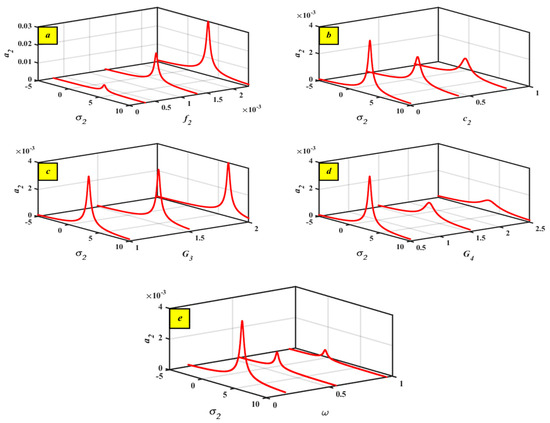
Figure 7.
Through the detuning parameter , the controlled structures interact with the amplitude of (a) at different values of (b) at different values of (c) at different values of (d) at different values of (e) at different values of the natural frequency .
We will now illustrate the effect of changing the value of the parameters via the detuning parameter and the system , as shown in Figure 7. The second system amplitude against is shown in Figure 7a. There is a single peak around . The FRC demonstrates that the amplitude of increases as f increases. It depicts the decreasing amplitude curves for Figure 7b,d,e. These outcomes were achieved by raising the values of , , and . The consequence of on the FRC is demonstrated in Figure 7c, revealing that the beak relocated to the right and the amplitude of rose as the quantity of increased.
6. Verification Within FRC Before and After PHPD
The performance of the uncontrolled systems and in the FRC before and after introducing PHPD are shown in Figure 8. The best option for lowering the vibration amplitude is the PHPD controller, while the detuning parameters and fall within the ranges of and , respectively.
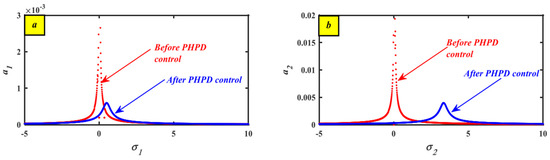
Figure 8.
FRC before and after PHPD: (a) via and (b) via .
7. Bifurcation Classification
To comprehend the intricacy of nonlinear dynamical phenomena, it is essential to examine chaotic actions in this section. When the framework’s characteristics are altered, as they are in our situation, the system undergoes a change that can result in a variety of behaviors, ranging from complete chaos to stable periodic motions. The bifurcation schematic, which illustrates how the system reforms as a critical parameter changes, successfully captures this shift. An analysis of the Lyapunov Exponent is additionally available. The dynamic behavior of a nonlinear system regarding a variable control or mechanism parameter, represented by in Figure 9, is depicted by two bifurcation diagrams, labeled as (a) and (b). We will now present the findings of the first section, which examines the relationship between and . The framework displays a chaotic state for small amounts of (), as indicated by the dense and scattered spots in the bifurcation diagram of against what Figure 9a depicts. The system then experiences bifurcations as rises above , ultimately moving toward periodic or quasi-periodic behavior (more organized and distinct points). The system seems to stabilize at the last area, exhibiting more regular oscillations or steady-state behavior, with larger amounts of (). The behavior bifurcation diagram is shown in Figure 9b ( via ). For low levels, chaotic dynamics are seen, much like in diagram (a). As increases (), bifurcations and a shift to periodicity are suggested by the scatter becoming less dense and more ordered. The LLE is displayed in the illustration of Figure 10 as a function of . For , the chaotic regime is confirmed by the extreme LLE, which also matches the bifurcation charts showing scattered points. Then, for (), the mechanism moves via bifurcations toward more regular behavior when LLE drastically drops and varies, indicating that chaos is being repressed. At the last region (), LLE steadies with minor fluctuations around its smallest value, which implies that the more structured periodic activity in the bifurcation diagrams is consistent with reduced chaos or weakly chaotic behavior. Two-phase portraits in Figure 11 depict the state-space trajectories of a nonlinear dynamical system at a particular parameter value, . The previously displayed bifurcation diagrams and Lyapunov exponent support the idea that this value belongs to a regime in which the system behaves in a chaotic manner. At , we can concentrate on some points. In either state-space projection, the entire system behaves chaotically, and the framework is in a classical weird attractor condition where its paths never repeat but are nonetheless bounded. A coherent picture of chaos is presented by these graphs in conjunction with the earlier bifurcation and Lyapunov exponent diagrams. Lastly, the chaotic nature is confirmed by the absence of periodicity or transitions to order, which may be detected using the red Poincaré sections.
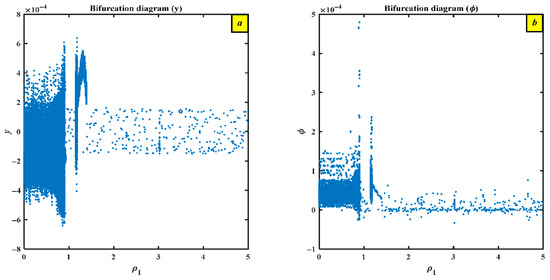
Figure 9.
Bifurcation diagrams of (a) vs. (b) vs. .
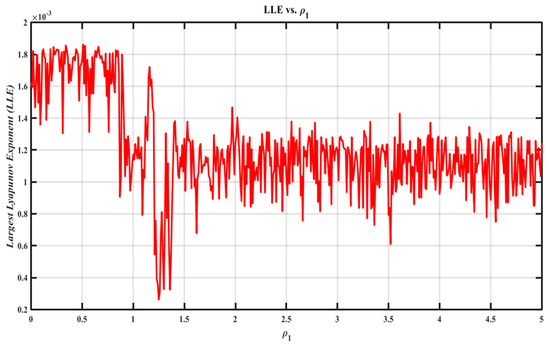
Figure 10.
LLE as a function of .
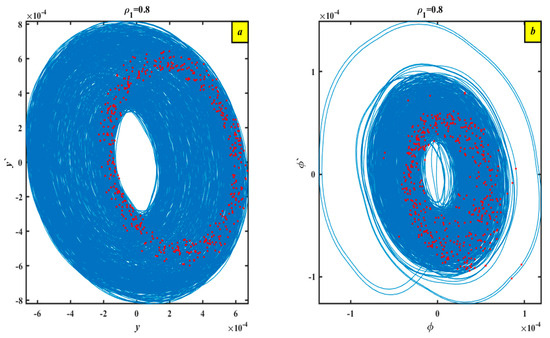
Figure 11.
The chaotic action phase portraits and Poincaré maps when (a) vs. (b) vs. .
Two-phase pictures (subplots a and b) of a nonlinear dynamical system with a parameter estimate are displayed in Figure 11. Both visualizations show intricate and possibly chaotic dynamics with dispersed points and dense trajectories, suggesting a substantial change in the behavior of the system in comparison to earlier instances. Plotting and while examining the route creates a toroidal or donut-like shape, as shown in Figure 11a. A quasi-periodic or chaotic attractor with dense non-repeating motion is represented by the blue lines. The central hole implies that the track continuously circles the center rather than ever crossing it. Because of their irregular dispersion, the red spots are probably Poincaré section points or markers that demonstrate discontinuous sampling of the trajectory, verifying chaotic or quasi-periodic activity. Figure 11b, which plots and , has a different scale and form but displays a toroidal structure that is comparable to that in Figure 11a. Uneven spacing and inner loops point to chaotic evolution. Additionally, the red pixels are dispersed erratically, which lends credence to the idea of chaotic dynamics. Two subplots (designated as a and b) in Figure 12 display phase portraits of a nonlinear structure for a given parameter measurement, . Zoomed-in insects that display significant centralized variations in behavior are included in both charts, which also demonstrate the way the system responds in phase space. The dominant configuration in the first section of Figure 12a is a closed and smooth limit cycle, which suggests periodic behavior. The system trajectory is shown by the dense blue curve. Critical dynamics or a region of interest is indicated by a tiny red segment. The graph focuses on a loop construction, which is probably a sign of a fine-scale limit cycle, supplementary oscillation, or mild nonlinear activity inside the larger cycle. Poincaré sections or extensive data sampling are indicated by white line shading. In the second section of Figure 12b, a closed periodic orbit once more displays a limit cycle. Regular fluid motion is delineated by the blue curve. An important area of interest is shown by the red section. The red section of the trajectory is the focus of the zoomed-in figure. Like Figure 12a, which displays a little loop or lobe, this one most probably represents a subharmonic oscillation or a dynamic transition region. Phase space trajectories are used to illustrate the evolution of system variables in Figure 13. Figure 13a shows the variable phase plane trajectory together with its time derivative . A nonlinear and potentially chaotic or multi-periodic behavior is indicated by the red curve. A reference solution, such as a theoretical prediction or numerical baseline, is represented by a thin black dashed line. The phase picture for the variable and its time derivative is shown in Figure 13b. More intricacy in the trajectory could be a sign of bifurcation, multi-stability, or even chaotic motion. With obvious folds and numerous loops, the red trajectory once more takes a nonlinear course. Again, a baseline or steady-state solution might be represented by the dashed black line.
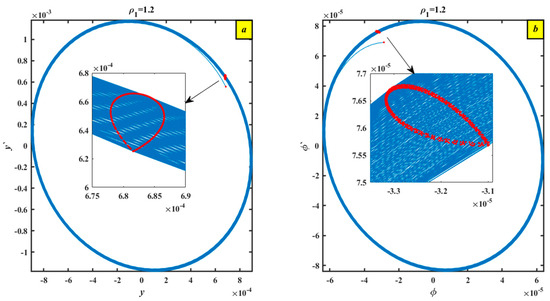
Figure 12.
The chaotic action phase portraits and Poincaré maps when (a) vs. (b) vs. .
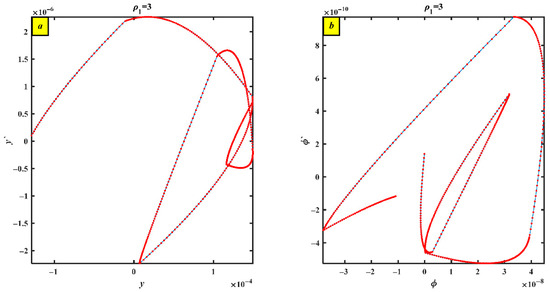
Figure 13.
A nonlinear dynamical mechanism’s phase portraits (blue) and Poincaré maps (red) with the value of the parameter (a) vs. (b) vs. .
8. Comparison with Earlier Published Works
The authors examined the nonlinear lively performance of the damped linear oscillator, which is its main component, in conjunction with an unstretched pendulum, in contrast to a recently published study [25]. In addition, a piezoelectric transducer was incorporated into the dynamical system under different excitation force quantities. The stability was taken into consideration, and MSPT was used to provide an analytical explanation. Additionally, they examined the mechanism in several primary external resonance settings.
The three-degree-of-freedom system was used to show how we added the PHPD controller to the system model of [25] in this article. We were able to numerically reduce the vibrations in the identical system for 1:1 internal and primary resonance situations. Numerical representations are provided of the stability and vibration bandwidth regions at various system and control factor values. The most important observation and the most significant result that favor this work over the previous work in [25] is the system’s damping time. In the last study [25], it was found that the system’s vibration level was reduced to a time of , whereas the system with PHPD control eliminated the vibration at . This is a significant difference that deserves further research and explanation.
9. Conclusions
- A Piezoelectric Harvester Proportional–Derivative (PHPD) controller was successfully proposed, integrating the harvester’s electrical output into the feedback loop for simultaneous vibration suppression and energy utilization.
- The nonlinear electromechanical system, originally modeled as 2DOF, was extended to a 3DOF model after incorporating control input, enabling a more comprehensive representation of system dynamics.
- The third-order Multiple-Scale Perturbation Technique (MSPT) was applied to derive accurate reduced-order analytical solutions, effectively capturing the system’s nonlinear behavior.
- The PHPD controller showed significant vibration amplitude reduction, especially near resonant frequencies, demonstrating its high effectiveness.
- By studying the effect of parameters on the existence of the detuning parameter , we found that the amplitude of is increased as increases but decreases with an increase in , , and .
- By studying the effect of parameters on the existence of the detuning parameter , we found that the amplitude of is increased as and increase but decreases with an increase in the other parameters.
- Stability analysis via 3D frequency response surfaces confirmed the controller’s ability to ensure robust and predictable dynamic responses.
- Analytical predictions were validated through numerical simulations using the fourth-order Runge–Kutta method, showing excellent agreement.
- When the PHPD controllers are used, the vibration amplitudes for the primary system become 0.00025744 (), 5.10093 × 10−35 () as shown in Figure 4. This indicates that the vibrations are suppressed to about 99.67% () and 100% () of their values. This percentage is given using the following relationship: Percentage = (amplitude before-amplitude after)/(amplitude before) %.
- Detailed bifurcation diagrams and LLE computations verified transitions between periodic, quasi-periodic, and chaotic regimes, improving the reliability of stability assessment.
- The results demonstrate a new pathway for energy-efficient, high-performance control in nonlinear electromechanical systems, with potential applications in smart structures and vibration energy harvesting.
Future Research Directions
- Implement intelligent control techniques (e.g., fuzzy logic, adaptive control, or neural networks) to enhance system robustness and improve vibration suppression.
- Analyze the influence of external disturbances and noise on the stability and efficiency of the piezoelectric energy-harvesting system.
- Conduct experimental investigations to evaluate the actual energy-harvesting efficiency of the proposed PHPD-controlled piezoelectric system. These measurements will validate the simulation results shown in Figure 7 and provide insight into the system’s real-world performance.
- Optimize controller parameters to maximize both vibration suppression and harvested energy under various operating conditions.
- Extend the model to include fractional-order controllers or time-delayed feedback mechanisms to improve dynamic response and efficiency.
- Investigate the system’s performance under varying environmental and operational conditions to ensure adaptability and reliability.
- Compare simulation-based predictions with experimental data to refine the control strategy and improve the accuracy of energy-harvesting estimations.
- Apply the proposed control strategy to experimental prototypes or real-world mechanical systems to demonstrate practical feasibility.
Author Contributions
F.T.E.-B.: Methodology, software, validation, data curation, reviewing, and editing. R.K.H.: Investigation, methodology, formal analysis, reviewing and editing, and funding acquisition. A.T.E.-S.: Conceptualization, investigation, resources, software, methodology, writing—original draft preparation, visualization, reviewing, and editing. M.W.: Investigation, methodology, data curation, validation, reviewing, and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2503).
Data Availability Statement
All data generated or analyzed during this study are included in this published article.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU), KSA, for funding this research work through the project number “IMSIU-DDRSP2503”.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix B
The Lagrangian function for a dynamical system has the formula ; so, it will be in the following form:
where primes represent the derivatives with respect to time .
Lagrange’s equation is critical in our study for deriving the equation of motion, as follows:
where represents the generalized velocities and indicates the generalized coordinates.
The generalized forces and correspond to the coordinates, as follows:
Given the following descriptions of the dimensionless parameters:
Equations (A1), (A3), and (A4) are inserted into (A4) to generate the dimensionless version of the equation of motion of the system (1)–(3).
References
- Masood, A.; Khan, N.M.; Khan, F. Multi-degrees of freedom energy harvesting for broadband vibration frequency range. Sens. Actuators A Phys. 2022, 344, 113690. [Google Scholar] [CrossRef]
- Bai, X.; Wen, Y.; Li, P.; Yang, J.; Xiao, P.; Yue, X. Multimodal vibration energy harvesting utilizing spiral cantilever with magnetic coupling. Sens. Actuators A 2014, 209, 78–86. [Google Scholar] [CrossRef]
- Sun, S.; Leng, Y.; Hur, S.; Sun, F.; Chen, X.; Song, H.C.; Kang, C.Y. Force and stability mechanism analysis of two types of nonlinear mono-stable and multi-stable piezoelectric energy harvesters using cantilever structure and magnetic interaction. Smart Mater. Struct. 2023, 32, 035003. [Google Scholar] [CrossRef]
- Brzeski, P.; Perlikowski, P.; Yanchuk, S.; Kapitaniak, T. The dynamics of the pendulum suspended on the forced Duffing oscillator. J. Sound Vib. 2012, 331, 5347–5357. [Google Scholar] [CrossRef]
- Amer, T.S.; Bek, M.A.; Hassan, S.S.; Elbendary, S. The stability analysis for the motion of a nonlinear damped vibrating dynamical system with three degrees of freedom. Results Phys. 2021, 28, 104561. [Google Scholar] [CrossRef]
- Chatterjee, S. Resonant locking in viscous and dry friction damper kinematically driving mechanical oscillators. J. Sound Vib. 2013, 332, 3499–3516. [Google Scholar] [CrossRef]
- Abohamer, M.K.; Awrejcewicz, J.; Starosta, R.; Amer, T.S.; Bek, M.A. Influence of the motion of a spring pendulum on energy-harvesting devices. Appl. Sci. 2021, 11, 8658. [Google Scholar] [CrossRef]
- Saeed, N.; Kamel, M. Nonlinear PD-controller to suppress the nonlinear oscillations of horizontally supported Jeffcott-rotor system. Int. Non-Linear Mechanics. 2016, 87, 109–124. [Google Scholar] [CrossRef]
- Yan, J.; Yang, X.; Luo, X.; Guan, X. Dynamic gain control of teleoperating cyber-physical system with time-varying delay. Nonlinear Dyn. 2019, 95, 3049–3062. [Google Scholar] [CrossRef]
- Eissa, M.; Kandil, A.; El-Ganaini, W.A.; Kamel, M. Analysis of a nonlinear magnetic levitation system vibrations controlled by a time-delayed proportional derivative controller. Nonlinear Dyn. 2015, 79, 1217–1233. [Google Scholar] [CrossRef]
- Eissa, M.; Kandil, A.; Kamel, M.; El-Ganaini, W. On controlling the response of primary and parametric resonances of a nonlinear magnetic levitation system. Meccanica 2015, 50, 233–251. [Google Scholar] [CrossRef]
- Alluhydan, K.; EL-Sayed, A.T.; El-Bahrawy, F.T. The Effect of Proportional, Proportional-Integral, and Proportional-Integral-Derivative Controllers on Improving the Performance of Torsional Vibrations on a Dynamical System. Computation 2024, 12, 157. [Google Scholar] [CrossRef]
- Zi, B.; Duan, B.; Du, J.; Bao, H. Dynamic modeling and active control of a cable-suspended parallel robot. Mechatronics 2008, 18, 1–12. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, Y.; Feng, Z. Transactions on Intelligent Welding Manufacturing; Springer: Berlin/Heidelberg, Germany, 2019; Volume III, No. 4. [Google Scholar] [CrossRef]
- Homayounzade, M.; Khademhosseini, A. Disturbance Observer-based Trajectory Following Control of Robot Manipulators. Int. J. Control. Autom. Syst. 2019, 17, 203–211. [Google Scholar] [CrossRef]
- Nayfeh, J.F.; Nayfeh, A.H.; Mook, D.T. Nonlinear Response of Thick Laminated Composite Plates. In Proceedings of the ASME 1991 Design Technical Conferences, 13th Biennial Conference on Mechanical Vibration and Noise: Machinery Dynamics and Element Vibrations, Miami, FL, USA, 22–25 September 1991; ASME: New York, NY, USA; p. 321. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Perturbation Methods; Wiley: New York, NY, USA, 2000. [Google Scholar] [CrossRef]
- Nayfeh, A. Resolving controversies in the application of the method of multiple scales and the generalized method of averaging. Nonlinear Dyn. 2005, 40, 61–102. [Google Scholar] [CrossRef]
- Mousa, A.A.; Sayed, M.; Eldesoky, I.M.; Zhang, W. Nonlinear stability analysis of a composite laminated piezoelectric rectangular plate with multi-parametric and external excitations. Int. J. Dyn. Control. 2014, 2, 494–508. [Google Scholar] [CrossRef]
- Sayed, M.; Mousa, A.A.; Mustafa, I.H. Stability analysis of a composite laminated piezoelectric plate subjected to combined excitations. Nonlinear Dyn. 2016, 86, 1359–1379. [Google Scholar] [CrossRef]
- Sayed, M.; Mousa, A.A. Vibration, stability, and resonance of angle-ply composite laminated rectangular thin plate under multi excitations. Math. Probl. Eng. 2013, 2013, 1–26. [Google Scholar] [CrossRef]
- Ashour, O.N.; Nayfeh, A.H. Adaptive control of flexible structures using a nonlinear vibration absorber. Nonlinear Dyn. 2002, 28, 309–322. [Google Scholar] [CrossRef]
- Bauomy, H.S.; EL-Sayed, A.T.; El-Bahrawy, F.T.; Salem, A.M. Safety of a continuous spinning Shaft’s structure from nonlinear vibration with NIPPF. Alex. Eng. J. 2023, 67, 193–207. [Google Scholar] [CrossRef]
- Bauomy, H.S.; EL-Sayed, A.T.; El-Bahrawy, F.T. Integral resonant negative derivative feedback suppression control strategy for nonlinear dynamic vibration behavior model. Chaos Solitons Fractals 2024, 189, 115686. [Google Scholar] [CrossRef]
- Amer, T.S.; Abdelhfeez, S.A.; Elbaz, F.R.; Abohamer, M.K. Investigation of the Dynamical Analysis, Stability, and Bifurcation for a Connected Damped Oscillator with a Piezoelectric Harvester. J. Vib. Eng. Technol. 2025, 13, 155. [Google Scholar] [CrossRef]
- Xu, C.J.; Wu, Y.S. Bifurcation control for a duffing oscillator with delayed velocity feedback. Int. J. Autom. Comput. 2016, 13, 596–606. [Google Scholar] [CrossRef]
- Wang, C.C.; Jang, M.J.; Yeh, Y.L. Bifurcation and nonlinear dynamic analysis of a flexible rotor supported by relative short gas journal bearings. Chaos Solitons Fractals 2007, 32, 566–582. [Google Scholar] [CrossRef]
- Bahnasy, T.A.; Amer, T.S.; Abohamer, M.K.; Abosheiaha, H.F.; Elameer, A.S.; Almahalawy, A. Stability and bifurcation analysis of a 2DOF dynamical system with piezoelectric device and feedback control. Sci. Rep. 2024, 14, 26477. [Google Scholar] [CrossRef]
- Abohamer, M.K.; Amer, T.S.; Arab, A.; Galal, A. Analyzing the chaotic and stability behavior of a duffing oscillator excited by a sinusoidal external force. J. Low Freq. Noise Vib. Act. Control. 2024, 44, 969–986. [Google Scholar] [CrossRef]
- Amer, T.; Abdelhfeez, S.A.; Elbaz, R.F.; Abohamer, M. Exploring dynamics, stability, and bifurcation in a coupled damped oscillator with piezoelectric energy harvester. J. Low Freq. Noise Vib. Act. Control. 2024, 44, 938–958. [Google Scholar] [CrossRef]
- Strogatz, S.H. Symmetry in Nonlinear Dynamics and Chaos II. Symmetry 2025, 17, 846. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, L. On stability of a class of switched nonlinear systems. Automatica 2013, 49, 305–307. [Google Scholar] [CrossRef]
- Meng, Q.; Yang, H. Small-time Local Controllability of Switched Nonlinear Systems. IEEE Trans. Autom. Control. 2020, 66, 5422–5428. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).