High-Temperature Degradation of Throttling Performance in While-Drilling Jars Induced by Thermal Expansion and Fluid Rheology
Abstract
1. Introduction
2. The Throttling Principle of Drilling Jar
3. Mathematical Modeling of Throttling of Throttle Valve
3.1. Mathematical Modeling of Throttling
3.1.1. Basic Assumptions
- (1)
- The hydraulic oil is treated as a continuous medium;
- (2)
- The density variation of hydraulic oil during flow is minimal, and it is considered as incompressible fluid;
- (3)
- The interior of the drilling jar is assumed to be completely filled with hydraulic oil;
- (4)
- The throttling effect is primarily concentrated near the throttle valve, and pressure losses in other flow passages are considered negligible;
- (5)
- The sealing performance of the drilling jar is assumed to remain intact under high-temperature downhole conditions.
3.1.2. Mathematical Modeling
3.2. Governing Equations
3.2.1. Mass Conservation Equation
3.2.2. Momentum Conservation Equation
3.2.3. Energy Conservation Equation
3.3. RNG k-ε Model
4. Experimental Test
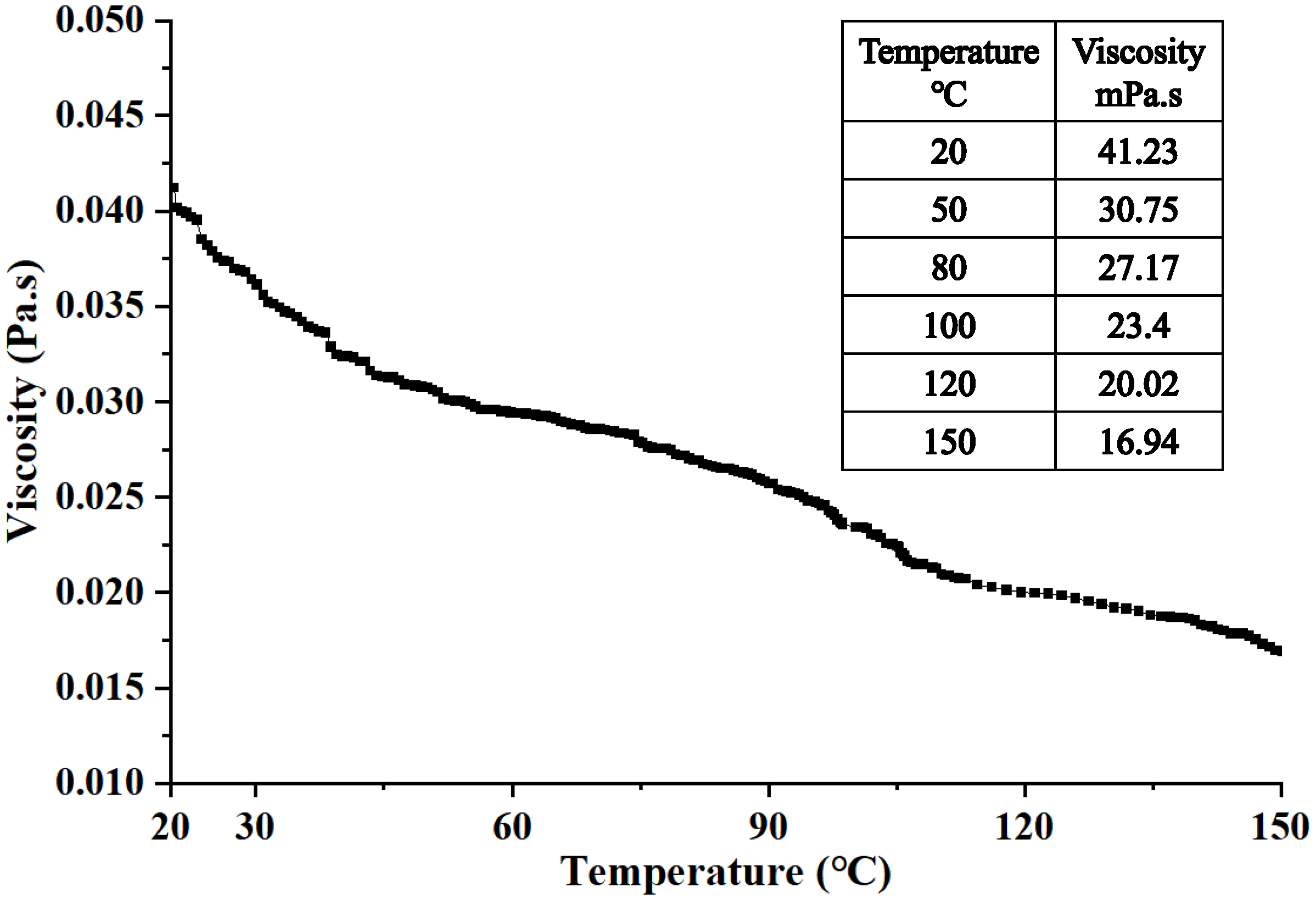
4.1. Hydraulic Oil Rheological Property Test
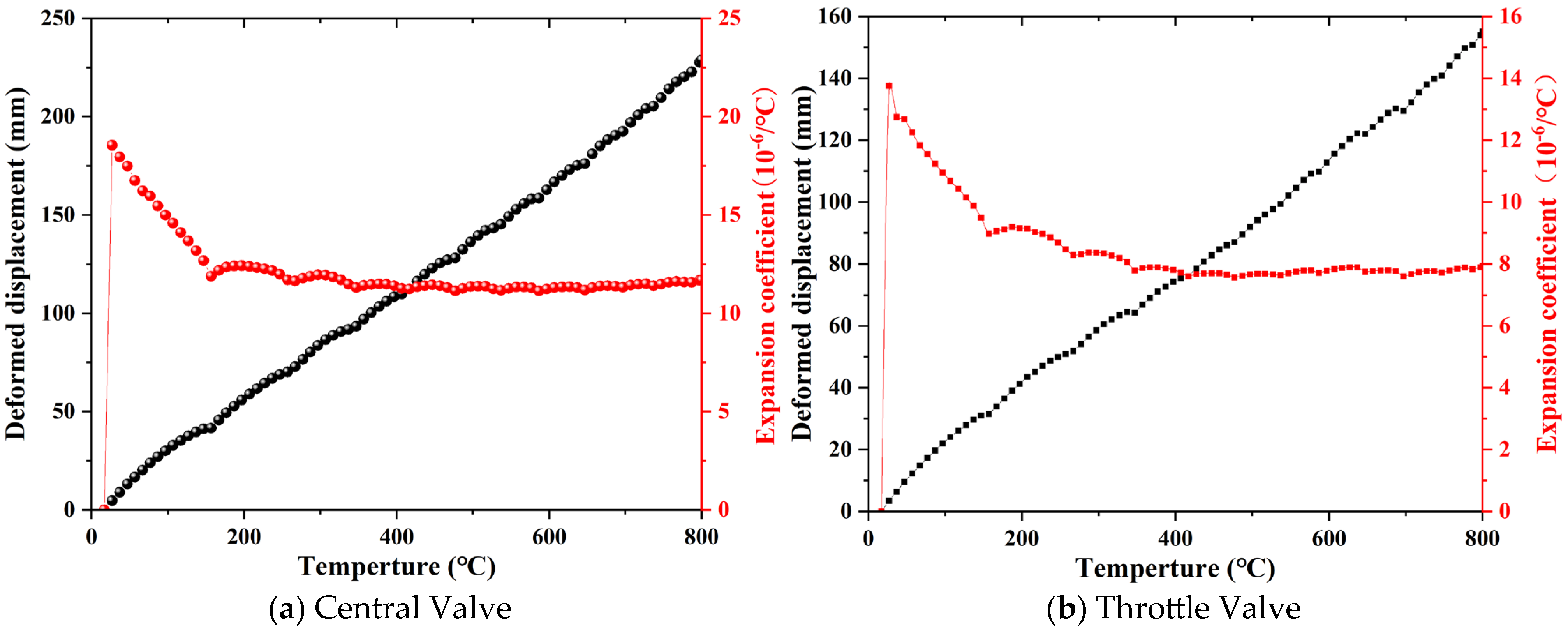
4.2. Thermal Expansion Performance of Metal Components
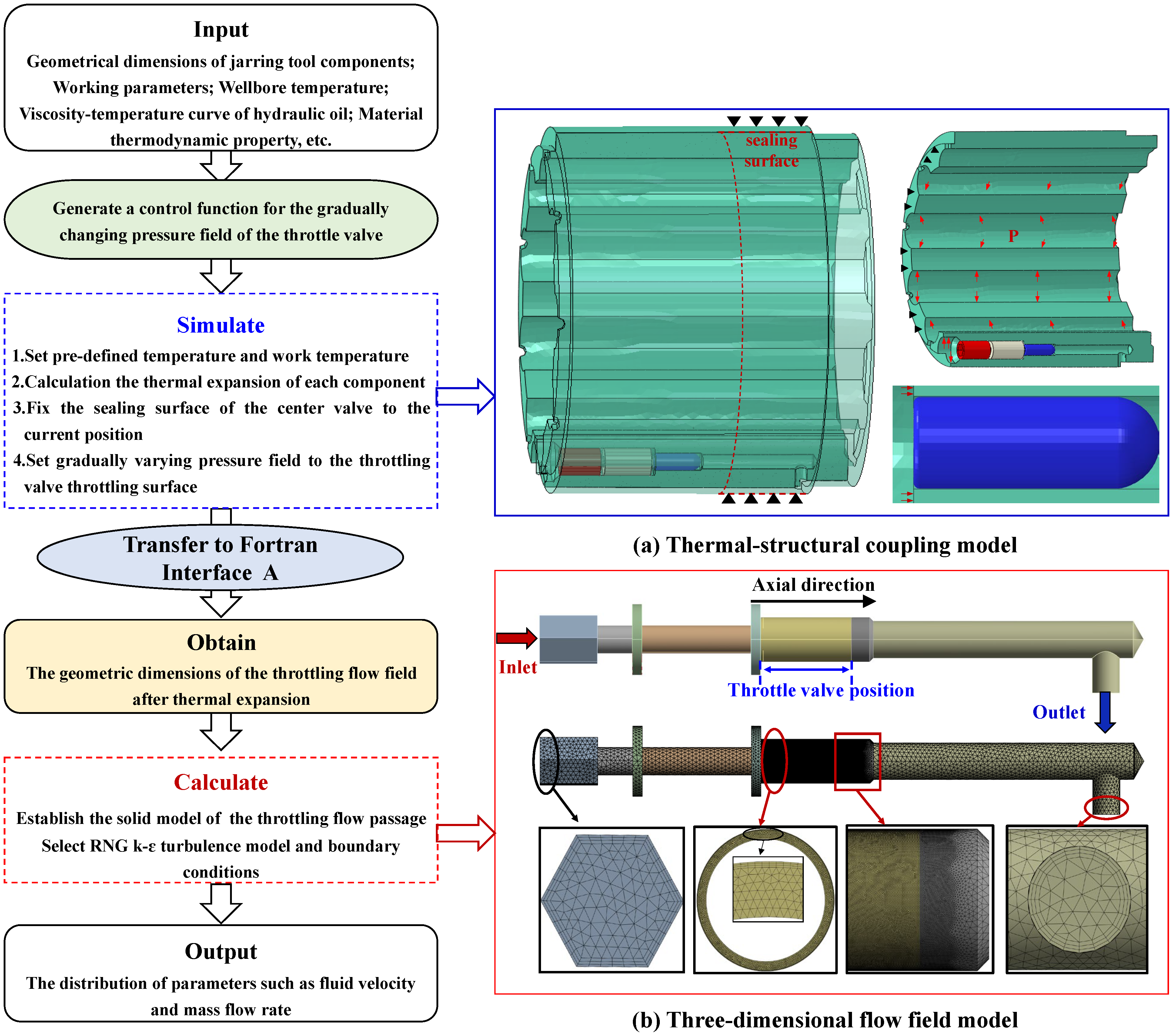
5. Numerical Simulation
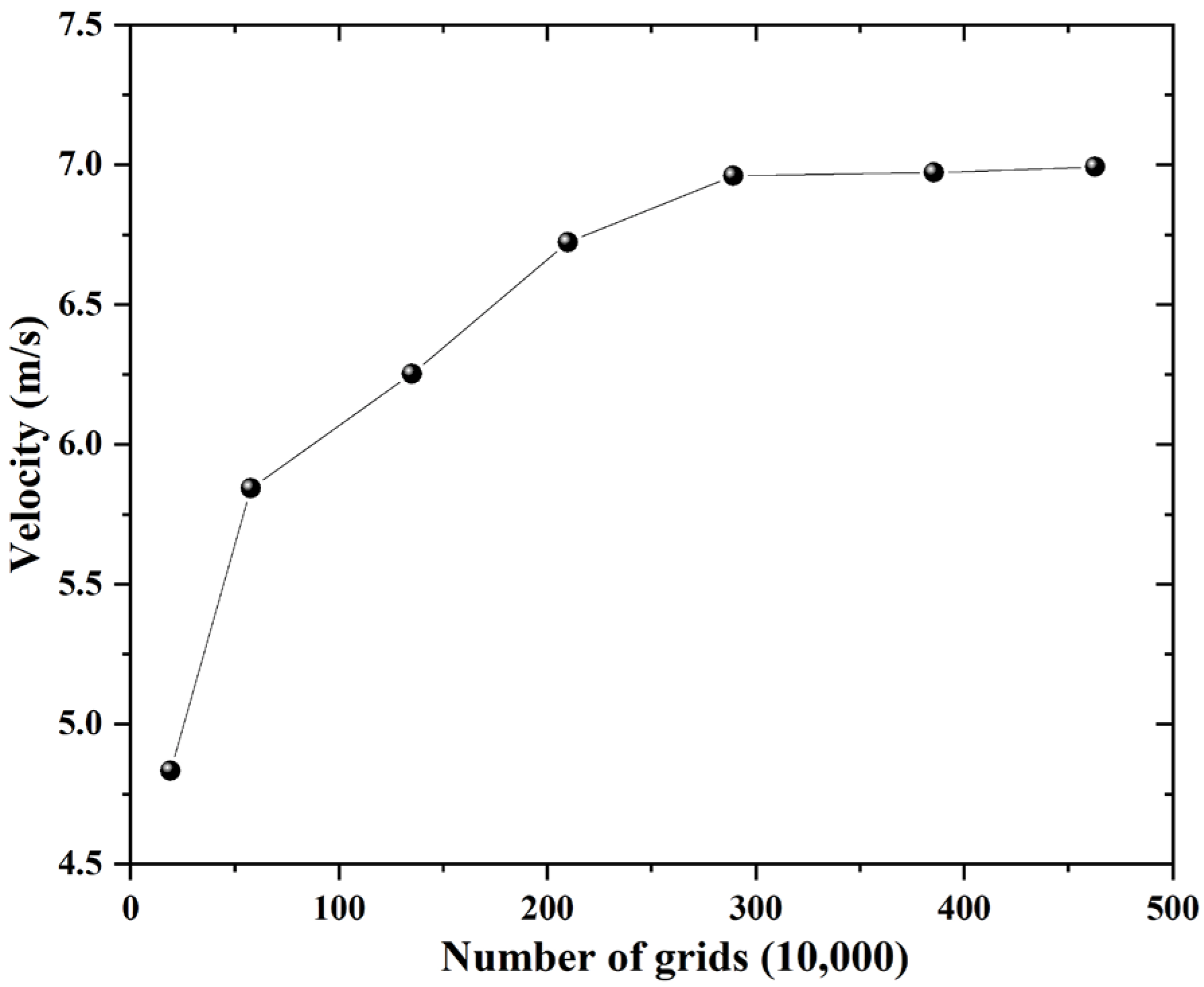
5.1. Simulation Model
5.2. Simulation Result
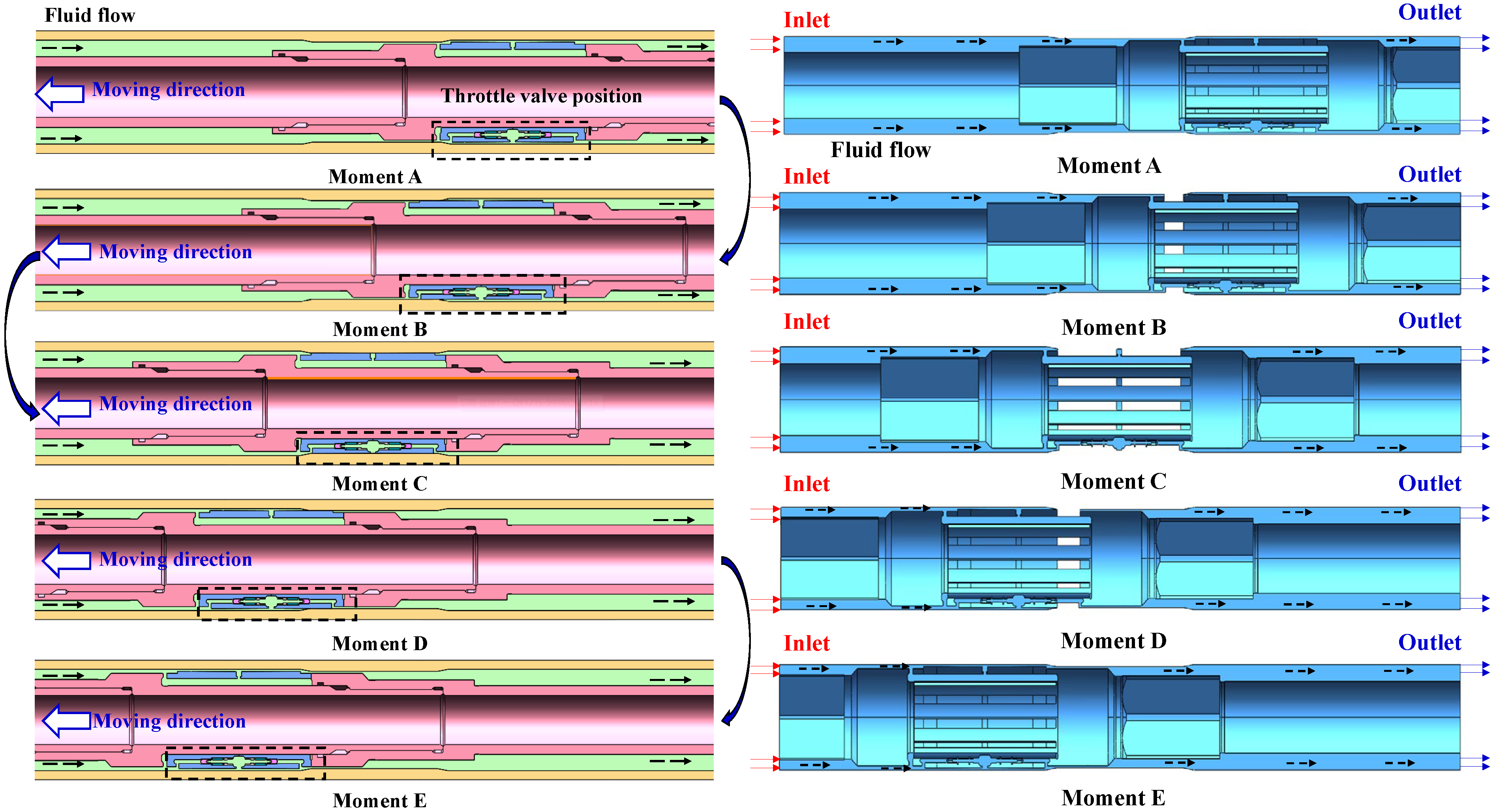
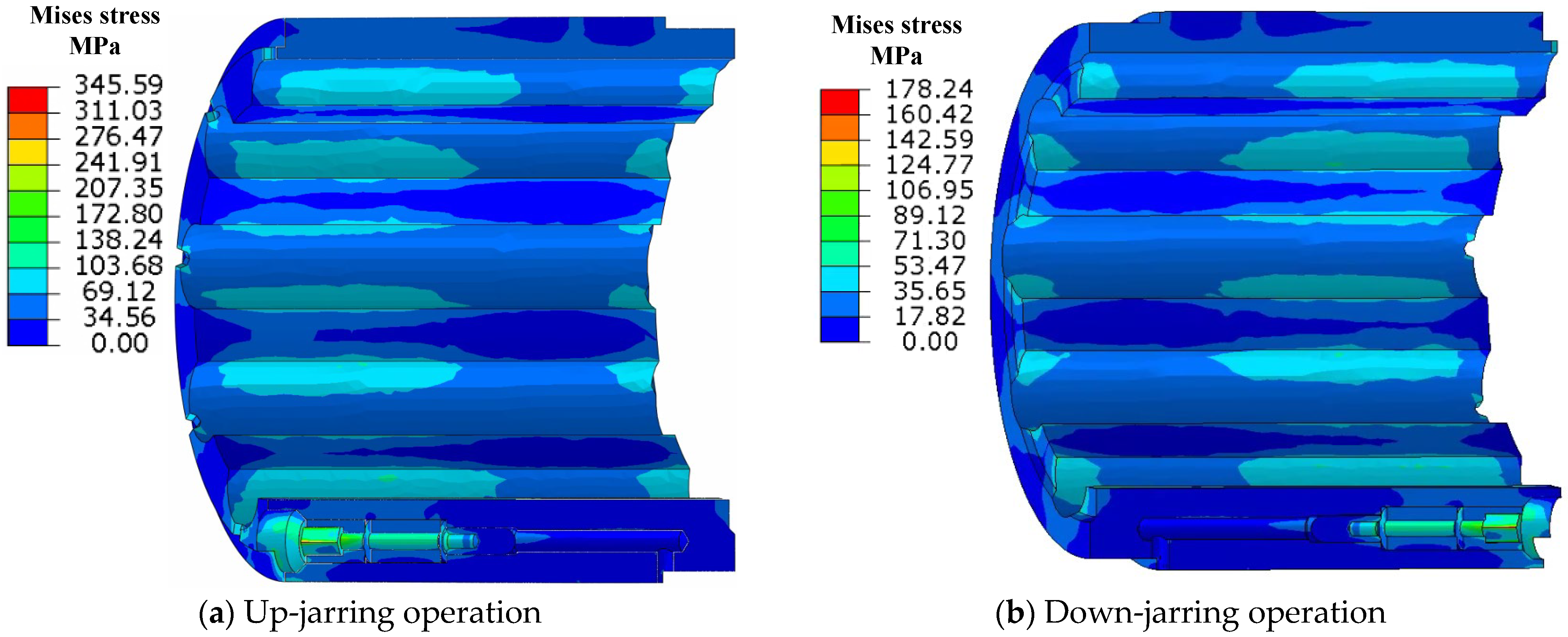
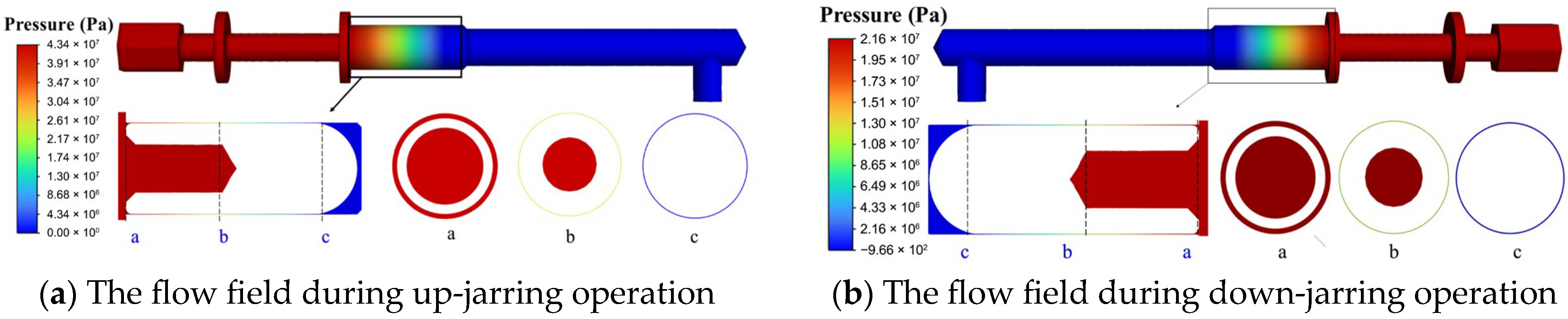
5.2.1. Analysis of Throttling Characteristics Under Conventional Working Conditions
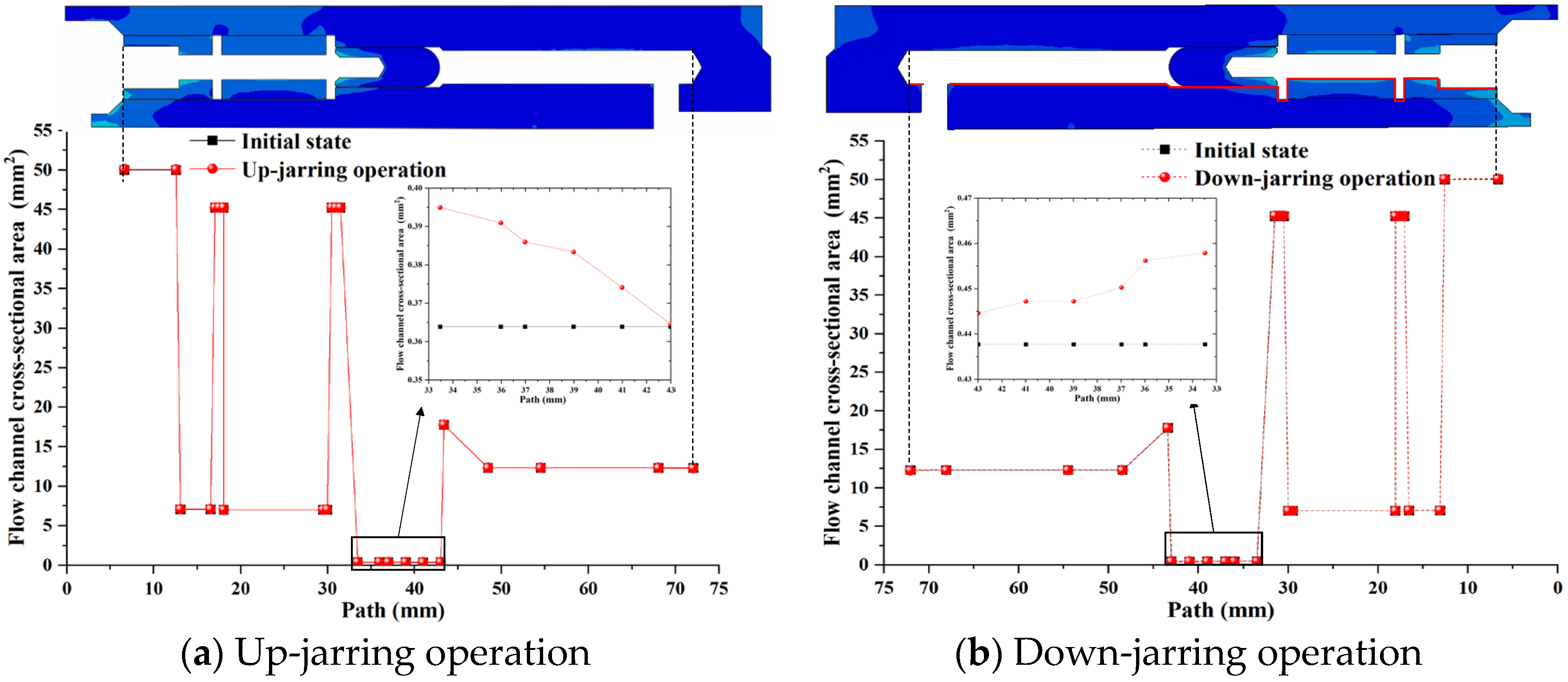
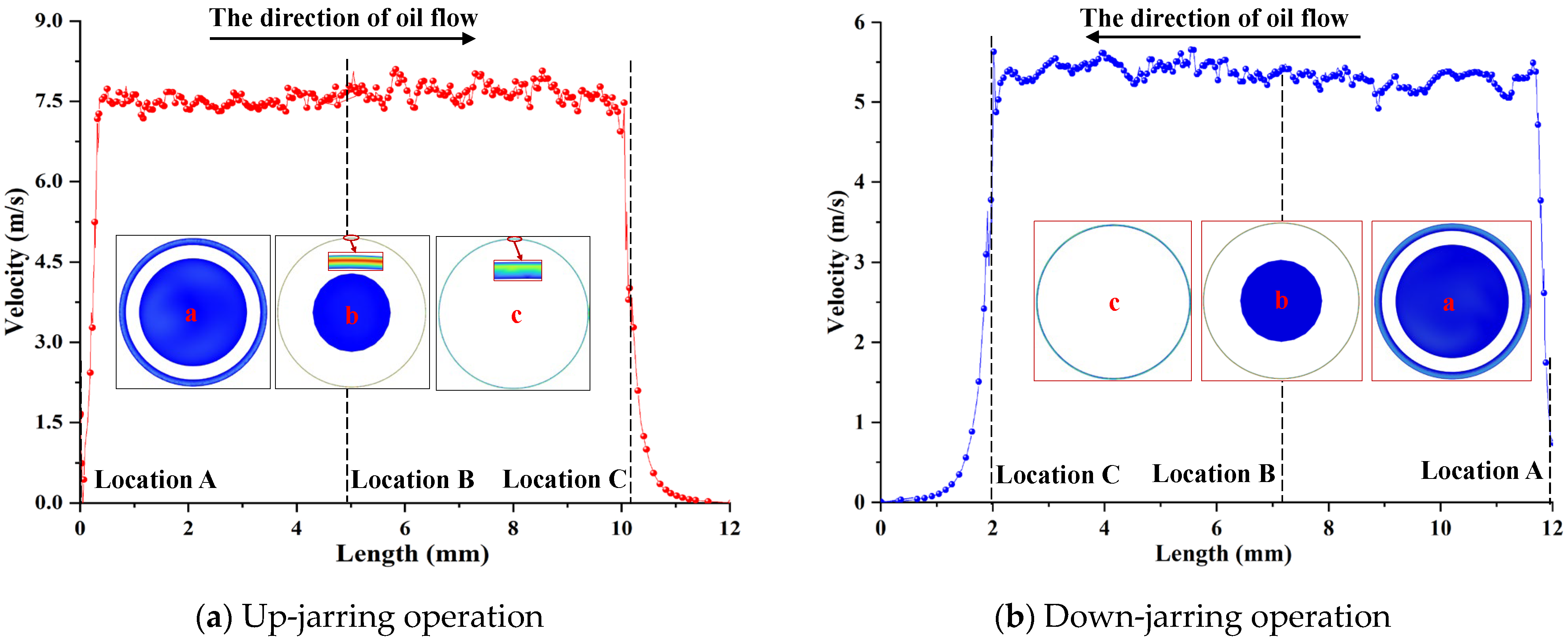
5.2.2. Distribution Characteristics of the Throttle Valve Flow Field
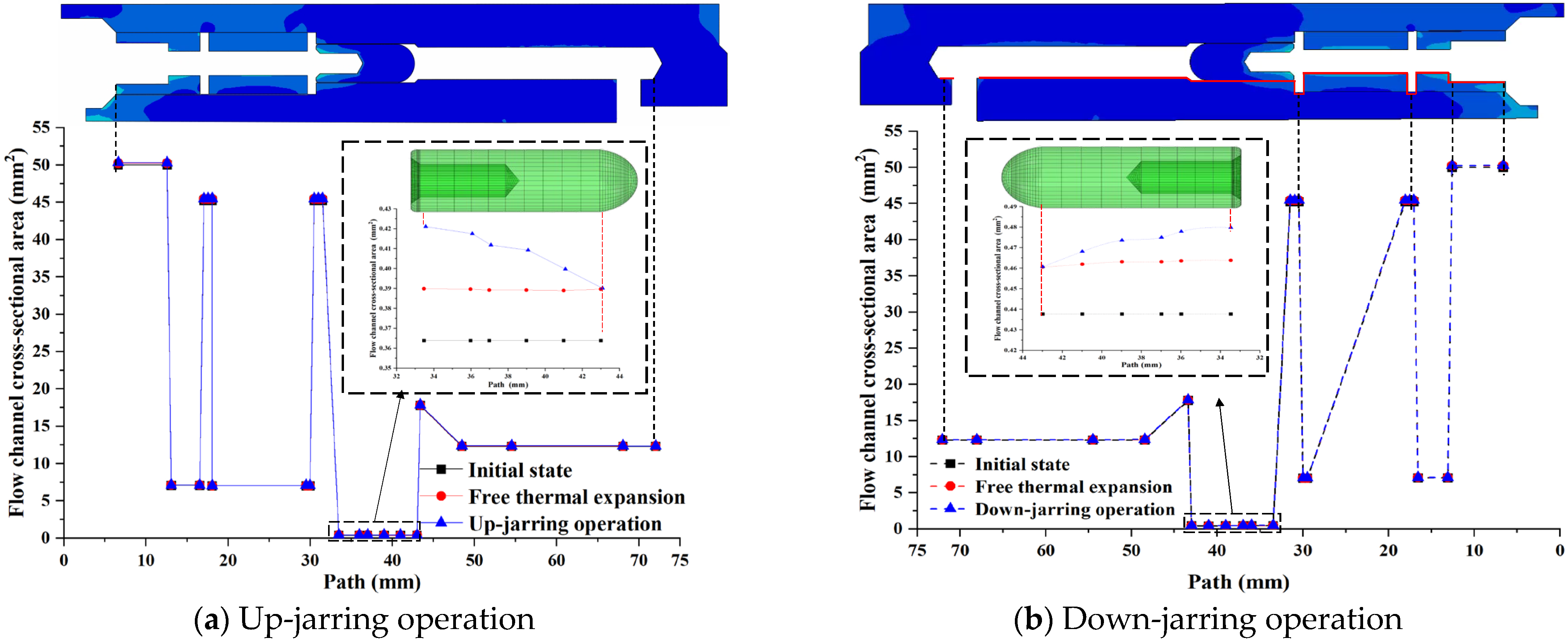
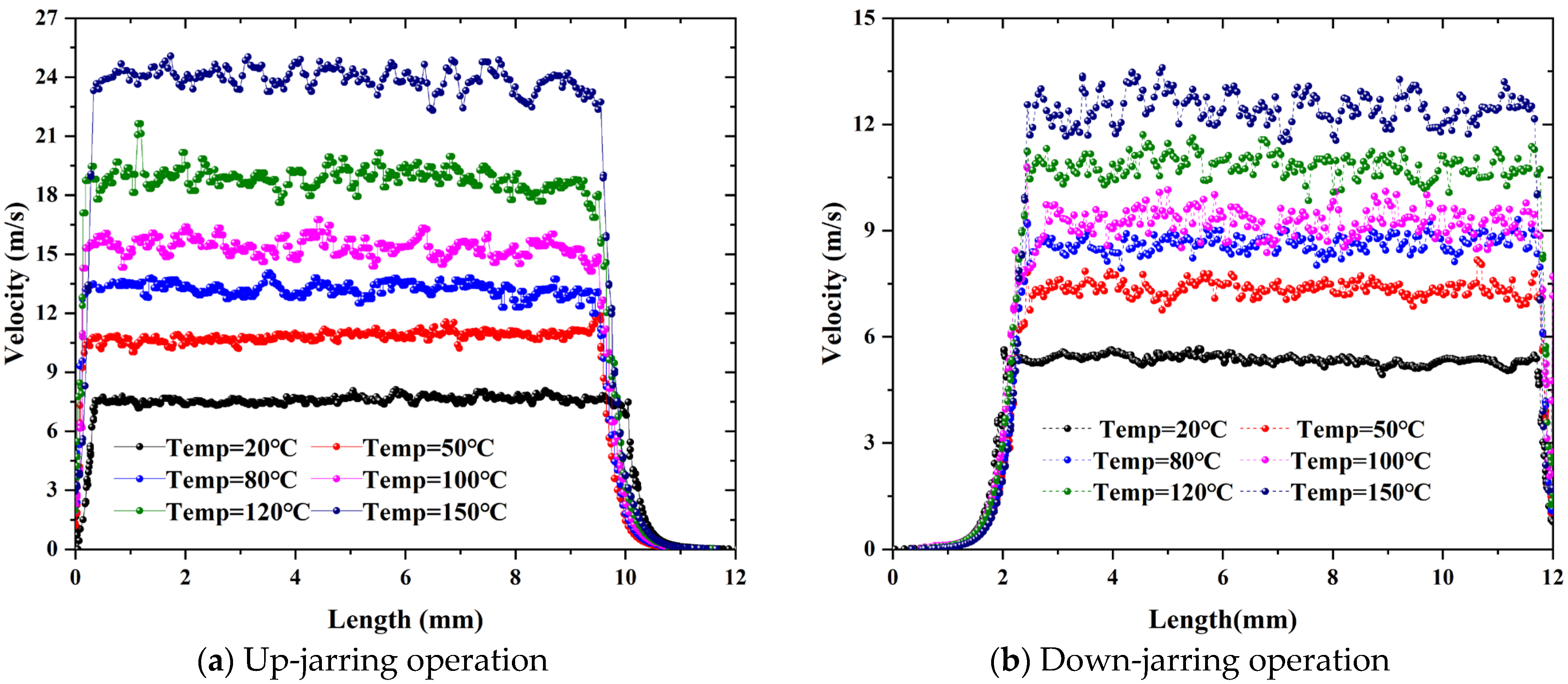
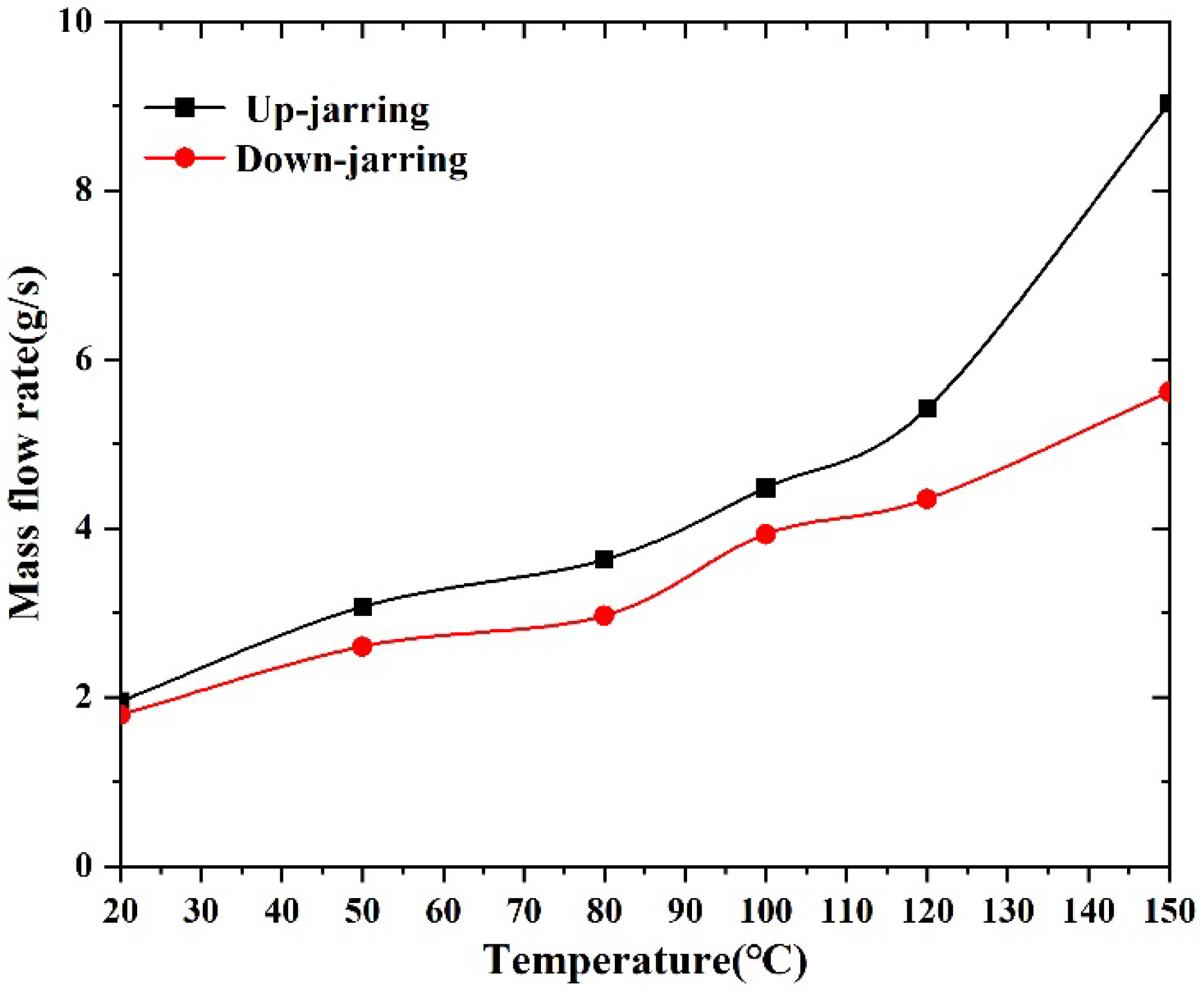
5.2.3. The High-Temperature Sensitivity of Throttling Performance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mercado, J.L. Planning for Successful Jarring Operations-Effective Use of Drilling Impact System Helps Release Stuck Pipe. Presented at the SPE/IADC Drilling Conference and Exhibition, Amsterdam, The Netherlands, 5–7 March 2013. [Google Scholar]
- Li, Q.C.; Zhao, D.F.; Yin, J.K.; Zhou, X.; Li, Y.; Chi, P.; Han, Y.; Ansari, U.; Cheng, Y. Sediment instability caused by gas production from hydrate-bearing sediment in Northern South China Sea by horizontal wellbore: Evolution and mechanism. Nat. Resour. Res. 2023, 32, 1595–1620. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.C.; Wang, F.L.; Xu, N.; Wang, Y.; Bai, B. Settling behavior and mechanism analysis of kaolinite as a fracture proppant of hydrocarbon reservoirs in CO2 fracturing fluid. Colloids Surf. A Physicochem. Eng. Asp. 2025, 724, 137463. [Google Scholar] [CrossRef]
- Evans, C.D.; Reitsma, R.; Ramsay, E. Reducing Safety Incidents While Lifting and Handling Drilling Jars: A Case Study. Presented at the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 25–28 September 2011. [Google Scholar]
- Oliveira, V.C.; Martinez, M.A.; Zahrani, B.S.; Abouelnaaj, K.K. A Study of Drilling Jar Utilization and Effectiveness in the Kingdom of Saudi Arabia. Presented at the SPE Oil and Gas India Conference and Exhibition, Mumbai, India, 4–6 April 2017. [Google Scholar]
- Fu, Y.K.; Liu, Q.Y.; Wang, G.R. Mathematical Modeling and Validation on a New Valve Core of the Throttle Valve in MPD. Adv. Mech. Eng. 2013, 5, 125936. [Google Scholar] [CrossRef]
- Wang, G.R.; Tao, S.Y.; Liu, Q.Y. Experimental Validation on a New Valve Core of the Throttle Valve in Managed Pressure Drilling. Adv. Mech. Eng. 2014, 6, 324219. [Google Scholar] [CrossRef]
- Abdelrahman, A.M.; Hussein, I.A.; Nasser, M.S.; Karami, H.; Ahmed, R. CFD modeling of particle settling in drilling fluids: Impact of fluid rheology and particle characteristics. J. Pet. Sci. Eng. 2021, 199, 108326. [Google Scholar] [CrossRef]
- Boyko, E. Interplay between complex fluid rheology and wall compliance in the flow resistance of deformable axisymmetric configurations. J. Non-Newton. Fluid Mech. 2025, 336, 105380. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, B.J.; Wang, Z.Y. Multiphase throttling characteristic analysis and structure optimization design of throttling valve in managed pressure drilling. Energy 2023, 262, 125619. [Google Scholar] [CrossRef]
- Wang, X.D.; Li, Y.; Gao, Y.; Gao, C.; Fu, W. DSMC Simulation of the Effect of Needle Valve Opening Ratio on the Rarefied Gas Flows inside a Micronozzle with a Large Length-to-Diameter Ratio. Aerospace 2023, 10, 126. [Google Scholar] [CrossRef]
- Singh, D.; Aliyu, A.M.; Charlton, M.; Mishra, R.; Asim, T.; Oliveira, A.C. Local multiphase flow characteristics of a severe-service control valve. J. Pet. Sci. Eng. 2020, 195, 107557. [Google Scholar] [CrossRef]
- Okhotnikov, I.; Noroozi, S.; Sewell, P.; Godfrey, P. Evaluation of steady flow torques and pressure losses in a rotary flow control valve by means of computational fluid dynamics. Int. J. Heat Fluid Flow 2017, 64, 89–102. [Google Scholar] [CrossRef]
- Ye, J.J.; Cui, J.x.; Hua, Z.; Xie, J.; Peng, W.; Wang, W. Study on the high-pressure hydrogen gas flow characteristics of the needle valve with different spool shapes. Int. J. Hydrogen Energy 2023, 48, 11370–11381. [Google Scholar] [CrossRef]
- Zhao, J.G.; Zheng, H.T.; Xie, C.; Peng, H. Research on the Throttling Performance and Anti-Erosion Structure of Trapezoidal Throttle Orifices. Energies 2024, 17, 3196. [Google Scholar] [CrossRef]
- Zhu, H.J.; Pan, Q.; Zhang, W.; Feng, G.; Li, X. CFD simulations of flow erosion and flow-induced deformation of needle valve: Effects of operation, structure and fluid parameters. Nucl. Eng. Des. 2014, 273, 396–411. [Google Scholar] [CrossRef]
- Wu, Z.; Lu, Y.F.; Liu, M.; Wang, F.; Wang, Y.; Du, S.; Wang, W.; Hong, B. The Erosion Characteristics of a Needle Throttle Valve with Multiple Placement Schemes in a Shale Gas Field Based on CFD-DEM. Processes 2025, 13, 1833. [Google Scholar] [CrossRef]
- Zhao, Z.H.; Wu, Z.; Wang, W.; Wang, X.; Du, S.; Chen, X.; Li, P.; Wang, Y. CFD-DPM Model of Gas–Solid Two-Phase Flow Erosion of Needle Throttle Valve. Coatings 2025, 15, 248. [Google Scholar] [CrossRef]
- Kibar, A.; Korkmaz, Y.S.; Yigit, K.S. Flow Analysis of a Needle Type Throttle Valves via Experimental and Numerical Methods. Iran. J. Sci. Technol. Trans. Mech. Eng. 2024, 49, 429–444. [Google Scholar] [CrossRef]
- Ye, Y.G.; Fan, H.H.; Liu, Y.H. A new approach for predicting the rheological properties of oil-based drilling fluids under high temperature and high pressure based on a parameter-free method. Appl. Sci. 2023, 13, 8592. [Google Scholar] [CrossRef]
- Hou, C.W.; Qian, J.Y.; Chen, F.; Jiang, W.; Jin, Z. Parametric analysis on throttling components of multi-stage high pressure reducing valve. Appl. Therm. Eng. 2018, 128, 1238–1248. [Google Scholar] [CrossRef]
- Chen, F.Q.; Jin, Z.J. Fluid dynamics analysis and optimized throttling design of L-shaped multi-stage high pressure reducing valve. Flow Meas. Instrum. 2023, 89, 102296. [Google Scholar] [CrossRef]
- Chen, F.Q.; Ren, X.D.; Hu, B.; Li, X.; Gu, C.; Jin, Z. Parametric analysis on multi-stage high pressure reducing valve for hydrogen decompression. Int. J. Hydrogen Energy 2019, 44, 31263–31274. [Google Scholar] [CrossRef]
- Al Alsayednassir, A.; Alvarez, O.; Aitmaganbetov, S.; Radhakrishnan, V. Enhancing Impact Tool Reliability and Efficiency: Advances in Technology and Design. In Proceedings of the SPE 225706, SPE/IADC Middle East Drilling Technology Conference and Exhibition, Abu Dhabi, United Arab Emirates, 27–29 May 2025. [Google Scholar]
- Chen, F.; Jin, Z. Throttling components effect on aerodynamic performance of superheated steam flow in multi-stage high pressure reducing valve. Energy 2021, 230, 120769. [Google Scholar] [CrossRef]
- Darmawan, S.; Tanujaya, H. CFD investigation of flow over a backward-facing step using an RNG k-ε turbulence model. Int. J. Technol. 2019, 10, 280–289. [Google Scholar]
- ASTM D2270; Standard Test Method for Calculating Viscosity Index from Kinematic Viscosity at 40 and 100 °C. ASTM International: West Conshohocken, PA, USA, 2016.
- ASTM E228; Standard Test Method for Linear Thermal Expansion of Solid Materials with a Push-Rod Dilatometer. ASTM International: West Conshohocken, PA, USA, 2016.




| Type | Temperature | ||
|---|---|---|---|
| 20–150 (10−6/°C) | 20–500 (10−6/°C) | 20–800 (10−6/°C) | |
| Throttle Valve | 11.35 | 9.08 | 8.57 |
| Central Valve | 16.7 | 12.74 | 12.21 |
| Parameter | Initial Temperature/°C | Wellbore Temperature/°C | Upward Triggering Load/kN |
|---|---|---|---|
| Value | 20 | 150 | 350 |
| Downward triggering load/kN | Up-jarring inlet pressure/MPa | Down-jarring inlet pressure/MPa | Outlet pressure /MPa |
| 180 | 42.06 | 21.61 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Lian, Z.; Yu, H.; Sun, W.; Liu, S.; Wan, Z.; Nie, J. High-Temperature Degradation of Throttling Performance in While-Drilling Jars Induced by Thermal Expansion and Fluid Rheology. Machines 2025, 13, 824. https://doi.org/10.3390/machines13090824
Zhao Z, Lian Z, Yu H, Sun W, Liu S, Wan Z, Nie J. High-Temperature Degradation of Throttling Performance in While-Drilling Jars Induced by Thermal Expansion and Fluid Rheology. Machines. 2025; 13(9):824. https://doi.org/10.3390/machines13090824
Chicago/Turabian StyleZhao, Zhaoyang, Zhanghua Lian, Hao Yu, Wei Sun, Senyan Liu, Zhiyong Wan, and Jiachang Nie. 2025. "High-Temperature Degradation of Throttling Performance in While-Drilling Jars Induced by Thermal Expansion and Fluid Rheology" Machines 13, no. 9: 824. https://doi.org/10.3390/machines13090824
APA StyleZhao, Z., Lian, Z., Yu, H., Sun, W., Liu, S., Wan, Z., & Nie, J. (2025). High-Temperature Degradation of Throttling Performance in While-Drilling Jars Induced by Thermal Expansion and Fluid Rheology. Machines, 13(9), 824. https://doi.org/10.3390/machines13090824






