Abstract
Chatter vibration in machining operations has been identified as one of the major obstacles to improving surface quality and productivity. Therefore, efficiently and accurately predicting stable cutting regions is becoming increasingly important, especially in high-speed milling processes. In this study, on the basis of a predictor–corrector scheme, the following three error correction methods are developed for milling stability analysis: the Correction Hamming–Milne-based method (CHM), the Correction Adams–Milne-based method (CAM) and the Predictor–Corrector Hamming–Adams–Milne-based method (PCHAM). Firstly, we employ the periodic delay differential equations (DDEs), which are usually adopted to describe mathematical models of milling dynamics, and the time period of the coefficient matrix is divided into two unequal subintervals based on an analysis of the vibration modes. Then, the Hamming method and the fourth-order implicit Adams–Moulton method are separately utilized to predict the state term, and the Milne method is adopted to correct the state term. Based on local truncation error, combining the Hamming and Milne methods creates a CHM that can more precisely approximate the state term. Similarly, combining the fourth-order implicit Adams–Moulton method and the Milne method creates a CAM that can more accurately approximate the state term. More importantly, the CHM and the CAM are employed together to acquire the state transition matrix. Thereafter, the effectiveness and applicability of the three error correction methods are verified by comparing them with three existing methods. The results demonstrate that the three error correction methods achieve higher prediction accuracy without sacrificing computational efficiency. Compared with the 2nd SDM, the calculation times of the CHM, CAM and PCHAM are reduced by around 56%, 56% and 58%, respectively. Finally, verification experiments are carried out using a CNC machine (EMV650) to further validate the reliability of the proposed methods, where ten groups of cutting tests illustrate that the stability lobes predicted by the three error correction methods exhibit better agreement with the experimental results.
1. Introduction
In the modern manufacturing industry, machining chatter is commonly recognized as a phenomenon of violent self-excited vibration between the tool and workpiece and has a considerable negative effect on surface finish, tool life and productivity efficiency. Therefore, many researchers have been primarily focused on the prediction [1,2,3], identification [4,5] and suppression [6,7] of chatter. However, predicting the limit of cutting stability is an important and effective strategy for selecting appropriate machining parameter combinations to avoid chatter vibration. During milling operations, regenerative chatter is considered to be the primary cause of undesirable instability, and DDEs are often utilized to formulate mathematical models of milling dynamics [8,9]. By solving the DDEs, a stability lobe diagram (SLD) can be directly determined to improve machining productivity and surface quality. It is important to select suitable cutting parameters based on stability analysis to avoid the occurrence of chatter.
To achieve stable cutting conditions using SLDs, many methods for chatter stability prediction have been proposed, such as numerical, analytical and experimental methods. These methods include the zeroth-order approximation (ZOA) method [10], multi-frequency solution (MFS) method [11], semi-discretization method (SDM) [12,13], numerical integration scheme–based SDM (NISDM) [14], full-discretization method (FDM) [15], updated version of FDM (UFDM) [16], holistic-discretization method (HDM) [17], precise integration method (PIM) [18], numerical integration method (NIM) [19], updated NIM (UNIM) [20], Simpson-based method (SBM) [21], generalized Runge–Kutta method (GRKM) [22], Adams–Moulton-based method (AMM) [23], Newton–Cotes-based method (NCM) [24], Milne–Simpson-based predictor–corrector method (SSM) [25], Correction Milne–Simpson method (CMM) [26] and linear multi-step predictor–corrector method (PCM) [27]. Altintas et al. [10] retained only the zeroth-order term of Fourier series utilizing the Fourier transform method and were the first to present an effective ZOA method based on the average of dynamic milling coefficients. This method can achieve extremely high efficiency for large radial immersion milling while maintaining reasonable computational accuracy. However, it is not applicable for instances of small radial immersion. To overcome the major limitation of the ZOA method, Merdol and co-workers [11] took advantage of the greater number of harmonics terms obtained using the MFS method to predict the locations of stable cutting regions. By approximating the delay term of DDEs with piecewise constant functions, Insperger et al. [12,13] reported on the zeroth-order SDM and first-order SDM (0th SDM and 1st SDM) to construct an SLD based on the direct difference scheme and Floquet theory. Higher-order SDMs were recommended by Jiang et al. [28] and Yan et al. [29] to enhance prediction precision by utilizing the different high-order interpolation polynomials, in which the exponential matrixes were approximated by precise integration. Zhang et al. [14] suggested the NISDM, which estimates the state term-related part with numerical integration schemes. It was found that the NISDM exhibits higher convergence rates and better prediction accuracy than the high-order vector numerical integration methods.
With the help of the direct integration scheme (DIS), the first-order FDM (1st FDM) was found to be effective by Ding and co-workers [15], who solved the Duhamel term of the precise response using linear interpolation. Compared with the 1st SDM, the 1st FDM exhibited superior calculation efficiency without loss of precision. Furthermore, in the framework of the 1st FDM, many higher-order versions of FDMs [30,31,32,33,34] have been reported to achieve higher approximation accuracy. With an increase in interpolation order, the computational time required for these extension algorithms will gradually increase. Liu et al. [35] adopted fourth-order Lagrange interpolation to accurately approximate the time-delayed part of an FDM and introduced an updated FDM (E-FDM) to analyze milling stability. To enhance computational speed, Tang and co-workers [16] employed the 2nd UFDM to analyze milling stability by utilizing the second-order Lagrange polynomial, in which the state transition matrix was constructed directly. Then, Yan et al. [36] developed the 3rd UFDM, which interpolates the state term and delay term of DDEs using the third-order Newton interpolation polynomial, which is more accurate compared with the 2nd UFDM due to the small axial depth of the cut. By estimating the state term with cubic spline interpolation, Ma et al. [37] established a novel UFDM with higher prediction accuracy. Based on the Newton and Lagrange polynomials, Xia et al. [38] presented an FDM with improved stability prediction. With the aid of a holistic-interpolation scheme, Qin et al. [17,39] utilized second-order Lagrange interpolation to estimate the integral nonhomogeneous term and presented two HDMs (HDM and PCHDM) for milling stability analysis. Song et al. [40] considered discrete vibration velocities and introduced a whole discretization method that uses third-order Hermite interpolation polynomials. Dai and co-workers [18] expanded the nonhomogeneous term using the Taylor formula and established the PIM for predicting the stability of milling operations. With the aid of the second-order Taylor formula, Li et al. [41] established an improved PIM (IPIM) for predicting milling stability, which achieved a higher convergence rate compared with the PIM. Based on numerical integration formulas, Ding et al. [19] demonstrated the effectiveness of the well-known NIM for milling stability prediction with single- and multi-delays. Based on Hermite numerical interpolation, Dong et al. [20] developed an updated NIM (UNIM) for determining milling stability lobes, and its efficacy was verified through a milling test experiment. To increase calculation speed, Zhang et al. [21] utilized the Simpson formula to estimate the state term and proposed the SBM, the convergence rate of which is better than that of the 1st SDM and 2nd FDM. Niu et al. [22] established the GRKM by combining the classical fourth-order Runge–Kutta and Simpson methods, in which the mid-point value was approximated by three-point barycentric Lagrange interpolation. However, this method has a relatively complicated structure, resulting in extremely low computational efficiency. To achieve higher convergence rates, Qin et al. [23,42] suggested the AMM and the Adams–Simpson-based method (ASM) for predicting the stability of milling operations using a predictor–corrector scheme. Zhi et al. [43] introduced the implicit Adams method for analyzing milling stability, in which the state term was approximated by the fourth-order Adams–Moulton formula. Li et al. [24] adopted the Newton–Cotes rules to deduce the numerical solutions and developed the Newton–Cotes-based method (NCM) for achieving higher computational efficiency. To improve computational performance, Mei et al. [25] suggested the SSM for constructing SLDs based on the Milne and Simpson methods. Within the framework of the SDM, Yan et al. [44] updated two methods using the two-step Simpson formula. Based on 1/3 and 3/8 Simpson formulas, Zhan et al. [45] recommended a hybrid multi-step method for higher calculation speed and accuracy. Liu et al. [46] applied Simpson’s 3/8 rule to obtain algebraic equations and introduced a novel method for analyzing the stability of milling operations. By combining the Milne and Simpson methods, Wu et al. [26] presented the CMM for determining milling stability lobes based on the local truncation error. According to the predictor–corrector scheme, Qin et al. [27] established the PCMs by applying the three different linear multi-step methods. Finally, Du et al. [47] proposed the Simpson’s 3/8-based method for higher prediction accuracy. Of the above methods, linear multi-step methods can be directly applied to approximate the state term, and the application of the trapezoidal rule may lead to accuracy of existing algorithms. It is worth mentioning that the Hamming, Milne and fourth-order implicit Adams–Moulton methods have the same algebraic order precision. To improve computational performance, we attempt to present the Correction Hamming–Milne-based method and the Correction Adams–Milne-based method, which involve the linear combination of two different multi-step methods based on error correction. Moreover, the CHM and the CAM serve as a predictor–corrector pair form to further enhance the calculation accuracy and efficiency of stability lobes.
In this paper, three error correction methods based on linear multi-step formulas are presented for accurately predicting the stability of milling operations. Based on local truncation error, combining the Hamming and Milne methods creates a CHM that can more precisely approximate the state term. Similarly, combining the fourth-order implicit Adams–Moulton method and the Milne method creates a CAM that can more accurately estimate the state term. More importantly, the CHM is used to predict the state term, and the CAM is utilized to correct the state term based on the predictor–corrector scheme. The CHM and CAM serve as a predictor–corrector pair that enable us to acquire the state transition matrix. The remainder of this paper is organized as follows. Section 2 presents the three error correction methods based on the predictor–corrector scheme; Section 3 illustrates the effectiveness of the three error correction methods though detailed comparisons with the 2nd SDM, UNIM and CMM; Section 4 validates the reliability of the three error correction methods through experimental verifications; and Section 5 presents the main conclusions of this paper.
2. Mathematical Model and Numerical Algorithms of Milling Operations
Generally, establishing a dynamic model of milling operations that considers regenerative effects is an important prerequisite for stability analysis. Based on Refs. [8,13], the corresponding milling dynamics model can be formulated as the following second-order DDE:
where the matrixes M, C and K represent modal mass, modal damping and modal stiffness matrixes, respectively; and denote the modal displacement vector of the tool and the axial depth of the cut, respectively; matrix represents the cutting force coefficient satisfying ; and T indicates the time delay period of the milling system that can be computed by , where Ω denotes the rotation speed of the spindle (rpm) and N represents the number of cutter teeth.
State space transformation is represented by and the state vector . Using matrix transformation, the governing Equation (1) can easily be rewritten as the following state-space form:
where
Based on the DIS [15], Equation (2) can be deduced as follows:
where represents the initial time point.
According to Equations (2) and (3), the milling vibration form depends on the value of the cutting force coefficient matrix . Based on the above analysis, the time period of the milling system can be split into the free- and forced-vibration phases, according to [19,42]. When the matrix becomes a null matrix, it exhibits free vibration, as analytically deduced in Equation (4):
In this work, we equally divide the forced vibration phase into m very short time intervals with a step length of h. The corresponding time points are given by
During the time span , Equation (4) at arbitrary time points can be equivalently re-expressed as follows:
2.1. Correction Hamming–Milne-Based Method (CHM)
In order to solve Equation (7), the Hamming and Milne methods are employed to construct the state transition matrix. At the discrete time points , the abbreviated expressions , and represent the nodal values , and , respectively. Based on the Hamming formula, the state term of Equation (7) can be approximated by
where the local truncation error of the Hamming method is given as follows [27]:
Simultaneously, the state term of Equation (7) can be obtained by the Milne formula and expressed as
where the local truncation error of the Milne method is given as follows [26]:
On this basis, the Hamming and Milne methods have the same fourth-order algebraic precision, and a more accurate Correction Hamming–Milne-based method is obtained by using linear combinations. Based on the local truncation errors of the Hamming and Milne methods, the correction state term can be obtained as follows:
Based on the Correction Hamming–Milne-based method, the correction state term can be re-expressed as
By reorganizing Equation (13), the relationship is further rewritten as follows:
where
In addition, the two-step Adams–Moulton formula is adopted to approximate the third state term . Consequently, Equation (7) can be re-expressed as
where
The 1/3 Simpson formula is adopted to approximate the third state term . Consequently, Equation (7) can be further expressed as
where
The 3/8 Simpson formula is adopted to approximate the fourth state term . Consequently, Equation (7) can be further expressed as
where
According to Equations (5), (14), (16), (18) and (20), a discrete map can be produced and graphically depicted as
where
and
Consequently, the state transition matrix with the Correction Hamming–Milne-based method (CHM) can be deduced as follows:
On the basis of the Floquet theory, the milling stability can be determined by using the Correction Hamming–Milne-based method. Then, the milling operation is stable when the spectral radius of are all less than one; otherwise, it is unstable.
2.2. Correction Adams–Milne-Based Method (CAM)
Similarly, the Adams and Milne methods are utilized to solve Equation (7). Based on the fourth-order Adams–Moulton formula, the state term of Equation (7) can be approximated by
where the local truncation error of the fourth-order Adams–Moulton method is given by [27]:
Similarly, the fourth-order Adams–Moulton and Milne methods have the same fourth-order algebraic precision. A Correction Adams–Milne-based method with better accuracy and efficiency is obtained by using linear combinations. Based on the local truncation errors of the fourth-order Adams–Moulton and Milne methods, the correction state term can be expressed as follows:
Based on the Correction Adams–Milne-based method, the correction state term can be obtained as follows:
By reorganizing Equation (29), the relationship can be further rewritten as follows:
where
According to Equations (5), (16), (18), (20) and (30), a discrete map can be produced and graphically depicted as
where
and
Consequently, the state transition matrix with the Correction Adams–Milne-based method (CAM) can be deduced as follows:
On the basis of the Floquet theory, the milling stability can be determined by using the Correction Adams–Milne-based method.
2.3. Predictor–Corrector Hamming–Adams–Milne-Based Method (PCHAM)
Based on the predictor–corrector scheme, we utilize the Correction Hamming–Milne-based method to predict the milling stability and then use the Correction Adams–Milne-based method to correction this prediction. In addition, the 1/3 Simpson and 3/8 Simpson formulas are employed to estimate the third and fourth state terms, respectively. By combining Equations (5), (18), (20), (14) and (30), a linear discrete map based on the predictor–corrector scheme can be defined as
where
and
Consequently, the state transition matrix with the Predictor–Corrector Hamming–Adams–Milne-based method (PCHAM) can be deduced as follows:
On the basis of the Floquet theory, the milling stability can be determined by using the Predictor–Corrector Hamming–Adams–Milne-based method.
3. Numerical Comparison and Discussion
In this section, the effectiveness and characteristics of the proposed error correction methods are validated from the perspective of the convergence rates and SLDs. We use two typical benchmark milling models commonly selected for numerical illustration, and the corresponding machining parameters taken from Refs. [13,15] are often used for fair comparison, as shown in Table 1. Comprehensive comparisons among the 2nd SDM [28], UNIM [20], CMM [26], CHM, CAM and PCHAM are carried out under the same computational conditions. For algorithm verification, the mathematical model expressions of single- and two-DOF milling operations can be written as [15,19]

Table 1.
Milling parameters of single-DOF model.
3.1. Analysis of Convergence Rate
Without loss of generality, the variation in local discretization errors (LDEs) with increasing time intervals m can be taken as a significant criterion indicating algorithm accuracy. The precision of different algorithms can be directly visualized using a convergence rate curve, which indicates how fast the LDE asymptotically converges to zero. The LDE will approach zero more rapidly when the prediction method has consistently high convergence performances. Similarly to [28], we found that the LDE for the 2nd SDM is denoted by , where h represents the discrete step. Following a similar method to that in Ref. [20], the LDE of the UNIM can be determined as . As is well known, the Hamming, Milne and three-step implicit Adams–Moulton methods have fourth-order algebraic precision. Based on the local truncation error, the LED of the CMM can be proven to be . Similarly to the CMM, we demonstrate that the LDE of the CHM and the CAM are both . Moreover, the CHM and the CAM are combined to form a novel predictor–corrector method, where the CHM is used as the predictor variable and the CAM is utilized as the corrector variable. Consequently, the LED of the Predictor–Corrector Hamming–Adams–Milne-based method is larger than . For this reason, the three proposed methods are expected to achieve better accuracy than the 2nd SDM, UNIM and CMM under identical time intervals m. To further prove the above results, two different conditions of radial immersion are thoroughly studied for convergence rate analysis.
During down milling operations, four groups of milling parameter combinations are selected to intuitively investigate the convergence rates of the three proposed methods. To begin with, we set the radial immersion ratio to 0.5 and employ the single-DOF milling model to examine convergence performance. Based on the same program structure, two combinations of machining parameters are adopted to validate the convergence rates of the three error correction methods, i.e., = 7000 rpm, = 1.0, 2.0 and 3.0 mm; = 10,000 rpm, = 0.8, 1.6 and 2.4 mm. Here, the approximate spectral radius is computed based on the 2nd SDM, UNIM, CMM, CHM, CAM and PCHAM under different time intervals m. Meanwhile, the exact spectral radius is determined based on the CHM with sufficiently large time intervals (m = 1000). Figure 1 exhibits the convergence rate curves of the 2nd SDM, UNIM, CMM, CHM, CAM and PCHAM as the time intervals m increases.
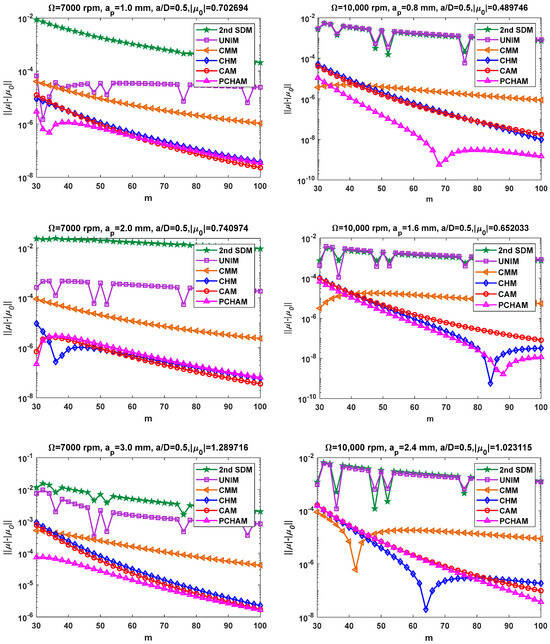
Figure 1.
Convergence rates of the 2nd SDM, UNIM, CMM, CHM, CAM and PCHAM with medium radial immersion ratio.
Figure 1 shows that the CHM, CAM and PCHAM converge to the exact spectral radius much more rapidly than the 2nd SDM, UNIM and CMM under conditions of medium radial immersion. For example, when m = 60 and = 2.0 mm, the LDEs acquired by the 2nd SDM, UNIM, CMM, CHM, CAM and PCHAM are 1.67 × , 3.31 × , 1.17 × , 4.88 × , 4.16 × and 6.57 × , respectively. In most cases, the PCHAM converges only slightly faster than the CHM and CAM, especially when the spindle speed is 10,000 rpm and the axial depth of the cut is 0.8 mm, and it is found that the convergence rate of the PCHAM is notably faster than that of the CHM and CAM. Moreover, the numerical stabilities of the three proposed methods are obviously superior to those of the 2nd SDM and UNIM for half radial immersion milling. Hence, the three proposed methods achieve faster convergence and better precision than the 2nd SDM, UNIM and CMM under conditions of medium radial immersion.
To further assess the convergence effect of the three proposed methods, two combinations of machining parameters are selected for algorithm verification, including two spindle speeds ( = 6000 and 9000 rpm), six axial cut depths = (0.6, 1.8, 3.0, 0.7, 1.9, and 3.1) mm and a small radial immersion ratio ( = 0.05). Figure 2 illustrates the convergence rates of the 2nd SDM, UNIM, CMM, CHM, CAM and PCHAM with low radial immersion milling. The exact spectral radius is still determined based on a CHM with m = 1000. Figure 2 shows that the convergence rates of the three error correction methods are significantly better than those of the 2nd SDM, UNIM and CMM. For example, when m = 60 and = 3.1 mm, the LDEs acquired by the 2nd SDM, UNIM, CMM, CHM, CAM and PCHAM are 2.22 × , 3.99 × , 6.09 × , 1.04 × , 1.08 × and 1.86 × , respectively. At the same time, the convergence rate of the PCHAM is slightly higher than that of the CHM and CAM, especially when the spindle speed is 6000 rpm and the axial depth of the cut is 0.6 mm; it is found that the convergence rate of the PCHAM obviously outweighs that of the CHM and CAM. Moreover, the numerical stabilities of the three proposed methods are obviously superior to those of the 2nd SDM and UNIM. Overall, Figure 1 and Figure 2 validate that the three proposed methods achieve faster convergence and better precision than the 2nd SDM, UNIM and CMM under conditions of both medium and low radial immersion.
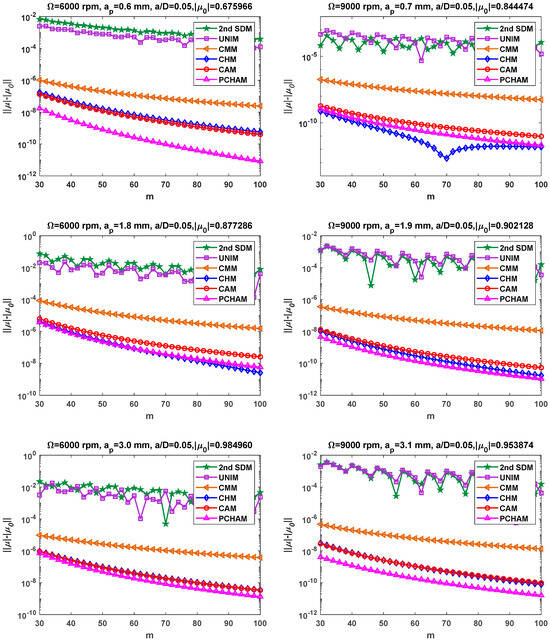
Figure 2.
Convergence rates of the 2nd SDM, UNIM, CMM, CHM, CAM and PCHAM with small radial immersion ratio.
3.2. Prediction and Comparison of Milling Stability
3.2.1. Single-DOF Milling Process
In order to evaluate the effectiveness of the three proposed methods, the SLDs of the 2nd SDM, UNIM, CMM, CHM, CAM and PCHAM are determined over an equidistance grid with a size of . The SLDs of these six methods at time intervals m of 12 and 4 are presented in Figure 3, and the corresponding calculation times are summarized in Figure 4. Based on the single-DOF milling model, two different radial immersion ratios ( = 0.5 and 0.05) are selected to construct the SLDs. As depicted in Figure 3, the reference stability lobes represented by the red solid line are determined by the CHM with a relatively large time interval (m = 1000). Meanwhile, the predicted stability lobes represented by the blue solid line are calculated via the three existing methods and the three proposed methods under identical time intervals m. Figure 3 indicates that with respect to the reference stability lobes, those predicted by the CHM, CAM and PCHAM exhibit better agreement, those predicted by the CMM exhibit only small deviations, and those predicted by the 2nd SDM and the UNIM show noticeable deviations; this means that the prediction accuracy of the SLDs for the three error correction methods are much better than those computed by the 2nd SDM, UNIM and CMM under conditions of small and medium radial immersion. In addition, Figure 4 shows that when the radial immersion ratio is 0.5 and the time interval m is 12, the 2nd SDM, UNIM, CMM, CHM, CAM and PCHAM take 3.06 s, 2.72 s, 2.42 s, 2.45 s, 2.44 s and 2.32 s, respectively, to generate SLDs. In comparison with the 2nd SDM, the calculation time of the CHM, CAM and PCHAM can be reduced by nearly 20%, 20% and 24%, respectively. These results demonstrate that under the same conditions, the three proposed methods achieve faster computing speeds than the 2nd SDM. Meanwhile, the three proposed methods require approximately the same amount of calculation time as the UNIM and CMM. Hence, the CHM, CAM and PCHAM have significantly better prediction accuracy with a small loss of computational efficiency.
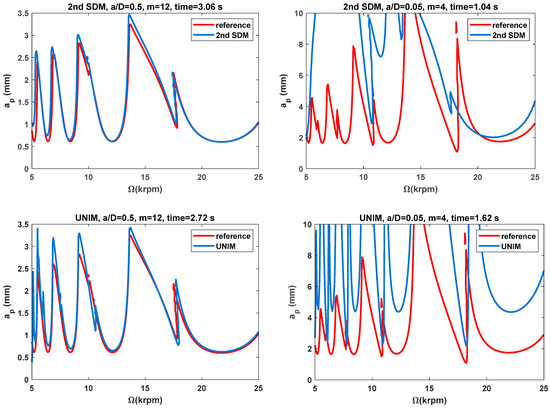
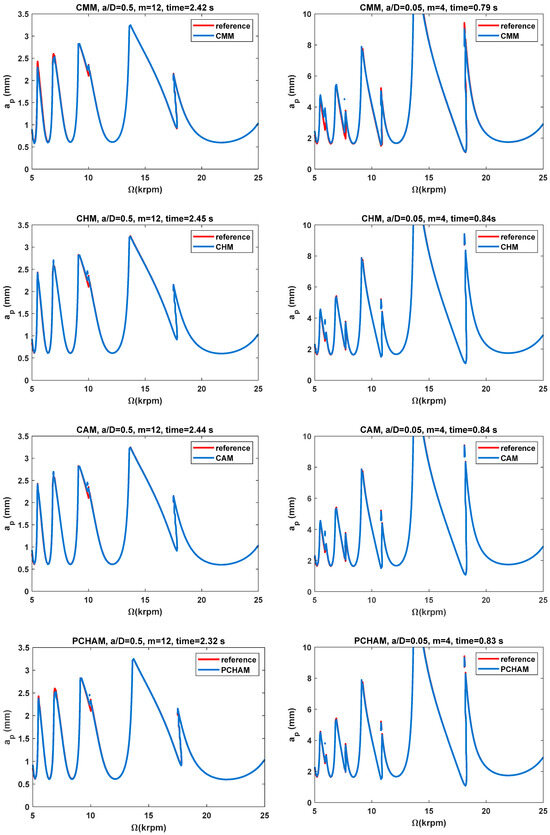
Figure 3.
The SLDs of single-DOF milling model predicted by the 2nd SDM, UNIM, CMM, CHM, CAM and PCHAM with = 0.5 and 0.05.
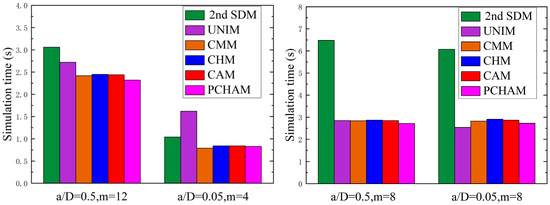
Figure 4.
Comparisons of calculation times required by the 2nd SDM, UNIM, CMM, CHM, CAM and PCHAM.
To examine the predictive accuracy of the three error correction methods under conditions of marginal stability, the SLDs of the 2nd SDM, UNIM, CMM, CHM, CAM and PCHAM with = 0.05 and m = 4 are recalculated over an equidistance grid with a size of . Figure 5 illustrates the predicted stability lobes and their local subgraphs. To further investigate the precision of the three existing methods and the three error correction methods, the time responses of six marginal parameter points A (5600 rpm, 4.10 mm), B (5600 rpm, 3.95 mm), C (5840 rpm, 2.95 mm), D (5840 rpm, 2.70 mm), E (6500 rpm, 1.85 mm) and F (6500 rpm, 1.55 mm) are calculated by using MATLAB (R2021a) routine dde23. Based on the vibration displacement response, six marginal parameter points are used to intuitively judge whether these parameter points are stable.
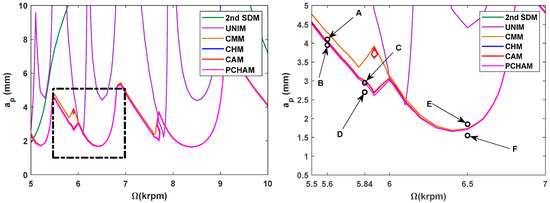
Figure 5.
Comparison of stability lobes predicted by different methods over spindle speed changes from 5 to 10 krpm at .
The relative tolerance and maximal solver step size are both set to , and the initial conditions of the DDE23 function are set to 25 and 0 m/s, to calculate the vibration displacement responses of six groups of parameter points, as depicted in Figure 6. In the low-speed region, it can be seen that parameter points A (5600 rpm, 4.10 mm), C (5840 rpm, 2.95 mm) and E (6500 rpm, 1.85 mm) are unstable, while points B (5600 rpm, 3.95 mm), D (5840 rpm, 2.70 mm) and F (6500 rpm, 1.55 mm) are stable. It is indicated that when the spindle speed is 5600 rpm, the stability curves are obtained at axial cut depths ranging from 3.95 mm to 4.10 mm; when the spindle speed is 5840 rpm, the stability curves are obtained at axial cut depths ranging from 2.70 mm to 2.95 mm; and when the spindle speed is 6500 rpm, the stability curves are obtained at axial cut depths ranging from 1.55 mm to 1.85 mm. In the 2nd SDM and UNIM, all of the predicted cutting states are completely incorrect. The cutting states of points A and C are always misjudged in the CMM, and the cutting state of point C is easily misjudged in the CHM and the CAM. However, the predicted results of the PCHAM are basically consistent with the cutting states. These results demonstrate that the accuracy of stability lobes computed by the PCHAM is much better than the stability of those computed by the 2nd SDM, UNIM, CMM, CHM and CAM under conditions of marginal stability.
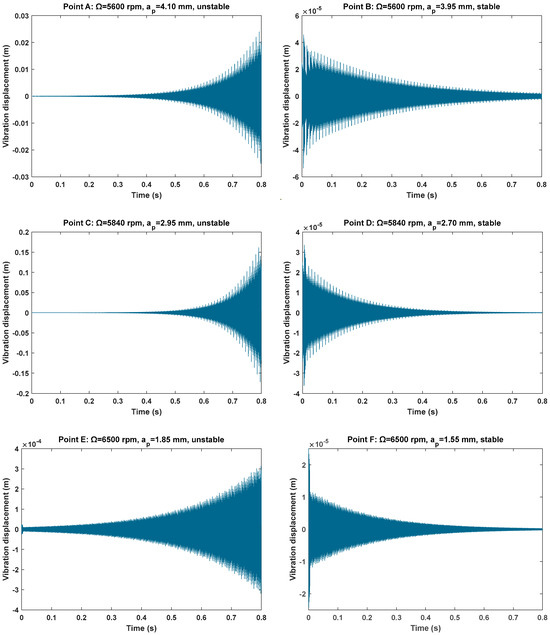
Figure 6.
Vibration displacement responses of six marginal parameter points using MATLAB dde23.
3.2.2. Two-DOF Milling Process
To further illustrate the effectiveness of the three proposed methods and examine the two radial immersion conditions, the modal parameters of the two-DOF milling dynamics system and the three conventional methods are employed. Therefore, the 2nd SDM, UNIM, CMM, CHM, CAM and PCHAM are applied directly to construct SLDs over an equidistance grid with a size of . The SLDs of these six methods with a time interval m of 8 are presented in Figure 7, and the corresponding computation times are summarized in Figure 4. Based on the two-DOF milling model, two different radial immersion ratios, = 0.5 and 0.05, are selected to construct the SLDs. As shown in Figure 7, the reference stability lobes, denoted by the solid red line, are determined by the CHM with a relatively large time interval (m = 1000). Meanwhile, the predicted stability lobes denoted by the solid blue line, are calculated via the three existing methods and the three proposed methods under the same time interval m. Figure 7 indicates that with respect to the reference stability lobes, those predicted by the CHM, CAM and PCHAM reveal better agreement, those predicted by the CMM exhibit only small deviations, and those predicted by the 2nd SDM and UNIM reveal noticeable deviations; this means that the prediction accuracy of the SLDs computed by the three proposed methods are much better than that of the SLDs computed by the 2nd SDM, UNIM and CMM under conditions of small and medium radial immersion. In addition, Figure 4 shows that when the radial immersion ratio is 0.5 and discrete number m is 8, the 2nd SDM, UNIM, CMM, CHM, CAM and PCHAM require 6.48 s, 2.85 s, 2.84 s, 2.87 s, 2.85 s and 2.72 s, respectively, to generate SLDs. When compared with the 2nd SDM, the calculation time of the CHM, CAM and PCHAM can be reduced by around 56%, 56% and 58%, respectively. This demonstrates that the three proposed methods achieve faster computing speeds than the 2nd SDM under the same conditions. Simultaneously, the three error correction methods require approximately the same amount of calculation time as the UNIM and the CMM. Therefore, the three error correction methods can achieve better prediction accuracy than the 2nd SDM, UNIM and CMM without loss of computational efficiency.
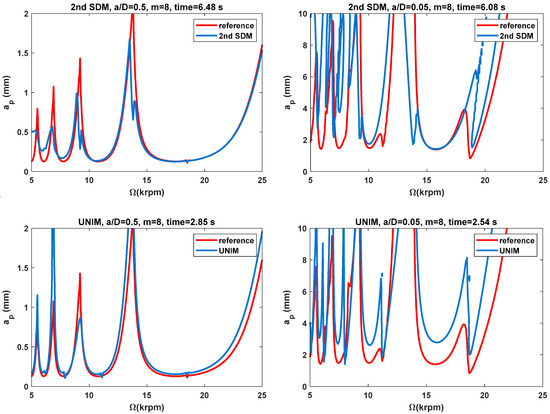
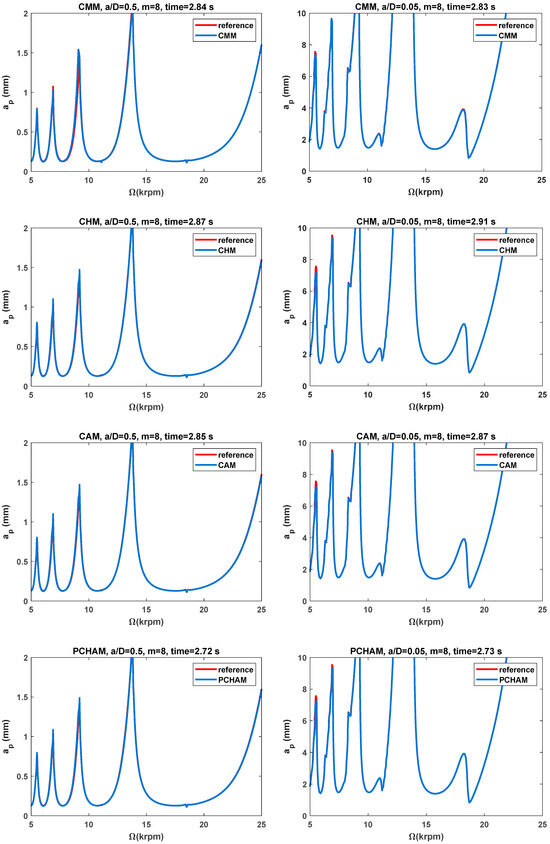
Figure 7.
The SLDs of the two-DOF milling model predicted by the 2nd SDM, UNIM, CMM, CHM, CAM and PCHAM with .
4. Experimental Verification and Analysis
To evaluate the effectiveness and applicability of the three proposed error correction methods, a series of slot-milling experiments were conducted using a CNC machine (EMV650). In all of the cutting tests, a four-flute end-milling cutter with a 10 mm diameter and helix angle was mounted on the spindle. Simultaneously, the aluminum alloy AL6061 was chosen as the material for the workpiece. The apparatus for obtaining the modal parameters comprised a Donghua LC02 impact hammer, a Dytran 3224A1 acceleration sensor, and a Donghua DH5922 signal acquisition instrument, as shown in Figure 8. In the impact tests, the Donghua LC02 impact hammer was employed to hit the cutter tip of the tool in the x and y directions to create an exciting force, the Dytran 3224A1 acceleration sensor was used to collect the corresponding vibration signals, and the Donghua DH5922 signal acquisition instrument was employed for modal parameter identification. Subsequently, the cutting force coefficients were calibrated via five groups of full slots milling experiments. The average cutting forces in the x and y directions under a constant spindle speed and axial cut depth, and different speeds of feed per tooth, are displayed in Figure 8.
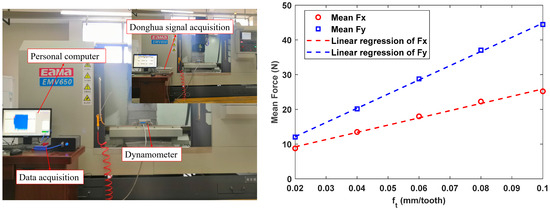
Figure 8.
An image of the experimental site and a graph depicting the linear regression of the average cutting forces.
Based on the rational fraction polynomials and linear regression results, the identified modal parameters of the cutter in the x and y directions and the cutting force coefficients are acquired and are listed in Table 2.

Table 2.
Milling parameters of the tool–machine system.
Based on the identified milling parameters of the tool–machine system, the SLDs calculated by the CHM, CAM and PCHAM with a radial immersion ratio of 1.0 and a time interval m of 80 are displayed in Figure 9. During the cutting confirmation experiments, a Kistler 9257B dynamometer with a sampling frequency of 10 kHz was applied to measure the instantaneous cutting forces, and an HRU-1213MA data acquisition device was adopted to collect the milling force signals. Figure 9 shows that the stability lobes predicted by the CHM, CAM and PCHAM exhibit excellent agreement with the actual cutting test results under conditions of large radial immersion.
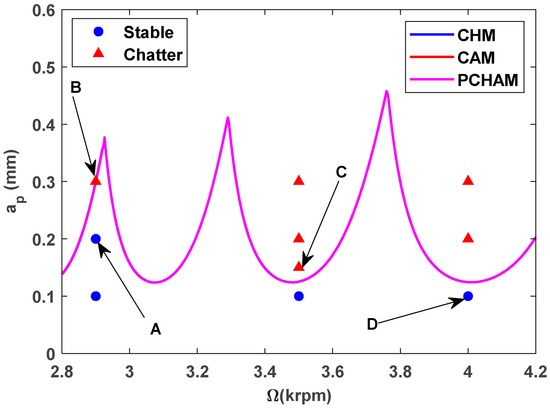
Figure 9.
The SLDs predicted using the CHM, CAM and PCHAM and the actual cutting tests results.
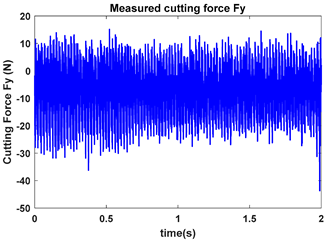
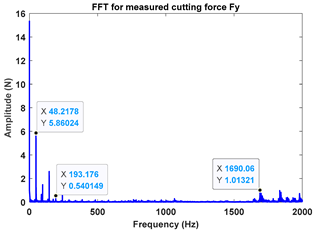
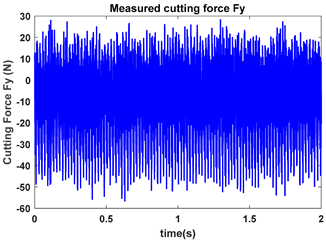
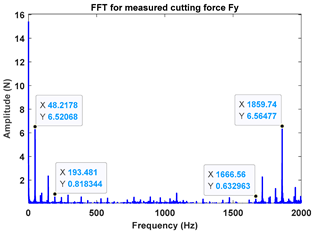
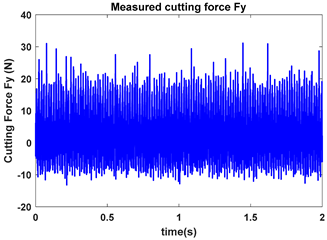
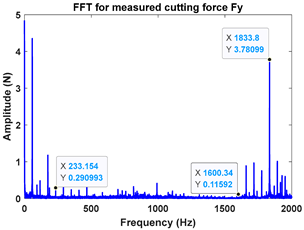
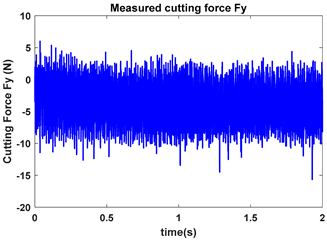
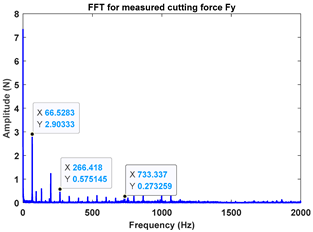
As depicted in Figure 9, the ten observation points can be directly divided into four stable points and six unstable points. The solid red triangle represents an unstable cutting state, and the solid blue circle represents a stable cutting state. To conduct a detailed analysis, the cutting force signals and their frequency spectra for the four observed parameter combinations, i.e., A (2900 rpm, 0.20 mm), B (2900 rpm, 0.30 mm), C (3500 rpm, 0.15 mm) and D (4000 rpm, 0.10 mm), were selected to perform actual cutting force tests, as exhibited in Table 3. It can be seen that points A (2900 rpm, 0.20 mm) and D (4000 rpm, 0.10 mm) are stable, and the frequency spectra of their cutting forces do not contain chatter frequencies, particularly the tooth passing frequencies (193 Hz, 266 Hz,) and its harmonic frequencies. In the case of point B (2900 rpm, 0.30 mm), the tooth passing frequency is 2900/60 × 4 = 193 Hz, but the chatter frequencies of point B (2900 rpm, 0.30 mm) occur at (1666 Hz, 1859 Hz), and the difference in these adjacent chatter frequencies is equal to 193 Hz. For point C (3500 rpm, 0.15 mm), the tooth passing frequency is 3500/60 × 4 = 233 Hz, but the chatter frequencies of point C (3500 rpm, 0.15 mm) occur at 1600 Hz and 1833 Hz, and the difference in these adjacent chatter frequencies is equal to 233 Hz. Hence, points of B (2900 rpm, 0.30 mm) and C (3500 rpm, 0.15 mm) are unstable. According to the above analysis, the CHM, CAM and PCHAM have the ability to accurately predict the SLDs for actual milling operations.

Table 3.
Cutting force signal and corresponding frequency spectra of different parameter points.
5. Conclusions
Based on a predictor–corrector scheme, three error correction methods are proposed in this paper for accurately predicting milling stability. The main conclusions of this study are summarized as follows:
(1) The Correction Hamming–Milne-based method (CHM), the Correction Adams–Milne-based method (CAM) and the Predictor–Corrector Hamming–Adams–Milne-based method (PCHAM) based on a predictor–corrector scheme are proposed for accurate stability prediction. Based on the local truncation error, combining the Hamming method and the Milne method creates a CHM that can more precisely approximate the state term. Similarly, combining the fourth-order implicit Adams–Moulton method and the Milne method creates a CAM that can more accurately approximate the state term.
(2) More importantly, the CHM is used to predict the state term, and the CAM is utilized to correct the state term based on the predictor–corrector scheme. The CHM and the CAM serve as a predictor–corrector pair to acquire the state transition matrix.
(3) The convergence rates of the three proposed error correction methods are analyzed and compared with those of the three existing methods for a single-DOF milling system. The numerical results demonstrate that the CHM, CAM and PCHAM achieve much higher convergence rates than the 2nd SDM, UNIM and CMM under different radial immersion conditions. When m = 60 and = 3.1 mm, the LDEs acquired by the 2nd SDM, UNIM, CMM, CHM, CAM and PCHAM are 2.22 × , 3.99 × , 6.09 × , 1.04 × , 1.08 × and 1.86 × , respectively.
(4) In comparison with the three existing methods, the SLDs determined by the CHM, CAM and PCHAM are mostly consistent with the reference stability lobes under an identical discrete number. When compared with the 2nd SDM, the calculation time of the CHM, CAM and PCHAM can be reduced by approximately 56%, 56% and 58%, respectively. The calculation speeds of the CHM, CAM and PCHAM are comparable to those of the UNIM and CMM. Therefore, the CHM, CAM and PCHAM are proven to have exhibited performance for predicting milling stability lobes without sacrificing computational efficiency.
(5) Experimental verification is conducted using a CNC machine (EMV650), and ten groups of cutting tests are performed to demonstrate the applicability and reliability of the three proposed error correction methods. The stability lobes predicted by the CHM, CAM and PCHAM exhibit excellent agreement with the actual cutting test results, which indicate that the three proposed methods have the ability to accurately predict the stability lobes for actual milling operations.
Author Contributions
Conceptualization, Y.W. and B.D.; Methodology, Y.W., Q.Z. and W.M.; Software, Q.Z.; Data Curation, Q.Z., W.M., T.Y. and W.M.; Investigation, W.J.; Resources, Y.W., T.Y. and B.D.; Writing—Original Draft Preparation, Y.W.; Writing—Review and Editing, Y.W. and B.D.; Visualization Y.W. and T.Y.; Supervision T.Y. and W.M.; Validation, Q.Z. and W.J.; Project Administration, Y.W. and B.D.; Funding Acquisition, Y.W. and B.D. All authors have read and agreed to the published version of the manuscript.
Funding
The research described in this paper was supported by the Hunan Provincial Natural Science Foundation of China (grant number 2024JJ7113), the Scientific Research Fund of Hunan Provincial Education Department of China (grant numbers 23B0832 and 23C0400), the Guiding plan project of Hengyang city (grant numbers 202323016881 and 202222015981), and the Scientific Research Project of Hunan Institute of Technology (grant numbers HQ22011 and KFA22014).
Data Availability Statement
The original contributions presented in this study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Qinghua Zhao and Wenbo Jiang were employed by the company Hunan Meibeida Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Quintana, G.; Ciurana, J. Chatter in machining processes: A review. Int. J. Mach. Tools Manuf. 2011, 51, 363–376. [Google Scholar] [CrossRef]
- Rusinek, R.; Wiercigroch, M.; Wahi, P. Modelling of frictional chatter in metal cutting. Int. J. Mech. Sci. 2014, 89, 167–176. [Google Scholar] [CrossRef]
- Qin, C.; Tao, J.; Shi, H.; Xiao, D.; Li, B.; Liu, C. A novel Chebyshev-wavelet-based approach for accurate and fast prediction of milling stability. Precis. Eng. 2020, 62, 244–255. [Google Scholar] [CrossRef]
- Rafal, R.; Pawel, L.; Krzysztof, K.; Bogdan, K.; Jerzy, W. Chatter identification methods on the basis of time series measured during titanium superalloy milling. Int. J. Mech. Sci. 2015, 99, 196–207. [Google Scholar] [CrossRef]
- Tao, J.; Qin, C.; Liu, C. A synchroextracting-based method for early chatter identification of robotic drilling process. Int. J. Adv. Manuf. Technol. 2019, 100, 273–285. [Google Scholar] [CrossRef]
- Munoa, J.; Beudaert, X.; Dombovari, Z.; Altintas, Y.; Budak, E.; Brecher, C.; Stepan, G. Chatter suppression techniques in metal cutting. CIRP Ann. 2016, 65, 785–808. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, X.; Yan, R.; Chen, X.; Cao, H. Multi harmonic spindle speed variation for milling chatter suppression and parameters optimization. Precis. Eng. 2019, 55, 268–274. [Google Scholar] [CrossRef]
- Altintas, Y.; Weck, M. Chatter stability of metal cutting and grinding. CIRP Ann. 2004, 53, 619–642. [Google Scholar] [CrossRef]
- Catania, G.; Mancinelli, N. Theoretical–experimental modeling of milling machines for the prediction of chatter vibration. Int. J. Mach. Tools Manuf. 2011, 51, 339–348. [Google Scholar] [CrossRef]
- Altintas, Y.; Budak, E. Analytical prediction of stability lobes in milling. CIRP Ann. Manuf. Technol. 1995, 44, 357–362. [Google Scholar] [CrossRef]
- Merdol, S.D.; Altintas, Y. Multi frequency solution of chatter stability for low immersion milling. J. Manuf. Sci. Eng. 2004, 126, 459–466. [Google Scholar] [CrossRef]
- Insperger, T.; Stépán, G. Semi-discretization method for delayed systems. Int. J. Numer. Methods Eng. 2002, 55, 503–518. [Google Scholar] [CrossRef]
- Insperger, T.; Stépán, G. Updated semi-discretization method for periodic delay-differential equations with discrete delay. Int. J. Numer. Methods Eng. 2004, 61, 117–141. [Google Scholar] [CrossRef]
- Zhang, C.; Yan, Z.; Jiang, X. Numerical integration scheme–based semi-discretization methods for stability prediction in milling. Int. J. Adv. Manuf. Technol. 2021, 115, 397–411. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H. A full-discretization method for prediction of milling stability. Int. J. Mach. Tools Manuf. 2010, 50, 502–509. [Google Scholar] [CrossRef]
- Tang, X.; Peng, F.; Yan, R.; Gong, Y.; Li, Y.; Jiang, L. Accurate and efficient prediction of milling stability with updated full-discretization method. Int. J. Adv. Manuf. Technol. 2017, 88, 2357–2368. [Google Scholar] [CrossRef]
- Qin, C.; Tao, J.; Liu, C. A novel stability prediction method for milling operations using the holistic-interpolation scheme. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4463–4475. [Google Scholar] [CrossRef]
- Dai, Y.; Li, H.; Xing, X.; Hao, B. Prediction of chatter stability for milling process using precise integration method. Precis. Eng. 2018, 52, 152–157. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H. Numerical integration method for prediction of milling stability. J. Manuf. Sci. Eng. 2011, 133, 031005. [Google Scholar] [CrossRef]
- Dong, X.; Qiu, Z. Stability analysis in milling process based on updated numerical integration method. Mech. Syst. Signal Process. 2020, 137, 106435. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, H.; Meng, G.; Liu, C. A novel approach for the prediction of the milling stability based on the Simpson method. Int. J. Mach. Tools Manuf. 2015, 99, 43–47. [Google Scholar] [CrossRef]
- Niu, J.; Ding, Y.; Zhu, L.; Ding, H. Runge–Kutta methods for a semi-analytical prediction of milling stability. Nonlinear Dyn. 2014, 76, 289–304. [Google Scholar] [CrossRef]
- Qin, C.; Tao, J.; Li, L.; Liu, C. An Adams-Moulton-based method for stability prediction of milling processes. Int. J. Adv. Manuf. Technol. 2017, 89, 3049–3058. [Google Scholar] [CrossRef]
- Li, W.; Wang, L.; Yu, G. An accurate and fast milling stability prediction approach based on the Newton-Cotes rules. Int. J. Mech. Sci. 2020, 177, 105469. [Google Scholar] [CrossRef]
- Mei, Y.; Mo, R.; Sun, H.; He, B.; Wan, N. Stability prediction in milling based on linear multistep method. Int. J. Adv. Manuf. Technol. 2019, 105, 2677–2688. [Google Scholar] [CrossRef]
- Wu, Y.; You, Y.; Liu, A.; Deng, B.; Ye, T.; Chen, W. A correction method for milling stability analysis based on local truncation error. Int. J. Adv. Manuf. Technol. 2021, 115, 2873–2887. [Google Scholar] [CrossRef]
- Qin, G.; Lou, W.; Wang, H.; Wu, Z. High efficiency and precision approach to milling stability prediction based on predictor–corrector linear multi-step method. Int. J. Adv. Manuf. Technol. 2022, 122, 1933–1955. [Google Scholar] [CrossRef]
- Jiang, S.; Sun, Y.; Yuan, X.; Liu, W. A second-order semi-discretization method for the efficient and accurate stability prediction of milling process. Int. J. Adv. Manuf. Technol. 2017, 92, 583–595. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, C.; Jia, J.; Ma, B.; Jiang, X.; Wang, D.; Zhu, T. High-order semi-discretization methods for stability analysis in milling based on precise integration. Precis. Eng. 2022, 73, 71–92. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H. Second-order full-discretization method for milling stability prediction. Int. J. Mach. Tools Manuf. 2010, 50, 926–932. [Google Scholar] [CrossRef]
- Quo, Q.; Sun, Y.; Jiang, Y. On the accurate calculation of milling stability limits using third-order full-discretization method. Int. J. Mach. Tools Manuf. 2012, 62, 61–66. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, D.; Wu, B. An efficient full-discretization method for prediction of milling stability. Int. J. Mach. Tools Manuf. 2012, 63, 44–48. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, X.; Liu, Z.; Wang, H.; Yan, Z. An updated full-discretization milling stability prediction method based on the higher-order Hermite–Newton interpolation polynomial. Int. J. Adv. Manuf. Technol. 2018, 95, 2227–2242. [Google Scholar] [CrossRef]
- Ozoegwu, C.G. High order vector numerical integration schemes applied in state space milling stability analysis. Appl. Math. Comput. 2016, 273, 1025–1040. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y. A refined and accurate method for stability analysis of milling process. Alex. Eng. J. 2025, 116, 306–320. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, X.; Liu, Z.; Wang, D.; Jiao, L.; Ji, Y. Third-order updated full-discretization method for milling stability prediction. Int. J. Adv. Manuf. Technol. 2017, 92, 2299–2309. [Google Scholar] [CrossRef]
- Ma, J.; Li, Y.; Zhang, D.; Zhao, B.; Wang, G.; Pang, X. A Novel Updated Full-Discretization Method for Prediction of Milling Stability. Micromachines 2022, 13, 160. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Wan, Y.; Luo, X.; Liu, Z.; Song, Q. Milling stability prediction based on the hybrid interpolation scheme of the Newton and Lagrange polynomials. Int. J. Adv. Manuf. Technol. 2021, 112, 1501–1512. [Google Scholar] [CrossRef]
- Qin, C.; Tao, J.; Liu, C. A predictor-corrector-based holistic-discretization method for accurate and efficient milling stability analysis. Int. J. Adv. Manuf. Technol. 2018, 96, 2043–2054. [Google Scholar] [CrossRef]
- Song, C.; Peng, Z.; Zhao, D.; Jin, X. A whole discretization method for milling stability prediction considering the discrete vibration velocities. J. Sound Vib. 2023, 553, 117687. [Google Scholar] [CrossRef]
- Li, H.; Dai, Y.; Fan, Z. Improved precise integration method for chatter stability prediction of two-DOF milling system. Int. J. Adv. Manuf. Technol. 2018, 101, 1235–1246. [Google Scholar] [CrossRef]
- Qin, C.; Tao, J.; Liu, C. Stability analysis for milling operations using an Adams-Simpson-based method. Int. J. Adv. Manuf. Technol. 2017, 92, 969–979. [Google Scholar] [CrossRef]
- Zhi, H.; Zhang, T.; Du, J.; Yan, X. An Efficient Full-Discretization Method for Milling Stability Prediction. Int. J. Adv. Manuf. Technol. 2020, 107, 4955–4967. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, C.; Jia, J.; Ma, B.; Jiang, X.; Wang, D.; Wang, W.; Yang, C. Two updated methods based on Simpson formula for chatter stability prediction in milling. Int. J. Adv. Manuf. Technol. 2022, 121, 8357–8378. [Google Scholar] [CrossRef]
- Zhan, D.; Jiang, S.; Li, S.; Sun, Y. A Hybrid Multi-Step Method Based on 1/3 and 3/8 Simpson Formulas for Milling Stability Prediction. Int. J. Adv. Manuf. Technol. 2022, 120, 265–277. [Google Scholar] [CrossRef]
- Liu, C.; Tang, D.; Li, S.; Ding, G. Simpson’s 3/8–based method stability analysis for milling processes. Int. J. Adv. Manuf. Technol. 2021, 114, 671–682. [Google Scholar] [CrossRef]
- Du, X.; Ren, P.; Zheng, J. Predicting Milling Stability Based on Composite Cotes-Based and Simpson’s 3/8-Based Methods. Micromachines 2022, 13, 810. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).