1. Introduction
In the modern industrial system, rotating machinery occupies a pivotal position. As the rolling bearing is a core component, its operating condition plays a decisive role in the system’s overall safety and reliability [
1,
2]. Condition monitoring and fault diagnosis of rolling bearings have therefore been the focus of research in recent decades [
3,
4].
Presently, the identification of faults in rolling bearings is predominantly predicated on signal processing methodologies, incorporating machine learning and deep learning algorithms. These methodologies entail the analysis of measured signals within the time domain, frequency domain, and time–frequency domain, thereby enhancing the efficacy of fault diagnosis [
5]. As is well documented in the relevant literature, the following tools are commonly used: the fast Fourier transform (FFT) [
6], the wavelet packet transform (WPT) [
7], empirical mode decomposition (EMD) [
8], and the Hilbert–Huang transform (HHT) [
9]. However, the employment of signal processing-based methodologies frequently necessitates a sophisticated comprehension of signal analysis, thereby impeding the efficacy of fault diagnosis due to the inevitable presence of human interference.
Machine learning methods have been extensively utilized in the field of bearing fault diagnosis, with prominent examples including support vector machines (SVMs) [
10], random forests (RFs) [
11], and k-nearest neighbor algorithms (KNNs) [
12]. However, it should be noted that conventional machine learning algorithms also impose limitations on the diagnostic capabilities of the model, primarily due to their relatively shallow structure.
In recent years, deep learning algorithms, including convolutional neural networks (CNNs) and multi-layer perceptrons (MLPs), have been extensively employed in the field of bearing fault diagnosis. The 1DCNN has been developed to simplify the structure of CNNs, with the objective of maximizing classification accuracy. The 1DCNN is combined with the self-correcting CEEMD algorithm, as proposed by Gao et al. [
13]. This algorithm is an enhanced signal processing algorithm, derived from the CEEMD. This algorithm represents an enhanced signal processing technique, founded upon CEEMD, which incorporates the concepts of fuzzy entropy and kurtosis with a view to attenuating noise and identifying impulse signals, thereby enhancing the accuracy of classification. Guo et al. [
14] employed motor speed signals and CNN models for the purpose of diagnosing a range of motor faults. Li et al. [
15] combined the 1DCNN with gated recurrent units (GRUs). The 1DCNN has the capacity to automatically extract features from data, whilst GRUs can also perform this function. The GRU compensates for the deficiencies of CNN in processing time-series data, thereby ensuring the comprehensiveness of the extracted features and enhancing the accuracy of circuit fault diagnosis. He et al. [
16] integrated 1DCNN with transfer learning (TL) to formulate a 1DCNN-TL model to predict the inlet gas volume fraction of a rotary vane pump, achieving a satisfactory fit. Mystkowski, Arkadiusz et al. [
17] applied a multi-layer perceptron (MLP) with two hidden layers to detect faults in rotary weeders, achieving favorable results in both laboratory conditions and real-world tests. Zou, Fengqian et al. [
18] proposed a depth-optimized 1DCNN that automatically extracts features from background noise while maintaining high accuracy even in noisy conditions. Xie, Suchao et al. [
19] developed a multi-scale multi-layer perceptron (MSMLP) and used complementary integrated empirical modal decomposition (CEEMD) for fault diagnosis. However, the aforementioned studies are limited in scope as they begin from a single scale, such as the time or frequency domain, and the added noise is regular. In contrast, this study aims to address these limitations by expanding the scope to include multiple scales and by introducing a more diverse range of added noises.
In recent years, scholars have utilized fusion models for the purpose of fault diagnosis. For instance, Sinitsin et al. [
20] combined CNN and MLP to form a CNN-MLP model for the diagnosis of bearings. Similarly, Song et al. [
21] combined CNN and BiLSTM to construct the CNN-BiLSTM algorithm, which they then tuned using the improved PSO algorithm. In a recent study, Bharatheedasan, Kumaran et al. [
22] explored the potential of combining a multi-layer perceptron (MLP) with long short-term memory (LSTM) to predict bearing life. Similarly, Wang, Hui et al. [
23] investigated the efficacy of integrating multi-head attention with convolutional neural network (CNN) and optimizing the CNN structure using the attention mechanism to enhance the recognition rate of fault diagnosis. Qing et al. [
24] embedded Transformer in the dual-head integration algorithm (DHET) and used the dual-input time–frequency architecture to effectively capture the long-range dependencies in the data. Cui, Long et al. [
25] introduced the self-attention mechanism into the bearing fault diagnosis. The study proposed a self-attention-based signal converter, which was able to learn the feature extraction capability from a large amount of unlabeled data by using a comparison learning method with only positive samples. In addition, Peng et al. [
26] embedded the attention mechanism in a traditional residual network to evaluate the bearing state.
Notably, these studies were conducted in a laboratory setting with experimental conditions that excluded noise effects. The studies mainly focus on attention mechanisms within a single scale. In real industrial scenarios, the models may be disturbed by irregular random noise, which may significantly limit their effectiveness in applications. Therefore, the method proposed in this paper can maintain high accuracy under laboratory conditions and effectively deal with strong noise. Therefore, this method has the potential to achieve good performance in the face of a large amount of noise while maintaining high accuracy in the laboratory environment. The main contributions of this paper include the following:
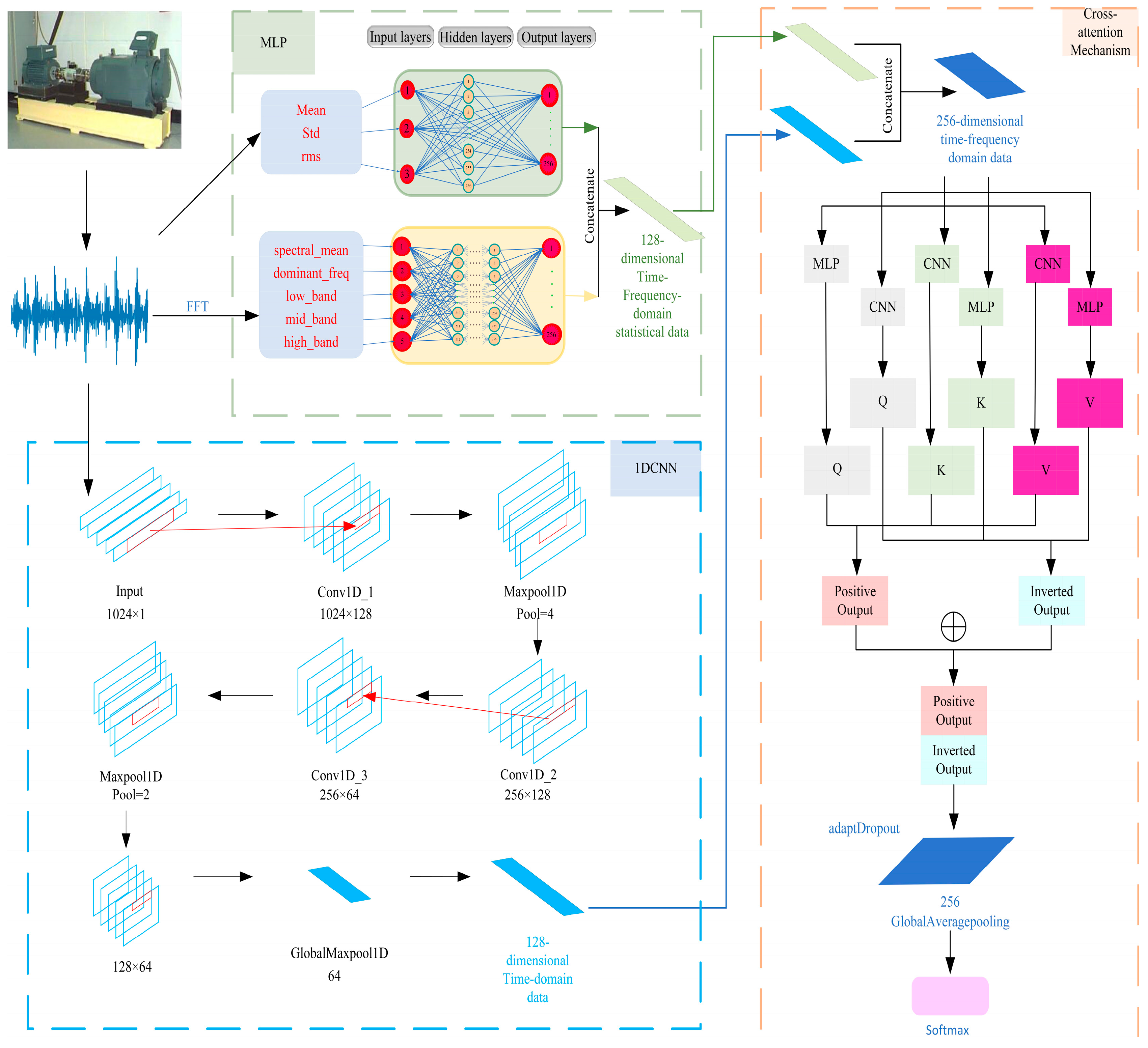
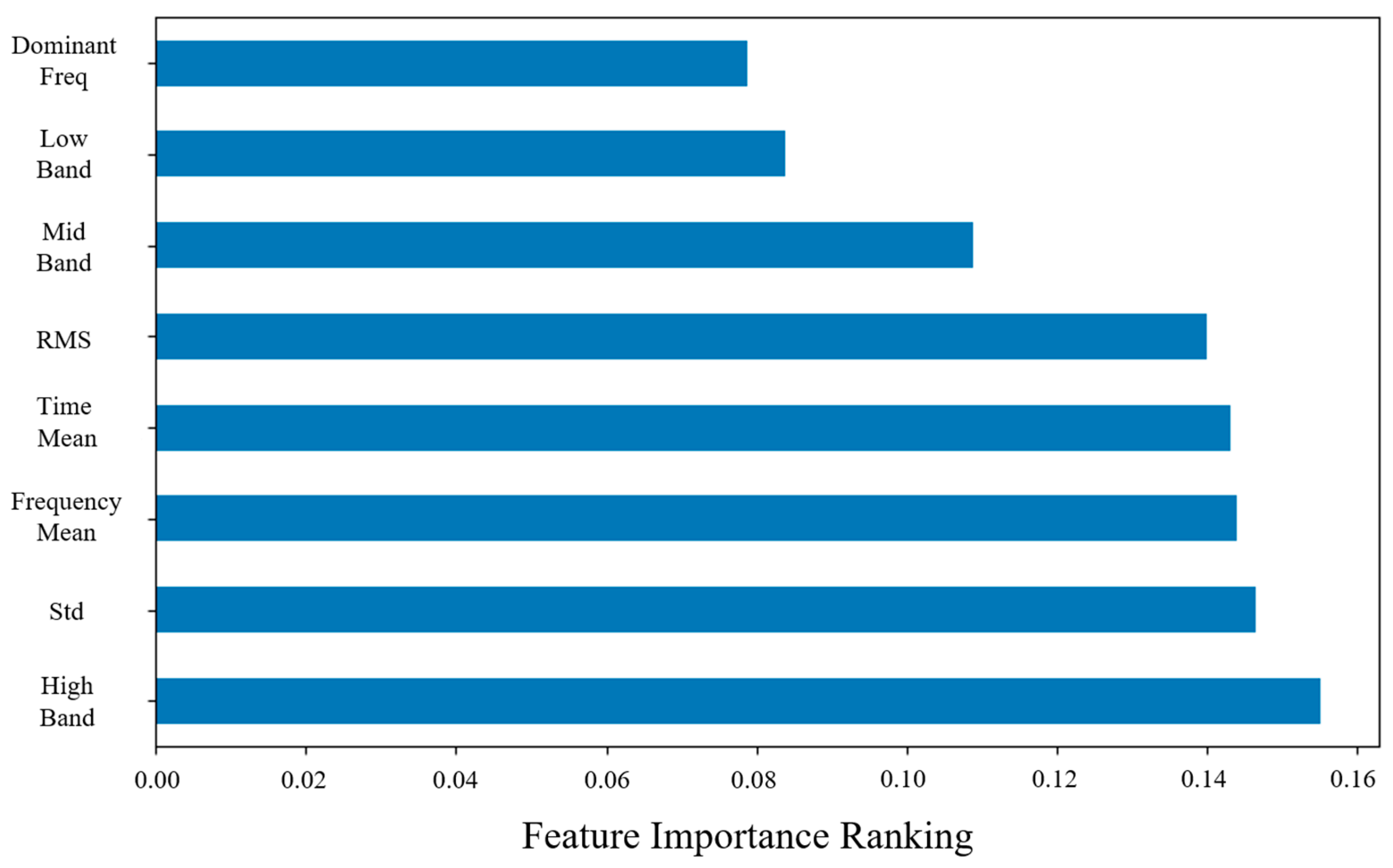
The innovation of this work lies not in the individual components but in the integration strategy of dual MLP and 1DCNN and application scenarios under high noise. Our dual MLP extracts high- and low-frequency information from the data, solving the problem that the current Transformer-based models have a weak ability to capture local minute details and are vulnerable to noise interference at low signal-to-noise ratios.
The enhanced 1DCNN+dual MLP multimodal feature extraction structure has been designed to extract time- and frequency-domain features from the original data in depth.
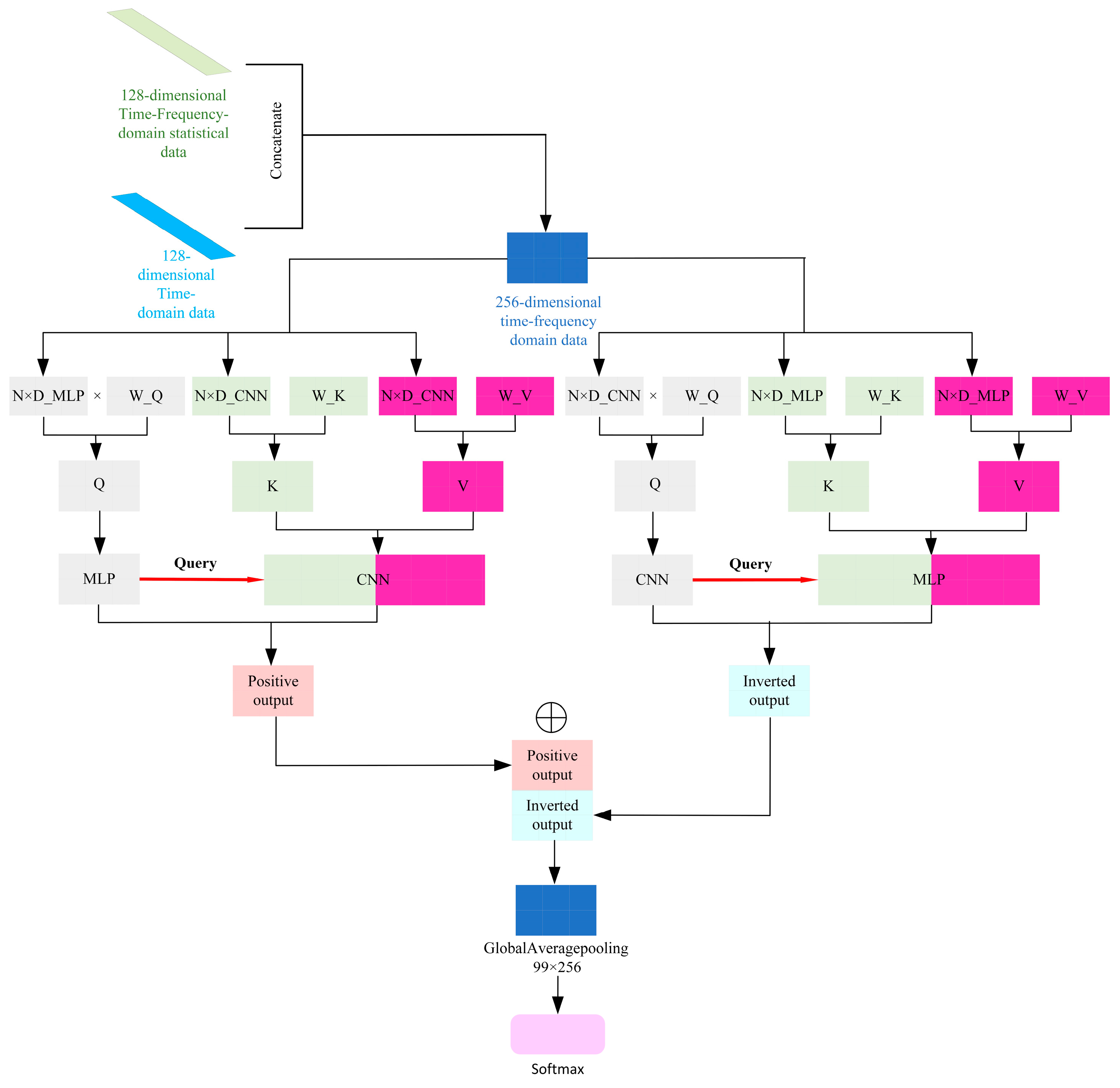
A refined cross-attention mechanism is utilized to comprehensively capture signal characteristics from both the temporal and frequency domains. This approach demonstrates exceptional performance under diverse noise conditions.
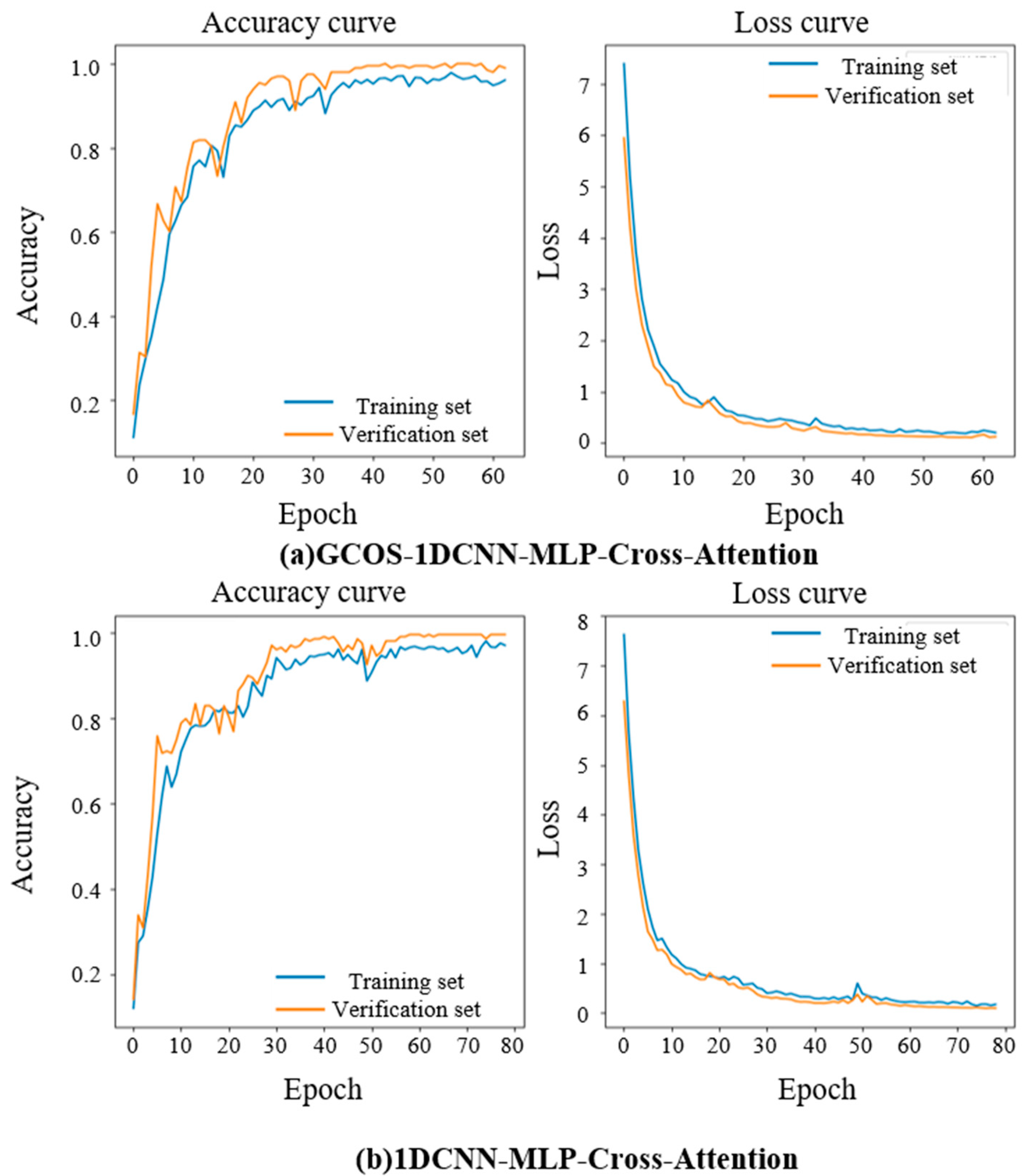
The development of the GCOS learning rate scheduler constitutes a significant advancement in the field of automatic learning rate adjustment. This tool has been designed to address the challenge of manually selecting the learning rate by automatically adjusting it.
The experimental verification of the model’s performance was conducted in two distinct settings: the laboratory environment and a high-noise environment.
4. Conclusions and Future Work
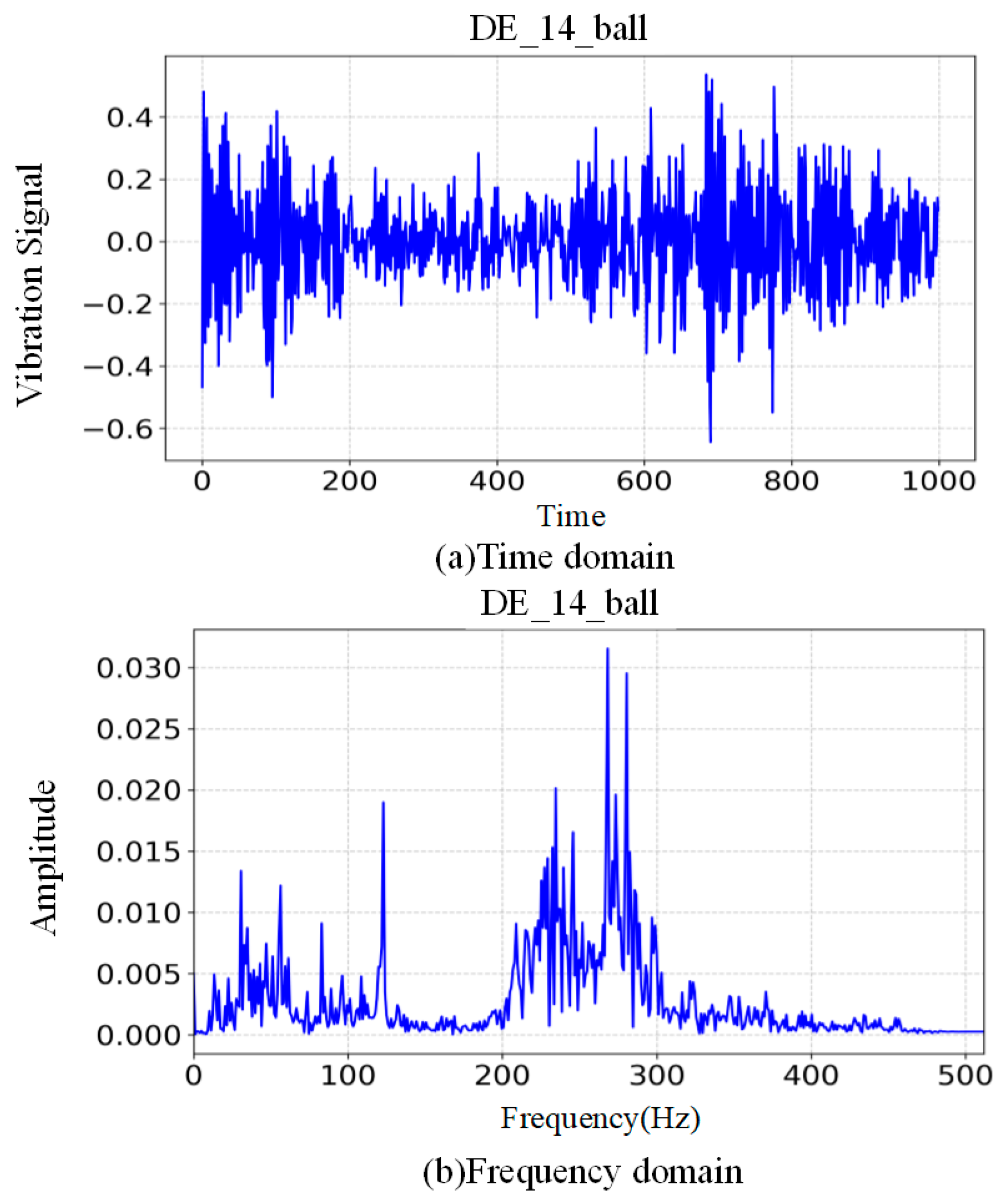
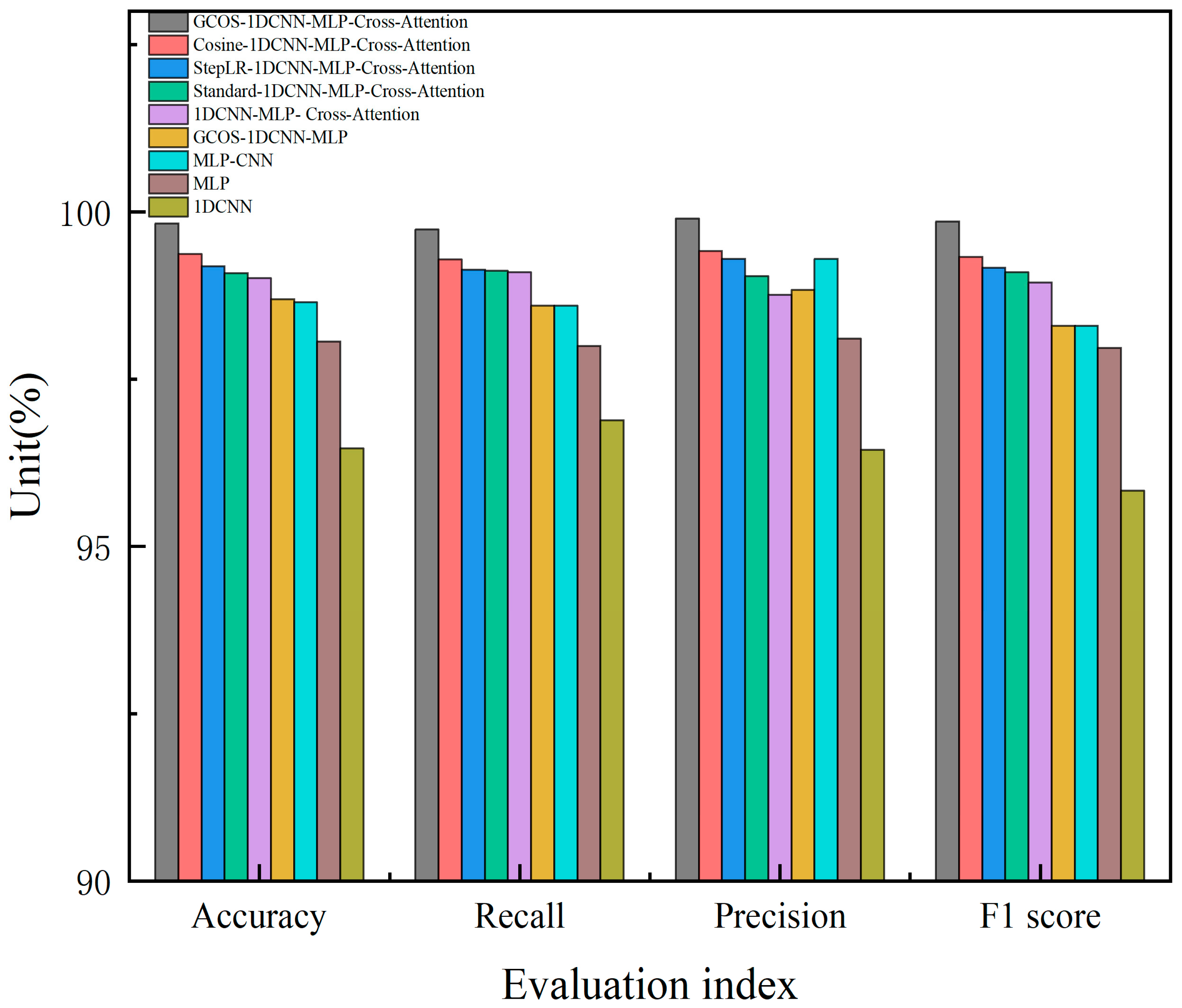
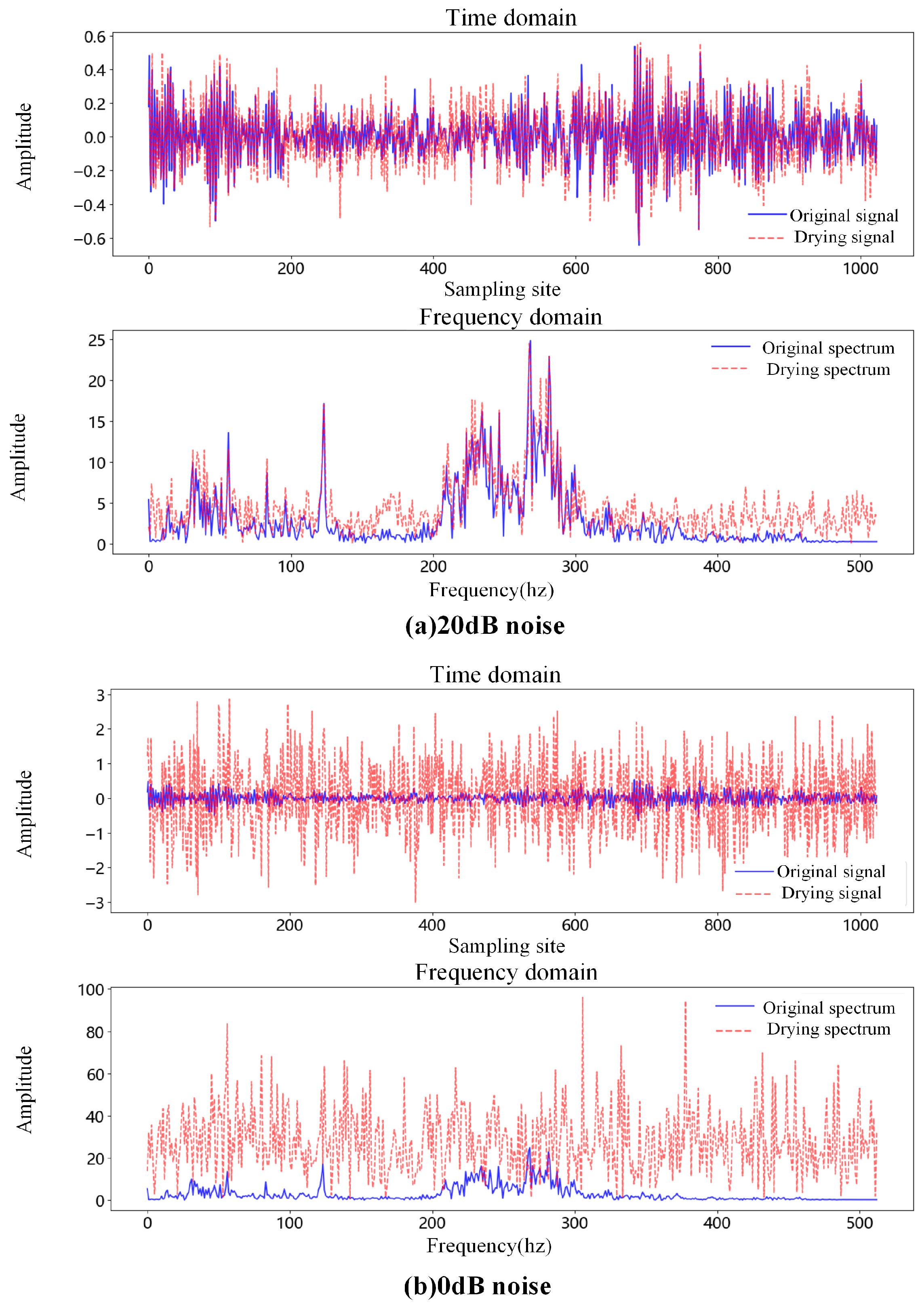
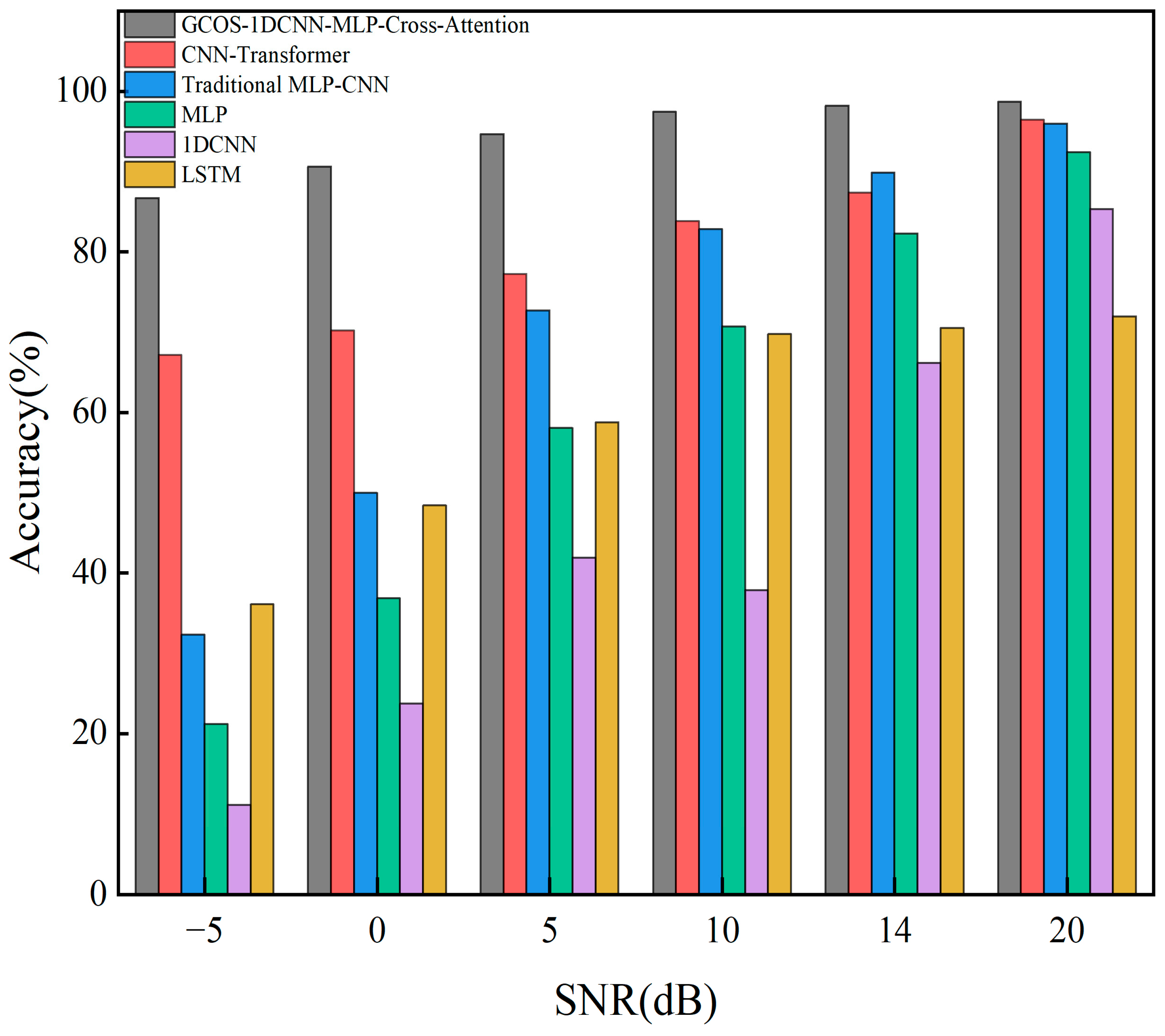
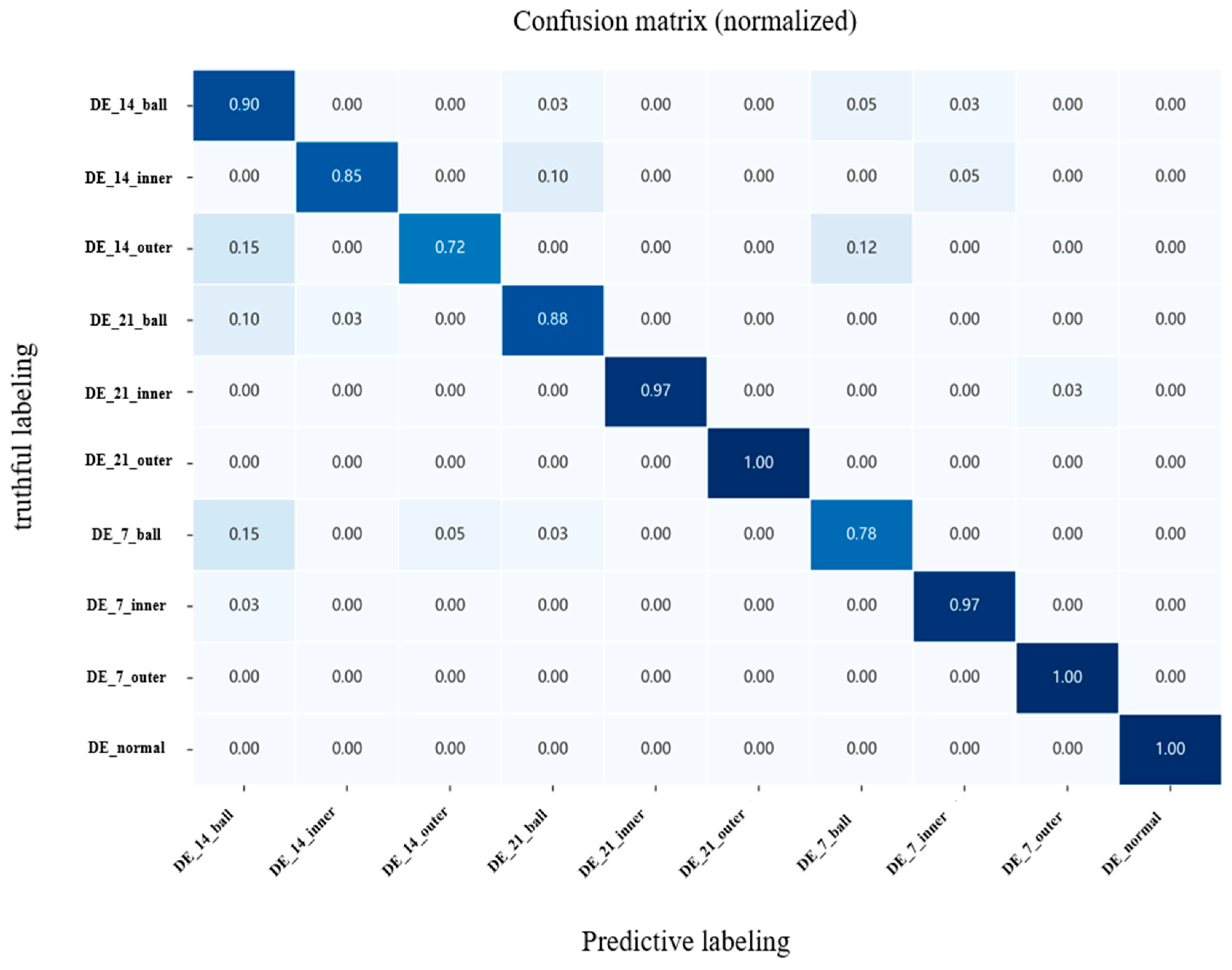
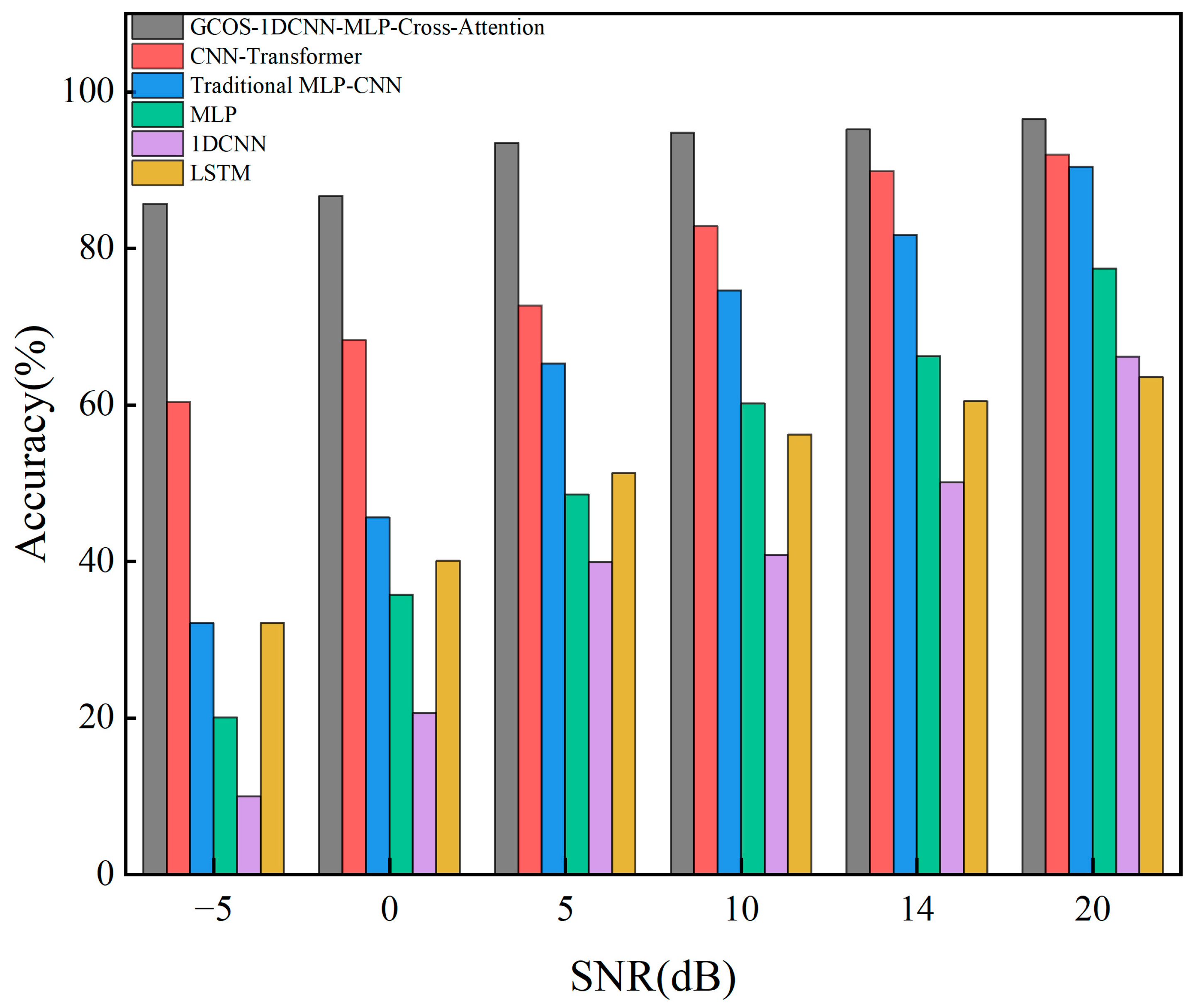
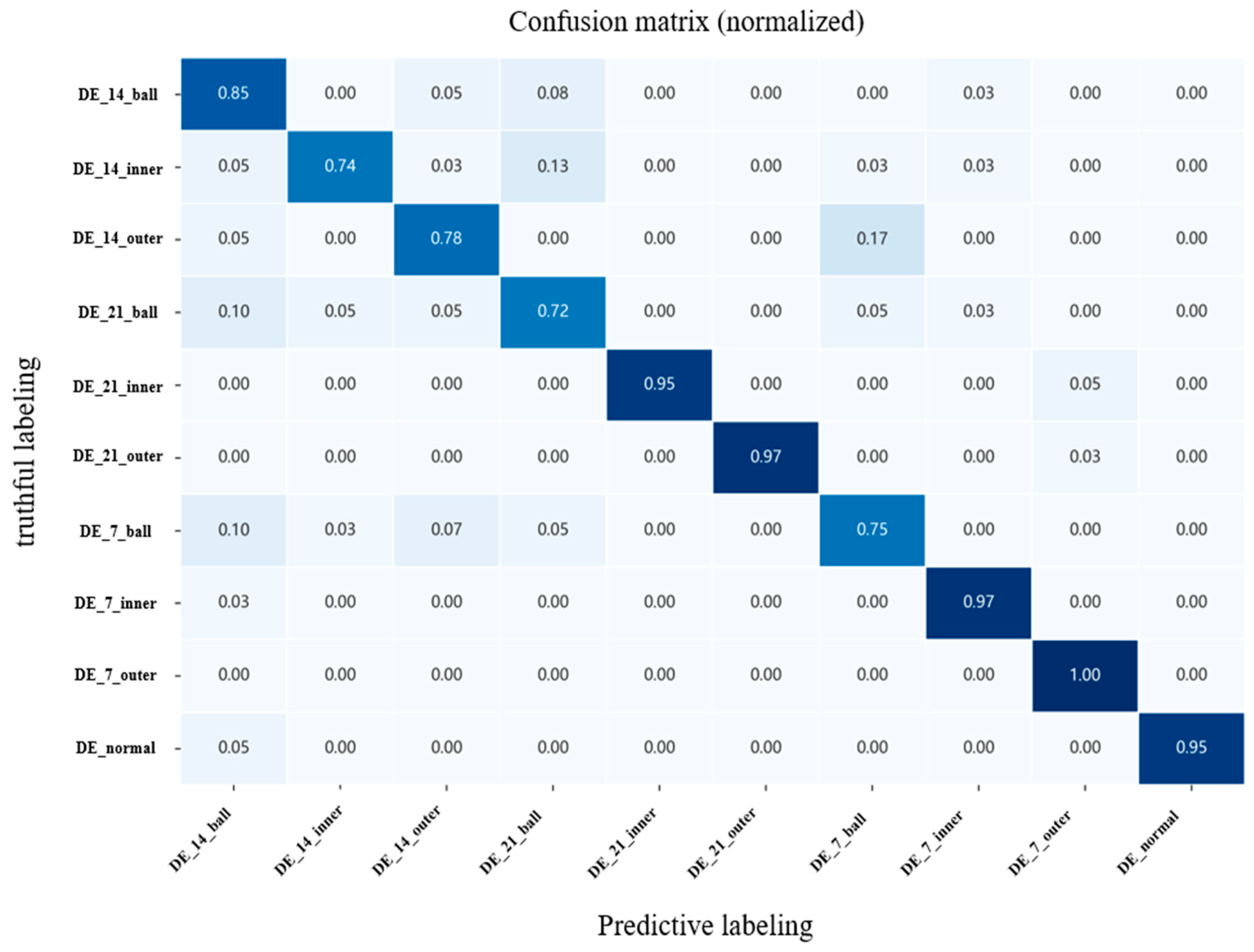
In order to cope with the problems of insufficient feature extraction and poor model performance in high-noise environments in current bearing fault diagnosis methods, this paper designs a GCOS-1DCNN-dual MLP-bidirectional cross-attention mechanism model, which gives full play to the advantages of 1DCNN for extracting temporal data and bidirectional cross-attention mechanism for feature fusion. The model constructed in this paper provides a new way and idea of extracting fault diagnosis for bearings, including the ability of dual MLP to deeply extract time-domain and frequency-domain features while using bidirectional cross-attention mechanism to deeply fuse multimodal features, and also designed a learning rate optimizer, which can automatically adjust the learning rate during the model learning process to cope with the shortcomings of slow learning speed and overfitting of the model. In fifteen independent validation experiments using the Case Western Reserve University bearing dataset, the model demonstrated an average accuracy of 99.83%, exhibiting exceptional robustness. Meanwhile, noise is added to the original dataset, noise experiments are conducted, and the results show that the model proposed in this paper still maintains a high accuracy of 90.66% and 86.72% under the strong noise levels of 0 dB and −5 dB. This shows that the model proposed in this paper has the advantages of high recognition accuracy, good robustness, and strong noise resistance.
Future work should evaluate the model’s adaptability to noise scenarios beyond Gaussian noise—such as pink noise and impulse/impact noise—to better address diverse noise conditions encountered in industrial applications. Additionally, research into scheduler sensitivity is warranted.