Nonlinear Dynamic Analysis of High-Speed Aerostatic Conical Bearing–Rotor System with Micro-Orifice Frictional Loss
Abstract
1. Introduction
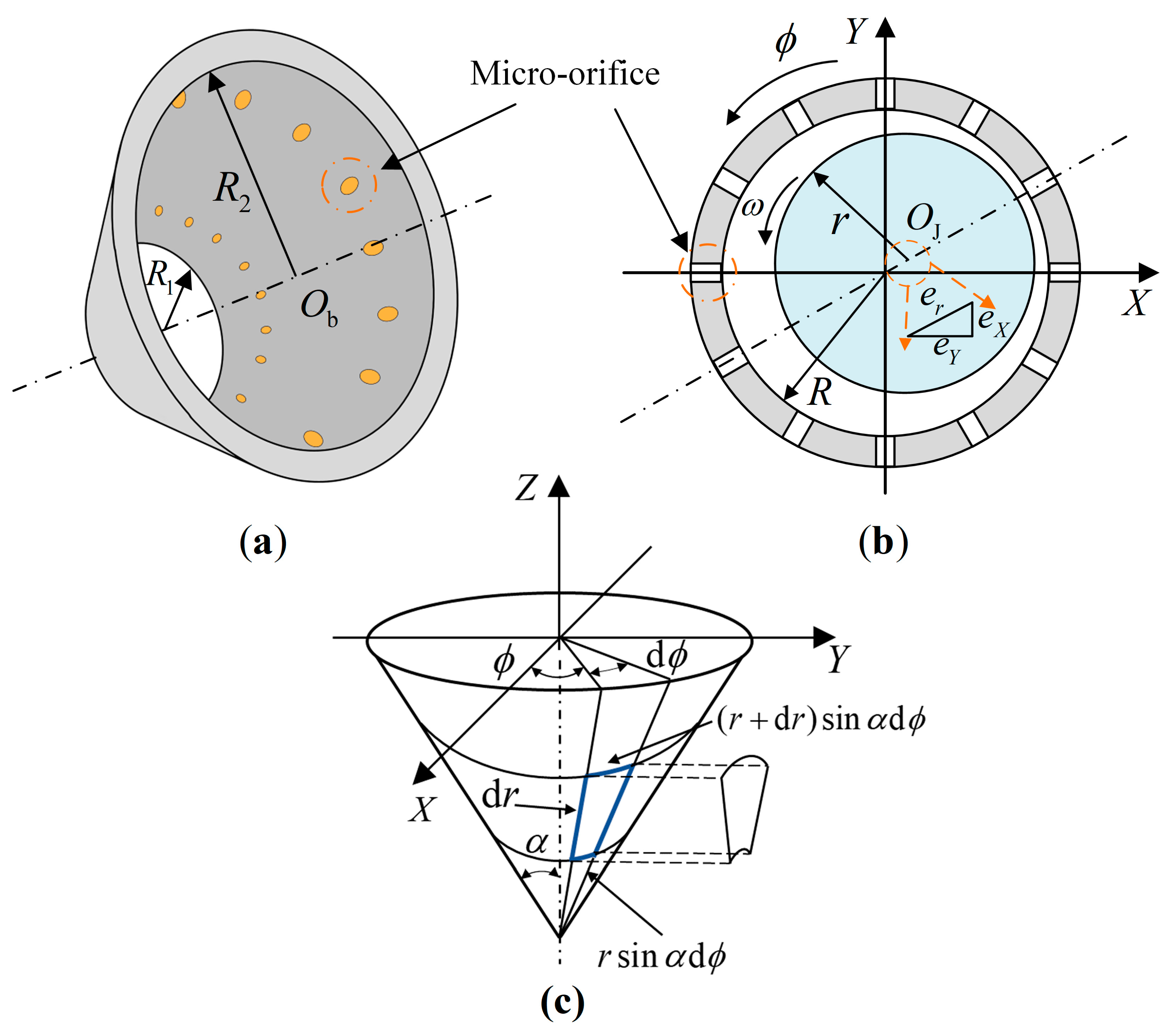
2. Mathematical Model of Bearing–Rotor System with Frictional Loss
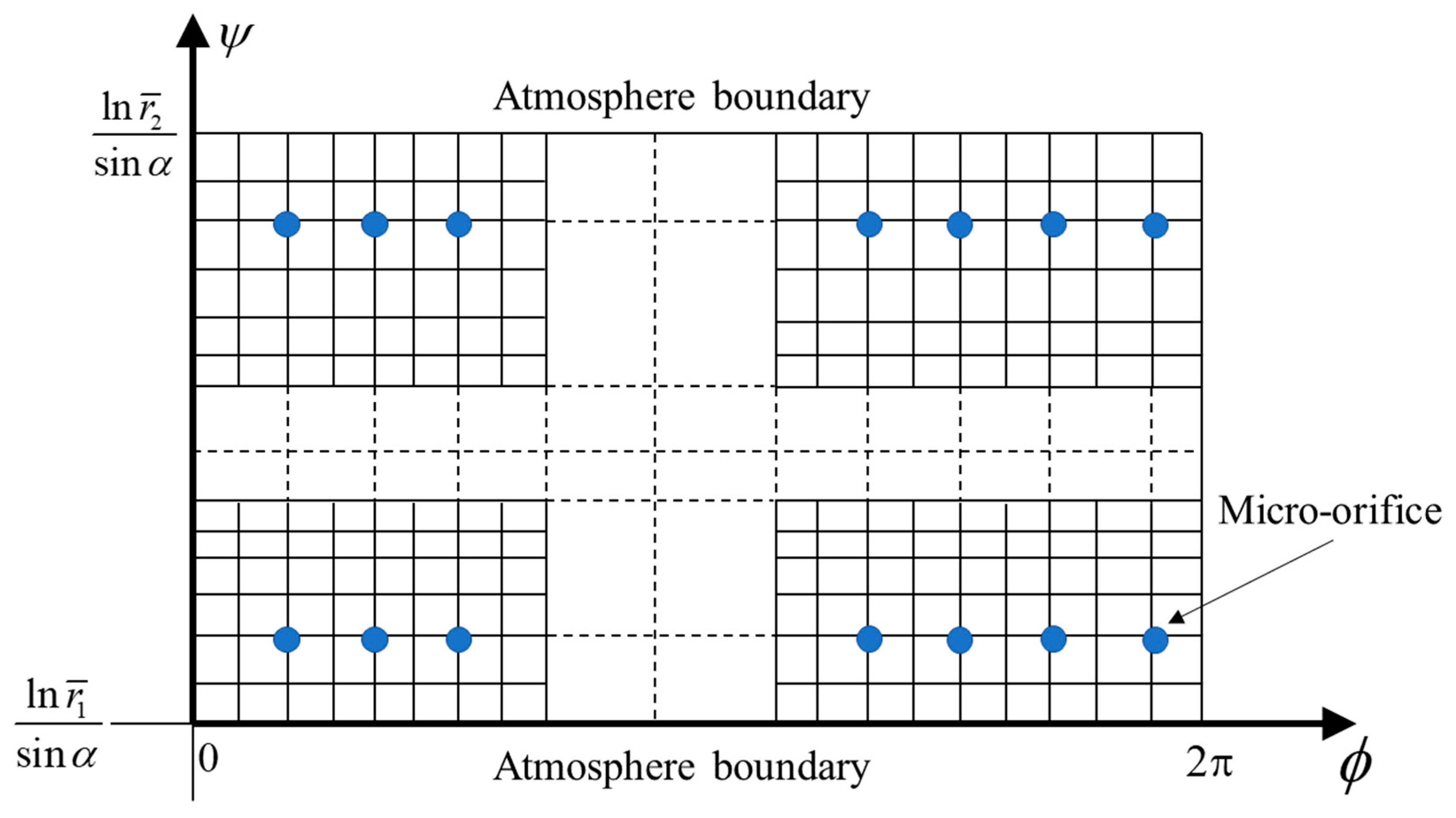
2.1. The Governing Equation of Air Film Flow
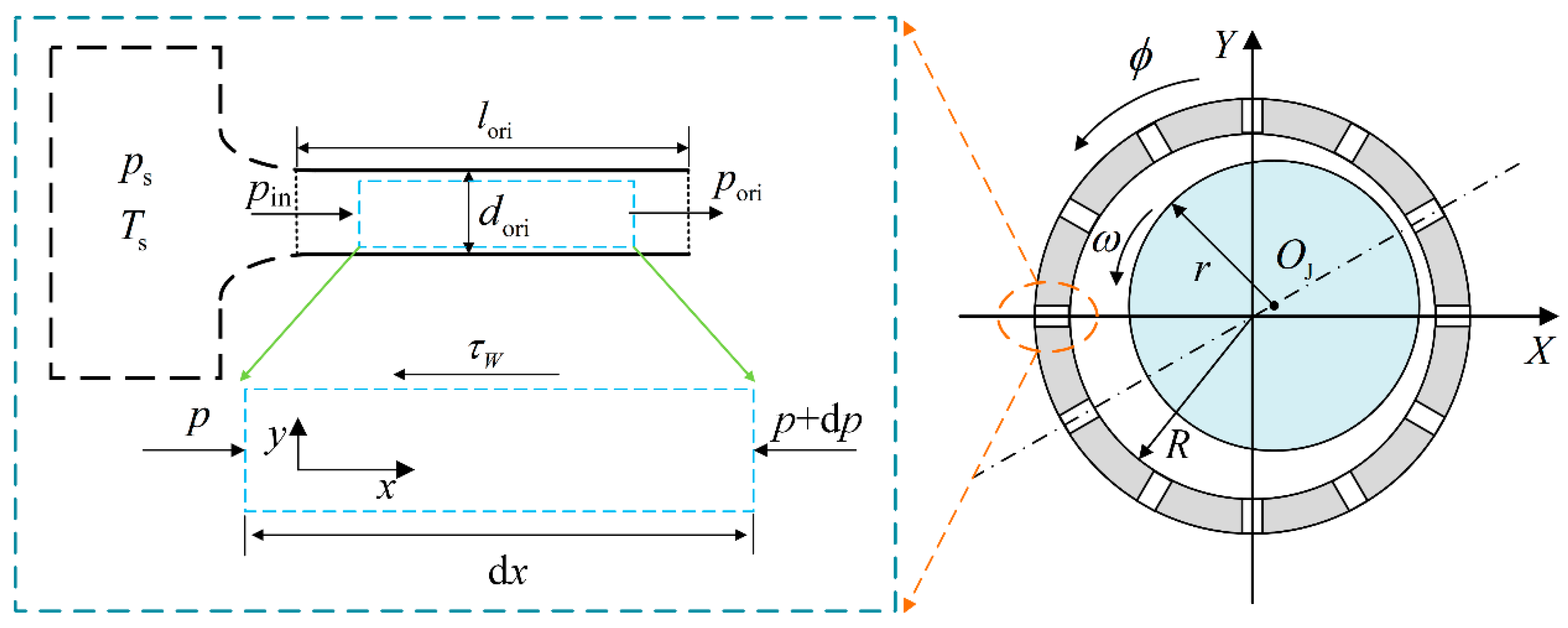
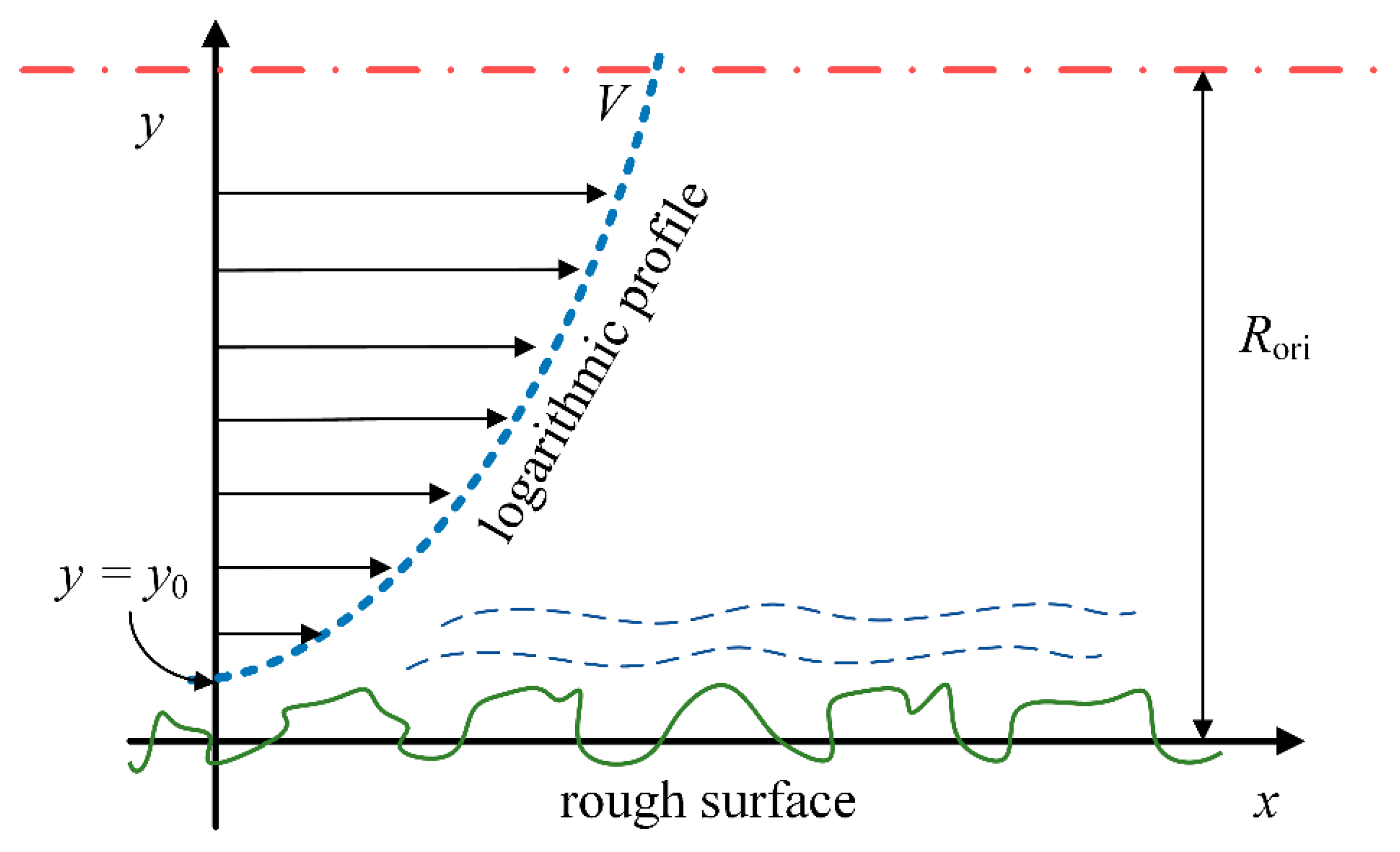
2.2. Micro-Orifice Model with Frictional Loss in Aerostatic Conical Bearings
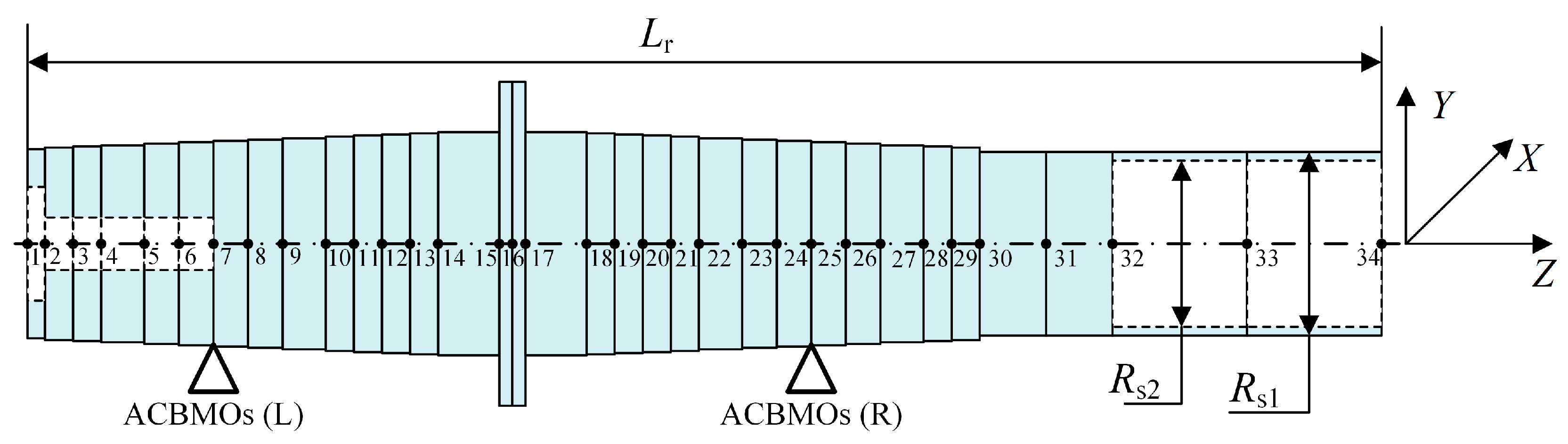
2.3. Dynamic Model of the ACBMO–Rotor System
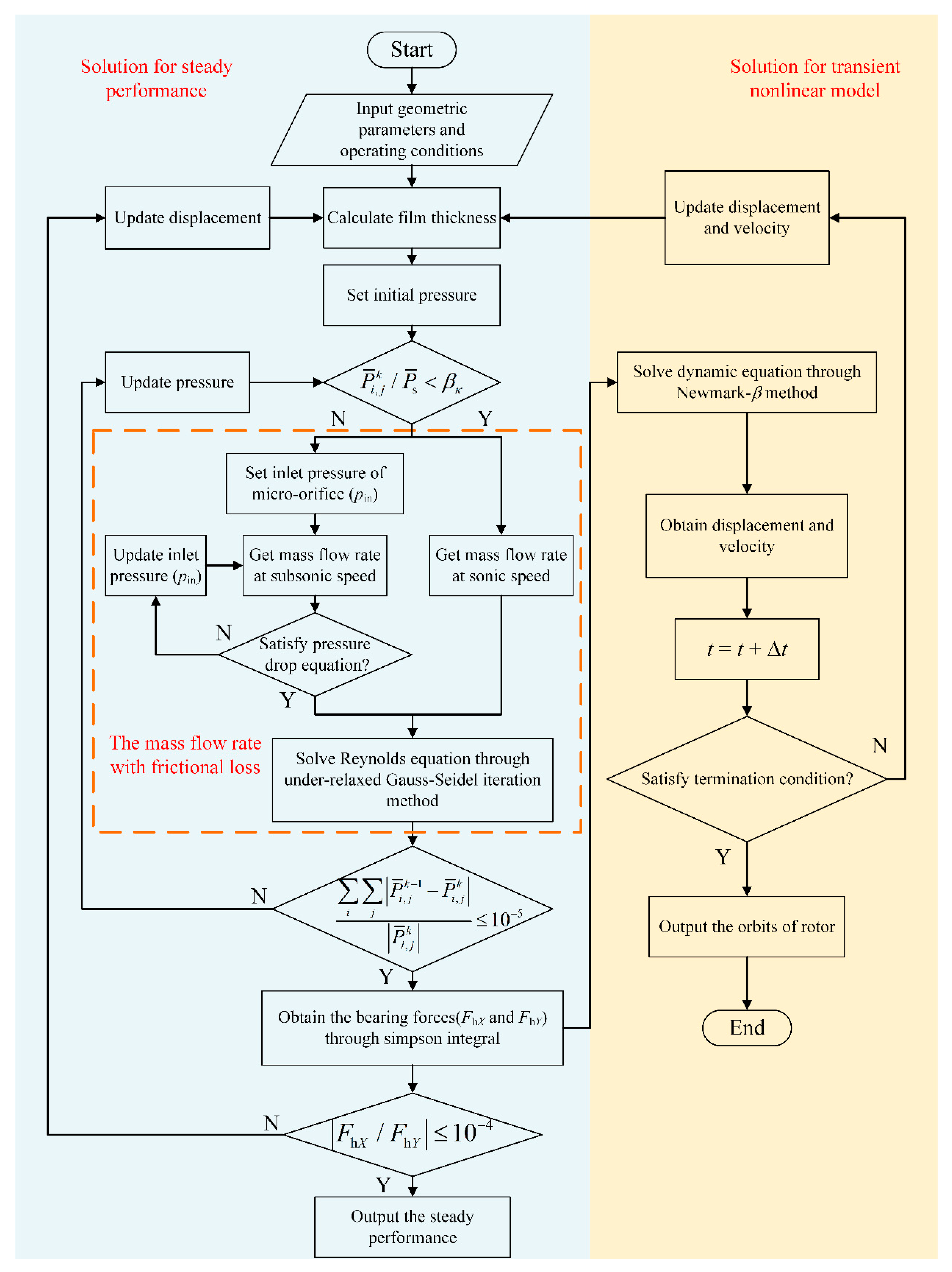
2.4. Numerical Calculation
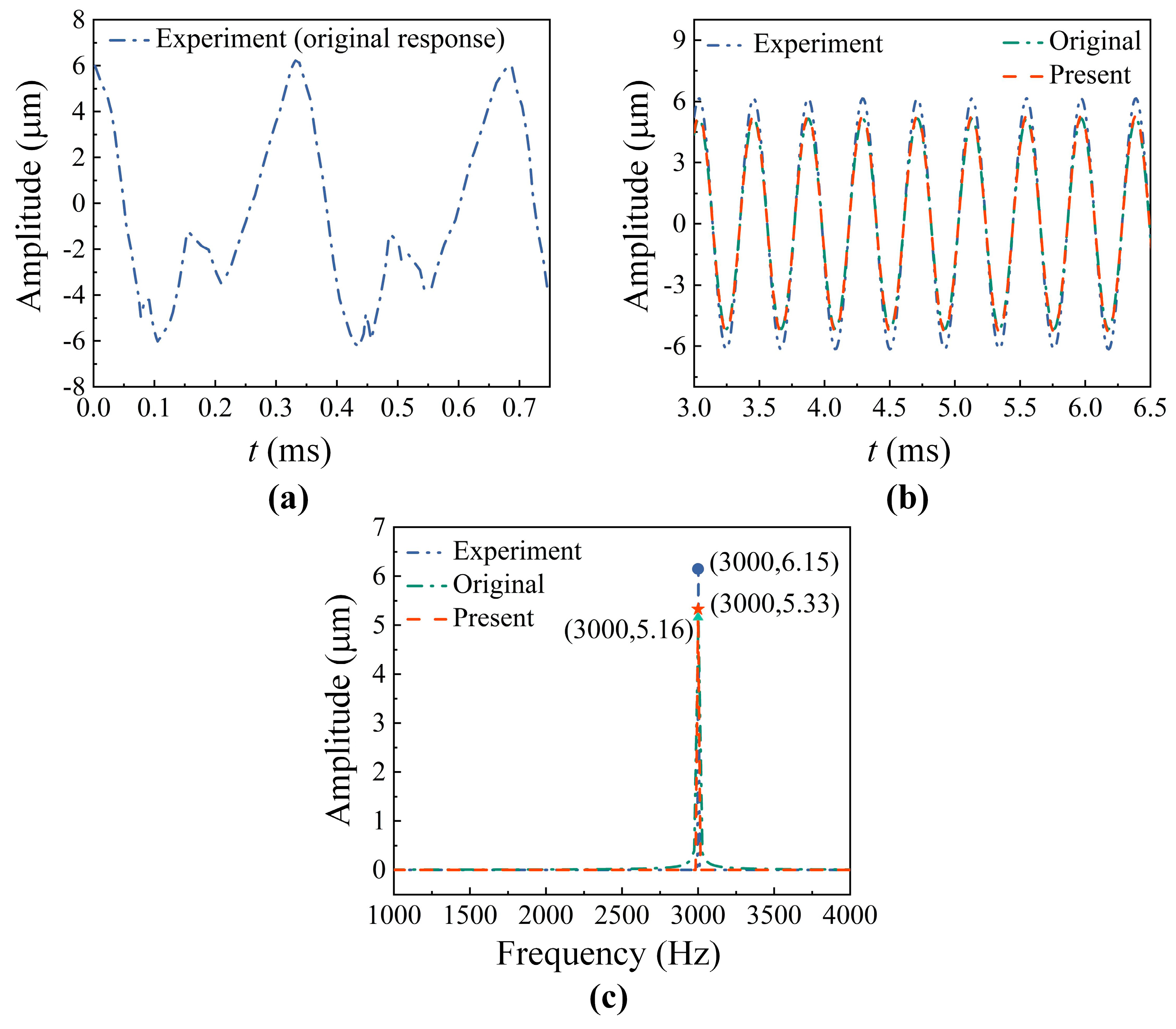
2.5. Numerical Model Validation
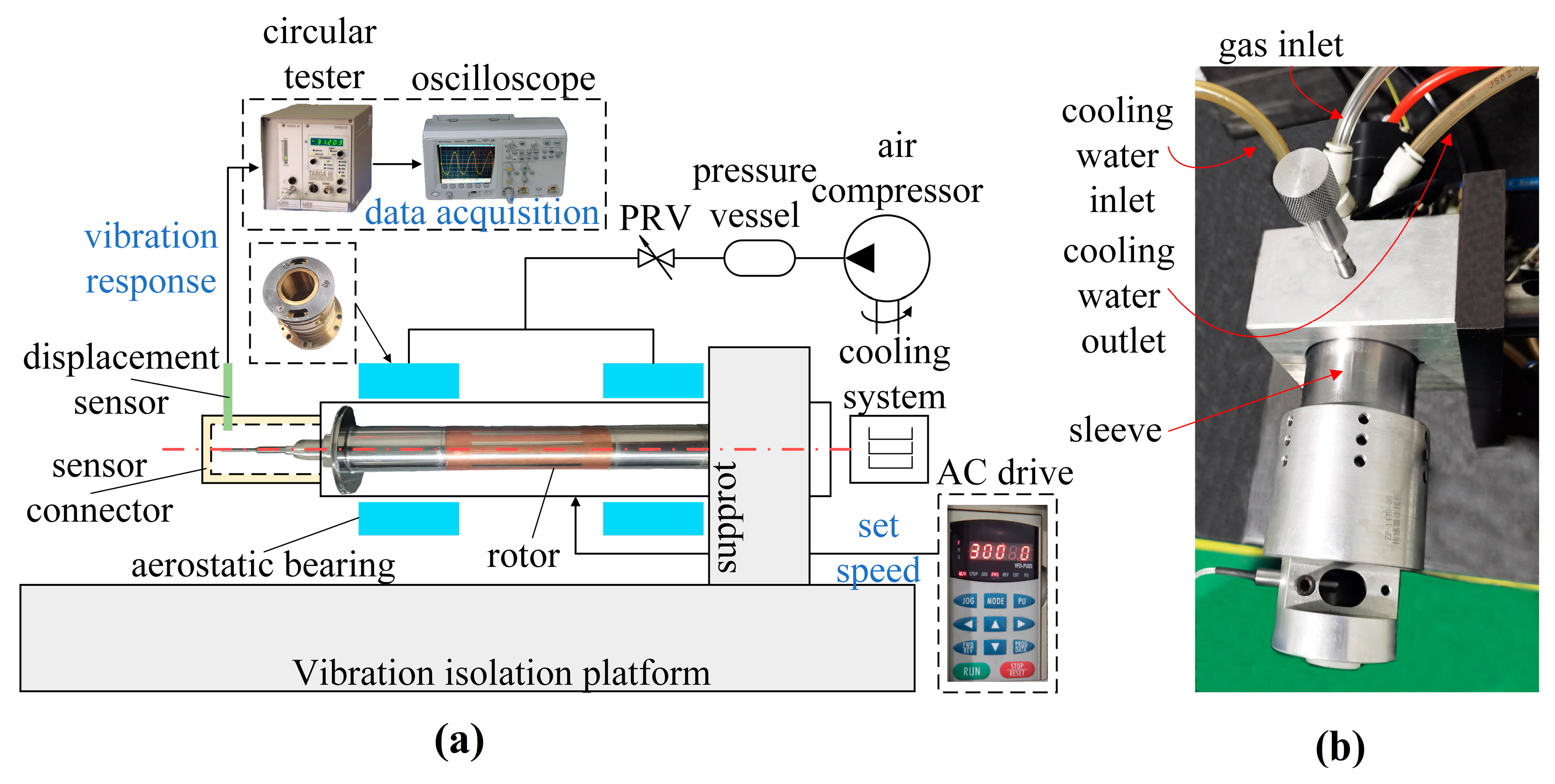
3. Experiment Validation
4. Results and Discussion
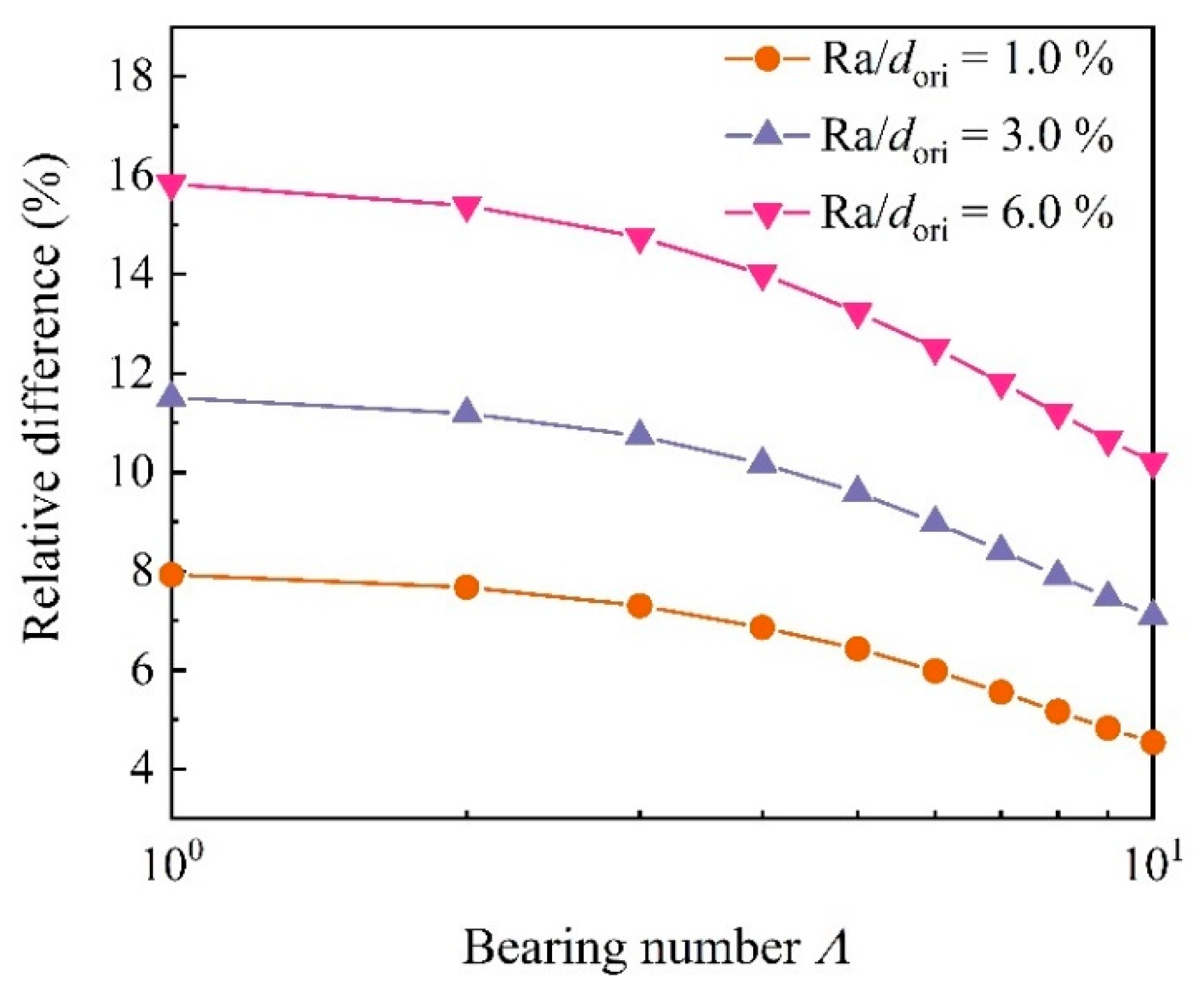
4.1. Effects of Frictional Loss on Micro-Orifice Performance
4.2. Effects of Frictional Loss on the Lubrication Performance of ACBMOs
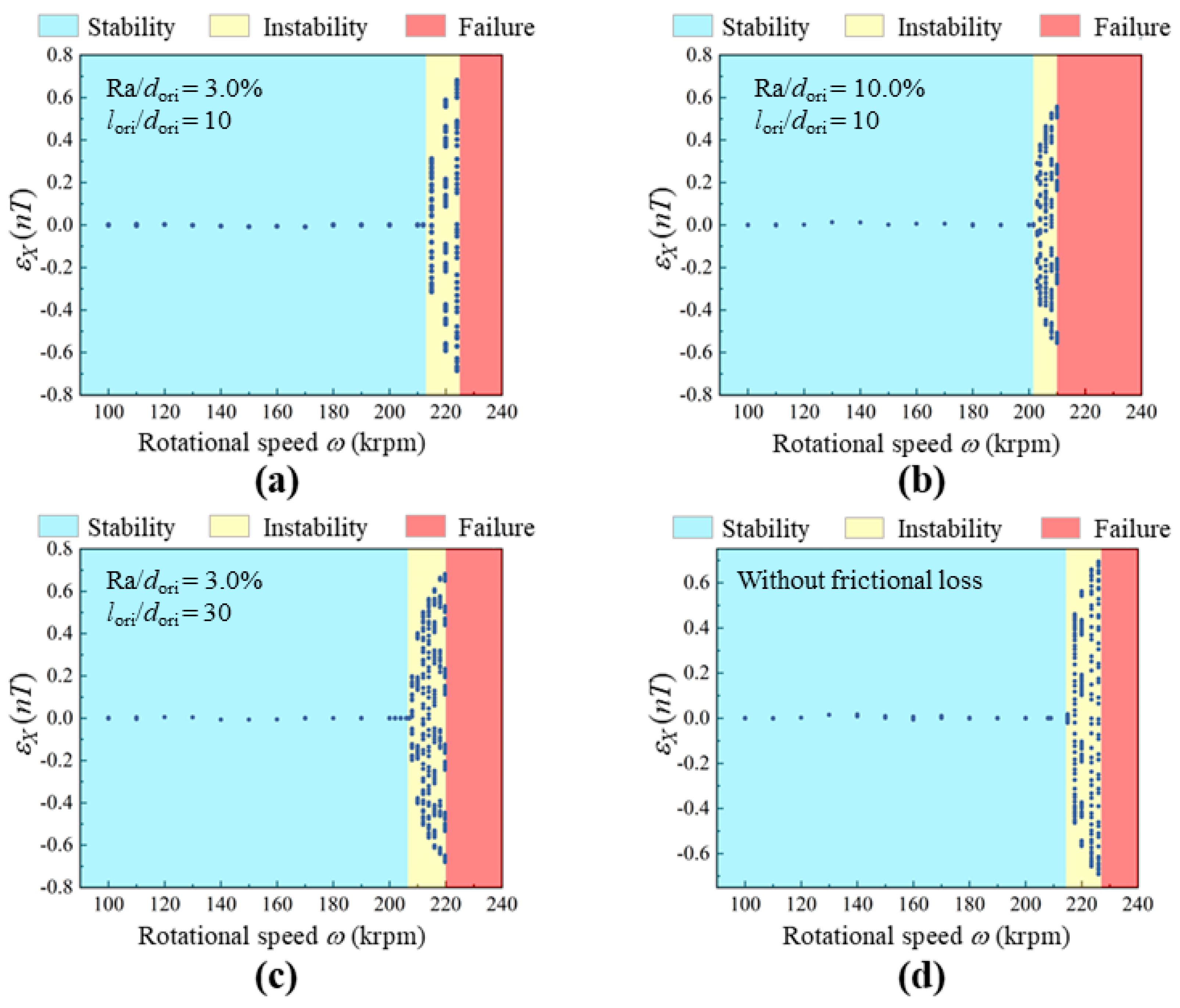
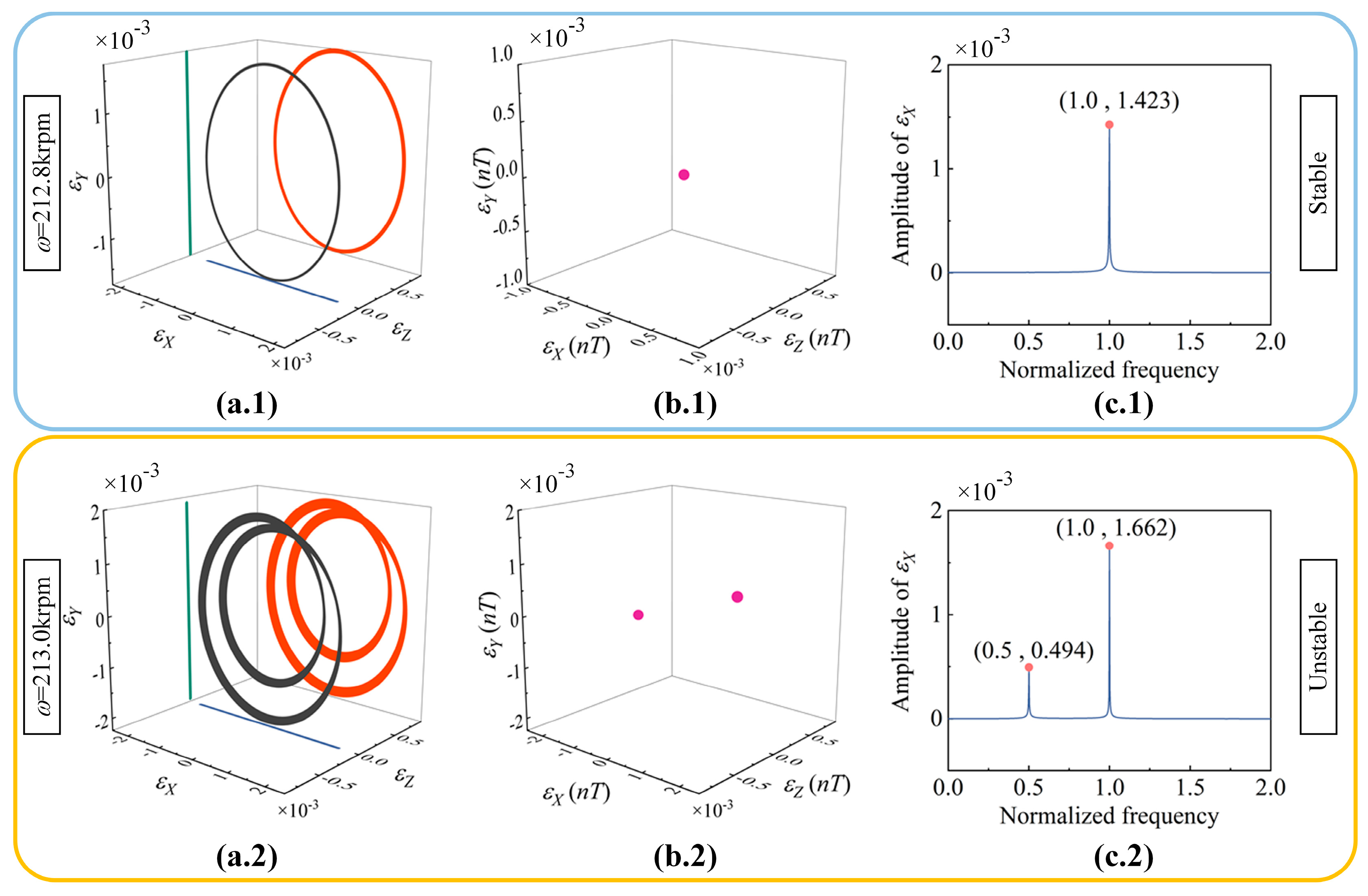
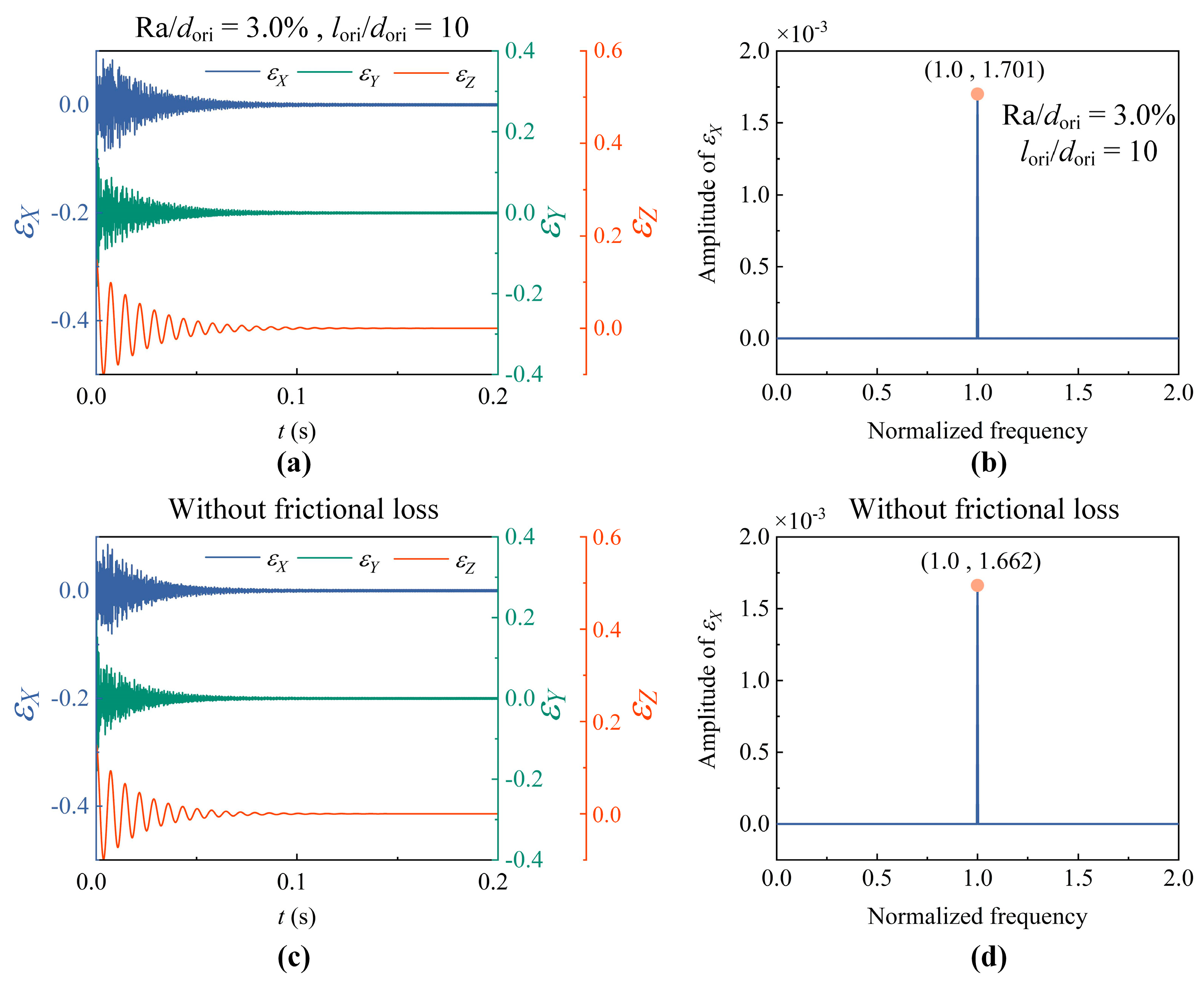
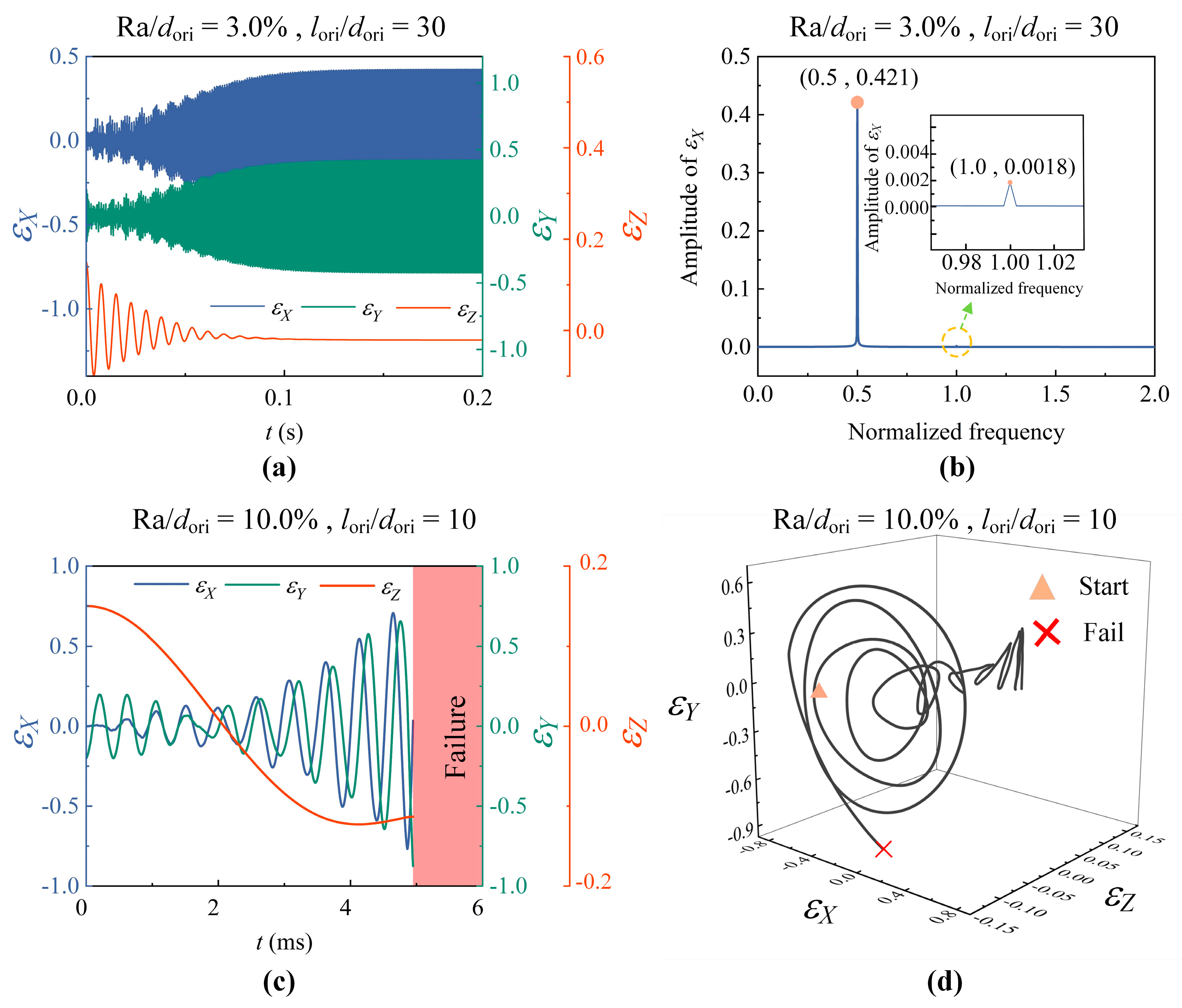
4.3. Effects of Frictional Loss on Nonlinear Behaviors and Stability
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
Nomenclature
| R | Bearing radius, m |
| r, ϕ | Conical coordinates, m and ° |
| t | Time, s |
| u | Node displacement of rotor, m |
| α | Semi-cone angle, ° |
| Ra | Mean bearing radius, m |
| p | Pressure, Pa |
| ps | Supply pressure, Pa |
| Er | Young’s modulus of rotor, Pa |
| νr | Poisson’s ratio of rotor |
| Ts | Supply temperature, K |
| pin | Inlet pressure of orifices, Pa |
| pori | Downstream pressure of orifices, Pa |
| lori | Length of orifices, m |
| dori | Diameter of orifices, m |
| Aori | Area of orifices, m2 |
| Aeff | Effective area of orifices, m2 |
| τW | Shear stress, Pa |
| hf | Frictional loss, m |
| Ma | Mach number |
| ug | Velocity of gas flow, m/s |
| Cd | Discharge coefficient |
| κ | Ratio of specific heat of gas |
| X, Y, Z | Cartesian coordinates, m |
| in | Inlet mass inflow rate, kg/s |
| ori | Outlet mass inflow rate, kg/s |
| *ori | *ori = Cd × ori |
| er | Radial eccentricity, m |
| V | Average velocity of flow, m/s |
| h | Film thickness, m |
| κ1,κ2 | Experiment coefficients |
| τturb | Shear stress of turbulent flow, Pa |
| l0 | Distance between orifices and edges, m |
| L | Bearing length, m |
| δk | Kronecker function |
| mr | Rotor mass, kg |
| Ra | Average roughness of orifice, m |
| pa | Ambient pressure, Pa |
| βκ | Critical pressure ratio |
| R1, R2 | Bearing radius of bearing edges, m |
| Re | Reynolds numbers |
| Gr | Shear modulus of rotor, Pa |
| Dimensionless r, | |
| c0 | Clearance, m |
| τ | Dimensionless t, τ = ωt |
| ρ | Air density, kg/m3 |
| ρr | Rotor density, kg/m3 |
| ω | Rotational speed, rad/s |
| Dimensionless p, = p/pa | |
| Λ | Bearing number |
| ψ | Axial coordinate after conformal map |
| ζ | Conformal map coefficient |
| Fhr | Bearing radial load capacity, N |
| Fer | Radial external force, N |
| f | Friction factor |
| u* | Shear velocity of gas flow, s−1 |
| Ai | Rotor area of section i, m2 |
| Φi | Φi = 12ErId,i/(ks,iGrAiL2i) |
| Rs1, Rs2 | Outer and inner radius of rotor, m |
| Id,i | Inertia moment of section i, m4 |
| Li | Rotor length of section i, m |
| Dimensionless h, | |
| ks,i | Shear coefficient of section i |
| No | Number of orifices |
| μ | Air dynamic viscosity, Pa∙s |
| τ | Non-dimensional time variable |
| eu | Rotating unbalance offset, m |
| kori | Coefficient of experience |
| c | Sonic speed, m/s |
| lmix | Prandtl mixing length, m |
| Qori | Volume inflow rate, m3/s |
| Qo | The gas mass flow factor of the orifices |
| X, Y, Z | Displacement vector on X, Y, Z axis |
| MXY | Radial mass matrix |
| MZ | Axial mass matrix |
| mR,i | Element rotational mass matrix |
| mT,i | Element translational mass matrix |
| mZ,i | Element axial mass matrix |
| KXY | Radial stiffness matrix |
| KZ | Axial stiffness matrix |
| ke,i | Element stiffness matrix |
| kZ,i | Element axial stiffness matrix |
| GXY | Radial gyroscopic matrix |
Appendix A
References
- An, C.H.; Zhang, Y.; Xu, Q.; Zhang, F.H.; Zhang, J.F.; Zhang, L.J.; Wang, J.H. Modeling of dynamic characteristic of the aerostatic bearing spindle in an ultra-precision fly cutting machine. Int. J. Mach. Tools Manuf. 2010, 50, 374–385. [Google Scholar] [CrossRef]
- Zhang, G.; Huang, M.; Chen, G.; Li, J.; Liu, Y.; He, J.; Zheng, Y.; Tang, S.; Cui, H. Design and optimization of fluid lubricated bearings operated with extreme working performances—A comprehensive review. Int. J. Extrem. Manuf. 2024, 6, 022010. [Google Scholar] [CrossRef]
- Feng, K.; Wang, P.; Zhang, Y.; Hou, W.; Li, W.; Wang, J.; Cui, H. Novel 3-D printed aerostatic bearings for the improvement of stability: Theoretical predictions and experimental measurements. Tribol. Int. 2021, 163, 107149. [Google Scholar] [CrossRef]
- Wu, Y.; Li, C.; Li, J.; Du, J. Lubrication mechanism and characteristics of aerostatic bearing with close-spaced micro holes. Tribol. Int. 2024, 192, 109278. [Google Scholar] [CrossRef]
- Gao, S.; Jiang, T.; Li, Z.; Yang, H.; Zhu, M.; Shang, Y.; Song, L.; Lu, L.; Gao, Q.; Zhang, H. Performance Investigation of the Micro-Hole High-Speed Aerostatic Thrust Bearing Based on the Finite Element Method. Machines 2025, 13, 477. [Google Scholar] [CrossRef]
- Talukder, H.M.; Stowell, T.B. Pneumatic hammer in an externally pressurized orifice-compensated air journal bearing. Tribol. Int. 2003, 36, 585–591. [Google Scholar] [CrossRef]
- Chen, X.; Chen, H.; Luo, X.; Ye, Y.; Hu, Y.; Xu, J. Air Vortices and Nano-Vibration of Aerostatic Bearings. Tribol. Lett. 2011, 42, 179–183. [Google Scholar] [CrossRef]
- Chen, X.; Chen, H.; Zhu, J.; Jiang, W. Vortex suppression and nano-vibration reduction of aerostatic bearings by arrayed microhole restrictors. J. Vib. Control. 2016, 23, 842–852. [Google Scholar] [CrossRef]
- Mohiuddin Mala, G.; Li, D. Flow characteristics of water in microtubes. Int. J. Heat Fluid Flow 1999, 20, 142–148. [Google Scholar] [CrossRef]
- Chen, Q.L.; Wu, K.J.; He, C.H. Investigation on liquid flow characteristics in microtubes. AIChE J. 2014, 61, 718–735. [Google Scholar] [CrossRef]
- Yao, Z.; Hao, P.; Zhang, X. Effects of gas compressibility and surface roughness on the flow in microfluidic devices. Sci. China Phys. Mech. Astron. 2011, 54, 711–715. [Google Scholar] [CrossRef]
- Tang, G.H.; Li, Z.; He, Y.L.; Tao, W.Q. Experimental study of compressibility, roughness and rarefaction influences on microchannel flow. Int. J. Heat Mass Transf. 2007, 50, 2282–2295. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Z.; Ji, Y.; Wang, L.; Li, D. Influence of surface roughness on the fluid flow in microchannel. J. Phys. Conf. Ser. 2024, 2740, 012059. [Google Scholar] [CrossRef]
- Hu, H.; Feng, M.; Ren, T. Study on the performance of novel gas foil conical bearings. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 235, 883–900. [Google Scholar] [CrossRef]
- Liu, W.; Bättig, P.; Wagner, P.H.; Schiffmann, J. Nonlinear study on a rigid rotor supported by herringbone grooved gas bearings: Theory and validation. Mech. Syst. Signal Process. 2021, 146, 106983. [Google Scholar] [CrossRef]
- An, L.; Wang, W.; Wang, C. Dynamic modeling and analysis of high-speed aerostatic journal bearing-rotor system with recess. Tribol. Int. 2023, 187, 108686. [Google Scholar] [CrossRef]
- Chen, P.; Ding, J.; Zhuang, H.; Chang, Y. A novel method for studying fluid-solid interaction problems of the rotor system in air bearings with manufacturing errors. Mech. Syst. Signal Process. 2023, 202, 110709. [Google Scholar] [CrossRef]
- Zheng, C.; Wang, X.; Zhang, X.; Wang, C.; Han, Q. Three-dimensional nonlinear behaviors and stability analysis of high-speed aerostatic conical bearing-rotor system. Nonlinear Dyn. 2025, 113, 17613–17636. [Google Scholar] [CrossRef]
- Belforte, G.; Raparelli, T.; Viktorov, V.; Trivella, A. Discharge coefficients of orifice-type restrictor for aerostatic bearings. Tribol. Int. 2007, 40, 512–521. [Google Scholar] [CrossRef]
- Li, D.; Yang, R.; Cao, H.; Yao, F.; Shen, C.; Zhang, C.; Wu, S. Experimental Study on Gas Flow in a Rough Microchannel. Front. Energy Res. 2022, 10, 863733. [Google Scholar] [CrossRef]
- Morini, G.L.; Lorenzini, M.; Salvigni, S.; Spiga, M. Thermal performance of silicon micro heat-sinks with electrokinetically-driven flows. A preliminary version of this paper was presented at ICMM05: Third International Conference on Microchannels and Minichannels, held at University of Toronto, June 13–15, 2005, organized by S.G. Kandlikar and M. Kawaji, CD-ROM Proceedings. Int. J. Therm. Sci. 2006, 45, 955–961. [Google Scholar] [CrossRef]
- Eckert, M. Turbulence Research in the 1920s and 1930s between Mathematics, Physics, and Engineering. Sci. Context 2018, 31, 381–404. [Google Scholar] [CrossRef]
- Zeghadnia, L.; Robert, J.L.; Achour, B. Explicit solutions for turbulent flow friction factor: A review, assessment and approaches classification. Ain Shams Eng. J. 2019, 10, 243–252. [Google Scholar] [CrossRef]
- Chen, W.J.; Gunter, E. Dynamics of Rotor-Bearing Systems—Ch. 5 Shaft Finite Element Equations; Chen, W.J., Gunter, E.J., Eds.; Trafford Publishing: Bloomington, IN, USA, 2023; p. 155. [Google Scholar]
- Nelson, H.D. A finite rotating shaft element using Timoshenko beam theory. J. Mech. Des. Trans. ASME 1980, 102, 793–803. [Google Scholar] [CrossRef]
- Nelson, H.D.; McVaugh, J.M. The dynamics of rotor-bearing systems using finite elements. J. Manuf. Sci. Eng. Trans. ASME 1976, 98, 593–600. [Google Scholar] [CrossRef]
- Zhang, J.; Deng, Z.; Zhang, K.; Jin, H.; Yuan, T.; Chen, C.; Su, Z.; Cao, Y.; Xie, Z.; Wu, D.; et al. The Influences of Different Parameters on the Static and Dynamic Performances of the Aerostatic Bearing. Lubricants 2023, 11, 130. [Google Scholar] [CrossRef]
- Yang, P.; Zhu, K.-Q.; Wang, X.-L. On the non-linear stability of self-acting gas journal bearings. Tribol. Int. 2009, 42, 71–76. [Google Scholar] [CrossRef]

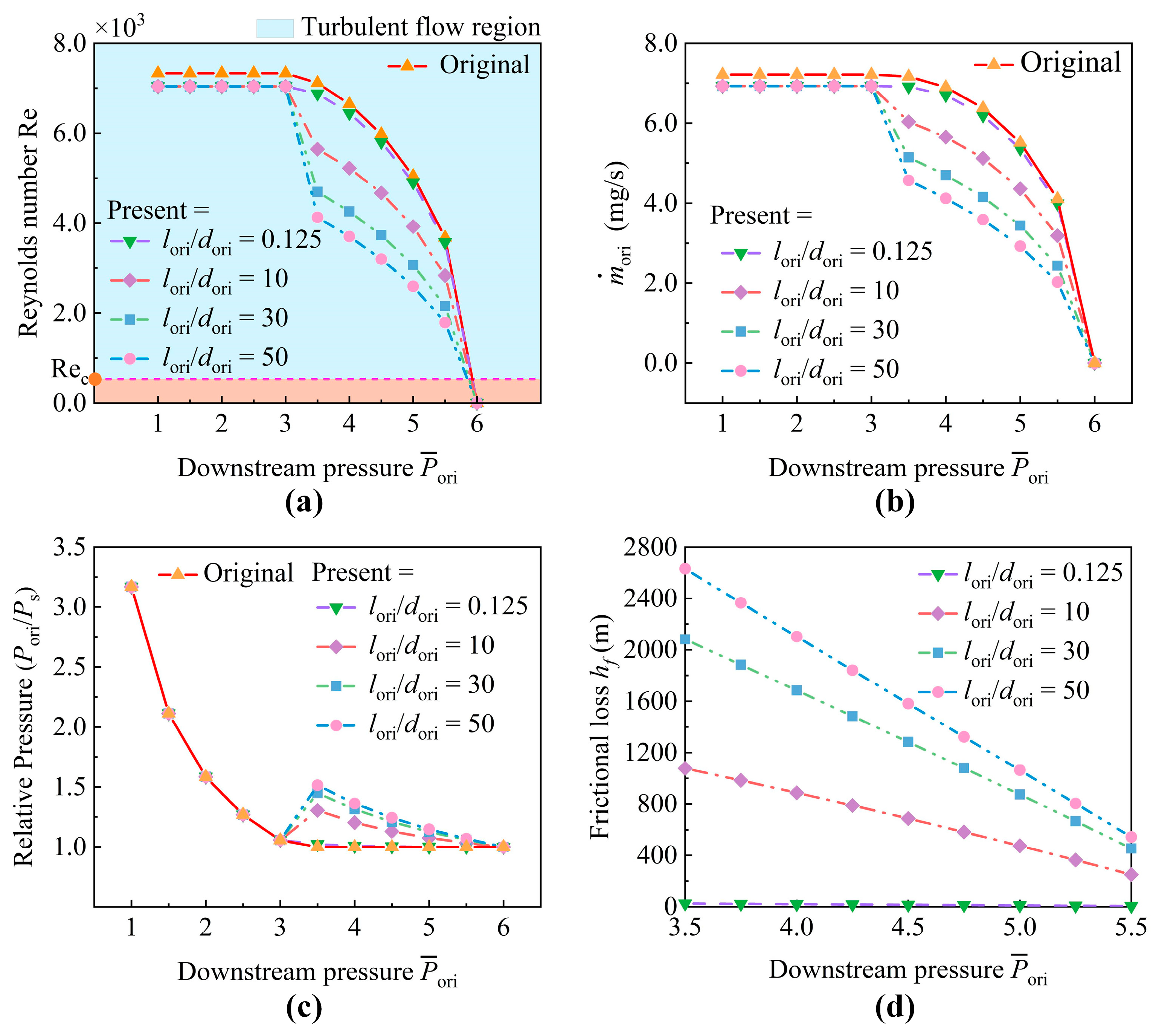
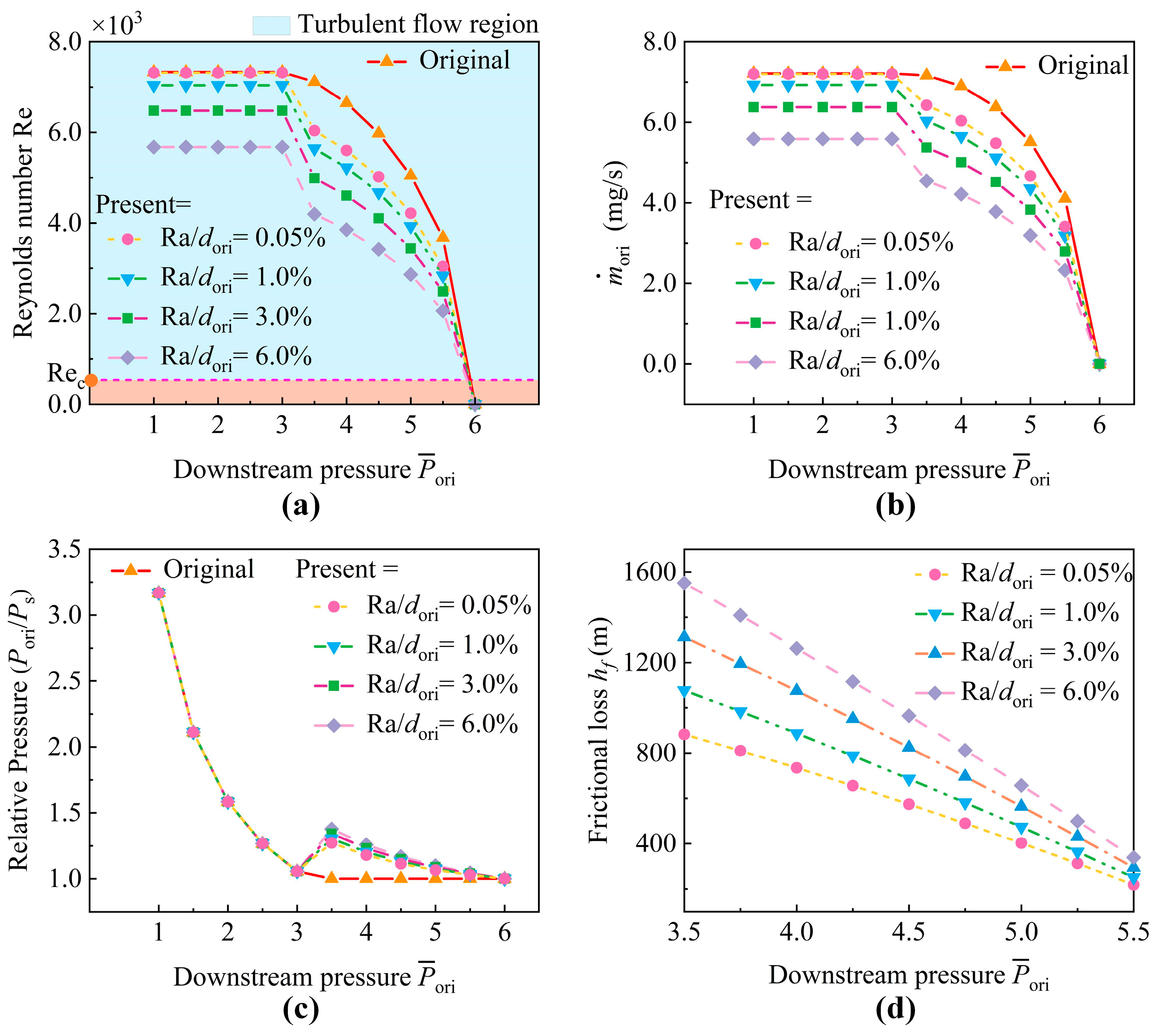

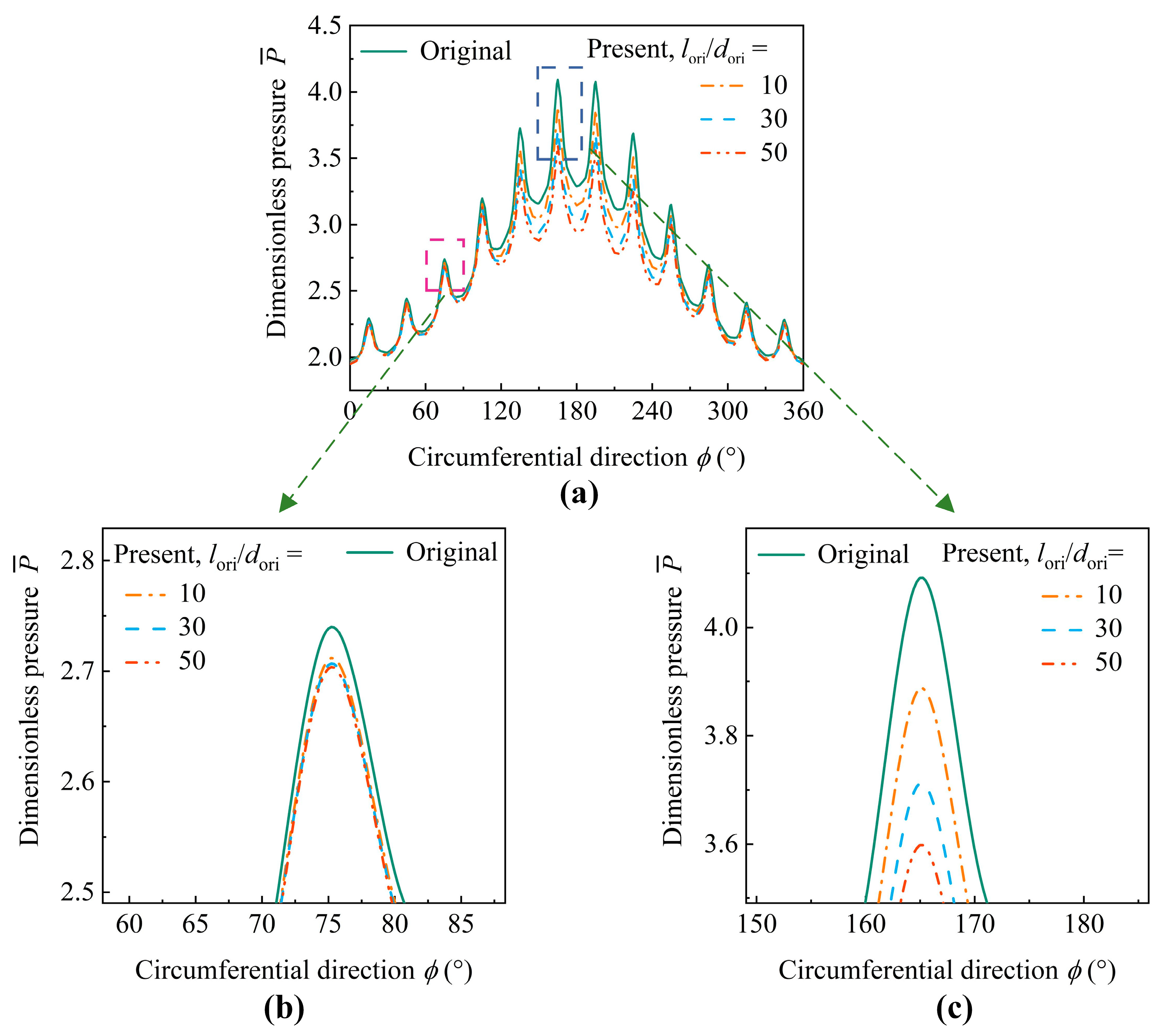
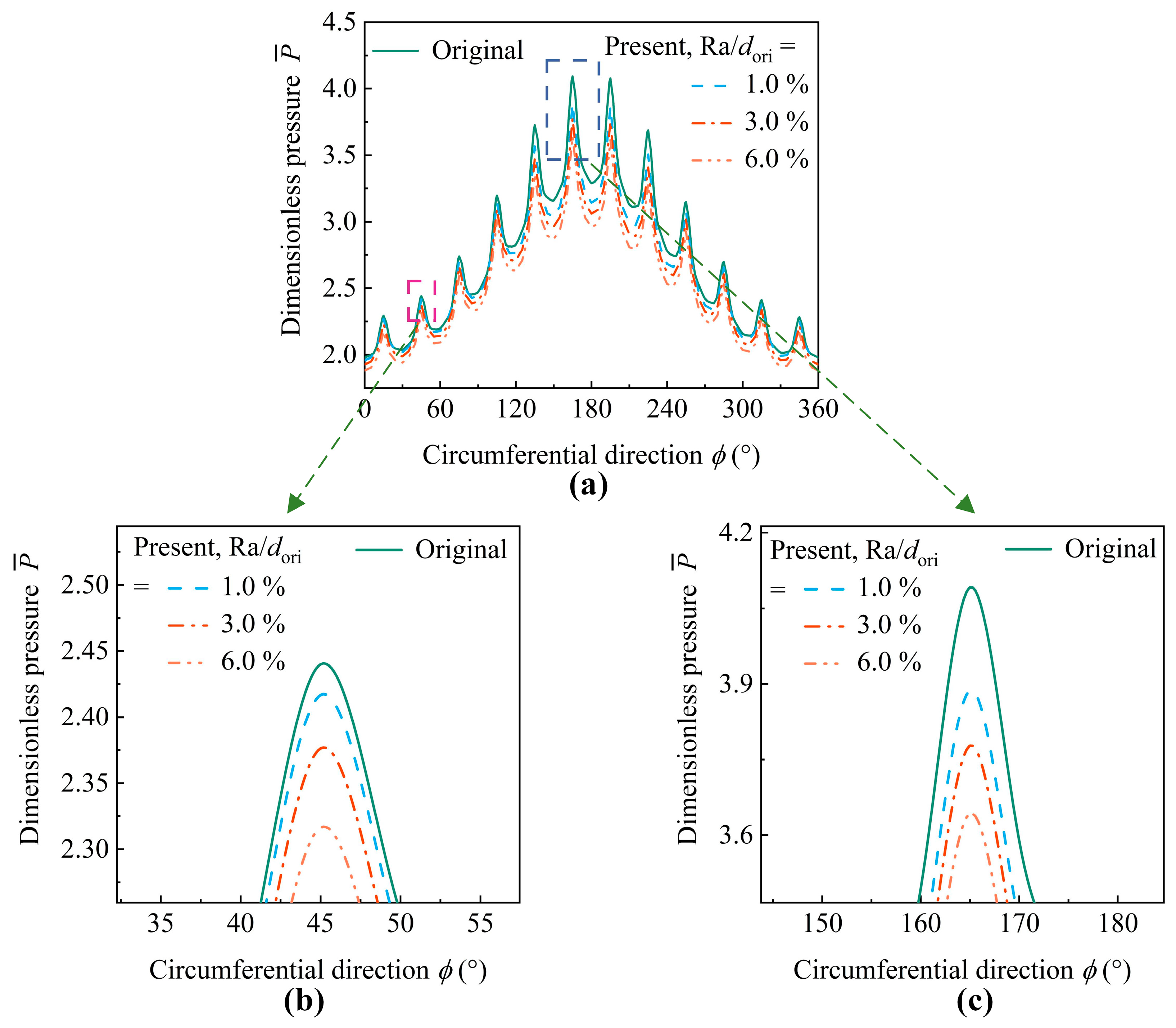

| Parameters | Value |
|---|---|
| Semi-cone angle (α) | 0.0001° |
| Bearing length (L) | 24.5 mm |
| Mean radius of bearing (Ra) | 10.355 mm |
| No. of orifices | 2 column × 8 row |
| Supply pressure (ps) | 0.8 MPa |
| Length of orifice (lori) | 0.1 mm |
| Average roughness (Ra) | 1.6 μm |
| Distance between orifices and bearing edge (l0) | 4 mm |
| Rotational speed (ω) | 180k rpm |
| Mass of rotor (mr) | 0.19 kg |
| Clearance (c0) | 40.0 μm |
| Diameter of orifice (dori) | 0.1 mm |
| Parameters | Value |
|---|---|
| Gas density (ρ) | 1.204 kg/m−3 |
| Gas viscosity (μ) | 1.82∙10−5 Ns/m2 |
| Ration of specific heat of gas (κ) | 1.401 |
| Atmosphere pressure (pa) | 101,325 Pa |
| Supply pressure (ps) | 0.6 MPa |
| Parameters | Value |
|---|---|
| Mean radius of bearing (Ra) | 12.0 mm |
| Bearing length (L) | 25.71 mm |
| No. of micro-orifices (No) | 2 column × 12 row |
| Supply pressure (ps) | 0.6 MPa |
| Distance between orifices and bearing edge (l0) | 5 mm |
| Semi-cone angle (α) | 2.227 ° |
| Rotational speed (ω) | 50 krpm |
| Clearance (c0) | 15.0 μm |
| Dimensionless radial eccentricity ratio (εr) | 0.3 |
| Dimensionless axial eccentricity ratio (εz) | 0.1 |
| Parameters | Value |
|---|---|
| Mass of rotor (mr) | 0.438 kg |
| Density of rotor (ρr) | 7700 kg/m3 |
| Clearance (c0) | 5.0 μm |
| Poisson’s ratio (νr) | 0.28 |
| Young’s modulus (Er) | 210 GPa |
| Diameter of orifice (dori) | 0.03 mm |
| Length of orifice (lori) | 0.3 mm |
| Node of unbalance | 16, 31 |
| Phase of unbalance (φu) | 0°, 180° |
| Unbalance (mreu) | 2.08 × 10−3 g∙mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Q.; Wang, X.; Zheng, C. Nonlinear Dynamic Analysis of High-Speed Aerostatic Conical Bearing–Rotor System with Micro-Orifice Frictional Loss. Machines 2025, 13, 797. https://doi.org/10.3390/machines13090797
Han Q, Wang X, Zheng C. Nonlinear Dynamic Analysis of High-Speed Aerostatic Conical Bearing–Rotor System with Micro-Orifice Frictional Loss. Machines. 2025; 13(9):797. https://doi.org/10.3390/machines13090797
Chicago/Turabian StyleHan, Qilong, Xiaoli Wang, and Chen Zheng. 2025. "Nonlinear Dynamic Analysis of High-Speed Aerostatic Conical Bearing–Rotor System with Micro-Orifice Frictional Loss" Machines 13, no. 9: 797. https://doi.org/10.3390/machines13090797
APA StyleHan, Q., Wang, X., & Zheng, C. (2025). Nonlinear Dynamic Analysis of High-Speed Aerostatic Conical Bearing–Rotor System with Micro-Orifice Frictional Loss. Machines, 13(9), 797. https://doi.org/10.3390/machines13090797






