Unsupervised Bearing Fault Diagnosis Using Masked Self-Supervised Learning and Swin Transformer

Abstract

Bearings are vital to rotating machinery, where undetected faults can cause severe failures. Conventional fault diagnosis methods depend on manual feature engineering and labeled data, struggling with complex industrial conditions. This study introduces an innovative unsupervised framework combining masked self-supervised learning with the Swin Transformer for bearing fault diagnosis. The novel integration leverages masked Auto Encoders to learn robust features from unlabeled vibration signals through reconstruction-based pretraining, while the Swin Transformer’s shifted window attention mechanism enhances efficient capture of fault-related patterns in long-sequence signals. This approach eliminates reliance on labeled data, enabling precise detection of unknown faults. The proposed method achieves 99.53% accuracy on the Paderborn dataset and 100% accuracy on the CWRU dataset significantly, surpassing other unsupervised Auto Encoder-based methods. This method’s innovative design offers high adaptability and substantial potential for predictive maintenance in industrial applications.

1. Introduction

Bearings, as the core fundamental components of rotating machinery, play an irreplaceable role in critical industrial equipment such as wind turbines, high-speed trains, and aircraft engines [1,2,3]. Their operational condition directly affects the reliability, energy efficiency, and safety performance of the entire mechanical system [4]. However, due to long-term exposure to alternating loads, variable-speed operation, and harsh working conditions, bearings are highly susceptible to various failure modes, including fatigue spalling, cracks, and lubrication failure. Undetected faults may lead to cascading equipment damage, unplanned down-time, and significant economic losses. Therefore, developing accurate and efficient bearing fault diagnosis methods is crucial for achieving predictive maintenance and ensuring industrial safety [5,6,7].

Traditional fault diagnosis techniques, such as Fast Fourier Transform (FFT) [8], wavelet analysis [9], and envelope demodulation [10], primarily rely on signal processing methods to extract fault features from vibration or acoustic data. While these approaches perform well in certain scenarios, they exhibit notable limitations when dealing with non-stationary signals, weak fault signatures, and complex operating conditions. More importantly, their effectiveness heavily depends on expert experience and manual feature engineering, making them difficult to adapt to diverse industrial environments.

With the rapid advancement of artificial intelligence, data-driven fault diagnosis methods have demonstrated significant advantages. Deep learning approaches, represented by Convolutional Neural Networks (CNNs) and Recurrent Neural Networks (RNNs), can automatically extract discriminative features directly from raw sensor data [11,12,13]. Li et al. [14] proposed an interpretable deep learning model based on attention mechanisms for rolling bearing fault diagnosis. By incorporating attention mechanisms, the network can autonomously focus on critical fault-related segments in vibration signals while utilizing attention weight visualization to provide intuitive decision explanations, effectively addressing the “black-box” nature of traditional deep learning models and bridging the gap with engineering diagnostic knowledge. Yang et al. [15] introduced a federated semi-supervised transfer fault diagnosis method based on distribution barycenter mediation to overcome the limitations of conventional transfer learning in decentralized data scenarios. However, most existing methods rely on supervised learning paradigms, requiring large amounts of labeled fault data for model training—a major challenge in real-world industrial settings where fault samples are scarce and annotation costs are prohibitively high.

The Swin Transformer is particularly suited for vibration signal analysis due to its unique combination of local precision and global context awareness. Its shifted window mechanism efficiently captures both high-frequency impulse features and long-range periodic patterns, addressing the key challenge of detecting fault signatures that span multiple timescales. The hierarchical architecture naturally aligns with vibration physics—early-stage faults manifest in localized waveform distortions while severe faults induce system-wide vibrations—enabling more physiologically meaningful feature learning than CNNs with fixed receptive fields or RNNs with sequential processing constraints.

To overcome this limitation, unsupervised learning techniques have garnered increasing attention due to their ability to learn meaningful representations from unlabeled data. While methods like Auto Encoders [16], contrastive learning [17], and clustering algorithms [18] have shown promise in detecting unknown fault patterns, they face three critical challenges: (1) limited capacity for long-range feature dependency modeling, (2) sensitivity to noise and missing data in industrial environments, and (3) computational inefficiency when processing long vibration sequences. The Swin Transformer [19,20,21], with its hierarchical shifted window attention mechanism, offers potential solutions through its unique combination of local feature extraction and global information interaction. However, its application in unsupervised bearing fault diagnosis remains underexplored, particularly regarding two key aspects: (a) effective adaptation to 1D vibration signals, and (b) integration with reconstruction-based self-supervised paradigms.

This study addresses these gaps through three innovative contributions: First, we develop the first masked self-supervised framework specifically designed for Swin Transformer-based bearing fault diagnosis, enabling robust feature learning through a novel vibration signal reconstruction task [22,23]. Our approach introduces two key innovations: First, we develop a novel vibration signal masking strategy that preserves critical fault signatures while enabling efficient self-supervised learning. Second, we establish an effective framework for adapting the Swin Transformer’s architecture to 1D vibration analysis, demonstrating its superiority in capturing both local and global fault patterns compared to conventional methods. Importantly, our methodology maintains computational efficiency while eliminating the need for labeled training data—a crucial advantage for real-world industrial applications where labeled fault samples are scarce.

2. Methodology

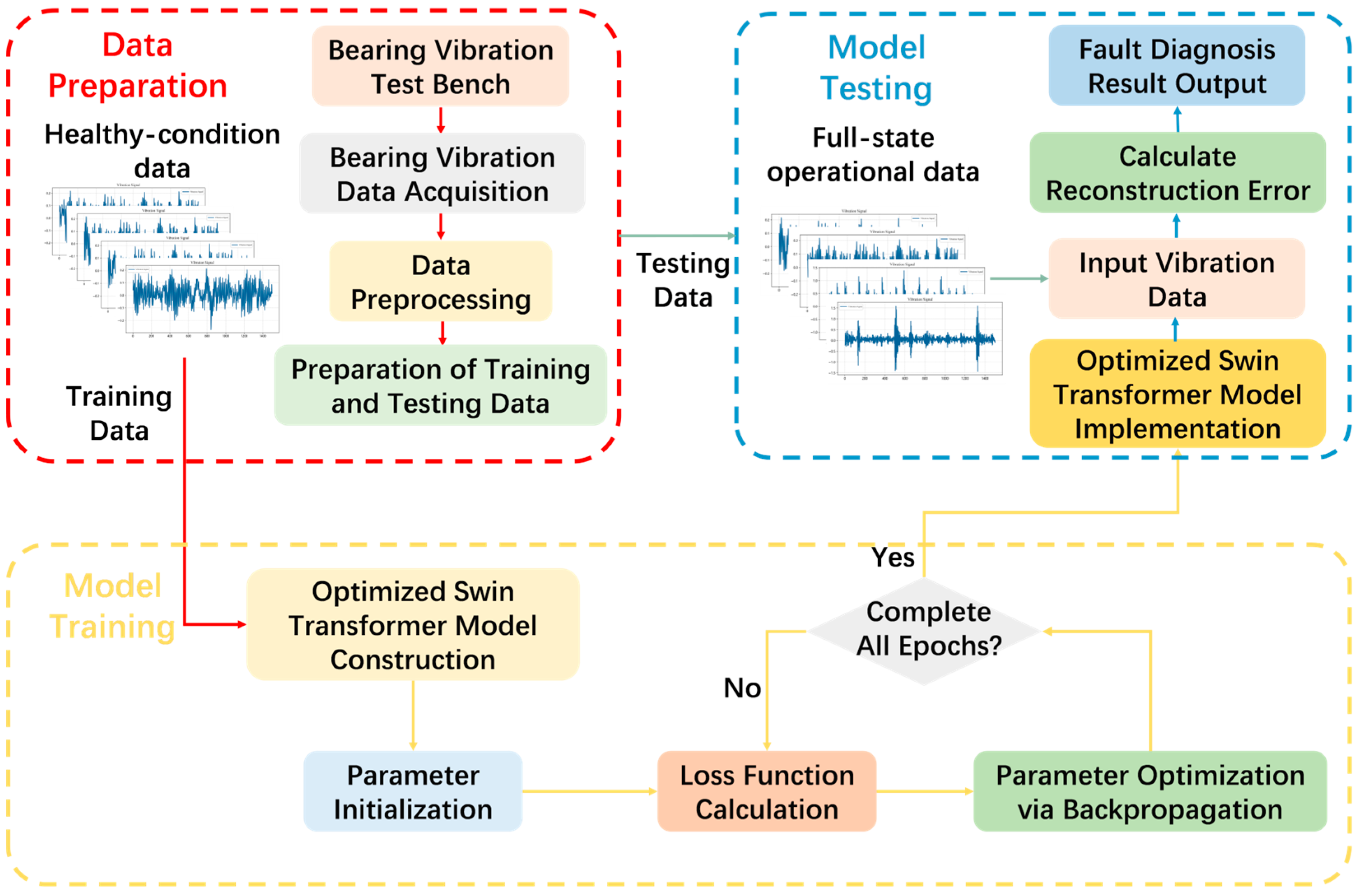
The research framework of this study is illustrated in Figure 1. The proposed method trains a deep neural network using preprocessed vibration signals from healthy bearing conditions, eliminating the need for labeled data. Leveraging a data reconstruction approach, the model autonomously captures the intrinsic structure of healthy data. During data processing, all label-dependent operations are excluded, ensuring a fully unsupervised learning process.

In the model training phase, the Huber loss function is utilized to compute reconstruction errors, while the 3σ criterion establishes an effective detection threshold. The 3σ threshold (μ + 3σ) is calculated from healthy training data reconstruction losses, where μ and σ represent the mean and standard deviation, respectively. This approach assumes: (1) health state errors approximate normal distribution, and (2) training data contains no latent faults. During the testing phase, vibration data of unknown health status are fed into the trained neural network. If the reconstruction error surpasses the predefined threshold, the data is classified as faulty, enabling robust unsupervised fault diagnosis.

The proposed method employs the 3σ criterion to define a statistical threshold for fault diagnosis. While effective for stationary conditions, two limitations should be noted: (1) sensitivity to non-Gaussian noise (e.g., impulsive disturbances), (2) required recalibration for variable-speed operations. By calculating the mean (μ) and standard deviation (σ) of reconstruction loss values from healthy training data, the detection threshold is established as μ + 3σ. As the training set comprises solely healthy samples, this threshold effectively encompasses the range of data fluctuations under typical operating conditions. In practical applications, test data with reconstruction loss exceeding this threshold is identified as anomalous or faulty, ensuring reliable fault detection.

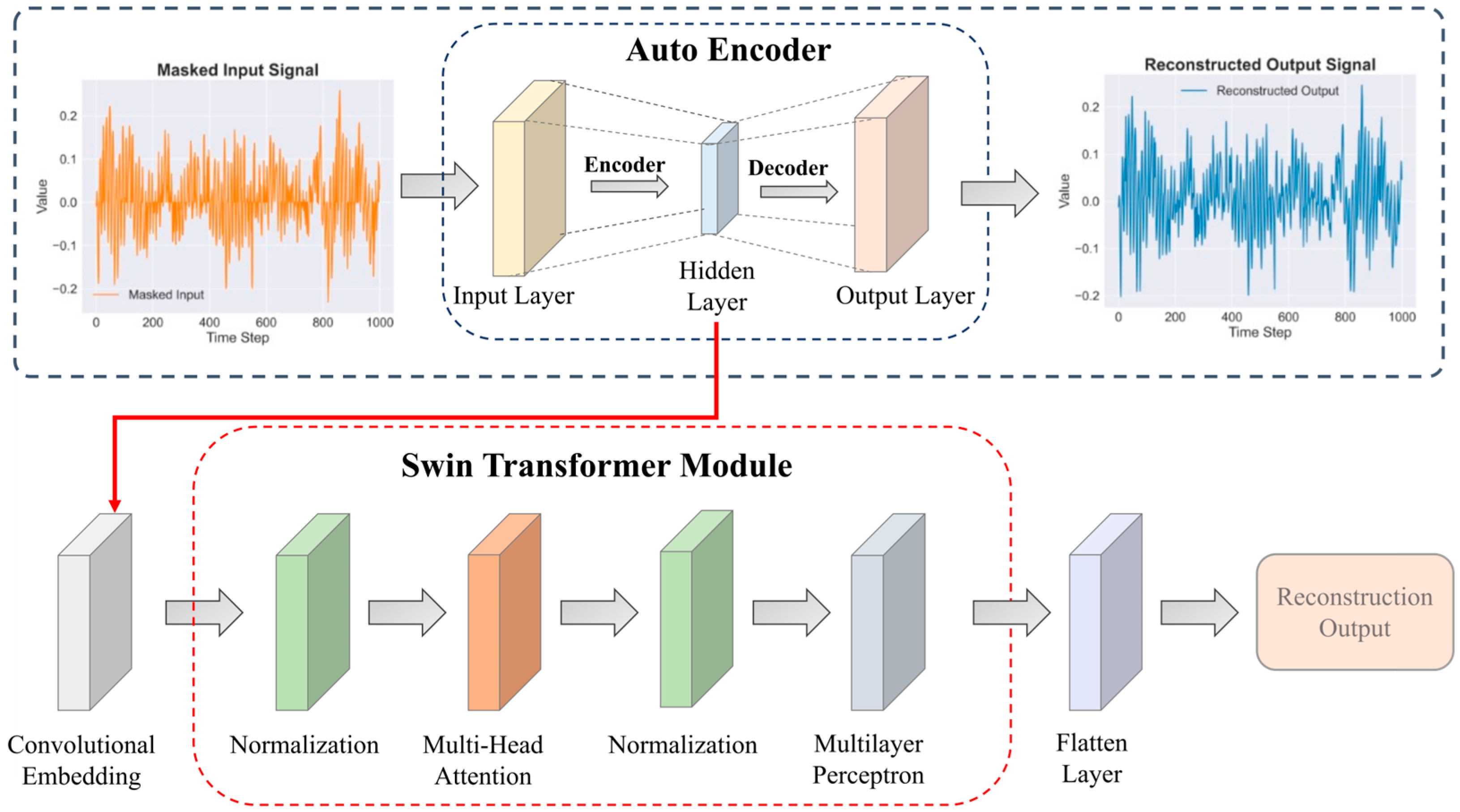
This study presents an intelligent bearing fault diagnosis model leveraging masked self-supervised learning. The model’s architecture, illustrated in Figure 2, integrates a mask-reconstruction self-supervised learning task with a Swin Transformer neural network to enhance diagnostic accuracy and robustness.

The self-supervised learning component employs an Auto Encoder architecture consisting of an input layer, a hidden layer, and an output layer. The model applies random masking to standardized vibration signals to mimic sensor failures or data loss in real-world operating conditions. By minimizing reconstruction error, the Auto Encoder learns to recover masked data using visible information. The features extracted from the hidden layer are fed into the Swin Transformer for subsequent feature reconstruction tasks.

To clarify the architecture: the model operates as a sequential pipeline where the Auto Encoder serves solely as a self-supervised pre-training module. Once pre-trained, its encoder is fixed and functions as a feature extractor, producing robust embeddings from the input signals. These embeddings are then passed to the Swin Transformer module, which performs the subsequent hierarchical feature reconstruction and analysis, leveraging its attention mechanism to model complex dependencies in the data. This two-stage design effectively separates representation learning from advanced feature processing.

The Swin Transformer is an advanced model based on the Transformer architecture, with its core structure primarily including convolutional embedding layers, multi-head self-attention mechanisms, multilayer perceptron, and feedforward neural networks. By combining local feature extraction with global information interaction, the model can effectively capture long-range dependencies in vibration signals. Compared to traditional methods, the Swin Transformer demonstrates stronger generalization capabilities and higher recognition accuracy in fault diagnosis under complex operating conditions.

Self-supervised learning utilizes randomly masked segments of vibration signals in the time domain, framing the reconstruction of these masked segments as a pretext task. This strategy drives the model to autonomously discover meaningful patterns, capturing the intricate relationships between time-frequency features, periodic behaviors, and fault signatures. By training under such artificially induced data imperfections, the model develops inherent robustness against real-world challenges like noise contamination, missing data, and irregular sampling rates. Consequently, it achieves reliable fault detection even in non-ideal industrial conditions. The result is a more adaptable and resilient diagnostic system capable of handling the complexities of actual operational environments.

As shown in Figure 3, the workflow progresses from raw waveform input through masked processing to final model reconstruction. During preprocessing, the model randomly obscures selected time-domain segments of vibration signals, generating training samples with deliberate localized information gaps. This masking strategy compels the model to develop the ability to reconstruct complete fault characteristics from partial observations. The approach achieves two key benefits: (1) it substantially strengthens the model’s capacity to extract discriminative fault representations, and (2) it significantly enhances diagnostic reliability when dealing with real-world industrial challenges such as signal noise and data incompleteness.

During the pre-training phase, an Auto Encoder architecture incorporating a masking strategy is employed to learn discriminative features from vibration signals. The model processes randomly masked input signals through an encoder network, which projects them into a low-dimensional latent space. Subsequently, the decoder network reconstructs the complete signals from these latent representations. This self-supervised approach forces the model to develop robust feature extraction capabilities while learning meaningful patterns from partially observed data. Given the original vibration signal ${\rm X}\in {ℝ}^T$, where $T$ is the input sequence length and x_t represents the vibration amplitude at timestep $\mathrm{t}\in \left\{1,2,\dots ,T\right\}$, random masking is performed on the amplitude x_t at each timestep:

$$X_{masked }=\left\{\begin{array}{c}0, if time step t is masked\\ x_t, otherwise\end{array}\right.$$

(1)

where X_masked represents the randomly masked 1D vibration signal sequence, and x_t is the original value at time step t. The core task of the encoder is to map the masked vibration signals to a low-dimensional latent space, expressed as follows:

$$Z=f_{enc}(X_{masked};{\theta }_{enc})$$

(2)

where f_enc denotes the encoder network with parameters θ, and Z represents the extracted latent features. The decoder then maps the latent features $Z\in {ℝ}^m$ back to the original data space $\widehat{X}\in {ℝ}^n$, i.e., reconstructs the input data, expressed as follows:

$$\widehat{X}=f_{dec}(Z;{\theta }_{dec})$$

(3)

where $f_{dec}$ is the mapping function of the decoder, and ${\theta }_{dec}$ represents the decoder’s parameters. The training objective of the Auto Encoder is to minimize the discrepancy between the original vibration signal $f_{dec}$ and the reconstructed signal ${\theta }_{dec}$. This paper employs the Huber loss as the loss function to measure the reconstruction error:

$$L(y,F(x))=\left\{\begin{array}{l}{\displaystyle \frac{1}{2}}{(y-f(x))}^2,if\left|y-f(x)\right|\le \delta \\ \delta \left|y-f(x)\right|-{\displaystyle \frac{1}{2}}{\delta }^2,if\left|y-f(x)\right|\ge \delta \end{array}\right.$$

(4)

Among them, $\left|y-f(x)\right|$ represents the reconstruction error of the t sampling point, and $\delta$ is the decision threshold. This loss function combines the advantages of L2 and L1 loss: it maintains the favorable convergence of L2 loss when the error is small, while automatically switching to L1 loss for larger errors. This mechanism enhances the model’s robustness to vibration signals and ensures training stability.

Following pre-training, the encoder’s primary function transitions from signal reconstruction to discriminative feature extraction. Having learned robust representations of bearing vibration characteristics, the encoder now efficiently projects high-dimensional raw vibration data into a meaningful low-dimensional latent space. In this operational phase, the encoder exclusively focuses on deriving the most salient features from input signals rather than performing reconstruction. These compressed yet informative latent representations are subsequently processed by the Swin Transformer for hierarchical feature reconstruction. Crucially, these embeddings encode distinctive patterns corresponding to different bearing health conditions, substantially enhancing the model’s diagnostic capability and state discrimination performance.

3. Experiment and Result

3.1. Datasets Description and Data Processing

For experimental validation, we selected two benchmark bearing fault datasets: the Paderborn University dataset [24] (featuring controlled fault progression under various operational conditions) and the CWRU dataset [25] (containing well-characterized fault signatures across multiple bearing configurations), both widely adopted in the fault diagnosis literature.

Paderborn Bearing Dataset: The Paderborn University Bearing Dataset includes eight different operating conditions: healthy state, Level 1 inner race fault, Level 2 inner race fault, Level 3 inner race fault, Level 1 outer race fault, Level 2 outer race fault, Level 2 combined fault, and Level 3 combined fault. The CWRU Bearing Dataset contains twelve state categories: healthy state, Level 1 to Level 4 inner race faults, Level 1 to Level 3 outer race faults, and Level 1 to Level 4 rolling element faults.

For the Paderborn dataset, a resampling technique is employed for data processing. Each sample comprises 2000 fixed data points, with subsequent samples generated by shifting a fixed number of data points backward, enabling continuous extraction of multiple samples. Data construction is based on the standard operating condition of 1500 rpm, 0.7 N·m load torque, and 1000 N radial force. The training set consists of 80% of the healthy state data under this condition, while the test set includes the remaining 20% of healthy data and all fault state data. This configuration facilitates effective fault state recognition under unsupervised conditions by training exclusively on healthy data. The operating conditions and data partitioning scheme are detailed in

Table 1. Paderborn Bearing Dataset Configuration.

Data Source	Sample Length	Shift Length	Load (N·m)	Speed (rpm)
N15_M07_F10 Healthy (80%, Training Set)	2000	1500	0.7	1500
N15_M07_F10 All Faults (Test Set)	2000	1500	0.7	1500
N15_M07_F10 Healthy (20%, Test Set)	2000	1500	0.7	1500

.

CWRU Bearing Dataset: For the CWRU Bearing Dataset, a resampling technique is utilized for data processing. Each sample consists of 1000 fixed data points, with subsequent samples generated by shifting a fixed number of data points backward, facilitating continuous extraction of multiple samples. During data construction, 80% of the healthy state data is allocated to the training set, while the remaining 20% of healthy data and all fault state data across four operating conditions constitute the test sets. The specific operating conditions and data partitioning scheme are presented in

Table 2. CWRU Bearing Dataset Configuration.

	Data Source	Sample Length	Shift Length	Load (N·m)
Training Set	80% Healthy Data (All Conditions)	1000	500	0–3
Test Set	20% Healthy Data (Condition 1)	1000	500	0
	All Fault Data (Condition 1)	1000	500	0

.

3.2. Comparative Methods

This study evaluates the proposed Swin Transformer-based unsupervised neural network model against several established unsupervised learning methods, including Auto Encoder (AE), Deep Auto Encoder (DAE), Convolutional Auto Encoder (CAE), and Sparse Auto Encoder (SAE), to demonstrate its superior performance in fault identification tasks.

(1)

Auto Encoder:

We implemented a standard AE with single hidden layer 500 units, LeakyReLU activation α = 0.01, trained using Adam optimizer (lr = 1 × 10⁻⁴, batch = 64). LeakyReLU maintains activation in all neurons during training, thereby enhancing network stability and training efficiency.

(2)

Deep Auto Encoder:

Our DAE configuration stacked three fully connected layers (500-1000-500 units) with layer-wise pretraining and dropout (p = 0.2). Through multilayer nonlinear mapping, the DAE hierarchically extracts abstract features from data, significantly improving reconstruction performance and generalization ability.

(3)

Convolutional Auto Encoder:

The CAE architecture employed three convolutional blocks (kernel sizes 5-3-5, channels 32-64-32) with max-pooling (stride = 2). Compared to standard Auto Encoders and Deep Auto Encoders, the CAE maintains robust modeling performance while reducing the number of parameters and computational complexity, making it particularly well-suited for processing vibration signal data with spatial structures.

(4)

Sparse Auto Encoder:

The Sparse Auto Encoder introduces sparsity constraints into the Auto Encoder architecture by restricting the activation ratio of hidden neurons, effectively suppressing interference from redundant information. Incorporating KL divergence sparsity constraint (target activation = 0.05) and L1 regularization (λ = 1 × 10⁻⁴). This sparse structure enhances the model’s representational capacity and robustness while mitigating the risk of overfitting, thereby enabling more efficient feature learning.

3.3. Experimental Results

This section presents experimental validation of the proposed method on both the Paderborn bearing dataset and Case Western Reserve University bearing dataset. To mitigate the impact of model randomness, all experimental results represent the average values from five independent trials. The experiments were conducted on a workstation equipped with an Intel Gold 5117 @2.00GHz CPU, 64GB RAM, and an NVIDIA GeForce RTX 3080 GPU. The model employs the Adam optimizer with an initial learning rate of 1 × 10⁻⁴, a batch size of 64, and incorporates a dropout rate of 0.2 during training to prevent overfitting.

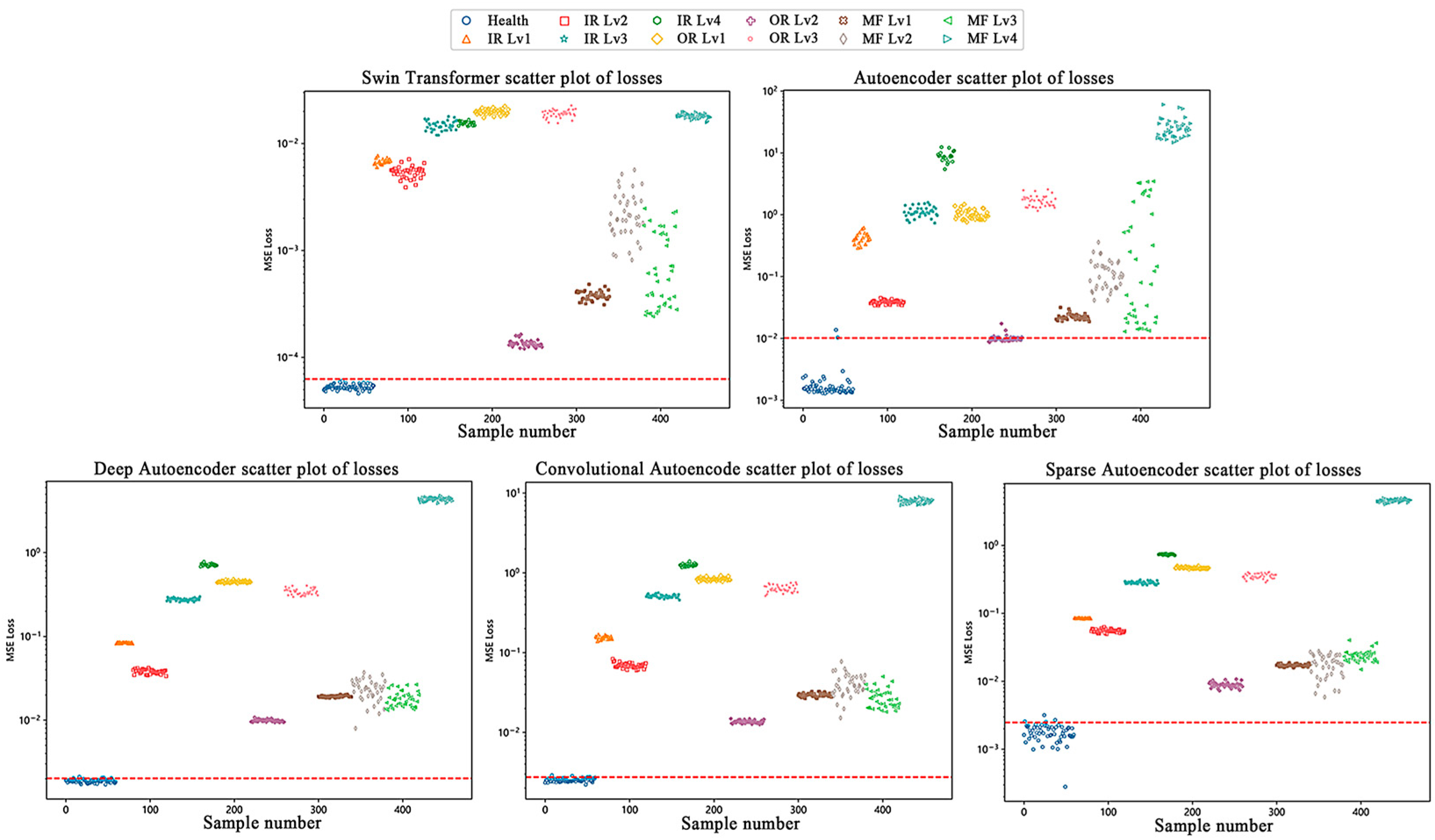
Figure 4 and Figure 5 present the experimental results and corresponding loss distribution visualizations for the Paderborn bearing dataset, with detailed experimental data provided in

Table 3. Fault diagnosis results of different methods on the Paderborn bearing dataset.

Network	Proposed Method	Auto Encoder	Deep Auto Encoder	Convolutional Auto Encoder	Sparse Auto Encoder
Accuracy (%)	99.53%	81.26%	75.30%	60.44%	71.67%
Precision (%)	100.00%	98.77%	98.29%	99.02%	98.69%
Recall (%)	99.46%	79.23%	72.57%	54.59%	67.99%

. The red line represents the threshold plotted based on 3σ. The results demonstrate that the proposed masked self-supervised learning model along with the Swin Transformer achieves superior performance across all metrics, attaining an accuracy of 99.53%, precision of 100.00%, and recall of 99.46%.

The loss distribution plots illustrate that the loss values for healthy samples are consistently concentrated below the established diagnostic threshold, whereas those for fault samples are uniformly distributed above it, demonstrating the model’s robust fault discrimination capability.

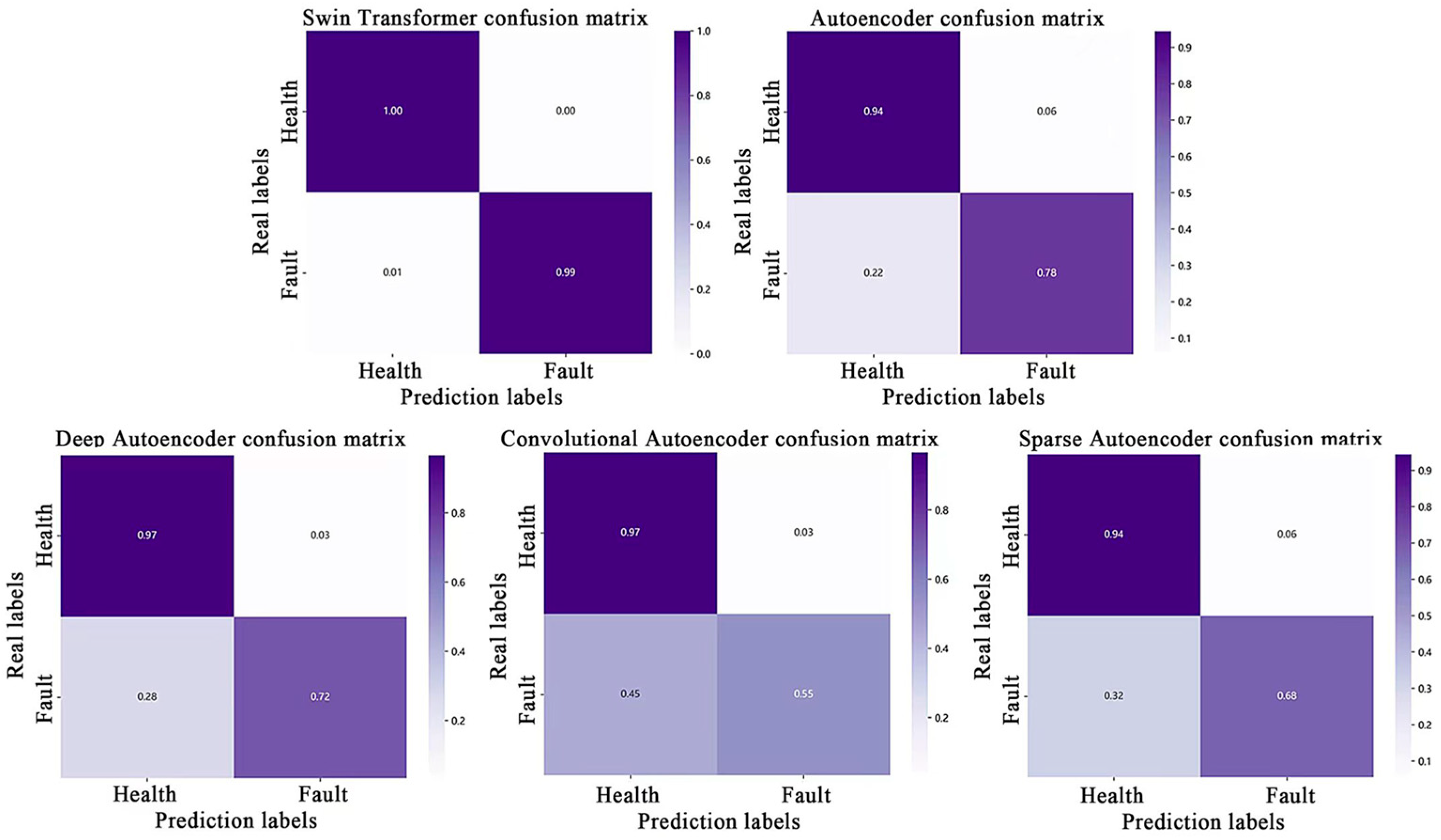
In comparative experiments, the four traditional Auto Encoder networks exhibited suboptimal performance, with none surpassing an accuracy of 82% or a recall of 80%. Analysis revealed that misclassified samples were predominantly associated with inner race faults and Level 1 outer race faults, highlighting significant limitations in the ability of traditional methods to effectively capture these fault features.

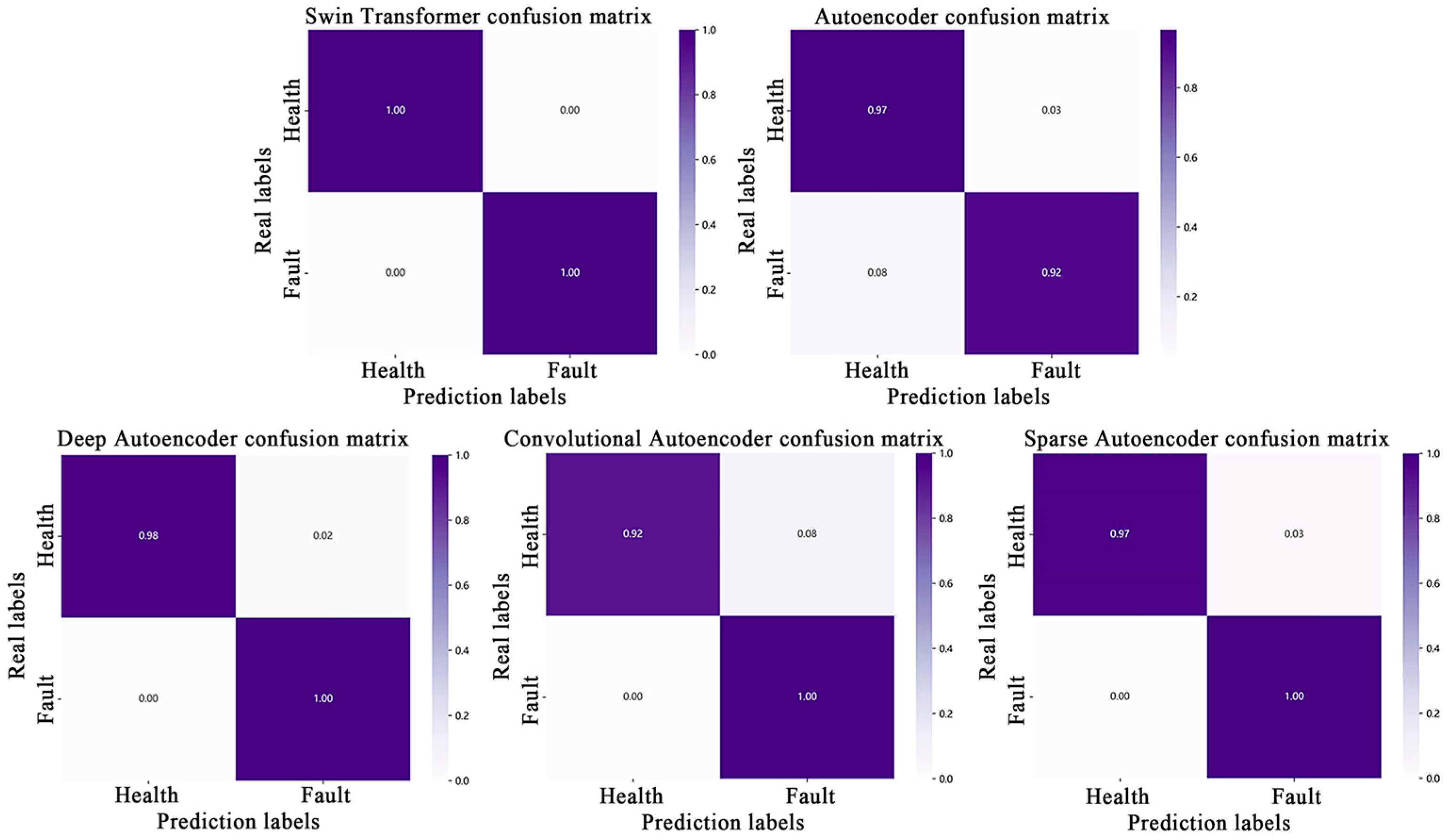
Figure 6 and Figure 7 present the experimental results and loss distribution visualizations for the Case Western Reserve University bearing dataset under a 0 N load condition at 1797 rpm rotational speed, with detailed data presented in

Table 4. Fault diagnosis results of different methods on the CWRU bearing dataset.

Network	Proposed Method	Auto Encoder	Deep Auto Encoder	Convolutional Auto Encoder	Sparse Auto Encoder
Accuracy (%)	100.00%	92.82%	99.56%	98.91%	99.56%
Precision (%)	100.00%	99.46%	99.50%	98.77%	99.50%
Recall (%)	100.00%	92.25%	100.00%	100.00%	100.00%

. The results demonstrate that the proposed method achieves perfect diagnostic performance in this operating condition, with 100% accuracy, precision, and recall. The red line represents the threshold plotted based on 3σ. The loss distribution plot clearly indicates that the loss values of all healthy samples fall strictly below the diagnostic threshold, while those of fault samples consistently exceed it, showcasing exceptional fault discrimination characteristics.

The experimental results confirm the superior adaptability and robustness of the proposed method. In contrast to conventional approaches, which exhibited significant performance degradation and notable missed detection issues that compromised system stability and safety, our method achieved 100% fault identification accuracy without any omissions under identical operating conditions. This consistently exceptional performance across all test scenarios underscores the method’s distinct advantages and practical engineering value in complex industrial environments.

4. Discussion

The superior performance of our method, as evidenced by the results in Table 3 and Table 4, can be primarily attributed to the Swin Transformer’s unique ability to learn multi-scale representations. The key innovation lies in its shifted-window self-attention mechanism, which overcomes a fundamental limitation of conventional autoencoders. While CNNs are constrained by fixed kernel sizes and struggle with long-range dependencies, our model dynamically adjusts its receptive field. This allows it to simultaneously resolve fine-grained temporal details and integrate contextual information across the entire sequence—a capability that is crucial for diagnosing real-bearing faults where symptoms are often manifested across multiple timescales. This mechanistic advantage directly explains the significant performance improvement, especially on complex fault types [19].

4.1. Why the Swin Transformer Outperforms Conventional Auto Encoders

The superior performance of our approach stems from fundamental differences in how the Swin Transformer processes vibration signals compared to conventional Auto Encoders. While Auto Encoders rely on fixed compression of input data through dense or convolutional layers, our model’s shifted-window attention mechanism [19] naturally adapts to key challenges in vibration analysis.

Auto Encoders struggle with three critical aspects of bearing fault detection: (1) capturing long-range dependencies between periodic impacts, (2) handling multi-scale features from early to severe fault stages, and (3) adapting to non-stationary operating conditions. The Swin Transformer addresses these through its hierarchical attention—local windows detect impulse signatures while cross-window interactions correlate them into diagnostic patterns [19].

Particularly for complex faults like combined inner/outer race damage, the model succeeds where Auto Encoders fail, which we hypothesize is because its attention weights automatically learn to disentangle overlapping vibration patterns. The masked pretraining further enhances this by forcing the model to reconstruct physically meaningful signal characteristics rather than memorizing superficial features. This is substantiated by our results on the Paderborn dataset (Table 3), where the proposed method significantly outperformed all conventional Autoencoders, especially in detecting subtle early-stage faults (e.g., Level 1 inner race faults). The superior performance on these challenging cases indicates that our model learned robust generalized features related to the underlying fault physics, rather than overfitting to superficial noise or simple patterns in the data [22].

This architectural advantage is most apparent in variable-speed conditions, where the Swin Transformer’s adaptive attention outperforms conventional methods that require explicit retraining. The model naturally develops speed-invariant representations through its reconstruction objective, demonstrating the inherent benefits of transformer-based approaches for vibration analysis [20].

4.2. Limitations and Future Improvements

The primary limitation of our current framework lies in its reliance on the 3σ threshold for fault detection. Although this method effectively distinguishes between healthy and faulty states—as clearly visualized in the loss distribution plots (Figure 4 and Figure 6), where healthy and faulty samples are well separated relative to the threshold—it operates as a binary classifier that cannot differentiate between specific fault types or severity levels. This is evident in the confusion matrices (Figure 5 and Figure 7), which show that while overall accuracy is high, the method lacks granularity in identifying exact fault categories (e.g., inner race vs. outer race faults, or Level 1 vs. Level 3 faults). Moreover, traditional thresholding methods like 3σ assume Gaussian-distributed errors and stationarity in data, assumptions often violated in real-world industrial environments with dynamic operating conditions, non-Gaussian noise, and varying load/speed profiles.

To overcome these limitations, future research should focus on integrating the strengths of traditional model-based approaches with modern deep learning techniques to develop adaptive multi-threshold mechanisms. Specifically, we propose hybrid frameworks that combine the interpretability and stability of traditional methods (e.g., clustering algorithms or density estimation) with the representational power of deep neural networks.

4.3. Industrial Context and Broader Implications

Our work demonstrates the practical value of unsupervised learning for industrial condition monitoring, particularly in scenarios where only healthy-state data is available for training. This approach addresses a critical industrial challenge: faults occur randomly in real-world applications, with unknown types and severity levels that are often impossible to replicate in laboratory environments. Many complex fault patterns emerge uniquely under specific operational conditions, material fatigue states, or environmental factors that cannot be fully simulated experimentally.

The proposed method aligns with industrial needs by utilizing solely healthy vibration data for training, eliminating the requirement for difficult-to-obtain fault examples. This capability is especially valuable in practical applications where fault data is scarce, unpredictable, and where early detection of novel fault types is essential for preventing catastrophic failures. By leveraging unlabeled data from normal operations, our approach provides a feasible solution for real-world industrial systems where comprehensive fault data collection is impractical or economically unviable.

Our research contributes to the growing adoption of self-supervised learning in industrial automation, offering a practical pathway for implementing intelligent fault diagnosis in environments where labeled fault data remains unavailable or insufficient.

5. Conclusions

This study innovatively proposes an unsupervised bearing fault diagnosis method that integrates masked self-supervised learning with the Swin Transformer, significantly improving the accuracy and robustness of fault diagnosis. The key innovations include:

1

A self-supervised pre-training method is proposed based on randomly masked vibration signals. By reconstructing the masked time-series segments, the model is compelled to learn deep spatiotemporal features of vibration signals, enhancing sensitivity to subtle fault characteristics.

2

The Huber loss function is employed to optimize the reconstruction task, combining the advantages of L1 and L2 losses to improve the model’s robustness against noise and non-stationary signals.

3

Real-world industrial noise and missing data problems are simulated through random masking, ensuring stable diagnostic performance under complex operating conditions. This provides a reliable technical solution for predictive maintenance of industrial equipment.