Experimental Innovative Prototype Solution for a Specialized Handling Trolley for Sampling Devices
Abstract
1. Introduction
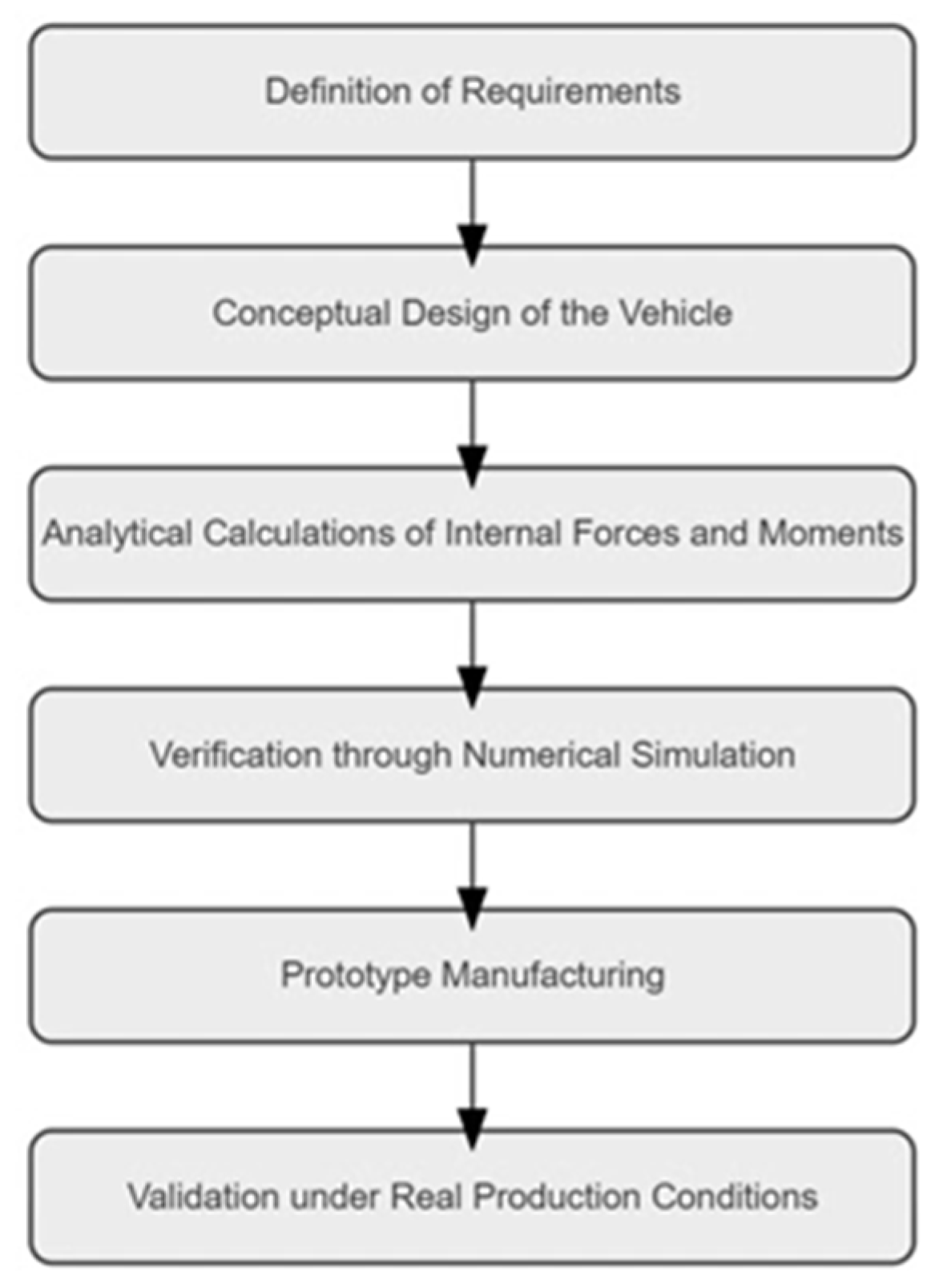
2. Materials and Methods
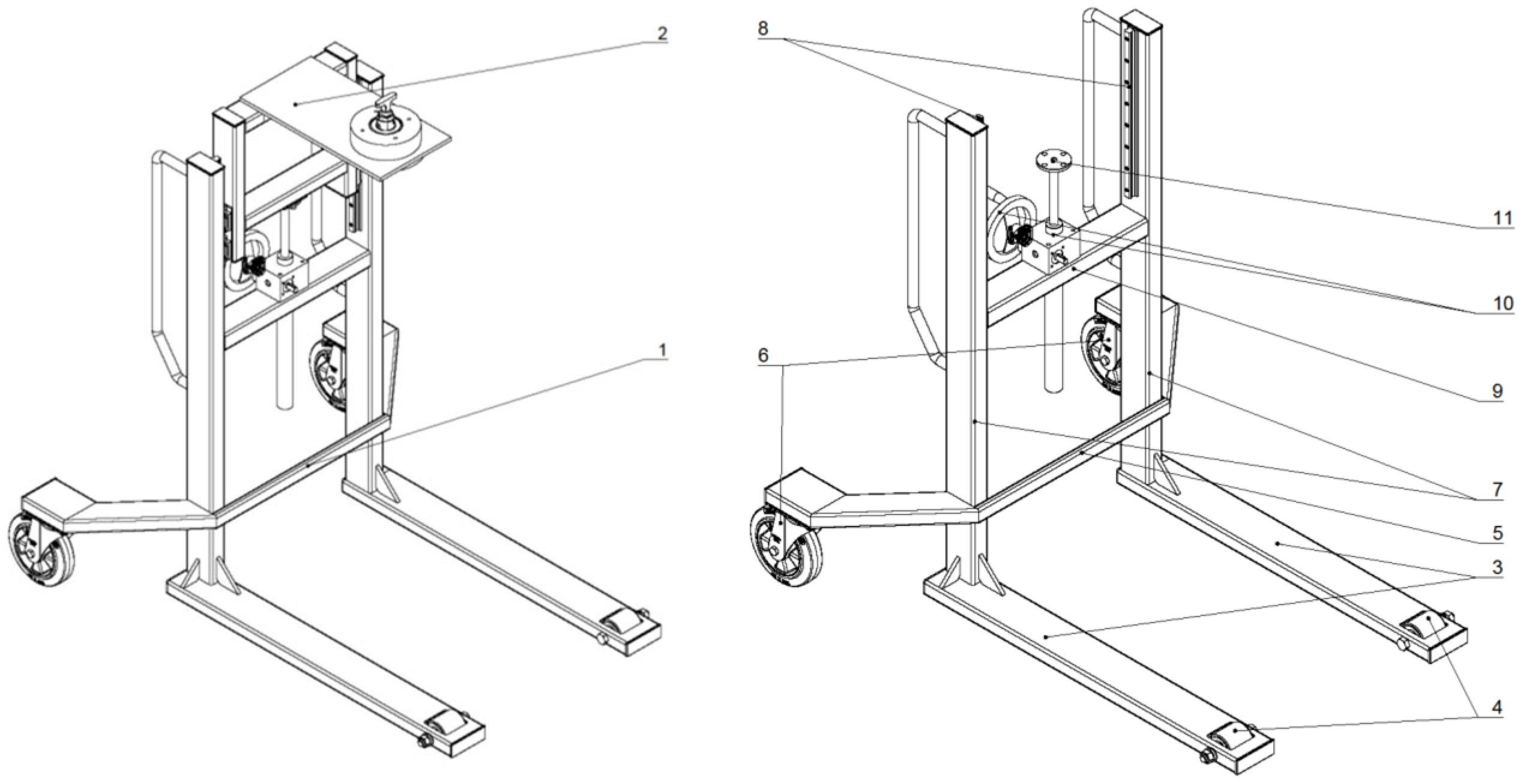
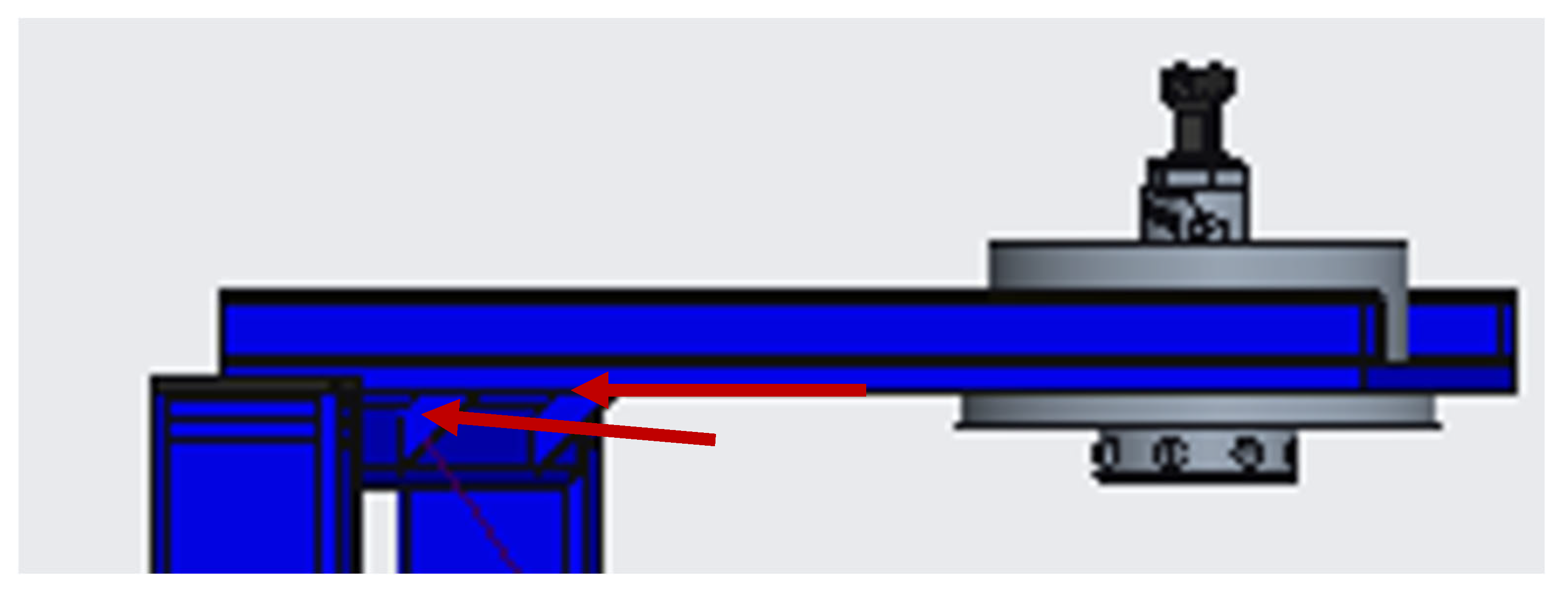
2.1. Conceptual Design and Definition of Input Parameters
2.2. Material Solution and Its Justification
2.3. Calculation of Structural Forces
2.3.1. Total Load of the Trolley
- Load from nominal load:
- Load from clamping device:
- Load from the bearing:
- Total load capacity of the trolley:
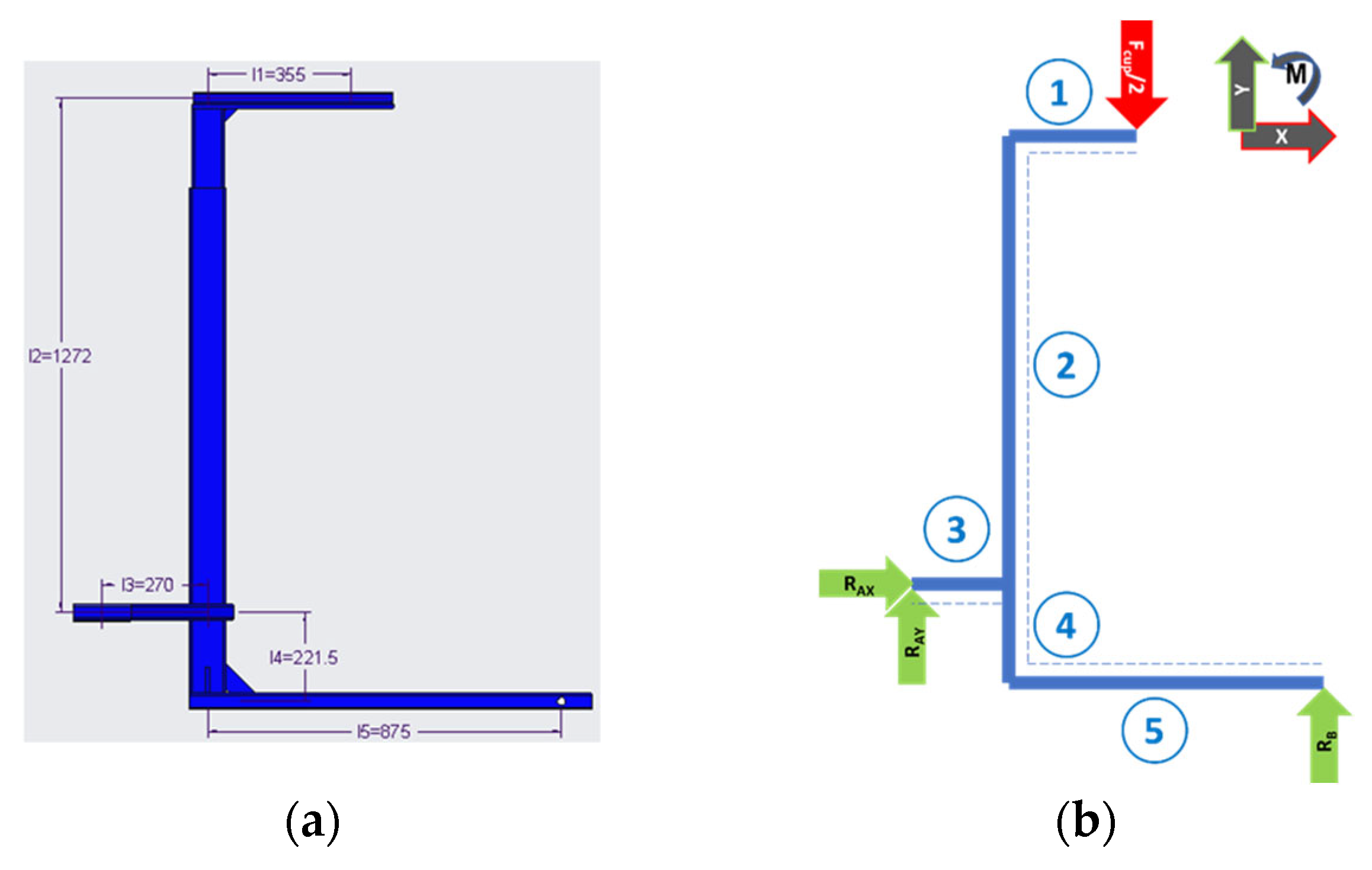
2.3.2. Calculation of External and Internal Force Effects
- Calculation of external reactions on the structure:
−1357.750 + 616.620 + 𝑅𝐵 = 0
𝑅𝐵 = 741.130 N
1357.750 · (0.875 − 0.355) − 𝑅𝐴𝑌(0.270 + 0.875) = 0
𝑅𝐴𝑌 = 616.620 N
- -
- Simple tension (pressure)—the only internal force is the axial force 𝑁;
- -
- Simple shear—the only internal force is the transverse force 𝑇;
- -
- Simple bending—the only internal force is the bending moment 𝑀𝑜;
- -
- Simple torsion—the only internal force is the torsional moment 𝑀k [13].
- Solution for Section 1: 0 ≤ x1 ≤ l1
T1 = 1357.75 N
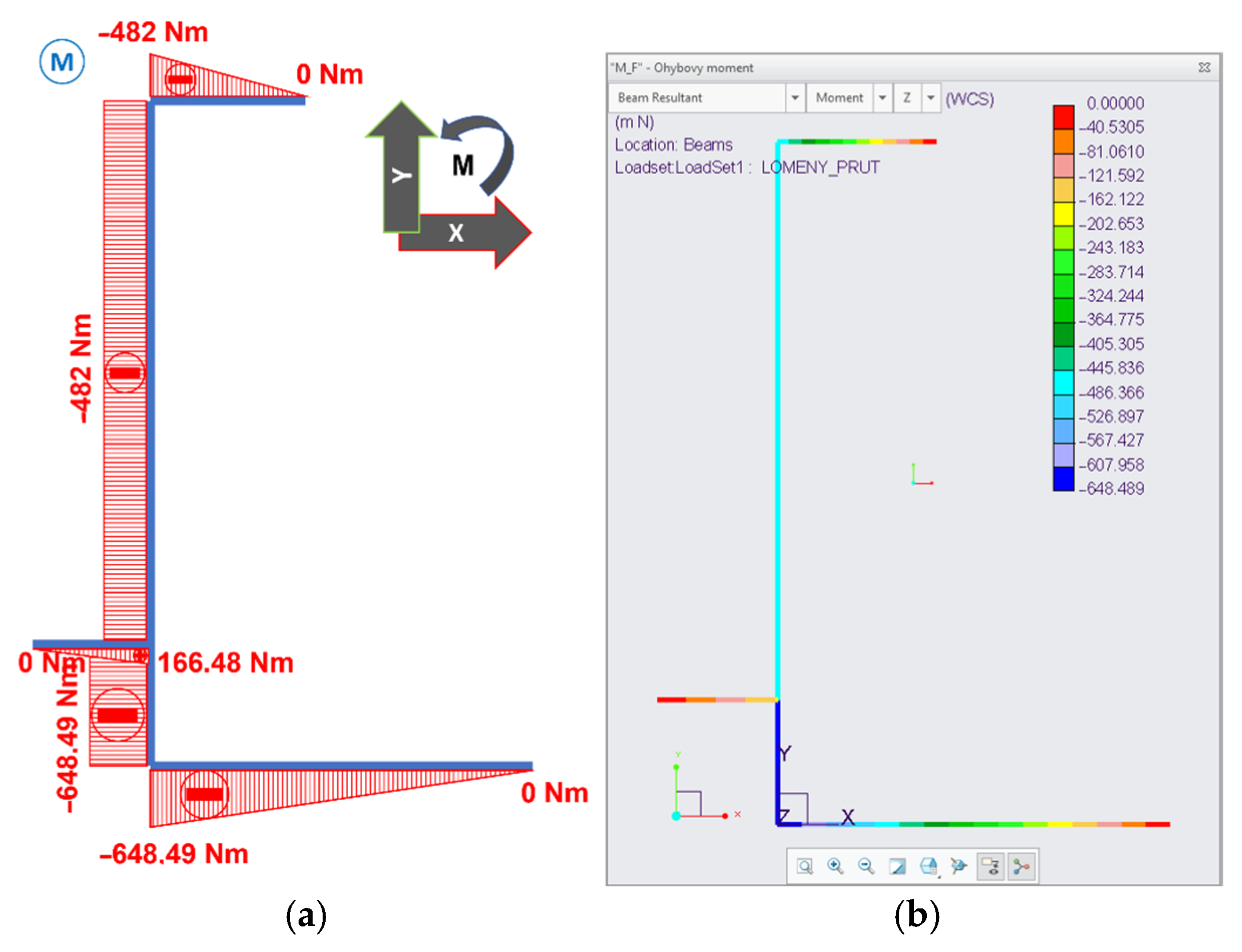
𝑀1(0) = −1357.75 · 0 = 0 Nm
𝑀1(𝑙1) = −1357.75 · 0.335 = −482.001 Nm
- 2.
- Solution for Section 2: 0 ≤ x2 ≤ l2
𝑁2 = − 1357.75 N
𝑀2 = −1357.75 · 0.335 = −482.001 Nm
- 3.
- Solution for Section 3: 0 ≤ x3 ≤ l3
𝑇3 = 616.62 N
𝑀3(0) = 616.62 · 0 = 0 Nm
𝑀3(l1) = 616.62 · 0.355 = 166.487 Nm
- 4.
- Solution for Section 4: 0 ≤ x4 ≤ l4
𝑁4 = −1357.75 + 616.62 = –741.13 N
𝑀4 = −616.62 · 0.27 − 1357.75 · 0.355 = −648.488 Nm
- 5.
- Solution for Section 5: 0 ≤ x5 ≤ l5
𝑇5 = −1357.75 + 616.620 = −741.129 N
𝑀5 = −616.620 · 0.27 − 1357.75 · 0.355 = −648.488 Nm
2.4. Design Proposal
- 1.
- Section 1:
- Calculation of permissible stress σD1:
- Calculation of the minimum section modulus Wo1min:
- Cross-sectional modulus in bending Wo1:
- Static moment S1:
- Area moment of inertia J1:
- Section modulus in sheet metal and hollow structural section (HSS) Wo1:
- Cross-sectional area A1:
- Shear stress τ1:
- Normal stress σ1:
- Hypothesis of strain energy for shape change σ1red:
- 2.
- Section 2:
- Calculation of permissible stress σD2:
- Calculation of minimum section modulus Wo2min:
- Shear stress τ2: does not apply, equals 0.
- Normal stress σ2:
- 3.
- Section 3:
- Calculation of the minimum cross-sectional modulus Wo3min:
- Shear stress τ3:
- Normal stress σ3:
- Hypothesis of strain energy for shape change σ1red:
- 4.
- Section 4:
- Calculation of the minimum section modulus Wo4min:
- Shear stress τ4: does not apply, equals 0.
- Normal stress σ4:
- 5.
- Section 5:
- Calculation of minimum section modulus Wo5min:
- Shear stress τ5:
- Normal stress σ5:
- Hypothesis of strain energy for shape change σ5red:
3. Results and Discussion
3.1. Comparison of Internal Force Effects Results with Creo Simulate
3.2. Comparison of Stress Results with Creo Simulate
3.3. Patent Protection and Practical Implementation
- Vargovská, M.; Čierťažský, R.; Minárik, M. Handling trolley for sand core clamping fixture. Slovak Republic utility model SK 10144 Y1, 25 September 2024 (in Slovak).
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blatnicky, M.; Dizo, J.; Gerlici, J.; Saga, M.; Lack, T.; Kuba, E. Design of a robotic manipulator for handling products of automotive industry. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420906290. [Google Scholar] [CrossRef]
- Zajacko, I.; Gál, T.; Ságová, Z.; Mateichyk, V.; Wiecek, D. Application of artificial intelligence principles in mechanical engineering. In Proceedings of the 3rd International Scientific Conference on Innovative Technologies in Engineering Production (ITEP), Bangkok, Thailand, 12–14 December 2018; Volume 244. [Google Scholar] [CrossRef]
- Kuric, I.; Klarak, J.; Bulej, V.; Saga, M.; Kandera, M.; Hajducik, A.; Tucki, K. Approach to Automated Visual Inspection of Objects Based on Artificial Intelligence. Appl. Sci. 2022, 12, 864. [Google Scholar] [CrossRef]
- Vargovská, M.; Minárik, M. Innovative Solutions for Handling Mechanisms at Handling Wood Material, 1st ed.; Technical University in Zvolen: Zvolen, Slovakia, 2024. (In Slovak) [Google Scholar]
- Banský, M.; Michna, S.; Plagany, J.; Radi, J. Universal CNC Grinding Machine; Technical University in Zvolen: Zvolen, Slovakia, 2007. (In Slovak) [Google Scholar]
- Siddharta, R. Introduction to Materials Handling; National Institute of Technical: Kolkata, India, 2015. [Google Scholar]
- Leggieri, S.; Falco, V.; D’Andrea, C.N. Online Ergonomic Evaluation in Realistic Manual Material Handling Task. Bioengineering 2023, 11, 14. [Google Scholar] [CrossRef] [PubMed]
- Umar, R.Z.R.; Ahmad, N.; Halim, I.; Lee, P.Y.; Hamid, M. Design and Development of an Ergonomic Trolley-Lifter for Sheet Metal Handling Task. Saf. Health Work 2019, 10, 327–335. [Google Scholar] [CrossRef] [PubMed]
- STN EN 10219-1:2007; Cold Formed Hollow Sections of Non-Alloy and Fine-Grained Structural Steels. Part 1: Technical Delivery Conditions. Slovak Institute of Technical Standardization: Bratislava, Slovakia. (In Slovak)
- STN EN 10305-3:2010; Precision Steel Tubes. Part 3: Cold Drawn Welded Tubes. Slovak Institute of Technical Standardization: Bratislava, Slovakia. (In Slovak)
- STN EN 10025-2:2019; Hot-Rolled Products of Structural Steels. Part 2: Technical Delivery Conditions for Non-Alloy Structural Steels. Slovak Institute of Technical Standardization: Bratislava, Slovakia. (In Slovak)
- Structural Steels. Available online: http://old.konstrukce.cz/clanek/volba-konstrukcnich-oceli-pro-stavebni-svarovane-konstrukce-podle-vyznamu-oznaceni/ (accessed on 26 February 2023).
- Bodnár, F. Elasticity and Strength I; Technical University in Zvolen: Zvolen, Slovakia, 2008. (In Slovak) [Google Scholar]
- Vita, L.; Gattamelata, D. Analytical Method for Assessing Stability of a Counterbalanced Forklift Truck Assembled with Interchangeable Equipment. Appl. Sci. 2023, 13, 1206. [Google Scholar] [CrossRef]
- Oh, H.J.H.; Liew, K.W.; Ng, P.K.; Lim, B.K.; Tay, C.H.; Khoh, C.L. An Innovative Solution for Stair Climbing: A Conceptual Design and Analysis of a Tri-Wheeled Trolley with Motorized, Adjustable, and Foldable Features. Inventions 2025, 10, 57. [Google Scholar] [CrossRef]
- Van der Woude, L.H.V.; Geurts, C.; Winkelman, H.; Veeger, H.E.J. Measurement of wheelchair rolling resistance with a handle bar push technique. J. Med. Eng. Technol. 2003, 27, 249–258. [Google Scholar] [CrossRef] [PubMed]
- Sauret, C.; Bascou, J.; de Saint Rémy, N.; Pillet, H.; Vaslin, P.; Lavaste, F. Assessment of field rolling resistance of manual wheelchairs. J. Rehabil. Res. Dev. 2012, 49, 63–74.S. [Google Scholar] [CrossRef] [PubMed]
- Sandfeld, J.; Rosgaard, C.; Jensen, B.R. L4-L5 compression and anterior/posterior joint shear forces in cabin attendants during the initial push/pull actions of airplane meal carts. Ergonomics 2014, 45, 1067–1075. [Google Scholar] [CrossRef] [PubMed]
- Leban, B.; Fabbri, D.; Lecca, L.I.; Uras, M.; Monticone, M.; Porta, M.; Pau, M.; Campagna, M. Characterization of hand forces exerted during non-powered hospital bed pushing and pulling tasks. Int. J. Occup. Saf. Ergon. 2022, 28, 991–999. [Google Scholar] [CrossRef] [PubMed]
- Sprigle, S.; Huang, M.; Misch, J. Measurement of rolling resistance and scrub torque of manual wheelchair drive wheels and casters. Assist. Technol. 2019, 34, 91–103. [Google Scholar] [CrossRef] [PubMed]
- Silva, L.C.A.; Dedini, F.G.; Corrêa, F.C.; Eckert, J.J.; Becker, M. Measurement of wheelchair contact force with a low cost bench test. Med. Eng. Phys. 2016, 38, 163–170. [Google Scholar] [CrossRef] [PubMed]
- Al-Eisawi, K.W.; Kerk, C.J.; Congleton, J.J.; Amendola, A.A.; Jenkins, O.C.; Gaines, W. Factors affecting minimum push and pull forces of manual carts. Appl. Ergon. 1999, 30, 235–245.S. [Google Scholar] [CrossRef] [PubMed]
- Banský, M.; Svoreň, J.; Plagany, J. Obrábacie Centrum pre Porez Drevnej Suroviny; Technická Univerzita vo Zvolene: Zvolen, Slovakia, 2006. [Google Scholar]
- Zhang, Y.; Lin, K.Y.; Lin, J.H. Factors Affecting Material-Cart Handling in the Roofing Industry. Int. J. Environ. Res. Public Health 2021, 18, 1510. [Google Scholar] [CrossRef]
- Amio, F.F.; Ahmed, N.; Jeong, S.; Jung, I.; Nam, K. Optimizing Precision Material Handling: Elevating Performance and Safety through Enhanced Motion Control in Industrial Forklifts. Electronics 2024, 13, 1732. [Google Scholar] [CrossRef]
- Anggono, W.; Rakhmawati, R.; Saputra, A. Redesign Materials Handling System by Using Ergonomic Approaches to Reduce Back Pain Risk. In Advances in Intelligent Systems and Computing; Springer: Singapore, 2018; Volume 605, pp. 469–475. [Google Scholar] [CrossRef]
- Gille, S. Design of Manual Handling Carts: A Novel Approach Combining Corrective Forces and Modelling to Prevent Injuries. Safety 2025, 11, 25. [Google Scholar] [CrossRef]
- Ahmad, I.; Abidin, A.A.Z.; Mohd Yusoff, H.H.; Sapuan, S.M.; Ahmad, R.; Jamil, M.A. Sheet Metal Manual Handling Aids: Effects of Design Differences on Muscle Activity and Subjective Assessment. IIUM Eng. J. 2023, 24, 45–55. Available online: https://journals.iium.edu.my/ejournal/index.php/iiumej/article/view/3397 (accessed on 8 August 2025). [CrossRef]
- Gumasing, M.J. An Ergonomic Design of Six-Wheeled Trolley for Transportation of a 100-kg Weight Load. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Dubai, United Arab Emirates, 10–12 March 2020; Available online: https://index.ieomsociety.org/index.cfm/article/view/ID/4301 (accessed on 8 August 2025).
- Siska, R.; Syahbana, A. Design of an Ergonomic Trolley for Plate Handling Task Using OWAS and Ergonomic Function Deployment. Spektrum Ind. 2020, 18, 47–58. [Google Scholar] [CrossRef]
- Singh, T.; Kumar, R.; Sharma, S. Development of a Trolley-Lifter for Sheet Metal Handling: Ergonomic Evaluation and Pilot Testing. Int. J. Occup. Saf. Ergon. 2019, 25, 523–531. [Google Scholar]
- Industrial Property Office of the Slovak Republic. Úžitkový vzor č. 25-2024. Available online: https://wbr.indprop.gov.sk/WebRegistre/UzitkovyVzor/Detail/25-2024 (accessed on 31 July 2025).
- ClearCalcs. Free Moment of Inertia Calculator. Available online: https://clearcalcs.com/freetools/free-moment-of-inertia-calculator/au (accessed on 26 February 2023).
- Han, B.; Gabriel, J.-C.P. Thin-film nanocomposite (TFN) membrane technologies for the removal of emerging contaminants from wastewater. J. Clean. Prod. 2024, 480, 144043. [Google Scholar] [CrossRef]
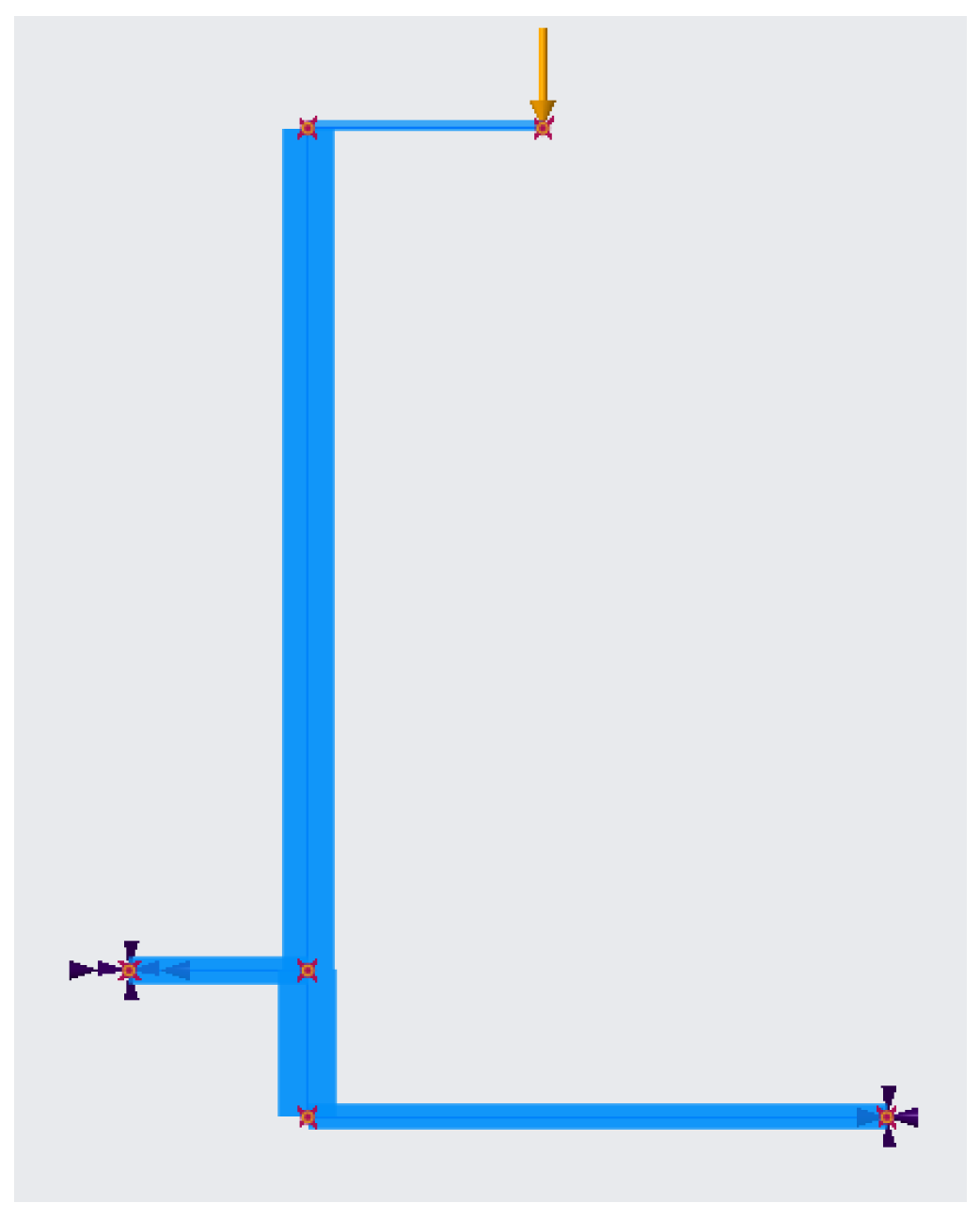




| Force/Section | Value | Conversion of Units |
|---|---|---|
| 𝐹 = 𝐹Cup/2 | 3075.5/2 N | 1357.75 N |
| l1 | 355 mm | 0.355 m |
| l2 | 1272 mm | 1.272 m |
| l3 | 270 mm | 0.270 m |
| l4 | 221.5 mm | 0.2215 m |
| l5 | 875 mm | 0.875 m |
| Variable | Calculated Result (MPa) | Result of Creo Simulate Analysis (MPa) |
|---|---|---|
| σ(1(0)) σ(1(l1)) | 0 → (Equation (37)) | 1.620 × 10−3 ≐ 0 |
| 411.15 → (Equation (38)) | 1.265 × 10 = 12.65 | |
| σ2 | 39.13 → (Equation (42)) | 3.650 × 10 = 36.5 |
| σ(3(0)) σ(3(l3)) | 0 → (Equation (45)) | 7.896 × 10−3 ≐ 0 |
| 12.9 → (Equation (46)) | 1.248 × 10 = 12.48 | |
| σ4 | 36.59 → (Equation (49)) | 3.469 × 10 = 34.69 |
| σ(5(0)) | 0 → (Equation (52)) | 3.160 × 10−13 ≐ 0 |
| σ(5(l5)) | 50.27 → (Equation (53)) | 4.862 × 10 = 48.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Čierťažský, R.; Vargovská, M.; Pivarčiová, E. Experimental Innovative Prototype Solution for a Specialized Handling Trolley for Sampling Devices. Machines 2025, 13, 775. https://doi.org/10.3390/machines13090775
Čierťažský R, Vargovská M, Pivarčiová E. Experimental Innovative Prototype Solution for a Specialized Handling Trolley for Sampling Devices. Machines. 2025; 13(9):775. https://doi.org/10.3390/machines13090775
Chicago/Turabian StyleČierťažský, Roman, Mária Vargovská, and Elena Pivarčiová. 2025. "Experimental Innovative Prototype Solution for a Specialized Handling Trolley for Sampling Devices" Machines 13, no. 9: 775. https://doi.org/10.3390/machines13090775
APA StyleČierťažský, R., Vargovská, M., & Pivarčiová, E. (2025). Experimental Innovative Prototype Solution for a Specialized Handling Trolley for Sampling Devices. Machines, 13(9), 775. https://doi.org/10.3390/machines13090775






