Stator Fault Diagnostics in Asymmetrical Six-Phase Induction Motor Drives with Model Predictive Control Applicable During Transient Speeds †
Abstract
1. Introduction
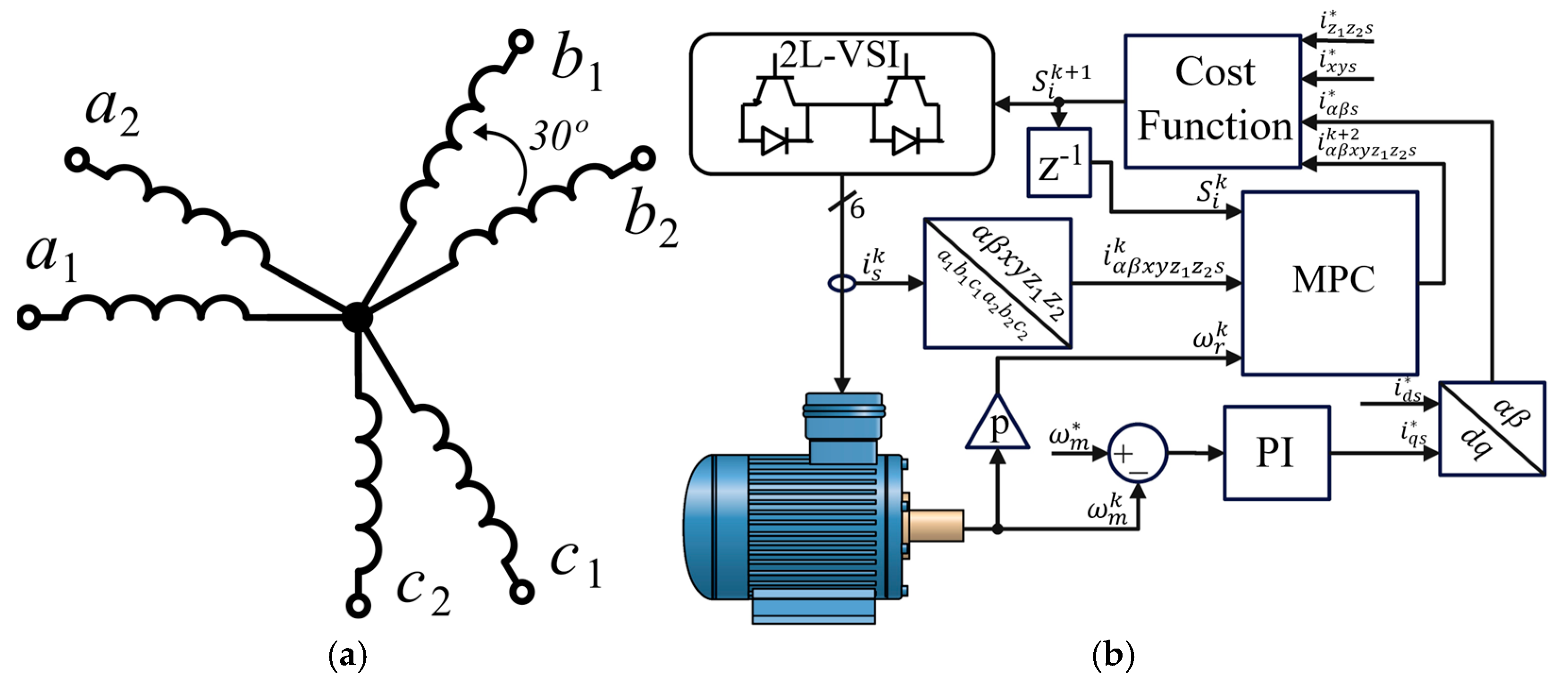
2. A6PIM Drive with MPC
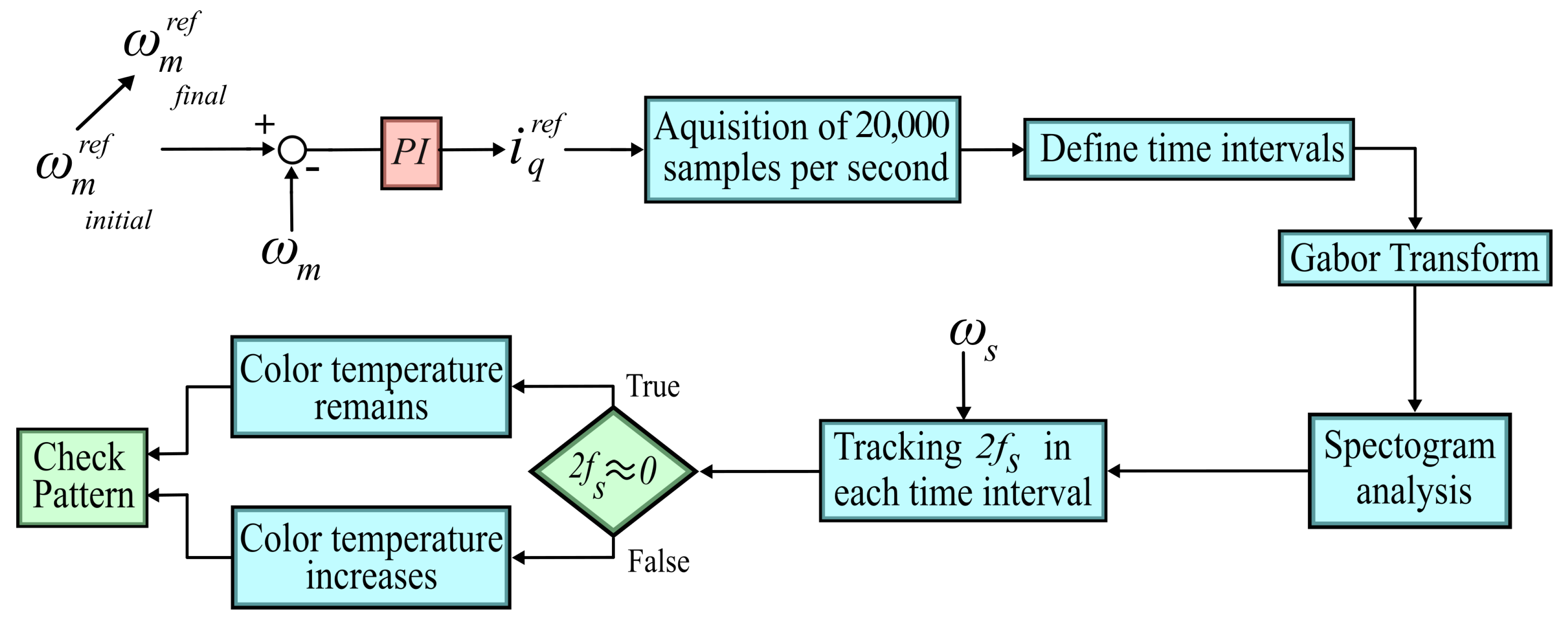
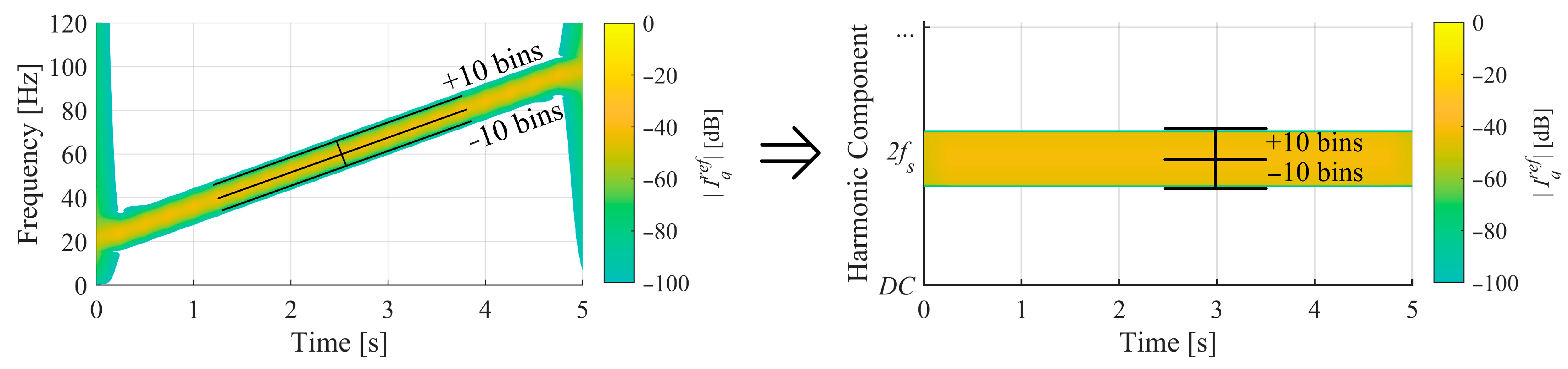
3. Fault Diagnostic Technique
4. Experimental Validation
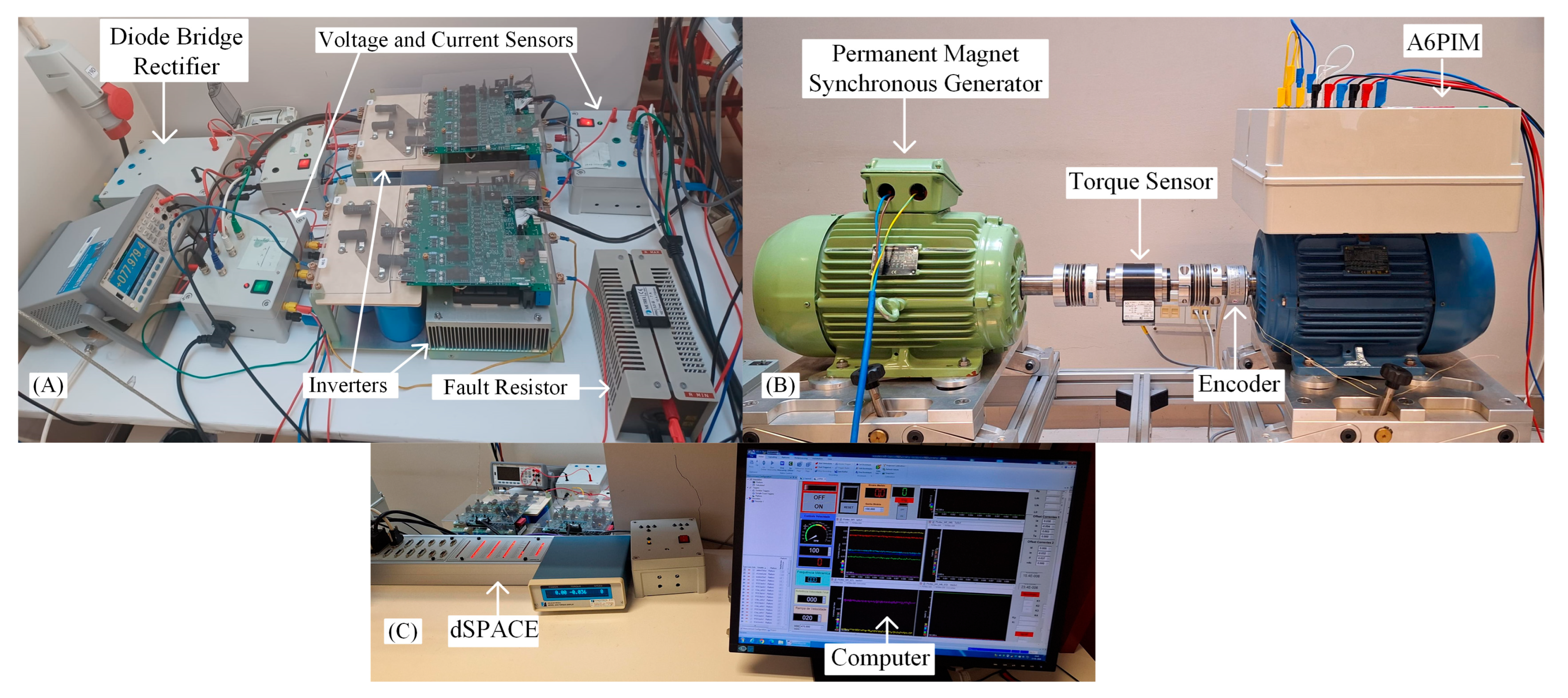
4.1. Experimental Setup
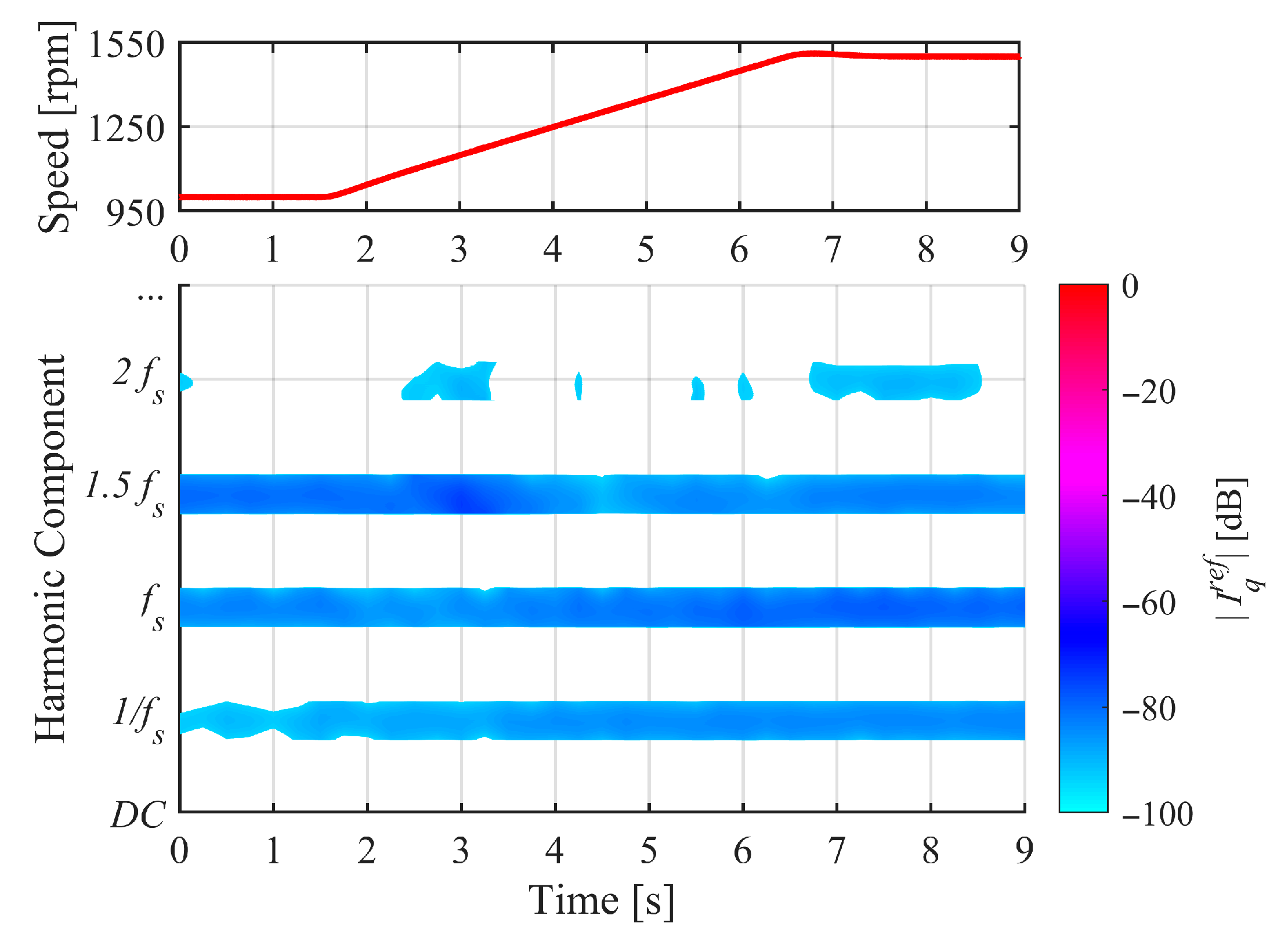
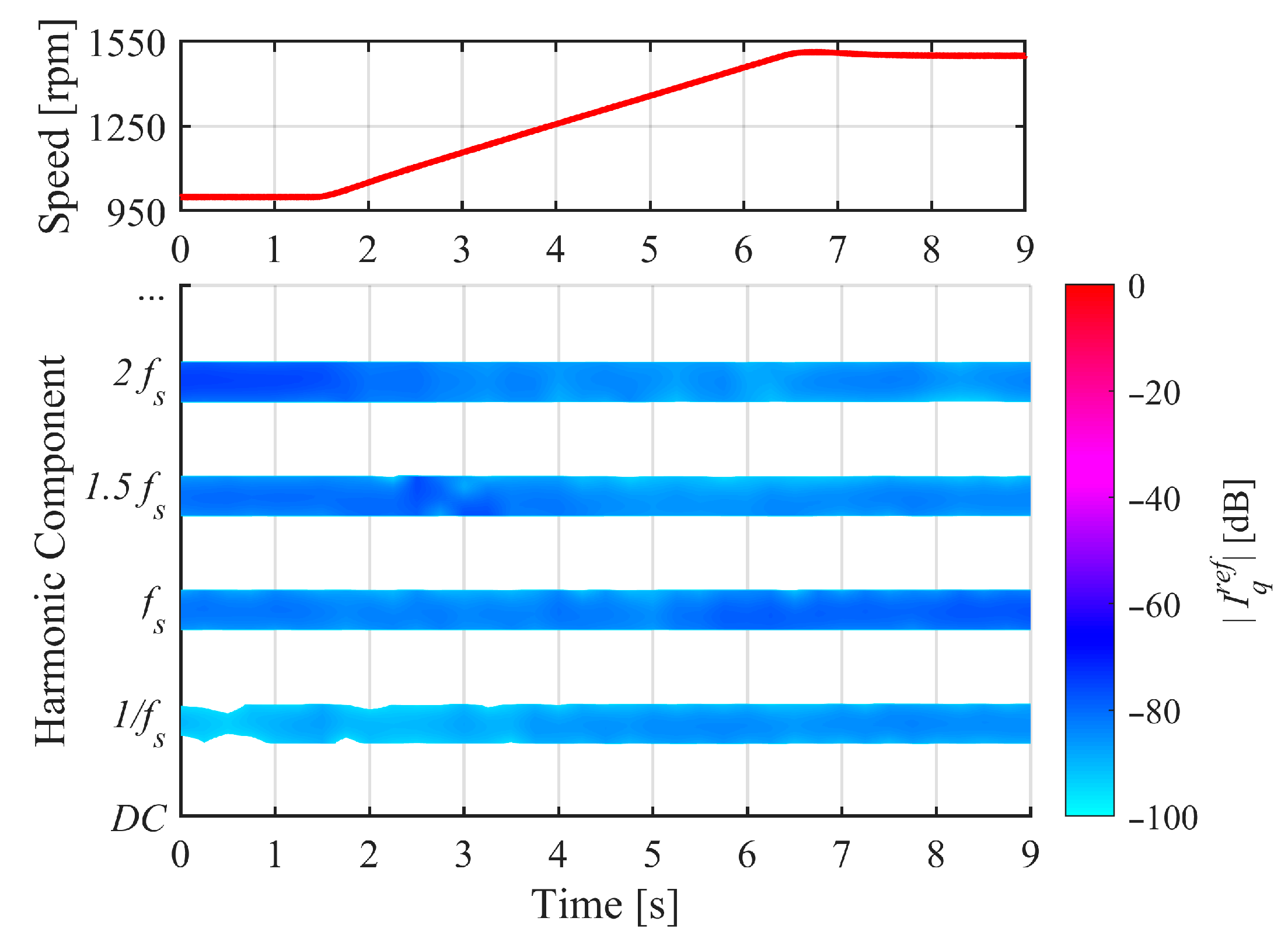
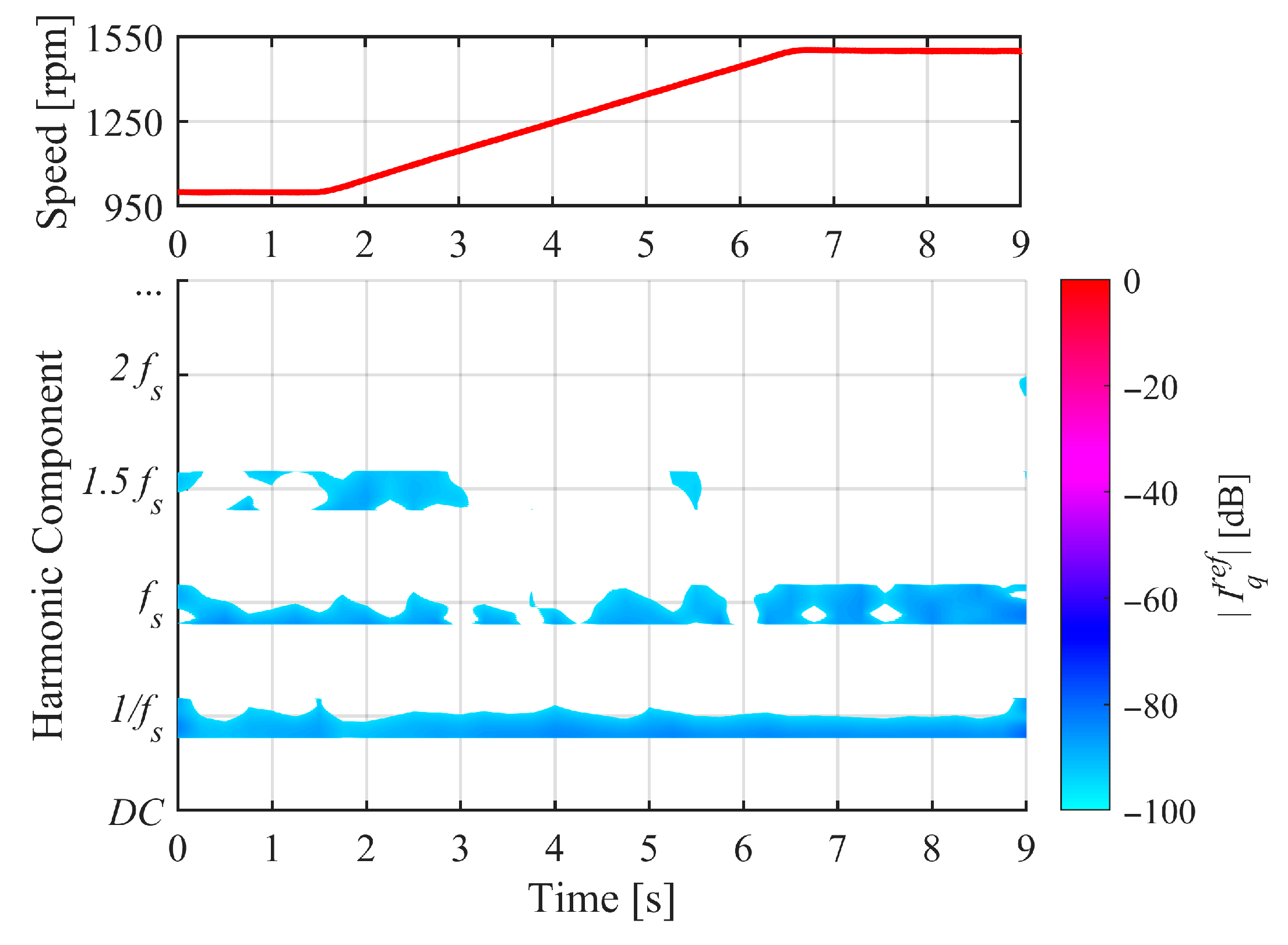
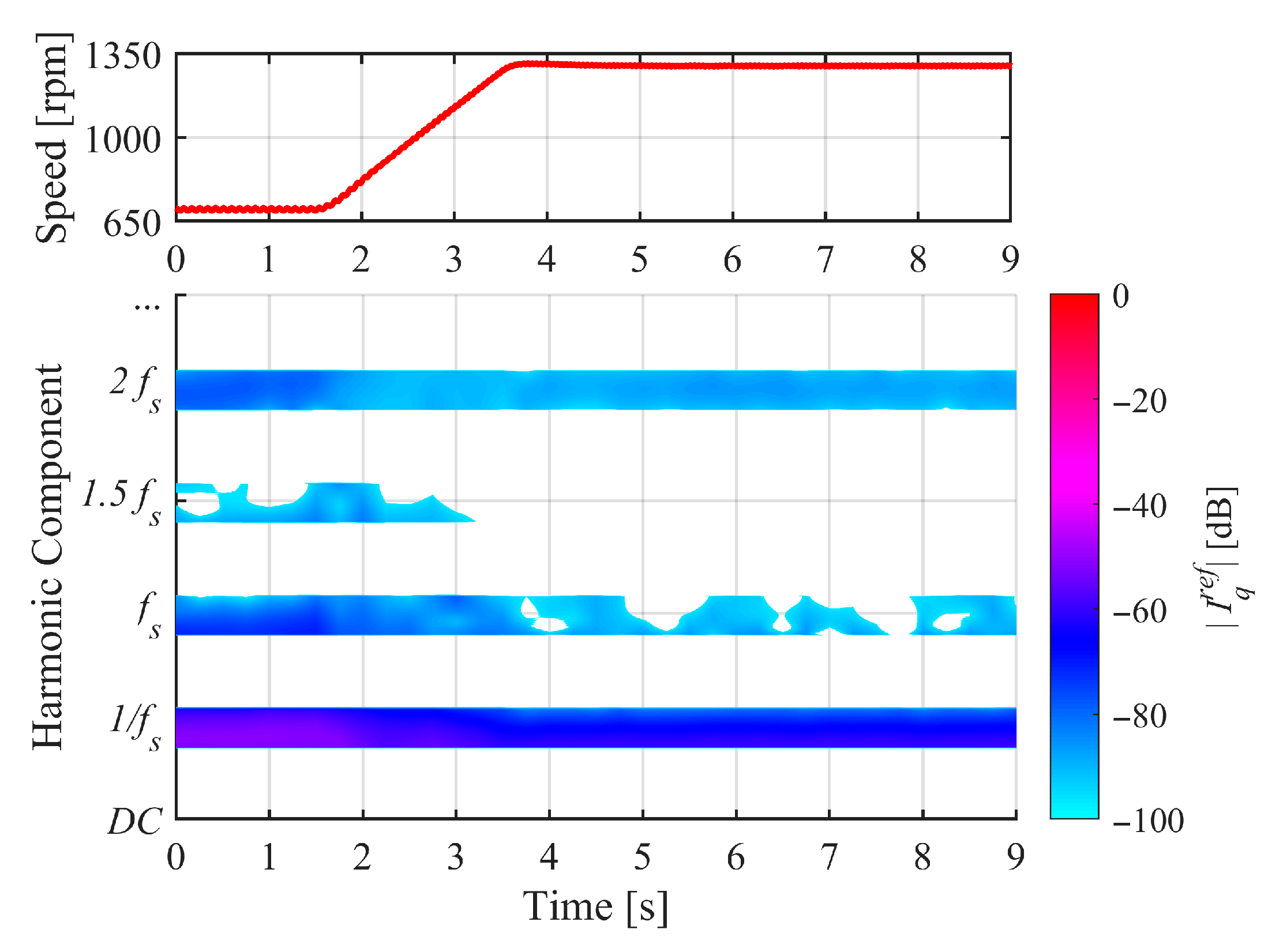
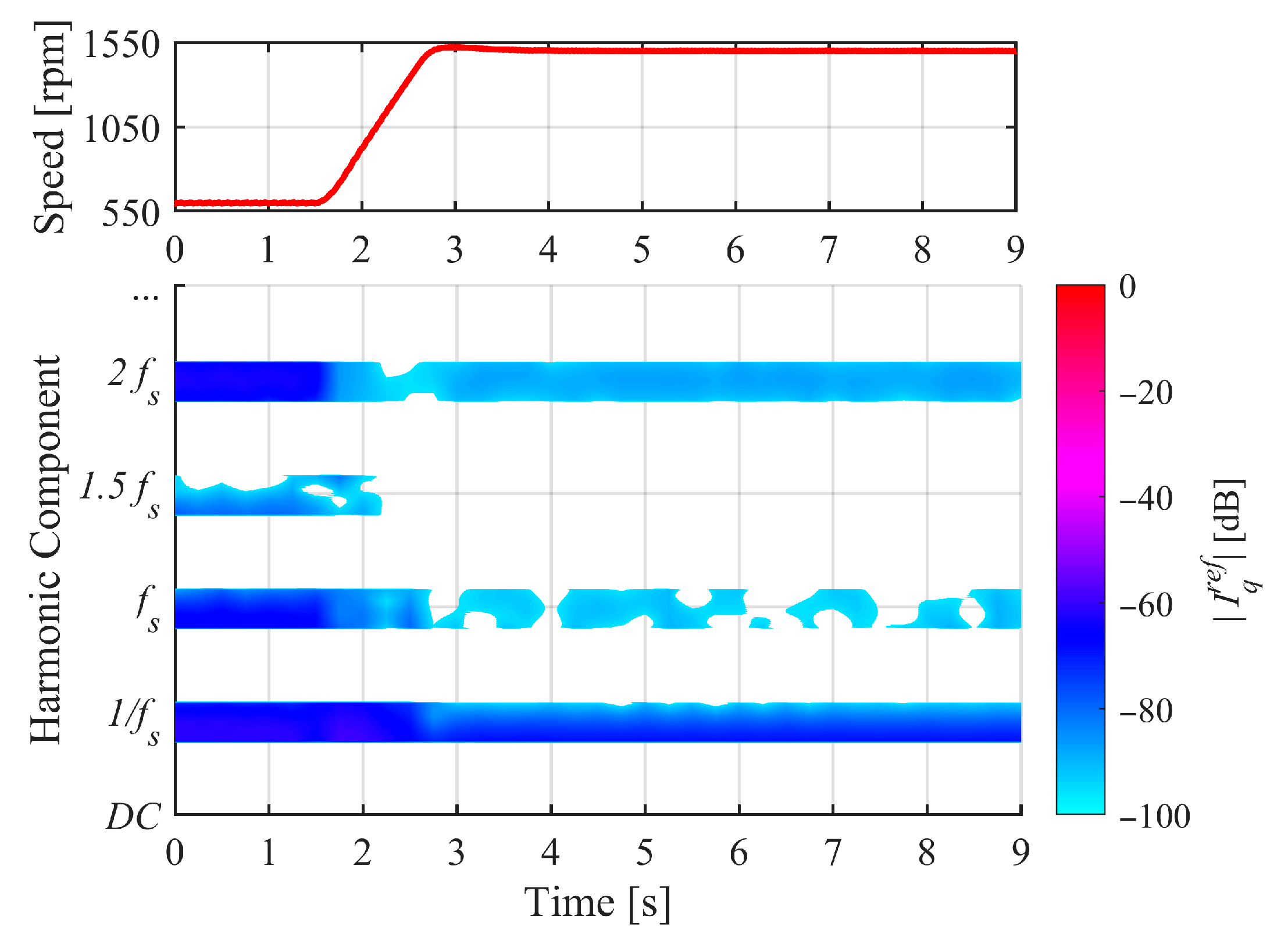
4.2. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DTC | Direct torque control |
| FOC | Field-oriented control |
| MPC | Model predictive control |
| ITSCF | Inter-turn short circuit fault |
| PMSM | Permanent magnet synchronous motor |
| 3PIM | Three-phase induction motor |
| FFT | Fast Fourier transform |
| A6PIM | Asymmetrical six-phase induction motor |
| WT | Wavelet transform |
| STFT | Short-time Fourier transform |
| GT | Gabor transform |
| VSD | Vector space decomposition |
| PMSG | Permanent magnet synchronous generator |
References
- Levi, E. Multiphase Electric Machines for Variable-Speed Applications. IEEE Trans. Ind. Electron. 2008, 55, 1893–1909. [Google Scholar] [CrossRef]
- Levi, E. Advances in Converter Control and Innovative Exploitation of Additional Degrees of Freedom for Multiphase Machines. IEEE Trans. Ind. Electron. 2006, 63, 433–448. [Google Scholar] [CrossRef]
- Bojoi, R.; Farina, F.; Profumo, F.; Tenconi, A. Dual-Three Phase Induction Machine Drives Control—A Survey. IEEJ Trans. Ind. Appl. 2006, 126, 420–429. [Google Scholar] [CrossRef]
- Barrero, F.; Duran, M.J. Recent Advances in the Design, Modeling, and Control of Multiphase Machines—Part I. IEEE Trans. Ind. Electron. 2016, 63, 449–458. [Google Scholar] [CrossRef]
- Rodriguez, J.; Garcia, C.; Mora, A.; Davari, S.A.; Rodas, J.; Valencia, D.F.; Elmorshedy, M.; Wang, F.; Zuo, K.; Tarisciotti, L.; et al. Latest Advances of Model Predictive Control in Electrical Drives—Part II: Applications and Benchmarking With Classical Control Methods. IEEE Trans. Power Electron. 2022, 37, 5047–5061. [Google Scholar] [CrossRef]
- Serra, J.; Jlassi, I.; Cardoso, A.J.M. A Computationally Efficient Model Predictive Control of Six-Phase Induction Machines Based on Deadbeat Control. Machines 2021, 9, 306. [Google Scholar] [CrossRef]
- Zhang, P.; Du, Y.; Habetler, T.G.; Lu, B. A Survey of Condition Monitoring and Protection Methods for Medium-Voltage Induction Motors. IEEE Trans. Ind. Appl. 2011, 47, 34–46. [Google Scholar] [CrossRef]
- Gyftakis, K.N.; Sumislawska, M.; Kavanagh, D.F.; Howey, D.A.; McCulloch, M.D. Dielectric Characteristics of Electric Vehicle Traction Motor Winding Insulation Under Thermal Aging. IEEE Trans. Ind. Appl. 2016, 52, 1398–1404. [Google Scholar]
- Cardoso, A.J.M. Diagnosis and Fault Tolerance of Electrical Machines, Power Electronics and Drives; The Institution of Engineering and Technology: London, UK, 2018; ISBN 978-1-78561-531-3. [Google Scholar]
- Wolbank, T.M.; Loparo, K.A.; Wohrnschimmel, R. Inverter statistics for online detection of stator asymmetries in inverter-fed induction motors. IEEE Trans. Ind. Appl. 2003, 39, 1102–1108. [Google Scholar] [CrossRef]
- Bellini, A.; Filippetti, F.; Franceschini, G.; Tassoni, C. Closed-loop control impact on the diagnosis of induction motors faults. IEEE Trans. Ind. Appl. 2000, 36, 1318–1329. [Google Scholar] [CrossRef]
- Obeid, N.H.; Boileau, T.; Nahid-Mobarakeh, B. Modeling and Diagnostic of Incipient Interturn Faults for a Three-Phase Permanent Magnet Synchronous Motor. IEEE Trans. Ind. Appl. 2016, 52, 4426–4434. [Google Scholar] [CrossRef]
- Kim, K.-h.; Gu, B.-G.; Jung, I.-S. Online fault-detecting scheme of an inverter-fed permanent magnet synchronous motor under stator winding shorted turn and inverter switch open. IET Electr. Power Appl. 2011, 5, 529–539. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, J.; Xiong, J.; Wu, Y.; Cheng, M. An Improved High-Frequency Voltage Injection Method for Interturn Short-Circuit Fault Detection in PMSMs. IEEE Trans. Transp. Electrif. 2023, 9, 3228–3239. [Google Scholar] [CrossRef]
- Li, W.; Hang, J.; Ding, S.; Wang, Q. Common Predictive Model for PMSM Drives With Interturn Fault Considering Torque Ripple Suppression. IEEE Trans. Transp. Electrif. 2023, 9, 4071–4079. [Google Scholar] [CrossRef]
- Fang, J.; Sun, Y.; Wang, Y.; Wei, B.; Hang, J. Improved ZSVC-based fault detection technique for incipient stage inter-turn fault in PMSM. IET Electr. Power Appl. 2019, 13, 2015–2026. [Google Scholar] [CrossRef]
- Hang, J.; Zhang, J.; Xia, M.; Ding, S.; Hua, W. Interturn Fault Diagnosis for Model-Predictive-Controlled-PMSM Based on Cost Function and Wavelet Transform. IEEE Trans. Power Electron. 2020, 35, 6405–6418. [Google Scholar] [CrossRef]
- Hu, R.; Wang, J.; Mills, A.R.; Chong, E.; Sun, Z. Current-Residual-Based Stator Interturn Fault Detection in Permanent Magnet Machines. IEEE Trans. Ind. Electron. 2021, 68, 59–69. [Google Scholar] [CrossRef]
- Hu, J.; Wang, H.; Li, Y. Model-Based Severity Monitoring for Interturn Short Circuit Faults in Symmetrical Six-Phase PMSMs Using Subspace Current Residuals. IEEE Trans. Power Electron. 2023, 38, 16142–16152. [Google Scholar] [CrossRef]
- Wang, H.; Hu, J.; Li, Y. Fault Phase Location for Interturn Short-Circuit Faults in Symmetrical Six-Phase PMSMs Based on Subspace Current Residual. IEEE Trans. Transp. Electrif. 2024, 10, 8336–8345. [Google Scholar] [CrossRef]
- Wolkiewicz, M.; Tarchała, G.; Orłowska-Kowalska, T.; Kowalski, C.T. Online Stator Interturn Short Circuits Monitoring in the DFOC Induction-Motor Drive. IEEE Trans. Ind. Electron. 2016, 63, 2517–2528. [Google Scholar] [CrossRef]
- Cheng, S.; Zhang, P.; Habetler, T.G. An Impedance Identification Approach to Sensitive Detection and Location of Stator Turn-to-Turn Faults in a Closed-Loop Multiple-Motor Drive. IEEE Trans. Ind. Electron. 2011, 58, 1545–1554. [Google Scholar] [CrossRef]
- Drif, M.; Cardoso, A.J.M. Stator Fault Diagnostics in Squirrel Cage Three-Phase Induction Motor Drives Using the Instantaneous Active and Reactive Power Signature Analyses. IEEE Trans. Ind. Inform. 2014, 10, 1348–1360. [Google Scholar] [CrossRef]
- Berzoy, A.; Eldeeb, H.H.; Mohammed, O.A. On-Line Detection of Stator Faults in DTC-Driven IM Using SC Impedance Matrix Off-Diagonal Term. IEEE Trans. Ind. Appl. 2019, 55, 5906–5915. [Google Scholar] [CrossRef]
- Cruz, S.M.A.; Cardoso, A.J.M. Diagnosis of stator inter-turn short circuits in DTC induction motor drives. IEEE Trans. Ind. Appl. 2004, 40, 1349–1360. [Google Scholar] [CrossRef]
- Jia, Z.; Song, W.; Ma, C.; Zhang, B.; Sun, N. An MPC-Based Online Interturn Fault Diagnosis Method for Induction Motors With Fault Localization. IEEE Trans. Transp. Electrif. 2025, 11, 75–85. [Google Scholar] [CrossRef]
- Ma, C.; Song, W.; Jia, Z.; Zhang, B.; Huang, W. A Residual Stator Flux Angle-Based Interturn Short-Circuit Fault Diagnosis Method Alongside MPTC for Induction Motor Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 2296–2306. [Google Scholar] [CrossRef]
- Şahin, İ.; Keysan, O. Model Predictive Controller Utilized as an Observer for Inter-Turn Short Circuit Detection in Induction Motors. IEEE Trans. Energy Convers. 2021, 36, 1449–1458. [Google Scholar] [CrossRef]
- Laadjal, K.; Bento, F.; Serra, J.; Cardoso, A.J.M. An Integrated Strategy for the Real-Time Detection and Discrimination of Stator Inter-Turn Short-Circuits and Converter Faults in Asymmetrical Six-Phase Induction Motors. IEEE Trans. Ind. Appl. 2024, 60, 377–387. [Google Scholar]
- Urresty, J.-C.; Riba, J.-R.; Saavedra, H.; Romeral, L. Detection of inter-turns short circuits in permanent magnet synchronous motors operating under transient conditions by means of the zero sequence voltage. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August–1 September 2011; pp. 1–9. [Google Scholar]
- Rosero, J.; Cusido, J.; Garcia, A.; Romeral, L.; Ortega, J.A. Detection of Stator Short Circuits in PMSM by mean of joint Time-Frequency Analysis. In Proceedings of the 2007 IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives, Cracow, Poland, 6–8 September 2007; pp. 420–425. [Google Scholar]
- Rosero, J.A.; Romeral, L.; Ortega, J.A.; Rosero, E. Short-Circuit Detection by Means of Empirical Mode Decomposition and Wigner–Ville Distribution for PMSM Running Under Dynamic Condition. IEEE Trans. Ind. Electron. 2009, 56, 4534–4547. [Google Scholar] [CrossRef]
- Dlamini, M.; Barendse, P.S.; Khan, A.M. Detecting faults in inverter-fed induction motors during startup transient conditions. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 3131–3138. [Google Scholar]
- Bonet-Jara, J.; Pons-Llinares, J.; Morinigo-Sotelo, D.; Gyftakis, K.N. A Novel Approach for Early Detection of Inter-turn Faults in Induction Motors during Start-up. In Proceedings of the 2023 IEEE 14th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Chania, Greece, 28–31 August 2023; pp. 56–62. [Google Scholar]
- Riera-Guasp, M.; Antonino-Daviu, J.A.; Pineda-Sanchez, M.; Puche-Panadero, R.; Perez-Cruz, J. A General Approach for the Transient Detection of Slip-Dependent Fault Components Based on the Discrete Wavelet Transform. IEEE Trans. Ind. Electron. 2008, 55, 4167–4180. [Google Scholar] [CrossRef]
- Pons-Llinares, J.; Antonino-Daviu, J.; Roger-Folch, J.; Moríñigo-Sotelo, D.; Duque-Pérez, O. Mixed eccentricity diagnosis in Inverter-Fed Induction Motors via the Adaptive Slope Transform of transient stator currents. Mech. Syst. Signal Process. 2014, 48, 423–435. [Google Scholar] [CrossRef]
- Fernandez-Cavero, V.; Pons-Llinares, J.; Duque-Perez, O.; Morinigo-Sotelo, D. Detection and quantification of bar breakage harmonics evolutions in inverter-fed motors through the dragon transform. ISA Trans. 2021, 109, 352–367. [Google Scholar] [CrossRef] [PubMed]
- Antonino-Daviu, J.A.; Zamudio-Ramirez, I.; Osornio-Rios, R.A.; Dunai, L.; Quijano-Lopez, A. Application of Transient Analysis to Detect Rotor and Stator Asymmetries in Wound Rotor Induction Motors: A Field Case. In Proceedings of the 2021 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Modena, Italy, 8–9 April 2021; pp. 237–242. [Google Scholar]
- Antunes, H.R.P.; Fonseca, D.S.B.; Serra, J.; Cardoso, A.J.M. Stator Fault Diagnostics in Asymmetrical Six-phase Induction Motor Drives With Model Predictive Control under Transient Regimes. In Proceedings of the 2024 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Napoli, Italy, 19–21 June 2024; pp. 1204–1209. [Google Scholar]
- Cruz, S.M.A.; Cardoso, A.J.M. Multiple reference frames theory: A new method for the diagnosis of stator faults in three-phase induction motors. IEEE Trans. Energy Convers. 2005, 20, 611–619. [Google Scholar] [CrossRef]
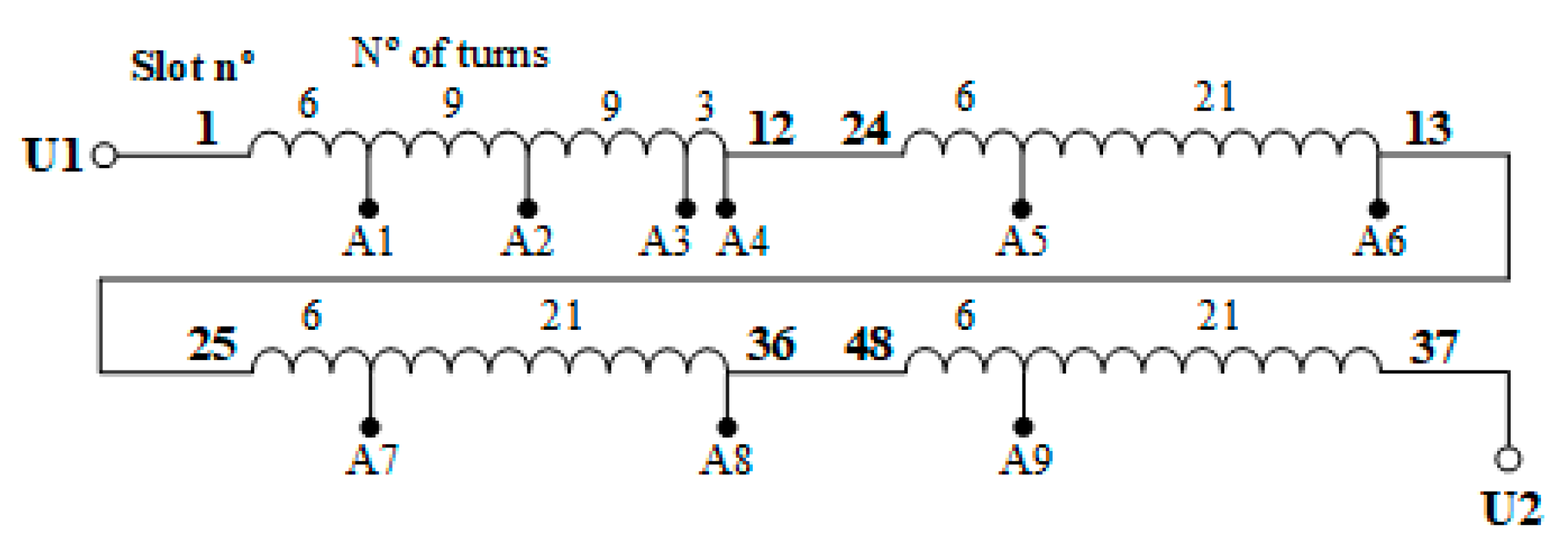
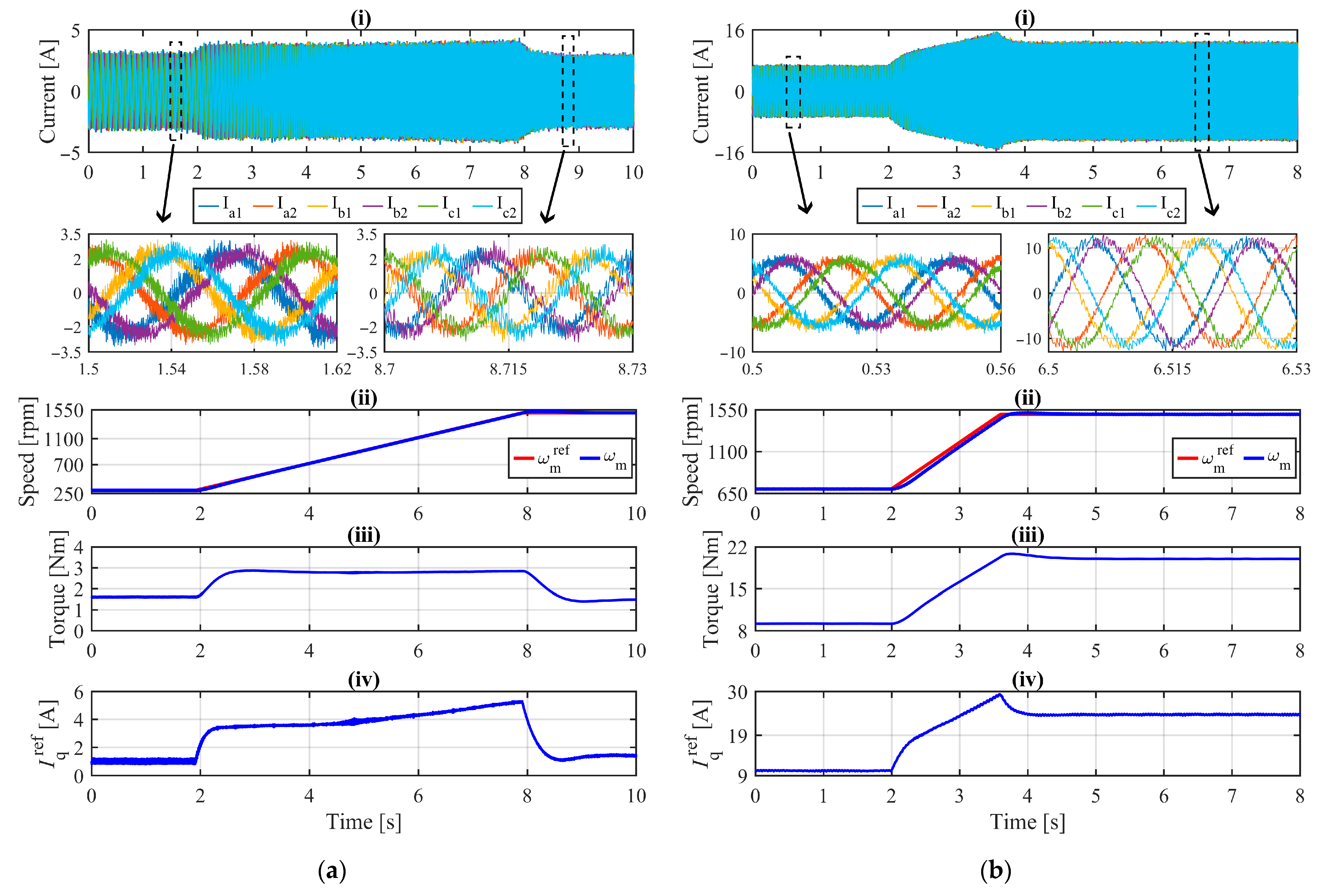
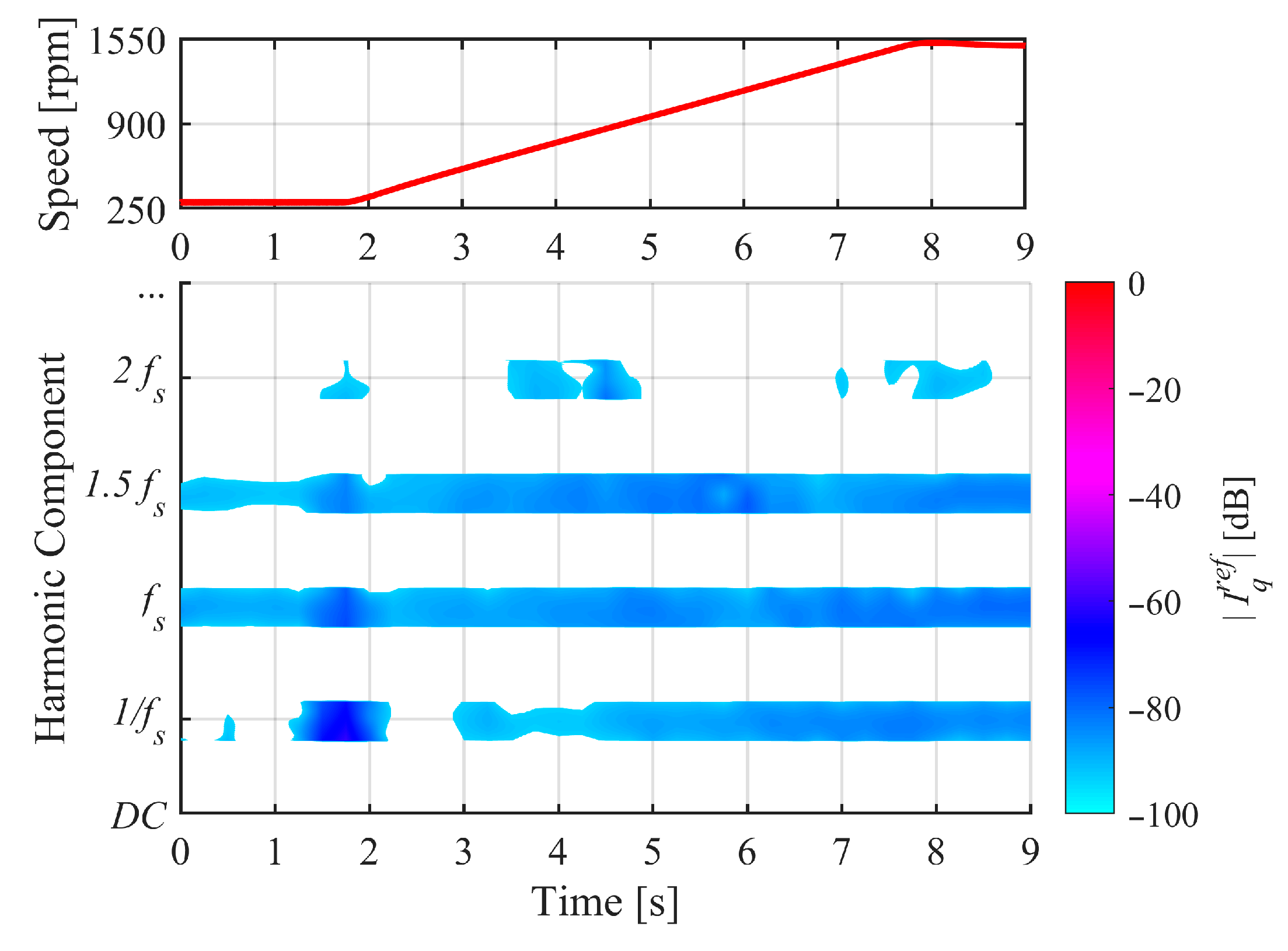
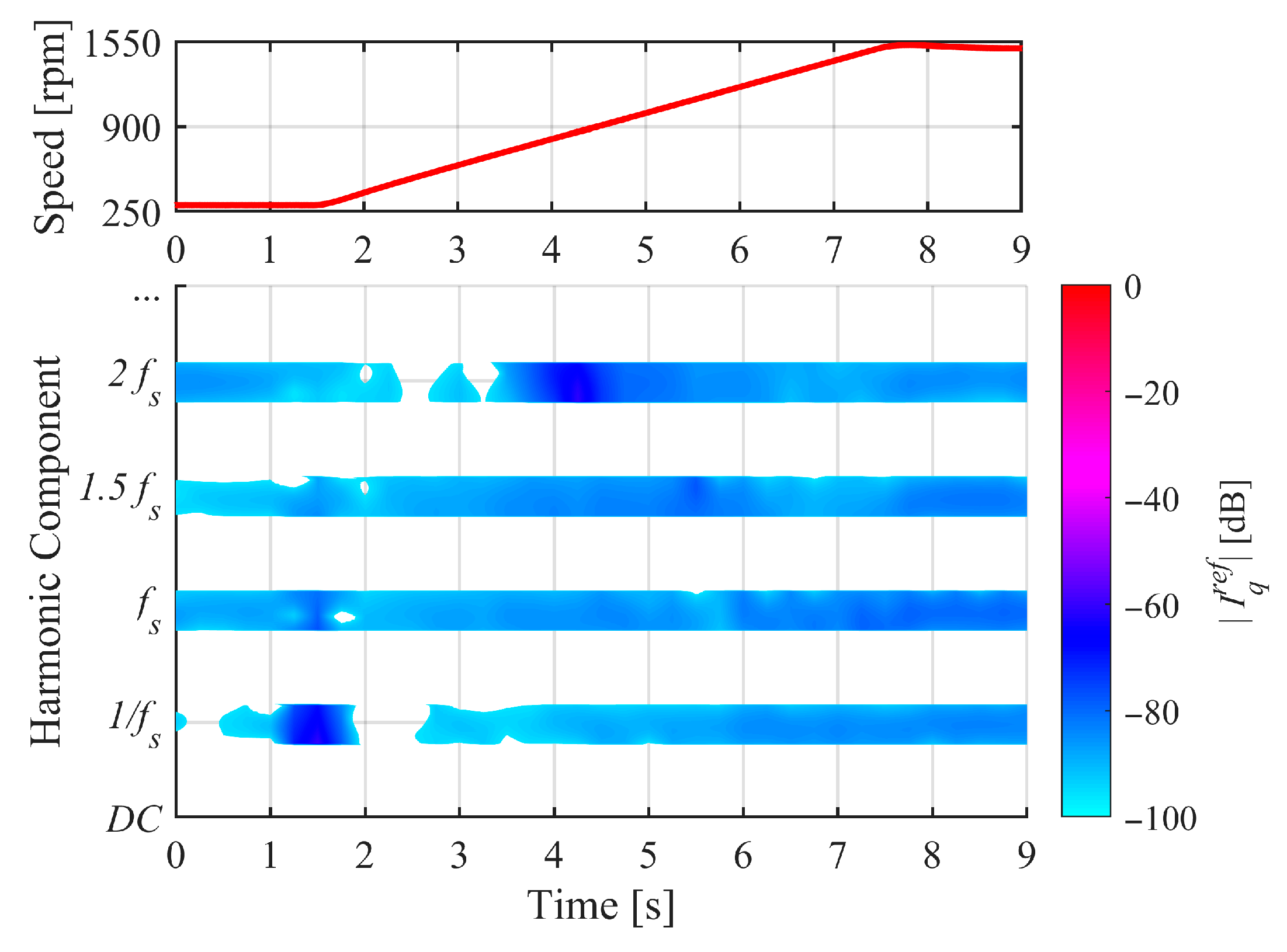




| Parameter | Value |
|---|---|
| Stator phase resistance (RS) | 1.03 Ω |
| Rotor phase resistance (Rr) | 0.89 Ω |
| Stator phase leakage inductance (Lσs) | 9.7 mH |
| Rotor leakage inductance (Lσr) | 9.7 mH |
| Magnetizing inductance (Lm) | 220.3 mH |
| Moment of inertia (J) | 0.0563 kg·m2 |
| Number of pole pairs (p) | 2 |
| Proportional gain () | 0.08 |
| Integral gain () | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antunes, H.R.P.; Fonseca, D.S.B.; Serra, J.; Marques Cardoso, A.J. Stator Fault Diagnostics in Asymmetrical Six-Phase Induction Motor Drives with Model Predictive Control Applicable During Transient Speeds. Machines 2025, 13, 740. https://doi.org/10.3390/machines13080740
Antunes HRP, Fonseca DSB, Serra J, Marques Cardoso AJ. Stator Fault Diagnostics in Asymmetrical Six-Phase Induction Motor Drives with Model Predictive Control Applicable During Transient Speeds. Machines. 2025; 13(8):740. https://doi.org/10.3390/machines13080740
Chicago/Turabian StyleAntunes, Hugo R. P., Davide. S. B. Fonseca, João Serra, and Antonio J. Marques Cardoso. 2025. "Stator Fault Diagnostics in Asymmetrical Six-Phase Induction Motor Drives with Model Predictive Control Applicable During Transient Speeds" Machines 13, no. 8: 740. https://doi.org/10.3390/machines13080740
APA StyleAntunes, H. R. P., Fonseca, D. S. B., Serra, J., & Marques Cardoso, A. J. (2025). Stator Fault Diagnostics in Asymmetrical Six-Phase Induction Motor Drives with Model Predictive Control Applicable During Transient Speeds. Machines, 13(8), 740. https://doi.org/10.3390/machines13080740









