Condition-Based Maintenance in Complex Degradation Systems: A Review of Modeling Evolution, Multi-Component Systems, and Maintenance Strategies
Abstract
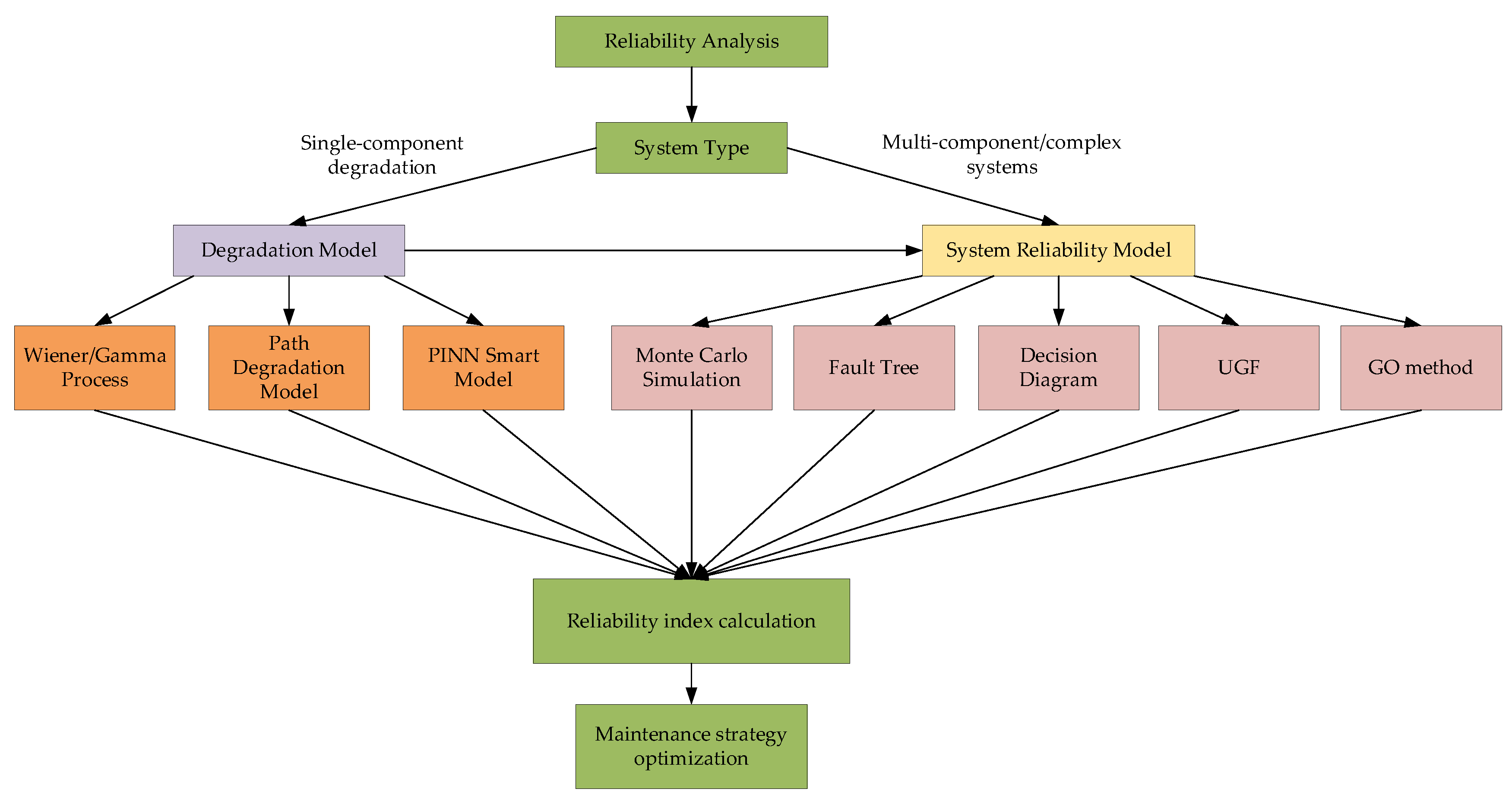
1. Introduction
2. Component Degradation Modeling
2.1. The Degradation Path Model
2.1.1. Random Slope-Intercept Model
2.1.2. Paris Law
2.1.3. Power-Law Model
2.1.4. Damage Theory Model
2.2. The Random Process Model
2.3. The Intelligence Model (PINN)
3. Reliability Modeling of Complex Degradation Systems
3.1. The System Modeling
3.1.1. The Monte Carlo Simulation Model
3.1.2. Multi-State Fault Tree Model
3.1.3. The Multi-Valued Decision Diagrams Model
3.1.4. The Universal Generating Function Model
3.1.5. The GO Method Model
3.2. System Reliability Analysis
3.2.1. Degradation Characteristics of Key System Components
3.2.2. Internal Interconnection Structures
3.2.3. Special-Structured Degradation Systems
4. Maintenance Strategies for Complex Degradation Systems
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, N.; Chen, C.; Jiang, B. Latest Progress on Maintenance Strategy of Complex System: From Condition-based Maintenance to Predictive Maintenance. Acta Autom. Autom. Sinica 2021, 47, 1–17. [Google Scholar]
- Wu, Y.; Jia, X.; Wen, L. A Review of Reliability Centered Maintenance (RCM): Development and Application. J. Ordnance Eng. Coll. 2016, 28, 13–21. [Google Scholar]
- Li, H.; Liu, R.; Wang, X.; Yao, R.; Lai, W. Review on Package Degradation Monitoring Methods of Press-Pack IGBT Modules. Trans. China Electrotech. Soc. 2021, 36, 2505–2521. [Google Scholar]
- Xiong, G.; Li, S.; Li, H.; Zhao, H.; Xiao, Y.; Zhang, Z.; Shen, M. Surface Mechanical Behaviors of Aging Rubber by Nanoindentation Technology. Polym. Mater. Sci. Eng. 2021, 37, 109–115. [Google Scholar]
- Zhang, Y.; Li, Y.; Sun, B. Fatigue Reliability Evaluation Method for Hold Down Spring of Reactor Vessel Internals Considering StressRelaxation and Irradiation. Nucl. Power Eng. 2021, 42, 141–147. [Google Scholar]
- Guo, H.; Lei, J.; Hu, L. Influencing Factors of Contact Fatigue Failure of Rolling Bearings and Their Research Status. Fail. Anal. Prev. 2019, 14, 206–211. [Google Scholar]
- Gopikrishnan, A. Reliability Inference Based on Degradation and Time to Failure Data: Some Models, Methods and Efficiency Comparisons; University of Michigan: Ann Arbor, MI, USA, 2004. [Google Scholar]
- Freitas, M.A.; De, T.; Maria, L.G. Using Degradation Data to Assess Reliability: A Case Study on Train Wheel Degradation. Qual. Reliab. Eng. Int. 2009, 25, 607–629. [Google Scholar] [CrossRef]
- Yuan, X.X.; Pandey, M.D. A Nonlinear Mixed-effects Model for Degradation Data Obtained from In-service Inspections. Reliab. Eng. Syst. Saf. 2009, 94, 509–519. [Google Scholar] [CrossRef]
- Gebraeel, N.Z.; Lawley, M.A.; Li, R. Residual-life Distributions from Component Degradation Signals: A Bayesian Approach. IIE Trans. 2005, 37, 543–557. [Google Scholar] [CrossRef]
- Chen, L.; Huang, T.; Zhou, H. Stochastic Modelling Of Metal Fatigue Crack Growthusing Proportional Paris Law and Inversegaussian Process. Eng. Mech. 2021, 38, 238–247. [Google Scholar]
- Ma, B.; Zhai, B.; Peng, Q. Useful life prediction of rolling element bearings based on a particle filtering model and the state space model at different degradation stages. J. Beijing Univ. Chem. Technol. (Nat. Sci.) 2017, 44, 81–86. [Google Scholar]
- Luo, B.; Shen, H.X.; Lin, L. Mechanical Property Statistical Analysis of Gd50Al30Co20 Amorphous Wires for Providing Reference to Design Requirements of Cooling System. J. Iron Steel Res. Int. 2018, 25, 261–267. [Google Scholar] [CrossRef]
- Chun, K.C.; Boulanger, M.; Tortorella, M. Analysis of Parameter-degradation Data Using Life-data Analysis Programs. In Proceedings of the Annual Reliability and Maintainability Symposium, Anaheim, CA, USA, 24–27 January 1994; pp. 288–291. [Google Scholar]
- Song, J.; Zhu, J.; Han, L. Prediction of Relaxation Modulus for Asphalt Rubber Based on Power Law Model. J. Wuhan Univ. Technol. (Transp. Sci. Eng.) 2021, 45, 779–786. [Google Scholar]
- Carey, M.B.; Koenig, R.H. Reliability Assessment Based on Accelerated Degradation: A Case Study. IEEE Trans. Reliab. 1991, 40, 499–506. [Google Scholar] [CrossRef]
- Tseng, S.T.; Peng, C.Y. Optimal Burn-in Policy by Using an Integrated Wiener Process. IIE Trans. 2004, 36, 1161–1170. [Google Scholar] [CrossRef]
- Hu, Y.F.; Ye, X.R.; Zheng, B.K. Degradation mechanisms-based reliability modeling for metallized film capacitors under temperature and voltage stresses. Microelectron. Reliab. 2022, 138, 114609. [Google Scholar] [CrossRef]
- Dong, Q.L.; Cui, L.R.; Si, S.B. Reliability and Availability Analysis of Stochastic Degradation Systems Based on Bivariate Wiener Processes. Appl. Math. Model. 2020, 79, 414–433. [Google Scholar] [CrossRef]
- Ye, Z.S.; Chen, N.; Shen, Y. A New Class of Wiener Process Models for Degradation Analysis. Reliab. Eng. Syst. Saf. 2015, 139, 58–67. [Google Scholar] [CrossRef]
- Si, X.S.; Wang, W.B.; Hu, C.H.; Zhou, D.H.; Pecht, M.G. Remaining Useful Life Estimation Based on a Nonlinear Diffusion Degradation Process. IEEE Trans. Reliab. 2012, 61, 50–67. [Google Scholar] [CrossRef]
- Limon, S.M.; Yadav, O.P. Remaining Useful Life Estimation Considering Prior Accelerated Degradation Data and Bayesian Inference for Multi-Stress Operating Conditions. Int. J. Math. Eng. Manag. Sci. 2021, 6, 103–117. [Google Scholar] [CrossRef]
- Van Noortwijk, J.M. A Survey of the Application of Gamma Processes in Maintenance. Reliab. Eng. Syst. Saf. 2009, 94, 2–21. [Google Scholar] [CrossRef]
- Sun, B.; Yan, M.C.; Feng, Q.; Li, Y.; Ren, Y.; Zhou, K. Gamma Degradation Process and Accelerated Model Combined Reliability Analysis Method for Rubber O-Rings. IEEE Access 2018, 6, 10581–10590. [Google Scholar] [CrossRef]
- Zhang, C.H.; Lu, X.; Tan, Y.Y.; Wang, Y.H. Reliability Demonstration Methodology for Products with Gamma Process by Optimal Accelerated Degradation Testing. Reliab. Eng. Syst. Saf. 2015, 142, 369–377. [Google Scholar] [CrossRef]
- Lu, J.; Luo, B. Reliability Analysis of Vertical Cavity Surface-Emitting Lasers Based on the Gamma Process. IEEE Access 2020, 8, 10686–10692. [Google Scholar] [CrossRef]
- Peng, W.W.; Li, Y.F.; Yang, Y.J.; Huang, H.Z.; Zuo, M.J. Inverse Gaussian Process Models for Degradation Analysis: A Bayesian Perspective. Reliab. Eng. Syst. Saf. 2014, 130, 175–189. [Google Scholar] [CrossRef]
- Huang, Y.; Lu, Z.; Dai, W.; Zhang, W.; Wang, B. Remaining Useful Life Prediction of Cutting Tools Using an Inverse Gaussian Process Model. Appl. Sci. 2021, 11, 5011. [Google Scholar] [CrossRef]
- Sun, B.; Li, Y.; Wang, Z.L.; Ren, Y.; Feng, Q.; Yang, D.Z. An Improved Inverse Gaussian Process with Random Effects and Measurement Errors for RUL Prediction of Hydraulic Piston Pump. Meas. J. Int. Meas. Confed. 2021, 173, 108604. [Google Scholar] [CrossRef]
- Cross, E.J.; Rogers, T.J.; Pitchforth, D.J.; Gibson, S.J.; Zhang, S.K.; Jones, M.R. A spectrum of physics-informed Gaussian processes for regression in engineering. Data-Centric Eng. 2024, 5, e8. [Google Scholar] [CrossRef]
- Grall, A.; Dieulle, L.; Bérenguer, C.; Roussignol, M. Continuous-time predictive-maintenance scheduling for a deteriorating system. IEEE Trans. Reliab. 2002, 51, 141–150. [Google Scholar] [CrossRef]
- Barlow, E.; Bedford, T.; Revie, M.; Tan, J.; Walls, L. A performance-centred approach to optimising maintenance of complex systems. Eur. J. Oper. Res. 2021, 292, 579–595. [Google Scholar] [CrossRef]
- Bérenguer, C.; Grall, A.; Castanier, B. Simulation and evaluation of condition-based maintenance policies for multi-component continuous-state deteriorating systems. In Proceedings of the ESREL’2000 and SRA-Europe Annual Conference Foresight and Precaution, Edinburgh, UK, 11–17 May 2000. [Google Scholar]
- Zhang, Z. Data Mining Approaches for Intelligent Condition-Based Maintenance—A Framework of Intelligent Fault Diagnosis and Prognosis System (IFDPS); Norwegian University of Science and Technology: Trondheim, Norway, 2014. [Google Scholar]
- Marseguerra, M.; Zio, E.; Podofillini, L. Condition-based maintenance optimization by means of genetic algorithms and Monte Carlo simulation. Reliab. Eng. Syst. Saf. 2002, 77, 151–165. [Google Scholar] [CrossRef]
- Kang, K.; Subramaniam, V. Integrated control policy of production and preventive maintenance for a deteriorating manufacturing system. Comput. Ind. Eng. 2018, 118, 266–277. [Google Scholar] [CrossRef]
- Keizer, M.C.A.O.; Flapper, S.D.P.; Teunter, R.H. Condition-based maintenance policies for systems with multiple dependent components: A review. Eur. J. Oper. Res. 2017, 261, 405–420. [Google Scholar] [CrossRef]
- Wang, F.; Zhai, Z.; Zhao, Z.; Di, Y.; Chen, X. Physics-informed neural network for lithium-ion battery degradation stable modeling and prognosis. Nat. Commun. 2024, 15, 4332. [Google Scholar] [CrossRef] [PubMed]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Shu, W.; Meng, Y.Q.; Deng, F.; Jiang, J.G.; Wu, J.C. Inversion of seepage parameters for one-dimensional unconfined aquifer flow equations based on PINNs algorithm. J. Nanjing Univ. (Nat. Sci.) 2024, 60, 317–327. [Google Scholar]
- Ni, Q.; Ji, J.C.; Halkon, B.; Nandi, A.K. Physics-Informed Residual Network (PIResNet) for rolling element bearing fault diagnostics. Mech. Syst. Signal Process. 2023, 200, 110544. [Google Scholar] [CrossRef]
- Meng, Z.; Qian, Q.C.; Xu, M.Q.; Yu, B.; Yıldız, A.R.; Mirjalili, S. PINN-FORM: A new physics-informed neural network for reliability analysis with partial differential equation. Comput. Methods Appl. Mech. Eng. 2023, 414, 116172. [Google Scholar] [CrossRef]
- Zhu, Q.; Shi, Y.; Feng, Y.; Wang, Y. Physics-Informed Neural Networks for RUL Prediction. In Proceedings of the 2024 China Automation Congress (CAC), Qingdao, China, 1–3 November 2024; pp. 6361–6366. [Google Scholar]
- Park, Y.; Kang, M. How does PDE order affect the convergence of PINNs. Adv. Neural Inf. Process. Syst. 2024, 37, 73–131. [Google Scholar]
- Su, P. Reliability Analysis of Several Classes of Multi-State Complex Systems; Southeastern University: Nanjing, China, 2020. [Google Scholar]
- Billinton, R.; Li, W. Reliability Assessment of Electric Power Systems Using Monte Carlo Methods; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Geng, L.; Zhao, Y.; Chen, G. Simplified Sequential Simulation of Bulk Power System Reliability Via Chronological Probability Model of Load Supplying Capability. IEEE Trans. Power Syst. 2018, 33, 2349–2358. [Google Scholar] [CrossRef]
- Li, L.F.; Sun, Y.; Huang, Y.; Hu, B.; Hou, T.; Huang, W.; Guo, L.; Hu, Y.Z.; Ji, Y.K.; Xie, K.G. Reliability Evaluation of Offshore Wind Farm and VSC-HVDC Integrated System Considering the Influence of Extreme Weather. South. Power Syst. Technol. 2020, 14, 32–42. [Google Scholar]
- Chao, H.W.; Hu, B.; Xie, K.G.; Tai, H.M.; Yan, J.H.; Li, Y.L. A Sequential MCMC Model for Reliability Evaluation of Offshore Wind Farms Considering Severe Weather Conditions. IEEE Access 2019, 7, 132552–132562. [Google Scholar] [CrossRef]
- Goharian, E.; Zahmatkesh, Z.; Sandoval-Solis, S. Uncertainty Propagation of Hydrologic Modeling in Water Supply System Performance: Application of Markov Chain Monte Carlo Method. J. Hydrol. Eng. 2018, 23, 4018013. [Google Scholar] [CrossRef]
- Zhao, Y.; Tang, Y.; Li, W.; Yu, J. Composite power system reliability evaluation based on enhanced sequential cross-entropy Monte Carlo simulation. IEEE Trans. Power Syst. 2019, 34, 3891–3901. [Google Scholar] [CrossRef]
- Zhu, C.; Zhang, T. A review on the realization methods of dynamic fault tree. Qual. Reliab. Eng. Int. 2022, 38, 3233–3251. [Google Scholar] [CrossRef]
- Rubin, M.; Du, D. A Review of Dynamic Fault Tree Analysis and Capacity Degradation for Complex Redundant Systems. Qual. Reliab. Eng. Int. 2025, 41, 1161–1181. [Google Scholar] [CrossRef]
- Aslansefat, K.; Kabir, S.; Gheraibia, Y.; Papadopoulos, Y. Dynamic fault tree analysis: State-of-the-art in modeling, analysis, and tools. Reliab. Manag. Eng. 2020, 73–112. [Google Scholar]
- Dugan, J.B.; Bavuso, S.J.; Boyd, M.A. Dynamic fault-tree for fault-tolerant computer systems. IEEE Trans. Reliab. 1992, 41, 363–376. [Google Scholar] [CrossRef]
- Dugan, J.B.; Sullivan, K.J.; Coppit, D. Developing a low cost high-quality software tool for dynamic fault-tree analysis. IEEE Trans. Reliab. 2000, 49, 49–59. [Google Scholar] [CrossRef]
- Qi, J.P.; Jia, C.X.; Yu, Q.Y. Reliability analysis of EMU air-conditioning system based on multi-dimensional polymorphic T-S fault tree. J. Mech. Des. 2025, 42, 55–61. [Google Scholar]
- Li, Y.F.; Huang, H.Z.; Liu, Y.; Xiao, N.C.; Li, H.Q. A new fault tree analysis method: Fuzzy dynamic fault tree analysis. Maint. Reliab. 2012, 14, 208–214. [Google Scholar]
- Luo, X.; Li, Y.; Bai, X.; Tang, R.; Jin, H. A novel approach based on fault tree analysis and Bayesian network for multi-state reliability analysis of complex equipment systems. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2024, 238, 812–838. [Google Scholar] [CrossRef]
- Liu, Y.; Luo, D.L.; Shi, C.; Wu, H.X. Performance reliability of multi-state navigation system based on T-S fuzzy fault tree. J. Beijing Univ. Aeronaut. Astronaut. 2021, 47, 240–246. [Google Scholar]
- Gu, L.; Wang, G.; Zhou, Y. Reliability analysis and optimization of multi-state tree-structured systems with performance sharing mechanism. Reliab. Eng. Syst. Saf. 2025, 260, 110990. [Google Scholar] [CrossRef]
- Forgac, A.; Lukyanchuk, I. New algorithm for Multi-valued Decision Diagram construction. In Proceedings of the 2019 International Conference on Information and Digital Technologies (IDT), Zilina, Slovakia, 25–27 June 2019; pp. 142–148. [Google Scholar]
- Rushdi, A.M.A.; Al-Amoudi, M.A. Reliability analysis of a multi-state system using multi-valued logic. IOSR J. Electron. Commun. Eng. 2019, 14, 1–10. [Google Scholar]
- Miller, D.M. Multiple-valued logic design tools. In Proceedings of the Twenty-Third International Symposium on Multiple-Valued Logic, Sacramento, CA, USA, 24–27 May 1993; pp. 2–11. [Google Scholar]
- Shrestha, A.; Xing, L.D.; Dai, Y.S. Reliability analysis of multi-state phased-mission systems. In Proceedings of the 2009 Annual Reliability and Maintainability Symposium, Fort Worth, TX, USA, 26–29 January 2009; pp. 151–156. [Google Scholar]
- Xing, L.D.; Dai, Y.S. A New Decision-Diagram-Based Method for Efficient Analysis on Multistate Systems. IEEE Trans. Dependable Secur. Comput. 2009, 6, 161–174. [Google Scholar] [CrossRef]
- Amari, S.V.; Xing, L.; Shrestha, A.; Akers, J.; Trivedi, K.S. Performability Analysis of Multistate Computing Systems Using Multivalued Decision Diagrams. IEEE Trans. Comput. 2010, 59, 1419–1433. [Google Scholar] [CrossRef]
- Wang, N.; Hu, D.W. Important measure for multi-state fault tree based on multi-state multi-value decision diagram. Comput.-Integr. Manuf. Syst. 2015, 21, 1301–1308. [Google Scholar]
- Shrestha, A.; Xing, L.; Dai, Y. Decision Diagram Based Methods and Complexity Analysis for Multi-State Systems. IEEE Trans. Reliab. 2010, 59, 145–161. [Google Scholar] [CrossRef]
- Ushakov, I.A. Universal generating function. Sov. J. Comput. Syst. Sci. 1986, 24, 85–95. [Google Scholar]
- Levitin, G. The Universal Generating Function in Reliability Analysis and Optimization; Springer: London, UK, 2005. [Google Scholar]
- Lisnianski, A.; Levitin, G. Multi-State System Reliability: Assessment, Optimization, and Application; World Scientific: Singapore, 2003. [Google Scholar]
- Levitin, G. A universal generating function approach for the analysis of multi-state systems with dependent elements. Reliab. Eng. Syst. Saf. 2004, 84, 285–292. [Google Scholar] [CrossRef]
- Lisnianski, A.; Ding, Y. Redundancy analysis for repairable multi-state system by using combined stochastic processes methods and universal generating function technique. Reliab. Eng. Syst. Saf. 2009, 94, 1788–1795. [Google Scholar] [CrossRef]
- Wang, G.; Duan, F.; Zhou, Y. Reliability evaluation of multi-state series systems with performance sharing. Reliab. Eng. Syst. Saf. 2018, 173, 58–63. [Google Scholar] [CrossRef]
- Sun, R.J.; Gayan, A.; Mu, Q.; Liang, J. Reliability and Economic Evaluation of Offshore Wind Power Collection System Based on Universal Generating Function. Autom. Electr. Power Syst. 2022, 46, 159–173. [Google Scholar]
- Jiang, X.H.; Duan, F.H.; Tian, H.; Wei, X.D. Optimization of reliability centered predictive maintenance scheme for inertial navigation system. Reliab. Eng. Syst. Saf. 2015, 140, 208–217. [Google Scholar] [CrossRef]
- Jiang, X.H.; Duan, F.H.; Hu, A.L. A New GO Operator and Its Application in Multi-state System. Acta Armamentarii 2019, 40, 857–864. [Google Scholar]
- Ren, Y.; Zeng, C.; Fan, D.; Liu, L.L.; Feng, Q. Multi-State Reliability Assessment Method Based on the MDD-GO Model. IEEE Access 2018, 6, 5151–5161. [Google Scholar] [CrossRef]
- Yi, X.J.; Dhillon, B.S.; Shi, J.; Mu, H.N.; Dong, H.P. Reliability Analysis Method on Repairable System with Standby Structure Based on Goal Oriented Methodology. Qual. Reliab. Eng. Int. 2016, 32, 2505–2517. [Google Scholar] [CrossRef]
- Yi, X.J.; Dhillon, B.S.; Dong, H.P.; Shi, J.; Jiang, J.P. Quantitative reliability analysis of repairable systems with closed-loop feedback based on GO methodology. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 1845–1858. [Google Scholar] [CrossRef]
- Li, K.; Ren, Y.; Fan, D.; Liu, L.L.; Wang, Z.; Ma, Z. Enhance GO methodology for reliability analysis of the closed-loop system using Cyclic Bayesian Networks. Mech. Syst. Signal Process. 2018, 113, 237–252. [Google Scholar] [CrossRef]
- Yi, X.J.; Shi, J.; Dhillon, B.S.; Hou, P.; Lai, Y.H. A new reliability analysis method for repairable systems with multifunction modes based on goal-oriented methodology. Qual. Reliab. Eng. Int. 2017, 33, 2215–2237. [Google Scholar] [CrossRef]
- Qi, J.P. Research on Reliability Modeling Method of High Speed Railway EMUs—A Case Study of EMUs on Lanzhou-Xinjiang Passenger Dedicated Line. Ph.D. Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2018. [Google Scholar]
- Zhang, H.Q. Study on Polymorphic Time-varying Reliability of Radar Mechanical and Electrical System. Ph.D. Thesis, Xidian University, Xi’an, China, 2017. [Google Scholar]
- Fox, E.P.; Condra, L.W. Reliability Improvement with Design of Experiments. Technometrics 1994, 36, 316. [Google Scholar] [CrossRef]
- Meeker, W.Q.; Hamada, M. Statistical tools for the rapid development and evaluation of high-reliability products. IEEE Trans. Reliab. 1995, 44, 187–198. [Google Scholar] [CrossRef]
- Li, J.; Coit, D.W.; Elsayed, E.A. Reliability modeling of a series system with correlated or dependent component degradation processes. In Proceedings of the International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, Xi’an, China, 17–19 June 2011; pp. 388–393. [Google Scholar]
- Li, W.J.; Pham, H. Reliability modeling of multi-state degraded systems with multi-competing failures and random shocks. IEEE Trans. Reliab. 2005, 54, 297–303. [Google Scholar] [CrossRef]
- Gong, M.; Xie, M.; Yang, Y. Reliability assessment of system under a generalized run shock model. J. Appl. Probab. 2018, 55, 1249–1260. [Google Scholar] [CrossRef]
- Peng, B.H.; Zhou, J.L.; Liu, X.M. System Performance Reliability Assessment Based on Degradation Data from Components. Fire Control Command Control 2011, 36, 148–151. [Google Scholar]
- Majid, M.A.; Rashid, M.N. Multi-state availability and reliability assessment of electric chillers of a district cooling plant. In Proceedings of the 2011 IEEE Colloquium on Humanities, Science and Engineering, Penang, Malaysia, 5–6 December 2011; pp. 178–183. [Google Scholar]
- Reshid, M.N.; Majid, M.A. Availability and reliability modelling for chilled water generation of a cogenerated power plant using multi-state system theory. In Proceedings of the 3rd National Postgraduate Conference-Energy and Sustainability: Exploring the Innovative Minds, Perak, Malaysia, 19–20 September 2011; pp. 1–8. [Google Scholar]
- Li, X.Y.; Jiang, T.M.; Ma, J.; Lu, R.C. State tree analysis of FOG based on drift brownian motion. In Proceedings of the International Conference on Reliability, Maintainability and Safety, Chengdu, China, 20–24 July 2009; pp. 1322–1326. [Google Scholar]
- Lisnianski, A.; Levitin, G.; Ben-Haim, H.; Elmakis, D. Power system structure optimization subject to reliability constraints. Electr. Power Syst. Res. 1996, 39, 145–152. [Google Scholar] [CrossRef]
- Levitin, G.; Lisnianski, A.; Ben-Haim, H.; Elmakis, D. Redundancy optimization for series-parallel multi-state systems. IEEE Trans. Reliab. 1998, 47, 165–172. [Google Scholar] [CrossRef]
- Zhao, Z.C.; Song, B.W.; Wang, P. Reliability of load-sharing r-out-of-n:G system with components following Gamma degradation process. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2015, 43, 12–16. [Google Scholar]
- Jia, H.; Ding, Y.; Peng, R.; Song, Y.H. Reliability Evaluation for Demand-Based Warm Standby Systems Considering Degradation Process. IEEE Trans. Reliab. 2017, 66, 795–805. [Google Scholar] [CrossRef]
- Levitin, G.; Finkelstein, M.; Dai, Y. Redundancy optimization for series-parallel phased mission systems exposed to random shocks. Reliab. Eng. Syst. Saf. 2017, 167, 554–560. [Google Scholar] [CrossRef]
- Wang, C.; Xing, L.; Peng, R.; Pan, Z.S. Competing failure analysis in phased-mission systems with multiple functional dependence groups. Reliab. Eng. Syst. Saf. 2017, 164, 24–33. [Google Scholar] [CrossRef]
- Faghih-Roohi, S.F.; Min, X.; Kien, M.G.; Richard, C.M.Y. Dynamic availability assessment and optimal component design of multi-state weighted k-out-of-n systems. Reliab. Eng. Syst. Saf. 2014, 123, 57–62. [Google Scholar] [CrossRef]
- Liu, B.; Gong, C.; Li, M.M.; Wang, R. RMSST Design Based on Virtual Reality. Acta Armamentarii 2022, 43, 208–213. [Google Scholar]
- Bautista, L.; Castro, I.T.; Di Nardo, M.; Murino, T. Condition-based and age-based maintenance in a multi-component system with heterogeneous components incorporating imperfect preventive maintenance actions. Comput. Ind. Eng. 2025, 206, 111188. [Google Scholar] [CrossRef]
- Di Nardo, M.; Madonna, M.; Addonizio, P.; Gallab, M. A mapping analysis of maintenance in Industry 4.0. J. Appl. Res. Technol. 2021, 19, 653–675. [Google Scholar] [CrossRef]
- Zhang, C.; Gao, W.; Guo, S.; Li, Y.L.; Yang, T. Opportunistic maintenance for wind turbines considering imperfect, reliability-based maintenance. Renew. Energy 2017, 103, 606–612. [Google Scholar] [CrossRef]
- Heo, J.H.; Kim, M.K.; Lyu, J.K. Implementation of reliability-centered maintenance for transmission components using particle swarm optimization. Int. J. Electr. Power Energy Syst. 2014, 55, 238–245. [Google Scholar] [CrossRef]
- Yssaad, B.; Khiat, M.; Chaker, A. Reliability centered maintenance optimization for power distribution systems. Int. J. Electr. Power Energy Syst. 2014, 55, 108–115. [Google Scholar] [CrossRef]
- Alaswad, S.; Xiang, Y. A review on condition-based maintenance optimization models for stochastically deteriorating system. Reliab. Eng. Syst. Saf. 2017, 157, 54–63. [Google Scholar] [CrossRef]
- Zhu, X.; Wen, L.; Li, J.; Song, M.C.; Hu, Q.W. Condition-based Maintenance Optimization for Gamma Deteriorating Systems under Performance-based Contracting. Chin. J. Mech. Eng. 2023, 36, 18. [Google Scholar] [CrossRef]
- Han, D. Exploring the optimal condition-based maintenance policy under the gamma degradation process. Procedia Manuf. 2021, 55, 132–138. [Google Scholar] [CrossRef]
- Do, P.; Voisin, A.; Levrat, E.; Iung, B. A proactive condition-based maintenance strategy with both perfect and imperfect maintenance actions. Reliab. Eng. Syst. Saf. 2015, 133, 22–32. [Google Scholar] [CrossRef]
- Grall, A.; Omshi, E.M.; Shemehsavar, S. Bayesian update and aperiodic maintenance policy for deteriorating systems with unknown parameters. In Proceedings of the 28th European Safety and Reliability Conference, ESREL 2018, Trondheim, Norway, 17–21 June 2018. [Google Scholar]
- Dieulle, L.; Bérenguer, C.; Grall, A.; Roussignol, M. Sequential condition-based maintenance scheduling for a deteriorating system. Eur. J. Oper. Res. 2003, 150, 451–461. [Google Scholar] [CrossRef]
- Nguyen, K.A.; Do, P.; Grall, A. Condition-based maintenance for multi-component systems using importance measure and predictive information. Int. J. Syst. Sci. Oper. Logist. 2014, 1, 228–245. [Google Scholar] [CrossRef]
- Nguyen, K.A.; Do, P.; Grall, A. Multi-level predictive maintenance for multi-component systems. Reliab. Eng. Syst. Saf. 2015, 144, 83–94. [Google Scholar] [CrossRef]
- Guo, C.; Wang, W.; Guo, B.; Si, X.S. A maintenance optimization model for mission-oriented systems based on Wiener degradation. Reliab. Eng. Syst. Saf. 2013, 111, 183–194. [Google Scholar] [CrossRef]
- Zhou, Y.F.; Zhang, Z.; Lin, T.R.; Ma, L. Maintenance optimisation of a multi-state series-parallel system considering economic dependence and state-dependent inspection intervals. Reliab. Eng. Syst. Saf. 2013, 111, 248–259. [Google Scholar] [CrossRef]
- Zhao, H.S.; Xu, F.H.; Liang, B.T.; Zhang, J.P. A condition-based opportunistic maintenance strategy for multi-component system. Struct. Health Monit. 2019, 18, 270–283. [Google Scholar] [CrossRef]
- Huynh, T.K.; Barrosa, A.; Bérenguerb, C. A reliability-based opportunistic predictive maintenance model for k-out-of-n deteriorating systems. Chem. Eng. Trans. 2013, 33, 493–498. [Google Scholar]


| Model | Mathematical Formulation | Key Parameters | Typical Applications |
|---|---|---|---|
| Random Slope-Intercept | β0: Random initial degradation β1: Degradation rate ε(t): White noise | Bearings, linear degradation systems | |
| Paris’ Law | C, m: Material constants ΔK: Stress intensity factor range | Metal fatigue crack propagation | |
| Power-Law | α: Scale parameter β: Shape parameter ε(t): Error term | Electronics aging, nonlinear degradation | |
| Damage Theory | D(t): Cumulative damage ni/Ni: Cycle ratio | Mechanical systems under multi-stress |
| Model | Mathematical Formulation | Key Parameters | Increment Properties | Typical Applications |
|---|---|---|---|---|
| Wiener Process | μ: Drift coefficient σ: Diffusion coefficient B(t): Standard Brownian motion | Independent Gaussian increments (can be positive/negative) | LED light decay, Capacitor wear, | |
| Gamma Process | αt: Shape parameter β: Scale parameter | Non-negative, Strictly increasing increments | Rubber aging, bearing wear | |
| Inverse Gaussian (IG) Process | μt: Mean degradation at time t λt2: Shape parameter | Non-negative, flexible-distributed increments | tool wear |
| Method Name | Features | Advantages and Disadvantages | Typical Applications |
|---|---|---|---|
| Monte Carlo Simulation | Avoids complex modeling; efficient for large-scale/intricate systems. | Advantage: No need for complex modeling. Disadvantage: Time-consuming simulation with approximate results. | Large-capacity power systems, offshore wind systems, complex pipeline networks. |
| Fault Tree Analysis | Handles multi-failure modes and dynamic traits. | Advantage: Addresses multi-failure systems. Disadvantage: Poor for repairable systems with fault dependence. | Fault-tolerant computer systems, CNC hydraulic systems, complex equipment safety assessment. |
| Multi-Valued Decision Diagrams | Reduces computational complexity. | Advantage: Extends binary diagram applicability. Disadvantage: Higher complexity in traditional models. | Multi-stage multi-state systems, simplified evaluation algorithms. |
| Universal Generating Function | Directly represents system-component state relations. | Advantage: High computational efficiency. Disadvantage: Requires integration for complex structures. | Redundant systems, shared-performance series systems, offshore AC/DC collector systems. |
| GO Method | Simple, intuitive modeling process. | Advantage: Intuitive modeling. Disadvantage: Increased complexity due to common signals. | Inertial navigation systems, redundant backup systems, feedback engineering systems, repairable systems. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, H.; Yu, J.; Duan, F. Condition-Based Maintenance in Complex Degradation Systems: A Review of Modeling Evolution, Multi-Component Systems, and Maintenance Strategies. Machines 2025, 13, 714. https://doi.org/10.3390/machines13080714
Cao H, Yu J, Duan F. Condition-Based Maintenance in Complex Degradation Systems: A Review of Modeling Evolution, Multi-Component Systems, and Maintenance Strategies. Machines. 2025; 13(8):714. https://doi.org/10.3390/machines13080714
Chicago/Turabian StyleCao, Hui, Jie Yu, and Fuhai Duan. 2025. "Condition-Based Maintenance in Complex Degradation Systems: A Review of Modeling Evolution, Multi-Component Systems, and Maintenance Strategies" Machines 13, no. 8: 714. https://doi.org/10.3390/machines13080714
APA StyleCao, H., Yu, J., & Duan, F. (2025). Condition-Based Maintenance in Complex Degradation Systems: A Review of Modeling Evolution, Multi-Component Systems, and Maintenance Strategies. Machines, 13(8), 714. https://doi.org/10.3390/machines13080714






