An Integrated Path Planning and Tracking Framework Based on Adaptive Heuristic JPS and B-Spline Optimization

Abstract

In this paper, we propose a navigation synthesis method for indoor mobile robots based on the Improved Jumping Point Search (JPS) framework. Although traditional JPS has high search efficiency, it often leads to excessive node expansion and sharp turns in complex environments, which limits its practical application. In order to overcome these problems, we introduced three key strategies. First, we used a density-sensing heuristic function calculated by integrating the image to improve the adaptability of complex areas. Secondly, we extracted structural key points from the path and used third-order B-splines to fit them to enhance smoothness and continuity. Third, a curvature-driven Regulated Pure Pursuit (RPP) controller adjusts the look-ahead distance and speed based on path curvature, improving tracking stability. Simulation results show that the proposed method reduces planning time and node redundancy while generating smoother and more executable paths than the conventional JPS framework.

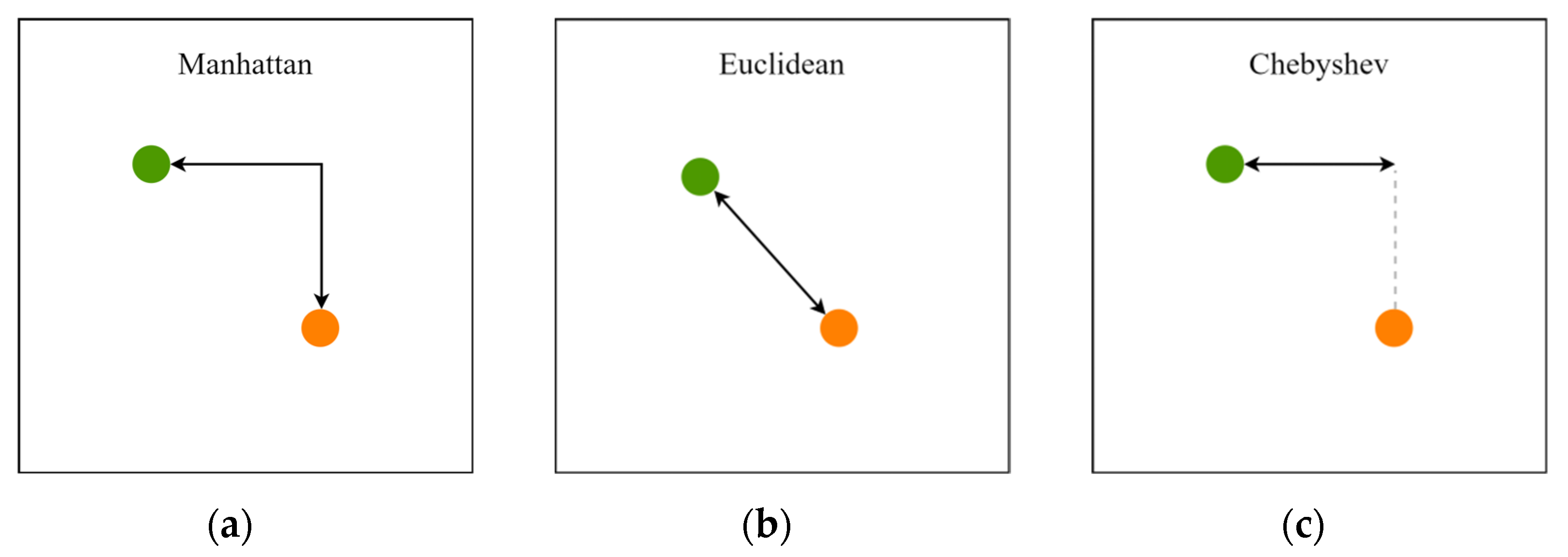
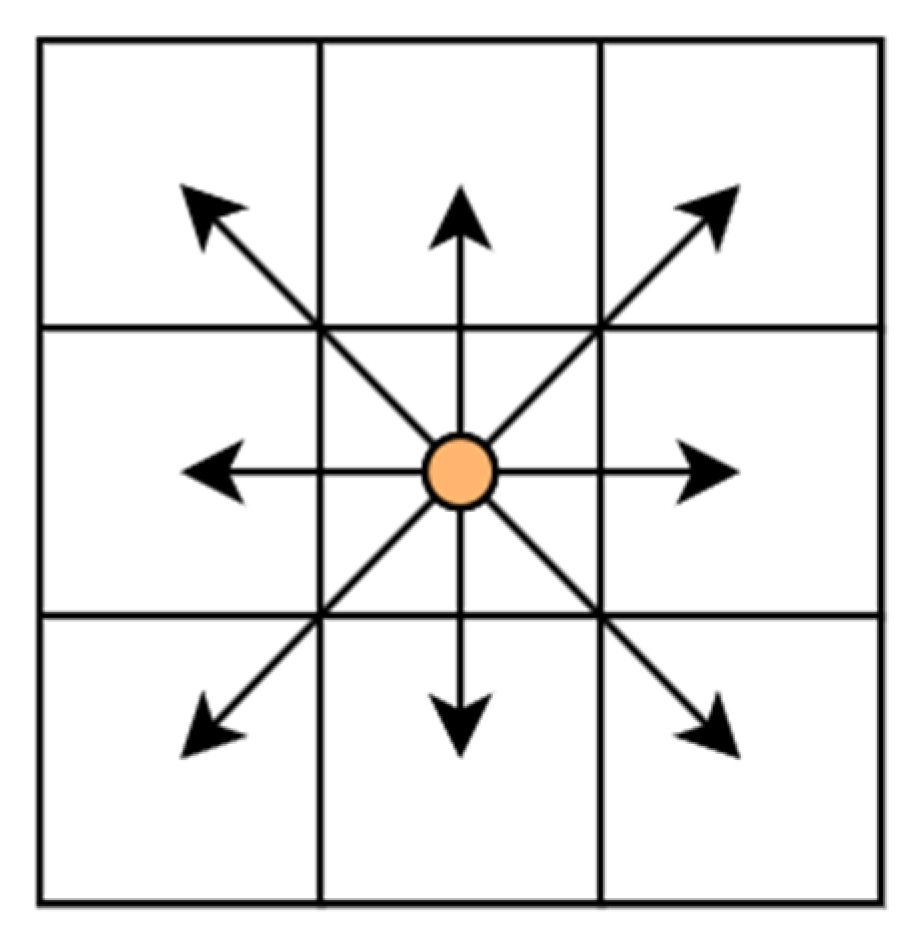
1. Introduction

In the context of a regular grid environment, path planning and trajectory tracking are the basic technologies that enable mobile robots to achieve autonomous navigation. As an outstanding example of a heuristic search method, the A* algorithm [1] has optimality and completeness, making it a popular choice in various application scenarios. When faced with large-scale maps, the A* algorithm often expands too many nodes during the search process, resulting in unsatisfactory computing efficiency and facing challenges in meeting the actual needs of efficient path generation [2].

To enhance search efficiency, the JPS algorithm [3], an optimized variant of the A* algorithm, has been extensively utilized in global path planning for static grid maps. This algorithm effectively minimizes redundant nodes and markedly improves search performance through the application of jump expansion and symmetric pruning techniques. Despite this, the initial trajectory generated by the JPS algorithm has a large number of discrete jump points, which leads to insufficient continuity and poor smoothness of the path. This limitation limits its application in practical robot control systems [4]. This problem is particularly significant in environments with a high density of obstacles, where problems such as the frequent expansion of jump points, unstable jump directions, and sudden changes in paths become more evident. These factors have a negative impact on both path quality and execution stability.

In recent years, researchers have put forth a range of enhancement strategies designed to address the shortcomings of the JPS algorithm in environments characterized by a high density of obstacles. Traish et al. [5] introduced a swift boundary jump point identification mechanism to reduce the redundancy associated with extensions. Luo et al. [6] introduced an angle propagation strategy to solve the problem of sudden change in path direction. Yang et al. [7] proposed a bidirectional extension and endpoint correction mechanism to improve search efficiency. This method has insufficient environment perception in local complex environments, resulting in poor path stability. Wang et al. [8] further advanced the field by implementing redundant jump point elimination and local arc reconstruction strategies to improve path feasibility, although the path continuity of these methods is still insufficient. In addition to these efforts, recent studies have explored hybrid strategies that integrate JPS with global–local fusion frameworks. For instance, Liu et al. [9] incorporated Theta* into JPS to reduce detours caused by excessive turning, while Wang et al. [8] coupled JPS with the Dynamic Window Approach (DWA) to achieve real-time obstacle avoidance albeit with limited curvature smoothness. Meanwhile, Zhao et al. [10] adapted JPS to honeycomb raster environments, improving direction resolution but facing challenges in downstream smoothing. Guo et al. [11] and An et al. [4] have successively improved bidirectional JPS structures to accelerate pathfinding in dense environments, yet they struggled to maintain feasible curvature in narrow passages. In addition, Bai et al. [12] introduced artificial potential fields into weighted JPS to encourage obstacle-aware navigation, although the method may cause excessive detouring in sparse areas. Zhang et al. [13] combined JPS with polynomial fitting, but path overshooting near sharp corners remained problematic. Although existing enhancement methods have made progress in search efficiency and jumping point behavior management, they still have shortcomings in establishing a mechanism that can effectively combine jumping point generation strategies with obstacle distribution characteristics. This limitation hinders the potential for improvement in the continuity and controllability of the path from a given starting point.

To overcome these challenges, post-processing methods based on spline curves have been increasingly adopted to improve the geometric quality of paths generated by discrete search algorithms. Due to their advantageous characteristics such as geometric continuity, local adjustability, and micro-machinability, spline curves—particularly B-splines—have become a common solution in path refinement tasks [14,15]. Xu et al. [16] introduced a gradient-driven B-spline trajectory optimization technology specifically designed for drone dynamic obstacle avoidance scenarios. This method generates a distance gradient field based on visual input, which helps achieve real-time path smoothing and demonstrates effective continuity and obstacle avoidance capabilities in a dynamic environment. Zhang et al. [17] developed a multi-objective B-spline smoothing method that combines curvature, comfort, and safety distance constraints for intelligent vehicle polygonal path fitting, which improves path smoothness and tracking stability in actual vehicle testing. Choi et al. [18] combined B-splines with incremental path flattening (IPF) to achieve efficient and safe continuous path generation in autonomous driving trajectory optimization, adopting a structure-aware collision correction mechanism and a curvature penalty strategy. Although these methods have made significant progress in path continuity and control effectiveness, they rely mainly on the equidistant or heuristic selection of control points, which limits their ability to systematically incorporate skip path structure semantics. Moreover, the optimization process of some of these methods may conflict with real-time requirements in barrier-dense environments.

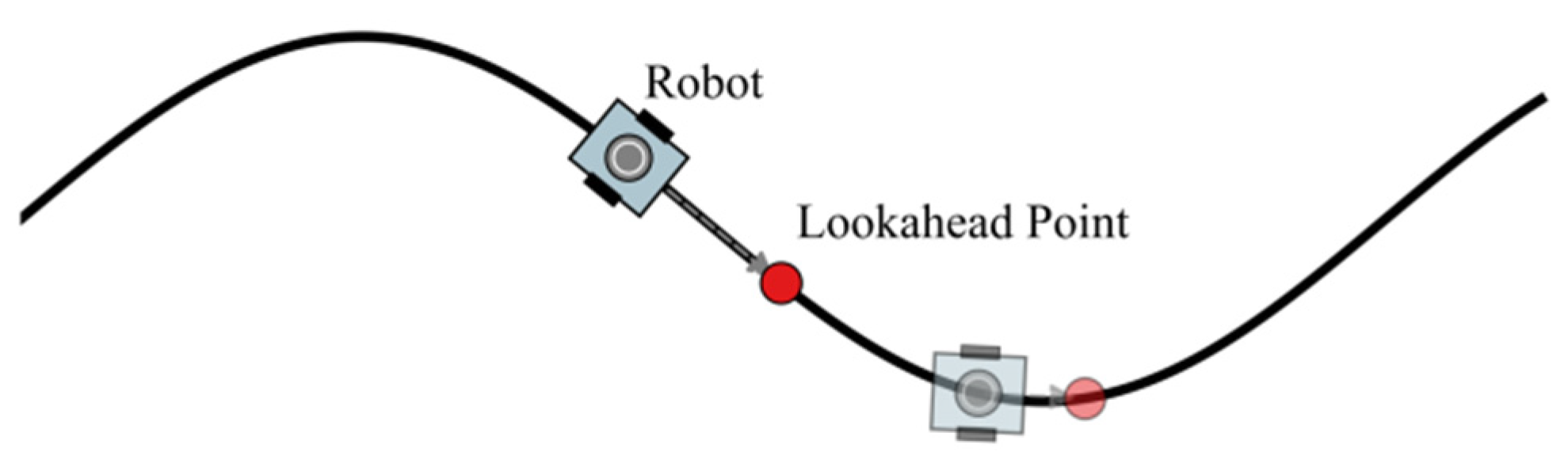
On the contrary, geometric discontinuities of the trajectory will significantly affect the execution stability of the controller. Pure tracking (PP) algorithms [19,20] have attracted widespread attention in many fields including agricultural machinery, intelligent driving, and mobile robots because of their simple structure and easy implementation. The algorithm formulates control arcs based on specified look-ahead points to achieve path tracking. When dealing with road sections with high curvature or folded paths, it often encounters problems such as direction fluctuations and tracking jitter. In order to enhance the robustness of the PP algorithm, the researchers proposed an integrated fuzzy control mechanism [21] and speed regulation strategy [22], and they achieved certain improvements. In addition, Miao et al. [23] proposed a decoupling controller for agricultural vehicles that considers steering delay, while Wang et al. [24] integrated nonlinear model predictive control (NMPC) into PP tracking to enhance motion adaptability in water-based robotic platforms. These methods improve local stability but still struggle under sudden curvature transitions. However, the overall control performance still relies heavily on the continuity and smoothness of the path itself. In order to further improve response capabilities in complex path segments, Macenski et al. [25] introduced an RPP controller, which adjusts the look-ahead distance and line speed based on the perception of path curvature, thereby improving system stability to a certain extent. The RPP controller is still susceptible to angular velocity fluctuations in sections with discrete path structures or sudden changes in curvature, which limits its control effectiveness. Improving the geometric continuity and control compatibility of the path during the path generation stage is a key prerequisite for developing a highly robust trajectory tracking system.

To improve the feasibility and continuity of robot navigation in cluttered indoor environments, this paper proposes an integrated path planning and control framework based on an enhanced JPS algorithm. The goal is to enhance planning efficiency while ensuring smooth and executable trajectories for real-time control. This paper offers the following contributions:

• Density-aware heuristic planning:

An integral image is used to estimate the local obstacle density via a density-aware heuristic approach. In densely crowded environments, this method reduces needless node expansions and improves path feasibility by enabling adaptive adjustment of the search direction and heuristic cost.

• Structure-guided B-spline smoothing:

A structure-guided B-spline smoothing method is applied to reduce the discontinuities of discrete jump point pathways. Using this technique, important geometric points are extracted from the JPS path and used as control nodes for third-order B-spline interpolation, producing curvature-continuous and trackable trajectories.

• Curvature-driven trajectory tracking:

An RPP controller driven by curvature is used to improve tracking stability. This controller smooths out the path-following experience and increases system responsiveness by adjusting the look-ahead distance and velocity according to local curvature.

Section 2 introduces the basic principles of the traditional JPS algorithm, covering its heuristic structure and core extension mechanism. Section 3 introduces our improved path-planning method, which is characterized by having a density-aware adaptive heuristic function, that can improve search efficiency in complex environments. Section 4 details the B-spline-based path smoothing strategy and the curvature-driven RPP controller for stable trajectory tracking. Section 5 gives comprehensive simulation results. It compares and analyzes different map sizes and obstacle densities with the A* algorithm and the traditional JPS algorithm. Section 6 discusses key observations, focusing on trade-offs between path efficiency, smoothness, and tracking stability. Section 7 summarizes the paper and lists future research directions.

2. Traditional Jump Point Search

To establish a clearer context for the proposed improvements, this section commences with an examination of the fundamental principles underpinning the traditional JPS algorithm. As a widely utilized optimization technique for grid-based A* search, JPS efficiently reduces redundant node expansions by eliminating symmetrical paths [26]. A comprehensive understanding of its operational mechanisms and intrinsic limitations provides the basis for the advanced methodologies introduced in Section 3.

2.1. Evaluation Functions and Heuristics

JPS adopts the framework of the evaluation function as established by the A* algorithm.

$$f\left(n\right)=g\left(n\right)+h\left(n\right)$$

(1)

where $f\left(n\right)$ represents the overall cost evaluation value associated with the node, $g\left(n\right)$ signifies the actual cost incurred from the starting node to the current node, and $h\left(n\right)$ indicates the heuristic estimate of the cost from the current node to the target node.

Widely utilized heuristic function types encompass the Manhattan distance, Euclidean distance, and Chebyshev distance, each of which is suited to various raster connectivity contexts [27], as illustrated in Figure 1. In the present study, all subsequent analyses employ Euclidean distance as the foundational heuristic function, represented by the following Formula (2), and implement an eight-neighborhood search, as depicted in Figure 2.

$$h\left(n\right)=\sqrt{{\left(x_n-x_{goal}\right)}^2+{\left(y_n-y_{goal}\right)}^2}$$

(2)

Let $\left(x_n,y_n\right)$ represent the coordinates of the current node, while $\left(x_{goal},y_{goal}\right)$ denotes the coordinates of the target node.

2.2. The Core Mechanism of the Jump Point Search

The primary benefit of the Jump Point Search (JPS) algorithm lies in its ability to circumvent unnecessary path expansion through the implementation of a jumping strategy. This approach allows the algorithm to maintain only the essential “jump points” within the path, which are critical for indicating changes in direction, thereby significantly reducing the search space. The fundamental mechanism of JPS can be categorized into three distinct types of operations [7].

2.2.1. Unnatural Neighbor Pruning

In conventional grid-based search, every node examines its full neighborhood, often leading to redundant expansions. The JPS algorithm optimizes this step by identifying unnatural neighbors—nodes that can be reached more efficiently from the parent without passing through the current node.

Let $p\left(x\right)$ be the parent node, node $x$ the current node, and $n$ a neighbor of $x$. If

$$\mathrm{cost}\left(P\left(x\right),n\right)\le \mathrm{cost}\left(P\left(x\right),x\right)+\mathrm{cost}\left(x,n\right)$$

(3)

then node $n$ is deemed an unnatural neighbor and can be safely pruned, as illustrated in Figure 3.

This pruning reduces unnecessary branching and ensures that only direction-changing nodes are retained in the search.

2.2.2. Forced Neighborhood Extension

In grid environments containing obstacles, certain expansion directions may become partially obstructed, limiting access to direct successors. To preserve path connectivity in such cases, forced neighbors must be identified and included in the search process. These are successor nodes that would not typically be part of the natural expansion direction but become necessary due to the presence of obstacles.

Let $p\left(x\right)$ denote the parent of the current node $x$, and let $d$ represent the main direction of expansion. If a side-adjacent node in the direction orthogonal to $d$ is blocked, yet the corresponding diagonal node is free, then this diagonal node must be considered a forced neighbor and retained for further expansion.

The detection logic can be described as

$$\mathrm{If} \mathrm{Blocked}\left(x+d_{\perp }\right)\wedge \neg \mathrm{Blocked}\left(x+d+d_{\perp }\right)\Rightarrow x+d+d_{\perp }\mathrm{is} \mathrm{a} \mathrm{forced} \mathrm{neighbor}$$

(4)

This strategy ensures that the path search does not overlook viable alternatives around obstacles. As depicted in Figure 4, both straight-line and diagonal directions are evaluated for forced neighbor conditions with gray cells representing obstacles and key forced neighbors indicated explicitly.

2.2.3. Jump Point Recognition

The identification of jump points constitutes a critical component of the JPS framework. Its objective is to eliminate redundant intermediate nodes along straight or diagonal segments while preserving essential turning points required for direction changes. This strategy significantly reduces the search space and accelerates the pathfinding process.

During the path expansion phase, JPS performs a recursive directional search from a given node $x$ in a specified expansion direction $d$. The goal is to determine whether a jump point $y=J\left(x,d\right)$ exists in that direction, which is subject to one of the following conditions:

• A forced neighbor is encountered at any point along the path;
• The goal node is reached.

Formally, the jump point can be defined recursively as

$$J\left(x,d\right)=\left\{\begin{array}{l}\mathrm{None}, \mathrm{if} x \mathrm{is} \mathrm{not} \mathrm{traversable} \\ x, \mathrm{if} x \mathrm{is} \mathrm{the} \mathrm{goal} \mathrm{or} \mathrm{has} \mathrm{forced} \mathrm{neighbors}\\ J\left(x+d,d\right), \mathrm{otherwise} \end{array}\right.$$

(5)

In the case of diagonal movements, it is necessary to recursively verify the horizontal and vertical components of the diagonal direction to ensure that any jump points along those axes are not overlooked. Specifically, let $d=\left(d_x,d_y\right)$; then, the following apply:

• Perform checks along $\left(d_x,0\right)$ and $\left(0,d_y\right)$;
• If either subdirection yields a valid jump point, then the diagonal path must be retained.

This recursive process guarantees the inclusion of all critical nodes that contribute to preserving optimality and connectivity while avoiding unnecessary expansions. An illustration of the jump point recognition process, including diagonal propagation and forced neighbor evaluation, is provided in Figure 5. Green indicates the start point, blue indicates the goal point, gray represents obstacles, and orange denotes forced neighbors.

3. Improved Path-Planning Methods

In conventional JPS path planning, the process of node expansion is dependent on a static geometric distance estimation, which inadequately captures the structural characteristics of the environment. This limitation is particularly pronounced in areas with a high density of obstacles, where the search path is susceptible to local oscillations and redundant extensions, thereby compromising both search efficiency and path quality [28]. To address this issue, the present study introduces a density-aware adaptive heuristic function optimization strategy. This approach develops an effective local obstacle density estimation method utilizing an integral map and dynamically modifies the heuristic weights to facilitate adaptive adjustments in response to varying environmental structures.

3.1. Local Barrier Density Modeling and Acceleration

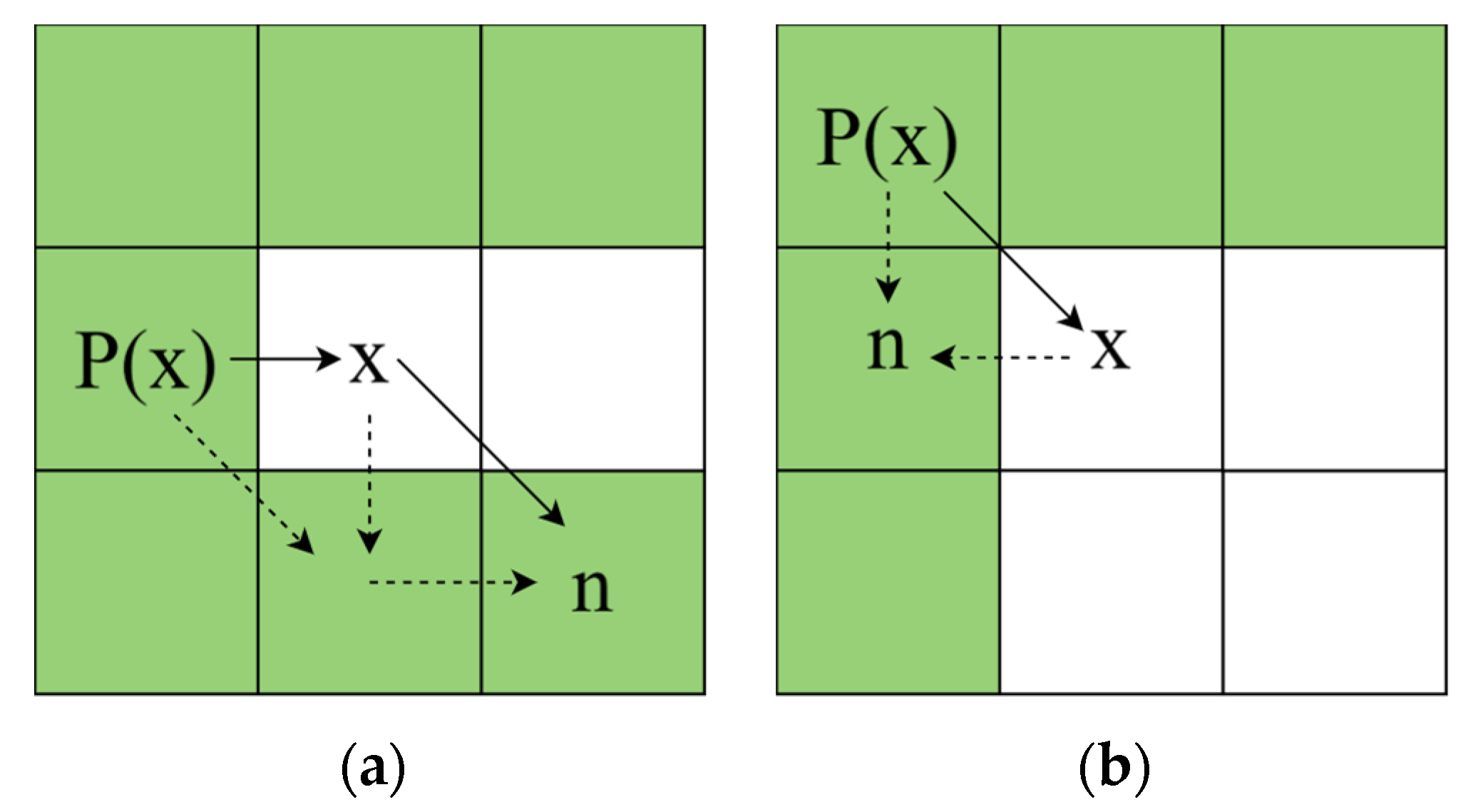
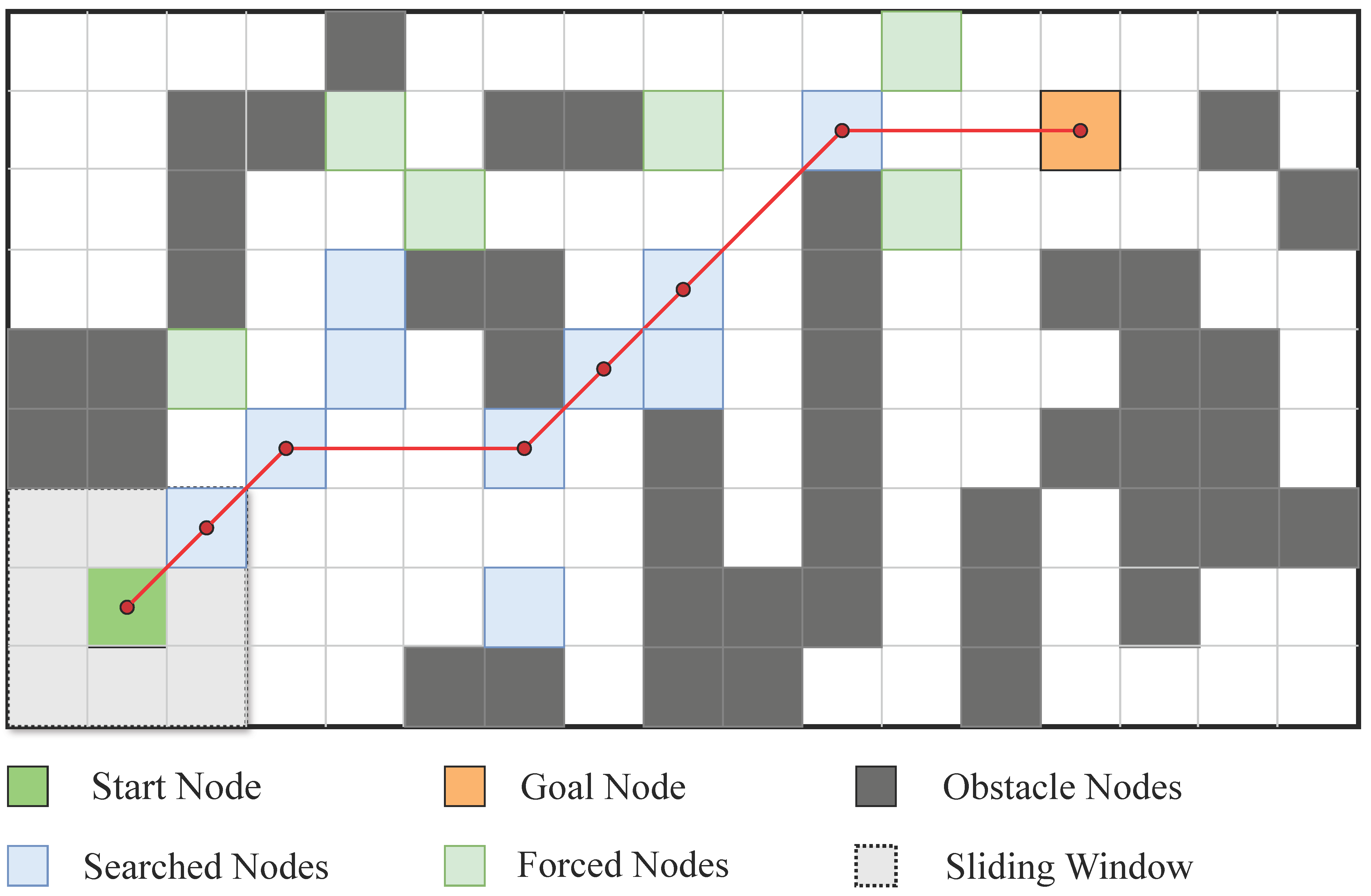
To acquire the structural information surrounding the node, this study employs the sliding window statistics approach to develop a local obstacle density model, as illustrated in Figure 6. For a given node location $\left(x,y\right)$, a local window with a width of $W=2w+1$ is established at its center, and the density is subsequently computed as follows:

$$D\left(x,y\right)={\displaystyle \frac{1}{W^2}}{\displaystyle \sum _{i=-w}^w{\displaystyle \sum _{j=-w}^{w}M\left(x+i,y+i\right)}}$$

(6)

where $M\left(i,j\right)\in \left\{0,1\right\}$ represents the state of the grid, where a value of 1 indicates the presence of an obstacle and a value of 0 signifies a passable area. While this approach is both intuitive and effective, it necessitates conducting local traversals for each individual node. Consequently, the computational complexity is denoted as $O\left(W^2\right)$, which constrains its efficiency when applied to large-scale maps.

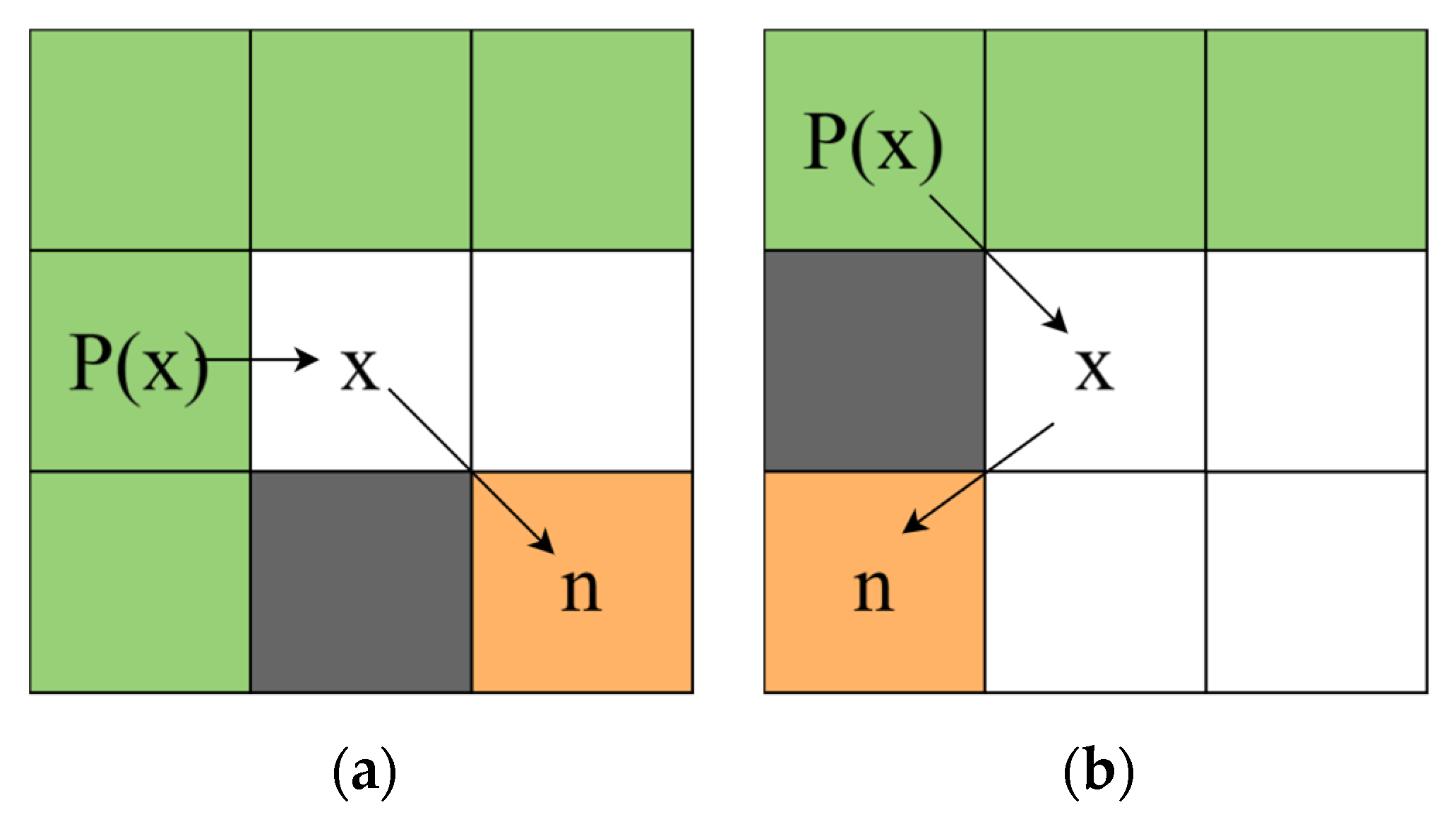
To improve computational efficiency, this study presents an integral graph designed to expedite the aforementioned window summation process, as illustrated in Figure 7. The integral map $I\left(x,y\right)$ denotes the cumulative count of obstacles within the area extending from the map’s origin to the coordinates $\left(x,y\right)$.

$$I\left(x,y\right)=M\left(x,y\right)+I\left(x-1,y\right)+I\left(x,y-1\right)-I\left(x-1,y-1\right)$$

(7)

The synthesis of obstacles within a specified interval from $\left(x_1,y_1\right)$ to $\left(x_2,y_2\right)$ can be efficiently calculated using an integral map.

$$S=I\left(x_2,y_2\right)-I\left(x_1-1,y_2\right)-I\left(x_2,y_1-1\right)+I\left(x_1-1,y_1-1\right)$$

(8)

The ultimate density of the barrier is

$$D\left(x,y\right)={\displaystyle \frac{S}{W^2}}=\rho \in \left[0,1\right]$$

(9)

In contrast to the conventional sliding window approach, this method decreases the computational complexity to $O\left(1\right)$ while preserving the accuracy of density evaluation. This enhancement notably increases the efficiency of environmental modeling in the context of pathfinding.

3.2. Adaptive Heuristic Function

In light of the aforementioned density modeling, this study proposes a dynamically weighted heuristic function. This function is intended to augment the heuristic efficacy in expediting the search process within sparse obstacle areas while simultaneously diminishing the heuristic guidance in regions characterized by dense obstacles, thereby enhancing overall global robustness.

The enhanced heuristic function is characterized by the following structure:

$$f\left(n\right)=g\left(n\right)+\left(1+\alpha \left(\rho \right)\right)\cdot h\left(n\right)$$

(10)

where $g\left(n\right)$ represents the actual cost incurred from the initial point to the specified node, $h\left(n\right)$ denotes the Euclidean distance, and $\alpha \left(\rho \right)$ signifies the density adjustment factor. This factor is subject to dynamic modification in response to variations in the local obstacle density, which is denoted as $\rho \in \left[0,1\right]$.

$$\alpha \left(\rho \right)={\alpha }_0\cdot \left(1-{\displaystyle \frac{\rho }{{\rho }_{\max }}}\right), {\alpha }_0\in R^{+}$$

(11)

In this context, $\alpha \left(\rho \right)$ represents the obstacle density at the present location, which denotes the maximum weight, and ${\rho }_{\max }$ indicates the maximum density across the entire map. This approach guarantees that $\alpha \left(\rho \right)$ approaches the maximum value ${\alpha }_0$ in scenarios where obstacles are sparse, which is characterized by robust inspiration and rapid search capabilities. Conversely, when obstacles are densely populated, $\alpha \left(\rho \right)$ tends to approximate 0, reflecting diminished guidance and increased cost estimation. The comprehensive execution of this adaptive heuristic function is detailed in the pseudo-code presented in Algorithm 1.

Algorithm 1 Adaptive Heuristic Function for Density-Aware JPS

1: function ADAPTIVEHEURISTIC(n, g, I, W, ρ_max, α0) 2:           x, y ← coordinates of node n 3:           ρ ← GETDENSITY(I, x, y, W) 4:           α ← α0 × (1 − ρ/ρ_max) 5:           α ← CLAMP(α, 0, α0) 6:           D ← EUCLIDEANDISTANCE(n, g) 7:           h(n) ← (1 + α) × D 8:           f(n) ← g(n) + h(n) 9:           return f(n) 10: end function 11: function GETDENSITY(I, x, y, W) 12:         half_w ← W//2 13:         x1 ← max(x − half_w, 0) 14:         y1 ← max(y − half_w, 0) 15:         x2 ← min(x + half_w, width − 1) 16:         y2 ← min(y + half_w, height − 1) 17:         sum ← I[x2][y2] − I[x1][y2] − I[x2][y1] + I[x1][y1] 18:         return sum/((x2 − x1 + 1) × (y2 − y1 + 1)) 19: end function

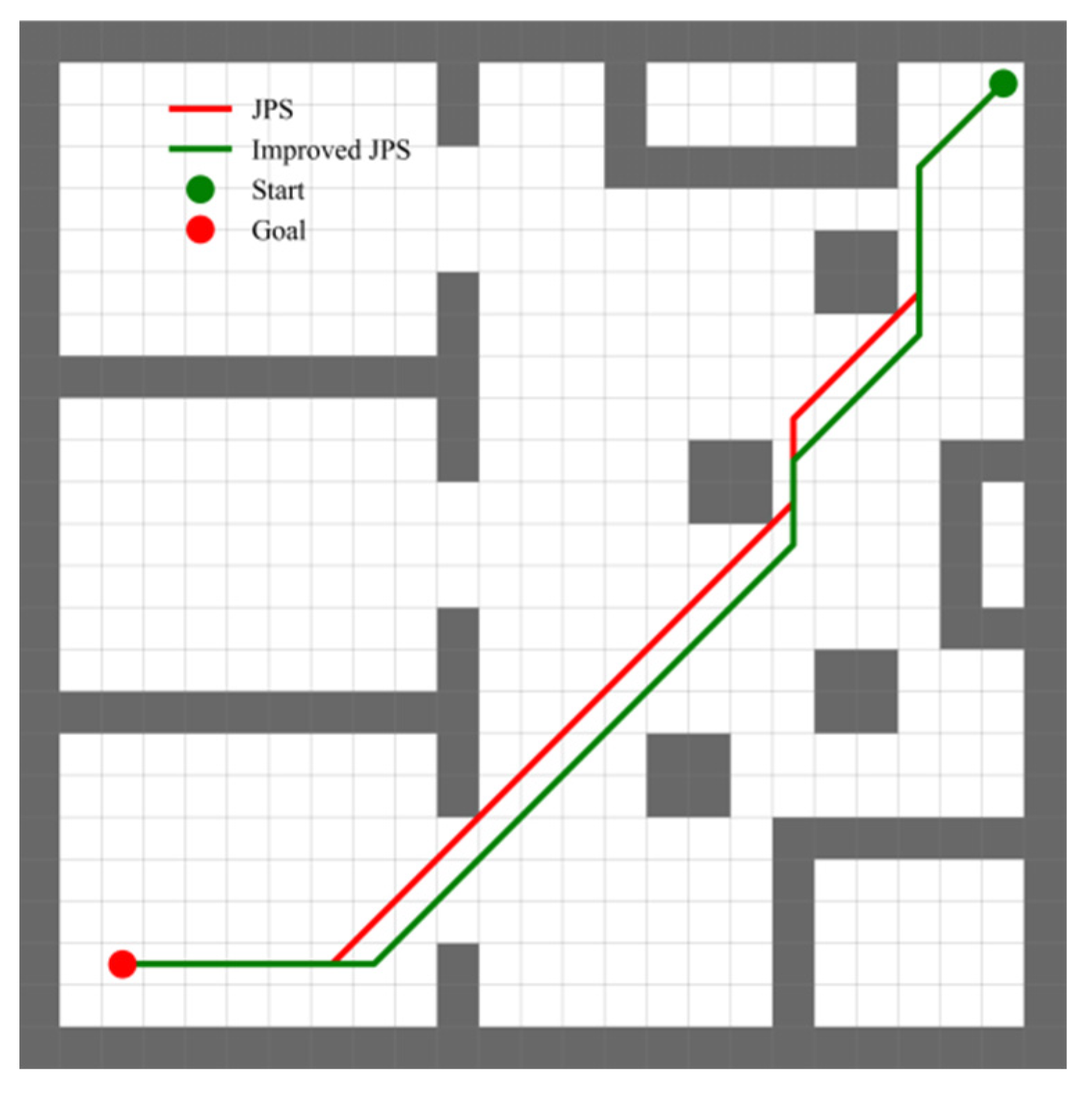
To assess the efficacy of the proposed adaptive heuristic function, this study conducts a comparative analysis of the search processes of the traditional JPS and the improved JPS, utilizing identical starting and ending conditions. As illustrated in Figure 8, the improved JPS demonstrates a decrease in the number of extended nodes from 48 to 18 alongside a reduction in planning time from 1.60 milliseconds to 1.17 milliseconds. These changes represent a decrease of 62.5% in the number of extended nodes and 26.9% in planning time, respectively. It is noteworthy that this improvement in search efficiency and path security is accompanied by a slight increase in path length of approximately 1.8%.

3.3. Parameter Configuration and Sensitivity Analysis

The density-aware heuristic proposed in this study depends on several critical parameters. The window size was set to $W=5$ to achieve a balance between sensitivity to local structural variations and computational efficiency. Smaller window sizes (e.g., $W=3$) resulted in unstable density estimations, whereas larger sizes (e.g., $W=7$) diminished spatial resolution in confined areas.

The maximum local density, denoted as ${\rho }_{\max }$, was derived from the integral image during the map initialization phase to facilitate normalization of the heuristic scaling across diverse environmental contexts.

The weighting coefficient α0 was evaluated over the range [0.1, 1.0]. Lower values (e.g., ${\alpha }_0=0.1$) yielded limited pruning and performance close to that of standard A*, while higher values (e.g., ${\alpha }_0=1.0$) led to excessive pruning, occasionally omitting viable narrow passages. Intermediate values (approximately 0.2–0.8) improved efficiency but required fine tuning.

This study used a value of ${\alpha }_0=0.3$ to guarantee effective expansion performance in congested interior situations. This conservative selection proved beneficial when integrated with B-spline smoothing and curvature-aware tracking, as evidenced in Section 5.

Future research may investigate the adaptive adjustment of this parameter in relation to environmental complexity or the dynamics of the robotic platform.

4. Path Smoothing and Tracking Control

To improve the controllability and continuity of the JPS path during the execution phase, this study presents a B-spline curve reconstruction strategy during the path-smoothing stage. Additionally, it optimizes the curvature feedback-based RPP controller, thereby establishing a comprehensive closed-loop system that integrates path generation with execution control.

4.1. B-Spline-Based Path Smoothing Reconstruction

The conventional path generated by JPS is characterized by a series of linear segments, which can lead to issues such as sudden changes in direction and discontinuities in curvature. These characteristics are not conducive to effective control of real-world robotic systems. Consequently, this study employs third-order B-splines to enhance the smoothness and reconstruction of the JPS-generated path.

Let the jump point path $n+1$ be characterized by a single control point, which is referred to as $\left\{P_0,P_1,\dots ,P_n\right\}\in R^2$. Consequently, the third-order B-spline path can be articulated as follows:

$$P\left(u\right)={\displaystyle \sum _{i=0}^n{N}_{i,3}\left(u\right)}\cdot P_i,u\in \left[u_3,u_{n+1}\right]$$

(12)

where $N_{i,3}\left(u\right)$ represents the third-order B-spline basis function that is formulated using the series of incremental nodes denoted as $\left\{u_0,u_1,\dots ,u_{n+4}\right\}$.

In order to maintain the viability and consistency of trajectories within intricate environments, this study employs a systematic key-point extraction methodology for the selection of control points. As illustrated in Figure 9, the initial point, terminal point, and turning points characterized by notable directional changes are preserved in the enhanced JPS path as the key control points $\left(kps\right)$ of the B-spline curve. The resultant red curve represents the B-spline smoothed trajectory, which is constructed based on these control points.

To characterize the local curvature of the path and subsequent controller adaptation, the local curvature is further computed for the smooth path:

$$\kappa \left(u\right)={\displaystyle \frac{\left|x^{\prime }\left(u\right)\cdot y^{″}\left(u\right)-y^{\prime }\left(u\right)\cdot x^{″}\left(u\right)\right|}{{\left(x^{\prime }{\left(u\right)}^2+y^{\prime }{\left(u\right)}^2\right)}^{3/2}}}$$

(13)

where $x^{\prime }\left(u\right)$ and $y^{\prime }\left(u\right)$ represent the velocity components of the trajectory at the parameter $u$, while $x^{″}\left(u\right)$ and $y^{″}\left(u\right)$ correspond to its acceleration components. The curvature is employed not only to define the geometric properties of the trajectory but also serves as the fundamental metric upon which the curvature feedback adjustment during the control phase is reliant.

4.2. RPP Tracking Control

To improve the adaptability of the robot to continuous curved trajectories, this study proposes a Regulated Pure Pursuit (RPP) control strategy [25], which is an extension of the traditional Pure Pursuit (PP) controller [29]. This approach utilizes the smoothed path curvature as the foundation for regulation. The proposed method integrates the geometric characteristics of the trajectory to dynamically modify the look-ahead distance and linear velocity, thereby accommodating the tracking requirements associated with varying curvature segments.

The RPP controller continues to utilize the geometric tracking model of the vehicle’s coordinate system, as illustrated in Figure 10, which includes the equation for controlling angular velocity:

$$\omega ={\displaystyle \frac{2\nu \cdot \sin \left(\alpha \right)}{L}}$$

(14)

where $\nu$ represents the present linear velocity, $\alpha$ denotes the angle of deflection between the vehicle and the designated look-ahead point, and $L$ signifies the distance to the look-ahead point.

In contrast to conventional probabilistic programming (PP) algorithms, the RPP methodology possesses the capability to dynamically modify the parameters $L$ and $\nu$ in response to the curvature of the current $\kappa$ path point. The formula is as follows:

$$L=L_{\max }\cdot \left(1-\kappa /{\kappa }_{\max }\right)$$

(15)

$$\nu ={\nu }_{\max }\cdot \left(1-\kappa /{\kappa }_{\max }\right)$$

(16)

In this context, $\kappa$ represents the curvature at the current point along the path, while ${\kappa }_{\max }$ signifies the global maximum curvature within the planned trajectory. The parameters $L_{\max }$ and ${\nu }_{\max }$ correspond to the maximum look-ahead distance and the maximum linear velocity constant, respectively. As illustrated in Figure 11, the controller dynamically adjusts the look-ahead distance and linear speed in response to variations in path curvature. Specifically, in areas characterized by higher curvature, the controller reduces both the look-ahead distance and the speed to enhance the precision and responsiveness of path tracking. Conversely, in sections where the path is relatively flat and straight, the controller increases the look-ahead distance and speed to optimize overall operational efficiency.

This study employs the analytical formulation of the third-order B-spline trajectory for the purpose of calculating curvature, as delineated in Equation (17). Additionally, to prevent the occurrence of excessive curvature that may lead to peak angular velocity, a minimum threshold, denoted as $L_{\min }$, is established for the forward-looking distance within the practical control framework.

$$L=\max \left(L_{\min },L_{\min }\cdot \left(1-{\displaystyle \frac{\kappa }{{\kappa }_{\max }}}\right)\right)$$

(17)

While the RPP controller provides direct outputs of angular velocity, its control behavior can be assessed indirectly at the path level by examining the angle of change in direction between consecutive segments of the trajectory. Denote the sequence of smooth path points as $\left(x_i,y_i\right)$; the angle of change in direction for each segment can be determined by calculating the angle formed by three consecutive significant points.

$${\theta }_i=\arccos \left({\displaystyle \frac{\left(P_i-P_{i-1}\right)\cdot \left(P_{i+1}-P_i\right)}{‖P_i-P_{i-1}‖\cdot ‖P_{i+1}-P_i‖}}\right)$$

(18)

This perspective serves to accurately represent the variations in local steering amplitude within the trajectory of the controller output. In this study, the average and maximum values of all ${\theta }_i^{\prime }s$ along the path are employed as metrics for assessing smoothness and extreme deflection during the process of path tracking, respectively.

The path-planning framework delineated in this study incorporates adaptive JPS path planning, a path-smoothing algorithm utilizing third-order B-splines, and a curvature-aware RPP tracking controller. The comprehensive workflow is illustrated in Figure 12.

5. Simulation Experiment

To systematically assess the applicability and performance benefits of the path planning and execution methodology proposed in this study across various scenarios, experiments are conducted at three distinct levels: search efficiency, path quality, and trajectory execution feasibility. The experimental framework is organized into four components:

(1) A comparative analysis of the search performance of three algorithms under varying obstacle density conditions while maintaining a constant map size;

(2) An examination of how changes in map size affect the performance of each algorithm under a fixed obstacle density;

(3) An investigation into the trend of node expansion for the enhanced JPS algorithm across different environmental combinations;

(4) An evaluation of the enhanced JPS algorithm’s capacity to improve path smoothness and executability through the integration of a B-spline and RPP controller within the ROS simulation environment.

To assess the performance of the algorithm in a thorough manner, this study employs the following evaluation metrics: path length, planning time, number of expanded nodes, maximum and average curvature, as well as maximum and average turning angles.

5.1. Experimental Configuration

The algorithm comparison experiments were conducted on the Windows 11 (Microsoft Corporation, Redmond, WA, USA) operating system, while the system simulation experiments were performed on the Ubuntu 20.04 platform (Canonical Ltd., London, UK). The simulation utilized the TurtleBot3 Waffle Pi robot model (ROBOTIS, Seoul, Republic of Korea), as illustrated in Figure 13, and to ensure the reproducibility and clarify the experimental settings, the detailed parameters of the TurtleBot3 Waffle Pi used in the simulation are summarized in

Table 1. Hardware configuration and component specifications of the TurtleBot3 Waffle Pi robot platform.

Category	Specification
Dimensions	281 × 306 × 141 mm (L × W × H)
Wheelbase/Diameter	160 mm/66 mm
Weight	Approx. 1.8 kg
Max Speed	Linear: 0.26 m/s; Angular: 180 deg/s
Controller	Raspberry Pi 3/4 + OpenCR 1.0
LiDAR	HLS-LFCD LDS-02 (360° scanning)
Camera	Raspberry Pi Camera V2 (8 MP)
Motor	DYNAMIXEL XM430-W210-R x 2
Battery	11.1 V 1800 mAh Li-Po (approx. 2–3 h runtime)

. These include its kinematic structure, maximum speed, wheel configuration, and sensor specifications. All experiments were executed on a standardized hardware platform with detailed specifications provided in

Table 2. Hardware and software configuration of the experimental platform.

Component	Specification
Operating System	Windows 11 Ubuntu 20.04
CPU	Intel Core i5-12400F
GPU	NVIDIA GeForce RTX 4060
Simulation Platform	ROS Noetic with Gazebo 11 and RViz
Robot Model	TurtleBot3 Waffle Pi

.

5.2. Comparison of Algorithm Performance for Different Barrier Densities

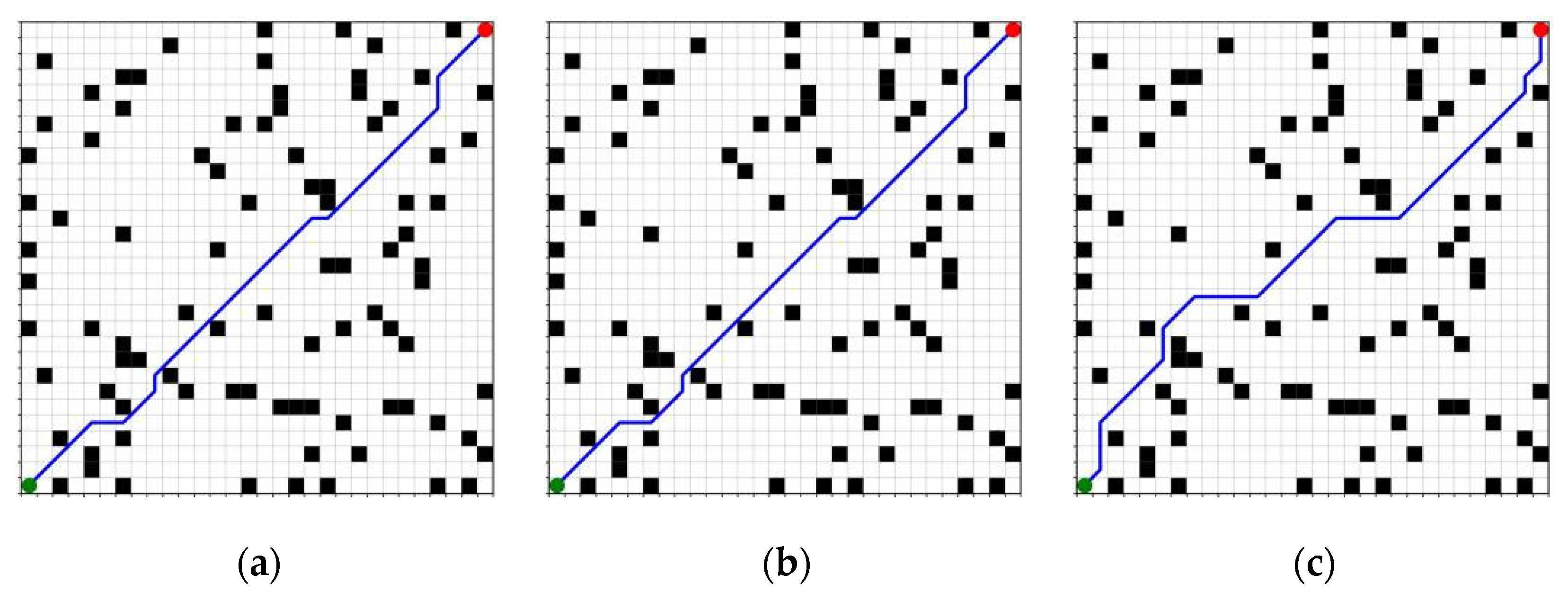
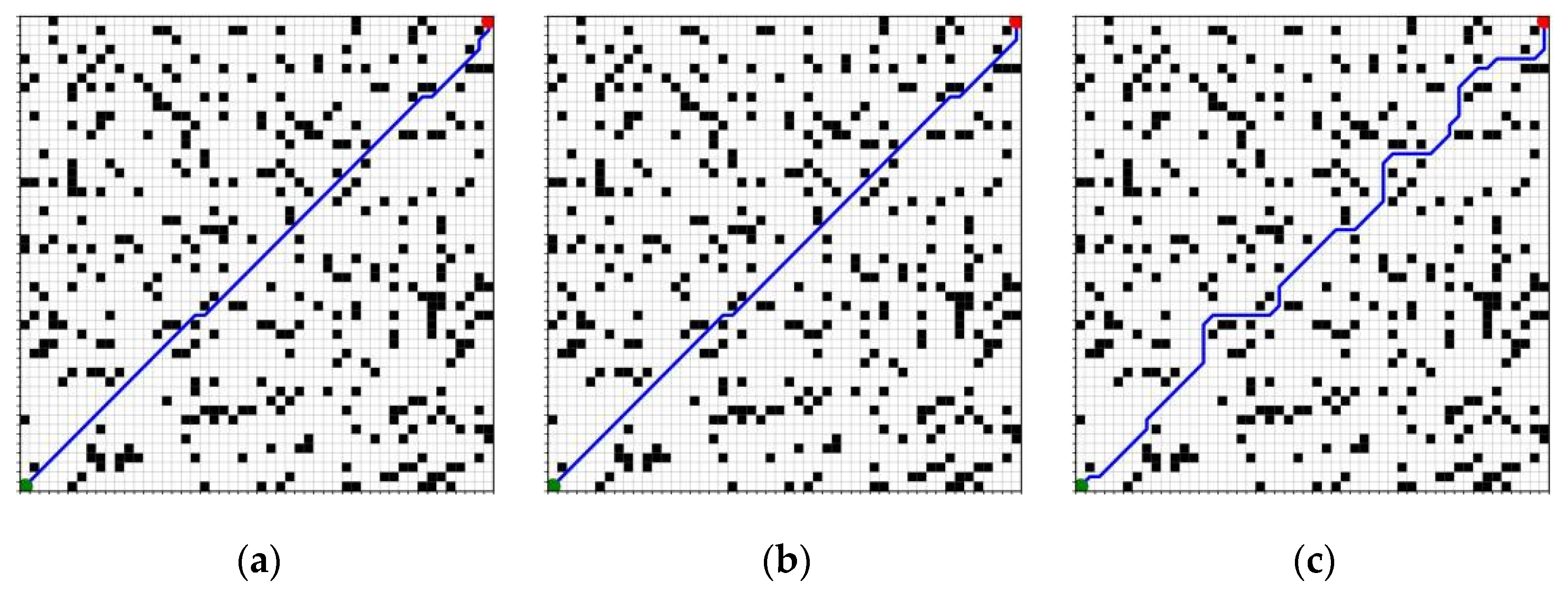
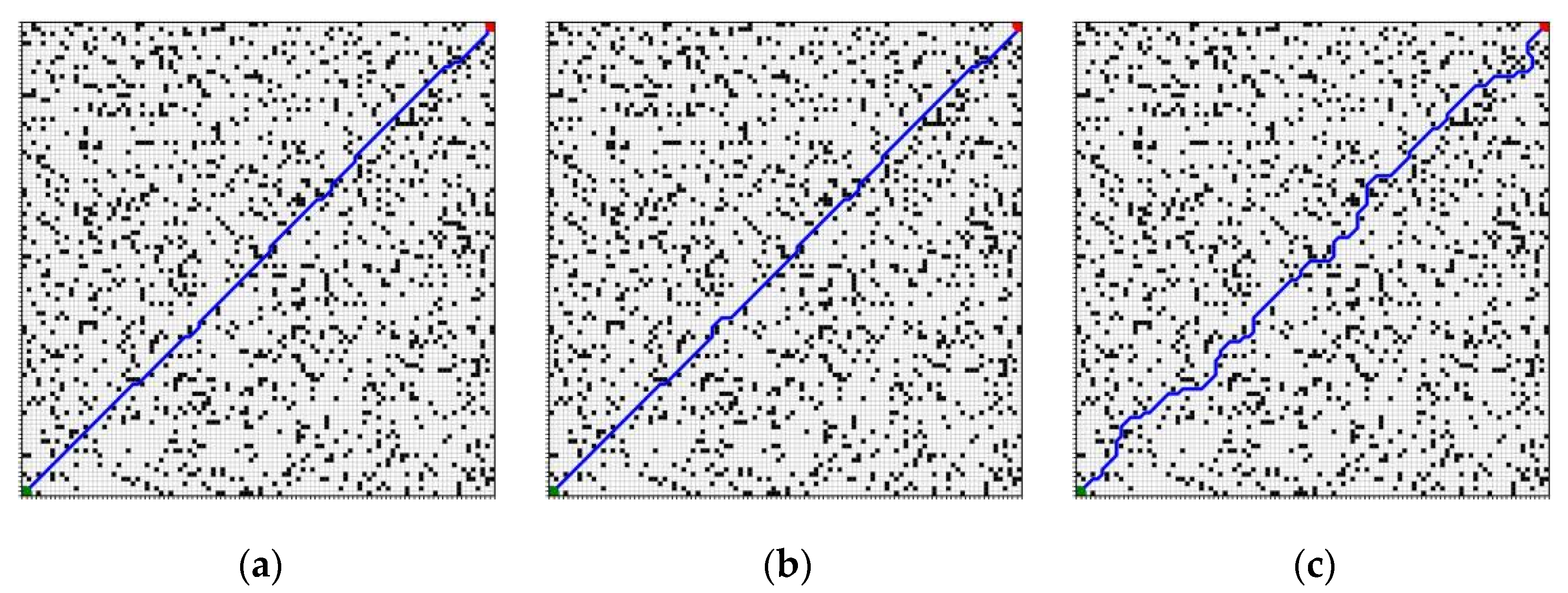
To assess the robustness and adaptability of various path-planning algorithms in intricate environments, this study establishes three levels of obstacle densities: low (0.1), medium (0.15), and high (0.2), while maintaining a constant map size of 25 × 25. The research involves a comparative analysis of the A* algorithm, the traditional Jump Point Search (JPS) algorithm, and an enhanced version of the JPS algorithm. For each density configuration, multiple sets of obstacle map instances are generated randomly, and the experimental outcomes are averaged to improve statistical reliability and confidence. The results of path generation for the three algorithms across different obstacle density conditions are illustrated in Figure 14, Figure 15 and Figure 16. In these figures, green indicates the start point, and red indicates the goal point. The same color scheme is applied consistently throughout the subsequent figures.

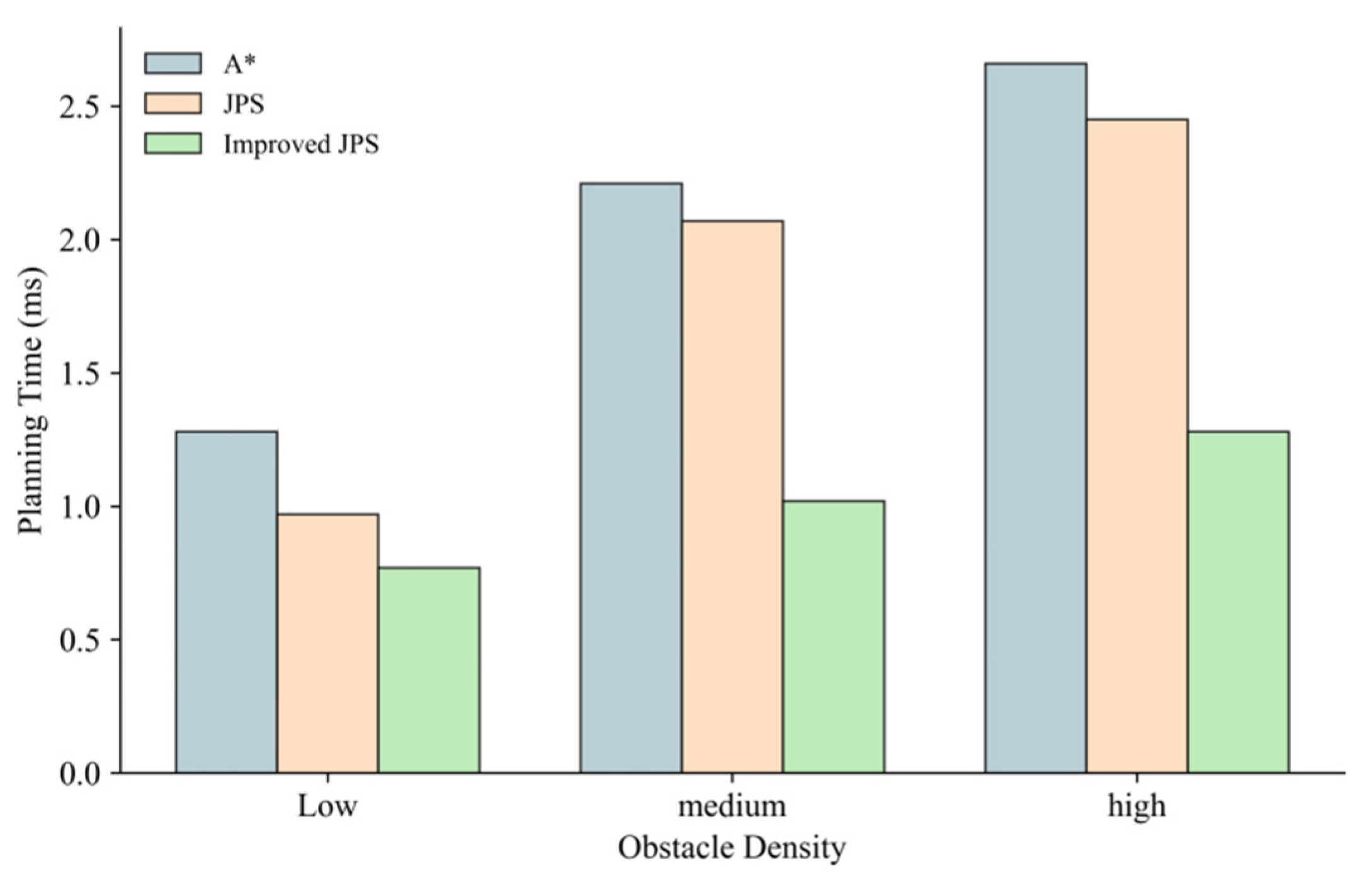
The statistical findings presented in

Table 3. Performance comparison of three algorithms under different obstacle densities.

Obstacle Density	Algorithm	Path Length	Time (ms)	Number of Expanded Nodes
Low (0.1)	A*	42.77	1.28	110
	JPS	42.77	0.97	71
	Improved JPS	45.70	0.77	31
Medium (0.15)	A*	42.18	2.21	175
	JPS	42.18	2.07	101
	Improved JPS	46.28	1.02	35
High (0.2)	A*	43.94	2.66	270
	JPS	43.94	2.45	146
	Improved JPS	49.21	1.28	48

and Figure 17 indicate that an increase in obstacle density leads to a notable rise in both the number of expansion nodes and the planning time for the A* and traditional JPS algorithms. Specifically, in high-density scenarios, the traditional JPS algorithm expands the number of nodes to a maximum of 146, resulting in a planning time of 2.45 ms, which signifies a marked decline in search efficiency. In contrast, the enhanced JPS algorithm effectively reduces the search space within the same environment, limiting the number of expanded nodes to 48 and decreasing the planning time to 1.28 ms, representing reductions of approximately 67% and 47%, respectively. This improvement in performance can be attributed to the implementation of a density-aware adaptive heuristic function that dynamically modifies the heuristic term based on the local distribution of obstacles, thereby minimizing unnecessary expansions while preserving path coherence. Although the path lengths generated by the improved JPS may be slightly longer in certain scenarios compared to the traditional JPS, this is primarily due to the algorithm’s tendency to circumvent obstacle edges and regions of high density during the search process. This approach enhances the feasibility of the paths and increases the safety margin, resulting in a minimal impact on the overall planning performance. To prevent redundancy, any similar phenomena that arise in the following sections will be considered as stemming from the same underlying cause and will not be reiterated.

5.3. Algorithm Performance Comparison for Different Map Sizes

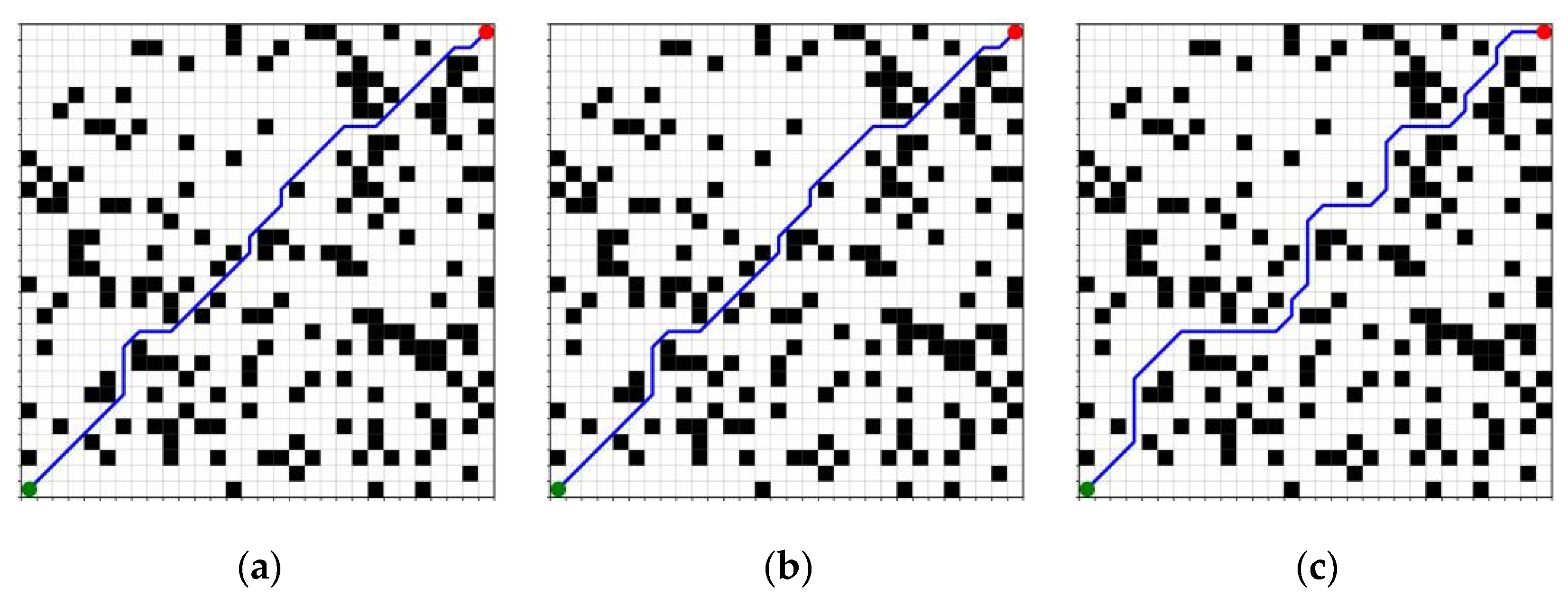
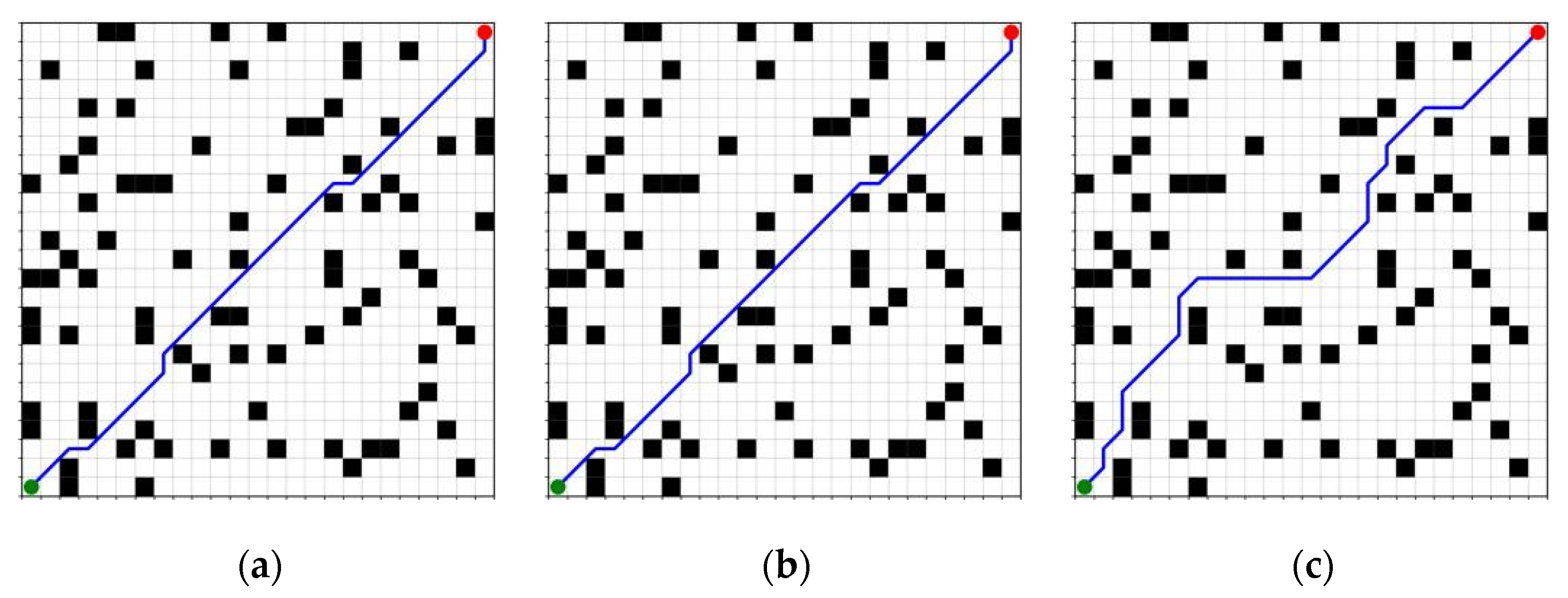
In order to evaluate the scalability and stability of each algorithm under different environmental scales, this section examines three different map sizes, which are 25 × 25, 50 × 50, and 100 × 100, respectively, while keeping the obstacle density constant at 0.15. The path length, planning time, and number of expansion nodes will be compared under these different map sizes for A*, traditional JPS, and improved JPS. This analysis aims to clarify the performance trends of algorithms in large-scale search spaces. The results of the path generation for the three algorithms across the specified map configurations are illustrated in Figure 18, Figure 19 and Figure 20.

As illustrated in

Table 4. Performance comparison of three algorithms under different map sizes.

Map Size	Algorithm	Path Length	Time (ms)	Number of Expanded Nodes
25 × 25	A*	35.11	1.38	83
	JPS	35.11	1.01	53
	Improved JPS	38.63	0.77	24
50 × 50	A*	70.47	3.93	262
	JPS	70.47	2.54	160
	Improved JPS	79.84	2.40	86
100 × 100	A*	142.94	24.84	1630
	JPS	142.94	18.66	957
	Improved JPS	159.58	4.16	154

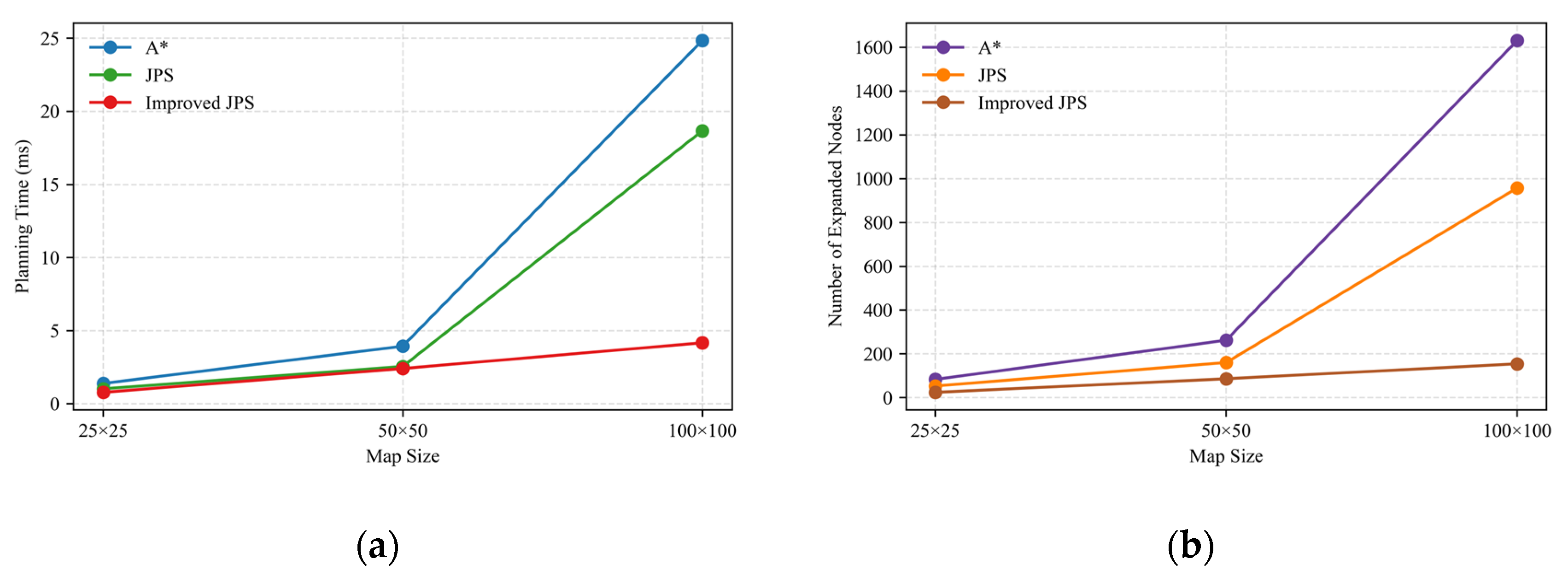
and Figure 21, the expansion of map size results in a pronounced increase in both the number of expansion nodes and planning time for the A* and traditional JPS algorithms, which is particularly evident in the 100 × 100 scenario. The expansion nodes for these two algorithms reach 1630 and 957, respectively, indicating a substantial rise in search costs. In contrast, the enhanced JPS algorithm exhibits a more consistent performance in terms of expansion scale and time efficiency on larger maps, with the number of expansion nodes limited to 154 under identical conditions and the planning time maintained at 4.16 ms. This demonstrates the improved JPS algorithm’s superior scalability and computational stability.

5.4. Trend Analysis of Expanded Nodes for Improved JPS Algorithm Under Multivariate Conditions

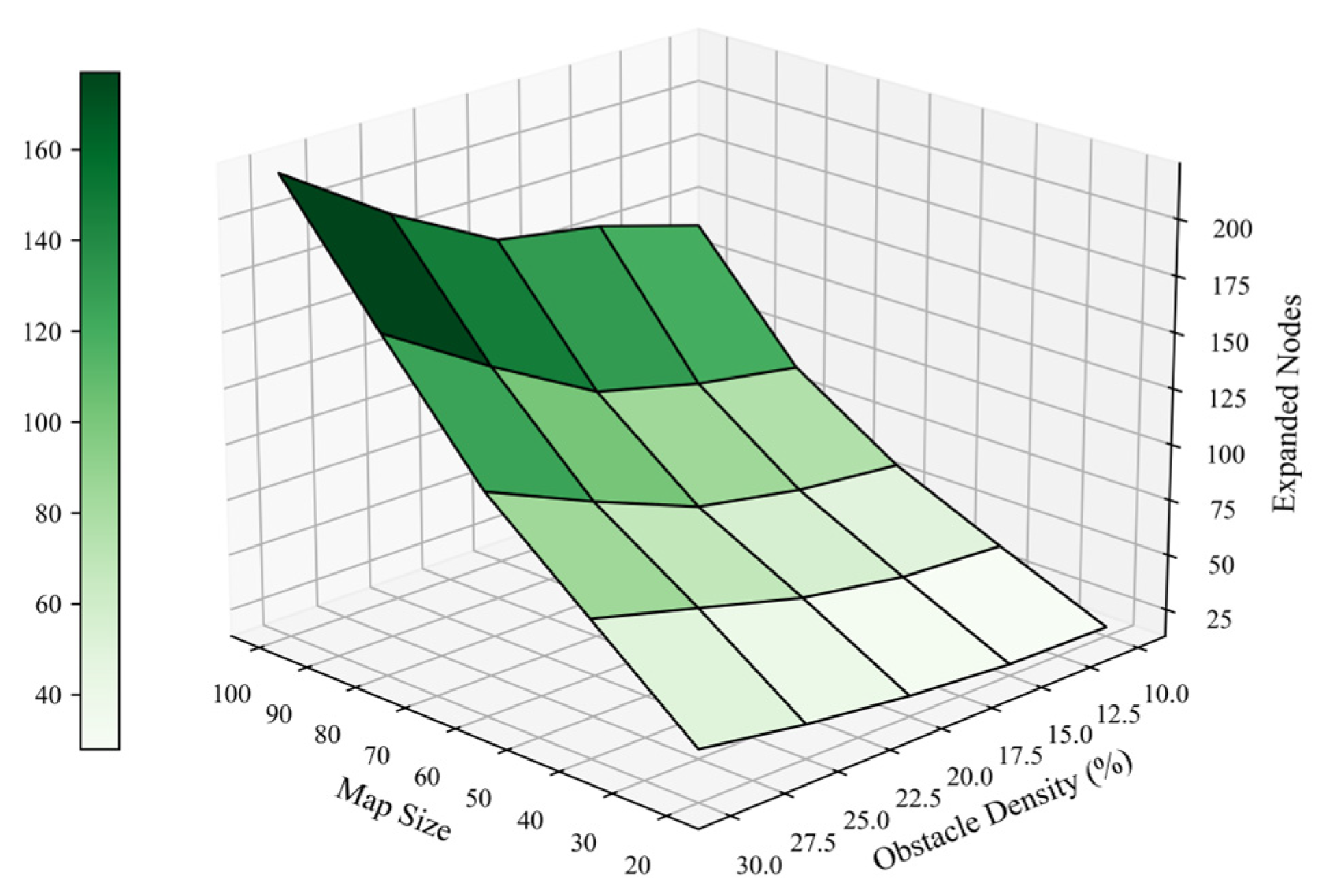
In order to evaluate the expansion performance of the enhanced JPS algorithm in various environmental configurations, this study built a two-dimensional experimental framework to conduct relevant experiments with map size and obstacle density as the main variables. The analysis process covers quantitative statistics on the number of extended nodes under five different map sizes and five different obstacle ratios. The obtained data are presented in the form of a three-dimensional surface map, as shown in Figure 22. Research results show that the number of extended nodes will gradually increase with the increase in map size and obstacle density, which means that these two variables have a cumulative impact on search complexity. Further analysis shows that when the map specifications are controlled, the impact of obstacle density on the number of extended nodes is more significant. This observation supports the ability of the density-aware heuristic to adaptively adjust to local environmental complexity.

The overall surface structure presents a smooth texture, and expansion control is maintained at a stable level. This shows that the improved JPS algorithm can effectively handle unnecessary flower clusters even in complex environmental conditions. It demonstrates the significant scalability and robustness of the algorithm, highlighting its huge potential in terms of environmental adaptability and practical engineering applications.

5.5. Path Performance Evaluation of the Complete System in a Simulation Environment

To assess the execution performance of the proposed method and its control efficacy in practical scenarios, this section develops two representative indoor environment maps (Map_1 and Map_2) utilizing the ROS simulation platform, as illustrated in Figure 23. Additionally, three distinct types of representative paths are established: task 1 (short-range), task 2 (medium-range), and task 3 (long-range). For each task group, a comparison is made between two system configurations: one in which the improved JPS algorithm generates paths for direct execution, and another in which the improved JPS algorithm is integrated with B-spline path smoothing and the RPP controller for enhanced trajectory optimization and tracking.

Figure 24 shows the effect of trajectory execution in the simulation environment for a typical task under the two maps. In the figure, the blue path represents the original planning path generated by the improved JPS algorithm, the green path is the smooth trajectory based on the third-order B-spline reconstruction, and the red dots are the look-ahead point positions computed in real time by the RPP controller during the execution process. In contrast, the baseline path has an obvious folding structure in the corner region, while the optimized scheme is significantly smoother in the turning section and makes the robot control commands more stable and natural by dynamically adjusting the look-ahead point position.

The statistical findings are presented in

Table 5. Comparison of path smoothness and executability.

Map	Version	Task	Path Length (m)	Max Curvature (1/m)	Avg. Curvature (1/m)	Max Turning Angle(rad)	Avg. Turning Angle(rad)
Map_1	Original	1	9.511	4.142	1.631	0.785	0.785
		2	15.188	4.142	1.566	0.785	0.703
		3	23.856	4.142	1.210	0.785	0.553
	Optimized	1	9.615	2.448	0.368	0.669	0.092
		2	15.256	1.419	0.478	0.496	0.123
		3	24.014	1.595	0.414	0.337	0.094
Map_2	Original	1	8.014	7.388	3.995	0.785	0.717
		2	17.808	7.388	4.023	0.785	0.668
		3	24.931	7.388	3.824	0.785	0.703
	Optimized	1	8.204	3.155	0.506	0.537	0.109
		2	17.651	3.242	0.349	0.631	0.079
		3	24.855	3.542	0.494	0.701	0.122

, which details the primary execution metrics, including the path length, maximum and average curvature, and maximum and average turning angle. The optimized system demonstrates superior performance relative to the baseline solution across all curvature and corner metrics for each task and map configuration, particularly in scenarios characterized by greater path complexity, such as tasks 2 and 3. For instance, in task 3 of Map_2, the optimization strategy results in a reduction in the maximum curvature from 7.388 to 3.542 and a decrease in the maximum rotation angle from 0.785 rad to 0.701 rad. Additionally, both the mean curvature and average rotation angle exhibit significant reductions, thereby enhancing the geometric continuity of the trajectory and the smoothness of control. Although there is a slight increase in path length compared to the baseline scheme, this can be attributed to the inherent structural redundancy introduced during the smooth reconstruction process. This redundancy contributes positively to the executability and tracking stability of the path, thereby aligning with the actual control requirements.

Figure 25 and Figure 26 illustrate histograms depicting the mean curvature and mean corner, respectively, to provide a more detailed quantification of the differences in smoothness and controllability between the two schemes across various tasks. The data presented in these charts show that the optimization scheme exhibits a reduction in overall curvature and a reduction in direction change across all path tasks, which confirms the effectiveness of the trajectory reconstruction process and adaptive control mechanisms in mitigating high-frequency changes in attitude.

Beyond enhancing curvature continuity and mitigating sudden directional changes, the application of B-spline smoothing results in a slight increase in path length attributable to the inherent characteristics of curve fitting. This trade-off is anticipated, given that achieving smooth transitions necessitates the introduction of additional curvature between critical points. Nonetheless, the extent of the path lengthening remains within acceptable limits and is warranted by the demonstrated improvements in tracking stability and control efficacy [30].

6. Discussion

The experimental outcomes demonstrate that the proposed planning and control system is effective across multiple evaluation dimensions. In particular, the improved JPS algorithm significantly decreases both the number of expanded nodes and the total planning time with advantages becoming more apparent as map complexity increases. The findings demonstrate the efficacy of the density-sensitive heuristic in effectively guiding the search process while preserving the capacity to explore globally feasible paths.

While B-spline smoothing results in a slight augmentation in path length, it provides significant advantages for geometric smoothness. The generated trajectories demonstrate less abrupt changes in heading and more gradual curvature transitions, hence substantially improving path-tracking stability. The structure-guided smoothing approach preserves essential path details while adhering to the robot’s motion limitations.

The curvature-adaptive Regulated Pure Pursuit controller enhances the accuracy and resilience of trajectory tracking, especially in regions with significant curvature. The controller enhances stability in diverse settings by dynamically modifying forward velocity and look-ahead distance in reaction to local geometric alterations, adapting more proficiently to intricate path configurations.

However, the existing method is tailored for static and completely known grid-based systems, potentially constraining its practical application in dynamic or partially observable contexts. Future endeavors will concentrate on incorporating sophisticated sensing modules and real-time replanning mechanisms to enhance adaptability. Moreover, improving computing efficiency would be crucial for implementing the suggested system on resource-constrained embedded robotic platforms.

7. Conclusions

This research provides a comprehensive framework for the path planning and control of indoor mobile robots, integrating an improved JPS algorithm, B-spline-based trajectory smoothing, and a curvature-adaptive RPP controller. The proposed framework solves the major shortcomings of traditional JPS by introducing density-aware heuristics and adaptive extension mechanisms, and it jointly improves planning efficiency and path feasibility in dense environments. The B-spline smoothing component identifies structure-dependent control points from the sequence of jump points to generate a geometrically continuous trajectory that conforms to curvature constraints, ensuring it is suitable for tracking purposes. During operation execution, the RPP controller adjusts the look-ahead distance and line speed based on local curvature, improving tracking stability and response capabilities.

The results of the simulation indicate that the proposed methodology surpasses the baseline approach in terms of planning efficiency, path smoothness, and tracking accuracy. The framework has been validated within ROS-based environments, underscoring its practical significance for real-world robotic applications.

It is essential to acknowledge that the existing methodology is limited to static environments and is predicated on the assumption of comprehensive map knowledge. Subsequent research endeavors will aim to broaden the algorithm’s applicability to dynamic environments by incorporating real-time perception, online re-planning, and coordination strategies for multi-robot systems. This advancement is expected to improve adaptability and robustness in intricate operational contexts.