Support-Vector-Regression-Based Intelligent Control Strategy for DFIG Wind Turbine Systems
Abstract
1. Introduction
1.1. Background Research
1.2. Motivation for the Research
1.3. Literature Review
1.4. Problem Statement
1.5. Purpose of the Research
1.6. Research Goals
- To create a single intelligent control approach based on support vector regression (SVR) for the coordinated control of the RSC and GSC in DFIG-based wind turbine systems (WTSs).
- To lessen mechanical torque oscillations and rotor speed overshoot in windy and variable conditions.
- To strengthen DC-link voltage regulation and the system’s capacity to effectively control the flow of active and reactive power.
- To evaluate and validate the performance of the proposed SVR controller against conventional PI and other advanced controllers through extensive time-domain simulations.
- To establish the computational efficiency, robustness, and real-time applicability of the SVR-based control framework in dynamic and fault-prone grid environments.
1.7. Contributions
- Designed an SVR-based intelligent controller for real-time optimization of RSCs and GSCs in DFIG-based wind turbine systems.
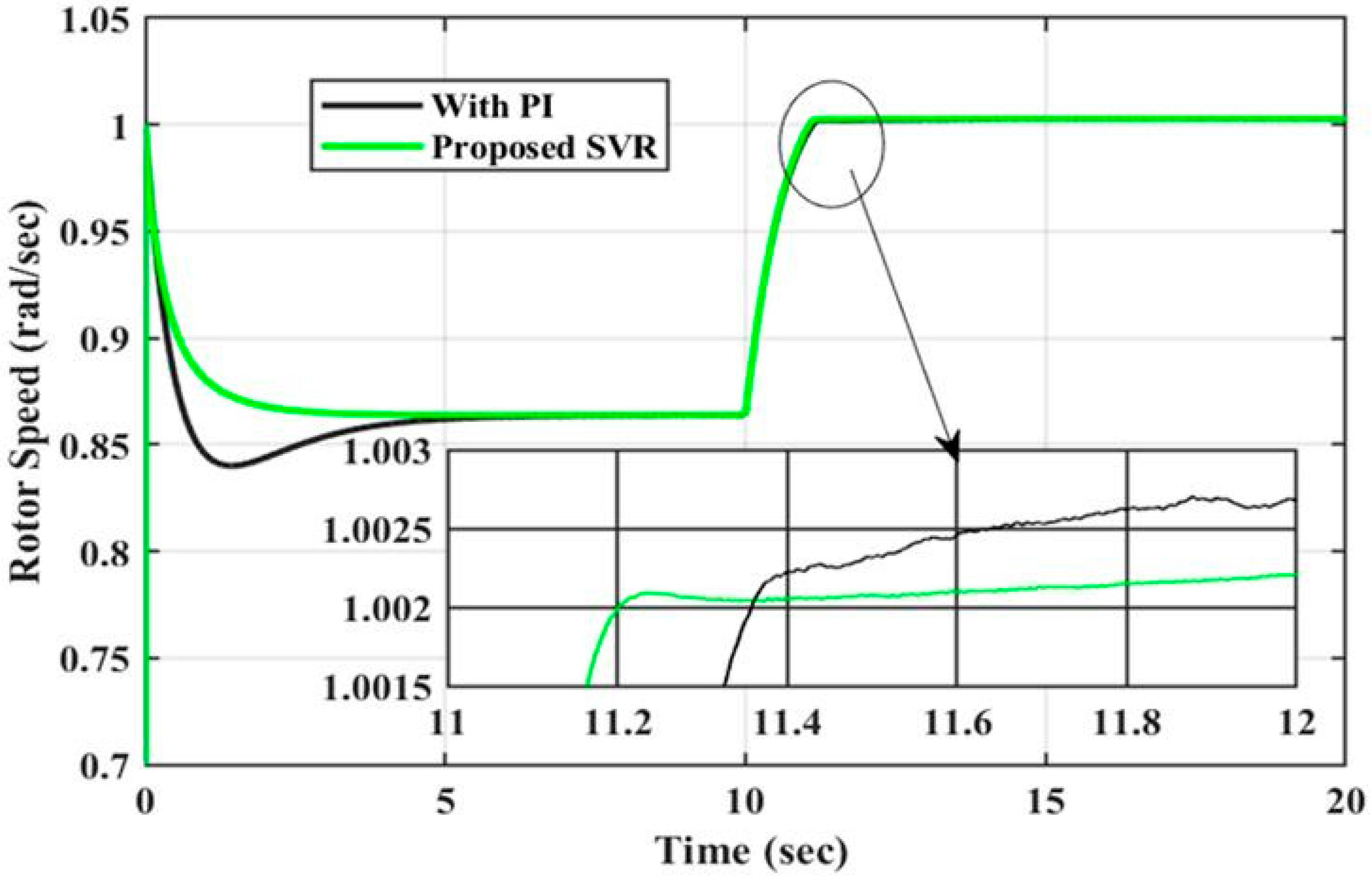
- Improved dynamic performance with ~17.2% less rotor speed overshoot and 30.2% faster settling time compared to PI controllers.
- Outperformed hybrid ANFIS-PI controllers with 8.3% lower overshoot, 12.4% quicker settling, and reduced computational complexity.
- Achieved accurate, scalable control without requiring large training datasets, ensuring feasibility for real-time grid integration.
2. Mathematical Modeling and Configuration of WECS Components
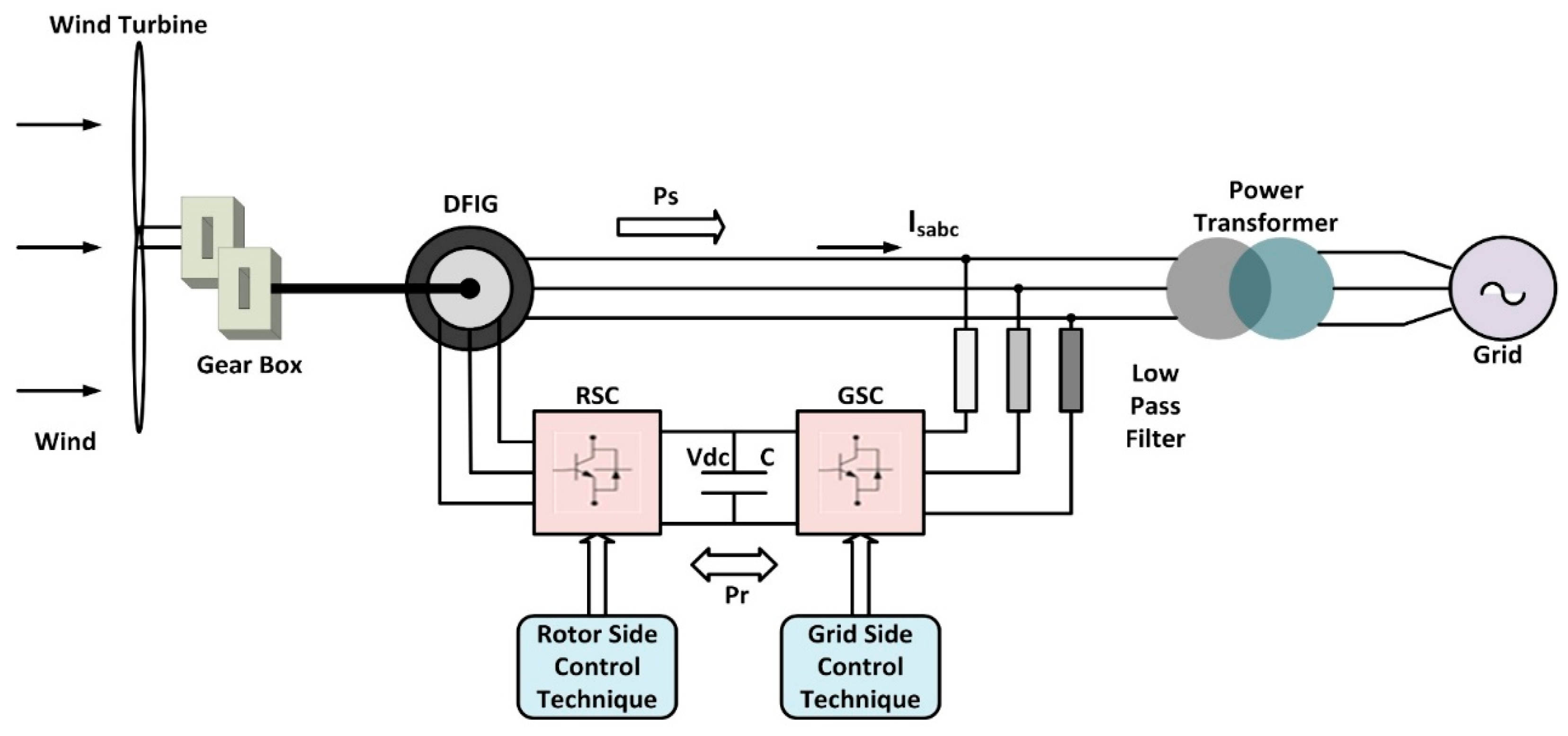
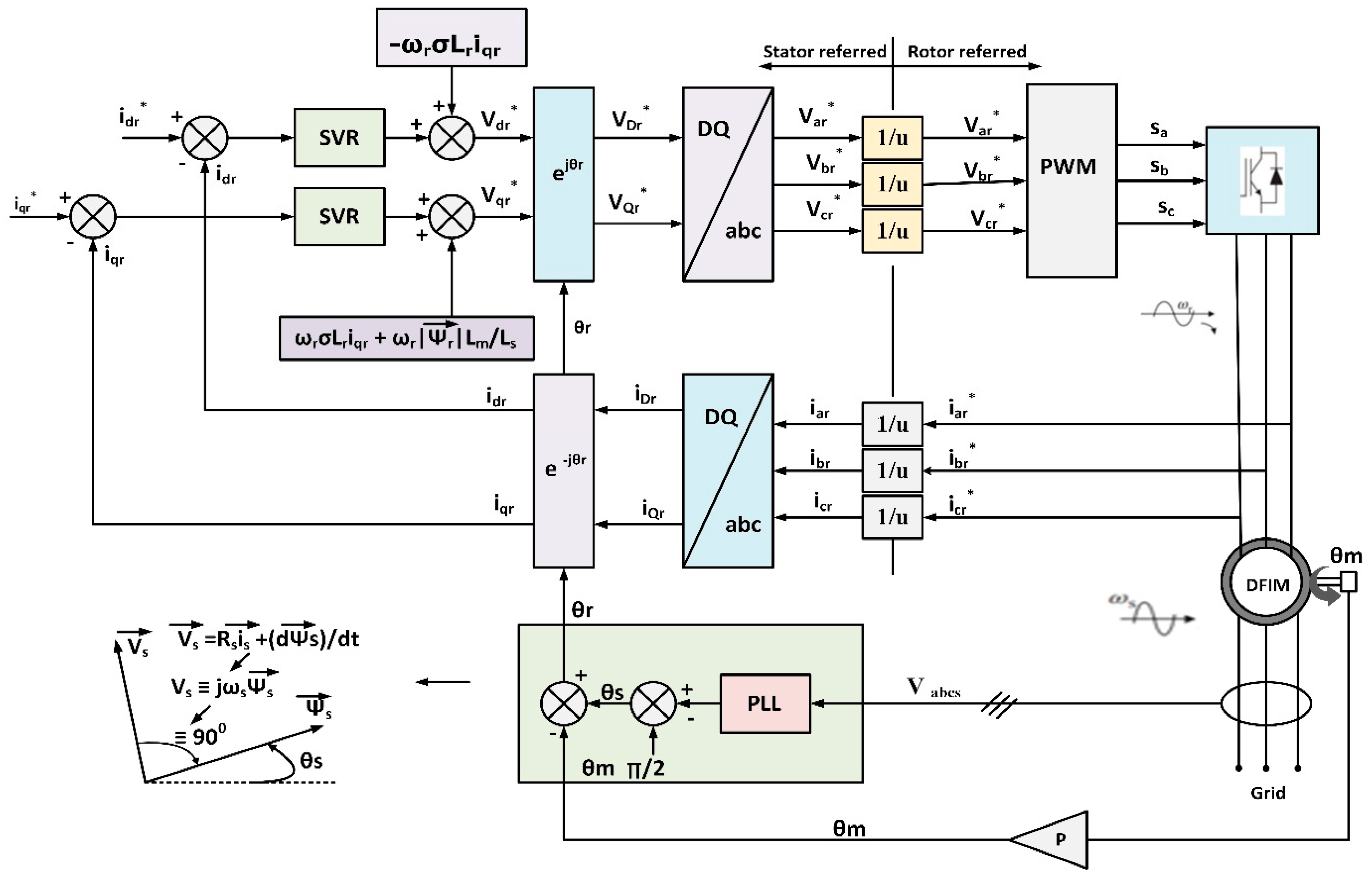
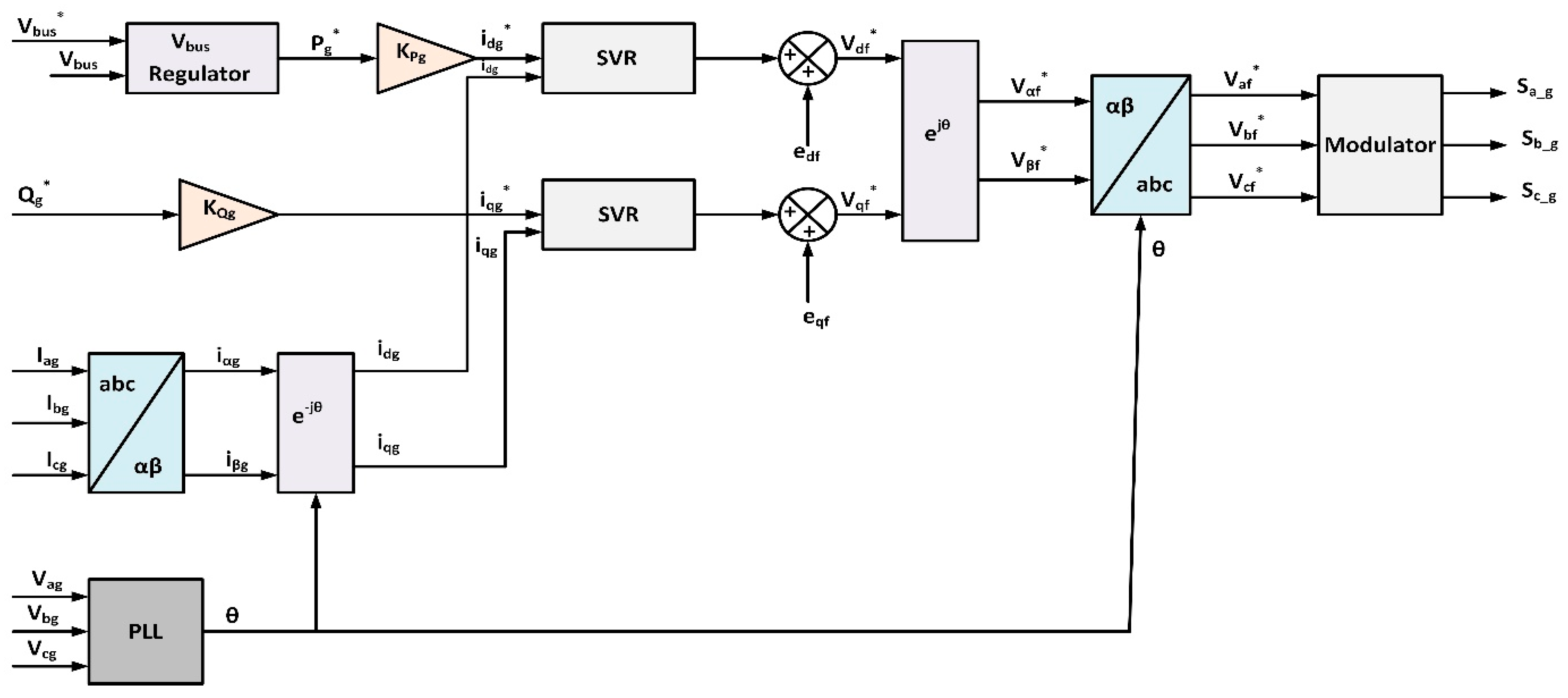
2.1. System Configuration
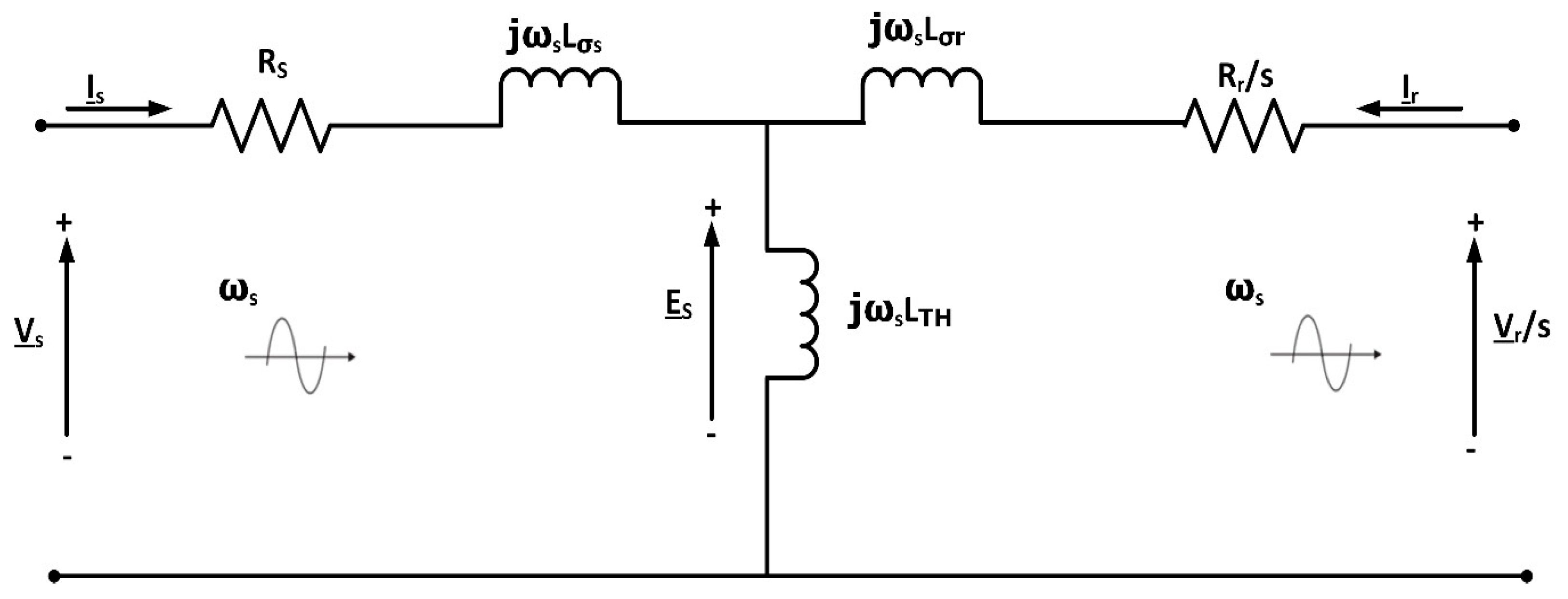
2.2. Dynamic Modeling of DFIG
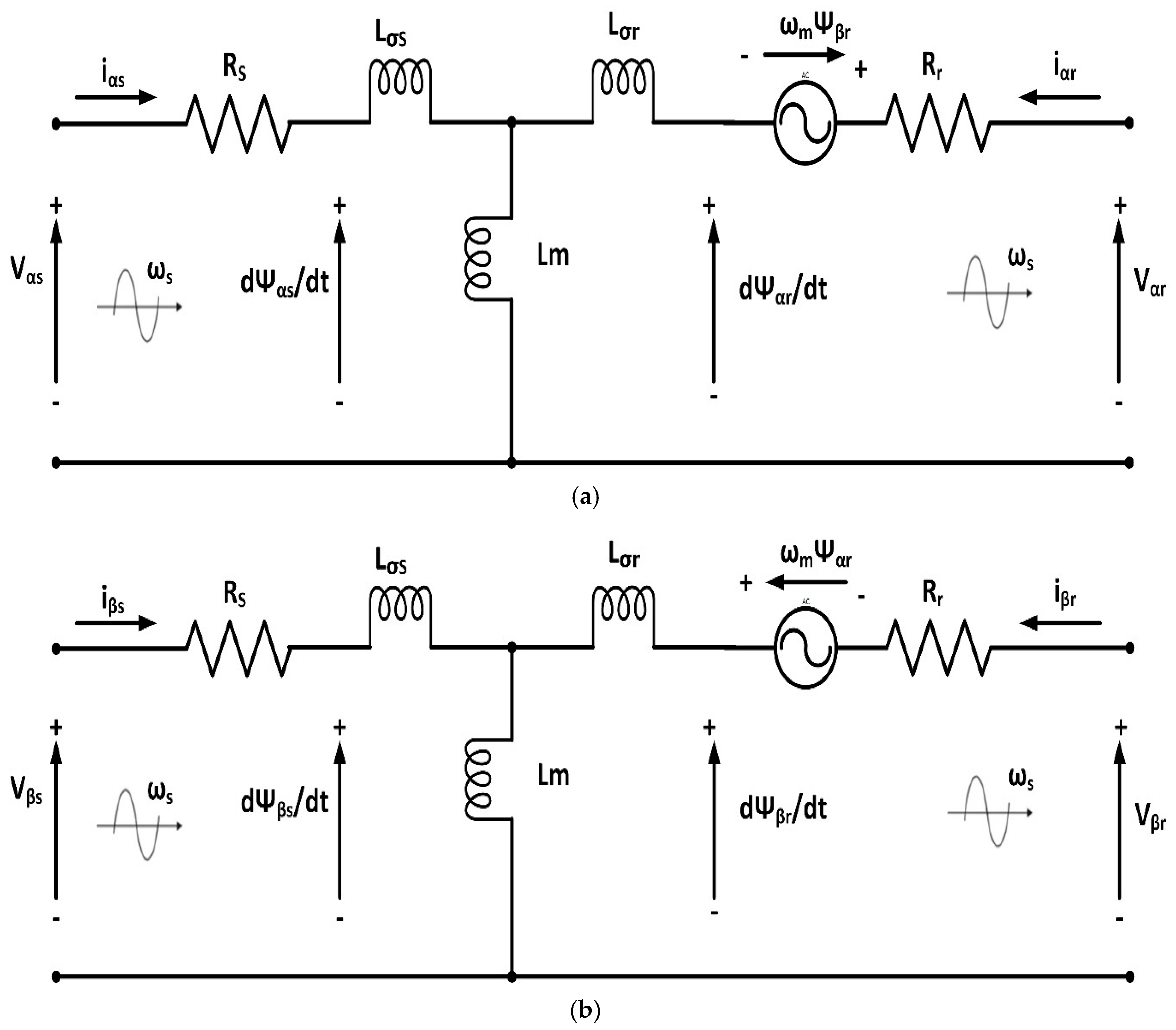
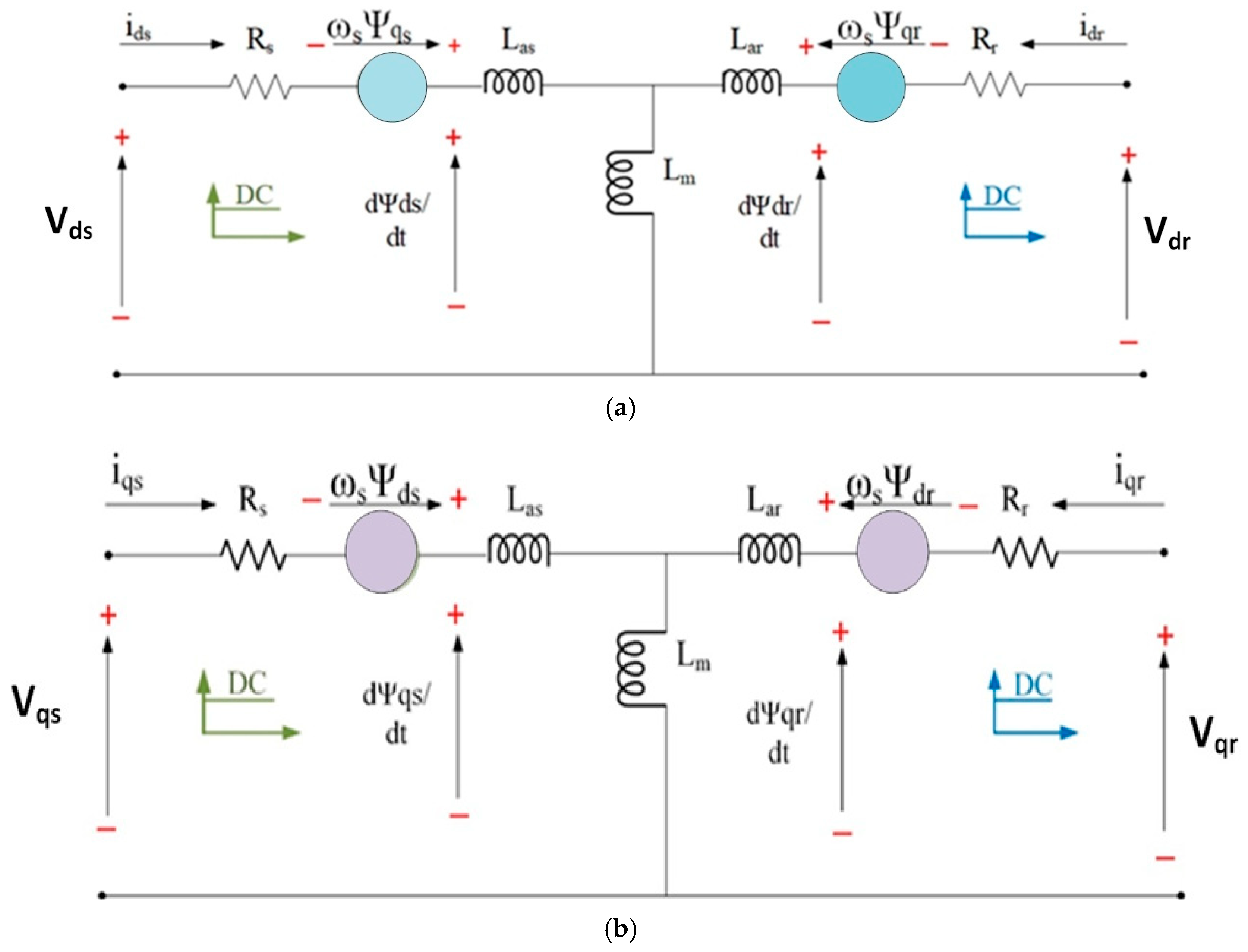
2.2.1. αβ Modeling
2.2.2. dq Modeling of DFIG
2.3. DFIG in State-Space Equations
2.4. Active, Reactive Power and Torque Calculation
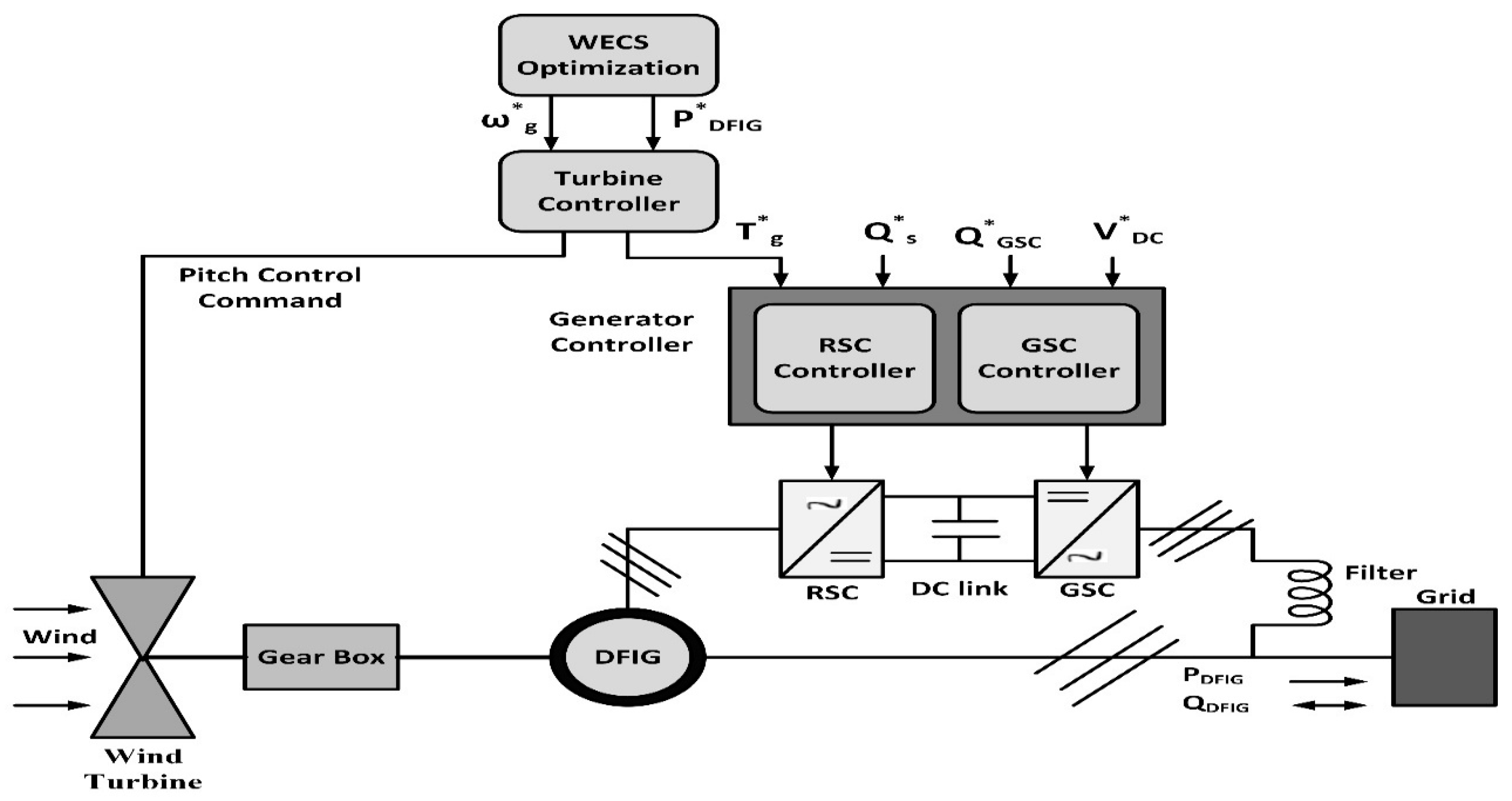
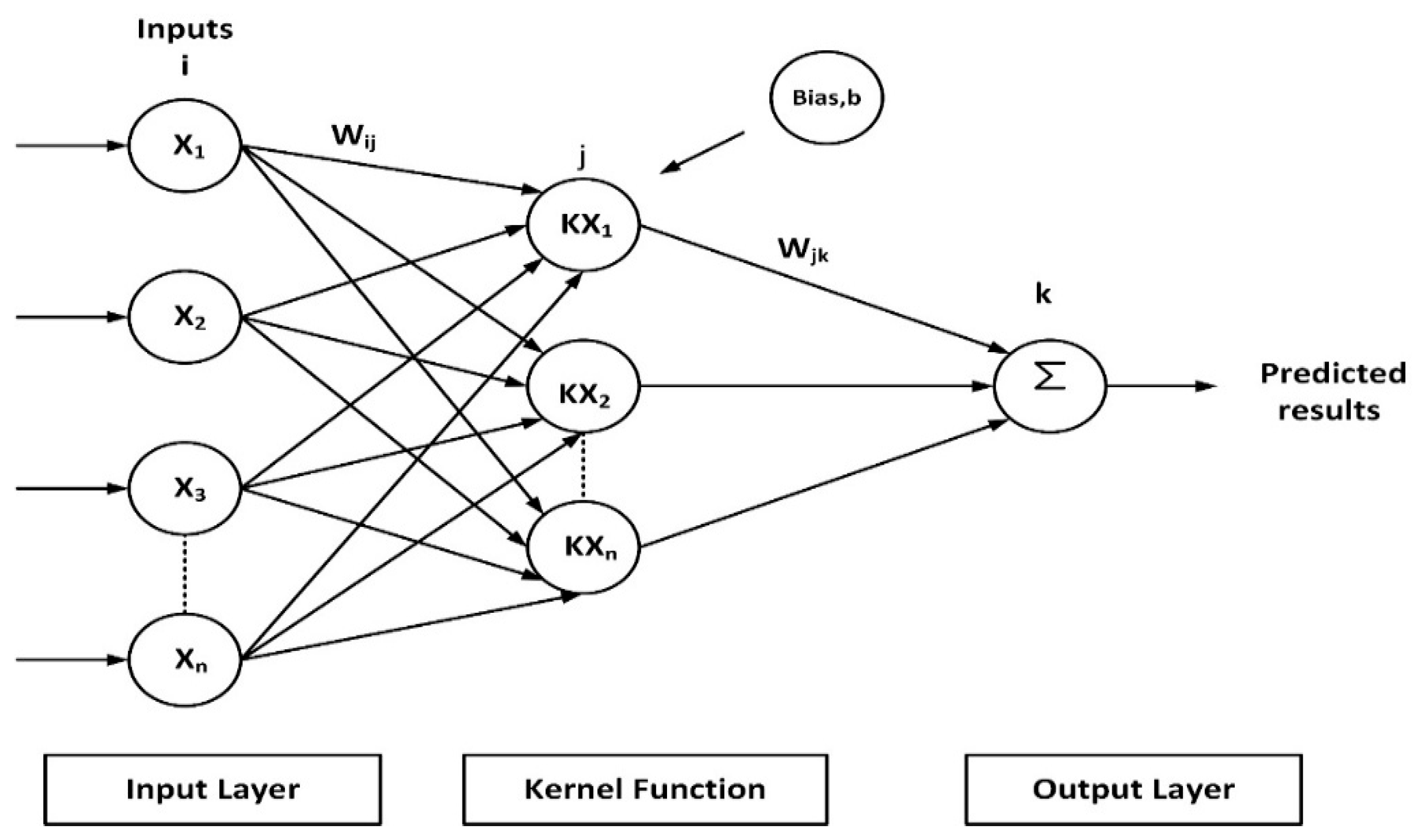
3. Proposed Support Vector Regression (SVR)-Based Controller
Implementation of Proposed SVR-Based Controller in WECS Model
- Training Set (65%)—Used to train the SVR model by optimizing support vectors, kernel function parameters (e.g., RBF kernel width), and penalty coefficients. This phase ensures the model captures the underlying dynamics of the system based on simulation data.
- Validation Set (15%)—Utilized during the training process to fine-tune the SVR model and prevent overfitting. This subset helps adjust the model to generalize well to new, unseen data conditions.
- Testing Set (20%)—Independently used to evaluate the predictive accuracy and control performance of the trained SVR model.
4. Result and Discussion
4.1. Computational Performance and Real-Time Feasibility
4.2. Statistical Validation of SVR Performance
5. Limitation of the Proposed Method
- The SVR model has a relatively high number of support vectors (42,977), which represent approximately 10.7% of the dataset. This increases the model’s computational complexity and may limit scalability in real-time or embedded applications. Although this configuration yielded strong predictive accuracy, it reflects a trade-off between model performance and compactness.
- The current work evaluates the SVR controller under a step-change wind profile, which, while effective for initial validation, does not encompass the full spectrum of dynamic operating conditions. Scenarios such as wind turbulence, random noise, and grid disturbances were not included in this study. Future work will extend testing to include these complex conditions to assess controller robustness and real-world applicability.
- While experimental validation is highly valuable, it was not feasible within the current scope due to resource and infrastructure limitations. However, we fully acknowledge this limitation and agree that future work should involve hardware-in-the-loop (HIL) testing or real-time lab-scale implementation using digital control platforms (e.g., dSPACE, OPAL-RT, or FPGA-based controllers) to validate the controller’s practical performance, latency, and robustness under real-world disturbances.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- GWEC: Global Wind Report 2024. Global Wind Energy Council. 2024. Available online: https://www.gwec.net/ (accessed on 2 June 2025).
- Hete, R.R.; Shrivastava, T.; Dash, R.; Anupallavi, L.; Fathima, M.; Reddy, K.J.; Dhanamjayalu, C.; Mohammad, F.; Khan, B. Design and develop a PI controller for DFIG grid integration using a neural tuning method ensembled with dense plexus terminals. Sci. Rep. 2024, 14, 7916. [Google Scholar] [CrossRef]
- Sahito, G.M.; Korai, J.J.; Korai, M.B.; Shaikh, A.R.S. Design of PI controller for wind energy conversion system using MATLAB/Simulink. Int. J. Electr. Eng. Emerg. Technol. 2022, 5, 6–10. [Google Scholar]
- Chojaa, H.; Derouich, A.; Chehaidia, S.E.; Taoussi, M.; Zamzoum, O.; Mosaad, M.I.; Benbouhenni, H. Advanced Control Techniques for Doubly-Fed Induction Generators Based Wind Energy Conversion Systems. In Proceedings of the 2022 Global Energy Conference (GEC), Batman, Turkey, 26–29 October 2022; pp. 282–287. [Google Scholar] [CrossRef]
- Boudjema, Z.; Taleb, R.; Djeriri, Y.; Yahdou, A. A novel direct torque control using second order continuous sliding mode of a doubly fed induction generator for a wind energy conversion system. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 965–975. [Google Scholar] [CrossRef]
- Bekhada, H.; Boudjema, Z.; Golea, A.; Benalla, H. Comparative study of PI, RST, sliding mode and fuzzy supervisory controllers for DFIG based wind energy conversion system. Int. J. Renew. Energy Res. 2015, 5, 1174–1185. [Google Scholar] [CrossRef]
- Mohammed, A.; Ahmed, E.; Tamou, N.; Haitam, C. Comparative analysis of ADRC & PI controllers used in wind turbine system driving a DFIG. Int. J. Renew. Energy Res. 2017, 7, 1816–1824. [Google Scholar] [CrossRef]
- Chetouani, E. Self-adapting PI controller for grid-connected DFIG wind turbines based on recurrent neural network optimization control under unbalanced grid faults. Electr. Power Syst. Res. 2023, 214, 108829. [Google Scholar] [CrossRef]
- Nadour, M.; Essadki, A.; Nasser, T. Comparative analysis between PI and backstepping control strategies of DFIG driven by wind turbine. Int. J. Renew. Energy Res. 2017, 7, 1307–1316. [Google Scholar] [CrossRef]
- Sara, M.; Ahmed, E.; Tamou, N.; Badr, B.I. An efficient nonlinear backstepping controller approach of a wind energy conversion system based on a DFIG. Int. J. Renew. Energy Res. 2017, 7, 1520–1528. [Google Scholar] [CrossRef]
- Adel, K.; Nihel, K.; Mohamed, F.M. Wind energy conversion system using DFIG controlled by backstepping and sliding mode strategies. Int. J. Renew. Energy Res. 2012, 2, 421–430. [Google Scholar]
- Lekhchine, S.; Rayane, L. Fuzzy logic controller-based power control of DFIG based on wind energy systems. Int. J. Smart Grid 2024, 8, 74–80. [Google Scholar]
- Sanjeev, K.G.; Sundram, M.; Madhu, S. Performance enhancement of DFIG based grid connected SHPP using ANN controller. Int. J. Renew. Energy Res. 2019, 9, 1165–1179. [Google Scholar] [CrossRef]
- Ismail, M.M.; Bendary, A.F. Protection of DFIG wind turbine using fuzzy logic control. Alex. Eng. J. 2016, 55, 2437–2446. [Google Scholar] [CrossRef]
- El Azzaoui, M.; Mahmoudi, H. Fuzzy-PI control of a doubly fed induction generator-based wind power system. Int. J. Autom. Control 2017, 11, 123–135. [Google Scholar] [CrossRef]
- Maafa, A.; Mellah, H.; Benaouicha, K.; Babes, B.; Yahiou, A.; Sahraoui, H. Fuzzy Logic-Based Smart Control of Wind Energy Conversion System Using Cascaded Doubly Fed Induction Generator. Sustainability 2024, 16, 9333. [Google Scholar] [CrossRef]
- Kasbi, A.; Rahali, A. Adaptive FOPI controller based on the fuzzy supervisory for wind power conversion system equipped by DFIG. Int. Trans. Electr. Energy Syst. 2021, 31, e12892. [Google Scholar] [CrossRef]
- Rodríguez, J.A. Meta-heuristic Algorithm and Laser Projection for Adjusting the Model of the Last Lower Surface to a Footprint. Biomimetics 2024, 9, 699. [Google Scholar] [CrossRef] [PubMed]
- Dardabi, C.; Cóbreces Álvarez, S.; Djebli, A. An artificial-neural-network-based direct power control approach for doubly fed induction generators in wind power systems. Energies 2025, 18, 1989. [Google Scholar] [CrossRef]
- Ngamroo, I. Review of DFIG wind turbine impact on power system dynamic performances. IEEJ Trans. Electr. Electron. Eng. 2017, 12, 301–311. [Google Scholar] [CrossRef]
- Dzung, P.Q.; Bao, A.N.; Lee, H.H. New artificial neural network based direct virtual torque control and direct power control for DFIG in wind energy systems. In Proceedings of the 2011 IEEE Ninth International Conference on Power Electronics and Drive Systems, Singapore, 5–8 December 2011; pp. 219–227. [Google Scholar]
- Maafa, A.; Mellah, H.; Sahraoui, H.; Yahiou, A. Performance Improvement of a DPC-FPID Strategy with Matrix Converter Using CDFIG in Wind Power System. Wind. Eng. 2025, 49, 375–386. [Google Scholar] [CrossRef]
- Vu, N.T.T.; Nguyen, H.D.; Nguyen, A.T. Reinforcement Learning-Based Adaptive Optimal Fuzzy MPPT Control for Variable Speed Wind Turbine; IEEE Access: New York, NY, USA, 2022; pp. 95771–95780. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Al-Saud, M.S.; Sayed, K. Sensorless active and reactive control for DFIG wind turbines using opposition-based learning technique. Sustainability 2020, 12, 3583. [Google Scholar] [CrossRef]
- Wang, D.; Xu, M.; Zhu, G.; Luo, F.; Gao, J.; Chen, Y. Enhancing Wind Power Forecasting Accuracy through LSTM with Adaptive Wind Speed Calibration (C-LSTM). Sci. Rep. 2025, 15, 5352. [Google Scholar] [CrossRef]
- Krevnevičiūtė, J.; Mitkevičius, A.; Naujokaitis, D.; Lagzdinytė-Budnikė, I.; Marčiukaitis, M. The Forecast of the Wind Turbine Generated Power Using Hybrid (LTC + XGBoost) Model. Appl. Sci. 2024, 15, 7615. [Google Scholar] [CrossRef]
- Kamal, S.A.; Li, Y. Wind power forecasting based on support vector regression and particle swarm optimization. IEEE Trans. Sustain. Energy 2019, 10, 208–215. [Google Scholar]
- Abo-Khalil, A.G.; Lee, D.C. MPPT control of wind generation systems based on estimated wind speed using SVR. IEEE Trans. Ind. Electron. 2008, 55, 1489–1490. [Google Scholar] [CrossRef]
- Chhipa, A.A.; Kumar, V.; Joshi, R.R.; Chakrabarti, P.; Jasinski, M.; Burgio, A.; Chakrabarti, T. Adaptive neuro-fuzzy inference system-based maximum power tracking controller for variable speed WECS. Energies 2021, 14, 6275. [Google Scholar] [CrossRef]
- Xia, S.; Chen, Z.; Zhu, Y. Performance comparison of SVR-based and PI-based controllers for grid-connected wind turbines. Energies 2021, 14, 2631. [Google Scholar]
- Yan, X.; Cheng, M. Backstepping-based direct power control for dual-cage rotor brushless doubly fed induction generator. IEEE Trans. Power Electron. 2023, 38, 2668–2680. [Google Scholar]
- Fezai, R.; Dhibi, K.; Mansouri, M.; Trabelsi, M.; Hajji, M.; Bouzrara, K.; Nounou, H.; Nounou, M. Effective Random Forest-Based Fault Detection and Diagnosis for Wind Energy Conversion Systems. IEEE Sens. J. 2021, 21, 6914–6921. [Google Scholar] [CrossRef]
- Tavoosi, J.; Mohammadzadeh, A.; Pahlevanzadeh, B.; Kasmani, M.B.; Band, S.S.; Safdar, R.; Mosavi, A.H. A Machine Learning Approach for Active/Reactive Power Control of Grid-connected Doubly-fed Induction Generators. Ain. Shams. Eng. J. 2022, 13, 101564. [Google Scholar] [CrossRef]
- Shaque, M.; Laghari, J.A.; Bhayo, M.A.; Chandio, S.; Mahariq, I. Hybrid ANFIS-PI-Based Robust Control of Wind Turbine Power Generation System. Int. Trans. Electr. Energy Syst. 2024, 2024, 2389751. [Google Scholar]
- Nasim, F.; Khatoon, S.; Ibraheem Urooj, S.; Shahid, M.; Ali, A.; Nasser, N. Hybrid ANFIS-PI-Based Optimization for Improved Power Conversion in DFIG Wind Turbine. Sustainability 2025, 17, 2454. [Google Scholar] [CrossRef]
- Ouhssain, S.; Chojaa, H.; Aljarhizi, Y.; Al Ibrahmi, E.; Maarif, A.; Mossa, M.A. Enhancing the Performance of a Wind Turbine Based DFIG Generation System Using an Effective ANFIS Control. Int. J. Robot. Control Syst. 2024, 4, 1617–1640. [Google Scholar] [CrossRef]
- Martínez, J.C.; Amenedo, J.L.R.; Gómez, S.A.; Alonso-Martínez, J. Grid-forming control of doubly-fed induction generators based on the rotor flux orientation. Renew. Energy 2023, 207, 162–176. [Google Scholar] [CrossRef]
- Mossa, M.A.; Echeikh, H.; Iqbal, A. Enhanced control technique for a sensor-less wind driven doubly fed induction generator for energy conversion purpose. Energy Rep. 2021, 7, 5815–5833. [Google Scholar] [CrossRef]
- Boubzizi, S.; Abid, H.; El Hajjaji, A.; Chaabane, M. Comparative study of three types of controllers for DFIG in wind energy conversion system. Prot. Control Mod. Power Syst. 2018, 3, 21. [Google Scholar] [CrossRef]
- Nasim, F.; Khatoon, S.; Shahid, M.; Baranwal, S.; Ahmad Wani, S. Ziegler-Nichols Based Controller Optimization for DFIG Wind Turbines. Tuijin Jishu/J. Propuls. Technol. 2024, 45, 2024. [Google Scholar] [CrossRef]
- Ibrahim, A.K. 1.5MW DFIG Wind Turbine with Variable Speed Operation Connected to a Grid, MATLAB Central File Exchange. 2025. Available online: https://www.mathworks.com/matlabcentral/fileexchange/58202-1-5mw-dfig-wind-turbine-with-variable-speed-operation-connected-to-a-grid (accessed on 2 June 2025).
- Nasim, F.; Khatoon, S.; Ibraheem; Shahid, M. Machine Learning Approach Using SVR for Optimized Control of DFIG Wind Turbine Systems. Arab. J. Sci. Eng. Under Rev. 2025. [Google Scholar]




| Serial Number | Ref. | Control Technique Implemented | Parameters Used | Input Signal | Advantages | Limitations | Training Required |
|---|---|---|---|---|---|---|---|
| 1. | [1,2,3,4,5] | PI controller | Rotor current, stator voltage | Variable wind speed | Simple design, effective for steady-state conditions, easy implementation | Fixed tuning, poor adaptability, degraded performance under nonlinear dynamics | No |
| 2. | [6,7,8] | 2DOF PI controller | Rotor current, stator voltage | Variable wind speed | Improves disturbance rejection, reduces overshoot | Still static in tuning, limited flexibility under highly dynamic grids | No |
| 3. | [9] | PI + Fuzzy | Rotor current, stator voltage | Variable wind speed | Better power quality, handles uncertainties better | More complex design, needs fuzzy tuning | No |
| 4. | [10] | ANN-based PI controller | Rotor current, stator voltage | Variable wind speed | Adapts dynamically, better for real-time control | Higher computational needs, training required | Yes |
| 5. | [11,12,13] | Fuzzy logic controllers (FLCs) | Stator voltage, reactive power | Variable wind conditions | Handles nonlinearities, no precise model needed, enhances stability | Complex design, requires expert rules, sensitive to membership design | No |
| 6. | [14,15,16] | Artificial neural networks (ANNs) | Active/reactive power, torque | Grid variations | Learns system dynamics, adapts to changes, accurate control | Needs large training dataset, risk of overfitting, black-box behavior | Yes |
| 7. | [17,18] | Hybrid ANFIS-PI controller | RSC and GSC parameters | Wind speed variation | Combines ANN and FLC, better controls accuracy, improves response time | High computational cost, complex tuning, long training | Yes |
| 8. | [19,20] | Extreme learning machine (ELM) | Rotor flux, stator voltage | Grid disturbances | Fast training speed, simple architecture | Sensitive to the number of hidden neurons | Yes |
| 9. | [21,22] | Random forest (RF) | Fault diagnosis parameters | Grid faults | High accuracy for classification tasks | Large memory requirements, limited real-time control | Yes |
| 10. | [23,24] | Reinforcement learning (RL) | Frequency, active/reactive power control | Variable wind and load | Self-learning capability, real-time adaptability | Long exploration time, high training cost | Yes |
| 11. | [25] | LSTM | MSE or MAE for regression | Time-series data (e.g., wind speed) | Handles temporal patterns, strong prediction capability | High training cost, large data requirement, not suited for real-time control | Yes |
| 12. | [26] | XGBoost | Usually “reg:squarederror” for regression | Static features | High accuracy, fast convergence | Not suitable for dynamic control loops, no temporal memory | Yes |
| 13. | [27] | SVR | Kernel, C, ε, support vectors | Wind speed, temperature, historical power output | Accurate wind power forecasting; robust to noisy inputs; generalizes well with limited data; suitable for nonlinear regression problems | Not designed for real-time control; requires preprocessed historical data | Yes |
| 14. | Proposed | SVR-based controller | RSC and GSC control parameters | Step wind speed change (10.0 m/s to 12.0 m/s) | Achieves a 17.2% decrease in rotor speed overshoot and enhances settling time by 30.2%, while maintaining low computational cost | Effectiveness depends on appropriate tuning of SVR parameters like kernel function and penalty values | Yes |
| Serial Number | Symbol | Parameter |
|---|---|---|
| 1. | Stator, rotor voltages of dq axis | |
| 2. | Stator, rotor currents of dq axis | |
| 3. | Rotor resistance | |
| 4. | Stator resistance | |
| 5. | Stator and rotor angular velocities | |
| 6. | Stator and rotor magnetic flux linkages | |
| 7. | dq axes stator flux components | |
| 8. | dq axes rotor flux components | |
| 9. | Stator and rotor windings leakage inductance | |
| 10. | Mutual inductance | |
| 11. | p | Pole pairs |
| 12. | Stator active and reactive power | |
| 13. | Rotor active and reactive power | |
| 14. | Electromagnetic torque | |
| 15. | Rotor’s inertia | |
| 16. | Load torque | |
| 17. | Rotor speed | |
| 18. | Friction coefficient | |
| 19. | J | Rotor inertia |
| 20. | Mechanical torque | |
| 21. | x | State vector |
| 22. | y | Yield vector |
| Serial Number | Symbol | Parameter | Value and Unit |
|---|---|---|---|
| 1. | Rated Power | 1.56 MVA | |
| 2. | Inductance | 0.312 pu | |
| 3. | DC Voltage | 1.154 KV | |
| 4. | Frequency | 50 Hz | |
| 5. | Rated L-L Voltage | 575.5 V | |
| 6. | Resistance | 0.00323 pu |
| Serial Number | Parameters | Value |
|---|---|---|
| 1. | Kernel Function | Gaussian (RBF) |
| 2. | Kernel Scale (σ) | 1 |
| 3. | Regularization Parameter (C) | 10 (Tuned via Grid Search) |
| 4. | Epsilon-insensitive Zone (ε) | 0.01(Tuned via Grid Search) |
| 5. | Dataset (Input–Output Pairs) | 400,001 |
| 6. | Test Input (V Wind) at 10 s | From 10.0 m/s to 12.0 m/s |
| 7. | No. of Inputs | 1 |
| 8. | No. of Outputs | 1 |
| 9. | Number of Support Vectors | 42,977 |
| 10. | Training Algorithm | SVR |
| Serial Number | Parameters | Value |
|---|---|---|
| 1. | MSE | 0.0067 |
| 2. | RMSE | 0.082 |
| 3. | MAE | 0.079 |
| 4. | R2 | 0.8 |
| Serial Number | Parameters | Value |
|---|---|---|
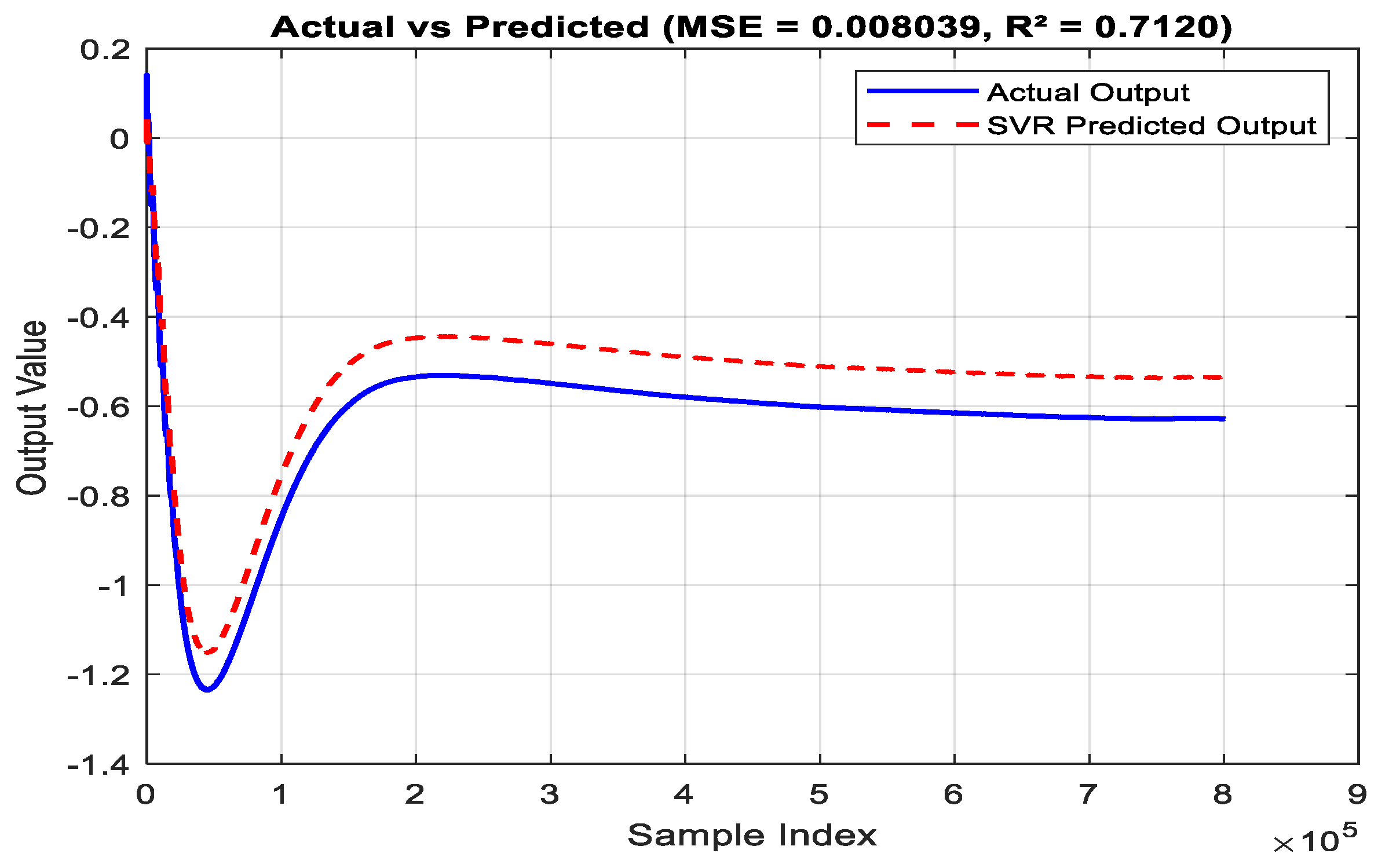
| 1. | MSE | 0.008 |
| 2. | RMSE | 0.089 |
| 3. | MAE | 0.089 |
| 4. | R2 | 0.71 |
| Serial Number | Parameters | Mean | SD | 95% Confidence Interval (±) |
|---|---|---|---|---|
| 1. | Rotor Speed Overshoot (%) | 0.0 | 0.12 | ±0.04 |
| 2. | Torque Overshoot (%) | 1.0 | 0.20 | ±0.07 |
| 3. | Settling Time (s) | 2.1 | 0.25 | ±0.09 |
| 4. | DC-link Voltage Error (V) | 0 | 0.18 | ±0.06 |
| Serial Number | Parameter | Control Scheme | Rise Time (s) | Overshoot (%) | Settling Time (s) | Steady-State Error |
|---|---|---|---|---|---|---|
| 1. | Rotor Speed | With PI | 2.5 | 6.5 | 6.0 | 0.002 |
| With SVR | 1.4 | 0 | 1.8 | 0 | ||
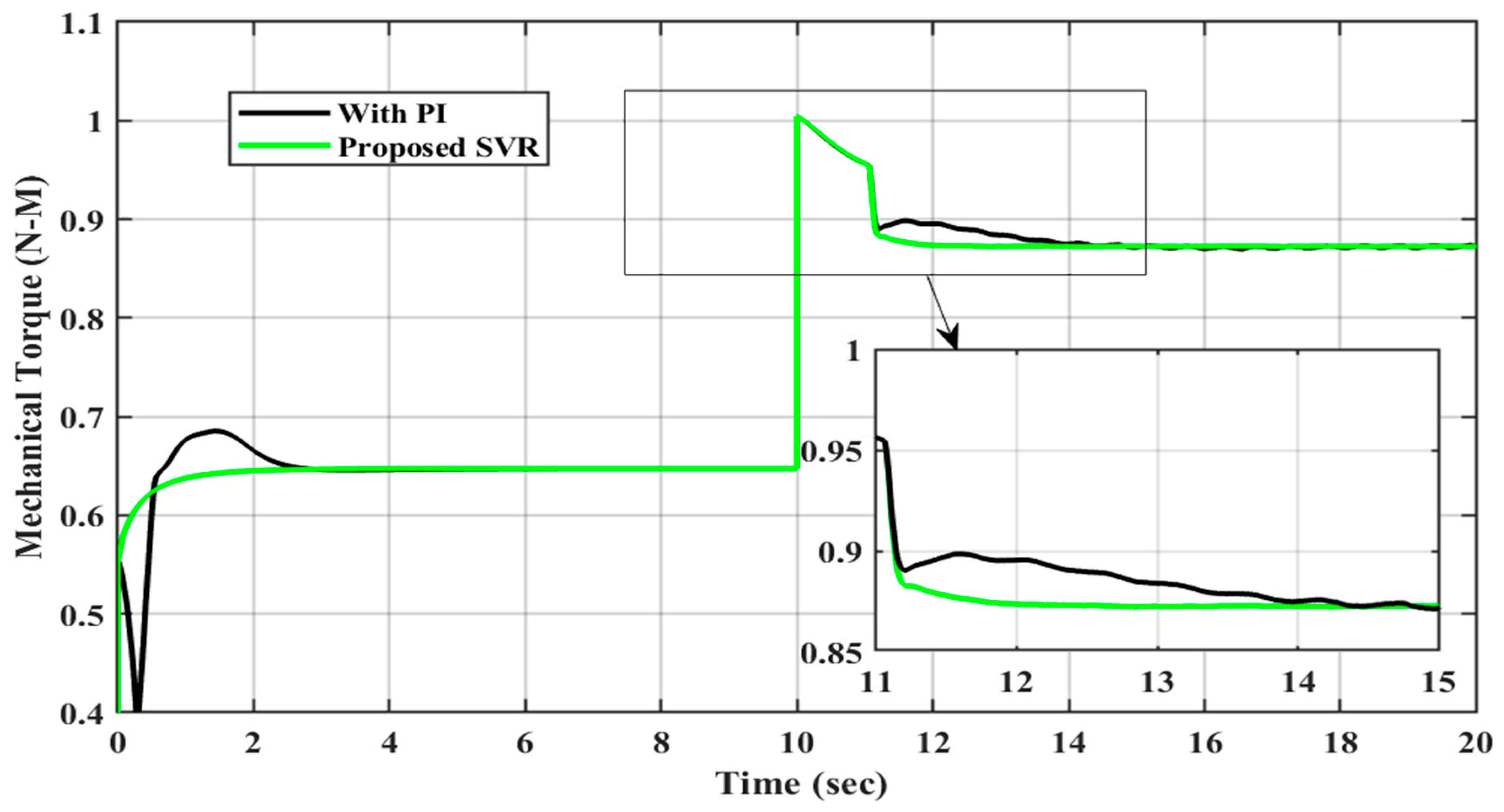
| 2. | Torque | With PI | 2.2 | 9 | 6.0 | 0.004 |
| With SVR | 1.4 | 1 | 2.0 | 0 | ||
| 3. | Active Power | With PI | 2.0 | 14 | 6.5 | 0.003 |
| With SVR | 1.4 | 1 | 2.5 | 0 | ||
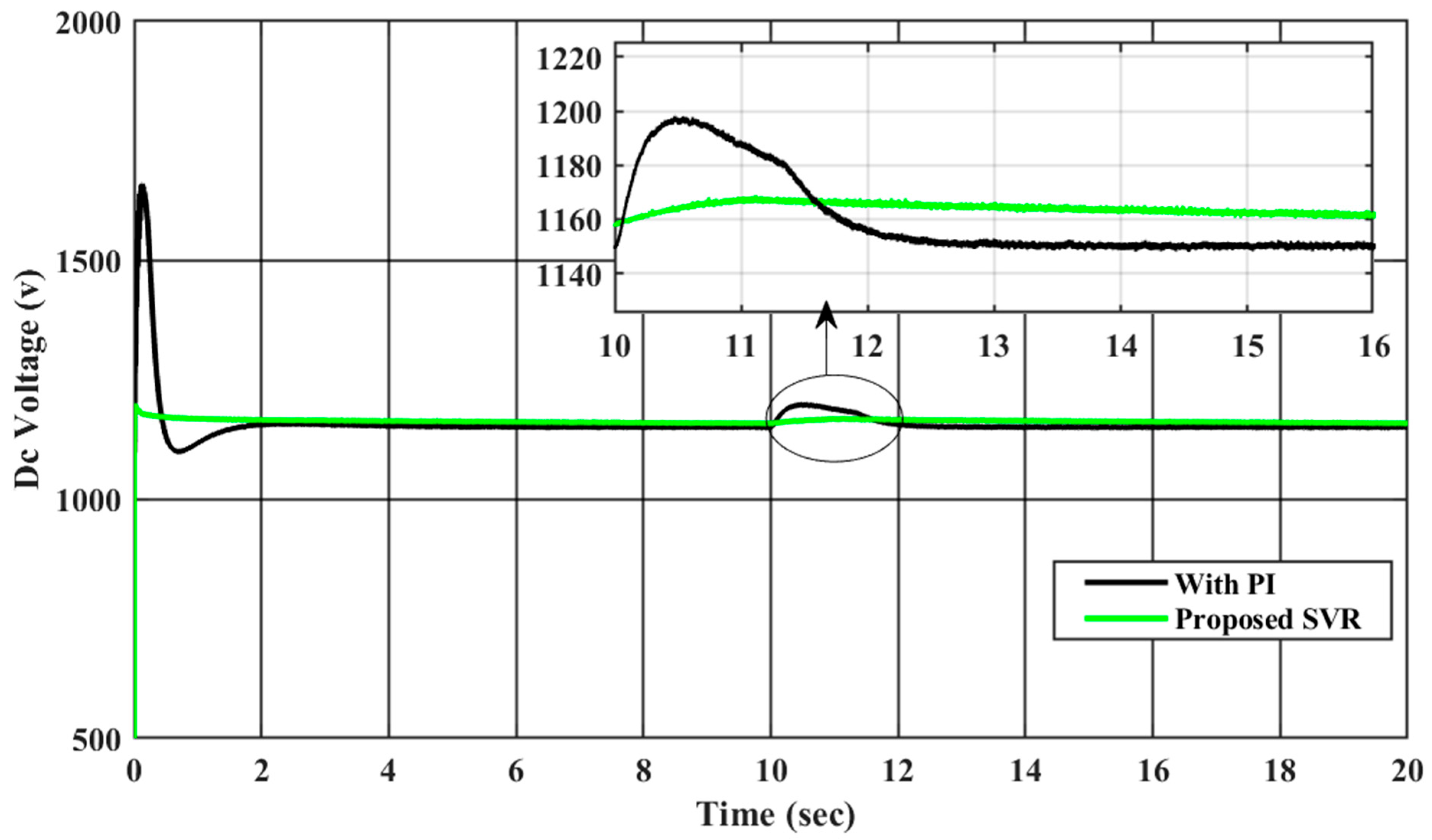
| 4. | DC Bus Voltage | With PI | 2.5 | 6.5 | 8.5 | 5 |
| With SVR | 1.5 | 1 | 2.5 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nasim, F.; Khatoon, S.; Nasiruddin, I.; Shahid, M.; Urooj, S.; Bilal, B. Support-Vector-Regression-Based Intelligent Control Strategy for DFIG Wind Turbine Systems. Machines 2025, 13, 687. https://doi.org/10.3390/machines13080687
Nasim F, Khatoon S, Nasiruddin I, Shahid M, Urooj S, Bilal B. Support-Vector-Regression-Based Intelligent Control Strategy for DFIG Wind Turbine Systems. Machines. 2025; 13(8):687. https://doi.org/10.3390/machines13080687
Chicago/Turabian StyleNasim, Farhat, Shahida Khatoon, Ibraheem Nasiruddin, Mohammad Shahid, Shabana Urooj, and Basel Bilal. 2025. "Support-Vector-Regression-Based Intelligent Control Strategy for DFIG Wind Turbine Systems" Machines 13, no. 8: 687. https://doi.org/10.3390/machines13080687
APA StyleNasim, F., Khatoon, S., Nasiruddin, I., Shahid, M., Urooj, S., & Bilal, B. (2025). Support-Vector-Regression-Based Intelligent Control Strategy for DFIG Wind Turbine Systems. Machines, 13(8), 687. https://doi.org/10.3390/machines13080687







