Nose-Wheel Steering Control via Digital Twin and Multi-Disciplinary Co-Simulation
Abstract
1. Introduction
2. Materials and Methods
2.1. Ground Taxiing Dynamics Modeling Based on Digital Twin
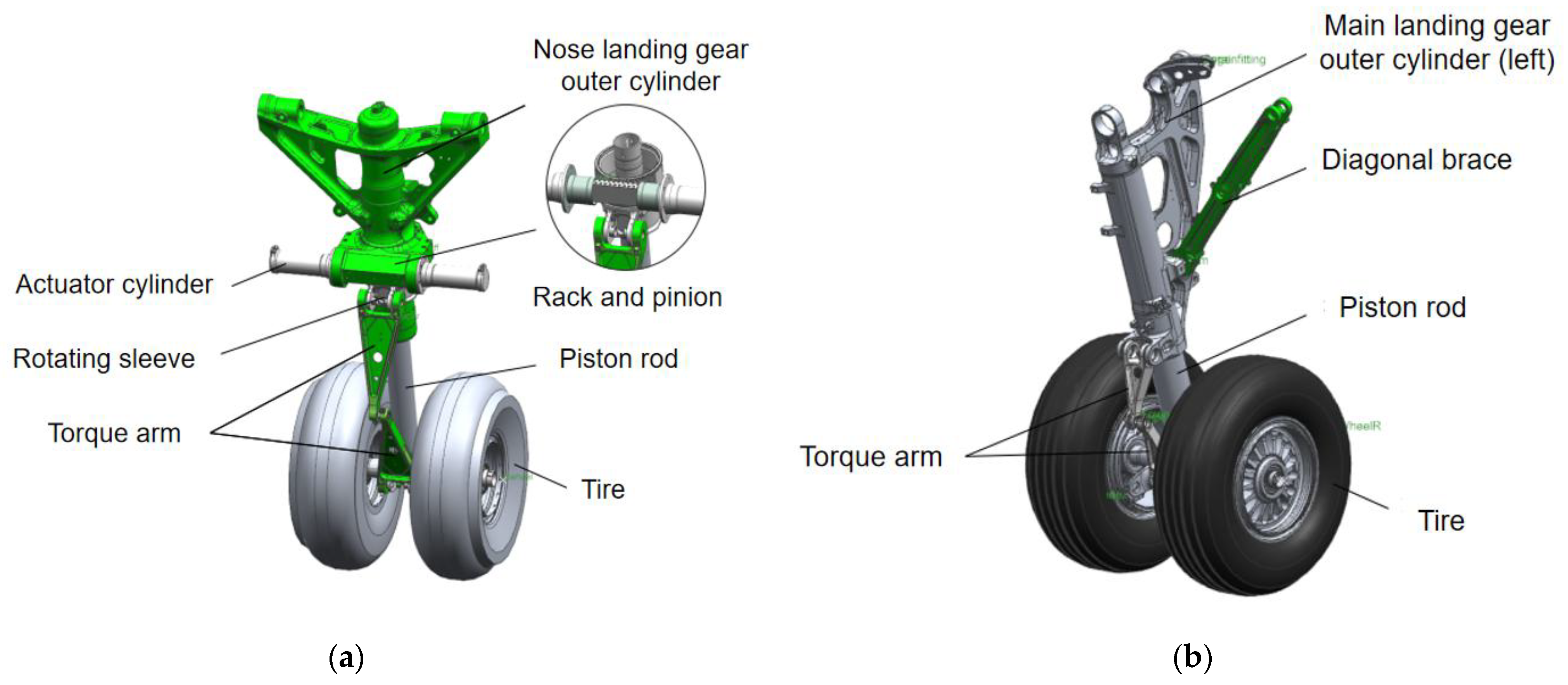
2.1.1. Landing Gear Model Simplification
- Component simplification of landing gear: secondary components with negligible impact on steering—such as bolts, nuts, washers, and other fasteners—are omitted;
- Rigid-body assumption: all landing gear components (excluding tires) and associated structures are treated as rigid bodies, disregarding material elastic deformation and structural vibrations [19];
- Aerodynamic force exclusion: aerodynamic forces (lift, drag) acting on the nose-wheel during taxiing are neglected to avoid unnecessary higher-order nonlinear complexities.
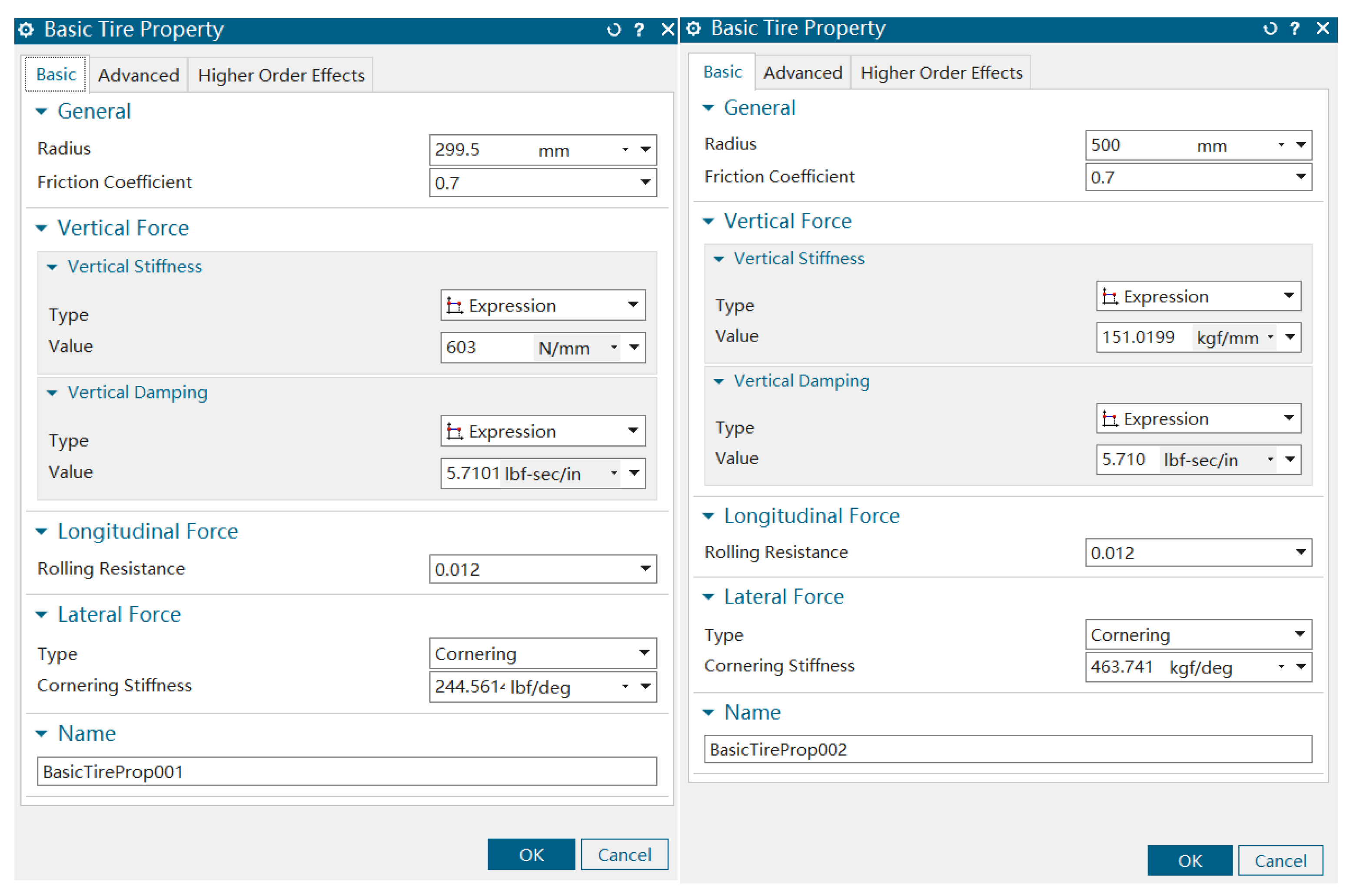
2.1.2. Tire Mechanical Model
2.1.3. Tire Subsystem
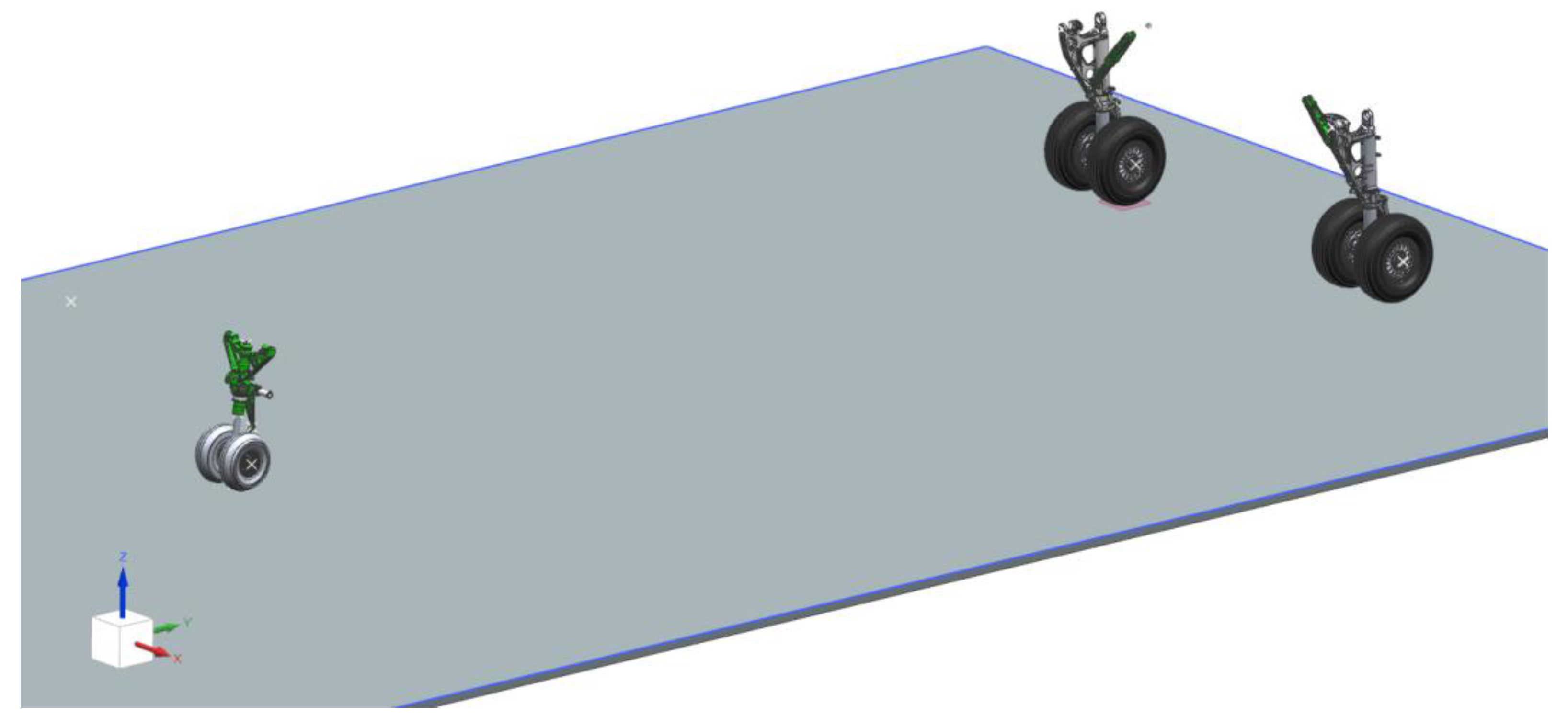
2.1.4. Full-Aircraft Virtual Model Construction
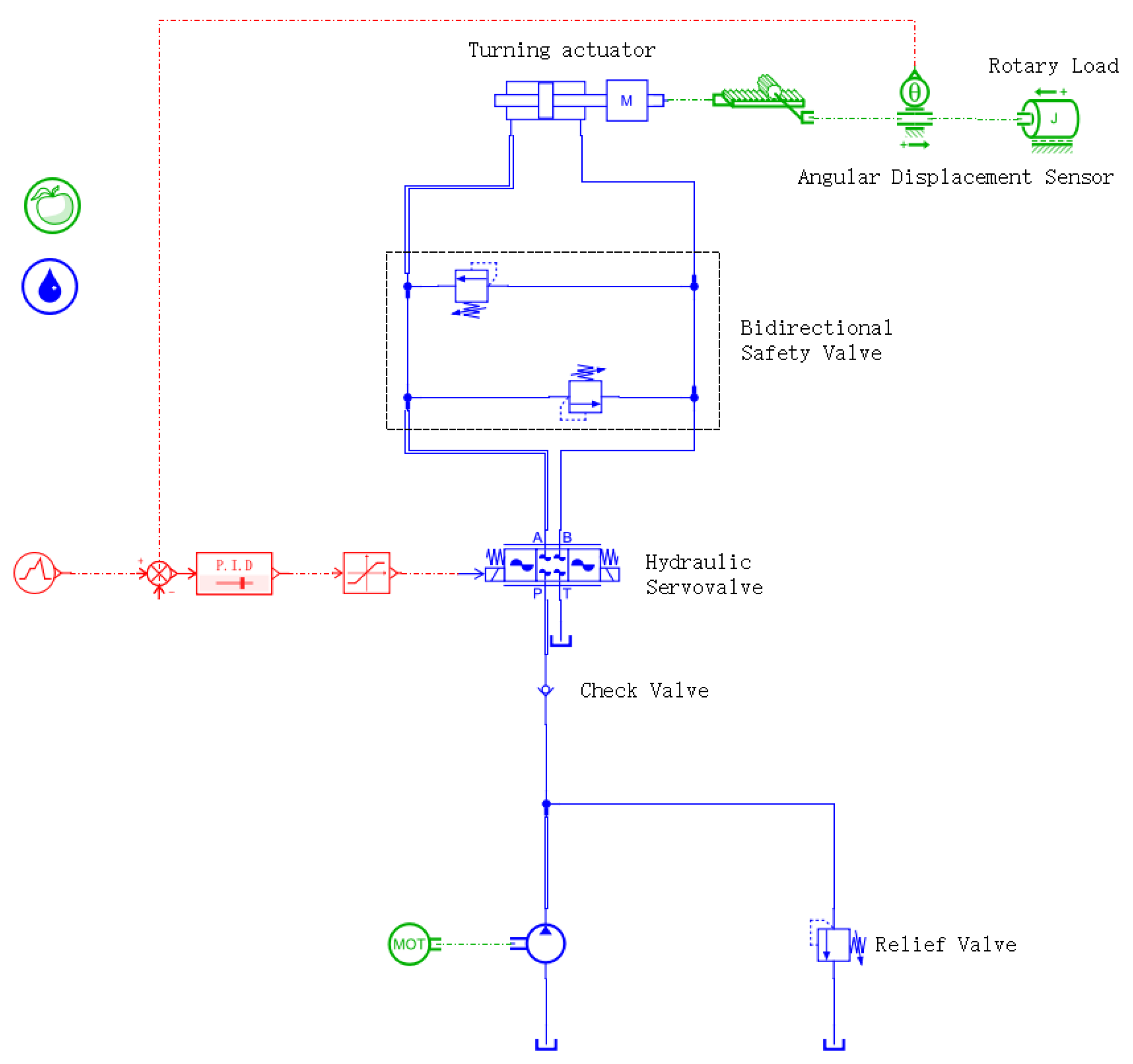
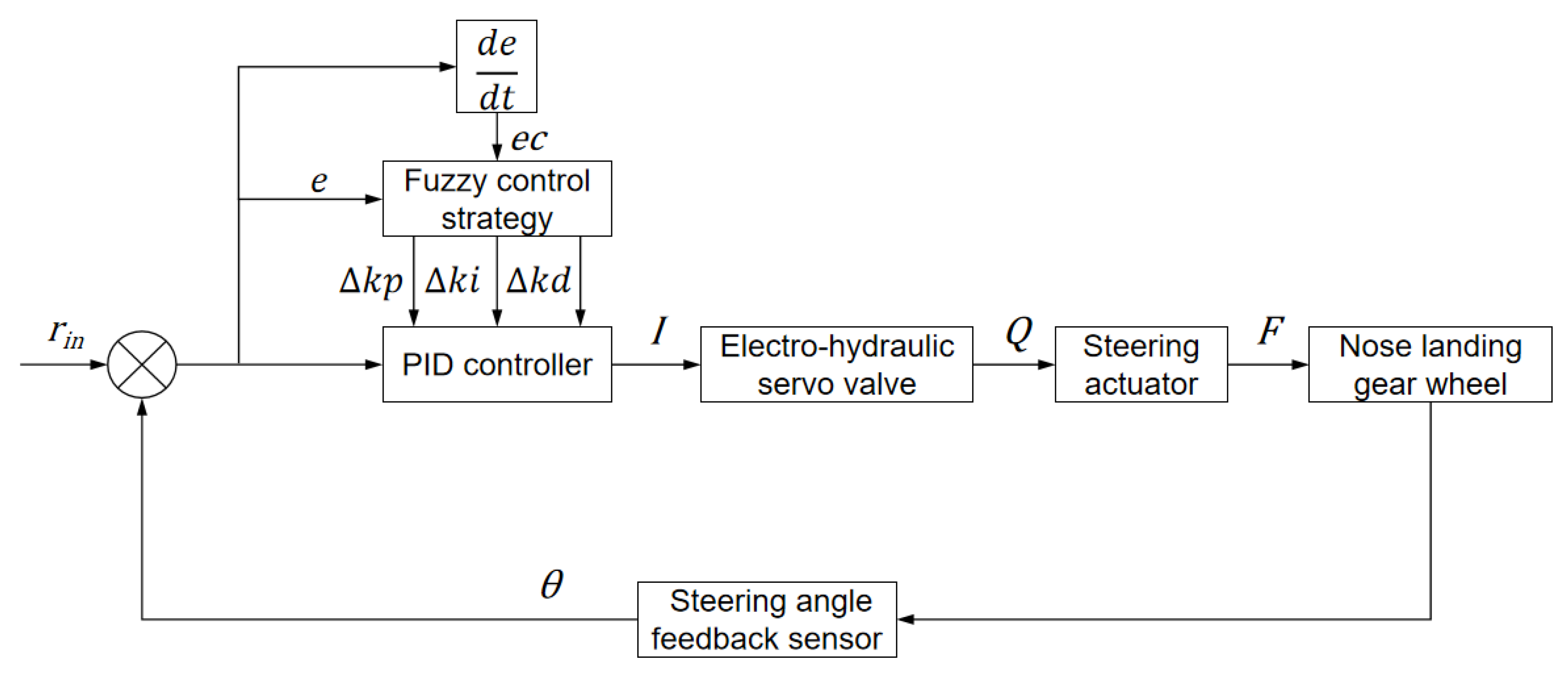
2.2. Physical Modeling of Nose-Wheel Electro-Hydraulic Servo Steering System
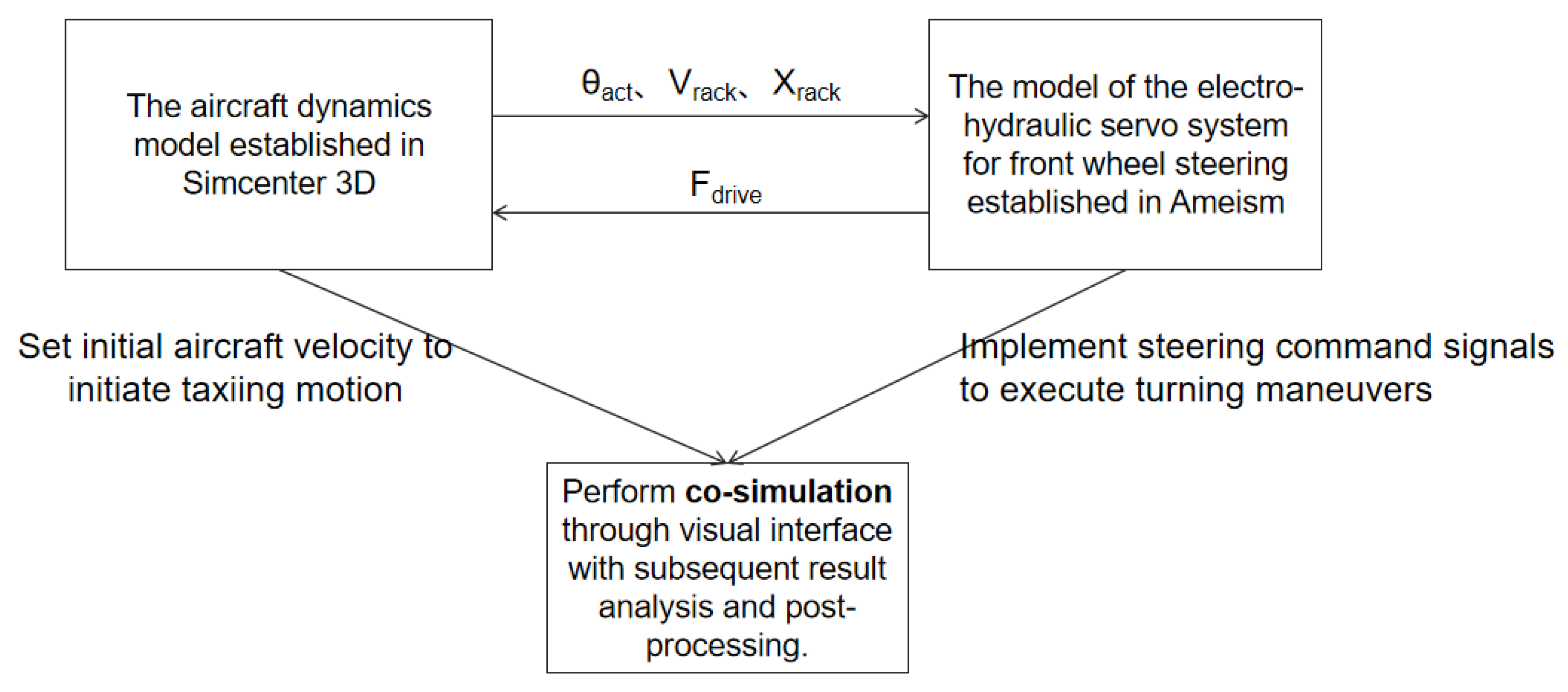
2.3. Multidisciplinary Co-Simulation
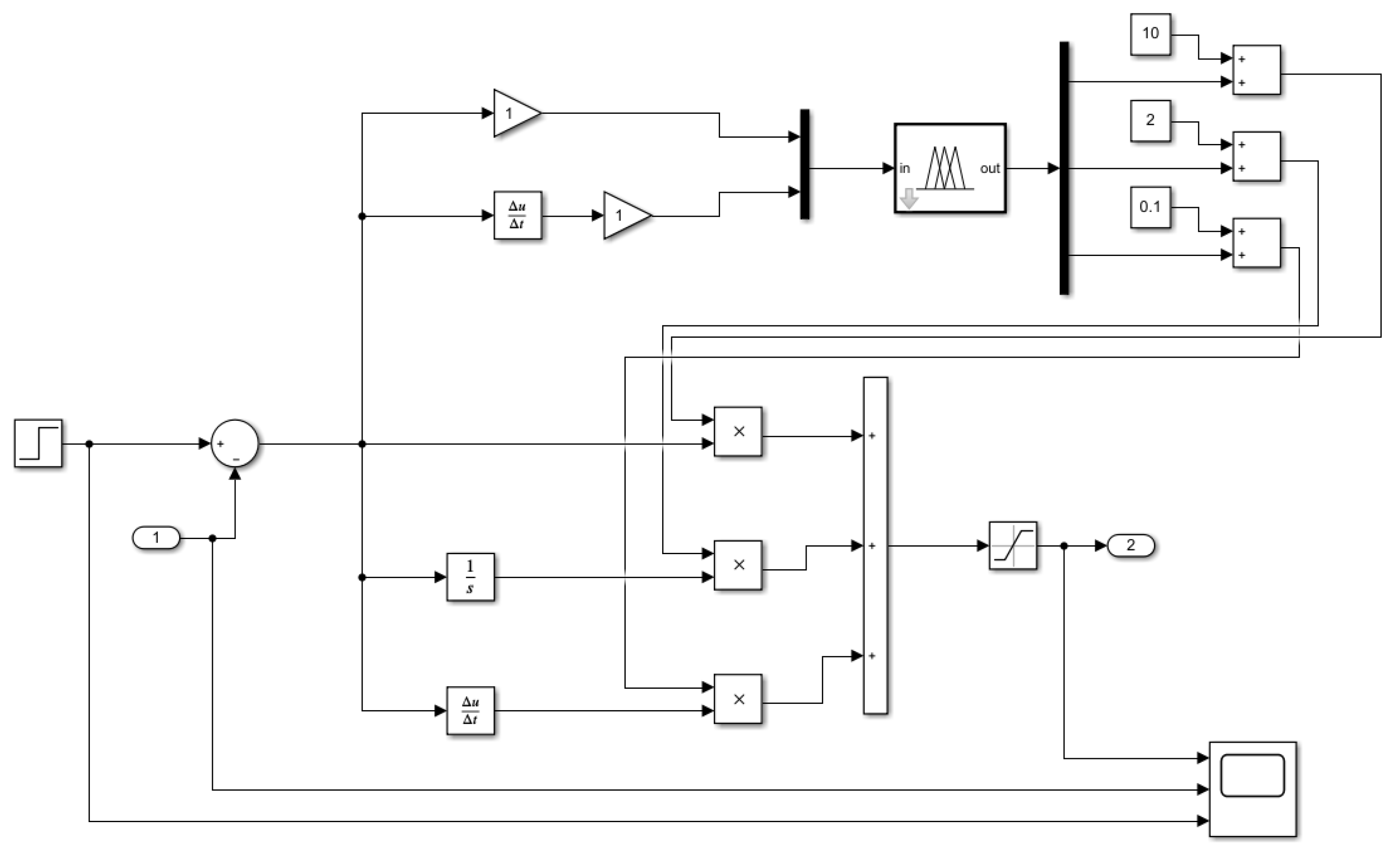
2.4. Design of Fuzzy Adaptive PID Controller
- Dynamic parameter self-tuning capability: real-time adjustment of control parameters based on error signals, resolving traditional PID’s inability to adapt to complex disturbances such as time-varying runway–tire friction and nonlinear hysteresis in hydraulic systems;
- Enhanced robustness and anti-windup properties: suppression of integral windup via fuzzy rules, preventing control instability caused by actuator output saturation under extreme conditions; in conventional PID control, anti-windup functionality typically requires an additional independent module (e.g., integrator clamping or back-calculation). However, in our proposed fuzzy adaptive controller, anti-windup capability is embedded directly within the fuzzy inference rules, demonstrating greater design integration and functional advancement.
- Multi-objective collaborative optimization: balancing overshoot suppression with response speed, addressing the inherent conflict between steady-state accuracy and dynamic performance in traditional PID tuning.
2.4.1. Fuzzy Controller Architecture Design
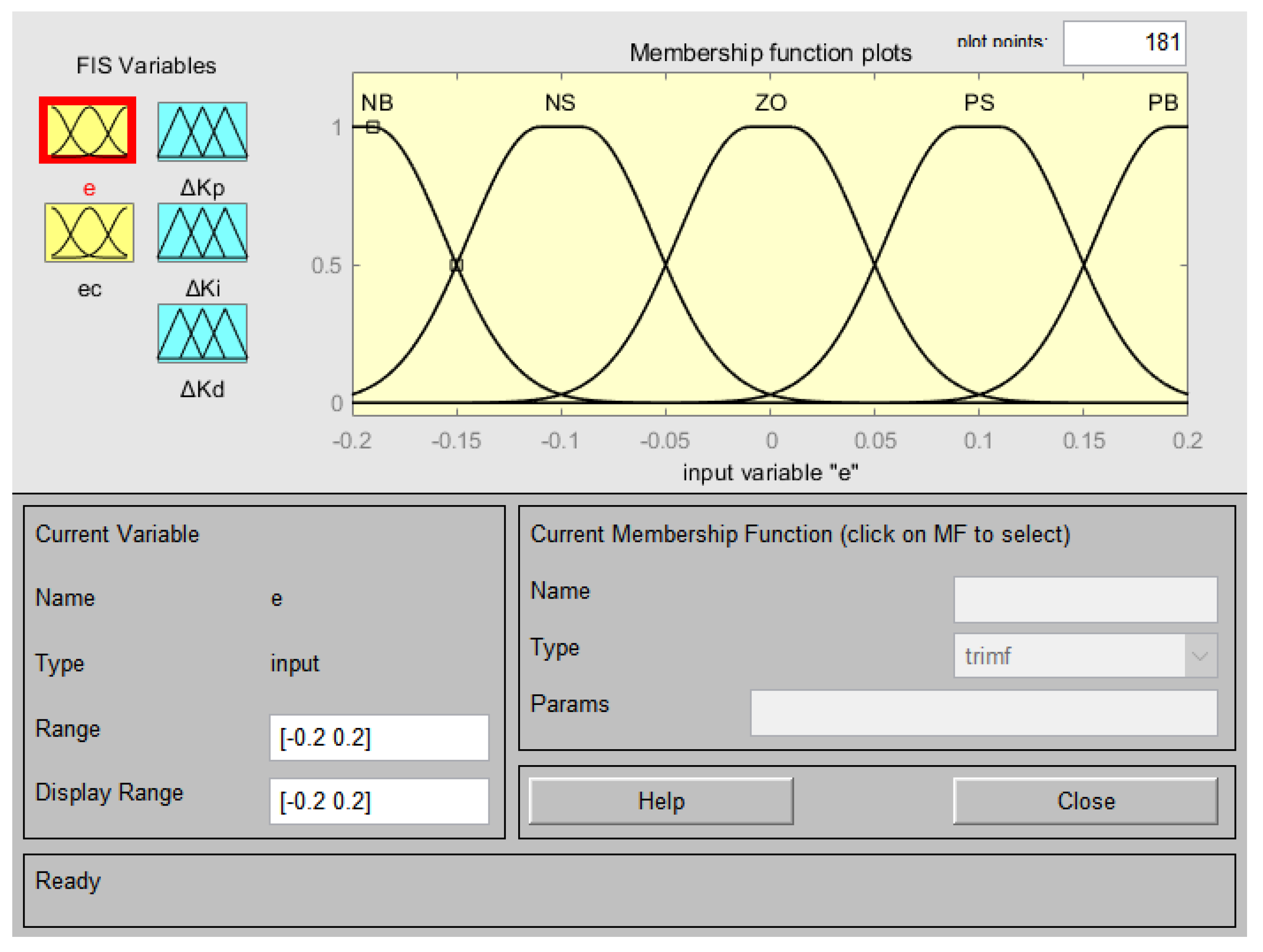
2.4.2. Design of Linguistic Variables and Membership Functions
2.4.3. Fuzzy Controller Rule-Base Formulation
- Large Negative Deviation with Stabilizing Trend (e = NB, ec = ZO): significantly increase Kp (ΔKp = PB) to enhance rapid response to substantial deviations; moderately reduce Ki(∆Ki = NS) to prevent integral windup caused by persistent deviations; maintain Kd (∆Kd = ZO) unchanged, as the zero deviation rate minimizes derivative influence;
- Zero Deviation with Gradual Positive Increase (e = ZO, ec = PS): slightly decrease Kp (ΔKp = NS) to avoid overshoot from excessive response; moderately increase Ki (∆Ki = PS) to eliminate residual steady-state errors; enhance Kd (∆Kd = PS) to preemptively suppress oscillations induced by rising deviation rates;
- Large Positive Deviation with Rapid Reduction (e = PB, ec = NB): maximize Kp (ΔKp = PB) to expedite residual error elimination; disable Ki (∆Ki = NB) to prevent overshoot from cumulative integral action during late-stage correction; sharply increase Kd (∆Kd = PB) to counteract oscillations arising from rapid convergence;
- Anti-Windup Mechanism (e = PB/NB): when system error e is large, the mechanism outputs a negative integral gain adjustment (∆Ki = NB), effectively reducing or temporarily disabling the integral action. This prevents unlimited accumulation of the integral term, achieving anti-windup functionality.
2.4.4. Encapsulation of the Fuzzy Controller
3. Results
3.1. Analysis of Co-Simulation Results for Nose-Wheel Steering System
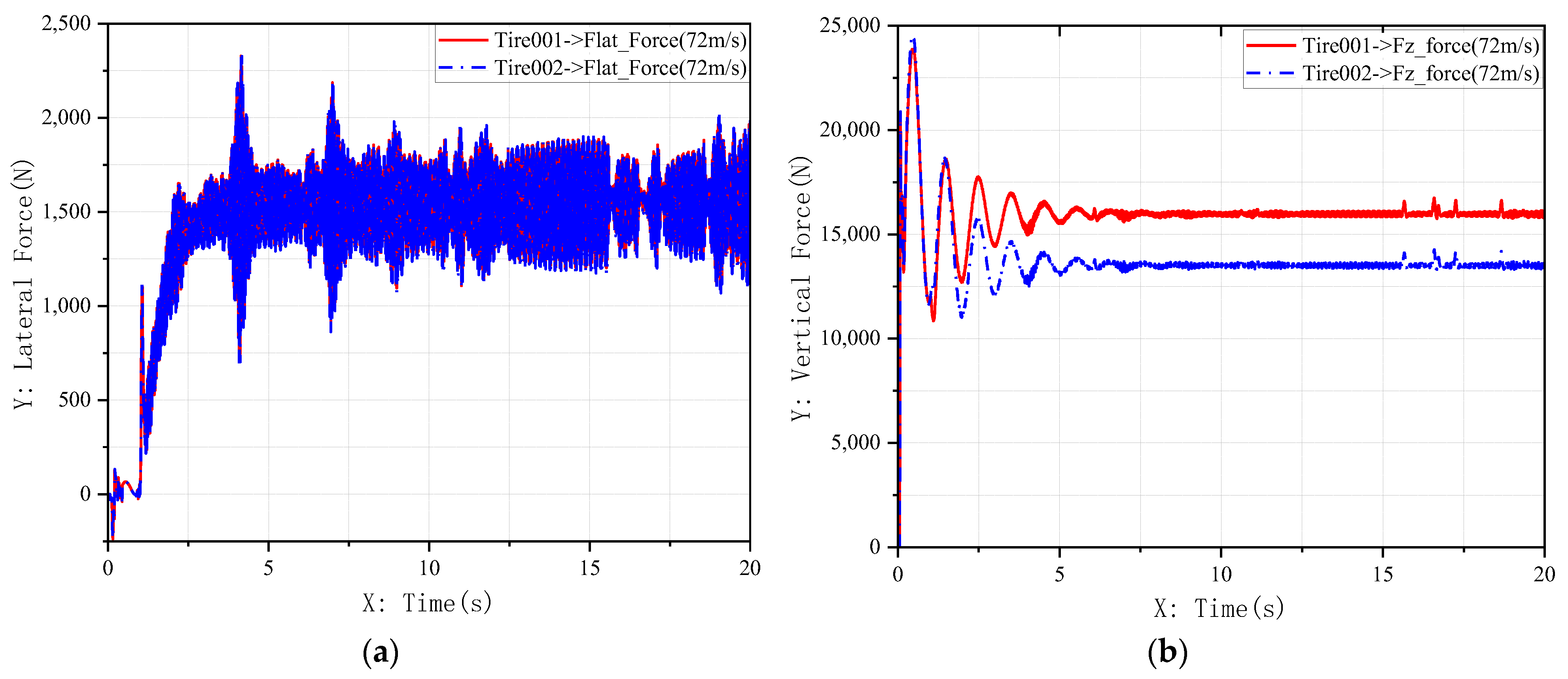
3.1.1. Step Control During High-Speed Landing
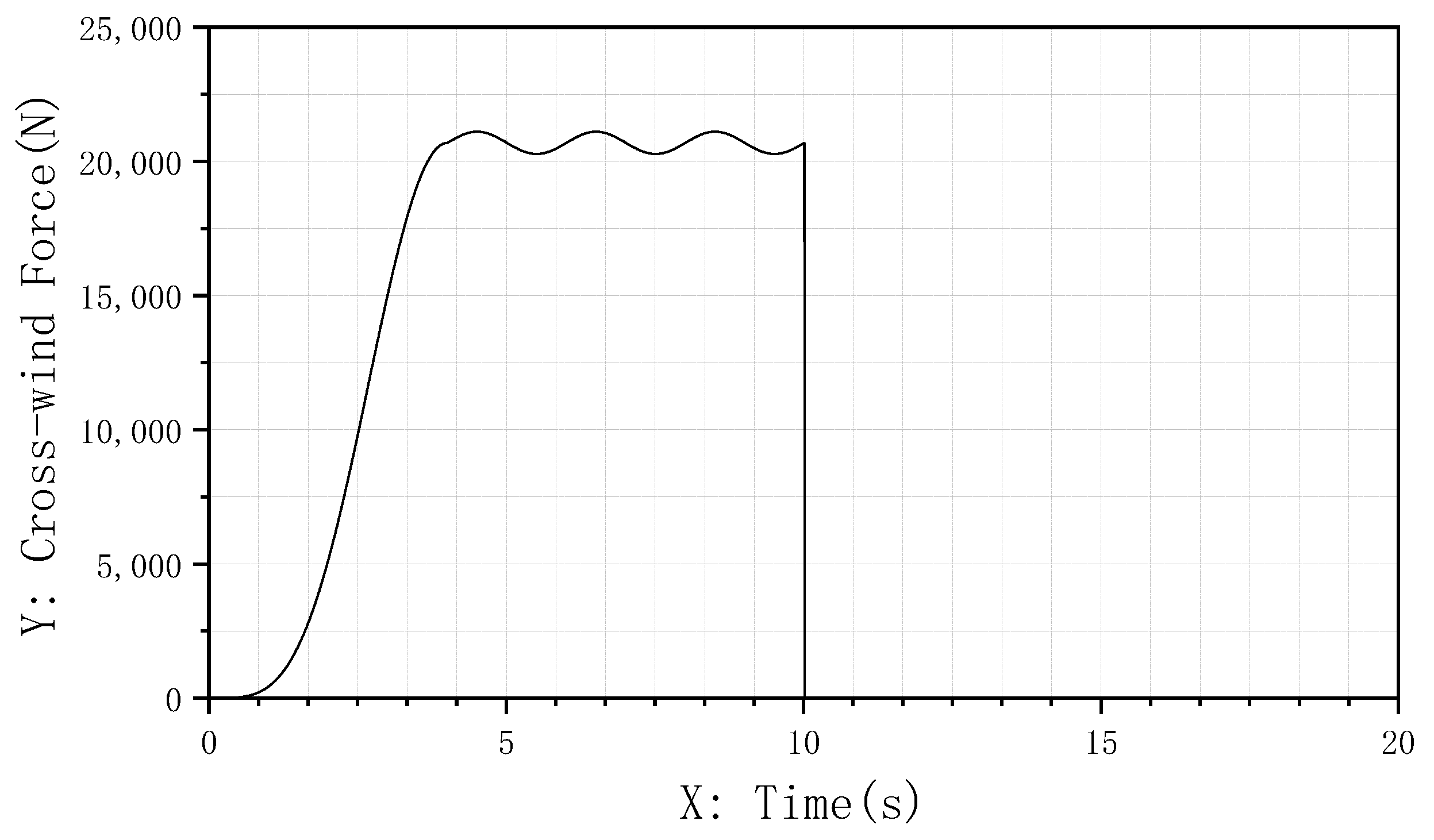
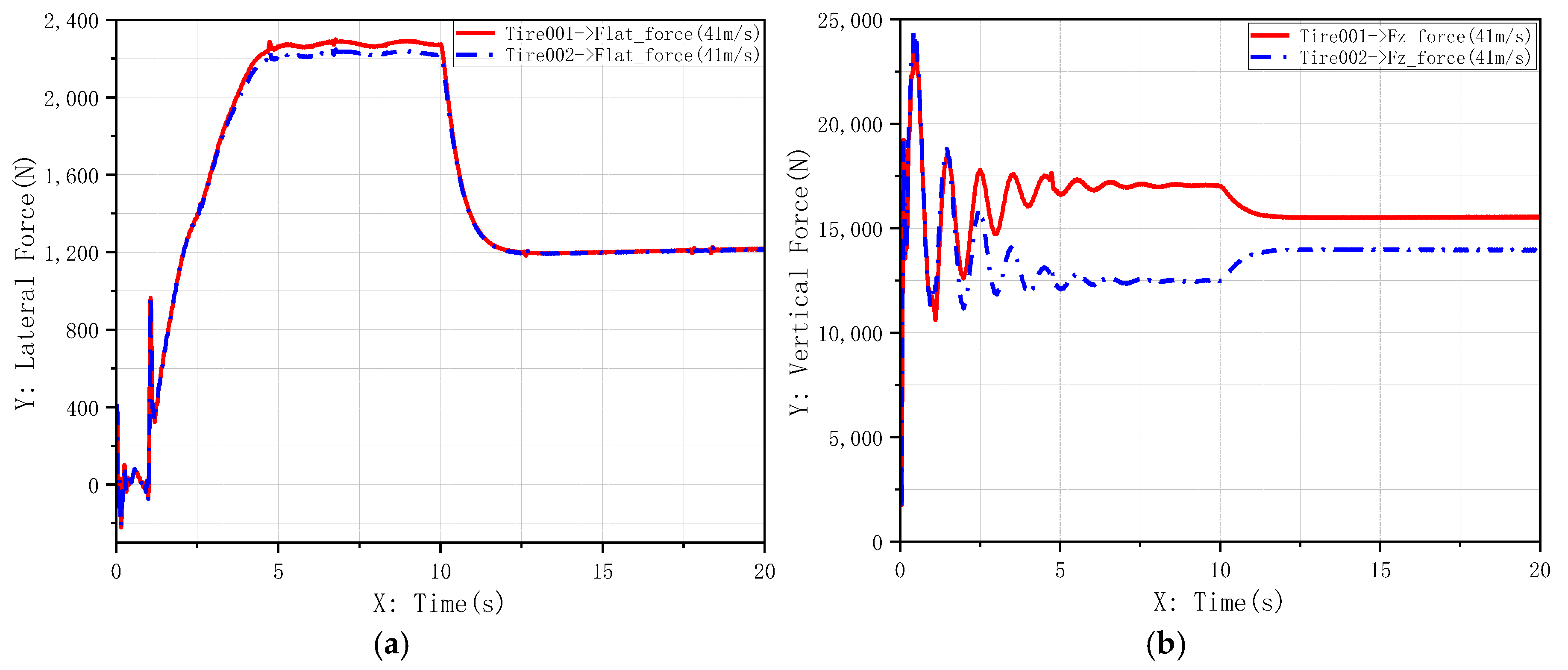
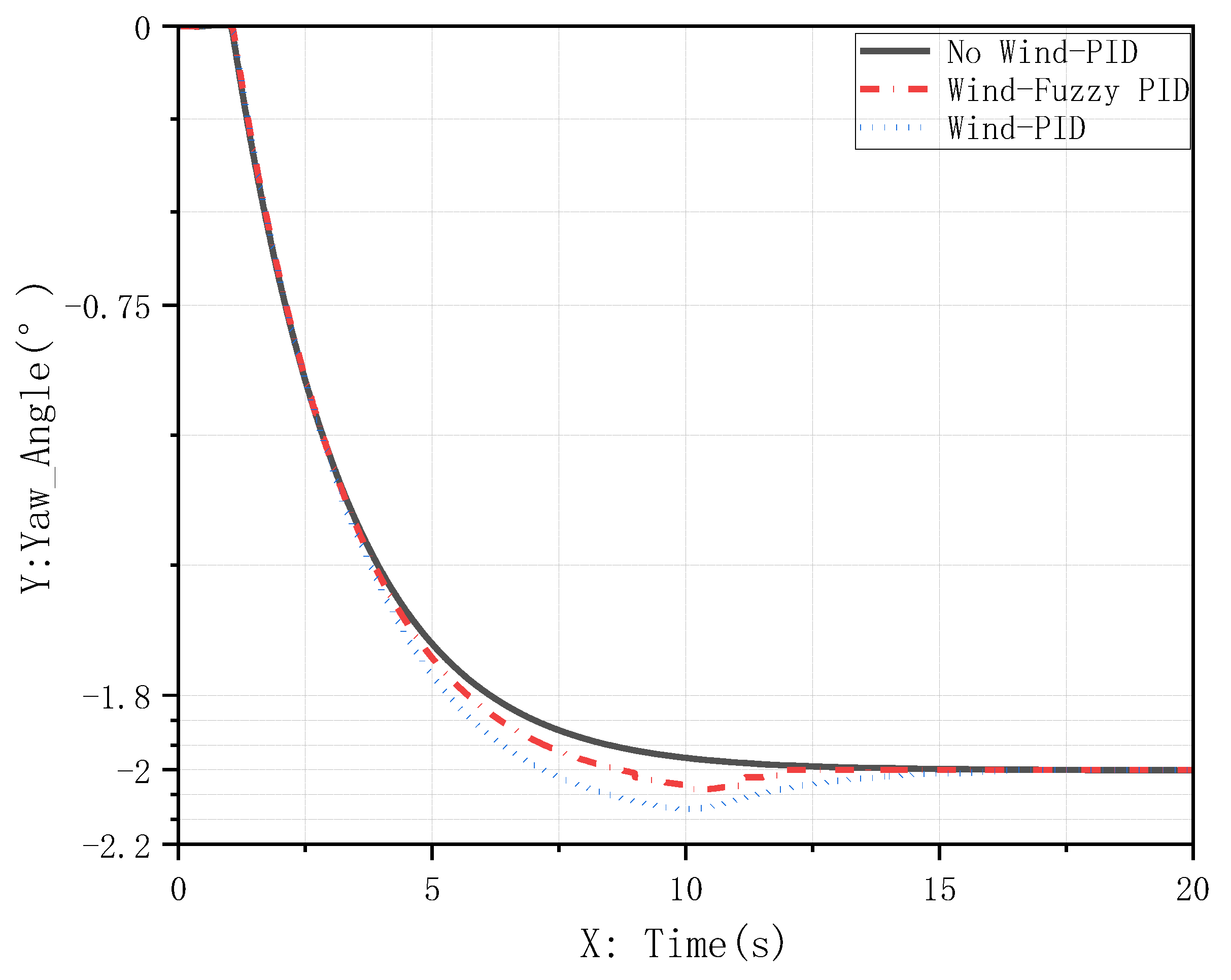
3.1.2. Robustness Analysis Under Crosswind Disturbance
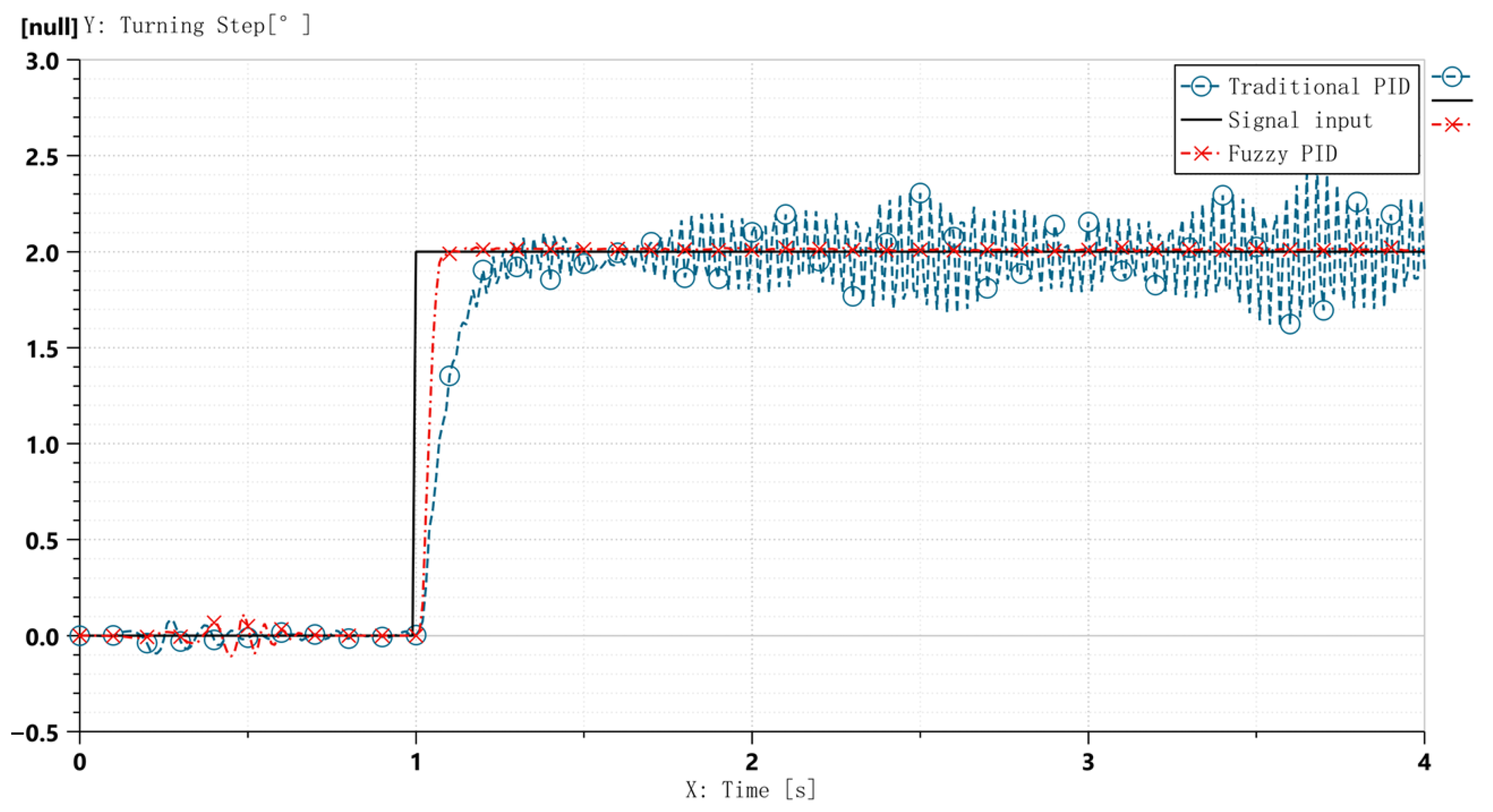
- Heading Maintenance (Figure 21): after crosswind impact, the aircraft with conventional PID control exhibited a maximum yaw deviation exceeding 0.12° and required extended time to fully suppress the yaw; in contrast, the fuzzy adaptive PID controller rapidly adjusted its gains to actively suppress disturbances, limiting maximum lateral deviation to within 0.05° and achieving swift stabilization;
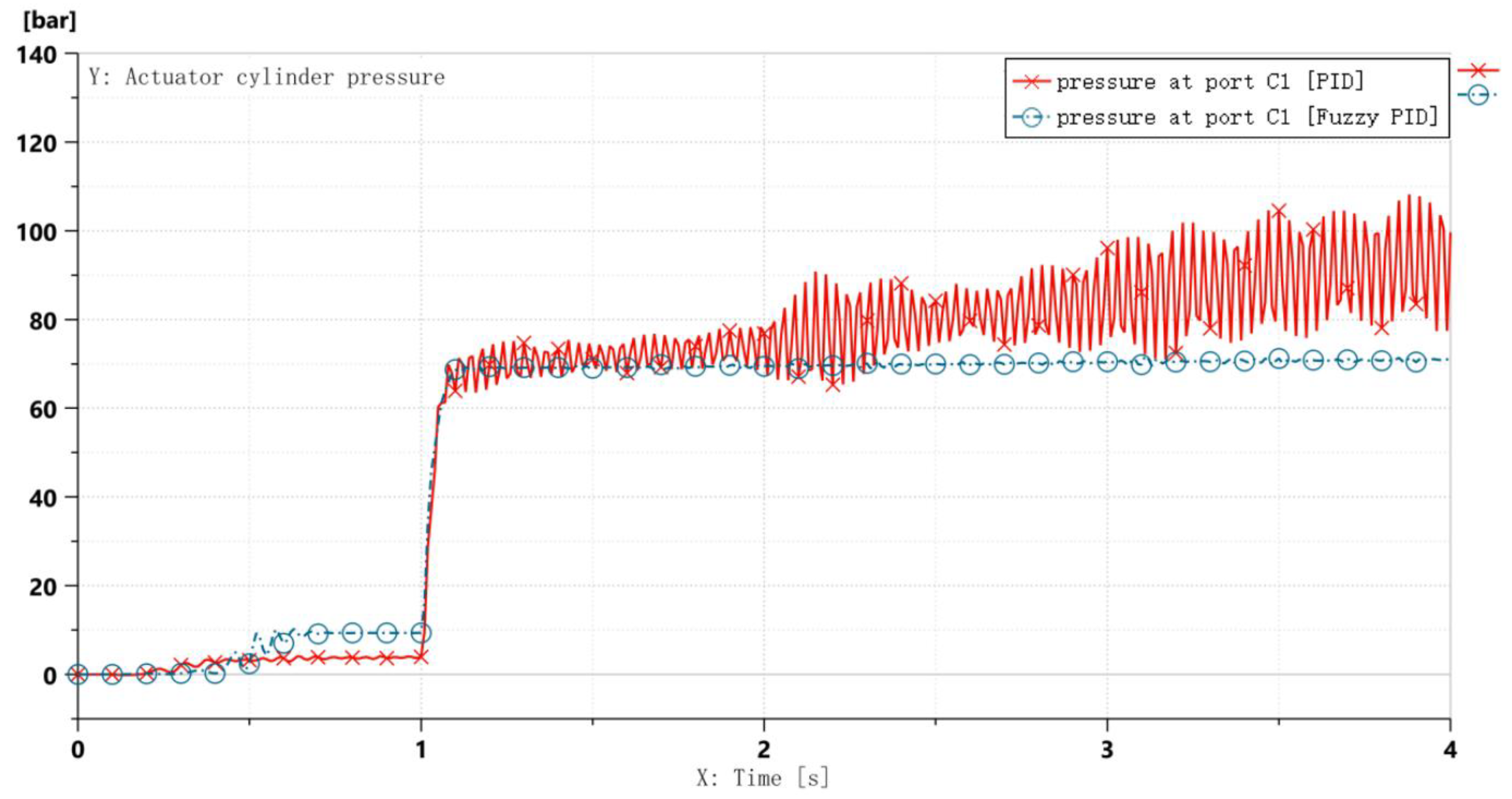
- Hydraulic System Stability (Figure 22): under external crosswind disturbance, the hydraulic pressure of the conventional PID controller showed sustained oscillations, increasing the risk of component fatigue and failure; the pressure response of the fuzzy adaptive PID controller remained significantly smoother, reaffirming its advantage in suppressing hydraulic fluctuations.
4. Conclusions
- Addressing the bottleneck of traditional single-discipline modeling in simulating mechanical–hydraulic-control coupling effects, this study innovatively adopts a high-fidelity co-simulation architecture integrating multidisciplinary tools. By leveraging the strengths of Simcenter 3D (mechanical dynamics), AMESim (hydraulic systems), and MATLAB/Simulink (control algorithms), a digital twin with both precision and real-time capability is constructed through millisecond-level data interaction. This framework provides an authentic simulation environment for subsequent research on steering control laws.
- To resolve the control stability challenges caused by fixed PID parameters under nonlinear conditions, a novel fuzzy adaptive control strategy is proposed. By dynamically optimizing PID parameters (K_p, K_i, K_d) through online fuzzy rule-based tuning, this method overcomes the poor adaptability of conventional steering control strategies in nonlinear scenarios. It offers a solution to stability degradation caused by unstable nose-wheel loads during landing phases, thereby enhancing deviation correction capability and landing safety.
- Comparative simulation analyses demonstrate that the proposed control strategy achieves superior performance over traditional PID methods, including accelerated system response, significantly reduced overshoot, and over 85.2% suppression of hydraulic pressure fluctuations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, W.; Chen, Y.; Xu, Y.; Jiang, Y. Study on the Test and Adjustment Method of Civil Aircraft Taxiing Deviation. Aerospace 2024, 11, 732. [Google Scholar] [CrossRef]
- Davis, P.A.; Stubbs, S.M.; Tanner, J.A. Langley Aircraft Landing Dynamics Facility; NASA Reference Publication: Washington, DC, USA, 1987.
- Dai, Y.; Song, J.; Yu, L.; Lu, Z.; Zheng, S.; Li, F. The lateral control during aircraft-on-ground deceleration phases. Aerosp. Sci. Technol. 2019, 95, 105482. [Google Scholar] [CrossRef]
- Tao, F.; Xiao, B.; Qi, Q.; Cheng, J.; Ji, P. Digital twin modeling. J. Manuf. Syst. 2022, 64, 372–389. [Google Scholar] [CrossRef]
- Li, L.; Aslam, S.; Wileman, A.J.; Perinpanayagam, S. Digital Twin in Aerospace Industry: A Gentle Introduction. IEEE Access 2022, 10, 9543–9562. [Google Scholar] [CrossRef]
- Yin, Z.H.; Wang, L. Application and Development Prospect of Digital Twin Technology in Aerospace. In Proceedings of the 3rd IFAC Workshop pn Cyber-Physical and Human Systems (CPHS), Beijing, China, 3–5 December 2020. [Google Scholar]
- Kabashkin, I. Digital Twin Framework for Aircraft Lifecycle Management Based on Data-Driven Models. Mathematics 2024, 12, 2979. [Google Scholar] [CrossRef]
- Wu, Z.; Li, J. A Framework of Dynamic Data Driven Digital Twin for Complex Engineering Products: The Example of Aircraft Engine Health Management. In Proceedings of the 30th International Conference on Flexible Automation and Intelligent Manufacturing (FAIM), Athens, Greece, 15–18 June 2021. [Google Scholar]
- Zhou, H.; Xie, F.; Ji, T.; Zhang, X.; Zheng, C.; Zheng, Y. Fast transonic flow prediction enables efficient aerodynamic design. Phys. Fluids 2023, 35, 026109. [Google Scholar] [CrossRef]
- Dong, Q.; Wang, J.; Zhang, X.; Wang, H.; Zhao, J. Dynamic response analysis of airport pavements during aircraft taxiing for evaluating pavement bearing capacity. J. Zhejiang Univ. Sci. A 2021, 22, 736–750. [Google Scholar] [CrossRef]
- Shi, X.; Cai, L.; Wang, G.; Liang, L. A New Aircraft Taxiing Model Based on Filtering White Noise Method. IEEE Access 2020, 8, 10070–10087. [Google Scholar] [CrossRef]
- Shan, D.; Gu, X.; Huang, Q.; Gu, X.; Lan, Y. A Digital-Twin Assisted Simulation for the Electromechanical System of Aircraft. In Proceedings of the Asia-Pacific International Symposium on Aerospace Technology (APISAT), Lingshui, China, 16–18 October 2023. [Google Scholar]
- Young, D.W.S.; Ohly, B. European Aircraft Steering Systems; SAE International: Warrendale, PA, USA, 1985. [Google Scholar]
- Sadien, E.; Roos, C.; Birouche, A.; Carton, M.; Grimault, C.; Romana, L.-E.; Basset, M. A simple and efficient control allocation scheme for on-ground aircraft runway centerline tracking. Control Eng. Pract. 2020, 95, 104228. [Google Scholar] [CrossRef]
- Wang, D.; Hemming, S.; Yang, Y.; Poorfakhraei, A.; Zhou, L.; Liu, C.; Emadi, A. Multilevel Inverters for Electric Aircraft Applications: Current Status and Future Trends. IEEE Trans. Transp. Electrif. 2024, 10, 3258–3282. [Google Scholar] [CrossRef]
- Nie, Q.; Nie, H.; Zhang, M. Design and Dynamic Analysis of Dual Actuator Nose Wheel Steering System on Large Civil Aircraft. J. Nanjing Univ. Aeronaut. 2012, 44, 503–510. [Google Scholar]
- Wu, Z.; Peng, H.; Li, F.; Huang, T.; Yang, C.; Gui, W. Extended dissipative analysis and taxiing control of fuzzy model based aircraft-on-ground systems via sliding mode approach. J. Frankl. Inst. 2022, 359, 4623–4641. [Google Scholar] [CrossRef]
- Chang, Q.-C.; Xue, C.-J. Reliability Analysis and Experimental Verification of Landing-Gear Steering Mechanism Considering Environmental Temperature. J. Aircr. 2018, 55, 1154–1164. [Google Scholar] [CrossRef]
- Yin, Q.; Kong, D.; Song, J.; Wei, X.; Nie, H. Influence of asymmetrical factors on aircraft ground steering stability. Aerosp. Sci. Technol. 2023, 142, 108698. [Google Scholar] [CrossRef]
- He, H.; Wu, R.; Huang, W. Design of Aircraft Antiskid Brake System with ANN and FNN. Acta Aeronaut. Astronaut. Sin. 2005, 1, 116–120. [Google Scholar]
- Neto, M.M.; Sandoval Goes, L.C. Use of LMS Amesim® model and a bond graph support to predict behavior impacts of typical failures in an aircraft hydraulic brake system. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 414. [Google Scholar] [CrossRef]
- Li, D.; Lin, M.; Zhang, T. Design and co-simulation of a nose wheel steering system for a civil aircraft. Proc. Inst. Mech. Eng. Part G-J. Aerosp. Eng. 2022, 236, 1388–1395. [Google Scholar] [CrossRef]
- Soumya, N.; Jee, G.; Kavitha, C.S.; Nair, A.P.; Rajeev, U.P.; Padmakumar, E.S. Modelling and Lateral-Directional Control of a Winged Re-entry Vehicle on Runway. IFAC-Pap. 2022, 55, 504–509. [Google Scholar] [CrossRef]
- Petrov, M.; Ganchev, I.; Taneva, A. Fuzzy PID control of nonlinear plants. In Proceedings of the 1st International IEEE Symposium on Intelligent Systems, Varna, Bulgaria, 10–12 September 2002. [Google Scholar]
- Lee, B.-K.; Kim, I.-H.; Kim, J.-H. Stability Analysis and Proposal of a Simple Form of a Fuzzy PID Controller. J. Adv. Mar. Eng. Technol. 2004, 28, 1299–1312. [Google Scholar]
- Dogan, A.; Lewis, T.A.; Blake, W. Flight Data Analysis and Simulation of Wind Effects During Aerial Refueling. J. Aircr. 2008, 45, 2036–2048. [Google Scholar] [CrossRef]




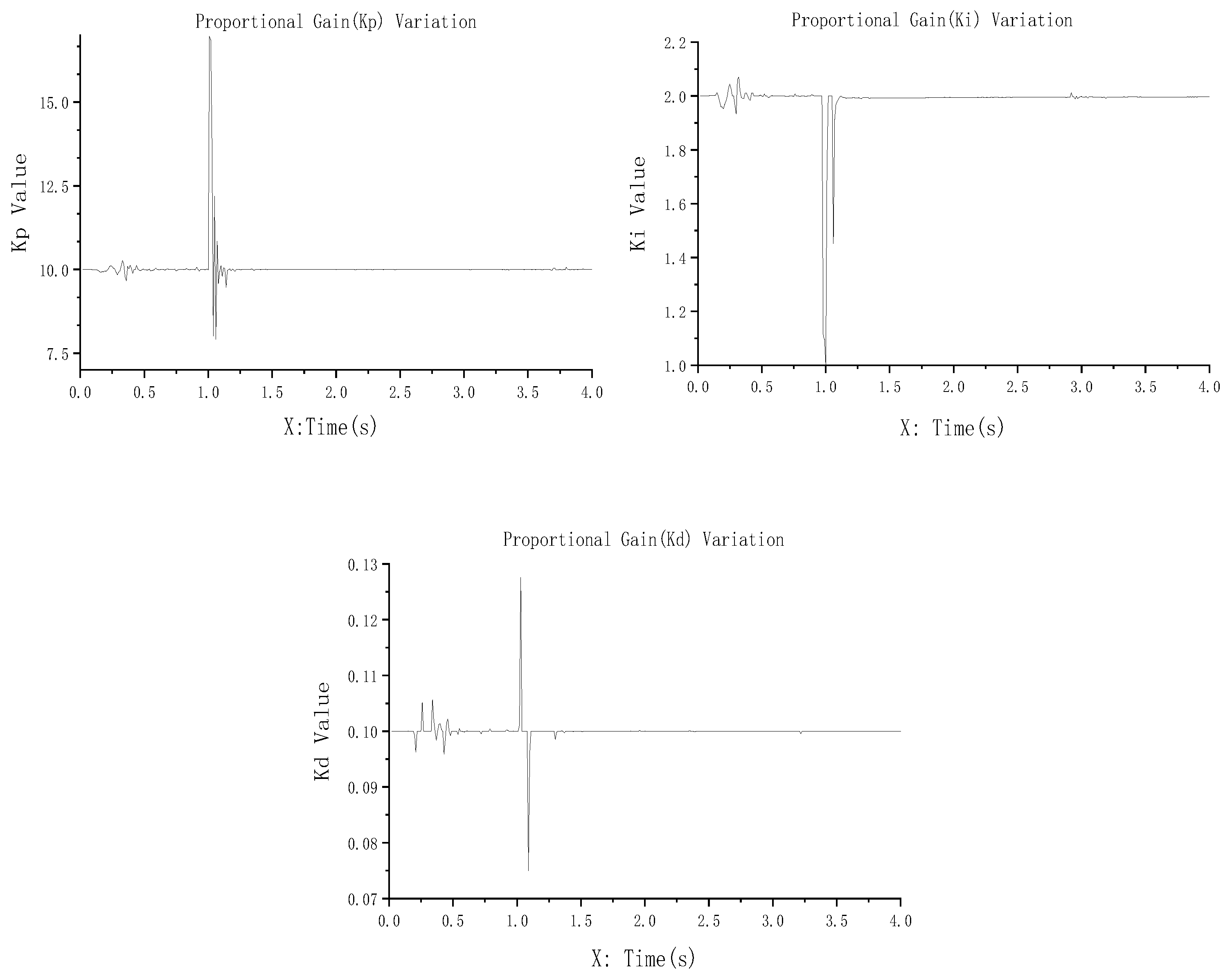



| PID Parameter | e | |||||
|---|---|---|---|---|---|---|
| NB | NS | ZO | PS | PB | ||
| ec | NB | ΔKp = PB, ΔKi = NB, ΔKd = NB | ΔKp = PB, ΔKi = NB, ΔKd = NS | ΔKp = PS, ΔKi = NB, ΔKd = NB | ΔKp = PS, ΔKi = NB, ΔKd = PB | ΔKp = PB, ΔKi = NB, ΔKd = PB |
| NS | ΔKp = PB, ΔKi = NB, ΔKd = NS | ΔKp = PS, ΔKi = NB, ΔKd = NS | ΔKp = PS, ΔKi = NS, ΔKd = NS | ΔKp = ZO, ΔKi = NS, ΔKd = PS | ΔKp = PB, ΔKi = NB, ΔKd = PS | |
| ZO | ΔKp = PB, ΔKi = NS, ΔKd = ZO | ΔKp = PS, ΔKi = NS, ΔKd = ZO | ΔKp = ZO, ΔKi = ZO, ΔKd = ZO | ΔKp = NS, ΔKi = ZO, ΔKd = ZO | ΔKp = PB, ΔKi = NS, ΔKd = ZO | |
| PS | ΔKp = PS, ΔKi = ZO, ΔKd = PS | ΔKp = ZO, ΔKi = ZO, ΔKd = PS | ΔKp = NS, ΔKi = PS, ΔKd = PS | ΔKp = NS, ΔKi = PS, ΔKd = NS | ΔKp = PS, ΔKi = ZO, ΔKd = NS | |
| PB | ΔKp = PS, ΔKi = PS, ΔKd = PB | ΔKp = NS, ΔKi = PS, ΔKd = PB | ΔKp = NS, ΔKi = PS, ΔKd = PB | ΔKp = NB, ΔKi = PB, ΔKd = NB | ΔKp = PS, ΔKi = PS, ΔKd = PB | |
| Parameters | Values |
|---|---|
| wind yaw angle | 90° |
| 1.225 Kg/m3 | |
| 79.86 m2 | |
| 0.94 | |
| 15 m/s | |
| 4 s | |
| wind duration—t | 10 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Zhang, L.; Tong, Z.; Liu, L. Nose-Wheel Steering Control via Digital Twin and Multi-Disciplinary Co-Simulation. Machines 2025, 13, 677. https://doi.org/10.3390/machines13080677
Chen W, Zhang L, Tong Z, Liu L. Nose-Wheel Steering Control via Digital Twin and Multi-Disciplinary Co-Simulation. Machines. 2025; 13(8):677. https://doi.org/10.3390/machines13080677
Chicago/Turabian StyleChen, Wenjie, Luxi Zhang, Zhizhong Tong, and Leilei Liu. 2025. "Nose-Wheel Steering Control via Digital Twin and Multi-Disciplinary Co-Simulation" Machines 13, no. 8: 677. https://doi.org/10.3390/machines13080677
APA StyleChen, W., Zhang, L., Tong, Z., & Liu, L. (2025). Nose-Wheel Steering Control via Digital Twin and Multi-Disciplinary Co-Simulation. Machines, 13(8), 677. https://doi.org/10.3390/machines13080677




