Dynamic Modeling and Validation of Dual-Cable Double-Pendulum Systems for Gantry Cranes
Abstract
1. Introduction
2. Methodology
2.1. Kane’s Method for Multibody Dynamics
2.2. Modeling Assumptions
- Planar motion: The analysis is limited to two-dimensional (planar) motion, and any out-of-plane dynamics are neglected. This is justified because heavy-duty crane operations typically separate motions in orthogonal directions, and lateral wind loads are not considered in this study.
- Ideal joints and connections: All joints and connections are modeled as perfect kinematic pairs. The influence of auxiliary mechanisms, such as pulleys within equalizer beams, is neglected.
- Rigid bodies: The crane carts, equalizer beams, and payload are treated as rigid bodies. The rotational inertia of point masses is ignored, and only translational dynamics are considered. Since the system studied in this paper operates at low speeds and rotational effects are even smaller, the influence of rotational inertia is neglected.
- Cables: All suspension cables are modeled as massless, inextensible, and always taut. This is justified for large-scale gantry cranes, where the cable mass is negligible relative to the payload and equalizer beams, and cable elasticity has minimal effect on the system dynamics of slow movements.
- External disturbances: Effects such as friction, aerodynamic forces, and mechanical vibrations are neglected. Only gravitational forces and the horizontal control force applied to the crane carts are included.
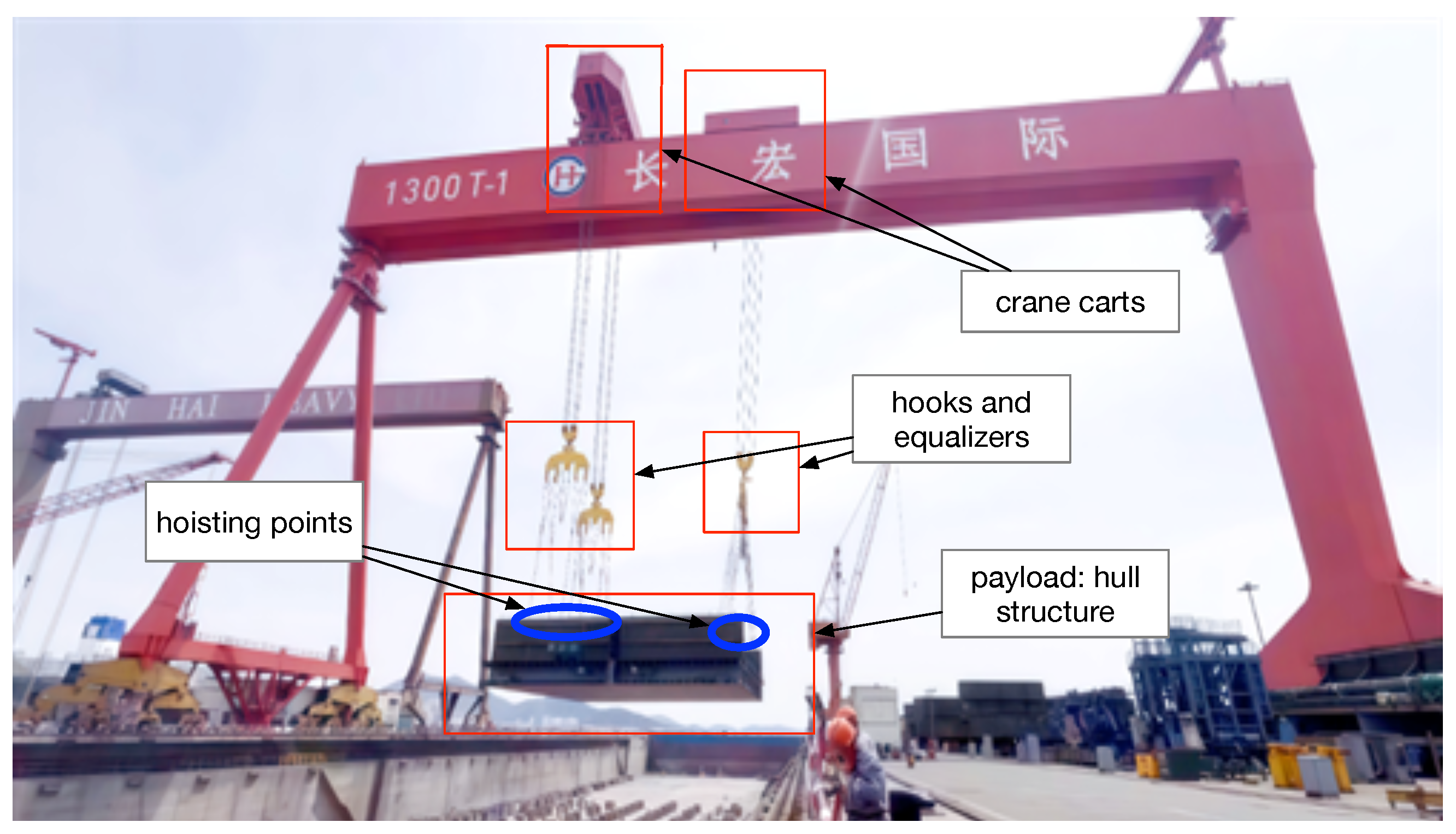
2.3. System Description
2.3.1. System Composition
- Carts: Two movable bases traveling horizontally along rails, providing primary positioning.
- Equalizer beams: Devices suspended between the carts and payload to balance and distribute the load.
- Payload: The lifted object, typically large and heavy.
- Cables: Suspension elements connecting the carts, equalizer beams, and payload, forming the basis for double-pendulum dynamics.
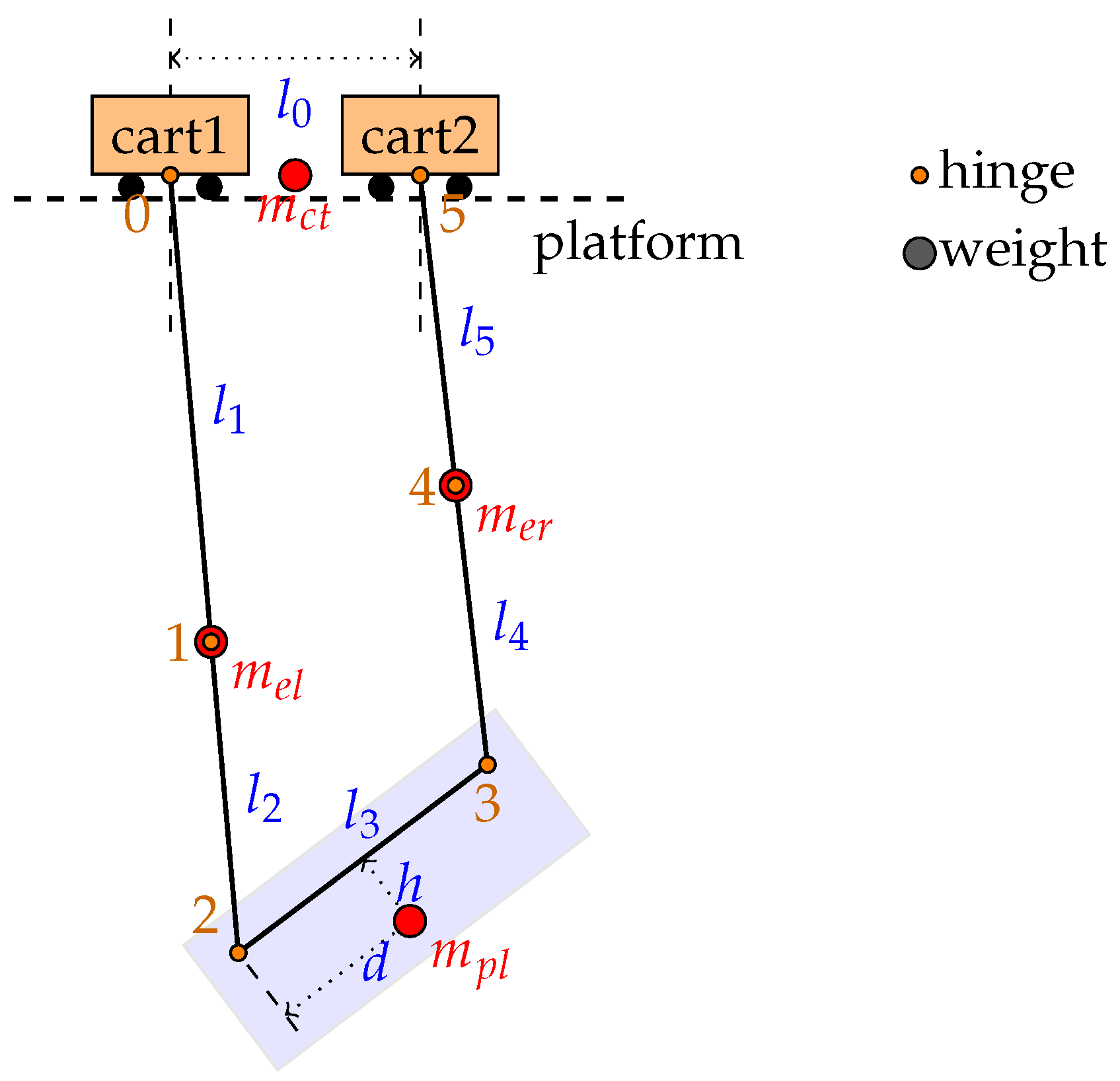
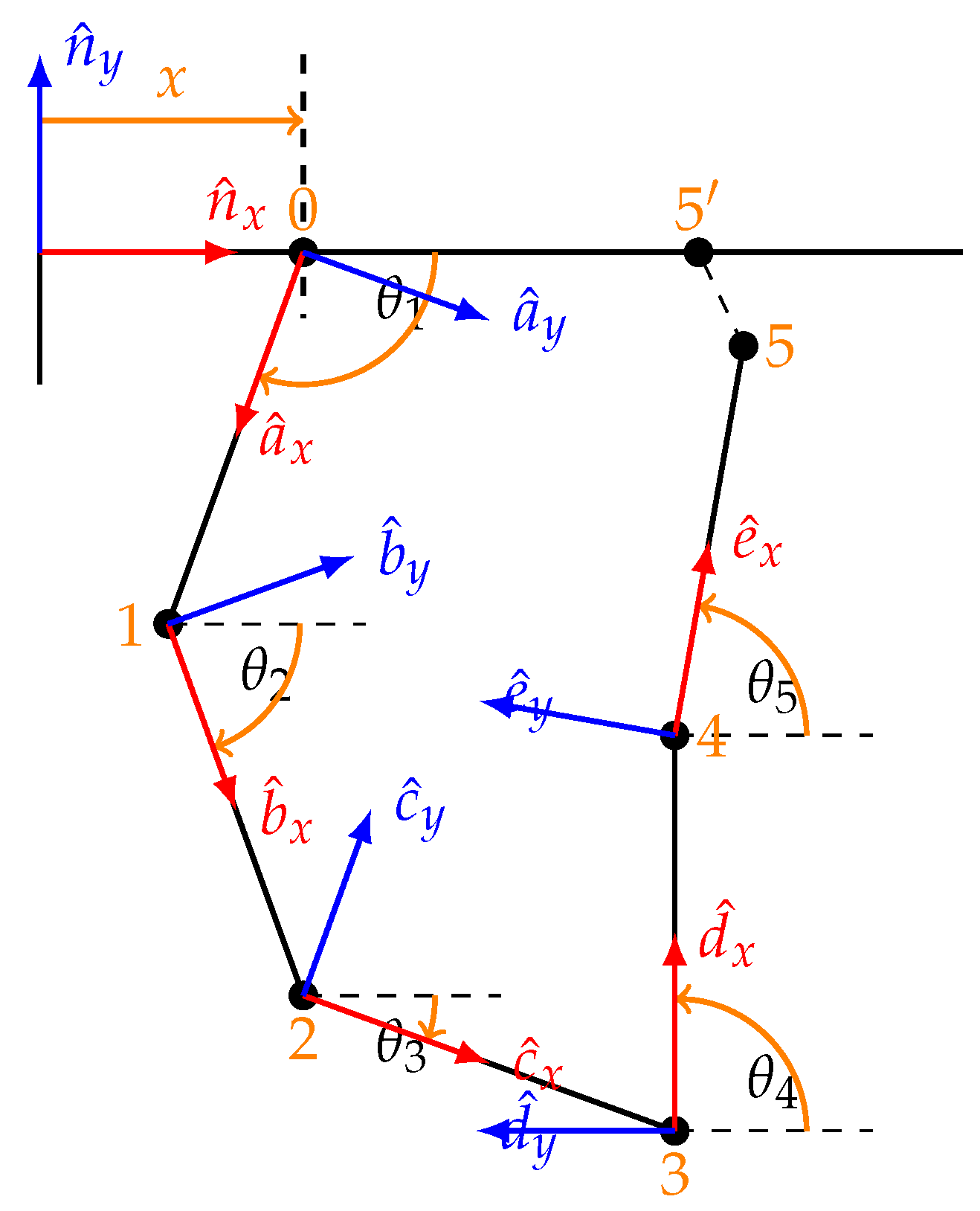
2.3.2. Mathematical Model and Coordinates
3. Dynamic Formulation
3.1. Kinematic Equations
3.2. Holonomic Constraints
3.3. Partial Velocity Matrix
3.4. Dynamic Equations
4. Numerical Implementation
4.1. Simulation Framework
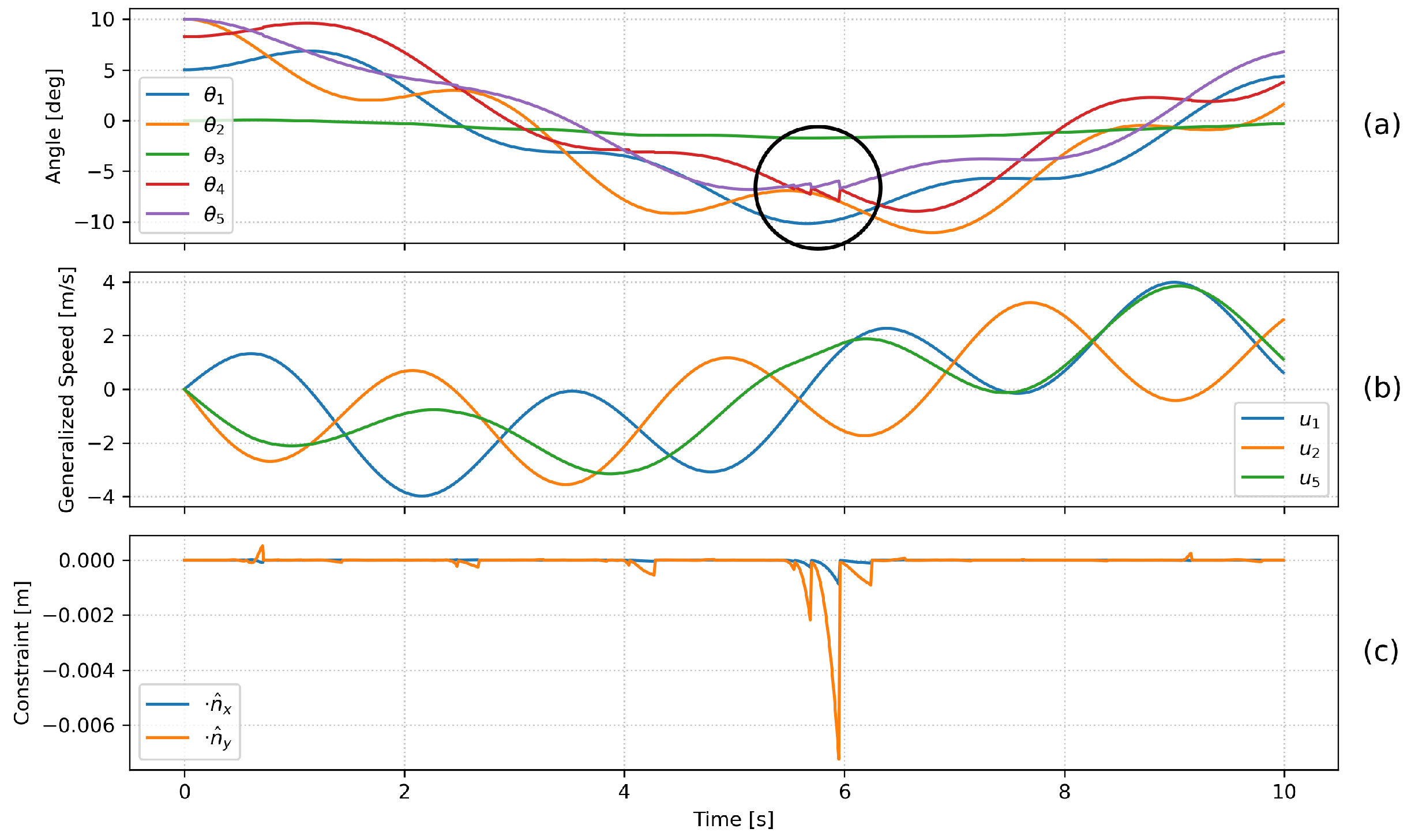
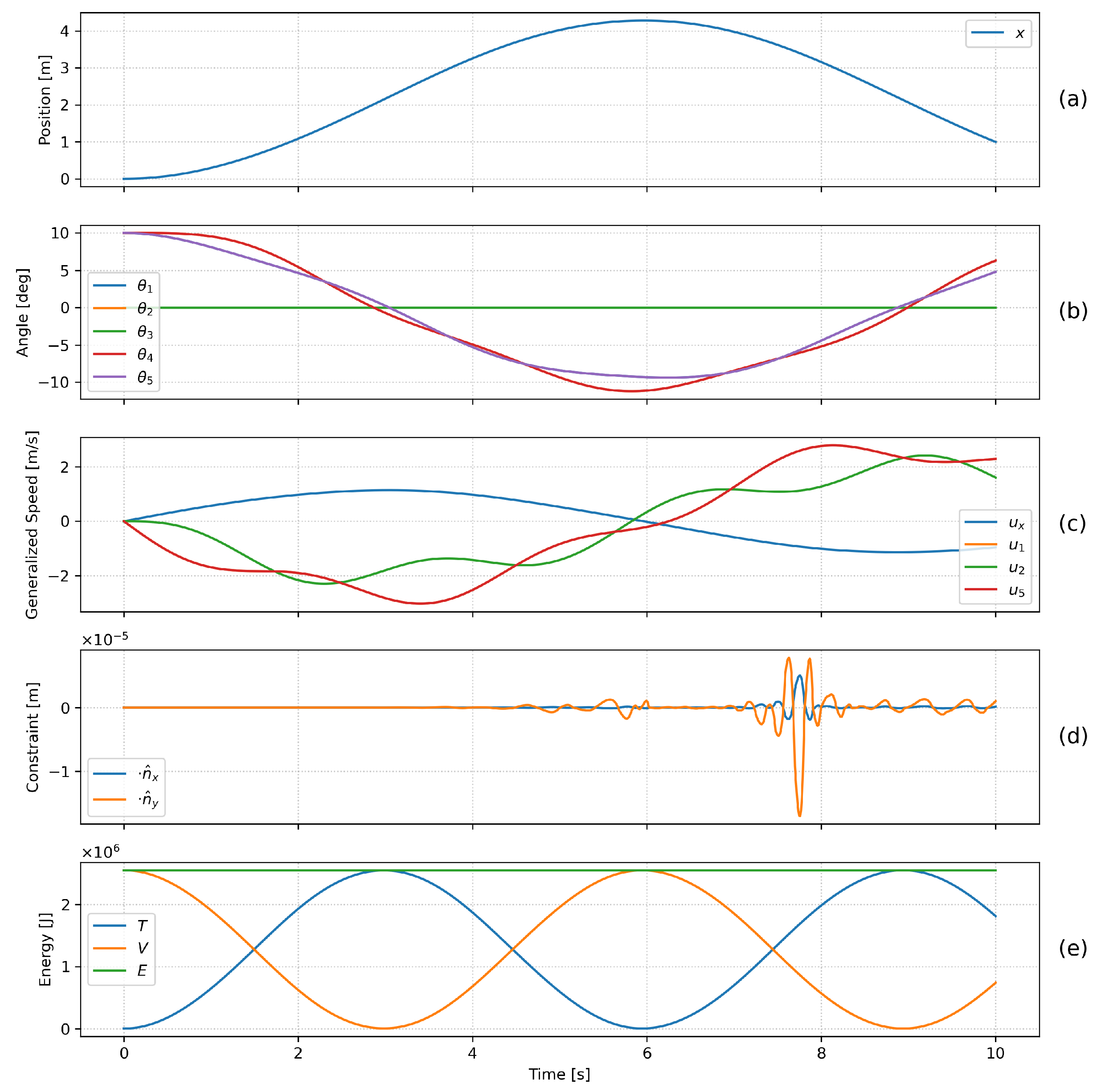
4.2. Special Case Simulation and Modeling Insights
- Cable lengths: , , , , , .
- Payload center of gravity: , .
- Mass distribution: , , , .
- Initial state: , , , , , , with all initial velocities set to zero.
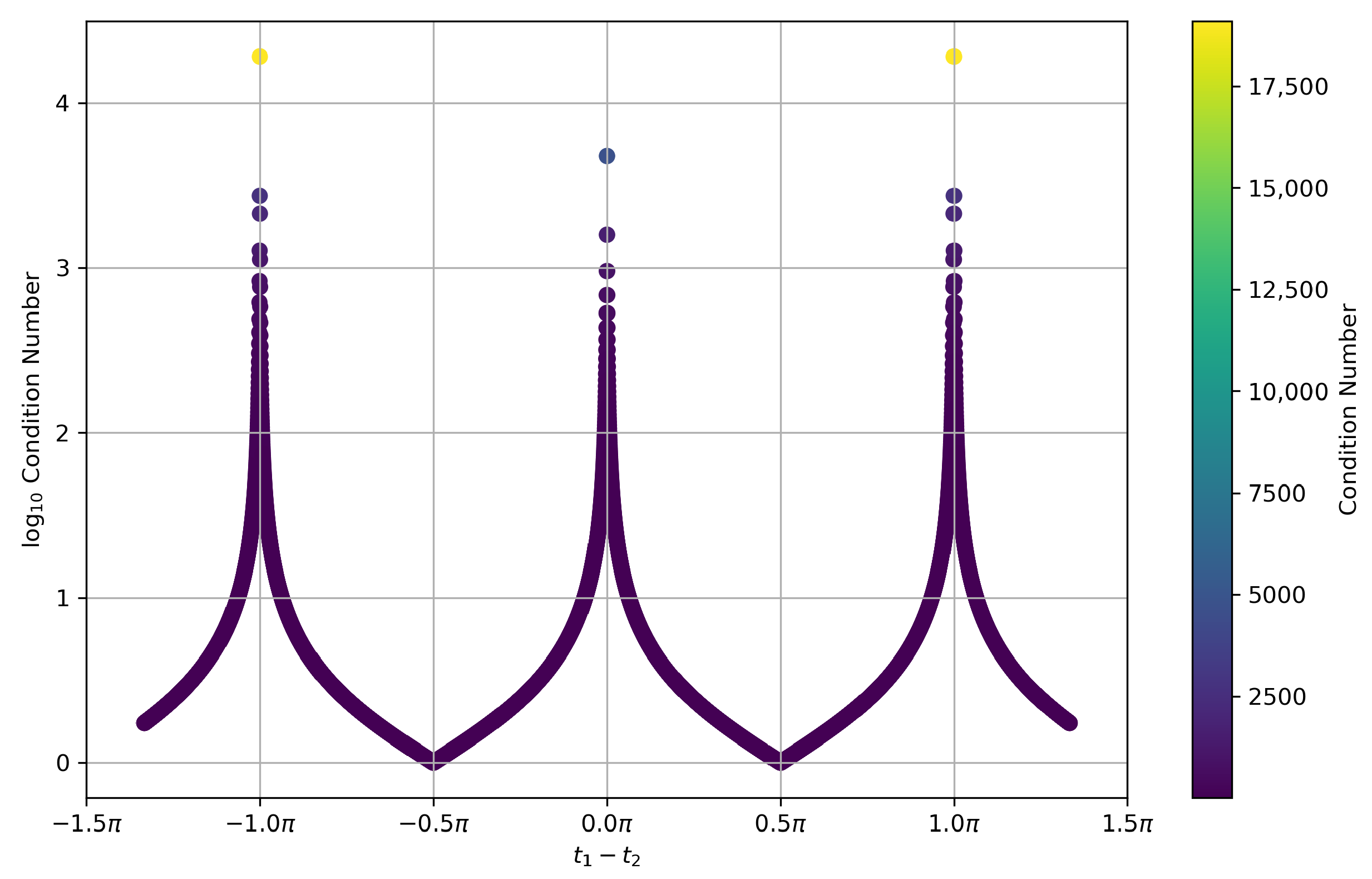
4.3. Variable Selection and Numerical Stability
- As (), the condition number rapidly approaches infinity, indicating singularity within a narrow range.
- Away from these singular points, the condition number decreases significantly, improving the numerical stability.
- : Typically fluctuate around .
- : Typically fluctuate around .
- : Generally varies between and , depending on specific conditions.
5. Validation and Model Comparison
5.1. Energy Conservation Analysis
- Cable lengths: , , , , , .
- Payload center of gravity: , .
- Mass distribution: , , , .
- Initial state: , , , , , , with all initial velocities set to zero.
- Cable lengths: , , , , , .
- Payload center of gravity: , .
- Mass distribution: identical to the symmetric case.
- Initial state: , , , , , , with all initial velocities set to zero.
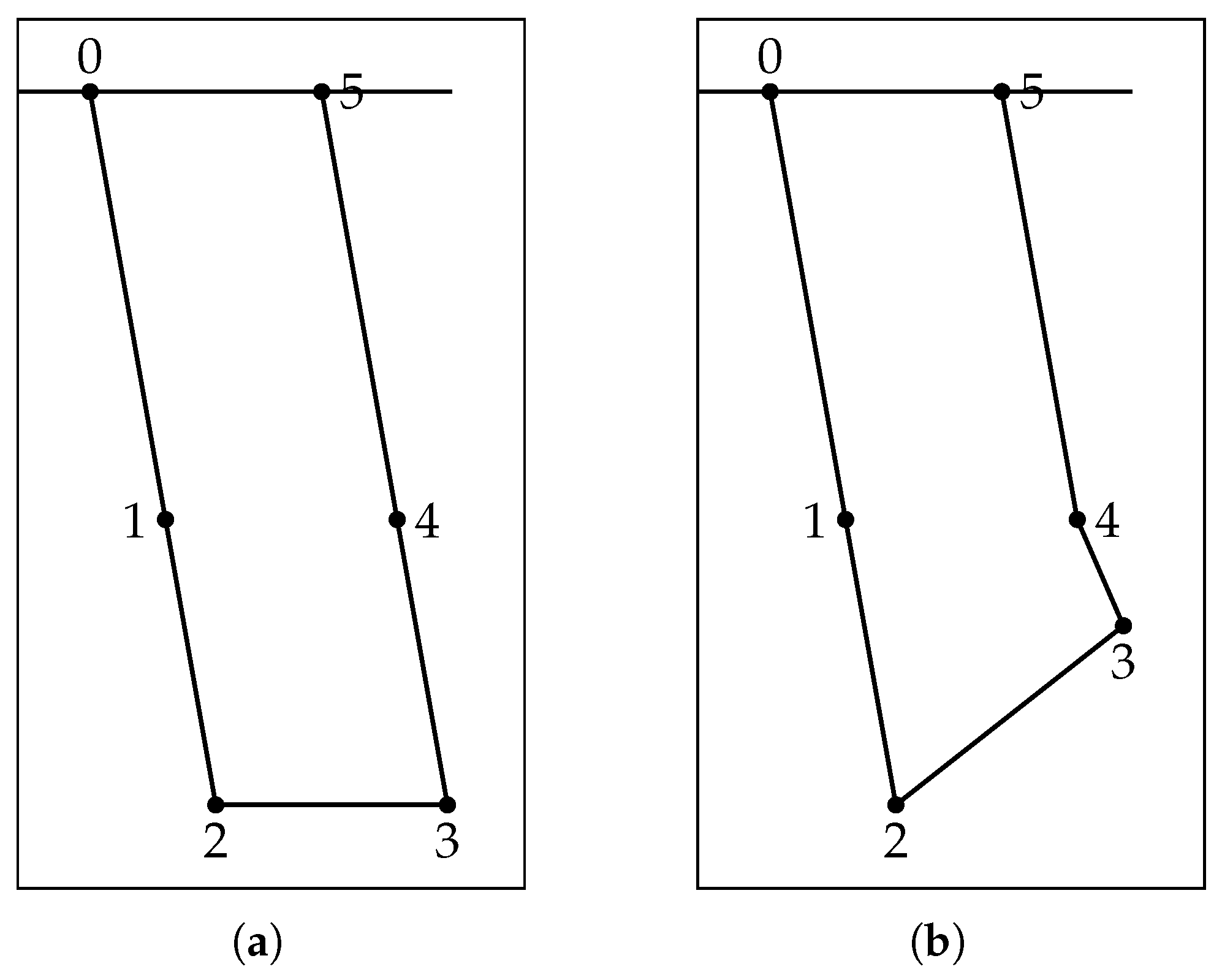
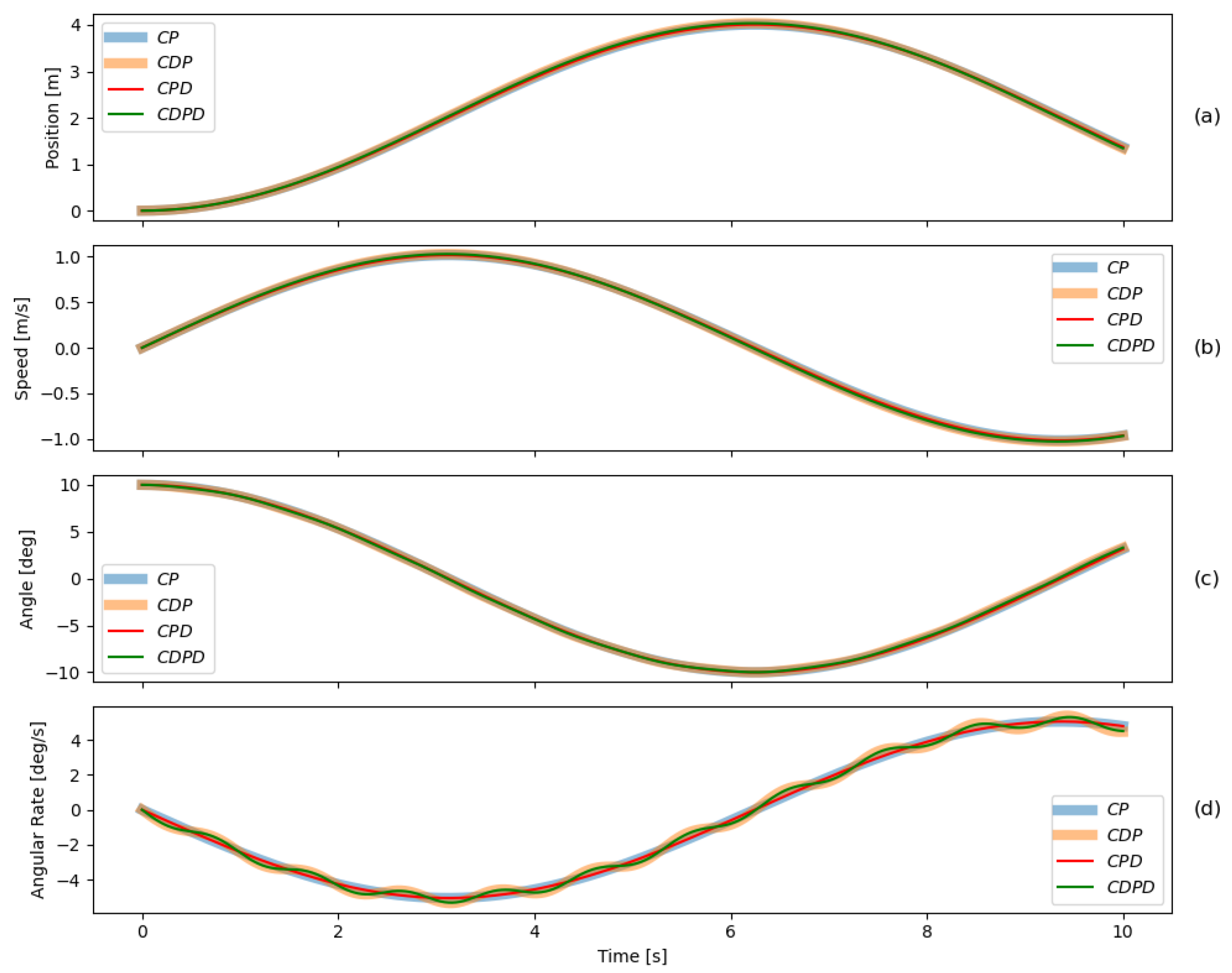
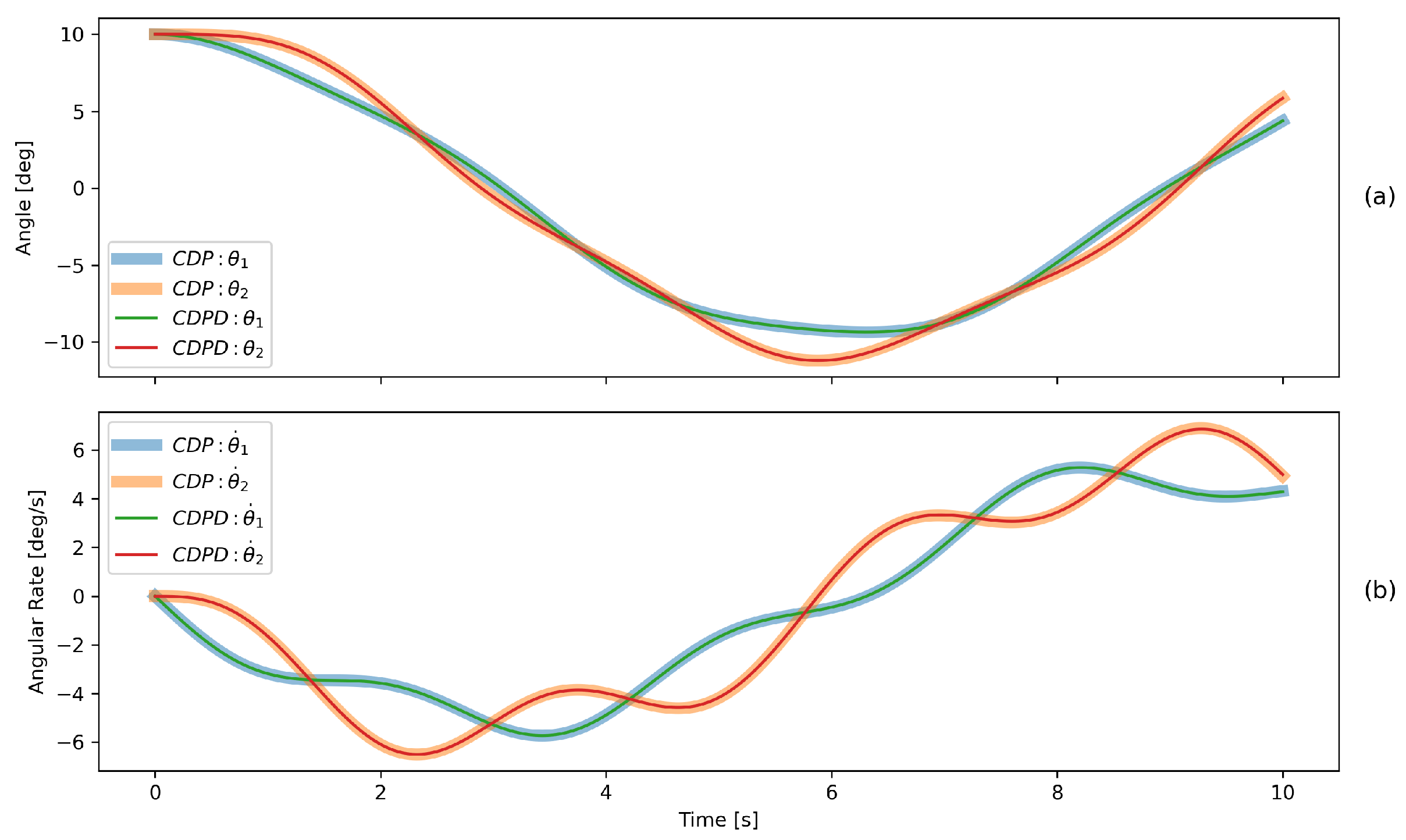
5.2. Comparison with Traditional Models
5.2.1. Model Types and Degeneration
5.2.2. Parameter Mapping
5.2.3. Simulation Scenarios and Results
Case 1: Negligible Equalizer Beam Mass
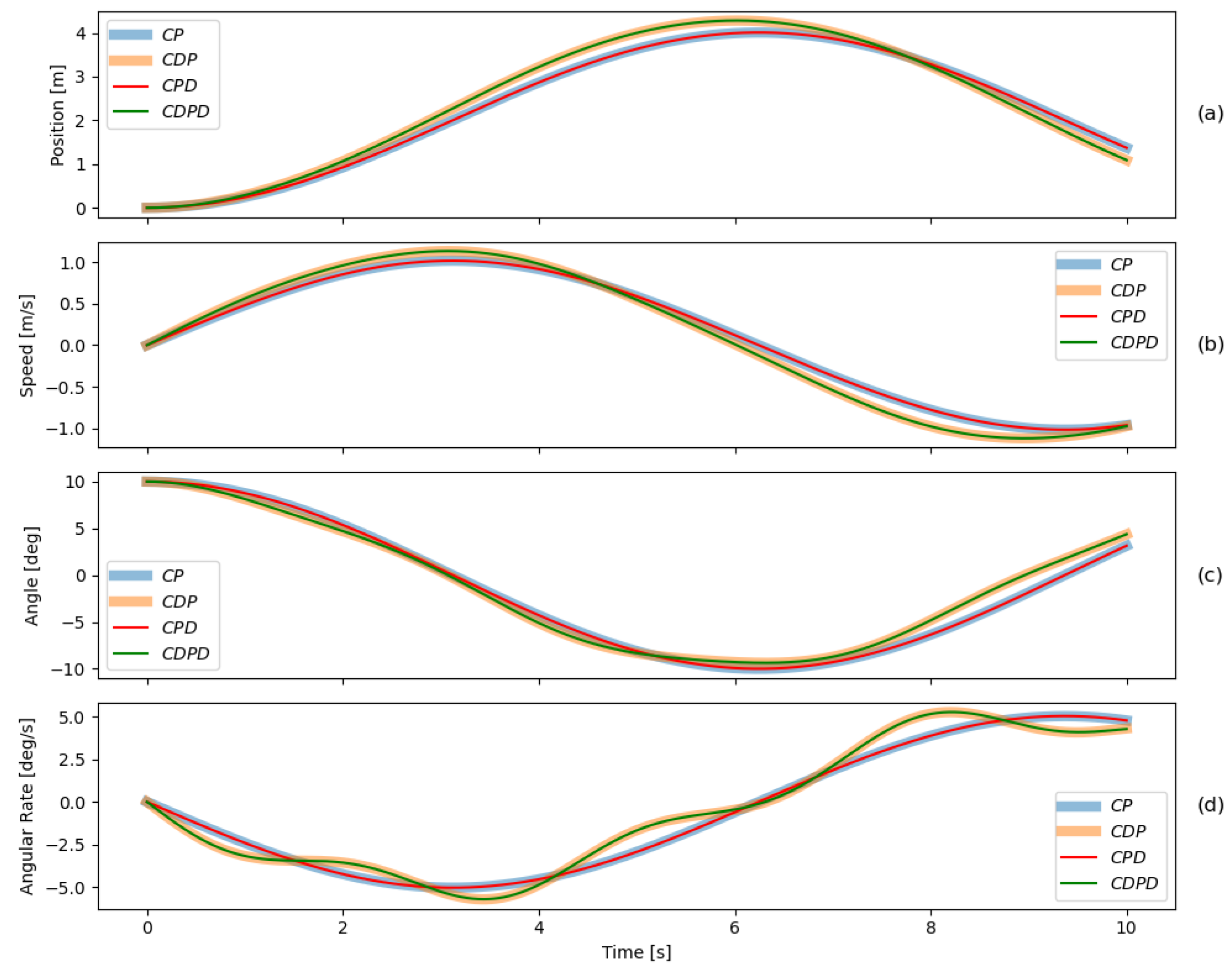
Case 2: Increased Equalizer Beam Mass
Case 3: Asymmetric Cable Lengths
5.3. Summary
6. Case Studies
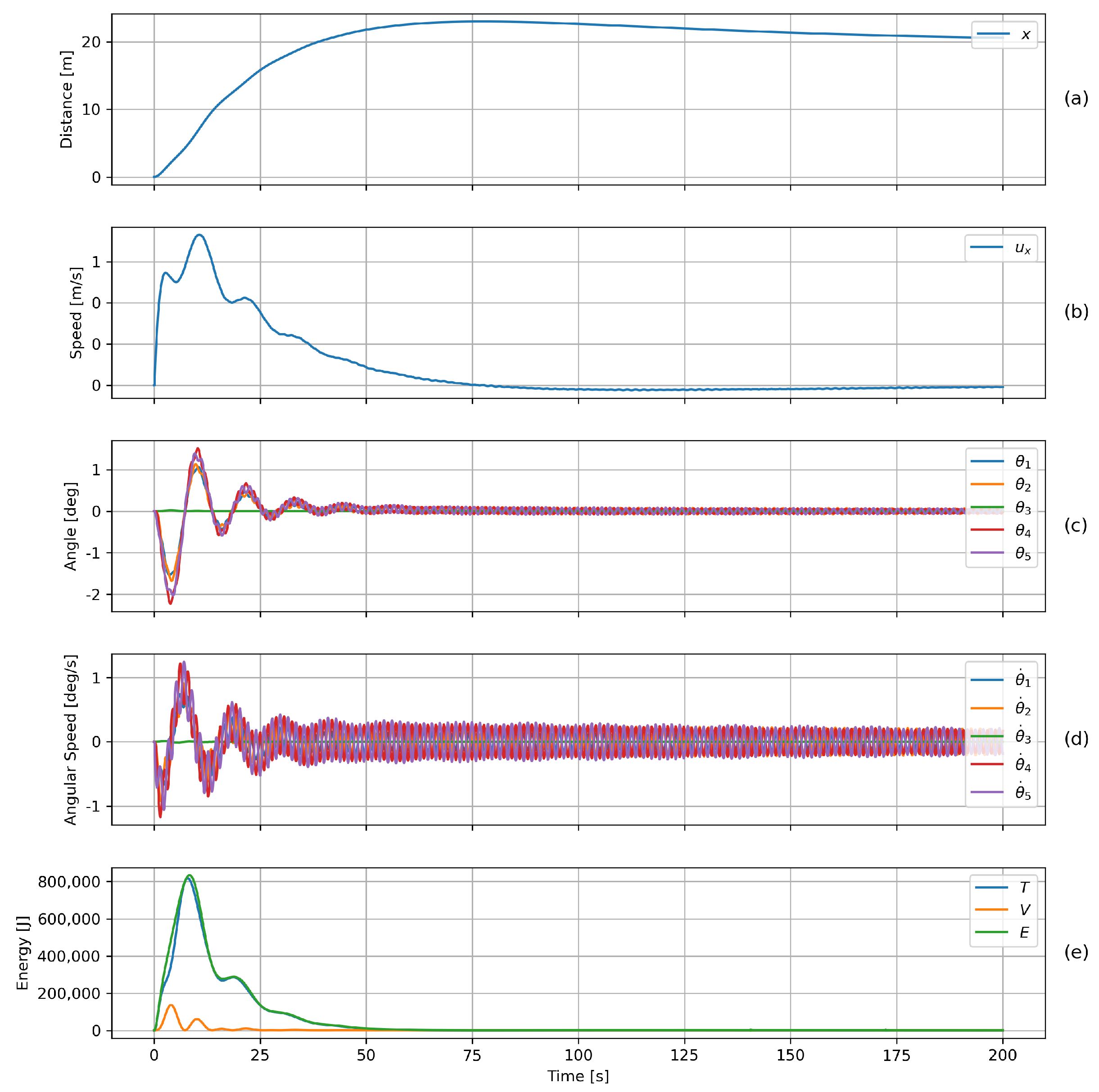
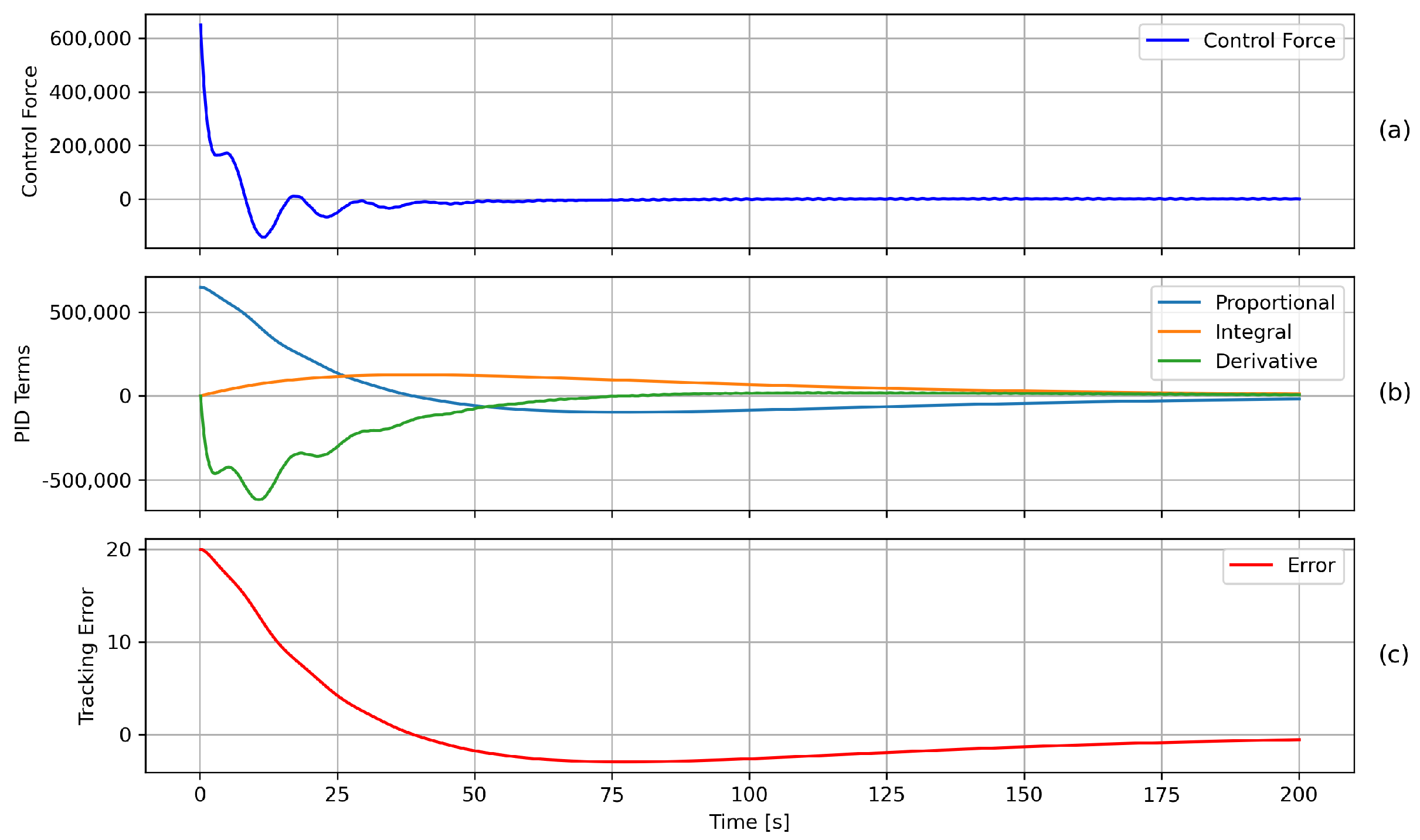
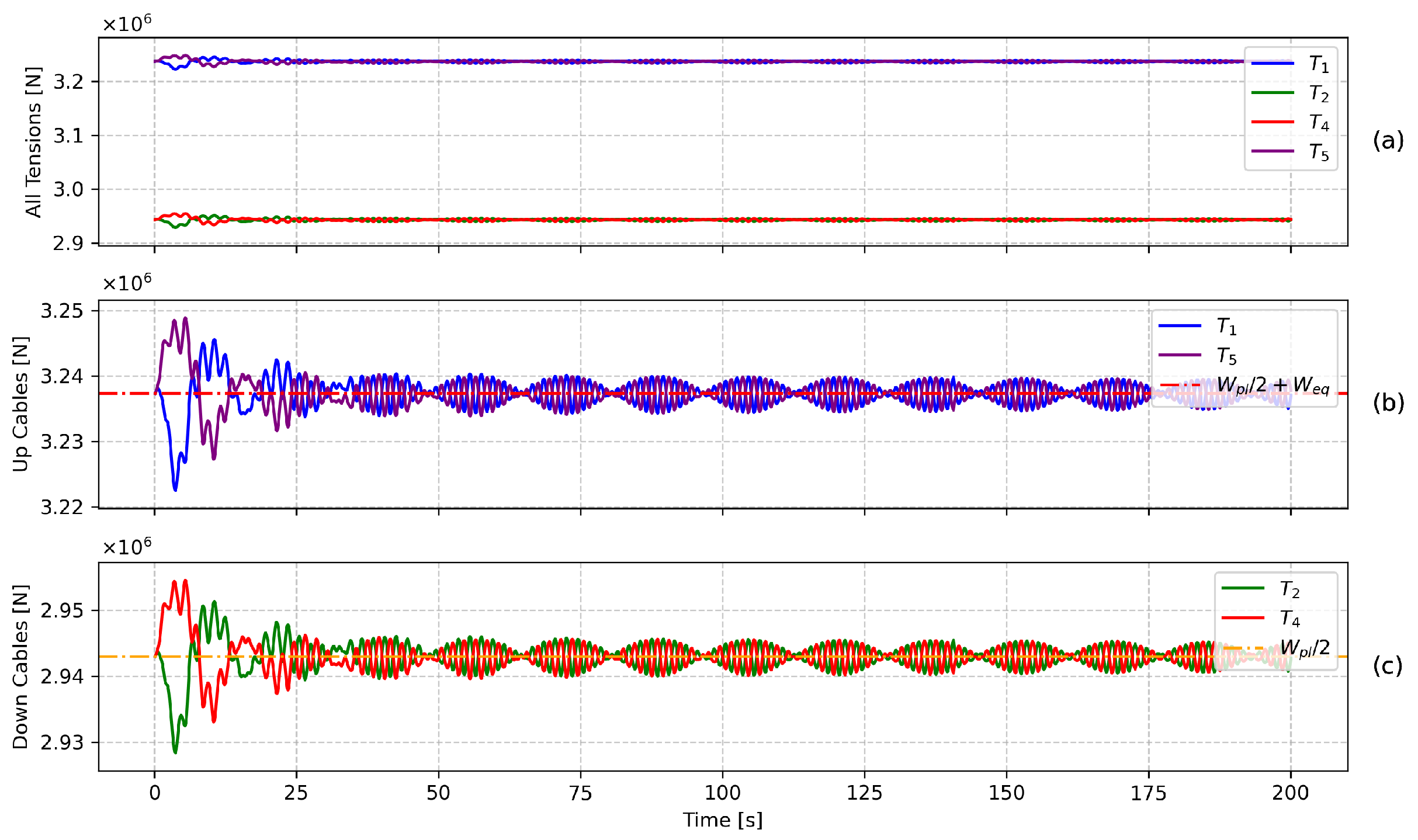
6.1. Discrete PID Control Algorithm
- : The control input at the k-th sampling instant; in this study, it represents the horizontal control force applied to the crane cart.
- : The error between the reference value and the measured output ; here, is the target position of the cart, and is the current cart position x.
- , , : The proportional, integral, and derivative gain coefficients, respectively.
- : The sampling period.
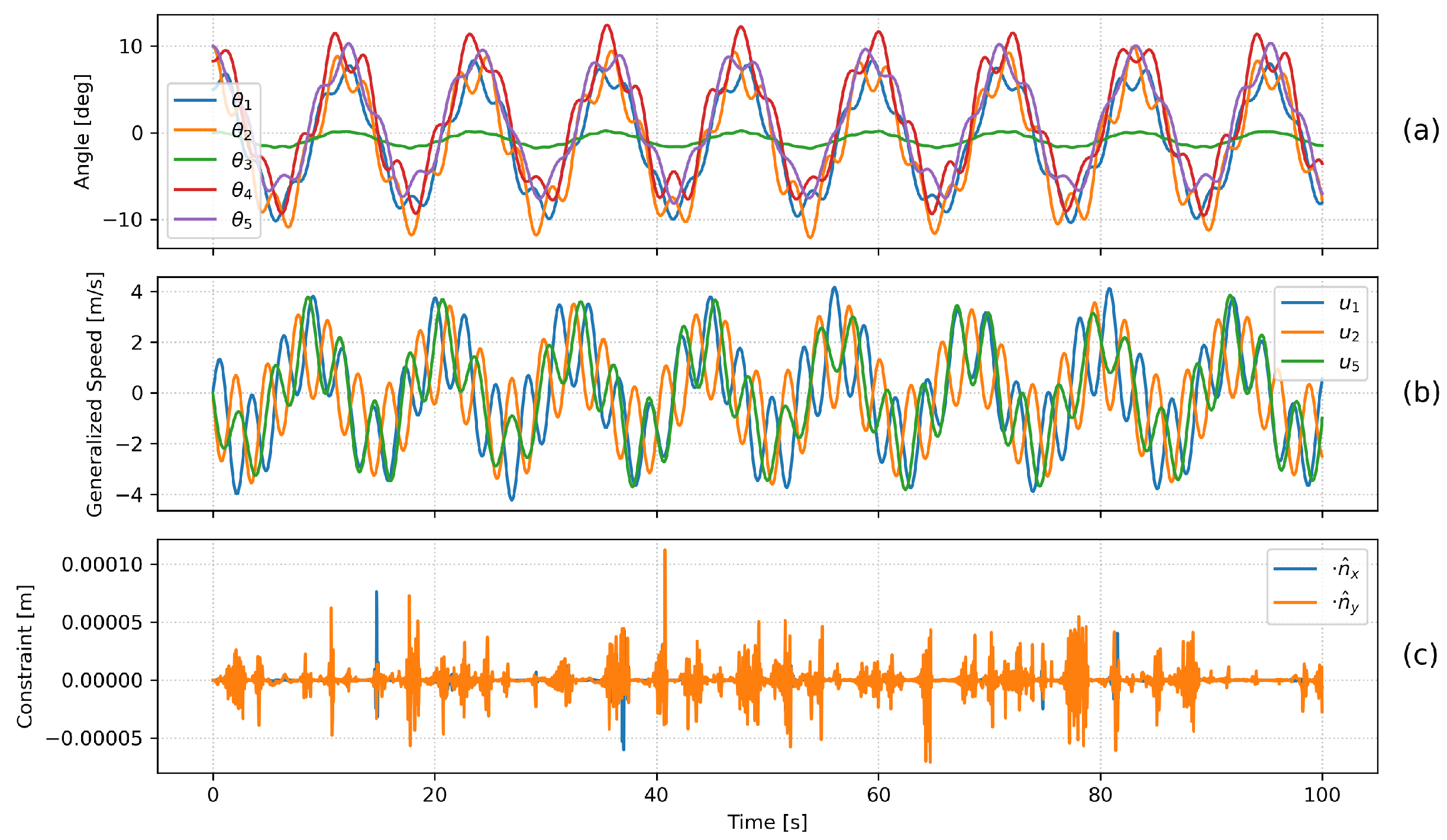
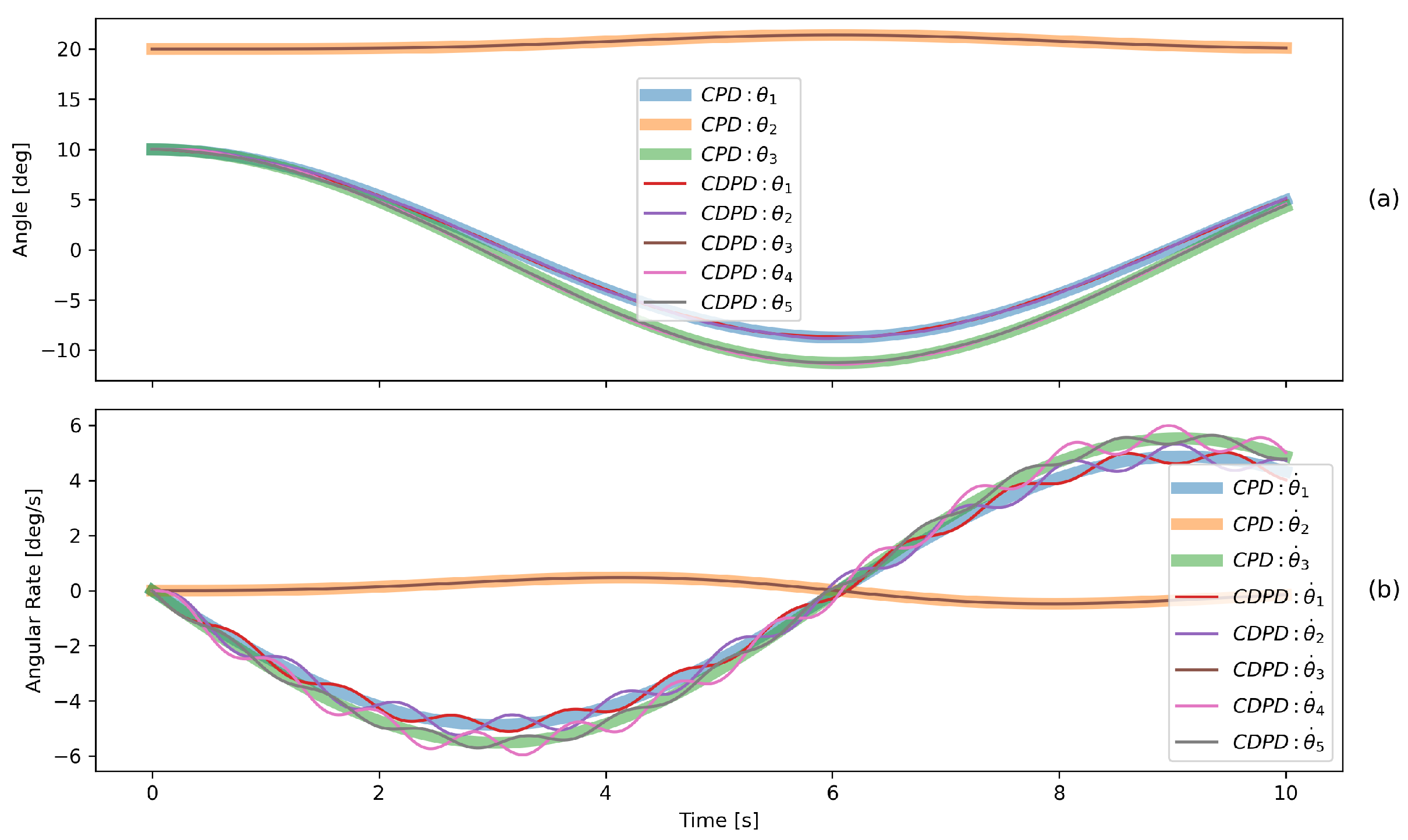
6.2. Hoisting with Unequal Suspension Heights
- Simulation time: .
- Cable lengths: , , , , , .
- Mass parameters: , , .
- Initial conditions: , , , ; all initial velocities are zero.
6.3. Simulation Result
7. Conclusions
- The explicit consideration of the equalizer beam mass and closed-chain constraints, which are critical for accurate force transmission and load sharing in practical engineering applications;
- The formulation of a unified dynamic model based on Kane’s method, with the systematic selection of independent and dependent variables to achieve a concise and numerically stable set of equations suitable for complex hoisting scenarios.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CDPD | Cart double pendulum with dual cables |
| CKC | Closed kinematic chain |
| CP | Cart pendulum |
| CPD | Cart pendulum with dual cables |
| CDP | Cart double pendulum |
| PID | Proportional–integral–derivative (controller) |
| ODEs | Ordinary differential equations |
| CoG | Center of gravity |
| DAEs | Differential–algebraic equations |
| SMC | Sliding mode control |
References
- Abdel-Rahman, E.M.; Nayfeh, A.H.; Masoud, Z.N. Dynamics and Control of Cranes: A Review. J. Vib. Control 2003, 9, 863–908. [Google Scholar] [CrossRef]
- Ramli, L.; Mohamed, Z.; Abdullahi, A.M.; Jaafar, H.I.; Lazim, I.M. Control strategies for crane systems: A comprehensive review. Mech. Syst. Signal Process. 2017, 95, 1–23. [Google Scholar] [CrossRef]
- Hong, K.S.; Shah, U.H. Dynamics and Control of Industrial Cranes; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Muddassir, M.; Zayed, T.; Ali, A.H.; Elrifaee, M.; Abdulai, S.F.; Yang, T.; Eldemiry, A. Automation in tower cranes over the past two decades (2003–2024). Autom. Constr. 2025, 170, 105889. [Google Scholar] [CrossRef]
- Mojallizadeh, M.R.; Brogliato, B.; Prieur, C. Modeling and control of overhead cranes: A tutorial overview and perspectives. Annu. Rev. Control 2023, 56, 100877. [Google Scholar] [CrossRef]
- Kim, G.H.; Yoon, M.; Jeon, J.Y.; Hong, K.S. Data-driven Modeling and Adaptive Predictive Anti-swing Control of Overhead Cranes. Int. J. Control. Autom. Syst. 2022, 20, 2712–2723. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, S.; Chen, H.; Li, G.; Zhang, H. Dynamic Modeling and Anti-swing Control of Double Pendulum Payload System of Overhead Crane. In Proceedings of the 2022 IEEE 17th International Conference on Control & Automation (ICCA), Naples, Italy, 27–30 June 2022. [Google Scholar] [CrossRef]
- Fatehi, M.H.; Eghtesad, M.; Necsulescu, D.S.; Fatehi, A.A. Tracking control design for a multi-degree underactuated flexible-cable overhead crane system with large swing angle based on singular perturbation method and an energy-shaping technique. J. Vib. Control 2019, 25, 1752–1767. [Google Scholar] [CrossRef]
- Rome, T.; Adams, C.; Singhose, W. Dynamic Model for Improved Controller Design in Tower Crane Disassembly. In Proceedings of the 2024 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 15–19 July 2024; pp. 1118–1125. [Google Scholar] [CrossRef]
- Shi, H.; Yao, F.; Yuan, Z.; Tong, S.; Tang, Y.; Han, G. Research on nonlinear coupled tracking controller for double pendulum gantry cranes with load hoisting/lowering. Nonlinear Dyn. 2022, 108, 223–238. [Google Scholar] [CrossRef]
- Chen, Q.; Cheng, W.; Liu, J.; Du, R. Partial state feedback sliding mode control for double-pendulum overhead cranes with unknown disturbances. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2022, 236, 3902–3911. [Google Scholar] [CrossRef]
- Rigatos, G. Nonlinear Optimal Control for the Underactuated Double-Pendulum Overhead Crane. J. Vib. Eng. Technol. 2023, 12, 1203–1223. [Google Scholar] [CrossRef]
- Tuan, L.A.; Lee, S.G. Sliding mode controls of double-pendulum crane systems. J. Mech. Sci. Technol. 2013, 27, 1863–1873. [Google Scholar] [CrossRef]
- Wang, J.; Liu, K.; Wang, S.; Chen, H.; Sun, Y.; Niu, A.; Li, H. Dynamic Analysis and Experiment of Underactuated Double-Pendulum Anti-Swing Device for Ship-Mounted Jib Cranes. Pol. Marit. Res. 2022, 29, 145–154. [Google Scholar] [CrossRef]
- Miao, X.; Zheng, S.; Ouyang, H. Fault-tolerant controller design for tower cranes considering distributed payload beams. Int. J. Robust Nonlinear Control 2023, 34, 3516–3547. [Google Scholar] [CrossRef]
- Li, Z.; Ma, X.; Li, Y. Nonlinear partially saturated control of a double pendulum offshore crane based on fractional-order disturbance observer. Autom. Constr. 2022, 137, 104212. [Google Scholar] [CrossRef]
- Guo, Q.; Chai, L.; Liu, H. Anti-swing sliding mode control of three-dimensional double pendulum overhead cranes based on extended state observer. Nonlinear Dyn. 2022, 111, 391–410. [Google Scholar] [CrossRef]
- Maleki, E.; Singhose, W.; Hawke, J.; Vaughan, J. Dynamic Response of a Dual-Hoist Bridge Crane. In Proceedings of the ASME 2013 Dynamic Systems and Control Conference, V003T48A002, Palo Alto, CA, USA, 21–23 October 2013; Volume 3. [Google Scholar] [CrossRef]
- Arena, A.; Casalotti, A.; Lacarbonara, W.; Cartmell, M.P. Three-Dimensional Modeling of Container Cranes. In Proceedings of the ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, V07AT10A069, Portland, OR, USA, 4–7 August 2013; Volume 7A. [Google Scholar] [CrossRef]
- Arena, A.; Casalotti, A.; Lacarbonara, W.; Cartmell, M.P. Dynamics of container cranes: Three-dimensional modeling, full-scale experiments, and identification. Int. J. Mech. Sci. 2015, 93, 8–21. [Google Scholar] [CrossRef]
- Lu, B.; Fang, Y.; Sun, N. Modeling and verification for a four-rope crane. In Proceedings of the 2015 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), Shenyang, China, 8–12 June 2015. [Google Scholar] [CrossRef]
- Lu, B.; Fang, Y.; Sun, N. Adaptive trajectory tracking control for a four-rope crane. In Proceedings of the 2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Busan, Republic of Korea, 7–11 July 2015. [Google Scholar] [CrossRef]
- Lu, B.; Fang, Y.; Sun, N. Nonlinear control for underactuated multi-rope cranes: Modeling, theoretical design and hardware experiments. Control Eng. Pract. 2018, 76, 123–132. [Google Scholar] [CrossRef]
- Lu, B.; Fang, Y.; Sun, N. Adaptive Output-Feedback Control for Dual Overhead Crane System With Enhanced Anti-Swing Performance. IEEE Trans. Control Syst. Technol. 2020, 28, 2235–2248. [Google Scholar] [CrossRef]
- Wen, T.; Fang, Y.; Lu, B. Neural network-based adaptive sliding mode control for underactuated dual overhead cranes suffering from matched and unmatched disturbances. Auton. Intell. Syst. 2022, 2, 1. [Google Scholar] [CrossRef]
- Leban, F.A.; Diaz-Gonzalez, J.; Parker, G.G.; Zhao, W. Inverse Kinematic Control of a Dual Crane System Experiencing Base Motion. IEEE Trans. Control Syst. Technol. 2015, 23, 331–339. [Google Scholar] [CrossRef]
- Fu, Y.; Yang, T.; Sun, N.; Zhang, J.; Fang, Y. Dynamics modeling and analysis for cooperative dual rotary crane systems. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 5492–5497. [Google Scholar]
- Sun, N.; Yang, T.; Fang, Y.; Lu, B.; Qian, Y. Nonlinear Motion Control of Underactuated Three-Dimensional Boom Cranes With Hardware Experiments. IEEE Trans. Ind. Inform. 2018, 14, 887–897. [Google Scholar] [CrossRef]
- Sun, N.; Fu, Y.; Yang, T.; Zhang, J.; Fang, Y.; Xin, X. Nonlinear Motion Control of Complicated Dual Rotary Crane Systems Without Velocity Feedback: Design, Analysis, and Hardware Experiments. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1017–1029. [Google Scholar] [CrossRef]
- Liu, Z.; Fu, Y.; Sun, N.; Yang, T.; Fang, Y. Collaborative Antiswing Hoisting Control for Dual Rotary Cranes With Motion Constraints. IEEE Trans. Ind. Inform. 2022, 18, 6120–6130. [Google Scholar] [CrossRef]
- Zhao, X.; Huang, J. Distributed-mass payload dynamics and control of dual cranes undergoing planar motions. Mech. Syst. Signal Process. 2019, 126, 636–648. [Google Scholar] [CrossRef]
- Huang, J.; Zhu, K. Dynamics and control of three-dimensional dual cranes transporting a bulky payload. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2020, 235, 1956–1965. [Google Scholar] [CrossRef]
- Feng, X.; Yang, T.; Zhang, T.; Wang, J.; Pang, R.; Chen, X.; Wu, Q.; Sun, N. Dynamic Modeling of Variable-Length Dual Cable Boom Cranes with Postural Adjustments. In Proceedings of the International Conference on Guidance, Navigation and Control, Changsha, China, 9–11 August 2024; Springer: Singapore, 2024; pp. 140–151. [Google Scholar]
- Sarkar, S.; Fitzgerald, B. Use of Kane’s Method for Multi-Body Dynamic Modelling and Control of Spar-Type Floating Offshore Wind Turbines. Energies 2021, 14, 6635. [Google Scholar] [CrossRef]
- Qiu, S.; Ren, H.; Li, H.; Zhou, Y.; Wang, D. Multibody Dynamics Model and Simulation for the Totally Enclosed Lifeboat Lowered From Ship in Rough Seas. IEEE Access 2021, 9, 32171–32187. [Google Scholar] [CrossRef]
- Zhong, Y.; Wang, L. A Method to Establish the Dynamic Models of Multibody System Based on Kane’s Equations. In Proceedings of the the 2nd International Conference on Modelling, Identification and Control, Paris, France, 9–10 August 2015; Atlantis Press: Dordrecht, The Netherlands, 2015; pp. 21–26. [Google Scholar] [CrossRef]
- Marques, F.; Roupa, I.; Silva, M.T.; Flores, P.; Lankarani, H.M. Examination and comparison of different methods to model closed loop kinematic chains using Lagrangian formulation with cut joint, clearance joint constraint and elastic joint approaches. Mech. Mach. Theory 2021, 160, 104294. [Google Scholar] [CrossRef]
- Wang, Z.; Ghorbel, F.H. Modeling Closed Kinematic Chains for Control: A Comparative Study. In Proceedings of the ASME 2005 International Mechanical Engineering Congress and Exposition, Orlando, FL, USA, 5–11 November 2005. [Google Scholar] [CrossRef]
- Zahedi, A.; Shafei, A.M.; Shamsi, M. On the dynamics of multi-closed-chain robotic mechanisms. Int. J. Non-Linear Mech. 2022, 147, 104241. [Google Scholar] [CrossRef]
- Kane, T.R.; Levinson, D.A. Dynamics, Theory and Applications; McGraw Hill: New York, NY, USA, 1985. [Google Scholar]
- Vallery, H.; Schwab, A.L. Advanced Dynamics; Delft University of Technology: Delft, The Netherlands, 2017. [Google Scholar]


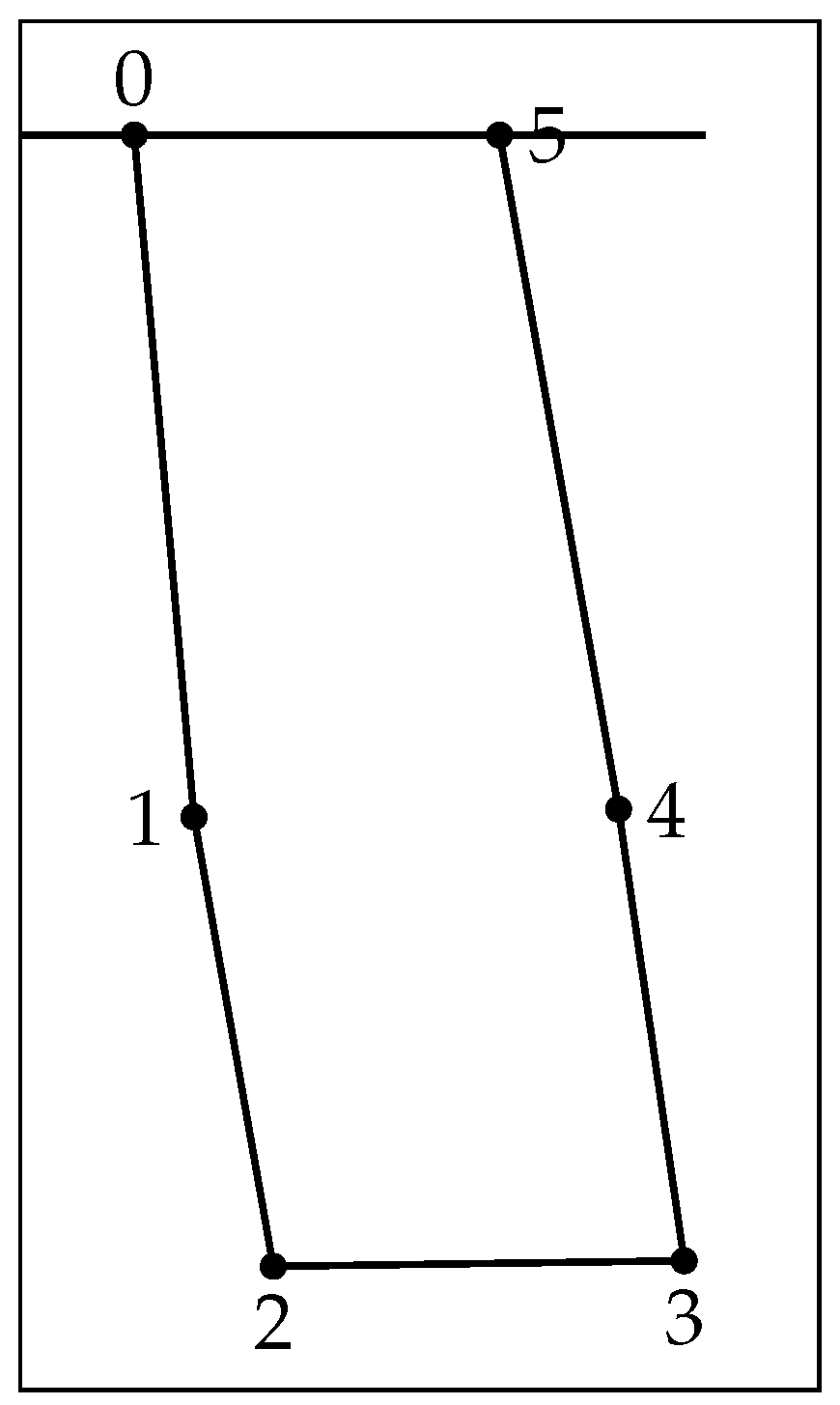


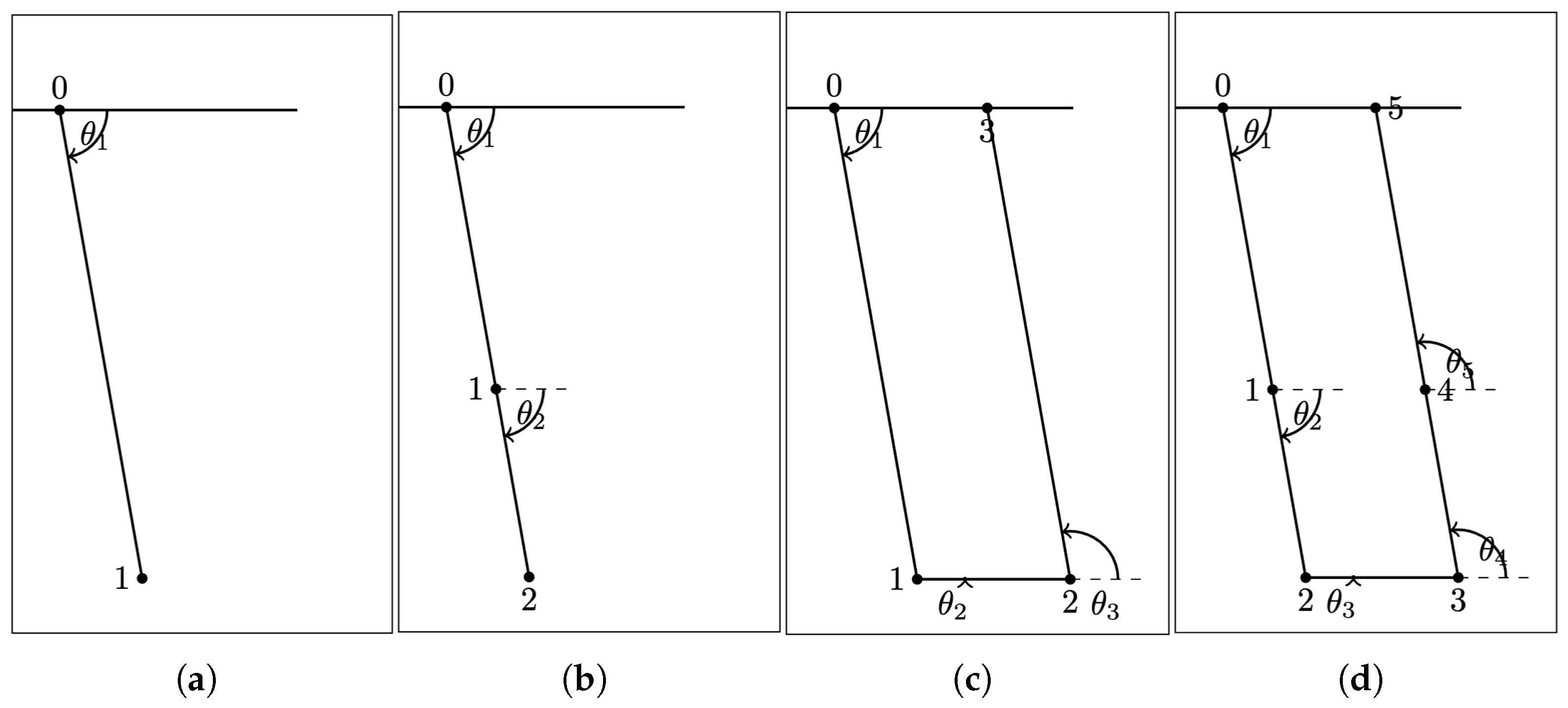
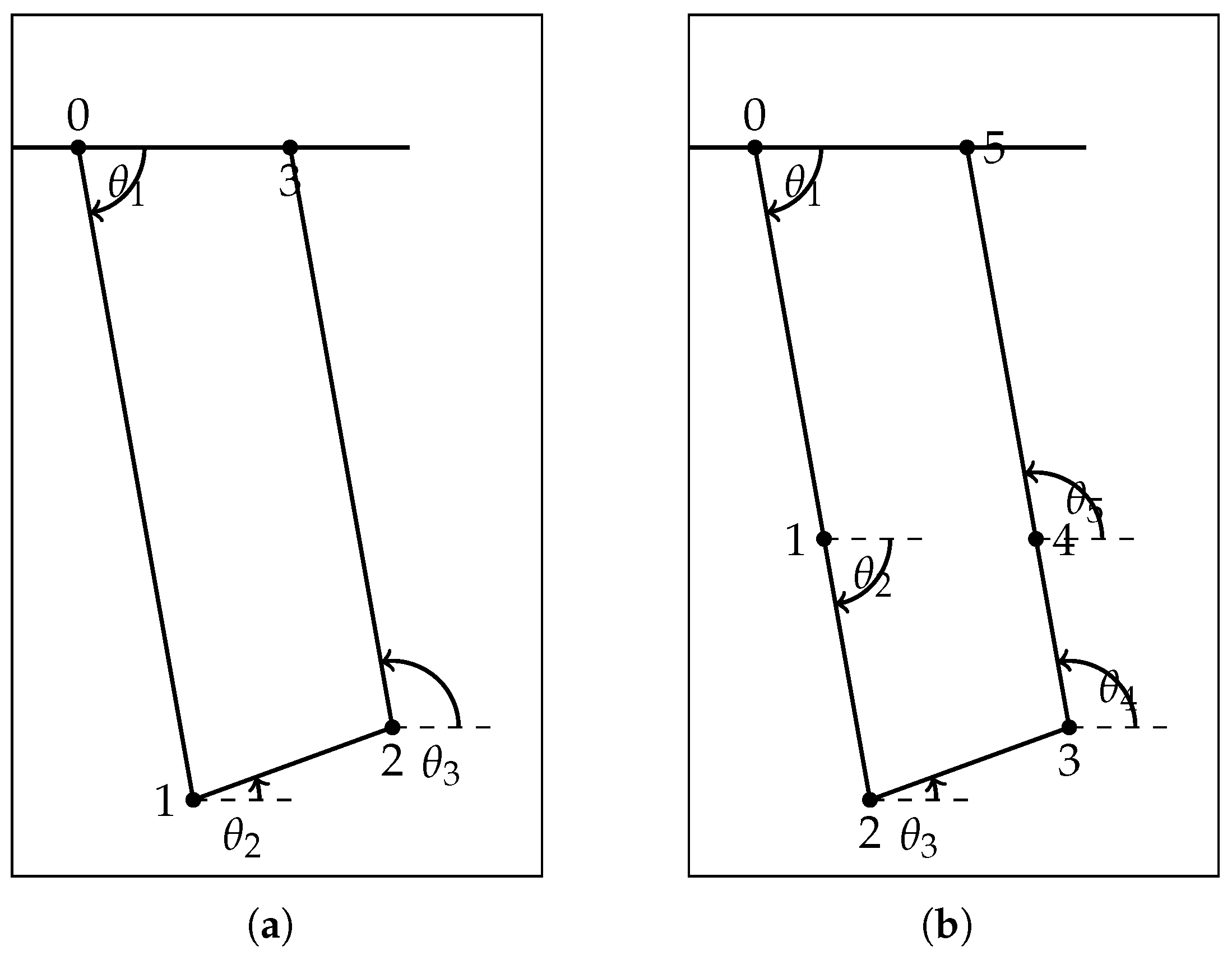
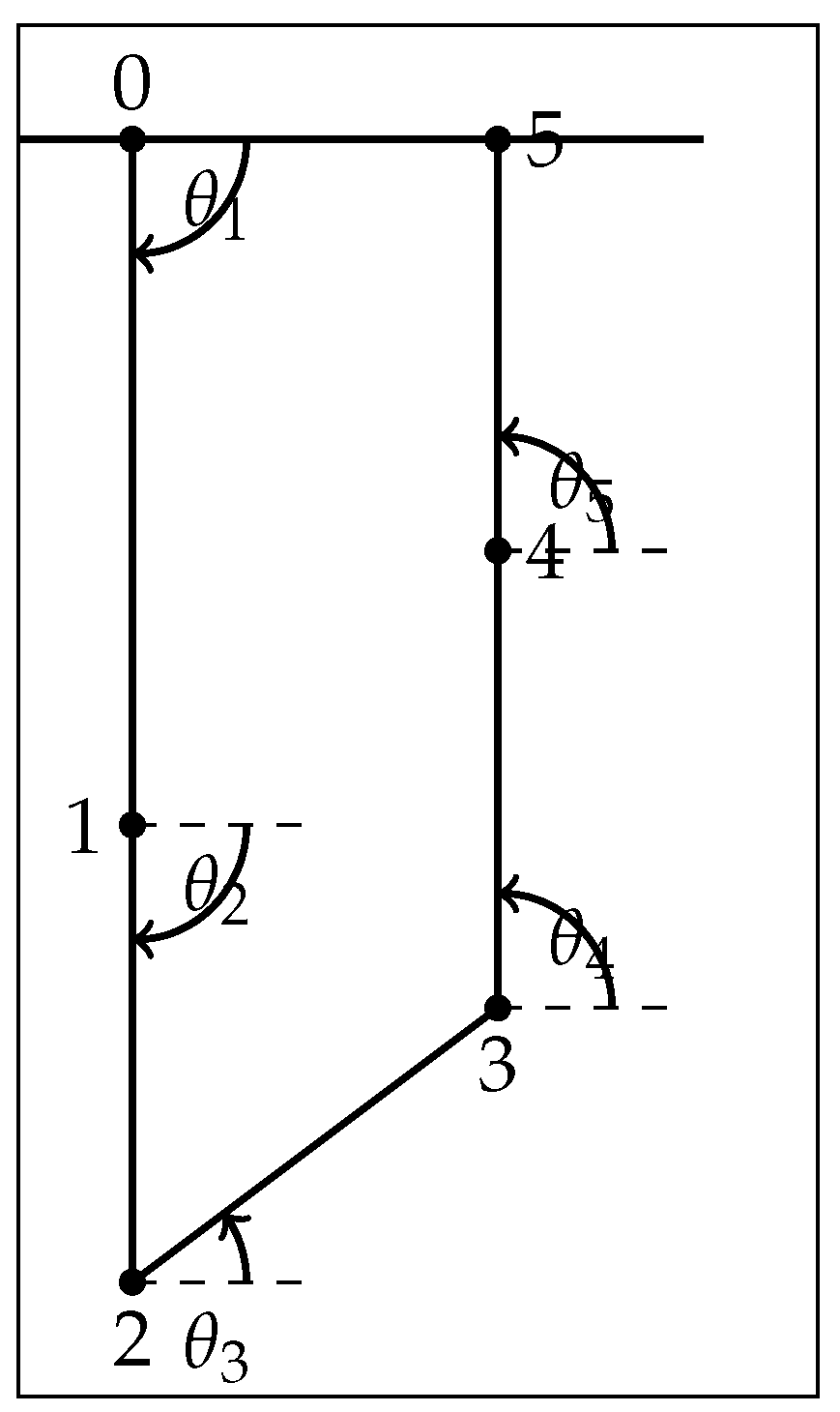
| Coordinate System | Associated Body |
|---|---|
| N (inertial frame) | Ground (fixed reference) |
| A | Cart 1 to left equalizer beam (nodes 0–1) |
| B | Left equalizer beam to left hoisting point (nodes 1–2) |
| C | Payload (left to right hoisting points, nodes 2–3) |
| D | Right hoisting point to right equalizer beam (nodes 3–4) |
| E | Right equalizer beam to Cart 2 (nodes 4–5) |
| Node | Physical Meaning | Position Vector Expression |
|---|---|---|
| Cart 1 position (left cart) | ||
| Left equalizer beam | ||
| Left payload suspension point | ||
| Right payload suspension point | ||
| Right equalizer beam | ||
| Cart 2 position (right cart) | ||
| the position of the payload’s CoG |
| Symbol | Description | Unit / Value |
|---|---|---|
| x | Horizontal position of cart 1 (left cart) | m |
| Distance between carts (platform length) | m | |
| Length of left upper cable | m | |
| Length of left lower cable | m | |
| Length between payload suspension points | m | |
| Length of right lower cable | m | |
| Length of right upper cable | m | |
| d | Horizontal offset of payload CoG from node 2 | m |
| h | Vertical offset of payload CoG from node 2 | m |
| Mass of crane carts (total) | ton or kg | |
| Mass of left equalizer beam | ton or kg | |
| Mass of right equalizer beam | ton or kg | |
| Mass of payload | ton or kg | |
| Horizontal control force on cart(s) | N | |
| g | Gravitational acceleration | |
| Absolute angle of the i-th link | rad or deg () | |
| Generalized speed of cart 1 (horizontal) | m/s | |
| Generalized speed of the i-th link | m/s () | |
| Tension in the i-th cable | N () |
| Method 1 | Method 2 | Method 3 | |
|---|---|---|---|
| Constraint Error | |||
| Mean | |||
| Median | |||
| Max | |||
| Constraint Error | |||
| Mean | |||
| Median | |||
| Max |
| Configuration 1 | Configuration 2 | |||||
|---|---|---|---|---|---|---|
| Dependent Variables | ||||||
| Condition Number | 111.524 | 108.072 | 111.524 | 108.072 | ||
| Using Method 1 (s) | 7.139 | 10.567 | 6.639 | 8.657 | 10.857 | 6.805 |
| Using Method 2 (s) | 7.499 | 11.208 | 6.999 | 10.716 | 11.608 | 7.005 |
| Using Method 3 (s) | - | 7.188 | 3.659 | - | 5.790 | 2.604 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, B.; Zeng, J.; Gao, P.; Zhang, H.; Ge, S. Dynamic Modeling and Validation of Dual-Cable Double-Pendulum Systems for Gantry Cranes. Machines 2025, 13, 676. https://doi.org/10.3390/machines13080676
Jin B, Zeng J, Gao P, Zhang H, Ge S. Dynamic Modeling and Validation of Dual-Cable Double-Pendulum Systems for Gantry Cranes. Machines. 2025; 13(8):676. https://doi.org/10.3390/machines13080676
Chicago/Turabian StyleJin, Bowen, Ji Zeng, Pan Gao, He Zhang, and Shenwei Ge. 2025. "Dynamic Modeling and Validation of Dual-Cable Double-Pendulum Systems for Gantry Cranes" Machines 13, no. 8: 676. https://doi.org/10.3390/machines13080676
APA StyleJin, B., Zeng, J., Gao, P., Zhang, H., & Ge, S. (2025). Dynamic Modeling and Validation of Dual-Cable Double-Pendulum Systems for Gantry Cranes. Machines, 13(8), 676. https://doi.org/10.3390/machines13080676





