Motion Sickness Suppression Strategy Based on Dynamic Coordination Control of Active Suspension and ACC
Abstract
1. Introduction
2. Materials and Methods
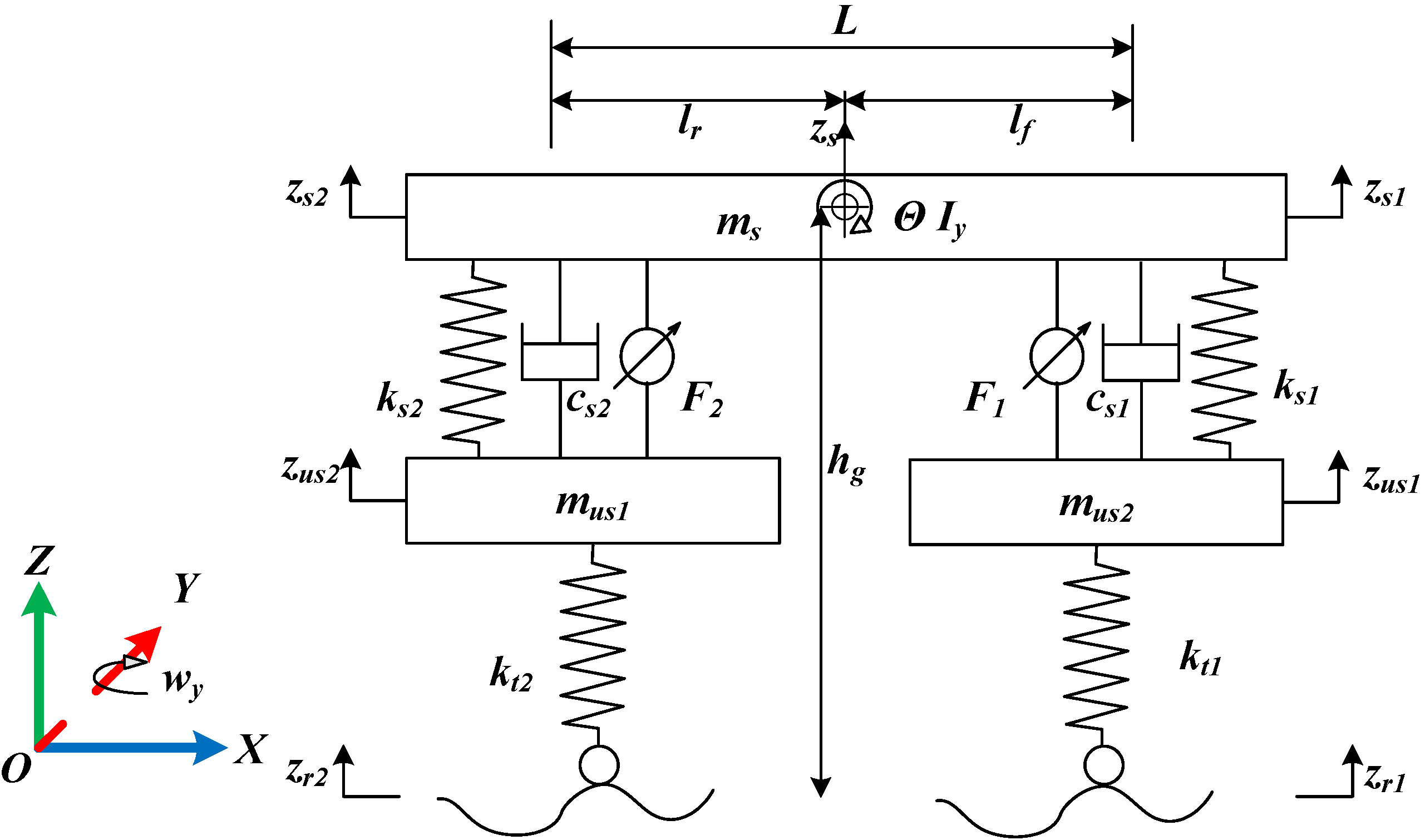
2.1. Vertical Dynamics
- Model Control Variables:
- Model Disturbance Inputs:
- Model State Variables:
- Model Output Variables:
2.2. ACC Control
- Model Control Variables:
- Model Disturbance Inputs:
- Model State Variables:
- Model Output Variables:
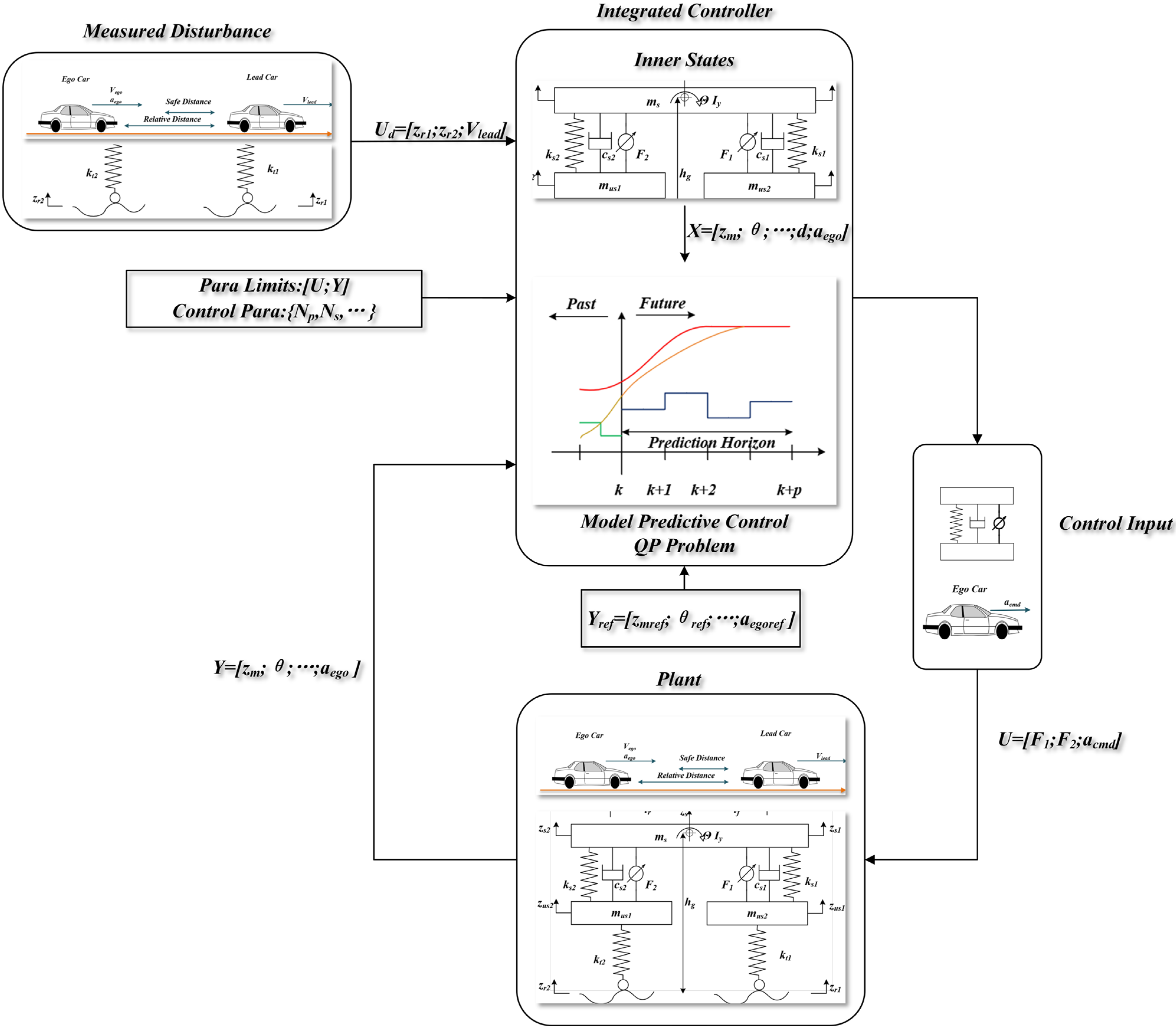
2.3. Coupled Dynamics Integration
- Model Control Variables:
- Model Disturbance Inputs:
- Model State Variables:
- Model Output Variables:
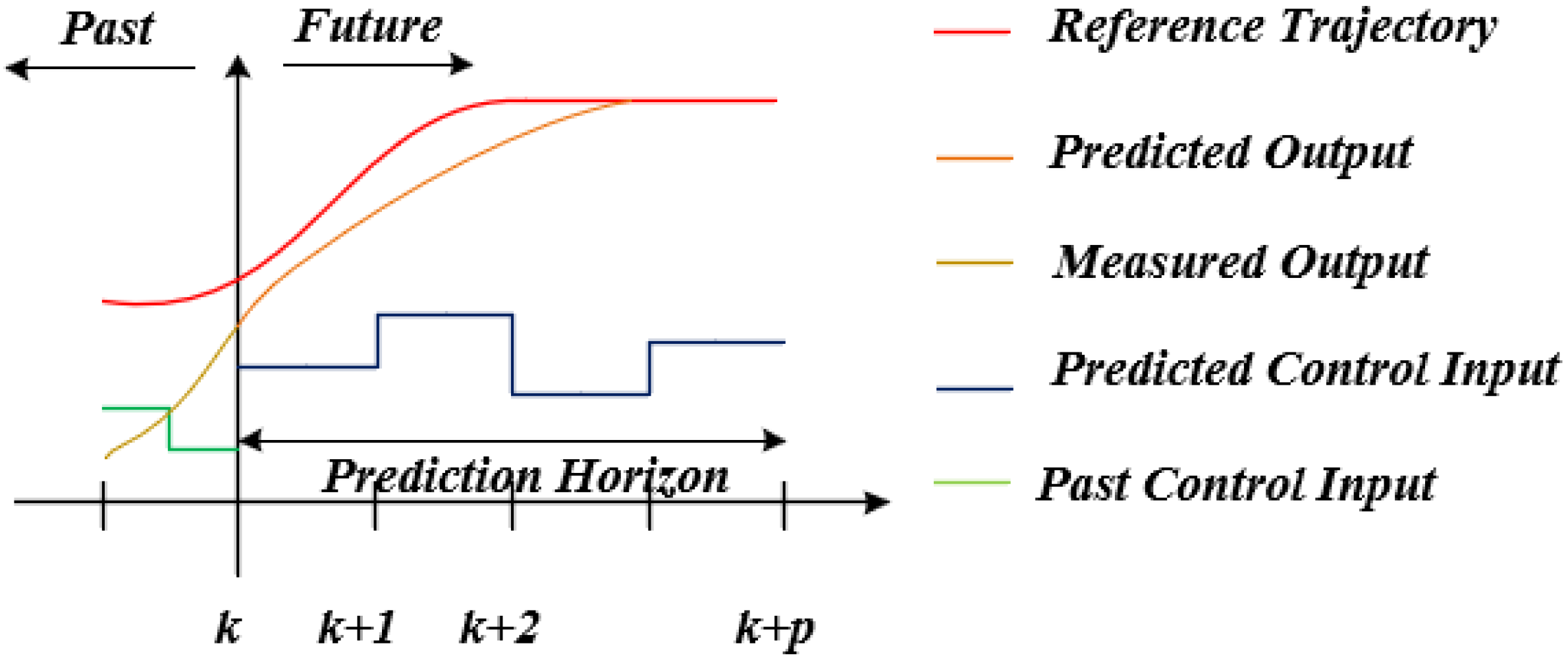
2.4. MPC-Based Integrated Controller Design
3. Results
3.1. Coupled Control System Architecture
3.2. System Decoupled Simulation
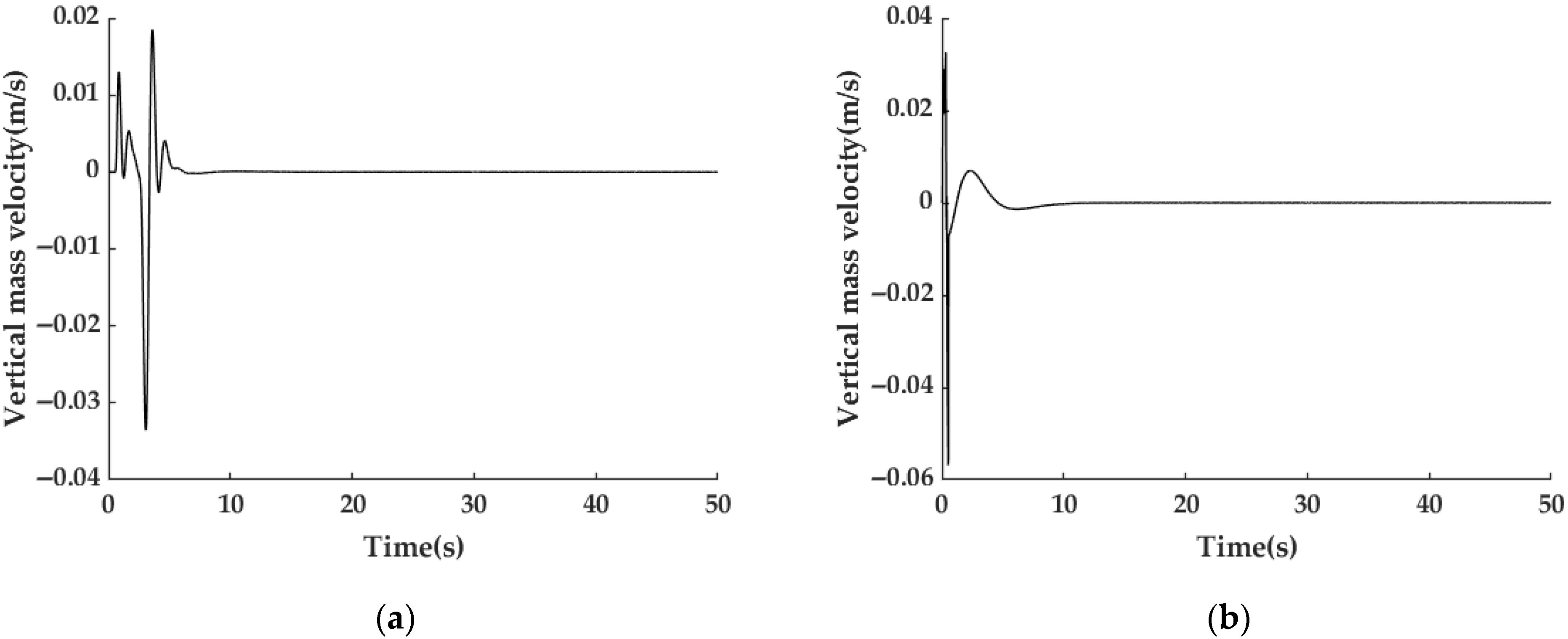
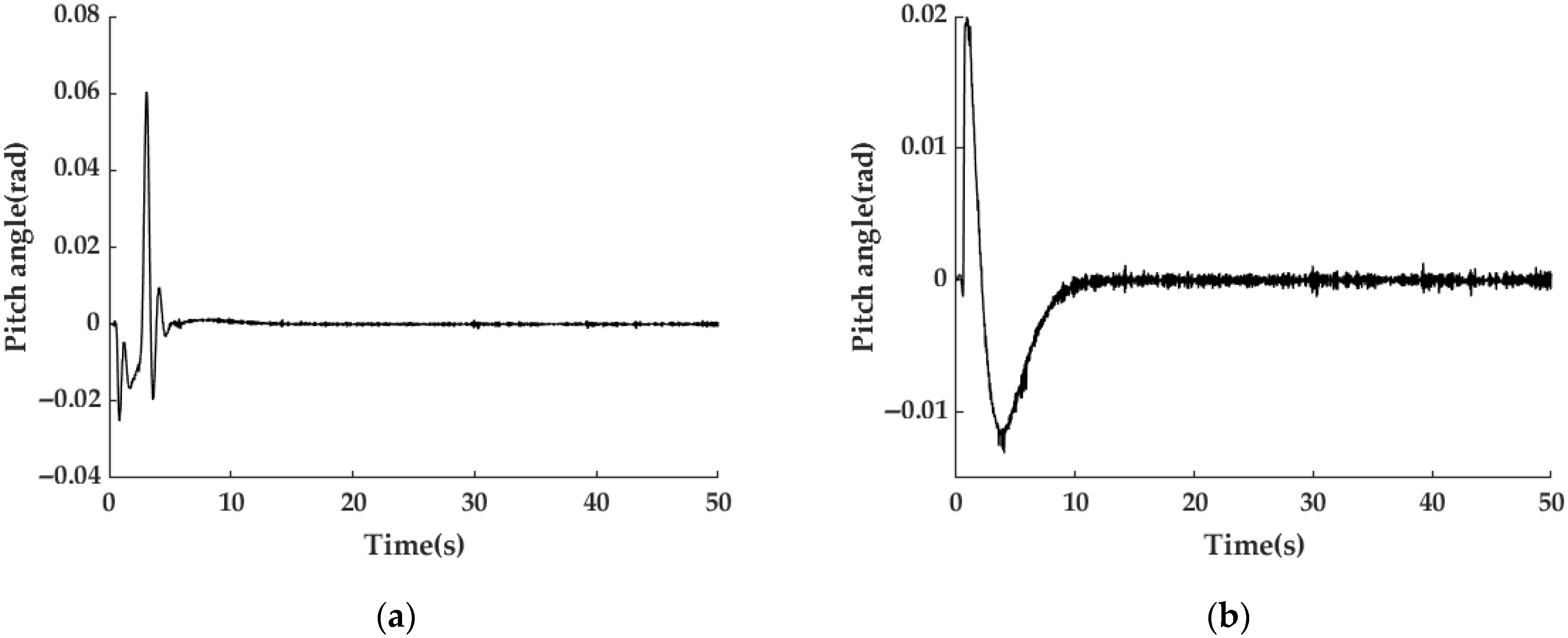
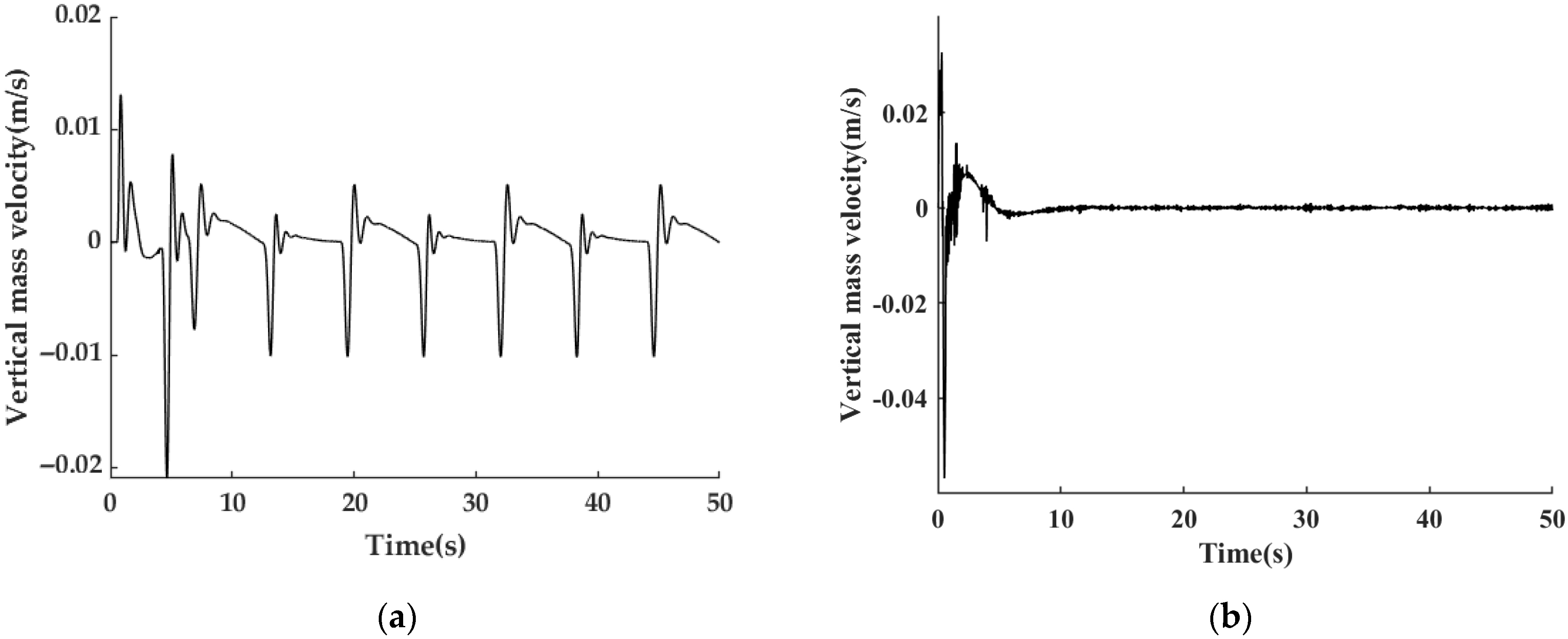
3.2.1. Suspension Control Simulation
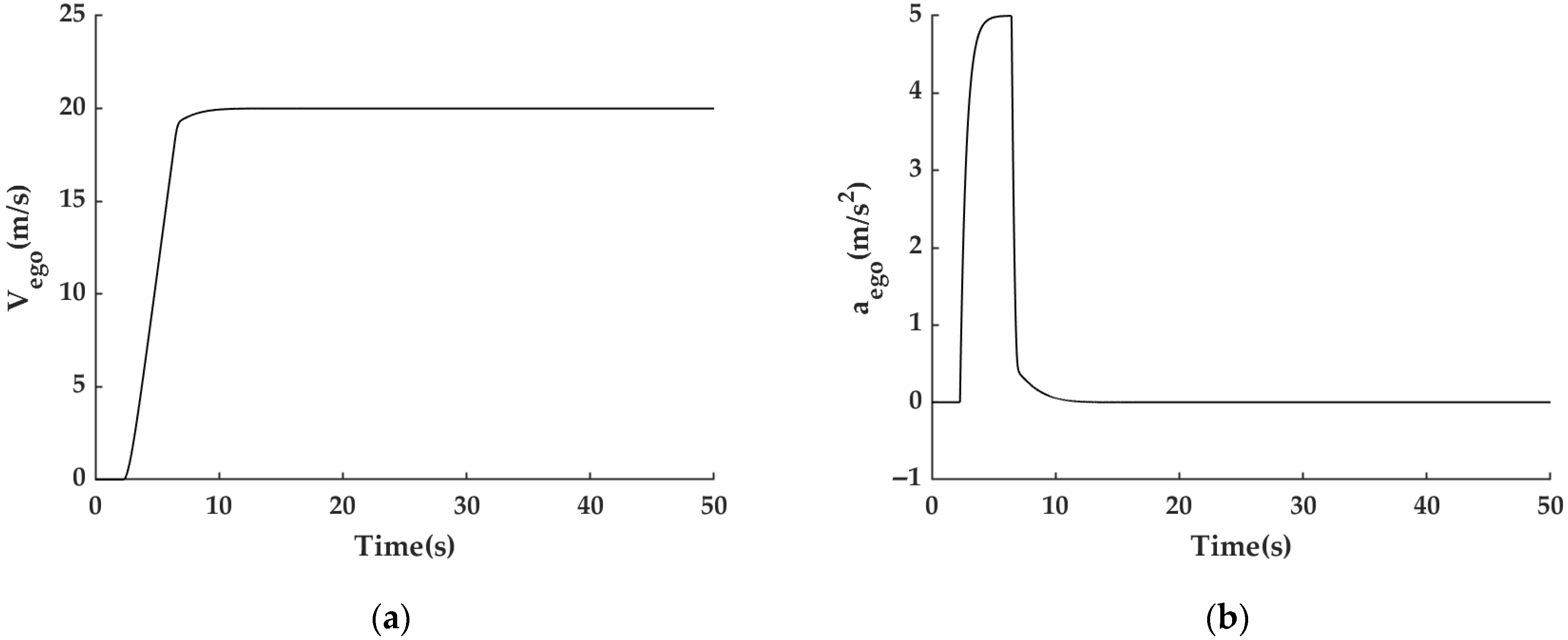
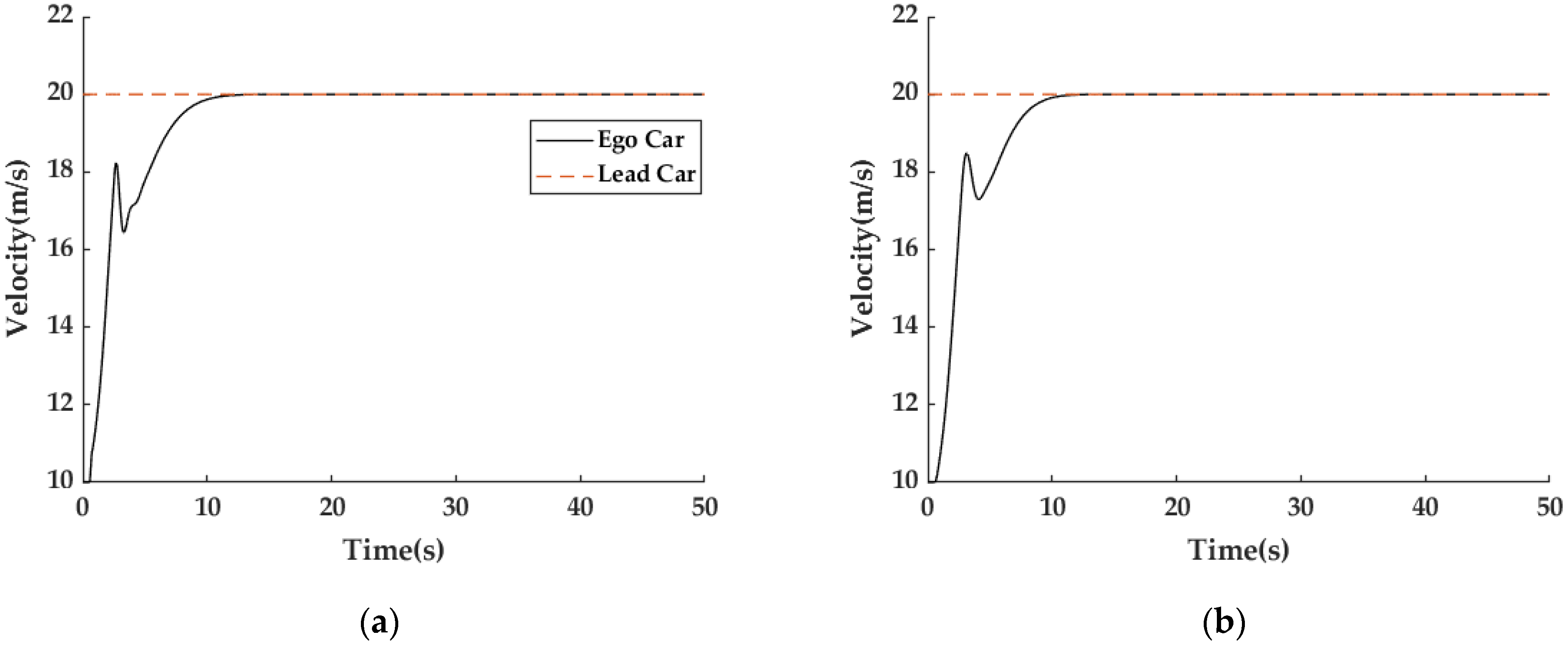
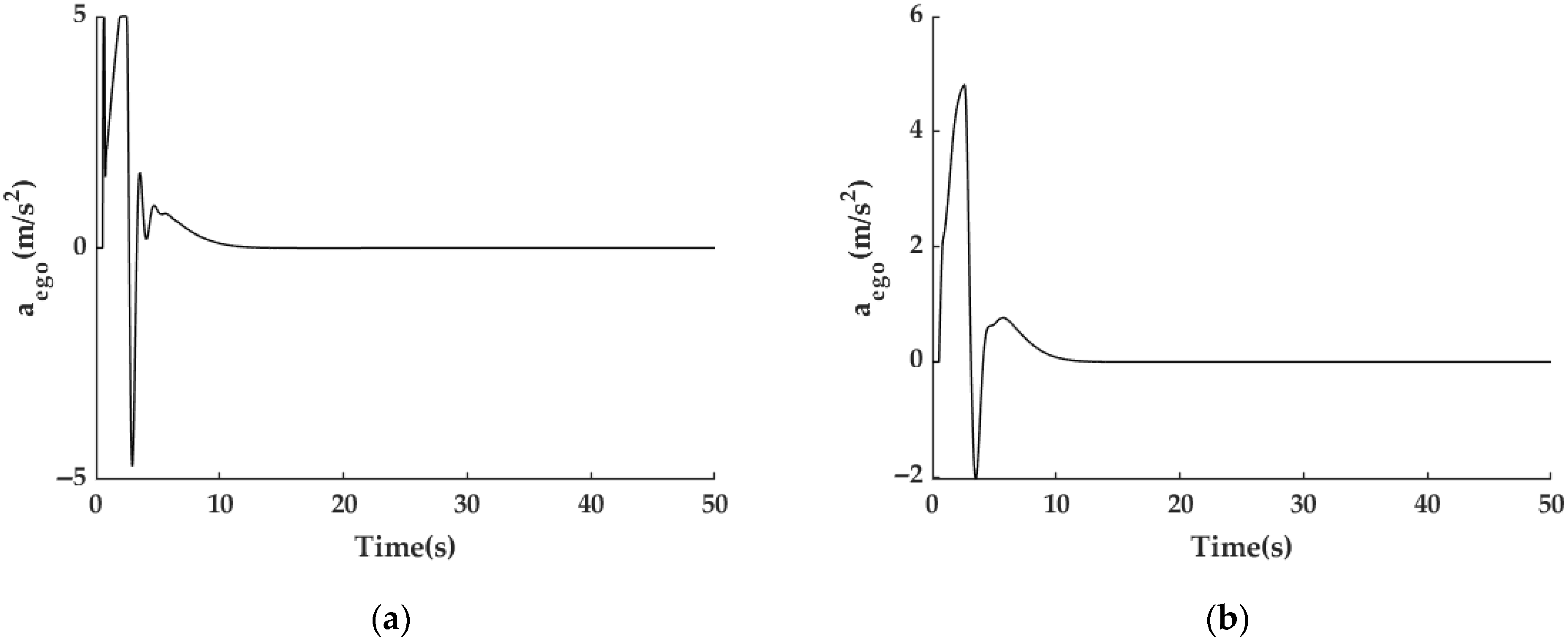
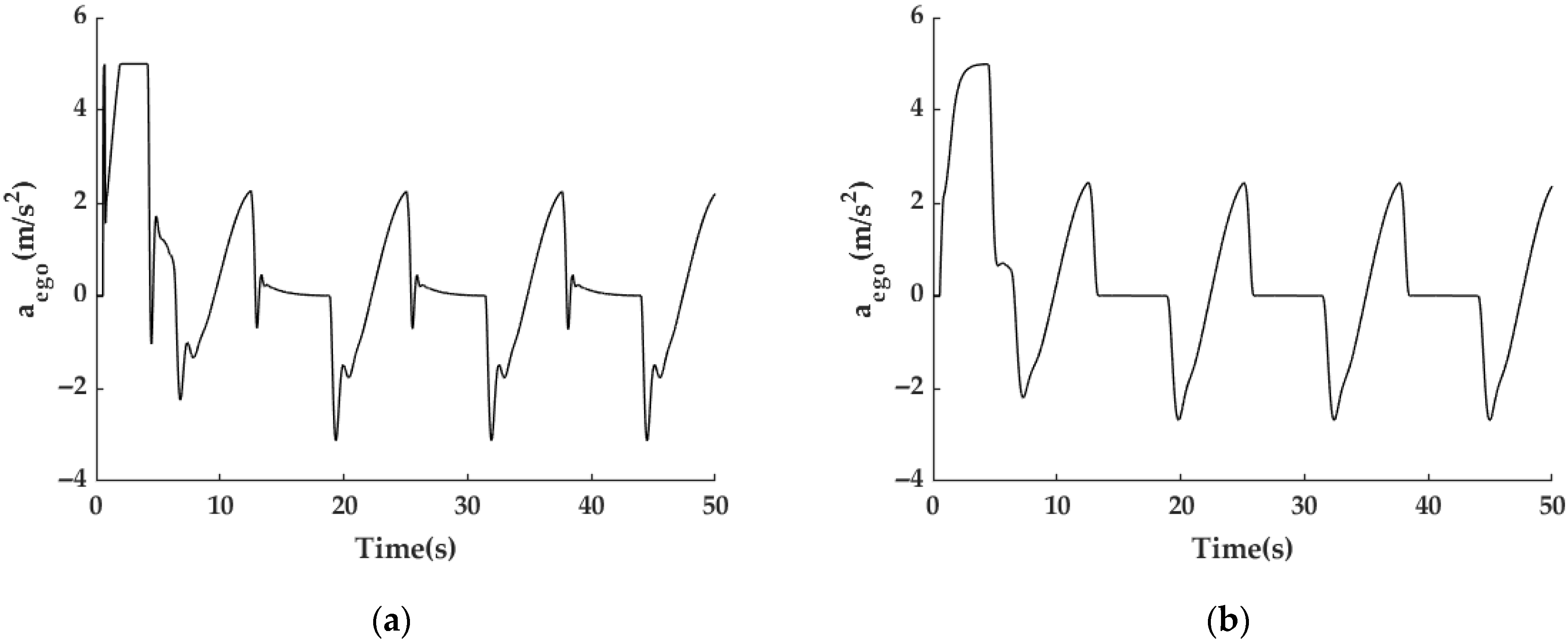
3.2.2. ACC Simulation
3.3. System Integrated Simulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EVs | Electric Vehicles |
| AVs | Autonomous Vehicles |
| VR | Virtual Reality |
| EGG | Electrogastrography |
| EEG | Electroencephaogram |
| AFS | Active Front Steering |
| ASS | Active-suspension System |
| MDMPC | Multi-constrained Distributed Model Predictive Control |
| SSQ | Simulator Sickness Questionnaire |
| MSI | Motion Sickness Incidence |
| MSDV | Motion Sickness Dose Value |
| EDA | Electrodermal activity |
| WBV | Whole-body Vibration |
| LMI | Linear Matrix Inequality |
| MOGA | Multi-objective Genetic Algorithm |
| DRL | Deep Reinforcement Learning |
| ADAS | Advanced Driving Assistance System |
| MPC | Model Predictive Control |
| QP | Quadratic Programming |
| MIMO | Multiple-Input Multiple-Output |
References
- Diels, C.; Ye, Y.; Bos, J.E.; Maeda, S. Motion Sickness in Automated Vehicles: Principal Research Questions and the Need for Common Protocols. SAE Int. J. Connect. Autom. Veh. 2022, 5, 121–134. [Google Scholar] [CrossRef]
- Li, Z.H.; Khajepour, A.; Song, J.C. A comprehensive review of the key technologies for pure electric vehicles. Energy 2019, 182, 824–839. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Shyrokau, B.; Keviczky, T. Mitigating Motion Sickness With Optimization-Based Motion Planning. IEEE Trans. Intell. Veh. 2024, 9, 2553–2563. [Google Scholar] [CrossRef]
- Shi, Z.S.; He, L.; Wang, M.W.; Bian, Y.J.; Cui, S.H.; Chen, P.P. Ideal comfort ellipses and comfort dynamics model for mitigating motion sickness in battery electric vehicle. In Vehicle System Dynamics; Taylor & Francis: Abingdon, UK, 2024. [Google Scholar]
- Asua, E.; Gutiérrez-Zaballa, J.; Mata-Carballeira, O.; Ruiz, J.A.; del Campo, I. Analysis of the Motion Sickness and the Lack of Comfort in Car Passengers. Appl. Sci. 2022, 12, 3717. [Google Scholar] [CrossRef]
- Keshavarz, B.; Golding, J.F. Motion sickness: Current concepts and management. Curr. Opin. Neurol. 2022, 35, 107–112. [Google Scholar] [CrossRef] [PubMed]
- Laessoe, U.; Abrahamsen, S.; Zepernick, S.; Raunsbaek, A.; Stensen, C. Motion sickness and cybersickness—Sensory mismatch. Physiol. Behav. 2023, 258, 114015. [Google Scholar] [CrossRef] [PubMed]
- Ng, A.K.T.; Chan, L.K.Y.; Lau, H.Y.K. A study of cybersickness and sensory conflict theory using a motion-coupled virtual reality system. Displays 2020, 61, 101922. [Google Scholar] [CrossRef]
- Gruden, T.; Popovic, N.B.; Stojmenova, K.; Jakus, G.; Miljkovic, N.; Tomazic, S.; Sodnik, J. Electrogastrography in Autonomous Vehicles-An Objective Method for Assessment of Motion Sickness in Simulated Driving Environments. Sensors 2021, 21, 550. [Google Scholar] [CrossRef]
- Huang, J.; Liu, X.Z.; Hu, L. Review of Motion Sickness-associated Comfort Studies for Occupants in Autonomous Vehicles. China J. Highw. Transp. 2024, 37, 356–369. [Google Scholar]
- Brietzke, A.; Xuan, R.P.; Dettmann, A.; Bullinger, A.C. Influence of dynamic stimulation, visual perception and individual susceptibility to car sickness during controlled stop-and-go driving. Forsch. Ingenieurwes 2022, 12, 3717. [Google Scholar] [CrossRef]
- Deng, Z.X.; Yuan, K.; Xiao, X. Investigative examination of motion sickness indicators for electric vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2025, 239, 3347–3357. [Google Scholar] [CrossRef]
- Zhao, S.E.; Tian, Z.S.; Wei, H.b.B.; Xiao, X.; Wang, K.; Zeng, J. Evaluation Model of Passenger Motion Sickness Based on Vehicle Motion Parameters. China J. Highw. Transp. 2025, 38, 274–285. [Google Scholar]
- Tian, Z.S.; Zhao, S.E.; Xiao, X.; Wei, H.B.; Wang, K.; Zeng, J. Evaluation of intelligent electric vehicle carsickness performance considering passenger motion sensitivity. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2025. [Google Scholar]
- Iskander, J.; Attia, M.; Saleh, K.; Nahavandi, D.; Abobakr, A.; Mohamed, S.; Asadi, H.; Khosravi, A.; Lim, C.P.; Hossny, M. From car sickness to autonomous car sickness: A review. Transp. Res. Part F Traffic Psychol. Behav. 2019, 62, 716–726. [Google Scholar] [CrossRef]
- Kia, K.; Johnson, P.W.; Kim, J.H. The effects of different seat suspension types on occupants? physiologic responses and task performance: Implications for autonomous and conventional vehicles. Appl. Ergon. 2021, 93, 103380. [Google Scholar] [CrossRef] [PubMed]
- Jin, S.; Lee, C.; Rhee, E.; Jung, J.; Lee, C. Analysis of the Effects of Motion Sickness According to Damping Characteristics of Suspension. Int. J. Auto. Technol. 2025, 26, 991–999. [Google Scholar] [CrossRef]
- Cui, M.; Fu, Z.J.; Rakheja, S.; Zhen, R.; Liu, Y.G. Adaptive Preview H. Control of Active Suspension Based on Road Recognition. Automot. Eng. 2025, 47, 508–518. [Google Scholar]
- Chen, X.K.; Wang, H.Y.; Liu, H.Y.; Liu, X. Research on Coordinated Control of Semi-active Suspension of Intelligent Chassis and Ground Tangential Force. J. Mech. Eng. 2024, 60, 1–10. [Google Scholar]
- Feng, J.W.; Liang, J.H.; Lu, Y.B.; Zhuang, W.C.; Pi, D.W.; Yin, G.D.; Xu, L.W.; Peng, P.; Zhou, C.B. An Integrated Control Framework for Torque Vectoring and Active Suspension System. Chin. J. Mech. Eng. 2024, 37, 10. [Google Scholar] [CrossRef]
- Liang, J.H.; Lu, Y.B.; Pi, D.W.; Yin, G.D.; Zhuang, W.C.; Wang, F.A.; Feng, J.W.; Zhou, C.B. A Decentralized Cooperative Control Framework for Active Steering and Active Suspension: Multi-Agent Approach. IEEE Trans. Transp. Electrif. 2022, 8, 1414–1429. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Shyrokau, B.; Keviczky, T.; Al Sakka, M.; Dhaens, M. Curve Tilting with Nonlinear Model Predictive Control for Enhancing Motion Comfort. IEEE Trans. Control Syst. Technol. 2022, 30, 1538–1549. [Google Scholar] [CrossRef]
- Winkel, K.N.D.; Irmak, T.; Happee, R.; Shyrokau, B. Standards for passenger comfort in automated vehicles: Acceleration and jerk. Appl. Ergon. 2023, 106, 103881. [Google Scholar] [CrossRef]
- Htike, Z.; Papaioannou, G.; Siampis, E.; Velenis, E.; Longo, S. Fundamentals of Motion Planning for Mitigating Motion Sickness in Automated Vehicles. IEEE Trans. Veh. Technol. 2022, 71, 2375–2384. [Google Scholar] [CrossRef]
- Geng, G.Q.; Wu, Z.; Jiang, H.B.; Sun, L.Q.; Duan, C. Study on Path Planning Method for Imitating the Lane-Changing Operation of Excellent Drivers. Appl. Sci. 2018, 8, 814. [Google Scholar] [CrossRef]
- Li, D.F.; Hu, J.K. Mitigating Motion Sickness in Automated Vehicles with Frequency-Shaping Approach to Motion Planning. IEEE Robot. Autom. Lett. 2021, 6, 7714–7720. [Google Scholar] [CrossRef]
- Rajesh, N.; Zheng, Y.G.; Shyrokau, B. Comfort-Oriented Motion Planning for Automated Vehicles Using Deep Reinforcement Learning. IEEE Open J. Intell. Transp. Sys. 2023, 4, 348–359. [Google Scholar] [CrossRef]
- Gysen, B.L.J.; Paulides, J.J.H.; Janssen, J.L.G.; Lomonova, E.A. Active Electromagnetic Suspension System for Improved Vehicle Dynamics. IEEE Trans. Veh. Technol. 2010, 59, 1156–1163. [Google Scholar] [CrossRef]
- Papaioannou, G.; Ning, D.H.; Jerrelind, J.; Drugge, L. A K-Seat-Based PID Controller for Active Seat Suspension to Enhance Motion Comfort. SAE Int. J. Connect. Autom. Veh. 2022, 5, 189–199. [Google Scholar] [CrossRef]
- ISO 2631-1:1997; Mechanical Vibration and Shock—Evaluation of Human Exposure to Whole-Body Vibration—Part 1: General Requirements. International Organization for Standardization: Geneva, Switzerland, 1997.





| Parameter | Value |
|---|---|
| ms | 1200 kg |
| Iy | 1500 kg·m2 |
| mus1 | 40 kg |
| mus1 | 45 kg |
| ks1 | 25,000 N/m |
| ks2 | 27,000 N/m |
| cs1 | 1500 N·s/m |
| cs2 | 1600 N·s/m |
| kt1 | 200,000 N/m |
| kt2 | 210,000 N/m |
| lf | 1.2 m |
| lr | 1.5 m |
| hg | 0.5 m |
| Hyperparameter | Value |
|---|---|
| Discretization Period | 0.02 s |
| Prediction Horizon | 30 |
| Control Horizon | 20 |
| Parameter | Min. | Max. |
|---|---|---|
| F1 | −2000 N | 2000 N |
| F2 | 2000 N | 2000 N |
| acmd | −5 m/s2 | 5 m/s2 |
| −0.3 m/s | 0.3 m/s | |
| θ | −8·π/180 rad | 8·π/180 rad |
| −3·π/180 rad/s | 3·π/180 rad/s | |
| zs1−zus1 | −0.1 m | 0.1 m |
| zs2−zus2 | −0.1 m | 0.1 m |
| d | 50 m | 250 m |
| vego | 0 m/s | 50 m/s |
| aego | −5 m/s2 | 5 m/s2 |
| Driving Condition | Parameter | Method | RMS | MSDV |
|---|---|---|---|---|
| Vlead: constant | aego | decoupled | 0.936 | / |
| coupled | 0.846 | / | ||
| jerk | decoupled | 4.18 | / | |
| coupled | 1.39 | / | ||
| θy | decoupled | 0.0057 | / | |
| coupled | 0.0036 | / | ||
| vsz | decoupled | 0.0032 | 0.0295 | |
| coupled | 0.0033 | 0.1696 | ||
| wy | decoupled | 0.03 | / | |
| coupled | 0.018 | / | ||
| Vlead: sinusoidal | aego | decoupled | 1.72 | / |
| coupled | 1.68 | / | ||
| jerk | decoupled | 4.4 | / | |
| coupled | 1.72 | / | ||
| θy | decoupled | 0.0068 | / | |
| coupled | 0.0035 | / | ||
| vsz | decoupled | 0.0031 | 0.0255 | |
| coupled | 0.0038 | 0.1721 | ||
| wy | decoupled | 0.0296 | / | |
| coupled | 0.0176 | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, F.; Zhao, D.; Zhong, Y.; Wang, P.; Jiang, J.; Wang, Z.; Fu, Z. Motion Sickness Suppression Strategy Based on Dynamic Coordination Control of Active Suspension and ACC. Machines 2025, 13, 650. https://doi.org/10.3390/machines13080650
Zhou F, Zhao D, Zhong Y, Wang P, Jiang J, Wang Z, Fu Z. Motion Sickness Suppression Strategy Based on Dynamic Coordination Control of Active Suspension and ACC. Machines. 2025; 13(8):650. https://doi.org/10.3390/machines13080650
Chicago/Turabian StyleZhou, Fang, Dengfeng Zhao, Yudong Zhong, Pengpeng Wang, Junjie Jiang, Zhenwei Wang, and Zhijun Fu. 2025. "Motion Sickness Suppression Strategy Based on Dynamic Coordination Control of Active Suspension and ACC" Machines 13, no. 8: 650. https://doi.org/10.3390/machines13080650
APA StyleZhou, F., Zhao, D., Zhong, Y., Wang, P., Jiang, J., Wang, Z., & Fu, Z. (2025). Motion Sickness Suppression Strategy Based on Dynamic Coordination Control of Active Suspension and ACC. Machines, 13(8), 650. https://doi.org/10.3390/machines13080650






