Relationship Analysis Between Helicopter Gearbox Bearing Condition Indicators and Oil Temperature Through Dynamic ARDL and Wavelet Coherence Techniques
Abstract
1. Introduction
2. Material and Methods
2.1. HUMS Data Collection
2.2. Model Specification
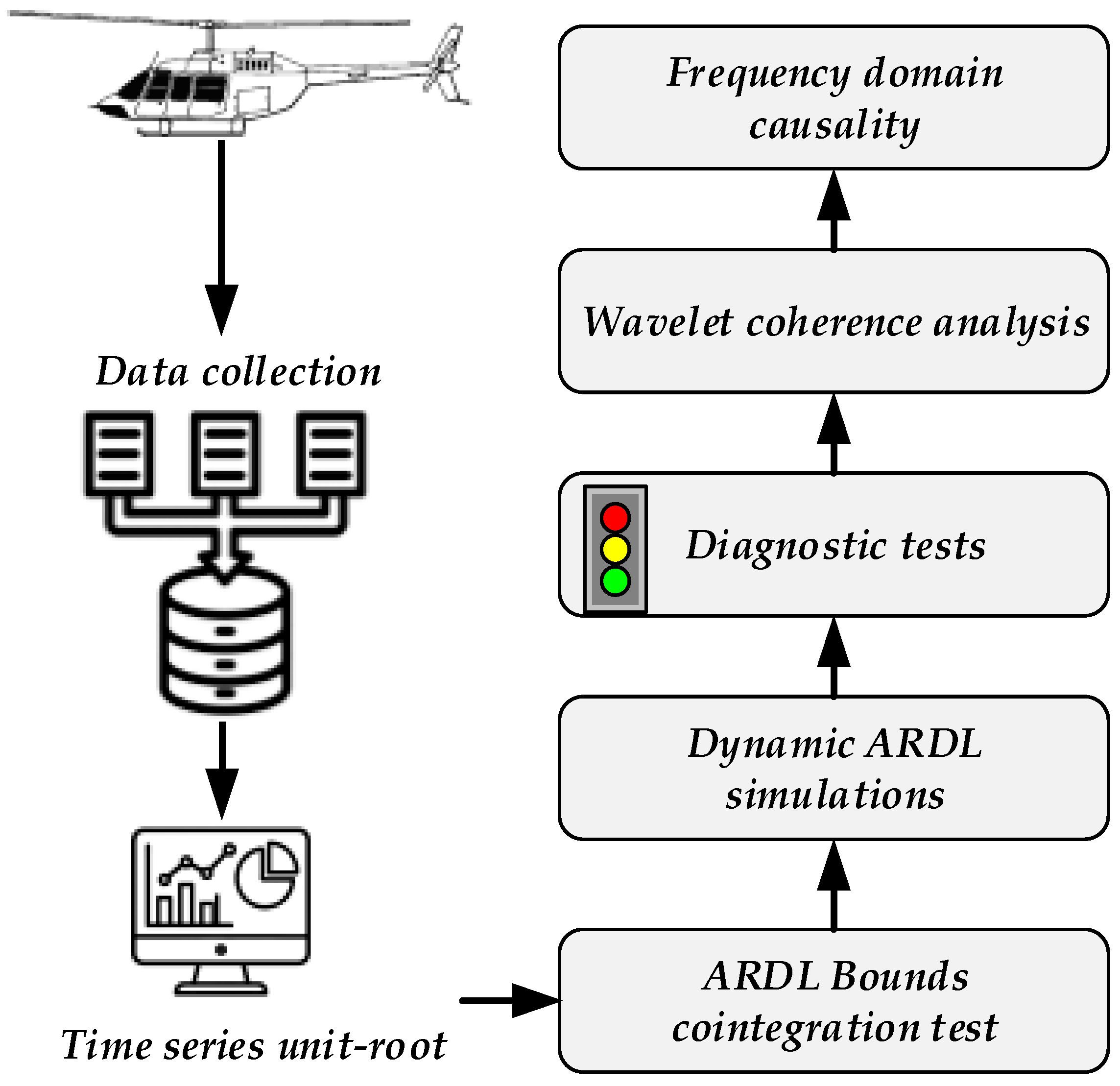
2.3. Algorithmic Procedure for Experimental Analysis
- -
- Data Acquisition: Vibration and OT data are collected from HUMS-equipped Bell 407 helicopters under steady-state flight conditions.
- -
- Preprocessing: Raw signals are log-transformed and smoothed to ensure the stationarity and comparability of CIs.
- -
- Unit Root Testing: The stationarity of the time series is assessed using the ADF and KPSS tests.
- -
- ARDL Bounds Testing: Cointegration relationships between the OT and BGCIs are verified.
- -
- DARDL Simulation: The DARDL model is applied to simulate the short- and long-term impacts of the BGCIs on the OT.
- -
- Wavelet coherence analysis: A WCA is conducted to examine the time–frequency correlations between variables.
- -
- Frequency-domain causality: Spectral Granger causality is tested across short-, medium-, and long-term bands.
- -
- Diagnostics and validation: Statistical tests (LM, RESET, Jarque-Bera) validate the model robustness.
3. Empirical Analysis Procedure
4. Empirical Results and Discussion
4.1. Unit Root Test
4.2. ARDL Cointegration Test
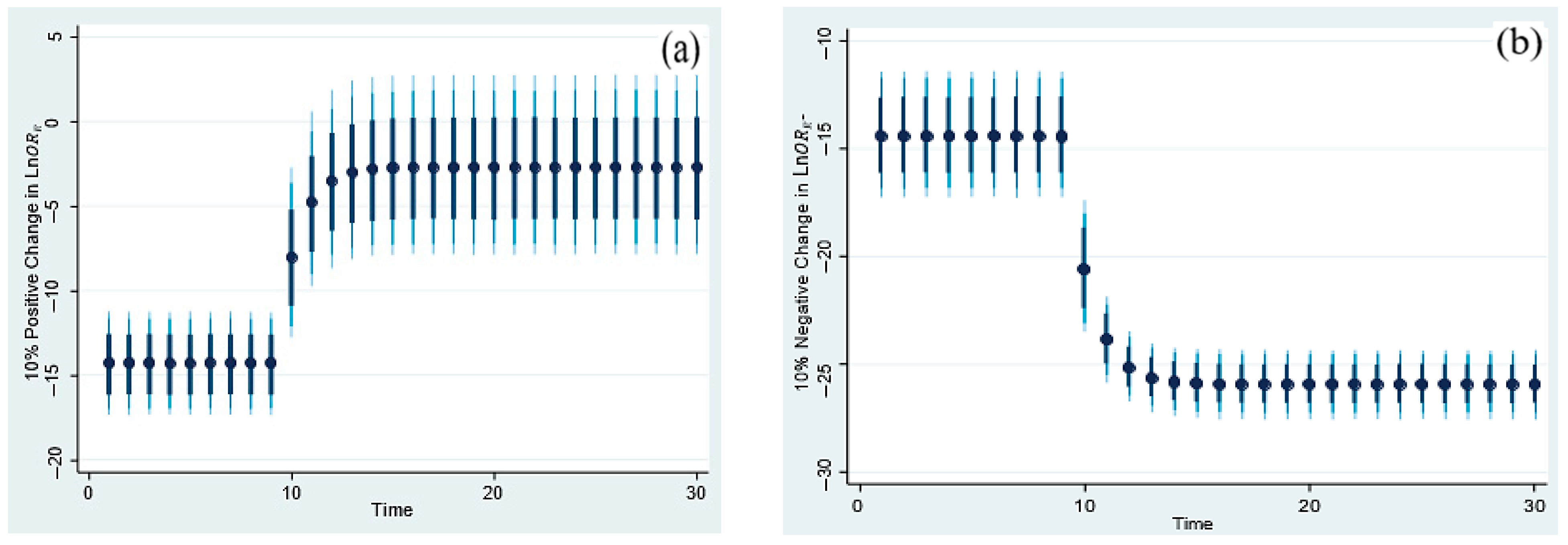
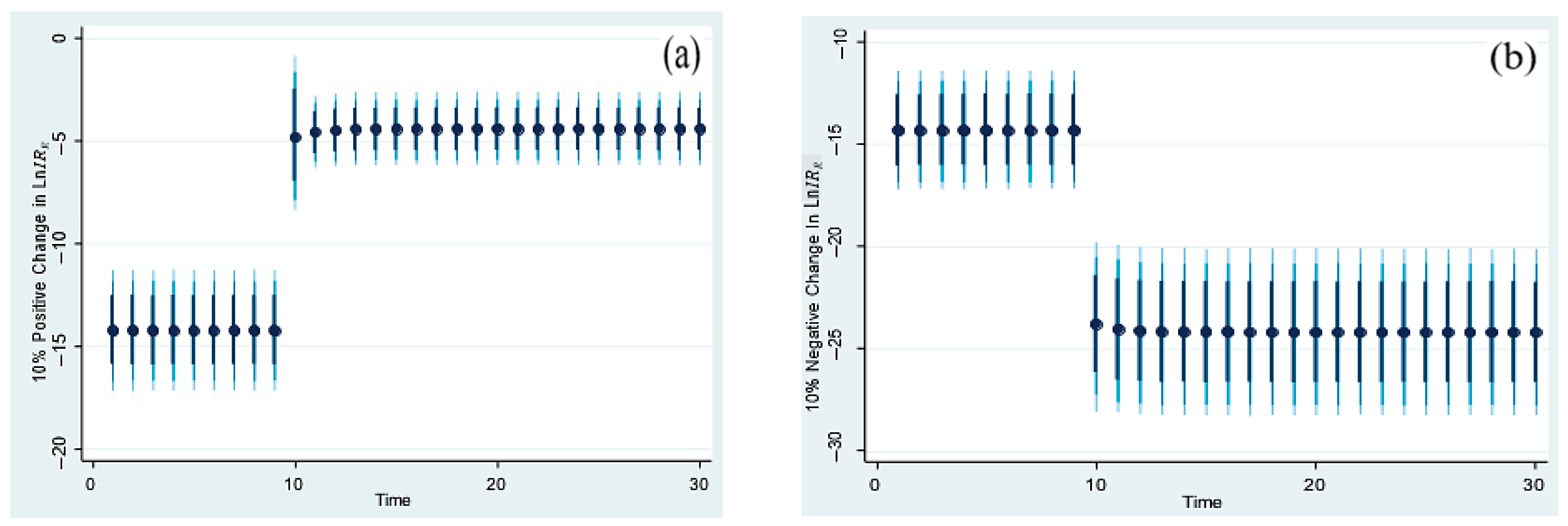
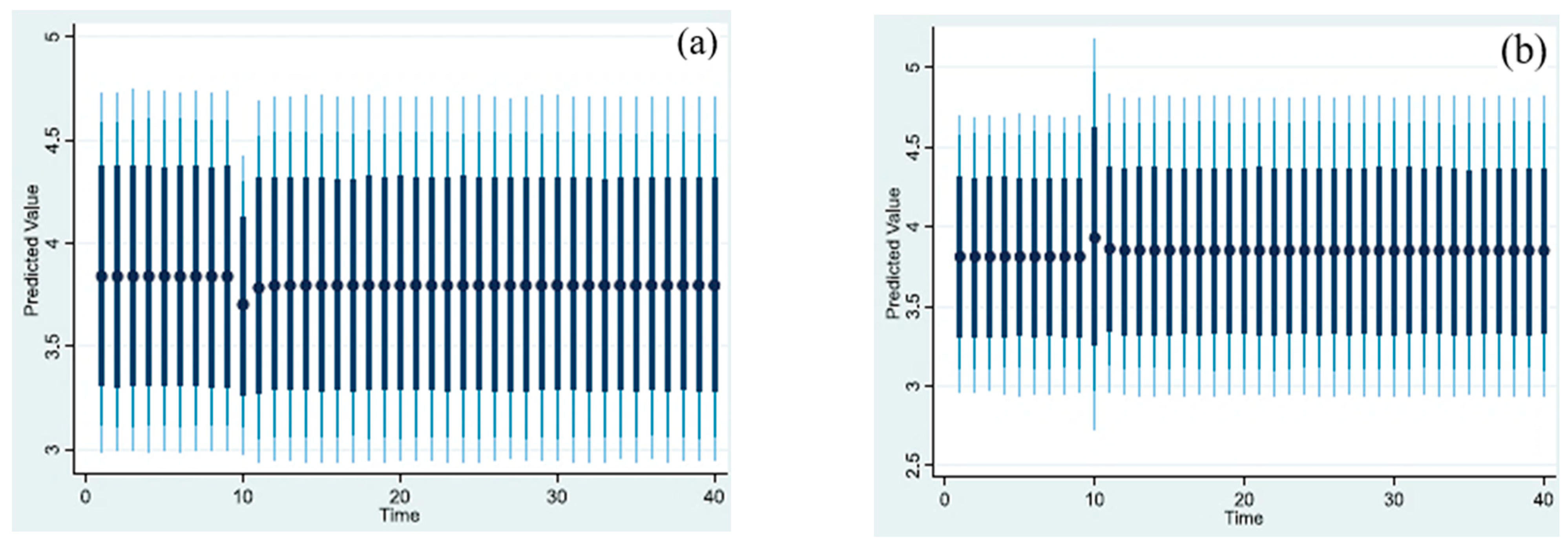
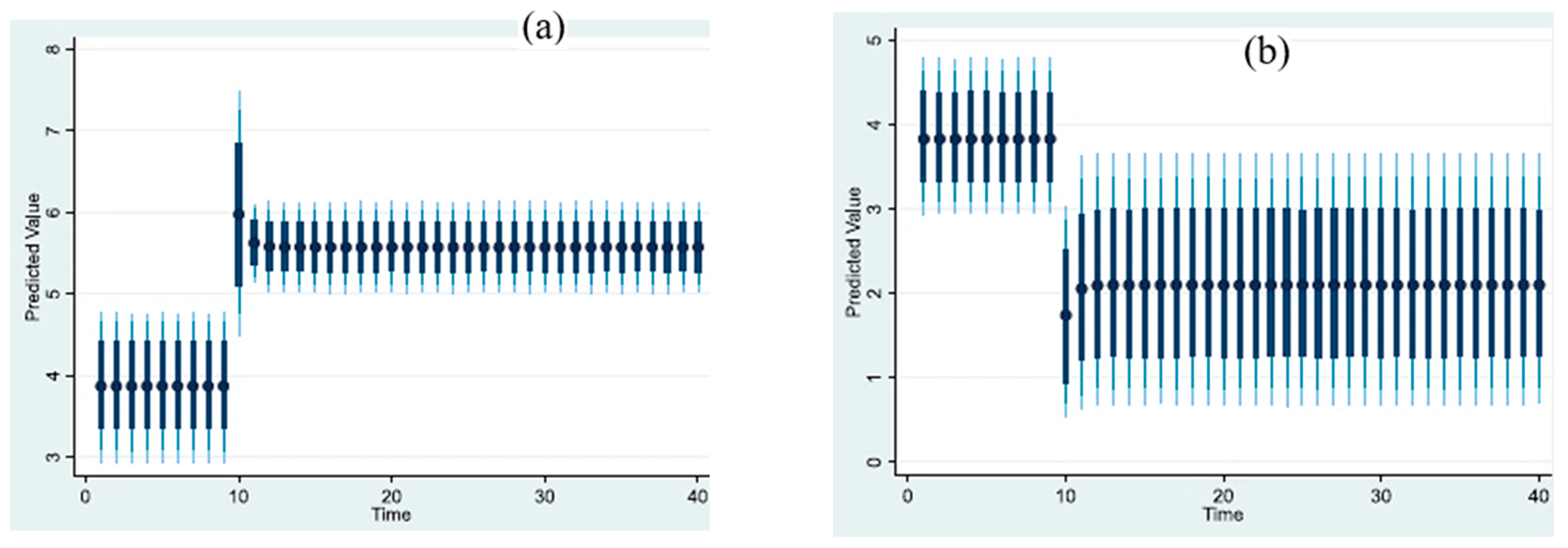
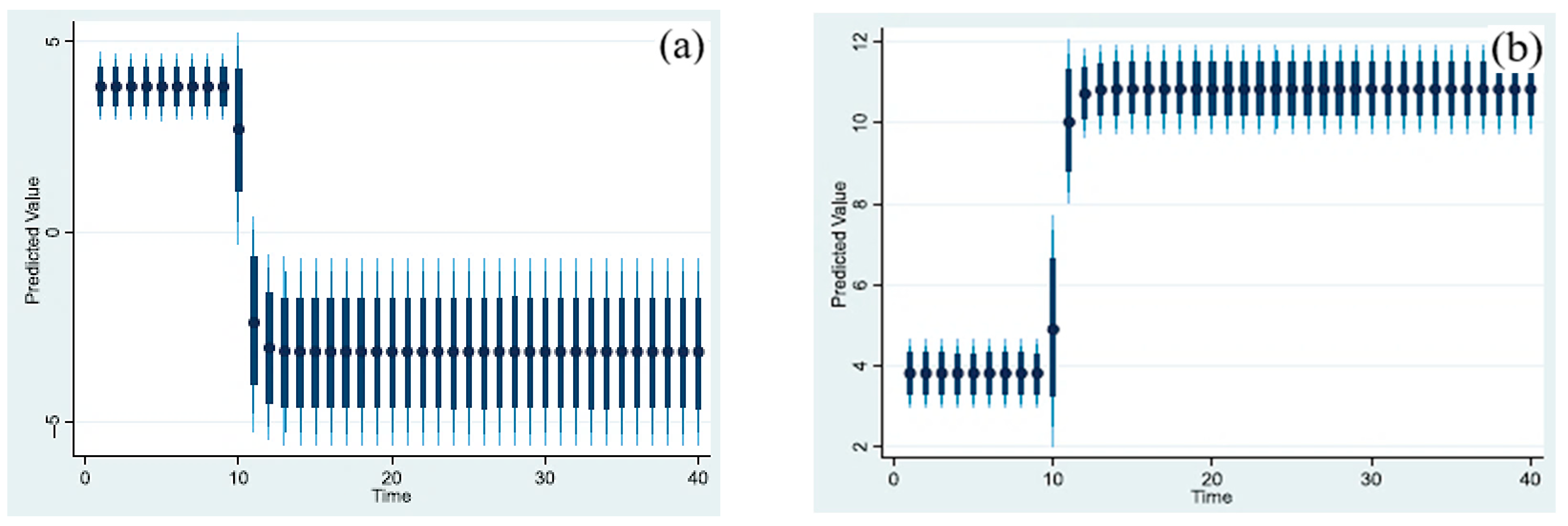
4.3. Dynamic Autoregressive Distributed Lag Simulations
4.4. Wavelet Coherence Analysis
4.5. Frequency-Domain Causality
5. Conclusions and Policy Implications
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BGCI | Bearing Gearbox Condition Indicator |
| CWT | Continuous Wavelet Transformation |
| OT | Oil Temperature |
| HUMS | Health and Usage Monitoring System |
| DARDL | Dynamic Autoregressive Distributed Lag |
| CIs | Condition Indicators |
| WCA | Wavelet Coherence Analysis |
| ORE | Outer Race Energy |
| IRE | Inner Race Energy |
| CE | Cage Energy |
| BE | Ball Energy |
| SK | Spectral Kurtosis |
| Ln | Natural Logarithm |
| KPSS | Kwiatkowski–Phillips–Schmidt–Shin |
| AIC | Akaike Information Criterion |
| ECT | Error Correction Terms |
| CUSUM | Cumulative Sum of Recursive Residuals |
| CUSUMSQ | Cumulative Sum of Recursive Residual Squares |
| WPS | Wavelet Power Spectrum |
| FDC | Frequency-Domain Causality |
| LM | Lagrange Multiplier |
References
- Ranasinghe, K.; Kapoor, R.; Gardi, A.; Sabatini, R.; Wickramanayake, V.; Ludovici, D. Vehicular Sensor Network and Data Analytics for a Health and Usage Management System. Sensors 2020, 20, 5892. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Wu, Z.; An, B.; Sun, R.; Cui, Y. Digital Twin-Based Technical Research on Comprehensive Gear Fault Diagnosis and Structural Performance Evaluation. Sensors 2025, 25, 2775. [Google Scholar] [CrossRef] [PubMed]
- Kannan, V.; Zhang, T.; Li, H. A Review of the intelligent condition monitoring of rolling element bearings. Machines 2024, 12, 484. [Google Scholar] [CrossRef]
- Qiu, S.; Cui, X.; Ping, Z.; Shan, N.; Li, Z.; Bao, X.; Xu, X. Deep Learning Techniques in Intelligent Fault Diagnosis and Prognosis for Industrial Systems: A Review. Sensors 2023, 23, 1305. [Google Scholar] [CrossRef] [PubMed]
- Tiboni, M.; Remino, C.; Bussola, R.; Amici, C. A Review on Vibration-Based Condition Monitoring of Rotating Machinery. Appl. Sci. 2022, 12, 972. [Google Scholar] [CrossRef]
- Xie, F.; Liu, H.; Dong, J.; Wang, G.; Wang, L.; Li, G. Research on the Gearbox Fault Diagnosis Method Based on Multi-Model Feature Fusion. Machines 2022, 10, 1186. [Google Scholar] [CrossRef]
- Wei, L.; Cheng, Z.; Cheng, J.; Hu, N.; Yang, Y. A Fault Detection Method Based on an Oil Temperature Forecasting Model Using an Improved Deep Deterministic Policy Gradient Algorithm in the Helicopter Gearbox. Entropy 2022, 24, 1394. [Google Scholar] [CrossRef] [PubMed]
- Saidi, L.; Benbouzid, M. Prognostics and Health Management of Renewable Energy Systems: State of the Art Review, Challenges, and Trends. Electronics 2021, 10, 2732. [Google Scholar] [CrossRef]
- Babay, O.; Saidi, L.; Bechhofer, E.; Benbouzid, M. Investigation of the dynamic relationship between oil temperature and bearing gearbox condition indicator values for the Bell 407 helicopter based on cointegration analysis. In Proceedings of the Annual Conference of the PHM Society, Salt Lake City, UT, USA, 4–7 November 2024. [Google Scholar]
- Wu, J.; Wang, Z.; Cao, H.; Huang, Y.; Liu, Y. Deep Clustering Variational Network for Helicopter Regime Recognition in HUMS. Aerosp. Sci. Technol. 2022, 124, 107553. [Google Scholar] [CrossRef]
- Modaresahmadi, S.; Chittenden, R.; Mueller, M. Convective Heat Transfer Analysis of a Laminated Flux Focusing Magnetic Gearbox. Therm. Sci. Eng. Prog. 2020, 18, 100552. [Google Scholar] [CrossRef]
- Rashid, H.S.J.; Yang, Z.; Wang, J. Reliability Model for Helicopter Main Gearbox Lubrication System Using Influence Diagrams. Reliab. Eng. Syst. Saf. 2015, 139, 50–57. [Google Scholar] [CrossRef]
- Saidi, L.; Bechhofer, E.; Benbouzid, M. Dynamic Relationship Between Oil Temperature and BGCI in Bell 407 Helicopter: A Cointegration and Autoregressive Distributed Lag Approach. Int. J. Progn. Health Manag. 2025, 16, 1. [Google Scholar] [CrossRef]
- Bechhoefer, E.; Hajimohammadali, M. Process for Turboshaft Engine Performance Trending. Annu. Conf. PHM Soc. 2023, 15, 1. [Google Scholar] [CrossRef]
- Ayad, M.; Saoudi, K.; Rezki, M.; Benziane, M.; Arabi, A.; Chikouche, D. Early detection of defects in gear systems using autocorrelation of Morlet wavelet transforms. Stroj. Vestn. J. Mech. Eng. 2022, 68, 56–65. [Google Scholar] [CrossRef]
- Praveen, H.M.; Sabareesh, G.R. Wavelet based real-time planetary gearbox health monitoring under non-stationary operation. Exp. Tech. 2022, 46, 861–875. [Google Scholar] [CrossRef]
- Lupea, I.; Lupea, M. Continuous Wavelet Transform and CNN for Fault Detection in a Helical Gearbox. Appl. Sci. 2025, 15, 950. [Google Scholar] [CrossRef]
- Majeed, R.; Haddar, M.; Chaari, F.; Haddar, M. Exponentially Weighted Moving Average Control Chart for Fault Detection of the Spur Gear Transmission System. In Proceedings of the International Conference on Acoustics and Vibration; Springer: Cham, Switzerland, 2022; pp. 123–132. [Google Scholar] [CrossRef]
- Jordan, S.; Philips, A.Q. Cointegration testing and dynamic simulations of autoregressive distributed lag models. Stata J. 2018, 18, 902–923. [Google Scholar] [CrossRef]
- Breitung, J.; Candelon, B. Testing for short-and long-run causality: A frequency-domain approach. J. Econom. 2006, 132, 363–378. [Google Scholar] [CrossRef]
- Łuczak, D. Machine Fault Diagnosis through Vibration Analysis: Continuous Wavelet Transform with Complex Morlet Wavelet and Time–Frequency RGB Image Recognition via Convolutional Neural Network. Electronics 2024, 13, 452. [Google Scholar] [CrossRef]
- Habbouche, H.; Benkedjouh, T.; Amirat, Y.; Benbouzid, M. A Wavelet Transform-Based Transfer Learning Approach for Enhanced Shaft Misalignment Diagnosis in Rotating Machinery. Electronics 2025, 14, 341. [Google Scholar] [CrossRef]
- Lee, J.-H.; Okwuosa, C.N.; Hur, J.-W. Extruder Machine Gear Fault Detection Using Autoencoder LSTM via Sensor Fusion Approach. Inventions 2023, 8, 140. [Google Scholar] [CrossRef]
- Gao, Z.-W.; Zhao, R.; Zhang, J.; Zhang, X.; Zhang, Y. An optimized updating adaptive federated learning for pumping units collaborative diagnosis with label heterogeneity and communication redundancy. Eng. Appl. Artif. Intell. 2025, 152, 110724. [Google Scholar] [CrossRef]
- Zhou, F.; Yang, Y.; Wang, C.; Hu, X. Federated Learning Based Fault Diagnosis Driven by Intra-Client Imbalance Degree. Entropy 2023, 25, 606. [Google Scholar] [CrossRef] [PubMed]
- GPMS. Available online: https://www.gpms-vt.com/ (accessed on 15 June 2025).
- GPMS International. GPMS Foresight MX HUMS for MD530F. Heli-Expo 2023. 2023. Available online: https://www.helis.com/database/news/heliexpo23-gpms-md530f-hums (accessed on 17 June 2025).
- GPMS International. GPMS Foresight MX HUMS for Airbus Models. Heli-Expo 2023. 2023. Available online: https://www.helis.com/database/news/heliexpo23-gpms-as350b2-ec145 (accessed on 17 June 2025).
- Pesaran, M.H.; Shin, Y.; Smith, R.J. Bounds testing approaches to the analysis of level relationships. J. Appl. Econom. 2001, 16, 289–326. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar] [CrossRef] [PubMed]
- Kwiatkowski, D.; Phillips, P.C.; Schmidt, P.; Shin, Y. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? J. Econom. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- Narayan, P.K. The saving and investment nexus for China: Evidence from cointegration tests. Appl. Econ. 2005, 37, 1979–1990. [Google Scholar] [CrossRef]
- Goupillaud, P.; Grossmann, A.; Morlet, J. Cycle-octave and related transforms in seismic signal analysis. Geoexploration 1984, 23, 85–102. [Google Scholar] [CrossRef]
- Hainmueller, J.; Hazlett, C. Kernel regularized least squares: Reducing misspecification bias with a flexible and interpretable machine learning approach. Polit. Anal. 2014, 22, 143–168. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Huang, W.; Wang, H.; Li, C.; Zi, Y.; He, Z. Feature Extraction for Rolling Element Bearing Faults Using Resonance Sparse Signal Decomposition. Exp. Tech. 2017, 41, 251–265. [Google Scholar] [CrossRef]
- Bechhoefer, E.; He, D. Case Study of a Faulted Planet Bearing. Proc. Annu. Conf. PHM Soc. 2016, 8, 1. [Google Scholar] [CrossRef]
- Saidi, L.; Benbouzid, M.; Diallo, D.; Amirat, Y.; Elbouchikhi, E.; Wang, T. Higher-order spectra analysis-based diagnosis method of blades biofouling in a PMSG driven tidal stream turbine. Energies 2020, 13, 2888. [Google Scholar] [CrossRef]
- Saidi, L.; Bechhoefer, E.; Ben Ali, J.; Benbouzid, M. Wind turbine high-speed shaft bearing degradation analysis for run-to-failure testing using spectral kurtosis. In Proceedings of the 16th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Monastir, Tunisia, 16–18 December 2015. [Google Scholar]
- Vasić, M.; Stojanović, B.; Blagojević, M. Failure analysis of idler roller bearings in belt conveyors. Eng. Fail. Anal. 2020, 117, 104898. [Google Scholar] [CrossRef]
- Pastukhov, A.; Timashov, E. Procedure for simulation of stable thermal conductivity of bearing assemblies. Adv. Eng. Lett. 2023, 2, 58–63. [Google Scholar] [CrossRef]
- Vertical Aviation International (VAI); GPMS International. VAI Partners with GPMS to Expand Access to Advanced HUMS. 2025. Available online: https://verticalavi.org/vai-daily/vai-partners-with-gpms-to-expand-access-to-advanced-hums/ (accessed on 17 June 2025).
- Airbus Helicopters. Connected Services. 2023. Available online: https://www.airbus.com/en/products-services/helicopters/hcare-services/connected-services (accessed on 17 June 2025).
- SciELO Brazil. Addressing Gearbox Health Monitoring Challenges for Helicopters: A Machine Learning Approach. 2023. Available online: https://www.scielo.br/j/aabc/a/ZBmSydzGg6GdMWycGn8RDjL/ (accessed on 17 June 2025).
- Helicopted. The Role of Predictive Maintenance in Helicopter Fleet Management. 2023. Available online: https://helicopted.com/the-role-of-predictive-maintenance-in-helicopter-fleet-management/ (accessed on 17 June 2025).


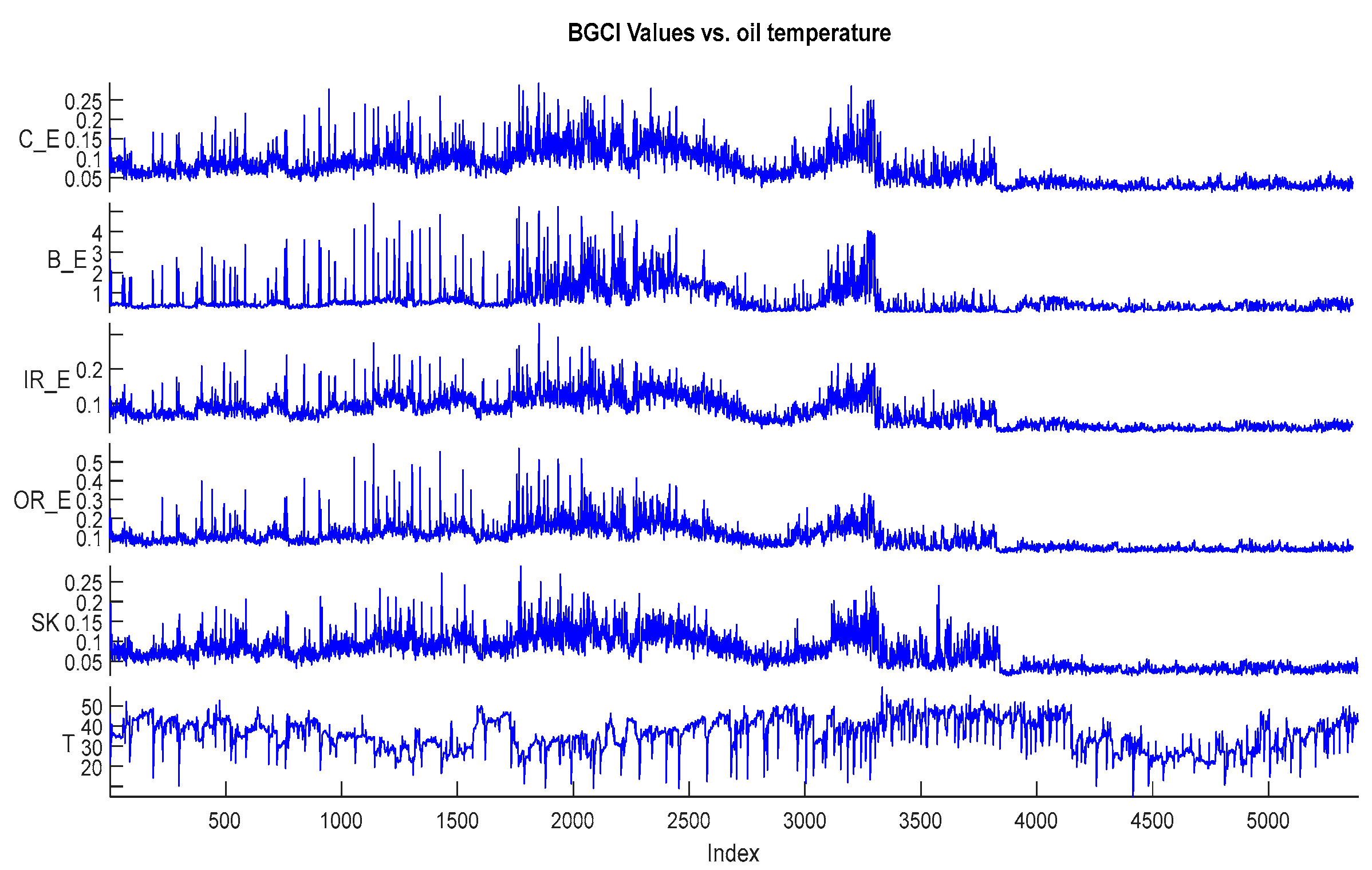
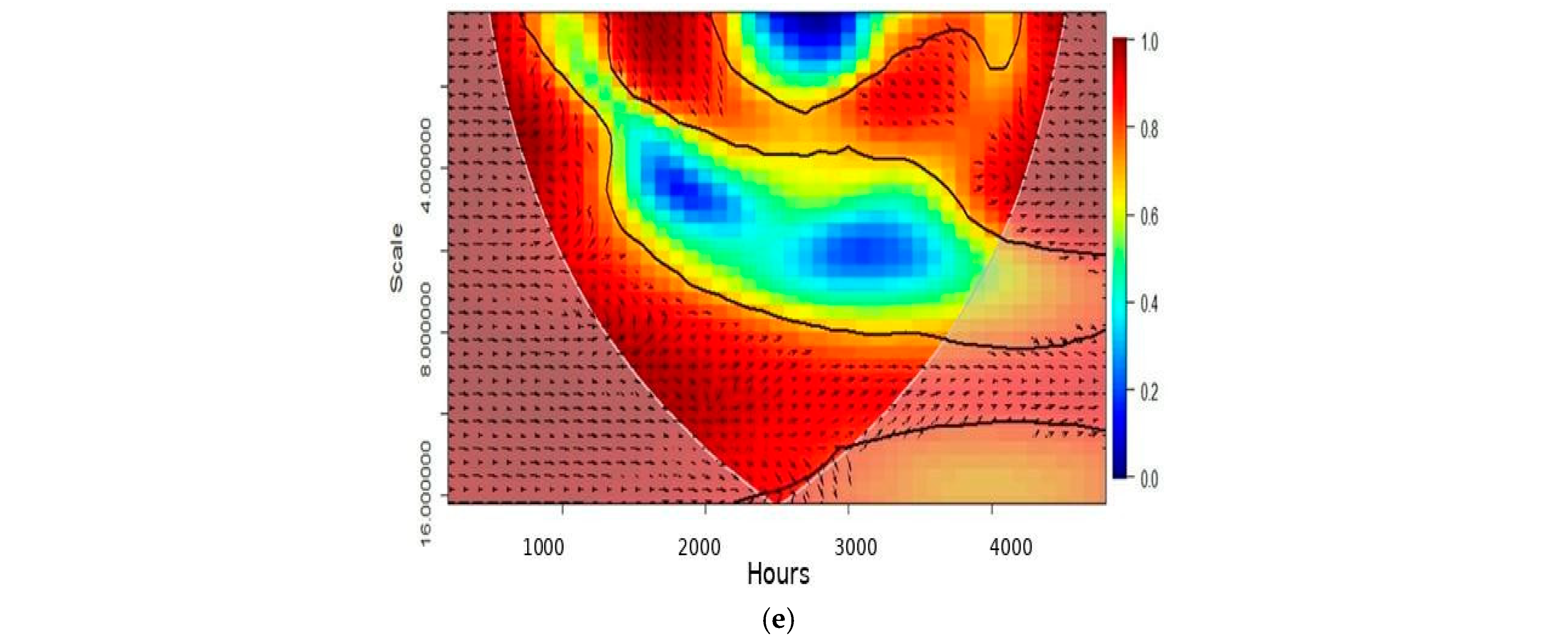
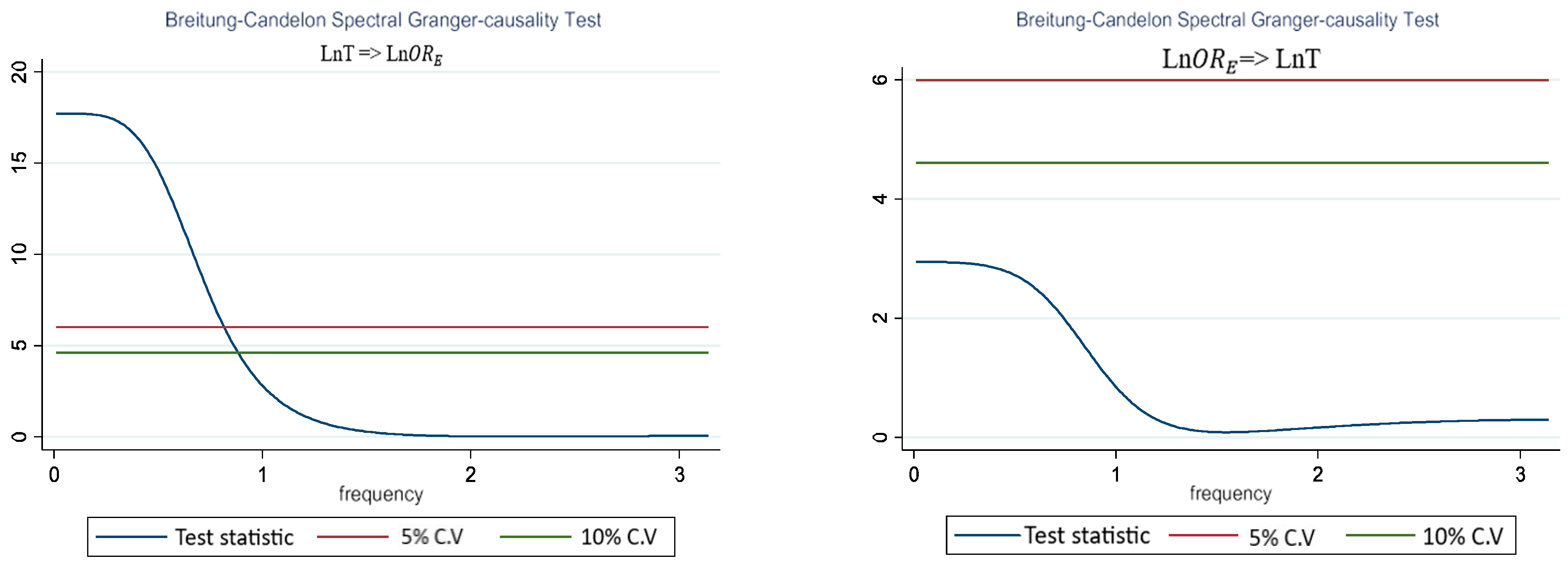
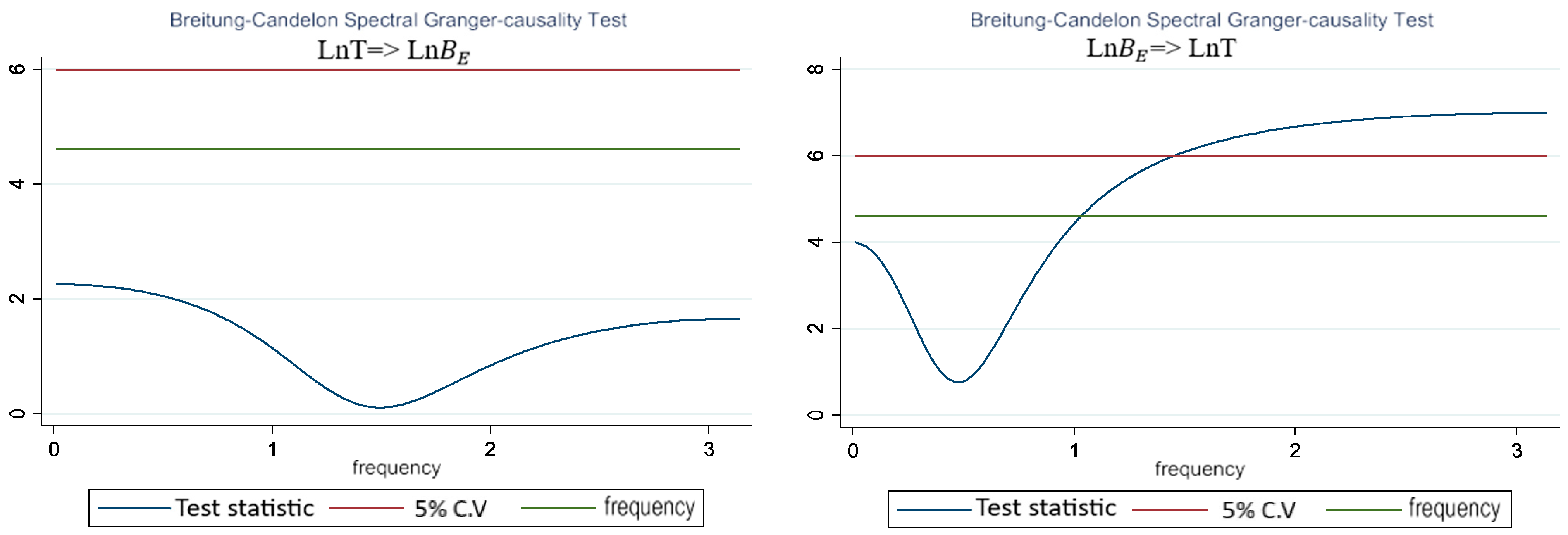
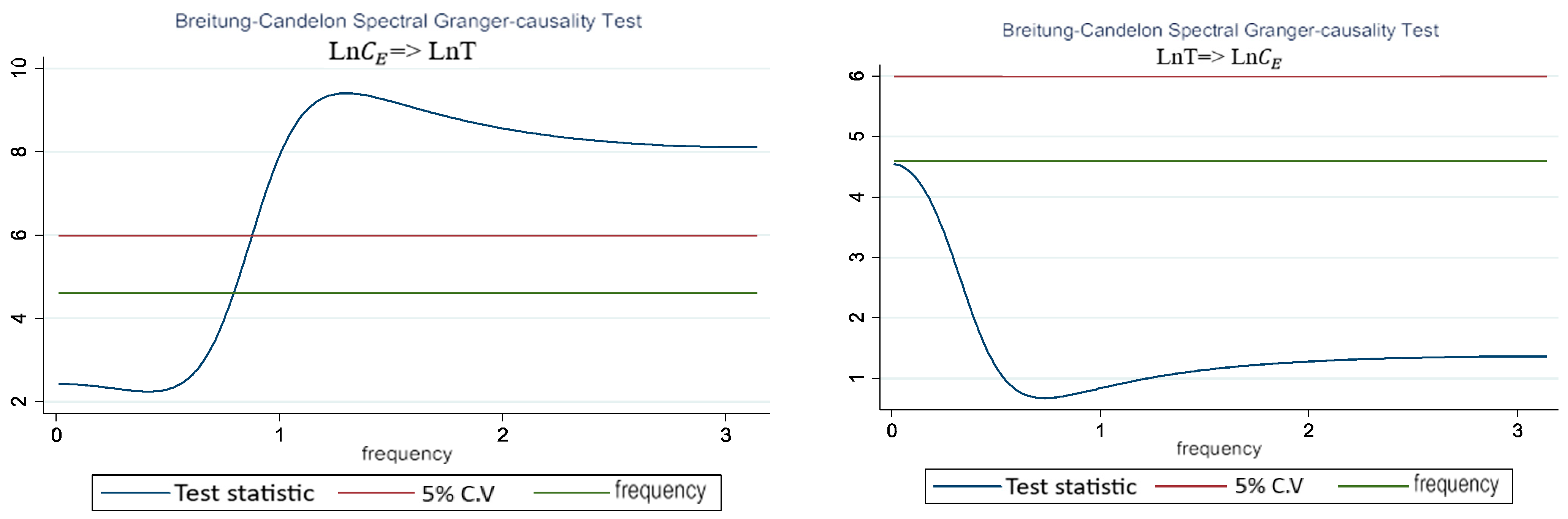
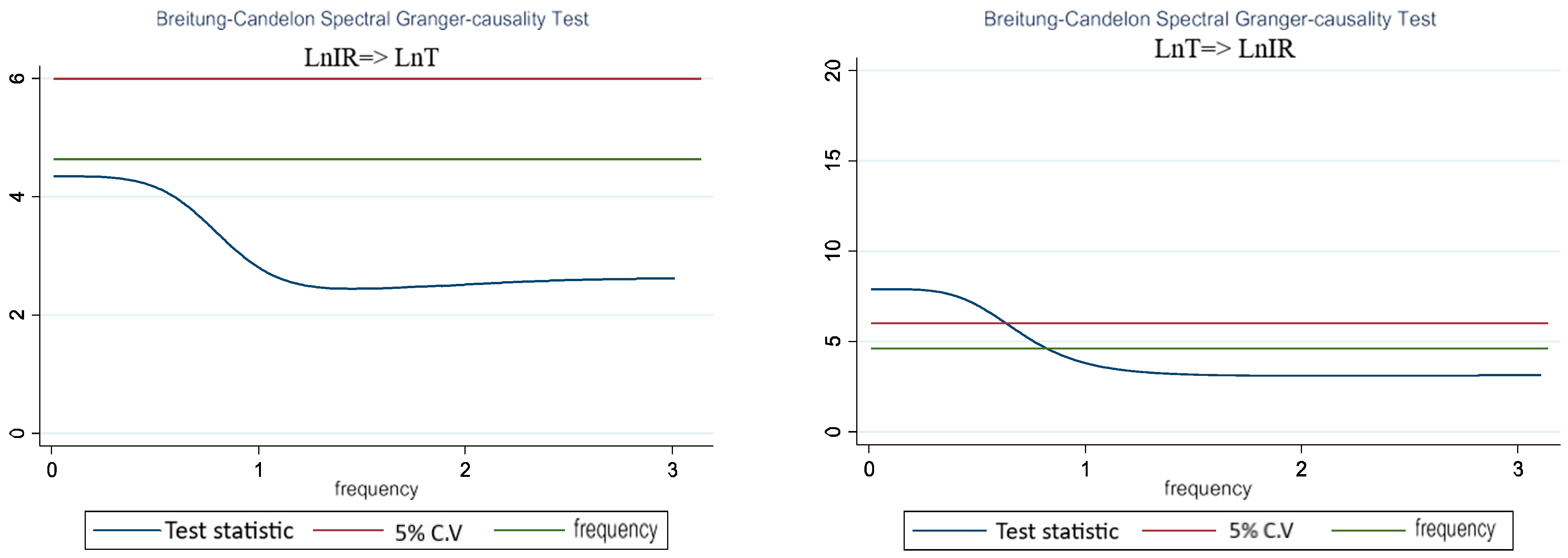
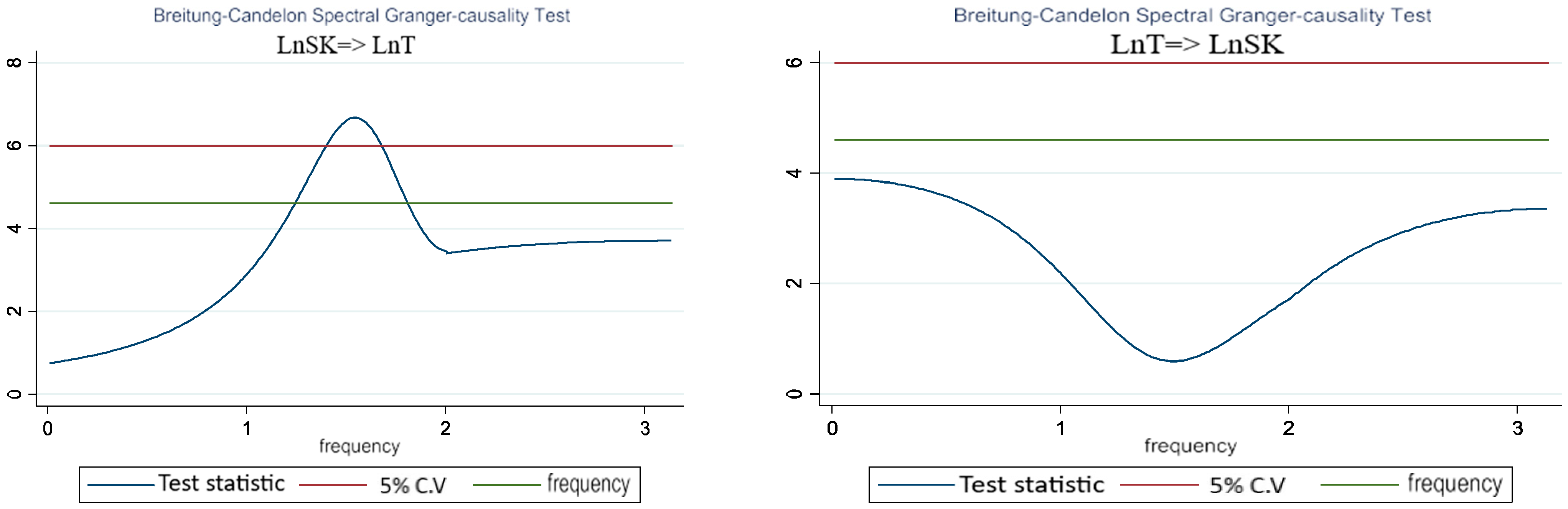
| CIs | ADF | KPSS | ||
|---|---|---|---|---|
| Level | First Difference | Level | First Difference | |
| LnOT | −0.460 | −32.875 *** | −0.013 | −23.324 *** |
| LnCE | −3.619 *** | −32.923 *** | −9.183 *** | −32.202 *** |
| LnBE | −5.725 *** | −30.881 *** | −8.252 *** | −35.617 *** |
| LnIRE | −0.703 | −35.604 *** | −1.356 | −31.267 *** |
| LnORE | −4.548 *** | −30.650 *** | −15.142 *** | −30.262 *** |
| LnSK | −3.817 *** | −34.203 *** | −10.461 *** | −30.166 *** |
| Estimated Model | F-Statistics | |
|---|---|---|
| LnOTt = f(LnCEt, LnBEt, LnIREt, LnOREt, LnSKt) | 5.534 * | |
| Significance level | Lower bound | Upper bound |
| 1% | 3.09 | 3.86 |
| 5% | 2.93 | 3.83 |
| 10% | 2.101 | 3.869 |
| CIs | Coefficient | St. Error | t-Value |
|---|---|---|---|
| ECT | −0.778 | 0.163 | −2.96 *** |
| LnORE | 0.205 | −5.287 | 0.000 *** |
| LnOREt−1 | 0.122 | 2.366 | 0.000 *** |
| LnSK | 0.025 | 0.636 | 0.250 |
| LnSKt−1 | 0.020 | 0.211 | 0.704 |
| LnIRE | 0.262 | 3.139 | 0.000 *** |
| LnIREt−1 | 0.292 | 3.766 | 0.000 *** |
| LnCE | 0.374 | 0.712 | 0.010 |
| LnCEt−1 | −0.020 | −0.110 | 0.028 |
| LnBE | 0.120 | 4.448 | 0.000 *** |
| LnBEt−1 | 0.266 | 4.883 | 0.000 *** |
| Cons | 3.281 | 0.069 | 0.000 *** |
| Adj R-squared | 0.7850 | Root MSE | 0.008 |
| R2 | 0.772 | ||
| Simulation | 5000 |
| Diagnostic Test | X2 (p-Value) | Result |
|---|---|---|
| Breusch–Godfrey LM | 0.16 (0.863) | No evidence of serial correlations |
| Breusch–Pagan–Godfrey | 0.388 (0.960) | No evidence of heteroscedasticity |
| Ramsey RESET test | 2.839 (0.213) | Model specified correctly |
| Jarque–Bera test | 0.144 (0.930) | Residuals are normally estimated |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saidi, L.; Bechhofer, E.; Benbouzid, M. Relationship Analysis Between Helicopter Gearbox Bearing Condition Indicators and Oil Temperature Through Dynamic ARDL and Wavelet Coherence Techniques. Machines 2025, 13, 645. https://doi.org/10.3390/machines13080645
Saidi L, Bechhofer E, Benbouzid M. Relationship Analysis Between Helicopter Gearbox Bearing Condition Indicators and Oil Temperature Through Dynamic ARDL and Wavelet Coherence Techniques. Machines. 2025; 13(8):645. https://doi.org/10.3390/machines13080645
Chicago/Turabian StyleSaidi, Lotfi, Eric Bechhofer, and Mohamed Benbouzid. 2025. "Relationship Analysis Between Helicopter Gearbox Bearing Condition Indicators and Oil Temperature Through Dynamic ARDL and Wavelet Coherence Techniques" Machines 13, no. 8: 645. https://doi.org/10.3390/machines13080645
APA StyleSaidi, L., Bechhofer, E., & Benbouzid, M. (2025). Relationship Analysis Between Helicopter Gearbox Bearing Condition Indicators and Oil Temperature Through Dynamic ARDL and Wavelet Coherence Techniques. Machines, 13(8), 645. https://doi.org/10.3390/machines13080645








