Yaw Control and Yaw Actuator Synchronised Control of Large Wind Energy Converters Using a Non-Linear PI Approach
Abstract
1. Introduction
2. Control System Background
2.1. Basic Nonlinear PID
2.2. Extended Nonlinear PID
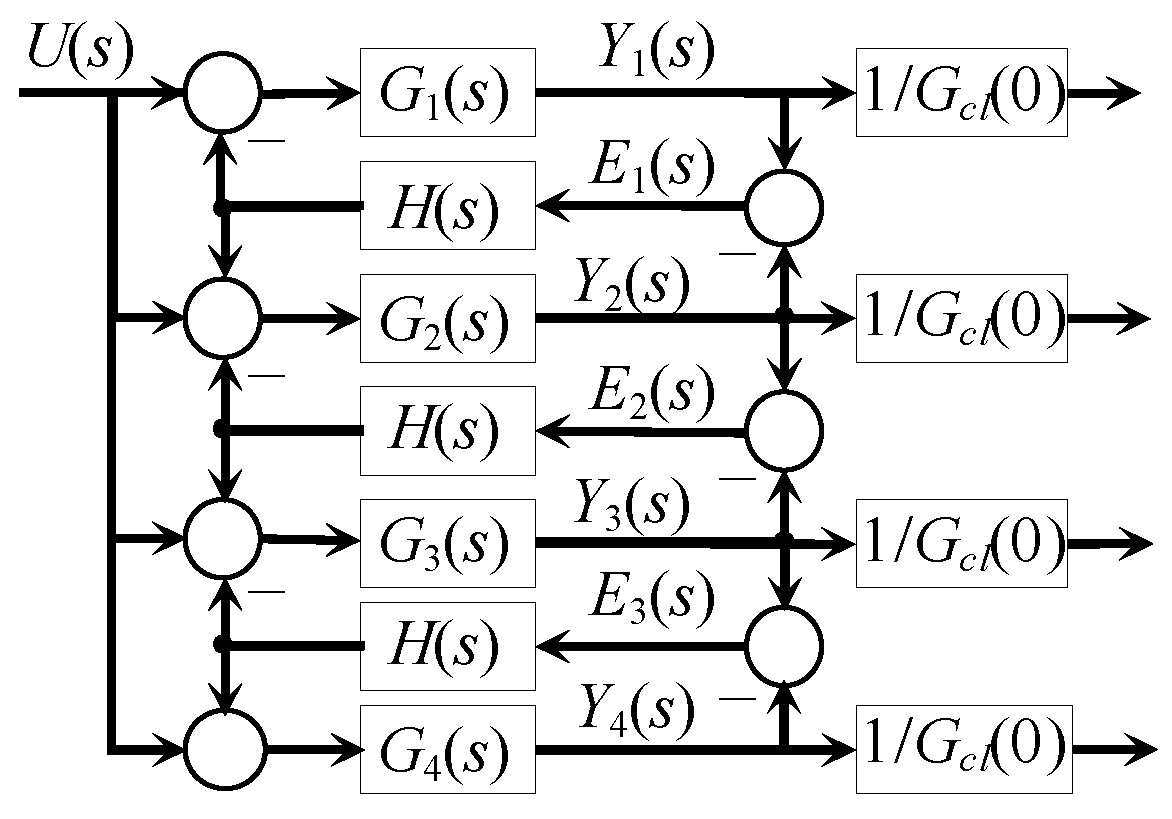
2.3. Synchronised Operation of Multiple Actuators
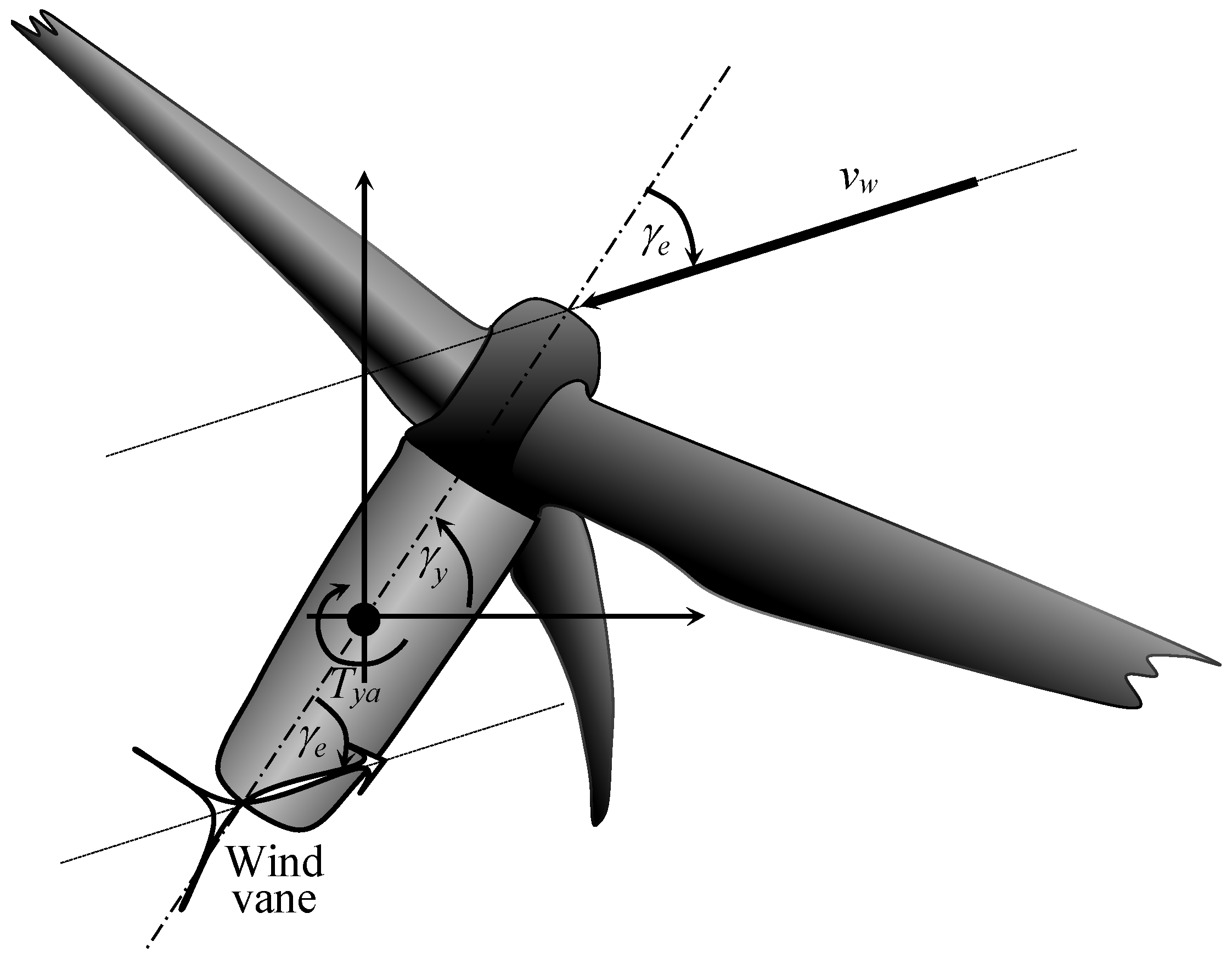
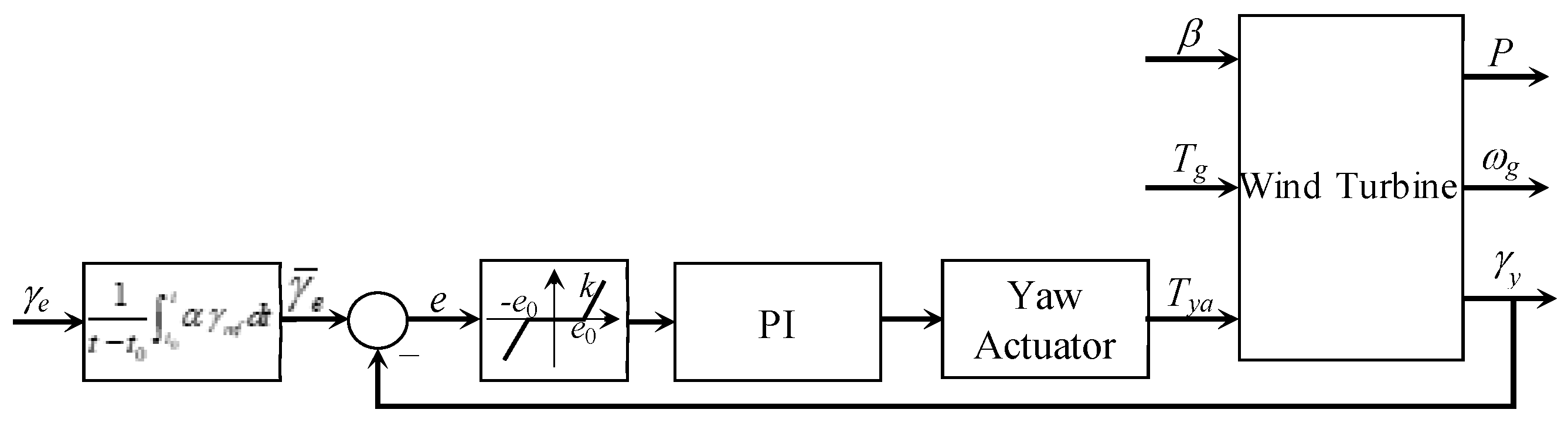
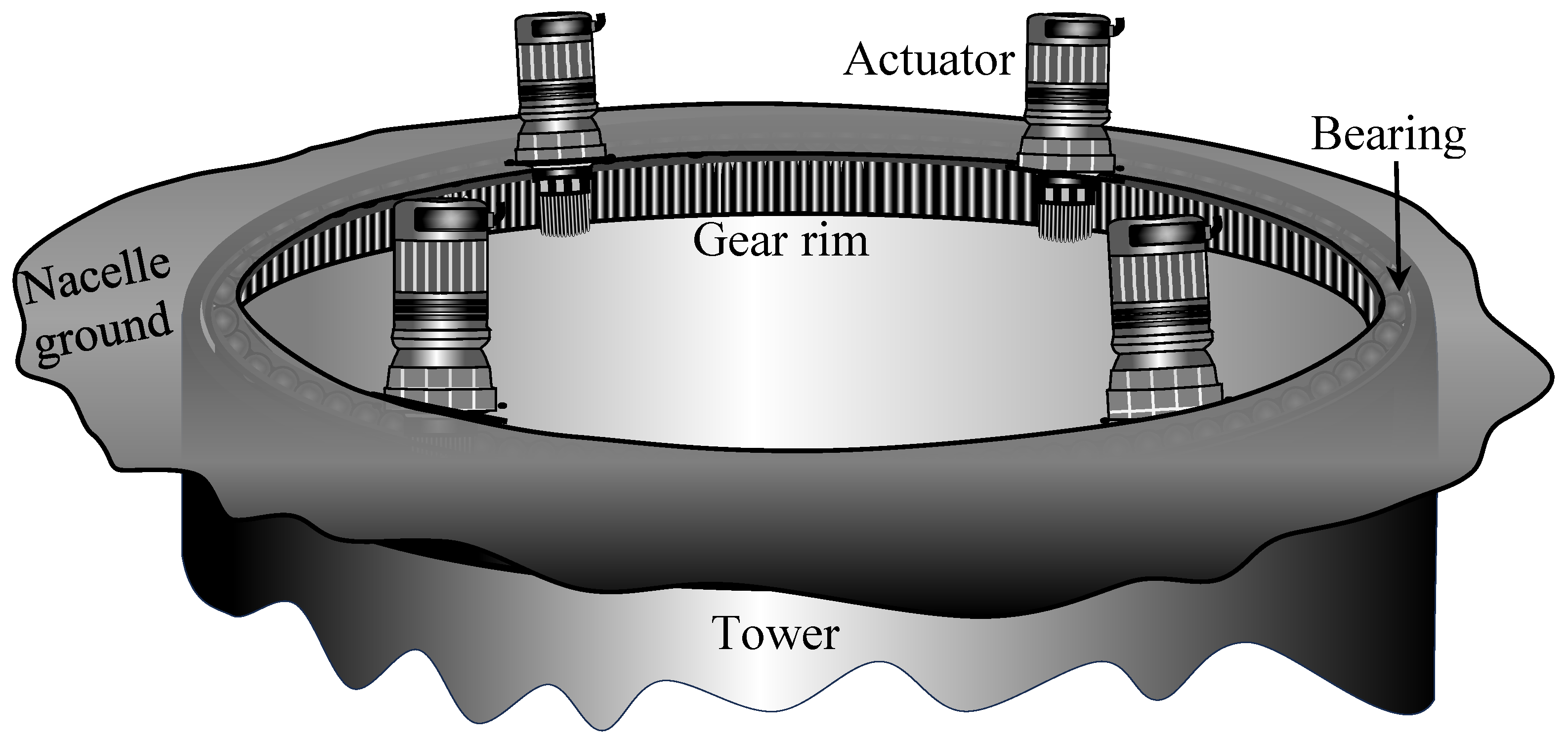
3. Yaw Control of Wind Turbines
4. Yaw Actuator Control
4.1. Control System for an Individual Actuator
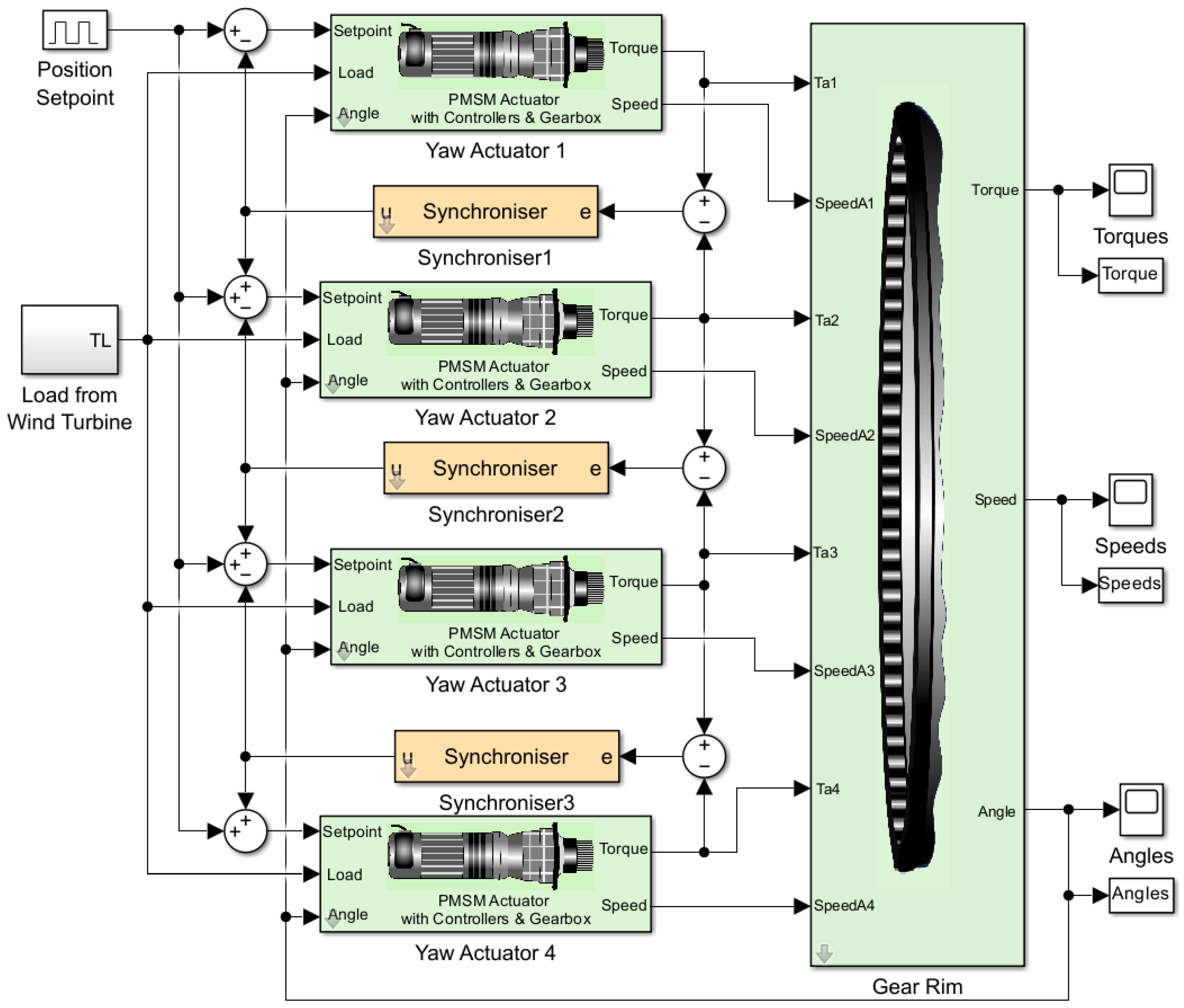
4.2. Synchronised Operation of Multiple Yaw Actuators
5. Application Study
5.1. Parametrisation of the Reference Wind Turbine
5.2. Parametrisation of the Yaw Actuator Model
5.3. Control Systems and Controller Parametrisation
5.3.1. Control Loops and Controller Parameters for the Yaw System
5.3.2. Control Loops and Controller Parameters for the Yaw Actuators
5.4. Setup for the Simulation Environment
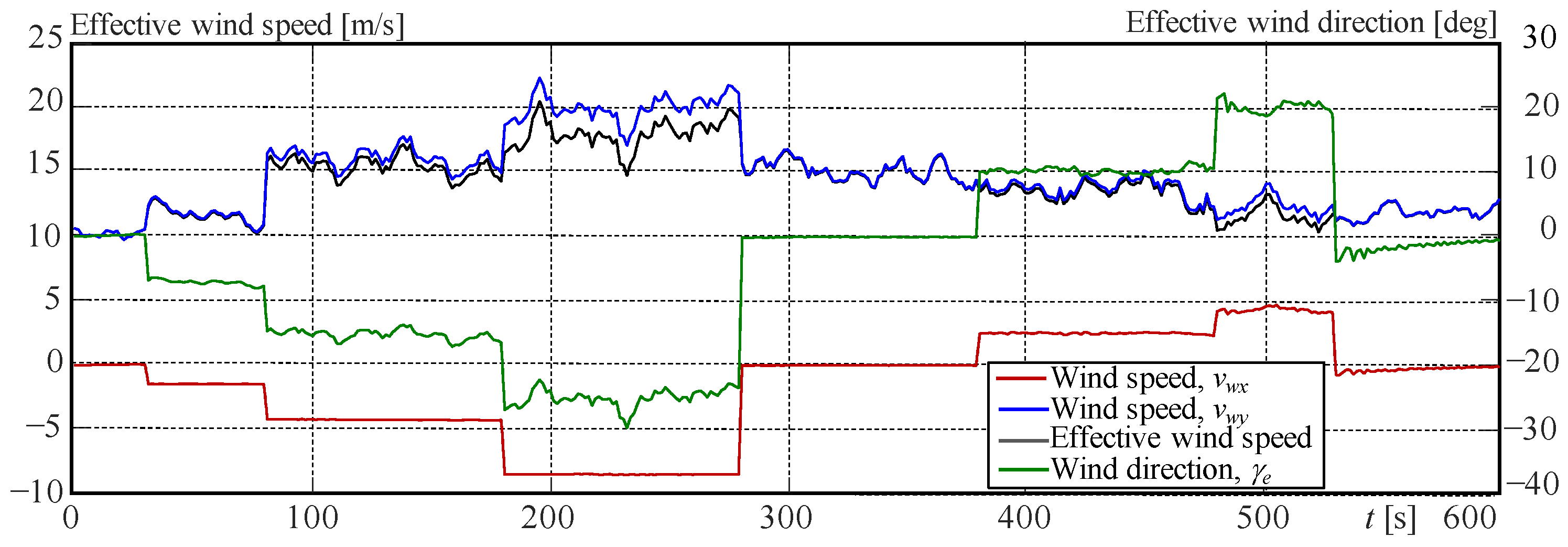
5.5. Description of the Simulation Experiments
6. Simulation Results and Analysis
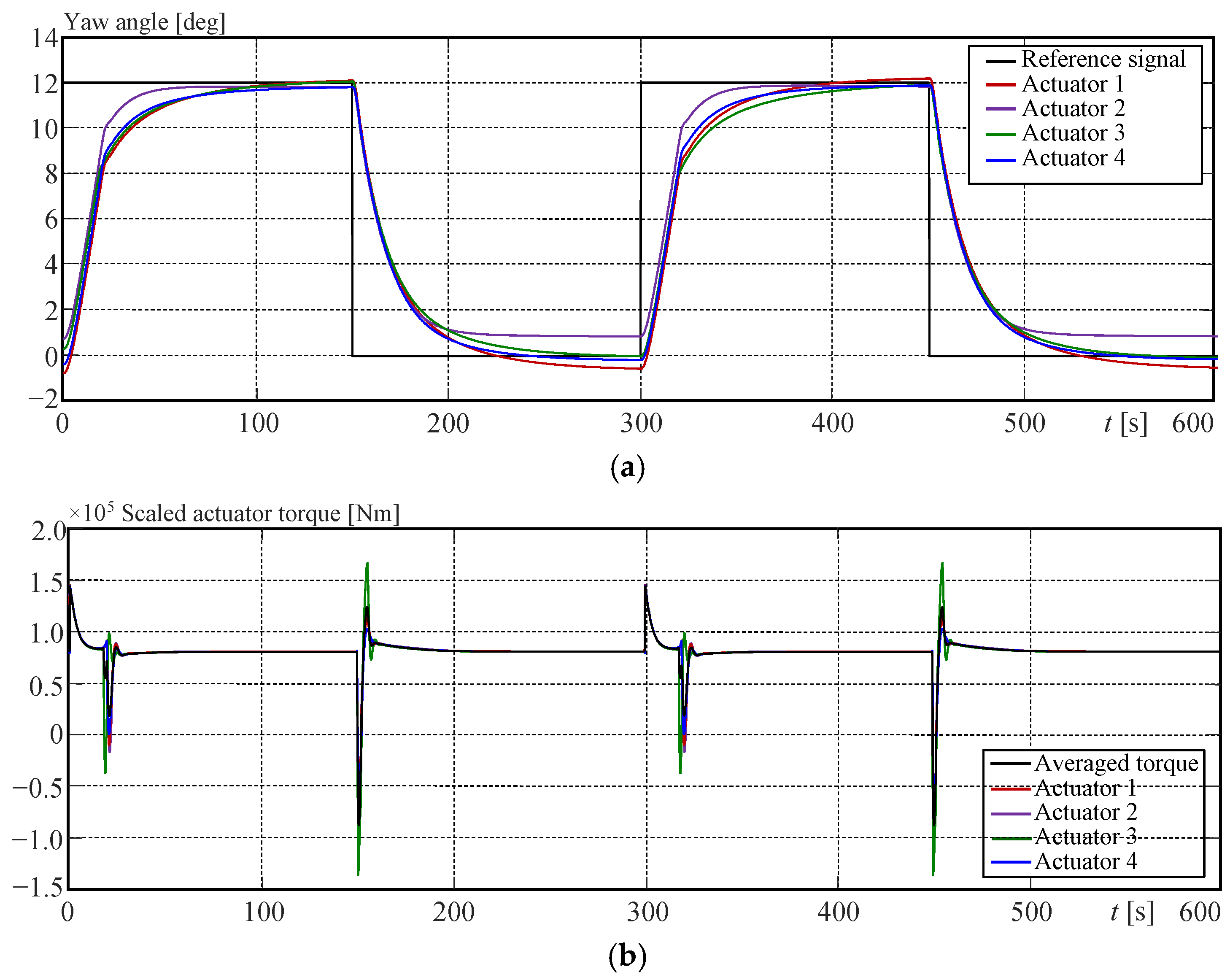
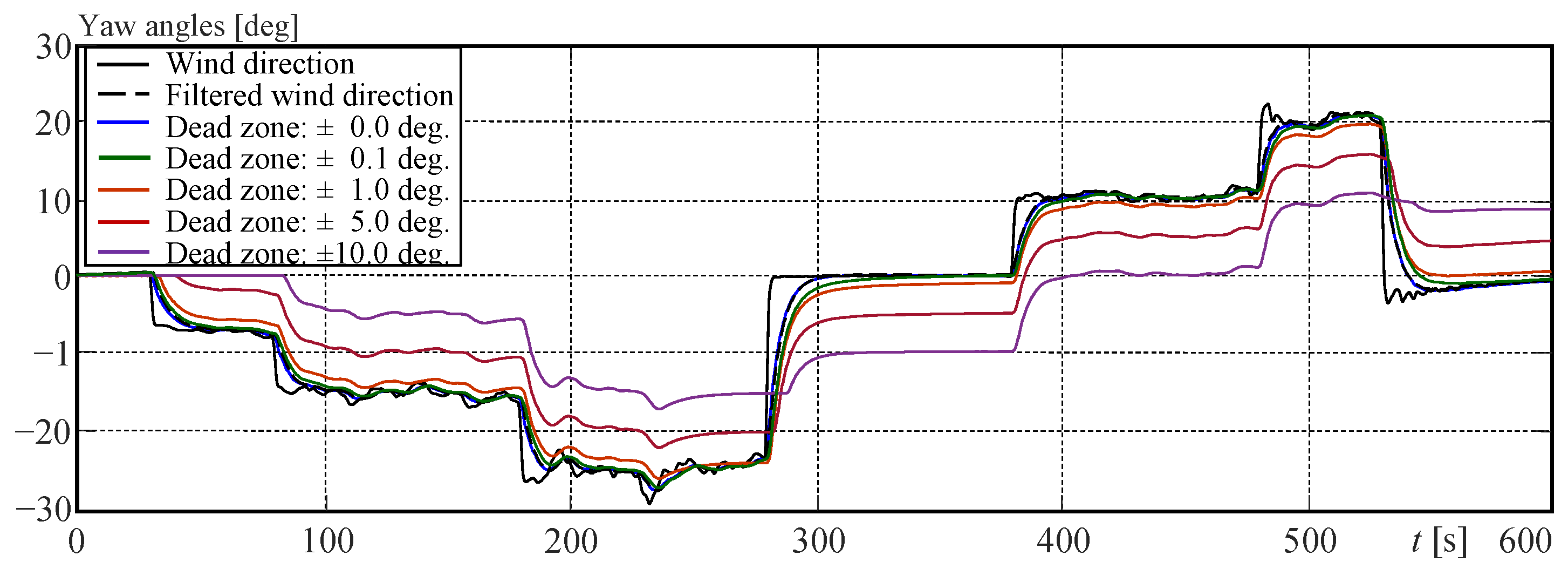
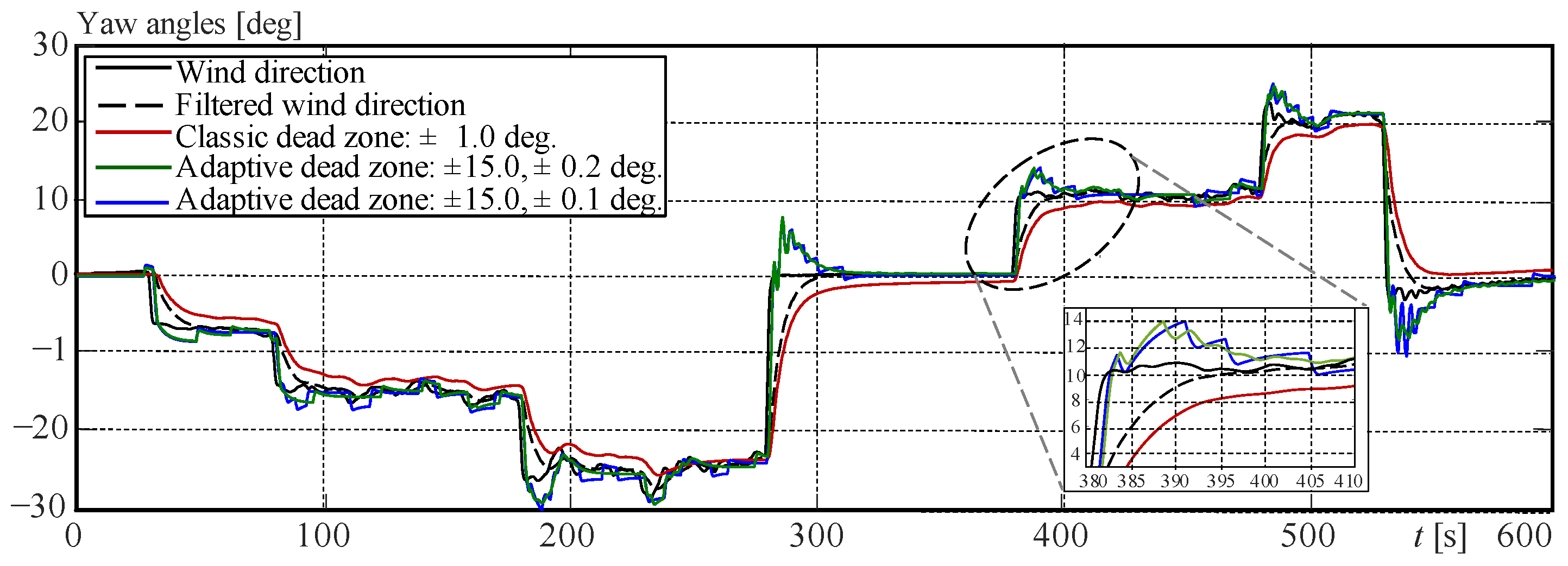
6.1. Simulation Results for the Yaw Control Experiment
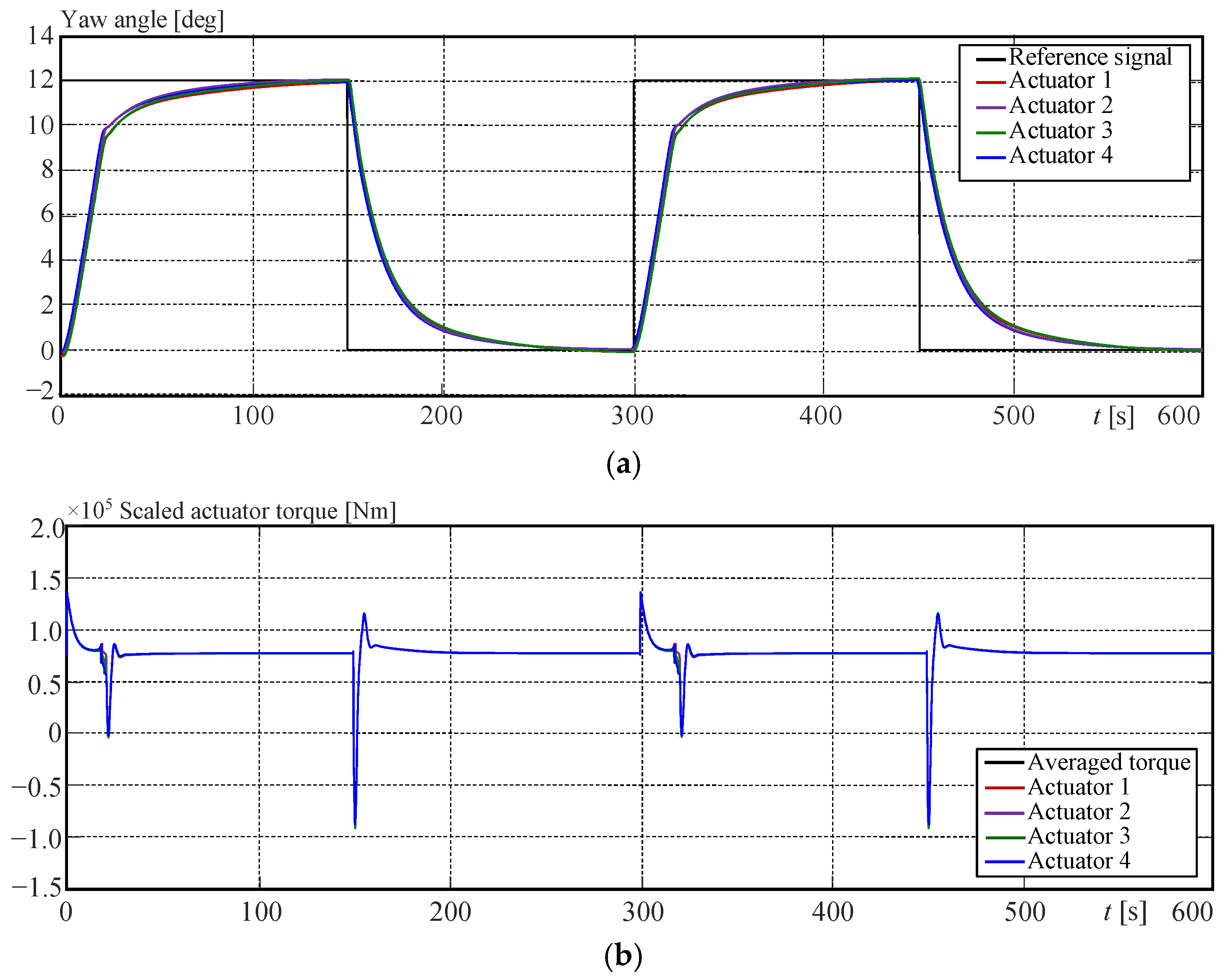
6.2. Simulation Results for the Yaw Actuator Control Experiment
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HCS | Hill climb searching |
| ISE | Integral square error |
| ITSE | Integral time-weighted squared error |
| ITSU | Integral time-weighted squared control |
| LiDAR | Light detection and ranging |
| NREL | National Renewable Energy Laboratory |
| PMSG | Permanent magnet synchronous motor |
| P, PI, PID | Proportional, proportional–integral, proportional–integral–derivative control |
| NP, NPI, NPID | Nonlinear P, nonlinear PI, nonlinear PID control |
Nomenclature
| Parameters | |
| ai, bi, pi, qi | Elements of polynomials A(s), B(s), P(s), Q(s) |
| Bm | Torsional viscous friction of motor shaft, Nm s/rad |
| Jm | Second moment of inertia of motor, kg m2 |
| Kpq, Kvff, | Parameters of the position control |
| Kpd, Kid, Kid, Kiq, | Gains of the current controllers (d and q axis) |
| Kpw, Kiw | Gains of the speed controller |
| K0, K1, K2 | Gains for the nonlinear controllers |
| Kp, Ki, Kd, Ka, b, f | Parameters of P, PI, PID controllers |
| Ld Lq | Self-inductances, H |
| na | Number of actuators |
| nx, nm | Gearbox and gear rim ratios, -- |
| p | Number of pole pairs, -- |
| dp | Pinion diameter, m |
| dt | Tower top diameter, m |
| Rs | Stator resistance, Ohm |
| TLmax | Maximum load torque, Nm |
| λf | Flux linkage between rotor and stator |
| wgn | Rated yaw speed |
| Variables | Flapwise root bending moments |
| isd, isq | d and q currents, in the dq reference frame, A |
| idref, iqref | d and q reference currents, in the dq reference frame, A |
| s | Laplace variable |
| t | Time |
| Tg | Yaw torque, Nm |
| TL | Load torque, Nm |
| u | Control variable |
| y | Output variable |
| va, vb, vc | Three-phase input voltages, V |
| vd, vq | d and q input voltages, in the dq reference frame, V |
| vwe | Effective wind speed |
| ge, gy, | Yaw error angle and yaw angle, rad |
| we, wm, wg | Electric, mechanical, and yaw speeds, rad/s |
| Qm, Qmref | Laplace transform of angle and angle reference, rad |
| Functions | |
| Ai(s), As(s) | Denominators of transfer function |
| Bi(s), Bs(s), BT(s) | Numerators of transfer functions |
| f(e), g(e) | Nonlinear function of the nonlinear PID controllers |
| G1(s), G2(s), G3(s), G4(s) | Transfer functions |
| Gdf(s), Gdq(s) | Transfer functions of filters in the d and q axis |
| H(s) | Transfer function of the synchroniser |
| Q(s), P(s), | Numerator and denominator of controller or Synchroniser |
| Id(s), Iq(s), Idref(s), Iqref(s) | Laplace transformed currents and current references |
| U(s), E(s), Y(s), R(s), | Laplace transformed input, error, output and reference |
| Wm(s),Qm(s),Wmref(s), Qmref(s) | Laplace transformation of wm, qm, wmref, qmref |
References
- Liu, Y.; Liu, S.; Zhang, L.; Cao, F.; Wang, L. Optimization of the yaw control error of wind turbines. Front. Energy Res. 2021, 9, 626681. [Google Scholar] [CrossRef]
- Bastankhaha, M.; Porté-Agelb, F. Wind farm power optimization via yaw angle control: A wind tunnel study. J. Renew. Sustain. Energy 2019, 11, 023301. [Google Scholar] [CrossRef]
- Howland, M.F.; Lele, S.K.; Dabiria, J.O. Wind farm power optimization through wake steering. Proc. Natl. Acad. Sci. USA 2019, 116, 14495–14500. [Google Scholar] [CrossRef] [PubMed]
- Knudsen, T.; Bak, T.; Svenstrup, M. Survey of wind farm control—Power and fatigue optimization. Wind Energy 2015, 18, 1333–1351. [Google Scholar] [CrossRef]
- Yang, J.; Fang, L.; Song, D.; Su, M.; Yang, X.; Huang, L.; Joo, Y.H. Review of control strategy of large horizontal-axis wind turbines yaw system. Wind Energy 2021, 24, 97–115. [Google Scholar] [CrossRef]
- Song, D.; Yang, J.; Fan, X.; Liu, Y.; Liu, A.; Chen, G.; Joo, Y.H. Maximum power extraction for wind turbines through a novel yaw control solution using predicted wind directions. Energy Convers. Manag. 2018, 157, 587–599. [Google Scholar] [CrossRef]
- Chen, W.; Liu, H.; Lin, Y.; Li, W.; Sun, Y.; Zhang, D. LSTM-NN yaw control of wind turbines based on upstreamWind information. Energies 2020, 13, 1482. [Google Scholar] [CrossRef]
- Fleming, P.A.; Scholbrock, A.K.; Jehu, A.; Davoust, S.; Osler, E.; Wright, A.D.; Clifton, A. Field-test results using a nacelle-mounted lidar for improving wind turbine power capture by reducing yaw misalignment. J. Phys. Conf. Ser. 2014, 524, 012002. [Google Scholar] [CrossRef]
- Yang, M.; Fan, S.; Lee, W.J. Probabilistic short-term wind power forecast using componential sparse Bayesian learning. IEEE Trans. Ind. Appl. 2013, 49, 2783–2792. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Khosravi, A.; Nahavandi, S. A new fuzzy-based combined prediction interval for wind power forecasting. IEEE Trans. Power Syst. 2016, 31, 18–26. [Google Scholar] [CrossRef]
- Ouyang, T.; Kusiak, A.; He, Y. Predictive model of yaw error in a wind turbine. Energy 2017, 123, 119–130. [Google Scholar] [CrossRef]
- Karakasis, N.; Mesemanolis, A.; Nalmpantis, T.; Mademlis, C. Active yaw control in a horizontal axis wind system without requiring wind direction measurement. IET Renew. Power Gener. 2016, 10, 1441–1449. [Google Scholar] [CrossRef]
- Guo, F.; Jiang, W.; Shao, H.; Du, Y.; She, J. Research on the wind turbine yaw system based on PLC. In Proceedings of the 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 5164–5168. [Google Scholar]
- Farret, F.A.; Pfitscher, L.L.; Bernardon, D.P. Sensorless active yaw control for wind turbines. In Proceedings of the 27th Annual Conference of the IEEE Industrial Electronics Society, Denver, CO, USA, 29 November–2 December 2001; pp. 1370–1375. [Google Scholar] [CrossRef]
- Wu, X.; Liu, Y.; Teng, W. Modified hill climbing method for active yaw control in wind turbine. In Proceedings of the 31st Chinese Control Conference, Hefei, China, 25–27 July 2012; pp. 6677–6680. [Google Scholar]
- Ekelund, T. Yaw control for reduction of structural dynamic loads in wind turbines. J. Wind. Eng. Ind. Aerodyn. 2000, 85, 241–262. [Google Scholar] [CrossRef]
- Hure, N.; Turnar, R.; Vasak, M.; Bencic, G. Optimal wind turbine yaw control supported with very short-term wind predictions. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 385–391. [Google Scholar] [CrossRef]
- Kragh, K.A.; Hansen, M.H. Load alleviation of wind turbines by yaw misalignment. Wind Energy 2014, 17, 971–982. [Google Scholar] [CrossRef]
- Hu, S.; Ren, X.; Zhao, W. Synchronous control of multi-motor driving servo systems. In Lecture Notes in Electrical Engineering; Jia, Y., Du, J., Zhang, W., Eds.; Springer: Singapore, 2017; Volume 459, pp. 611–620. [Google Scholar] [CrossRef]
- Li, M.; Meng, X. Analysis and design of system for multi-motor synchronous control. In Advances in Computer Science, Environment, Ecoinformatics, and Education; Lin, S., Huang, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 217, pp. 268–273. [Google Scholar] [CrossRef]
- Niu, F.; Sun, K.; Huang, S.; Hu, Y.; Liang, D. A review on multimotor synchronous control methods. IEEE Trans. Transp. Electrif. 2023, 9, 22–33. [Google Scholar] [CrossRef]
- Gambier, A. Synchronised control of multiple actuators of wind turbines. Actuators 2025, 14, 264. [Google Scholar] [CrossRef]
- Koren, Y. Cross-coupled biaxial computer control for manufacturing systems. J. Dyn. Syst. Meas. Control 1980, 102, 265–271. [Google Scholar] [CrossRef]
- Zhao, D.; Li, C.; Ren, J. Speed synchronization of multiple induction motors with adjacent cross coupling control. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC), Shanghai, China, 15–18 December 2009; pp. 6805–6810. [Google Scholar] [CrossRef]
- Unbehauen, H.; Vakilzadeh, I. Synchronization of n non-identical simple-integral plants. Int. J. Control 1989, 50, 543–574. [Google Scholar] [CrossRef]
- Vakilzadeh, I.; Mansour, M. Synchronization of ‘n’ integral-plus-times constant plants with non-identical gain and time constants. Control Theory Adv. Technol. 1989, 5, 569–585. [Google Scholar] [CrossRef]
- Vakilzadeh, I.; Mansour, M. Synchronization of ‘n” integral-plus-double time constant plants with non-identical gain and time constants. J. FrankIm. Inst. 1990, 327, 579–593. [Google Scholar] [CrossRef]
- Unbehauen, H.; Vakilzadeh, I. Synchronization of ‘n’ decentralized non-identical plants with integral behavior and two complex poles. Control Theory Adv. Technol. 1994, 10, 385–402. [Google Scholar]
- Vakilzadeh, I.; Unbehauen, H. Four rendezvous problems for n non-identical simple-integral plants. Int. J. Syst. Sci. 1993, 24, 1455–1472. [Google Scholar] [CrossRef]
- Shahruz, S.M.; Schwartz, A.L. Design of optimal nonlinear PI compensators. In Proceedings of the 32nd IEEE Conference on Decision and Control, San Antonio, TX, USA, 15–17 December 1993; pp. 3564–3565. [Google Scholar]
- Xu, Y.; Hollerbach, J.M.; Ma, D. A nonlinear PD controller for force and contact transient control. IEEE Control Syst. Mag. 1995, 15, 15–21. [Google Scholar]
- Gambier, A.; Nazaruddin, Y. Collective pitch control with active tower damping of a wind turbine by using a nonlinear PID approach. IFAC 2018, 51, 238–243. [Google Scholar] [CrossRef]
- Åström, K.J.; Hagglund, T. Advanced PID control, ISA-The Instrumentation, Systems, and Automation Society; Research Tringle Park: Durham, NC, USA, 2006. [Google Scholar]
- Visioli, A. Practical PID Control; Springer: London, UK, 2006. [Google Scholar]
- Seraji, H. A new class of nonlinear PID controllers with Robotic Applications. J. Robot. Syst. 1998, 15, 161–181. [Google Scholar] [CrossRef]
- Su, Y.X.; Sun, D.; Duan, B.Y. Design of an enhanced nonlinear PID controller. Mechatronics 2005, 15, 1005–1024. [Google Scholar] [CrossRef]
- Taylor, J.H.; Strobel, K.L. Nonlinear compensator synthesis via sinusoidal-input describing functions. In Proceedings of the 1985 American Control Conference, Boston, MA, USA, 19–21 June 1985; pp. 1242–1247. [Google Scholar]
- Isayed, B.M.; Hawwa, M.A. A nonlinear PID control scheme for hard disk drive servosystems. In Proceedings of the 15th Mediterranean Conference on Control and Automation, Athens, Grecce, 27–29 June 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Junoh, S.C.K.; Salim, S.N.S.; Abdullah, L.; Anang, N.A.; Chiew, T.H.; Retas, Z. Nonlinear PID triple hyperbolic controller. Int. J. Mech. Mechatron. Eng. Des. XY Table Ball-Screw Drive Syst. 2017, 17, 1–10. [Google Scholar]
- Slotine, J.-J.; Li, W. Applied Nonlinear Control; Prentice Hall, Englewood Cliffs: New Jersey, NJ, USA, 1991. [Google Scholar]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook Edition, 2nd ed.; John Wiley and Sons: Chichester, UK, 2011. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scot, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development. Technical Report; NREL: Golden, CO, USA, 2009. [Google Scholar]
- Jonkman, J.M.; Buhl Jr, L.M. FAST User’s Guide; Research report, NREL; Battelle: Golden, CO, USA, 2005. [Google Scholar]
- Wang, L.; Chai, S.; Yoo, D.; Gan, L.; Ng, K. PID and Predictive Control of Electrical Drives and Power Converters Using MATLAB®/Simulink®; John Wiley & Sons: Singapore, 2015. [Google Scholar]
- Bonfiglioli. Wind Solutions: Product Range. Product Description; Bonfiglioli Riduttori S.p.A.: Carpiano, Italy, 2020. [Google Scholar]





| Parameters | Actuator 1 | Actuator 2 | Actuator 3 | Actuator 4 |
|---|---|---|---|---|
| Jm [kg m2] | 1.6134 | 1.5327 | 1.6457 | 1.6505 |
| Bm [N m/(rad/s)] | 0.0147 | 0.018919 | 0.0075661 | 0.009241 |
| Ld [H] | 0.00035934 | 0.00034138 | 0.00053901 | 0.00048511 |
| Lq [H] | 0.00035934 | 0.00034138 | 0.00053901 | 0.00048511 |
| Rs [Ω] | 0.80455 | 0.76432 | 1.2068 | 1.0861 |
| lf [Wb] | 0.07072 | 0.068217 | 0.076378 | 0.076095 |
| p | 6 | 6 | 6 | 6 |
| Parameters | Proportional Gain | Integral Gain | Actuator 3 | Reference Weight |
|---|---|---|---|---|
| PI | Kpy = 7.372 | Kiy = 3.443 | Kay = 5 | b = 1 |
| NPI | K0py = 4.4173 K1py = 8.6107 K2py = 0.0143 | K0iy = 4.4173 K1iy = 8.6107 K2iy = 0.0143 | Kay = 5 | b = 1 |
| Parameters | Actuator 1 | Actuator 2 | Actuator 3 | Actuator 4 | |
|---|---|---|---|---|---|
| Current controllers | Kpd = 0.0870 Kid = 0.1710 Kpq = 1.0489 Kiq = 2.5310 | Kpd = 0.0870 Kid = 0.1710 Kpq = 1.0489 Kiq = 2.5310 | Kpd = 0.0870 Kid = 0.1710 Kpq = 1.0489 Kiq = 2.5310 | Kpd = 0.0870 Kid = 0.1710 Kpq = 1.0489 Kiq = 2.5310 | |
| Speed controllers | Kpt = 4.1952 Kit = 0.0290 | Kpt = 1.5646 Kit = 0.0215 | Kpt = 3.5038 Kit = 0.0192 | Kpt = 5.7635 Kit = 0.0294 | |
| Position controllers | FF | Kvff = 20.6395 | Kvff = 20.6395 | Kvff = 22.2367 | Kvff = 26.2889 |
| P | Kpp = 20.1020 | Kpp = 20.2919 | Kpp = 20.8031 | Kpp = 20.3189 | |
| NP | Kpp1 = 15.4355 Kpp2 = 2.3869 Kpp3 = 1.0000 | Kpp1 = 1.2978 Kpp2 = 16.4546 Kpp3 = 1.0000 | Kpp1 = 12.6032 Kpp2 = 5.0307 Kpp3 = 1.0000 | Kpp1 = 9.8339 Kpp2 = 8.0440 Kpp3 = 1.0000 | |
| P Position Controller | NP Position Controller | |||||||
| Actuator 1 | Actuator 2 | Actuator 3 | Actuator 4 | Actuator 1 | Actuator 2 | Actuator 3 | Actuator 4 | |
| Je | 685.5 | 543.5 | 743.4 | 564.5 | 211.4 | 480.6 | 598.5 | 559.3 |
| Dead Zone | PI | NPI | ||||
|---|---|---|---|---|---|---|
| Je | Ju | E | Je | Ju | E | |
| 0 deg | 0.3566 | 68.5939 | 262.0 | 0.0071 | 68.5942 | 262.8 |
| ±0.1 deg | 0.4182 | 69.1778 | 262.0 | 0.0269 | 68.9010 | 263.0 |
| ±1.0 deg | 1.2507 | 68.1147 | 261.4 | 0.4072 | 65.6015 | 262.8 |
| ±5.0 deg | 17.6656 | 62.3505 | 256.1 | 6.8705 | 78.0999 | 258.2 |
| ±10.0 deg | 100.9248 | 73.2117 | 242.0 | 26.3100 | 77.2117 | 252.7 |
| Adaptive: (±0.2, ±15.0) deg | 0.4775 | 69.1624 | 261.9 | 0.0380 | 69.4918 | 261.9 |
| Adaptive: (±0.1, ±15.0) deg | 0.4009 | 69.2013 | 262.0 | 0.0290 | 68.8906 | 262.0 |
| PI Synchronisers | NPI Synchronisers | |||||||
| Actuator 1 | Actuator 2 | Actuator 3 | Actuator 4 | Actuator 1 | Actuator 2 | Actuator 3 | Actuator 4 | |
| Je | 206.03 | 432.01 | 151.09 | 154.91 | 30.20 | 47.85 | 45.23 | 95.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gambier, A. Yaw Control and Yaw Actuator Synchronised Control of Large Wind Energy Converters Using a Non-Linear PI Approach. Machines 2025, 13, 644. https://doi.org/10.3390/machines13080644
Gambier A. Yaw Control and Yaw Actuator Synchronised Control of Large Wind Energy Converters Using a Non-Linear PI Approach. Machines. 2025; 13(8):644. https://doi.org/10.3390/machines13080644
Chicago/Turabian StyleGambier, Adrian. 2025. "Yaw Control and Yaw Actuator Synchronised Control of Large Wind Energy Converters Using a Non-Linear PI Approach" Machines 13, no. 8: 644. https://doi.org/10.3390/machines13080644
APA StyleGambier, A. (2025). Yaw Control and Yaw Actuator Synchronised Control of Large Wind Energy Converters Using a Non-Linear PI Approach. Machines, 13(8), 644. https://doi.org/10.3390/machines13080644






