Re-Optimized Design for the ADR-Based Dual-Loop Controller of 100 m Class Aperture Radio Telescope

Abstract

Pointing accuracy is a crucial performance index for a fully steerable large-aperture radio telescope and is subject to external and internal disturbances. Improvement of the antenna’s servo control performance is meaningful for pointing, especially for blind pointing of the antenna. This paper firstly establishes a multi-motor-driving four-degrees-of-freedom (DOF) model of an antenna servo system, then optimizes the original design consisting of the active disturbance rejection (ADR)-based velocity controller and lead–lag-based position controller, making the velocity controller a novel linear ADR-based controller coupled with a disturbance-velocity compensation (DLADRC) and the position controller the simplest proportional (P) controller. Simulation results based on a 100 m class radio telescope servo model indicate that the new control system’s velocity-loop response is smoother, the position-loop peak disturbance response is reduced by 17.8%, the position-loop dynamic performance with the short settling time and slight overshoot remains the same as the former PD-LADRC system, and the RMS pointing/tracking error is 2.16 arcsec under a mean wind of 3 m/s, less than the design specification of 2.5 arcsec RMS required.

1. Introduction

The fully steerable reflector radio telescope plays a crucial role in radio-astronomy observations because of its larger observational sky coverage and longer observational time (integration time). For higher sensitivity and angular resolution, the antenna aperture of a single-dish radio telescope becomes larger and larger. The 100 m × 110 m Green Bank Telescope (GBT) and the 100 m aperture Effelsberg Radio Telescope are the biggest fully steerable antennas in service. Xinjiang Astronomical Observatory, CAS is building the larger aperture QiTai Radio Telescope (QTT), which has a 110 m aperture dish and works at frequencies from 115 MHz up to 115 GHz [1].

Pointing accuracy is a crucial index, as important as the angular resolution and sensitivity of a fully steerable radio telescope. The pointing accuracy of large-aperture antennas is required to be a few arcseconds; e.g., QTT required an initial pointing accuracy of better than 2.5 arcsec and about 1 arcsec ultimately, which is challenging. In addition, astronomical observation also requires the antenna to switch fast between the goal and calibrator when operating at higher-frequency observations or VLBI [2]. The good dynamic performance of the antenna’s servo system implies a shorter settling time, a tiny/zero overshoot for switching, meaning higher observation efficiency for the antenna. Making an antenna’s aperture larger makes its sensitivity and resolution higher; however, it requires higher pointing accuracy at the same frequency, consequently asking for better servo control performance. Comparing the pointing accuracy, blind pointing accuracy is more closely related to the antenna’s mechanical performance, and improvement in it is regarded as a better way to achieve high-accuracy pointing and is more meaningful [3]. An antenna’s pointing performance is beset by various challenges [4]. The negative effect of an imperfect antenna structure, such as uneven track and axis-related errors, can be reduced by astronomical pointing correction [5,6]. In addition to an antenna’s imperfect structure, antennas built outdoors are subject to nonlinear friction [7,8] and many environmental disturbances, like wind gusts and temperature, which make the antenna’s servo control accuracy challenging. The design of a better main-axis controller is regarded as a way to reduce the negative effects, and thus, improve the antenna servo system’s performance.

Electromechanical servo systems like antennas apply the current, velocity, and position to a three-loop control structure. The velocity- and position-loops are more relevant to the antenna’s servo performance; so, they are crucial to the antenna’s high-precision pointing control. Traditionally, integer-order proportional–integral–derivative (IOPID) controllers are employed in each loop; however, IOPID cannot simultaneously meet the requirements for the tracking accuracy and stability of a servo control system. Therefore, compound control based on IOPID and/or advanced control algorithms has been researched and utilized for antenna-pointing control. Advanced control algorithms can reduce major issues and increase the performance of the servo system, so their utilization is the major way to improve pointing control performance [9].

The advanced algorithms used for antennas mainly include linear quadratic Gaussian (LQG)/H₂, H_∞, quantitative feedback technique (QFT), disturbance observer-based control (DOBC), equivalent input disturbance approach (EID), active disturbance rejection control (ADRC), sliding mode control (SMC), etc.

LQG/H₂ controllers are well studied for achieving high-performance control of antennas under disturbances. In [10], Gawronski et al. compared and studied the tracking and disturbance rejection performances of a feedback controller and LQG controller for the Deep Space Network (DSN) antenna. In [11], Zhang et al. considered the influence of the antenna reflector structure deformation under wind on pointing and employed the LQG controller to reject wind disturbances. Li et al. [12] proposed a compound control strategy to address the coupling between flexible deformation and rigid displacement in a large reflector antenna, in which the PID controller is for rigid-body model control, while the LQG is for flexible control. Perrotta et al. [13] improved an LQG controller in the position-loop to attenuate flexible factors to increase the gain of the PI, consequently reducing the position errors. Although the model-based LQG/H₂ controller claims it is an optimal design and can attenuate structural resonance, it cannot obtain the desired control performance due to the existing model uncertainties, which are universal and non-negligible for the controlled plant.

H_∞ is proposed to deal with the model uncertainties; thus, it is insensitive to model uncertainties and can achieve better control performance than LQG/H₂ in the presence of model uncertainties [14]. The applications of H_∞ in antenna servo systems have been widely studied. In [15], H_∞ is used for improving the ship-mounted tracking antenna’s tracking accuracy. Wu et al. [16] designed a robust H_∞ double-feedback controller based on a typical PD controller cascaded with a structure filter to deal with the flexible structure uncertainty. In [17], a bi-objective control architecture is proposed for achieving an optimal H₂ tracking performance by a central controller under low-level disturbance, and a robust H_∞ anti-disturbance performance at significant disturbance via a disturbance filter. Rationally estimating the plant’s model uncertainty is challenging, especially for control engineers without comprehensive knowledge of the plant operating conditions. Furthermore, since these two kinds of methods are model-based, the order of the designed controller is not less than that of the plant models. A controller with high orders may be limited in application without considering order reduction. QFT is also an H_∞ control approach; it is designed on a Nichols diagram and can directly design a low-order robust controller. García-Sanz [18,19] applied the QFT to a large radio telescope’s servo system to improve its control performance. However, the design was made on an exclusive design platform, thus bringing a limit to its application.

SMC [20] is also used for antenna servo control to improve response rapidity and control accuracy; however, it leads to chattering due to the switch between different sliding mode surfaces, which is detrimental for a multiple-body flexible system like a large antenna. So, it is not common in the field of antenna control.

DOBC, EID, and ADRC are classes of active anti-disturbance control approaches. Liao et al. [21] augmented a disturbance observer (DOB) on the base of the original controller in an antenna’s position-loop to estimate and compensate for the equivalent disturbance in the input channel, thus enhancing the pointing properties of the antenna. The DOB, however, cannot work due to unstable poles when the plant model is in the non-minimum phase, thus limiting its application. Yang et al. [22] considered the non-minimum-phase properties in antenna servo systems due to communication lag, and designed an EID controller to achieve high-accuracy control of an antenna. Like H₂ and H_∞, the EID controller is also model-based, and the high order of the controller makes it more parameterized, limiting its application to some extent.

Different from DOBC and EID, the typical ADRC is a model-free active anti-disturbance control method. It has a lot of successful engineering applications. For example, Qiu et al. [23] applied it to a DSN antenna to achieve a good anti-wind-disturbance performance. Ranka [24] employed the extended state observer (ESO) of the ADRC to attenuate the adverse effect of the uncertainties of the GBT. Chen et al. [25] applied ADRC to the position-loop of the Leighton Chajnantor telescope to strengthen the wind-disturbance rejection ability of the antenna servo system. The order of ADRC can be chosen according to the controlled plant model’s relative order, and thus, may be much less than the model’s order, mainly due to the ADRC’s different understanding of the controlled plant model. The scenario in which ADRC is used in this paper is a typical example.

The contributions of this paper are as follows:

(1) A single-input, multiple-motor-driven, multi-output (SIMO) motor-load model of an antenna servo system is developed. The antenna load that causes shaft-load speed fluctuation is considered a disturbance term for the motor-gearbox velocity control.

(2) A linear ADR-based controller coupled with disturbance-rate compensation (DLADRC) is designed for the velocity-loop, which improves the initial dynamic response and enhances the anti-disturbance performance of the complex antenna system. A first-order low-pass filter and a notch filter are further introduced to improve the speed-tracking characteristics of the off-velocity-loop antenna’s structure. The position-loop employs a proportional controller in the base of the DLADRC-based velocity controller, simplifying the parameter-tuning of the position controller.

(3) The proposed control scheme is characterized by less dependence on the controlled plant information, a simple controller structure, easy parameter tuning, good command tracking, disturbance rejection, and high robustness against parametric perturbations.

In the rest of this paper, we introduce our studies on multiple-motor-driven antenna modeling in Section 2 and controller design in Section 3. Simulation and analysis of the control scheme are illustrated in Section 4, and finally, a summary is given.

2. Multiple-Motor-Driven Antenna Servo System Modeling

Since it is a small ratio between weight and aperture, low cost, easy installation and maintenance, and high structural accuracy, a wheel-track azimuth-elevation-fully-steerable radio telescope is widely adopted in radio astronomy. Large-aperture radio telescopes in service, such as GBT, and Effisberg, and the under-construction QTT, employ this type of antenna. The azimuth and elevation axes of the azimuth–elevation antenna are geometrically orthogonal to each other, and their structures are similar. Since the azimuth axis subsystem is subject to the influence of the elevational pose changing, making its control performance susceptible, engineers usually undertake controller design and analysis on it.

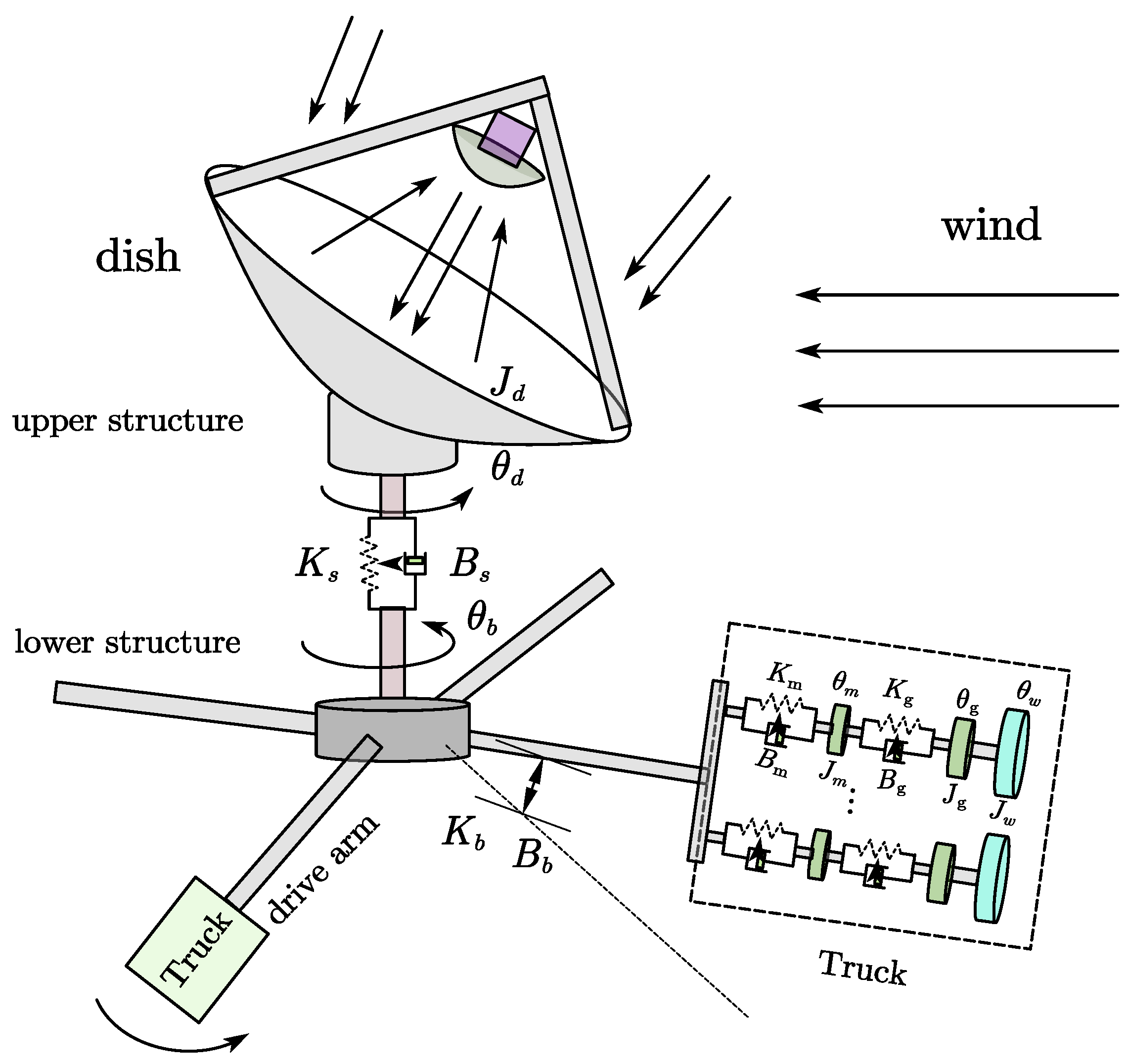
The azimuthal system of a wheel-track large-aperture antenna consists of a track and a mount with several driving arms and balancing arms, in which each driving arm is rotated by a truck with several motors with gearboxs; for example, there are four driving arms, each employing four motors in the GBT azimuthal system [19]. Figure 1 shows a simplified azimuth structure of the multiple-motor-driven antenna of a radio telescope. It considers four principal degrees of freedom (4DOF): the dish (major reflector) angular displacement ${\theta }_{\mathrm{d}}$, the base angular displacement ${\theta }_{\mathrm{b}}$, the truck system angular displacement ${\theta }_{\mathrm{t}}$, and the gearbox angular displacement ${\theta }_{\mathrm{g}}$. The azimuth system has n (n = 2 or 4) driving arms and n balancing arms. Each driving arm connects a truck consisting of k (k = 1, 2, 3, 4) wheels, and motors with gearboxes. The n drive arms have the same motor and structure parameters, so Figure 1 only shows one driving arm for the schematic drawing. In Figure 1, $J_{\mathrm{d}}$, $J_{\mathrm{b}}$, $J_{\mathrm{t}}$, $J_{\mathrm{w}}$, $J_{\mathrm{g}}$, $J_{\mathrm{m}}$ are the inertia moments of the dish, base, truck, wheel, gearbox, and motor, respectively; $K_s$, $K_{\mathrm{b}}$, $K_{\mathrm{g}}$, $K_{\mathrm{m}}$ and $B_{\mathrm{s}}$, $B_{\mathrm{b}}$, $B_{\mathrm{g}}$, $B_{\mathrm{m}}$ are the coefficients of the torsional stiffness and damping of the upper structure, one drive arm, gearbox, and motor shaft, respectively.

Because of the relatively much lower damping and more significant stiffness of the gearbox, the motor shaft and gearbox are regarded as a whole. The equivalent inertia amount at the gearbox output of these two parts can be represented in Equation (1) under the condition of ignoring the gearbox damping $B_{\mathrm{g}}$ and marking the reduction ratio as N.

$${\overline{J}}_{\mathrm{m}}=N^2{J}_{\mathrm{m}}+J_{\mathrm{g}},$$

(1)

When the little $J_{\mathrm{g}}$ is neglected, the equivalent inertia amount ${\overline{J}}_{\mathrm{m}}$ can further be rewritten as ${\overline{J}}_{\mathrm{m}}=N^2{J}_{\mathrm{m}}$. Let the radius ratio between the base and the wheel be R, then ${\theta }_{\mathrm{w}}=R{\theta }_{\mathrm{t}}$. The kinetic, potential, and dissipated energy equations of the 4DOF azimuthal system shown in Figure 1 can be denoted as follows.

$$E_{\mathrm{k}}=\frac{1}{2}{J}_{\mathrm{d}}{\dot{\theta }}_{\mathrm{d}}^2+\frac{1}{2}{J}_{\mathrm{b}}{\dot{\theta }}_{\mathrm{b}}^2+n\left(\frac{1}{2}{J}_{\mathrm{t}}{\dot{\theta }}_{\mathrm{t}}^2+\frac{k}{2}{J}_{\mathrm{w}}{R}^2{\dot{\theta }}_{\mathrm{t}}^2+\frac{k}{2}{\overline{J}}_{\mathrm{m}}{\dot{\theta }}_{\mathrm{g}}^2\right),$$

(2)

$$E_{\mathrm{p}}=\frac{1}{2}{K}_{\mathrm{s}}{({\theta }_{\mathrm{d}}-{\theta }_{\mathrm{b}})}^2+n\left(\frac{1}{2}{K}_{\mathrm{b}}{({\theta }_{\mathrm{b}}-{\theta }_{\mathrm{t}})}^2+\frac{k}{2}{K}_{\mathrm{m}}{(R{\theta }_{\mathrm{t}}-{\theta }_{\mathrm{g}})}^2\right),$$

(3)

$$D_{\mathrm{b}}=\frac{1}{2}{B}_{\mathrm{s}}{({\dot{\theta }}_{\mathrm{d}}-{\dot{\theta }}_{\mathrm{b}})}^2+n\left(\frac{1}{2}{B}_{\mathrm{b}}{({\dot{\theta }}_{\mathrm{b}}-{\dot{\theta }}_{\mathrm{t}})}^2+\frac{k}{2}{B}_{\mathrm{m}}{(R{\dot{\theta }}_{\mathrm{t}}-{\dot{\theta }}_{\mathrm{g}})}^2\right),$$

(4)

Choosing the antenna’s four displacement outputs as the generalized coordinate vector $q={\left[\begin{array}{cccc}{\theta }_{\mathrm{d}}\hfill & {\theta }_{\mathrm{b}}\hfill & {\theta }_{\mathrm{t}}\hfill & {\theta }_{\mathrm{g}}\hfill \end{array}\right]}^T$, the antenna system satisfies Newton’s second law and the Euler–Lagrange equation as follows.

$$M\ddot{q}+\mathbb{C}\dot{q}+Kq=F\left(u\right),$$

(5)

$$L=E_{\mathrm{k}}-E_{\mathrm{p}},$$

(6)

$$\frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{q}}_j}\right)-\frac{\partial L}{\partial q_j}+\frac{\partial D_{\mathrm{b}}}{\partial {\dot{q}}_j}=F_j\left(u\right),$$

(7)

where M, $\mathbb{C}$, K, F denote the system’s mass matrix, damping matrix, stiffness matrix, and the generalized input forces, respectively, and $j,j=1,2,3,4$, represents the number of the generalized coordinate components. Simplifying Equation (7), the following three equations can be obtained:

$$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}}\right)=\frac{d}{dt}\frac{\partial E_{\mathrm{k}}}{\partial \dot{q}}=\left[\begin{array}{cccc}{J}_{\mathrm{d}}& 0& 0& 0\\ 0& J_{\mathrm{b}}& 0& 0\\ 0& 0& n\left(J_{\mathrm{t}}+R^{2}k{J}_{\mathrm{w}}\right)& 0\\ 0& 0& 0& nk{\overline{J}}_{\mathrm{m}}\end{array}\right]\left[\begin{array}{c}{\theta }_{\mathrm{d}}\hfill \\ {\theta }_{\mathrm{b}}\hfill \\ {\theta }_{\mathrm{t}}\hfill \\ {\theta }_{\mathrm{g}}\hfill \end{array}\right]=M\dot{q},$$

(8)

$$\frac{\partial L}{\partial q}=-\frac{\partial E_{\mathrm{p}}}{\partial q}=\left[\begin{array}{cccc}{K}_{\mathrm{s}}& -K_{\mathrm{s}}& 0& 0\\ -K_{\mathrm{s}}& (K_{\mathrm{s}}+n{K}_{\mathrm{b}})& -n{K}_{\mathrm{b}}& 0\\ 0& -n{K}_{\mathrm{b}}& n\left(K_{\mathrm{b}}+R^{2}k{K}_{\mathrm{m}}\right)& -nkRk{K}_{\mathrm{m}}\\ 0& 0& -nRk{K}_{\mathrm{m}}& nk{K}_{\mathrm{m}}\end{array}\right]\left[\begin{array}{c}{\theta }_{\mathrm{d}}\\ {\theta }_{\mathrm{b}}\\ {\theta }_{\mathrm{t}}\\ {\theta }_{\mathrm{g}}\end{array}\right]=Kq,$$

(9)

$$\frac{\partial D_{\mathrm{b}}}{\partial \dot{q}}=\left[\begin{array}{cccc}{B}_{\mathrm{s}}& -B_{\mathrm{s}}& 0& 0\\ -B_{\mathrm{s}}& B_{\mathrm{s}}+n{B}_{\mathrm{b}}& -n{B}_{\mathrm{b}}& 0\\ 0& -n{B}_{\mathrm{b}}& n\left(B_{\mathrm{b}}+R^{2}k{B}_{\mathrm{m}}\right)& -nkR{B}_{\mathrm{m}}\\ 0& 0& -nkR{B}_{\mathrm{m}}& nk{B}_{\mathrm{m}}\end{array}\right]\left[\begin{array}{c}{\dot{\theta }}_{\mathrm{d}}\hfill \\ {\dot{\theta }}_{\mathrm{b}}\hfill \\ {\dot{\theta }}_{\mathrm{t}}\hfill \\ {\dot{\theta }}_{\mathrm{g}}\hfill \end{array}\right]=\mathbb{C}\dot{q},$$

(10)

The input vector of the system is

$$F\left(u\right)=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ nk\end{array}\right]T_m=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ nk{K}_{\mathrm{t}}\end{array}\right]i=\Re u,$$

(11)

where $T_{\mathrm{m}}$ is the motor’s output torque, $K_{\mathrm{t}}$ is the torque constant, ℜ is the input matrix, and i is the input current. The system’s dynamic equation can be as shown in Equation (12) by rectifying.

$$\ddot{q}=-M^{-1}\mathbb{C}-M^{-1}Kq+M^{-1}\Re u,$$

(12)

Choosing $x={\left[\begin{array}{cc}\dot{q}\hfill & q\hfill \end{array}\right]}^T$ as the system states and letting C be the output matrix, and $y=Cx$ be the system outputs, then the state equation of the antenna servo system can be denoted as follows:

$$\begin{array}{ccc}\hfill \dot{x}& =& \left[\begin{array}{cc}-M^{-1}\mathcal{C}& -M^{-1}K\\ I& 0\end{array}\right]x+\left[\begin{array}{c}{M}^{-1}\Re \\ 0\end{array}\right]u,\hfill \\ & =& Ax+Bu\hfill \\ \hfill y& =& Cx\hfill \end{array}$$

(13)

The azimuthal system’s system matrix A and the input matrix B of the radio telescope are shown in Equation (14).

$$\begin{array}{c}\hfill A=\left[\begin{array}{cccccccc}-\frac{B_{\mathrm{s}}}{J_{\mathrm{d}}}& \frac{B_{\mathrm{s}}}{J_{\mathrm{d}}}& 0& 0& -\frac{K_{\mathrm{s}}}{J_{\mathrm{d}}}& \frac{K_{\mathrm{s}}}{J_{\mathrm{d}}}& 0& 0\\ \frac{B_{\mathrm{s}}}{J_{\mathrm{b}}}& -\frac{(B_{\mathrm{s}}+n{B}_{\mathrm{b}})}{J_{\mathrm{b}}}& \frac{n{B}_{\mathrm{b}}}{J_{\mathrm{b}}}& 0& \frac{K_{\mathrm{s}}}{J_{\mathrm{b}}}& -\frac{(K_{\mathrm{s}}+n{K}_{\mathrm{b}})}{J_{\mathrm{b}}}& \frac{n{K}_{\mathrm{b}}}{J_{\mathrm{b}}}& 0\\ 0& \frac{B_{\mathrm{b}}}{\overline{J}}& -\frac{(R^{2}k{B}_{\mathrm{m}}+B_{\mathrm{b}})}{\overline{J}}& \frac{Rk{B}_{\mathrm{m}}}{\overline{J}}& 0& \frac{K_{\mathrm{b}}}{\overline{J}}& -\frac{(R^{2}k{K}_{\mathrm{m}}+K_{\mathrm{b}})}{\overline{J}}& \frac{Rk{K}_{\mathrm{m}}}{\overline{J}}\\ 0& 0& \frac{R{B}_{\mathrm{m}}}{{\overline{J}}_{\mathrm{m}}}& -\frac{B_{\mathrm{m}}}{{\overline{J}}_{\mathrm{m}}}& 0& 0& \frac{R{K}_{\mathrm{m}}}{{\overline{J}}_{\mathrm{m}}}& -\frac{K_{\mathrm{m}}}{{\overline{J}}_{\mathrm{m}}}\\ 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0\end{array}\right],\\ \hfill B={\left[\begin{array}{cccccccc}0& 0& 0& \frac{K_{\mathrm{t}}}{{\overline{J}}_{\mathrm{m}}}& 0& 0& 0& 0\end{array}\right]}^T,\end{array}$$

(14)

where $\overline{J}=J_{\mathrm{t}}+k{R}^2{J}_{\mathrm{w}}$.

Equation (13) shows that the simplified antenna azimuthal model in Figure 1 is an eighth-order system. When the number k of motors in each driving arm is one, the model shown in Equation (14) becomes the single-motor-driven model, as shown in [19]. The Bode diagram of this model with relevant parameters is similar to that of the actual model of the GBT [26] in non-high-frequency bands, indicating its validity. So, the model can be used for controller design and performance analysis.

3. Re-Optimized Design of the Dual-Loop Controller

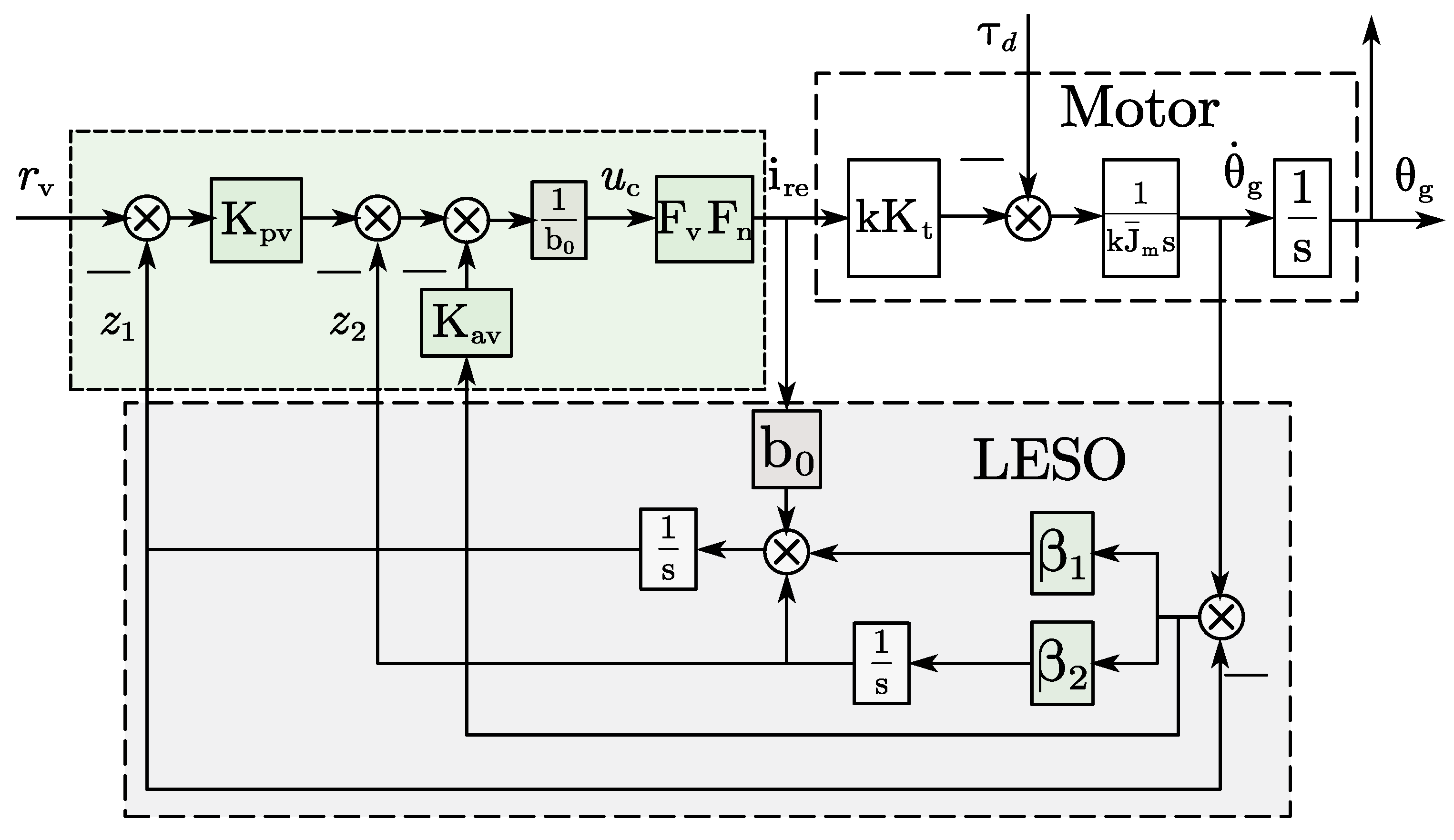
The controller design of a servo system is usually carried out under the context of the triple-loop control structure: current-, velocity-, and position-loops. Figure 2 shows the block diagram of the 4DOF antenna servo system, which is driven by multiple DC motors (denoted as $nk$) in the context of a triple-loop control structure. Where G_p, G_v, and G_c denote the position-, the velocity-, and the current-loop controller, respectively. The current-loop controller related to the motor driving performance generally does not need a special design; in addition, the magnitude of the closed current-loop transfer function is unity within the velocity-loop bandwidth since the bandwidth of the current-loop is much higher than that of the velocity- and position-loops. So, the antenna servo controller design mainly focuses on the velocity- and the position-loop controllers. The position feedback point depends on the actual need and is usually chosen at the base. Figure 2 also presents the wind loads (in terms of torque ${\tau }_{\mathrm{wind}}$) acting on the antenna dish.

We have designed an active disturbance rejection-based dual-loop controller on this 4DOF model [27]. To further improve the performance of the servo control system of the large radio telescope, and thus, the pointing accuracy, we have re-optimized the designed controllers, i.e., the velocity controller re-optimization and position controller simplification.

3.1. Velocity Controller Re-Optimization

From Figure 2, it can be easily seen that the load torque ${\tau }_{\mathrm{d}}$ is an external disturbance for the motor’s speed control system. The load torque ${\tau }_{\mathrm{d}}$ can be represented as

$${\tau }_{\mathrm{d}}=k(K_{\mathrm{t}}{r}_i-{\overline{J}}_{\mathrm{m}}{\ddot{\theta }}_{\mathrm{g}}),$$

(15)

where ${\ddot{\theta }}_{\mathrm{g}}$ is the motor angular acceleration.

If the disturbance can be compensated, the motor speed control performance can be improved, which is the basis of designing an active disturbance suppression-based controller.

Active disturbance rejection control (ADRC) [28,29] is a valuable engineering application approach in the disturbance/uncertainty estimation and attenuation (DUEA) methods. The method has now been developed as linear ADRC (LADRC) [30] and other derivatives. Since only one integrator exists in the closed-current-loop motor’s speed control system, we have used a first-order LADRC. The equation of the linear extended state observer (LESO) of the first-order LADRC algorithm that we employed to observe and compensate for the load torque disturbance ${\tau }_{\mathrm{d}}$ is

$$\left[\begin{array}{c}{\dot{z}}_1\\ {\dot{z}}_2\end{array}\right]=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]\left[\begin{array}{c}{z}_1\\ z_2\end{array}\right]+\left[\begin{array}{c}{b}_0\\ 0\end{array}\right]u+\left[\begin{array}{c}{\beta }_1\\ {\beta }_2\end{array}\right]({\dot{\theta }}_{\mathrm{g}}-z_1),$$

(16)

where $b_0$ is the estimated forward gain of the motor from the input voltage to the output velocity, u is the controller output, $z_1$ and $z_2$ are the velocity and disturbance observed by the LESO, ${\left[\begin{array}{cc}{\beta }_1\hfill & {\beta }_2\hfill \end{array}\right]}^T$ is the observation vector of the LESO to be designed. The equation for the first-order LADRC’s typical output is shown below.

$$u_{c1}=\frac{K_{\mathrm{pv}}(r_{\mathrm{v}}-z_1)-z_2}{b_0},$$

(17)

where $K_{\mathrm{pv}}$ is the controller gain.

Theoretically, the disturbance can be suppressed entirely. In practice, the disturbance ${\tau }_{\mathrm{d}}$ cannot be directly measured but observed/identified with the help of an observer. It is well known that the estimated disturbance lags relative to the real one. Thus, only compensating for the disturbance has a limited effect, and the impact of the load disturbance is still significant on the motor’s velocity.

It can be seen from Equation (16) that the error $({\dot{\theta }}_{\mathrm{g}}-z_1)$ used to calculate the disturbance is approximately equal to the disturbance velocity. The anti-disturbance performance of the system is further enhanced if it compensates for both the observed disturbance and its velocity. Therefore, it can be considered to add a disturbance-velocity compensation term with a factor of $K_{\mathrm{av}}$ to the conventional first-order LADRC control equation, and then, the new controller equation is

$$u_c=\frac{K_{\mathrm{pv}}(r_{\mathrm{v}}-z_1)-z_2-K_{\mathrm{av}}({\dot{\theta }}_{\mathrm{g}}-z_1)}{b_0},$$

(18)

In addition to this, we also utilize a notch filter $F_{\mathrm{n}}$ to filter the fundamental mechanical resonance frequency of the antenna and a first-order low-pass filter $F_{\mathrm{v}}$ to limit the controller’s bandwidth. It is valuable to note that applying these two filters mainly attenuates the antenna resonances during the motor control rather than achieving better motor velocity control. The transfer functions of the low-pass filter $F_{\mathrm{v}}$ and notch filter $F_{\mathrm{n}}$ are shown in Equations (18) and (19), respectively.

$$F_{\mathrm{v}}=\frac{1}{s/{\omega }_{\mathrm{F}}+1},$$

(19)

$$F_{\mathrm{n}}=\frac{s^2+2{\xi }_1{\omega }_{\mathrm{n}1}s+{\omega }_{\mathrm{n}1}^2}{s^2+2{\xi }_2{\omega }_{\mathrm{n}1}s+{\omega }_{\mathrm{n}1}^2},$$

(20)

where ${\omega }_F$ is the filter cutoff frequency, ${\omega }_{\mathrm{n}1}$ is the resonant frequency to be filtered, and the value $20lg({\xi }_1/{\xi }_2)$ is the notch depth. The final block diagram of the antenna’s velocity-loop control is shown in Figure 3.

Combining Equations (16) and (18), then the LADRC can be rewritten as a combination of a feedback controller $G\left(s\right)$ and feedforward controller $H\left(s\right)$, as shown in the following equations:

$$G\left(s\right)=\frac{1}{b_0}\frac{K_{av}{s}^2+(K_{pv}{\beta }_1+{\beta }_2)s+K_{pv}{\beta }_2}{s[s+(K_{pv}+{\beta }_1-K_{av})]},$$

(21)

$$H\left(s\right)=K_{pv}\frac{s^2+{\beta }_{1}s+{\beta }_2}{K_{av}{s}^2+(K_{pv}{\beta }_1+{\beta }_2)s+K_{pv}{\beta }_2},$$

(22)

Equation (21) shows that the equivalent feedback controller $G\left(s\right)$ is a PID control cascading a low-pass filter (PID-F), and Equation (22) shows that the equivalent feedforward controller $H\left(s\right)$ is a notch filter. Equation (21) explains the reason for adding disturbance velocity compensation to improve the system’s anti-disturbance performance from the PID point of view, i.e., both reducing the low-pass filter cutoff frequency (bandwidth) and introducing the derivative term in the original PI. The $H\left(s\right)$ can also be rewritten as a combination of a unit-magnitude feedforward controller and a bypass lead–lag compensator on the equivalent closed-loop feedback controller output. The transfer function of this lead–lag compensator $F_{\mathrm{r}}$ is

$$F_{\mathrm{r}}=\frac{(K_{pv}-K_{\mathrm{av}})s-{\beta }_2}{s+(K_{pv}+{\beta }_2-K_{\mathrm{av}})},$$

(23)

Equation (23) shows that the equivalent bypass feedforward controller is similar to command-speed compensation. Thus, it can be seen through Equations (21)–(23) that the first-order LADRC can be comparable to a combination of conventional PID-F with command-speed feedforward compensation. It is worth noting that despite this equivalence, the first-order LADRC explains the combination from an anti-disturbance point of view and gives a complete set rather than dispersive parameter-tuning methods.

3.2. Position Controller Simplification

The amplitude of the closed-velocity-loop transfer function is approximated as unity within the position-loop bandwidth; therefore, a single integrator exists in the whole position system. A proportional controller for the single-integrator system is sufficient for step tracking without static error. The typical trajectory of a radio telescope for astronomical observation is a ramp, which means that utilizing a position-loop proportional controller will create a static tracking error. Therefore, a PID controller is used for non-static-error tracking for non-step signals and enhancing the response rapidity. However, for the adverse effect of the measurement noise and integrator saturation, the coefficients of the integral and the derivative terms in the PID are smaller than the proportional term coefficient, making the PID control manifest primarily proportional control; some radio telescopes even employ a pure proportional control in their position-loop system. Some radio telescope position-loops, such as GBT, utilize a lead–lag compensator. The nature of the lead–lag compensator is a PD cascading a first-order low-pass filter, and it also cannot achieve static-error-free tracking for non-step signals.

In fact, a radio telescope does not need to achieve static-error-free tracking for a position signal; instead, it is sufficient to achieve command-tracking with a certain static error. Correction by a pointing model can eliminate the negative effect of the position tracking error. Therefore, a proportional controller in the position-loop is sufficient for a radio telescope.

Finally, the block diagram of the re-optimized dual-loop control structure used for the 100 m class antenna is shown in Figure 4, which consists of a position proportional (P) controller and a velocity-controller-based LADRC with disturbance derivative (DLADRC).

4. Simulation Results and Analysis

We apply the set of parameters of a 100 m class radio telescope in [19] to the established multiple-motor-driven 4DOF model shown in Equation (14) to verify the performance of the re-optimized dual-loop controller, where we set the number of the motors in the driving arm to one. The quantitative feedback theory (QFT)-based robust PID (RPID) controller in [19] is used for comparison.

Inspired by the bandwidth parameterization tuning approach of LADRC [30], we also tuned LADRC here via the system’s frequency, based on the fundamental resonance frequency but not the closed-loop bandwidth frequency. The system’s feedforward gain $b_0$ and the fundamental resonant frequency ${\omega }_{n1}$ are the first factors to determine. We obtain $b_0$ by an open-loop test, and thus, it includes the information of the antenna load. The 100 m class antenna’s fundamental resonance frequency is 4.27 rad/s (0.68 Hz), and consequently, the central angular frequency of the notch filter can be chosen as 4 rad/s; the low-pass filter’s cutoff frequency is usually chosen to be two times bigger than ${\omega }_{n1}$ and is five times it here (during tuning an interesting phenomenon is found that a cutoff frequency not less than 2${\omega }_{n1}$ is sufficient, indicating the robustness of the LADRC). The bandwidth of the first-order LESO is chosen to be five times ${\omega }_{n1}$. The prominent difference to the bandwidth parameterization approach is that the choice of the LESO’s gains is not according to pole assignment but to the open-loop test. The factor $K_{\mathrm{pv}}$ is chosen by an empirical formula of ${\omega }_{n1}/4$, while $K_{\mathrm{av}}$ is tuned by trial and error.

The well-tuned parameters of the velocity-loop DLADRC controller and the filters are shown in Equations (24) and (4), respectively.

$$\begin{array}{ccc}\hfill b_0& =& 5.6\times {10}^{-5},{\omega }_{n1}=4,{\omega }_o=k{\omega }_{\mathrm{n}1}=20\hfill \\ \hfill {\beta }_1& =& k_1{\omega }_o=8\times 20,{\beta }_2=k_2{\omega }_o^2=2\times {20}^2,K_{\mathrm{pv}}=0.8,K_{\mathrm{av}}=200,\hfill \end{array}$$

(24)

$$F_{\mathrm{n}}=\frac{s^2+2\times 0.1\times 4s+4^2}{s^2+2\times 1\times 4s+4^2},F_{\mathrm{v}}=\frac{1}{s/20+1},$$

(25)

The robust PID controller in the velocity-loop is as below.

$$G_{\mathrm{v}}\left(s\right)=\frac{1900(s/0.2+1)}{s(s/5+1)}·\frac{s^2+0.8s+16}{s^2+8s+16},$$

(26)

Wind loads are the most significant environmental disturbances for an antenna’s pointing. The velocity $v_{\mathrm{wind}}$ of the wind loads can be expressed as the sum of the steady-state (average) velocity V and the transient gust velocity $\mathsf{\Delta }v$, i.e., $v_{\mathrm{wind}}=(V+\mathsf{\Delta }v)$. The wind loads impact the antenna’s primary reflector (dish) and the feed arms in terms of disturbance torque, causing a static displacement and dynamic effects, consequently deteriorating the antenna’s pointing accuracy. The wind-induced torque ${\tau }_{\mathrm{wind}}$ is related to the square of the wind speed $v_{\mathrm{wind}}^2$ , air density ${\rho }_{\mathrm{air}}$, antenna aperture D, as well as relative angle ${\mathsf{\Delta }}_{\theta }$. Assume that the 100 m aperture antenna suffers from oncoming wind with an average speed $V=$ 6 m/s and turbulivity (it can be used for calculating a gust velocity) of 0.15 from the time of 35 s. The wind-induced torque can be written in the following form:

$${\tau }_{\mathrm{wind}}=\frac{1}{2}{\rho }_{\mathrm{air}}{C}_{\mathrm{T}}{(V+\mathsf{\Delta }v)}^2·\frac{\pi D^2}{8}\frac{1}{3}D,$$

(27)

where the air density is ${\rho }_{\mathrm{air}}=1.225$ ${\mathrm{kg}/\mathrm{m}}^3$, and the aerodynamic thrust coefficient is $C_{\mathrm{T}}=0.1$.

4.1. Single-Velocity-Loop Performance Analysis

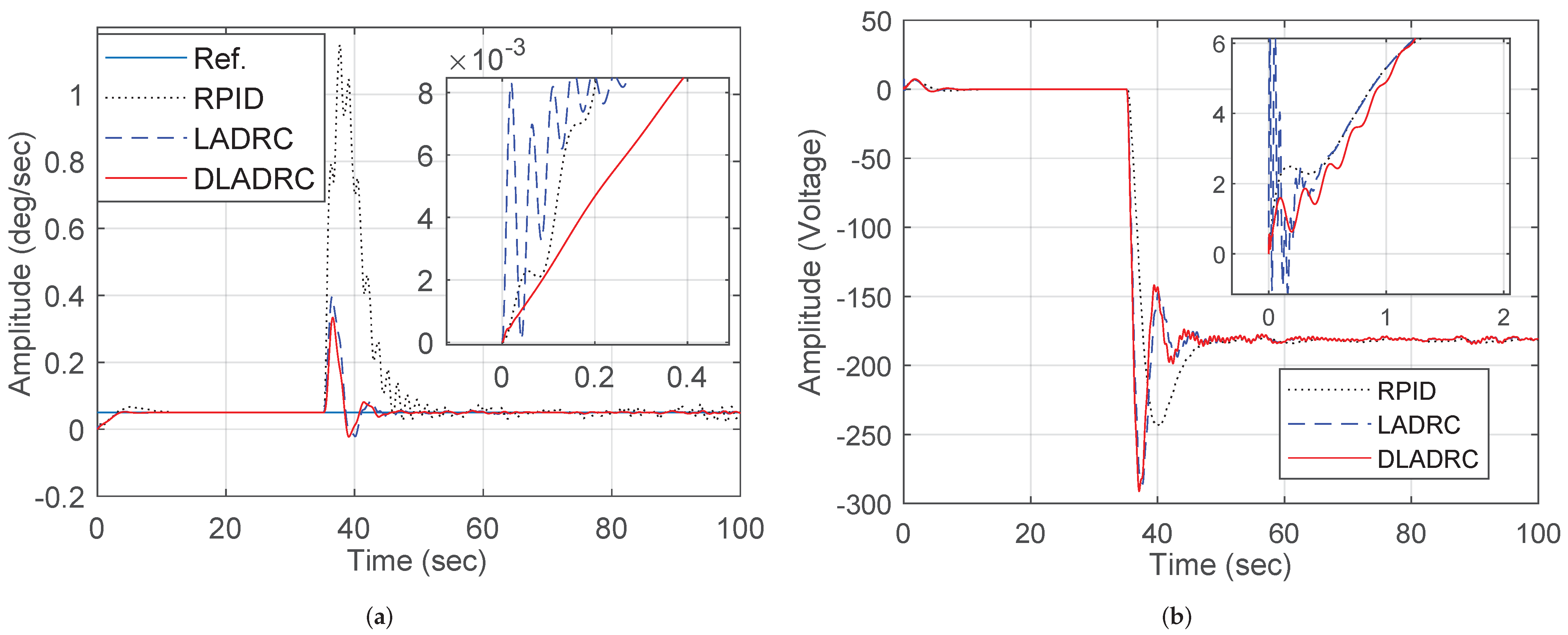
In the open-position-loop case, the motor’s velocity and input voltage responses of the system are shown in Figure 5. The mean, maximum, median, and root mean square values of the tracking errors due to disturbances and response times are shown in

Table 1. Tracking errors (in deg/s) and response times (in s) of motor speed responses with three control methods in wind disturbances.

	RPID	LADRC	DLADRC
Mean error	0.0710	0.0076	0.0052
Max. error	1.0987	0.3457	0.2836
Median error	0.0002	0.0000	0.0000
RMS error	0.2255	0.0480	0.0362
Response time	20	8.8	8.8

.

It is clear from Figure 5a that both LADRC and DLADRC achieve fast and overshoot-free tracking responses to the speed command relative to RPID. When the system is subjected to external wind disturbances, LADRC and DLADRC can also quickly achieve anti-disturbance; the maximum response amplitudes to the disturbance are reduced by 3.18 times and 3.87 times compared with RPID, and their disturbance response times are reduced by 1 time compared to RPID; in addition, the disturbance response is smoother than that of RPID. Compared with LADRC, DLADRC has smoother initial velocity responses curves, a 20% reduction in the peak disturbance response amplitude, and smoother steady-state responses, indicating the effectiveness and superiority of the re-optimized method. The relatively smoother input voltage responses of the motor controlled by DLADRC in Figure 5b show that it is easier for it to obtain excellent control performance than the traditional LADRC.

4.2. Position-Loop Controller Simplification Analysis

In the closed-velocity DLADRC controller case, we analyze the position response performance of the system with the proportional (P) controller and the lead–lag compensator (denoted PD), respectively.

Figure 6a presents the position response curves of the system under the P controller of $K_{\mathrm{p}}$ = 16 and the PD of $G=16\frac{0.05s+1}{1/10s+1}$, respectively. It can be seen that there is not much difference in the system’s response curves under these two controllers, except that the PD-controlled system arrives at the steady-state response slightly faster. When the coefficient $K_{\mathrm{d}}$ of the derivative term in the lead–lag compensator is increased to 0.55, the response curve is shown in Figure 6b. The response performance of the lead–lag compensator at this time is not as good as that of the P controller. Figure 6c presents the motor’s input voltages at $K_{\mathrm{d}}$ = 0.55. Though the motor’s input voltages of the PD are convergent, they fluctuate more than those of P-DLADRC, which is terrible for the achievement of high-performance control.

Table 2. Error statistics (in deg) of position responses under two position controllers in $K_{\mathrm{p}}=16$ and $K_{\mathrm{d}}=0.55$.

	Mean	Max.	Median	RMS
PD-DLADRC	−0.0005	0.0161	0.0010	0.0086
P-DLADRC	−0.0005	0.0169	0.0010	0.0087

lists four kinds of statistical values for the overall response errors of the two methods; it can be seen that the difference between the correspondence errors is very tiny. Therefore, we can conclude that a pure proportional controller in the position-loop is sufficient under the same speed controller.

4.3. Position Switching Performance Analysis

Astronomical observations require radio telescopes to be able to switch quickly between target sources and calibration sources to reduce their overhead time for gain/phase calibration. The fast switching performance corresponds to the step response in servo control. Typical switching angles for radio telescopes are related to their sensitivity, and the typical switching angles for 100 m class radio telescopes such as the GBT do not exceed 2 deg. The switching angle can be used to test the performance of the telescope servo system. Due to an actual telescope system’s speed and acceleration saturation limitations, the step signal used for servo system performance testing is usually a small-angle signal; a 0.05 deg test signal was used for the 100 m class antenna in this paper, after careful consideration.

The feedback and feedforward controllers of the RPID-controlled system’s position-loop are

$$G_{\mathrm{p}1}\left(s\right)=\frac{800(s+0.6)}{s+25},G_{\mathrm{F}}\left(s\right)=0.485\frac{(s+0.3)}{{(s+0.38)}^2},$$

(28)

The position controller of the LADRC-controlled system is

$$G_{\mathrm{p}2}\left(s\right)=16\frac{0.05s+1}{(1/10s+1)},$$

(29)

The position response curves of the motor, the base, and the dish of the system are shown in Figure 7a. Figure 7b,c shows the motor speed and input voltage response curves of the system, respectively. The response curves of the system using LADRC and DLADRC are smoother than those of RPID in the double-closed-loop case, which indicates that these two methods are less likely to excite the structural resonance of the system compared with the RPID. When encountering external disturbances, they not only can quickly suppress disturbance but also have a lower peak response magnitude, giving the advantages of high control precision and saving power.

Table 3. Switching performance indicators and tracking errors for wind disturbances of V = 6 m/s and 3 m/s.

	RPID	LADRC	DLADRC
Overshoot (%)	0	2.4	4
Settling time (5%, in s)	11.9	5.12	5.26
Settling time (2%, in s)	17.5	8.4	10.8
Mean (V = 6 m/s)	0.0042	0.0007	0.0006
Max. (V = 6 m/s)	0.0385	0.0185	0.0153
Median (V = 6 m/s)	0.0006	0.0000	0.0000
RMS (V = 6 m/s)	0.0092	0.0032	0.0025
Response time	100	44	44
Mean (V = 3 m/s)	0.0013	0.0002	0.0001
Max. (V = 3 m/s)	0.0102	0.0047	0.0039
Median (V = 3 m/s)	0.0004	0.0000	0.0000
RMS (V = 3 m/s)	0.0025	0.0008	0.0006

gives the indicators measuring the system switching performance in terms of the overshoot (in %), settling time (in s), and the typical four kinds of wind-response errors under an average wind of V = 6 m/s and 3 m/s, respectively. The maximum disturbance response amplitudes of the base under the LADRC and DLADRC are reduced by 51.9% and 60.2% compaed to that of RPID, respectively, and the response times of the LADRC and DLADRC are reduced by about 50 s, indicating their better anti-disturbance performance. The maximum disturbance response amplitude of DLADRC is reduced by 17.3%, and the response time is slightly reduced compared to LADRC. The RMS pointing errors of the systems controlled by the RPID, LADRC, and DLADRC at the base are 0.0092 deg (33.12 arcsecs), 0.0032 deg (11.52 arcsecs), and 0.0025 deg (9 arcsecs) at a wind of 6 m/s, respectively, while they are 9 arcsecs, 2.88 arcsecs, and 2.1 arcsecs (0.0006 deg) at a wind of 3 m/s, indicating the DLADRC meets the design specification of 2.5 arcsec RMS. So, Figure 7 and Table 3 illustrate the advantages of DLADRC over LADRC and RPID.

The difference in response between the base and the dish in Figure 7a is due to the structure flexibility of the antenna. When the antenna system is in a steady state, there are stable response errors between the base and the dish, which are independent of the control method.

4.4. Ramp-Tracking Performance Analysis

The trajectory of a radio telescope for star tracking can be considered a ramp curve, and its typical velocity is 0.0042 deg/s. So, a ramp signal with a slope of 0.004 deg/s is employed as the test signal. When performing ramp tracking, the position controllers shown above result in tracking errors related to the ramp signal’s slope. An additional command-rate feedforward controller with a gain of 50 for LADRC and DLADRC, and a gain of 83.1 for RPID is used to eliminate the error.

Figure 8 illustrates the results of the system’s ramp response under the same wind disturbances, where Figure 8a,b show the results without and with command-rate feedforward, respectively. From Figure 8, it can be seen that the command-rate feedforward eliminates the static error during ramp tracking. The DLADRC-controlled system can quickly suppress the disturbance and track the ramp command. DLADRC can also achieve overshoot-free tracking with sharp steering in the command trajectory. The smooth response curves of the motor’s input voltage and velocity in Figure 9 indicate that the active anti-disturbance approaches succeed in the motor velocity control. Comparing the errors in

Table 4. Ramp-tracking errors (in deg) of the base under the three control methods in an average wind of V = 6 m/s.

	RPID	LADRC	DLADRC
Mean	0.0046	0.0007	0.0006
Max.	0.0384	0.0185	0.0153
Median	0.0018	0.0000	0.0000
RMS	0.0090	0.0032	0.0025

with Table 3, it is easy to see that the ramp-tracking errors of the system controlled by RPID, LADRC, and DLADRC under the same wind disturbance are almost the same as the pointing errors, indicating the wind effect on the system is constant and independent of the input signal.

The simulation and analysis of the above four aspects all show that good rate-loop control performance is the basis of high-precision servo control. Using an active anti-disturbance controller in the velocity-loop can improve the system’s response speed and reduce the peak magnitude and time of the system’s response to disturbance. LADRC with the disturbance-derivative compensation can perform better initial dynamic and anti-disturbance performance than the original LADRC. A simple position proportional controller rather than other controllers can also achieve good position-tracking performance in the context of the active disturbance suppression-based velocity controller.

4.5. Frequency-Domain Analysis

The Bode diagram of the antenna’s 4DOF model used for the controller algorithm test, shown in Figure 10, indicates obvious anti-resonance (at 0.25 Hz, 5 Hz) and multiple resonance points in the antenna 4DOF model, suggesting the antenna is a rigid–flexible coupled system. It is the flexible structure that increases the difficulty of high-precision control for the antenna. Figure 11 presents the frequency-domain responses of the motor, the base, and the dish of the system with RPID, LADRC, and DLADRC control in terms of the Bode diagram, respectively.

Comparing Figure 10 and Figure 11, smaller depth and narrower width at the anti-resonance frequency points, and little magnitudes at other resonance points of the DLADRC-controlled motor system can be seen. The structure resonance at about 1.5 Hz is suppressed by the DLADRC rather than RPID or LADRC. The three methods suppress the motor system’s first-order resonance frequency (0.68 Hz) due to a notch filter. The changes in phase curves in the DLADRC-controlled system are more monotonous than others, which also indicates DLADRC’s excellent control performance. These response characteristics indicate that DLADRC has better flexibility suppression performance than the other two algorithms.

Compared with RPID, the DLADRC enhances the bandwidth of the motor’s and the dish’s transfer function, thus reaching the desired position faster. Figure 11b presents the bandwidth of DLADRC as a little smaller than the LADRC, suggesting a slower response of DLADRC. The smaller magnitudes of the base and the dish in the middle frequencies of the DLADRC-controlled system make the response curves smoother than those of RPID and LADRC. Figure 11 also presents the DLADRC’s higher stability margin over the other two approaches, thus giving smoother response curves.

5. Conclusions

This paper established an antenna (azimuth) servo system’s multiple-motor-driven 4DOF model and re-optimized the design of an active disturbance rejection-based dual-loop controller used for a 100 m class aperture radio telescope. The re-optimized design mainly centers on enhancing the anti-disturbance performance of the velocity-loop LADRC by adding disturbance-derivative compensation (DLADRC) and simplifying the position-loop controller to a proportional controller. The optimal scheme has good dynamic performance and strong attenuation to external disturbances. The research also shows that a superior velocity-loop controller is essential for a high-precision antenna servo control system.

Future work will validate the proposed control strategy via experiments and further optimize it for higher-accuracy pointing of a radio telescope.