An Optimized 1-D CNN-LSTM Approach for Fault Diagnosis of Rolling Bearings Considering Epistemic Uncertainty
Abstract
1. Introduction
- A physics-guided method based on fault characteristic frequencies was developed to take sections (optimal sizes) from the original signals, containing information regarding all possible types of ball bearing faults;
- Grid search was utilized to optimize the training parameters to enhance the classification accuracy and reduce associated epistemic uncertainty;
- The proposed optimized 1-D CNN-LSTM methodology outscored other state-of-the-art algorithms while testing under different operational conditions with limited data for two benchmark datasets.
2. Materials and Methods
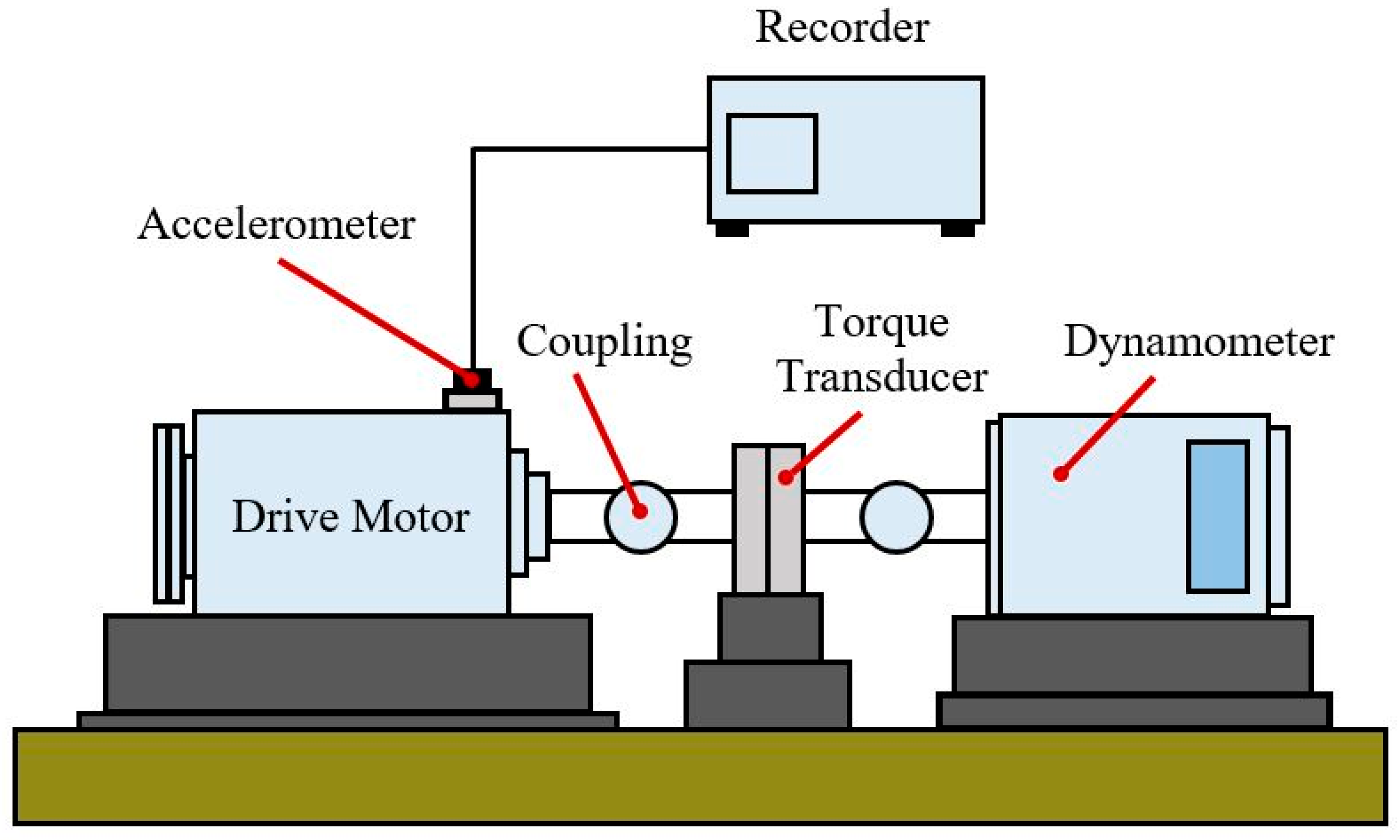
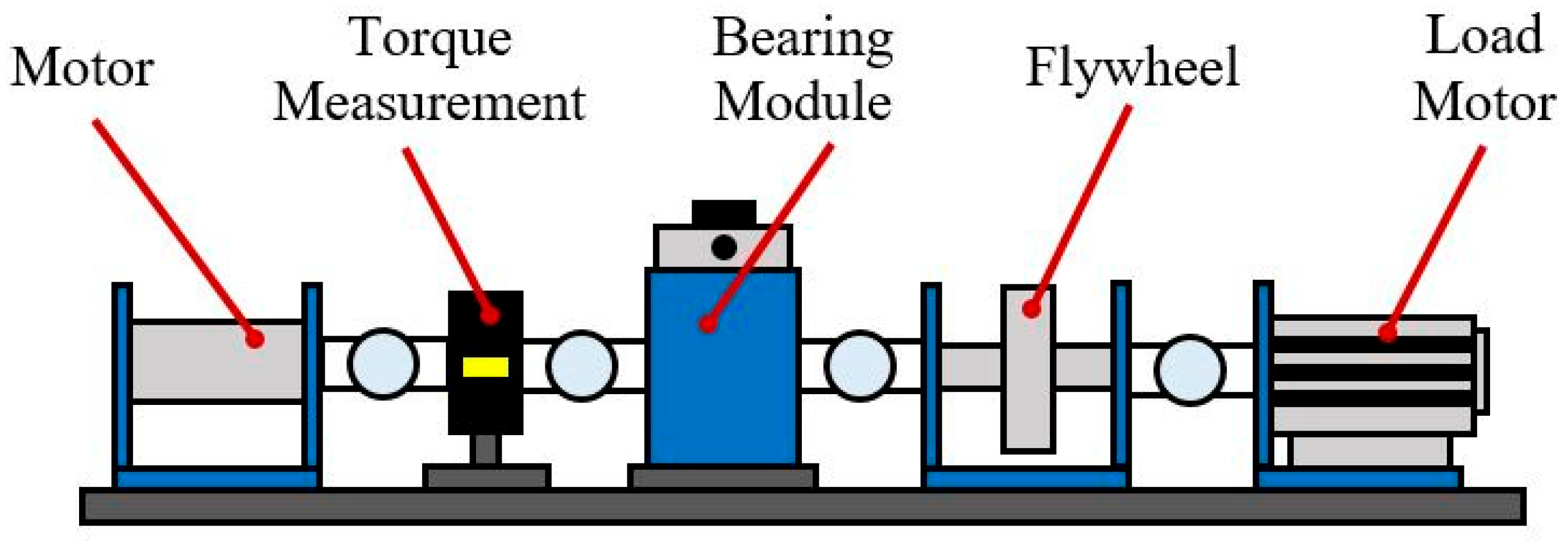
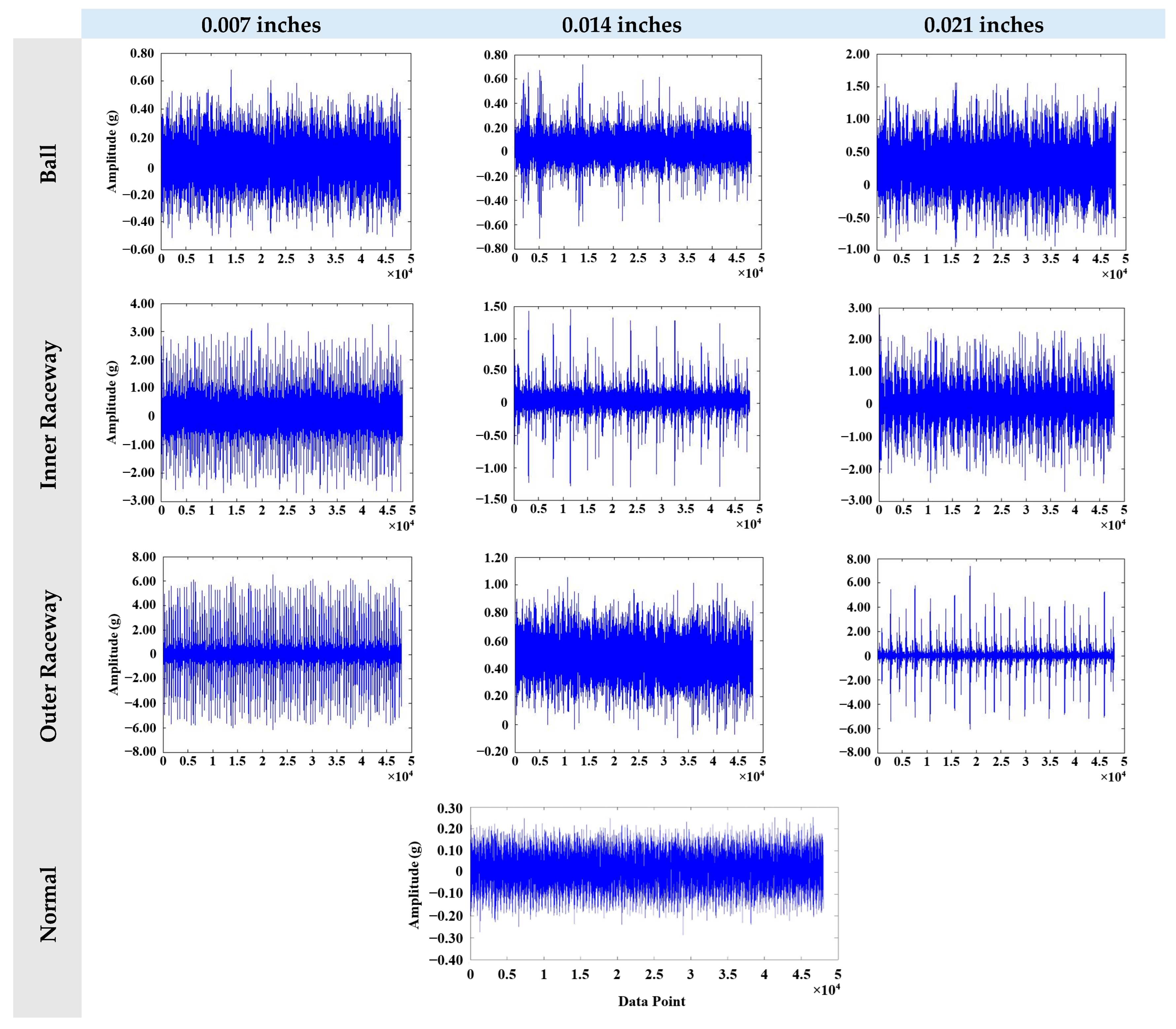
2.1. Preliminaries of Experimental Datasets
2.1.1. CWRU Dataset
2.1.2. PU Dataset
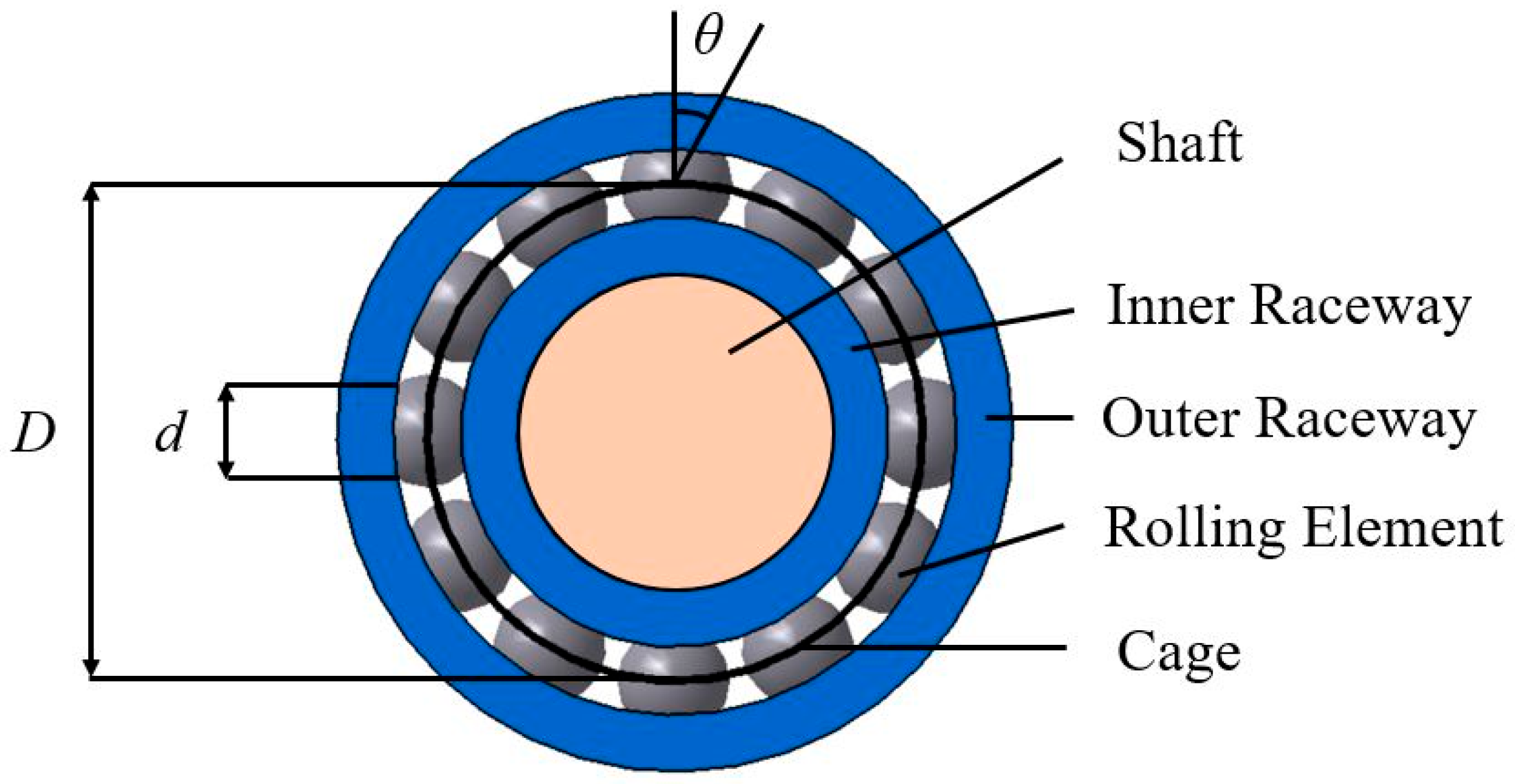
2.2. Physics-Guided Input Size Selection
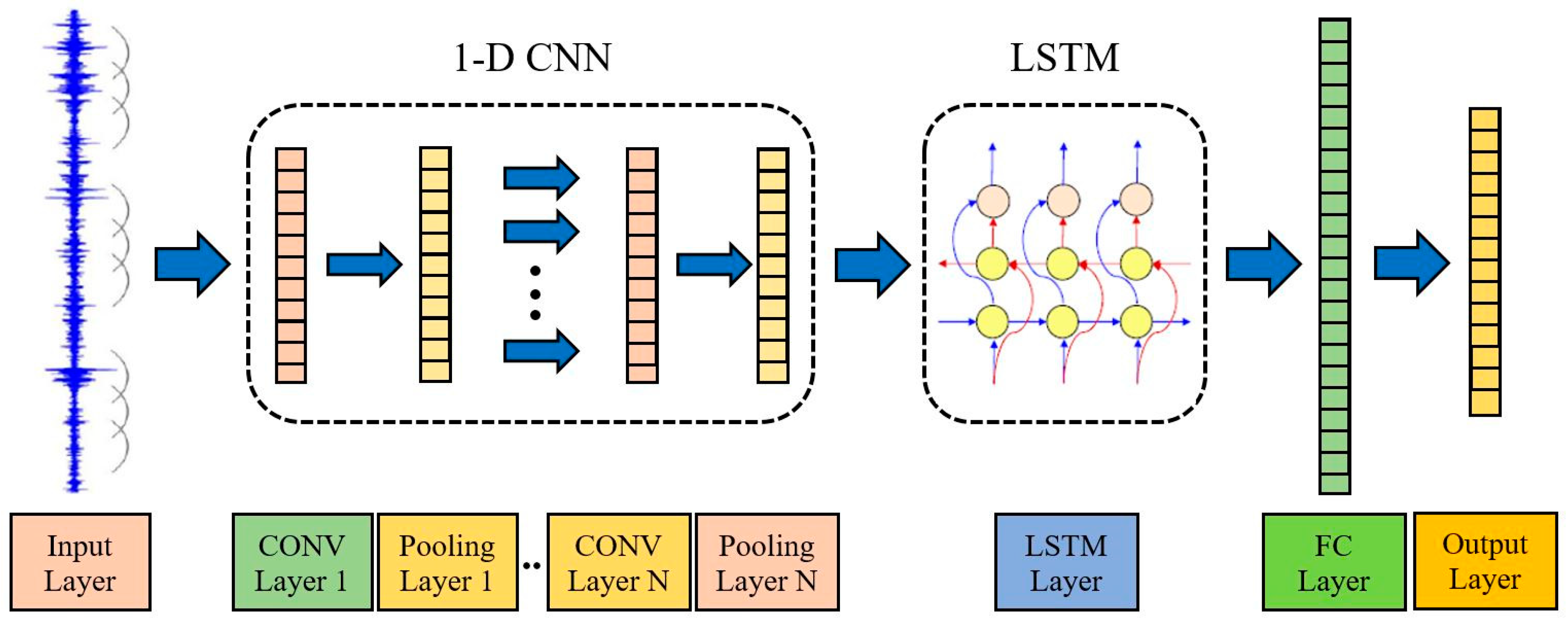
2.3. The Proposed Optimized 1-D CNN-LSTM Method
2.3.1. Convolutional Neural Networks
2.3.2. Long Short-Term Memory
2.3.3. Proposed Methodology
- Batch size: 32~256;
- Dropout rate: 0.3~0.6;
- Number of epochs: 10~50.
2.4. Uncertainty in Machine Learning
3. Results
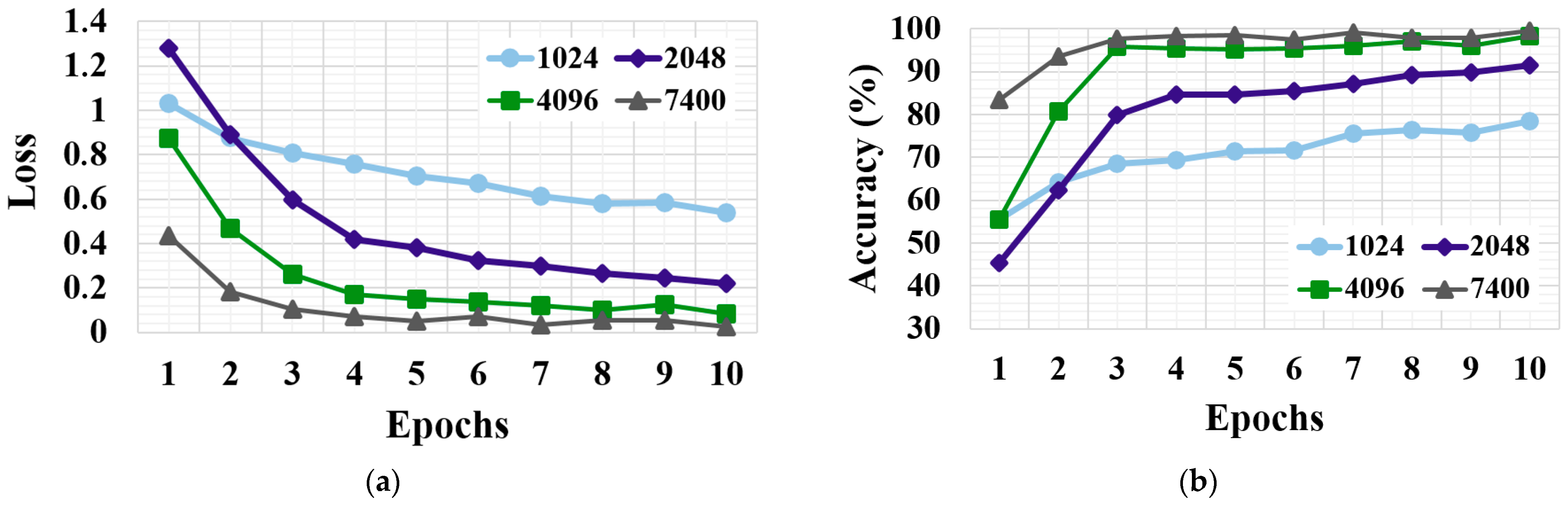
3.1. Input Length
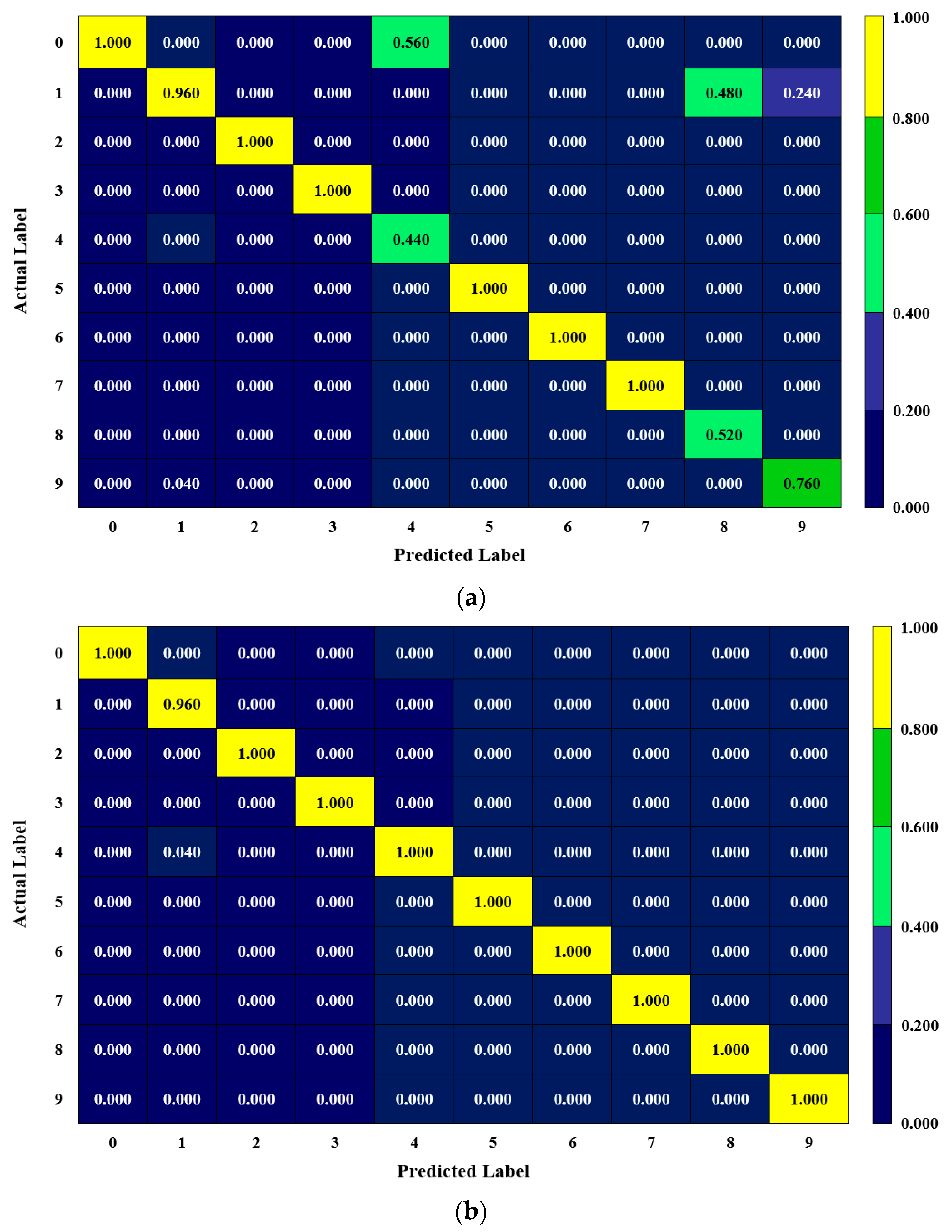
3.2. Evaluation of the Proposed Optimized 1-D CNN-LSTM Model
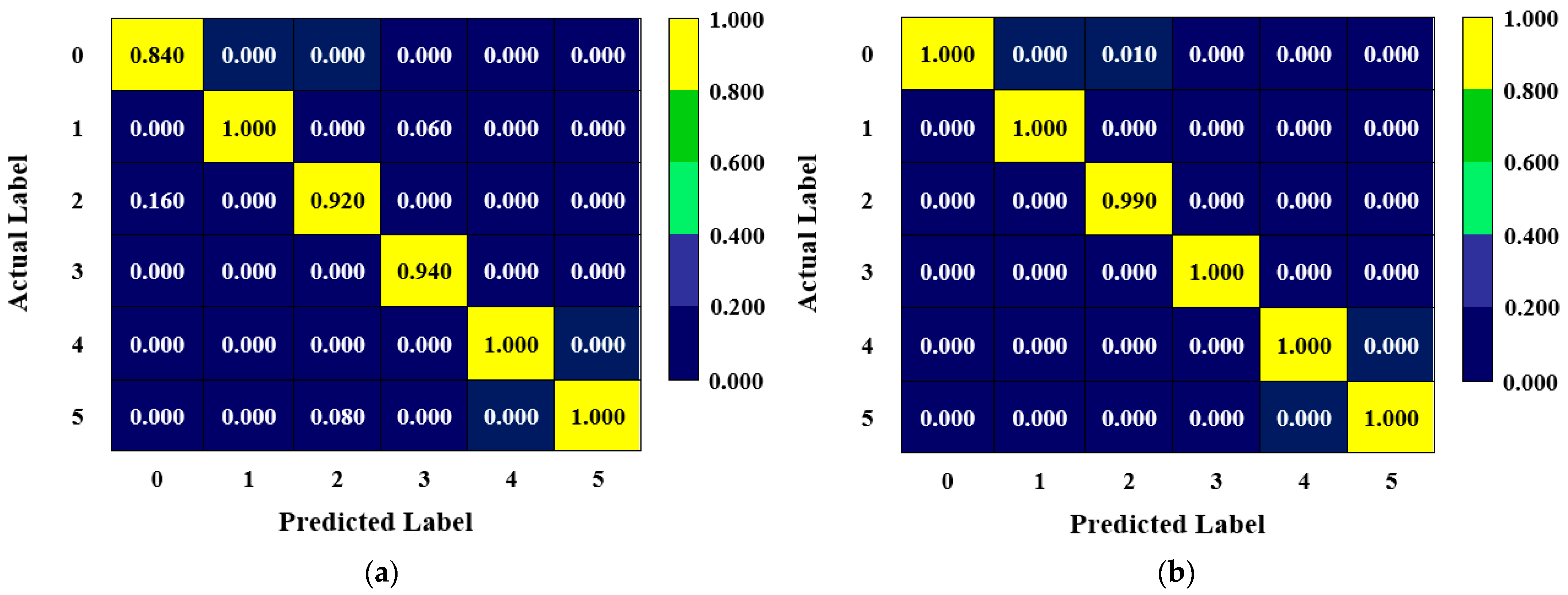
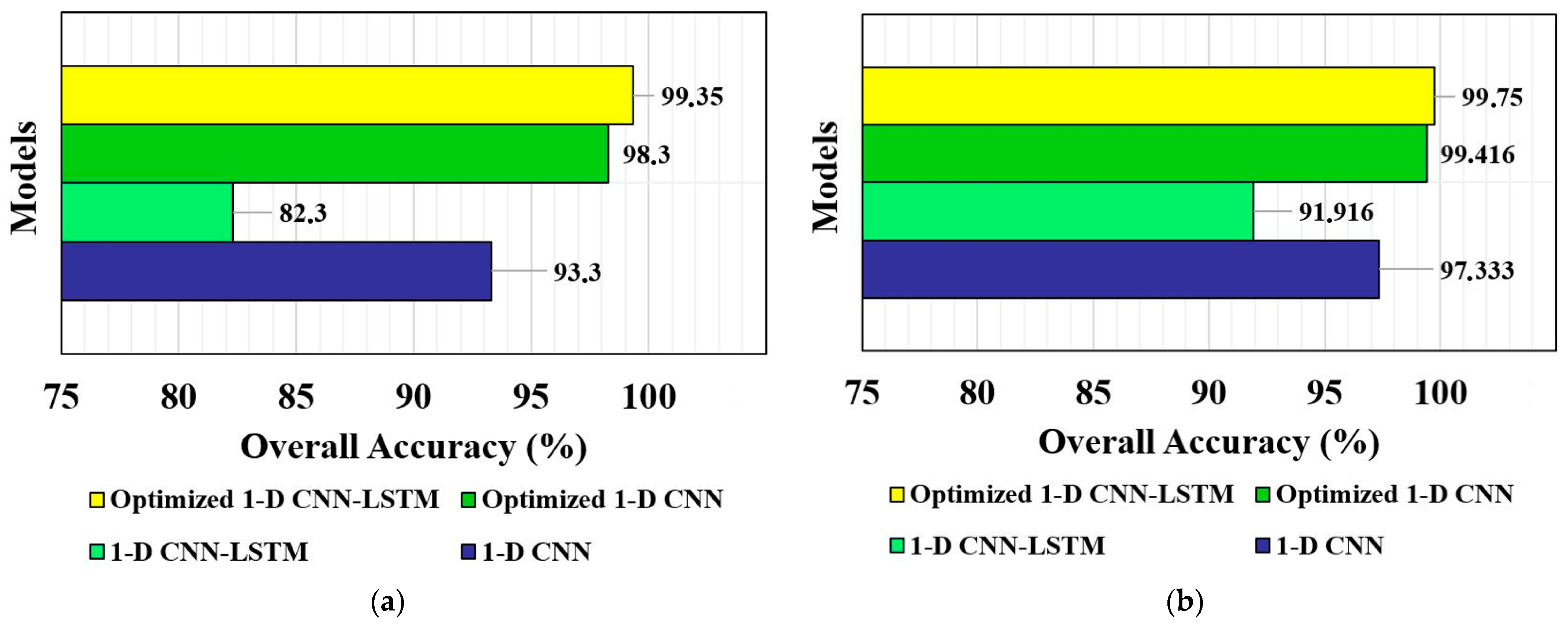
- If we compare the non-optimized cases, the 1-D CNN model outscored the 1-D CNN-LSTM regarding its overall accuracy for both datasets. The difference was 13.365% in favor of 1-D CNN for the CWRU dataset, while the difference was 5.893% for the PU dataset. Still, one should remember that these structures were run considering a baseline model [10; 110; 0.55], and, for the CWRU dataset, the 1-D CNN-LSTM algorithm needs more epochs to enhance (or maximize) its performance.
- Following the optimization, the average accuracy of the 1-D CNN algorithm was enhanced by around 5.359% and 2.140% for the CWRU and PU datasets, respectively. The increment in performance seems to be low for the PU dataset, as even the baseline algorithm performed relatively well for this dataset (>95%).
- A considerable performance increment was observed in favor of the 1-D CNN-LSTM model following the optimization process. The pertinent improvement was 20.717% and 8.523% for the CWRU and PU datasets, respectively.
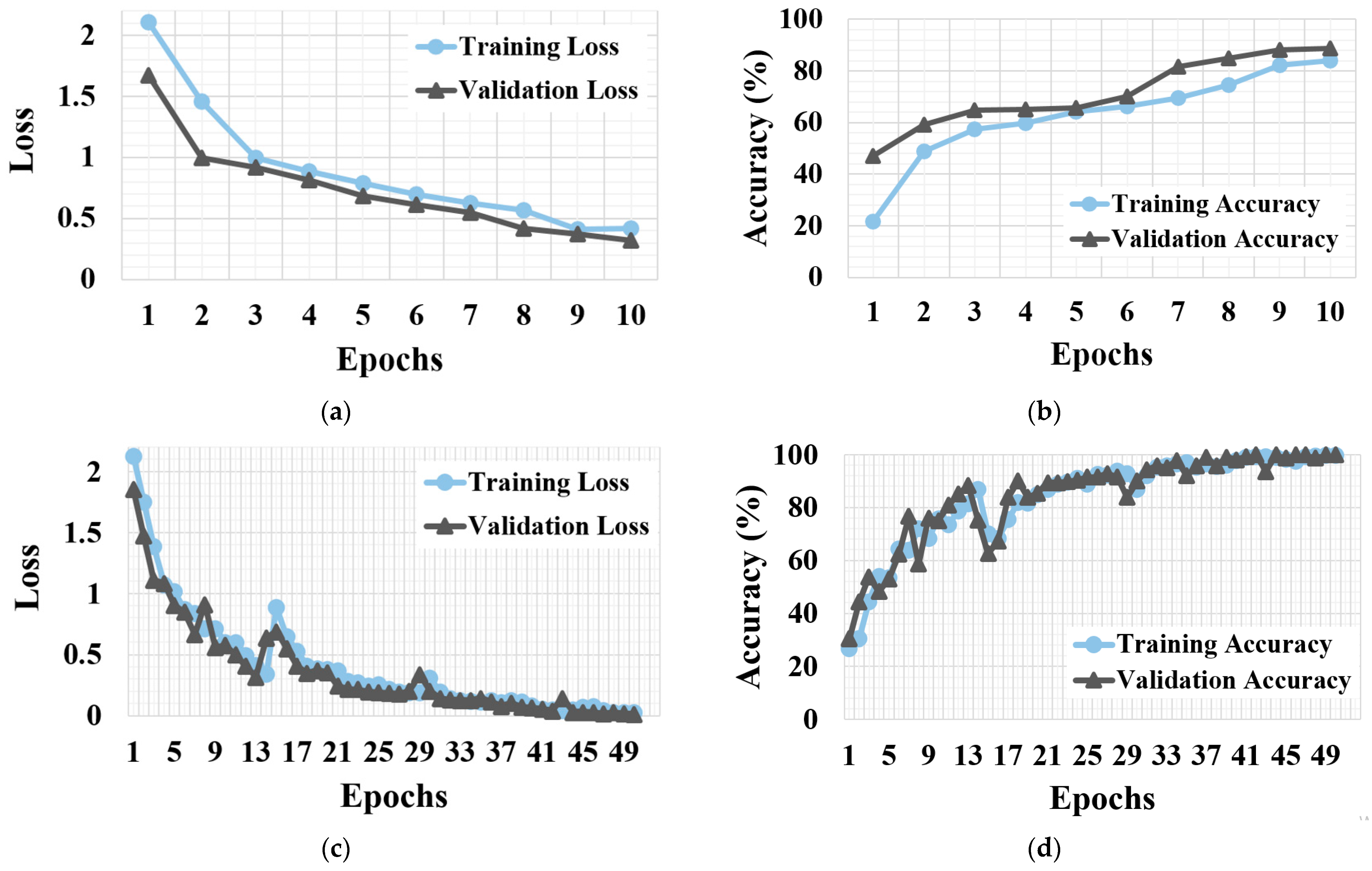
- Following the optimization, the models’ performance became notably stable and consistent. This enhancement can also be seen in minimal epistemic (model-related) uncertainties. The translation of the relevant improvement is that the models’ accuracy deviates each time the user runs the code, but the deviations happen within a narrow band. Therefore, incorporating optimization enhances the trustworthiness of the predictions [34,42]. Its impact was the most on 1-D CNN-LSTM for both datasets.
4. Discussion
5. Conclusions
- The results showed that the average accuracy of the physics-guided 1-D CNN-LSTM model was enhanced approximately by up to 20.717% and 8.523% for CWRU and PU datasets, respectively, following the optimization;
- Incorporating the optimization also made the model predictions more consistent and trustworthy by reducing (model-related) epistemic uncertainties.
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; He, Y.; Wang, H.; Hu, A.; Zhang, X. A novel hybrid approach for damage identification of wind turbine bearing under variable speed condition. Mech. Mach. Theory 2022, 169, 104629. [Google Scholar] [CrossRef]
- Xue, F.; Zhang, W.; Xue, F.; Li, D.; Xie, S.; Fleischer, J. A novel intelligent fault diagnosis method of rolling bearing based on two-stream feature fusion convolutional neural network. Meas. J. Int. Meas. Confed. 2021, 176, 109226. [Google Scholar] [CrossRef]
- Sun, H.; Cao, X.; Wang, C.; Gao, S. An interpretable anti-noise network for rolling bearing fault diagnosis based on FSWT. Meas. J. Int. Meas. Confed. 2022, 190, 110698. [Google Scholar] [CrossRef]
- Zhu, Y.; Xie, B.; Wang, A.; Qian, Z. Fault diagnosis of wind turbine gearbox under limited labeled data through temporal predictive and similarity contrast learning embedded with self-attention mechanism. Expert. Syst. Appl. 2024, 245, 123080. [Google Scholar] [CrossRef]
- Karpat, F.; Kalay, O.C.; Dirik, A.E.; Karpat, E. Fault classification of wind turbine gearbox bearings based on convolutional neural networks. Transdiscipl. J. Eng. Sci. 2022, SP-2, 71–83. [Google Scholar] [CrossRef]
- Li, H.; Wu, X.; Liu, T.; Li, S.; Zhang, B.; Zhou, G.; Huang, T. Composite fault diagnosis for rolling bearing based on parameter-optimized VMD. Meas. Int. J. Meas. Confed. 2022, 201, 111637. [Google Scholar] [CrossRef]
- Xu, Z.; Li, C.; Yang, Y. Fault diagnosis of rolling bearing of wind turbines based on the variational mode decomposition and deep convolutional neural networks. Appl. Soft Comput. 2020, 95, 106515. [Google Scholar] [CrossRef]
- Karpat, F.; Kalay, O.C.; Dirik, A.E.; Doğan, O.; Korcuklu, B.; Yüce, C. Convolutional neural networks based rolling bearing fault classification under variable operating conditions. In Proceedings of the IEEE International Conference on Innovations in Intelligent Systems and Applications, Kocaeli, Turkey, 25–27 August 2021. [Google Scholar] [CrossRef]
- Alhams, A.; Abdelhadi, A.; Badri, Y.; Sassi, S.; Renno, J. Enhanced bearing fault diagnosis through trees ensemble method and feature importance analysis. J. Vib. Eng. Technol. 2024, 12, 109–125. [Google Scholar] [CrossRef]
- Qi, M.; Zhou, R.; Zhang, Q.; Yang, Y. Feature classification method of frequency cepstrum coefficient based on weighted extreme gradient boosting. IEEE Access 2021, 9, 72691–72701. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 1–74. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Han, P.; Xu, L.; Zhang, F.; Wang, Y.; Gao, L. Research on bearing fault diagnosis of wind turbine gearbox based on 1DCNN-PSO-SVM. IEEE Access 2020, 8, 192248–192258. [Google Scholar] [CrossRef]
- Hatipoğlu, A.; Süpürtülü, M.; Yılmaz, E. Enhanced fault classification in bearings: A multi-domain feature extraction approach with LSTM-attention and LASSO. Arab. J. Sci. Eng. 2024, 1–18. [Google Scholar] [CrossRef]
- Neupane, D.; Seok, J. Bearing fault detection and diagnosis using Case Western Reserve University dataset with deep learning approaches: A review. IEEE Access 2020, 8, 93155–93178. [Google Scholar] [CrossRef]
- Yu, T.; Li, C.; Huang, J.; Xiao, X.; Zhang, X.; Li, Y.; Fu, B. ReF-DDPM: A novel DDPM-based data augmentation method for imbalanced rolling bearing fault diagnosis. Reliab. Eng. Syst. Saf. 2024, 251, 110343. [Google Scholar] [CrossRef]
- Gong, W.; Chen, H.; Zhang, Z.; Zhang, M.; Wang, R.; Guan, C.; Wang, Q. A novel deep learning method for intelligent fault diagnosis of rotating machinery based on improved CNN-SVM and multichannel data fusion. Sensors 2019, 19, 1693. [Google Scholar] [CrossRef] [PubMed]
- Sahu, D.; Dewangan, R.K.; Matharu, S.P.S. Hybrid CNN-LSTM model for fault diagnosis of rolling element bearings with operational defects. Int. J. Interact. Des. Manuf. 2025, 19, 5737–5748. [Google Scholar] [CrossRef]
- Zhou, Q.; Tang, J. An interpretable parallel spatial CNN-LSTM architecture for fault diagnosis in rotating machinery. IEEE Internet Things J. 2024, 11, 31730–31744. [Google Scholar] [CrossRef]
- Han, K.; Wang, W.; Guo, J. Research on a bearing fault diagnosis method based on a CNN-LSTM-GRU model. Machines 2024, 12, 927. [Google Scholar] [CrossRef]
- Song, B.; Liu, Y.; Fang, J.; Liu, W.; Liu, X. An optimized CNN-BiLSTM network for bearing fault diagnosis under multiple working conditions with limited training samples. Neurocomputing 2024, 574, 127284. [Google Scholar] [CrossRef]
- Huang, T.; Zhang, Q.; Tang, X.; Zhao, S.; Lu, X. A novel fault diagnosis method based on CNN and LSTM and its application in fault diagnosis for complex systems. Artif. Intell. Rev. 2022, 55, 1289–1315. [Google Scholar] [CrossRef]
- Novello, P.; Poëtte, G.; Lugato, D.; Congedo, P.M. Goal-oriented sensitivity analysis of hyperparameters in deep learning. J. Sci. Comput. 2023, 94, 45. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Liu, X.; Wu, R.; Wang, R.; Zhou, F.; Chen, Z.; Guo, N. Bearing fault diagnosis based on particle swarm optimization fusion convolutional neural network. Front. Neurorobot. 2022, 16, 1044965. [Google Scholar] [CrossRef] [PubMed]
- Dong, S. An integrated method of rolling bearing fault diagnosis based on convolutional neural network optimized by sparrow optimization algorithm. Sci. Program. 2022, 6234169. [Google Scholar] [CrossRef]
- Ruan, D.; Wang, J.; Yan, J.; Gühmann, C. CNN parameter design based on fault signal analysis and its application in bearing fault diagnosis. Adv. Eng. Inform. 2023, 55, 101877. [Google Scholar] [CrossRef]
- Shenfield, A.; Howarth, M. A novel deep learning model for the detection and identification of rolling element-bearing faults. Sens. 2020, 20, 5112. [Google Scholar] [CrossRef] [PubMed]
- Mostafavi, A.; Siami, M.; Friedmann, A.; Barszcz, T.; Zimroz, R. Probabilistic uncertainty-aware decision fusion of neural network for bearing fault diagnosis. In Proceedings of the 8th European Conference of the Prognostics and Health Management Society, Prague, Czech Republic, 3–5 July 2024. [Google Scholar] [CrossRef]
- Zhou, T.; Zhang, L.; Han, T.; Lopez Droguett, E.; Mosleh, A.; Chan, F.T.S. An uncertainty-informed framework for trustworthy fault diagnosis in safety-critical applications. Reliab. Eng. Syst. Saf. 2023, 229, 108865. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Li, G.-H. Uncertainty-aware fault diagnosis under calibration. IEEE Trans. Syst. Man. Cybern. Syst. 2024, 54, 6469–6481. [Google Scholar] [CrossRef]
- Das, L.; Gjorgiev, B.; Sansavini, G. Uncertainty-aware deep learning for monitoring and fault diagnosis from synthetic data. Reliab. Eng. Syst. Saf. 2024, 251, 110386. [Google Scholar] [CrossRef]
- Ren, J.; Wen, J.; Zhao, Z.; Yan, R.; Chen, X.; Nandi, A.K. Uncertainty-aware deep learning: A promising tool for trustworthy fault diagnosis. IEEE/CAA J. Autom. Sin. 2024, 11, 1317–1330. [Google Scholar] [CrossRef]
- Kafunah, J.; Ali, M.I.; Breslin, J.G. Uncertainty-aware ensemble combination method for quality monitoring fault diagnosis in safety-related products. IEEE Trans. Industr. Inform. 2024, 20, 1975–1986. [Google Scholar] [CrossRef]
- Hüllermeier, E.; Waegeman, W. Aleatoric and epistemic uncertainty in machine learning: An introduction to concepts and methods. Mach. Learn. 2021, 110, 457–506. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center. Available online: https://engineering.case.edu/bearingdatacenter/welcome (accessed on 8 June 2025).
- Lessmeier, C.; Kimotho, J.K.; Zimmer, D.; Sextro, W. Condition monitoring of bearing damage in electromechanical drive systems by using motor current signals of electric motors: A benchmark data set for data-driven classification. In Proceedings of the 3th European Conference of the Prognostics and Health Management Society, Bilbao, Spain, 5–8 July 2016. [Google Scholar] [CrossRef]
- Magadán, L.; Ruiz-Cárcel, C.; Granda, J.C.; Suárez, F.J.; Starr, A. Explainable and interpretable bearing fault classification and diagnosis under limited data. Adv. Eng. Inform. 2024, 62, 102909. [Google Scholar] [CrossRef]
- Kalay, O.C.; Karpat, F. A comparative experimental research on the diagnosis of tooth root cracks in asymmetric spur gear pairs with a one-dimensional convolutional neural network. Mech. Mach. Theory 2024, 201, 105755. [Google Scholar] [CrossRef]
- Scherer, D.; Müller, A.; Behnke, S. Evaluation of pooling operations in convolutional architectures for object recognition. In Proceedings of the International Conference on Artificial Neural Networks, Thessaloniki, Greece, 11–15 September 2010. [Google Scholar] [CrossRef]
- Ravikumar, K.N.; Yadav, A.; Kumar, H.; Gangadharan, K.V.; Narasimhadhan, A.V. Gearbox fault diagnosis based on multi-scale deep residual learning and stacked LSTM model. Meas. J. Int. Meas. Confed. 2021, 186, 110099. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, H.; Pourpanah, F.; Zeng, T.; Wang, X. A survey on epistemic (model) uncertainty in supervised learning: Recent advances and applications. Neurocomputing 2022, 489, 449–465. [Google Scholar] [CrossRef]
- Valdenegro-Toro, M.; Mori, D.S. A deeper look into aleatoric and epistemic uncertainty disentanglement. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, New Orleans, LA, USA, 19–20 June 2022. [Google Scholar] [CrossRef]
- Hou, L.; Jiang, R.; Tan, Y.; Zhang, J. Input feature mappings-based deep residual networks for fault diagnosis of rolling element bearing with complicated dataset. IEEE Access 2020, 8, 180967–180976. [Google Scholar] [CrossRef]
- Karpat, F.; Kalay, O.C.; Dirik, A.E.; Karpat, E. Fault diagnosis of rolling bearing under variable operating conditions based on deep learning. In Proceedings of the 10th International Scientific Conference on Research and Development of Mechanical Elements and Systems, Belgrade, Serbia, 26 May 2022. [Google Scholar]
- Wang, C.; Chen, X.; Qiang, X.; Fan, H.; Li, S. Recent advances in mechanism/data-driven fault diagnosis of complex engineering systems with uncertainties. AIMS Math. 2024, 9, 29736–29772. [Google Scholar] [CrossRef]
- Qiang, X.; Wang, C.; Fan, H. Hybrid interval model for uncertainty analysis of imprecise or conflicting information. Appl. Math. Model. 2024, 129, 837–856. [Google Scholar] [CrossRef]
- Wang, C.; Qiang, X.; Xu, M.; Wu, T. Recent advances in surrogate modeling methods for uncertainty quantification and propagation. Symmetry 2022, 14, 1219. [Google Scholar] [CrossRef]
- Tian, H.; Fan, H.; Feng, M.; Cao, R.; Li, D. Fault diagnosis of rolling bearing based on HPSO algorithm optimized CNN-LSTM neural network. Sensors 2023, 23, 6508. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Zhao, K.; Wang, J.; Bashir, M. Physics-informed probabilistic deep network with interpretable mechanism for trustworthy mechanical fault diagnosis. Adv. Eng. Inform. 2024, 62, 102806. [Google Scholar] [CrossRef]
- Chen, J.; Jiang, J.; Guo, X.; Tan, L. A self-adaptive CNN with PSO for bearing fault diagnosis. Syst. Sci. Control. Eng. 2021, 9, 11–22. [Google Scholar] [CrossRef]


| Fault Location | Ball | Inner Raceway | Outer Raceway |
|---|---|---|---|
| 4.7135 Hz | 5.4152 Hz | 3.5848 Hz |
| Fault Characteristic Frequency (Hz) | Order | ||||
|---|---|---|---|---|---|
| 1st | 2nd | 3th | 4th | 5th | |
| fball | 141.16 | 282.32 | 423.48 | 564.64 | 705.8 |
| fIR | 162.18 | 324.36 | 486.54 | 648.72 | 810.9 |
| fOR | 107.36 | 214.72 | 322.08 | 429.44 | 536.8 |
| Layer | Output Shape | Number of Parameters |
|---|---|---|
| Conv1D | (None, 21,060, 4) | 8 |
| MaxPooling1D | (None, 10,530, 4) | 0 |
| Conv1D | (None, 10,530, 4) | 20 |
| MaxPooling1D | (None, 5265, 4) | 0 |
| Conv1D | (None, 5265, 4) | 20 |
| MaxPooling1D | (None, 2632, 4) | 0 |
| Conv1D | (None, 2632, 8) | 40 |
| MaxPooling1D | (None, 877, 8) | 0 |
| Conv1D | (None, 877, 8) | 72 |
| MaxPooling1D | (None, 292, 8) | 0 |
| Dropout | (None, 292, 8) | 0 |
| LSTM | (None, 32) | 5248 |
| Flatten | (None, 32) | 0 |
| Dense | (None, 256) | 8448 |
| Dense | (None, 128) | 32,896 |
| Dense | (None, 64) | 8256 |
| Dense | (None, 10) | 650 |
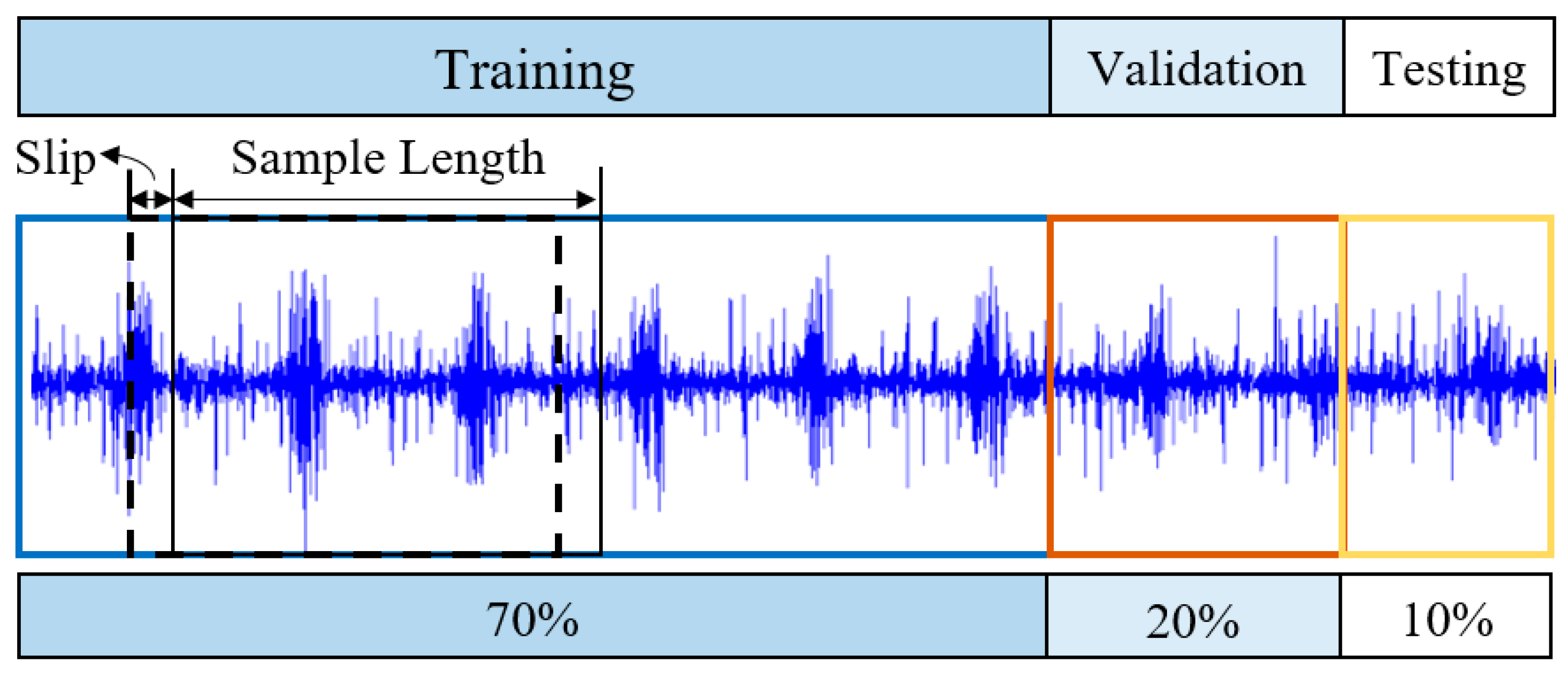
| Health Status | Data Points lp | Slip Length Slip | Number of Samples ns | Label |
|---|---|---|---|---|
| Normal | 243,938 | 220 | 1000 | 0 |
| 0.007″ BF | 244,739 | 220 | 1000 | 1 |
| 0.014″ BF | 249,146 | 220 | 1000 | 2 |
| 0.021″ BF | 243,938 | 220 | 1000 | 3 |
| 0.007″ IRF | 243,938 | 220 | 1000 | 4 |
| 0.014″ IRF | 63,788 | 40 | 1000 | 5 |
| 0.021″ IRF | 244,339 | 220 | 1000 | 6 |
| 0.007″ ORF | 243,538 | 220 | 1000 | 7 |
| 0.014″ ORF | 245,140 | 220 | 1000 | 8 |
| 0.021″ ORF | 246,342 | 220 | 1000 | 9 |
| Health Status | Data Points lp | Slip Length Slip | Number of Samples ns | Label |
|---|---|---|---|---|
| Normal @ 1500 | 257,407 | 245 | 1000 | 0 |
| Normal @ 900 | 256,608 | 245 | 1000 | 1 |
| IRF @ 1500 | 256,001 | 245 | 1000 | 2 |
| IRF @ 900 | 256,762 | 245 | 1000 | 3 |
| ORF @ 1500 | 256,000 | 245 | 1000 | 4 |
| ORF @ 900 | 256,000 | 245 | 1000 | 5 |
| Dataset | Input Length | Test-1 | Test-2 | Test-3 | Test-4 | Overall Accuracy |
|---|---|---|---|---|---|---|
| CWRU | 1024 | 82.500% | 83.000% | 83.700% | 81.800% | 82.750% |
| 2048 | 88.100% | 89.800% | 90.100% | 89.500% | 89.375% | |
| 4096 | 89.900% | 90.600% | 91.100% | 90.700% | 90.575% | |
| 21,060 | 90.000% | 94.000% | 94.400% | 94.800% | 93.300% | |
| PU | 1024 | 75.333% | 75.500% | 77.500% | 76.667% | 76.250% |
| 2048 | 88.500% | 90.667% | 87.833% | 88.833% | 88.958% | |
| 4096 | 97.333% | 96.667% | 96.000% | 93.167% | 95.791% | |
| 7400 | 95.500% | 98.500% | 97.167% | 98.167% | 97.333% |
| Algorithm | Test-1 | Test-2 | Test-3 | Test-4 | Overall Accuracy | Parameters | Epistemic Uncertainty |
|---|---|---|---|---|---|---|---|
| 1-D CNN | 90.000% | 94.000% | 94.400% | 94.800% | 93.300% | [10; 110; 0.55] | 16.900 × 10−5 |
| 1-D CNN-LSTM | 81.600% | 86.800% | 78.400% | 82.400% | 82.300% | [10; 110; 0.55] | 36.100 × 10−5 |
| Optimized 1-D CNN | 98.400% | 97.200% | 98.400% | 99.200% | 98.300% | [30; 32; 0.5] | 2.500 × 10−5 |
| Optimized 1-D CNN-LSTM | 99.100% | 99.200% | 99.600% | 99.500% | 99.350% | [50; 192; 0.6] | 0.400 × 10−5 |
| Algorithm | Test-1 | Test-2 | Test-3 | Test-4 | Overall Accuracy | Parameters | Epistemic Uncertainty |
|---|---|---|---|---|---|---|---|
| 1-D CNN | 95.500% | 98.500% | 97.167% | 98.167% | 97.333% | [10; 110; 0.55] | 1.112 × 10−5 |
| 1-D CNN-LSTM | 86.333% | 92.000% | 94.333% | 95.000% | 91.916% | [10; 110; 0.55] | 75.625 × 10−5 |
| Optimized 1-D CNN | 99.000% | 99.500% | 99.333% | 99.833% | 99.416% | [30; 256; 0.45] | 0.277 × 10−5 |
| Optimized 1-D CNN-LSTM | 99.833% | 99.833% | 99.667% | 99.667% | 99.750% | [20; 64; 0.5] | 0.068 × 10−5 |
| Algorithm * | Overall Accuracy | Sampling Ratio | Number of Classes | Sample Length | |
|---|---|---|---|---|---|
| Xue et al. [2] | TSFFCNN-PSO-SVM | 98.500% | 48 kHz | 10 | 1024 |
| Zhang et al. [12] | 1-D CNN-PSO-SVM | 98.200% | 48 kHz | 10 | 864 |
| Han et al. [19] | CNN-LSTM with Gated Recurrent Unit | 99.290% | – | 10 | – |
| Song et al. [20] | CNN-BiLSTM with Grid Search | 99.285% | 12 kHz | 10 | 2048 |
| Proposed Method | Optimized 1-D CNN-LSTM | 99.350% | 48 kHz | 10 | 21,060 |
| Algorithm * | Overall Accuracy | Sampling Ratio | Number of Classes | Sample Length | |
|---|---|---|---|---|---|
| Ruan et al. [26] | PGCNN | 99.719% | 64 kHz | 5 | 7921 |
| Hou et al. [43] | IFMs-based ResNet | 99.700% | 64 kHz | 4 | 4096 |
| Karpat et al. [44] | 1-D CNN | 96.670% | 64 kHz | 6 | 25,000 |
| Proposed Method | Optimized 1-D CNN-LSTM | 99.750% | 64 kHz | 6 | 7400 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalay, O.C. An Optimized 1-D CNN-LSTM Approach for Fault Diagnosis of Rolling Bearings Considering Epistemic Uncertainty. Machines 2025, 13, 612. https://doi.org/10.3390/machines13070612
Kalay OC. An Optimized 1-D CNN-LSTM Approach for Fault Diagnosis of Rolling Bearings Considering Epistemic Uncertainty. Machines. 2025; 13(7):612. https://doi.org/10.3390/machines13070612
Chicago/Turabian StyleKalay, Onur Can. 2025. "An Optimized 1-D CNN-LSTM Approach for Fault Diagnosis of Rolling Bearings Considering Epistemic Uncertainty" Machines 13, no. 7: 612. https://doi.org/10.3390/machines13070612
APA StyleKalay, O. C. (2025). An Optimized 1-D CNN-LSTM Approach for Fault Diagnosis of Rolling Bearings Considering Epistemic Uncertainty. Machines, 13(7), 612. https://doi.org/10.3390/machines13070612






