Abstract
Driven by the urgent demand for low-frequency vibration and noise control in engineering scenarios such as automobiles, acoustic metamaterials (AMs), as a new class of functional materials, have demonstrated significant application potential. This paper proposes a low-frequency band gap optimization design method for local resonance acoustic metamaterials (LRAMs) based on a multi-objective genetic algorithm. Within a COMSOL Multiphysics 6.2 with MATLAB R2024b co-simulation framework, a parameterized unit cell model of the metamaterial is constructed. The optimization process targets two objectives: minimizing the band gap’s deviation from the target and reducing the structural mass. A multi-objective fitness function is formulated by incorporating the band gap deviation and structural mass constraints, and non-dominated sorting genetic algorithm II (NSGA-II) is employed to perform a global search over the geometric parameters of the resonant unit. The resulting Pareto-optimal solution set achieves a unit cell mass as low as 26.49 g under the constraint that the band gap deviation does not exceed 2 Hz. The results of experimental validation show that the optimized metamaterial configuration reduces the peak of the low-frequency frequency response function (FRF) at 63 Hz by up to 75% in a car door structure. Furthermore, the simulation predictions exhibit good agreement with the experimental measurements, confirming the effectiveness and reliability of the proposed method in engineering applications. The proposed multi-objective optimization framework is highly general and extensible and capable of effectively balancing between the acoustic performance and structural mass, thus providing an efficient engineering solution for low-frequency noise control problems.
1. Introduction
Vibration and noise control is one of the most important research directions in the engineering field and is widely used in industries such as machinery, construction, aerospace, and automotive manufacturing. In modern automotive design, noise, vibration, and harshness (NVH) are key indicators for measuring vehicle comfort and quality [1]. With continuous improvements in people’s needs during the riding experience, traditional passive noise reduction methods are no longer able to meet these needs. In the traditional vibration and noise control methods, reducing noise by adding damping materials or changing the structural design is the most commonly used approach [2,3,4]. However, these methods often have limitations, such as the use of damping materials that increase the vehicle’s weight and complex structural designs that can lead to increased manufacturing costs [5]. Therefore, researchers have begun to explore new vibration and noise control technologies.
Acoustic metamaterials (AMs) are functional materials with artificially designed structures that achieve precise control over sound wave propagation through artificially designed sub-wavelength structures, demonstrating revolutionary potential in the field of low-frequency noise control [6,7,8,9]. In the automotive industry, thin-walled structures such as car doors are prone to resonance in the low-frequency range due to engine or road excitation, leading to significant low-frequency noise problems [10]. The traditional sound-absorbing materials are limited by the law of mass and find it difficult to effectively suppress such low-frequency vibrations. AMs based on the principle of local resonance form band gaps through the coupling effect of structural resonance and matrix vibrations, providing new ideas for breaking through this bottleneck [11,12,13,14]. However, the existing research has mostly focused on band gap design under free field conditions, and there are still significant bottlenecks in customized AM design for practical engineering structures with complex boundary constraints. On the one hand, low-frequency sound waves have longer wavelengths, requiring AM structures to have larger feature sizes or more complex resonance mechanisms, resulting in low efficiency of the traditional design methods based on empirical trial and error or single objective optimization [15,16,17]. On the other hand, although multi-material composite structures can broaden the band gap, material stacking leads to a 60–80% increase in the mass density, which goes against the demand for engineering lightweighting [18,19].
In recent years, reverse design methods based on numerical simulation and optimization algorithms have gradually become a hot topic in AM research. For example, Huang et al. proposed a deep-learning-based framework for reverse engineering of cylindrical AMs which generated a dataset through finite element simulation and established nonlinear mapping between the structural parameters and the band gap, significantly improving the design efficiency [20]. However, deep learning methods rely on a large amount of training data and may face convergence issues in multi-objective optimization. In contrast, genetic algorithms (GAs) [21] have demonstrated unique advantages in AM optimization due to their global search capability and adaptability to multi-objective problems. Maamoun et al. used GAs to optimize the design of vibration plate openings, successfully reducing the acoustic power response and verifying the effectiveness of GAs in complex acoustic vibration coupling problems [22]. In addition, Hu et al. further combined non-dominated sorting with a GA to achieve synergistic optimization of the sound absorption and energy absorption in shell-based lattice AMs [23,24]. However, the above research focuses on idealized models and lacks validation of actual engineering structures. There is still a lack of systematic methods for optimizing AMs for ultra-low frequencies, and few studies have simultaneously considered the band gap performance and lightweight requirements. Unlike these studies, our work integrates precision band gap targeting and strict mass minimization within an automated co-simulation workflow, validated under complex automotive boundary conditions.
In response to the above issues, this article aims to propose a multi-objective GA optimization framework based on COMSOL and MATLAB joint simulations for designing localized resonant acoustic metamaterials (LRAMs) with low-frequency wide band gaps. Firstly, a design space containing the geometric parameters of the local resonance elements was generated through parametric modeling, and a finite element analysis of the band gap characteristics was conducted using COMSOL Multiphysics. Then, the initial structural model and the method of combining the structural model with a GA were introduced, and the fitness function corresponding to iterative optimization was derived. Finally, a multi-objective GA [25] optimization model based on MATLAB was constructed, with the optimization objectives of minimizing the width of the band gap and the structural mass. The Pareto-optimal solution set was selected through non-dominated sorting and elite retention strategies [19]. Finally, the optimization effect was verified through experiments, and the research results showed that the designed AMs had a significant vibration suppression ability in the low-frequency range.
2. The Method
2.1. COMSOL with MATLAB Joint Simulation Optimization Process
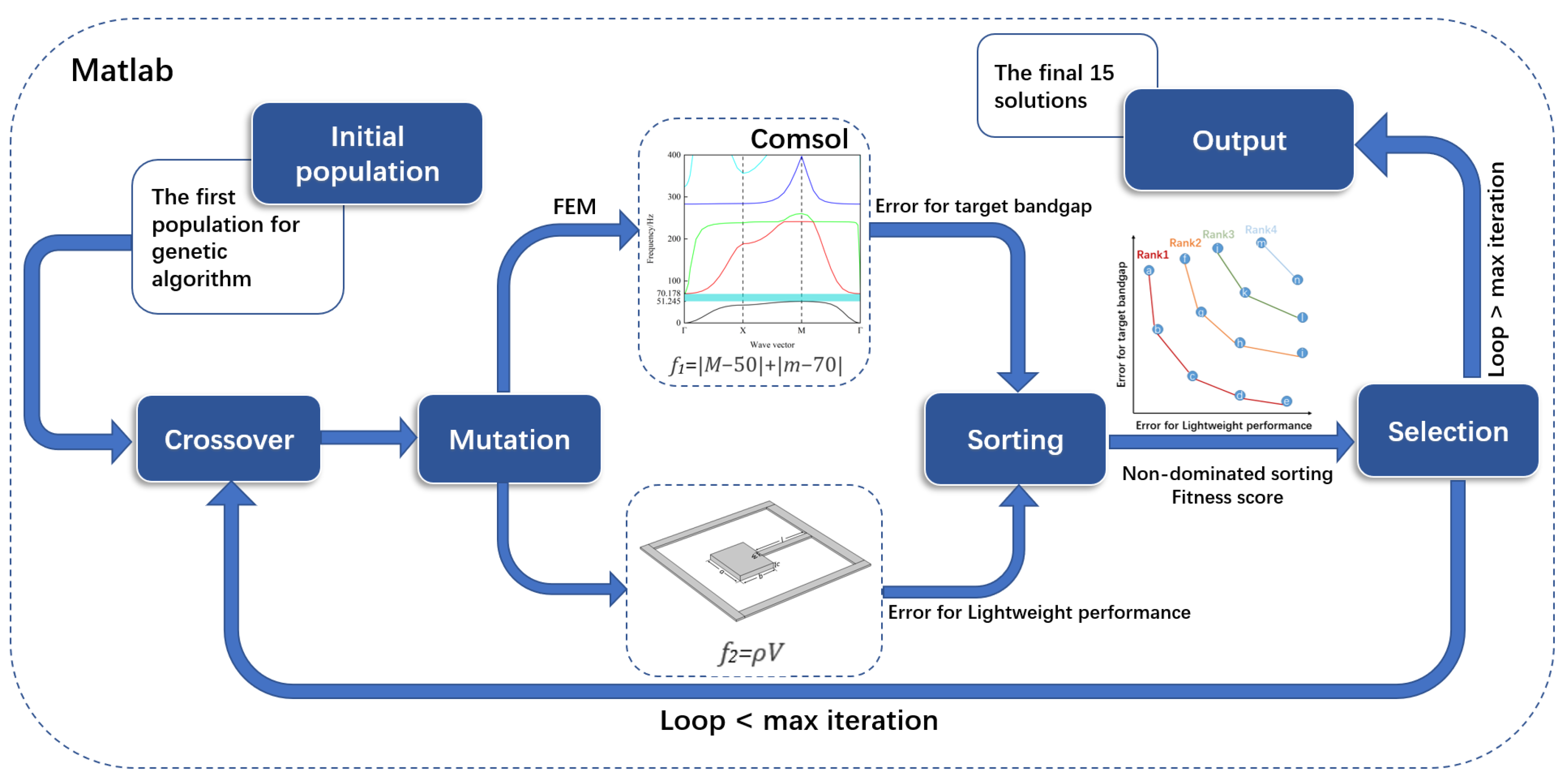
The structural optimization method adopts the non-dominated classification genetic algorithm II (NSGA-II), taking the initial structural parameters of the local resonance unit as the design variables and their value ranges as the design space. This framework uniquely addresses the precision band gap and lightweighting trade-offs in automotive NVH applications, advancing beyond generic band gap maximization. This work synchronously processes two competitive objectives through a multi-objective optimization framework: the primary objective is to reduce the error with the target band gap by adjusting the dispersion curves of the local resonant unit. The maximum frequency of the first dispersion curve and the minimum frequency of the second dispersion curve constitute the first-order band gap of the optimized unit. The sum of the errors between the upper and lower limits of the first-order band gap of the optimized unit and the upper and lower limits of the target band gap is taken as the fitness function for the primary objective. The secondary objective is to establish a constraint function for minimizing the mass of the local resonance element through material efficiency optimization so as to achieve the purpose of lightweighting. At the algorithm implementation level, the Pareto frontier solution set of the two objectives is coordinated by NSGA-II’s non-dominated sorting mechanism.
The specific process is as follows: Firstly, the parameters of the local resonance unit are randomly generated into the first-generation population in the design space, and the dual-objective function values for each individual are obtained through finite element calculation; then, the elite retention strategy is adopted to directly pass the non-dominated solution set to the next generation, and the design variables of the local resonance unit are iteratively optimized using optimization operators such as crossover, selection, and mutation in the GA to obtain the second-generation parameter combination group; finally, the population diversity is maintained through a crowding comparison operator, and a non-dominated sorting mechanism is used to coordinate the Pareto frontier solution sets of the two objectives. After multiple iterations, the best parameter combination that meets the band gap requirements and has the minimum quality is selected from the Pareto-optimal solution set. The specific process is shown in Figure 1.
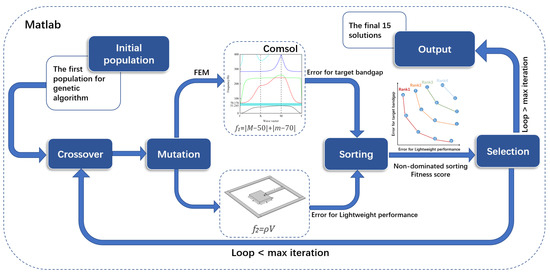
Figure 1.
The entire flowchart of the COMSOL and MATLAB multi-objective optimization genetic algorithm.
2.2. A Multi-Objective Genetic Algorithm and Fitness Function Design
Multi-objective optimization problems aim to achieve a balance between multiple objective functions. In AM design, there is often a conflicting demand between band gap performance and structural quality. To solve this type of problem, this paper adopts NSGA-II, which retains the basic mechanism of a GA and introduces non-dominated sorting and crowding distance comparisons, effectively identifying the Pareto-optimal solution set.
This method sets two optimization objectives: objective 1 is to minimize the band gap error, defined by Equation (1), where is the return value of the fitness function for the first objective. The smaller the fitness function value, the closer the first-order band gap of the local resonance unit is to the target. Here, M is the maximum frequency of the first dispersion curve, and m is the minimum frequency of the second dispersion curve. The smaller the fitness function value, the closer the first-order band gap of the local resonance unit is to Hz − Hz.
Objective 2 is to minimize the mass of the unit cell structure. The mass is defined as the second objective fitness function , as shown in Equation (2), where a smaller fitness value indicates the better lightweight performance of the designed local resonance unit. Here, denotes the material density, and V is the total volume of the structure composed of the unit cell structure.
2.3. The Elite Strategy and Sorting Mechanism
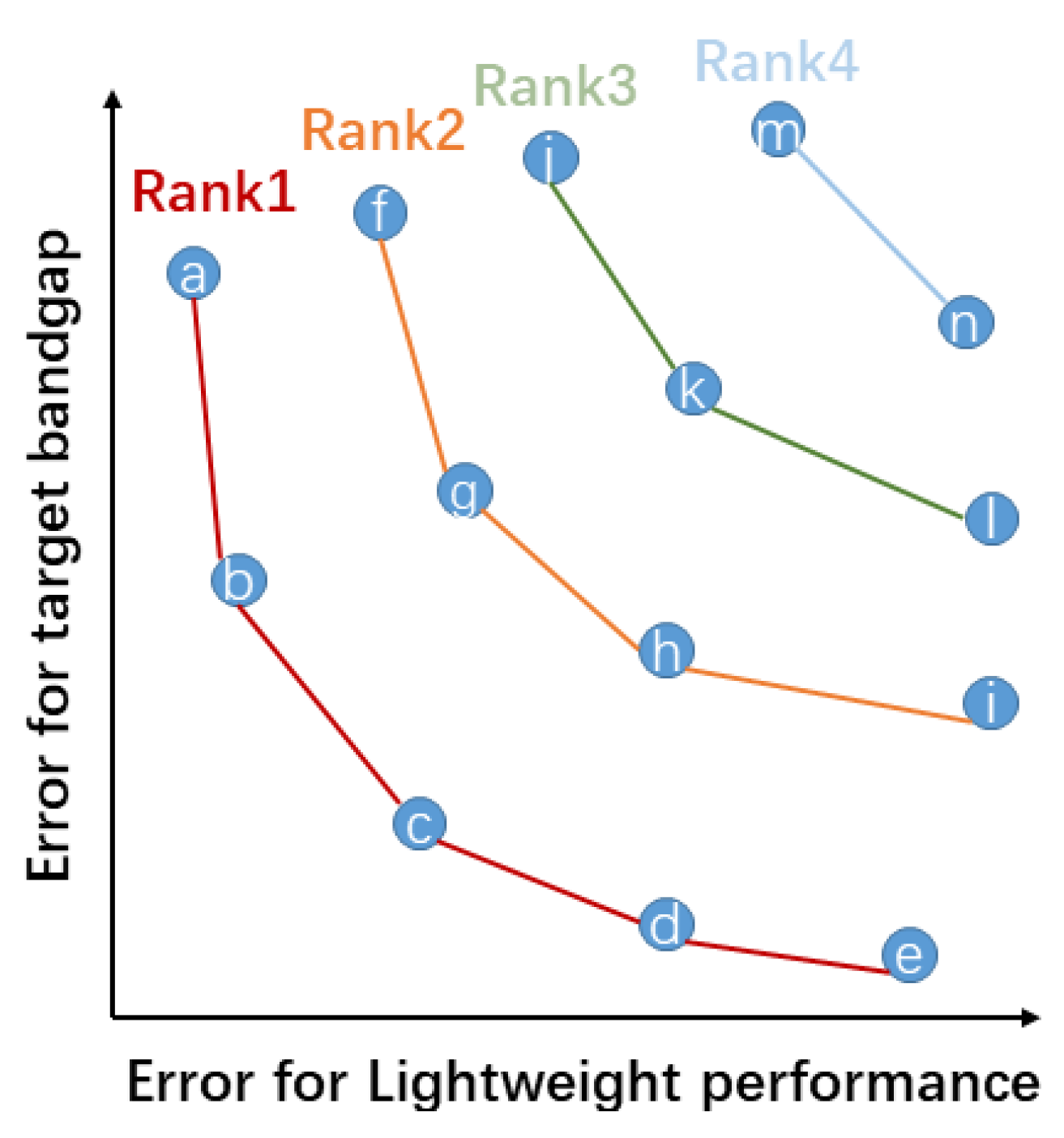
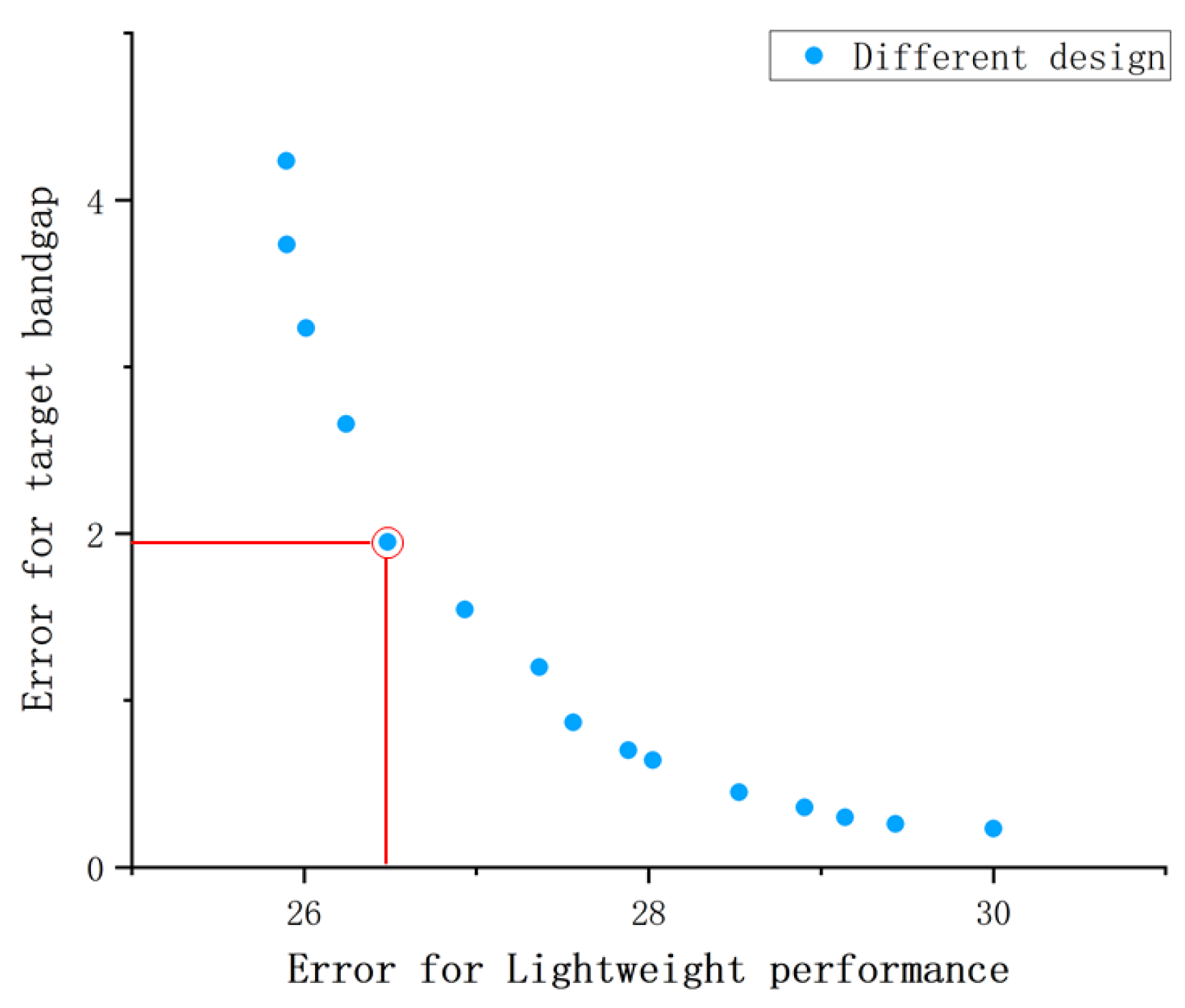
The principles of dominance and ranking are illustrated in Figure 2. For data point , if its objective values—the band gap error and structural quality—are lower than those of data point , then dominates over . This relationship is exemplified in Figure 2, where data point c dominates over data point g. Subsequently, individuals not dominated by any others are classified as the first Pareto front (Rank 1), as depicted in Figure 2. The next set of individuals, who are only dominated by those in Rank 1, form the second Pareto front (Rank 2), and so on [19,25]. Following this sorting principle, a finite element analysis is employed to evaluate the properties of all parameter combinations. The results are then organized into their respective Pareto fronts, as shown in Figure 2 [26].
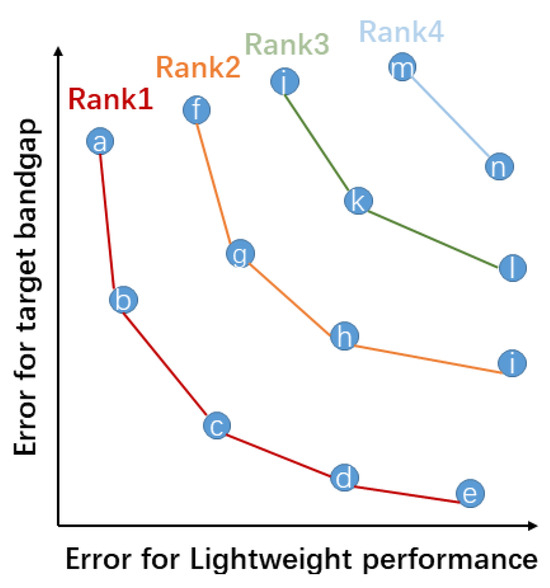
Figure 2.
Pareto solution set ranking method for data points with different parameter combinations in multi-objective genetic algorithm, Each letter represents the data points obtained by different design parameters.
3. Optimization of the Design
3.1. Parameterized Modeling of Local Resonance Units
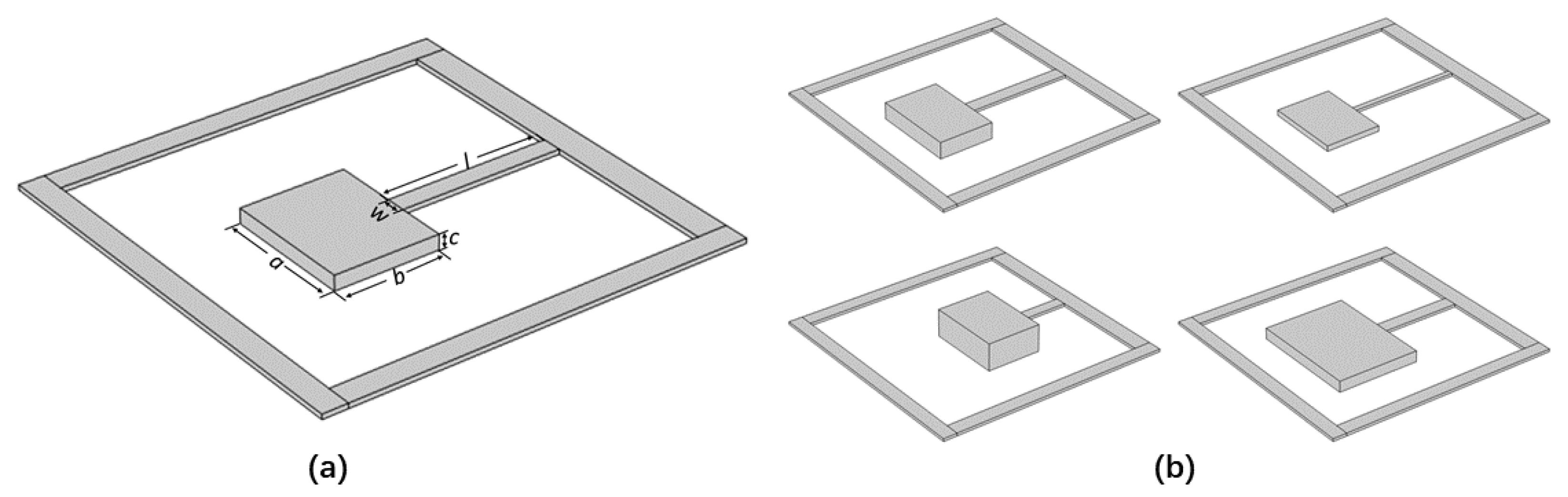
In the study of AMs, researchers have increasingly replaced traditional straight-rod arrays with framework structures incorporating local resonant units in order to achieve more flexible low-frequency wide-band-gap tuning [26,27]. A multi-objective GA optimization framework based on COMSOL with MATLAB co-simulation was employed to optimize the unit cell model depicted in Figure 3a, which comprises a square frame connected to a central oscillator via a thin beam. Further investigations revealed that the geometric parameters of the beam and the oscillator significantly influence the range and width of the band gap. The general parameters are set as follows: the side length of the square frame is 85 mm, the frame width is 5 mm, and both the frame thickness and beam thickness are 1 mm. The design parameters include the beam width w; the beam length l; and the oscillator’s length, width, and height, denoted as a, b, and c, respectively. These parameters collectively define the structural characteristics of the unit cell. Considering industrial manufacturing tolerances and formability limits, the design parameter ranges are prescribed as
with a uniform step size of . After defining the initial configuration, a numerical model was constructed in COMSOL Multiphysics with the specific parameter settings
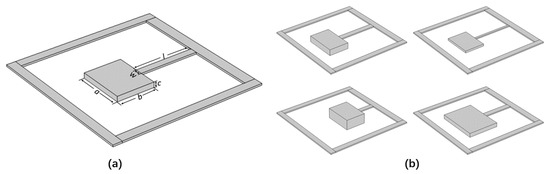
Figure 3.
Combination diagram of LRAM: (a) schematic diagram of design parameters for single-cell model and (b) different single-cell models obtained by combining different design parameters.
The mesh was generated using the physics-controlled meshing sequence, and structural steel was selected as the material, with an elastic modulus of , a Poisson’s ratio , and a density . Figure 3b illustrates the various lattice models obtained by varying these geometric parameters.
3.2. Dispersion Curve Solution
In elastic heterogeneous media, the governing equation for vibration and wave propagation can be written as
where ∇ is the differential operator, is the displacement vector, denotes the material’s density, and and are the Lamé constants. By applying Bloch’s theorem, the displacement field in a periodic structure can be expressed as
where is the wave vector, is a lattice-periodic function satisfying , and is the position vector of a lattice point.
Substituting (4) into (3) and performing a finite element discretization yields the unit cell eigenvalue problem
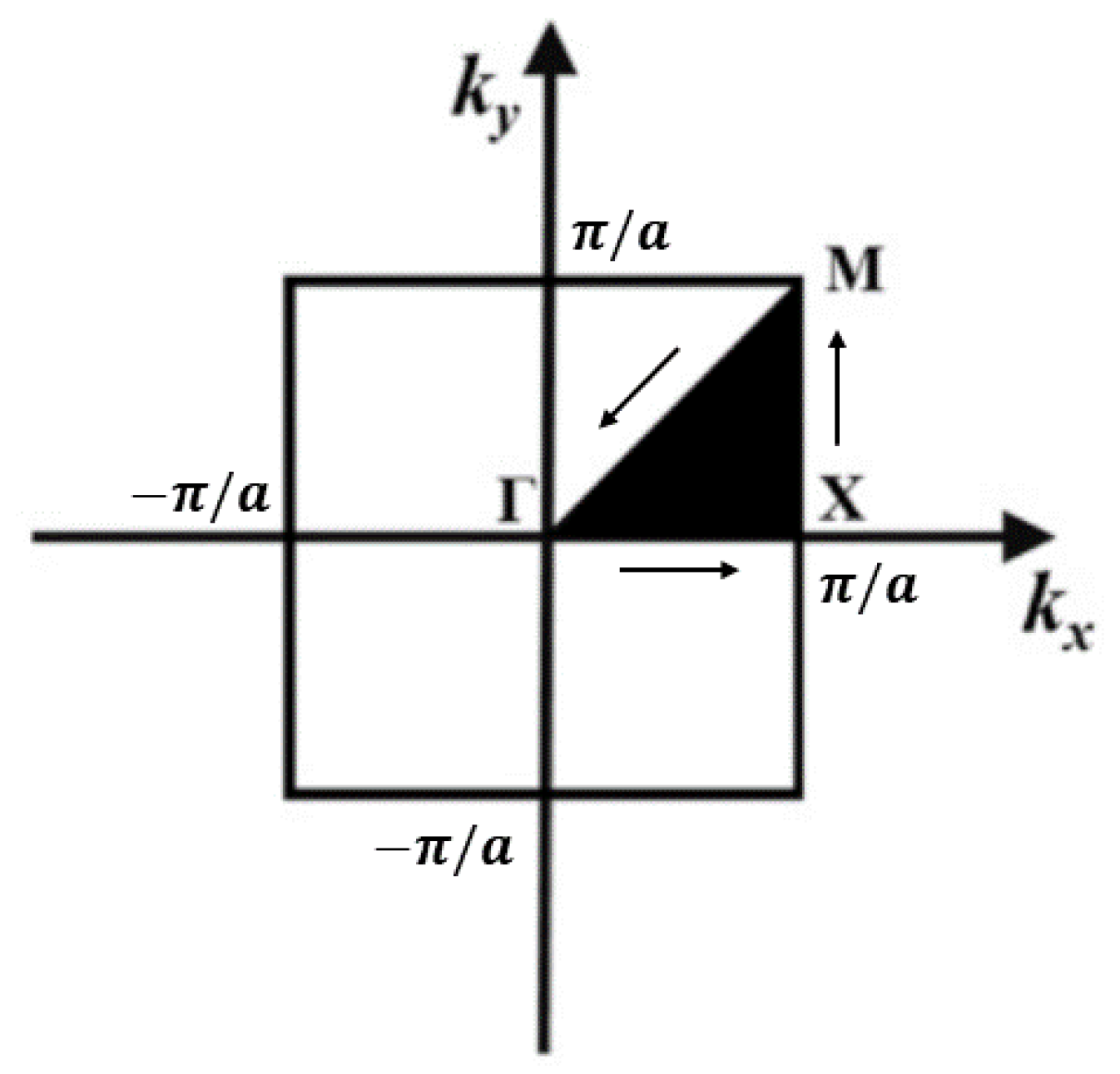
where K and M are the stiffness and mass matrices of the structure, respectively. Due to periodicity, the wave vector may be confined to the first irreducible Brillouin zone shown in Figure 4, with a lattice constant . By tracing the high-symmetry path on the Brillouin-zone boundary, one obtains the dispersion curves. To reduce the computational cost, only the first six bands are computed, each sampled at 30 wave vector points along the boundary [28].
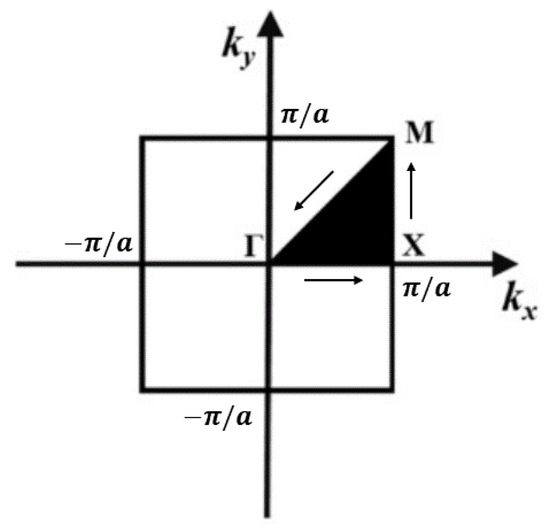
Figure 4.
Division of the first irreducible Brillouin zone.
3.3. The Optimization Design Method Based on NSGA-II
To validate the performance of the optimized local resonance unit for low-frequency vibration suppression in automobile doors, we constructed the experimental setup shown in Figure 5. The car door under test was suspended using elastic cords to emulate the free–boundary conditions of the numerical model. A modal hammer was used to provide impact excitation, and tri-axial accelerometers were installed at designated measurement points to capture vibration acceleration signals. The acquired data were subsequently analyzed and processed using LMS Test.Lab.

Figure 5.
Experimental test platform.
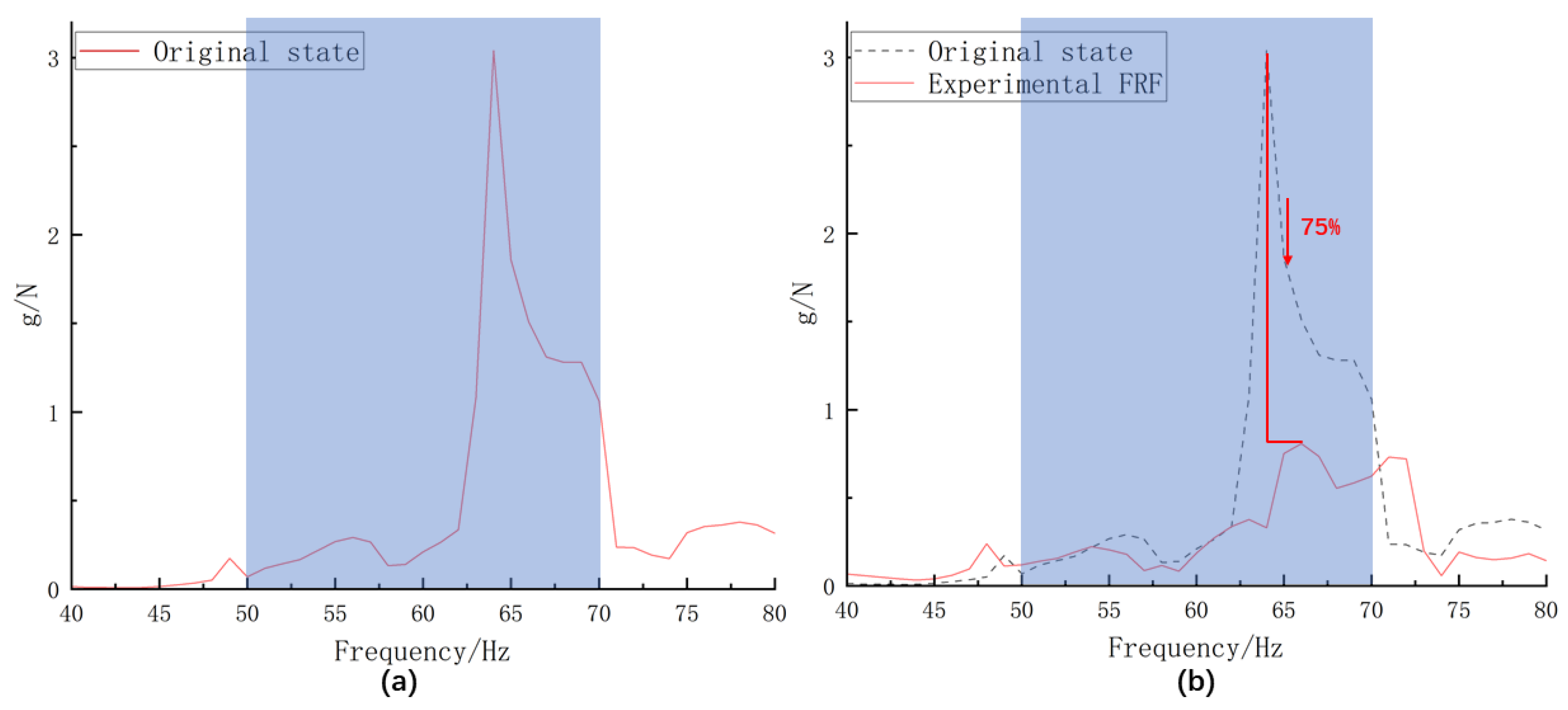
As shown in Figure 6a, the experimentally obtained frequency response function (FRF) of the car door exhibits pronounced peaks in the 50–70 Hz frequency band. Under driving conditions, the natural vibrational characteristics in this range readily induce structural resonance, thereby deteriorating the vehicle’s NVH performance. Based on this observation, the target band gap design frequency range of the LRAM is defined as 50–70 Hz to specifically suppress the dominant resonance peaks (52–68 Hz) observed in the door’s experimental FRF (Figure 6a). The tolerance of ±2 Hz was determined according to the manufacturing tolerance (a geometric error of +0.5 mm), which caused a frequency deviation of less than 1.5 Hz in the simulated analysis. This lightweight design strategy effectively controls the change in the vehicle’s body mass introduced by the integration of the LRAM on the door, thus reducing the associated additional energy losses.
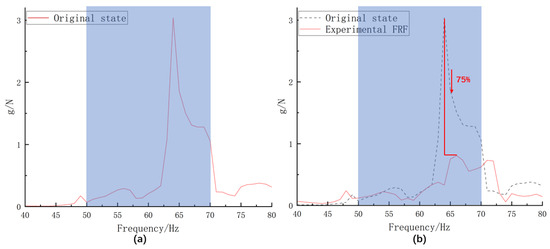
Figure 6.
(a) The FRF of the door is measured experimentally before arranging the LRAM; (b) the FRF of the door after arranging the LRAM is compared with the FRF in the original state.
The optimization component of our method is embodied by the NSGA-II, which iteratively “learns” the optimal mapping between the geometric parameters of the unit cell and the performance of the acoustic band gap. Through a COMSOL–MATLAB co-simulation loop, COMSOL computes the real-time dispersion curves for a candidate design and transmits the first branch maximum and second branch minimum frequencies to MATLAB, and MATLAB evaluates two fitness functions—the band gap error minimization and mass reduction—to guide the selection, crossover, and mutation operators. After 200 generations (population size = 15, crossover rate = 0.8, mutation rate = 0.2), Pareto-optimal designs are identified for fabrication and subsequent tests.
An initial unit cell model of the locally resonant structure was constructed in a finite element environment with the following geometric parameters:
This model was exported in code form and imported into MATLAB. By integrating a multi-objective genetic algorithm with the COMSOL-based structural model via co-simulation, the optimization loop was fully automated: COMSOL computes the dispersion curve data in real time and transmits it to MATLAB, where the maximum frequency M of the first branch and the minimum frequency m of the second branch are extracted to determine the current first-order band gap range.
Two fitness functions were defined for the optimization: 1. The first fitness value corresponds to the band gap error minimization, such that smaller values drive the first-order band gap toward the target range of 50–70 Hz. 2. The second fitness value represents the mass of the unit cell structure. The mass is defined as the second objective fitness function , as shown in Equation (2), where a smaller fitness value indicates the better lightweight performance of the designed local resonance unit. Here, denotes the material’s density, and V is the total volume of the structure composed of the unit cell structure.
The constant term 1600 represents the invariant mass contribution from the fixed square frame, which remains unchanged during optimization. This term ensures full accounting of the baseline structural mass while optimizing the variable components.
The genetic algorithm was configured with a population size of 15, a crossover rate of 0.8, a mutation rate of 0.2, and a maximum of 200 generations. Non-dominated sorting was used to trace the Pareto front for the two objectives. After convergence, the Pareto-optimal set is shown in Figure 7. From this set, the design exhibiting a cumulative band gap deviation within Hz and the minimal mass was selected, yielding the optimal parameters
with a total unit cell mass of .
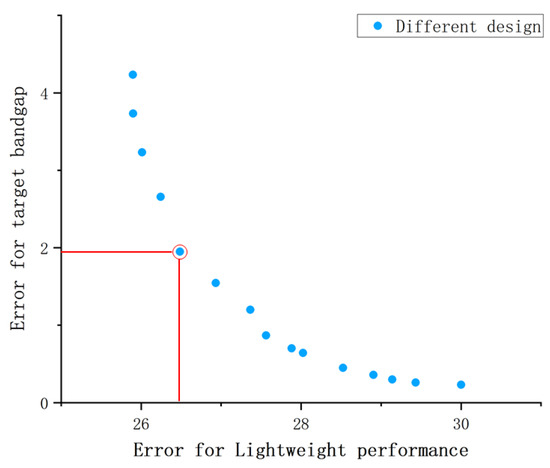
Figure 7.
Pareto-optimal solution set and we marked the selected data point and created the corresponding design parameters for the LRAM.
4. Results and Discussion
To validate the practical performance of the optimized LRAM for low-frequency vibration suppression, experimental tests were conducted focusing on the resonance modes of the automobile door. A 1 mm thick 201 stainless-steel plate was laser-cut into the main geometry. To achieve a designed oscillator thickness of mm, identical 1 mm thick 201 stainless-steel sheets were bonded to both the top and bottom surfaces of the central resonator, as illustrated in Figure 8a.

Figure 8.
(a) Manufactured LRAM; (b) LRAM layout.
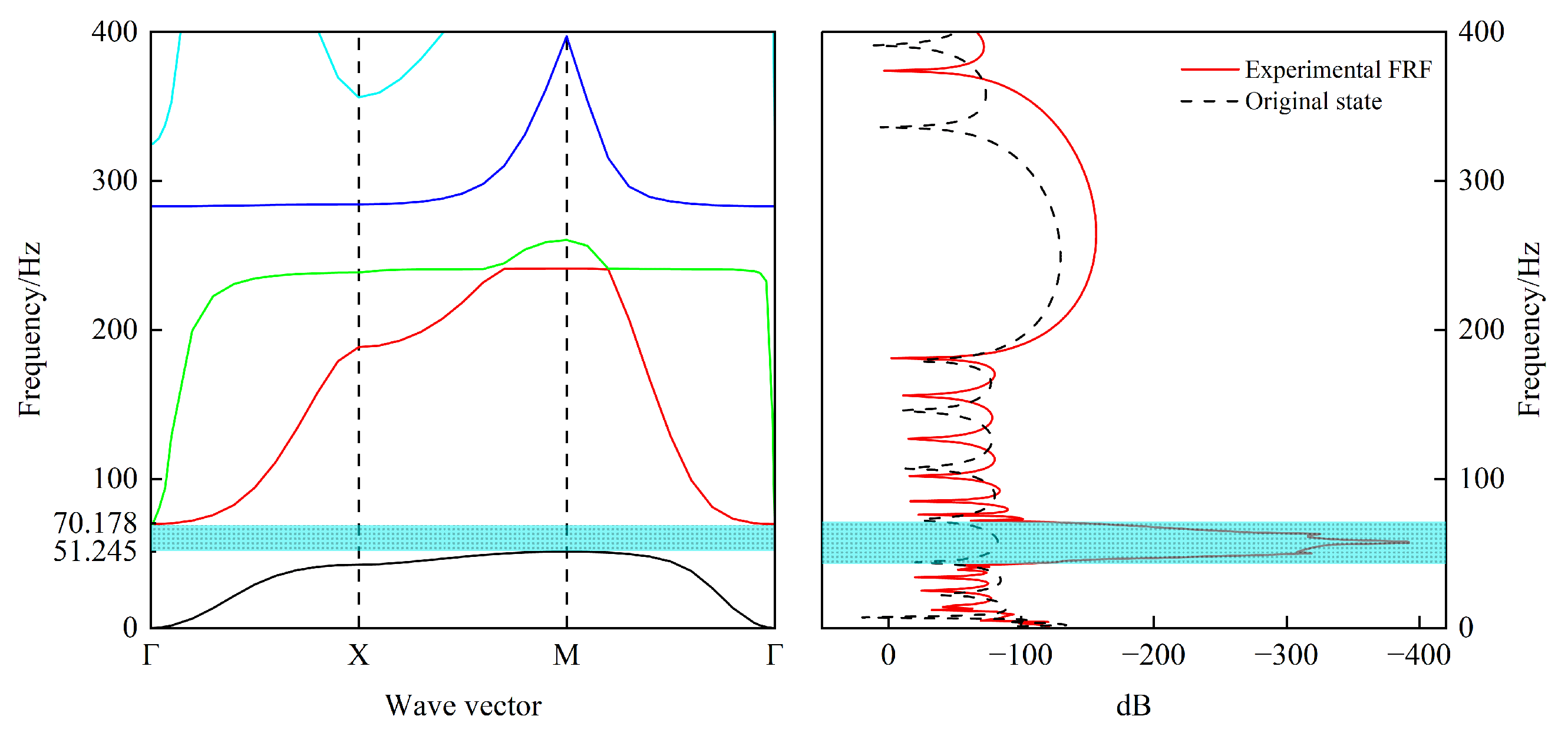
First, the vibration attenuation performance of the designed LRAM was evaluated via simulations. In COMSOL Multiphysics, both the dispersion relations and the transfer function of the structure were computed, as shown in Figure 9. The first-order band gap was found to range from to , demonstrating excellent vibration suppression capabilities within the 50–70 Hz band.
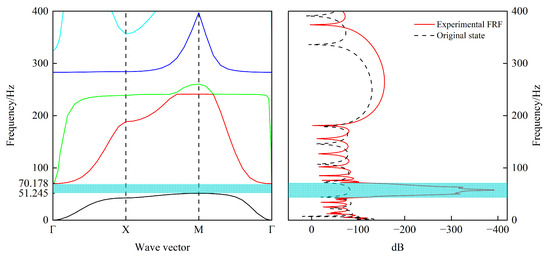
Figure 9.
The dispersion curve and the FRF of the optimized unit are calculated using COMSOL. The dispersion curve indicates that the band gap of the designed LRAM is 51.245 Hz–70.178 Hz, and the FRF also confirms this.
Subsequently, the vibration attenuation performance of the designed LRAM was evaluated experimentally. As illustrated in Figure 6b, four optimized AM units were arranged in a ring around the measurement point. The resulting FRF of the car door after AM deployment is presented in Figure 8b.
Subsequently, the first-order band gap predicted from the optimized dispersion curves was found to span 51.245–70.178 Hz, while the experimental measurements revealed the most pronounced vibration attenuation at 63 Hz. This central frequency closely aligns with the simulation’s prediction, demonstrating that the proposed COMSOL and MATLAB co-simulation multi-objective genetic algorithm optimization framework achieves high accuracy in band gap localization and validates the reliability of the model parameterization and sampling resolution. Moreover, the Pareto-optimal solutions strike a significant balance between the band gap deviation and structural lightweighting, overcoming the traditional AM trade-off of “broad bandwidth at the expense of mass” and confirming the global search capability of the genetic algorithm. In automotive NVH control applications, the lightweight design avoids additional energy consumption from the extra mass, while precise band gap coverage directly enhances the noise reduction efficacy, yielding clear engineering value.
The numerical simulations and experimental tests both confirm that the optimized LRAM exhibits excellent vibration suppression within the target frequency band. From the attenuation depth of the measured transfer function, the acceleration amplitude peak at 63 Hz decreases by approximately 75% compared to that for the untreated door, indicating that the local resonance unit provides substantial energy dissipation and effectively improves the in-cabin low-frequency noise experience. Further analysis shows that this high attenuation results from strong coupling between the local resonance unit and the substrate vibration and that the resonant frequency can be finely tuned via the geometric parameters to achieve precise coverage of the desired band.
5. Conclusions
This study presents a co-simulation framework integrating COMSOL Multiphysics and MATLAB, employing a multi-objective genetic algorithm (NSGA-II) for the design of LRAMs targeting low-frequency vibration suppression in automotive applications.
(1) Optimization Efficacy: The framework effectively balances band gap accuracy and unit cell mass. By minimizing the squared deviation from the target first-order band gap (50–70 Hz) and the unit cell mass, the Pareto front achieved an optimal design with a mass of 26.49 g and a band gap deviation within ±2 Hz.
(2) Experimental Validation: The experimental results corroborate the simulation predictions, with significant vibration attenuation observed at 63 Hz—aligning closely with the simulated band gap range of 51.245–70.178 Hz. This validates the framework’s predictive accuracy and robustness under complex boundary conditions.
(3) Design Flexibility: The modular framework supports adaptation to diverse frequency requirements, including multi-band or broadband AM design, via generalized fitness functions. While extending to n target band gaps increases the computational load proportionally, the co-simulation architecture leverages parallel processing to maintain feasibility. Future work will implement this approach for multi-band NVH control.
(4) Practical Considerations: While the optimization framework demonstrates advantages under validated free-boundary conditions (Figure 5 and Figure 6), its practical deployment requires further investigation of the performance under real-world operating environments—including dynamic mechanical loading, thermal variations, and complex structural coupling. Future work will integrate these factors into the co-simulation framework and conduct on-road NVH testing. Nevertheless, the current experimental results confirm the metamaterial’s efficacy in suppressing target resonances (e.g., a 75% reduction at 63 Hz), establishing a foundation for application-specific refinements.
In summary, the proposed framework offers a robust approach to designing lightweight AMs with precise low-frequency band gap characteristics, holding significant potential for applications in automotive NVH control.
Author Contributions
Conceptualization: Y.W., Y.Q. and Y.H.; Methodology: J.D., Y.W. and Y.Q.; Software: X.Z. and W.M.; Validation, J.D., X.C. and Y.S.; Formal Analysis: S.L. and Y.H.; Investigation: J.D. and X.C.; Resources: Y.W. and Y.Q.; Data Curation: J.D., Y.S. and W.M.; Writing—Original Draft Preparation: Y.Q. and Y.W.; Writing—Review and Editing: Y.H. and S.L.; Visualization: X.Z.; Supervision: Y.W.; Project Administration: Y.H.; Funding Acquisition: Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the 2023 Open Foundation of the State Key Laboratory of Advanced Vehicle Integration and Control [RBJ33], the Talent Program (Ph.D. Fund) of Chengdu Technological University [2024RC025], and the Science and Technology Program of Yibin [2024JC017].
Data Availability Statement
The data are available from the authors on reasonable request.
Acknowledgments
The author thanks China First Automobile Co., Ltd.; Chengdu Technological University; and Southwest Jiaotong University for their support in completing this work.
Conflicts of Interest
Authors Jianjiao Deng, Xi Chen, Yu Song, Xinpeng Zhang, Wenting Ma and Shoukui Li were employed by the company China FAW Group Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Masri, J.; Amer, M.; Salman, S.; Ismail, M.; Elsisi, M. A survey of modern vehicle noise, vibration, and harshness: A state-of-the-art. Ain Shams Eng. J. 2024, 15, 102957. [Google Scholar] [CrossRef]
- Mishra, V.N.; Gupta, D.A.; Sarangi, D.S.K. Numerical and Experimental Study of Layered Beams with Vibration-Damping Coatings for Improved Vibration Mitigation. Mech. Res. Commun. 2025, 148, 104476. [Google Scholar] [CrossRef]
- AktaŞ, K.G.; GüvenÇ, M.A. Numerical and Analytical Free Vibration Analysis of Composite Plate with Auxetic Core Layer and Functionally Graded Surface Layers. Aerosp. Res. Lett. (ASREL) 2024, 3, 158. [Google Scholar] [CrossRef]
- Kang, X.; Li, H.; Zhu, X.; Zhang, A.; Tang, J.; Shi, X. Optimization of vibration control of adjacent buildings structures by a new inertial amplified mass-tuned damper. J. Inst. Eng. (India) Ser. A 2025, 106, 241–258. [Google Scholar] [CrossRef]
- Hansen, C.H.; Snyder, S.D.; Qiu, X.; Brooks, L.A.; Moreau, D.J. Active Control of Noise and Vibration; E & Fn Spon London: London, UK, 1997; p. 1267. [Google Scholar]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022. [Google Scholar] [CrossRef]
- Xu, J.; Mao, W.; Yu, X.; Liu, B. Prediction and optimization of acoustic absorption performance of quasi-Helmholtz acoustic metamaterials based on LightGBM algorithm. AIP Adv. 2025, 15, 015125. [Google Scholar] [CrossRef]
- Chen, Z.; Guo, B.; Yang, Y.; Cheng, C. Metamaterials-based enhanced energy harvesting: A review. Phys. B Condens. Matter 2014, 438, 1–8. [Google Scholar] [CrossRef]
- Liu, N.; Sun, Y.; Wang, Y.; Sun, P.; Li, W.; Guo, H. Mechanism of interior noise generation in high-speed vehicle based on anti-noise operational transfer path analysis. Proc. Inst. Mech. Eng. Part J. Automob. Eng. 2021, 235, 273–287. [Google Scholar] [CrossRef]
- Cummer, S.A.; Christensen, J.; Alù, A. Controlling sound with acoustic metamaterials. Nat. Rev. Mater. 2016, 1, 1–13. [Google Scholar] [CrossRef]
- Fahy, F.J. Sound and Structural Vibration: Radiation, Transmission and Response; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Zhang, Y.; Zhu, Z.; Sheng, Z.; He, Y.; Wang, G. Vibro-acoustic suppression of metamaterial plates in multi-bandgaps. Int. J. Mech. Sci. 2025, 286, 109873. [Google Scholar] [CrossRef]
- Wu, Y.; Yan, W.; Wen, G.; He, Y.; Deng, S.; Ding, W. Design and Application of a Lightweight Plate-Type Acoustic Metamaterial for Vehicle Interior Low-Frequency Noise Reduction. Crystals 2024, 14, 957. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, L.; Sun, L.; Li, N. Optimization of graded filleted lattice structures subject to yield and buckling constraints. Mater. Des. 2021, 206, 109746. [Google Scholar] [CrossRef]
- Yang, N.; Qian, Z.; Wei, H.; Zhao, M. Anisotropy and deformation of triply periodic minimal surface based lattices with skew transformation. Mater. Des. 2023, 225, 111595. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, D.Z.; Li, Z.; Zhang, T.; Zhou, H.; Ren, Z. Design, mechanical properties, and optimization of BCC lattice structures with taper struts. Compos. Struct. 2022, 295, 115830. [Google Scholar] [CrossRef]
- Yang, F.; Yang, J.S.; Wang, Y.; Li, S.; Chen, Y.Y. Low frequency bandgap characteristics of a 3D chiral acoustic metamaterial structure. Wave Motion 2024, 128, 103303. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Huang, J.; Chen, J.; Mai, H.; Wan, H.; Chen, R.; He, T. Performance prediction and inverse design of cylindrical plate-type acoustic metamaterials based on deep learning. Appl. Acoust. 2025, 234, 110633. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Maamoun, K.S.A.; Wrona, S.; Pawelczyk, M.; Karimi, H.R. Optimizing design of openings in vibrating plates for enhanced vibro-acoustic performance using a genetic algorithm approach. J. Sound Vib. 2025, 598, 118847. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Wang, Y.; Luo, Y. Ultra-wide low-frequency bandgap design of acoustic metamaterial via multi-material topology optimization. Compos. Struct. 2023, 306, 116584. [Google Scholar] [CrossRef]
- Hu, Z.; Ding, J.; Ding, S.; Ma, W.W.S.; Chua, J.W.; Li, X.; Zhai, W.; Song, X. Machine learning–enabled inverse design of shell-based lattice metamaterials with optimal sound and energy absorption. Virtual Phys. Prototyp. 2024, 19, e2412198. [Google Scholar] [CrossRef]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Z.; Wang, W.; Ji, W.; Yu, T.; Gao, P. Vibration Manipulation Properties of Phononic Crystals and Acoustic Metamaterials for Fluid-Conveying Pipeline Systems: A Review. J. Vib. Eng. Technol. 2025, 13, 114. [Google Scholar] [CrossRef]
- Sun, H.; Hai, H.; Zhou, C.; Wang, W.; Chen, C.; Xu, W. Attenuation effects of seismic metamaterials based on local resonance and Rayleigh wave dispersion phenomena. Mech. Res. Commun. 2025, 143, 104367. [Google Scholar] [CrossRef]
- Zhang, K.; Guo, Y.; Liu, X.; Hong, F.; Hou, X.; Deng, Z. Deep learning-based inverse design of lattice metamaterials for tuning bandgap. Extrem. Mech. Lett. 2024, 69, 102165. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).