Performance Analysis of a Reciprocating Refrigeration Compressor Under Variable Operating Speeds

Abstract

Variable-speed reciprocating compressors (VSRCs) have been increasingly used in domestic refrigeration due to their ability to modulate cooling capacity and reduce energy consumption. A detailed understanding of performance-limiting factors such as volumetric and exergetic inefficiencies is essential for optimizing their operation. An experimentally validated simulation model was developed using GT-SUITE to analyze a VSRC operating with R-600a across speeds from 1800 to 6300 rpm. Volumetric inefficiencies were quantified using a stratification methodology, while an exergy-based approach was adopted to assess the main sources of thermodynamic inefficiency in the compressor. Unlike traditional energy analysis, exergy analysis reveals where and why irreversibilities occur, linking them directly to power consumption and providing a framework for optimizing design. Results reveal that neither volumetric nor exergy efficiency varies monotonically with compressor speed. At low speeds, exergetic losses are dominated by the electrical motor (up to 19% of input power) and heat transfer (up to 13.5%). Conversely, at high speeds, irreversibilities from fluid dynamics become critical, with losses from discharge valve throttling reaching 5.8% and bearing friction increasing to 6.5%. Additionally, key volumetric inefficiencies arise from piston–cylinder leakage, which causes up to a 4.5% loss at low speeds, and discharge valve backflow, causing over a 5% loss at certain resonant speeds. The results reveal complex speed-dependent interactions between dynamic and thermodynamic loss mechanisms in VSRCs. The integrated modeling approach offers a robust framework for diagnosing inefficiencies and supports the development of more energy-efficient compressor designs.

1. Introduction

Refrigeration systems play a crucial role in modern society, with applications from thermal comfort and medical preservation to data center cooling and household use [1]. Within this context, reciprocating compressors are widely used in domestic refrigeration, particularly in small-capacity systems, due to their high efficiency, reliability, and cost-effectiveness.

Conventional hermetic reciprocating compressors used in household applications typically operate under thermostatic on–off control to maintain compartment temperature. Although being a straightforward and widely used approach, it has notable disadvantages that diminish the overall system efficiency. Variable-speed reciprocating compressors (VSRCs) present a more efficient alternative, allowing for the continuous modulation of refrigeration capacity while minimizing energy consumption. In fact, capacity control through VSRCs can lead to significant energy savings, with reductions of up to 7% reported in domestic refrigeration systems [2].

Improving the energy performance of a compressor requires methods capable of identifying and quantifying its primary inefficiencies. Traditionally, this has been performed by comparing the p-V diagrams of real and ideal compression cycles. However, such first-law-based approaches have become insufficient for optimizing compressors that already operate with high efficiency. In contrast, assessments based on the Second Law of Thermodynamics allow for more detailed and insightful analyses. As McGovern and Harte [3] observed, relying solely on isentropic efficiency does not always lead to optimal compressor design and may obscure the true sources of inefficiency. The Second Law directly addresses irreversibilities, the root of energy losses, and thus enables a more accurate inventory of inefficiencies. By allowing for a systematic breakdown of exergy destruction by component and physical mechanism (e.g., valve throttling, viscous friction in mufflers, leakage, and heat transfer), exergy analysis offers both component-specific and condition-dependent insights. This level of resolution provides a more actionable foundation for performance optimization than traditional energy balances. Ultimately, exergy analysis offers a rigorous and practical approach to reducing compressor power consumption by identifying and minimizing irreversibility. In other words, reducing total exergy destruction (${\dot{I}}_t$) directly decreases the required input power (${\dot{W}}_{sup}={\dot{W}}_{rev}+{\dot{I}}_t$). Following this approach, Posch et al. [4] developed a simulation model for a conventional hermetic reciprocating compressor and found that, at 3000 rpm, exergy losses associated with the fluid flow and electric motor accounted for approximately 70% of total compressor losses, with a substantial share attributed to fluid flow through the suction valve.

Volumetric efficiency, defined as the ratio of actual to ideal mass flow rates, is a critical parameter in compressor performance, as reductions in mass flow directly impair cooling capacity. This highlights the importance of identifying and understanding the factors that influence volumetric efficiency. McGovern [5] proposed a simplified method for reciprocating compressors, accounting for effects such as gas re-expansion in the clearance volume, leakage, valve backflow, pressure losses in the suction and discharge systems, and in-cylinder heat transfer. Although this approach offers a general overview, it requires empirical adjustments for practical application.

Pérez-Segarra et al. [6] advanced this approach by identifying the following six distinct sources of volumetric inefficiency: motor slip, gas re-expansion in the clearance volume, suction process losses, suction valve supercharging, discharge valve backflow, and leakage through the piston–cylinder gap. This framework contributed significantly to the detailed characterization of volumetric inefficiencies. Schreiner et al. [7] further refined the approach by incorporating effects of suction gas superheating, suction valve opening delays, and various factors influencing the re-expansion process, such as heat transfer, leakage, and discharge valve dynamics.

This manuscript presents a performance analysis of a variable-speed reciprocating compressor (VSRC) using a comprehensive simulation model validated through experimental data. The following two recently developed and complementary methodologies are applied to identify and quantify the main sources of inefficiency as a function of compressor speed: a volumetric inefficiency stratification procedure [8] and an exergy-based analysis approach [9]. The analysis focuses on a reciprocating compressor operating under fully developed cyclic conditions across a speed range from 1800 to 6300 rpm, considering ASHRAE low back pressure (LBP) and medium back pressure (MBP) conditions, with R600a (isobutane) as the working fluid.

2. Materials and Methods

2.1. Simulation Model

The simulation model was implemented with the assistance of the commercial software GT-SUITE (v.2021) and comprises sub-models for the compression cycle, heat transfer, and mechanical and electrical losses. Figure 1 presents a schematic diagram of the reciprocating compressor, identifying the key components considered in the model. The variable-speed motor drives a piston within the compression chamber, where refrigerant gas is compressed. This process gives rise to pressure pulsations; therefore, suction and discharge mufflers are included to attenuate pressure waves, noise and vibration, though they also introduce thermodynamic losses from viscous friction and heat transfer. The lubricating oil is located at the bottom of the hermetic shell, acting to decrease mechanical friction and aiding in the overall thermal management of the compressor.

The compression cycle model employs the methodology of Link and Deschamps [10], while the thermal model is based on the work of Diniz et al. [11]. A quasi-steady state approach is employed for the compression cycle simulation, justified by its significantly shorter time scale (milliseconds) relative to the compressor overall thermal transients (minutes).

2.1.1. Compression Cycle Model

The compression cycle model employs a lumped-parameter approach for the reciprocating compressor compression chamber. Unsteady state mass and energy conservation equations are solved for this chamber to evaluate its instantaneous volume, the thermodynamic properties of the gas (within the chamber and connected mufflers), valve dynamics, pressure pulsations in the suction and discharge mufflers, and mass flow rates through the valves and piston–cylinder clearance. Flow in the piston–cylinder clearance is modeled as one-dimensional and compressible [12]. Transient compressible flow within the suction and discharge mufflers is similarly treated using a one-dimensional approach, with the governing equations solved by the finite volume method for a network of interconnected tubes and volumes [10].

The dynamics of suction and discharge valves are modeled as single degree-of-freedom systems. Equivalent mass and stiffness for these valves are obtained via finite element analysis, and the damping coefficient is adjusted using experimental valve motion data. The flow-induced pressure load on each valve is calculated using the concept of effective force area, which is derived from three-dimensional numerical simulations. Similarly, mass flow rates through the suction and discharge orifices are determined by applying the effective flow area concept also obtained from the three-dimensional simulations.

2.1.2. Thermal Model

The accurate prediction of the compressor thermal profile is essential for understanding the thermodynamic processes within the compression cycle and the consequent entropy generation in hermetic reciprocating compressors. The thermal model in this study adapts the approach of Diniz et al. [11], incorporating modifications to better evaluate heat transfer in the suction and discharge muffler flows, which varies with compressor speed.

The modeling employs an integral formulation of the energy balance for its low computational cost. The compressor is divided into non-overlapping control volumes that exchange heat through global conductances. Based on Diniz et al. [11], the following eight control volumes are defined: compression chamber, suction and discharge mufflers, discharge tube, oil, electric motor, shell, and internal environment. These global conductances are calibrated using temperature measurements from various compressor locations. The thermal model also includes internal heat generation rates, such as motor heat dissipation, and heat exchange between components through solid walls. To account for the influence of oil pumping on thermal behavior, conductances are calibrated at two distinct rotational speeds, with linear interpolation applied for intermediate speeds. Wall temperatures for the suction muffler, discharge muffler, and discharge tube are determined by solving the energy equation for each control volume, using the Colburn correlation for internal convection.

The indirect suction system adopted in the compressor under analysis is modeled using a mixing factor, $\phi$ (Equation (1)), which is derived from an energy balance at the suction muffler inlet. This factor indicates the portion of refrigerant flowing directly into the suction muffler. The terms $h_{sl}$, $h_{ie}$, and $h_{se}$ represent the specific enthalpies of the gas at the suction line, internal environment, and suction muffler inlet, respectively. These are determined from component temperatures and the suction line pressure. The equation is shown as follows:

$$\phi ={\displaystyle \frac{h_{se}-h_{ie}}{h_{sl}-h_{ie}}}$$

(1)

2.1.3. Mechanical and Electrical Losses Model

Mechanical losses in the hermetic reciprocating compressor primarily originate from friction at the bearings and within the piston–cylinder clearance. Bearing losses, encompassing those from the crankshaft journal bearing, connecting rod large and small ends, and piston–liner contact, are calculated using the mobility method [13], an approach consistent with that of Tormos et al. [14]. Mechanical losses due to piston–cylinder clearance are also modeled, and the results are verified against the procedure outlined by Ferreira and Lilie [15]. Electrical losses are determined from manufacturer-provided electrical efficiency data for the compressor across its range of rotational speeds. Both mechanical and electrical losses are incorporated as heat sources in the thermal model and are considered in the exergy loss analysis.

2.1.4. Solution Procedure

The coupled compression cycle and thermal models are solved numerically using an explicit fifth order Runge–Kutta method. The time step is selected to ensure that the Courant number remains below 0.7. Input data for the simulation model are detailed in

Table 1. Input parameters for the simulation model.

Category	Input Variables
Operating conditions	Evaporating and condensing temperatures, ambient temperature, compressor speed.
Mufflers	Diameter and length of tubes, volume of muffler chambers, and mixing factor of indirect suction.
Crankshaft mechanism	Lengths of the connecting rod and crank, shaft eccentricity, and piston diameter.
Compression chamber	Cylinder bore and clearance volume.
Motor	Efficiency curve.
Lubricating oil	Viscosity as a function of temperature.
Valves	Stiffness, mass, damping coefficient, effective areas, Young’s modulus, diameter and number of orifices, minimum gap, reed thickness.
Thermal model	Global conductances.

.

The simulation initializes with arbitrary pressure and temperature values. After the first complete compression cycle (a full piston revolution), the thermal model is solved. Given that the compression cycle’s time scale is significantly shorter than that of the thermal model, the compression cycle equations are solved assuming constant temperatures over each cycle; its outputs are then time-averaged for use in the thermal model. For subsequent iterations, the end-state of the previous cycle serves as the initial condition for the next. This iterative process is repeated until a fully established cyclic condition is reached, signifying that predicted property values show no significant differences between consecutive cycles. In this work, convergence is achieved when the difference in pressure and mass between two consecutive cycles is less than 0.2%, and temperature variations are below 0.01 °C.

2.2. Inefficiency Sources

2.2.1. Volumetric Inefficiency Sources

Volumetric efficiency (${\mathsf{\eta }}_v$) quantifies the actual mass flow rate delivered by the compressor relative to an ideal theoretical rate (${\dot{m}}_{th}$). The estimation of this ideal mass flow rate assumes the following conditions: (i) no heat transfer or pressure drop occurs in the suction system; (ii) suction and discharge processes are isobaric and without backflow through the valves; (iii) there are no leaks from the compression chamber; (iv) there is no motor slip; and (v) the cylinder has no clearance volume. Under these assumptions, the ideal mass flow rate is expressed as follows:

$${\dot{m}}_{th}={\displaystyle \frac{N_{th}\mathrm{ }{\mathsf{\rho }}_{sl}{\forall }_{sw}}{60}}$$

(2)

where $N_{th}$ is the nominal rotational speed of the motor, ${\mathsf{\rho }}_{sl}$ is the refrigerant density at the suction line, and ${\forall }_{sw}$ is the piston displaced volume.

The volumetric efficiency is then defined by the following:

$${\mathsf{\eta }}_v={\displaystyle \frac{\dot{m}}{\dot{m_{th}}}}={\displaystyle \frac{\dot{m_{th}}-{\sum }_i\Delta \dot{m_i}}{\dot{m_{th}}}}=1\mathrm{ }-\sum _i\Delta {\mathsf{\eta }}_{v_i}$$

(3)

where $\Delta \dot{m_i}$ represents the reduction in mass flow rate due to a specific phenomenon $i$ within the compression cycle. The term $\Delta {\eta }_{v_i}$, which is the ratio of $\Delta \dot{m_i}$ to ${\dot{m}}_{th}$, quantifies the volumetric inefficiency attributed to that phenomenon. The primary sources contributing to mass flow rate reduction are listed in

Table 2. Volumetric inefficiency sources.

Source	Related Phenomena
Motor	Actual motor shaft speed is consistently lower than its nominal speed due to slip.
Suction muffler	Viscous friction and gas superheating.
Suction valve	Throttling, backflow, supercharging, pressure pulsation in suction and discharge chambers, valve opening delay, and oil stiction.
Clearance volume	Re-expansion of gas trapped in the clearance volume, considering heat transfer and leakage during the expansion process.
Piston–cylinder clearance	Leakage.
Discharge valve	Throttling, backflow, over compression, and closure delay, depending on valve dynamics and pressure pulsation in the discharge chamber.

. The detailed determination of $\Delta \dot{m_i}$ for each of these sources follows the methodology developed by [8].

2.2.2. Exergy Losses

An exergy-based method, based on the concept of exergy destruction (i.e., irreversibility or entropy generation), is employed to analyze sources of energy inefficiency. The total exergetic efficiency (${\eta }_{\mathrm{e}\mathrm{x}\mathrm{e},\mathrm{t}}$) of a system is defined as the ratio of the minimum required (reversible) power (${\dot{W}}_{\mathrm{r}\mathrm{e}\mathrm{v}}$) to the actual supplied power (${\dot{W}}_{\mathrm{s}\mathrm{u}\mathrm{p}}$) needed to change the thermodynamic state of a fluid. This efficiency can also be expressed in terms of the total exergy destruction or total irreversibility (${\dot{I}}_{\mathrm{t}}$), as follows:

$${\eta }_{\mathrm{e}\mathrm{x}\mathrm{e},\mathrm{t}}={\displaystyle \frac{{\dot{W}}_{\mathrm{r}\mathrm{e}\mathrm{v}}}{{\dot{W}}_{\mathrm{s}\mathrm{u}\mathrm{p}}}}={\displaystyle \frac{{\dot{W}}_{\mathrm{s}\mathrm{u}\mathrm{p}}-{\dot{I}}_{\mathrm{t}}}{\dot{{\dot{W}}_{\mathrm{s}\mathrm{u}\mathrm{p}}}}}$$

(4)

The Gouy–Stodola relation allows the total irreversibility to be disaggregated into a sum of local irreversibilities (${\dot{I}}_i$). When this method is applied to a compressor, the term ${\dot{W}}_{\mathrm{s}\mathrm{u}\mathrm{p}}$ represents the electric power supplied by the electric motor (${\dot{W}}_{\mathrm{e}\mathrm{l}\mathrm{e}}$). In this study, local irreversibilities within a VSRC are categorized into the following five main groups: fluid flow viscous friction, heat transfer, mechanical, electrical, and outlet losses. The normalized local irreversibility (${\eta }_{\mathrm{e}\mathrm{x}\mathrm{e},\mathrm{i}}$), representing the fraction of input power lost due to a specific source $i$, is formulated as follows:

$${\eta }_{\mathrm{e}\mathrm{x}\mathrm{e},\mathrm{i}}={\displaystyle \frac{{\dot{I}}_i}{{\dot{W}}_{e\mathrm{l}\mathrm{e}}}}$$

(5)

Table 3. Exergy loss (irreversibility) sources.

Source	Related Phenomena
Suction muffler	Gas superheating, viscous friction, and mixing.
Suction valve	Backflow, throttling, viscous friction, and mixing.
Piston–cylinder clearance	Energy dissipation due to friction in compressor bearings.
Discharge valve	Backflow, throttling, viscous friction, and mixing.
Discharge muffler	Energy dissipation due to friction in compressor bearings.
Heat transfer	Irreversibility arising from heat transfer between various compressor components.
Bearings	Energy dissipation due to viscous friction in bearings.
Electrical motor	Electrical energy dissipated as heat mainly due to copper and iron losses.
Outlet losses	Exergy difference between the actual thermodynamic state and the saturated state at the outlet.

details these irreversibility sources, including the various phenomena within the fluid flow. The determination of each local irreversibility (${\dot{I}}_i$) is based on established thermodynamic principles and detailed component modeling, drawing from the methodology proposed by [9].

3. Results

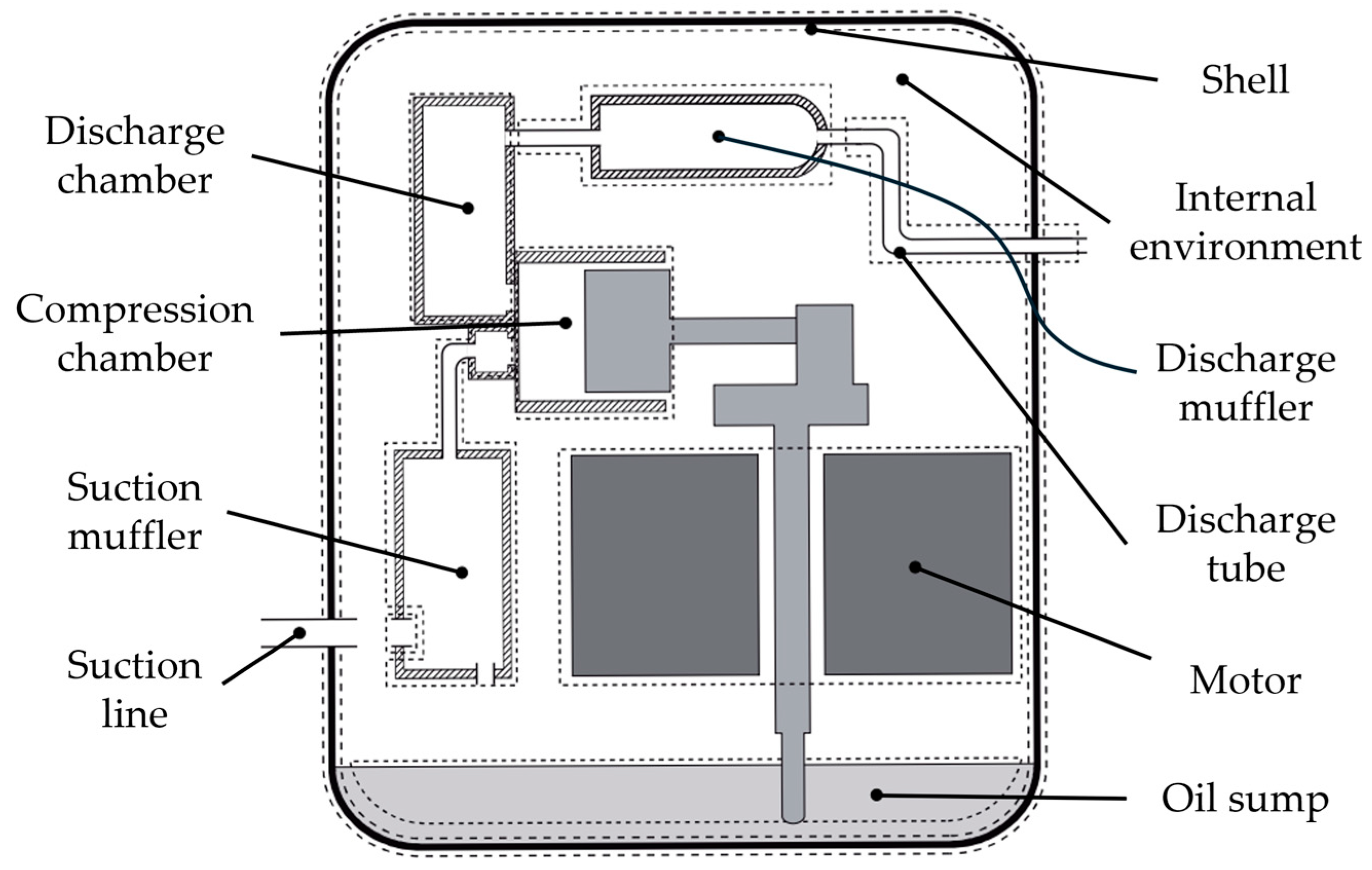
The analyses were conducted on a variable-speed hermetic reciprocating compressor (VSRC) with a 6.5 cm³ displacement, using R-600a as the refrigerant. This compressor features two distinct suction valves and two identical discharge valves. The study investigated rotational speeds from 1800 to 6300 rpm across various evaporating and condensing temperatures, with ambient and suction tube temperatures maintained at 32.2 °C.

3.1. Validation

Prior to experimental validation, a grid convergence study assessed numerical errors arising from the spatial discretization of the suction and discharge muffler tubes and chambers. Discretization errors were evaluated using the Grid Convergence Index (GCI) methodology proposed by Roache [16], which is based on Richardson’s extrapolation method. The ASHRAE low back pressure (LBP) condition (evaporating temperature $T_e$ = −23.3 °C, condensing temperature $T_c$ = 54.4 °C) at 1800 rpm and 6300 rpm (the lowest and highest speeds analyzed) was selected for this study. The results indicated that exergy loss predictions achieved asymptotic values with increasing grid refinement, and the solutions were confirmed to be in the asymptotic range of convergence. For the finest grid analyzed, the estimated errors for suction muffler exergy loss were 0.04% (at 1800 rpm) and 0.21% (at 6300 rpm). For the discharge muffler under the same conditions, the errors were 0.17% and 0.78%, respectively. The muffler discretization corresponding to this finest grid was used for all subsequent analyses.

The numerical model predictions were validated against experimental data obtained from a hot gas cycle calorimeter. The validation covered several key performance indicators, including p–V diagrams within the compression cylinder, pressure pulsations in the suction and discharge mufflers, refrigerant mass flow rates, compressor power consumption, and temperatures at various compressor components. The test bench allows the compressor to be evaluated independently of other refrigeration system components, ensuring well-defined and reproducible operating conditions.

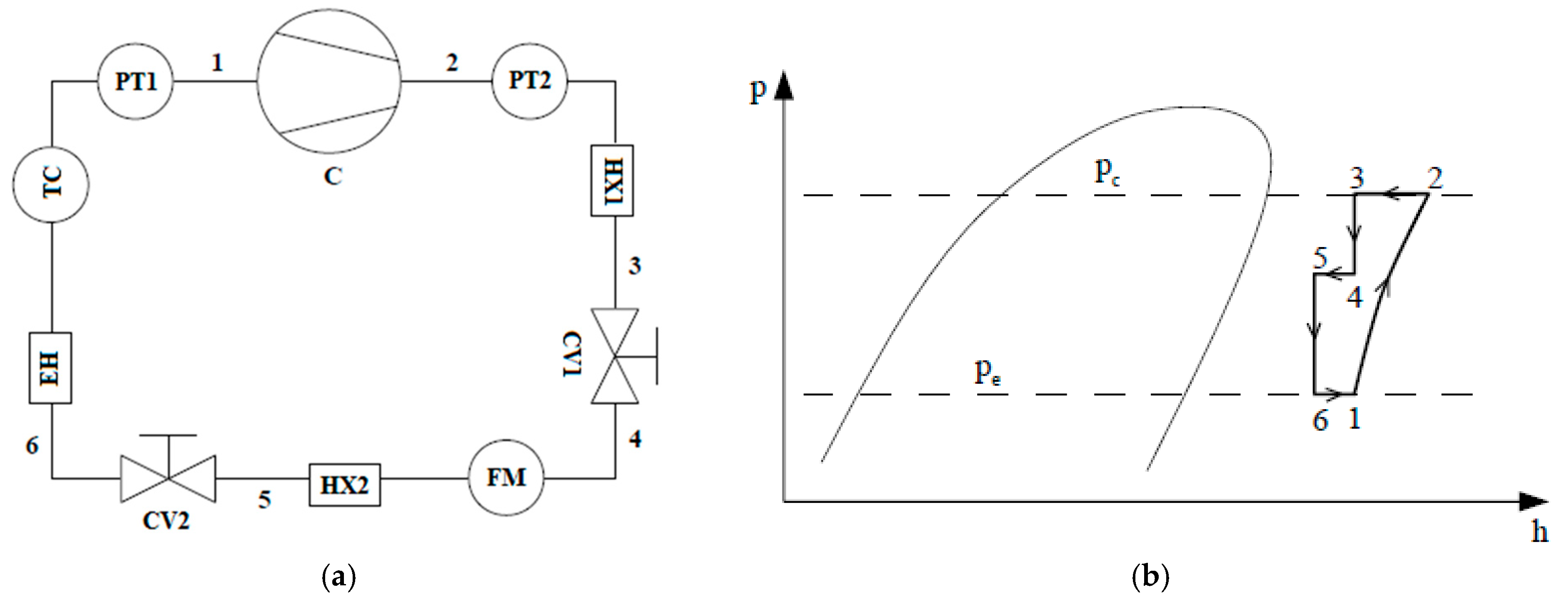
As shown in the schematic diagram of the calorimeter (Figure 2a), the experimental setup includes pipelines, servo-controlled needle valves (CV1 and CV2), a mass flow meter (FM), heat exchangers (HX1 and HX2), a thermocouple (TC), and pressure transducers (PT1 and PT2). The needle valves CV1 and CV2 are used exclusively to reduce the pressure from the condensing level to the evaporating level. This type of valve is particularly suitable for compressor testing, as it allows for the precise and independent control of suction and discharge pressures. By adjusting these valves, the compressor can be accurately set to operate under any desired condition.

The calorimeter is designed to ensure that the refrigerant flows through both the high- and low-pressure lines in a superheated state, as shown in the pressure–enthalpy diagram (Figure 2b). In this setup, refrigerant from the suction line (1) enters the compressor (C) and is compressed to the system’s condensing pressure $p_c$ (point 2). Pressure transducers PT1 and PT2 monitor the suction and discharge pressures, respectively. The fluid then passes through heat exchanger HX1, where its temperature is reduced (point 3), and is adiabatically expanded through control valve CV1 to an intermediate pressure (point 4). After the mass flow rate is measured by the flow meter FM, the fluid is further cooled in heat exchanger HX2 (point 5) and adiabatically expanded again through control valve CV2 to the evaporating pressure $p_e$ (point 6). Finally, an electrical heater (EH) and a thermocouple (TC) are used to adjust the fluid temperature in the suction line, returning it to the initial condition (point 1).

The thermodynamic conditions at the suction (1) and discharge (2) lines, and thus the operating conditions experienced by the compressor, are controlled by adjusting the refrigerant charge, the openings of the control valves, and the amount of thermal energy exchanged in the heat exchangers and by the electrical heater. In addition to the mass flow rate, the following parameters were measured during compressor operation: crankshaft angle, pressures in the suction and compression chambers, temperatures in the suction chamber and cylinder wall, and the suction valve opening. The experimental procedure involved mounting the compressor into the system, evacuating it to create a vacuum, admitting the desired amount of refrigerant, starting the compressor, and adjusting the control valves to establish the target operating conditions.

Measurements were conducted after the compressor had been operating for at least two hours to ensure that it reached a fully cyclic steady state regime. Data were then collected over a 30 min interval. Each test was repeated three times, with global parameters of the compression cycle (such as mass flow rate, indicated power, and local temperatures) reported as mean values. Parameters that vary with the crankshaft angle, such as p-V diagram, pressures in the suction and compression chambers, were taken from the cycle in which the global parameters most closely matched the overall mean.

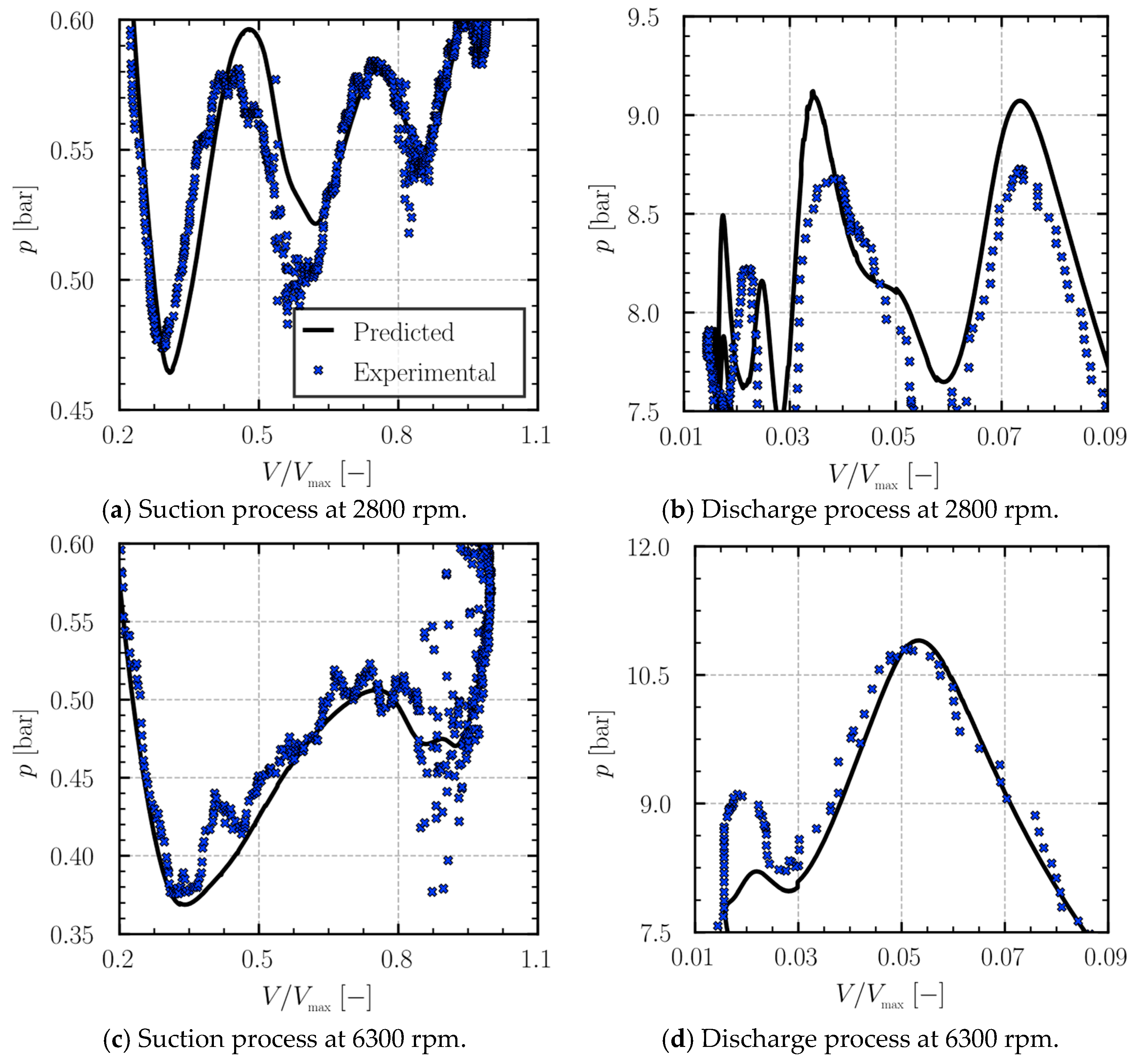
The p-V diagrams shown in Figure 3 for compressor speeds of 2800 and 6300 rpm demonstrated good agreement between predictions and measurements. Some minor deviations were observed, particularly during the discharge process at 2800 rpm. These discrepancies could be attributed to factors not fully captured by the model, such as the drilled channel in the cylinder wall for pressure transducer placement (which might induce high-frequency pulsations in the measurements) or simplifications in modeling valve phenomena like oil stiction on the seat and the precise assessment of effective force and flow areas.

Pressure pulsation predictions in both suction and discharge chambers (Figure 4) also aligned well with experimental data for 2800 and 6300 rpm. The model successfully captured the increase in pulsation amplitude with rising rotational speed, an effect also noted by Liu and Soedel [17]. Any slight differences observed may be due to the positioning of pressure transducers in the experimental setup or simplifications in the acoustic muffler and valve dynamic models.

Results of volumetric efficiency from predictions and measurements (

Table 4. Volumetric efficiency from predictions and measurements under the LBP condition and three compressor speeds.

Rotational Speed [rpm]	Volumetric Efficiency [-]		Difference [%]
	Experiment	Predicted
1800	0.72 ± 0.04	0.71	1.0
4000	0.71 ± 0.04	0.71	0.4
6300	0.64 ± 0.03	0.65	1.5

) across the 1800–6300 rpm range showed good agreement, with deviations falling within experimental uncertainty. Similarly, predicted power consumption (

Table 5. Power consumption from predictions and measurements under the LBP condition and three compressor speeds.

Rotational Speed [rpm]	Power Consumption [W]		Difference [%]
	Experiment	Predicted
1800	39.0 ± 2.0	39.8	2.1
4000	85.0 ± 4.2	85.5	0.5
6300	133.0 ± 6.7	131.6	−1.1

) matched experimental values closely. Finally, measured and numerically predicted temperatures at the suction chamber, discharge chamber, cylinder wall, and compressor shell are presented in

Table 6. Temperatures from predictions and measurements under the LBP condition and two compressor speeds.

Component	Temperature [°C]		Difference [°C]
	Experiment	Predicted
Rotational speed at 2200 rpm
Suction chamber	49.3	48.5	0.8
Shell	49.1	49.0	0.1
Cylinder wall	76.9	79.3	−2.4
Discharge chamber	87.7	88.7	−1.0
Rotational speed at 6300 rpm
Suction chamber	61.5	63.2	−1.7
Shell	56.0	56.6	−0.6
Cylinder wall	89.2	87.3	1.9
Discharge chamber	108.4	106.4	2.0

. The thermal model global conductances were calibrated using data from LBP conditions at rotational speeds ranging from 2800 to 6300 rpm. With these calibrated conductances, the simulation model demonstrated its ability to accurately predict compressor temperatures, including at speeds such as 2200 rpm, which is outside the direct calibration range but within the model’s predictive capability.

These comprehensive comparisons confirm that the simulation model can accurately predict p-V diagrams, pressure pulsations, mass flow rates, power consumption, and component temperatures across different rotational speeds. The developed simulation model is therefore considered validated and suitable for undertaking the subsequent performance analyses presented herein.

3.2. Volumetric Efficiency Analysis

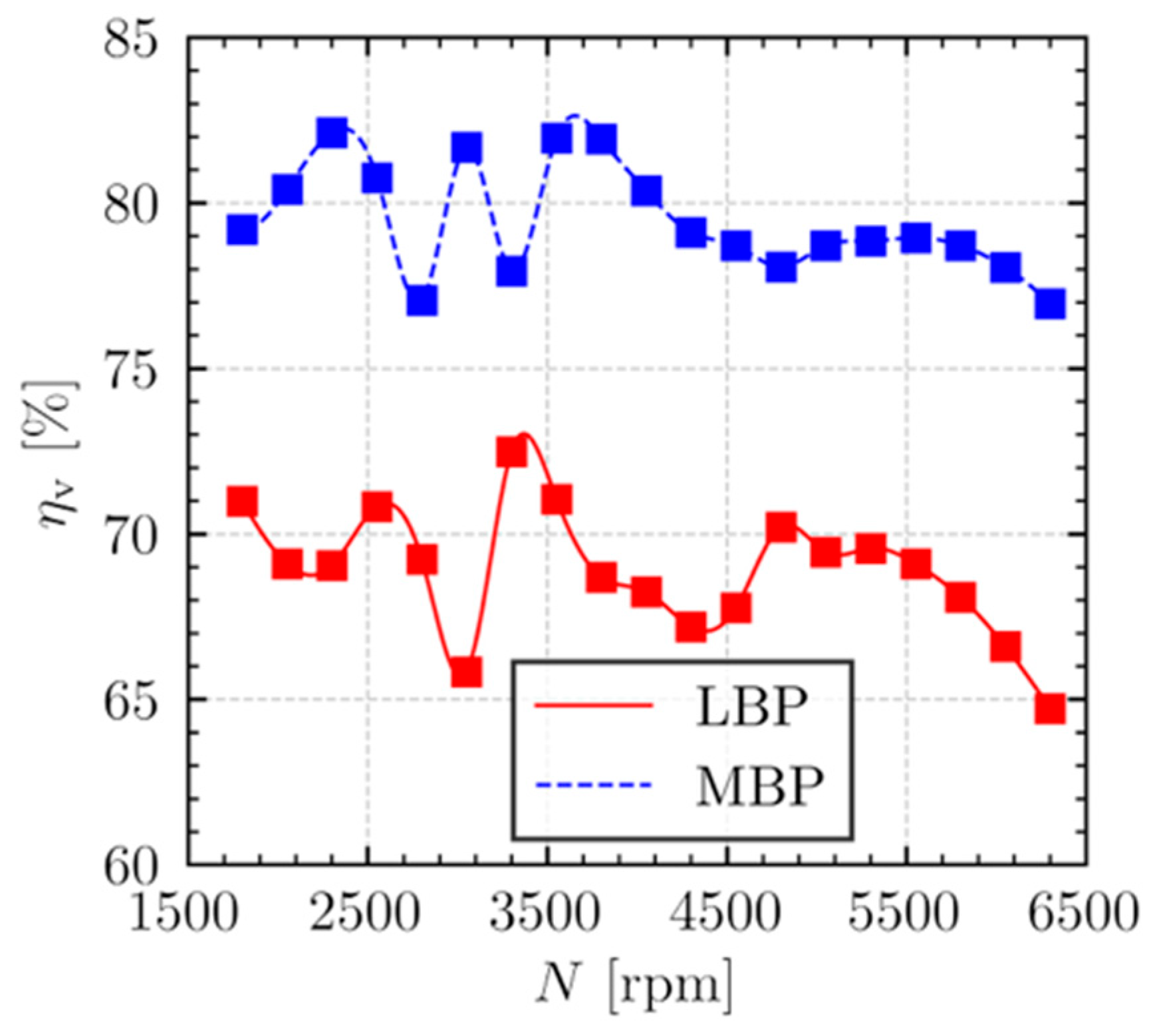
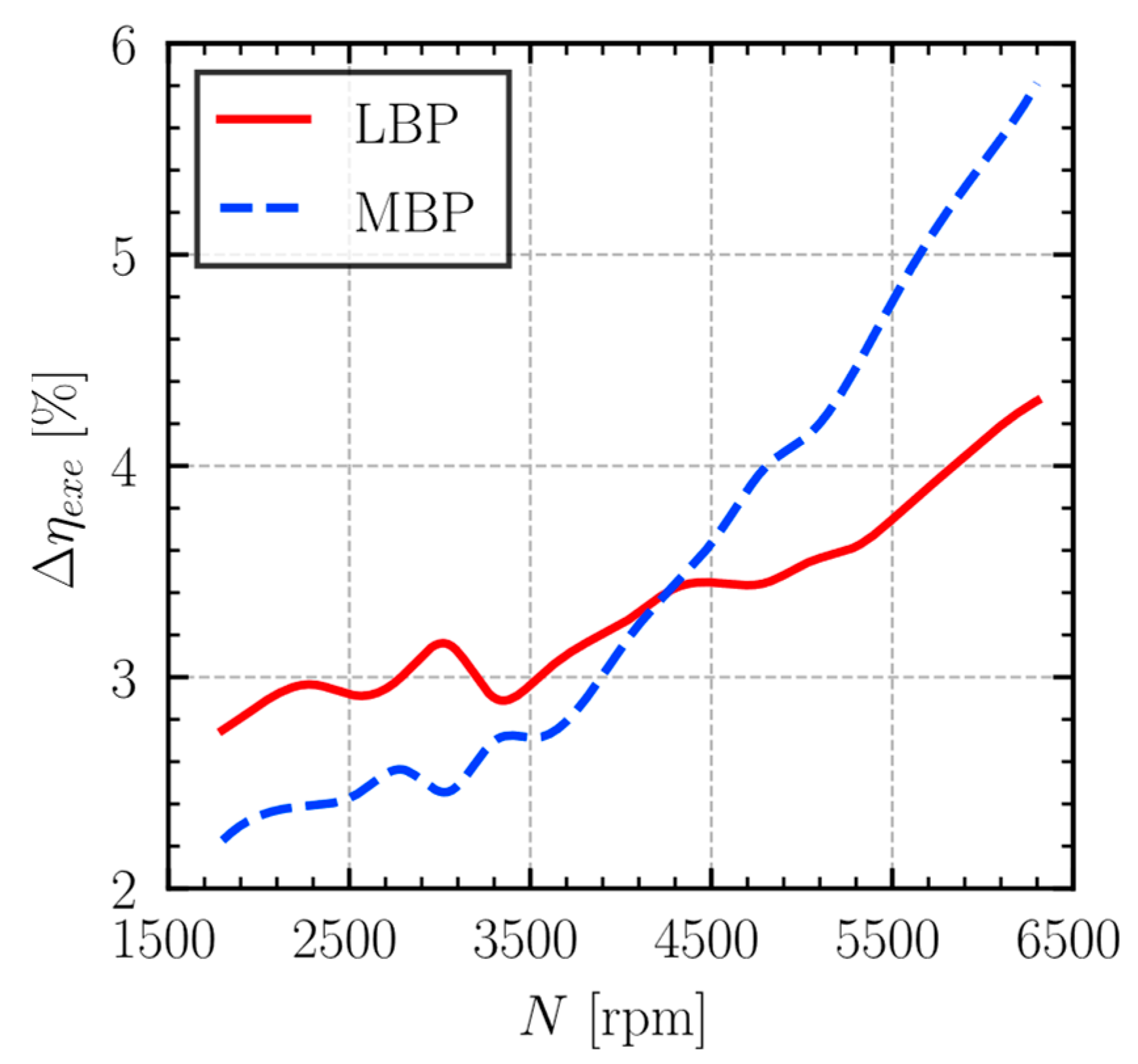
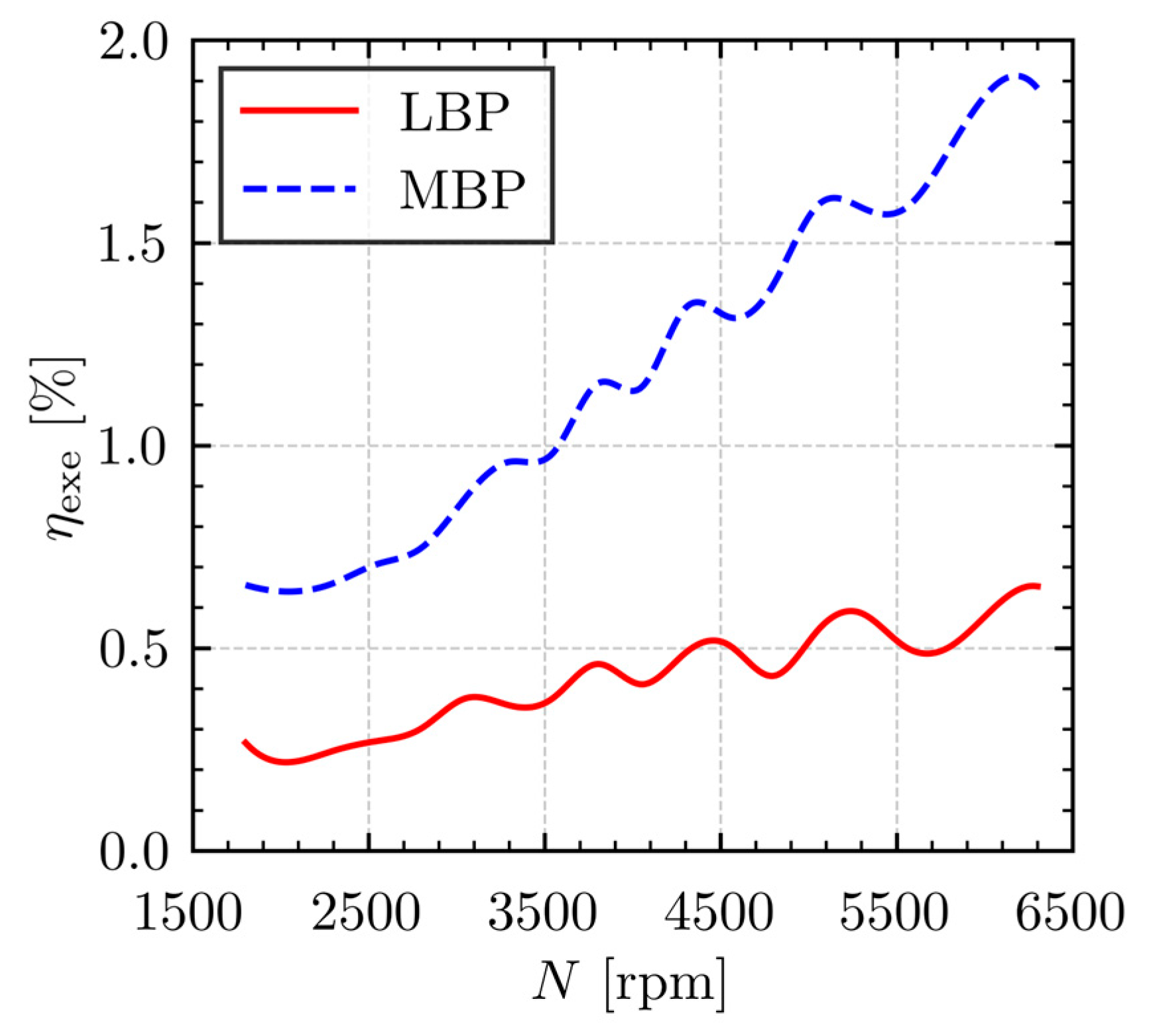
The relationship between overall volumetric efficiency and rotational speed, under the LBP ($T_e$ = −23.3 °C, $T_c$ = 54.4 °C) and MBP ($T_e$ = −6.7 °C, $T_c$ = 54.4 °C) operating conditions, is illustrated in Figure 5. Across the analyzed speed range of 1800–6500 rpm, a non-monotonic variation in volumetric efficiency is evident for both LBP and MBP conditions. Such oscillatory behavior with rotational speed is consistent with previous observations reported by Tao et al. [18]. Beyond the final efficiency peak observed around 3500 rpm, further increases in rotational speed predominantly led to a decline in the compressor volumetric efficiency under both operating conditions.

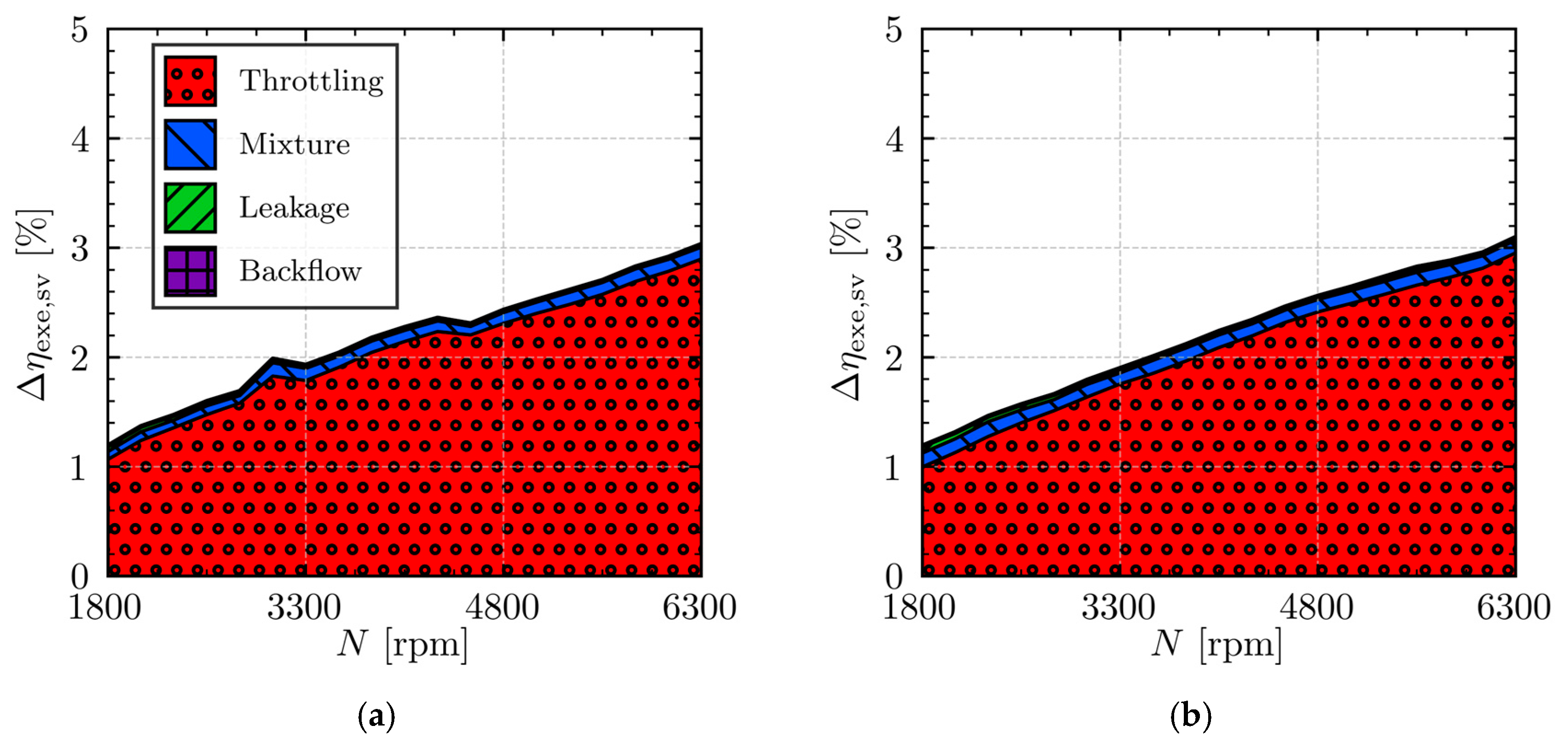
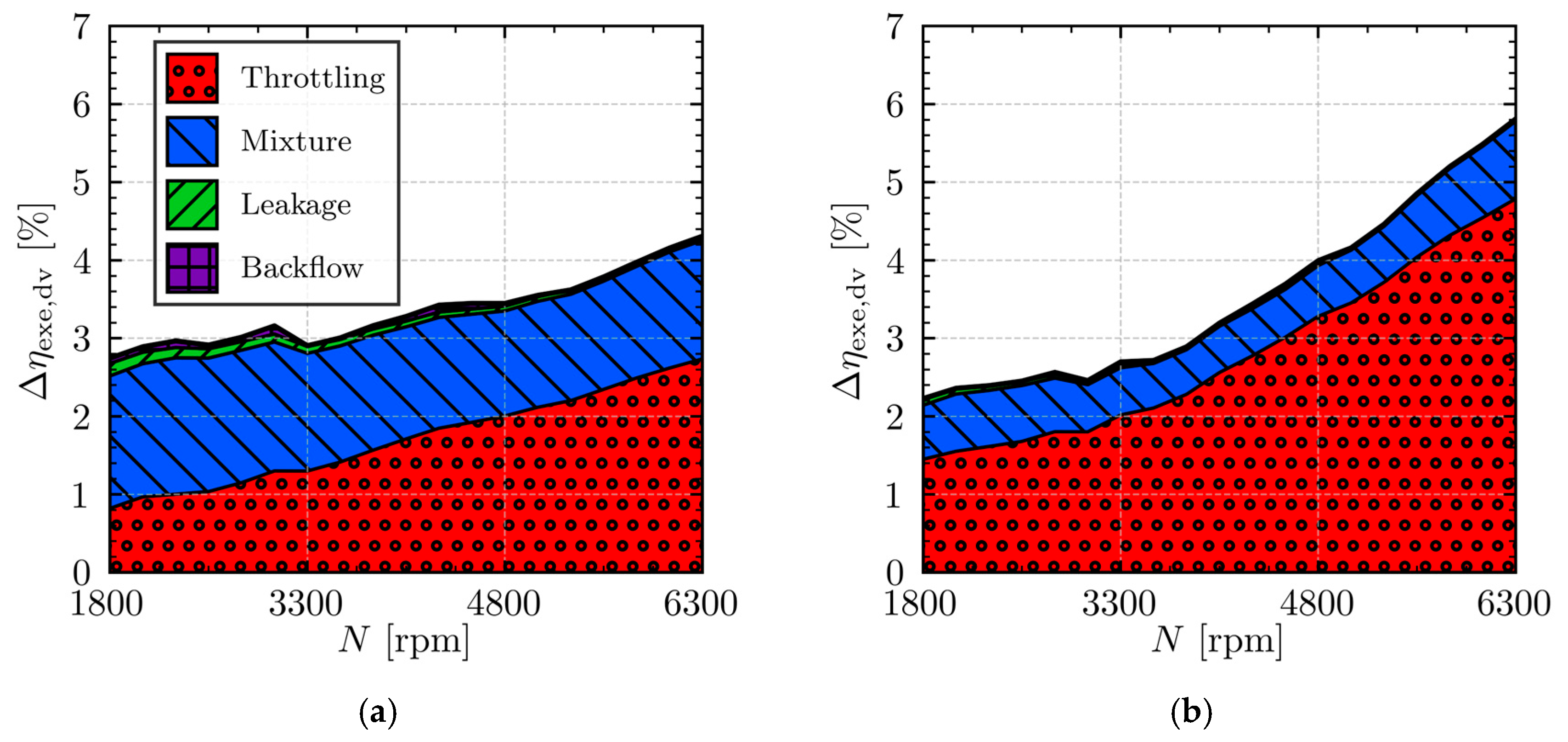
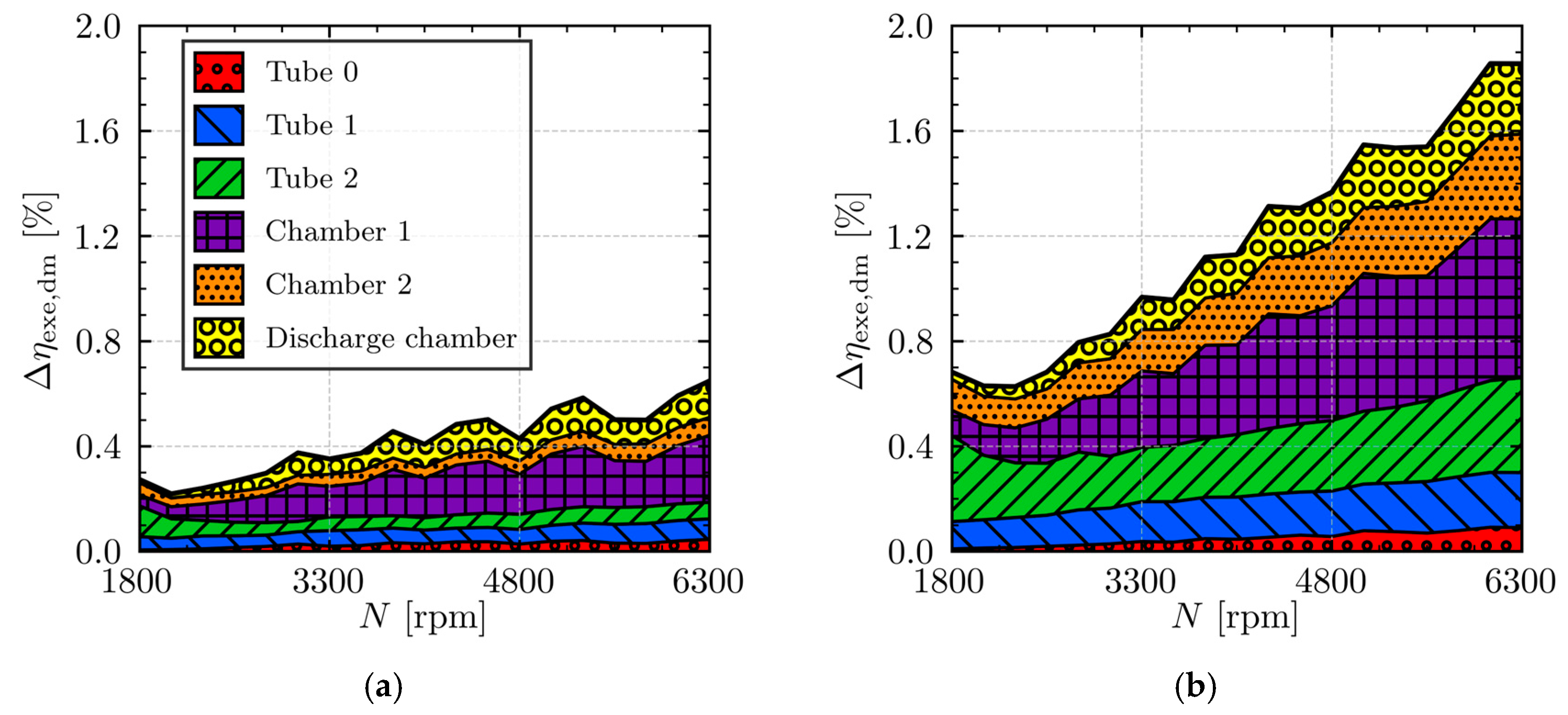
The volumetric inefficiencies that reduce the mass flow rate are associated with the individual sources (Table 2) under different operating conditions and compressor speed. It is important to note, however, that volumetric inefficiency due to motor slip is excluded from this specific breakdown, as detailed electric motor modeling is beyond the scope of the present study.

3.2.1. Suction Muffler

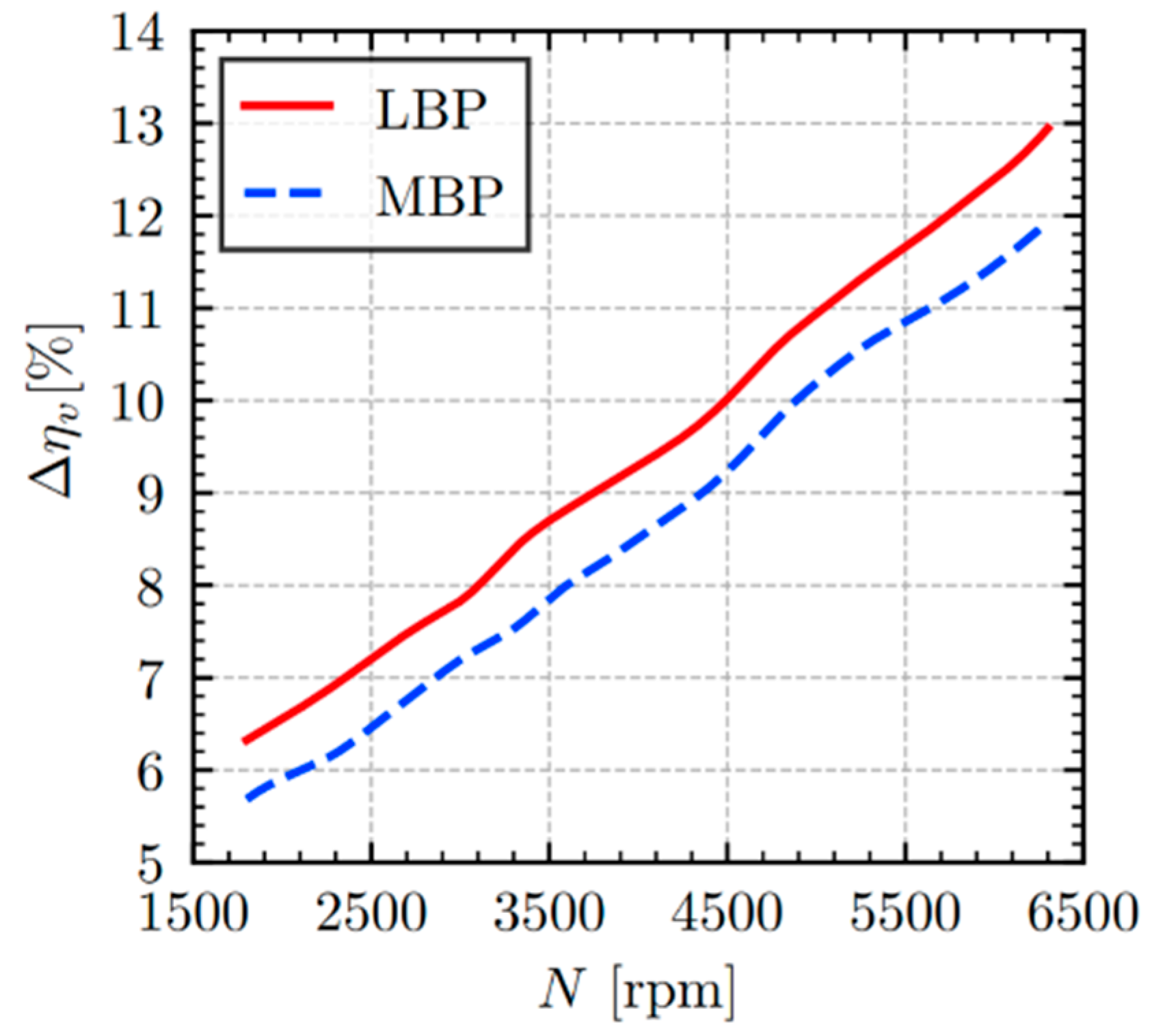
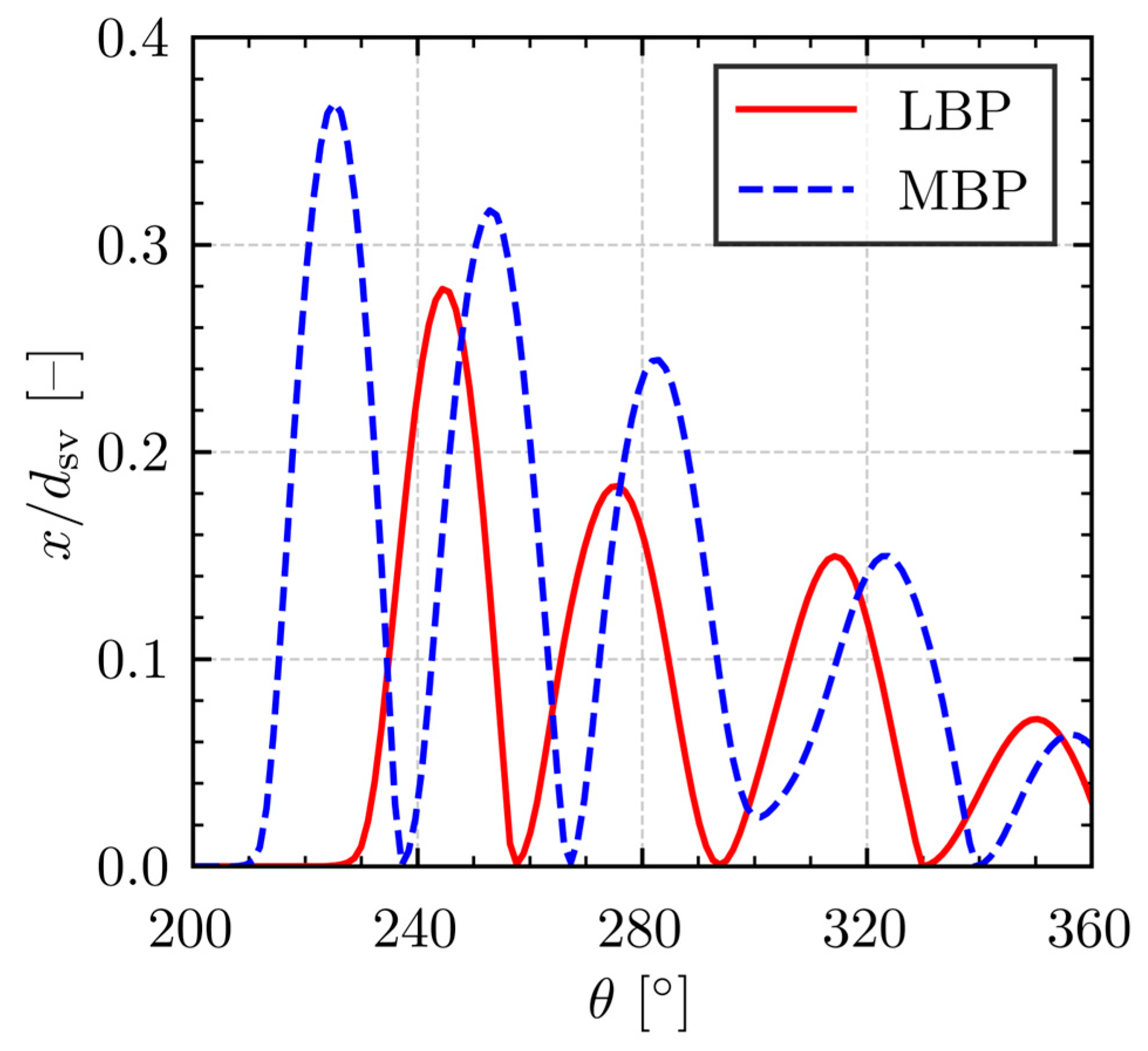
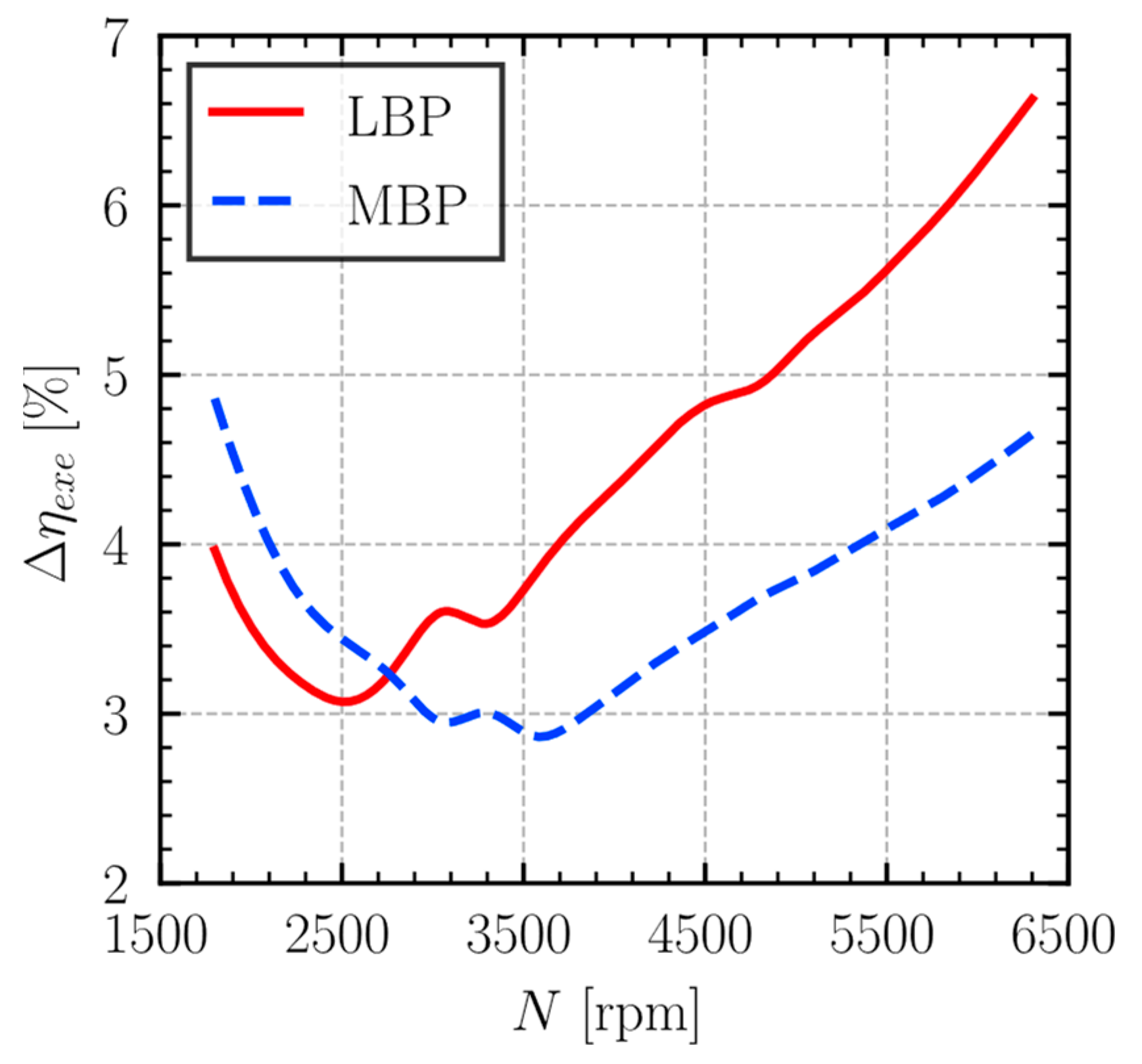
The volumetric inefficiency associated with fluid flow through the suction muffler increases significantly with compressor rotational speed, as shown in Figure 6 for both the LBP and MBP operating conditions. The LBP condition consistently exhibits higher levels of inefficiency across the entire speed range analyzed. The suction muffler volumetric inefficiency can be attributed to the following two primary components: losses due to viscous friction (pressure loss, Δη_v,hl) and heat transfer (gas superheating, Δη_v,ht).

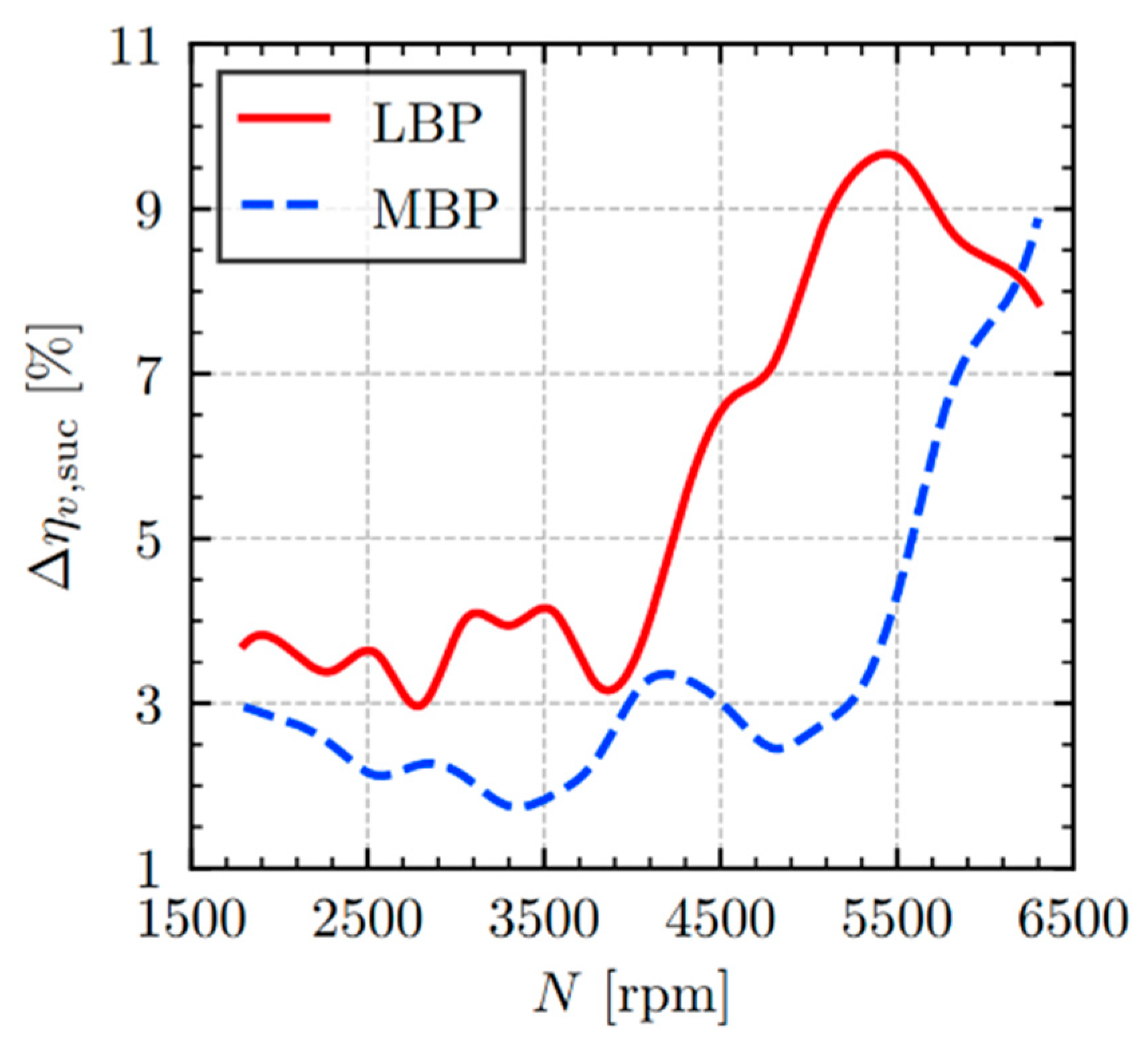
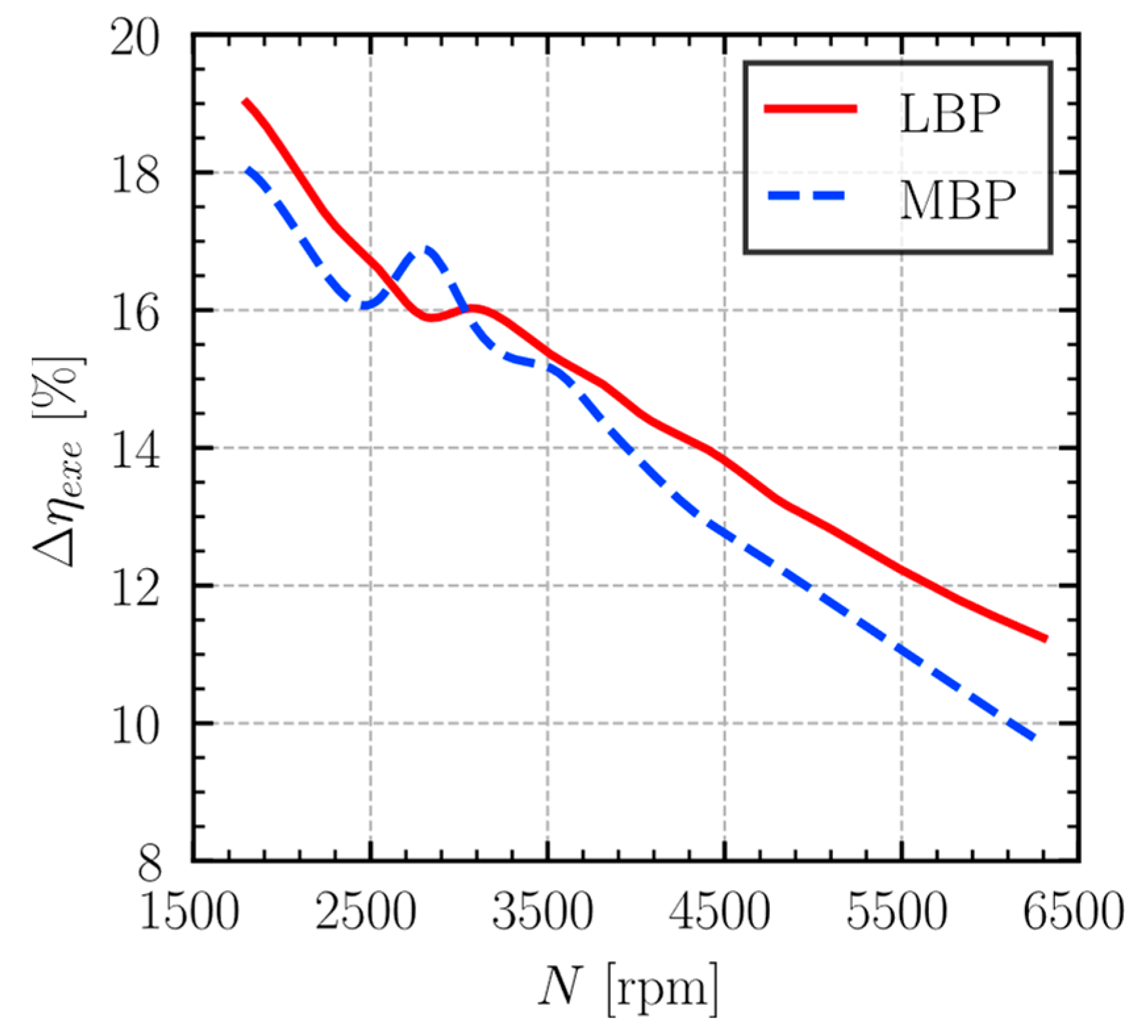
Figure 7 indicates that heat transfer (dashed line) accounts for much of the suction muffler inefficiency under both LBP and MBP conditions. However, the contribution from pressure loss (solid line) becomes significantly more pronounced with increasing rotational speed, rising from 0.6% at 1800 rpm to 6.2% at 6300 rpm under MBP conditions and from 0.6% to 5.1% under LBP conditions over the same speed range. The volumetric inefficiency linked to pressure loss is consistently greater for the MBP condition. This is a direct consequence of the higher mass flow rates inherent to MBP operation, which, when coupled with increasing compressor speed, result in greater refrigerant velocities within the muffler, thereby intensifying viscous friction and intensifying pressure loss. In contrast, the heat transfer component of inefficiency demonstrates less sensitivity to rotational speed and is typically more significant under the LBP condition.

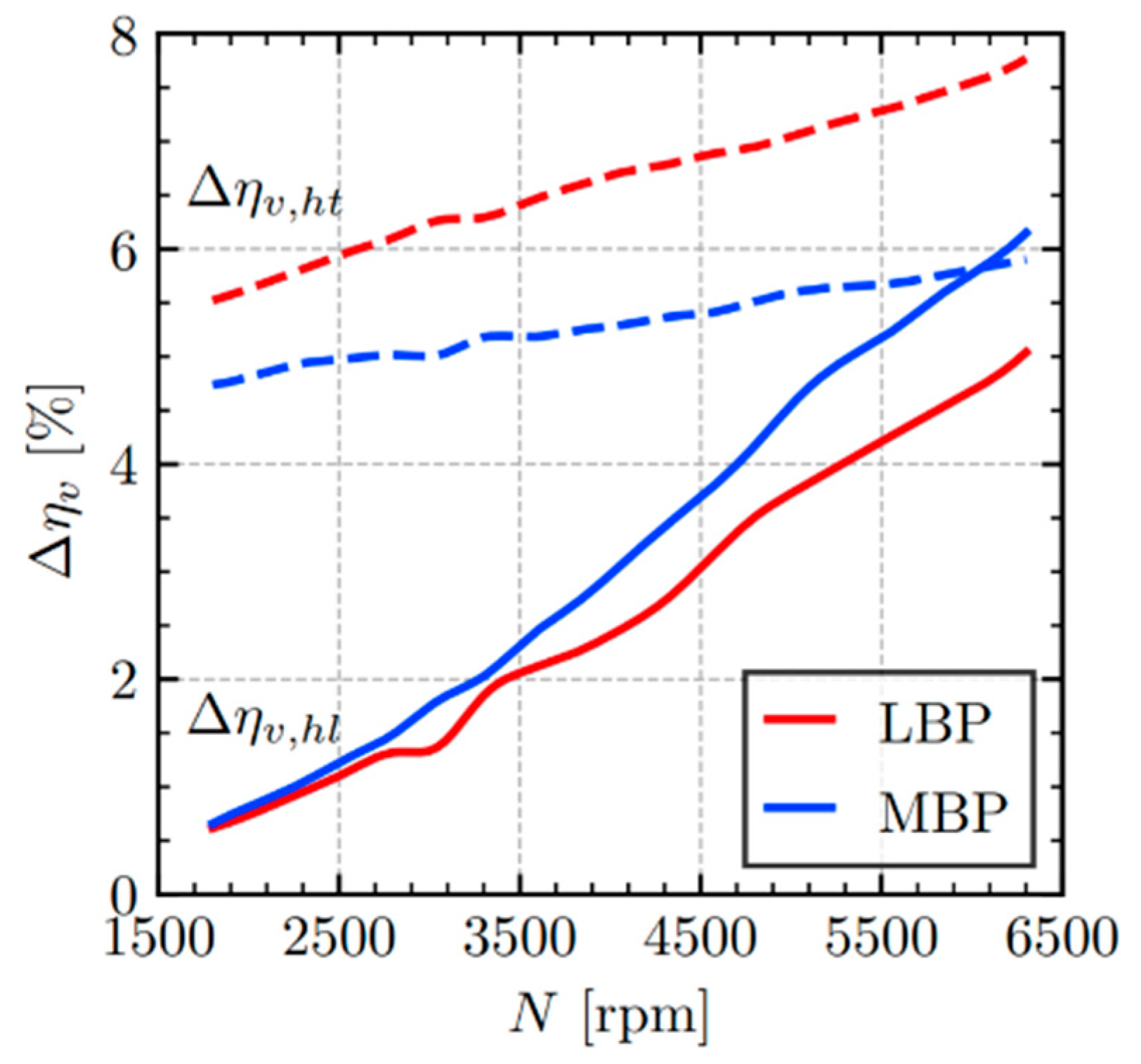
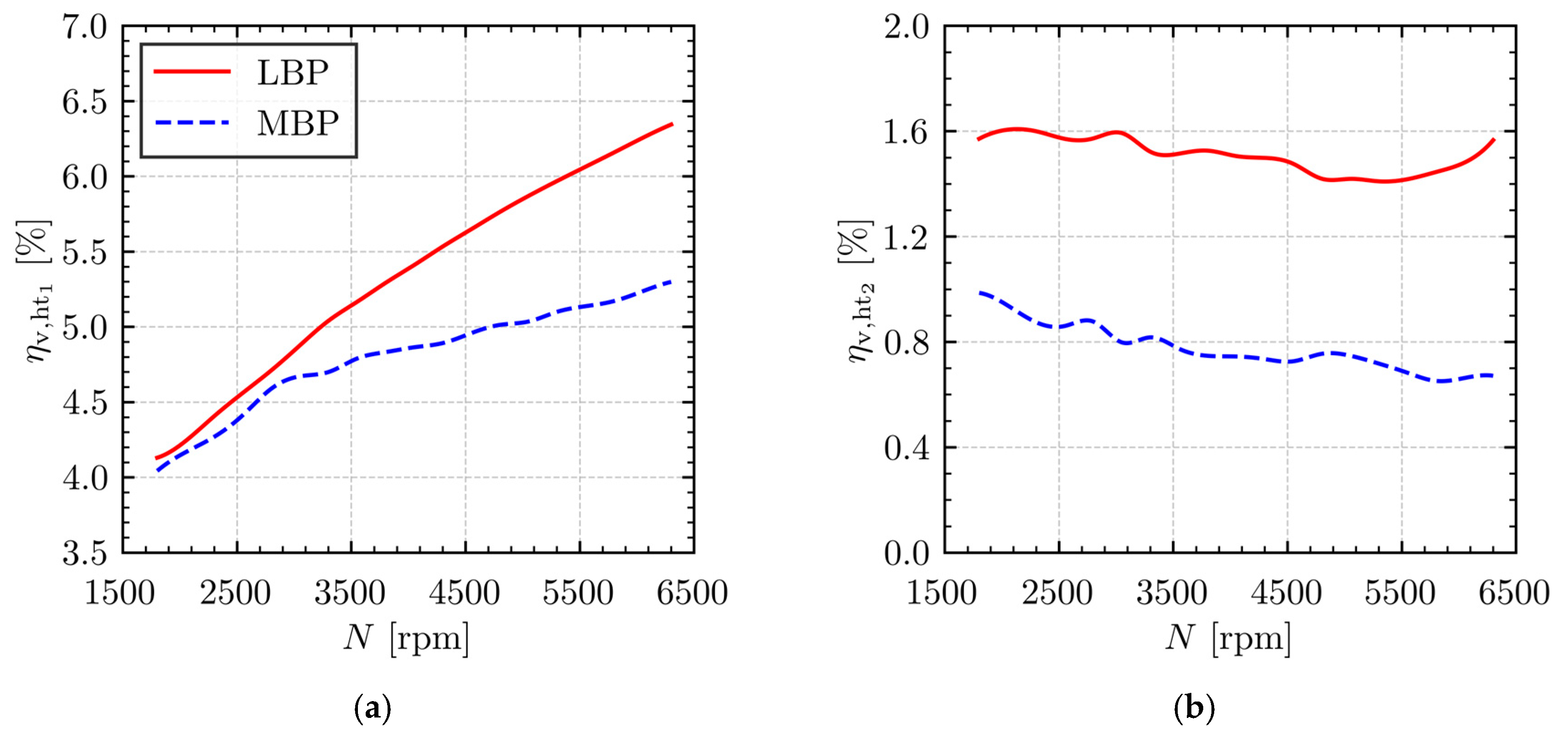
As shown in Figure 8, the volumetric inefficiency related to heat transfer can be divided into the following two components: one associated with indirect suction (Figure 8a) and the other with heat exchange between the muffler wall and the refrigerant fluid (Figure 8b). The results indicate that the greatest inefficiency arises from indirect suction, which leads to the mixing of gas portions at different temperatures coming from the suction line and the internal environment of the compressor. Moreover, this inefficiency increases with compressor speed, reaching 6.4% under LBP conditions and 5.2% under MBP conditions at 6300 rpm. On the other hand, the inefficiency caused by heat transfer throughout the suction muffler is considerably lower and shows little sensitivity to compressor speed, though it is also greater under LBP conditions. This occurs because, although the convective heat transfer coefficient increases with speed, this increase is not sufficient enough to offset the rise in the fluid’s thermal capacity due to higher mass flow rates. As a result, the temperature difference of the refrigerant at the inlet and outlet of the suction muffler decreases as the operating speed increases.

3.2.2. Clearance Volume

Reciprocating compressors feature a clearance volume in the compression chamber for operational reliability. Consequently, residual gas trapped in this volume at the end of the discharge process must expand before the next suction stroke can begin. The volumetric inefficiency component (Δη_v,exp) due to the isentropic re-expansion of real gas from condensing pressure to evaporating pressure is detailed in Figure 9. The extent of this re-expansion, and thus its contribution to volumetric inefficiency, directly correlates with the compressor pressure ratio. This explains why the re-expansion inefficiency is notably more critical under the LBP condition, which involves higher pressure ratios. The results indicate that rotational speed exerts only a small influence on this specific inefficiency, decreasing it by 0.8% for the LBP condition and by 0.4% for the MBP condition as the operational speed increases from 1800 to 6300 rpm.

Another minor factor is the non-isentropic nature of the re-expansion process for residual gas trapped in the clearance volume, which occurs due to concurrent heat transfer and refrigerant leakage. Simulation results indicate that this volumetric inefficiency source is small across the entire speed range for both LBP and MBP operating conditions, reaching a maximum absolute value of only 0.8%.

3.2.3. Suction Valve

Ideally, the suction process in reciprocating compressors would occur isobarically. In practice, however, refrigerant is admitted into the cylinder through suction valves that inherently restrict the flow, leading to pressure loss. As a result, the actual suction process is non-isobaric, with the in-cylinder pressure during intake typically falling below the pressure maintained in the suction chamber.

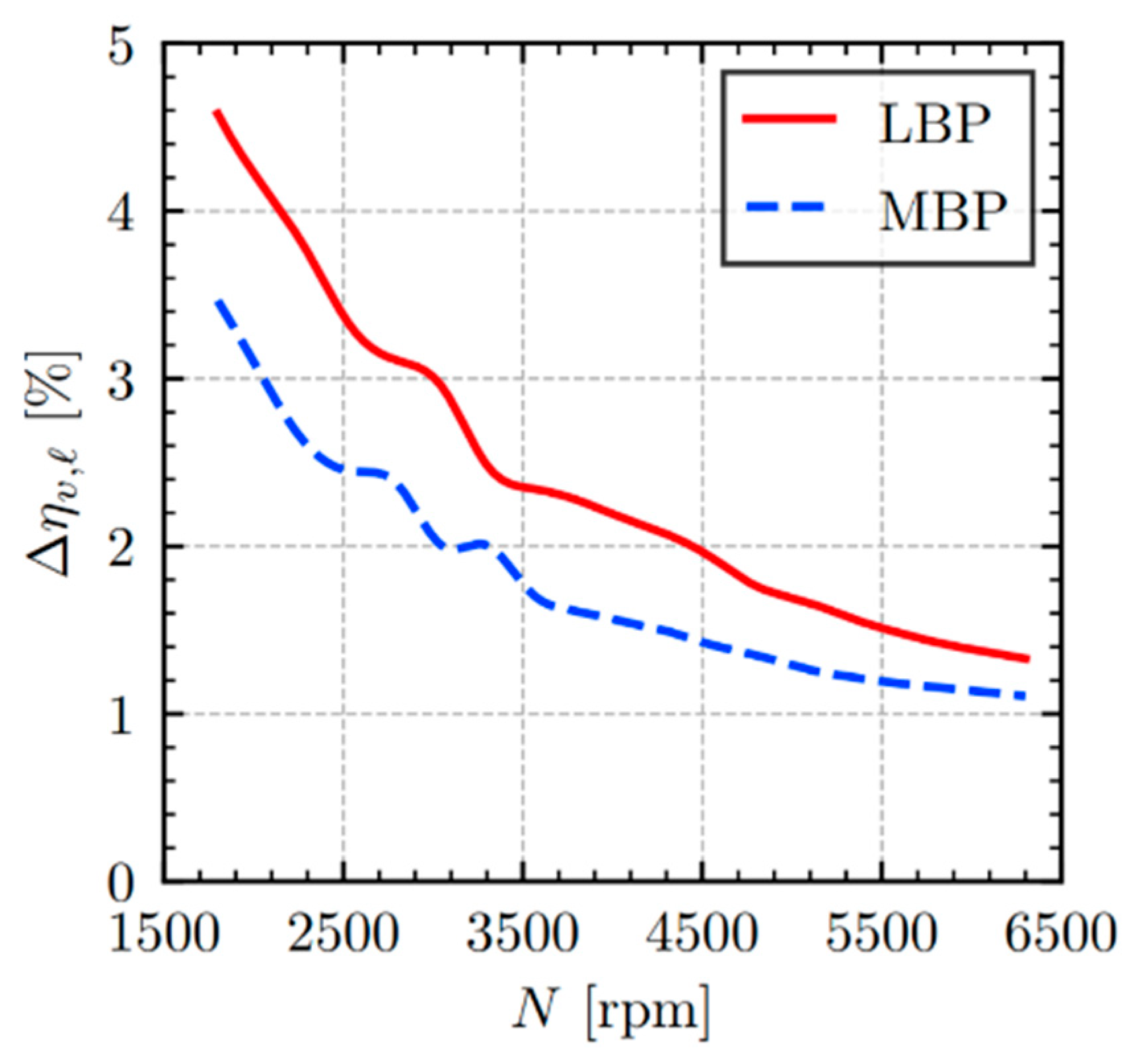
The volumetric inefficiencies specifically arising from this non-ideal suction process (Δη_v,suc) are detailed as a function of compressor speed for both LBP and MBP operating conditions in Figure 10. For most of the analyzed speed range, suction process inefficiencies are generally more pronounced under the LBP condition compared to the MBP condition. This difference is primarily attributed to the shorter duration of the suction process characteristic of LBP operation. During this shorter period, inducting the required mass of refrigerant requires higher instantaneous gas velocities through the valve, which in turn leads to greater pressure loss.

However, this general trend reverses at very high speeds, where the suction process inefficiency under MBP conditions can surpass that observed for the LBP condition. This behavior is linked to the complex dynamics of the valve reed. At these high speeds, especially under MBP conditions, the valve motion can be affected in such a way that it leads to an increased effective restriction to the flow, thereby altering the typical trend observed at lower and mid-range speeds.

In fact, valve dynamics, in conjunction with pressure pulsations within the suction and discharge chambers, frequently cause valve closure to lag relative to the timing in an idealized compressor cycle. This closure delay can have either a detrimental or a beneficial impact on the compressor volumetric efficiency. If, for instance, refrigerant flows in the reverse direction during this lag period, i.e., from the cylinder back into the suction chamber, a net reduction in the delivered mass flow rate occurs as previously discharged fluid returns via backflow. Conversely, should flow inertia cause refrigerant to continue entering the cylinder from the suction chamber while the valve is in the process of closing, an additional mass intake takes place. This phenomenon, also known as supercharging, enhances the compressor volumetric efficiency.

The volumetric inefficiency component specifically attributed to this supercharging effect (Δη_v,sch) is presented as a function of rotational speed in Figure 11a, in which negative values of inefficiency signify an increase in mass flow rate relative to an ideal compressor that features no valve closing delay. As previously indicated, the supercharging effect is primarily driven by the inertia of the flowing refrigerant, although it is also influenced by pressure pulsations within the suction chamber. The results for supercharging-related inefficiency demonstrate an oscillatory behavior with rotational speed. However, a substantial increase in mass flow rate (represented as significant negative inefficiencies) is consistently observed at the highest rotational speeds. This occurs because the refrigerant velocity through the valve escalates with increasing compressor speed, thereby enhancing flow inertia and, consequently, maximizing the supercharging phenomenon.

It should be noted that the positive impact of supercharging on volumetric efficiency tends to be more pronounced under LBP conditions than under MBP conditions. The higher-pressure ratio characteristic of the LBP operation leads to a longer expansion process, which in turn reduces the time available for the suction process. Therefore, for any given rotational speed, the gas velocity through the suction valve is typically greater under LBP conditions compared to MBP conditions. This higher velocity translates to increased flow inertia, thereby amplifying the supercharging effect observed.

On the other hand, simulation results depicted in Figure 11b indicate that the impact of backflow on this compressor volumetric efficiency is typically less pronounced than the gains from supercharging. Specifically, backflow-induced inefficiency remains negligible up to a rotational speed of 3800 rpm. Beyond this speed, under MBP conditions, the inefficiency due to backflow increases, reaching a peak of approximately 1% near 5100 rpm. Under LBP conditions, the impact of backflow is insignificant up to approximately 5500 rpm, reaching a maximum of 1.4%.

3.2.4. Piston–Cylinder Clearance

Reciprocating compressors have two primary refrigerant leakage paths that can be thermodynamically detrimental, which are the piston–cylinder clearance and the valve reed–seat gap. Figure 12 illustrates the volumetric inefficiencies arising from the piston–cylinder clearance (${∆\eta }_{v,l}$), revealing that this inefficiency is notably greater under the LBP condition compared to the MBP condition. This is because the pressure difference between the compression chamber and the compressor internal environment is the main driving force for this leakage, which is significantly larger under LBP conditions. In contrast, leakage through the suction valve reed–seat gap is found to be negligible for this compressor across all analyzed rotational speeds, contributing a maximum of only 0.08% to volumetric inefficiency.

Leakage inefficiencies are generally more significant at lower rotational speeds, a trend consistent with findings in the literature [19]. The mass flow rate due to leakage is largely independent of rotational speed, being primarily a function of the piston–cylinder gap size and the pressure difference determined by the operating condition. Given that the ideal theoretical mass flow rate increases with rotational speed, the relative impact of this leakage on the compressor net mass flow rate diminishes at higher speeds, as depicted in Figure 12.

3.2.5. Discharge Valve

Figure 13a shows the inefficiencies caused by overpressure during the discharge process. The discharge valve exhibits significant flutter, leading to multiple overpressure peaks in the cylinder during discharge. As a result, the associated inefficiency fluctuates considerably, with no clear trend in relation to rotational speed. Moreover, both negative and positive inefficiency values are observed, indicating that the pressure in the compression chamber when the piston reaches top dead center can be either above the condensation pressure, resulting in a longer expansion process, or below it, leading to a shorter expansion phase.

Figure 13b illustrates the effect of discharge valve closure delay on volumetric inefficiency, which may be either positive (pressure-boosted discharge) or negative (backflow). Within the range of speeds analyzed, the delay leads to a positive effect only at 3050 rpm under LBP conditions and at 3550 rpm under MBP conditions. The tendency toward a negative effect is greater because, unlike the supercharging observed on the suction side, the expansion process occurs faster than the compression process. After passing the top dead center, the piston reverses direction and quickly increases the chamber volume, which rapidly decreases the refrigerant pressure. This sharp pressure drop causes a strong deceleration of the flow through the discharge port, reversing its direction more quickly than the valve’s response time, favoring backflow.

Furthermore, like what was observed during suction, the inefficiency associated with discharge valve delay fluctuates with rotational speed, showing two local maxima under MBP conditions (2800 and 3300 rpm) and three under LBP conditions (2050, 3050, and 4800 rpm). These inefficiency peaks lead to corresponding oscillations in the compressor’s overall volumetric efficiency, as shown in Figure 5. These results are consistent with the observations of [18], although their study did not account for the influence of a valve opening limiter, which affects both the dynamics and oscillation behavior of the reed valve.

3.3. Exergy Losses Breakdown

Figure 14 presents the relationship between exergetic efficiency and compressor rotational speed, indicating higher efficiency under the MBP condition compared to the LBP condition. As can be seen, there is a range of rotational speeds associated with higher efficiency in both operating conditions. As was conducted for volumetric efficiency, the exergetic inefficiencies are quantified and analyzed in the following sections using the stratification described in Table 3.

3.3.1. Suction Muffler

Figure 15 shows that the irreversibility associated with indirect suction increases with compressor speed, parallel to what was observed for volumetric efficiency (Figure 8), since greater amounts of refrigerant fluid mix under such conditions. However, the trend between LBP and MBP conditions differs from that seen in volumetric inefficiency, i.e., irreversibilities are higher under the MBP condition across nearly the entire speed range analyzed.

This phenomenon can again be attributed to the amount of refrigerant fluid undergoing irreversible mixing. Since the mass flow rate is higher under MBP for a given compressor speed, the mixing irreversibility is also greater. It should be noted that this irreversibility also depends on the temperature difference between the refrigerant fluid in the suction muffler and the internal compressor environment. As the compressor speed increases, the internal environment temperatures under both conditions begin to converge. Because the suction pipe temperature is slightly higher for MBP conditions (35 °C in comparison with 32 °C adopted for LBP), this irreversibility tends to increase more for the LBP condition as speed increases, as shown by the convergence of the curves in Figure 15.

Figure 16 presents the irreversibility associated with the fluid flow throughout the suction muffler as a function of compressor speed. The results show trends like those observed for volumetric inefficiency due to pressure losses in the suction muffler (Figure 7). Exergetic inefficiencies are greater under the MBP condition, reaching 3.9% at the highest speed, compared to 3.0% under the LBP condition.

Figure 17 shows the exergy destruction in the suction muffler components. Except for the Helmholtz resonator, which proved to be irrelevant to exergy destruction, the irreversibilities from the other components are significant and increase considerably with compressor speed. The irreversibility due to viscous friction changed little between LBP and MBP conditions, due to similar flow velocity levels in the muffler.

3.3.2. Suction Valve

The results of the irreversibility associated with the suction valve in Figure 18 show a strong influence of rotational speed on exergy destruction. Unlike what was observed for the volumetric inefficiency in the suction valve (Figure 10), the exergetic inefficiency does not exhibit oscillatory behavior. Additionally, the operating condition (LBP or MBP) does not appear to significantly influence this irreversibility, as shown in Figure 18. The fact is that the valve dynamics under LBP conditions result in smaller opening amplitudes (Figure 19), thus imposing greater flow restriction and consequently higher pressure loss. On the other hand, although the restriction under MBP conditions is slightly smaller, the suction process occurs over a longer time interval, which tends to increase the pressure loss, making the irreversibility similar to that found under the LBP condition.

Figure 20 shows the following four sources of irreversibility in the suction valve: pressure loss, leakage, mixing, and backflow. As can be observed, the irreversibility caused by pressure loss is much greater than the others under both operating conditions and across the entire range of rotational speeds analyzed, and it is also the most affected by rotational speed. Although the backflow is found to reduce the compressor mass flow rate by up to 1.5% under MBP conditions, the exergy destruction associated with this phenomenon, as well as with leakage through the gap between the reed and the seat, proved negligible under both operating conditions. Finally, although greater than the irreversibilities from backflow and leakage, the irreversibility due to flow mixing is also negligible in comparison with pressure loss.

3.3.3. Piston–Cylinder Clearance

Figure 21 shows that irreversibility due to leakage in the piston–cylinder clearance decreases with increasing compressor speed, similarly to what was observed for its effect on volumetric inefficiency (Figure 12). As expected, this irreversibility is greater when the pressure differential between the suction and discharge lines is larger, which corresponds to the LBP condition, and is more critical at low compressor speeds, as also indicated in the literature [18,20].

3.3.4. Discharge Valve

The results for the irreversibility in the discharge valve are shown in Figure 22 and indicate that the highest irreversibility occurs under LBP conditions for speeds below 4300 rpm. Above this speed, entropy generation is greater under MBP conditions, with exergetic inefficiency increasing from 2.2% at 1600 rpm to 5.8% at 6300 rpm. When comparing Figure 17 and Figure 21, it is evident that the discharge valve reduces the compressor’s exergetic efficiency more than the suction valve.

To better understand the results in Figure 22, Figure 23 also breaks down the following four irreversibilities in the discharge valve: pressure loss, leakage, mixing, and backflow. Compared to what is observed for the suction valve, the irreversibility associated with the irreversible mixing of fluids is much more significant in the discharge valve. For instance, under LBP conditions and at 1800 rpm, this irreversibility reduces the compressor’s overall exergetic efficiency by approximately 1.8%.

As speed increases under LBP conditions, this irreversibility decreases due to the smaller temperature difference between the mixing fluids. This irreversibility of mixing is higher under LBP than MBP conditions because, given the higher pressure ratio, the discharge temperatures tend to be higher than the temperature in the discharge chamber, generating more entropy upon mixing.

Exergy destruction due to pressure loss is again the most affected by compressor speed, with a sharper increase under MBP conditions, rising from 1.6% at 1800 rpm to 4.9% at 6300 rpm. Irreversibility from valve leakage is noticeable only at low speeds under LBP conditions, but it remains negligible when compared to the irreversibilities from mixing and pressure loss. Although the backflow reduces the compressor’s flow rate by up to 6% under LBP conditions (Figure 13), its impact on exergetic efficiency is also negligible, with a maximum value of only 0.2%.

3.3.5. Discharge Muffler

Figure 24 presents the irreversibility associated with the discharge muffler as a function of compressor operating speed. The irreversibilities in the discharge muffler increase significantly with compressor speed, but their absolute values and rate of increase are smaller than those observed for the suction muffler. Lower irreversibilities in the discharge muffler compared to the suction muffler were also observed by [10,12] in low-capacity reciprocating compressors. This irreversibility is greater under MBP conditions due to the higher flow velocity in the discharge muffler. In addition, the observed oscillations in irreversibility values with compressor speed are associated with changes in valve dynamics.

Figure 25 breaks down the entropy generation in each component of the discharge muffler. A significant difference is noted in the exergy destruction in the tubes between the two operating conditions. While irreversibility due to viscous friction in the tubes is relatively insignificant under LBP conditions, it results in a reduction of approximately 0.7% in exergetic efficiency under MBP conditions. However, this irreversibility is considerably lower than that observed for the suction muffler. The irreversibility most affected by compressor speed variation occurs in the sudden expansion within the three chambers under both operating conditions. The higher flow velocity under MBP conditions explains the large difference observed between the two conditions.

3.3.6. Heat Transfer

Figure 26 presents the inefficiencies associated with heat transfer at different rotational speeds. It is noted that the effect of heat transfer decreases with increasing rotational speed in both operating conditions (LBP and MBP), but it is more significant under the LBP condition. The dependence on rotational speed aligns with the results for the so-called compression efficiency found by [19], although those authors attributed the trend to a combination of heat transfer and leakage effects.

It should be mentioned that [9] observed a greater importance of heat transfer at lower rotational speeds. Although not analyzing variable-speed compressors, ref. [20] by Jakobsen argued that the increase in flow velocity at higher rotations reduces the irreversibility of heat exchange and increases that associated with flow pressure losses. Moreover, the oil pumping rate tends to increase with compressor speed, raising the heat transfer coefficients and thereby reducing the temperature differences between components and, consequently, exergy destruction.

Figure 27 presents the results of exergy destruction associated with heat transfer between the following different components: (a) the shell and the external environment, (b) the shell and the internal environment, (c) the discharge chamber and the valve plate, (d) the cylinder and the refrigerant fluid both inside and outside, and (e) other heat transfers with little impact on the global exergy value (Δexe < 1%). A significant relevance of heat transfers between the shell and external environment and within the cylinder is observed in both operating conditions (LBP and MBP), accounting for more than half of the total irreversibility.

A local increase in irreversibility within the cylinder is also observed near 3000 rpm, coinciding with the point of maximum backflow at the discharge valve, which increases heat transfer. It should be noted that, except for heat transfer between the discharge chamber and the valve plate, the irreversibilities of all other heat exchanges decrease with increasing rotational speed. This is because the temperature difference between the discharge chamber and the valve plate changes with increased speed, as the discharge chamber temperature increases faster than that of the valve plate. Finally, it is worth emphasizing that the temperature difference between the shell and the external environment also varies with increasing speed, but the irreversibility of this heat exchange remains practically constant under both LBP and MBP conditions.

3.3.7. Bearings

Figure 28 shows the total irreversibility associated with the compressor bearings. At low speeds, oil viscosity is higher due to lower oil temperature. As compressor speed increases, oil temperature rises, reducing viscosity and mechanical losses. However, at high speeds, viscosity no longer varies much with temperature, and viscous friction increases with compressor speed. This occurs around 2500 rpm for the LBP condition and at approximately 3500 rpm for MBP. This result aligns with the findings of [21], and these losses can reduce by nearly 7% of the compressor exergy efficiency under LBP.

Figure 29 presents the contributions of different bearings to mechanical losses. As observed, the piston–cylinder clearance accounts for most of the losses, as also noted by [21]. Due to greater reaction forces, irreversibility in the main bearing is higher than in the secondary bearing under both operating conditions, and both increase with speed. Losses in the piston pin bearing are negligible across the entire speed range analyzed. Irreversibility in the eccentric bearing is also much smaller than in the main and piston bearings and is not significantly affected by compressor speed.

The increased viscosity due to lower temperatures at lower compressor speeds causes higher irreversibility in the main and eccentric bearings, especially under the MBP condition. In fact, bearing performance can be inadequate at low speeds, leading to contact between solid surfaces and thereby increasing power consumption further.

3.3.8. Electrical Motor

Figure 30 presents the irreversibility associated with the electric motor. As shown in this figure, this irreversibility plays a significant role in the exergy balance, reducing exergetic efficiency by more than 19%. The greater irreversibility at lower speeds is a result of the power–torque characteristic curve of the motor used in this study.

4. Conclusions

This study presented a comprehensive analysis of volumetric and exergetic inefficiencies in a variable-speed reciprocating compressor (VSRC), using a simulation model developed in GT-SUITE. The model incorporated detailed sub-models for the compression cycle, thermal profile, and mechanical and electrical losses, and it was successfully validated against experimental data, demonstrating its capability to accurately predict diverse aspects of compressor performance across a wide range of operating speeds and conditions.

In terms of volumetric efficiency, several trends emerged. Suction valve closure delays were found to promote beneficial supercharging effects at high speeds, although they could also induce minor backflow. Discharge valve delays, by contrast, more frequently caused backflow losses, with limited gains from super discharging. Suction muffler inefficiencies driven largely by heat transfer and viscous flow friction intensified significantly as speed increased. Additionally, refrigerant leakage through the piston–cylinder clearance proved especially detrimental at low speeds and under low back pressure (LBP) conditions.

The exergetic analysis further clarified how losses vary with compressor speed. Exergy destruction from viscous fluid flow and bearings increased with compressor speed, while heat transfer and electrical losses generally declined. At higher speeds, throttling effects and suction muffler behavior emerged as dominant contributors to fluid flow exergy losses. Losses from the discharge valve and from mixing in the indirect suction system remained significant across the entire speed range. Among heat-related losses, external heat transfer to the ambient environment became more pronounced with speed, whereas internal heat transfer paths tended to stabilize or diminish. Mechanical losses also shifted in character with operating speed, with crankshaft bearing losses dominating at low speeds due to suboptimal lubrication, while piston-assembly friction became the primary source at higher speeds.

In conclusion, this study highlights the intricate and speed-dependent interactions between dynamic and thermodynamic factors that influence the performance of variable-speed reciprocating compressors. The integrated modeling approach and the detailed analysis presented herein provide a robust framework for identifying key inefficiencies and guiding future efforts for the further optimization of compressor and system design aimed at achieving higher energy efficiency.