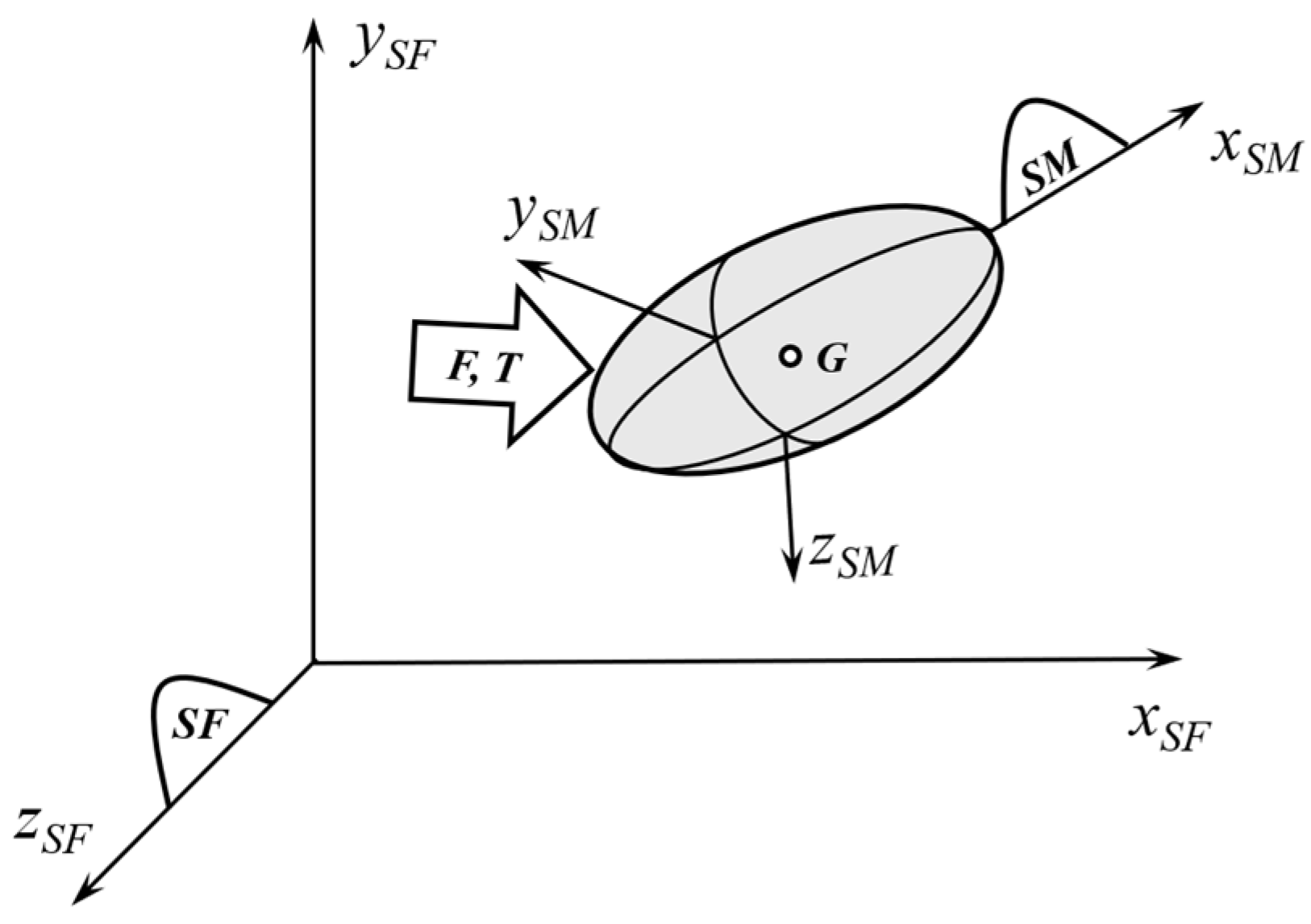
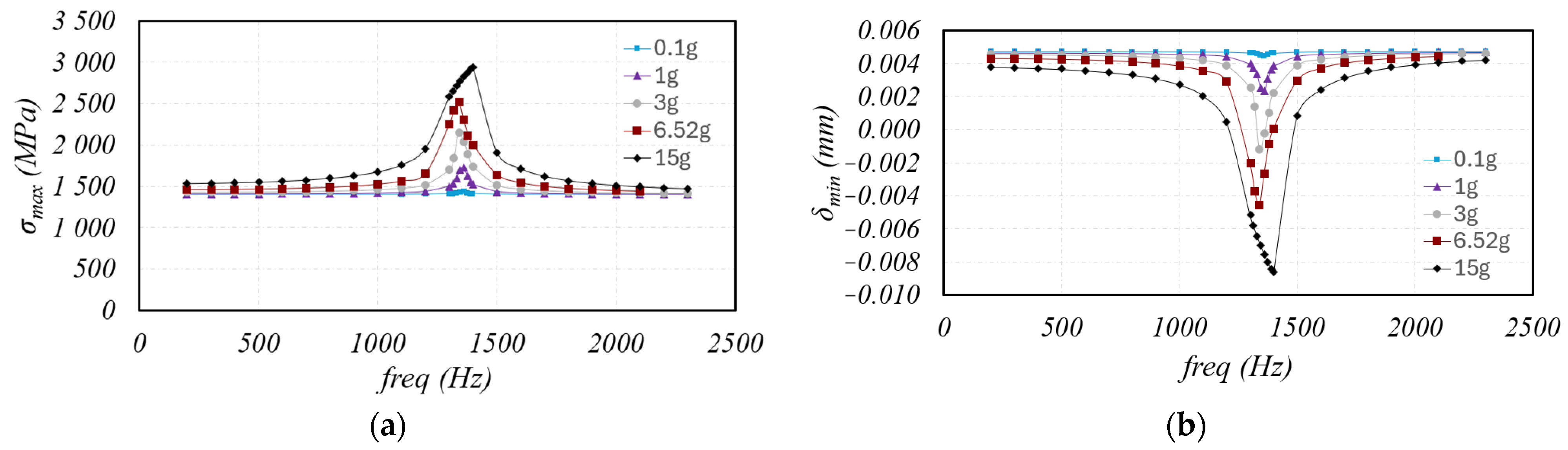
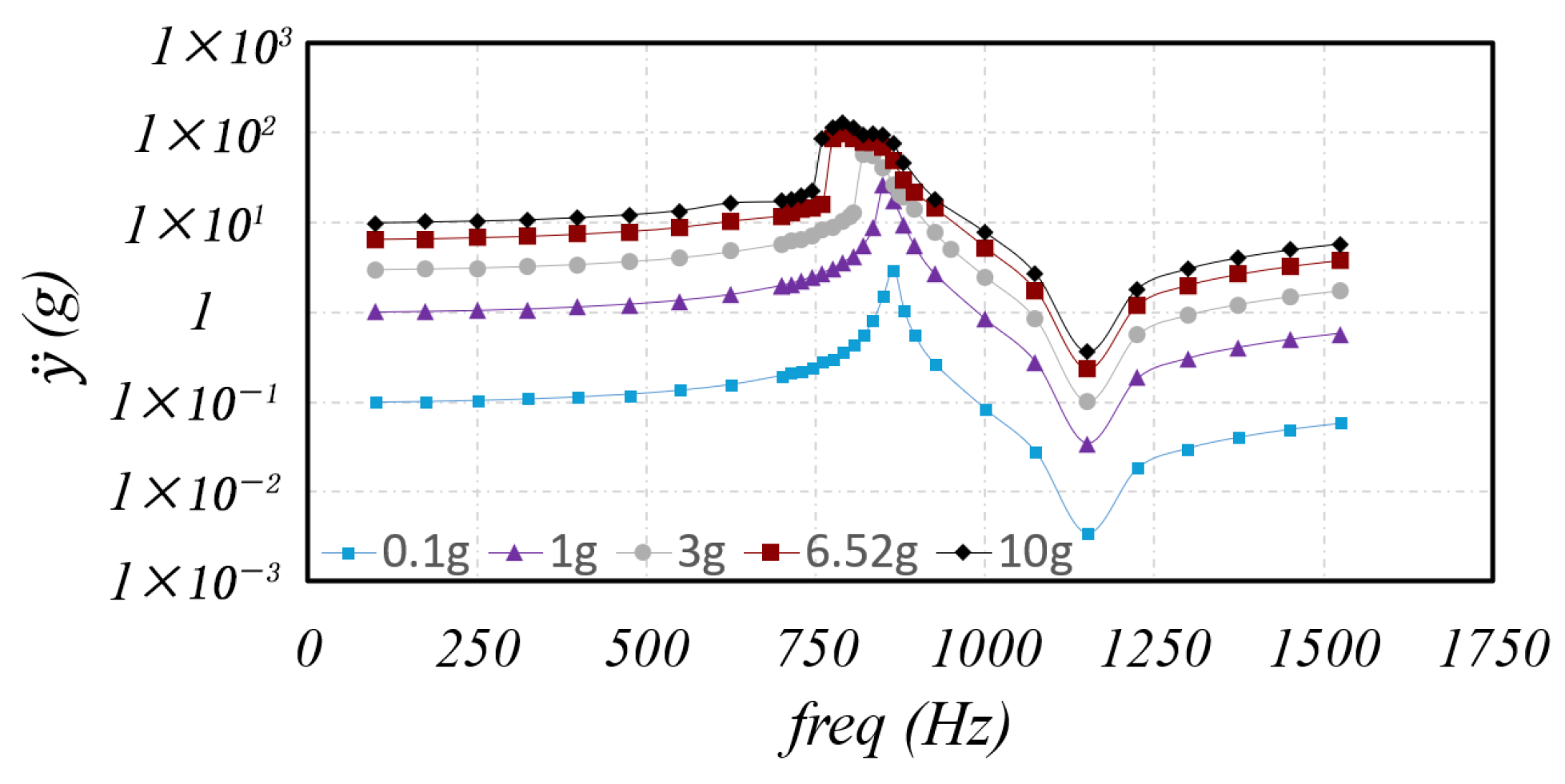
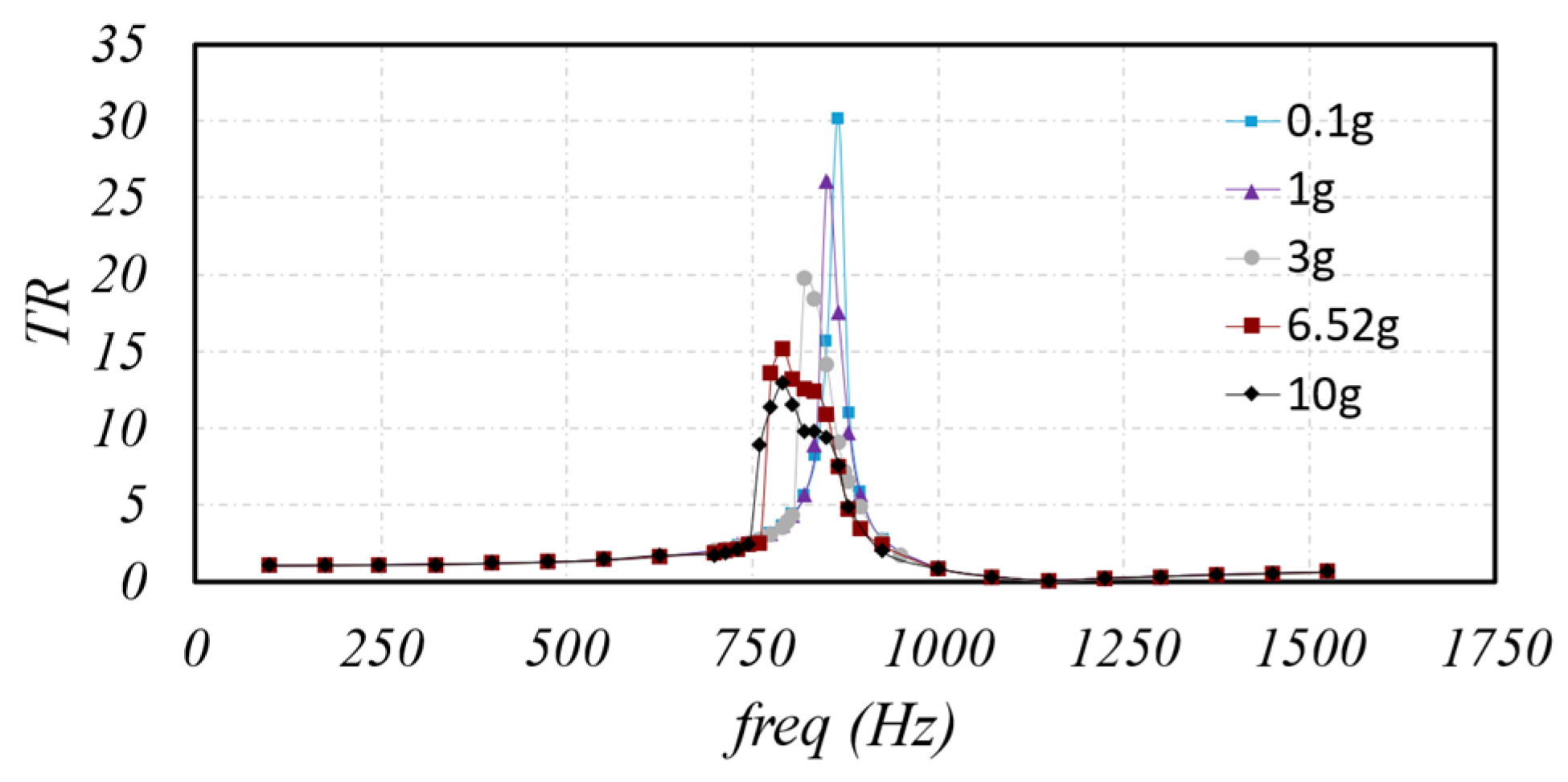
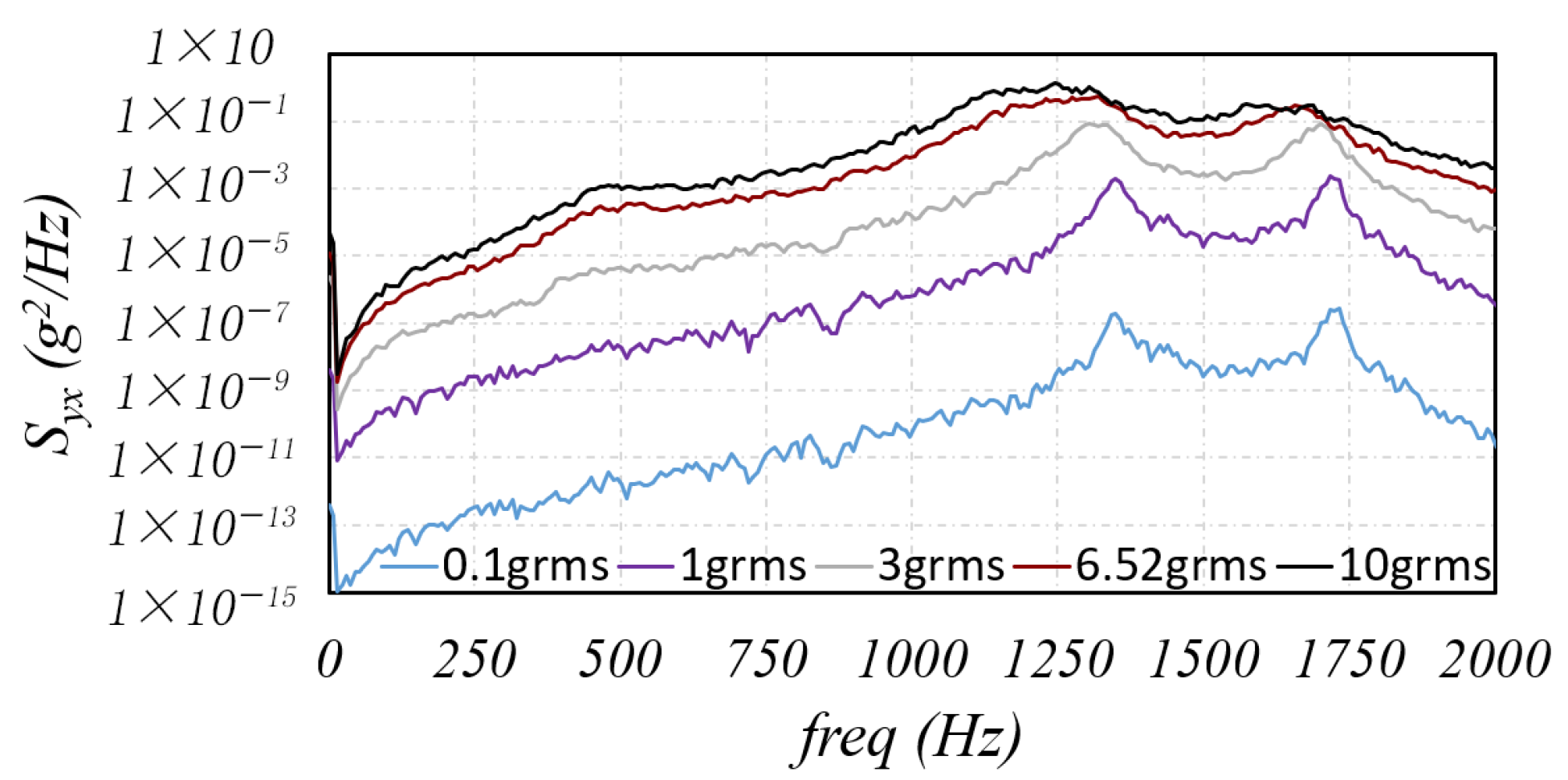
1. Introduction
Bearings are fundamental components in rotating systems, typically operating under vibrations induced by rotary motion. These vibrations originate from external loads and mechanical interactions among machine elements, such as gears and shafts, as well as internal interactions involving rolling elements, rings, cages, and also the lubricant within the bearing. However, bearings in space applications must face a different type of vibration inherent to any type of space mechanism. This occurs primarily during rocket launch when the satellites remain enclosed within the rocket, representing the most critical scenario for space bearings. Ensuring bearing survival during this phase is essential for proper satellite operation throughout its lifetime. To achieve this, simulations and tests are usually performed under the following loads: a static acceleration load equivalent to the rocket acceleration during launch, sine loads and random loads related to the rocket vibration, and a shock load equivalent to the satellite’s deployment.
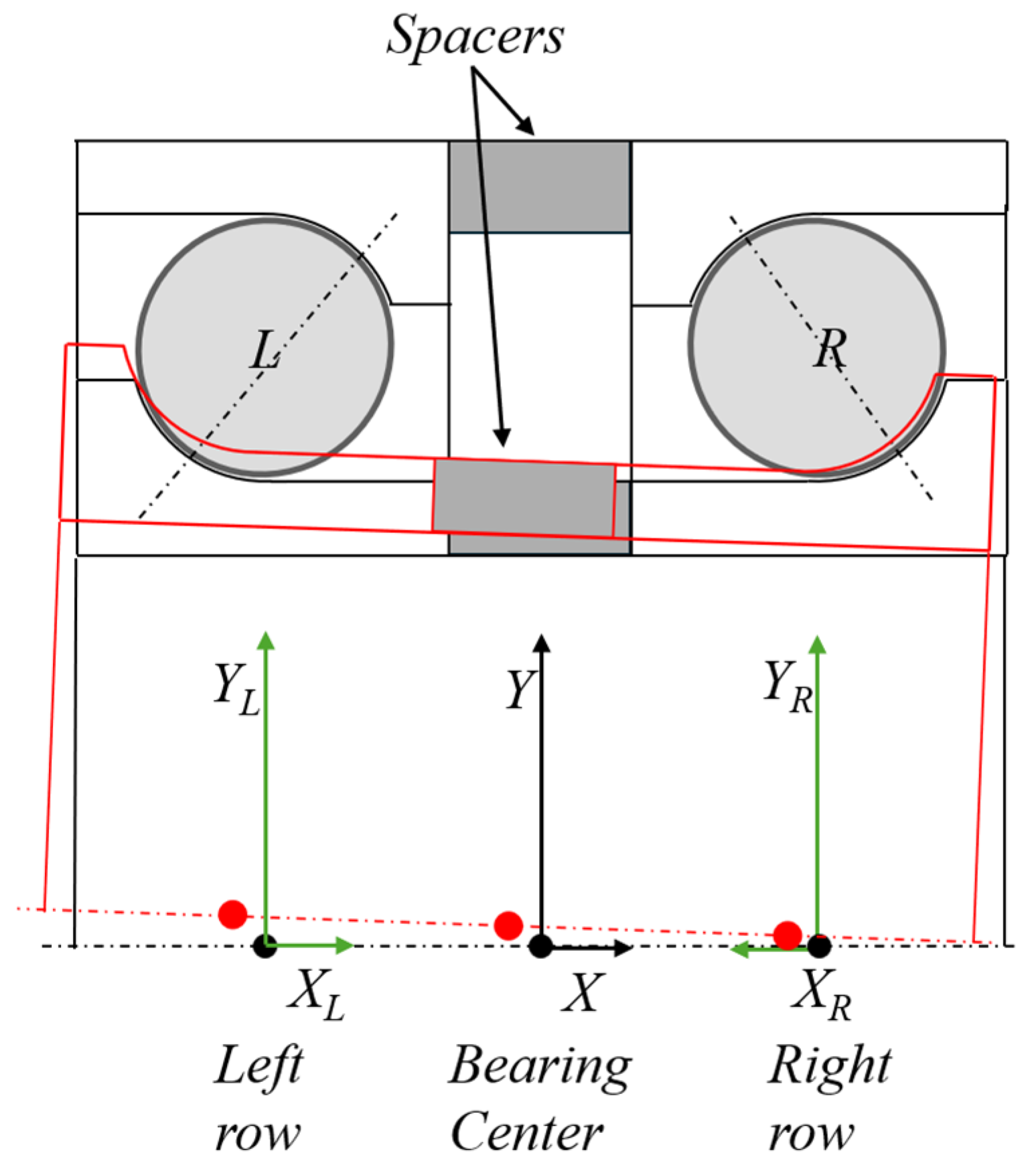
Double-row preloaded ball bearings form the joints between different movable components in space mechanisms. These bearings are arranged in either back-to-back or face-to-face configurations and can have either hard or soft preload, as described in [
1]. Among all satellite bearings, they withstand the highest loads and their preload must provide adequate stiffness for the survival of the bearing during rocket launch, thereby enabling proper satellite operation during its life. The integrity of these bearings is assessed verifying the contact stresses and gappings along the vibration response. Moreover, the preload not only affects the vibrational response but also the friction, which selecting a much higher preload than the minimum required one implies a higher friction that decreases the motorization margin of satellite’s electrical motors. Therefore, accurate modelling of all these aspects is a key factor to assess the survival and operability of the bearings.
Different models have been developed to estimate the static load distribution and stresses in ball bearings. Sjovall [
2] used finite element method (FEM) and a semi-analytical model to determine the radial load distribution within bearings. This model was later employed by Hernot et al. [
3] to compute the bearing stiffness matrix and by Liu et al. [
4] to asses load distribution and stiffness variations, incorporating ball preload and contact angle variations. Houpert [
5,
6] proposed point contact curve fitting approach for ball-raceway contacts, obtaining close results when comparing them with Hertz’s approach [
7]. Regarding the explicit dynamic modelling, the use of finite element analysis (FEA) for point contact modelization is not feasible due to the required computational cost. Consequently, this work uses the analytical model developed by Hertz [
7] for ball-raceway contact, along with the single-row ball bearing model developed by Harris and Kotzalas in [
8,
9] to develop the dynamic model. In this approach the dynamic forces are determined with the static model incorporating the contact damping effects.
In the field of bearing rotary dynamics, the current reference software is advanced dynamics of rolling elements (ADORE), developed by Gupta [
10]. This multibody simulation tool models the contact between rolling elements, rings and cage providing key insights such as cage forces, accelerations and friction. Stacke et al. [
11] developed bearing simulation tool (BEAST), a rolling bearing dynamic simulation tool which, in addition, includes other mechanical element forces for dynamic simulations. Xi et al. [
12] proposed a multibody model for ball bearings to analyse the ball-raceway contact path under different conditions, concluding that the axial force plays a decisive role in the contact path distribution. Bizarre et al. [
13] developed a bearing model simulating the elastohydrodynamic lubrication (EHL) contact evaluating the stiffness and damping characteristics of angular contact bearings under different conditions. Petersen et al. [
14] proposed a double-row ball bearing model under radial loads to investigate the dynamics of the system under different raceway defects, demonstrating strong correlation with the performed experimental tests. Luo et al. [
15] conducted dynamic simulations using FEA to analyse an angular contact ball bearing, incorporating the cage and balls at varying velocities to assess axial and radial stiffness. The simulations and the theoretical models showed agreement with the experimental data.
Rotor systems supported by a pair of bearings share structural design similarities with the hard-preloaded duplex bearings used in space applications, as both systems support a mass with two (bearing) rows. These rotor system models often incorporate bearing defects, rotor unbalance, preload variations and other excitations, with the damping defined either at a ball-raceway contact level, or through a global damping matrix for the entire bearing. Fang et al. [
16] analysed the influence of the different bearing stiffness matrix elements on rotor dynamics, clarifying the effects of the off-diagonal elements comparing
O (back-to-back) and
X (face-to-face) configurations. Liu and Shao [
17] developed a twelve degree of freedom rotor dynamic model considering housing stiffness, frictional moments and localized defects with particular focus on how housings properties affected the dynamics of the system across three different models. Cheng et al. [
18] investigated the dynamics of the rotor considering radial clearance, rotor-stator rubbing, rotor eccentricity, raceway defects and waviness of the bearings. The study concluded that a higher preload improves the load distribution, the rubbing leads to a sharpening in the displacement signal, and waviness influences the system only at a specific velocity. Sinou [
19] introduced a flexible shaft modeled by thirteen Timoshenko beam elements supported by two ball bearings, with an unbalanced disc attached to a flexible coupling. The study demonstrated the complexity of the nonlinear response for small changes in model parameters such as the radial clearance of the bearings. Young et al. [
20] analysed the rotor stability under random axial forces employing FEA to discretize the equations and the Itô method [
21,
22] to obtain the responses, concluding that reducing the bearing axial forces increased system instability. Gao et al. [
23] modeled a dual rotor system under barrel-roll flight loads, incorporating a defect in the outer raceway, proving the effects of the manoeuvre load, the defect and the rotating speed on the dynamic response.
Reaction wheel models also share similarities with the testing of space duplex bearings, as they support a high mass using two bearings and analyse system vibrational characteristics. Alkomy and Shan [
24] developed a reaction wheel micro-vibration model, simulating imbalance and bearing waviness, with simulations accurately predicting system forces and moments in agreement with experimental results. Addari et al. [
25] modeled a satellite cantilever reaction wheel which was validated with experimental results. The study highlighted the influence of the gyroscopic moment in the response of the system and proposed a methodology for the measurement of dynamic mass.
Rotor systems used for aeroengines response simulations also resemble the structural models of duplex bearings as they distribute different masses along the rotor supported by bearings. Chen [
26] developed a coupled rotor-ball bearing-stator dynamic model to analyse aeroengine vibrations, incorporating contact nonlinearities. The model effectively simulated rubbing faults, which were validated through experimental tests. Hou et al. [
27] investigated a dual rotor aeroengine system supported by five bearings with variable speed ratios, determining the bending-torsional coupling which affected the response. Lu et al. [
28] proposed another dual-rotor system of an aeroengine with four bearings, considering faults in one of the masses and reducing the model order to obtain dynamic responses. The results provided accurate solutions compared to those of the complete model, enabling the development of an efficient computational tool for designing large rotor systems with significant masses.
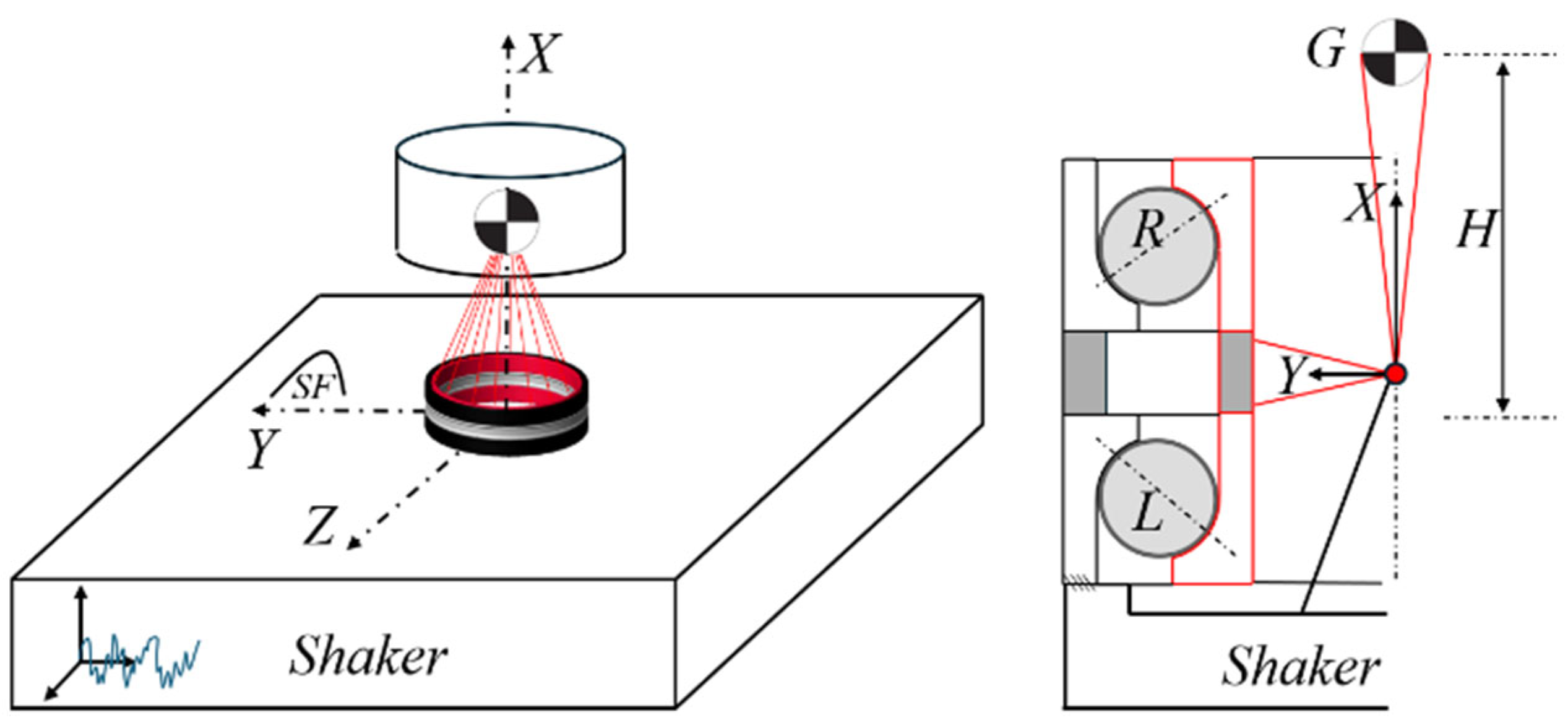
The models described above assess the dynamics of the bearings related to their own rotation. However, a significant part of the vibratory behaviour of space bearings is driven by large inertial excitations during rocket launch, while they are not rotating. These excitations can be classified into an equivalent set of loads for their analysis and testing [
29]: static acceleration load, sine load, random load and shock load. The common approach in the industry to analyse the bearing vibrations is to assume a linear stiffness for the bearing within the FEM and compute structural responses to the excitations by modal superposition. An alternative simplified method is using the Miles’ equation [
30], which determines the response grms of the system under random vibrations. However, neither approaches can capture the system’s nonlinear effects to estimate the maximum load appearing in the response, therefore, the simplification of 3σ
std approach [
31] is used to determine random loads. While FEM and Miles’ method provide a fast estimation about resonances and accelerations, they cannot capture the changes on bearings damping and natural frequencies under varying load levels which have been appreciated in tests.
Experimental studies have also been conducted to assess the vibrational behaviour of ball bearings and validate theoretical models. In this context, Söchting et al. [
32] performed harmonic axial vibration tests to measure the gapping between the rings of a ball bearing by means of two laser triangulation transducers. Additionally, friction measurements were carried out to evaluate the impact of vibrations on friction torque. The gapping results were compared to a linear axial model that integrated the stiffness obtained with Code for Analysis of Bearings in Rocket Engines Turbopumps (CABARET) [
33], showing similar results for low load levels. However, for higher load levels, the predicted gappings were higher than the gappings obtained through the experiments. Munro et al. [
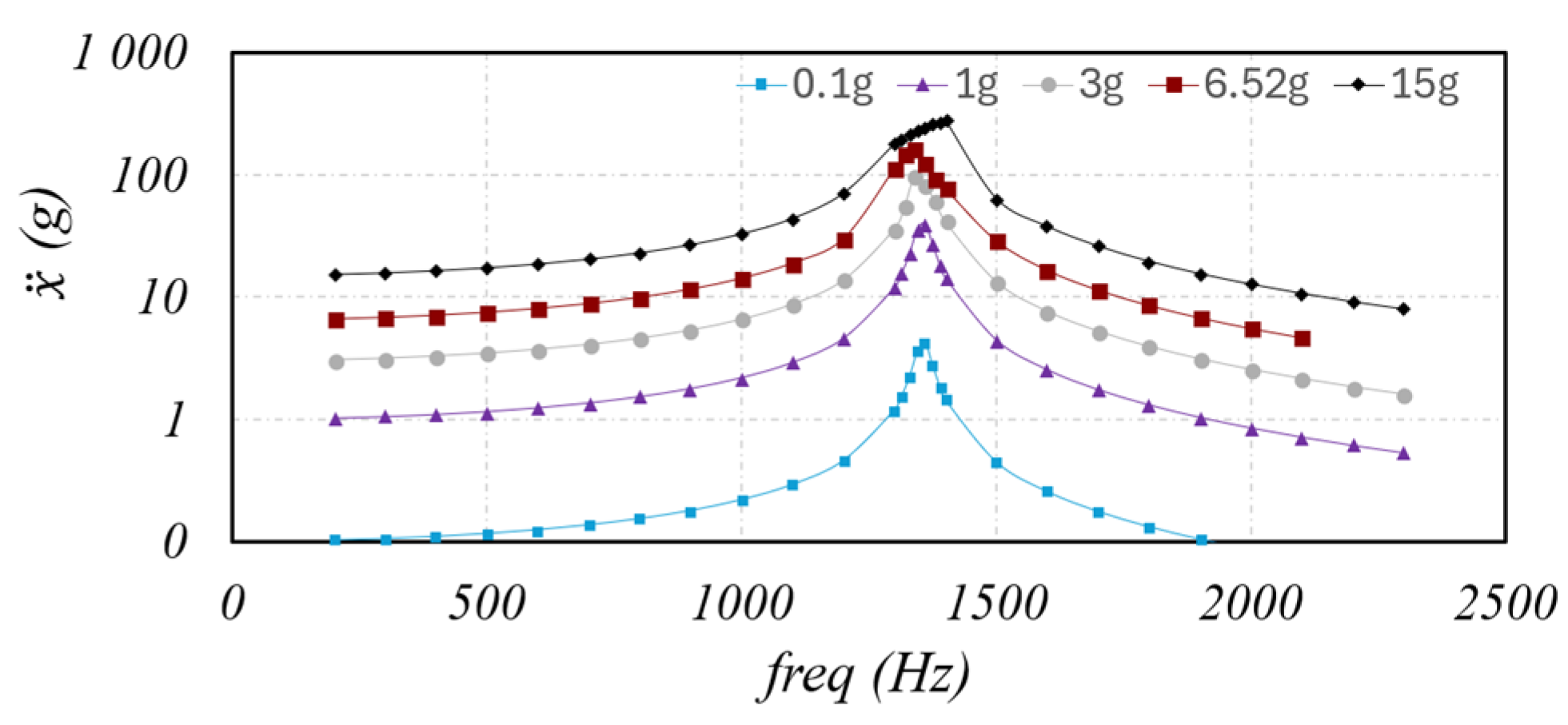
34] performed a series of axial vibration tests to different configurations of back-to-back duplex space ball bearings. The bearings were tested in different setups: soft preloaded without snubber, soft preloaded with various snubbers and hard preloaded. The results indicated that increasing load levels led to corresponding changes in natural frequencies and response amplitudes.
Continuing with the study, Hinque and Seiler [
35] developed perhaps the most complete work about axial vibrations of space bearings. He concluded that, for hard preloaded systems the gapping effect was almost linear, and that for soft preloaded systems it was necessary to simulate spring and snubber interactions to assess the nature of that gapping effect. Another key finding was that applying the rule of 3σ
std to assess the maximum load in a random vibration may not be a reliable approach, as some instantaneous loads observed in tests significantly exceeded the limits stated by the rule. To further investigate these effects, Hinque developed a single degree-of-freedom (DOF) dynamic axial model of the bearing, using load level test results to correlate model parameters. While the model obtained good correlation for resonant frequencies at low load levels, it exhibited limited sensitivity to frequency variations, and the damping was represented with a global damping matrix rather than being modeled at the ball-raceway contact, where most of the damping actually occurs. Additionally, the model only accounted for the axial DOF, overlooking the radial behaviour, which is a critical factor in the overall performance of space bearings.
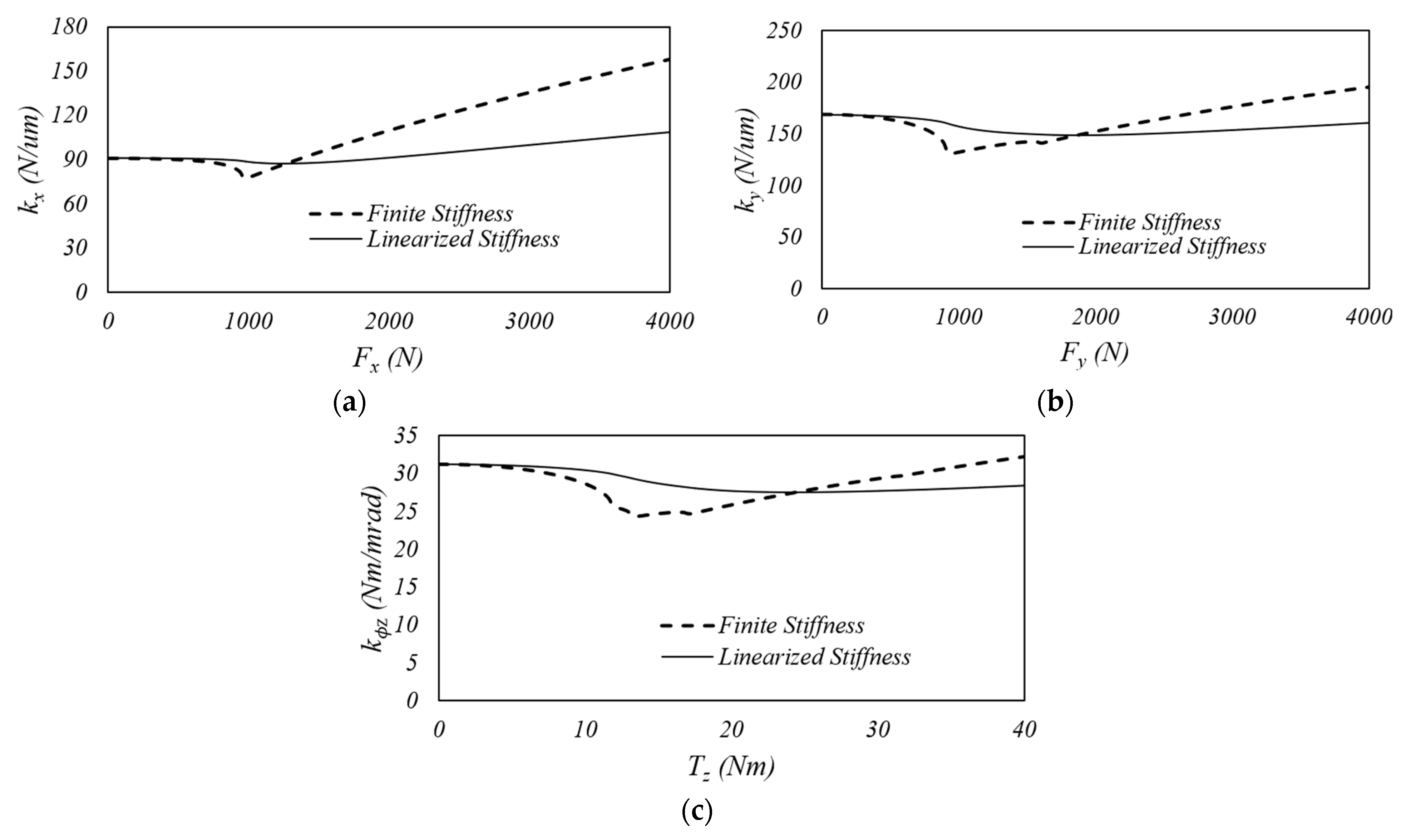
In this work, unlike previous models used for space applications, which rely on simplified representations such as linear stiffness assumptions or single-DOF dynamics, the proposed approach incorporates multiple-DOF, enabling the simulation of axial, radial and tilting combined responses, as well as non-centred masses and combined excitations. This multidirectional capability is essential to reproduce the complex dynamic behaviour experienced during satellite launches. The model includes contact-level damping at the ball–raceway interface using the Hunt and Crossley formulation, allowing a more accurate representation of energy dissipation compared to models that apply a global damping coefficient. Additionally, the use of quaternions to represent rigid body rotations eliminates the need for trigonometric functions, improving numerical stability and computational efficiency. These features collectively enhance the model’s ability to capture key nonlinear phenomena observed in experimental tests, such as shifts in natural frequencies, changes in transmissibility, stress and gapping effects under vibration.
In contrast to linear models, which provide constant natural frequencies and transmissibility values regardless of the load level or excitation type, the proposed model captures variations in both quantities as a function of the applied load. This difference arises because linear models rely on simplified amplification formulas directly related with a global damping, whereas the proposed model is based on an explicit formulation with damping directly applied at the ball–raceway contact. This representation allows to reproduce the nonlinear behaviour observed in tests in the simulations, capturing the cross-coupling effects. Moreover, compared to explicit models that incorporate damping as a general term based on the relative velocity between rings, the proposed approach integrates damping at the actual physical source of energy dissipation. By computing the local penetration velocities at the ball–raceway contacts, the model provides a more accurate and detailed representation of damping behaviour. The difference with general damping models increases when rotational dynamics are considered, where each ball dissipates a different amount of energy, an effect reproduced by the proposed model.
As a benchmark, this study takes the hard preloaded duplex bearing described in [
35] which was tested in [
34]. First, the static model of a duplex bearing is introduced revealing the geometrical nonlinearities of the system. Next, the ball-raceway contact damping model is presented, followed by the quaternion-based formulation used to describe the dummy mass dynamics. Afterwards, time dependent loads are applied to the model, revealing the changes on resonant frequencies and amplitudes showing strong correlation with the available axial vibration data [
34]. The analysis is further extended to radial simulations, demonstrating that the model successfully captures the cross-coupling modes, whose influence is underlaying the results of those published axial tests. Finally, the conclusions of the developed model and performed simulations are presented.
3. Dynamic Ball Bearing Model
In this section, the static models in
Section 2 are extended to obtain the corresponding dynamic models. For this purpose, velocities and damping effects are included in the arrangement. The single-row and duplex models are adapted for dynamic analysis substituting Equation (9) with Equation (23).
In the models used in [
16,
18,
19,
20,
21,
22,
23,
24,
25,
26,
35] the damping is included as a damping matrix for the whole bearing, relating the velocities of the inner and outer ring center nodes. This damping matrix is then incorporated into the equations of motion. However, there is an alternative approach with more physical representation than treating the damping as a “black box”, which is considering the damping in the ball-raceway contact. This perspective is supported by the work of Dietl et al. [
37], who performed different tests estimating the loss factor and concluded that damping was originated primarily from the ball-raceway contact interactions. Following this approach, studies such as [
10,
11,
12,
13,
14,
17] define the damping at each ball-raceway contact, offering a more accurate approach to model the damping behaviour in bearings. These contact damping models consider the effects of the lubricants and angular velocity of the bearing. Nevertheless, in this work the effect of EHL is not relevant, as the bearing is not rotating when it is suffering the vibration and the damping factor is adopted to account for all possible damping contributors.
Flores and Lankarani [
38] and Corral et al. [
39] reviewed the models for contact damping phenomena in multibody systems that may be closer for the conditions of simulation proposed in this work. Among those models, the one developed by Hunt and Crossley in [
40] is selected. This Hertz-damp model is represented as:
considers the effect of the contact load and the velocity of penetration for one contact. The first term of the equation is the Hertzian contact force, while the second term represents the damping force. The parameter
γ is the damping parameter of the model and
is the penetration velocity.
However, in the bearing model each ball represents an inner and an outer contact. Therefore, the expression defined by Hunt-Crossley needs to be extended for the model of this work to consider both contacts in a single equation. The formulation for this adaption is presented in the following equations:
With this formulation, the single-row dynamic bearing model remains identical to the static model described in
Section 2.1, except that Equation (9) is replaced by Equation (23). To complete the single-row dynamic model, the penetration velocity of the ball
must be determined. Assuming the outer ring fixed, and given the inner ring velocities
,
,
and angular velocities
,
, the penetration velocity of the ball
is determined using the equations:
It is important to note that the velocity of the inner ring center of curvature needs to be projected onto the line connecting inner and outer centers of curvature, which is done in Equation (28).
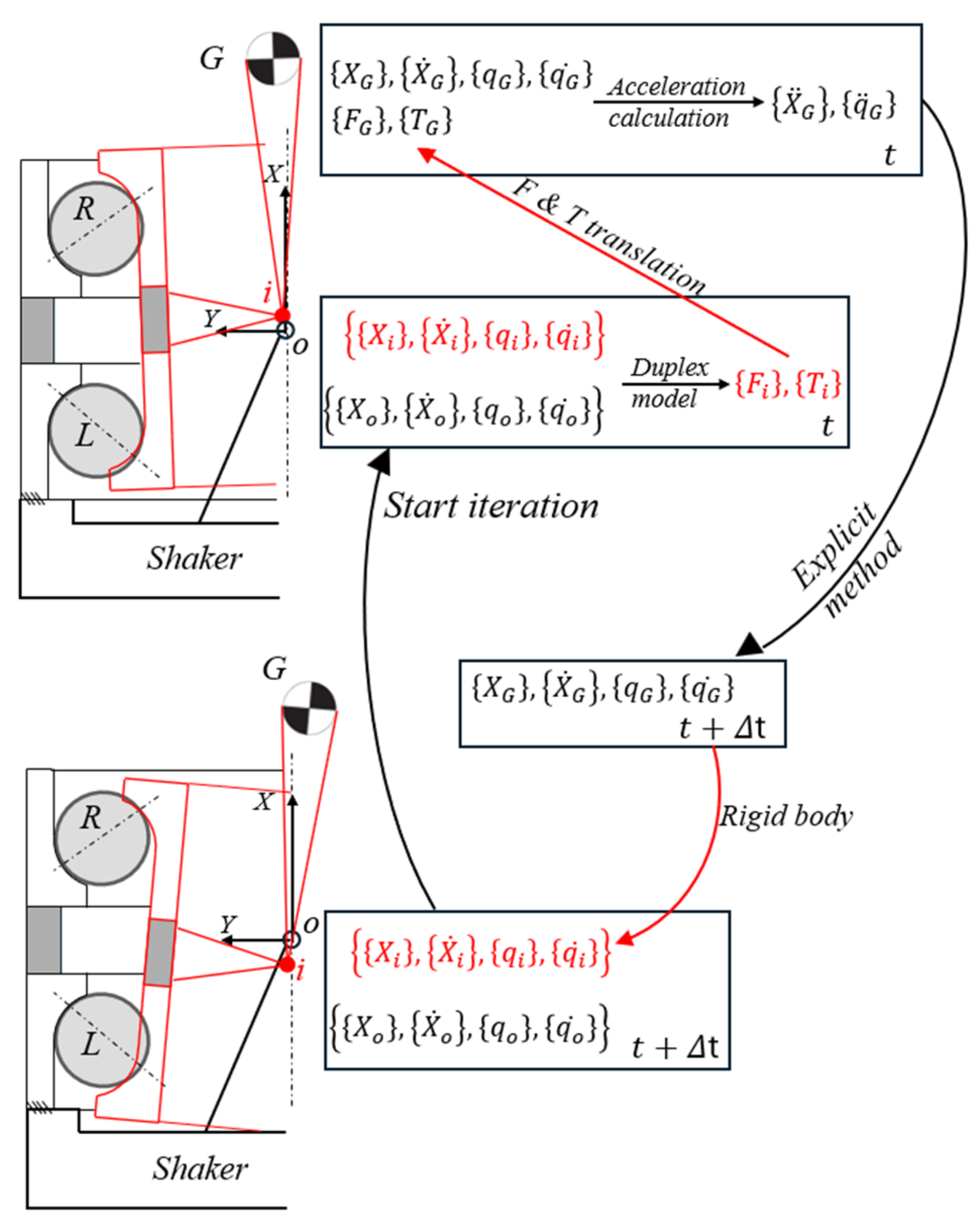
The dynamic model of the single-row bearing is then extended to the duplex bearing following the methodology described in
Section 2.2. Given the defined duplex center inner ring velocities
,
,
and angular velocities
,
, the velocities of the left and right row inner nodes are determined. Then, these nodal velocities are translated to the reference frames of their corresponding row and they are introduced in the single-row model for force calculation. After, the forces of each row, including elastic and damping forces, are translated to the center of the duplex. Therefore, introducing to this complete model the inner ring displacements and velocities relative to the outer ring, the forces and moments at both rings are obtained. Moreover, these reactions already contain the static and damping forces of the bearing. Hence, the duplex model can be easily included in multibody dynamic simulations.
6. Conclusions
This study presents a nonlinear model for analysing the dynamic behaviour of hard preloaded duplex ball bearings in space applications. The developed model incorporates multi-degree-of-freedom explicit nonlinear dynamics, using quaternions to represent rigid body rotations and the Hunt and Crossley model to describe ball-raceway contact, accounting for both elastic and damping forces. The use of quaternions simplifies the formulation of the equations of motion, eliminating the need for computationally expensive trigonometric functions. Additionally, by incorporating contact damping at the ball-raceway interface, the model provides a parameterizable framework for stiffness and damping characteristics. This contrasts with conventional models that apply global or generalized damping coefficients.
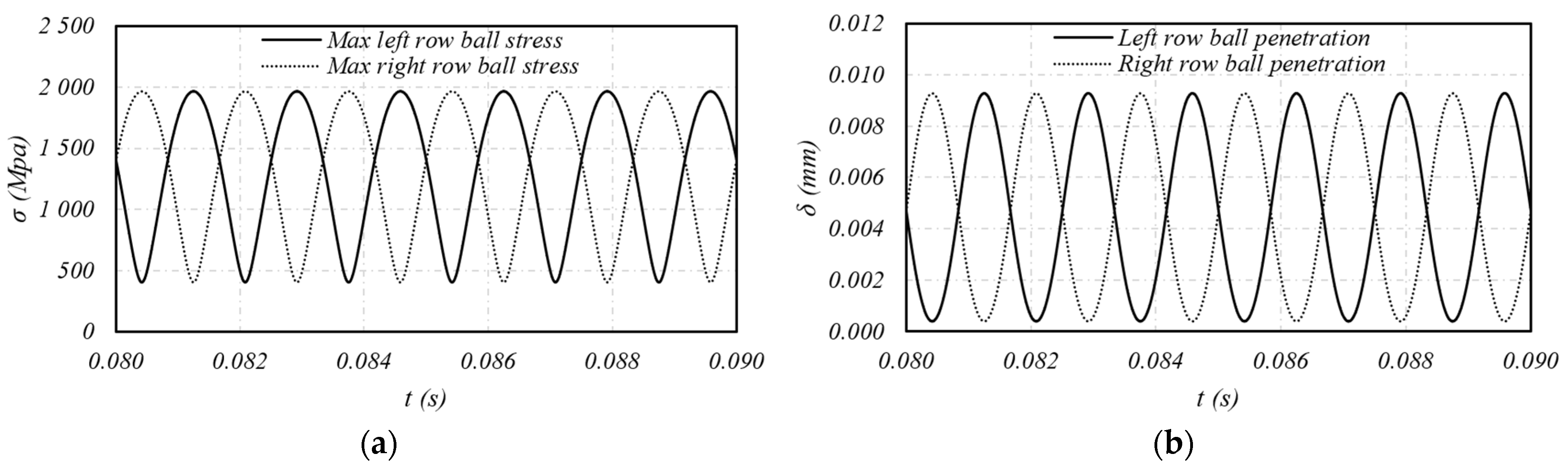
The static model, extended to a back-to-back duplex configuration, demonstrated the importance of considering nonlinearities in stiffness and stress responses under dynamic excitations. Meanwhile, the dynamic model effectively integrates damping and velocities, aligning well with published axial tests.
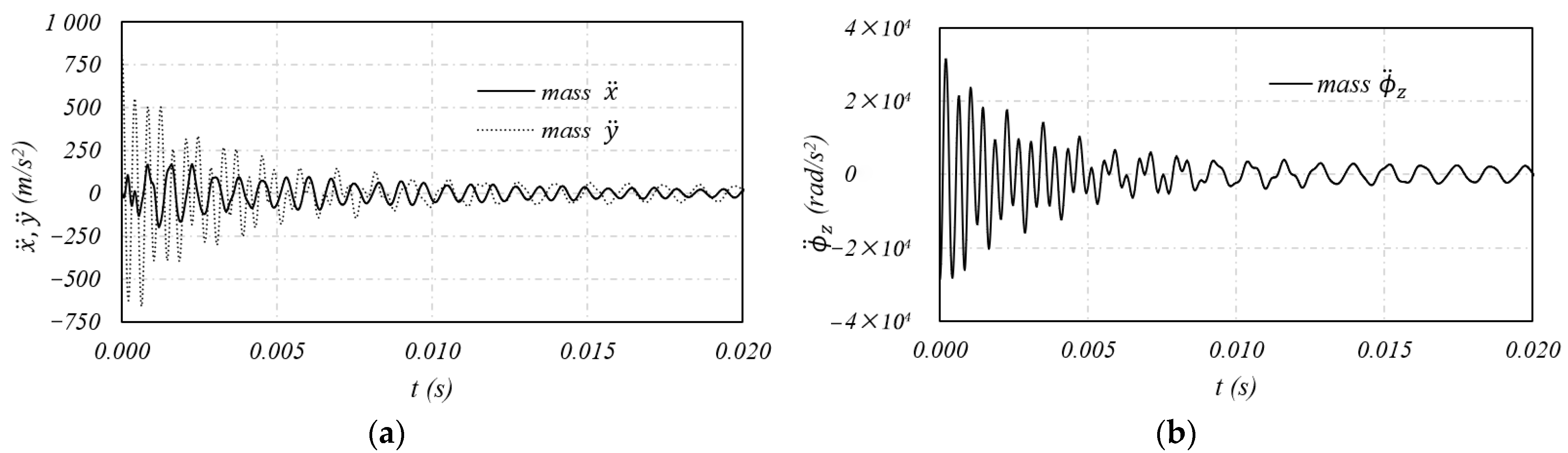
The duplex dynamic model with a dummy mass was specifically developed to simulate launch loads experienced by space mechanisms, capturing transmissibility variations, natural frequencies, stresses and gapping at different load levels. The model provides consistent results with experimental observations and is capable of evaluating conditions such as mass eccentricity and multidirectional excitations.
The axial and radial sine load simulations validate the model’s ability to capture both softening and stiffening effects, as well as cross-coupling phenomena, which is not detectable in purely axial or linear models. Furthermore, the random load simulations highlight the model’s ability to predict the system’s response, offering an alternative to the traditional 3σstd approach.
Although this study relies on experimental data from literature, these findings underscore the importance of considering nonlinear multi-DOF models to predict bearing behaviour under vibration conditions, thereby enhancing the reliability and performance of mechanisms in space applications. Moreover, the quaternion-based modelling technique will enable the consistent and systematic composition of models for complete space actuation mechanisms, including bearings, gears, shafts, and stiffener rings, and efficiently simulate the consequences of a rocket launch on them.