Abstract
Unmanned Aerial Vehicle (UAV) path planning is critical for ensuring flight safety and enhancing mission execution efficiency. This problem is typically formulated as a complex, multi-constrained, and nonlinear optimization task, often addressed using meta-heuristic algorithms. The Crested Porcupine Optimizer (CPO) has become an excellent method to solve this problem; however, the standard CPO has limitations, such as the lack of adaptive parameter tuning to adapt to complex environments, slow convergence, and the tendency to fall into local optimal solutions. To address these issues, this paper proposes an algorithm named QCPO, which integrates CPO with Q-learning to improve UAV path optimization performance. Q-learning is employed to adaptively adjust the key parameters of the CPO, thereby overcoming the limitations of traditional fixed-parameter settings. Inspired by the porcupine’s defense mechanisms, a novel audiovisual coordination strategy is introduced to balance visual and auditory responses, accelerating convergence in the early optimization stages. A refined position update mechanism is designed to prevent excessive step sizes and boundary violations, enhancing the algorithm’s global search capability. A B-spline-based trajectory smoothing method is also incorporated to improve the feasibility and smoothness of the planned paths. In this paper, we compare QCPO with four outstanding heuristics, and QCPO achieves the lowest path cost in all three test scenarios, with path cost reductions of 30.23%, 26.41%, and 33.47%, respectively, compared to standard CPO. The experimental results confirm that QCPO offers an efficient and safe solution for UAV path planning.
1. Introduction
In traditional engineering fields, many tasks depend on manual labor or conventional machinery for data collection and monitoring. These methods typically require substantial human intervention and incur high costs. They are also vulnerable to environmental factors, such as harsh weather, complex terrain, and remote locations. Moreover, these methods are plagued by inefficiencies, low accuracy, and delays in data updates [1,2,3]. As a novel platform, UAVs have garnered increasing attention due to their advantages, which include small size, low cost, and wide field of view. However, their autonomous nature makes mission planning particularly critical, with path planning (PP) serving as the core component [4]. Effective PP can help UAVs reduce flight distance and avoid threats [5].
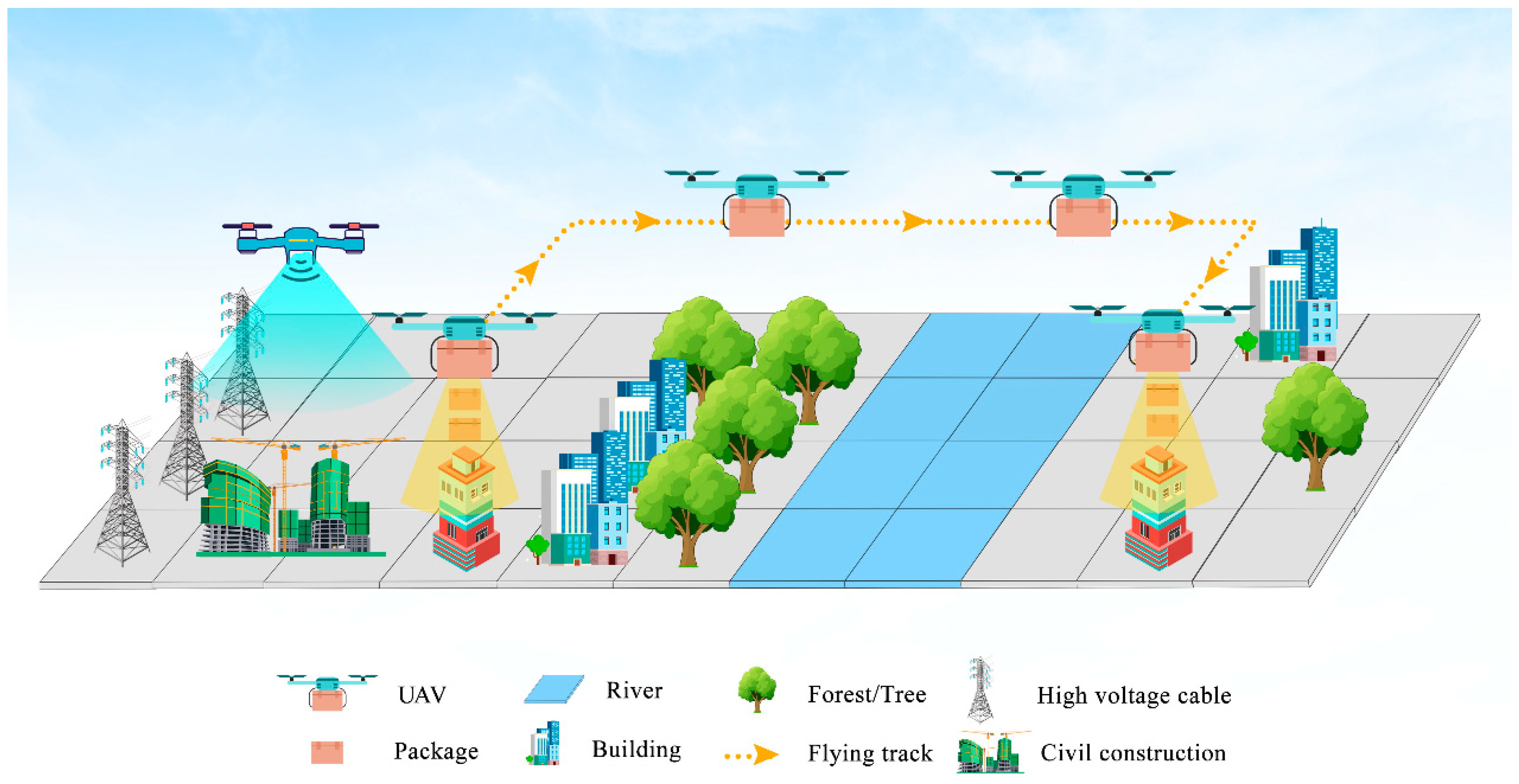
UAVs demonstrate remarkable efficiency in data acquisition within complex environments, thereby alleviating the burdens and hazards associated with manual inspections. They play a pivotal role, particularly in areas prone to high risks such as structural evaluations of buildings, power grid examinations, and logistical operations, as depicted in Figure 1. Despite these advantages, UAVs encounter challenges posed by intricate three-dimensional terrains [6]. Presently, the predominant PP algorithms encompass approaches such as reinforcement learning (RL), heuristic methods, and hybrid algorithms.
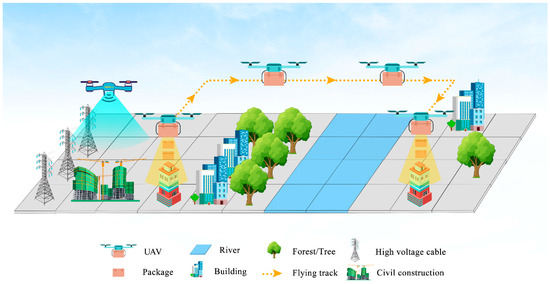
Figure 1.
Applications of UAVs in Engineering Fields.
RL represents a promising approach by offering an adaptive, efficient, and reliable intelligent solution for UAV PP in dynamic and complex environments. This method facilitates autonomous decision-making and interaction with the environment [7,8,9]. Sonny et al. proposed a Q-learning path planning algorithm that combines a shortest distance first strategy with a grid graph approach to effectively deal with dynamic and static obstacles [10]. de Carvalho et al. proposed a Q-learning-based offline path planning algorithm that optimizes path length, security, and energy consumption to optimize the path [11]. Cui et al. proposed A Q-learning path planning framework that combines control strategies with environmental uncertainty modeling to effectively improve the obstacle avoidance ability and path tracking accuracy of UAVs in dynamic threat environments [12]. Q-learning suffers from the problems of state-action space dimension explosion, difficulty in dealing with continuous variables, and slow convergence speed of training, which limits its effectiveness in the application of UAV path planning in complex three-dimensional environments. Boulares et al. introduced an adaptive experience replay mechanism based on deep Q-learning to tackle the three-dimensional PP challenge in partially observable environments. However, this method may still suffer from delayed responses when confronted with sudden dynamic obstacles [13]. Concurrently, Lee et al. developed a sub-goal-based UAV PP algorithm that employs goal-conditioned RL. This training enables UAVs to execute multiple flight tasks, thus allowing them to manage complex tasks across various scenarios and adapt to unknown environments without prior environmental knowledge [14]. Zhu et al. introduced an energy-efficient collaborative PP algorithm utilizing a hexagonal region search and a multi-agent deep Q-learning. This approach aims to maximize data collection from distributed sensors by multiple UAVs, while avoiding issues of overlapping coverage and collisions, although its effectiveness depends on robust network conditions [15]. Additionally, Jiang et al. enhanced collision avoidance and PP capabilities through a soft actor-critic model supplemented by posterior experience replay. However, the training requirements for this model are complex [16]. Swain et al. proposed a reinforcement learning-based cluster routing scheme, which incorporates transformer encoders designed to address the target tracking problem of UAVs in scenarios with communication disruptions or delays [17]. This approach effectively manages partially observable Markov decision processes, though it demands significant computational resources. In RL, particularly in Q-learning, the agent identifies the optimal action by learning the action-value function, which quantifies the expected utility derived from executing a specific action in a given state [18,19]. The Q-learning-based metaheuristic algorithm for dynamic parameter adjustment addresses the distributed assembly scheduling problem but incurs high parameter training costs despite its notable adaptability [20]. Similarly, the improved Spider Monkey Algorithm, which integrates Q-learning for dynamic parameter adjustment, efficiently adapts to various complex operational environments in PCB assembly lines, thereby improving environmental adaptability [21]. The application of Q-learning for dynamic parameter adjustment also significantly enhances adaptability and optimization efficiency in multi-objective scheduling algorithms for hybrid flow shops [20,21,22]. Despite substantial progress in the field of PP via RL, current methodologies continue to face challenges in real-time responsiveness, computational efficiency, and environmental adaptability. These issues underscore the need for the development of more robust and practical algorithms to navigate complex and dynamic real-world application scenarios [23].
Heuristic algorithms have emerged as the predominant method for UAV PP, offering the capability to generate near-optimal trajectories swiftly. This rapid generation facilitates prompt responses in emergency situations. Recent scholarly work has enhanced both the efficiency and accuracy of these algorithms in complex environments through the integration of multiple optimization techniques, thereby contributing significantly to the advancement of this field. Notable intelligent optimization algorithms employed in this context include the Cuckoo Search (CS) [24], Sparrow Search Algorithm (SSA) [25], Ant Colony Optimization (ACO) [26], Pigeon-Inspired Optimization (PIO) [27], Grey Wolf Optimizer (GWO) [28], Spider Wasp Optimizer (SWO) [29], and Crested Porcupine Optimizer (CPO) [30]. These algorithms have been successfully applied to UAV PP, yielding promising outcomes. However, while single-solution-based algorithms persist with a singular solution throughout the search process, hybrid algorithms—which amalgamate two or more techniques—tend to more effectively harness the benefits of PP.
The integration of metaheuristic algorithms with RL constitutes a pioneering collaborative framework, merging the adaptive capabilities of dynamic environments inherent in metaheuristics with the robust global search proficiency of RL, thereby creating a synergistic paradigm for intelligent optimization [18,31]. A multi-objective evolutionary algorithm, leveraging RL and information entropy, adeptly approximates the complex Pareto frontier by dynamically adjusting the distribution of reference vectors. However, the computational demands of this algorithm are notably high [32]. This hybrid methodology offers versatile and innovative solutions to intricate real-world challenges [33]. For example, Subramanian and Chandrasekar [34] have demonstrated that the integration of RL algorithms, through sophisticated decision-making mechanisms, facilitates dynamic optimization solutions for mobile robots, empowering them to autonomously generate optimal task sequences. Furthermore, Cheng et al. enhanced the global search capabilities by amalgamating an improved particle swarm optimization algorithm with a combination of grey wolf optimization and chaotic strategies, utilizing adaptive inertia weights and chaotic perturbations to effectively mitigate the limitations of traditional algorithms that typically stagnate at local optima [35]. Lu et al. introduced a method for optimizing logistics pathways in fourth-party logistics, employing an enhanced ant colony system integrated with a grey wolf algorithm, which optimizes both transportation time and costs while accommodating customer risk preferences under uncertain conditions, thereby elevating operational efficiency [36]. Chai et al. devised a multi-strategy fusion differential evolution algorithm, executing UAV three-dimensional PP in complex scenarios through strategic population division and adaptive mechanisms, adeptly balancing exploration and exploitation, and underscoring its adaptability [37]. Zhang et al. developed a heuristic crossover search rescue optimization algorithm, incorporating crossover strategies and real-time path adjustment mechanisms, which significantly improved the convergence speed and path quality in UAV PP [38]. Qu et al. formulated an RL-based grey wolf optimization algorithm (RLGWO) for UAV three-dimensional PP in complex environments, facilitated by adaptive operational switching [39]. Yin et al. [40] introduced an RL-based method for adaptive parameterization aimed at enhancing the convergence speed of the well-established PSO algorithm. This innovative fusion approach implements intelligent self-tuning of parameters in metaheuristic algorithms, enabling dynamic optimization informed by historical learning data, real-time environmental factors, and specific problem requirements [40]. The adaptive mechanism inherent in RL further amplifies the search efficiency within intricate solution spaces, achieving more precise dynamic parameter control [20]. These groundbreaking methodologies not only further the autonomy of UAVs but also prove their practical applicability in real-world engineering contexts. Despite these advancements, traditional heuristic algorithms still face limitations due to their strong dependence on parameters and slow convergence rates, which curtail their adaptability and robustness in complex and unpredictable environments. Consequently, enhancing the performance of these algorithms is crucial for their wider application.
In this study, we propose an integrated optimization algorithm that combines RL and the CPO to address the challenges of 3D PP for UAVs in engineering contexts. This algorithm aims to facilitate precise and efficient trajectory planning. The primary innovations and contributions of this research are outlined as follows:
- This study has incorporated a Q-learning strategy into the CPO algorithm, allowing for adaptive and dynamic parameter adjustment. This enhancement mitigates the dependency on manually tuned parameters inherent in the traditional CPO, thereby improving both the optimization efficiency and the stability of the algorithm in practical engineering applications.
- Drawing inspiration from symbiotic algorithms, we have implemented a vision-audio cooperative mechanism to balance visual and auditory defense strategies. This novel approach effectively addresses the issue of slow early convergence encountered in the original CPO when applied to engineering optimization problems.
- This study has developed a position update optimization strategy and integrated it into the CPO algorithm’s existing framework. This strategy is designed to prevent boundary violations that may occur due to excessive update amplitudes in later iterations, thus enhancing the algorithm’s capability to solve engineering optimization challenges.
2. Modeling of the UAV Path Planning Problem
2.1. Path Optimality
To ensure the efficient UAV flight, the PP must be optimized based on specific criteria. This research is primarily concerned with aerial remote sensing, aiming to minimize the path length. Given that UAV flights are centrally managed by the ground control station, the planned flight path is denoted as , which includes the key waypoints the UAV must traverse. Each waypoint corresponds to a node on the search map, represented as . The Euclidean distance between two consecutive nodes, , is employed to compute the path length cost, as defined in the following equation:
2.2. Security and Feasibility Constraints
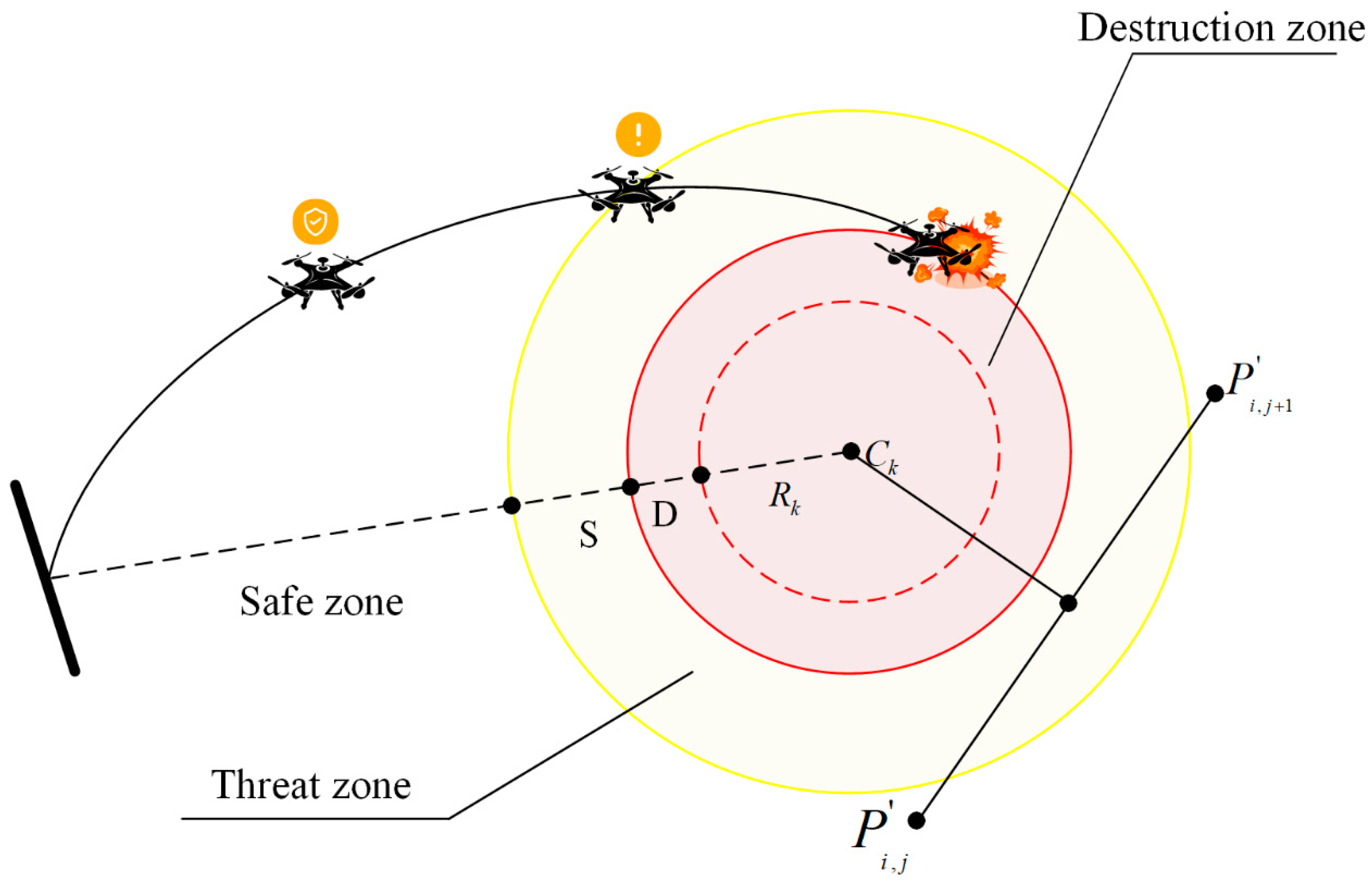
Beyond optimality, the planned UAV path must also enable the drone to navigate and mitigate threats posed by obstacles within the operational area, thereby ensuring safety. Let denote the set of all threats, with each threat assumed to be located within a region defined by its center coordinate and radius , as illustrated in Figure 2. The threat cost of any path segment is proportional to its distance from the threat area, determined by the proximity to and the radius . The threat cost along the waypoints is calculated by considering the diameter , the separation between the UAV and the threat, and the collision area, to evaluate the impact of obstacle regions. The set of obstacles is articulated as follows:
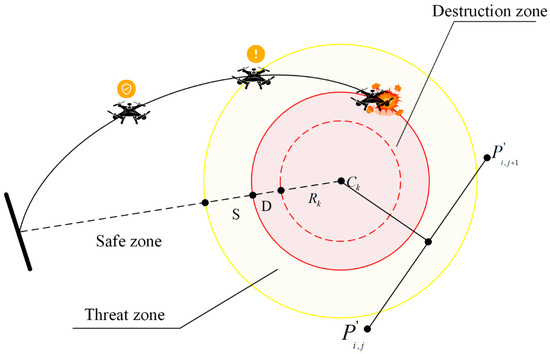
Figure 2.
Classification of threat zones.
It is important to note that while D is influenced by the size and distance of the UAV, S depends on multiple factors, including the application scenario, operational environment, and positioning accuracy.
Note that D is affected by the UAV’s physical dimensions and its relative distance, whereas S is affected by a combination of factors such as the use case, environmental conditions, and the accuracy of positioning systems.
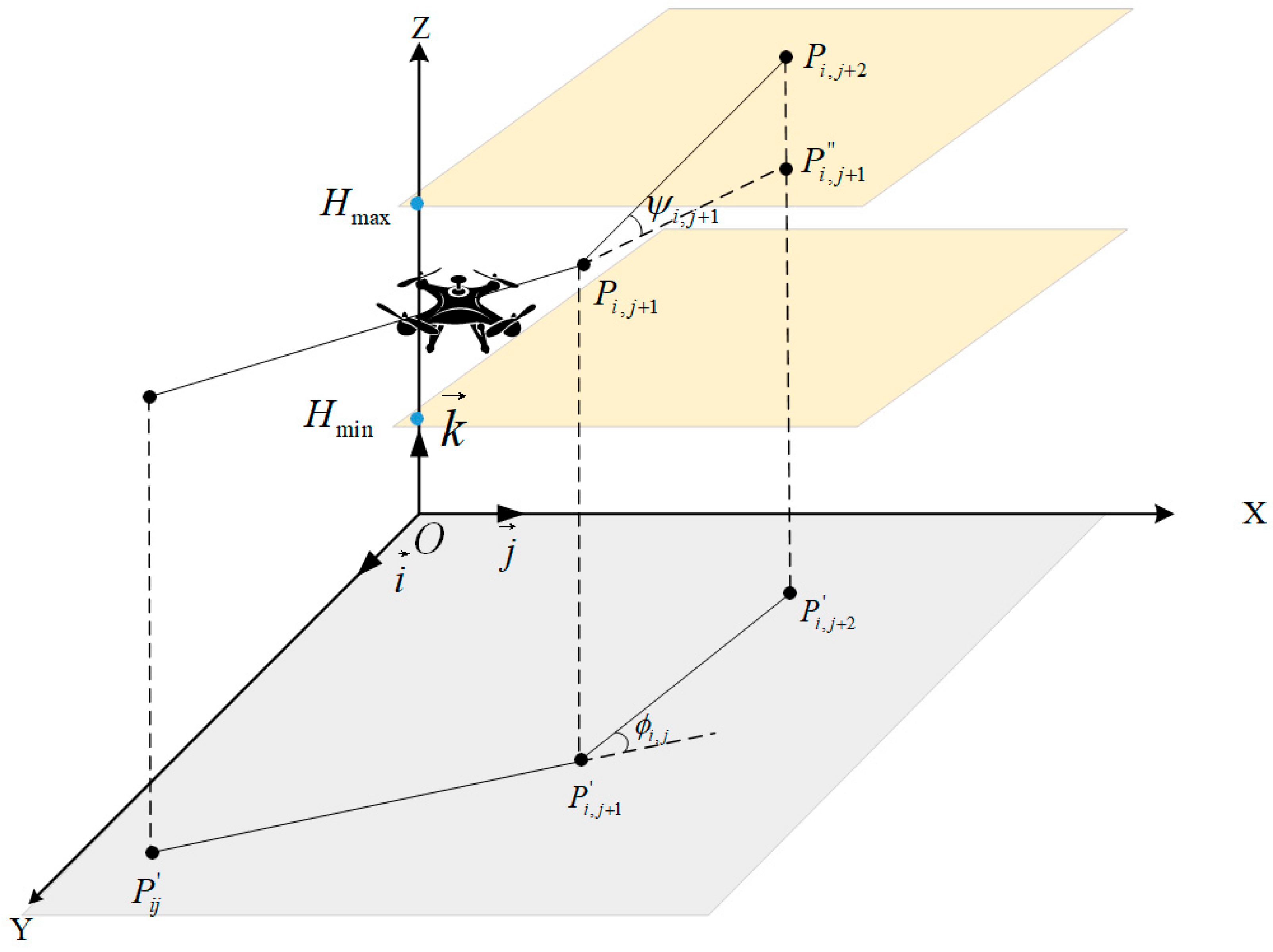
During operational phases, the flight altitude of UAVs is typically restricted within two predefined limits: a minimum and a maximum altitude. In engineering contexts, such as when onboard cameras are employed to capture visual data, the required resolutions and fields of view necessitate specific altitude constraints. Let these altitude boundaries be designated as and . The cost associated with altitude at waypoint is computed using the following equation:
Here, represents the altitude relative to the ground level, as depicted in Figure 3. It can be noted that aims to maintain an average altitude while penalizing deviations from the permissible range. Consequently, the altitude cost for all waypoints is summarized by:
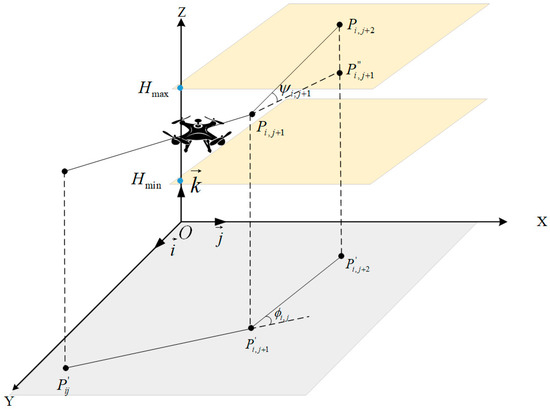
Figure 3.
UAV flight attitude parameters.
The assessment of the smoothness cost, which includes the rates of turning and climbing, is crucial for developing a viable path. As demonstrated in Figure 3, the turning angle is defined as the angle between two consecutive path segments, to , projected onto the horizontal plane “Oxy”. Let represent the unit vector along the z-axis. The projections of these vectors can be determined as follows:
Thus, the turning angle is calculated using:
The climbing angle is defined as the angle between the vector connecting two consecutive path segments and their projection on the horizontal plane:
Accordingly, the smoothness cost is calculated via:
In this context, and are penalty coefficients assigned to the turning and climbing angles, respectively.
Here, turning and climbing angles are penalized using the coefficients and , separately.
2.3. Total Cost Function
The total cost function is articulated by considering factors such as path optimality, safety, and the feasibility constraints , as articulated below:
Here, represents the weighting coefficient, and the cost components to correspond to the costs associated with path length, threat avoidance, flight altitude, and path smoothness, respectively. Among them, path length measures flight efficiency, threat avoidance ensures mission security, flight altitude constrains path executability, and path smoothness enhances flight stability. In this study, the weights are adjusted based on the actual needs and experience of the mission scenarios, prioritizing security and executability, while taking into account the path efficiency and smoothness. indicates the importance of controlling the total length of the path, and when the weights are large, it encourages the generation of shorter paths to enhance the efficiency; reflects the priority of avoiding the threat area, and the larger the weight, the paths will tend to be far away from the threat area to enhance security indicates the restriction of flight altitude change, which is suitable for scenarios that are sensitive to terrain or mission altitude requirements; reflects the smoothness of the constrained path, the larger the weight, the smoother the path will be, which is convenient for actual flight execution and control. The decision variable includes waypoints , where and denotes the operational space of the UAV. This specification of the cost function FFF serves as the foundation for the PP process. In addition, drawing on widely used trajectory smoothing techniques in existing research, this paper introduces a path smoothing method based on B-splines to further enhance the feasibility and continuity of the planned path [41].
3. Methods
3.1. System Framework
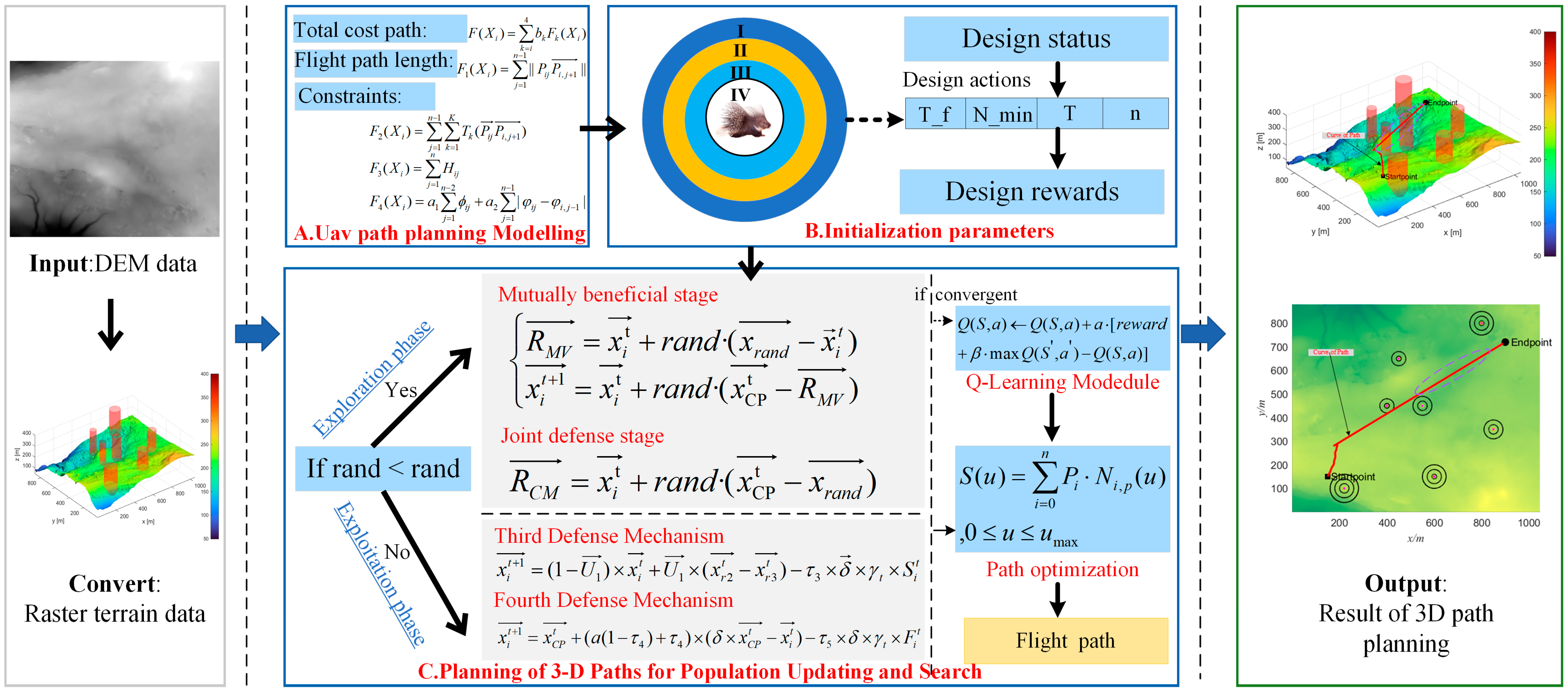
Figure 4 illustrates the structural framework of the developed QCPO approach, encompassing three principal phases: (1) Modeling the objectives of minimizing total flight distance and mitigating obstacle threats within given constraints; (2) Initializing individual and group paths; (3) Periodically updating the population and devising the three-dimensional path for navigation.
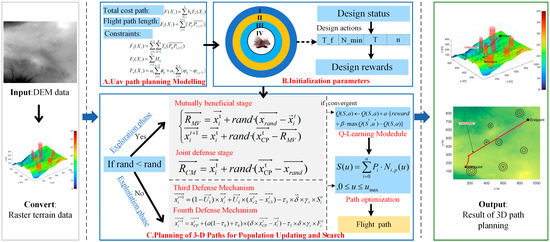
Figure 4.
System framework for UAV path planning based on QCPO approach.
3.2. CPO Algorithm
The CPO algorithm is an innovative metaheuristic inspired by the defensive behaviors exhibited by the crested porcupine [30]. It employs four strategic defensive mechanisms—visual, auditory, olfactory, and physical responses—to effectively balance global exploration with local exploitation, thereby addressing complex optimization challenges.
The initialization of the optimization process involves the creation of a population, denoted as , comprising candidate solutions , each confined within the defined boundaries of the search space. Mathematically, this is expressed as:
Here, and denote the lower and upper bounds of the search space, respectively, while is a vector populated with uniformly distributed random numbers between 0 and 1.
To enhance population diversity and accelerate convergence, the CPO algorithm integrates a cyclic population reduction strategy, which dynamically adjusts the population size (PS) during the optimization process, as described below:
In this context, specifies the number of cycles, indicates the current function evaluation count, is the maximum allowable function evaluation count, and represents the minimum permissible PS. This strategy simulates a scenario wherein not all porcupines deploy their defensive strategies simultaneously, thereby preserving diversity and promoting faster convergence.
During the exploration phase, CPO mimics the visual and auditory defensive tactics of the crested porcupine, aiming to systematically investigate various segments of the search space.
- (1)
- The initial defensive response is triggered when a porcupine perceives a threat from a distance, leading to the elevation and expansion of its quills to appear more formidable. This reaction is mathematically modeled as:
- (2)
- The second defensive mechanism: If the initial visual deterrent is ineffective, the porcupine resorts to auditory signals to ward off predators. This behavior is mathematically modeled as follows:
- (3)
- The third defensive mechanism: In the event that the first and second mechanisms prove ineffective, the porcupine releases an unpleasant odor as a repellent. This response is encapsulated by the following mathematical expressions:
- (4)
- The fourth defensive mechanism: As a final defensive measure, the porcupine engages in physical attacks against the predator. This strategy is represented by the subsequent mathematical formulas:
The fitness of each candidate solution is assessed using the objective function, with the best solution, denoted as , being iteratively updated based on new fitness evaluations. The optimization process is designed to continue until termination criteria—such as the maximum number of iterations or achieving a satisfactory fitness level—are met. This mechanism addresses critical issues like strong parameter dependence, slow convergence in CPO, and suboptimal performance [30].
3.3. Enhanced CPO Optimization Algorithm
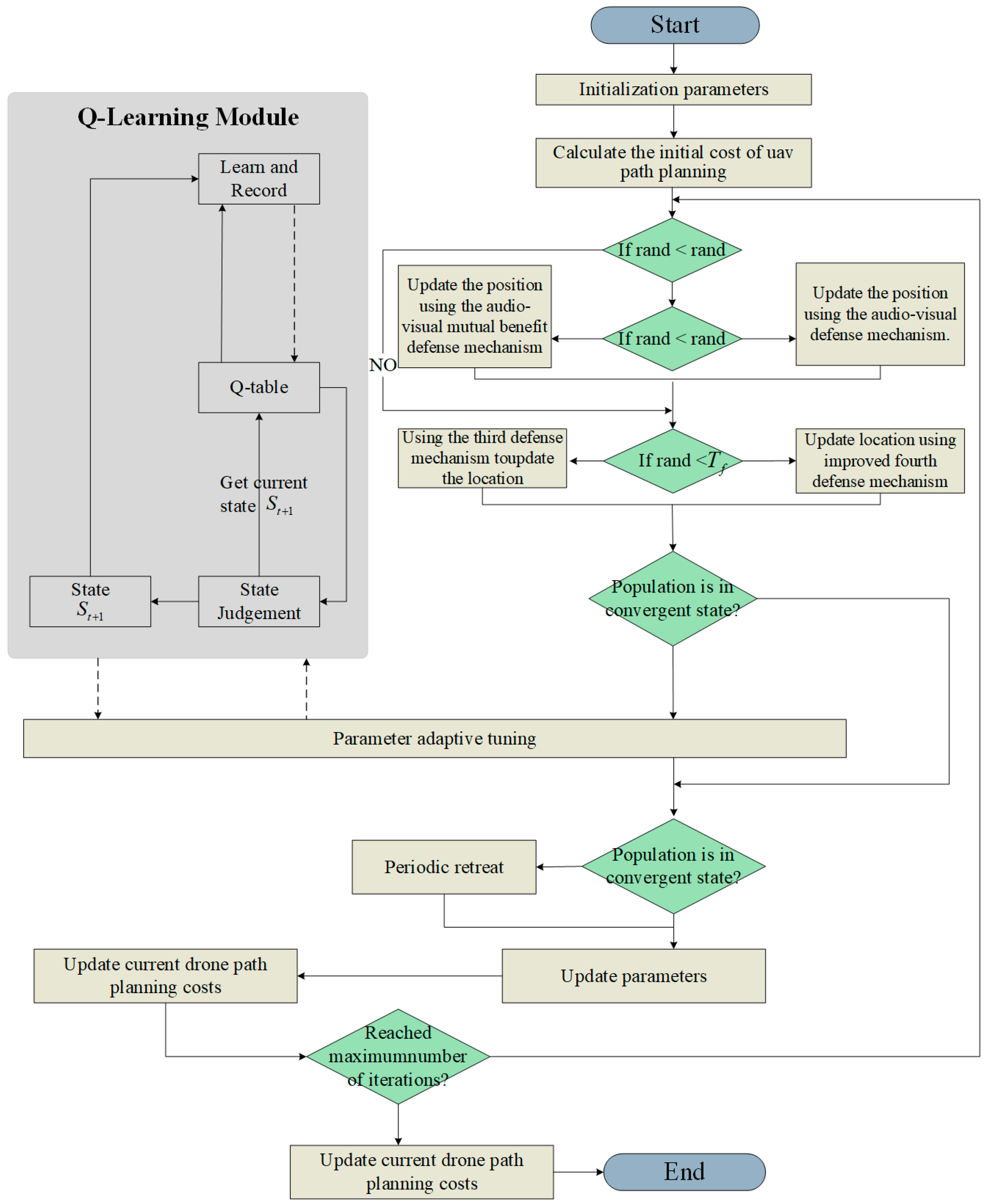
In this study, several improvement strategies for the QCPO algorithm are proposed. The algorithmic enhancements are illustrated in the flowchart depicted in Figure 5. In addition, this study provides pseudo-code for the algorithm, such as Algorithm 1
| Algorithm 1. The QCPO Algorithm. |
| 1 : Initialize: Maximum iterations Population size Initial parameters , , , State space , Action space Initialize population P = {, , …, } 2 : Evaluate initial fitness and path cost for each 3 : Set iteration counter t = 0 4 : while t < Tmax do 5 : for each individual do 6 : Generate random number 7 : if r < then 8 : Update using audio-visual mutual benefit mechanism 9 : else if r < then 10: Update using audio-visual defense mechanism 11: else if r < then 12: Update using third defense mechanism 13: else 14: Update using improved fourth defense mechanism 15: else if 16: end for 17: Evaluate fitness of new population P 18: Calculate population diversity and normalized fitness 19: Compute current state based on diversity and fitness measures 20: if population is converged then 21: Select action using policy based on Q(,·) 22: Apply action to adjust , , , 23: Re-evaluate fitness after parameter update 24: Compute reward based on fitness improvement 25: Observe next state 26: Update Q-table: 27: 28: Perform periodic retreat to increase diversity 29: end if 30: Update path planning cost of current population 31: t ← t + 1 32: end while 33: Return best solution in population P |
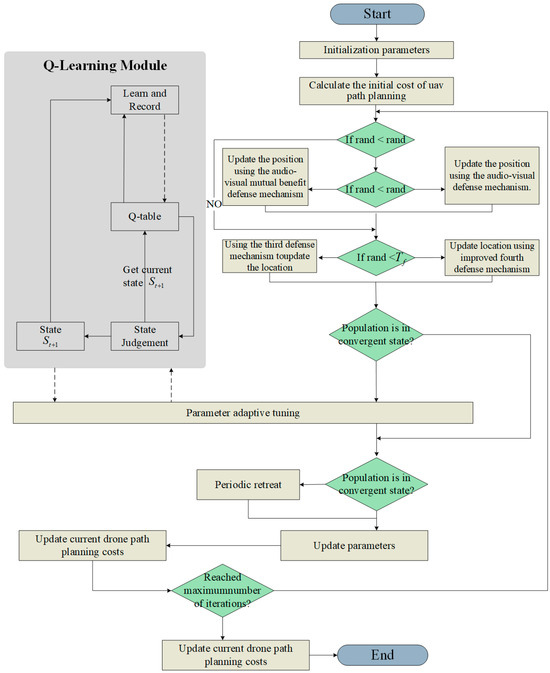
Figure 5.
QCPO algorithm flowchart.
3.3.1. Q-Learning Based on Adaptive Parameter Tuning
In the newly proposed QCPO algorithm, several parameters— between the third and fourth defense mechanisms, the minimum , the number of algorithmic cycles , and the convergence rate —are identified as crucial determinants of performance.
Due to the fact that the process of updating an individual’s position depends on the setting of key parameters, parameter values have a significant impact on algorithm performance. If fixed parameters are pre-set through experimental methods, it is difficult to achieve an effective balance between the global exploration and local development capabilities of the algorithm, which limits the sufficient search of the solution space and thus affects the acquisition of high-quality solutions. To optimize these parameters dynamically and adaptively, enhancing the algorithm’s adaptability and overall efficiency, we introduce a Q-learning-based method of adaptive parameter tuning in this investigation. In this study, Q-learning is not used as an independent optimization algorithm, but is embedded in the proposed QCPO algorithm, constituting its adaptive parameter adjustment module. The module intelligently adjusts the key control parameters including , , and based on the dynamic changes of the environmental state during the optimization process. By constructing a “state-action-reward” mechanism, Q-learning can continuously learn the optimal parameter adjustment strategy, thus increasing the environmental adaptability of parameter settings and effectively improving the overall optimization performance. Implementation of this method necessitates several critical steps for effective adjustment of parameters.
- (1)
- Design Status
In the QCPO algorithm, the evaluation of the state takes into account the diversity of the population. The fitness of the population is ascertained by calculating both average and maximum fitness values. To assess the diversity of the population, we calculate the average distance between individual members using Equations (24) and (25):
Here, denotes the Euclidean distance between two adjacent individuals, labeled as and . The terms and represent the maximum and minimum values of , respectively. indicates the total count of individuals within the population. The population’s fitness is computed through Equation (27), and the objective value is standardized using Equation (26). To derive the average and maximum fitness values, Equations (28) and (29) are employed. Equation (30) integrates the diversity and fitness metrics to evaluate the overall state of the population:
In this context, indicates the fitness of the individual at generation . The weights are assigned values of 0.35, 0.35, and 0.30, respectively, reflecting their contributions to . Based on the computed state value , the state space is segmented into ten discrete states, denoted as . Specifically, the state s is determined by the range within which falls; for instance, corresponds to , corresponds to the state , and aligns with .
- (2)
- Design Action
This phase involves the adjustment of four key parameters: . For example, can be dynamically updated according to Equation (30).
The terms denote the values at generation and respectively. The parameter defines the action space for , encompassing two potential actions: . The action space values for these four parameters are detailed in Table 1.

Table 1.
Action sets for the QCPO algorithm.
Within the context of the CPO algorithm, acts as a balancing parameter between the third and fourth defense mechanisms, dictating the switching behavior among various strategies. ensures a sufficient number of individuals throughout the execution of the algorithm. regulates the adjustment cycle of the population, permitting dynamic fluctuations in PS corresponding to different phases of the algorithm. The parameter , which manages the convergence rate, influences the step size of individuals and thus impacts the solution updating strategy during the search process.
- (3)
- Designing the Reward Function
The reward function represents feedback derived from state transitions, where the reward associated with each action correlates with changes in the population state. For each parameter , the respective rewards are . These rewards are calculated using Equations (32) and (33), while Equation (34) is employed to compute the updated value function of the agent. In this scheme, and denote the current and subsequent states, respectively, while represent the current and next actions. and are designated as hyperparameters.
3.3.2. Mutually Beneficial Audiovisual Defense Mechanisms
The Symbiotic Organisms Search algorithm is based on the concept of biological symbiosis [42], incorporates a novel position updating mechanism that provides valuable insights for the optimization process. In this research, a visual-auditory collaborative optimization strategy is introduced, leveraging the visual and auditory defense mechanisms of the crested porcupine. This strategy is designed to balance exploration and convergence speed, evade local optima, and expedite convergence towards the global optimum. The relevant formulas are specified as follows:
- (1)
- Mutual benefit phase:
Here, represents a randomly selected partner individual, and denotes the symbiotic parameter.
- (2)
- Joint Defense Phase:
Here, symbolizes the joint defense parameter. The subsequent equation delineates the position update:
3.3.3. QCPO Position Update Optimization Strategy
In the context of the fourth defense strategy of the CPO, position updating is executed through random adjustments near the previously best position. This approach, however, may lead to excessively large or small update steps. To mitigate this issue, the current study proposes an optimization strategy for position updates. This strategy employs an update factor, , derived from Equation (39).
Within this framework, represents a value randomly generated within the interval (0,1), and serves as a scaling factor. The parameters and denote the number of dimensions in the current solution, , that exceed the upper bound and fall below the lower bound, respectively. The value of is established based on the dimensional conditions from the prior iteration: is set to −1 if more than one-third of the dimensions exceed the upper bound ; is set to 1 if more than one-third of the dimensions are below the lower bound L; otherwise, is assigned a value of 0.
4. Results and Discussion
To ascertain the efficacy of the proposed QCPO method, this study conducts a comparative analysis with several leading-edge optimization algorithms, including the Enhanced GWO algorithm [43], Adaptive Evolutionary PSO algorithm [44], HHO algorithm [45], and the classical CPO [30]. All experiments were replicated 10 times to ensure the robustness of the findings, with results quantitatively assessed by calculating the mean and standard deviation.
4.1. Setting the Scene
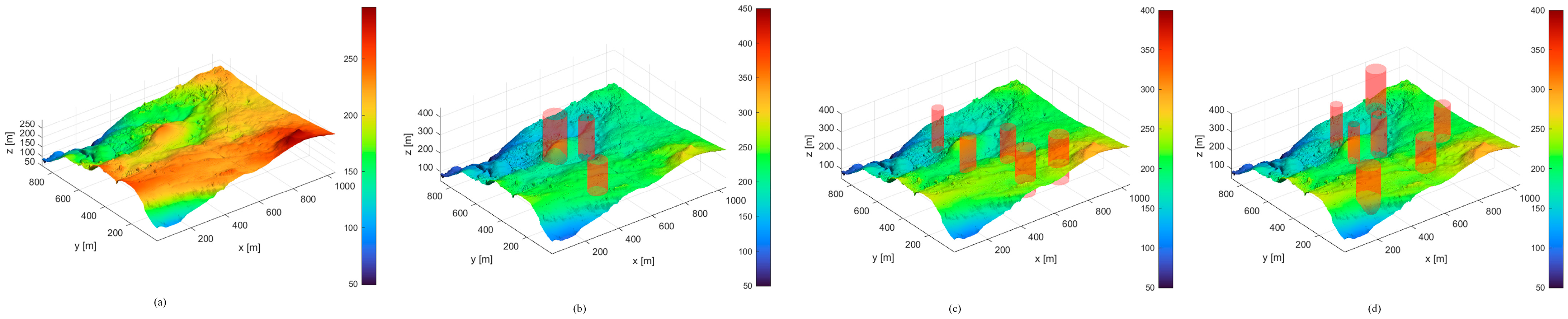
The experiments utilized real Digital Elevation Model (DEM) maps sourced from LiDAR sensors [46], focusing on two distinct terrain structures on Christmas Island, Australia. Three additional test scenarios were developed and visualized, as depicted in Figure 6. These scenarios varied in the number and spatial distribution of threats, represented as red cylindrical objects.

Figure 6.
Simulated terrain maps. (a) Original terrain, (b) simulated terrain for 3 threats in the first scenario, (c) simulated terrain for 5 threats in the second scenario, and (d) simulated terrain map for 7 threats in the third scenario.
4.2. Simulation Experiment Results and Analysis
This study performed experimental analyses on three sets of simulated terrains, setting the safe flight altitude at 300 m and providing 70 three-dimensional trajectory points for path searching. The experimental design incorporated the proposed QCPO method for UAV PP, with the number of iterations configured at 200 and the Population size was set to 100.
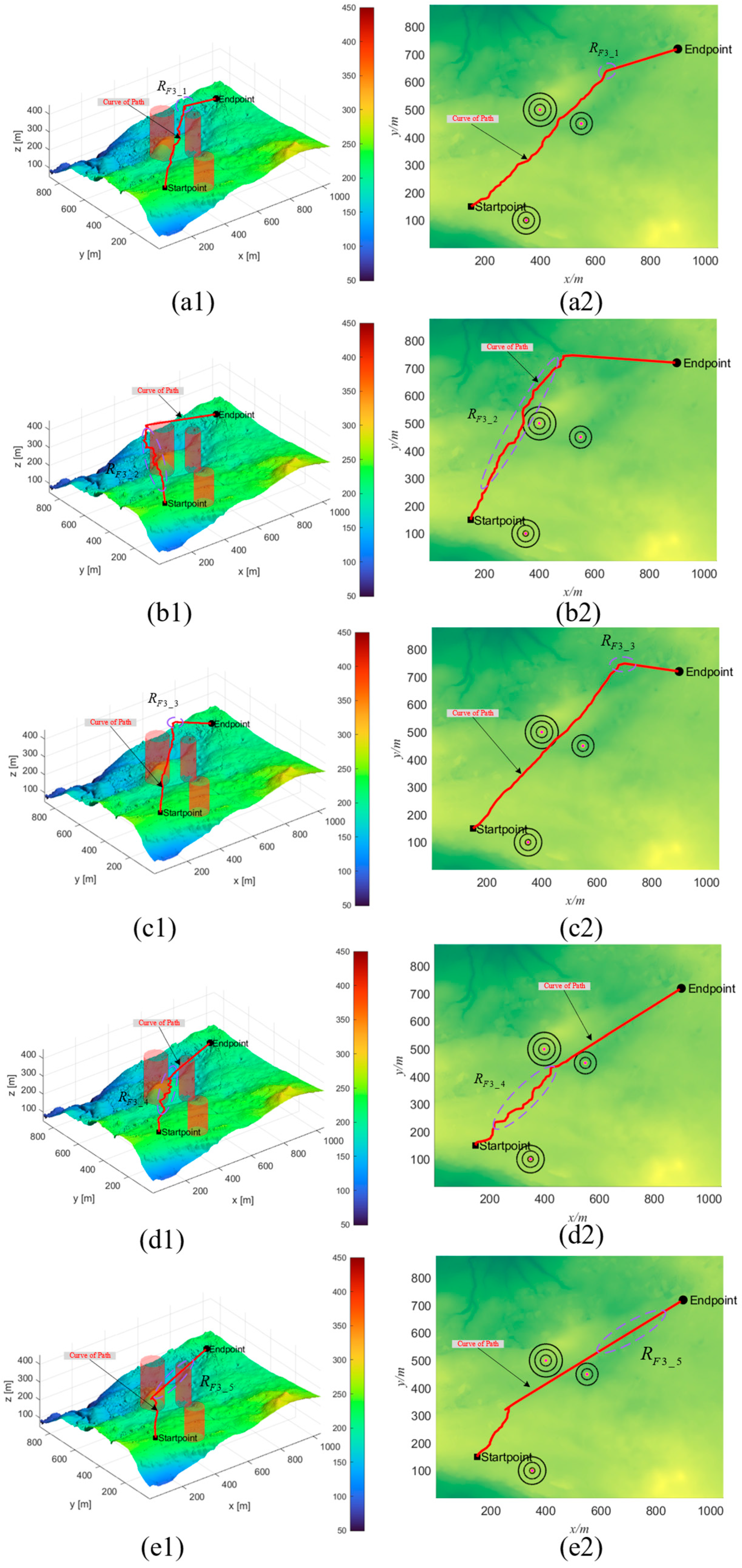
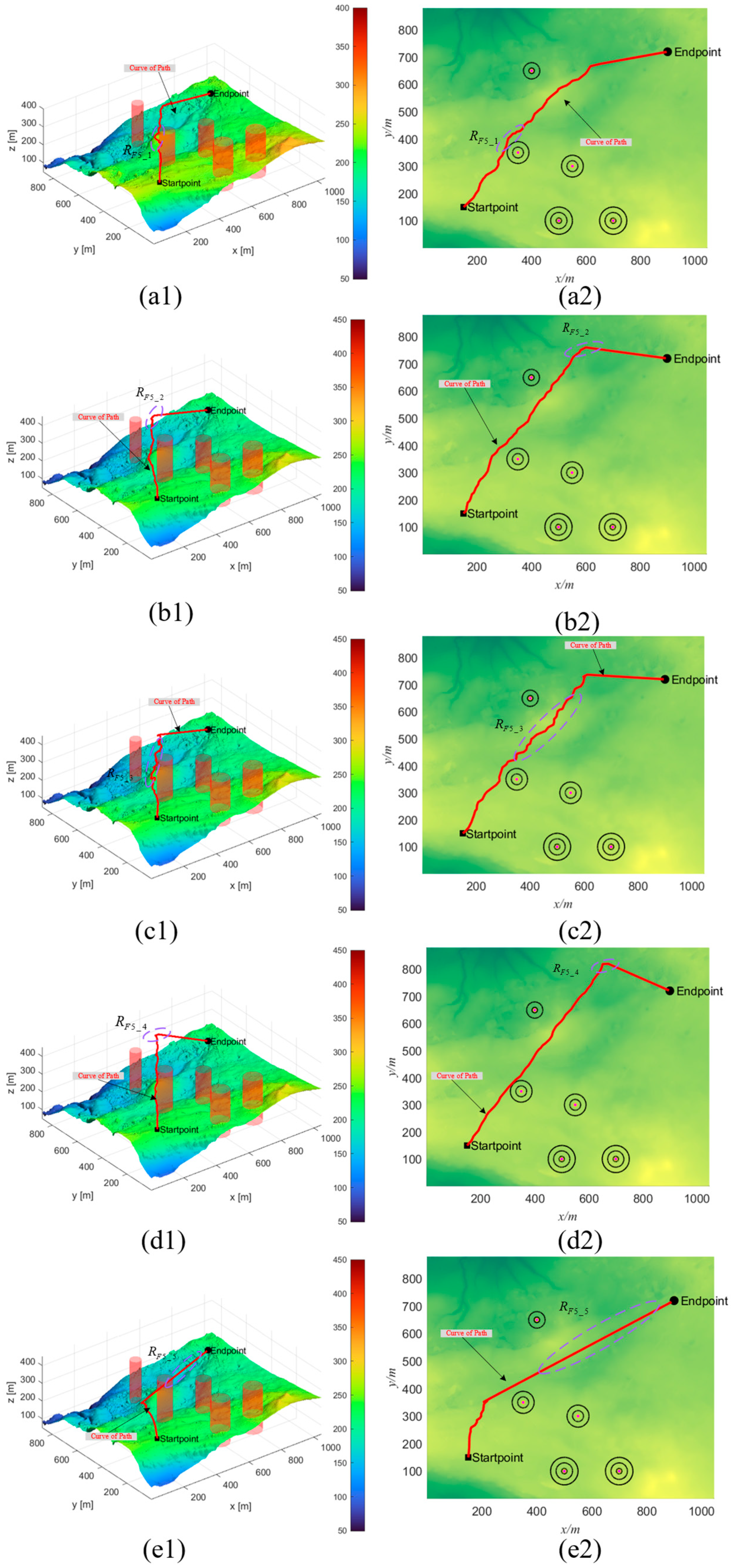
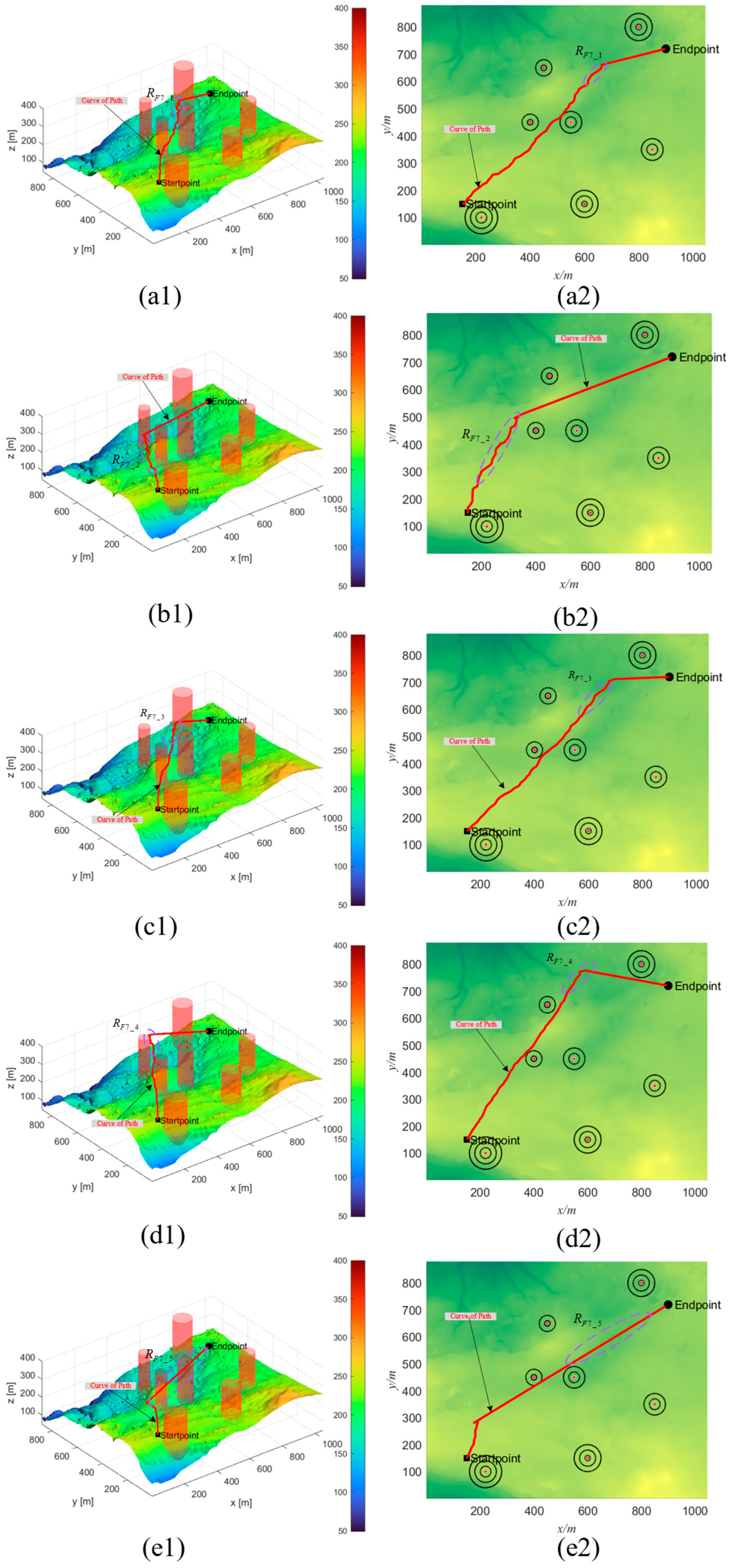
The results of the experiment are represented in Figure 7, Figure 8 and Figure 9. Visually, the path quality in the region appears inferior compared to that in the , , , and regions, as illustrated in Figure 7. When contrasted with the QCPO method, the PSO, HHO, GWO, and CPO methods demonstrate significant inaccuracies in controlling path angles. Additionally, in the evaluation of the primary regions , , , and , the QCPO method consistently generates superior paths, achieving the shortest flight distances and minimizing path risks. As the number of obstacles increases, the simulation results, as shown in Figure 8, indicate that the overall path length tends to increase. However, the QCPO method distinguishes itself by effectively adapting to complex environments and producing higher-quality paths, unlike the PSO, HHO, GWO, and CPO methods, which perform comparably in such settings. In the scenario depicted in Figure 9, which includes seven threats, the PSO method notably exhibits an increase in path turns. In an analysis of the primary regions , , , and , the QCPO method excels in path smoothness, outperforming other methods. In summary, visual analysis of the three sets of simulation experiments demonstrates that the QCPO method is capable of optimizing paths across various scenarios, thus exhibiting superior PP performance.
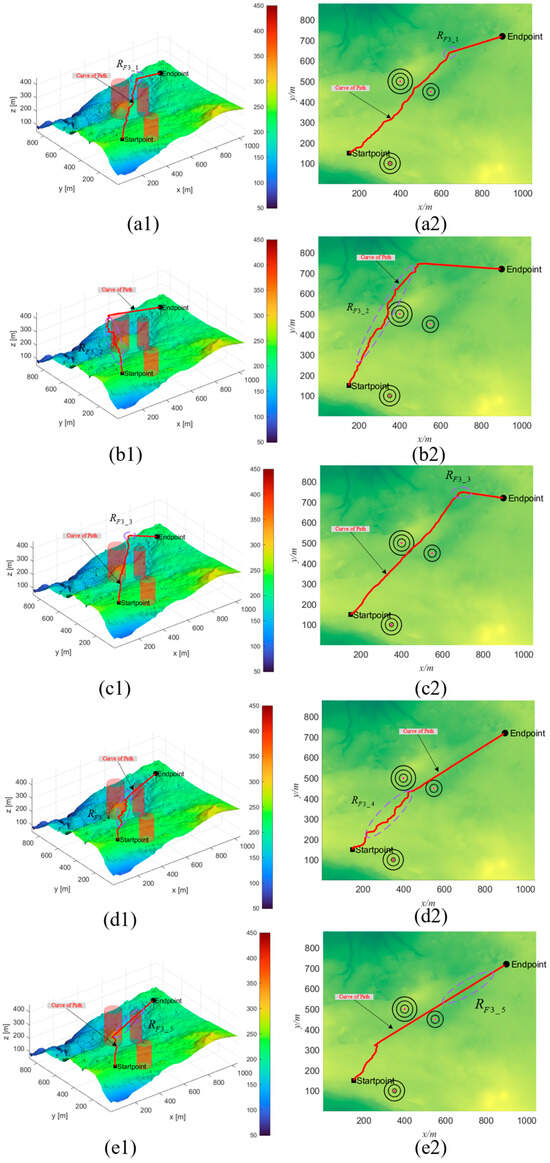
Figure 7.
Scenario 1 simulation experiment results. (a1) PSO_1. (a2) Top view of PSO_1. (b1) HHO_1. (b2) Top view of HHO_1. (c1) GWO_1. (c2) Top view of GWO_1. (d1) CPO_1. (d2) Top view of CPO_1. (e1) QCPO_1. (e2) Top view of QCPO_1.
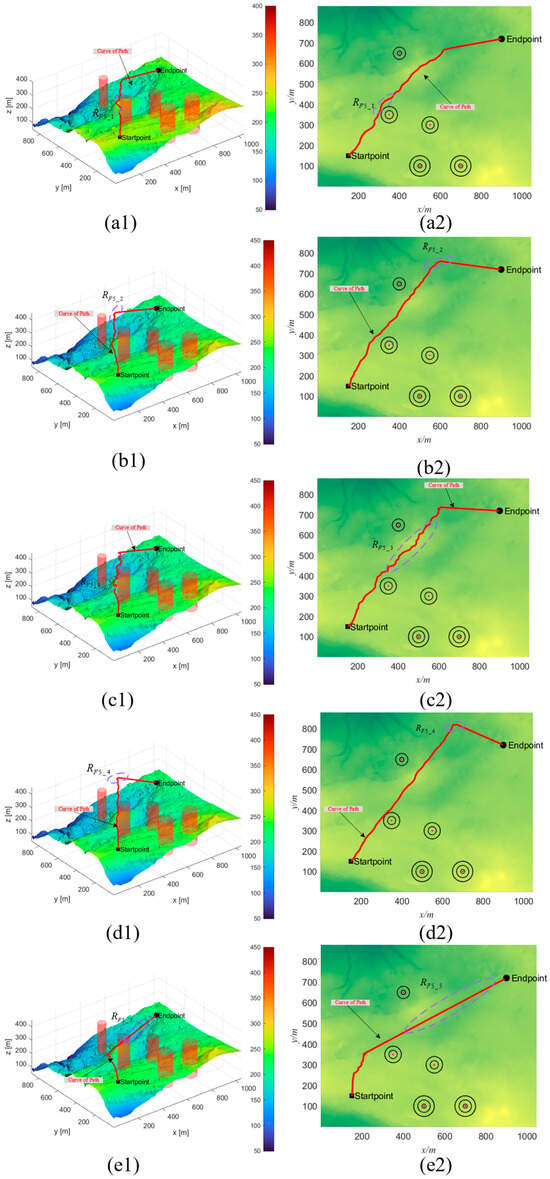
Figure 8.
Scenario 2 simulation experiment results. (a1) PSO_2. (a2) Top view of PSO_2. (b1) HHO_2. (b2) Top view of HHO_2. (c1) GWO_2. (c2) Top view of GWO_2. (d1) CPO_2. (d2) Top view of CPO_2. (e1) QCPO_2. (e2) Top view of QCPO_2.
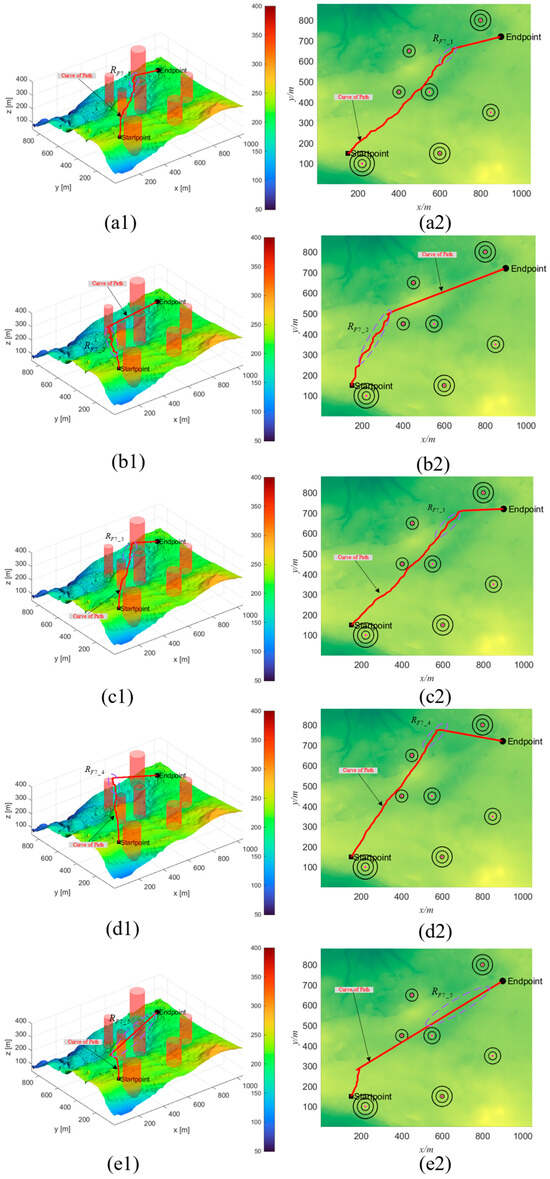
Figure 9.
Scenario 3 simulation experiment results. (a1) PSO_3. (a2) Top view of PSO_3. (b1) HHO_3. (b2) Top view of HHO_3. (c1) GWO_3. (c2) Top view of GWO_3. (d1) CPO_3. (d2) Top view of CPO_3. (e1) QCPO_3. (e2) Top view of QCPO_3.
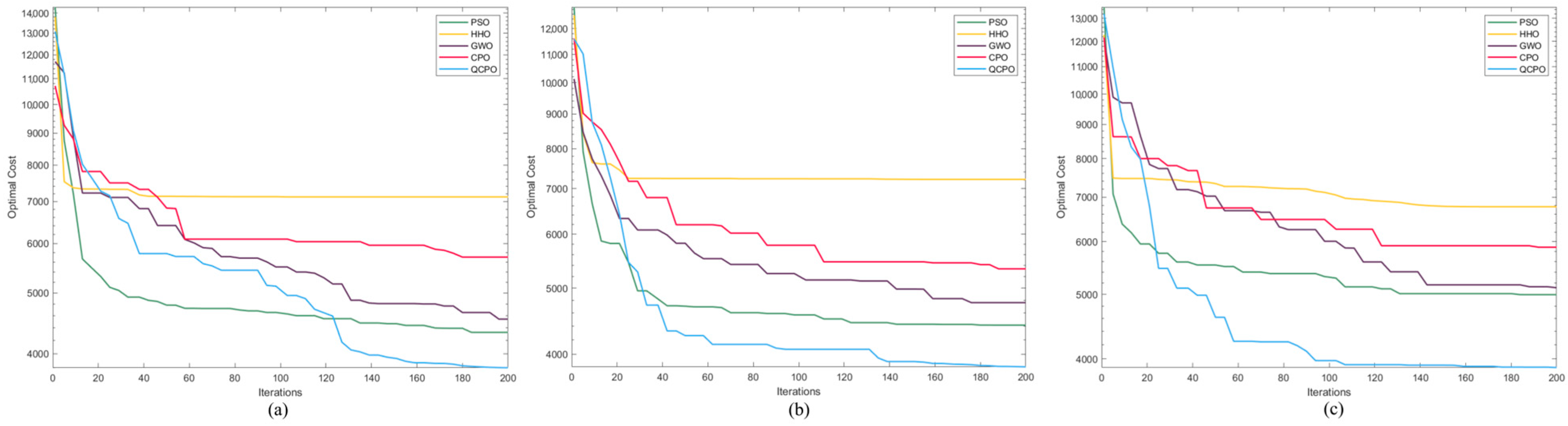
To evaluate the performance of the QCPO method, this study compares it with several advanced metaheuristic algorithms. Table 2 presents the mean and standard deviation of the fitness values obtained by each algorithm in the PP task, serving as indicators of their optimization ability and stability. The QCPO algorithm, however, achieves the optimal path, outperforming the others. Additionally, Figure 10 displays the fitness curves illustrating the optimization processes of each algorithm to visually compare various methods’ performance. The quantitative results detailed in Table 2 highlight that in Scenarios 1, 2, and 3, the QCPO method excels in both metrics and ranks first in terms of mean path values across all scenarios. The proposed method integrates more advantageous and practical constraints and effectively utilizes both global and local search capabilities, thereby enhancing the optimization performance of the algorithm in multidimensional objective spaces. Consequently, the optimal path in UAV 3D PP is achieved using the proposed QCPO method. Overall, both qualitative and quantitative results substantiate the superior optimization capabilities of the QCPO method.

Table 2.
Results of comparative algorithms for PP.
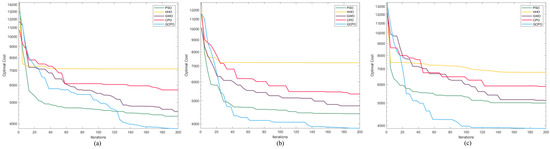
Figure 10.
Results of the comparative algorithms for PP. Results of the comparative algorithms for path planning. (a) indicates the first scenario, (b) indicates the second scenario, and (c) indicates the third scenario.
4.3. Parameters Tuning
The proposed QCPO algorithm is characterized by four pivotal parameters that significantly affect its optimization efficacy. These parameters include the fractional threshold among the three-stage defense mechanisms, , the number of iterations , and the convergence rate . To solve the UAV trajectory optimization problem, Taguchi’s method is used to determine the best combination of parameters that can improve the optimization performance. Table 3 delineates three distinct levels for each parameter. The Taguchi method is systematically executed through three phases: experimental design, signal-to-noise (S/N) ratio analysis, and the optimization process. Initially, an experimental setup was crafted using an orthogonal array (OA) , which facilitated the testing of nine unique combinations of the QCPO parameters for each scenario. This design was instrumental in evaluating each scenario under the specified parameter levels as outlined in the OA, followed by the computation of the respective objective function values. Subsequently, these values were transformed into S/N ratios to facilitate further analytical scrutiny.

Table 3.
Parameter values of the QCPO algorithm.
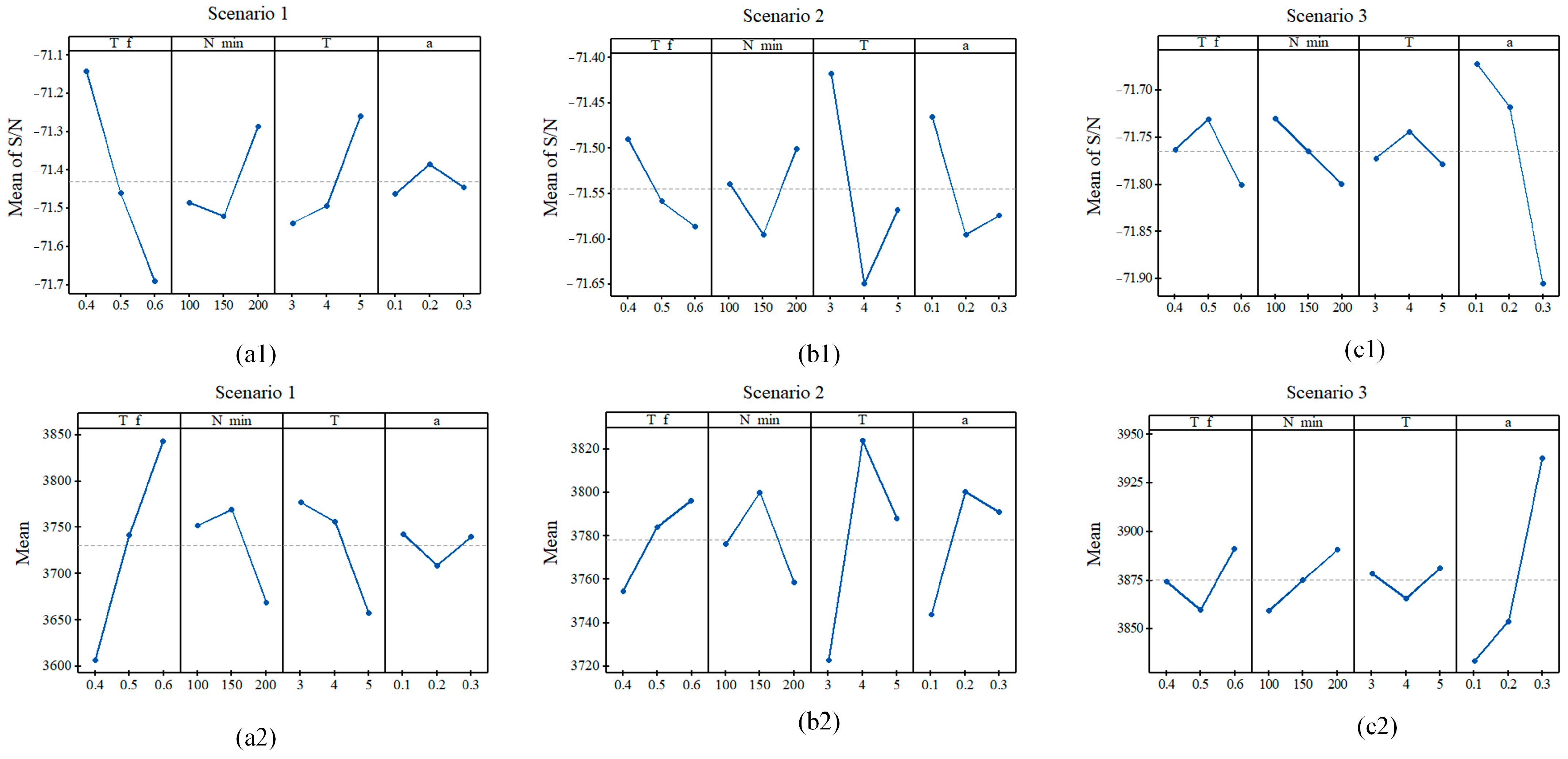
The assessment of each parameter’s impact on the S/N curve is depicted in Figure 11, where the mean S/N values were analyzed. This analysis was crucial in identifying the optimal parameters for different scenario instances. A graphical approach was employed to ascertain the target parameter levels for each specific case. The S/N ratios, contingent upon the intended outcomes and applications, can be categorized as continuous/discrete, nominal-the-best, smaller-the-better, or larger-the-better. In the present study, since the optimization objective is to minimize the response value, the ‘Smaller-the-Better’ signal-to-noise ratio criterion is used. For example, the analysis of Figure 11 reveals that in complex environments, optimal performance was achieved with . It was also noted that the optimal value of increased with the complexity of the environment. Moreover, the analysis led to the determination that for the first scenario, the best parameters were , , , and . These enhancements foster the QCPO algorithm’s ability to efficiently filter the population via the integrated heuristic strategies, thereby reducing computational overhead and expediting convergence to the optimal solution. Additionally, the incorporation of a continuous update module diminishes the risk of entrapment in local optima. Simultaneously, the dynamic parameter adjustment mechanism alleviates the decision-making burden during the evolutionary process, significantly reducing the operational costs associated with UAV flights.
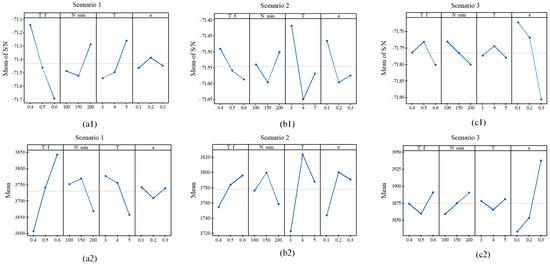
Figure 11.
Effect of key parameters on different scenarios. (a1,a2) represent the signal-to-noise ratio (S/N) mean and mean under Scenario 1, (b1,b2) represent the signal-to-noise ratio (S/N) mean and mean under Scenario 2, (c1,c2) represent the signal-to-noise ratio (S/N) mean and mean under Scenario 3.
4.4. Analysis of Ablation Experiments
The QCPO algorithm introduced in this study integrates three advanced strategies: (1) a Q-learning strategy for adaptive learning, (2) an audio-visual collaborative perspective for enhanced sensory integration, and (3) a position update optimization strategy for dynamic adjustment. To assess the efficacy and efficiency of these strategies, four algorithmic variants were defined: QCPO_(I) (QCPO without initialization), QCPO_(II) incorporating Q-learning, QCPO_(III) integrating the audio-visual collaborative perspective, and QCPO_(IV) implementing position update optimization. An ablation study was conducted to compare the performance of QCPO against these variants.
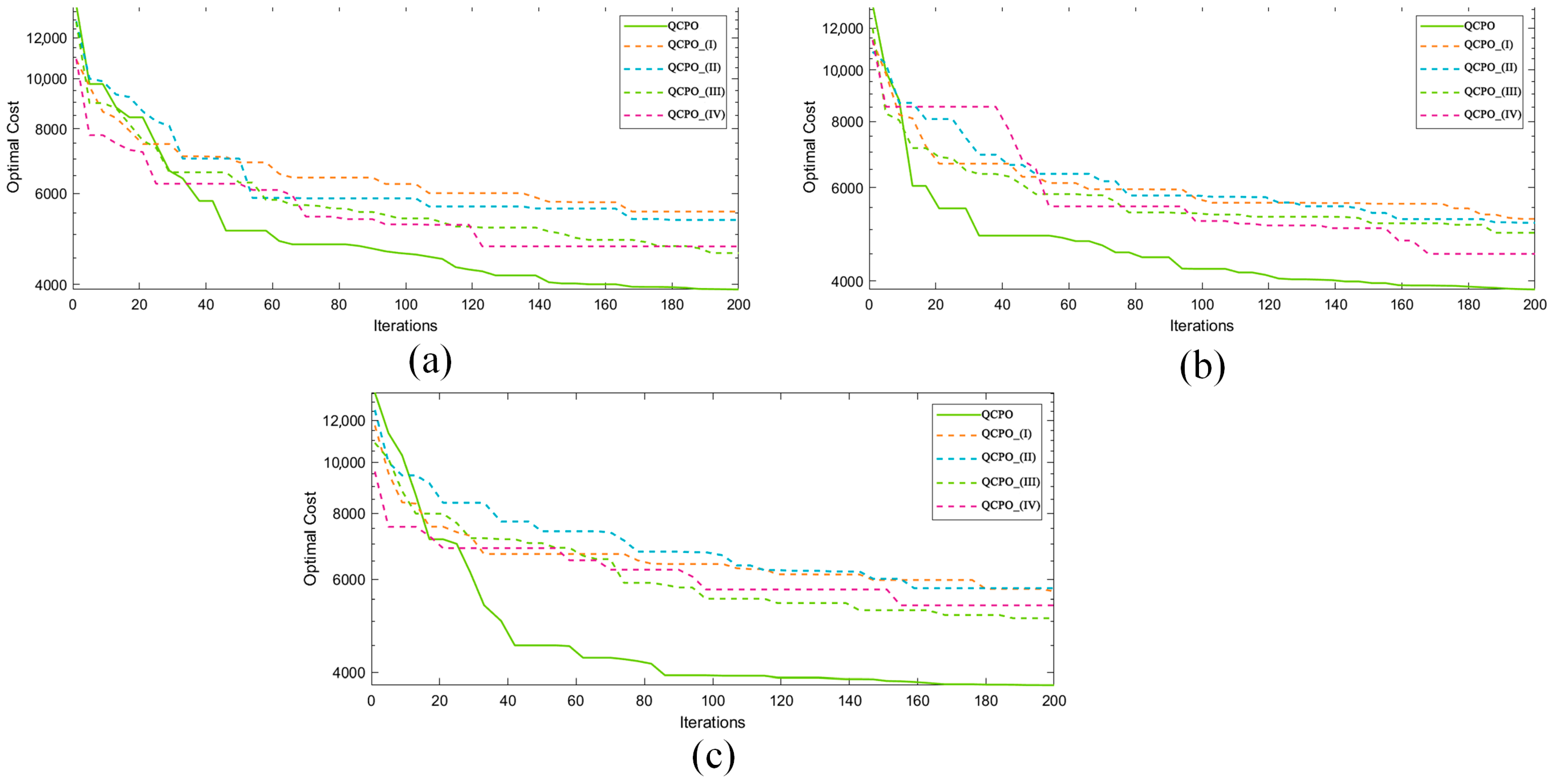
As shown in Figure 12, QCPO achieved the lowest fitness value, fully validating the synergistic optimization effect of the proposed strategies. For easy reading, this study gives the specific data of the ablation experiments in Table 4. The QCPO_(I) variant exhibited poor convergence during initial iterations, underscoring the vital role of solution initialization in producing high-quality solutions and facilitating rapid early convergence. QCPO_(II) utilized Q-learning for adaptive parameter adjustment, aimed at reducing the incidence of local optima resulting from static parameter settings. Nevertheless, experimental outcomes revealed that this approach resulted in slower convergence and inferior solution quality compared to other variants. These results validate the utility of Q-learning-based dynamic parameter adjustment in achieving a balance between exploration and exploitation. QCPO_(III) employed an audio-visual information fusion strategy, which enabled a balanced consideration of various search directions during decision-making. This integration enhanced population diversity, augmented exploration capabilities, and effectively circumvented local optima. QCPO_(IV) refined the individual update mechanism, allowing for a progressive narrowing of the search step size to an optimal range in later stages, thus improving solution stability and enhancing convergence accuracy.
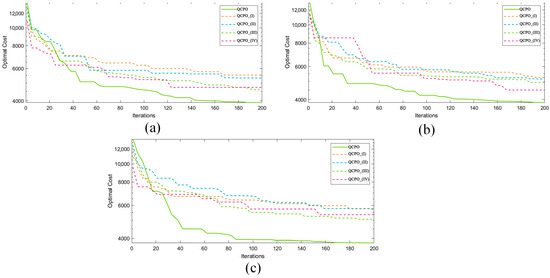
Figure 12.
Comparative validation of QCPO with and without the improved strategies across three scenarios. (a–c) represent the first, second, and third scenarios, separately.

Table 4.
Comparison of the results of ablation experiments with the QCPO algorithm.
4.5. Time Complexity Analysis
To examine the computational time complexity of the QCPO method, consider a specific UAV PP task with representing the three-dimensional waypoints’ number. Thus, the length of each solution individual is expressed as . Let denote the maximum number of iterations, and represent the PS. The time complexity of QCPO can be segmented into five primary stages:
- (1)
- Population Initialization: Initializing individuals, each of a length , results in a computational complexity of .
- (2)
- Population Evolution: During the global and local search processes, if denotes the number of individuals in , the corresponding computational complexity is .
- (3)
- Objective Function Evaluation: The computational complexity for evaluating the objective function is , assuming .
- (4)
- Main Iterative Loop: Considering iterations for the path search, the overall computational complexity is .
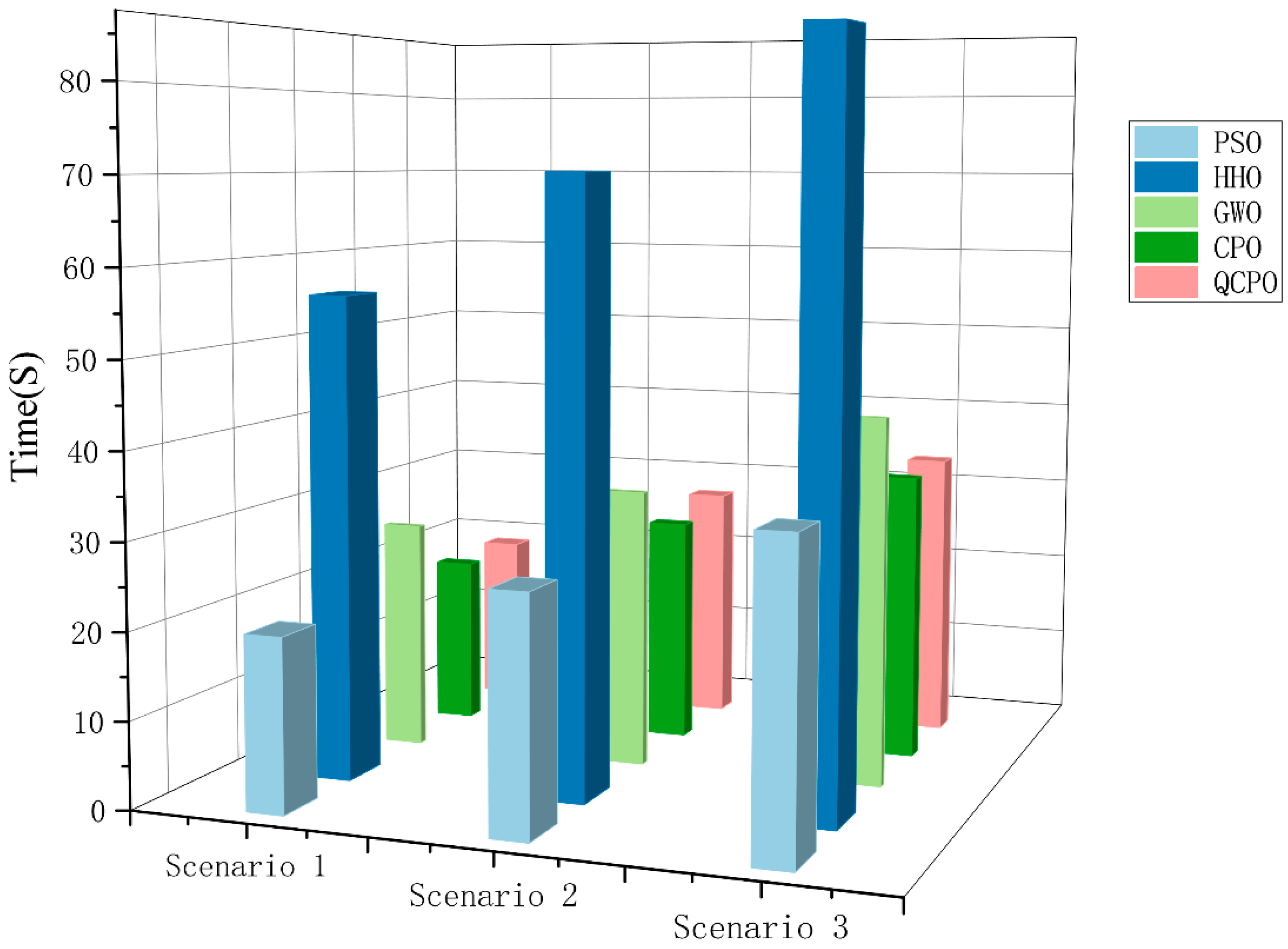
Figure 13 presents the actual computation times for various UAV PP methods, conducted on an Intel i9-14900KF processor (sourced from Intel Corporation, Santa Clara, CA, USA). The data illustrate that the time required for UAV PP increases proportionally with the complexity of the environment. Among the methods evaluated, the HHO algorithm exhibited the longest computation time and was less effective in complex environments. Conversely, the proposed QCPO method demonstrated optimal PP performance while maintaining a moderate computation time.
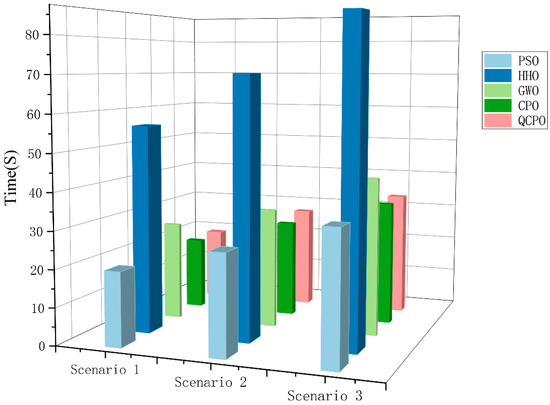
Figure 13.
Actual computation times of the different methods.
Despite the strong performance of the proposed QCPO algorithm in UAV 3D path planning under complex engineering scenarios, several limitations remain. First, the method relies on a fixed Q-learning framework for adaptive parameter tuning, which may not fully address temporal uncertainties in rapidly changing environments. As the tabular method is susceptible to dimensional catastrophe in the case of high or continuous state space dimensions, it is difficult to effectively portray the state-action relationship. Considering the introduction of deep reinforcement learning methods, deep Q-network DQN, dual DQN, Dueling DQN, and Actor-Critic frameworks, the deep reinforcement learning is able to abstract and generalize the representation of complex states through neural networks, which It helps to improve the expressive and generalization ability of strategy learning. Second, the study was primarily validated in a simulated environment using predefined digital elevation models and threat scenarios, and has not yet been comprehensively evaluated under real-world disturbances such as wind fields, sensor noise, and communication delays. Finally, although an audio-visual coordination mechanism was introduced to enhance the algorithm’s balance between exploration and exploitation, it is based on a simplified bio-inspired model, which may limit adaptability in multi-agent interaction scenarios. In addition, the study mainly chooses mainstream population intelligence optimization algorithms as reference objects in the comparison experiments, and although these algorithms are widely represented in the field of path planning, they fail to cover some of the advanced methods that have emerged in recent years, such as reinforcement learning models based on the Transformer architecture, Proximal Policy Optimization (PPO) algorithms, and modern multi-objective evolutionary algorithms, etc. This somewhat limits the comprehensive assessment of the performance of the proposed algorithms in more complex optimization scenarios.
The QCPO algorithm proposed in this paper integrates the bionic optimization strategy with the Q-learning adaptive adjustment mechanism to enhance the path planning capability of UAVs in complex environments. Experimental results show that the method achieves excellent results in terms of path planning length and algorithm convergence efficiency, especially in obstacle-dense scenarios, where it exhibits better stability and robustness. Compared with path planning studies based on meta-heuristic algorithms such as PSO, GWO, and CPO that use fixed parameters, QCPO shows better adaptability and stability in dealing with obstacle scenarios [30,43,44,45]. In multi-obstacle regions, traditional algorithms using fixed parameters are often difficult to adapt to the dynamic changes in the search space, and are prone to problems such as local optimum and slow convergence speed. The QCPO algorithms optimize paths through Q-learning adaptive adjustment of parameters, a bionic visual-auditory mechanism to guide the search, dynamic step-length limitation to avoid collisions, and B-spline smoothing. The current experiments are mainly based on the simulation environment, which lacks the comprehensive modeling and verification of the complex environmental factors in the real world. For example, the actual flight process is often accompanied by uncertainty disturbances (e.g., sudden wind speed changes, turbulence caused by terrain, GPS signal drift, multipath effects, sensor measurement errors) which will have a significant impact on the stability and robustness of the path planning algorithm.
In addition to path optimization at the algorithmic level, the passive structural stability and material design of the vehicle also play a key role in the path execution process, especially in the face of complex natural perturbations. Path planning algorithms can generate efficient trajectories under ideal conditions, but in real flight, the coupling between environmental perturbations and structural responses may lead to path deviation, attitude instability, and even flight failure. Therefore, relying only on algorithmic regulation has certain limitations. Karpenko et al. revealed the vibration-damping properties of porous extruded polystyrene in aerospace composite structures through theoretical analysis, showing that its porous structural fraction significantly enhances the passive control of UAV low-frequency and mid-frequency vibration [47]. In addition, sustainability factors are becoming increasingly important in UAV design. For example, biodegradable materials, ecological composite structures, and energy-efficient flight operations have become important directions in current research on green unmanned systems. These factors not only affect the structural design and load capacity of the vehicle but also introduce new constraints and optimization objectives for intelligent path planning. For example, Karpenko et al. applied renewable cork material instead of extruded polystyrene in composite laminated structures, which not only possesses similar vibration damping performance, but also improves the adaptability of passive control systems in the mid- to high-frequency region and promotes the development of UAV materials in a more environmentally sustainable direction [48].
Although this study focuses on single-intelligent body path planning, the QCPO algorithm has good scalability in its structural design and has the potential to be applied to multi-intelligent body systems. The algorithm can be further extended to multi-UAV collaborative path planning and task allocation problems, and the Q-learning adaptive adjustment mechanism based on state feedback in QCPO can provide personalized parameter adjustment strategies for each intelligent body to achieve dynamic adjustment and collaborative optimization under heterogeneous tasks or different environment sensing conditions; thus, improving the efficiency and safety of group path planning in complex environments. The following is an example of a multi-intelligence learning framework. Combined with the multi-intelligent body reinforcement learning framework, the robustness of the system’s decision-making under communication constraints and incomplete information conditions can be further enhanced. In addition, the effect of cluster size on the convergence speed and path quality of the algorithm can be explored, and strategies such as game-theoretic modeling and multi-task allocation optimization can be introduced to promote the application of the algorithm in real multi-UAV inspection, disaster rescue, and agricultural cooperative operation scenarios.
5. Conclusions
This study introduces a three-dimensional PP method, QCPO, that combines Q-learning with the CPO to address UAV monitoring tasks in complex engineering scenarios. QCPO employs an adaptive Q-learning strategy to dynamically adjust key parameters, enhancing the algorithm’s adaptability and optimization efficiency. Additionally, a multimodal mechanism that integrates visual and auditory cues is incorporated to improve the search capabilities of the traditional CPO framework. Furthermore, a position-update optimization strategy is introduced to accelerate convergence and enhance the algorithm’s ability to avoid local optima. To comprehensively evaluate the algorithm’s performance, comparative experiments were conducted in three complex environments between QCPO and four representative methods: GWO, PSO, HHO, and CPO. Ablation studies and computational complexity analyses were also performed. The experimental results demonstrate that QCPO outperforms the selected methods in terms of path cost, path length, and smoothness, exhibiting superior optimization capability and stability. The results affirm the practical value and reliability of QCPO for UAV PP tasks in complex engineering environments.
Future work could incorporate multi-agent reinforcement learning (MARL) to explore cooperative PP among multiple UAVs, aiming to improve monitoring coverage and overall operational efficiency. Additionally, incorporating constraints that better reflect real flight conditions—such as UAV speed limits and energy consumption restrictions—would enhance the realism and applicability of the simulation environment. Subsequent research could perform large-scale experiments in real-world engineering scenarios to systematically assess the feasibility and robustness of UAV monitoring tasks, advancing the practical deployment of UAVs in complex engineering environments.
Author Contributions
Conceptualization, Data curation, Methodology, Validation, Software, Resources, Investigation, Writing-original draft, J.L.; Validation, Formal analysis, Supervision, Funding acquisition and project administration, Y.H.; Methodology, Resources and Supervision, B.S.; Methodology and Resources, J.W.; Software, Writing-review and editing and Visualization, P.W.; Methodology and Resources, G.Z.; Methodology and Resources, X.Z.; Methodology and Resources, R.C.; Methodology and Resources, W.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Technology Innovation Project Fund of North China Institute of Aerospace Engineering, No. YKY-2024-90.
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ishiwatari, M. Leveraging drones for effective disaster management: A comprehensive analysis of the 2024 Noto Peninsula earthquake case in Japan. Prog. Disaster Sci. 2024, 23, 100348. [Google Scholar] [CrossRef]
- Kucharczyk, M.; Hugenholtz, C.H. Remote sensing of natural hazard-related disasters with small drones: Global trends, biases, and research opportunities. Remote Sens. Environ. 2021, 264, 112577. [Google Scholar] [CrossRef]
- Mishra, B.; Garg, D.; Narang, P.; Mishra, V. Drone-surveillance for search and rescue in natural disaster. Comput. Commun. 2020, 156, 1–10. [Google Scholar] [CrossRef]
- Evers, L.; Dollevoet, T.; Barros, A.I.; Monsuur, H. Robust UAV mission planning. Ann. Oper. Res. 2014, 222, 293–315. [Google Scholar] [CrossRef]
- Daud, S.M.S.M.; Yusof, M.Y.P.M.; Heo, C.C.; Khoo, L.S.; Singh, M.K.C.; Mahmood, M.S.; Nawawi, H. Applications of drone in disaster management: A scoping review. Sci. Justice 2022, 62, 30–42. [Google Scholar] [CrossRef]
- Jiang, S.; Jiang, W.; Wang, L. Unmanned Aerial Vehicle-Based Photogrammetric 3D Mapping: A survey of techniques, applications, and challenges. IEEE Geosci. Remote Sens. Mag. 2021, 10, 135–171. [Google Scholar] [CrossRef]
- Daud, S.M.S.M.; Yusof, M.Y.P.M.; Heo, C.C.; Khoo, L.S.; Singh, M.K.C.; Mahmood, M.S.; Nawawi, H. Towards autonomous multi-UAV wireless network: A survey of reinforcement learning-based approaches. IEEE Commun. Surv. Tutor. 2023, 25, 3038–3067. [Google Scholar]
- Luo, J.; Tian, Y.; Wang, Z. Research on Unmanned Aerial Vehicle Path Planning. Drones 2024, 8, 51. [Google Scholar] [CrossRef]
- Xie, R.; Meng, Z.; Wang, L.; Li, H.; Wang, K.; Wu, Z. Unmanned aerial vehicle path planning algorithm based on deep reinforcement learning in large-scale and dynamic environments. IEEE Access 2021, 9, 24884–24900. [Google Scholar] [CrossRef]
- Sonny, A.; Yeduri, S.R.; Cenkeramaddi, L.R. Q-learning-based unmanned aerial vehicle path planning with dynamic obstacle avoidance. Appl. Soft Comput. 2023, 147, 110773. [Google Scholar] [CrossRef]
- de Carvalho, K.B.; de O. B. Batista, H.; Fagundes-Junior, L.A.; de Oliveira, I.R.L.; Brandão, A.S. Q-learning global path planning for UAV navigation with pondered priorities. Intell. Syst. Appl. 2025, 25, 200485. [Google Scholar] [CrossRef]
- Cui, H.; Wei, R.X.; Liu, Z.C.; Zhou, K. UAV motion strategies in uncertain dynamic environments: A path planning method based on Q-learning strategy. Appl. Sci. 2018, 8, 2169. [Google Scholar] [CrossRef]
- Boulares, M.; Fehri, A.; Jemni, M. UAV path planning algorithm based on Deep Q-Learning to search for a floating lost target in the ocean. Robot. Auton. Syst. 2024, 179, 104730. [Google Scholar] [CrossRef]
- Lee, G.T.; Kim, K.J.; Jang, J. Real-time path planning of controllable UAV by subgoals using goal-conditioned reinforcement learning. Appl. Soft Comput. 2023, 146, 110660. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, L.; Li, Y.; Song, S.; Ma, S.; Yang, F.; Zhai, L. Path planning of multi-UAVs based on deep Q-network for energy-efficient data collection in UAVs-assisted IoT. Veh. Commun. 2022, 36, 100491. [Google Scholar] [CrossRef]
- Jiang, W.; Cai, T.; Xu, G.; Wang, Y. Autonomous obstacle avoidance and target tracking of UAV: Transformer for observation sequence in reinforcement learning. Knowl.-Based Syst. 2024, 290, 111604. [Google Scholar] [CrossRef]
- Swain, S.; Khilar, P.M.; Senapati, B.R. A reinforcement learning-based cluster routing scheme with dynamic path planning for mutli-uav network. Veh. Commun. 2023, 41, 100605. [Google Scholar] [CrossRef]
- Yu, H.; Gao, K.; Wu, N.; Zhou, M.; Suganthan, P.N.; Wang, S. Scheduling Multiobjective Dynamic Surgery Problems via Q-Learning-Based Meta-Heuristics. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 3321–3333. [Google Scholar] [CrossRef]
- Zhao, F.; Wang, Q.; Wang, L. An inverse reinforcement learning framework with the Q-learning mechanism for the metaheuristic algorithm. Knowl.-Based Syst. 2023, 265, 110368. [Google Scholar] [CrossRef]
- Yu, H.; Gao, K.Z.; Ma, Z.F.; Pan, Y.X. Improved meta-heuristics with Q-learning for solving distributed assembly permutation flowshop scheduling problems. Swarm Evol. Comput. 2023, 80, 101335. [Google Scholar] [CrossRef]
- Chen, Y.; Zhong, J.; Mumtaz, J.; Zhou, S.; Zhu, L. An improved spider monkey optimization algorithm for multi-objective planning and scheduling problems of PCB assembly line. Expert. Syst. Appl. 2023, 229, 120600. [Google Scholar] [CrossRef]
- Li, P.; Xue, Q.; Zhang, Z.; Chen, J.; Zhou, D. Multi-objective energy-efficient hybrid flow shop scheduling using Q-learning and GVNS driven NSGA-II. Comput. Oper. Res. 2023, 159, 106360. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, C.; Wang, Y.; Zhang, T.; Gong, Y. A fast formation obstacle avoidance algorithm for clustered UAVs based on artificial potential field. Aerosp. Sci. Technol. 2024, 147, 108974. [Google Scholar] [CrossRef]
- Ye, S.Q.; Zhou, K.Q.; Zhang, C.X.; Mohd Zain, A.; Ou, Y. An improved multi-objective cuckoo search approach by exploring the balance between development and exploration. Electronics 2022, 11, 704. [Google Scholar] [CrossRef]
- He, Y.; Wang, M. An improved chaos sparrow search algorithm for UAV path planning. Sci. Rep. 2024, 14, 366. [Google Scholar] [CrossRef]
- Tang, K.; Wei, X.F.; Jiang, Y.H.; Chen, Z.W.; Yang, L. An Adaptive Ant Colony Optimization for Solving Large-Scale Traveling Salesman Problem. Mathematics 2023, 11, 4439. [Google Scholar] [CrossRef]
- Ge, F.; Li, K.; Han, Y.; Xu, W.; Wang, Y.A. Path planning of UAV for oilfield inspections in a three-dimensional dynamic environment with moving obstacles based on an improved pigeon-inspired optimization algorithm. Appl. Intell. 2020, 50, 2800–2817. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert. Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Gao, Y.; Li, Z.; Wang, H.; Hu, Y.; Jiang, H.; Jiang, X.; Chen, D. An Improved Spider-Wasp Optimizer for Obstacle Avoidance Path Planning in Mobile Robots. Mathematics 2024, 12, 2604. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M. Crested Porcupine Optimizer: A new nature-inspired metaheuristic. Knowl.-Based Syst. 2024, 284, 111257. [Google Scholar] [CrossRef]
- Seyyedabbasi, A. A reinforcement learning-based metaheuristic algorithm for solving global optimization problems. Adv. Eng. Softw. 2023, 178, 103411. [Google Scholar] [CrossRef]
- Liang, P.; Chen, Y.; Sun, Y.; Huang, Y.; Li, W. An information entropy-driven evolutionary algorithm based on reinforcement learning for many-objective optimization. Expert. Syst. Appl. 2024, 238, 122164. [Google Scholar] [CrossRef]
- Osaba, E.; Villar-Rodriguez, E.; Del Ser, J.; Nebro, A.J.; Molina, D.; LaTorre, A.; Suganthan, P.N.; Coello, C.A.C.; Herrera, F. A tutorial on the design, experimentation and application of metaheuristic algorithms to real-world optimization problems. Swarm Evol. Comput. 2021, 64, 100888. [Google Scholar] [CrossRef]
- Subramanian, S.P.; Chandrasekar, S.K. Simultaneous allocation and sequencing of orders for robotic mobile fulfillment system using reinforcement learning algorithm. Expert. Syst. Appl. 2024, 239, 122262. [Google Scholar] [CrossRef]
- Cheng, X.; Li, J.; Zheng, C.; Zhang, J.; Zhao, M. An improved PSO-GWO algorithm with chaos and adaptive inertial weight for robot path planning. Front. Neurorobotics 2021, 15, 770361. [Google Scholar] [CrossRef] [PubMed]
- Lu, F.; Feng, W.; Gao, M.; Bi, H.; Wang, S. The Fourth-Party Logistics Routing Problem Using Ant Colony System-Improved Grey Wolf Optimization. J. Adv. Transp. 2020, 2020, 8831746. [Google Scholar] [CrossRef]
- Chai, X.; Zheng, Z.; Xiao, J.; Yan, L.; Qu, B.; Wen, P.; Wang, H.; Zhou, Y.; Sun, H. Multi-strategy fusion differential evolution algorithm for UAV path planning in complex environment. Aerosp. Sci. Technol. 2022, 121, 107287. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, W.; Qin, W.; Tang, W. A novel UAV path planning approach: Heuristic crossing search and rescue optimization algorithm. Expert. Syst. Appl. 2023, 215, 119243. [Google Scholar] [CrossRef]
- Qu, C.; Gai, W.; Zhong, M.; Zhang, J. A novel reinforcement learning based grey wolf optimizer algorithm for unmanned aerial vehicles (UAVs) path planning. Appl. Soft Comput. 2020, 89, 106099. [Google Scholar] [CrossRef]
- Yin, S.; Jin, M.; Lu, H.; Gong, G.; Mao, W.; Chen, G.; Li, W. Reinforcement-learning-based parameter adaptation method for particle swarm optimization. Complex Intell. Syst. 2023, 9, 5585–5609. [Google Scholar] [CrossRef]
- Chen, W.; Yang, Q.; Diao, T.; Ren, S. B-Spline Fusion Line of Sight Algorithm for UAV Path Planning. In International Conference on Guidance, Navigation and Control; Springer Nature: Singapore, 2022; pp. 503–512. [Google Scholar]
- Zhao, P.; Liu, S. An improved symbiotic organisms search algorithm with good point set and memory mechanism. J. Supercomput. 2023, 79, 11170–11197. [Google Scholar] [CrossRef]
- Jia, Y.; Qu, L.; Li, X. Automatic path planning of unmanned combat aerial vehicle based on double-layer coding method with enhanced grey wolf optimizer. Artif. Intell. Rev. 2023, 56, 12257–12314. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Zheng, H.; Li, Q.; Tian, Q. A spherical vector-based adaptive evolutionary particle swarm optimization for UAV path planning under threat conditions. Sci. Rep. 2025, 15, 2116. [Google Scholar]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Australia, G. Digital Elevation Model (DEM) of Australia Derived from LiDAR 5 Metre Grid; Commonwealth of Australia and Geoscience Australia: Canberra, Australia, 2015. [Google Scholar]
- Karpenko, M.; Stosiak, M.; Deptuła, A.; Urbanowicz, K.; Nugaras, J.; Królczyk, G.; Żak, K. Performance evaluation of extruded polystyrene foam for aerospace engineering applications using frequency analyses. Int. J. Adv. Manuf. Technol. 2023, 126, 5515–5526. [Google Scholar] [CrossRef]
- Karpenko, M. Nugaras Vibration damping characteristics of the cork-based composite material in line to frequency analysis. J. Theor. Appl. Mech. 2022, 60, 593–602. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).