Cascaded H-Bridge Multilevel Converter Topology for a PV Connected to a Medium-Voltage Grid

Abstract

When connecting a renewable energy source to a medium-voltage grid, it has to fulfil grid codes and be able to work in a medium-voltage range (>10 kV). Multilevel converters (MLCs) are recognized for their low total harmonic distortion (THD) and ability to work at high voltage compared to other converter types, making them ideal for applications connected to medium-voltage grids whilst being compliant with grid codes and voltage ratings. Cascaded H-bridge multilevel converters (CHBs-MLC) are a type of MLC topology, and they does not need any capacitors or diodes for clamping like other MLC topologies. One of the problems in these types of converters involves the double-frequency harmonics in the DC linking voltage and power, which can increase the size of the capacitors and converters. The use of line frequency transformers for isolation is another factor that increases the system’s size. This paper proposes an isolated CHBs-MLC topology that effectively overcomes double-line frequency harmonics and offers isolation. In the proposed topology, each DC source (renewable energy source) supplies a three-phase load rather than a single-phase load that is seen in conventional MLCs. This is achieved by employing a multi-winding high-frequency transformer (HFT). The primary winding consists of a winding connected to the DC sources. The secondary windings consist of three windings, each supplying one phase of the load. This configuration reduces the DC voltage link ripples, thus improving the power quality. Photovoltaic (PV) renewable energy sources are considered as the DC sources. A case study of a 1.0 MW and 13.8 kV photovoltaic (PV) system is presented, considering two scenarios: variations in solar irradiation and 25% partial panel shedding. The simulations and design results show the benefits of the proposed topology, including a seven-fold reduction in capacitor volume, a 2.7-fold reduction in transformer core volume, a 50% decrease in the current THD, and a 30% reduction in the voltage THD compared to conventional MLCs. The main challenge of the proposed topology is the use of more switches compared to conventional MLCs. However, with advancing technology, the cost is expected to decrease over time.

1. Introduction

1.1. Overview

Renewable energy is increasingly vital due to rising global energy demand and the depletion of fossil fuels, alongside its role in reducing greenhouse gas emissions, which is a significant international concern. In Saudi Arabia, electric power generation accounts for one-third of the country’s greenhouse gas emissions, yet the nation remains committed to renewable energy adoption despite having the world’s largest oil reserves and being a major oil producer. Electricity consumption in Saudi Arabia is mainly driven by the housing and air-conditioning sector (50%), with industry (21%), trade (15%), government facilities (12%), and other sectors accounting for the remainder [1]. The country’s rapid growth in energy consumption, spurred by economic development and population increases, saw electricity demand reach 65.301 GW in 2022, with projections to rise to 120 GW by 2030 [2,3]. This growing demand challenges the oil-dependent economy, as current electricity production relies heavily on fossil-fuel-based conventional power stations, contributing over 600 million tons of CO₂ emissions. To address this, Saudi Arabia has prioritized renewable energy investments under Vision 2030, aiming for 58.7 GW of renewable electricity by 2030, distributed across 40 GW of photovoltaic (PV) power, 16 GW of wind power, and 2.7 GW of concentrated solar power [4,5]. Solar energy, with its abundant natural resources, is a key focus due to Saudi Arabia’s geographic advantages, including 3000 h of sunshine annually and high solar radiation intensity. With a vast desert area of 2.15 million km², Saudi Arabia is poised to lead solar energy production in the Middle East. The country’s first solar power plant, the 300 MW Sakaka plant, began operations in 2018, reducing CO₂ emissions by 606 kilotons per year. Other projects, such as the 1.5 GW Sudair solar power plant, are underway, with additional plants planned for Madinah, Rafha, Qurayat, Rabigh, Jeddah, Shoiaba, Ar Rass, and SAAD, along with renewable-powered projects in NEOM and the Red Sea region [6,7].

1.2. Literature Review

The integration of photovoltaic (PV) systems into the power grid is becoming increasingly vital as the world transitions towards sustainable energy solutions. With growing concerns over climate change, fossil fuel depletion, and the need for cleaner energy sources, PV technology has emerged as one of the most promising alternatives. By harnessing solar energy, PV systems offer a renewable, environmentally friendly, and cost-effective solution to meet global energy demand. However, as more PV systems are deployed at various scales, their integration into the existing power grid presents several challenges and opportunities for enhancing grid reliability and power quality.

Addressing double-line frequency harmonics in medium-voltage PV systems is essential for enhancing power quality and reducing the size of filtering capacitors. In large-scale, high-voltage grid-connected PV systems, it is essential to provide galvanic isolation between the photovoltaic (PV) panels and the grid to avoid electrical shocks due to insulation failures and to mitigate leakage currents. Unlike single-stage cascaded multilevel inverters (CMIs), CMIs with high-frequency link (HFL)-based DC-DC converters offer the benefit of achieving galvanic isolation without the need for bulky line-frequency transformers. However, in three-phase wye-connected CMI PV systems that include a DC-DC stage, electrolytic capacitors are typically used as energy buffers in the DC link between the DC-DC and inverter stages to supply the double-line frequency (2ω) power to the grid. Despite their high capacitance density, electrolytic capacitors are considered less reliable, being about 30 times more prone to failure compared to non-electrolytic capacitors under similar conditions [8]. As a result, reducing capacitance is crucial to ensure high reliability, particularly when using non-electrolytic film capacitors, especially in high-voltage CMI PV systems. However, reducing the DC link capacitance can lead to a significant 2ω voltage ripple. If this ripple reaches the PV side, it can negatively impact the maximum power point tracking (MPPT) performance and reduce efficiency. To address this challenge, current-fed isolated DC-DC converters have distinct advantages over voltage-fed ones, as the input current in current-fed converters can be controlled directly. This enables the elimination of low-frequency power ripple at the input side through specialized current control, thus improving the overall system performance.

Adopting converter topologies like MMCs, cascaded H-bridge (CHB) converters, and medium-frequency link inverters, coupled with control techniques such as harmonic injection, phase-shifted PWM, and current control strategies, can effectively mitigate these harmonics. Implementing these methods leads to more efficient, compact, and reliable PV systems, facilitating their integration into the power grid.

The advancement of power electronics has led to greater reliance on photovoltaic (PV) systems. Modular multilevel inverters (MMIs) are preferred for integrating large-scale PV plants with the grid due to their excellent power quality, reliability, scalability, and high efficiency. MMIs also offer advantages such as replacing bulky transformers with smaller, high-frequency isolation transformers. Additionally, they help reduce total harmonic distortion (THD) and decrease the size and weight of filters compared to conventional low-voltage converters. However, MMIs face challenges related to galvanic isolation, submodule balancing, and distributed MPPT. A key MMI topology is the neutral point clamped (NPC) inverter, which uses multiple voltage levels to enhance the output voltage waveform and reduce stress on semiconductor devices [9]. However, the NPC topology requires a common DC link, limiting modularity and efficiency in MPPT control. An improved variant, the flying capacitor (FC) topology, replaces clamping diodes with auxiliary capacitors to manage high voltage and power. However, numerous capacitors are required to match the grid voltage, resulting in higher costs and more complex control. The most promising MMI topologies for large-scale PV applications are CHB converters and modular multilevel converter (MMCs). Both offer high efficiency, power density, and modularity while allowing for independent MPPT control. However, both topologies experience power mismatch issues, particularly under partial PV shading [10].

In [11], a CHB topology was proposed where the PV arrays were connected directly to the H-bridge cells and worked on the MPPT. This required the PV units to be connected in series, which increased the cost and complicated the control techniques. The authors in [12] proposed a CHB topology that reduced the number of power switches by the addition of an auxiliary circuit. However, the electrical isolation was poor, causing safety issues and high leakage currents. The isolation issue was resolved in [13] using a forward dual-active bridge converter with an isolating high-frequency transformer. The proposed topology allowed for galvanic isolation and increased the voltage while allowing the power flow to be bidirectional. Moreover, the performance at high power was efficient with the controllability of the PV modules. However, since it was a two-stage converter, the power loss was high, and the need for more filtering capacitors increased the converter’s size and reduced its lifetime. A CHB with a common DC link was proposed in [14], where the PV panels and the power converters were connected to a common DC bus before applying flyback converters that helped achieve the MPPT and galvanic isolation. However, this approach suffered from high harmonics and low conversion efficiency. Further, the high number of conversion stages increased the cost and weight and reduced the converters’ lifetime.

In [15,16], a PV system with CHB was connected to the grid through an isolated current-fed dual-active bridge (DAB) converter in order to achieve galvanic isolation while using film capacitors to reduce voltage ripples caused by PV converters. In [17], several cascaded H-bridge cells with isolated DC-DC converters were used to directly transmit the power from the PV arrays to the grid without dependence on online frequency transformers. In [18], a CHB with a common high-frequency magnetic link was proposed to directly connect multiple PV arrays with an improvement in PV array insulation, MPPT control, and voltage balancing. However, this topology had low reliability, high cost, and limited power rating disadvantages. In order to avoid these disadvantages, the authors of [19] proposed multiple low-power, high-frequency magnetic links (one primary winding and three secondary windings) connected to five-level H bridges. However, the design was complex, and the cost was high. The authors in [20] introduced a multi-string configuration with several PV strings with DC-DC converters connected to a common DC link. The MPPT was controlled independently through a grid tie inverter that was a multilevel CHB with a single DC input. In order to remove the power imbalance, a medium frequency isolation transformer was connected between each H-bridge and the common DC bus. Although the system had good galvanic isolation and MPPT control, it increased the cost and harmonics and reduced efficiency. A new topology was proposed in [21] that connected a large PV system to the grid via an MMC with three legs. The common DC link was constructed by connecting parallel high-gain DC-DC converters to distribute the MPPT. However, the PV system lacked galvanic isolation due to the use of boost converters, and the shaded PV strings needed to work on the MPPT when the DC link voltage was constant. A grid-tied MMC using voltage source H-bridge with MPPT tracking, high power quality, and high efficiency was proposed in [22]. The system was composed of multi-string PV strings that were a series of PV modules. The system achieved distributed MPPT, galvanic isolation, and power imbalance mitigation.

A grid-connected PV system based on an MMC topology in order to gain the maximum power under partial shading was proposed in [23]. The PV module was connected directly to a capacitor in each submodule of the paralleled MMC. The maximum power was gained by regulating the capacitor’s voltage to the maximum power point voltage. Therefore, the MPPT was controlled independently without DC-DC converters, which reduced the cost and losses but without galvanic isolation. The authors of [24] proposed a topology of an MMC-based PV system to eliminate the power mismatch. Multiple PV panels were connected to each submodule of the MMC through isolated DAB DC-DC converters to allow for independent MPPT control and PV grounding. However, this system required complex arm power imbalance control.

In medium-voltage (MV) photovoltaic multilevel converters, submodule (SM) circuits play a crucial role in ensuring the efficient and reliable operation of large-scale PV systems. These circuits are essential for providing galvanic isolation using high-frequency transformers (HFTs) and silicon carbide (SiC) switches between the PV arrays and the grid while also enabling distributed MPPT, which optimizes the power output from each PV string individually, thereby enhancing the overall system efficiency [25,26]. Several SM circuit topologies are addressed: Flyback converters are a cost-effective solution widely used in PV applications due to their simple structure and ability to provide both isolation and unidirectional power flow. However, flyback converters suffer from large leakage inductance and discontinuous current operation, which can reduce efficiency, particularly in multilevel converter applications where power quality is paramount [16,27]. On the other hand, DABs offer higher power density and zero-voltage switching (ZVS), making them more suitable for high-efficiency applications. They allow for high switching frequencies (up to 1 MHz), but their complexity increases due to the higher number of switches and bidirectional power flow, which are not always necessary for PV systems that typically involve unidirectional power flow. Moreover, MMCs are emerging as a favored topology due to their modularity, scalability, and independent MPPT control for each submodule, which is highly beneficial for large-scale PV applications. By connecting PV strings directly to each SM, MMCs remove the need for bulky low-frequency transformers (LFT), reducing system size, cost, and inefficiencies. However, power mismatch between the SMs, especially under partial shading conditions, remains a major challenge for MMC-based systems [28,29].

An MMC-based medium voltage PV system is presented in [30,31]. The presented topology can balance the power mismatches between the upper and lower arms. However, it fails to balance the power mismatches between different legs. A neural-network-based PV power mismatch elimination (NNPME) method is presented in [32]. The presented method can balance the capacitor voltages due to power mismatches in the MMC topology. However, the requirements of expert knowledge and a massive dataset for training the neural network hinder the applicability of this method. In addition, the presented method presented difficulty in balancing the power mismatches between legs. Another method is presented in [33] that is based on injecting a DC circulating current signal in the control loop. The exclusion of the AC component is presented to reduce the power converter’s internal losses and to improve the overall system stability.

After presenting a survey about the MLC topologies, it is important to highlight the topologies for increasing the power density of these converters. DC link capacitors and isolation transformers are the main bulk elements in this converter. One approach to reducing capacitor size in modular multilevel converters (MMCs) involves using an HFT to connect a battery with two submodules, which reduces the module’s capacitor size by 20% compared to the traditional MMC design presented in [34]. Another method for reducing both capacitor size and voltage ripples in MMCs is to connect the capacitor to three HFTs, with each transformer’s output linked to a different AC phase. This configuration allows the capacitor to supply three-phase power rather than just single-phase power [35]. Additionally, a single-stage HFT is proposed in [36] for MMCs, replacing the typical two-stage DC/AC HFT with a hybrid isolated module, which reduces the number of power electronic devices and passive components. For CHB converters, a multiple-input, single-output topology is introduced in [37] to decrease the DC link capacitor. This topology uses an HFT with multiple primary windings and a single secondary winding. Instead of multiple windings, a three-phase transformer is employed in [38], with a single DC supply connected to the three-phase transformers.

Table 1. Comparison of the existing configurations in the literature and the proposed contribution in the paper.

Reference	Scheme	Advantages	Disadvantages
Refs. [9,10]	Neutral point clamped (NPC) and flying capacitor (FC) topologies	Low number of components Multilevel output voltage Simple control	No independent MPPT control (cannot solve partial shading problems) Prone to failure and disconnection of the whole system Lower reliability
Ref. [11]	CHB topology	Direct connection of PV arrays with H-bridges Lower number of system components	Connection of PV units in series, and hence lower MPPT efficiency Complicated control requirements.
Ref. [12]	CHB topology with auxiliary circuit	Reduced number of power switches Multilevel CHB output	Poor electrical isolation High leakage currents Safety issues
Ref. [13]	Forward dual-active bridge converter	Galvanic isolation Bidirectional power flow Efficient MPPT control	High power losses Needs more filtering capacitors Reduced lifetime
Ref. [14]	CHB with a common DC link cascaded with a flyback converter	Efficient MPPT Galvanic isolation	High harmonic contents Low conversion efficiency Increased cost and weight of the PV system Low reliability
Refs. [15,16]	CHB with current-fed dual-active bridge (DAB)	Uses film capacitors Higher reliability Galvanic isolation	No elimination of double-line frequency harmonics Complex control of MPPT control
Ref. [17]	CHB with isolated DC-DC converters	Direct power transfer from PV to the grid No online frequency transformer requirements	High harmonic content Low efficiency
Ref. [18]	CHB with a common high-frequency magnetic link	Connection of multiple PV units Improved isolation Voltage balancing Improved MPPT control	Reduced reliability High cost Limited power ratings
Ref. [19]	Five-level H-bridge converter with high-frequency magnetic link	High-frequency magnetic link Connection of multiple PV units High MPPT efficiency	Complex design High cost Complicated design of the control system
Ref. [20]	Multilevel CHB with a single DC input	Multi-string PV configuration Independent control of MPPT Good galvanic isolation	Uses a medium-frequency isolation transformer Increased cost High harmonic content Reduced efficiency
Ref. [21]	MMC with three legs and boost converters	Possibility to connect large PV systems Distributed MPPT control	Sensitive to faults in the common DC-link Lacks galvanic isolation
Ref. [22]	MMC with voltage source H-bridge	Distributed MPPT Power imbalance mitigation Galvanic isolation	No elimination of harmonics Low efficiency
Ref. [23]	Parallel structure MMC	Distributed MPPT Direct connection of PV units to MMC capacitors	No imbalance between upper and lower arms No balance between different phases High imbalance between grid currents due to power mismatches
Ref. [24]	MMC topology with isolated DAB topologies	Elimination of power mismatch Distributed MPPT control	Complex control structures Complicated arm power balancing control
Proposed	Isolated MLC for PV applications connected to medium-voltage grid	Distributed MPPT Elimination of inter-arms imbalance and inter-legs imbalance Suitable for medium voltage applications Total elimination of double-line frequency components Reduced passive components requirements Lower THD distortion High reliability	Requires some cascaded control structures Specific design requirements Lack of experimental verification

shows a comparative study of the different configurations and topologies. Despite the advantages of MMCs, they have several drawbacks, such as circulating current, capacitor voltage imbalance, and the arm inductor, which impact the size and efficiency of the converter. The main advantage that makes CHBs be selected over MMC is that they require many sources. In PV applications, CHBs offer the following benefits:

• The ability to increase the system voltage/power without requiring significant modifications to the system.
• In the case of some PV panels being shaded, the other modules will not be affected.
• Each module has its own controller, which increases flexibility.
• In terms of faults, faulty modules can be bypassed.
• The proposed topology can be fit to different renewable energy sources.

1.3. Paper Contribution

This paper proposes an isolated MLC for PV applications connected to medium-voltage grids. Instead of using a centralized DC/battery supply, as occurs in MMCs, a separate DC supply/battery is proposed in this paper. The proposed configuration offers flexibility and expandability for the converter and simple battery energy management. Instead of using multiple port transformers or cascaded single-phase transformers, a single-input three-output transformer is employed in this paper. According to the aforementioned discussion, which explains the shortcomings of MMC converters in MV-PV, including increased voltage and current ripples and the increased size of the DC capacitors, a new topology is proposed to mitigate these problems. The proposed topology makes use of SB circuits equipped with a CHB and HFT. The contribution of the paper can be summarized in the following points:

○

An isolated MV-MLC is presented in this paper for medium-voltage PV applications. Compared to existing solutions, the proposed method provides a reduction in the double-frequency voltage on the DC link capacitor, a reduction in the required DC link capacitor, and a reduction in the transformer core size.

○

The proposed configuration produces high-quality voltage and current waveforms with lower THD distortion and higher reliability.

○

Compared to existing PV grid integration solutions, the proposed method provides better utilization of the PV output power and better performance under partially shaded PV panels. Moreover, the proposed configuration eliminates the interphase imbalance that exists in conventional solutions.

The remaining parts of the paper are organized as follows: Section 2 details the proposed MV-MLC circuit, including the different operating modes, component design, and closed-loop operation. Section 3 presents the obtained simulation results of the proposed topology and configuration. Section 4 provides paper discussions, and Section 5 gives conclusions.

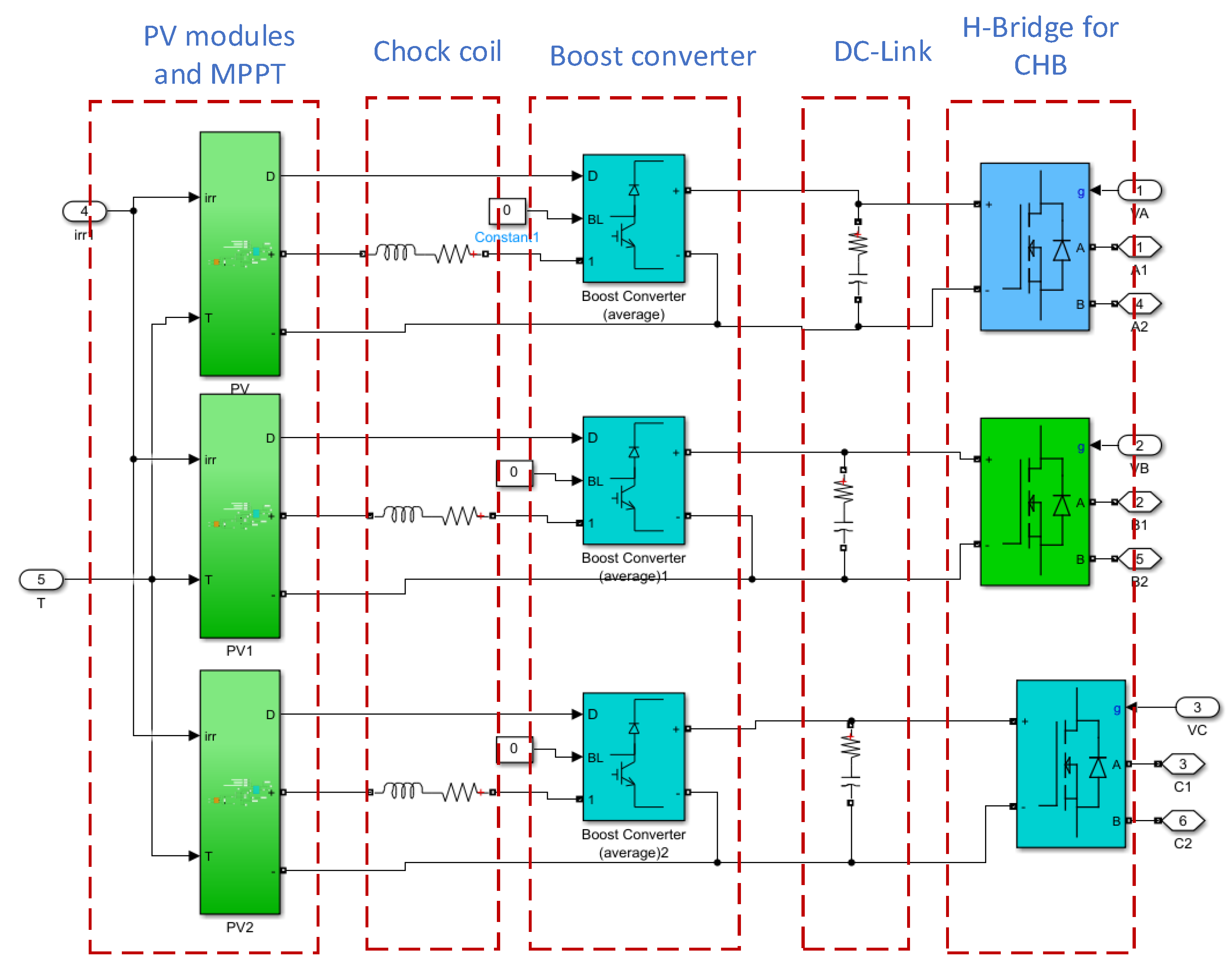
2. Proposed Multilevel Converters

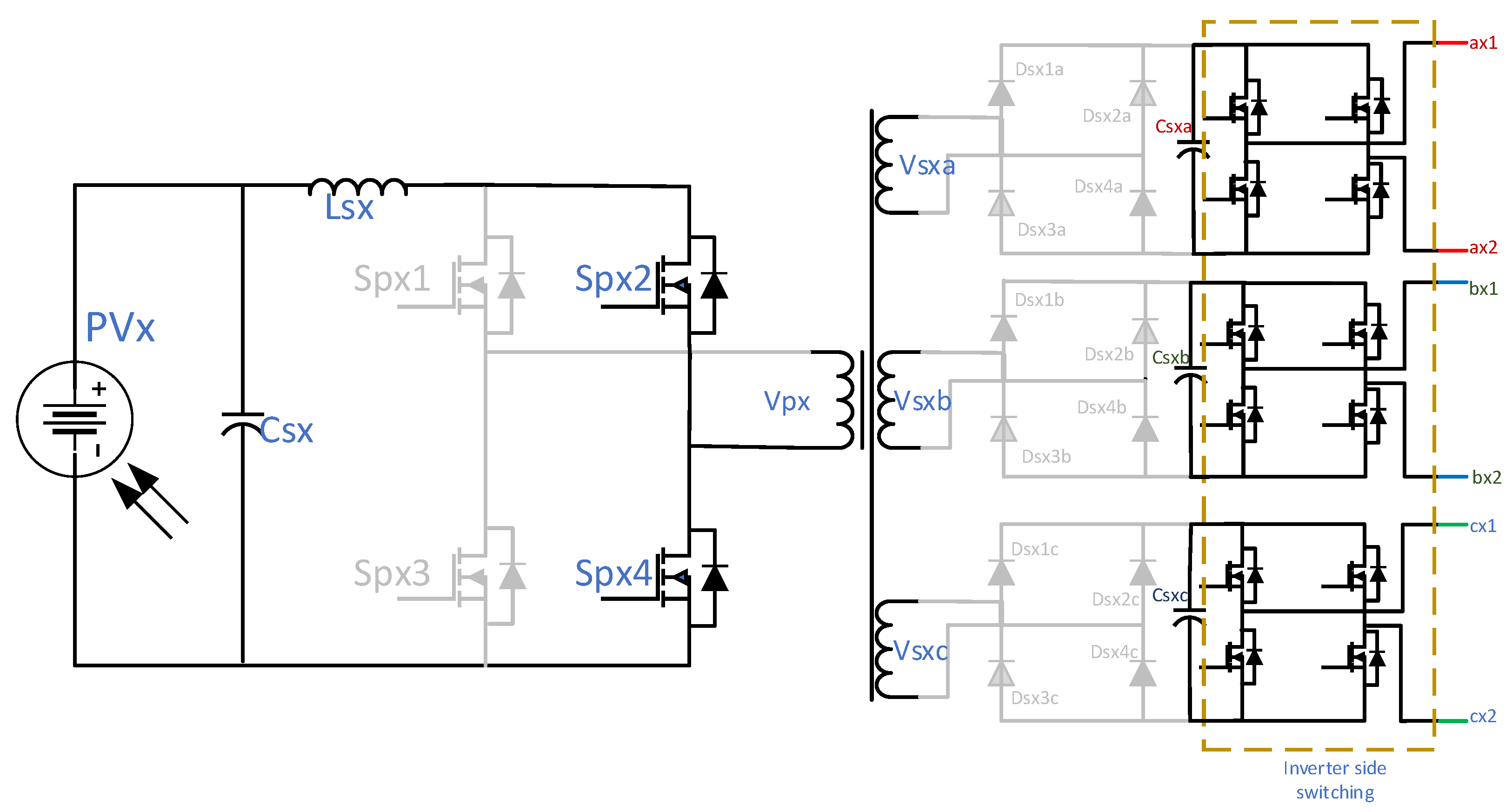
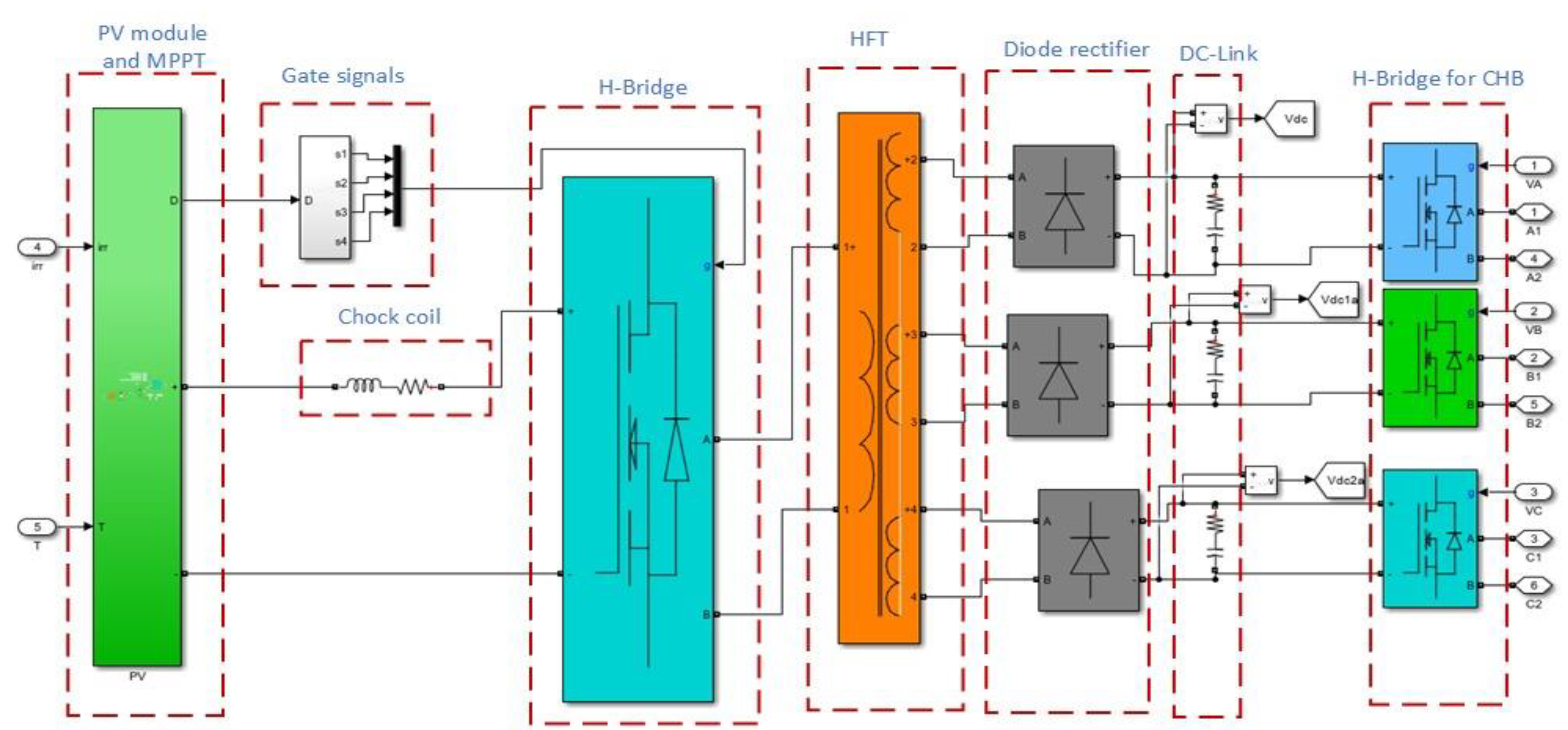
2.1. The Proposed MLC Circuit and Configuration

In most MLC converters, the DC sources, such as batteries and PV, are connected to supply a phase current/power to the load. This causes double-frequency harmonics on the power injected from these sources. These harmonics negatively affect the performance of the MLC. The proposed converter topology presented in this paper overcomes this problem by operating the DC sources to supply a three-phase load, not a single phase, as occurs in the published topologies. This can be achieved by employing an HFT with a single primary coil and three secondary coils. The primary HFT is connected to the DC sources (PV), and the secondary consists of three windings, wherein each winding is connected to one phase of the load. Therefore, the DC supplies (PV in this case) see the load side as a three-phase load, and the power is three-phase power. Three-phase power inherits less ripple compared to single-phase power. The layout of the proposed converter is shown in Figure 1. It consists mainly of an isolated power module connected in a series at the output to form the CHBs-MLC. Each isolated power module, as shown in Figure 2, consists of an HFT with a single winding at the primary and three windings at the secondary. This works as a single-phase to a three-phase transformer. Each winding in the primary or secondary is connected to an H-bridge. Each module has its PV connected to the primary side. In this configuration, the battery supplies three-phase power, which eliminates the double-frequency ripple in the DC voltage and current. Accordingly, the DC link capacitor can be reduced compared to conventional CHBs. The HF transformer can be a step-up or step-down transformer. This increases the flexibility of the proposed converter topology, which can be employed in many applications. The PVs are connected to an H-bridge to extract the maximum power from the PVs and invert the PV output voltage to an AC voltage under high frequency. The secondary side of the HFT is composed of three isolated windings. These three windings are connected to the diode rectifier with a DC link capacitor to smooth the output. The H-bridge inverter is connected to the output of the diode rectifier to generate the AC voltage with a line frequency.

2.2. Operation of the Proposed MLC

The proposed converter operates bidirectionally in both buck and boost modes. In the boost configuration, the high-frequency transformer’s (HFT) leakage inductance functions as the primary choke coil. For the buck mode of operation, where the HFT’s inherent inductance is insufficient, a supplementary inductor may be added. Operational analysis for a positive output voltage applies equally to a negative output polarity through complementary switch configurations. To simplify the explanation, this analysis considers only the DC/DC stage with a single secondary-side H-bridge. The converter exhibits four distinct operating modes, as follows:

• Mode 1: This mode is started by activating switches S_PX1 and S_PX3, which initiates charging of the choke coil (L_SX), causing its current to rise linearly. Simultaneously, the secondary-side DC link capacitor discharges to maintain power delivery to the load, ensuring continuous energy supply while the inductor stores energy, as shown in Figure 3.
• Mode 2: When S_PX1 and S_PX4 are turned ON, the choke coil discharges its stored energy into the transformer’s primary winding. This action generates a positive voltage across the winding, enabling power transfer to the load through the secondary-side diode rectifier, as shown in Figure 4.
• Mode 3: Activating switches S_PX2 and S_PX4 re-energizes the choke coil, inducing a monotonic increase in the inductor current. The DC link capacitor exclusively sustains the load current during this interval, as shown in Figure 5.
• Mode 4: Conduction of S_PX2 and S_PX3 discharges the choke coil energy into the transformer winding, inducing a negative voltage across its primary winding. The transformer transfers this energy to the load through the secondary-side diode rectifier, as shown in Figure 6. The duty cycle is generated from the MPPT algorithm.

2.3. System Design

A. 

Number of Voltage Levels Design

To connect the PV system to the grid, there are some regulations called grid codes. IEEE Standard 519 [39] is a PV grid connection code that defines the limits of the individual and THD of the voltage and current waveforms. According to this code, the maximum total THD for a grid voltage from 1 kV to 69 kV is 5%, according to IEEE Standard 519-1992 [40] and the updated IEEE Standard 519-2014 [41,42]. To meet this requirement, the number of MLC levels is selected. Figure 7 shows the relationship between the MLC levels and the THD on the output voltage. This curve was generated by running an MLC at a different number of levels as a stand-alone unit. The 24 levels for the MLC were selected to be away from the limit.

B. 

Transformer Design

The transformer design can be summarized into steps based on the design topology in [35] as follows:

• Selecting the transformer core flux density ($B_m$) and operating frequency ($f)$. These values can be selected according to the minimum total power losses where the iron losses are equal to the copper losses [42] or based on the optimization algorithm, as in [43].

The optimization methodology proposed in [43] is employed in this paper. The methodology considers all system losses, including transformer losses, choke coil losses, and losses from power electronics devices. To find the optimum combination of the flux density and operating frequency, a design procedure proposed in [43] is employed, where the objective function is based on maximizing efficiency or minimizing transformer volume. The volume is the combined volume of the transformer, choke coil, and converters’ heat sink. The optimization constraints for both objective functions are the voltage per turn, clearance between two coils, transformer core flux, and operating frequency. When the minimum volume is employed as the objective function, a minimum efficiency constraint can be set. The design procedure can be summarized as follows:

• Initially, the converter rated power, input, and output voltages are entered into the algorithm. Additionally, all constants used in the design are specified.
• The design constraints are established, along with the initial flux density and operating frequency. Using these initial values, the dimensions of the transformer core are calculated.
• Using the transformer dimensions, the core and copper losses are calculated.
• The power electronics losses are calculated.
• Based on the power electronics losses, the heat sink volume is then calculated. All the volumes and losses are determined. Depending on the optimization target (minimum losses or minimum volume), the optimization is carried out until the end criteria are met.
• The end criteria are the value difference between successive iterations, the number of iterations, and the constraints tolerance.

2.

Obtaining the voltage per turn of the transformer using Equation (1):

$$E_t=K\sqrt{{\displaystyle \raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{$1000$}\right.}}$$

(1)

where ${\mathrm{K}}_t=\sqrt{4.44fr}$, $S$ is the apparent power of the transformer, $r$ is a constant that depends on the flux and ampere-turn of the transformer, and $f$ is the operating frequency.

3.

Calculating the transformer core cross-sectional area $A_i$ and the transformer core window area $A_w$ using Equations (2) and (3):

$$A_i={\displaystyle \frac{E_t}{4.44f{B}_m{K}_i}}$$

(2)

$$A_w={\displaystyle \frac{S}{2.22J{A}_i{K}_s{K}_w{B}_{m}f}},$$

(3)

where $K_i$ is the transformer core staking factor and $K_w$ is the transformer winding fill factor

4.

Finding the transformer core volume using Equation (4):

$$V_c={2A}_i\left(\sqrt{{\displaystyle \frac{A_w}{r_w}}}\left(r_w+1\right)+{\displaystyle \frac{d_c}{\sqrt{K_c}}}\right)$$

(4)

where $r_w$ is the ratio of the winding window height to the width of the transformer core, $K_c$ is the ratio of the net core cross-sectional area to that of the circumscribing circle of the transformer, $A_w$ is the transformer core window area, and $d_c$ is the effective core diameter of the transformer and is given by:

$$d_c=\sqrt{4A_i/({\pi K}_c})$$

where $K_c$ is the ratio of the net core cross-sectional area to that of the circumscribing circle of the transformer. The optimization algorithm decides the operating switching frequency to obtain high efficiency under certain constraints. The core losses can be reduced at higher switching frequency by using different core material types, such as a nanocrystalline core [44].

C. 

Passive Elements Design

The main passive components are the inductor (choke coil) and DC link capacitor. The value of the choke coil depends on the duty cycle of the converter ($D)$, the switching frequency ($f_{sw})$, the supply voltage ($V_{dc})$, and the maximum allowance ripple in the DC current (${∆I}_{dc})$, as shown in Equation (5) for the boost operation of the SST system (battery discharging) [45].

$$L_b={\displaystyle \frac{\left(2D-1\right)V_{dc}}{f_{sw}{∆I}_{dc}}}$$

(5)

For the DC link capacitor, Equation (6) can be used to calculate the DC link capacitor [46].

$$C_o\ge {\displaystyle \frac{S}{4∆V_{dc}\omega V_{dc}}}$$

(6)

D. 

Closed-Loop Control

The main block diagram of the system controller is shown in Figure 8. It consists of five main blocks: PLL and measurements, V_DC link regulator, current regulator, v_abc reference generation, and MLC PWM generation. The PLL and measurement block converts the measured phase voltage and current to the dq components and regular frequency ωt. The V_DC link regulator controls the reference current to keep the DC link voltage at a preset value. The reference dq voltage and current are generated based on the dq components of the measured voltage and current in the current regulator block. The output of the current regulator block is fed to the v_abc reference generation to generate phase voltage references. The MLC PWM generation block generates the gate signals to all the modules based on time shift PWM topology.

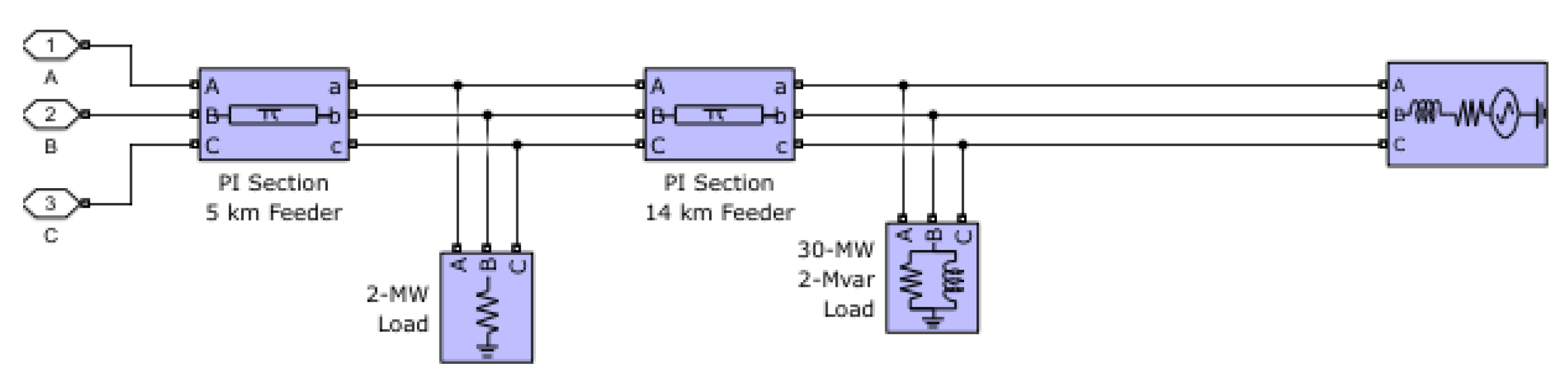
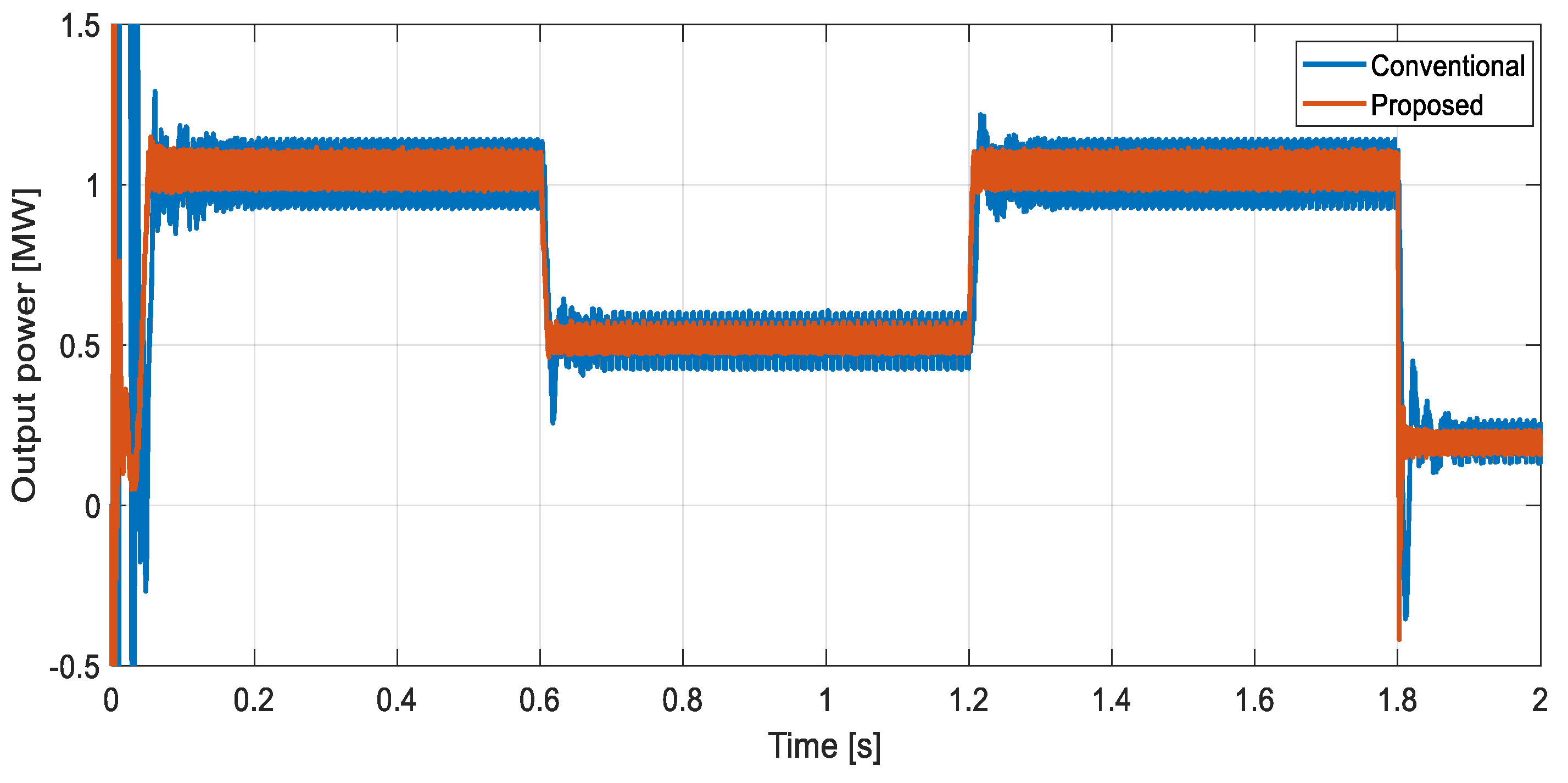
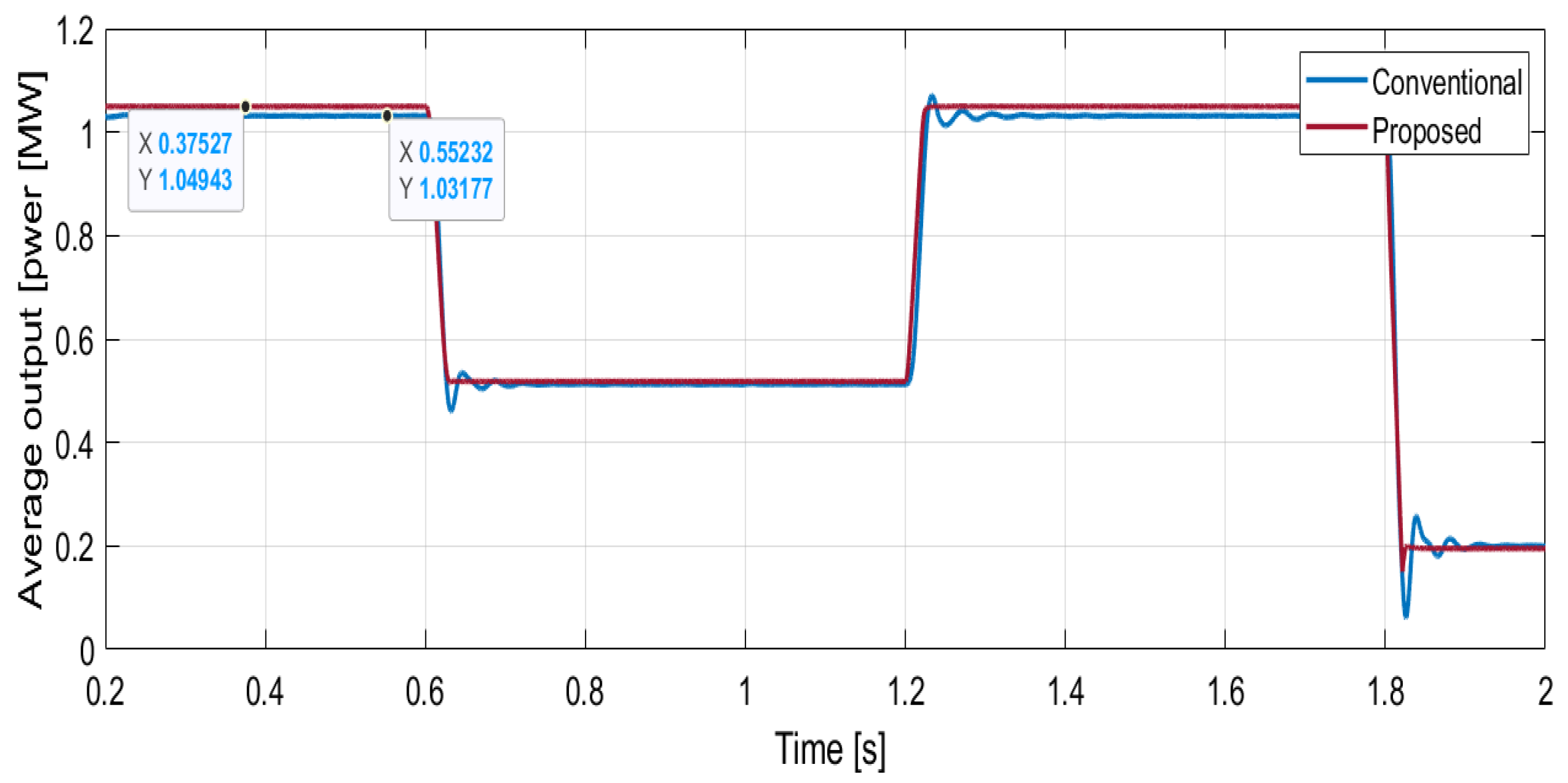
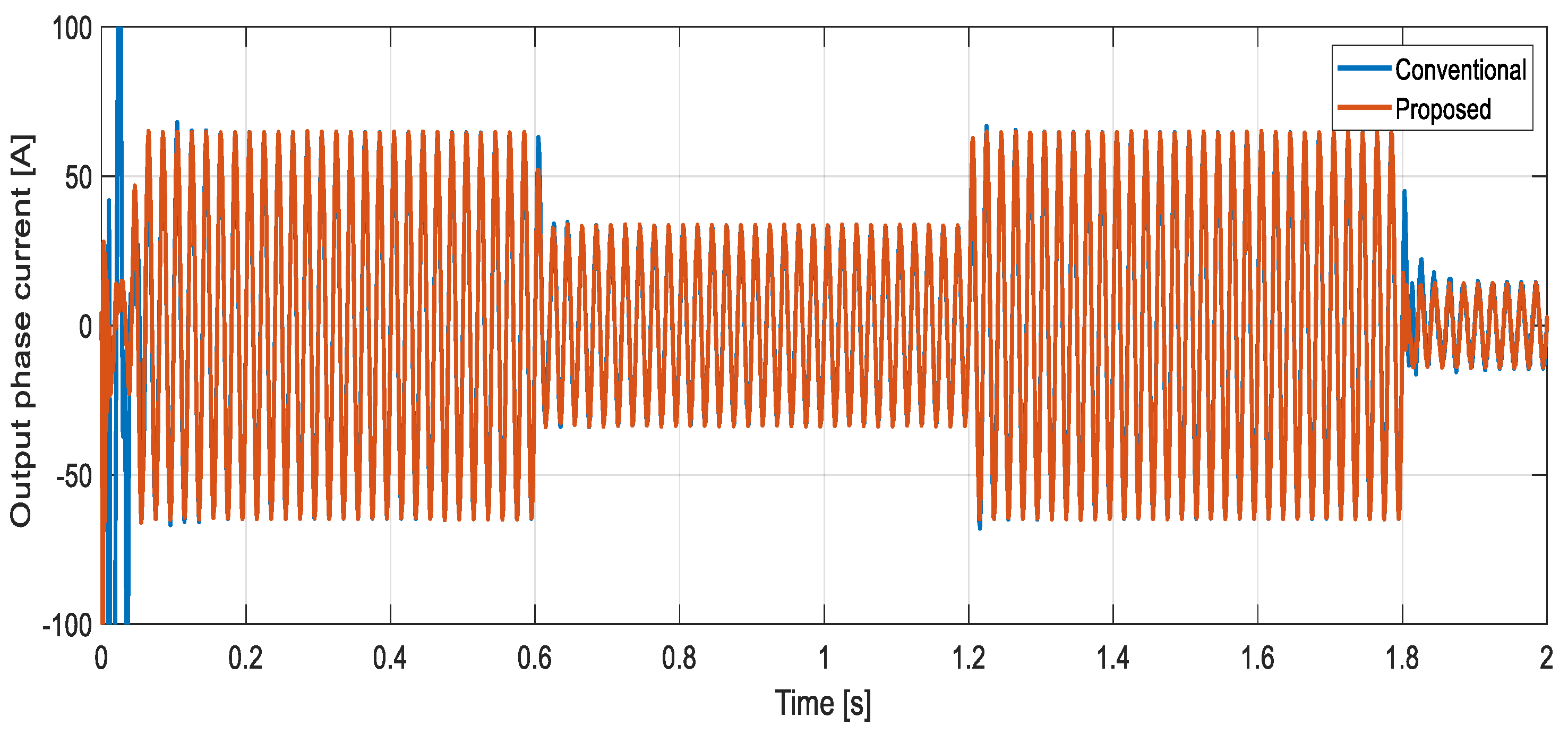
3. Simulation Results

The whole system was modeled using the MATLAB 2024 Simulink platform. The main block of the Simulink model for the conventional and the proposed CHBs-MLC are shown in Figure 9 and Figure 10, respectively. In both Simulink models, the grid was modeled by a three-phase voltage source, transmission line, and load, as shown in Figure 11. The CHBs-MLC module details are shown in Figure 12 and Figure 13 for the conventional and proposed models. To show the performance of the proposed converter and its benefits, the simulation results are compared with a conventional MLC. The conventional MLC was selected to show the benefits of the proposed MLC due to the following considerations:

• Based on the authors’ knowledge, it is not much work to address the problem of a double-frequency harmonic MLC.
• Recent work on MLCs employing high-frequency transformers focusing on improving the power density of the converter and control is not mature and has some drawbacks, such as the complexity of the system.
• Due to the simplicity of the proposed converter in terms of control and operation, the convention MLC is a suitable converter to compare with, as they share the same simplicity in terms of control and operation.

The parameters of the two systems are summarized in

Table 2. Main parameters of the ordinary and proposed CHBs-MLC.

	Proposed	Conventional
Power	1.2 MW
Voltage (line to line)	13.8 kV
Number of levels	24
Power of each module	41.67	13.89
Switching frequency	5 kHz for inverter 20 kHz for the HFT	5 kHz
DC link capacitor [mF]	0.12	6
PV
Maximum power Pmax	305.226
Voltage at Pmax	54.7

. Two scenarios for simulation are considered. The first scenario changes the irradiation for all PV panels. The second scenario shades 25% of the PV panels.

Scenario 1: In this scenario, the irradiation is changed from 1000 W/m² to 500 W/m² at 0.5 s, then changed to 1000 W/m² at 1.2 s, and then dropped to 200 W/m². All these changes take 1 ms to change their values. The output power of the proposed converter and the conventional one are shown in Figure 14, and the details of the output powers zoomed-in are shown in Figure 15. The details of the output power during the change in the irradiation from 1000 W/m² to 500 W/m² are shown in Figure 16. The proposed converter has a faster response to the disturbance, around two times faster than the conventional one. The double-frequency components in the output power of the conventional converter are high compared to the proposed converter. The average output power of the proposed and conventional converters is shown in Figure 17. Due to the double frequency content in the power, the MPPT cannot completely extract the maximum power from the PV compared to the proposed one, where the power has fewer fluctuations. The output power of the proposed one is 15% more than the conventional converter.

The phase current of the conventional and the proposed converter are shown in Figure 18. It can be seen that the proposed method performs better during transients. It achieves faster tracking of the output current with reduced overshoot values and a shorter settling time. Moreover, the proposed method eliminates the fluctuations at the start of the algorithm.

The FFT of the phase current under the conventional and proposed converter is shown in Figure 19. The THD of the phase current in the proposed converter is 50% less than the conventional one, and the odd harmonics order is very low in the proposed converter compared to the conventional one.

The DC link voltage of the proposed and conventional converters is shown in Figure 20, and the details during the irradiation change are shown in Figure 21 and Figure 22. The DC link voltage in the conventional converter has a higher double-frequency content than the proposed one.

The inverter phase voltage for the proposed and the conventional converters is shown in Figure 23. It is worth noting the THD of the converter voltage. Figure 24 shows the FFT and THD of the converter voltage. The proposed converter THD for the phase voltage is 10% less than the conventional converter, and the odd harmonics are 50% less in the proposed inverter.

Scenario 2: In this scenario, 25% of the PV panels are exposed to 800 W/m² irradiation and the rest (75%) are exposed to 1000 W/m² from the start, and then the irradiation drops to 500 W/m² for the 25% of the PV panels and the rest are kept at 1000 W/m². The output power of both converters, the conventional and the proposed, is shown in Figure 25, and details are shown in Figure 26. The conventional suffers from high fluctuations in power due to the double frequency, and the more nonuniform the distribution of the irradiation is, the more fluctuation there is. This effect on the average output is seen in Figure 27. There is a 2.5% mismatch between the conventional and the proposed converters for 800 W/m² and 2.7% for 500 W/m².

In terms of the converter phase current, Figure 28 shows the phase current of the two converters. The THD of the phase current when the irradiation of 25% of the PV panels is 800 W/m² and 75% are at 1000 W/m² is shown in Figure 29. For an irradiation of 500 W/m² for 25% and 1000 W/m² for 75% of the PV panels, Figure 30 shows the THD of the phase current.

The THD of the phase voltage when the irradiation of 25% of PV panels is 800 W/m² and 75% are at 1000 W/m² is shown in Figure 31. For an irradiation of 500 W/m² for 25% and 1000 W/m² for 75% of the PV panels, Figure 32 shows the THD of the phase voltage.

4. Discussion

This paper presents a proposed Cascaded H-bridge multilevel converter for PV systems connected to a medium-voltage grid. The proposed converter is mainly based on a high-frequency transformer topology. Instead of the PV supplying a single-phase power grid, it supplies a three-phase power grid. This offers a reduction in the capacitor size (50 times reduction), better performance in terms of THD reduction (200% for current and 30% for voltage), and a fast disturbance response (200%). High-frequency transformers offer a decrease in the transformer volume compared to ordinary line frequency transformers (2800% reduction). The performance and size of the proposed converter compared to the conventional one are presented in

Table 3. Sizing comparisons between the conventional and proposed CHBs-MLC.

	Proposed	Conventional	Difference
Capacitor size [µF]	0.12	6	50 times reduction
Capacitor volume [m3]	0.00204	0.0148	7 times reduction
Number of switches	384	360	7% increase
Number of diodes	288	72	4 times increase
Transformer core volume [m3]	0.023688	0.33844	28 times reduction
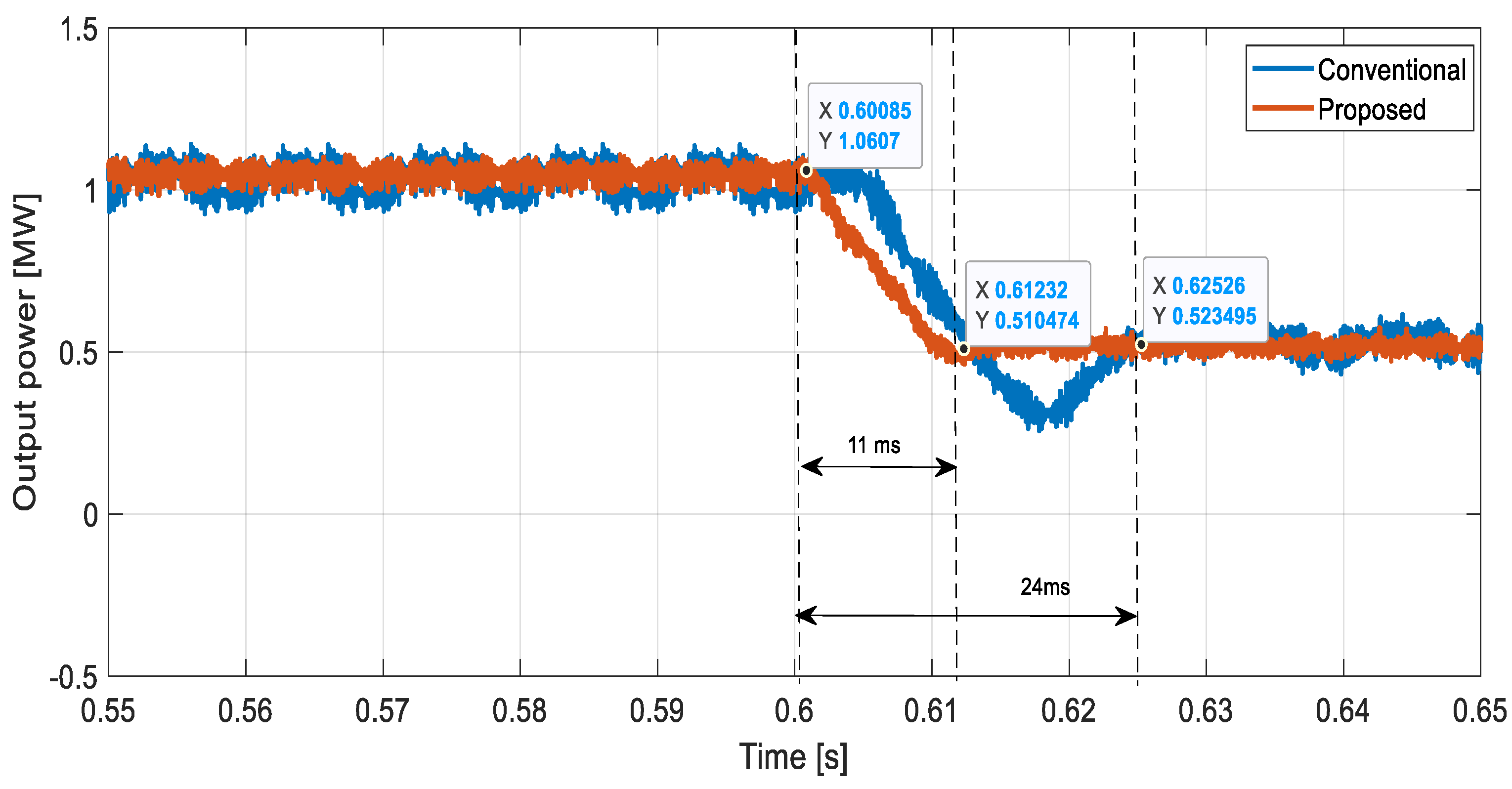
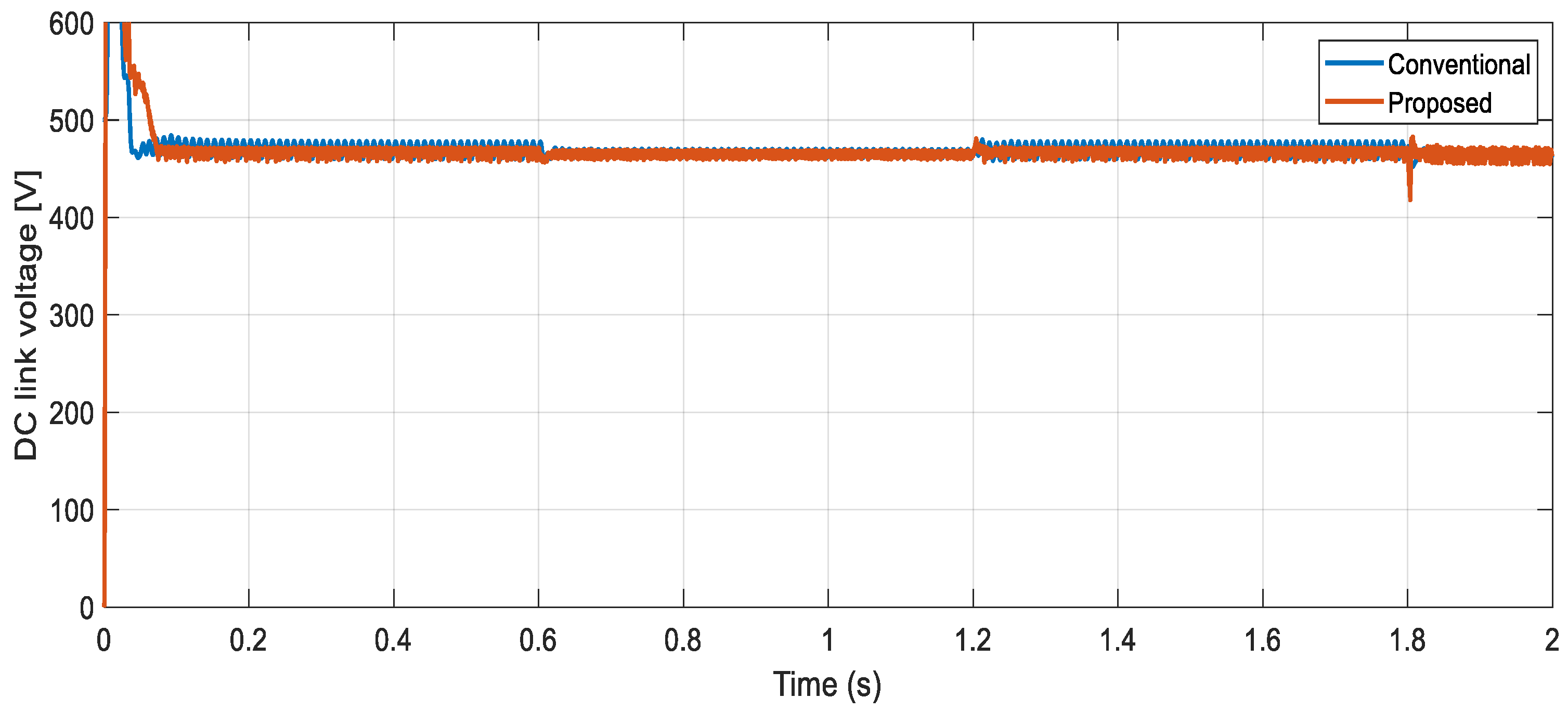
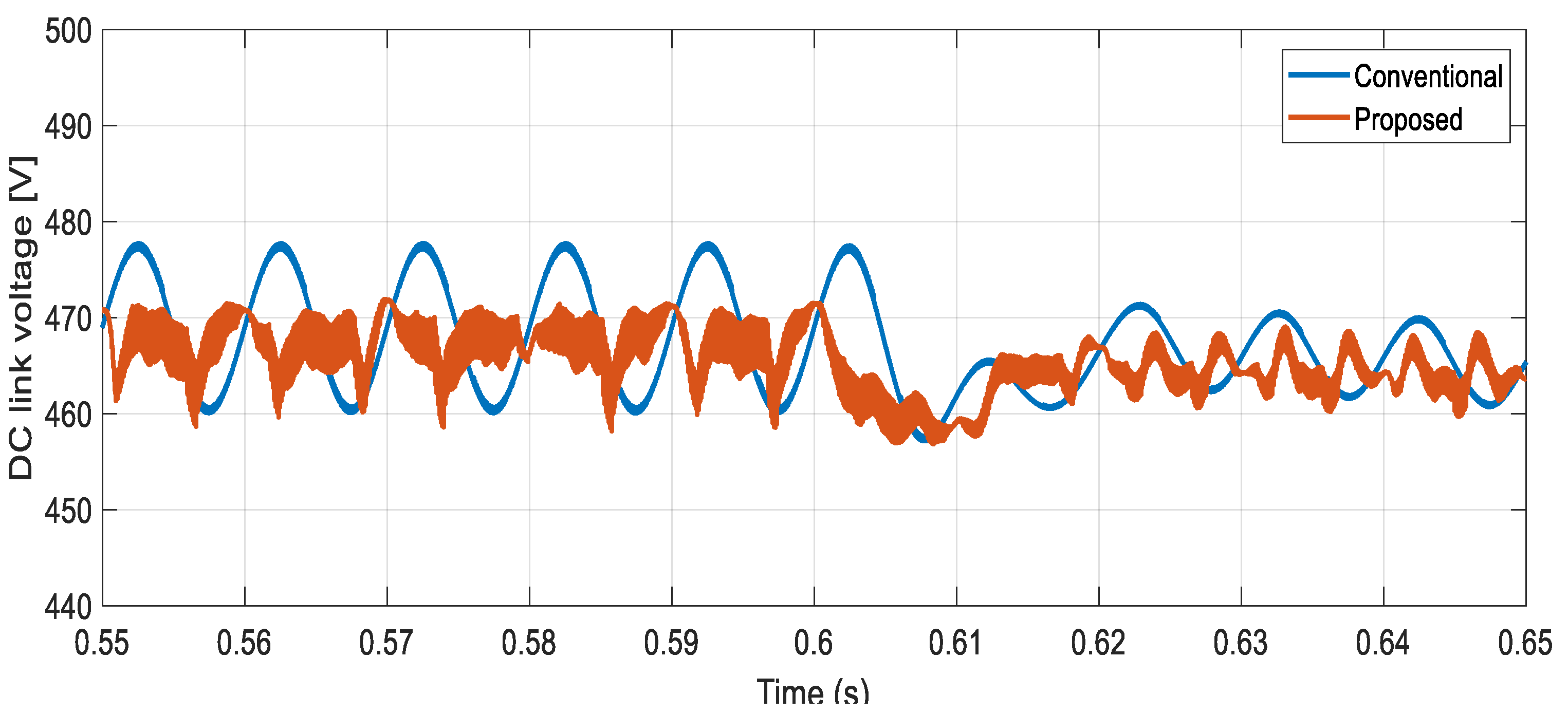
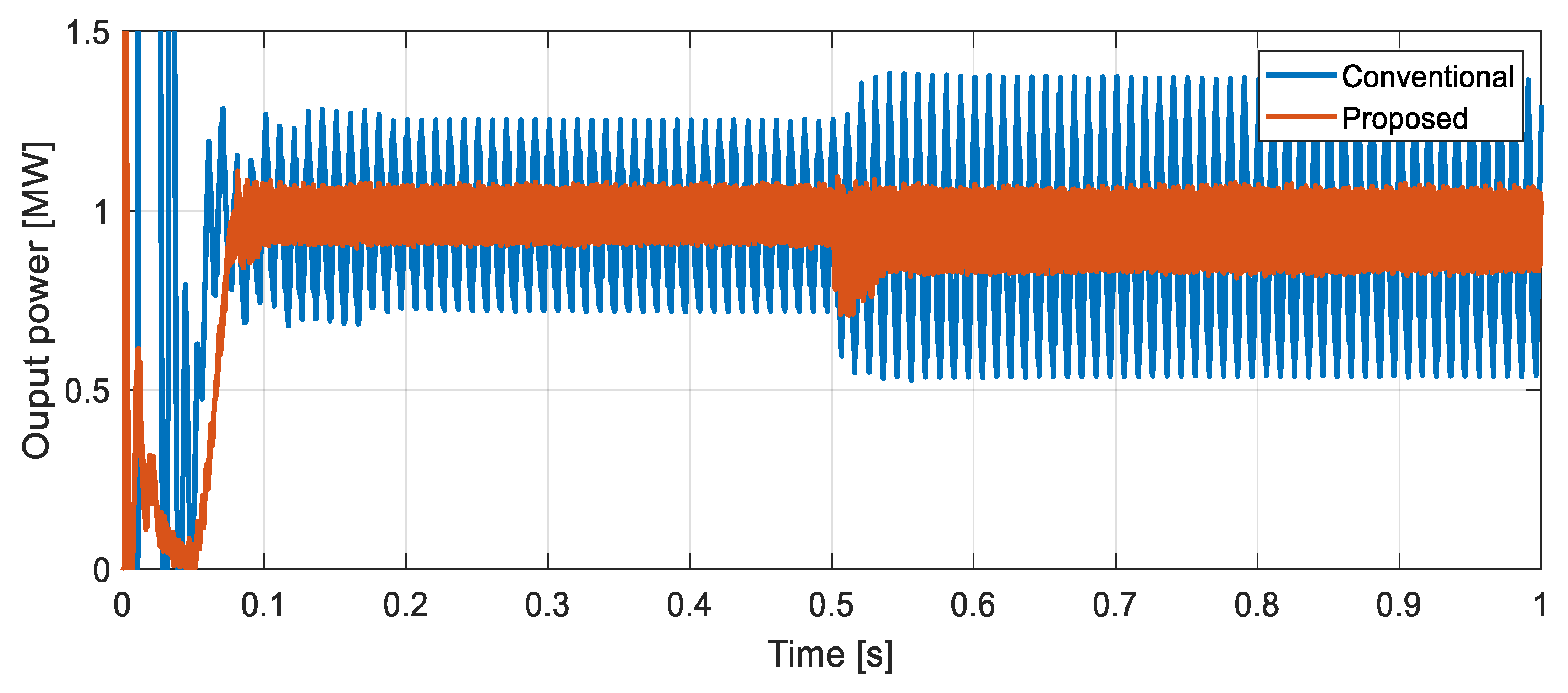
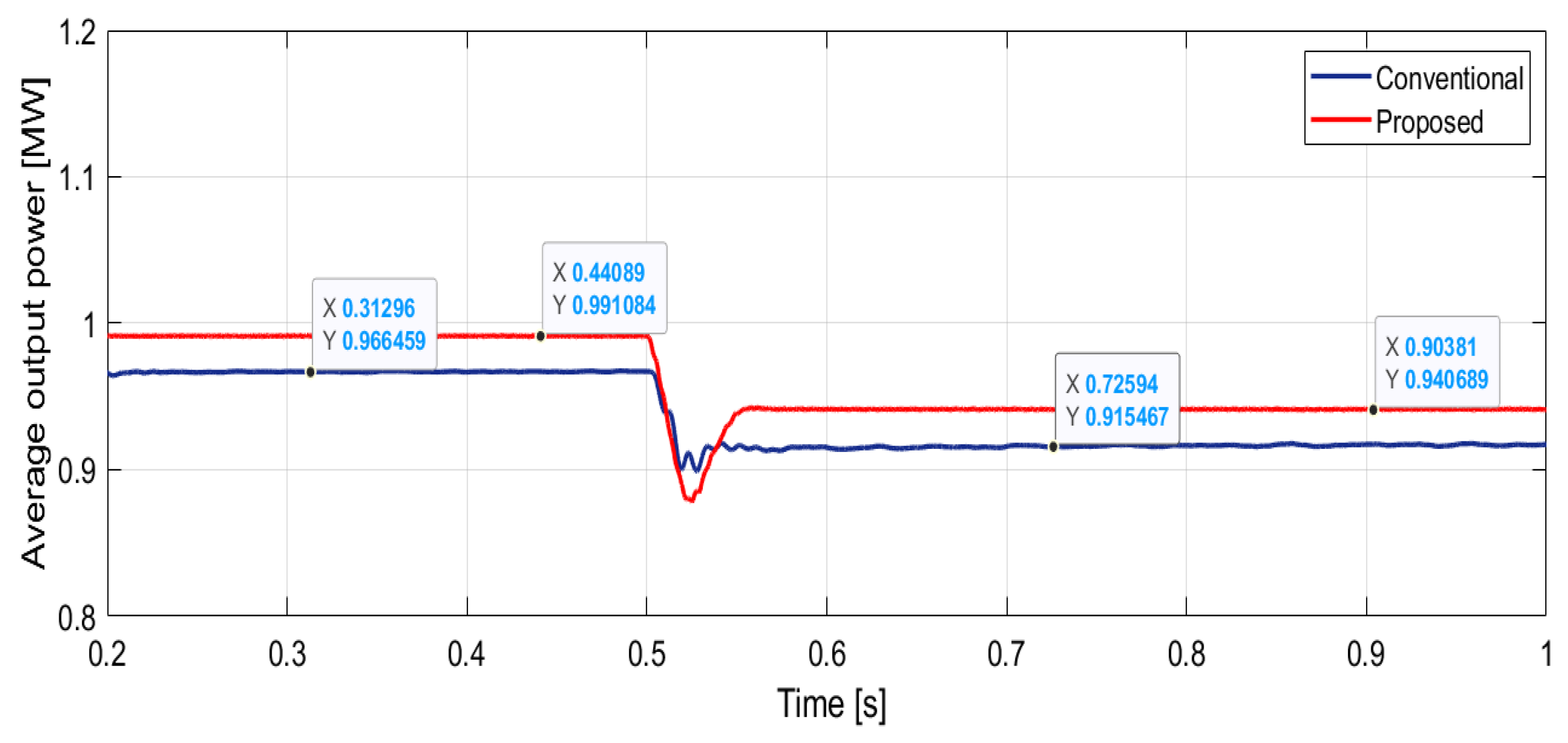
Time response to disturbance [ms]	11	22	2 times reduction
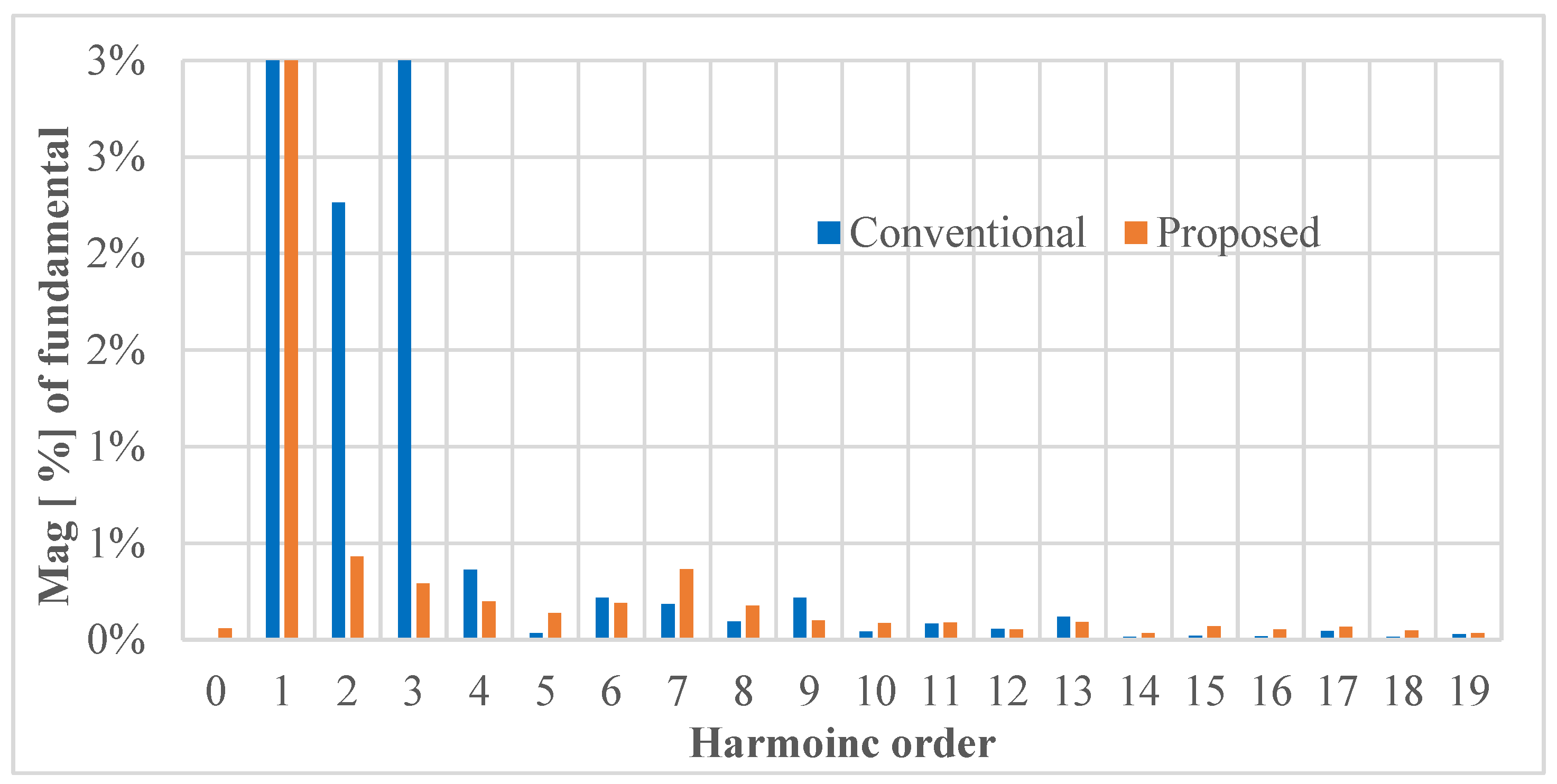
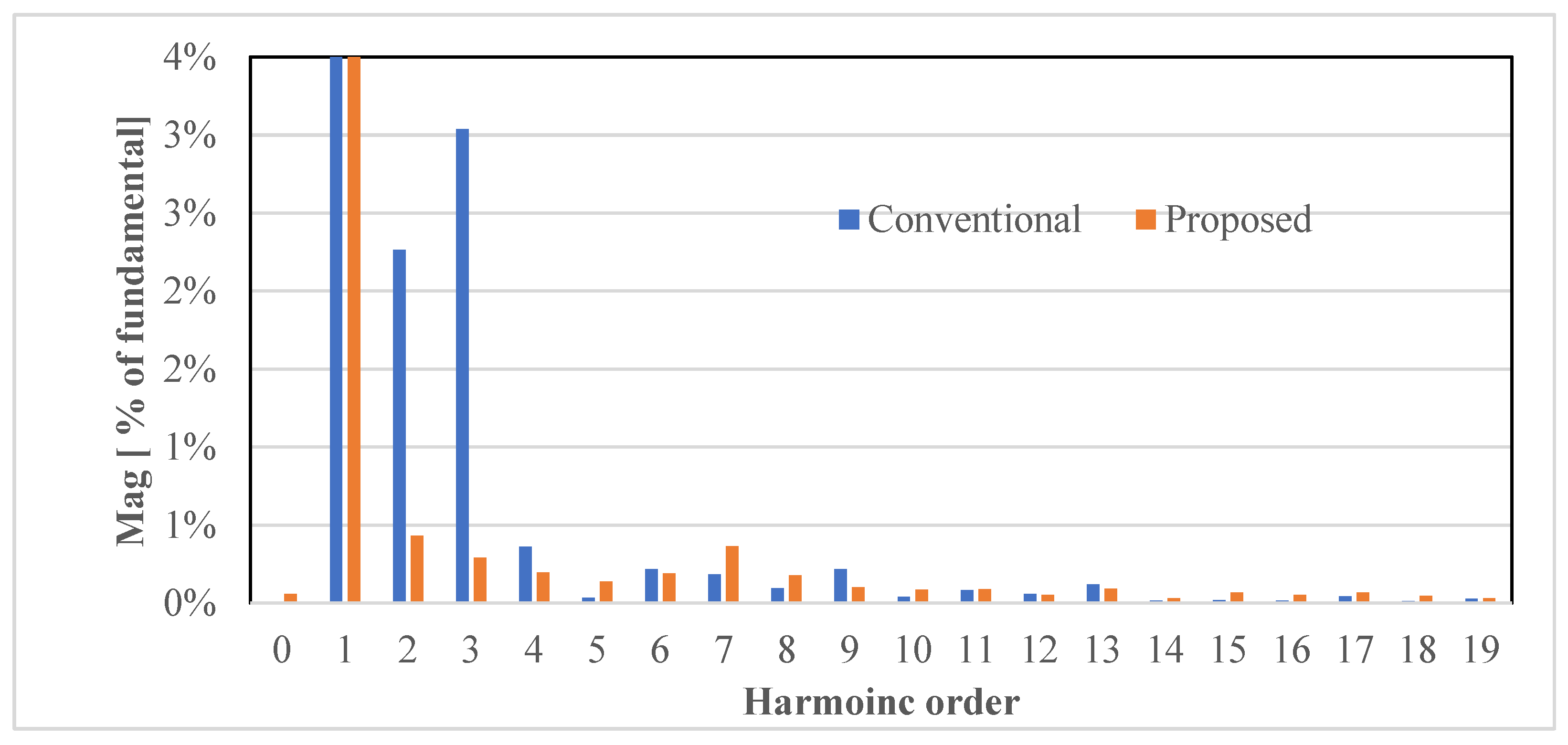
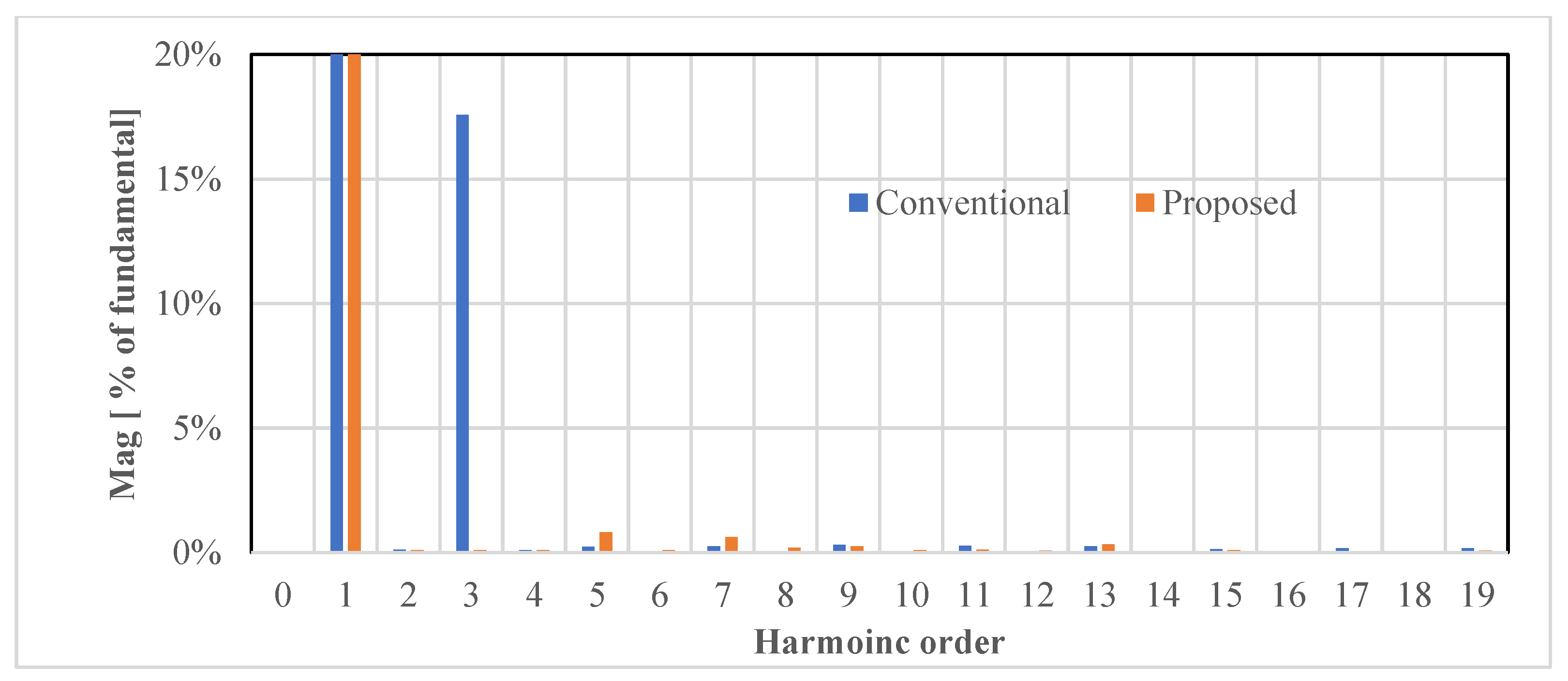
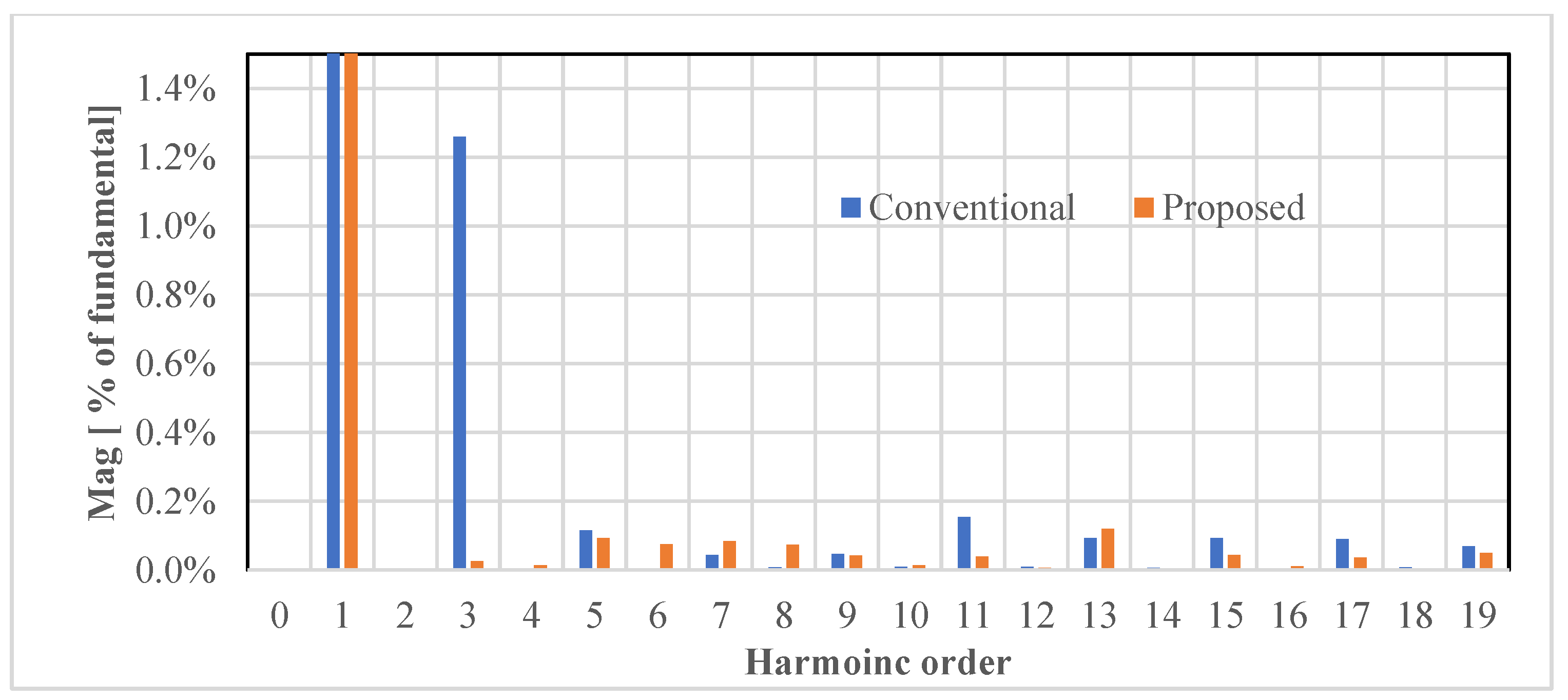
THD for current [%]	1.92%	3.88%	2 times reduction
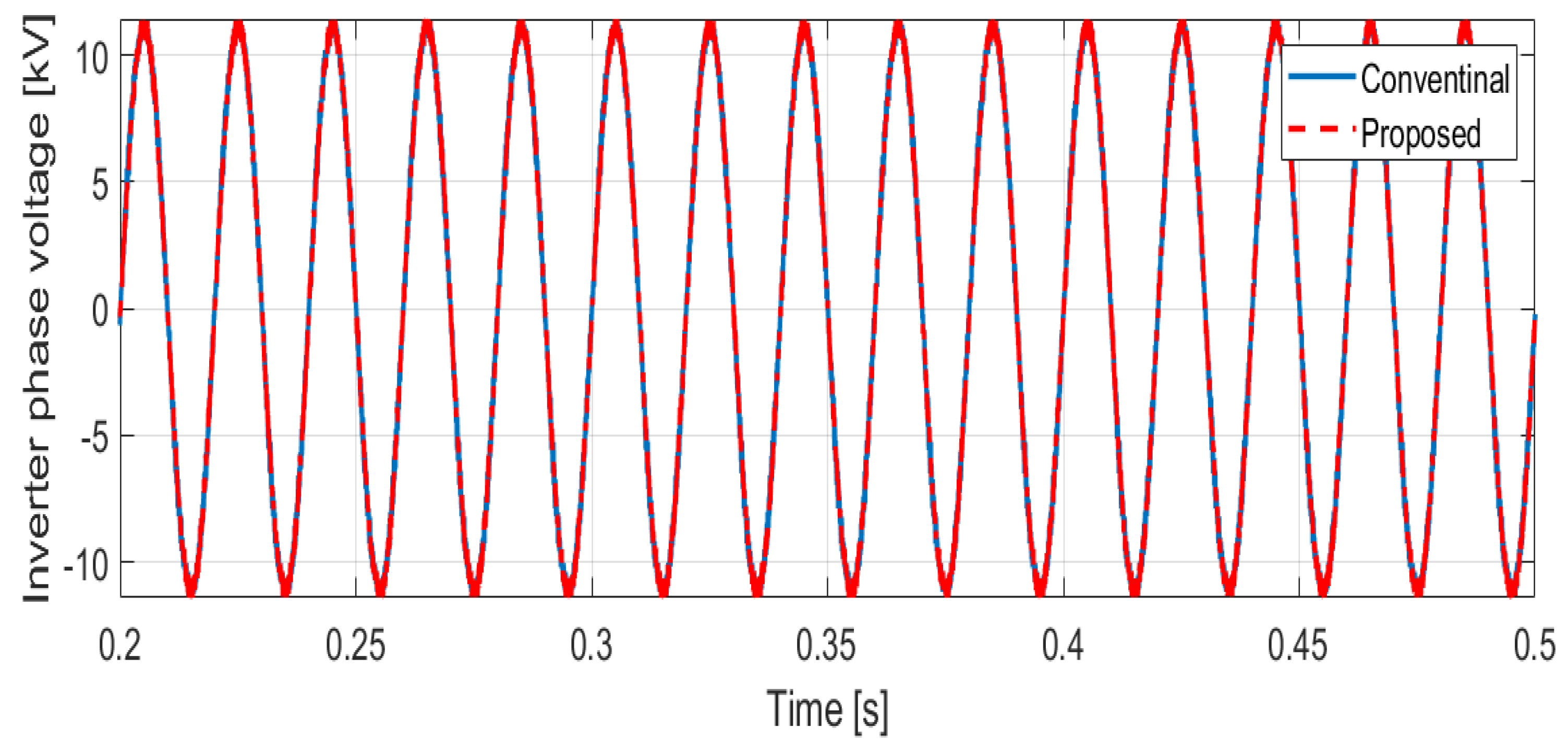
THD for voltage [%]	2.18%	2.42%	30% reduction

.

Table 4. Cost breakdown between the conventional and proposed CHBs-MLC.

Item	Proposed	Conventional
DC/AC converter (H-bridge at the load side)
Number of MOSFETs	288	288
MOSFET Id	IPW60R016CM8XKSA1	IPW60R016CM8XKSA1
Price	USD 7.66	USD 7.66
Total price	USD 2206.08	USD 2206.08
DC link capacitor
Number of capacitors	72.00	72.00
Value	0.12 µF	6 $\mu$F
Price	USD 0.26	USD 1.81
Caps Id	RSBPC1150DQ00J	C4AULBU4660M1CK
Caps total price	USD 19.01	USD 130.32
Rectifier (the secondary of the high-frequency transformer)
Number of diodes	288
Voltage	600
Current	23.14814815
Diode Id	BYC30M-650PQ
Price	USD 0.33
Total price	USD 93.60
DC/DC converter (H-bridge PV side)
Number of diodes		72
Diode Id		VS-30ETH06-N-S1
Price/diode		USD 0.62
Number of MOSFET s	96	72
MOSFET ID	IPW60R016CM8XKSA1	IPP65R110CFDXKSA2
Price of MOSFET	USD 7.66	USD 2.65
Total price	USD 735.36	USD 235.37
Total cost for the whole system excluding the transformer price	USD 3054.05	USD 2571.77

presents a cost breakdown for the power electronic components (switches, diodes, capacitors) in both the proposed and conventional topologies, derived from Mouser [47], with pricing for quantities exceeding 2000 units (tax excluded). The main transformer, being a customized component, lacks readily available supplier pricing. Although the proposed topology exhibits an 18.7% higher cost for these specific components, this comparison omits the transformer, which represents a substantial portion of the overall system cost. Critically, low-frequency transformers (LFTs) and their associated equipment required for the conventional topology incur significantly higher costs than the high-frequency transformer (HFT) used in the proposed solution.

While the proposed topology increases the MOSFET count by 7% (384 vs. 360) and the number of diodes by 300%, it achieves a 7-fold reduction in capacitor volume, substantially decreasing the component count and parallel arrangements required for ESR reduction. Crucially, the reliability analysis presented in [48] confirms that MOSFETs (35-year calculated lifetime) and electrolytic capacitors (40-year lifetime) exceed the PV system’s 25-year lifespan, rendering component replacements highly unlikely under normal operation. The capital savings from reduced capacitor volume (in materials, installation, and cooling) and operational benefits (reduced footprint and weight) outweigh the marginal cost increases for switches and diodes. This advantage amplifies at scale (>1 MW), where capacitor savings scale super-linearly, while switch costs remain near linear due to the modular design, confirming net lifecycle benefits.

Moreover, the primary objective of this paper is to introduce a topology that addresses the double frequency issue while reducing system volume, to explain the principle of operation, to outline the design and control, and to provide some simulation results to highlight the benefits. System losses, fault conditions, grid stability, unbalanced loads, scalability, total system cost, reliability, and high-level monitoring control are outside the scope of this paper.

It is worth mentioning that there are some issues regarding this proposed topology that can be summarized as follows:

○

The price of the converter could be higher than a conventional one due to a large number of power electronics switches and using a special core for the HFT. Mass production can reduce the converter price.

○

The losses of the proposed converter could be higher than an ordinary converter. Employing a lower-loss transformer core (at high frequency) and using WBG devices can reduce the total losses.

5. Conclusions

An advanced isolated topology based on a DAB converter was presented in this paper for grid-connected medium-voltage PV applications. The proposed configuration is modular and outputs a multilevel voltage waveform with high power quality. The output power of the PV system is fed to the primary side of the DAB topology, and the secondary side utilizes three different windings, each of which is connected to the phase leg. The proposed configuration eliminates unbalanced phase power in conventional CHB and MMC configurations. Furthermore, the proposed configuration eliminates the double-line frequency component from the DC-link capacitor, leading to longer lifetime operation and the use of lower capacitance. Moreover, the results showed the proposed circuit’s ability to operate at full PV power and partially shaded PV power. Future research will include extending the proposed concept to an MMC topology and conducting experimental verification with a higher number of PV inputs. The proposed concept offers a feasible and efficient integration methodology for multi-input PV generation systems, eliminating the issues of unbalanced phase powers at partial shading conditions and PV panel mismatches. The main disadvantage of the system appears to be its cost. However, as power electronics and high-frequency transformers continue to evolve, their prices are expected to decrease, potentially offsetting this drawback. Moreover, experimental validation is concurrently underway using a laboratory-scale prototype to verify its transient performance under dynamic shading conditions.

Future research includes the investigation of higher-level control design for the proposed configuration, which can be extended to several expected grid unbalance conditions, fault ride-through control, and various fault scenarios within the grid system. Furthermore, reliability analysis and fault tolerance of the proposed topology are also feasible future extensions, considering practical mission profiles and data. Future research will include the investigation of higher-level control design for the proposed configuration.