Design and Implementation of a Bionic Marine Iguana Robot for Military Micro-Sensor Deployment
Abstract
1. Introduction
- Based on the marine iguana’s motion characteristics, a dual-mode underwater sensor deployment robot is designed. The robot is driven by powerful limbs in crawling mode and by a tail swimming structure in swimming mode. It can ascend and descend through a flexible buoyancy adjustment mechanism and deploy underwater sensors using its head deployment structure, enabling flexible movement in complex terrains and overcoming the limitations of traditional equipment in complex waters.
- The robot’s crawling gait planning, trajectory planning, swimming posture planning, and dynamic analysis are conducted. The Trot gait and segmented composite foot trajectory are selected to enhance the robot’s environmental adaptability and task execution. Experimental results validate the effectiveness and rationality of the trajectory planning, showing that the robot can adapt well to complex terrains such as gravel and mud.
- The design and construction of the bionic marine iguana robot are completed, and its feasibility is verified through performance testing. The robot demonstrates excellent motion sensitivity and can perform underwater environmental detection and micro-sensor deployment tasks, providing an innovative solution for micro-sensor deployment in marine military applications.
2. Mechanical Structure Design of the Bionic Marine Iguana Robot
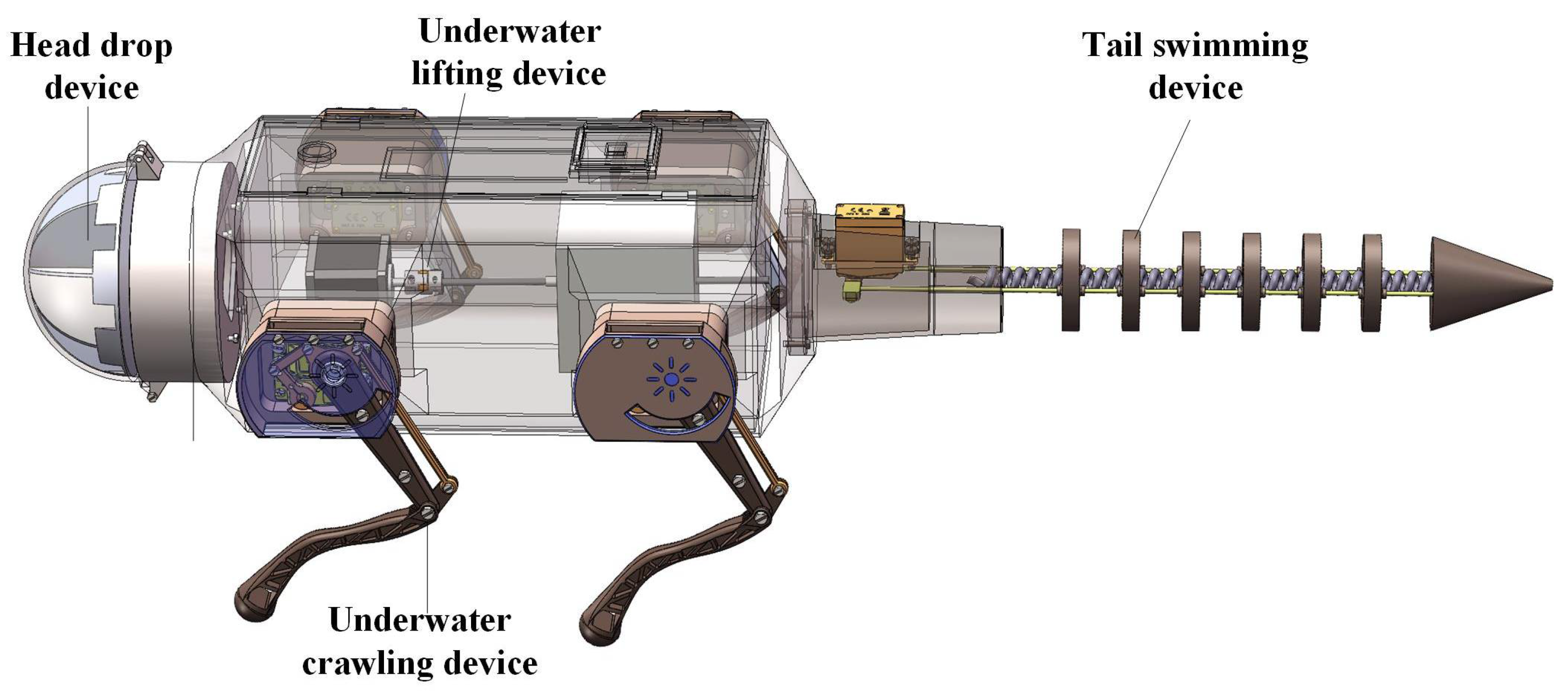
2.1. Overall Structure Design
2.2. Design of Deployment Mechanism
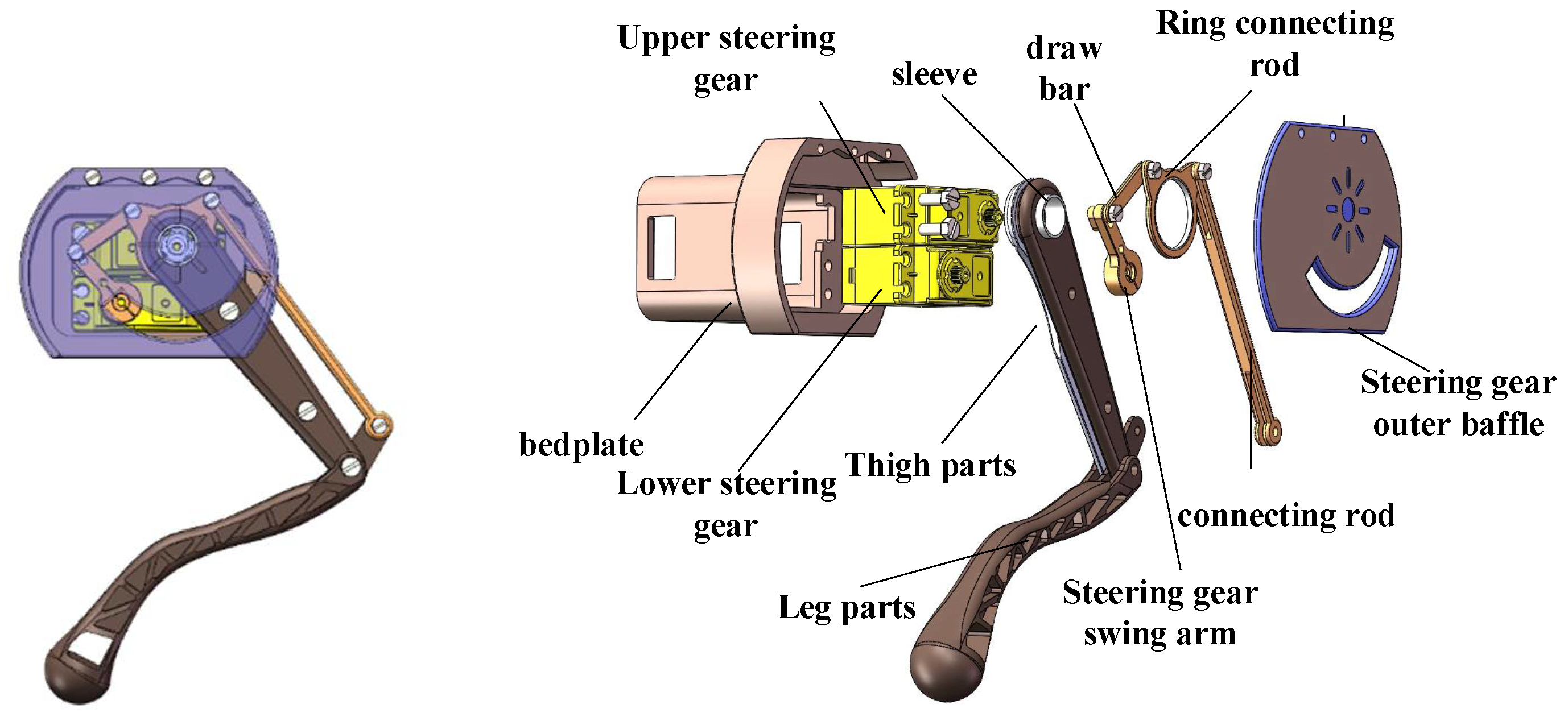
2.3. Design of Crawling Mechanism
2.4. Design of Swimming Mechanism
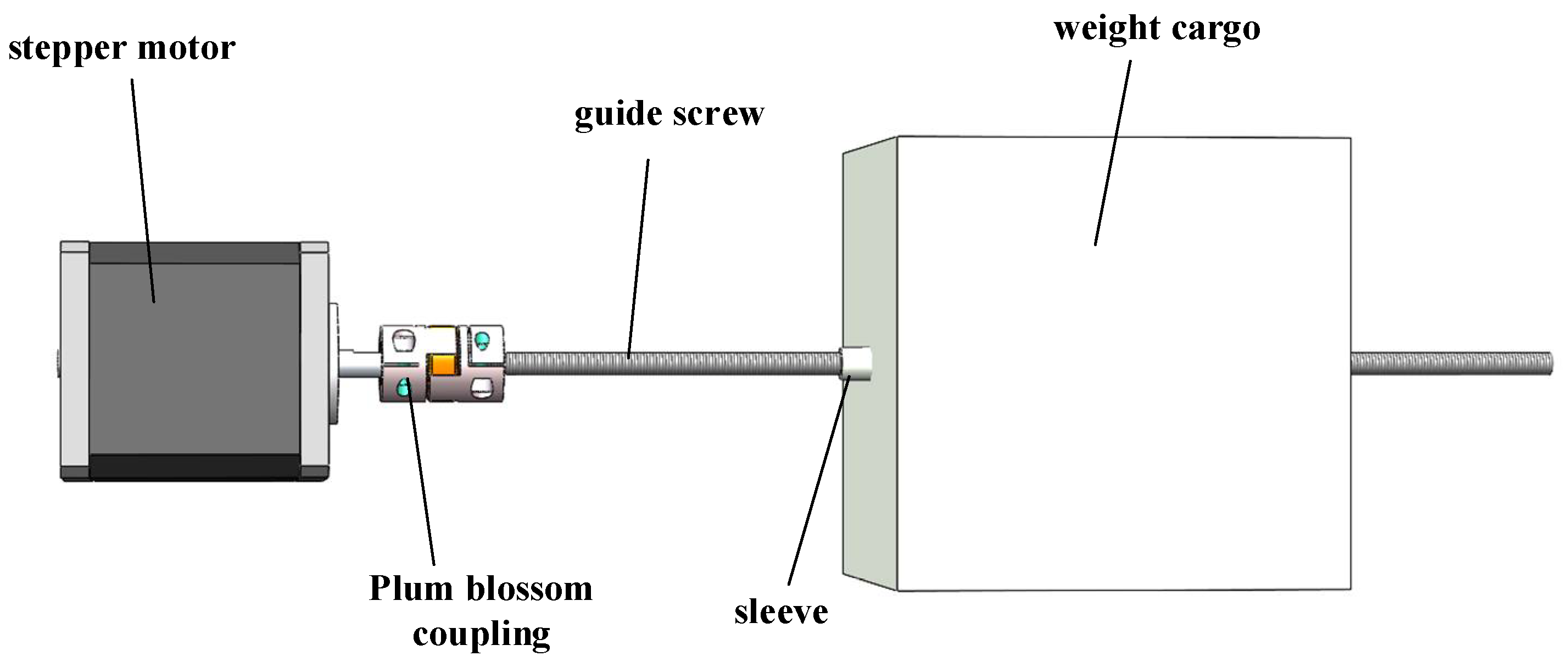
2.5. Design of Buoyancy Adjustment Mechanism
2.6. Motor Selection
3. Control System Design of the Bionic Marine Iguana Robot
3.1. Hardware System Design
3.2. Software System Design
4. Gait Planning and Kinematic Analysis of the Bionic Marine Iguana Robot
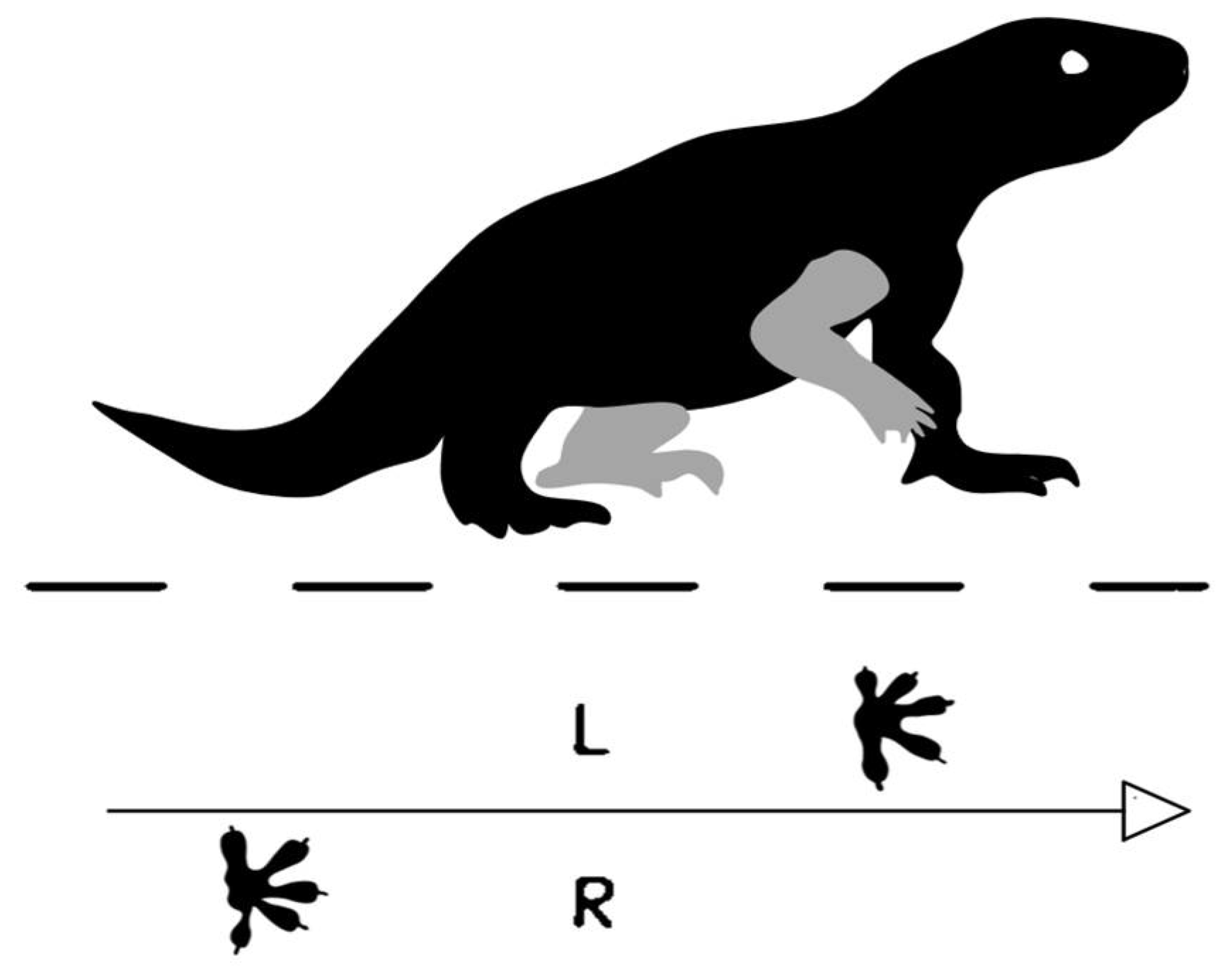
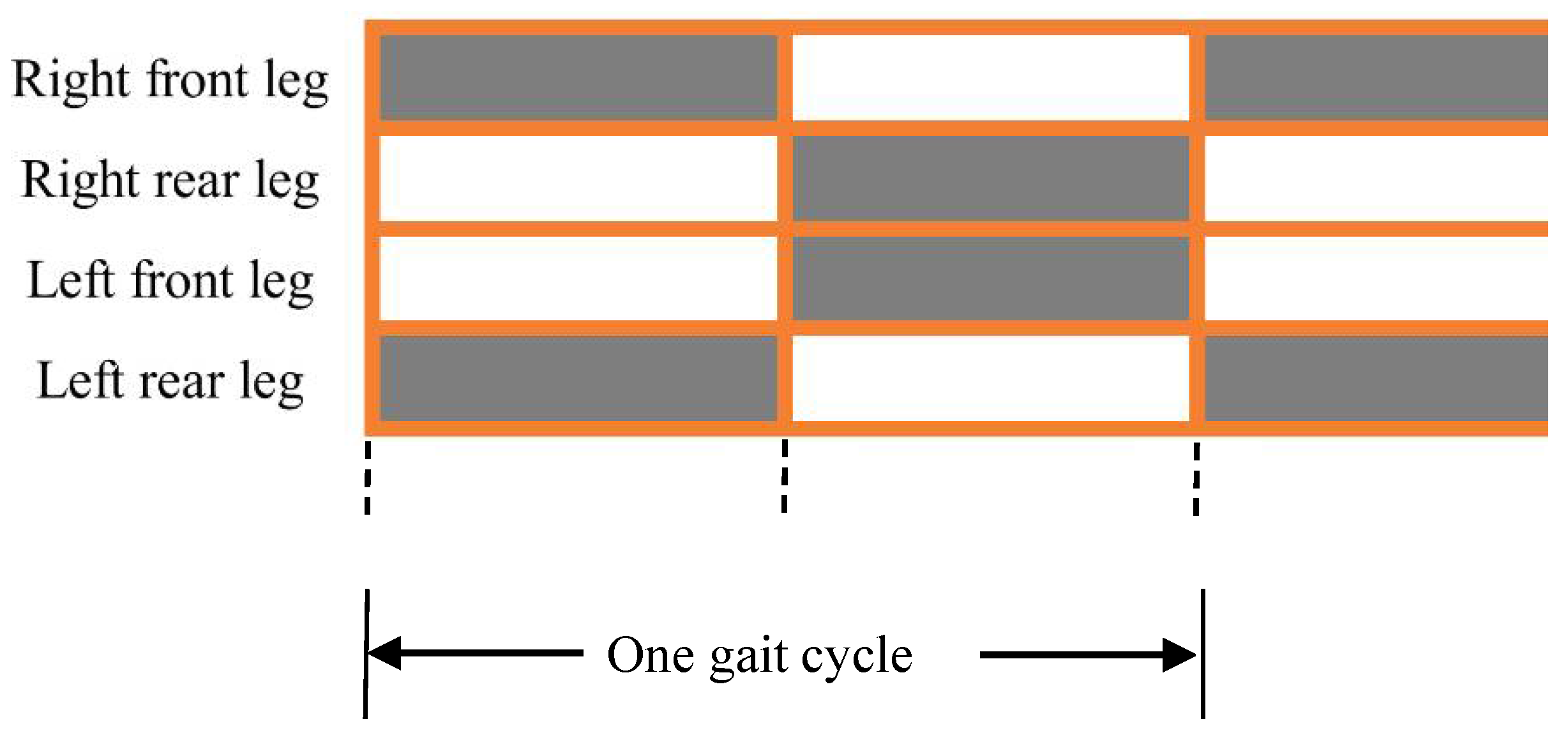
4.1. Crawling Gait Planning
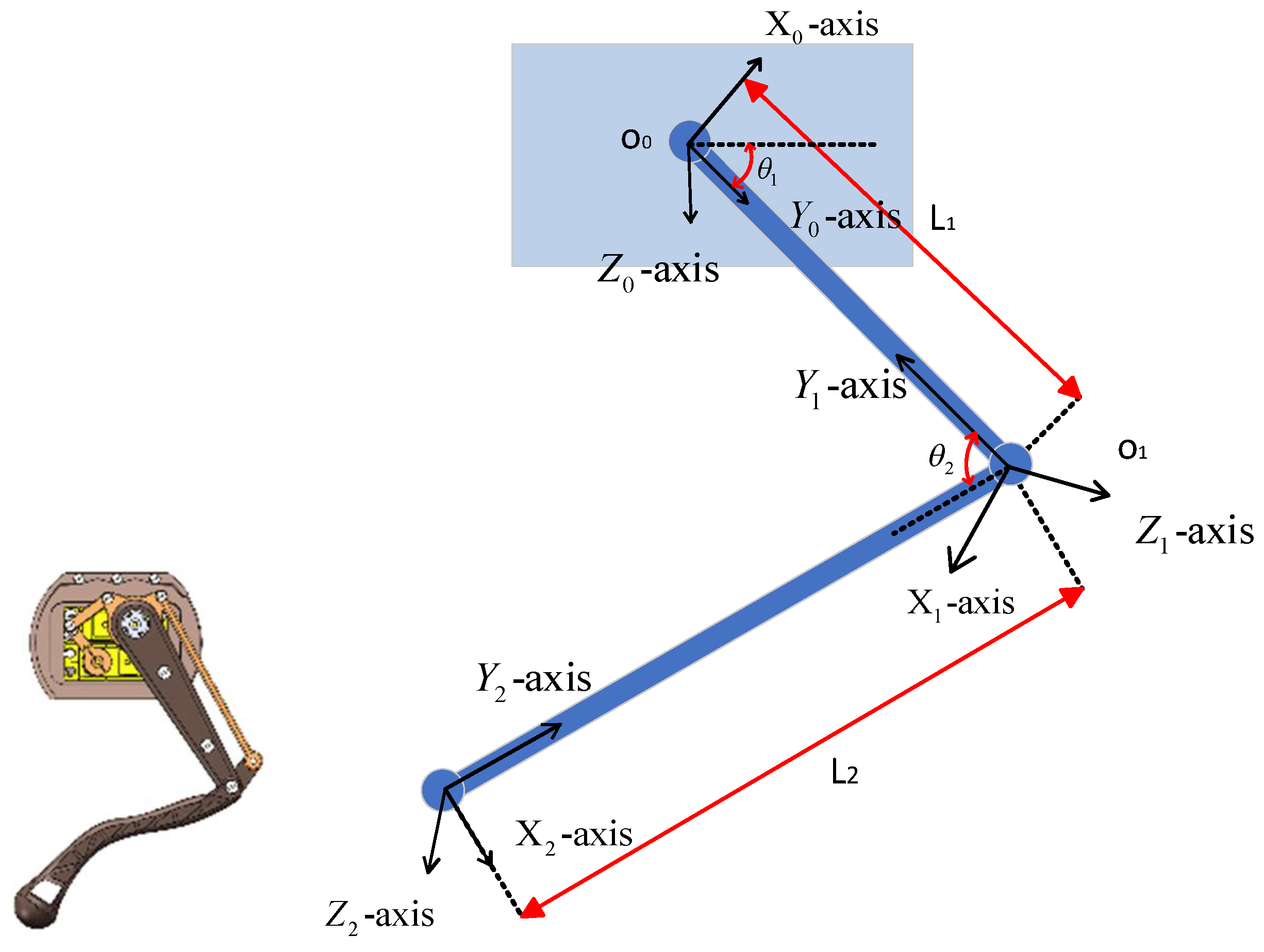
4.2. Leg Kinematic Modeling
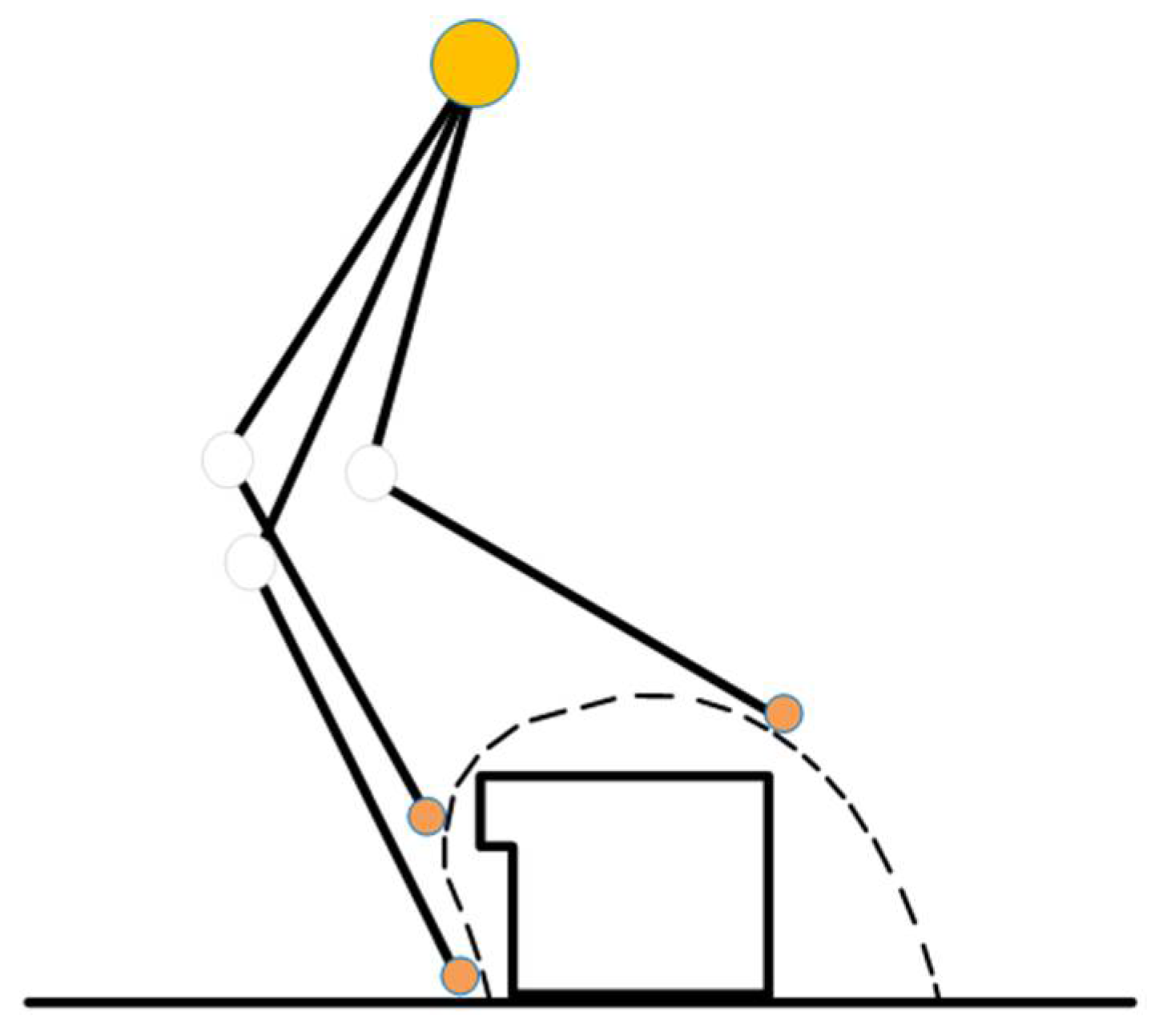
4.3. Crawling Trajectory Planning
4.4. Swimming Posture Planning
4.5. Swimming Kinematic Analysis
5. Performance Testing of the Bionic Marine Iguana Robot
5.1. Basic Function Testing
5.2. Underwater Crawling Test
5.3. Underwater Swimming Test
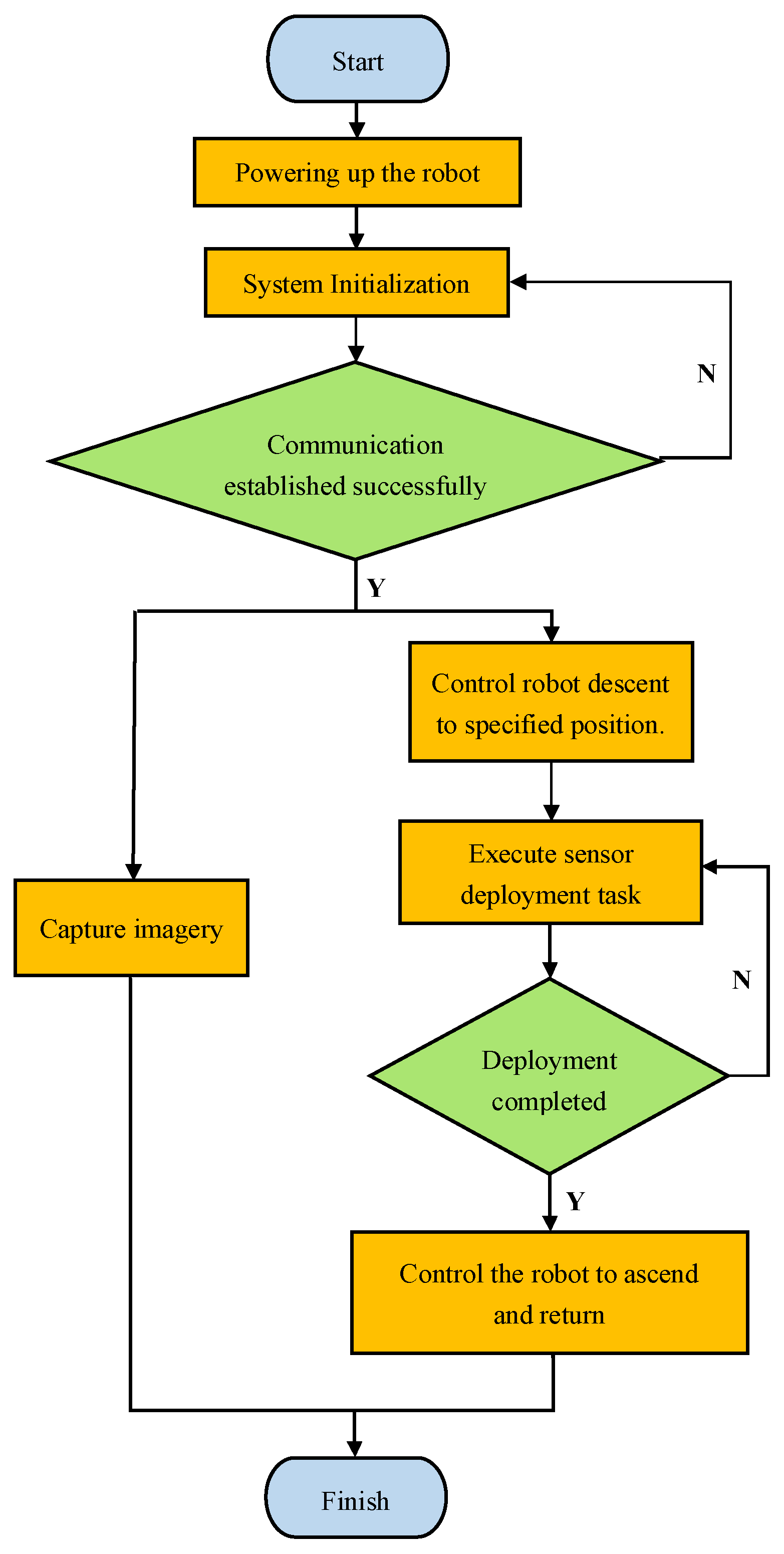
5.4. Sensor Deployment Testing
5.5. Theoretical and Experimental Data Comparative Analysis
- Unmodeled Fluid Dynamics
- Mechanical Efficiency Losses
- Elastic Deformation of Nylon Cords
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lloret, J. Underwater sensor nodes and networks. Sensors 2013, 13, 11782–11796. [Google Scholar] [CrossRef] [PubMed]
- Pompili, D.; Melodia, T.; Akyildiz, I.F. Three-dimensional and two-dimensional deployment analysis for underwater acoustic sensor networks. Ad Hoc Netw. 2009, 7, 778–790. [Google Scholar] [CrossRef]
- Luo, J.; Yang, Y.; Wang, Z.; Chen, Y. Localization algorithm for underwater sensor network: A review. IEEE Internet Things J. 2021, 8, 13126–13144. [Google Scholar] [CrossRef]
- Felemban, E.; Shaikh, F.K.; Qureshi, U.M.; Sheikh, A.A.; Qaisar, S.B. Underwater sensor network applications: A comprehensive survey. Int. J. Distrib. Sens. Netw. 2015, 11, 896832. [Google Scholar] [CrossRef]
- Xu, T.; Yu, J.; Vong, C.-I.; Wang, B.; Wu, X.; Zhang, L. Dynamic morphology and swimming properties of rotating miniature swimmers with soft tails. IEEE/ASME Trans. Mechatron. 2019, 24, 924–934. [Google Scholar] [CrossRef]
- Prahacs, C.; Saudners, A.; Smith, M.K.; McMordie, D.; Buehler, M. Towards legged amphibious mobile robotics. In Proceedings of the Canadian Engineering Education Association (CEEA), Montreal, QC, USA, 29–30 July 2004. [Google Scholar] [CrossRef]
- Chen, G.; Xue, H.; Meng, X.; Zhao, Z.; Liu, Z. Multi-performance index reinforcement learning training of beaver-like robot. Meas. Sci. Technol. 2025, 36, 036204. [Google Scholar] [CrossRef]
- Cao, Y.; Cao, Y.H.; Huang, Q.G.; Qu, Y.L.; Pan, G. A review of the underwater bionic flapping wing robots. Digit. Ocean Underw. Warf. 2023, 6, 380–405. [Google Scholar] [CrossRef]
- Gao, A.; Yang, E.H.; Zhang, J.N. Design of Dual-drive Bionic Jellyfish Based on Compliant Mechanism. Digit. Ocean Underw. Warefare 2023, 6, 504–510. [Google Scholar] [CrossRef]
- Ahmed, F.; Waqas, M.; Shaikh, B.; Khan, U.; Soomro, A.M.; Kumar, S.; Ashraf, H.; Memon, F.H.; Choi, K.H. Multi-material bio-inspired soft octopus robot for underwater synchronous swimming. J. Bionic Eng. 2022, 19, 1229–1241. [Google Scholar] [CrossRef]
- Chen, G.; Xu, Y.; Yang, C.; Yang, X.; Hu, H.; Chai, X.; Wang, D. Design and control of a novel bionic mantis shrimp robot. IEEE/ASME Trans. Mechatron. 2023, 28, 3376–3385. [Google Scholar] [CrossRef]
- Guo, S.; Ma, J.; Li, Z.; Zhang, J. Design and swimming test of myliobatid-inspired robot. Chin. J. Ship Res. 2022, 17, 139–144. [Google Scholar] [CrossRef]
- Berry, K.A.; Muñoz-Pérez, J.P.; Vintimilla-Palacios, C.P.; Clemente, C.J. Morphological and performance modifications in the world’s only marine lizard, the Galápagos marine iguana, Amblyrhynchus cristatus. Biol. J. Linn. Soc. 2021, 133, 68–80. [Google Scholar] [CrossRef]
- Chen, G.; Xu, Y.; Wang, Z.; Hu, H.; Wu, C. Motion stability analysis of beaver-like robot. Proc. Inst. Mech. Eng. Part M: J. Eng. Marit. Environ. 2025, 1–14. [Google Scholar] [CrossRef]
- Wang, H.; Yin, Q.; Song, Z.; Shang, J.; Luo, Z. Structure design of a novel self-adaptive climbing mechanism for the amphibious bionic robot. In 2020 Chinese Automation Congress (CAC); IEEE: Piscataway, NJ, USA, 2020; pp. 3519–3522. [Google Scholar] [CrossRef]
- Wang, C.; Liu, H.; Zhang, X.; Huang, C.; Chen, Q. Design and Simulation Analysis of Semi-Active Lifting and Sinking Compensation System. Acad. J. Sci. Technol. 2023, 5, 78–86. [Google Scholar] [CrossRef]
- da Cruz, A.L.; Vilela, B.; Klein, W. Morphological and physiological traits of the respiratory system in Iguana iguana and other non-avian reptiles. Zoology 2023, 157, 126079. [Google Scholar] [CrossRef]
- Groenhuis, V.; Rolff, G.; Bosman, K.; Abelmann, L.; Stramigioli, S. Multi-axis electric stepper motor. IEEE Robot. Autom. Lett. 2021, 6, 7201–7208. [Google Scholar] [CrossRef]
- Vo, C.D.; Dang, D.A.; Le, P.H. Development of multi-robotic arm system for sorting system using computer vision. J. Robot. Control. (JRC) 2022, 3, 690–698. [Google Scholar] [CrossRef]
- Zeng, X.; Zhang, S.; Zhang, H.; Li, X.; Zhou, H.; Fu, Y. Leg trajectory planning for quadruped robots with high-speed trot gait. Appl. Sci. 2019, 9, 1508. [Google Scholar] [CrossRef]
- Hao, Q.; Wang, Z.; Wang, J.; Chen, G. Stability-guaranteed and high terrain adaptability static gait for quadruped robots. Sensors 2020, 20, 4911. [Google Scholar] [CrossRef]
- Yi, S. Reliable gait planning and control for miniaturized quadruped robot pet. Mechatronics 2010, 20, 485–495. [Google Scholar] [CrossRef]
- Sun, P.; Gu, Y.; Mao, H.; Chen, Z.; Li, Y. Research on walking gait planning and simulation of a novel hybrid biped robot. Biomimetics 2023, 8, 258. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.P.; San, H.J.; Wu, X.; Xiong, B.Z. Structural design and gait research of a new bionic quadruped robot. Proc. Inst. Mech. Eng. Part B: J. Eng. Manuf. 2022, 236, 1912–1922. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, C.; Li, B.; Zheng, H. Motion planning of a dual manipulator system for table tennis. In Proceedings of the 12th International Conference IAS-12: Intelligent Autonomous Systems 12, Jeju Island, Republic of Korea, 26–29 June 2012; Springer: Berlin/Heidelberg, Germany, 2013; Volume 2, pp. 335–344. [Google Scholar] [CrossRef]
- Wang, Z.; Peng, W.; Zhang, B. Kinematics Analysis and Gait Study of Bionic Turtle Crawling Mechanism. Biomimetics 2024, 9, 147. [Google Scholar] [CrossRef] [PubMed]
- Yuan, S.D.; Zhou, Y.J.; Luo, C. Crawling Gait Planning Based on Foot Trajectory Optimization for Quadruped Robot. In Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 4–7 August 2019. [Google Scholar] [CrossRef]
- Yuan, S.; Zhou, Y.; Luo, C. Crawling gait planning based on foot trajectory optimization for quadruped robot. IEEE/ASME Trans. Mechatronics 2016, 21, 1711–1719. [Google Scholar] [CrossRef]
- Li, Z.; Chao, X.; Hameed, I.; Li, J.; Zhao, W.; Jing, X. Biomimetic omnidirectional multi-tail underwater robot. Mech. Syst. Signal Process. 2022, 173, 109056. [Google Scholar] [CrossRef]
- Chen, G.; Xu, Y.; Yang, C.; Yang, X.; Hu, H.; Dong, F.; Zhang, J.; Shi, J. Dynamic modeling and experimental analysis of a novel bionic mantis shrimp robot. J. Field Robot. 2025, 42, 493–509. [Google Scholar] [CrossRef]
- Di Santo, V.; Goerig, E.; Wainwright, D.K.; Akanyeti, O.; Liao, J.C.; Castro-Santos, T.; Lauder, G.V. Convergence of undulatory swimming kinematics across a diversity of fishes. Proc. Natl. Acad. Sci. USA 2021, 118, e2113206118. [Google Scholar] [CrossRef]













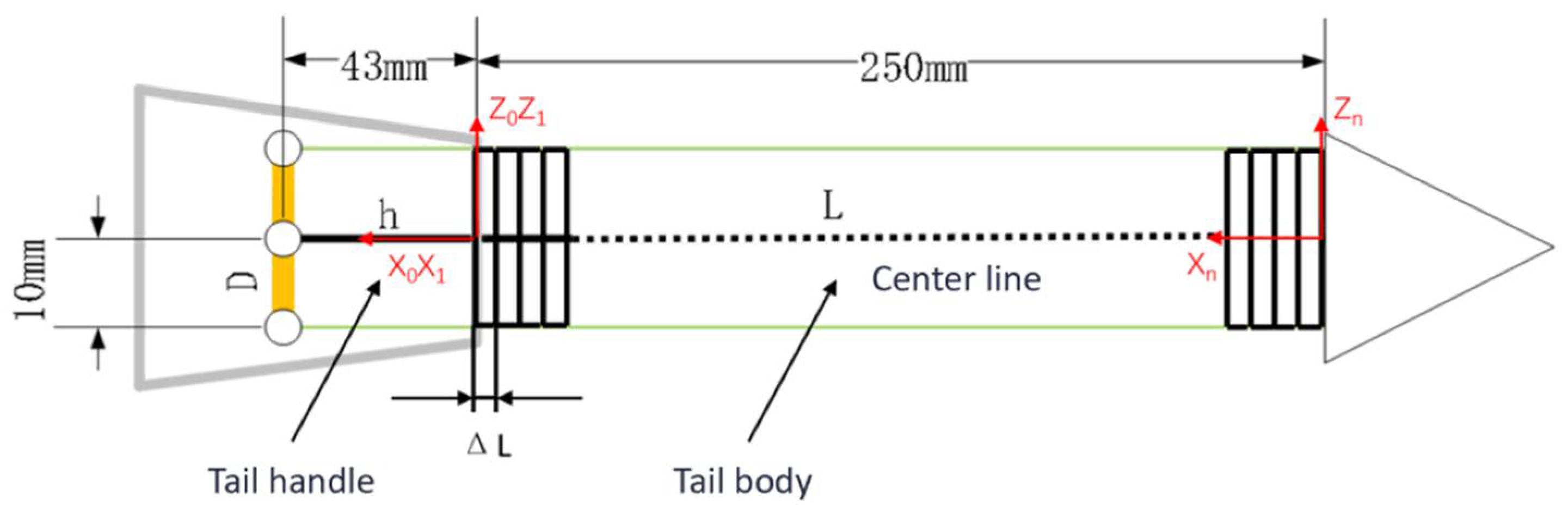
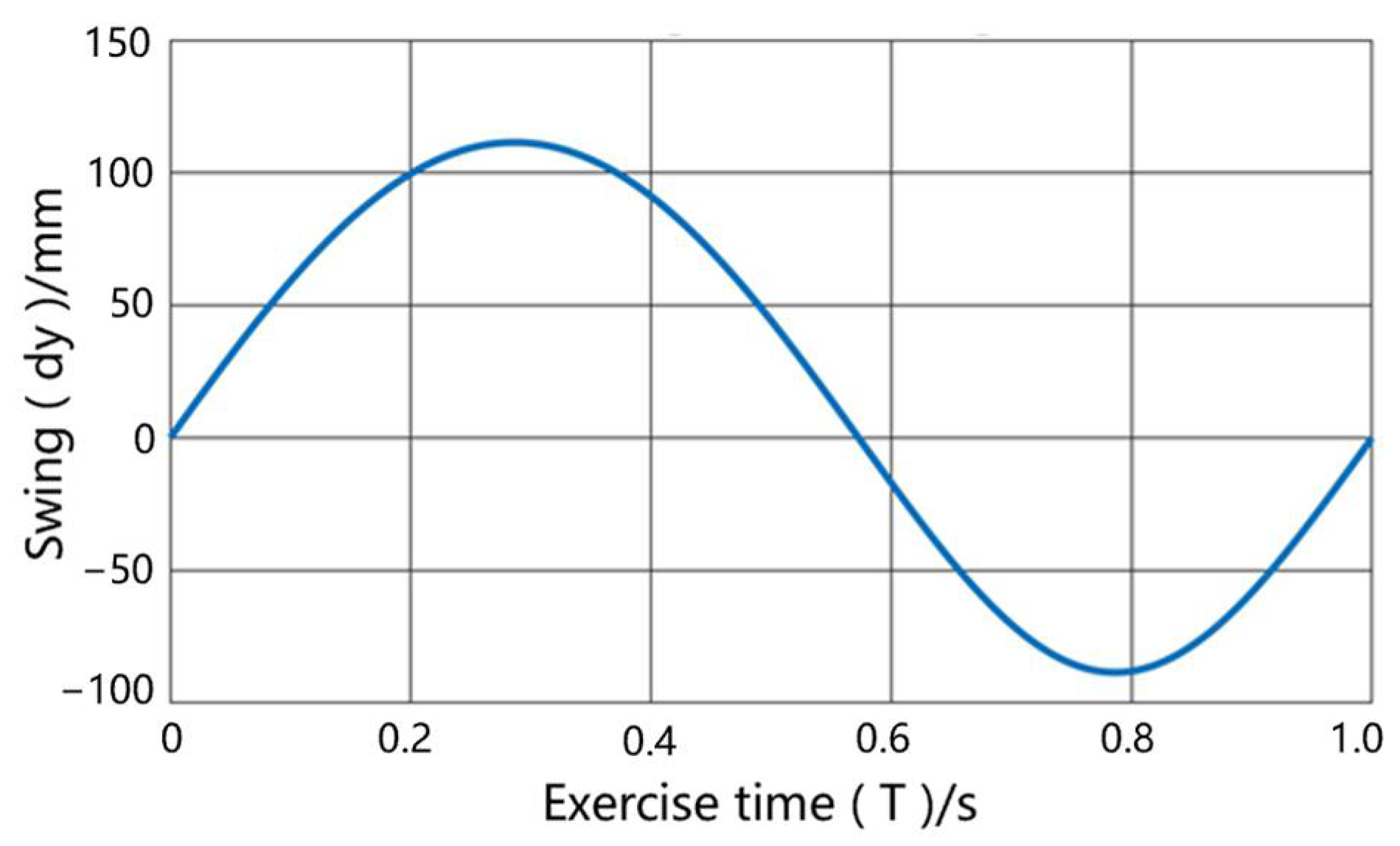

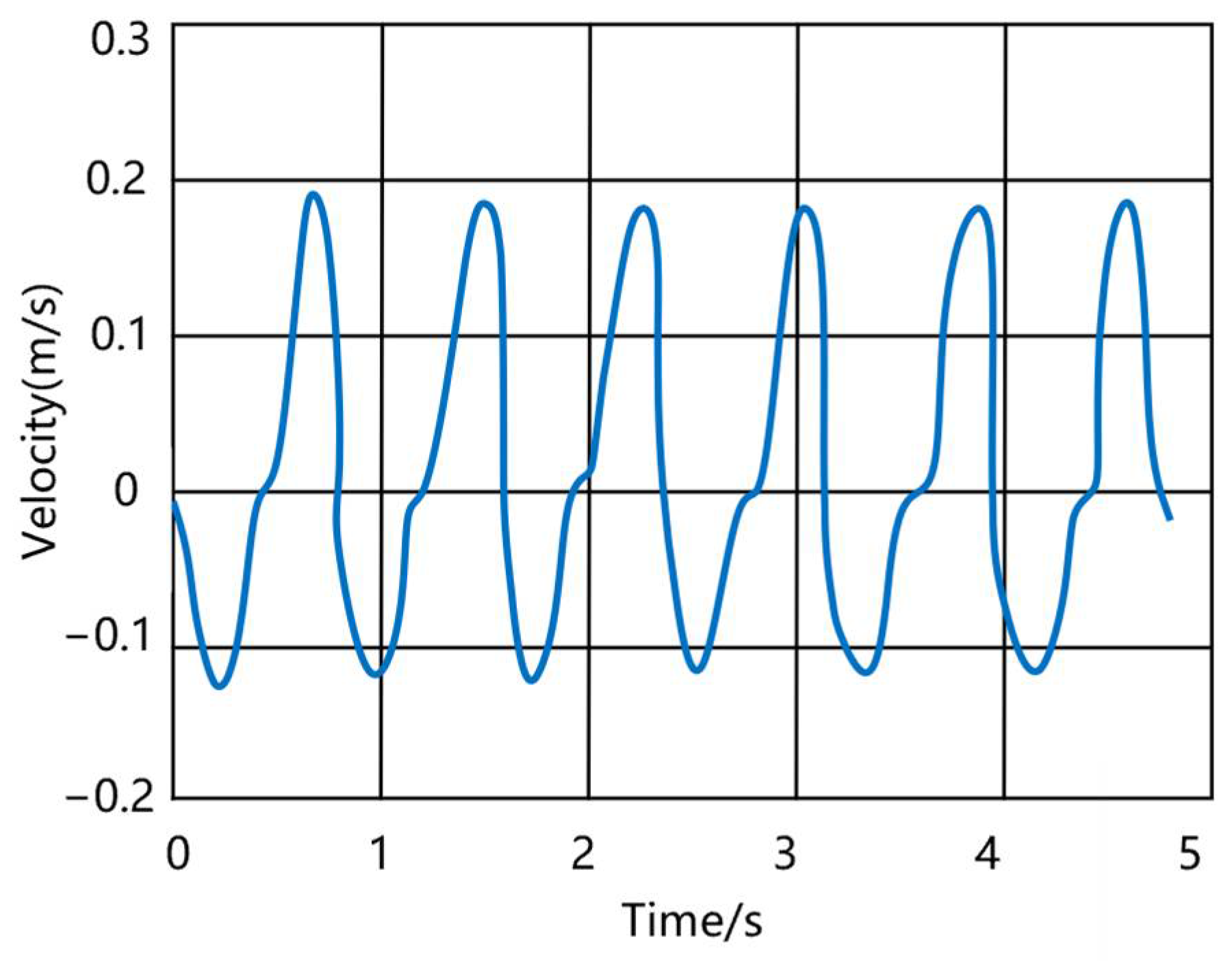





| Marine Iguana Robot Appearance Parameters | Quality (kg) | Maximum Length (m) | Maximum Width (m) | Maximum Height (m) | |
|---|---|---|---|---|---|
| 3.310 | 0.0031 | 0.830 | 0.320 | 0.281 |
| Actuator Type | Model | Waterproof Rating | Torque | Weight (g) | Power (W) | Unit Price (USD) |
|---|---|---|---|---|---|---|
| Joint Drive Servo | TD-9420MG | IP67 | 20 | 94 | 2.4 (6 V) | 11.2 |
| Alternative Option 1 | MG996R | IP54 | 15 | 55 | 1.8 (6 V) | 4.2 |
| Alternative Option 2 | Hiwonder | IP68 | 30 | 180 | 3.6 (12 V) | 21.1 |
| CG Adjustment Motor | 42-series Stepper Motor | IP66 | 4 | 280 | 10.2 (6 V) | 7.0 |
| Alternative Option | NEMA 17 Servo Motor | IP65 | 3 | 320 | 14.4 (12 V) | 16.9 |
| i | The Range of Values of Joint Variables | ||||
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0~180 | |
| 2 | 90 | 0 | 0~270 | ||
| 3 | 0 | 0 | 0 | -- |
| Parameter | Theoretical | Experimental | Absolute Error | RMSE | R2 | Primary Error Sources |
|---|---|---|---|---|---|---|
| Tail Max Thrust (N) | 4.21 | 3.954 | 0.256 | 0.18 | 0.92 | Unmodeled vortex shedding |
| Avg. Speed (m/s) | 0.22 | 0.196 | 0.024 | 0.03 | 0.88 | 12% mechanical efficiency loss |
| Undulation Freq. (Hz) | 1.5 | 1.2 | 0.3 | 0.25 | 0.85 | Elastic deformation of nylon cords |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Tang, X.; Guo, B.; Li, G.; Wu, Z.; Huang, W.; Xu, Y.; Lu, M.; Liang, J.; Liu, Z. Design and Implementation of a Bionic Marine Iguana Robot for Military Micro-Sensor Deployment. Machines 2025, 13, 505. https://doi.org/10.3390/machines13060505
Chen G, Tang X, Guo B, Li G, Wu Z, Huang W, Xu Y, Lu M, Liang J, Liu Z. Design and Implementation of a Bionic Marine Iguana Robot for Military Micro-Sensor Deployment. Machines. 2025; 13(6):505. https://doi.org/10.3390/machines13060505
Chicago/Turabian StyleChen, Gang, Xin Tang, Baohang Guo, Guoqi Li, Zhengrui Wu, Weizhe Huang, Yidong Xu, Ming Lu, Jianfei Liang, and Zhen Liu. 2025. "Design and Implementation of a Bionic Marine Iguana Robot for Military Micro-Sensor Deployment" Machines 13, no. 6: 505. https://doi.org/10.3390/machines13060505
APA StyleChen, G., Tang, X., Guo, B., Li, G., Wu, Z., Huang, W., Xu, Y., Lu, M., Liang, J., & Liu, Z. (2025). Design and Implementation of a Bionic Marine Iguana Robot for Military Micro-Sensor Deployment. Machines, 13(6), 505. https://doi.org/10.3390/machines13060505







