Multi-Agent Reinforcement Learning Tracking Control of a Bionic Wheel-Legged Quadruped
Abstract
1. Introduction
- We propose a novel multi-agent RL framework to learn the low-level dynamics of a wheeled quadruped robot and control it by the generated model.
- The framework addresses the issue of designing reward functions for MA-RL agents when no straightforward agent-specific feedback is available.
- We also propose to add expert input signals to guide agents’ policy (in training) for well-established quadruped static and locomotive gaits. Both reward function and expert signals are implemented using a motion guidance optimizer.
- We have trained four separate controllers for Pegasus, corresponding to the four motion modes of keeping and adjusting static pose, walking, trotting, and driving.
- Two variations of the trained model have been used to demonstrate the feasibility of the motion guidance signal. Finally, one of these trained models was deployed in the robot to demonstrate its real-world application with promising results.
2. Preliminary
2.1. Robot Structure and Modeling
2.2. RL Preliminary
2.2.1. Markov Games
2.2.2. Q-Learning
2.2.3. Policy Gradient (PG) Algorithms
2.2.4. Twin Delayed Deep Deterministic Policy Gradient (TD3)
2.2.5. Multi-Agent Deep Deterministic Policy Gradient (MADDPG)
2.2.6. MATD3
3. Motion Guidance
- .
- is the proportional gain.
- The configuration displacement maps the joint velocities
- .
- constraint matrix stacks and .
- constraint vector stacks and .
- is the lineraized approximation of Coulombic friction co-efficient.
- . Here, is the heightfield inclination input for the motion guidance.
3.1. Telescopic Vehicle Model
3.2. Motion Guidance Workflow
4. Procedural Framework
4.1. Observation and Action Space
4.2. Reward Function
- Torso
- Torso
- If a leg that is supposed to stay in stance loses contact.
- If the torso makes contact with the terrain.
- If there’s no movement for a locomotion task for time.
- If base height falls below
4.3. RL Environments
4.4. Training
5. Setup and Experiments
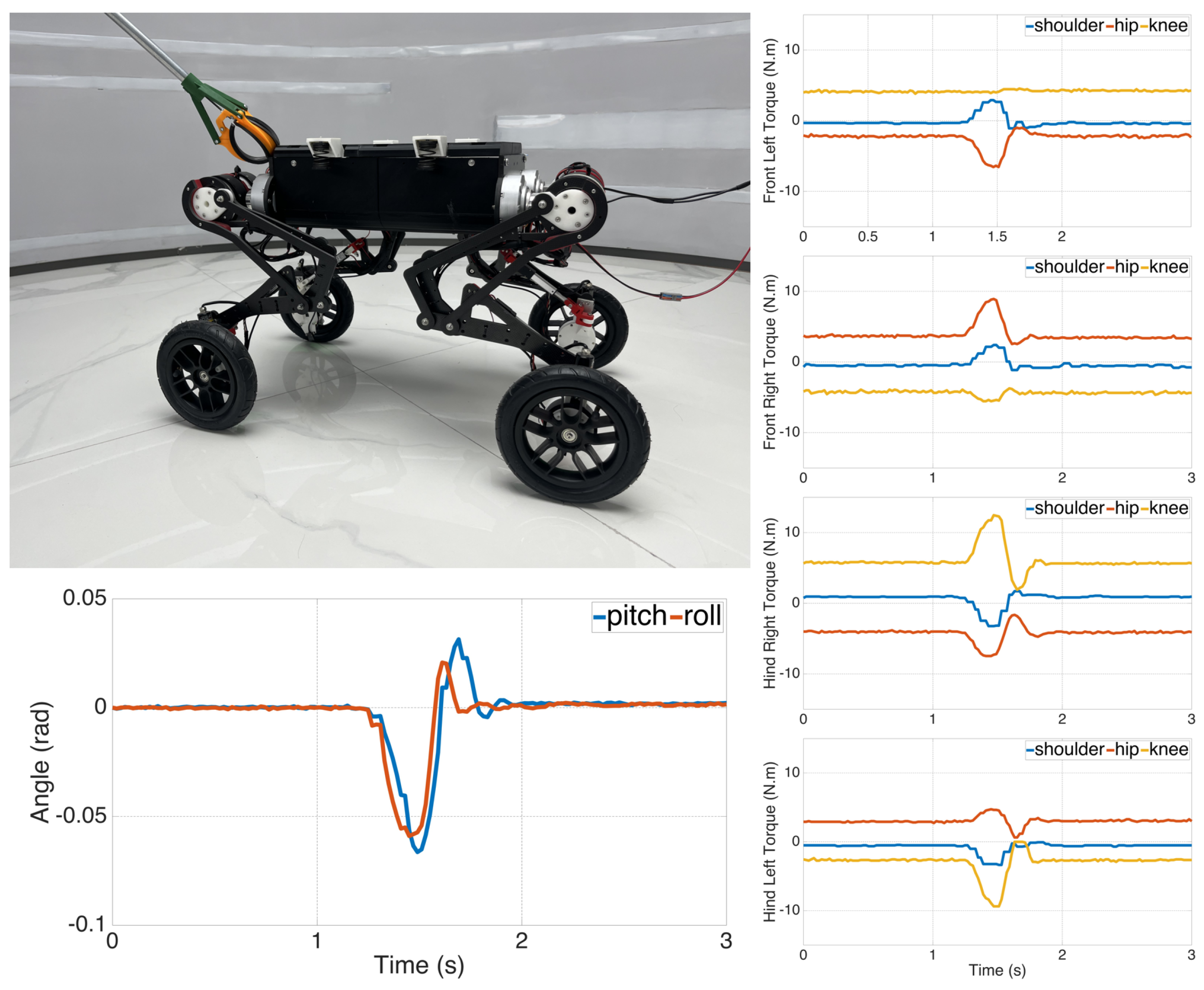
5.1. Real-World Experiments
5.1.1. Posture Balancing
5.1.2. Gait Test
5.1.3. Pure Driving Test
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vukobratović, M.; Borovac, B. Zero-moment point—Thirty five years of its life. Int. J. Humanoid Robot. 2004, 1, 157–173. [Google Scholar] [CrossRef]
- Kalakrishnan, M.; Buchli, J.; Pastor, P.; Mistry, M.; Schaal, S. Fast, robust quadruped locomotion over challenging terrain. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010. [Google Scholar] [CrossRef]
- Winkler, A.W.; Bellicoso, C.D.; Hutter, M.; Buchli, J. Gait and Trajectory Optimization for Legged Systems Through Phase-Based End-Effector Parameterization. IEEE Robot. Autom. Lett. 2018, 3, 1560–1567. [Google Scholar] [CrossRef]
- Jenelten, F.; Miki, T.; Vijayan, A.E.; Bjelonic, M.; Hutter, M. Perceptive Locomotion in Rough Terrain—Online Foothold Optimization. IEEE Robot. Autom. Lett. 2020, 5, 5370–5376. [Google Scholar] [CrossRef]
- Kim, D.; Carlo, J.D.; Katz, B.; Bledt, G.; Kim, S. Highly Dynamic Quadruped Locomotion via Whole-Body Impulse Control and Model Predictive Control. arXiv 2019, arXiv:1909.06586. [Google Scholar] [CrossRef]
- Bjelonic, M.; Sankar, P.K.; Bellicoso, C.D.; Vallery, H.; Hutter, M. Rolling in the Deep–Hybrid Locomotion for Wheeled-Legged Robots Using Online Trajectory Optimization. IEEE Robot. Autom. Lett. 2020, 5, 3626–3633. [Google Scholar] [CrossRef]
- Bjelonic, M.; Grandia, R.; Harley, O.; Galliard, C.; Zimmermann, S.; Hutter, M. Whole-Body MPC and Online Gait Sequence Generation for Wheeled-Legged Robots. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021. [Google Scholar] [CrossRef]
- Tan, J.; Zhang, T.; Coumans, E.; Iscen, A.; Bai, Y.; Hafner, D.; Bohez, S.; Vanhoucke, V. Sim-to-Real: Learning Agile Locomotion For Quadruped Robots. arXiv 2018, arXiv:1804.10332. [Google Scholar] [CrossRef]
- Lyu, S.; Lang, X.; Zhao, H.; Zhang, H.; Ding, P.; Wang, D. RL2AC: Reinforcement Learning-based Rapid Online Adaptive Control for Legged Robot Robust Locomotion. In Proceedings of the Robotics: Science and Systems 2024, Delft, The Netherlands, 15–19 July 2024. [Google Scholar] [CrossRef]
- Horak, P.; Trinkle, J.J. On the Similarities and Differences Among Contact Models in Robot Simulation. IEEE Robot. Autom. Lett. 2019, 4, 493–499. [Google Scholar] [CrossRef]
- Lee, J.; Hwangbo, J.; Wellhausen, L.; Koltun, V.; Hutter, M. Learning Quadrupedal Locomotion over Challenging Terrain. Sci. Robot. 2020, 5, eabc5986. [Google Scholar] [CrossRef] [PubMed]
- Kulkarni, P.; Kober, J.; Babuška, R.; Della Santina, C. Learning Assembly Tasks in a Few Minutes by Combining Impedance Control and Residual Recurrent Reinforcement Learning. Adv. Intell. Syst. 2022, 4, 2100095. [Google Scholar] [CrossRef]
- Tao, C.; Li, M.; Cao, F.; Gao, Z.; Zhang, Z. A Multiobjective Collaborative Deep Reinforcement Learning Algorithm for Jumping Optimization of Bipedal Robot. Adv. Intell. Syst. 2023, 6, 2300352. [Google Scholar] [CrossRef]
- Hwangbo, J.; Lee, J.; Dosovitskiy, A.; Bellicoso, D.; Tsounis, V.; Koltun, V.; Hutter, M. Learning agile and dynamic motor skills for legged robots. Sci. Robot. 2019, 4, eaau5872. [Google Scholar] [CrossRef] [PubMed]
- Rudin, N.; Hoeller, D.; Reist, P.; Hutter, M. Learning to Walk in Minutes Using Massively Parallel Deep Reinforcement Learning. In Proceedings of the 5th Conference on Robot Learning, London, UK, 8–11 November 2021. [Google Scholar]
- Margolis, G.; Agrawal, P. Walk These Ways: Tuning Robot Control for Generalization with Multiplicity of Behavior. In Proceedings of the 6th Conference on Robot Learning, Auckland, New Zealand, 14–18 December 2022. [Google Scholar]
- Jenelten, F.; He, J.; Farshidian, F.; Hutter, M. DTC: Deep Tracking Control. Sci. Robot. 2024, 9, eadh5401. [Google Scholar] [CrossRef] [PubMed]
- Melon, O.; Geisert, M.; Surovik, D.; Havoutis, I.; Fallon, M.F. Reliable Trajectories for Dynamic Quadrupeds using Analytical Costs and Learned Initializations. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020. [Google Scholar]
- Surovik, D.; Melon, O.; Geisert, M.; Fallon, M.; Havoutis, I. Learning an Expert Skill-Space for Replanning Dynamic Quadruped Locomotion over Obstacles. In Proceedings of the 2020 Conference on Robot Learning, Virtual, 16–18 November 2020; Kober, J., Ramos, F., Tomlin, C., Eds.; PMLR: Proceedings of Machine Learning Research. Volume 155, pp. 1509–1518. [Google Scholar]
- Melon, O.; Orsolino, R.; Surovik, D.; Geisert, M.; Havoutis, I.; Fallon, M.F. Receding-Horizon Perceptive Trajectory Optimization for Dynamic Legged Locomotion with Learned Initialization. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021. [Google Scholar]
- Brakel, P.; Bohez, S.; Hasenclever, L.; Heess, N.; Bousmalis, K. Learning Coordinated Terrain-Adaptive Locomotion by Imitating a Centroidal Dynamics Planner. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022. [Google Scholar]
- Bogdanovic, M.; Khadiv, M.; Righetti, L. Model-free Reinforcement Learning for Robust Locomotion Using Trajectory Optimization for Exploration. arXiv 2021, arXiv:2107.06629. [Google Scholar] [CrossRef]
- Gangapurwala, S.; Geisert, M.; Orsolino, R.; Fallon, M.F.; Havoutis, I. RLOC: Terrain-Aware Legged Locomotion using Reinforcement Learning and Optimal Control. IEEE Trans. Robot. 2022, 38, 2908–2927. [Google Scholar] [CrossRef]
- Tsounis, V.; Alge, M.; Lee, J.; Farshidian, F.; Hutter, M. DeepGait: Planning and Control of Quadrupedal Gaits using Deep Reinforcement Learning. IEEE Robot. Autom. Lett. 2020, 5, 3699–3706. [Google Scholar] [CrossRef]
- Xie, Z.; Da, X.; Babich, B.; Garg, A.; van de Panne, M. GLiDE: Generalizable Quadrupedal Locomotion in Diverse Environments with a Centroidal Model. In Proceedings of the Fifteenth Workshop on the Algorithmic Foundations of Robotics, College Park, MD, USA, 22–24 June 2022. [Google Scholar]
- Wu, J.; Xin, G.; Qi, C.; Xue, Y. Learning Robust and Agile Legged Locomotion Using Adversarial Motion Priors. IEEE Robot. Autom. Lett. 2023, 8, 4975–4982. [Google Scholar] [CrossRef]
- Cui, L.; Wang, S.; Zhang, J.; Zhang, D.; Lai, J.; Zheng, Y.; Zhang, Z.; Jiang, Z.P. Learning-Based Balance Control of Wheel-Legged Robots. IEEE Robot. Autom. Lett. 2021, 6, 7667–7674. [Google Scholar] [CrossRef]
- Lee, J.; Bjelonic, M.; Hutter, M. Control of Wheeled-Legged Quadrupeds Using Deep Reinforcement Learning. In Robotics in Natural Settings, Proceedings of the Climbing and Walking Robots Conference, Ponta Delgada, Portugal, 12–14 September 2022; Springer: Cham, Switzerland, 2022; pp. 119–127. [Google Scholar]
- Pan, Y.; Khan, R.A.I.; Zhang, C.; Zhang, A.; Shang, H. Pegasus: A Novel Bio-inspired Quadruped Robot with Underactuated Wheeled-Legged Mechanism. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 1464–1469. [Google Scholar] [CrossRef]
- Rezwan Al Islam, K.; Chenyun, Z.; Yuzhen, P.; Anzheng, Z.; Ruijiao, L.; Xuan, Z.; Huiliang, S. Hierarchical optimum control of a novel wheel-legged quadruped. Robot. Auton. Syst. 2024, 180, 104775. [Google Scholar] [CrossRef]
- Littman, M.L. Markov games as a framework for multi-agent reinforcement learning. In Proceedings of the Eleventh International Conference on International Conference on Machine Learning, ICML’94, New Brunswick, NJ, USA, 10–13 July 1994; pp. 157–163. [Google Scholar]
- Watkins, C.J.C.H. Learning from Delayed Rewards. Ph.D. Thesis, King’s College, Oxford, UK, 1989. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Hasselt, H. Double Q-learning. In Proceedings of the Advances in Neural Information Processing Systems 23: 24th Annual Conference on Neural Information Processing Systems 2010, Vancouver, BC, Canada, 6–9 December 2010; Volume 23. [Google Scholar]
- Sutton, R.S.; McAllester, D.; Singh, S.; Mansour, Y. Policy Gradient Methods for Reinforcement Learning with Function Approximation. In Proceedings of the Advances in Neural Information Processing Systems 12, NIPS Conference, Denver, CO, USA, 29 November–4 December 1999; Volume 12. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016, San Juan, Puerto Rico, 2–4 May 2016. Conference Track Proceedings. [Google Scholar]
- Fujimoto, S.; van Hoof, H.; Meger, D. Addressing Function Approximation Error in Actor-Critic Methods. In Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholmsmässan, Stockholm, Sweden, 10–15 July 2018; Dy, J.G., Krause, A., Eds.; PMLR: Proceedings of Machine Learning Research. Volume 80, pp. 1582–1591. [Google Scholar]
- Lowe, R.; Wu, Y.; Tamar, A.; Harb, J.; Abbeel, P.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. In Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17, Long Beach, CA, USA, 4–9 December 2017; pp. 6382–6393. [Google Scholar]
- Ackermann, J.; Gabler, V.; Osa, T.; Sugiyama, M. Reducing Overestimation Bias in Multi-Agent Domains Using Double Centralized Critics. arXiv 2019, arXiv:1910.01465. [Google Scholar] [CrossRef]
- Zhang, F.; Li, J.; Li, Z. A TD3-based multi-agent deep reinforcement learning method in mixed cooperation-competition environment. Neurocomputing 2020, 411, 206–215. [Google Scholar] [CrossRef]
- Pomax. A Primer on Bézier Curves. 2021–2024. Available online: https://pomax.github.io/bezierinfo/ (accessed on 22 November 2024).
- Miki, T.; Lee, J.; Hwangbo, J.; Wellhausen, L.; Koltun, V.; Hutter, M. Learning robust perceptive locomotion for quadrupedal robots in the wild. Sci. Robot. 2022, 7, eabk2822. [Google Scholar] [CrossRef] [PubMed]
- Coumans, E.; Bai, Y. PyBullet, a Python Module for Physics Simulation for Games, Robotics and Machine Learning. 2016–2021. Available online: http://pybullet.org (accessed on 25 October 2024).
- MathWorks. Identifying State-Space Models with Separate Process and Measurement Noise Descriptions. 2024. Available online: https://www.mathworks.com/help/ident/ug/identifying-state-space-models-with-independent-process-and-measurement-noise.html (accessed on 22 November 2024).
- Nvidia. Jetson Orin. 2024. Available online: https://www.nvidia.com/en-us/autonomous-machines/embedded-systems/jetson-orin/ (accessed on 25 October 2024).
- Unitree a1 Motor. Available online: https://shop.unitree.com/products/unitree-a1-motor (accessed on 25 February 2024).
- LK MG6010 Geared Motor. Available online: http://shop.smc-powers.com/MG6010-CAN-D.html (accessed on 25 February 2024).
- STM32F446 Resource. Available online: https://www.st.com/en/microcontrollers-microprocessors/stm32f446.html (accessed on 25 February 2024).
- Saber C4 Resource. Available online: http://www.atom-robotics.com/PC-EN/productC4.html (accessed on 25 February 2024).
- BRT25 Product Catalog. Available online: https://briterencoder.com/wp-content/uploads/2021/12/BriterEncoder-Product-Catalogue-V2.3.pdf (accessed on 25 February 2024).
- Busoniu, L.; Babuska, R.; Schutter, B.D. Multi-Agent Reinforcement Learning: An Overview; Technical Report; Delft University of Technology: Delft, The Netherlands, 2010. [Google Scholar]
- Albrecht, S.V.; Christianos, F.; Schäfer, L. Multi-Agent Reinforcement Learning: Foundations and Modern Approaches; MIT Press: Cambridge, MA, USA, 2024. [Google Scholar]
- Sebastian, E.; Duong, T.; Atanasov, N.; Montijano, E.; Sagues, C. Physics-Informed Multi-Agent Reinforcement Learning for Distributed Multi-Robot Problems. arXiv 2024, arXiv:2401.00212. [Google Scholar] [CrossRef]
- Perrusquía, A.; Yu, W.; Li, X. Redundant Robot Control Using Multi Agent Reinforcement Learning. In Proceedings of the 2020 IEEE 16th International Conference on Automation Science and Engineering (CASE), Hong Kong, China, 20–21 August 2020; pp. 1650–1655. [Google Scholar] [CrossRef]
- Brandão, B.; De Lima, T.W.; Soares, A.; Melo, L.; Maximo, M.R.O.A. Multiagent Reinforcement Learning for Strategic Decision Making and Control in Robotic Soccer Through Self-Play. IEEE Access 2022, 10, 72628–72642. [Google Scholar] [CrossRef]
- Orr, J.; Dutta, A. Multi-Agent Deep Reinforcement Learning for Multi-Robot Applications: A Survey. Sensors 2023, 23, 3625. [Google Scholar] [CrossRef]
- Yu, C.; Yang, X.; Gao, J.; Chen, J.; Li, Y.; Liu, J.; Xiang, Y.; Huang, R.; Yang, H.; Wu, Y.; et al. Asynchronous Multi-Agent Reinforcement Learning for Efficient Real-Time Multi-Robot Cooperative Exploration. arXiv 2023, arXiv:2301.03398. [Google Scholar] [CrossRef]










| Leg State | Gaits | Frame Projection in | ||
|---|---|---|---|---|
| x ‖ | y ⊥ | z n | ||
| Stance | Walk/Trot/ Static (mode 1) | 0 | 0 | 0 |
| Drive mode/ Static (mode 2) | 0 | 0 | ||
| Swing | Walk/Trot | order Bézier curve | ||
| Environment | Velocity | Distance | |
|---|---|---|---|
| Pose | 0 | rpy = , , | 0 |
| Walk | cm/s | ||
| Trot | cm/s | Optimized by motion guidance | 2–100 m |
| Drive | m/s |
| Component | Device Model | Parameter | Value |
|---|---|---|---|
| Joint Motor | Unitree A1 [46] | m | 20 kg |
| Wheel Motor | LK MG6010 [47] | 0.749 kg·m2 | |
| Linear Actuator | YiXing 50 mm stroke, 12VDC | 0.419 kg·m2 | |
| Onboard Computer | Jetson Orin NX [45] | 1.035 kg·m2 | |
| Microcontroller | STM32F446 [48] | 0.25 m | |
| IMU | Saber C4 [49] | 0.2 m | |
| Angle Sensor | BRT25-1024 [50] | 0.105 m | |
| Battery | Lithium 10AH | g | 9.81 m/s2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, R.A.I.; Zhang, C.; Deng, Z.; Zhang, A.; Pan, Y.; Zhao, X.; Shang, H.; Li, R. Multi-Agent Reinforcement Learning Tracking Control of a Bionic Wheel-Legged Quadruped. Machines 2024, 12, 902. https://doi.org/10.3390/machines12120902
Khan RAI, Zhang C, Deng Z, Zhang A, Pan Y, Zhao X, Shang H, Li R. Multi-Agent Reinforcement Learning Tracking Control of a Bionic Wheel-Legged Quadruped. Machines. 2024; 12(12):902. https://doi.org/10.3390/machines12120902
Chicago/Turabian StyleKhan, Rezwan Al Islam, Chenyun Zhang, Zhongxiao Deng, Anzheng Zhang, Yuzhen Pan, Xuan Zhao, Huiliang Shang, and Ruijiao Li. 2024. "Multi-Agent Reinforcement Learning Tracking Control of a Bionic Wheel-Legged Quadruped" Machines 12, no. 12: 902. https://doi.org/10.3390/machines12120902
APA StyleKhan, R. A. I., Zhang, C., Deng, Z., Zhang, A., Pan, Y., Zhao, X., Shang, H., & Li, R. (2024). Multi-Agent Reinforcement Learning Tracking Control of a Bionic Wheel-Legged Quadruped. Machines, 12(12), 902. https://doi.org/10.3390/machines12120902






