Contour Error Control for a Hybrid Robot Equipped with Grating Sensors
Abstract
1. Introduction
2. Prediction of Contour Error
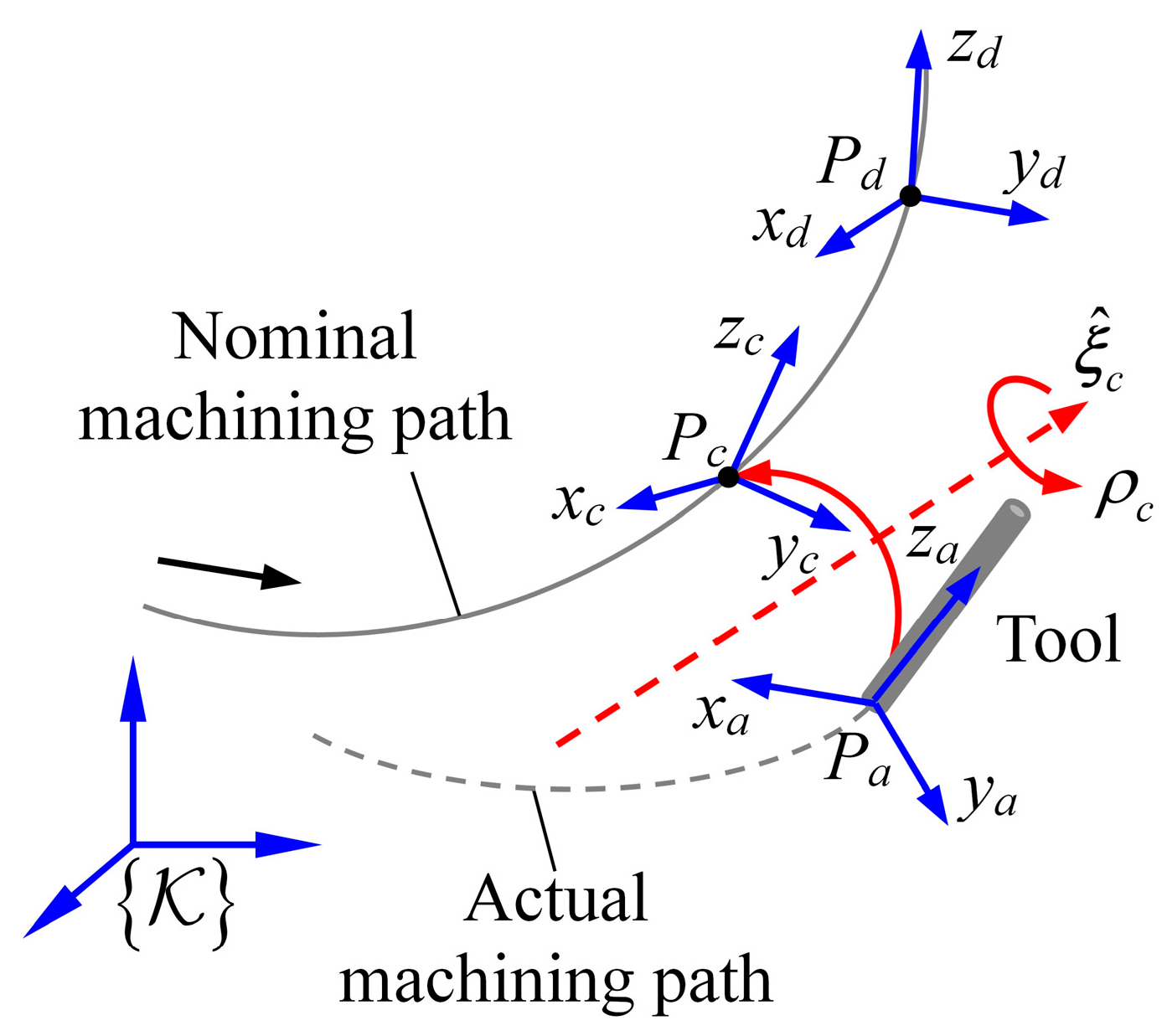
2.1. Definition of Contour Error
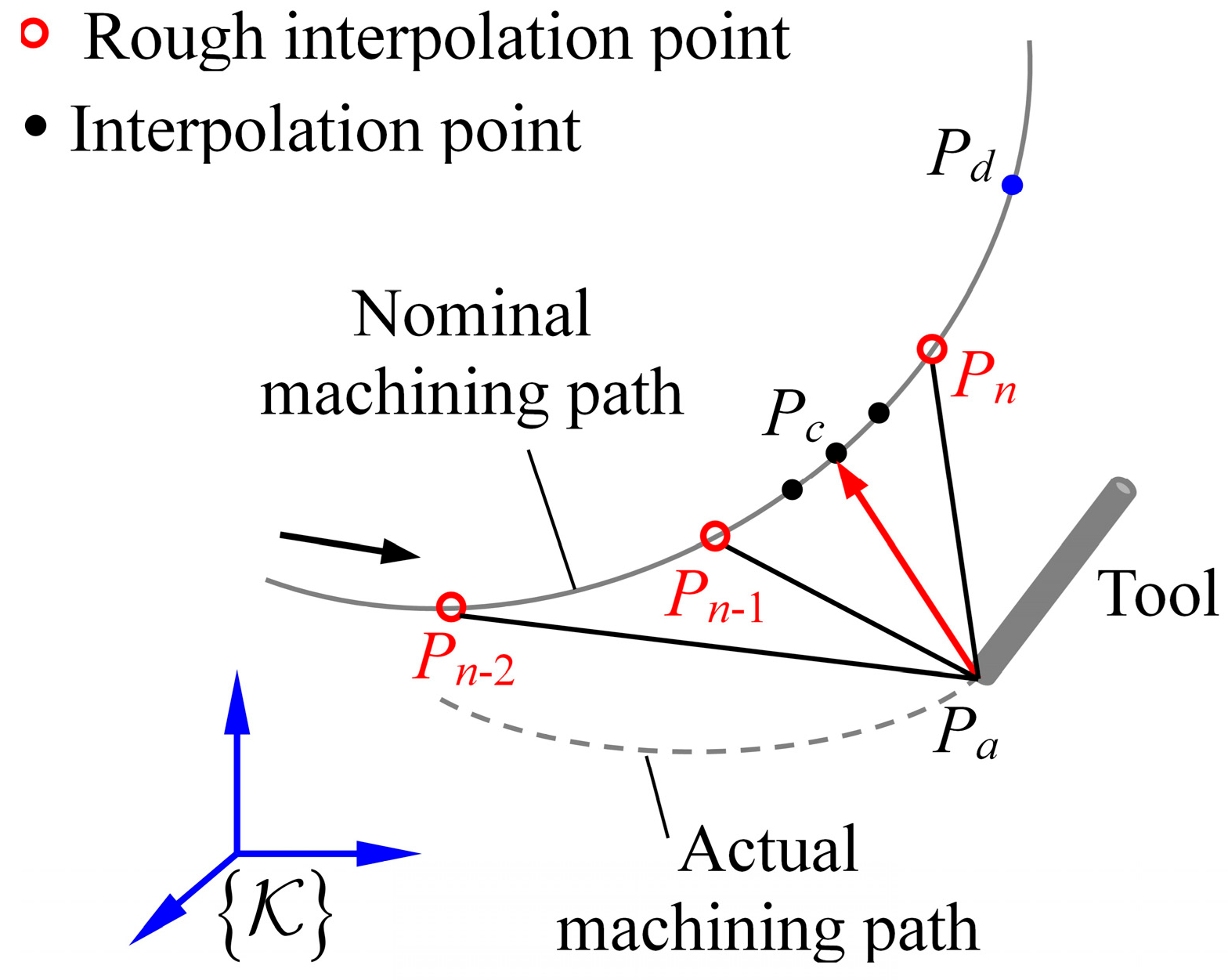
2.2. Modeling of Contour Error
3. Control Strategy of Contour Error
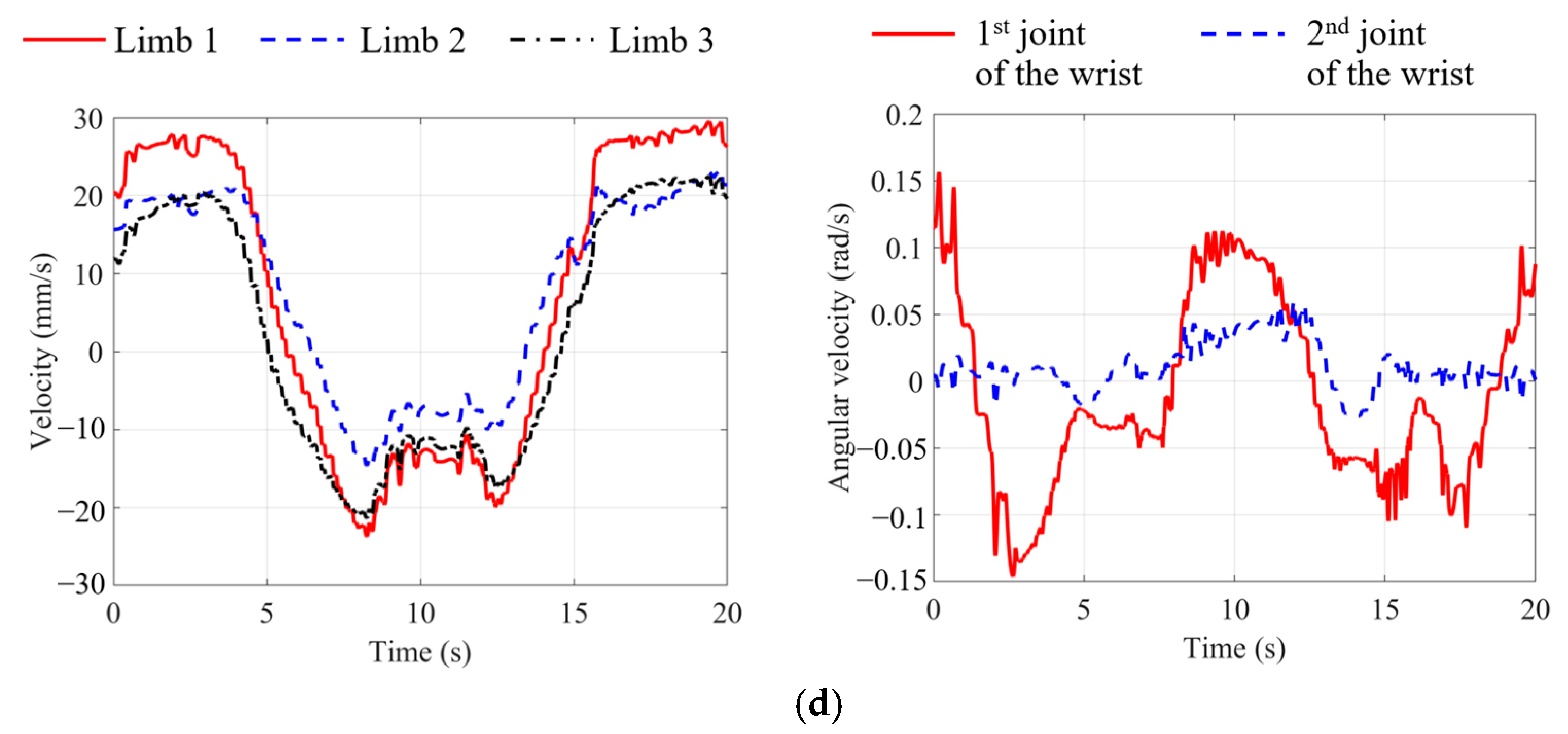
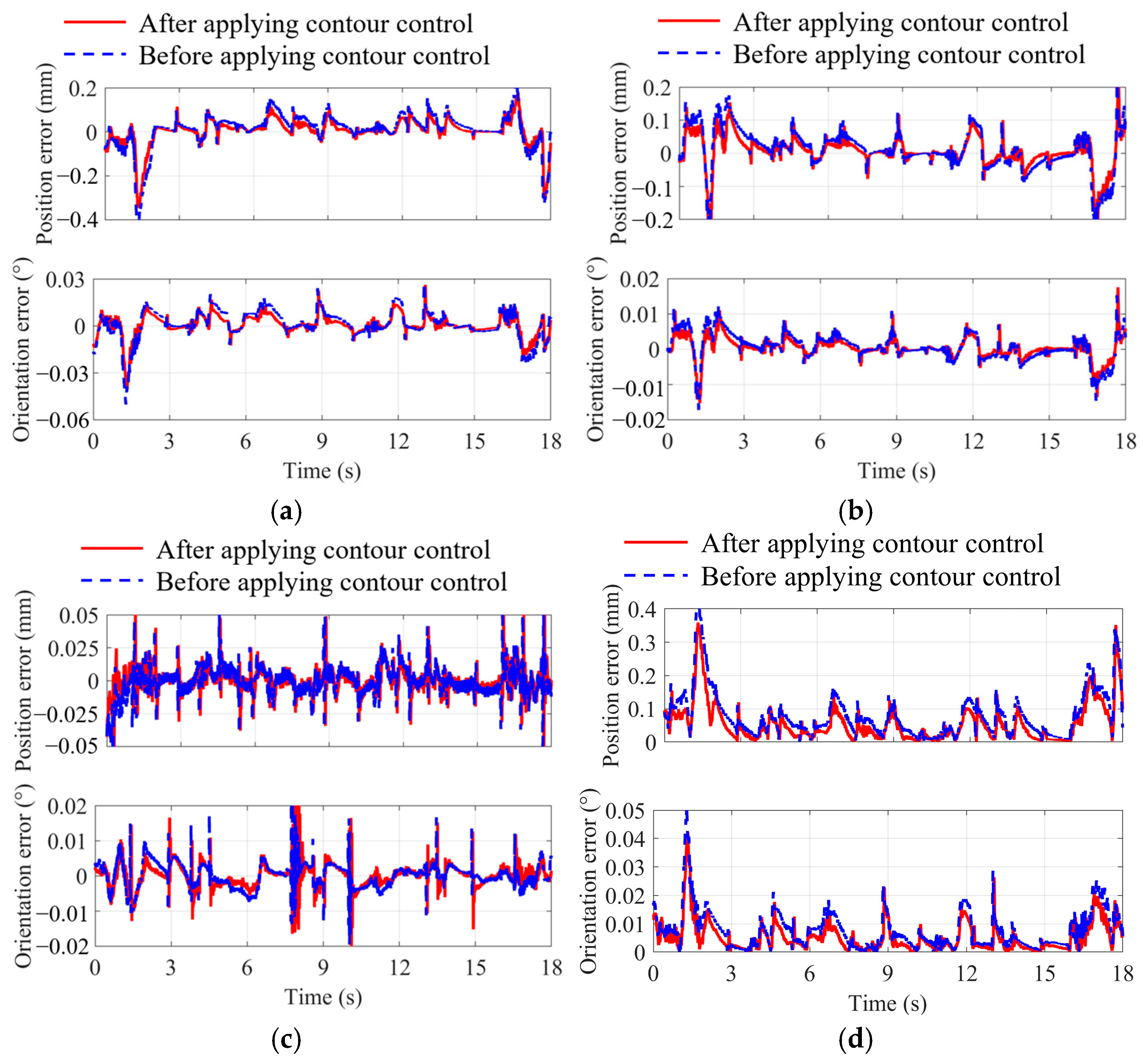
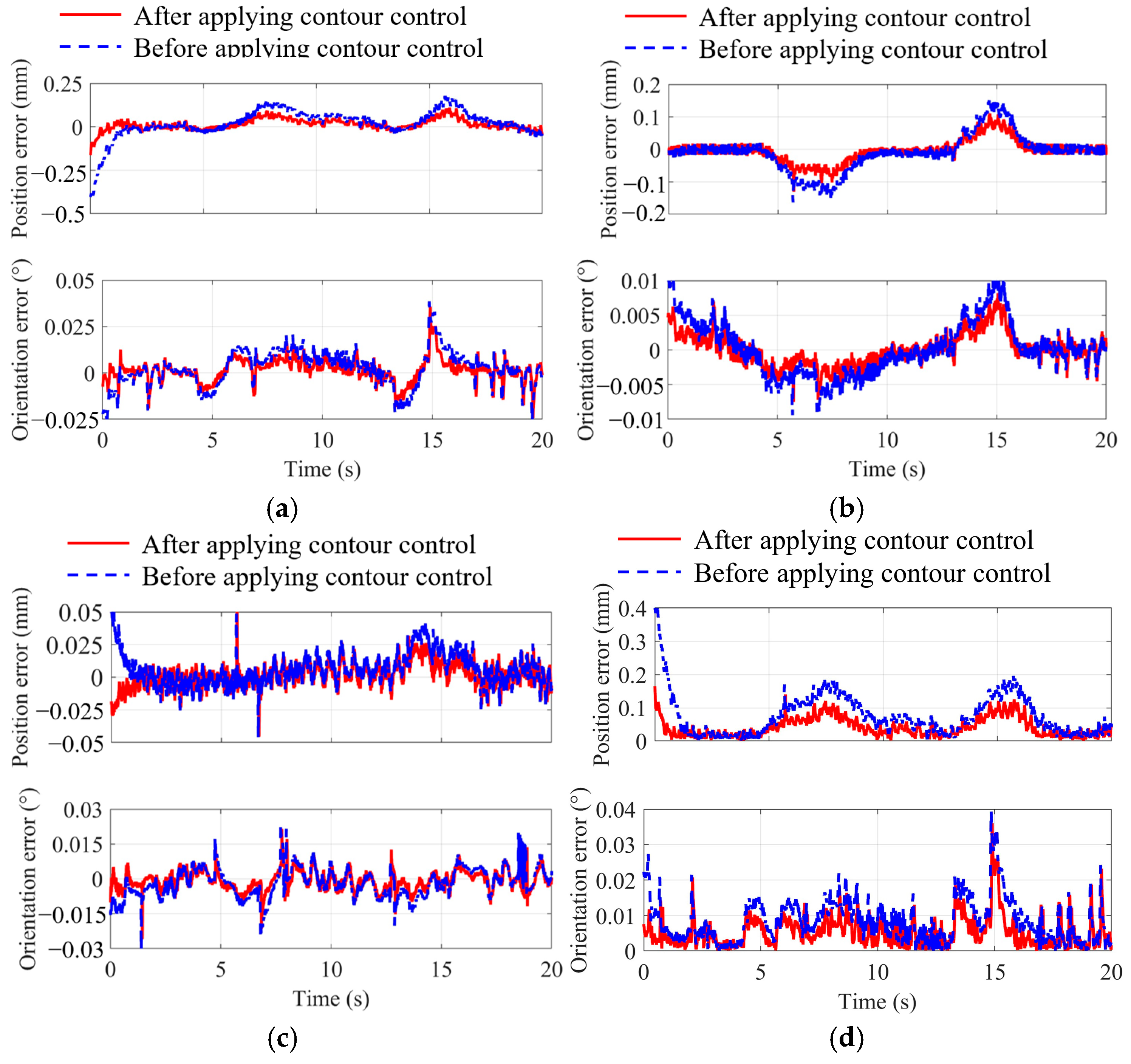
4. Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yue, W.; Liu, H.T.; Huang, T. An approach for predicting stiffness of a 5-dof hybrid robot for friction stir welding. Mech. Mach. Theory 2022, 175, 104941. [Google Scholar] [CrossRef]
- Dong, C.L.; Liu, H.T.; Huang, T.; Chetwynd, D.G. A screw theory-based semi-analytical approach for elastodynamics of the tricept robot. J. Mech. Robot. 2019, 11, 031005. [Google Scholar] [CrossRef]
- Aydin, M. Real-time sliding mode and moving sliding mode control of 3-dof linear parallel robot. Machines 2025, 13, 190. [Google Scholar] [CrossRef]
- Guechi, E.; Bouzoualegh, S.; Zennir, Y.; Blazic, S. MPC control and LQ optimal control of a two-link robot arm: A comparative study. Machines 2018, 6, 37. [Google Scholar] [CrossRef]
- Xiao, Q.B.; Wan, M.; Yang, Y.; Zhang, W.H. Pre-compensation of contour errors for five-axis machine tools through constructing a model reference adaptive control. Mech. Mach. Theory 2023, 187, 105258. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, C.X.; Zhu, Y.; Zhu, L.M. Prediction-model-based contouring error iterative precompensation scheme for precision multiaxis motion systems. IEEE-ASME Trans. Mechatron. 2021, 26, 2274–2284. [Google Scholar] [CrossRef]
- Zhao, H.; Li, X.F.; Ge, K.D.; Ding, H. A contour error definition, estimation approach and control structure for six-dimensional robotic machining tasks. Robot. Comput.-Int. Manuf. 2022, 73, 102235. [Google Scholar] [CrossRef]
- Jia, Z.Y.; Ma, J.W.; Song, D.N.; Wang, F.J.; Liu, W. A review of contouring-error reduction method in multi-axis CNC machining. Int. J. Mach. Tools Manuf. 2018, 125, 34–54. [Google Scholar] [CrossRef]
- Liu, Y.; Wan, M.; Xiao, Q.B.; Qin, X.B. Combined predictive and feedback contour error control with dynamic contour error estimation for industrial five-axis machine tools. IEEE Trans. Ind. Electron. 2022, 69, 6668–6677. [Google Scholar] [CrossRef]
- Li, J.A.; Yue, R.J.; Fei, Y.M. Five-axis contour error control based on numerical control data. Machines 2023, 11, 85. [Google Scholar] [CrossRef]
- Kim, S.H.; Min, B.K. Real-time tool path modification for machine tool contour error reduction. Int. J. Adv. Manuf. Technol. 2020, 120, 6969–6981. [Google Scholar] [CrossRef]
- Song, D.N.; Zhong, Y.G.; Ma, J.W. Third-order contour-error estimation for arbitrary free-form paths in contour-following tasks. Precis. Eng. 2019, 60, 85–92. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, C.X.; Zhu, Y. Double taylor expansion-based real-time contouring error estimation for multiaxis motion systems. IEEE Trans. Ind. Electron. 2019, 66, 9490–9499. [Google Scholar] [CrossRef]
- Yang, J.X.; Altintas, Y. A generalized on-line estimation and control of five-axis contouring errors of CNC machine tools. Int. J. Mach. Tools Manuf. 2015, 88, 9–23. [Google Scholar] [CrossRef]
- Li, X.F.; Zhao, H.; Zhao, X.; Ding, H. Interpolation-based contour error estimation and component-based contouring control for five-axis CNC machine tools. Sci. China Technol. Sci. 2018, 61, 1666–1678. [Google Scholar] [CrossRef]
- Yang, M.; Yang, J.X.; Ding, H. A high accuracy on-line estimation algorithm of five-axis contouring errors based on three-point arc approximation. Int. J. Mach. Tools Manuf. 2018, 130, 73–84. [Google Scholar] [CrossRef]
- Sencer, B.; Altintas, Y.; Croft, E. Modeling and control of contouring errors for five-axis machine tools-Part I: Modeling. J. Manuf. Sci. Eng. Trans. ASME 2009, 131, 031006. [Google Scholar] [CrossRef]
- Hu, C.X.; Yu, J.C.; Wang, Z.; Zhu, Y. An iterative contouring error compensation scheme for five-axis precision motion systems. Mech. Syst. Signal Process. 2022, 178, 109226. [Google Scholar] [CrossRef]
- Koren, Y. Cross-coupled biaxial computer control for manufacturing systems. J. Dyn. Sys. Meas. Control. ASME 1980, 102, 265–271. [Google Scholar] [CrossRef]
- Huo, F.; Poo, A.N. Improving contouring accuracy by using generalized cross-coupled control. Int. J. Mach. Tools Manuf. 2012, 63, 49–57. [Google Scholar] [CrossRef]
- Ouyang, P.R.; Dam, T.; Pano, V. Cross-coupled PID control in position domain for contour tracking. Robotica 2015, 33, 1351–1374. [Google Scholar] [CrossRef]
- Kang, Z.; Lin, W.Y.; Liu, Z.T.; Xu, R.Q. Accurate Contour Error Estimation-based robust contour control for dual-linear-motor-driven gantry stages. Mechatronics 2024, 100, 103174. [Google Scholar] [CrossRef]
- Hu, C.X.; Lin, S.Z.; Wang, Z.; Zhu, Y. Task space contouring error estimation and precision iterative control of robotic manipulators. IEEE Robot. Autom. Lett. 2022, 7, 7826–7833. [Google Scholar] [CrossRef]
- Chen, S.L.; Hsieh, S.M. Iterative learning contouring control: Theory and application to biaxial systems. Mechatronics 2023, 89, 102932. [Google Scholar] [CrossRef]
- Dai, J.; Wan, M.; Qin, X.B.; Zhang, W.H. A time-delay-based sliding mode controlling method for reducing contour errors of machine tools. J. Manuf. Process 2023, 106, 407–421. [Google Scholar] [CrossRef]
- Liu, Y.B.; Sun, W.C.; Buccella, C.; Cecati, C. Robust control of dual-linear-motor-driven gantry stage for coordinated contouring tasks based on feed velocity. IEEE Trans. Ind. Electron. 2023, 70, 6229–6238. [Google Scholar] [CrossRef]
- Sencer, B.; Altintas, Y. Modeling and control of contouring errors for five-axis machine tools-Part II: Precision contour controller design. J. Manuf. Sci. Eng. Trans. ASME 2009, 131, 031007. [Google Scholar] [CrossRef]
- Kornmaneesang, W.; Chen, S.L. MPC-based robust contouring control for a robotic machining system. Asian J. Control 2021, 23, 1212–1224. [Google Scholar] [CrossRef]
- Chen, S.L.; Hsieh, S.M.; Ta, T.Q. Iterative learning contouring control for five-axis machine tools and industrial robots. Mechatronics 2023, 94, 103030. [Google Scholar] [CrossRef]
- Kim, S.H. Feedforward compensation of contour errors in robotic machining system using compliance model. J. Manuf. Process 2023, 89, 142–149. [Google Scholar] [CrossRef]
- Kevin, M.L.; Frank, C.P. Modern Robotics-Mechanics, Planning, and Control; Cambridge University Press: Cambridge, UK, 2017; pp. 59–109. [Google Scholar]
- Featherstone, R. Rigid Body Dynamics Algorithms; Springer: Berlin/Heidelberg, Germany, 2008; pp. 7–87. [Google Scholar]
- Erkorkmaz, K.; Altintas, Y. High speed contouring control algorithm for CNC machine tools. In Proceedings of the ASME, IMECE98, Anaheim, CA, USA, 15–20 November 1998; pp. 463–469. [Google Scholar]
- Liu, H.T.; Yuan, H.; Shan, X.L.; Han, J.L.; Xiao, J.L. A grating sensor feedback-based dynamic accuracy control strategy of hybrid Robot. Aeronaut. Manuf. Technol. 2023, 66, 40–45. [Google Scholar]





| a | bx | by | e | dw | dv |
|---|---|---|---|---|---|
| 75 | 167 | 294.1 | 283.5 | 93.8 | 130 |
| j = 1 | j = 2 | j = 3 | j = 4 | j = 5 | j = 6 | |
|---|---|---|---|---|---|---|
| 1 × 10−2 | 1.5 × 10−2 | 1.5 × 10−2 | 3 × 10−3 | 2 × 10−3 | 1 × 10−3 | |
| 1 × 10−3 | 1.2 × 10−3 | 1.2 × 10−3 | 1 × 10−3 | 1.1 × 10−3 | 0.6 × 10−3 | |
| 2 × 10−2 | 2 × 10−2 | 2 × 10−2 | 1 × 10−3 | 1 × 10−3 | 1 × 10−3 |
| After Applying Contour Control | Before Applying Contour Control | |||
|---|---|---|---|---|
| Position Contour Error | Orientation Contour Error | Position Contour Error | Orientation Contour Error | |
| Butterfly-Shaped Trajectory | ||||
| MAX | 0.359 mm | 0.042° | 0.425 mm | 0.051° |
| RMS | 0.081 mm | 0.008° | 0.106 mm | 0.01° |
| Spatial S-shaped trajectory | ||||
| MAX | 0.166 mm | 0.036° | 0.408 mm | 0.04° |
| RMS | 0.05 mm | 0.007° | 0.099 mm | 0.01° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, X.; Zou, T.; Liu, H.; Deng, Y.; Xiao, J. Contour Error Control for a Hybrid Robot Equipped with Grating Sensors. Machines 2025, 13, 502. https://doi.org/10.3390/machines13060502
Shan X, Zou T, Liu H, Deng Y, Xiao J. Contour Error Control for a Hybrid Robot Equipped with Grating Sensors. Machines. 2025; 13(6):502. https://doi.org/10.3390/machines13060502
Chicago/Turabian StyleShan, Xianlei, Tianyu Zou, Haitao Liu, Yu Deng, and Juliang Xiao. 2025. "Contour Error Control for a Hybrid Robot Equipped with Grating Sensors" Machines 13, no. 6: 502. https://doi.org/10.3390/machines13060502
APA StyleShan, X., Zou, T., Liu, H., Deng, Y., & Xiao, J. (2025). Contour Error Control for a Hybrid Robot Equipped with Grating Sensors. Machines, 13(6), 502. https://doi.org/10.3390/machines13060502







