Prior Knowledge-Informed Graph Neural Network with Multi-Source Data-Weighted Fusion for Intelligent Bogie Fault Diagnosis
Abstract
1. Introduction
2. Related Work
2.1. Graph Neural Network
2.2. Graph Convolutional Network Model Construction
3. Proposed Method
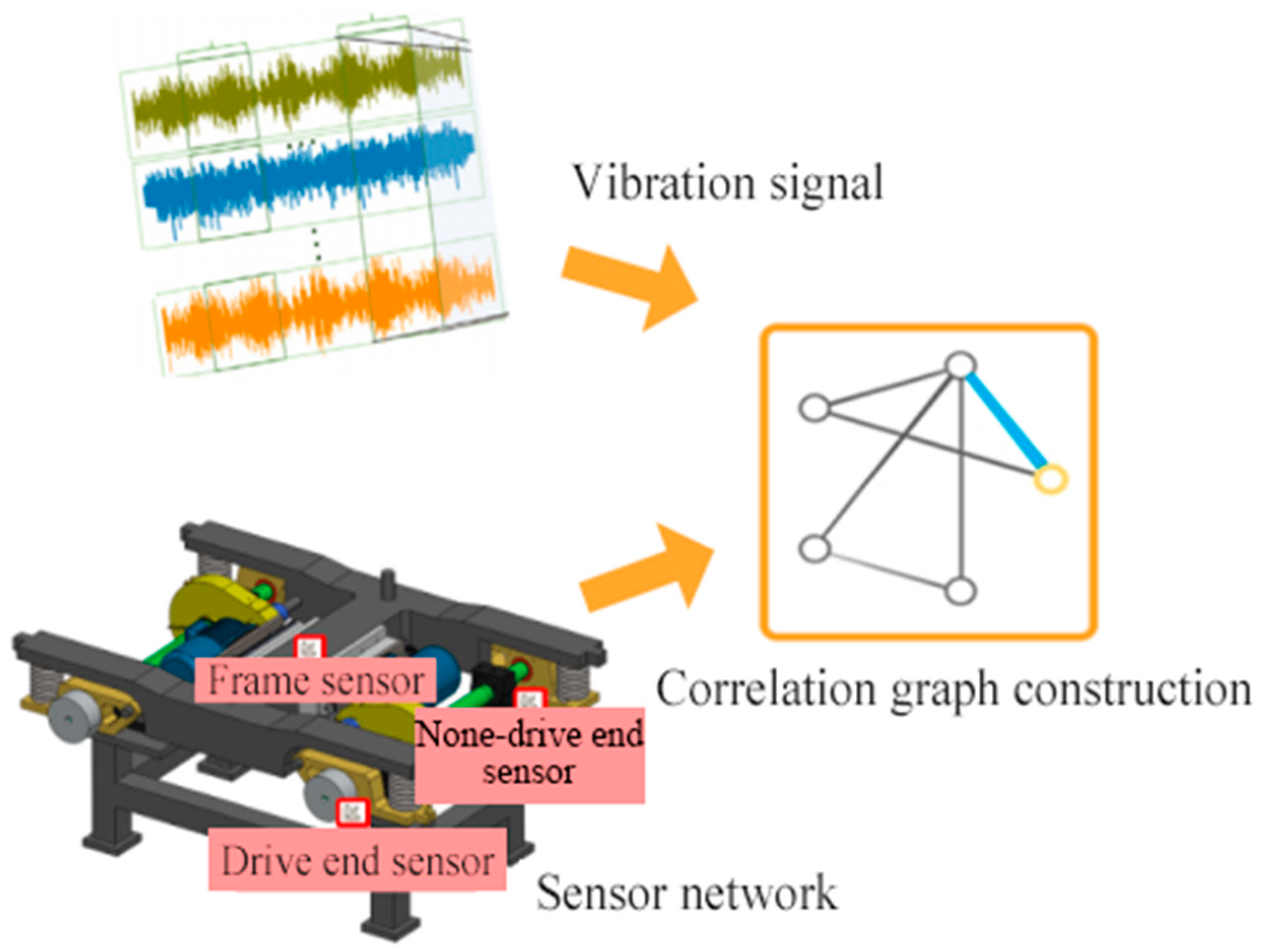
3.1. Principle of Multi-Source Sensor Weighted Fusion Optimization Method
3.2. Graph Data Set Construction Based on Prior Knowledge Embedding
4. Experimental Validation
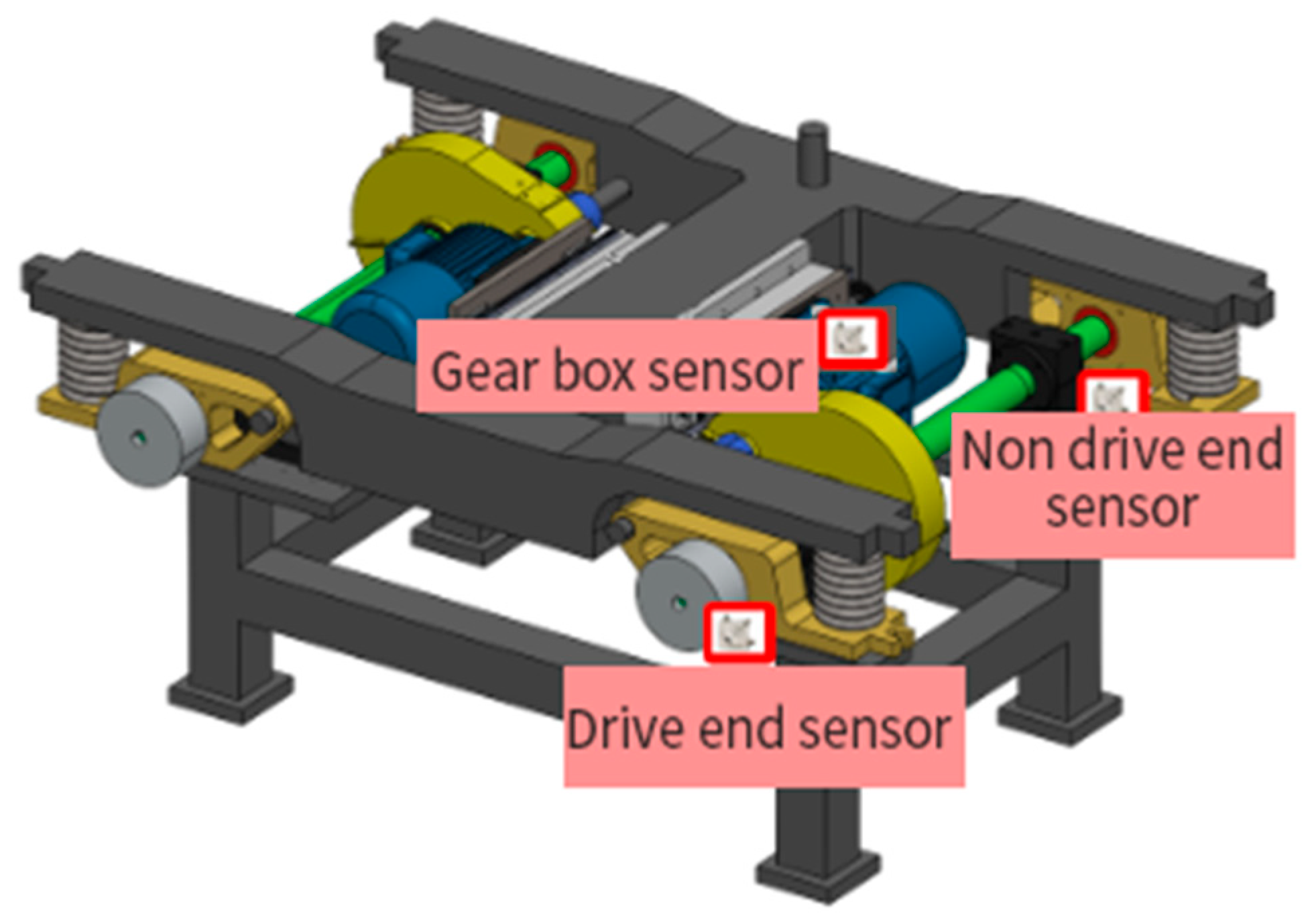
4.1. Experimental Verification of Bearing Fault Data Set Based on Bogie Comprehensive Performance Test Bench
4.1.1. Bearing Failure Data Set
4.1.2. Experimental Detail
4.1.3. Analysis of Results on Bearing Fault Data Set
4.1.4. Ablation Experiment
4.2. Experimental Verification of Gear Fault Data Set Based on Bogie Comprehensive Performance Test Bench
4.2.1. Introduction to Gear Data Set
4.2.2. Experimental Details
4.2.3. Analysis of Results on Gear Fault Data Set
4.3. Summary
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Li, W. Durability analysis of mechanical rotating parts in locomotive bogies. J. Mech. Eng. 2017, 53, 78–83. [Google Scholar]
- Huang, H.Z.; Cai, W.B.; Yang, Y.J. Research progress on bearings and their reliability of EMUs. J. Univ. Electron. Sci. Technol. China 2023, 52, 458–474. [Google Scholar]
- Kaewunruen, S.; Adesope, A.A.; Huang, J.H.; You, R.L.; Li, D. IAI-based technology to prognose and diagnose complex crack characteristics of railway concrete sleepers. Discov. Appl. Sci. 2024, 6, 217. [Google Scholar] [CrossRef]
- Chen, H.; Zhong, K.; Ran, G.; Cheng, C. Deep Learning-Based Machinery Fault Diagnostics. Machines 2022, 10, 690. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial Intelligence for Fault Diagnosis of Rotating Machinery: A Review. Mech. Syst. Signal Process. 2023, 172, 108802. [Google Scholar] [CrossRef]
- Bishara, J.A. Feature extraction methods in machine learning: Challenges and future trends. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2015; ACM: New York, NY, USA, 2015; pp. 120–125. [Google Scholar]
- Kaewunruen, S.; Sresakoolchai, J.; Huang, J.; Zhu, Y.; Ngamkhanong, C.; Remennikov, A.M. Machine Learning Based Design of Railway Prestressed Concrete Sleepers. Appl. Sci. 2022, 12, 10311. [Google Scholar] [CrossRef]
- Pan, T.; Chen, J.; Zhou, Z.; Wang, C.; He, S. A novel deep learning network via multiscale inner product with locally connected feature extraction for intelligent fault detection. IEEE Trans. Ind. Inf. 2019, 15, 5119–5128. [Google Scholar] [CrossRef]
- Ravikumar, K.; Yadav, A.; Kumar, H.; Gangadharan, K.; Narasimhadhan, A. Gearbox fault diagnosis based on multi-scale deep residual learning and stacked LSTM model. Measurement 2021, 186, 110099. [Google Scholar] [CrossRef]
- Zhiyi, H.; Haidong, S.; Lin, J.; Junsheng, C.; Yu, Y. Transfer fault diagnosis of bearing installed in different machines using enhanced deep auto-encoder. Measurement 2020, 152, 107393. [Google Scholar] [CrossRef]
- Pan, T.; Chen, J.; Zhang, T.; Liu, S.; He, S.; Lv, H. Generative adversarial network in mechanical fault diagnosis under small sample: A systematic review on applications and future perspectives. ISA Trans. 2022, 128, 1–10. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Wang, Y. An intelligent diagnosis scheme based on generative adversarial learning deep neural networks and its application to planetary gearbox fault pattern recognition. Neurocomputing 2018, 310, 213–222. [Google Scholar] [CrossRef]
- Fu, J.; Chu, J.; Guo, P.; Chen, Z. Condition Monitoring of Wind Turbine Gearbox Bearing Based on Deep Learning Model. IEEE Access 2019, 7, 57078–57087. [Google Scholar] [CrossRef]
- Wang, Y.; Li, H.; Zhang, J. Sensor-based fault diagnosis for high-speed train bogies: A comprehensive review. J. Rail Transp. Plan. Manag. 2020, 15, 100203. [Google Scholar]
- Fu, J.; Chu, J.; Guo, P.; Chen, Z. Adversarial embedding fusion network for multi-sensor fusion fault diagnosis of wheelset bearings. In Proceedings of the 2022 Global Reliability and Prognostics and Health Management, Yantai, China, 13–16 November 2022; pp. 1–7. [Google Scholar]
- Frundzhyan, V.G.; Ugarova, N. Research on the Application of the Multi-sensor Data Fusion Technology in Fault Diagnosis of Rolling Bearings. In Proceedings of the International Symposium on Test and Measurement, Johannesburg, South Africa, 19–21 November 2007. [Google Scholar]
- Azamfar, M.; Singh, J.; Bravo-Imaz, I.; Lee, J. Multisensor data fusion for gearbox fault diagnosis using 2-D convolutional neural network and motor current signature analysis. Mech. Syst. Signal Process 2020, 144, 106861. [Google Scholar] [CrossRef]
- Zou, L.; Zhuang, K.; Zhou, A.; Hu, J. Bayesian optimization and channel-fusion-based convolutional autoencoder network for fault diagnosis of rotating machinery. Eng. Struct. 2023, 280, 115708. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, J.; Liu, Y. Convolutional autoencoder-based feature extraction and Bayesian optimization for fault diagnosis considering sensor relevance and spatial topology. IEEE Trans. Ind. Inform. 2021, 17, 3900–3910. [Google Scholar]
- Ma, X.; Cao, J. Graph convolutional neural networks for multi-sensor information fusion. IEEE Trans. Signal Process. 2019, 67, 3164–3173. [Google Scholar]
- Chen, Z.; Xu, J.; Alippi, C.; Ding, S.X.; Shardt, Y.; Peng, T.; Yang, C. Graph Neural Network-Based Fault Diagnosis: A Review. IEEE Access 2021, 9, 147488–147507. [Google Scholar]
- Li, T.; Zhao, Z.; Sun, C.; Yan, R.; Chen, X. Multireceptive field graph convolutional networks for machine fault diagnosis. IEEE Trans. Ind. Electron. 2021, 68, 12739–12749. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, J.; He, S.; Li, F.; Feng, Y.; Zhou, Z. Triplet metric driven multihead GNN augmented with decoupling adversarial learning for intelligent fault diagnosis of machines under varying working condition. J. Manuf. Syst. 2022, 62, 1–16. [Google Scholar] [CrossRef]
- Li, T.; Zhao, Z.; Sun, C.; Yan, R.; Chen, X. Domain adversarial graph convolutional network for fault diagnosis under variable working conditions. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, J.; Peng, T.; Yang, C. Graph convolutional network-based method for fault diagnosis using a hybrid of measurement and prior knowledge. IEEE Trans. Cybern. 2021, 52, 9157–9169. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Zhou, K.; Liu, J. SuperGraph: Spatial-temporal graph-based feature extraction for rotating machinery diagnosis. IEEE Trans. Ind. Electron. 2021, 69, 4167–4176. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 2008, 20, 61–80. [Google Scholar] [CrossRef]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How Powerful are Graph Neural Networks? arXiv 2019, arXiv:1810.00826. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef]
- Li, Y.; Tarlow, D.; Brockschmidt, M.; Zemel, R. Gated graph sequence neural networks. arXiv 2015, arXiv:1511.05493. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Ying, R.; You, J.; Morris, C.; Ren, X.; Hamilton, W.L.; Leskovec, J. Hierarchical graph representation learning with differentiable pooling. Adv. Neural Inf. Process. Syst. 2018, 31, 4800–4810. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Wongkaew, W.; Muanyoksakul, W.; Ngamkhanong, C.; Sresakoolchai, J.; Kaewunruen, S. Data driven machine learning prognostics of buckling failure modes in ballasted railway track. Discov. Appl. Sci. 2024, 6, 212. [Google Scholar] [CrossRef]























| Network Structure | Type | Input Dimension | Output Dimension |
|---|---|---|---|
| Embedding | Embedding | 1 | 128 |
| Graph convolution layer | GCNConv | 128 | 128 |
| Pooling | Difpooling | 128 | 128 |
| Graph convolution layer | GCNConv | 128 | 128 |
| Pooling | Difpooling | 128 | 128 |
| Graph convolution layer | GCNConv | 128 | 128 |
| Pooling | Difpooling | 128 | 128 |
| Batch normalization | BatchNorm1d | 128 | 128 |
| Fully connected layer | linear | 128 | 64 |
| Batch normalization | BatchNorm1d | 64 | 64 |
| Fully connected layer | linear | 64 | 32 |
| Dropout layer | dropout | 32 | 32 |
| Fully connected layer | linear | 32 | 5 |
| Network Structure | Type | Input Dimension | Output Dimension |
|---|---|---|---|
| Embedding layer | Embedding | 1 | 128 |
| Weighting layer | Weighting | 128 | 128 |
| Graph convolution | GCNConv | 128 | 128 |
| Pooling layer | Difpooling | 128 | 128 |
| Graph convolution | GCNConv | 128 | 128 |
| Pooling layer | Difpooling | 128 | 128 |
| Graph convolution | GCNConv | 128 | 128 |
| Pooling layer | Difpooling | 128 | 128 |
| Batch normalization | BatchNorm1d | 128 | 128 |
| Fully connected layer | Linear | 128 | 64 |
| Batch normalization | BatchNorm1d | 64 | 64 |
| Fully connected layer | Linear | 64 | 32 |
| Dropout layer | Dropout | 32 | 32 |
| Fully connected layer | Linear | 32 | 6 |
| Experimental Class | Faulty Component | Fault Type | Degree of Failure | Sampling Rate |
|---|---|---|---|---|
| 0 | Axle box bearing | Normal | / | 12k |
| 1 | Axle box bearing | Cage crack | / | 12k |
| 2 | Axle box bearing | Roller pitting | mild | 12k |
| 3 | Axle box bearing | Roller crack | 0.4 mm | 12k |
| 4 | Axle box bearing | Outer pitting | mild | 12k |
| 5 | Axle box bearing | Outer crack | 0.5 mm | 12k |
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| SNM [34] | 87.05% | 85.07% | 82.82% | 85.04% | 81.92% | 85.74% |
| MCSA-CNN [17] | 96.52% | 97.32% | 95.01% | 96.60% | 94.41% | 93.45% |
| Bayes-CAE [18] | 97.91% | 98.86% | 96.85% | 97.90% | 97.82% | 96.87% |
| Proposed | 99.99% | 99.98% | 99.99% | 99.99% | 99.99% | 99.99% |
| SNR | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 0 dB | 99.99% | 99.98% | 99.99% | 99.99% | 99.99% | 99.99% |
| −3 dB | 98.34% | 98.48% | 98.53% | 98.24% | 98.43% | 98.62% |
| −6 dB | 96.56% | 96.43% | 95.75% | 95.68% | 96.53% | 95.79% |
| −9 dB | 91.48% | 90.68% | 92.75% | 90.46% | 92.35% | 93.42% |
| Number of Iterations | X1 (%) | Y1 (%) | Z1 (%) | X2 (%) | Y2 (%) | Z2 (%) | H (%) |
|---|---|---|---|---|---|---|---|
| 1 | 15.22 | 15.13 | 14.77 | 15.46 | 13.74 | 13.78 | 13.88 |
| 5 | 17.12 | 17.55 | 16.24 | 14.98 | 11.83 | 11.68 | 12.17 |
| 10 | 17.19 | 17.73 | 16.30 | 14.63 | 11.33 | 11.14 | 11.64 |
| 15 | 17.52 | 18.09 | 16.53 | 14.71 | 11.18 | 10.95 | 11.48 |
| 20 | 17.55 | 18.22 | 16.55 | 14.68 | 10.72 | 10.86 | 11.42 |
| Ranking | 2 | 1 | 3 | 4 | 6 | 7 | 5 |
| Model Name | |
|---|---|
| Model 1 | Multi-source measuring point weighting method is used to optimize the model |
| Model 2 | Basic graph neural network model |
| Method | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Multi-source measuring point weighting method is used to optimize the model | 99.99% | 99.91% | 99.52% | 99.99% | 99.95% | 99.98% |
| Basic graph neural network model | 99.67% | 99.86% | 99.79% | 99.94% | 99.98% | 99.88% |
| Experimental Class | Faulty Component | Fault Type | Degree of Failure | Rotational Speed | Sampling Rate |
|---|---|---|---|---|---|
| 0 | Drive gear | Normal | / | 1000 | 24k |
| 1 | Drive gear | Graze | Severe | 1000 | 24k |
| 2 | Drive gear | Pitting | Severe | 1000 | 24k |
| 3 | Drive gear | Partial denture | / | 1000 | 24k |
| 4 | Drive gear | Root crack | / | 1000 | 24k |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Cui, B.; Mao, X.; Yang, J. Prior Knowledge-Informed Graph Neural Network with Multi-Source Data-Weighted Fusion for Intelligent Bogie Fault Diagnosis. Machines 2024, 12, 838. https://doi.org/10.3390/machines12120838
Huang Y, Cui B, Mao X, Yang J. Prior Knowledge-Informed Graph Neural Network with Multi-Source Data-Weighted Fusion for Intelligent Bogie Fault Diagnosis. Machines. 2024; 12(12):838. https://doi.org/10.3390/machines12120838
Chicago/Turabian StyleHuang, Yuanxing, Bofeng Cui, Xianqun Mao, and Jinsong Yang. 2024. "Prior Knowledge-Informed Graph Neural Network with Multi-Source Data-Weighted Fusion for Intelligent Bogie Fault Diagnosis" Machines 12, no. 12: 838. https://doi.org/10.3390/machines12120838
APA StyleHuang, Y., Cui, B., Mao, X., & Yang, J. (2024). Prior Knowledge-Informed Graph Neural Network with Multi-Source Data-Weighted Fusion for Intelligent Bogie Fault Diagnosis. Machines, 12(12), 838. https://doi.org/10.3390/machines12120838






