Abstract
This paper proposes a multi-map path planning approach for rescue robots to address the challenges posed by complex obstacle information, high uncertainty, and the difficulties in mine disaster scenarios. Based on multiple possible environmental maps, each with associated subjective probabilities derived from prior knowledge and expert estimations, a mathematical model for multi-map path planning in mine disaster rescue scenarios is developed. An improved hybrid algorithm combining ant colony optimization (ACO) and genetic algorithm (GA) is then proposed to solve the established model. In the hybrid approach, the improved ACO is employed to overcome the limitations of traditional genetic algorithms, such as poor initial population quality, slow convergence, and suboptimal results. Additionally, a grid-based, rectangular-area, obstacle avoidance strategy is incorporated to precisely evaluate the obstacle avoidance path of each individual across different obstacle maps. Finally, the feasibility and effectiveness of the proposed hybrid algorithm are validated through simulations involving both single and multiple mine disaster maps. The results demonstrate the potential of the proposed approach for solving robot path optimization problems in complex multi-environment scenarios.
1. Introduction
After a mining disaster, the affected site often presents extremely complex conditions, accompanied by challenges such as extreme environments and limited visibility. Blind rescue attempts may lead to secondary casualties [1], and the narrow environment often makes locating trapped individuals difficult, resulting in low search efficiency during the initial stages of rescue operations. In recent years, advancements in robotic technology have opened new directions for search and rescue in complex scenarios [2]. Rescue robots, with their unique characteristics of non-contact operation, high efficiency, and adaptability, show great potential in confined, narrow, and hazardous mining disaster scenarios.
Scholars worldwide have been extensively studying various types of robots and applying them to rescue scenarios, including mining disasters. For instance, Li Y et al. [3] improved the environmental perception and planning systems of traditional Coal Mine Rescue Robots (CMRR), enhancing their adaptability to complex maps. Additionally, a 3D SLAM method based on normal distribution transformation can be applied to CMRRs [4], enabling real-time and accurate descriptions of mining tunnel spaces and constructing globally consistent scene maps. Other examples include Karo, a rescue robot designed with a tracked mobility platform [5], which maintains high maneuverability in unstructured and complex environments, and a four-legged robot [6], which mimics animal limb movements to autonomously explore challenging terrains. Furthermore, aerial robots such as drones utilize their hovering capabilities and graph search algorithms to achieve map generation, target localization, and aerial obstacle avoidance without direct exposure to hazardous environments [7]. Exploring the application and technological innovations of rescue robots in mining disasters and similar scenarios can leverage mature robotic technologies to enhance rescue efficiency. It also encourages the development of rescue robots tailored to specific scenarios, fostering technological innovation and interdisciplinary integration, thereby offering valuable insights for future disaster rescue operations.
To improve the precision and efficiency of path planning, researchers often construct maps tailored to different scenarios, ensuring that robots can maximize environmental information acquisition and execute path planning strategies. For instance, typical 2D firefighting rescue maps are used in fire scenarios [1], aerial images are generated by drones for post-flood environments [8], and in underground and enclosed mining disaster scenarios, rescue robots often combine mining information maps with SLAM technology to create high-precision point cloud maps of disaster sites [9].
However, most of the rescue scenario planning efforts mentioned above focus on a single deterministic environmental map, a limitation that significantly restricts the application of rescue robots in complex scenarios. In extreme rescue environments such as fires and mining accidents, single-map planning strategies often fail to address the uncertainties of real-world environments [10], leading to a disparity between planned paths and actual conditions, thereby reducing the usability of pre-planned paths. To overcome the limitations of single maps, researchers have attempted to build real-time environmental maps to enhance the usability of generated search and rescue paths. For example, Lee J, et al. [11] proposed a hierarchical path planning system for indoor fire rescue scenarios, dynamically adjusting maps by combining prior maps with real-time obstacle detection. Chen X et al. [12] utilized radar information and SLAM technology to sense the scene and construct real-time environmental maps in complex mining disaster scenarios, achieving global planning and local obstacle avoidance. Real-time detection and map generation technologies effectively address the issue of poor path planning performance based on single maps. However, their practical application in complex scenarios is challenged by high resource costs. Rescue robots often lack detailed map information at the initial stage and must construct maps through scene traversal and information collection. This process is time-consuming and requires substantial computational resources [13], significantly limiting the applicability of such technologies in time-critical search-and-rescue operations. From the above research survey, it is clear that existing single-map planning methods are unable to address two key challenges in rescue scenarios: the high uncertainty in obstacle distribution, where secondary collapses or unpredictable factors may block most of the pre-planned paths on a single map, and the real-time computation limitations, where typical methods like SLAM require considerable time to complete map updates.
To address the limitations of single-map planning, prior research has focused on handling uncertain environmental information by dynamically adjusting paths based on real-time detection during operations. This approach combines pre-planned paths using a single map with mid-operation adjustments. Nevertheless, even without accurate environmental data prior to rescue missions, expert knowledge can provide valuable prior information about the rescue environment. This paper aims to explore a multi-map-based path planning method for rescue robots, designed to overcome the shortcomings of existing approaches. By pre-generating and storing multiple prior maps and computing path plans for each, this method offers a solution that accounts for obstacle avoidance costs across diverse scenarios. Compared to single-map-based path planning, the multi-map approach demonstrates greater adaptability to various environmental conditions. It can identify optimal solutions across multiple potential map scenarios rather than being restricted to a single map, a significant advantage in complex, post-disaster environments. Furthermore, compared to real-time map generation technologies, the multi-map pre-planning method significantly reduces resource consumption while delivering high obstacle avoidance and highly usable pre-planned paths. This approach maximizes task efficiency with minimal computational cost, making it particularly suitable for resource-constrained and urgent rescue missions.
The choice of a suitable path planning algorithm for rescue robots is crucial for improving the efficiency of robotic operations. Currently, commonly used algorithms for rescue robots can be broadly categorized into graph search, random sampling, and swarm intelligence algorithms. Graph search algorithms represent the environment as a graph and traverse its nodes to find the shortest path in static, structured environments [14,15]. However, in complex scenarios, the large search space leads to high time complexity and significant computational resource consumption, while the adaptability to dynamic and unstructured environments is limited. Random sampling-based algorithms construct paths by randomly sampling and connecting nodes, selecting optimal paths through evaluation functions. These algorithms sample only in necessary regions, avoiding a comprehensive search of the entire space and quickly identifying feasible paths [16,17]. However, their inherent randomness often results in paths that are neither globally optimal nor sufficiently smooth. Swarm intelligence algorithms, inspired by biological interactions and adaptive processes, enable global search and optimization for complex problems. Examples include ant colony optimization (ACO) [18,19], genetic algorithms (GA) [20,21], and Particle Swarm Optimization (PSO) [22,23,24,25]. Swarm intelligence algorithms iteratively eliminate less fit individuals to approach optimal solutions. However, their computational speed remains a bottleneck for online applications.
Given the inherent limitations of swarm intelligence algorithms and other traditional path planning methods, a single algorithm often struggles to fully meet the demands of efficiency, accuracy, and robustness in complex rescue scenarios. As a result, hybrid strategies that combine multiple algorithms have become the optimal solution for path planning in such environments. For example, Jinjun Rao et al. [26] proposed combining the improved Artificial Potential Field (APF) method with the A-Star (A*) algorithm. By introducing the concept of repulsive force to optimize the heuristic function, their approach improves search efficiency while ensuring the generation of safe and reliable paths. Yonggang Li et al. [27] proposed an algorithm that combines an improved A* algorithm with the dynamic window approach, using an adaptive step-size adjustment and cubic Bézier curves to address issues such as sharp turns, long run times, and dynamic obstacle avoidance, while preventing local optimization. Zhenhua Yu et al. [28] improved the PSO algorithm by integrating simulated annealing, enhancing the global optimization capability, avoiding local convergence, and ensuring better robustness in complex environments by reducing particle oscillations and integrating beneficial information based on dimensional learning strategies. Sabeeh et al. [29] integrated the exploratory power of genetic algorithms (GA) with the global planning advantages of the Probabilistic Roadmap (PRM), achieving enhanced computational efficiency. Similarly, Zhang et al. [30] focused on multi-objective path planning in static nuclear accident environments and developed an improved ACO-A* algorithm based on a high-radiation dose avoidance strategy, aiming to minimize path length, cumulative radiation dose, and energy consumption. Despite the improvements achieved by integrating traditional heuristic methods with swarm intelligence algorithms, these hybrid algorithms still face challenges such as high computational complexity, susceptibility to local optima, and poor algorithmic stability in complex environments.
Recent efforts have focused on leveraging the global search capabilities of swarm-intelligenced algorithms to enhance efficiency and accuracy in path planning. For example, Chen et al. [31] introduced stochastic factors into the update formula of Particle Swarm Optimization (PSO) to adjust PSO parameters, applying this model to optimize the hyperparameters of the ACO algorithm. This approach reduced the number of optimization iterations, enabling the chaotic PSO-ACO algorithm to perform rapid searches in complex environments such as coal mines. Chao Liu et al. [32] proposed a novel improved heuristic mechanism ant colony optimization (IHMACO) algorithm. By incorporating four enhancement mechanisms for ant colony optimization, including the adaptive setting of pheromone concentration, the approach enhances the algorithm’s goal orientation in path planning, avoids getting trapped in local optima, and improves its search efficiency and global optimization capability. Yuting Liu et al. [33] proposed an Adaptive Double-Layer Ant Colony Optimization (ADL-ACO) algorithm for dynamic robot path planning, which accelerates convergence and enhances global search ability through adaptive parameter adjustment and pseudo-random state transition, addressing ACO’s limitations in convergence speed, search efficiency, local optima, and reliance on high-precision maps.
Among the above researches, ant colony optimization (ACO) has demonstrated significant potential in solving optimization problems such as robotic path planning and the traveling salesman problem. Meanwhile, it is known that the global optimization capability of genetic algorithms (GA) has been extensively validated both theoretically and practically. The fusion of these two algorithms not only maximizes their respective advantages but also enhances overall performance through complementary effects. And hence, Liu et al. [34] proposed a path planning algorithm that combined dynamic genetic algorithm (DGA) with an improved ant colony optimization algorithm (ACBIO) for scheduling multiple agricultural drones in tea plantations. The algorithm employed DGA to quickly search for initial solutions, which were then fine-tuned by ACBIO, significantly improving both search speed and precision. However, current research predominantly focuses on path planning in single-environment maps, overlooking the practical challenges of incomplete or imprecise map information in real-world rescue scenarios. Additionally, most existing global optimization algorithms often struggle to generate a sufficient number of initial feasible solutions, which adversely affects their overall performance.
This paper proposes an improved ACO-GA hybrid algorithm for path planning, designed to tackle challenges such as high complexity and limited usability in pre-disaster planning for mining rescue scenarios. The main contributions are as follows: (1) A mathematical model for multi-map path planning is developed, utilizing multiple known grid maps of mining disaster scenarios. The planning problem is addressed using a GA-based approach. (2) To overcome the limitations of traditional GA in managing complex environments, an improved ACO is introduced to generate the initial population. This enhancement accelerates convergence and improves the quality of path solutions. (3) An obstacle cost calculation strategy is incorporated into the proposed algorithm, enabling the formulation of a total fitness function that integrates multi-map obstacle avoidance costs. This ensures an accurate evaluation of path quality across multiple maps. (4) Comprehensive simulations are conducted on various grid maps representing mining disaster scenarios with different subjective probabilities. The multi-map fitness function is employed as the primary evaluation metric, demonstrating the reliability and applicability of the proposed ACO-GA hybrid algorithm for multi-map path planning problems.
Unlike existing approaches that focus on either single-map planning or computationally expensive real-time mapping, this study introduces three key innovations: (1) a novel multi-map probabilistic framework that systematically incorporates expert knowledge and historical data to generate diverse disaster scenarios, providing a robust foundation for pre-disaster planning, (2) an improved hybrid ACO-GA algorithm where the ant colony optimization not only generates high-quality initial populations but also incorporates a safety-aware pheromone update mechanism based on obstacle density across multiple maps, which is a critical feature for mine rescue operations, and (3) a computationally efficient rectangular obstacle avoidance strategy specifically designed for grid-based multi-map evaluation, which enables precise quantification of avoidance costs while maintaining path optimality across different environmental configurations. These innovations collectively address the fundamental challenges in mining rescue robotics: balancing planning accuracy with computational efficiency and ensuring solution robustness in highly uncertain environments.
The following section briefly describes rescue robot path planning with a single deterministic map. Section 3 proposes the multi-map-based, optimal path planning problem for rescue robots. An ant colony–genetic hybrid algorithm is proposed to solve multi-map-based, optimal path planning problems of rescue robots. Then, the detailed steps of the solution techniques are given in Section 5. Section 6 compares and analyzes the experimental results of the proposed hybrid algorithm and the traditional one; Section 7 provides the conclusions of this study.
2. Rescue Robot Path Planning with Single Deterministic Map
2.1. Grid Map Construction
The grid method is a traditional and effective approach for environmental map modeling, commonly used for constructing 2D maps in single rescue scenarios. This method discretizes the environmental space, mapping continuous environmental information onto discrete grids and classifying each grid according to the actual spatial state.
In rescue robot path planning, grid maps are divided into two types of grids: obstacle grids and free grids, representing obstacle areas and traversable areas, respectively. The specific representation of the grid array is shown in the following formula.
In the formula, represents a matrix, which is the grid map matrix. The represents the grid at the -th row and -th column of the matrix. The value of each grid is in the range of , as defined below:
In the formula, represents the grid set of the obstacle area, i.e., ; represents the grid set of the feasible region, i.e., . is the coordinate of the starting point, and satisfies the coordinate of the target point, with and . During the grid map construction, different colors are often used to represent the meaning of different grids. So, the grid matrix can be visualized by assigning corresponding colors to different types of grids, as follows:
In the formula, represents the color corresponding to the grid coordinate . According to the description above, the obstacle region grids are represented in black, the feasible region grids are represented in white, the starting point grid is represented in yellow, and the target point grid is represented in pink. In summary, the entire grid map can be formally described using the grid matrix and its value range. A sample of a colored grid map is fully described as shown in Figure 1.

Figure 1.
A sample of a colored grid map for path planning of rescuing robots.
2.2. Problem Description of Path Planning Problem Based on Grid Maps
The path optimization problem based on grid maps typically involves finding the optimal path within a grid environment. This type of problem is widely applied in fields such as robot path planning and mobility strategies. In the grid map of a mining disaster rescue scenario, each grid represents a potential path point or an obstacle. The goal of path planning is to find the optimal path from the starting point to the target point under given constraints. The definition of the optimal path can be determined based on specific requirements, such as the shortest path, minimum time, etc.
For a specific grid map, the starting point grid coordinates are , and the target point grid coordinates are . The optimal path must pass through every row between the starting point and the target point. Assuming that for any intermediate row , the horizontal coordinate is the column number , and there are column numbers. Path planning based on grid maps aims to find the optimal sequence such that the overall path achieves certain optimality.
For the path planning problem in the mining disaster grid map scenario, the following mathematical model can be established:
In the above formula, represents the column index in the -th row of the grid map. The decision variable represents the solution vector consisting of the column indices of intermediate grid points between the starting point and the target point on the grid map. This decision variable defines the unique path from the starting point to the target point. represents the total length of the path represented by the decision variable, and represents the total smoothness of the path. Smoothness optimization in path planning is essential for ensuring feasible and efficient robot navigation, particularly in rescue scenarios. Most ground-based rescue robots (e.g., tracked or wheeled platforms) have kinematic constraints, such as a minimum turning radius, making sharp or frequent turns impractical. Smooth paths reduce unnecessary deceleration, energy consumption, and mechanical wear while improving traversal speed and stability. By incorporating path smoothness into the fitness function—weighted alongside path length—the algorithm generates trajectories that are not only short but also executable, enhancing real-world applicability. Future work could explicitly model robot-specific motion constraints (e.g., turning radius) to further refine smoothness optimization for different robotic platforms. For rescue robots, shorter path lengths and higher path smoothness result in a better path. Thus, the objective function for the mining disaster rescue robot path planning is defined as maximizing the reciprocal of the total path length and the weighted sum of total smoothness, where and are the weight coefficients used to balance path length and smoothness.
The constraints in Formula (4) are mainly composed of three parts:
- (1)
- Obstacle Avoidance Node Constraint: The first equation represents the constraint that each node on the path must not be an obstacle grid;
- (2)
- Path Connectivity Constraint: The second equation represents the connectivity constraint, which requires that there must be at least one obstacle avoidance path (not limited to a straight-line connection) between adjacent points and on the grid map containing the obstacle set .The function represents the minimum number of steps required for the obstacle avoidance path between points and on the map containing the set . This path must ensure that each point along the path is not an obstacle grid. If no obstacle avoidance path exists, the value of the function is 0. In the case of a non-complex single grid map, the specific calculation of can be referenced in Section 2.3, where an iterative insertion method is used to find a connected path between two points, and the number of steps in the path can be calculated;
- (3)
- Boundary Constraint: The third equation represents the boundary constraint, stating that each point on the path must lie within the boundary of the grid map. The horizontal coordinate of each path node must not exceed the number of elements in each row of the map, ensuring that the coordinate is a positive integer and is less than the number of columns in the map.
2.3. GA for Rescue Robot Path Planning with Single Deterministic Map
The genetic algorithm is an optimization technique developed by simulating the natural selection and genetic mechanisms of Darwin’s theory of biological evolution. In optimization problems, the genetic algorithm initially computes the first generation of the population and then updates and evolves the population in generations to approach the optimal solution. During each generation’s updating process, the algorithm selects a new population of individuals based on a fitness function and uses genetic operators such as crossover and mutation to generate the next generation of individuals.
For path planning problems based on grid map models, the general steps of using genetic algorithm are as follows:
Step 1: Population Initialization
Randomly select a non-obstacle grid from each row between the starting point and the target point as the initial path node, generating an initial population (initial solution set) of a certain size.
Step 2: Individual Obstacle Avoidance Repair
For any individual solution, check if two adjacent nodes are continuous. If they are not continuous, use the median method to insert free grids between the two points until there are no interruptions in the path or until no feasible insertion points remain.
Step 3: Fitness Evaluation
For individuals where obstacle avoidance is successful, calculate their fitness function. For individuals where the median insertion failed, use a penalty function to calculate the fitness.
Step 4: Check for Optimization Criteria
If the optimization criteria are met, output the current best individual, i.e., the optimal path. Otherwise, proceed to the next step.
Step 5: Perform Genetic Algorithm Operations (Selection, Crossover, and Mutation)
Generate the new generation of candidate individuals, i.e., the new path planning solutions, and return to Step 2.
3. Multi-Map-Based Optimal Path Planning for Rescue Robot
3.1. Problem Description of Multi-Map-Based Path Planning for Rescue Robot
In the field of mining disaster rescue, traditional single-map path planning struggles to handle the complex and dynamic conditions of disaster sites. The terrain at disaster sites is often intricate, with obstacles distributed randomly and unpredictably. Relying solely on a single map for path planning can lead to early encounters with “dead ends” or path interruptions, resulting in an inefficient path search. To overcome this issue, it is crucial to introduce a path planning strategy based on multi-map scenarios.
This strategy is based on the core idea of utilizing existing prior information, such as geological survey reports, historical mining disaster data, and initial on-site detection data, to construct multiple map scenarios with subjective probabilities. These maps aim to reflect the possible real-world conditions. By considering multiple maps for path planning calculations and evaluating obstacle avoidance costs, the strategy can find the optimal safe path that covers multiple potential scenarios.
For multiple grid maps, let represent the set of multiple maps, i.e., , which represents the collection of known maps with associated subjective probabilities. Each map has a corresponding obstacle layout and a generation probability . Similar to the single-map path planning problem, the starting point coordinates are set as , and the target point grid coordinates as . The path must pass through each row from the starting point to the target point. Assuming the column coordinates of any intermediate row are denoted by , there are column indices. The multi-map path planning problem is to find an optimal sequence such that the path reaches a certain optimality.
For the multi-map path planning problem in the mining disaster rescue scenario, the following mathematical model is constructed to maximize the comprehensive fitness of the path in the multi-map environment:
In the above formula, represents the column number of the -th row in the grid map. The decision variable is a solution vector composed of the column numbers of intermediate points between the starting point and the target point in the grid map. This decision variable determines the unique path from the starting point to the target point.
In the objective function of Formula (5), represents the objective function to be maximized, where is the total fitness function of the path corresponding to the decision variable . In the calculation of the objective function, represents the obstacle avoidance path evaluation value of the path on the map , which is roughly calculated as follows. Firstly, based on a certain obstacle avoidance strategy, the path is adjusted for obstacle avoidance on the map , and then the evaluation value of the obstacle avoidance path is calculated by taking the weighted sum of the inverse of the path length and the path smoothness, denoted as . After obtaining the obstacle avoidance path evaluation value for path on each map, the comprehensive cost for path across multiple maps can be obtained by using a weighted sum approach as described in .
The constraints of Formula (5) are similar to the single-grid-map path planning problem and are mainly composed of three parts. The first equation represents the non-obstacle constraint for path nodes. Unlike the single-map path planning problem, each map in the multi-map set has a corresponding obstacle layout. These obstacles can be divided into two categories: The first category is fixed obstacles, which are obstacles that exist on every map. These mainly represent complex terrains that are present in the current scenario, and the set of grid cells corresponding to fixed obstacles can be represented as . The second category is random obstacles, which may not exist on all maps. These obstacles can be located at different positions of various maps, and the set of grid cells for random obstacles on each map can be represented as . Therefore, the non-obstacle constraint for path nodes in the multi-map route planning model primarily means that each node on the path cannot be a fixed obstacle grid on any map.
The second equation of Formula (5) represents the path connectivity constraint. In multi-map route optimization, this constraint ensures that there must be at least one obstacle avoidance path (not limited to a straight-line connection) between adjacent points and on the grid map containing the obstacle set . The function represents the minimum number of steps in the obstacle avoidance path between points and on the fixed obstacle map (the map containing the set ). The path must ensure that every point on the path is outside the fixed obstacle area. If there is no obstacle avoidance path, the value of the function is 0. The specific calculation of the function can refer to the operation of iteratively inserting intermediate points in Section 2.3 of this paper, where the connectivity path between two points is obtained and the number of steps is calculated.
The third equation of Formula (5) represents the path boundary constraint, which means that every point on the path must be within the boundary of the grid map. The horizontal coordinate of each path node must not exceed the number of elements in each row of the map, i.e., for to be a positive integer, must be less than the number of columns in the map.
3.2. GA for Path Planning Problem of Rescue Robot with Multi-Maps
Based on the established mathematical model for path planning across multiple maps, the general procedure for solving the multi-map path planning problem using a genetic algorithm is similar to that for solving a single-map path planning problem. The process involves initializing the population and iteratively performing selection, crossover, and mutation operations, allowing the population to progressively evolve towards an optimal solution with better fitness for multi-map scenarios. The specific steps are as follows:
Population Initialization:
Based on the three constraints of the multi-map path planning mathematical model, a non-fixed obstacle grid is randomly selected as the initial path node for each row between the start and target points. For the fixed obstacle map, an intermediate point insertion strategy is used to ensure that the function value between any adjacent nodes and is non-zero, creating a continuous and feasible initial population. However, when applied to large-scale, complex mine disaster grid maps, the population initialization method based on row-by-row point selection exhibits excessive randomness, often leading to infeasible or suboptimal solutions. Additionally, the approach of iteratively inserting intermediate points for individual repair results in a relatively small search space, which may discard feasible solutions, ultimately reducing the diversity of the population. This, in turn, affects the convergence speed of the algorithm and the quality of the final path.
Selection Operation:
Based on the constructed path planning model across multiple map scenarios, the objective function is used as the basis for the selection process. For each candidate individual, an obstacle avoidance strategy is applied firstly to calculate the precise avoidance path on each map. After that, the obstacle avoidance path evaluation value of for an individual on each map is determined by the weighted sum of the inverse of the path length and the smoothness. Then, the total fitness value of an individual across multiple maps is computed as . Finally, the roulette wheel selection method is employed to choose the next generation of individuals based on their fitness values.
Crossover and Mutation Operations:
After the selection operation, the crossover and mutation operations are executed. The crossover operation exchanges the overlapping sections of paths for selected path pairs in the population, generating two new paths. The mutation operation involves randomly selecting two grid nodes in a path and applying the intermediate point insertion method on the fixed obstacle map to generate a feasible new path between these two points. This increases the population diversity and guides the population toward better fitness.
Algorithm Iteration:
Based on the multi-grid map path planning model, the genetic algorithm first initializes the population. After initialization, the population undergoes iterations of selection, crossover, and mutation operations. The population is updated continuously until the maximum number of iterations is reached. Ultimately, the algorithm will obtain a population with better fitness, suited for path planning across multiple map environments.
4. Ant Colony–Genetic Hybrid Algorithm for Multi-Map-Based Optimal Path Planning Problem
In the context of complex grid maps, selecting an appropriate path planning algorithm is crucial. The algorithm must not only efficiently handle large-scale data but also possess the ability to find optimal paths in obstacle-filled environments. As previously mentioned, genetic algorithms (GAs) are known for their global search capabilities and powerful optimization performance, which help avoid local optima. However, they also suffer from slower convergence rates and a high dependency on the initial population.
For path planning problems involving multiple complex mining disaster grid maps, the obstacle distributions in the maps are often intricate, with large sizes and numerous obstacles, which significantly increases the map’s complexity. Additionally, each map’s obstacle layout may differ greatly. When using only traditional genetic algorithms, the randomness in the initialization of the population often results in numerous infeasible or poor solutions, leading to slow convergence when handling path planning for multiple complex maps. Furthermore, after selecting random points, the strategy of iteratively inserting intermediate points to ensure the continuous availability of paths reduces the search space. In complex maps with numerous and large obstacles, this strategy may fail to find insertion points, resulting in the elimination of feasible solutions and reduced population diversity during initialization.
In the case of multi-map planning, an accurate obstacle avoidance strategy is required to calculate the true obstacle avoidance cost for each path individual in different maps. Based on the avoidance paths for each map, an appropriate multi-map fitness function should be designed to accurately represent the path individual’s performance across multiple maps, ensuring that the optimal individual is selected for multi-map scenarios.
Thus, relying solely on genetic algorithms and their traditional strategies is inadequate for addressing path planning challenges in uncertain environments. This paper proposes the use of an improved ant colony–genetic hybrid algorithm. The approach involves using the population generated by the ant colony algorithm as the initial population for the genetic algorithm [35], which accelerates the convergence of the genetic algorithm while maintaining diversity in the population. The paper also introduces a grid map-based, rectangular-region obstacle avoidance strategy to ensure that each path individual can implement accurate and safe avoidance, specifically quantifying the avoidance path and costs for each map. Additionally, based on the rectangular obstacle avoidance strategy, a fitness function considering multi-map obstacle avoidance costs is proposed, which accurately calculates the total fitness of each path individual across multiple maps. This ensures that the population evolves towards the optimal solution for multi-map scenarios.
4.1. Population Initialization Based on the Improved Ant Colony Algorithm
To address the poor initial population quality in conventional genetic algorithms, this study employs an ant colony algorithm for initial population generation. The approach ensures production of high-quality, diverse initial solutions that enable subsequent genetic algorithm convergence to superior fitness path solutions. Ant colony optimization (ACO) simulates the foraging behavior of natural ant colonies, exhibiting remarkable distributed computation and self-organization capabilities [36]. By utilizing positive feedback and heuristic search, ACO can quickly find several feasible solutions in complex environments, providing a high-quality initial population for genetic algorithms. This paper chooses to use an improved ACO to generate a set of high-quality solutions to provide an initial solution for the genetic algorithm. The specific steps are as follows:
Step 1: For robustness and to ensure the algorithm can generate high-quality paths even in the most complex and “worst-case” mining disaster maps, the algorithm selects the map with the highest number of obstacles and the greatest complexity as the baseline map for the ant colony algorithm. This is performed by counting the number of obstacles on each available mining disaster grid map.
Step 2: Once the baseline map is determined, path planning is performed based on the principles of ACO for the most complex baseline map. This paper first adopts an improved pheromone initialization method. The initial pheromone concentration for each feasible grid is set differently based on its relative distance to the target point, with closer grids receiving higher pheromone concentrations. The specific initialization method is shown in the formula below. It is important to note that, unlike the traveling salesman problem, in the grid-based ACO path planning, each feasible grid in the map serves both as a potential node the ant can choose to move to and as part of the path the ant will traverse.
where , and represent the coordinates of the goal point, and and represent the coordinates of the path in the grid map. represents the Euclidean distance between the path ’s grid and the goal point. The initial pheromone of feasible grids is the inverse of the Euclidean distance from the grid to the goal point, while the pheromone concentration of obstacle grids is set to 0. Due to the differentiated pheromone concentration settings, ants are more likely to choose grids with higher pheromone concentration and closer to the goal point in the early stages. This accelerates the convergence speed of the ant colony towards the target area and avoids the potential invalid path loops caused by blind attempts during the initial search phase.
After selecting the reference map and initializing the pheromones, the iterative search of the ant colony algorithm can begin.
Step 3: In each iteration of the ant colony algorithm, each ant in the colony is sequentially placed at the starting point of the map. The next node is selected based on the state transition probability formula. Each node on the map can only be visited once by each ant. The ants continue to move forward until they reach a “dead-end” or the goal point. Ants that reach a “dead-end” discard the path, while ants that reach the goal point record the path for future pheromone updates. The state transition probability of each ant at a branch node can be expressed as the following formula:
In the formula, represents the -th ant in the colony, and represents the probability of the -th ant transitioning from node to node , i.e., the probability of selecting branch path at node . denotes the set of nodes not yet visited by the -th ant, represents the accessible neighboring nodes of node , represents the pheromone concentration of path at time (during the -th iteration), and represents the distance of the path at time . and are the influence factors of the pheromone and distance, respectively. The basic principle represented by this formula is that the larger the value of , the higher the probability of choosing the branch path at node .
Step 4: After all ants in the colony complete the path search, the recorded valid paths are subjected to pheromone updates [37]. To ensure the safety of the robot in real-world scenarios and reduce the likelihood of the robot traversing “dangerous paths”, this study adopts a pheromone concentration update strategy that incorporates safety considerations, as shown below:
In the formula, represents the pheromone evaporation rate, denotes the pheromone concentration on the path at time (i.e., during the -th iteration), and represents the amount of pheromone remaining on the path for the next iteration. denotes the pheromone deposited on the path by the ant during the current iteration. The specific calculation formula for is as follows:
In Formula (9), is a constant, is the total path length traversed by the ant, and is the penalty multiplier. The higher the number of obstacles around a path node, the greater the “risk” of that path in practical scenarios, resulting in a smaller value for the penalty multiplier and, consequently, a reduced pheromone increment . The detailed calculation formula for the penalty factor in the penalty coefficient is as follows:
In Formula (10), the penalty factor incorporates , the total number of maps, , the generation probability of the -th map, , the total number of neighboring nodes around node on the -th map (typically 8), and , the number of neighboring nodes around belonging to obstacle regions. The greater the number of obstacle nodes around across all maps, the larger the value of .
By introducing the penalty factor, the pheromone update strategy significantly improves the safety of the algorithm in mining disaster rescue scenarios while maintaining path planning efficiency. This encourages robots to prefer paths with fewer surrounding obstacles and safer traversal conditions, effectively reducing the risk of contact with obstacles in real-world applications.
Step 5: Once the pheromone concentrations of all recorded feasible paths have been updated, the current iteration concludes. If the number of iterations has not reached the maximum limit, the pheromone matrix on the map is retained, and the algorithm returns to Step 3 for the next iteration. In the next round, the ant colony is redeployed to search for new paths. If the maximum number of iterations has been reached, the ant colony algorithm terminates, preserving the high-quality path population generated during the final iteration as the initial population for the genetic algorithm.
In traditional genetic algorithms, the diversity of the initial population is often limited due to the randomness of selecting points row by row or the small search space of the intermediate point insertion strategy. The former can easily lead to infeasible solutions, while the latter tends to discard feasible solutions, ultimately reducing the convergence speed of the entire algorithm. Traditional search-based algorithms like A*, Dijkstra, etc., typically generate only one “optimal path”. These algorithms are prone to local optima, and due to their inherent characteristics, the paths they generate are often very close to obstacles, without taking into account safety issues in practical scenarios. On the other hand, sampling-based algorithms like RRT, while capable of generating multiple different paths, tend to produce paths with poor quality in terms of length, smoothness, and other metrics, due to their high randomness.
By contrast, the proposed improved ant colony optimization (ACO) algorithm in this paper can ensure both the diversity and optimality of the generated paths by leveraging the mechanisms of the ant colony itself and an improved pheromone initialization, thus avoiding local optima. Additionally, by introducing penalty factors for obstacles across multiple maps, the algorithm ensures that the generated path set has higher safety. This results in a high-quality and safe initial solution set, which can be further refined through subsequent operations in the genetic algorithm. Using these solutions as the initial population for the genetic algorithm enables the genetic algorithm to start from a higher baseline, thereby accelerating the convergence process.
4.2. Rectangular Region-Based Obstacle Avoidance Strategy for Grid Maps
This paper proposes a rectangular region-based obstacle avoidance strategy for grid maps. The core of this strategy lies in accurately computing obstacle avoidance paths for the initial route on each individual map, precisely quantifying the avoidance costs, which are subsequently integrated to evaluate the comprehensive fitness of the path across multiple maps.
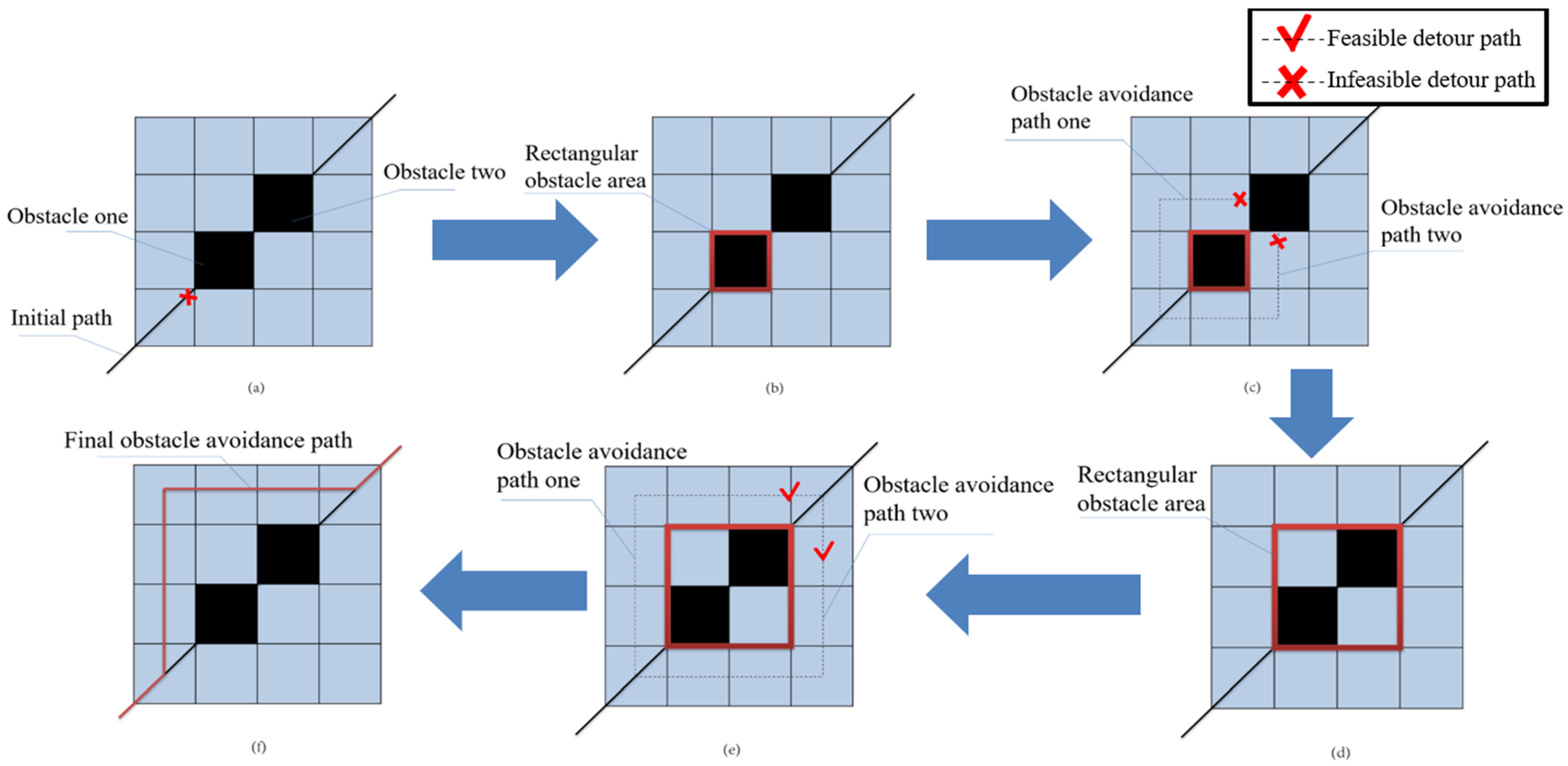
The process of the rectangular region-based obstacle avoidance strategy is as follows: Given the known path and map information, the strategy identifies the obstacle grids encountered by the initial path on a specific map. It starts with the first encountered obstacle, treats it as a rectangular obstacle region, and explores if there is an obstacle avoidance detour path around both sides of the rectangle that can connect the two nodes of the initial path.
If a detour path exists, it chooses the shorter one as the obstacle avoidance path and stops exploring the current rectangular obstacle region. The algorithm then proceeds from the terminal node of this avoidance path to traverse the next unexplored obstacle grid. If no detour path is found, the algorithm integrates obstacles from both detour paths into the rectangular zone, creating an enlarged new rectangular obstruction region. Then, it checks if the detour paths around this new rectangular region avoids obstacles and are feasible.
This process of expanding the rectangular obstacle region and checking for feasible detour paths around both sides is repeated until a valid detour path is found.
Once an avoidance path is found, the exploration of the current obstacle region ends. The same process continues to explore the next unexplored obstacle grids until all obstacle grids along the path on this map are fully traversed. The final output yields an optimized obstacle avoidance path incorporating the avoidance cost evaluation of the original path across this map. The general process of the rectangular region avoidance strategy is illustrated in Figure 2.
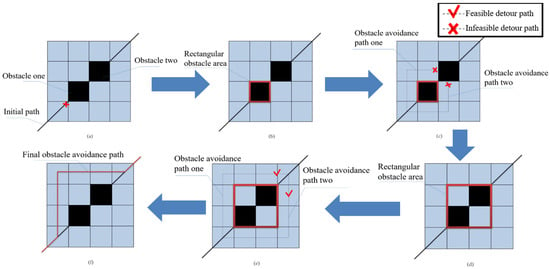
Figure 2.
(a–f) Flowchart of the obstacle avoidance strategy using rectangular regions.
The pseudocode for the rectangular-region obstacle avoidance strategy based on grid maps is shown in Algorithm 1.
| Algorithm 1. The Rectangular-Region Obstacle Avoidance Strategy Based on Grid Maps | |
| Input: | |
| path: Given the initial path node array grid map: Known map information array | |
| Output: | |
| Final_path: The final path after obstacle avoidance | |
| 1: | array1 = find_all_nodes(path,grid map) |
| 2: | array2 = find_obstacle(array1,grid map) |
| 3: | current_obstacle_node = array2(1) |
| 4: | obstacle_rect_area = array2(1) |
| 5: | while current_obstacle_node |
| 6: | detour_path = [] |
| 7: | while ~detour_path |
| 8: | [path1,path2] = find_detour_path(obstacle_rect_area,grid map) |
| 9: | if path1 && path2 |
| 10: | detour_path = min(path1,path2) |
| 11: | else if ~path1 && path2 |
| 12: | detour_path = path2 |
| 13: | else if path1 && ~path2 |
| 14: | detour_path = path1 |
| 15: | else |
| 16: | obstacle = find_min_dist_obstacle(path1,path2,obstacle_rect_area) |
| 17: | obstacle_rect_area = rect_area_extend(obstacle_rect_area,obstacle) |
| 18: | detour_path = [] |
| 19: | end |
| 20: | end |
| 21: | current_obstacle_node = find_next_obstacle(obstacle_rect_area,array2) |
| 22: | obstacle_rect_area = current_obstacle_node |
| 23: | detour_path_array = [detour_path_array;detour_path] |
| 24: | end |
| 25: | final_path = path_combition(detour_path_array,path) |
When handling a single obstacle using a rectangular obstacle avoidance strategy, two key operations are involved: rectangular region expansion and detour path search. In an m × n grid map (assuming the maximum map dimension is N), each rectangular expansion only needs to check the newly added boundary cells, resulting in a time complexity of . In the worst-case scenario, a single obstacle may require up to expansion steps to find a feasible path, leading to a total complexity of approximately for the expansion phase. The detour path search is performed using the Breadth-First Search (BFS) algorithm, which has a time complexity of per search. Therefore, the overall time complexity for handling a single obstacle is .
For the overall complexity, assuming the path encounters an average of k obstacles, the total complexity of the strategy is . In extreme cases, where the number of obstacles on the path is proportional to the map size ( = ), the complexity may reach . However, in practical applications, obstacles are usually locally clustered, and the number of critical obstacles along the path is limited. As a result, the average complexity of obstacle avoidance strategies in rectangular regions tends to be closer to .
This strategy treats obstacles as rectangular regions and identifies detour paths along their edges, thereby maximizing original path integrity while minimizing deviation. The rectangular approximation simultaneously simplifies avoidance cost computation, ultimately enhancing both the efficiency and robustness of path planning. In confined spaces, the rectangular region’s representation enables more intuitive and safer obstacle avoidance decisions. This approach effectively prevents robot–obstacle collisions by maintaining safe clearance, thus ensuring task execution stability and safety. By iteratively expanding the rectangular obstacle region and searching for feasible paths, this strategy demonstrates strong environmental adaptability and problem-solving ability. Even in extremely complex map combinations, it can plan a safe and efficient passage. In summary, the rectangular region-based obstacle avoidance strategy for grid maps provides a novel and effective solution for calculating avoidance costs in the context of path planning and evaluation across multiple map scenarios.
4.3. Fitness Evaluation Considering Multi-Map Obstacle Avoidance Costs
To accurately evaluate the fitness of each path candidate across multiple maps, the proposed rectangular-region avoidance strategy can be integrated into the multi-map fitness function calculation, yielding the following formulation:
In the above formula, represents the total multi-map fitness function of the path . represents the obstacle avoidance path’s evaluation value of the path on the map . The total fitness function of the path can be obtained by calculating the weighted sum of values across all maps. The calculation formula for , which incorporates the rectangular-region obstacle avoidance strategy, is as follows:
In the above formula, represents the path length fitness, which is obtained by calculating the reciprocal of the path length; represents the path smoothness fitness, which is mainly obtained by calculating the average turning angle of the entire path. The larger the values of both, the better the path. The final function for evaluating the obstacle avoidance path is a weighted sum of and , with and as their respective weights. The formulas for calculating , , and are as follows:
In Formula (13), the function represents the rectangular-region obstacle avoidance strategy. By inputting the obstacle map and the original path setting into the function, an obstacle avoidance path based on can be obtained on the map . The coordinates of the -th point on the obstacle avoidance path are denoted as , and represents the total number of nodes in the obstacle avoidance path.
In Formula (14), the function represents the path length fitness, which is calculated by continuously determining the Euclidean distance between two adjacent nodes to compute the path length. The fitness function evaluates the path length as the reciprocal of the total path length, where a larger value indicates a better path.
In Formula (15), the function represents the path smoothness, which is calculated by repeatedly summing the angles between two edges of three consecutive nodes on the obstacle avoidance path z using the arccosine function and then obtaining the average value. In this calculation, , , and represent segments formed by the first two points, the last two points, and the line connecting the first and last points, respectively. A larger value, closer to , indicates a smoother and more desirable path.
In summary, by applying the rectangular obstacle avoidance strategy to the original path on map , the obstacle avoidance path can be obtained. Subsequently, the path length fitness and path smoothness fitness of are calculated. By performing a weighted summation of these fitness values, the obstacle avoidance path evaluation value of the original path on map can be determined. Moreover, based on the definitions of and , a larger value of indicates a higher quality of the path.
After obtaining the obstacle avoidance path evaluation value of the original path on each map, the multi-map total fitness for each path can be calculated by performing a weighted summation.
The multi-map comprehensive fitness function, incorporating the rectangular-region obstacle avoidance strategy, allows for the precise calculation of the avoidance path required for each path individual on each map. This ensures that the improved fitness function accurately reflects the quality of a path individual in multi-map scenarios, guiding the population to iteratively update toward better multi-map fitness.
5. Detailed Steps of Ant Colony–Genetic Hybrid Algorithm for Multi-Map-Based Optimal Path Planning Problem
The specific steps for path planning of the rescue robot in mining disaster scenarios using the ant colony optimization (ACO) genetic hybrid algorithm and multi-map fitness evaluation system based on the improved strategy are as follows:
Step 1: For the existing multiple-mining-disaster-scenario grid maps with subjective probabilities, count the number of obstacles on each map. To ensure robustness, select the map with the highest number of obstacles and the highest complexity as the reference map for path planning.
Step 2: Initialize the parameters of the ACO algorithm, including the number of ants and the number of iterations. Use the improved strategy to initialize the pheromone matrix based on Euclidean distance, and set the pheromone and distance factors in the transfer probability Formula (7), as well as the evaporation factor and constants in the pheromone update Formula (8).
Step 3: In each iteration of the ACO algorithm, place each ant at the starting point of the reference map. The next node is selected according to the transfer probability Formula (7) and using roulette selection. The ants continue moving until they reach a dead-end or the target point. Ants that encounter a dead-end discard the path, while ants that reach the target record the path for pheromone concentration update.
Step 4: After all ants have completed their path search, perform the pheromone update. Collect the paths of ants that reached the destination in the previous step, and update the pheromone matrix using the pheromone concentration update Formula (8).
Step 5: Once the pheromone update is completed, the iteration process ends. If the iteration count has not reached the maximum number of iterations, retain the pheromone matrix on the map and proceed to Step 3 for the next iteration, sending ants out for another round of path search. If the maximum number of iterations has been reached, end the ACO algorithm, retain the high-quality path population from the last iteration, and proceed to Step 6 for the genetic algorithm.
Step 6: Initialize the parameters of the genetic algorithm, including the maximum number of iterations, the crossover and mutation probabilities, the path length and smoothness weights in Formula (4), and the known probabilities of each map. Use the path population left by the ACO algorithm as the initial population for the genetic algorithm, and set the new fitness function for the genetic algorithm based on the model for path planning across multiple environments.
Step 7: In each iteration, the total fitness of each initial path in the population is first calculated using the improved fitness function that takes into account the multi-map obstacle avoidance costs, as described in the calculation formula of in Formula (11). Subsequently, roulette wheel selection is performed based on each path’s fitness value, where paths with higher fitness scores are assigned proportionally greater selection probabilities for the next generation.
Step 8: Perform crossover and mutation operations on the new population according to probabilities. For mutation, apply the above-mentioned improved mutation operation considering the pheromone matrix. After completing all crossover and mutation operations, a new path population is generated. Record the total fitness of the entire population and the best individual in the current iteration, and retain the population for subsequent iterations.
Step 9: The best individual obtained in each iteration will be compared with the historical best individual from previous iterations to select the global best individual. This process continues until all iterations are completed, and the final comparison determines the optimal solution, which is the globally optimal path found by the algorithm.
Step 10: After completing the selection, crossover, and mutation operations, one iteration ends. Check the iteration count, and if the maximum number of iterations has not been reached, retain the population and proceed to Step 7 for the next iteration. If the maximum number of iterations has been reached, the algorithm ends, and the optimal path individual is determined by comparison, providing the final path for the rescue robot’s pre-run planning.
Following the above steps, experiments can be conducted on multiple mining disaster scenario grid maps with subjective probabilities. Using the improved ant colony–genetic hybrid algorithm, the optimal path for the rescue robot’s pre-run planning in a mining disaster scenario can be output.
6. Experimental Testing
6.1. Experimental Preconditions
For the multi-map experiments using the improved ant colony–genetic fusion algorithm, three complex mine disaster grid maps with subjective probabilities were selected. The subjective probabilities and complex obstacle weights of the three maps are shown in Table 1. Each map has a grid dimension of 50 × 50, with each grid cell representing an actual size of 0.5 m × 0.5 m. The obstacles in the mine disaster maps primarily include five categories.

Table 1.
Parameters of three representative mining disaster scenario maps.
The acquisition process of subjective probabilities for the maps can be summarized as follows: First, probability distribution models of typical obstacles are established by analyzing historical rescue scenarios and obstacle datasets. A large number of mine disaster scenario maps are then generated through Monte Carlo sampling based on these probability distribution models. Subsequently, according to practical requirements and expert knowledge, K-means clustering is employed to select several representative mine disaster scenario maps. The subjective probability of each representative map is determined by the proportion of maps in its cluster relative to the total number of generated maps. This approach ensures that the selected maps comprehensively cover various potential disaster scenarios while maintaining computational tractability.
From the comparison of obstacle complexity weights across the maps in the table, Map 3 exhibits the highest obstacle density. Therefore, to ensure robustness in the improved ant colony–genetic hybrid algorithm, Map 3 is selected as the benchmark map, with the start coordinate set to (6, 42) and the goal coordinate to (41, 7). The initial population is generated using the enhanced ant colony algorithm, followed by iterative optimization via a genetic algorithm incorporating the multi-map fitness function. This process ultimately yields the globally optimal path.
The parameter settings for the improved ant colony–genetic fusion algorithm in this study were configured as follows: population size m = 80, maximum iterations for ant colony algorithm set to 90, pheromone evaporation coefficient = 0.25, pheromone weight = 2, distance weight = 8, maximum iterations for genetic algorithm set to 60, crossover probability = 0.2, and mutation probability = 0.05. Following parameter determination, the multi-map experiments employed Formula (12) to compute the obstacle avoidance path evaluation metric for each individual map. Subsequently, Formula (11) was applied to perform weighted integration of these evaluation metrics, ultimately yielding the comprehensive multi-map fitness score as the optimal path selection criterion. All simulations were conducted on MATLAB R2023a platform, utilizing hardware with the following specifications: 12th Gen Intel(R) Core(TM) i7-12700 processor (2.10 GHz) manufactured by Intel Corporation, Santa Clara, California, USA and 32.0 GB RAM.
6.2. Feasibility Verification of the Algorithm
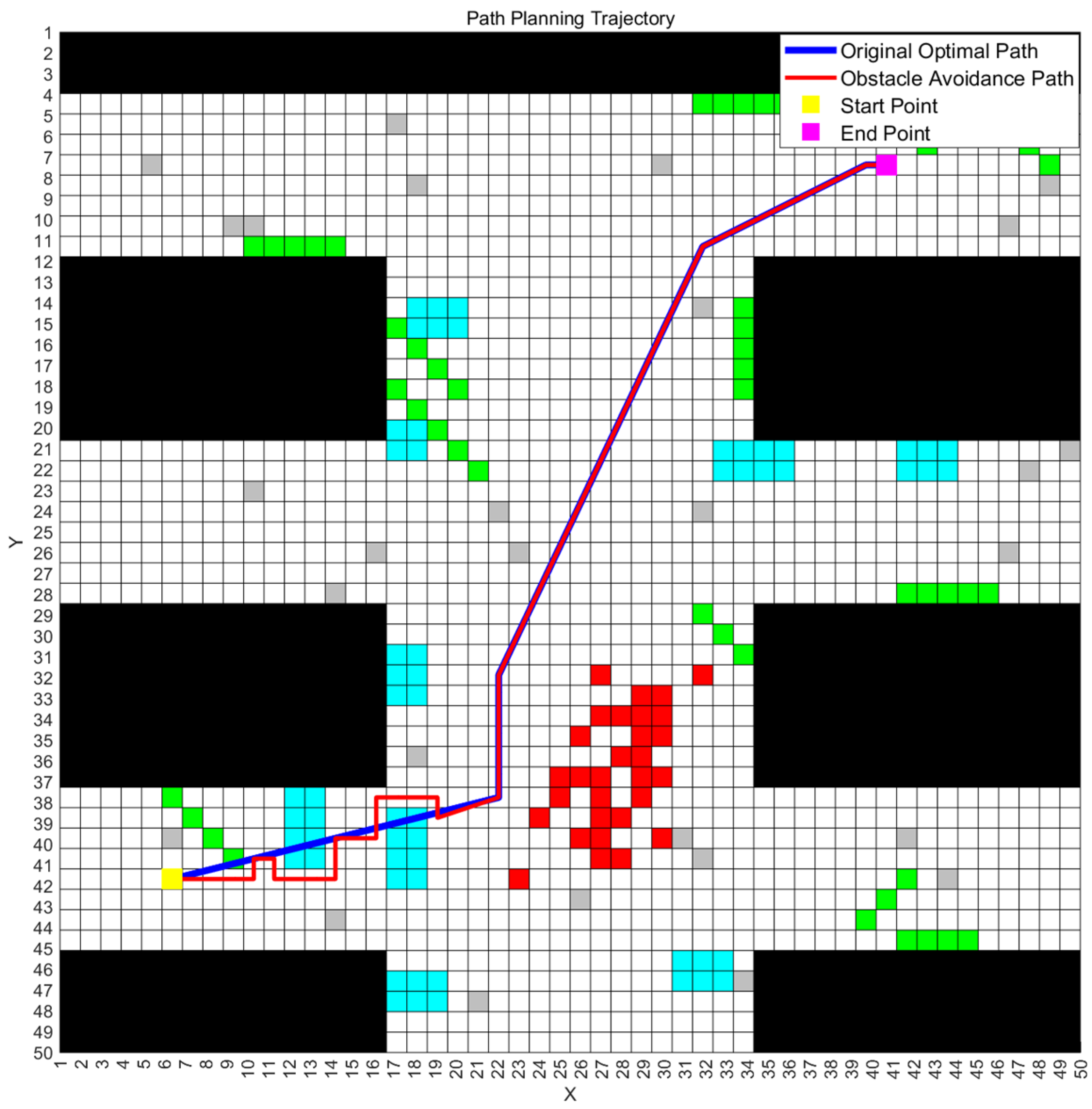
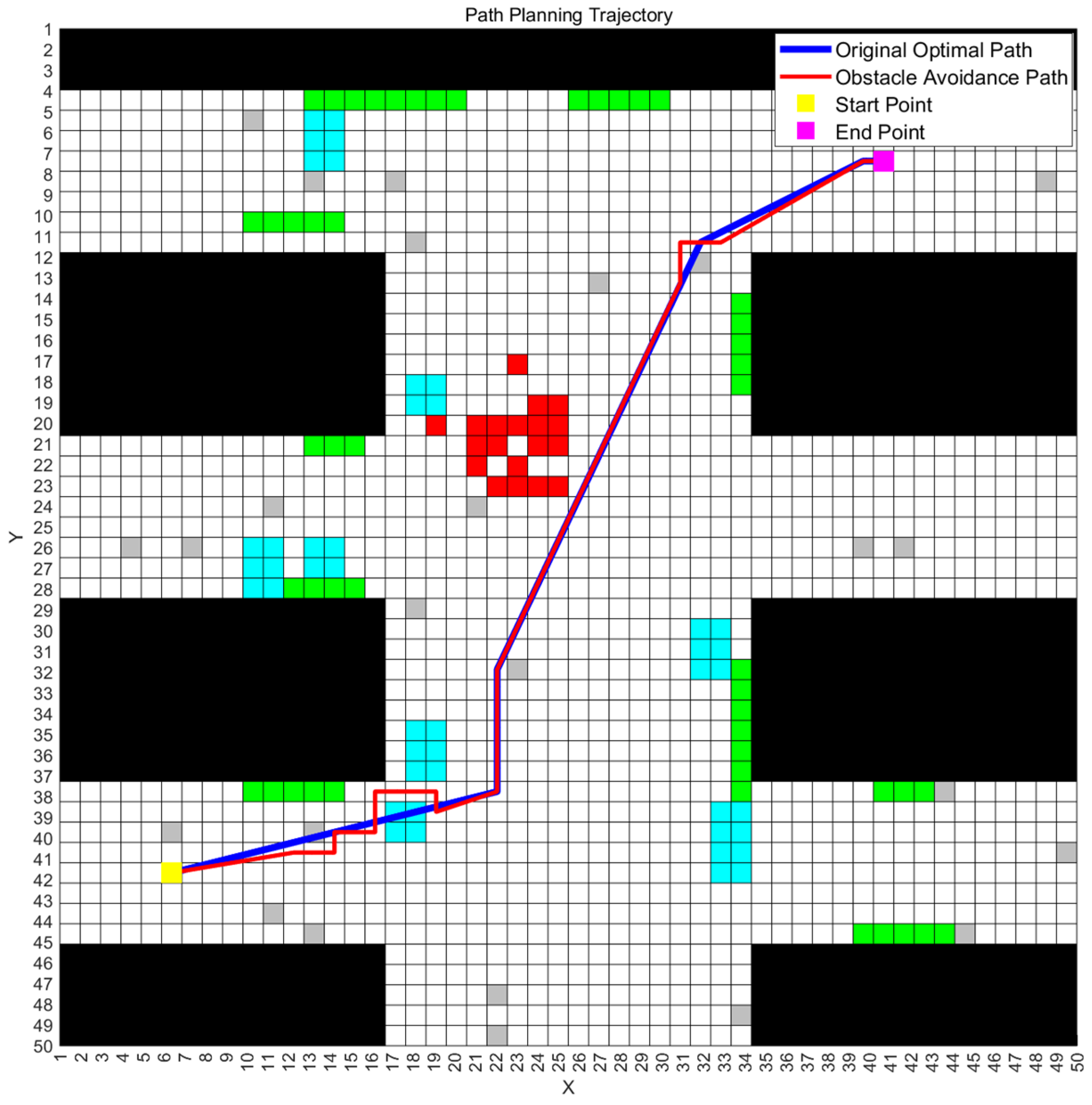
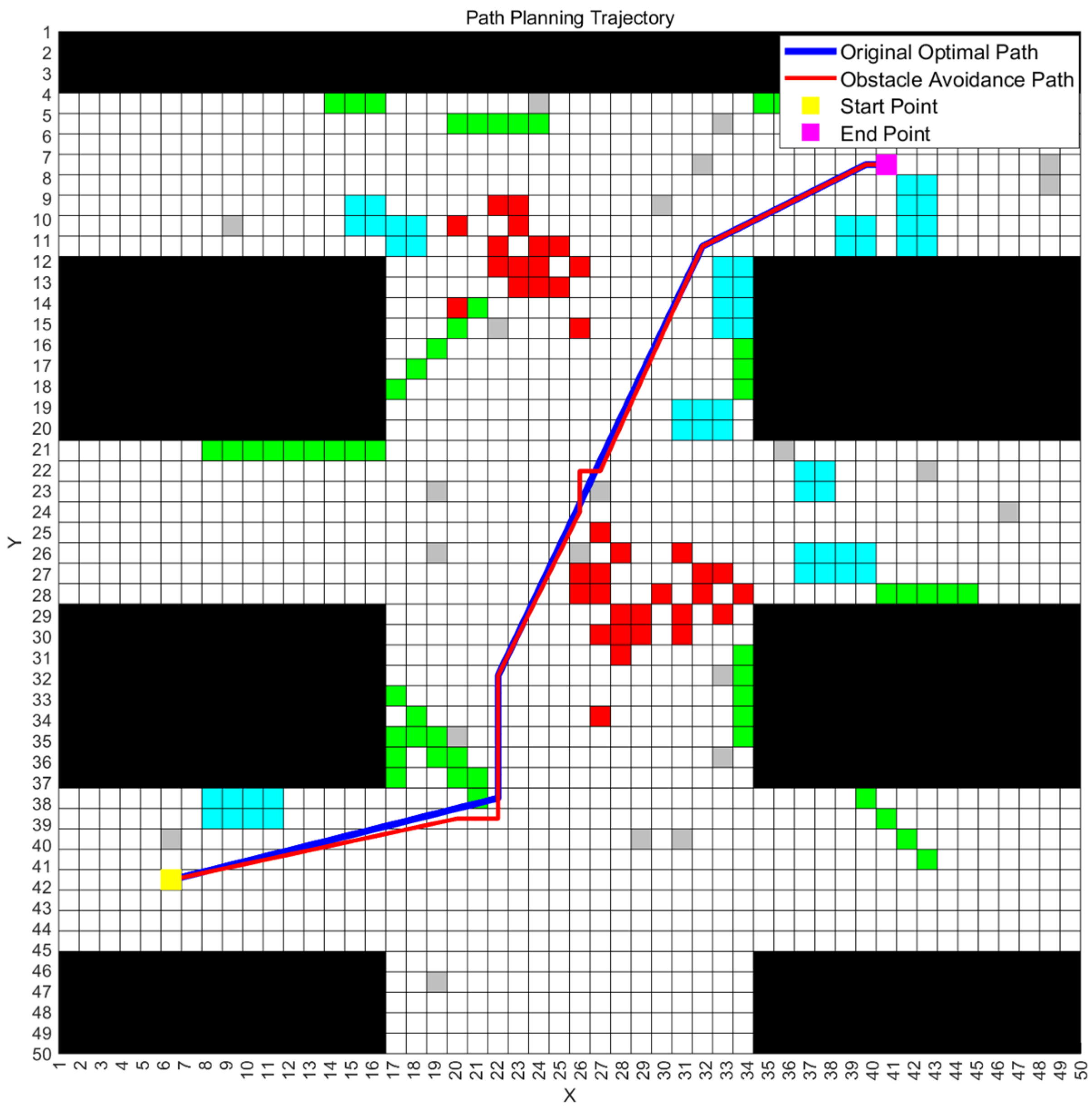
To validate the feasibility of the improved ant colony–genetic algorithm for multi-map path planning, we executed the algorithm on the three mine disaster scenario maps described earlier and recorded the final optimal path along with its fitness values. The optimal path obtained from a single experimental run, as well as the corresponding obstacle avoidance paths generated by the rectangular region strategy on all three maps, are illustrated in Figure 3, Figure 4 and Figure 5. The correspondence between obstacle types and grid colors in the figure is shown in the following Table 2.
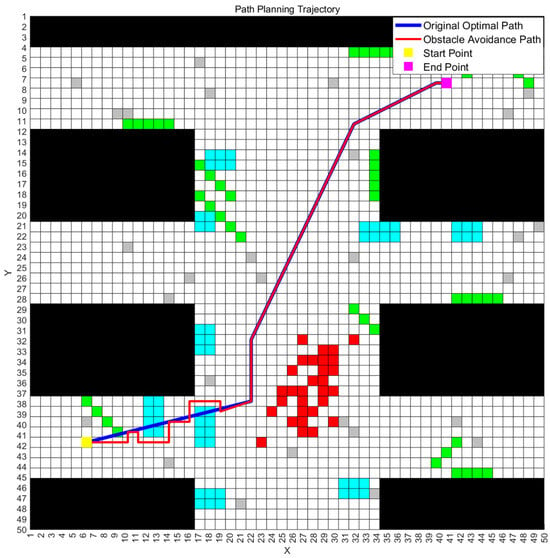
Figure 3.
The optimal path and obstacle avoidance path in Map 1.
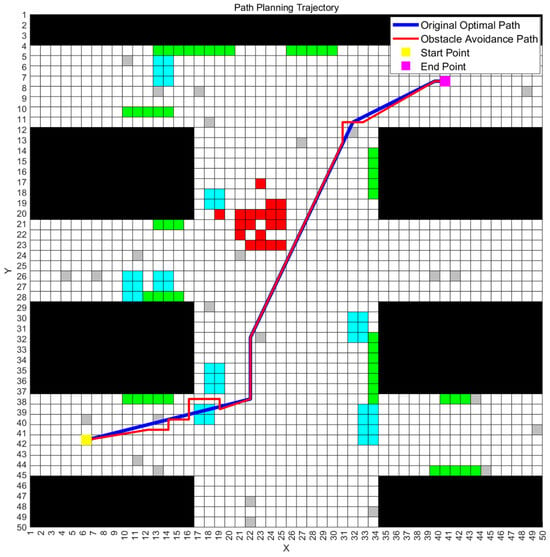
Figure 4.
The optimal path and obstacle avoidance path in Map 2.
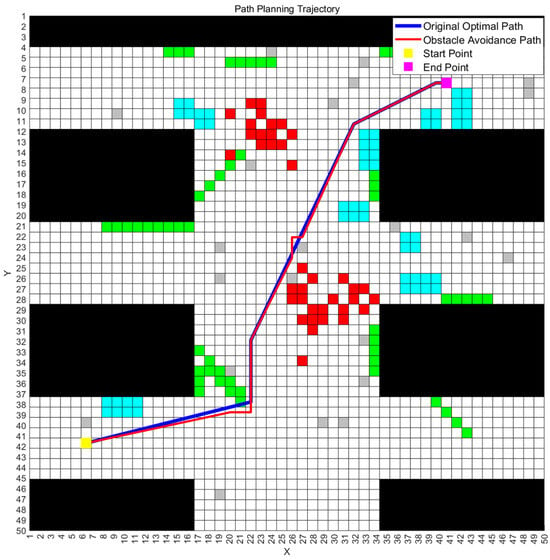
Figure 5.
The optimal path and obstacle avoidance path in Map 3.

Table 2.
Correspondence between grid colors and obstacle types.
Figure 3, Figure 4 and Figure 5 illustrate the optimal paths obtained by the improved hybrid algorithm, as well as the “obstacle-avoiding paths” derived from these optimal paths on the three mine disaster grid maps, with obstacle avoidance costs incorporated. From the figures, it is visually apparent that the improved ant colony–genetic fusion algorithm can generate high-quality original optimal paths that are relatively smooth and shorter in length for path planning across multiple environments, achieving a balance between path smoothness and length. Moreover, the figures show that the expected deviation of the optimal paths when encountering “possible obstacles” on all three maps is minimal. This effectively balances the inherent optimality of the paths with the environmental obstacle avoidance requirements, thus reducing unnecessary path adjustments. Table 3 presents the obstacle avoidance path evaluation metrics for all three maps and the corresponding weighted composite fitness values obtained by the improved ant colony–genetic fusion algorithm.

Table 3.
Optimal path fitness and obstacle avoidance path evaluation values for the three maps.
It should be noted that the obstacle avoidance path evaluation values in the table are derived by weighting the inverse of the path length (unit: meters) and the average path smoothness (unit: degrees), as indicated by Equation (4). The final fitness value is then obtained by weighting the obstacle avoidance path evaluation values for each map, as described in Equation (11). Therefore, the final fitness has no specific unit, and a higher fitness value indicates better path quality.
Analysis of the above table reveals that the improved ant colony–genetic algorithm consistently generates optimal paths with superior overall fitness values while maintaining high obstacle avoidance evaluation scores across all individual maps. This demonstrates the algorithm’s robust obstacle negotiation capability in multi-map environments, which effectively preserves path optimality while minimizing additional costs induced by avoidance maneuvers.
6.3. Statistical Performance Analysis
To further validate the stability and robustness of the proposed improved hybrid algorithm in path planning, this section conducts 30 independent path planning experiments under multi-map scenarios. Each experiment records the fitness value of the optimal path and the obstacle avoidance evaluation value for individual maps. The statistical results derived from these repeated experiments provide a comprehensive assessment of algorithmic stability. The following Table 4 presents the statistical outcomes of the 30 multi-map experiments, including the best optimal path fitness, worst optimal path fitness, mean fitness, median fitness, and variance of the optimal path fitness.

Table 4.
Statistical results of 30 multi-map experiments.
To further verify the stability and reliability of the algorithm, this paper also calculates the confidence intervals for the four aforementioned indicators. The confidence interval provides a quantitative description of the fluctuation range of the performance metrics, helping to understand the algorithm’s stability across multiple runs and its adaptability to different initial conditions and environments. To ensure the accuracy of the results, a 95% confidence level was used to compute the upper and lower bounds for each indicator, ensuring the reliability of the results within the given confidence level. The confidence intervals for each indicator are shown in the Table 5 below.

Table 5.
Confidence intervals for the four indicators on three maps.
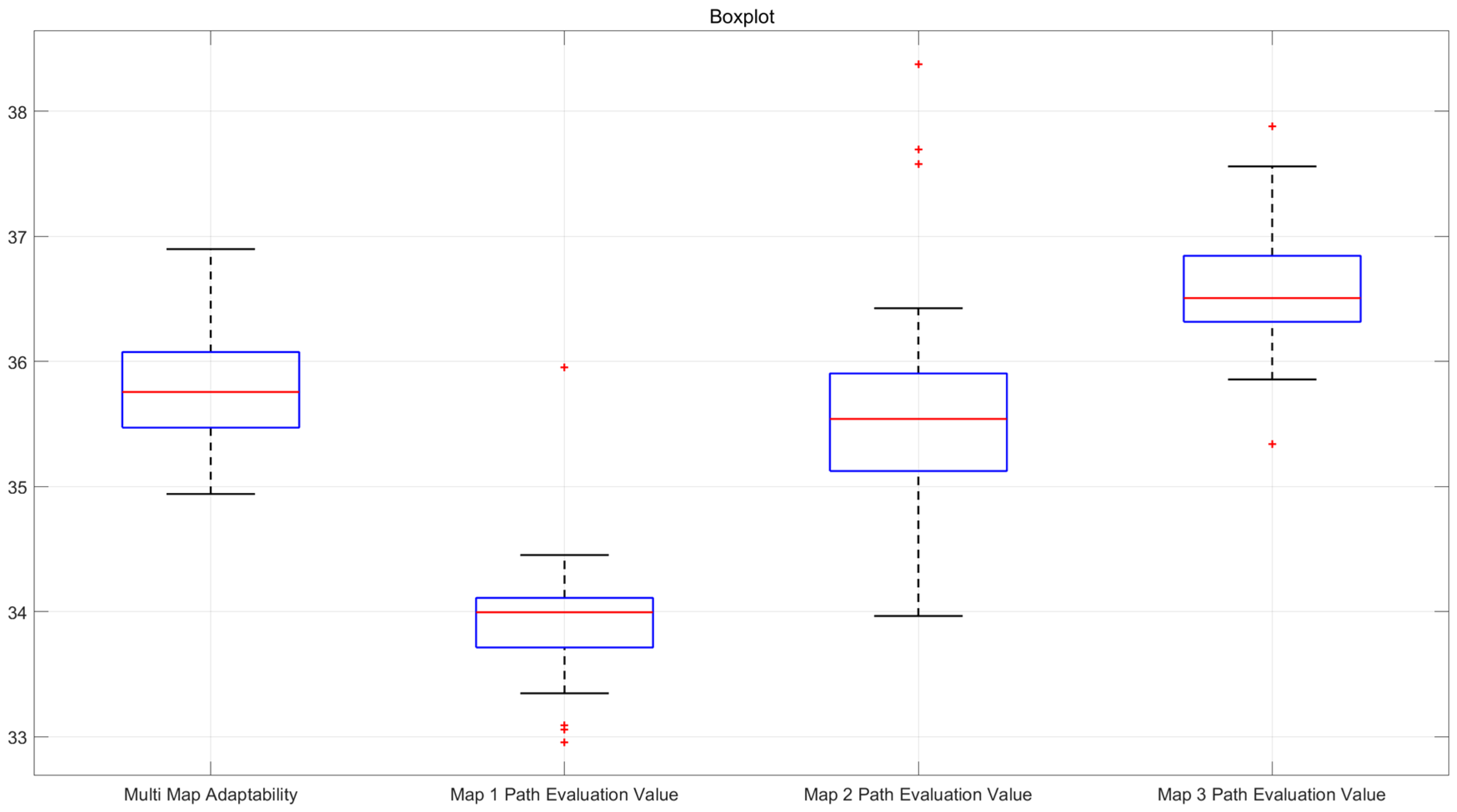
Based on the calculated confidence interval results, it can be observed that the confidence intervals for all indicators are small, further indicating that the optimal paths provided by the improved hybrid algorithm exhibit minimal fluctuation across different map scenarios, demonstrating good stability. The boxplots illustrating the obstacle avoidance path evaluation values for each map and the total fitness values of optimal paths are presented in the following Figure 6.
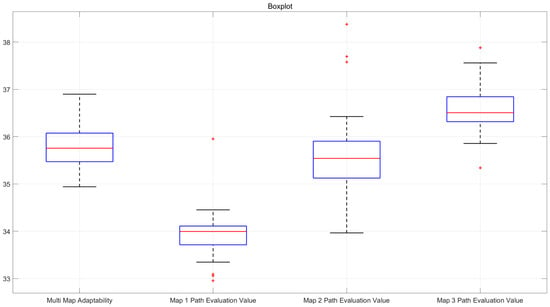
Figure 6.
Box plot of optimal path fitness and obstacle avoidance path evaluation values for the three maps.
Analysis of the statistical results demonstrates that the improved algorithm maintains consistent performance across multiple trials, as evidenced by favorable median and mean values with minimal variance—both in terms of the composite fitness across all three maps and individual obstacle avoidance evaluation value for each specific map. This robustness confirms that the enhanced hybrid algorithm reliably generates high-quality and stable solutions for multi-map path planning applications.
6.4. Validation of Effectiveness
To demonstrate the superiority and effectiveness of the improved ant colony–genetic fusion algorithm, this paper compares the proposed hybrid algorithm with other algorithms in the context of multi-map problems, exploring the improvements achieved by the hybrid algorithm over traditional and hybrid algorithms in multi-map scenarios. Since other algorithms cannot directly handle multi-map problems, this study selects the map with the highest generation probability from the multi-map set for path planning and then applies the rectangular obstacle avoidance strategy to compute the obstacle avoidance paths and costs for the other two maps. The Table 6 below shows a comparison of the obstacle avoidance path evaluation values for four algorithms across three maps in one experiment.

Table 6.
Comparison of obstacle avoidance path evaluation value on three maps.
In a comparative experiment, if an algorithm yields better obstacle avoidance path evaluation values across more maps, it can be considered superior in the experiment. As shown in the table, the proposed algorithm performs slightly better than the traditional genetic algorithm and RRT*–GA hybrid algorithm on Map 3 and significantly outperforms other algorithms on the other two maps. Therefore, it is concluded that the proposed hybrid algorithm demonstrates superiority in this experiment. In the case of multi-map problems, the proposed hybrid algorithm, by considering path planning across multiple maps simultaneously, ensures that the paths minimize the obstacle avoidance cost on each individual map. This indicates the algorithm’s superiority over traditional methods in handling multi-map problems. Furthermore, from the comparison of computational times, it is evident that, due to the iterative nature of the ant colony algorithm and the multi-map consideration, the proposed hybrid algorithm achieves a significant improvement in path quality across all maps with relatively minimal time cost. The following Table 7 shows the statistical results of 30 experiments on multi-map path planning using four algorithms.

Table 7.
Comparison of statistical results from 30 experiments of four algorithms on three maps.
The analysis of the table results shows that the highly stochastic RRT* algorithm, although having a shorter runtime, produces paths of lower quality and cannot compete with other algorithms. The improved hybrid algorithm yields obstacle avoidance evaluation values similar to those of the traditional genetic algorithm and RRT*–GA hybrid algorithm on Map 3 (the map with the highest probability) but demonstrates superior and more stable performance in multiple experiments on the other two maps. Furthermore, compared to the traditional genetic algorithm and RRT*–GA, the improved hybrid algorithm does not significantly increase computation time, indicating that the hybrid algorithm can achieve higher quality and more stable optimal paths with relatively low computational cost. These findings collectively confirm the enhanced stability and robustness of the hybrid algorithm in path planning applications across multiple environments.
6.5. Algorithm Adaptability Verification
To validate the adaptability of the improved hybrid algorithm in more complex experimental scenarios, this study selects six larger-scale mine disaster scenario maps with subjective probabilities. The map dimensions are expanded to 100 × 100 grids, with each grid maintaining a resolution of 0.5 m × 0.5 m. On these six maps, the algorithm’s feasibility and statistical performance are re-evaluated. The parameters of the six maps are detailed in the Table 8 below.

Table 8.
Parameters of six large-scale representative mining disaster scenario maps.
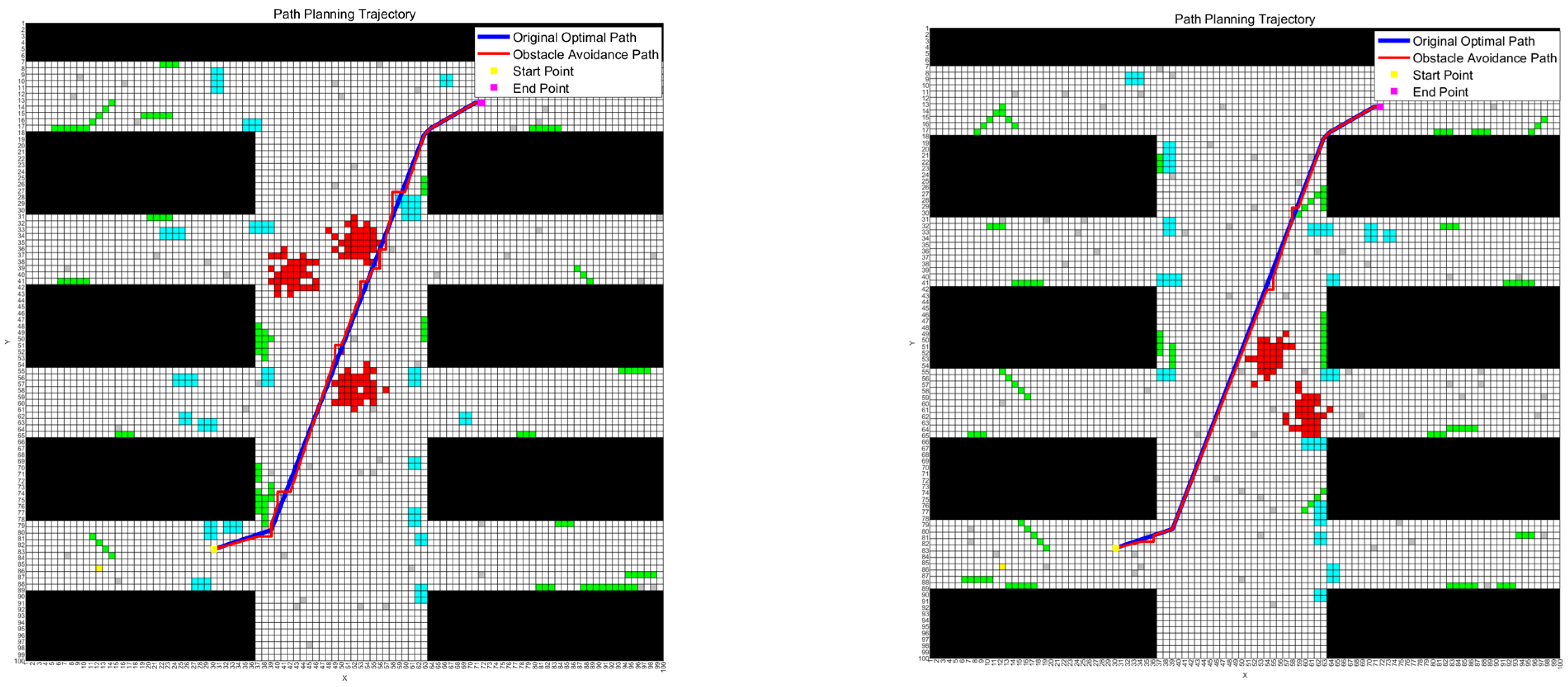
Analysis of the obstacle complexity weights across the maps in the table reveals that Map 1 exhibits the highest obstacle density. Consequently, in the adaptability experiments, the improved hybrid algorithm selects Map 1 as the benchmark map, with the start coordinate set to (30, 83) and the target point coordinate to (72, 13). The experimental results validating the algorithm’s feasibility are presented below Figure 7, Figure 8 and Figure 9. The statistical results of 30 experiments using four algorithms for multi-map path planning on six larger-scale maps are presented in Table 9.
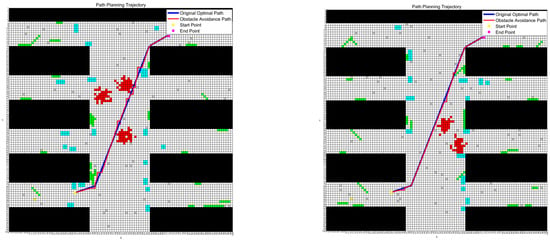
Figure 7.
The optimal path and obstacle avoidance path in Map 1 and Map 2.

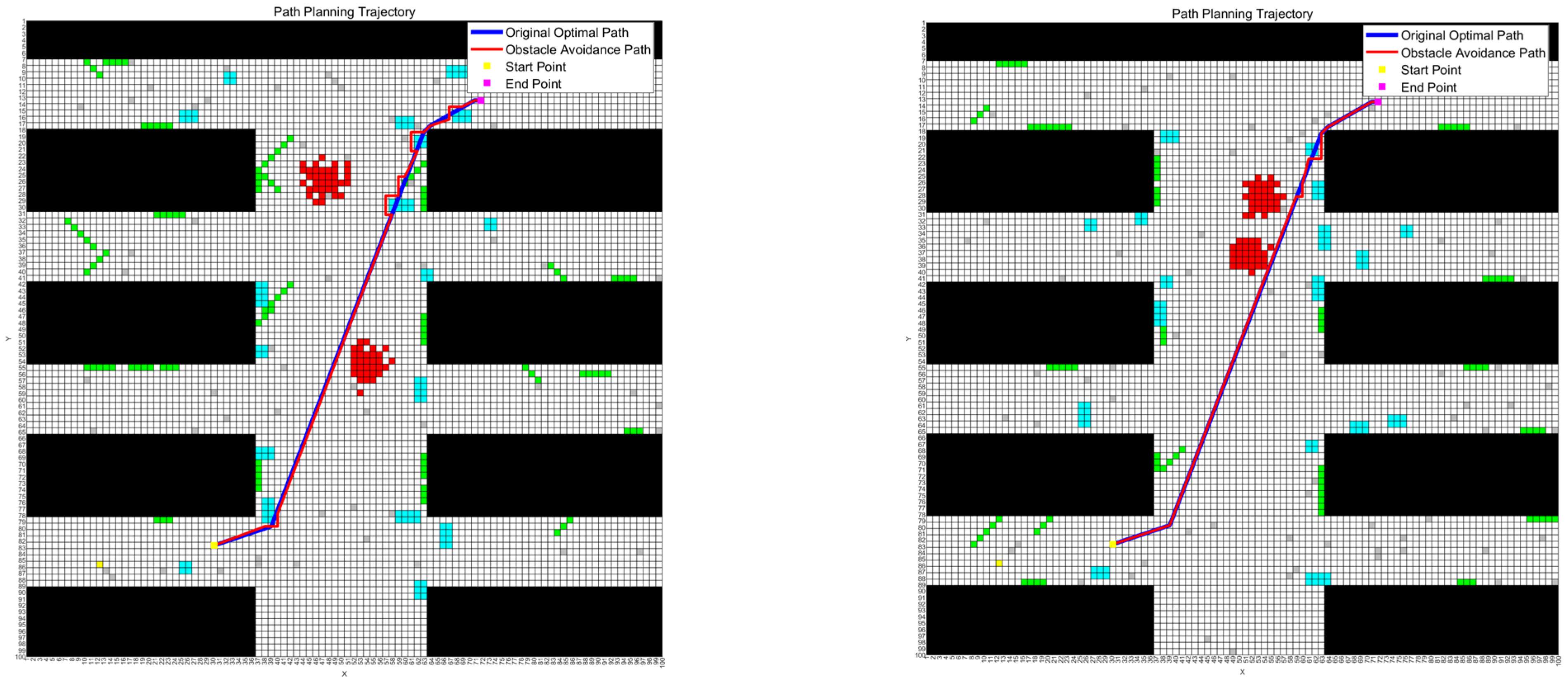
Figure 8.
The optimal path and obstacle avoidance path in Map 3 and Map 4.
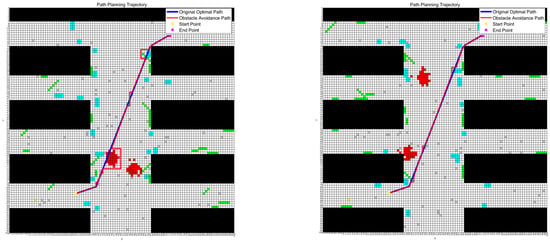
Figure 9.
The optimal path and obstacle avoidance path in Map 5 and Map 6.

Table 9.
Optimal path fitness and obstacle avoidance path evaluation values for six maps.
Analysis of the experimental results presented in the aforementioned figures demonstrates that the improved hybrid algorithm continues to generate high-quality primary optimal paths in larger-scale path planning scenarios across multiple maps, while maintaining excellent obstacle avoidance evaluation metrics across all individual maps. This balanced approach effectively reconciles path optimality with avoidance requirements, thereby minimizing unnecessary path modifications. These findings confirm that the enhanced ant colony–genetic algorithm can produce high-fitness optimal paths in expanded complex maps while preserving robust obstacle negotiation capabilities across increased map quantities.
To further validate the algorithm’s stability in enlarged map environments, we conducted 30 repeated experiments on the six mine disaster grid maps following the same methodology as Section 6.3. The statistical results of these experiments are presented in the Table 10 below.

Table 10.
Statistical results of 30 multi-map experiments on six maps.
The confidence intervals for each indicator are shown in the Table 11 below.

Table 11.
Confidence intervals for the seven indicators on six maps..
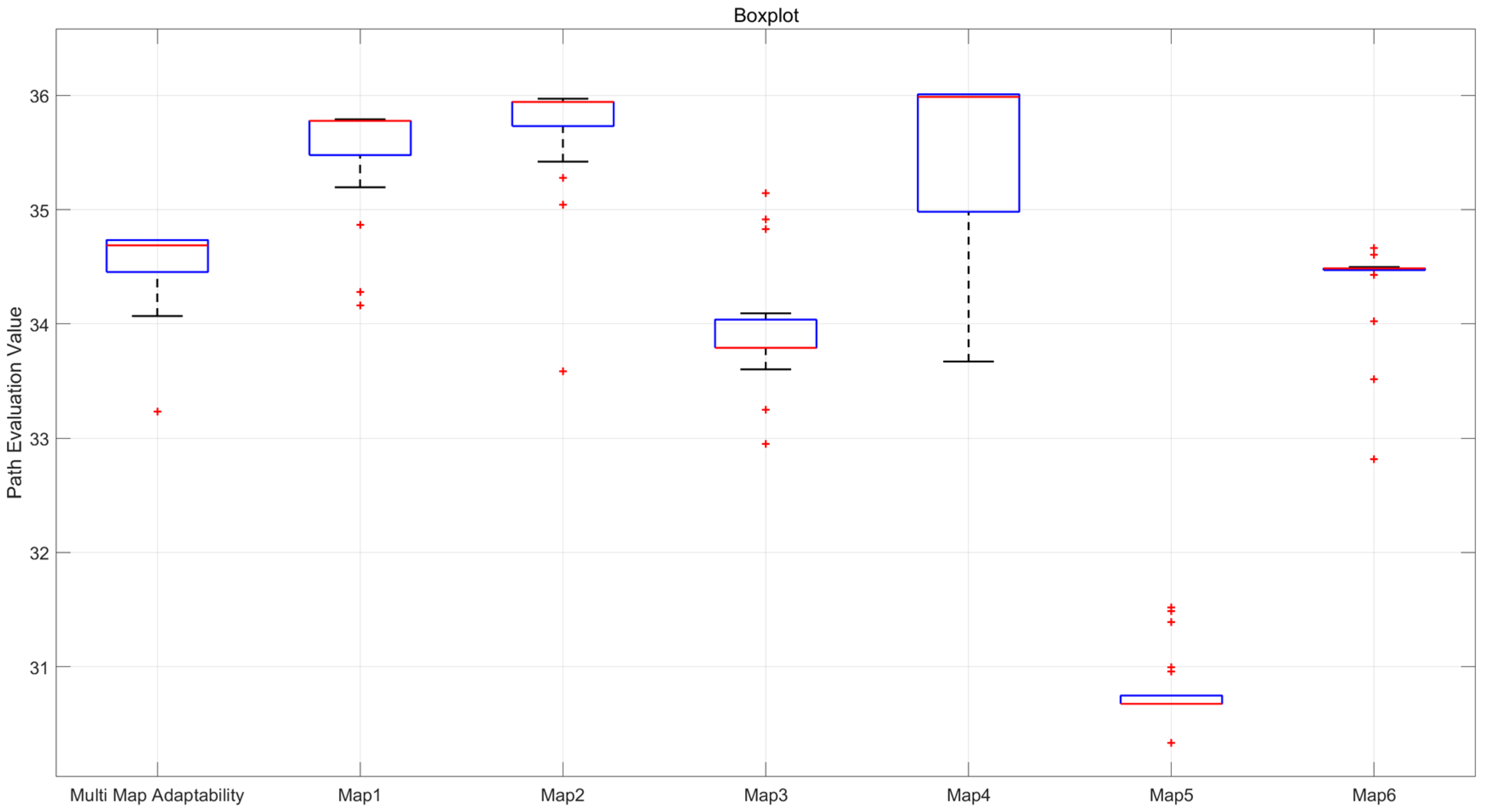
Based on the calculated confidence interval results, it can be observed that even across larger and more diverse map scenarios, the confidence intervals for all indicators remain small, indicating that the optimal paths provided by the improved hybrid algorithm also demonstrate good stability across maps of varying sizes and quantities. The boxplots illustrating the obstacle avoidance path evaluation values for each map and the total fitness values of optimal paths are presented in the following Figure 10.
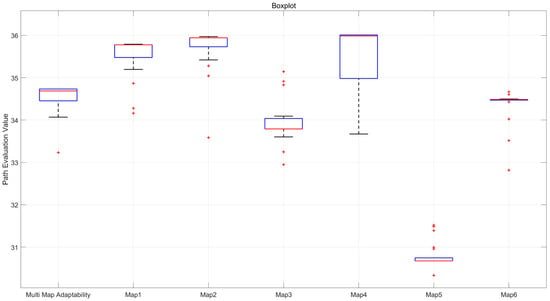
Figure 10.
Box plot of optimal path fitness and obstacle avoidance path evaluation values for the six maps.
The statistical results demonstrate that the improved algorithm maintains consistent performance across multiple trials, exhibiting favorable median and mean values with minimal variance for both the composite fitness across all six maps and individual obstacle avoidance evaluation value per map. This stability confirms the enhanced hybrid algorithm’s capability to generate high-quality and robust solutions for multi-scenario navigation tasks. The experimental findings further verify that the improved ant colony–genetic algorithm preserves superior performance even in larger-scale maps, underscoring its remarkable adaptability.
This study also conducts a comparative analysis of the proposed improved hybrid algorithm, traditional genetic algorithm, traditional RRT* algorithm, and the RRT*–genetic hybrid algorithm in larger and more complex map scenarios to demonstrate the superiority and adaptability of the proposed algorithm in more challenging experimental environments. The comparison results of the obstacle avoidance path evaluation values, obtained from 30 independent repetitions for each of the six representative maps, are shown in the Table 12 below.

Table 12.
Comparison of statistical results from 30 experiments of four algorithms on six maps.
From the comparison results in the above table, it can be seen that, in the larger, more numerous, and more complex multi-mining disaster map scenarios, the improved hybrid algorithm, despite having a higher time cost, outperforms traditional algorithms such as genetic algorithms, RRT*, and traditional hybrid algorithms like RRT*-GA in terms of path quality. This is primarily due to the ant colony algorithm’s ability to generate high-quality initial solutions and its consideration of obstacle avoidance costs across multiple maps. These results also demonstrate that the proposed improved hybrid algorithm has strong stability and adaptability, capable of producing stable and high-quality path solutions in more complex scenarios.
In summary, this chapter systematically validates the improved ant colony–genetic algorithm’s feasibility, stability, superiority, and adaptability in diverse experimental scenarios for multi-map path planning problems. The results collectively demonstrate that the enhanced hybrid algorithm effectively produces optimal paths with consistently high quality across multiple maps. The algorithm maintains excellent performance scalability in expanded environments, confirming its practical utility for complex scenario applications.
7. Conclusions
To address the issues of poor path population quality, slow convergence speed, and lack of consideration for actual obstacle avoidance costs in traditional genetic algorithms when faced with complex obstacle environments, this paper proposes an improved genetic algorithm path planning scheme for rescue robots based on multi-scenario map modeling and validates it through simulations. By introducing an improved ant colony algorithm to generate the initial population for the genetic algorithm, the quality of the initial population was enhanced, and the convergence speed of the algorithm was accelerated. A grid-map-based, rectangular obstacle avoidance strategy was proposed, which accurately calculates the actual obstacle avoidance path and costs for a predetermined route on the obstacle map. Based on this strategy, a fitness function that considers obstacle avoidance costs across multiple maps was developed to accurately reflect the quality of path individuals in multi-map scenarios and ensure that the population iteratively converges toward the optimal multi-map solution. Simulation results demonstrated that the proposed rectangular obstacle avoidance strategy can ensure minimal impact on the original path while accurately reflecting the actual obstacle avoidance costs on the obstacle map. In multi-map experimental scenarios, the improved ant colony–genetic hybrid algorithm demonstrated stable performance in identifying high-quality paths with minimized avoidance costs, thereby achieving an optimal balance between path efficiency and obstacle negotiation requirements. This comes at the cost of a moderately increased computational time due to the comprehensive multi-map evaluation and precise obstacle avoidance calculations.
The proposed improved hybrid algorithm demonstrates significant potential for real-world applications in mine disaster rescue scenarios. By generating high-quality pre-planned paths that account for multiple possible environmental conditions, the algorithm can effectively reduce rescue time in critical situations. In typical mining disasters, where every minute is crucial for saving lives, the algorithm’s ability to quickly provide optimal paths with minimal computational overhead ensures that rescue robots can be deployed immediately upon arrival at the disaster site. The rectangular obstacle avoidance strategy further enhances operational safety by minimizing unnecessary detours and ensuring reliable navigation through complex, obstacle-filled environments. This combination of efficiency, safety, and adaptability makes the proposed method particularly valuable for time-sensitive rescue operations in hazardous mining conditions.
Future research directions could focus on several aspects to further enhance the proposed method. First, integrating real-time sensor data with the multi-map planning approach could enable dynamic updates of environmental maps during rescue operations, improving adaptability to unforeseen changes. Second, exploring the use of deep reinforcement learning could potentially optimize the hybrid algorithm’s performance in highly dynamic and uncertain environments. Third, extending the algorithm to three-dimensional path planning would better address the complexities of multi-level mine structures. Additionally, field testing in actual mine disaster scenarios would provide valuable insights into the algorithm’s practical performance and identify areas for further refinement.
Author Contributions
Conceptualization, J.Z. and H.L.; Data curation, X.Z.; Formal analysis, X.Z.; Funding acquisition, J.Z. and H.L.; Investigation, J.Z., Z.X. and H.L.; Methodology, J.Z. and Z.X.; Resources, X.Z. and B.L.; Software, Z.X., H.L. and B.L.; Supervision, H.L.; Validation, B.L.; Visualization, Z.X., X.Z. and B.L.; Writing—original draft, Z.X.; Writing—review and editing, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Dreams Foundation of Jianghuai Advance Technology Center of China under Grant 2023-ZM01G001, National Natural Science Foundation of China under Grant 62173284 and 92248304, and Shenzhen Science Fund for Distinguished Young Scholars under Grant RCJC20210706091946001.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
Authors Xiaojun Zhu and Bin Lan are employed by Jianghuai Advance Technology Center; Author Houde Liu is partly employed by Jianghuai Advance Technology Center. The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Chou, J.S.; Cheng, M.Y.; Hsieh, Y.M.; Yang, I.T.; HsuH, T. Optimal path planning in real time for dynamic building fire rescue operations using wireless sensors and visual guidance. Autom. Constr. 2019, 99, 1–17. [Google Scholar] [CrossRef]
- Yu, X.B.; Li, C.L.; ZhouJ, F. A constrained differential evolution algorithm to solve UAV path planning in disaster scenarios. Knowl.-Based Syst. 2020, 204, 106209. [Google Scholar] [CrossRef]
- Li, Y.; Li, M.; Zhu, H.; Hu, E.; Tang, C.; Li, P.; You, S. Development and applications of rescue robots for explosion accidents in coal mines. J. Field Robot. 2020, 37, 466–489. [Google Scholar] [CrossRef]
- Li, M.; Zhu, H.; You, S.; Wang, L.; Tang, C. Efficient laser-based 3D SLAM for coal mine rescue robots. IEEE Access 2018, 7, 14124–14138. [Google Scholar] [CrossRef]
- Habibian, S.; Dadvar, M.; Peykari, B.; Hosseini, A.; Salehzadeh, M.H.; Hosseini, A.H.; Najafi, F. Design and implementation of a maxi-sized mobile robot (Karo) for rescue missions. Robomech J. 2021, 8, 1. [Google Scholar] [CrossRef]
- Miller, I.D.; Cladera, F.; Cowley, A.; Shivakumar, S.S.; Lee, E.S.; Jarin-Lipschitz, L.; Bhat, A.; Rodrigues, N.; Zhou, A.; Cohen, A.; et al. Mine tunnel exploration using multiple quadrupedal robots. IEEE Robot. Autom. Lett. 2020, 5, 2840–2847. [Google Scholar] [CrossRef]
- Dang, T.; Mascarich, F.; Khattak, S.; Nguyen, H.; Nguyen, H.; Hirsh, S.; Reinhart, R.; Papachristos, C.; Alexis, K. Autonomous search for underground mine rescue using aerial robots. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–8. [Google Scholar]
- Ozkan, M.F.; Carrillo, L.R.G.; King, S.A. Rescue boat path planning in flooded urban environments. In Proceedings of the 2019 IEEE International Symposium on Measurement and Control in Robotics (ISMCR), Houston, TX, USA, 19–21 September 2019. [Google Scholar]
- Ebadi, K.; Chang, Y.; Palieri, M.; Stephens, A.; Hatteland, A.; Heiden, E.; Thakur, A.; Funabiki, N.; Morrell, B.; Wood, S.; et al. LAMP: Large-scale autonomous mapping and positioning for exploration of perceptually-degraded subterranean environments. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 80–86. [Google Scholar]
- Li, X.Y.; Liang, X.D.; Wang, X.; Wang, R.; Shu, L.L.; Xu, W.T. Deep reinforcement learning for optimal rescue path planning in uncertain and complex urban pluvial flood scenarios. Appl. Soft Comput. 2023, 144, 110543. [Google Scholar] [CrossRef]
- Lee, J.; Park, H.; Kim, Y.; Park, C.G.; Lee, J.H. Multi-Level Indoor Path Planning and Clearance-Based Path Optimization for Search and Rescue Operations. IEEE Access 2023, 11, 40930–40943. [Google Scholar] [CrossRef]
- Chen, X.; Chen, Y.; Xu, J.; Zheng, Y. SLAM-based Navigation Technology for Rescue Robots in Post-disaster Scenarios. Highlights Sci. Eng. Technol. 2023, 52, 33–39. [Google Scholar] [CrossRef]
- Meng, X.; Gao, H.; Wang, J.; Wang, X.; Yu, H.; Zhang, J. Dynamic path planning of autonomous bulldozers using activity-value-optimised bio-inspired neural networks and adaptive cell decomposition. Appl. Soft Comput. 2024, 164, 111944. [Google Scholar] [CrossRef]
- Zhao, D.; Ni, L.; Zhou, K.; Lv, Z.; Qu, G.; Gao, Y.; Yuan, W.; Wu, Q.; Zhang, F.; Zhang, Q. A Study of the Improved A* Algorithm Incorporating Road Factors for Path Planning in Off-Road Emergency Rescue Scenarios. Sensors 2024, 24, 5643. [Google Scholar] [CrossRef] [PubMed]
- Mirahadi, F.; McCabe, B.Y. EvacuSafe: A real-time model for building evacuation based on Dijkstra’s algorithm. J. Build. Eng. 2021, 34, 101687. [Google Scholar] [CrossRef]
- Qi, J.; Yang, H.; Sun, H. MOD-RRT*: A sampling-based algorithm for robot path planning in dynamic environment. IEEE Trans. Ind. Electron. 2020, 68, 7244–7251. [Google Scholar] [CrossRef]
- Ravankar, A.A.; Ravankar, A.; Emaru, T.; Kobayashi, Y. HPPRM: Hybrid potential based probabilistic roadmap algorithm for improved dynamic path planning of mobile robots. IEEE Access 2020, 8, 221743–221766. [Google Scholar] [CrossRef]
- Fang, W.; Liao, Z.; Bai, Y. Improved ACO algorithm fused with improved Q-Learning algorithm for Bessel curve global path planning of search and rescue robots. Robot. Auton. Syst. 2024, 182, 104822. [Google Scholar] [CrossRef]
- Cui, J.; Wu, L.; Huang, X.; Xu, D.; Liu, C.; Xiao, W. Multi-strategy adaptable ant colony optimization algorithm and its application in robot path planning. Knowl.-Based Syst. 2024, 288, 111459. [Google Scholar] [CrossRef]
- Cheng, K.P.; Mohan, R.E.; Nhan, N.H.; Le, A.V. Multi-objective genetic algorithm-based autonomous path planning for hinged-tetro reconfigurable tiling robot. IEEE Access 2020, 8, 121267–121284. [Google Scholar] [CrossRef]
- Yang, K.; Duan, P.; Yu, H. An improved genetic algorithm for solving the helicopter routing problem with time window in post-disaster rescue. Math. Biosci. Eng. 2023, 20, 15672–15707. [Google Scholar] [CrossRef] [PubMed]
- Tao, B.; Kim, J.H. Mobile robot path planning based on bi-population particle swarm optimization with random perturbation strategy. J. King Saud Univ.-Comput. Inf. Sci. 2024, 36, 101974. [Google Scholar] [CrossRef]
- Wu, J.; Song, C.; Ma, J.; Wu, J.; Han, G. Reinforcement learning and particle swarm optimization supporting real-time rescue assignments for multiple autonomous underwater vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 23, 6807–6820. [Google Scholar] [CrossRef]
- Han, D.; Jiang, H.; Wang, L.; Zhu, X.; Chen, Y.; Yu, Q. Collaborative Task Allocation and Optimization Solution for Unmanned Aerial Vehicles in Search and Rescue. Drones 2024, 8, 138. [Google Scholar] [CrossRef]
- Liu, B.; Xu, M.; Gao, L.; Yang, J.; Di, X. A hybrid approach for high-dimensional optimization: Combining particle swarm optimization with mechanisms in neuro-endocrine-immune systems. Knowl.-Based Syst. 2022, 253, 109527. [Google Scholar] [CrossRef]
- Rao, J.; Xiang, C.; Xi, J.; Chen, J.; Lei, J.; Giernacki, W.; Liu, M. Path planning for dual UAVs cooperative suspension transport based on artificial potential field-A* algorithm. Knowl.-Based Syst. 2023, 277, 110797. [Google Scholar] [CrossRef]
- Li, Y.; Jin, R.; Xu, X.; Qian, Y.; Wang, H.; Xu, S.; Wang, Z. A mobile robot path planning algorithm based on improved A* algorithm and dynamic window approach. IEEE Access 2022, 10, 57736–57747. [Google Scholar] [CrossRef]
- Yu, Z.; Si, Z.; Li, X.; Wang, D.; Song, H. A novel hybrid particle swarm optimization algorithm for path planning of UAVs. IEEE Internet Things J. 2022, 9, 22547–22558. [Google Scholar] [CrossRef]
- Sabeeh, S.; Al-Furati, I.S. Efficient Path Planning in Medical Environments: Integrating Genetic Algorithm and Probabilistic Roadmap (GA-PRM) for Autonomous Robotics. Iraqi J. Electr. Electron. Eng. 2024, 20, 243–258. [Google Scholar] [CrossRef]
- Zhang, D.; Luo, R.; Yin, Y.B.; Zou, S.L. Multi-objective path planning for mobile robot in nuclear accident environment based on improved ant colony optimization with modified A*. Nucl. Eng. Technol. 2023, 55, 1838–1854. [Google Scholar] [CrossRef]
- Chen, P.; Li, Q.; Zhang, C.; Cui, J.; Zhou, H. Hybrid chaos-based particle swarm optimization-ant colony optimization algorithm with asynchronous pheromone updating strategy for path planning of landfill inspection robots. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419859083. [Google Scholar] [CrossRef]
- Liu, C.; Wu, L.; Xiao, W.; Li, G.; Xu, D.; Guo, J.; Li, W. An improved heuristic mechanism ant colony optimization algorithm for solving path planning. Knowl.-Based Syst. 2023, 271, 110540. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, S.; Tang, S.; Song, J.; Zhang, J. Path Planning for Robots Based on Adaptive Dual-Layer Ant Colony Optimization Algorithm and Adaptive Dynamic Window Approach. IEEE Sens. J. 2025, 99, 1. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, P.; Ru, Y.; Wu, D.; Wang, S.; Yin, N.; Meng, F.; Liu, Z. A scheduling route planning algorithm based on the dynamic genetic algorithm with ant colony binary iterative optimization for unmanned aerial vehicle spraying in multiple tea fields. Front. Plant Sci. 2022, 13, 998962. [Google Scholar] [CrossRef] [PubMed]
- Pehlivanoglu, Y.V.; Pehlivanoglu, P. An enhanced genetic algorithm for path planning of autonomous UAV in target coverage problems. Appl. Soft Comput. 2021, 112, 107796. [Google Scholar] [CrossRef]
- Kurdi, M. Ant colony optimization with a new exploratory heuristic information approach for open shop scheduling problem. Knowl.-Based Syst. 2022, 242, 108323. [Google Scholar] [CrossRef]
- Liu, C.; Wu, L.; Huang, X.; Xiao, W. Improved dynamic adaptive ant colony optimization algorithm to solve pipe routing design. Knowl.-Based Syst. 2022, 237, 107846. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).