Dynamic Error Compensation for Ball Screw Feed Drive Systems Based on Prediction Model
Abstract
1. Introduction
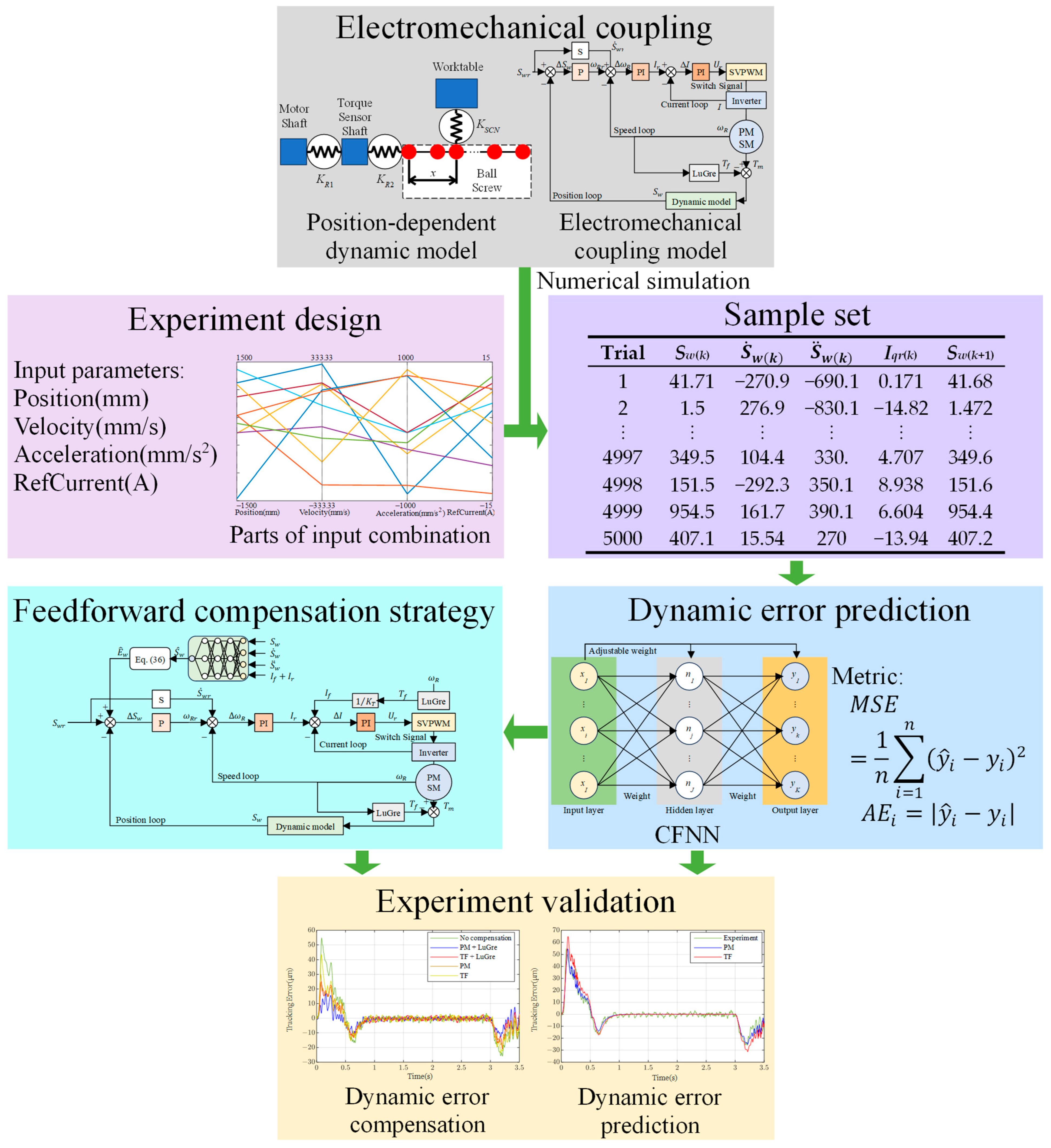
2. Methodology
3. Electromechanical Coupling Model of the Ball Screw Feed System
3.1. Position-Dependent Dynamics Modeling Based on the Lumped Mass Method and Distributed Mass Method
3.1.1. Lumped Mass Model of Two Shafts and Worktable
3.1.2. Position-Dependent Distributed Mass of the Screw
3.1.3. Position-Dependent Dynamic Model of Ball Screw Feed System
3.2. Friction Identification Based on the LuGre Model
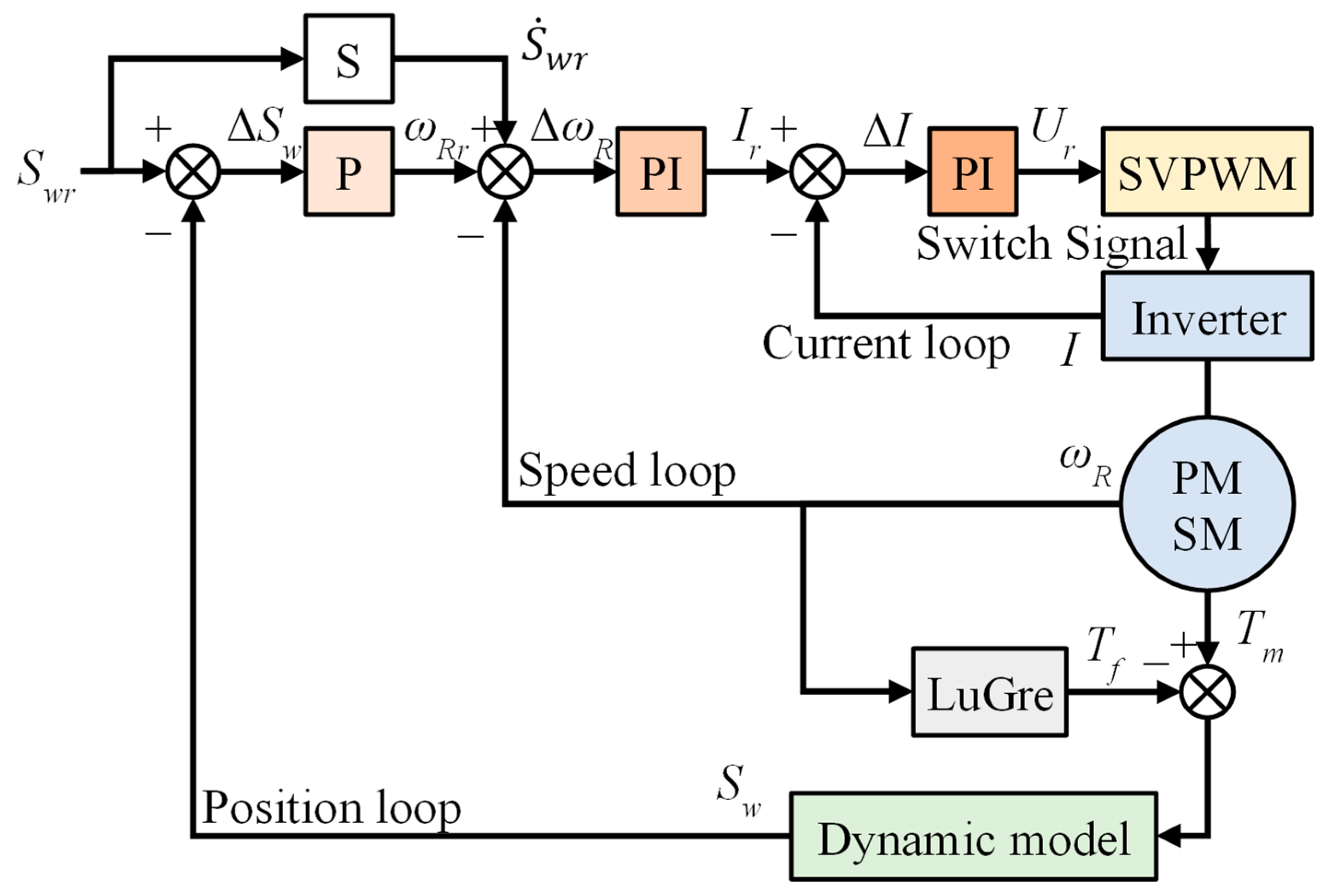
3.3. Electromechanical Coupling Modeling of the Ball Screw Feed System
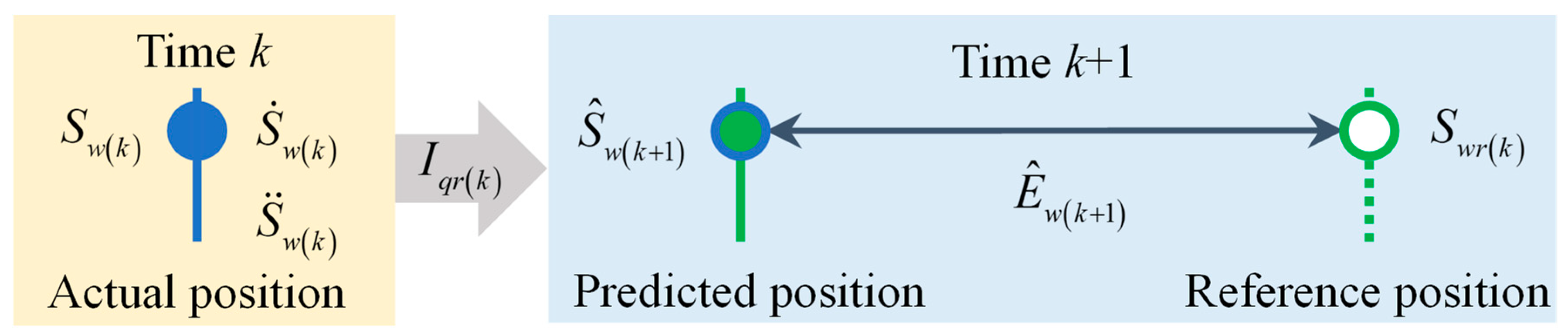
4. Dynamic Error Modeling of One Control Cycle and Feedforward Compensation
4.1. Basic Principles and Processes
4.2. Latin Hypercube Sampling Experimental Design
4.3. Dynamic Error Modeling Based on a CFNN Prediction Model
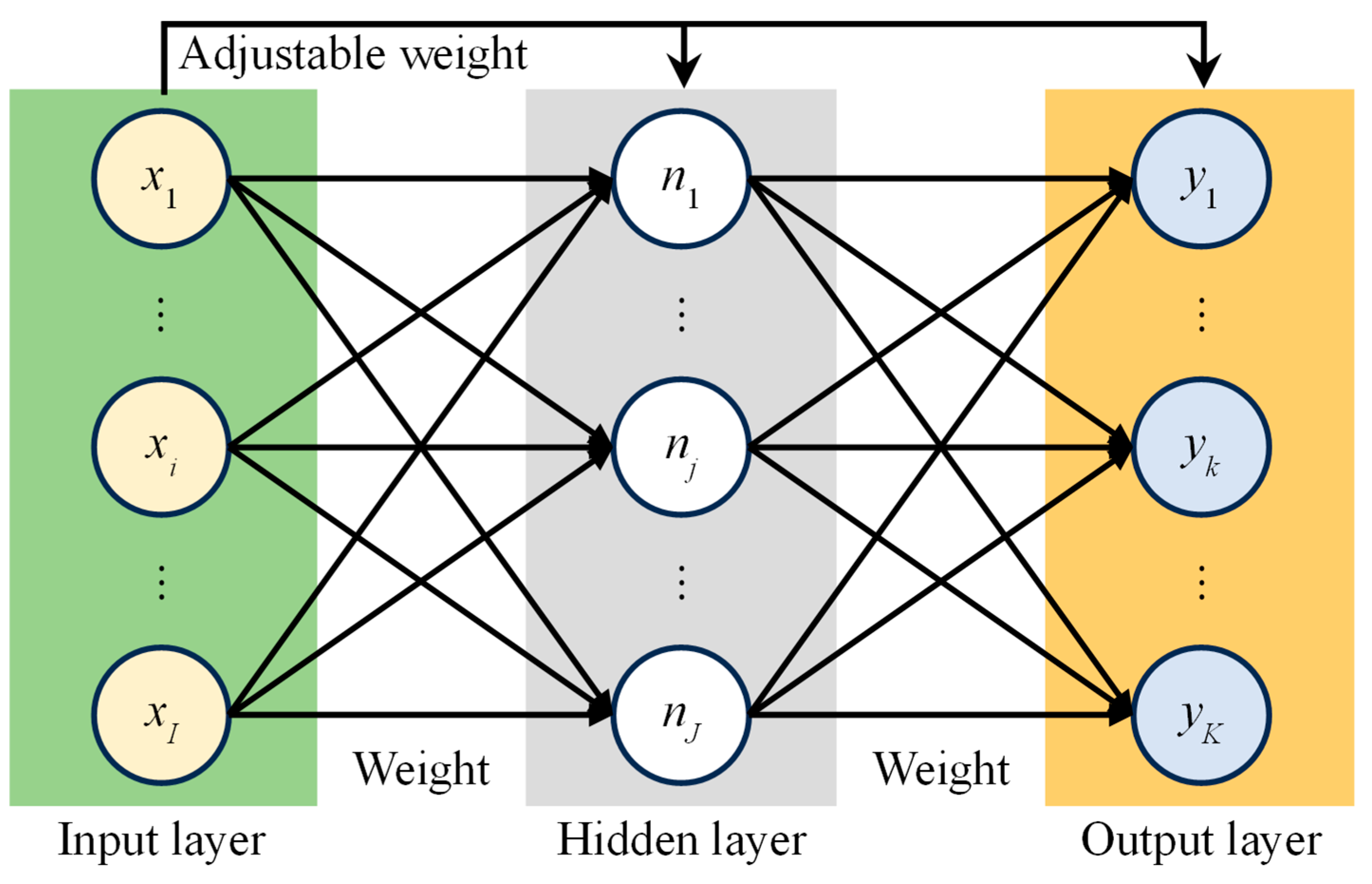
4.3.1. Cascade-Forward Neural Network
4.3.2. Training of the CFNN Prediction Model of Worktable’s Dynamic Error
4.3.3. Validation and Testing of CFNN
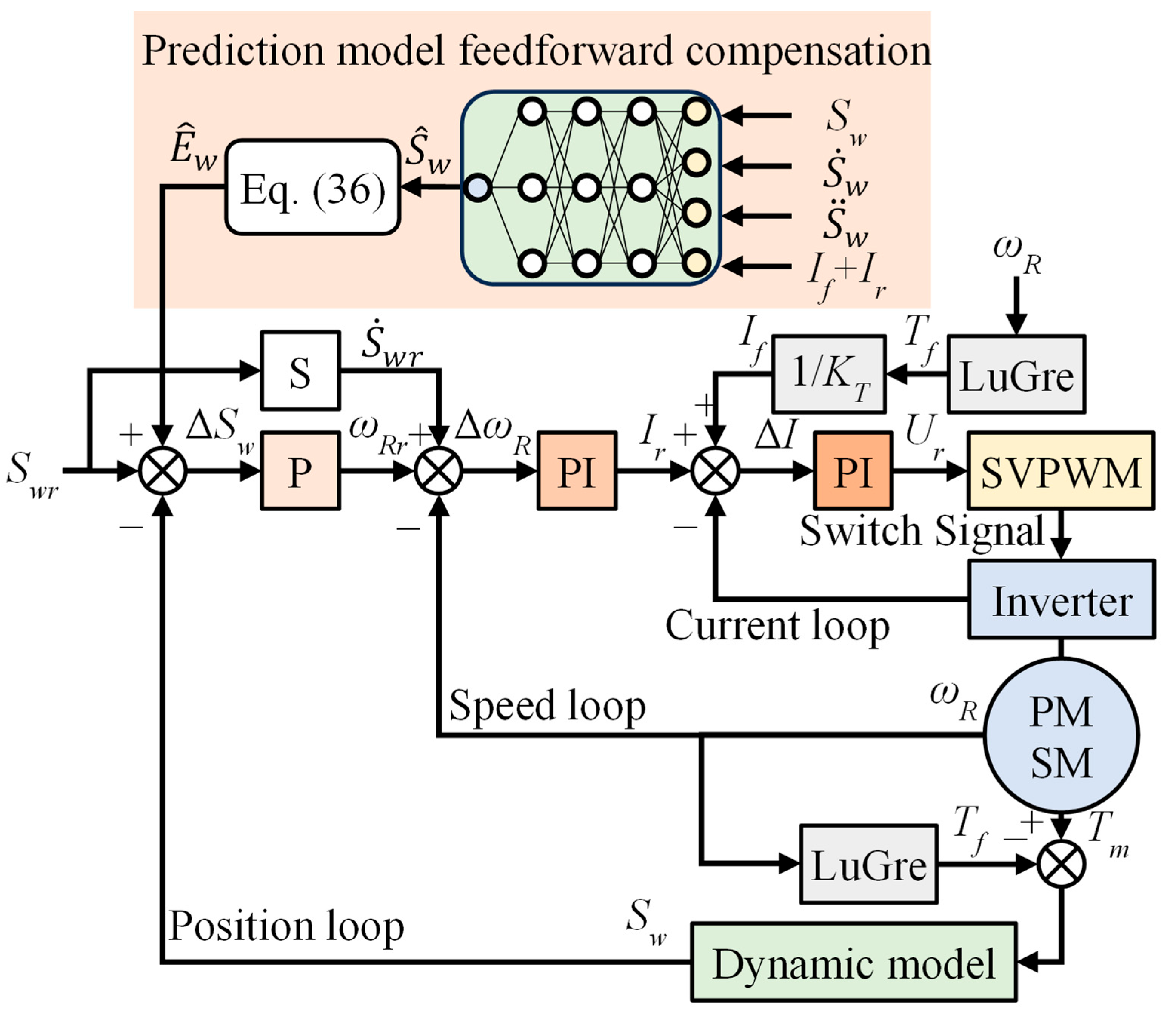
4.4. Feedforward Compensation Structure Based on the Prediction Model
5. Simulation and Experiment
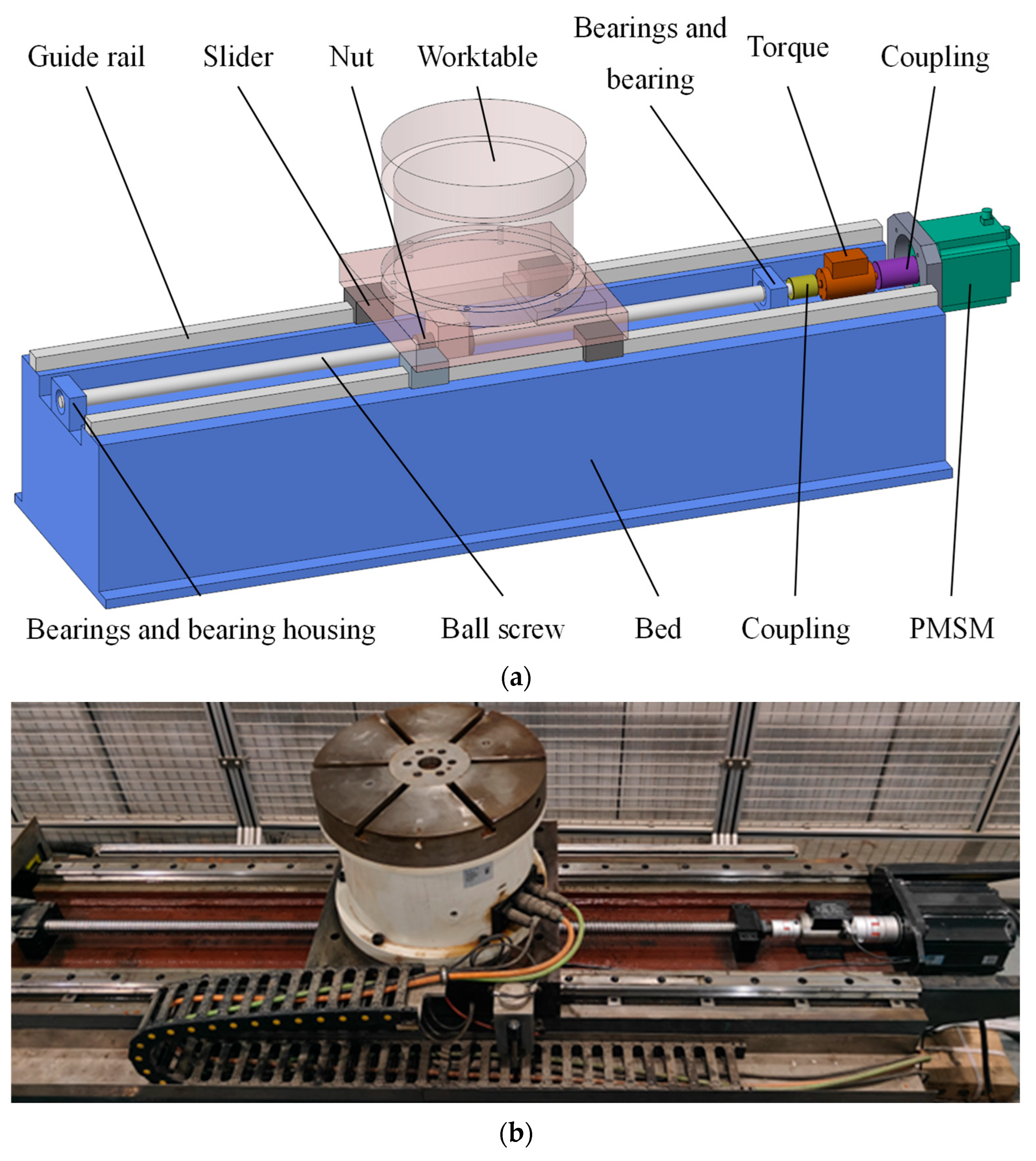
5.1. Ball Screw Feed System Experimental Test Platform
5.2. Simulation and Experimentation of Typical Trajectories
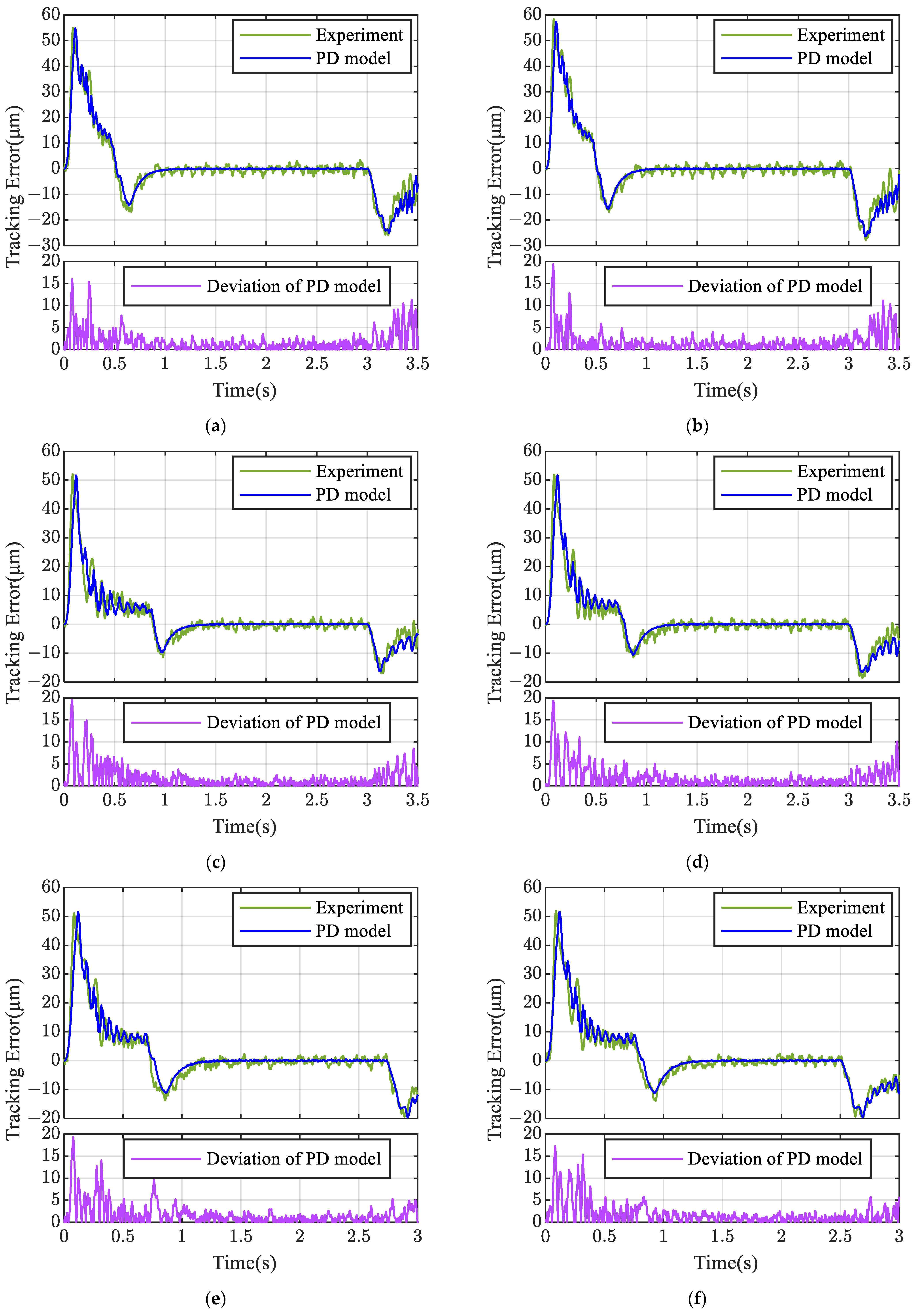
5.2.1. Electromechanical Coupling Model Simulation and Experimentation
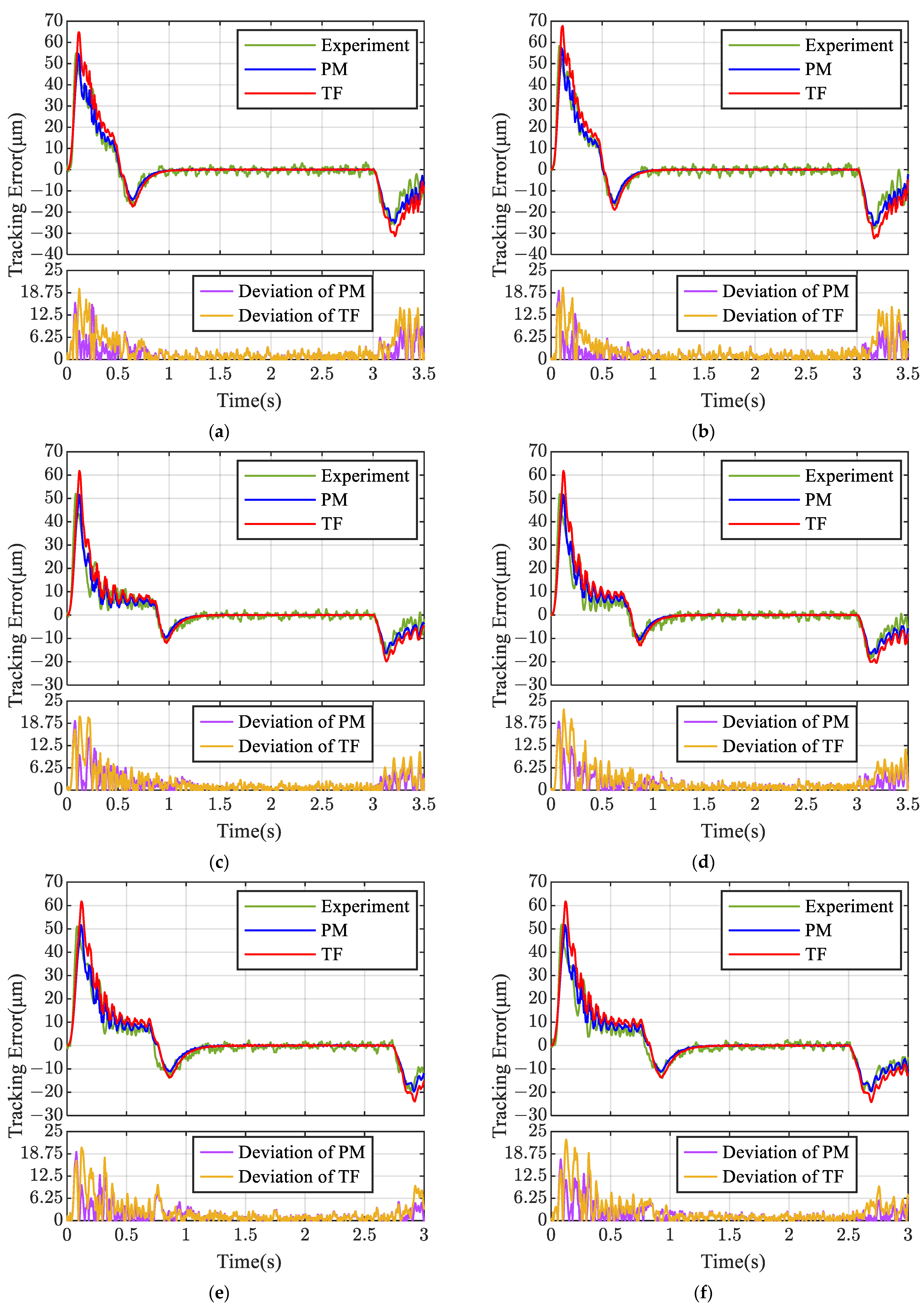
5.2.2. Dynamic Error Prediction
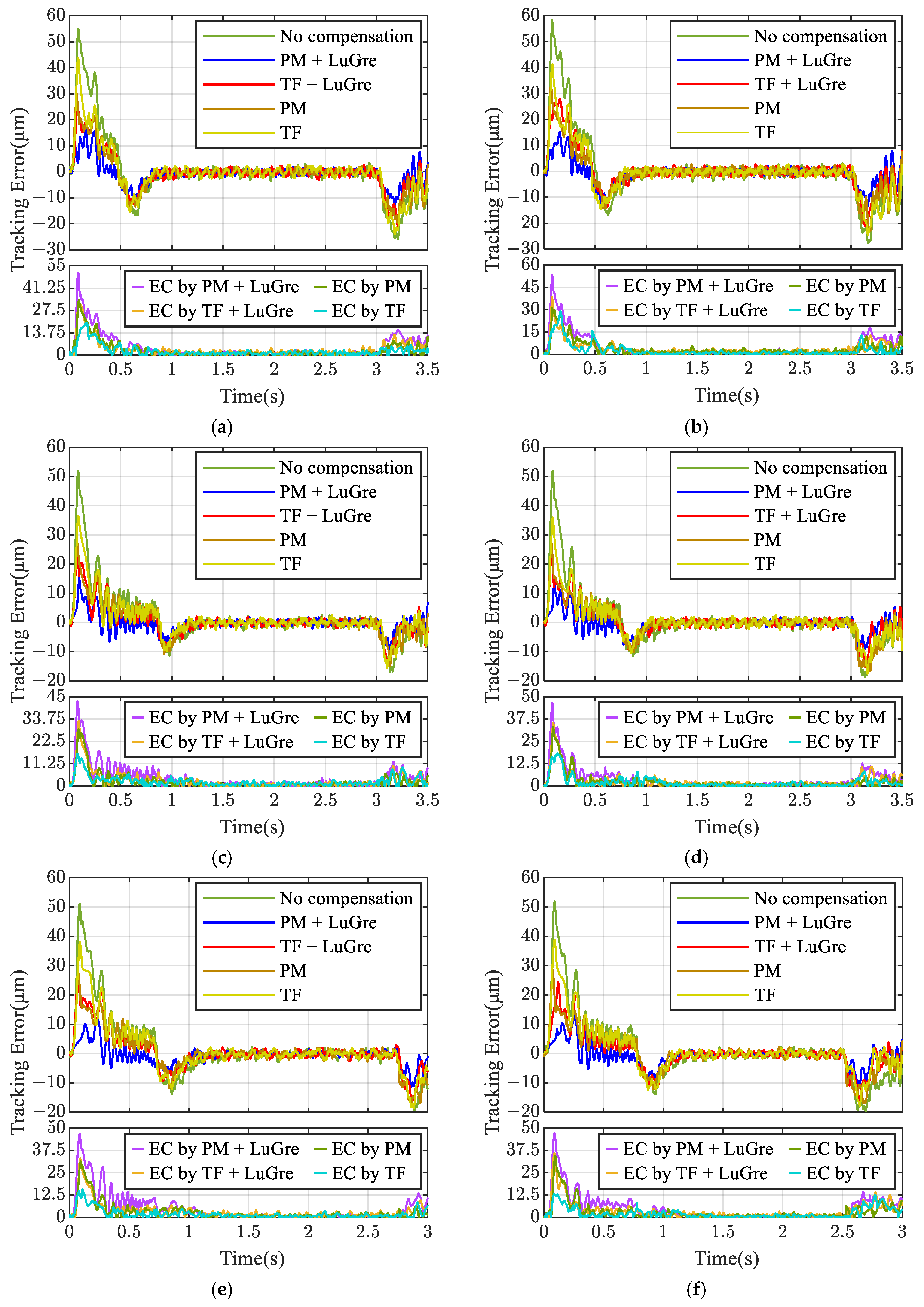
5.2.3. Dynamic Error Compensation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
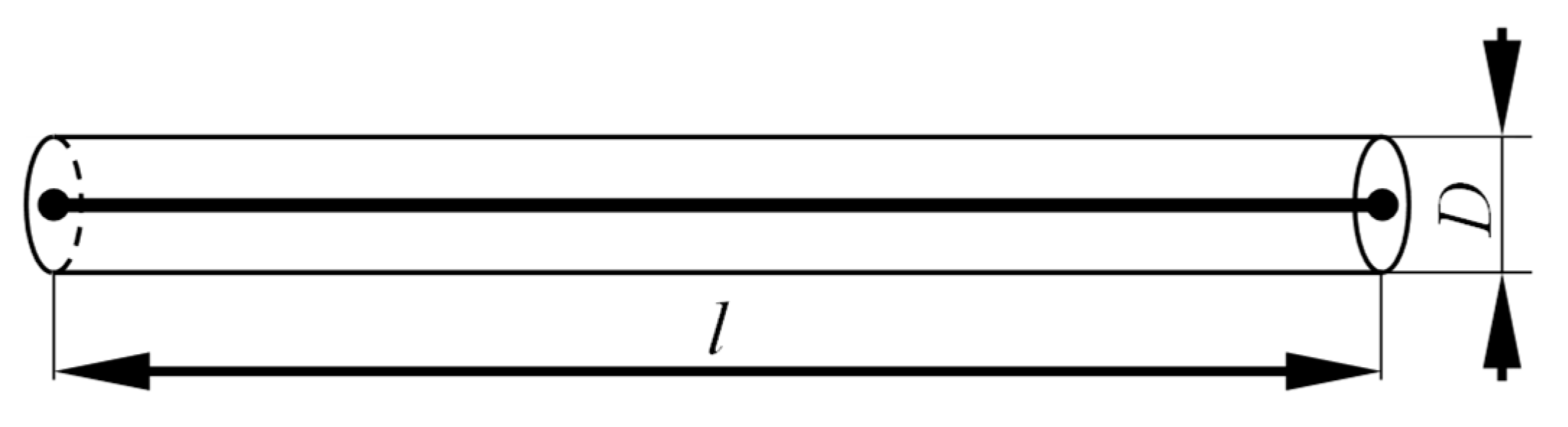

References
- Liu, X.; Li, Y.G.; Cheng, Y.G.; Cai, Y. Sparse identification for ball-screw drives considering position-dependent dynamics and nonlinear friction. Robot. Comput.-Integr. Manuf. 2023, 81, 102486. [Google Scholar] [CrossRef]
- Zhu, M.; Bao, D.; Huang, X. The Design of a Tracking Controller for Flexible Ball Screw Feed System Based on Integral Sliding Mode Control with a Generalized Extended State Observer. Robot. Actuators 2023, 12, 387. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, J.H.; Zhuang, C.B.; Yao, M.Q.; Chen, F.H.; Zhang, C.Y. Gain scheduling control of ball screw feed drives based on linear parameter varying model. Int. J. Adv. Manuf. Technol. 2023, 124, 4493–4510. [Google Scholar] [CrossRef]
- Liu, Z.D.; Li, C.Y.; Wang, G.D.; Yang, X.D.; Xu, M.T.; Li, Z.Y.; Li, J.J. Modeling and investigation on dynamic behaviors of ball screw feed system with bolt looseness. Int. J. Nonlinear Mech. 2025, 170, 104996. [Google Scholar] [CrossRef]
- Gong, X.X.; Zhao, J.S.; Zhao, C.Y.; Li, C.Y.; Hao, J.; Xu, M.T. Dynamic modeling and nonlinear characteristic analysis of the cross-axis ball screw feed system considering thermal deformation. Nonlinear Dyn. 2025, 113, 14515–14560. [Google Scholar] [CrossRef]
- Zhang, H.J.; Zhang, J.; Liu, H.; Liang, T.; Zhao, W.H. Dynamic modeling and analysis of the high-speed ball screw feed system. Proc. Inst. Mech. Eng. Part B-J. Eng. Manuf. 2014, 229, 870–877. [Google Scholar] [CrossRef]
- Vicente, D.A.; Hecker, R.L.; Villegas, F.J.; Flores, G.M. Modeling and vibration mode analysis of a ball screw drive. Int. J. Adv. Manuf. Technol. 2012, 58, 257–265. [Google Scholar] [CrossRef]
- Lu, H.J.; Rui, X.T.; Ma, Z.Y.; Ding, Y.Y.; Chen, Y.H.; Chang, Y.; Zhang, Y.P. Hybrid multibody system method for the dynamic analysis of an ultra-precision fly-cutting machine tool. Int. J. Mech. Syst. Dyn. 2022, 2, 290–307. [Google Scholar] [CrossRef]
- Miao, H.H.; Wang, C.Y.; Hao, J.; Li, C.Y.; Xu, M.T.; Liu, Z.D. Dynamic analysis of the column-spindle system considering the nonlinear characteristics of kinematic joints. Mech. Mach. Theory 2022, 174, 104922. [Google Scholar] [CrossRef]
- Hu, Y.J.; Wang, Y.Y.; Zhu, W.D.; Li, H.L. Dynamic Modeling of a Ball-Screw Drive and Identification of Its Installation Parameters. J. Dyn. Syst. Meas. Control-Trans. ASME 2021, 143, 041003. [Google Scholar] [CrossRef]
- He, W.W.; Wang, L.P.; Guan, L.W. A novel approach to calculating the dynamic error reflected on an S-shaped test piece. Proc. Inst. Mech. Eng. Part C-J. Eng. Mech. Eng. Sci. 2021, 235, 3273–3298. [Google Scholar] [CrossRef]
- Lyu, D.; Liu, Q.; Luo, S.Y.; Wang, D.W.; Liu, H. The influence of dynamic error outside servo-loop on the trajectory error. Int. J. Adv. Manuf. Technol. 2021, 113, 1517–1525. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, X.; Wang, L.; Zhao, W.H. Dynamic error of multi-axis machine tools considering position dependent structural dynamics and axis coupling inertial forces. Proc. Inst. Mech. Eng. Part B-J. Eng. Manuf. 2022, 236, 281–295. [Google Scholar] [CrossRef]
- Hu, J.J.; Yang, D.Z.; Sun, Z.C. Torque Fluctuation Suppression Strategy of Integrated Electric Drive System Based on the Principle of Minimization of Instantaneous Current Tracking Error. IEEE Access 2022, 10, 124673–124684. [Google Scholar] [CrossRef]
- Jiang, J.L.; LI, B.R.; Lin, F.Y.; Zhang, H.; Ye, P.Q. Prediction and compensation strategy of contour error in multi-axis motion system. Int. J. Adv. Manuf. Technol. 2022, 119, 163–175. [Google Scholar] [CrossRef]
- Zhang, J.; Li, B.; Zhou, C.X.; Zhao, W.H. Positioning error prediction and compensation of ball screw feed drive system with different mounting conditions. Proc. Inst. Mech. Eng. Part B-J. Eng. Manuf. 2016, 230, 2307–2311. [Google Scholar] [CrossRef]
- Liu, Q.; Lu, H.; Yonezawa, H.; Yonezawa, A.; Kajiwara, I.; Jiang, T.; He, J.J. Geometric and dynamic error compensation of dual-drive machine tool based on mechanism-data hybrid method. Mech. Syst. Signal Proc. 2025, 224, 112041. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, C.Y.; Wen, B.C. Dynamics analysis on the MDOF model of ball screw feed system considering the assembly error of guide rails. Mech. Syst. Signal Proc. 2022, 178, 109290. [Google Scholar] [CrossRef]
- Li, X.W.; Zhang, J.; Zhao, W.H.; Lu, B.H. A zero phase error tracking based path precompensation method for high-speed machining. Proc. Inst. Mech. Eng. Part C-J. Eng. Mech. Eng. Sci. 2016, 230, 230–239. [Google Scholar] [CrossRef]
- Zhang, D.L.; Chen, H.C. A data-driven iterative pre-compensation method of contouring error for five-axis machine tools. Int. J. Adv. Manuf. Technol. 2024, 135, 1669–1684. [Google Scholar] [CrossRef]
- Wu, H.; Meng, Y.X.; Zhao, Z.Y.; Zhu, Z.W.; Ren, M.J.; Zhang, X.Q.; Zhu, L.M. Surrogate model-based tool trajectory modification for ultra-precision tool servo diamond turning. Precis. Eng.-J. Int. Soc. Precis. Eng. Nanotechnol. 2025, 93, 46–57. [Google Scholar] [CrossRef]
- Li, H.C.; Li, Y.F.; Huang, S.M. Optimization strategy for the control of permanent magnet synchronous motors in numerical control machine tools based on intelligent feedforward self-learning. Rev. Adhes. Adhes. 2023, 11, 744–757. [Google Scholar] [CrossRef]
- Wang, Z.G.; Feng, X.Y.; Yang, H.T.; Jin, H.W. Research on low-speed characteristics of differential double-drive feed system. Mech. Sci. 2021, 12, 791–802. [Google Scholar] [CrossRef]
- Jin, L.; Li, C.H.; Wang, X.; Xie, L.M. A dynamic stiffness model for high-speed ball screw pair with the mass center of screw nut considered. Mech. Ind. 2023, 24, 21. [Google Scholar] [CrossRef]
- Li, F.; Jiang, Y.; Li, T.; Ehmann, K.F. Compensation of dynamic mechanical tracking errors in ball screw drives. Mechatronics 2018, 55, 27–37. [Google Scholar] [CrossRef]
- Li, X.T.; Xi, D.L.; Zhang, Y.L. Permanent magnet synchronous motor vector control based on MATLAB/Simulink. In Proceedings of the 2017 First International Conference on Electronics Instrumentation & Information Systems (EIIS), Harbin, China, 3–5 June 2017. [Google Scholar] [CrossRef]
- Lascu, C.; Trzynadlowski, A.M. A sensorless hybrid DTC drive for high-volume low-cost applications. IEEE Trans. Ind. Electron. 2004, 51, 1048–1055. [Google Scholar] [CrossRef]
- Preitl, S.; Precup, R.E. On the algorithmic design of a class of control systems based on providing the symmetry of open-loop Bode plots. Sci. Bull. UPT 1996, 41, 47–55. [Google Scholar]
- Meng, D.B.; Li, Y.; He, C.; Guo, J.B.; Lv, Z.Y.; Wu, P. Multidisciplinary design for structural integrity using a collaborative optimization method based on adaptive surrogate modelling. Mater. Des. 2021, 206, 109789. [Google Scholar] [CrossRef]
- Jesús, O.D.; Hagan, M.T. Backpropagation algorithms for a broad class of dynamic networks. IEEE Trans. Neural Netw. 2007, 18, 14–27. [Google Scholar] [CrossRef]
- Shohda, A.M.A.; Ali, M.A.M.; Ren, G.F.; Kim, J.G.; Mohamed, M.A. Application of Cascade Forward Backpropagation Neural Networks for Selecting Mining Methods. Sustainability 2022, 14, 635. [Google Scholar] [CrossRef]
- Nami, F.; Deyhimi, F. Prediction of activity coefficients at infinite dilution for organic solutes in ionic liquids by artificial neural network. J. Chem. Thermodyn. 2011, 43, 22–27. [Google Scholar] [CrossRef]
- Yavuz, M.; Iphar, M.; Once, G. The optimum support design selection by using AHP method for the main haulage road in WLC Tuncbilek colliery. Tunn. Undergr. Space Technol. 2008, 23, 111–119. [Google Scholar] [CrossRef]
- Zhang, J.S.; Tian, J.L.; Alcaide, A.M.; Leon, J.I.; Vazquez, S.; Franquelo, L.G.; Luo, H.; Yin, S. Lifetime extension approach based on the Levenberg–Marquardt neural network and power routing of DC-DC converters. IEEE Trans. Power Electron. 2023, 38, 10280–10291. [Google Scholar] [CrossRef]
- Wang, S.W.; Yuan, Y.; Zhou, A.H.; Yin, C. Environmental Study on Analysis of Characteristic Parameters of Rockfall Movement Based on Field Riprap Test and Establishment of SVM and LM-BPNN Prediction Models. Ekoloji Dergisi 2019, 28, 3319–3326. [Google Scholar]
- Dong, P.; Li, J.Q.; Guo, W.; Lai, J.B.; Mao, F.H.; Wang, K.F.; Xu, X.Y.; Wang, S.H. Surrogate-assisted multi-objective optimization for control parameters of adjacent gearshift process with multiple clutches. Control Eng. Practice. 2023, 135, 105519. [Google Scholar] [CrossRef]
- Cui, Y.X.; Zhong, B.; Qian, W.K.; Zheng, C.J. Identification of Time Series Transfer Function Parmeter. In Proceedings of the 2014 International Conference on Mechatronics Electronic industrial and Control Engineering (MEIC 2014), Shenyang, China, 15–17 November 2014. [Google Scholar] [CrossRef]




| Parameters | TC (N·mm) | TS (N·mm) | ΩS (rpm) | σ0(N) | σ1 (N·mm/rpm) | σ2 (N·mm/rpm) |
|---|---|---|---|---|---|---|
| value | 0.6757 | 0.7653 | 25.9147 | 1.5875 | 0.1593 | 0.0003 |
| Operational Specifications | Value |
|---|---|
| Rotor inertia | 0.0053 (kg·m2) |
| Torque constant | 1.641 (N·m/A) |
| Stator resistance | 0.75 (ohm) |
| The inductance of the quadrature axis | 13.2 (mH) |
| The inductance of the direct axis | 4.11 (mH) |
| Rated torque | 24 (N·m) |
| Rated current | 10 (A) |
| Rated speed | 2000 (RPM) |
| Coil pitch | 4 |
| Silicon steel grades | M270-35A |
| Permanent magnet grades | N42UH |
| Operational Specifications | Value |
|---|---|
| Ball screw manufacturer | HIWIN |
| Ball screw catalog | FDI 40-10T3 |
| Bed material grade | HT200 |
| Worktable material grade | HT200 |
| Rotary table material grade | QT450-10 |
| Torque sensor shaft stiffness | 1 × 105 (N·m/rad) |
| Coupling torsional stiffness | 2800 (N·m/rad) |
| Screw–nut pair axial stiffness | 7.45 × 107 (N/m) 1.04 × 107 (N/m) |
| PId | IId | PIq | IIq | PωR | IωR | PSw |
| 2.776 | 626.2 | 8.805 | 1003.3 | 0.0678 | 0.7122 | 280.2 |
| Parameters | Lower Bound | Upper Bound |
|---|---|---|
| Sw(k) (mm) | 0 | 1500 |
| (mm/s) | −333 | 333 |
| (mm/s2) | −1000 | 1000 |
| Iqr(k) (A) | −15 | 15 |
| Trial | Sw(k) | Iqr(k) | Sw(k+1) | ||
|---|---|---|---|---|---|
| 1 | 41.71 | −270.9 | −690.1 | 0.171 | 41.68 |
| 2 | 1.5 | 276.9 | −830.1 | −14.82 | 1.472 |
| ⁝ | ⁝ | ⁝ | ⁝ | ⁝ | ⁝ |
| 4997 | 349.5 | 104.4 | 330. | 4.707 | 349.6 |
| 4998 | 151.5 | −292.3 | 350.1 | 8.938 | 151.6 |
| 4999 | 954.5 | 161.7 | 390.1 | 6.604 | 954.4 |
| 5000 | 407.1 | 15.54 | 270 | −13.94 | 407.2 |
| u = 0.3 | u = 0.5 | u = 0.7 | |
|---|---|---|---|
| Maximum AE (mm) | 118.9 | 40.39 | 25.62 |
| Average AE (mm) | 15.08 | 5.559 | 2.622 |
| N = 1 | N = 2 | N = 3 | |
|---|---|---|---|
| Maximum AE (mm) | 118.9 | 26.62 | 15.23 |
| Average AE (mm) | 15.08 | 1.674 | 0.631 |
| Mh = 3 | Mh = 4 | Mh = 5 | |
|---|---|---|---|
| Maximum AE (mm) | 15.23 | 8.558 | 5.545 |
| Average AE (mm) | 0.631 | 0.309 | 0.112 |
| epochs = 100 | epochs = 150 | epochs = 200 | |
|---|---|---|---|
| Maximum AE(μm) | 15.2320 | 10.7695 | 7.0424 |
| Average AE (mm) | 0.6314 | 0.4880 | 0.3277 |
| Maximum AE (μm) | Average AE (μm) |
|---|---|
| 9.549 × 10−9 | 2.572 × 10−9 |
| Trajectories | Displacement | Maximum Velocity | Maximum Acceleration | Maximum Jerk |
|---|---|---|---|---|
| 1 | 300 | 100 | 225 | 1200 |
| 2 | 300 | 100 | 225 | 1400 |
| 3 | 300 | 100 | 120 | 1000 |
| 4 | 300 | 100 | 140 | 1000 |
| 5 | 300 | 110 | 160 | 1000 |
| 6 | 300 | 120 | 160 | 1000 |
| Trajectories | Experiment | Position-Dependent | ||
|---|---|---|---|---|
| Maximum Tracking Error (μm) | Average Tracking Error (μm) | Maximum Tracking Error (μm) | Average Tracking Error (μm) | |
| 1 | 54.86 | 6.753 | 54.75 | 5.757 |
| 2 | 58.35 | 7.013 | 57.3 | 5.848 |
| 3 | 51.98 | 5.056 | 51.64 | 4.482 |
| 4 | 51.89 | 5.279 | 51.64 | 4.771 |
| 5 | 51.08 | 6.38 | 51.64 | 5.552 |
| 6 | 51.91 | 6.719 | 51.64 | 6.052 |
| Trajectories | Experiment | Prediction Model | Transfer Function | |||
|---|---|---|---|---|---|---|
| Maximum Tracking Error (μm) | Average Tracking Error (μm) | Maximum Tracking Error (μm) | Average Tracking Error (μm) | Maximum Tracking Error (μm) | Average Tracking Error (μm) | |
| 1 | 54.86 | 6.804 | 54.75 | 6.574 | 64.75 | 7.573 |
| 2 | 58.35 | 7.098 | 57.3 | 6.173 | 67.75 | 7.694 |
| 3 | 51.98 | 5.056 | 51.64 | 4.709 | 61.79 | 5.878 |
| 4 | 51.89 | 5.279 | 51.64 | 5.098 | 61.79 | 6.261 |
| 5 | 51.08 | 6.414 | 51.64 | 5.862 | 61.79 | 7.313 |
| 6 | 51.91 | 6.719 | 51.64 | 6.407 | 61.79 | 7.995 |
| Trajectories | No Compensation | PM+ LuGre | TF+ LuGre | |||
|---|---|---|---|---|---|---|
| Maximum Tracking Error (μm) | Average Tracking Error (μm) | Maximum Tracking Error (μm) | Average Tracking Error (μm) | Maximum Tracking Error (μm) | Average Tracking Error (μm) | |
| 1 | 54.86 | 6.804 | 17.07 | 2.705 | 25.21 | 4.33 |
| 2 | 58.35 | 7.098 | 15.32 | 2.781 | 27.92 | 4.63 |
| 3 | 51.98 | 5.056 | 17.19 | 2.275 | 23.39 | 3.28 |
| 4 | 51.89 | 5.279 | 19.07 | 2.331 | 22.35 | 3.22 |
| 5 | 51.08 | 6.414 | 11.88 | 2.317 | 25.3 | 4.076 |
| 6 | 51.91 | 6.719 | 12.79 | 2.512 | 24.52 | 4.032 |
| Trajectories | PM | TF | ||
|---|---|---|---|---|
| Maximum Tracking Error (μm) | Average Tracking Error (μm) | Maximum Tracking Error (μm) | Average Tracking Error (μm) | |
| 1 | 30.09 | 4.443 | 43.67 | 5.177 |
| 2 | 33.21 | 4.404 | 41.22 | 5.183 |
| 3 | 27.39 | 3.337 | 36.50 | 3.666 |
| 4 | 27.16 | 3.432 | 36.01 | 3.872 |
| 5 | 27.10 | 4.152 | 38.20 | 4.860 |
| 6 | 28.59 | 4.340 | 38.84 | 4.912 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Guo, Y.; Liu, J.; Niu, W. Dynamic Error Compensation for Ball Screw Feed Drive Systems Based on Prediction Model. Machines 2025, 13, 433. https://doi.org/10.3390/machines13050433
Liu H, Guo Y, Liu J, Niu W. Dynamic Error Compensation for Ball Screw Feed Drive Systems Based on Prediction Model. Machines. 2025; 13(5):433. https://doi.org/10.3390/machines13050433
Chicago/Turabian StyleLiu, Hongda, Yonghao Guo, Jiaming Liu, and Wentie Niu. 2025. "Dynamic Error Compensation for Ball Screw Feed Drive Systems Based on Prediction Model" Machines 13, no. 5: 433. https://doi.org/10.3390/machines13050433
APA StyleLiu, H., Guo, Y., Liu, J., & Niu, W. (2025). Dynamic Error Compensation for Ball Screw Feed Drive Systems Based on Prediction Model. Machines, 13(5), 433. https://doi.org/10.3390/machines13050433





