Conceptual Design and Analysis of a Trans-Domain Aircraft Based on the Camber Morphing Wing
Abstract
1. Introduction
2. Concept of the Trans-Domain Aircraft
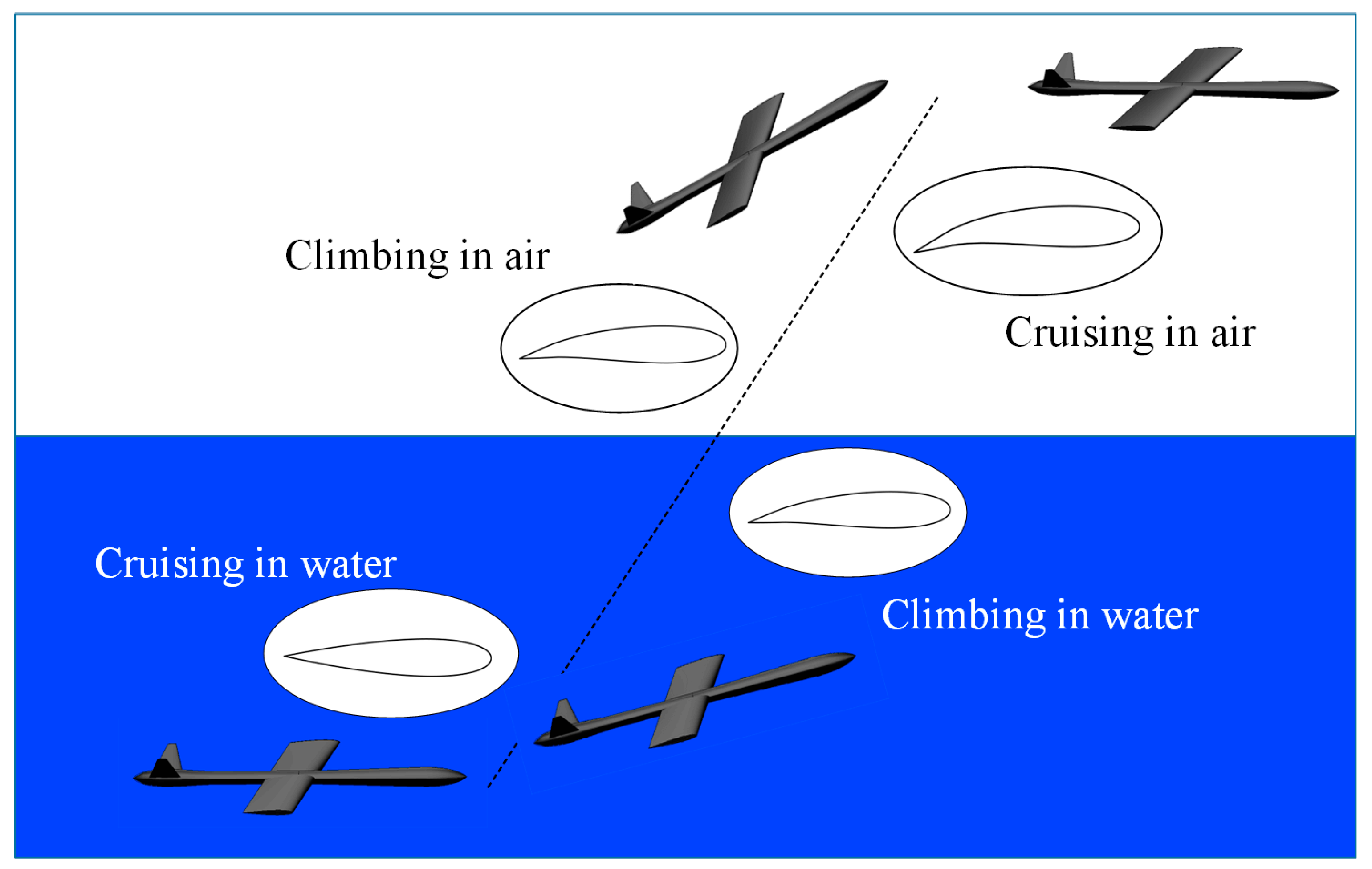
2.1. Proposed Working Process
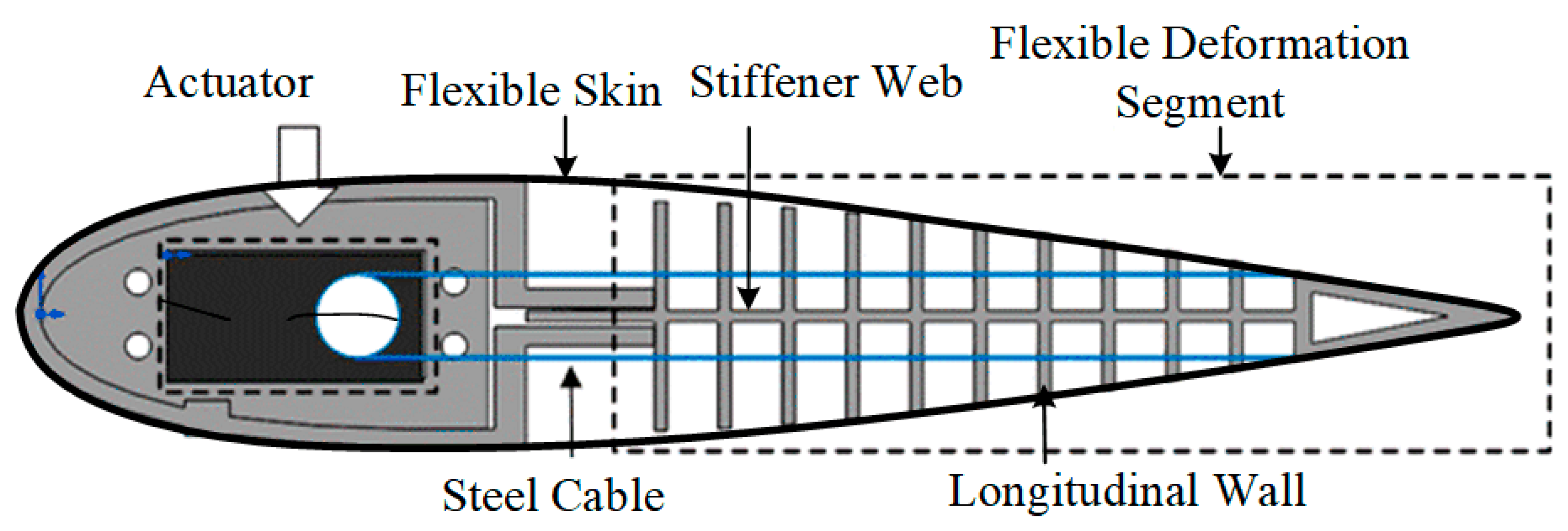
2.2. Conceptual Design of the Camber Morphing Wing
3. Analysis of the Camber Morphing Wing Considering Fluid–Structure Interaction
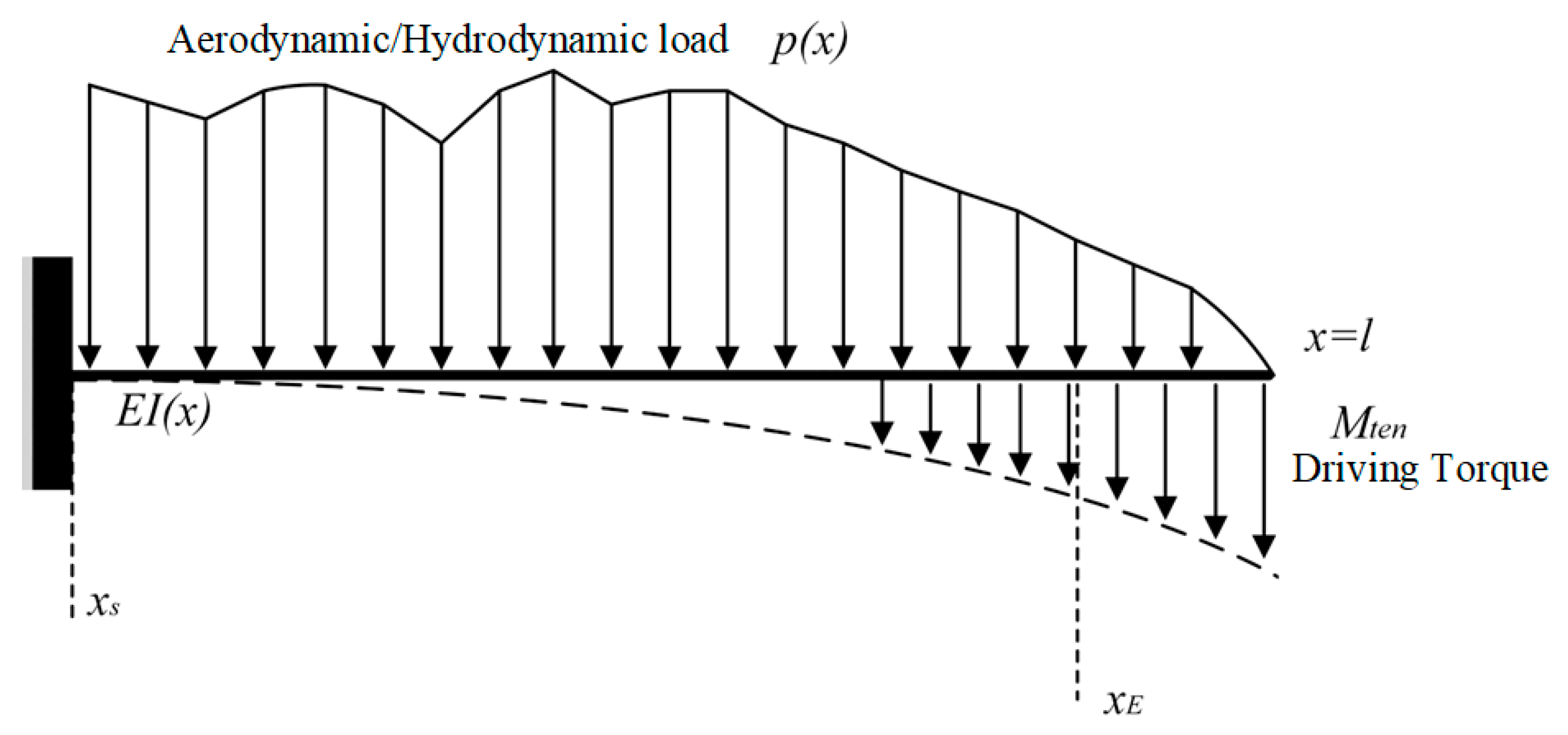
3.1. Modeling Method
3.2. Design Iteration
- (1)
- Objective
- (2)
- Variables
- (3)
- Constrains
- (4)
- Results
4. Experimental Demonstration
4.1. Demonstrator Preparation
4.2. Results and Discussions
5. Conclusions
- A conceptual design of the trans-domain aircraft is proposed, which is based on curvature change generated by the camber morphing wing. And the aircraft is supposed to maintain good performance both in the air and in the water.
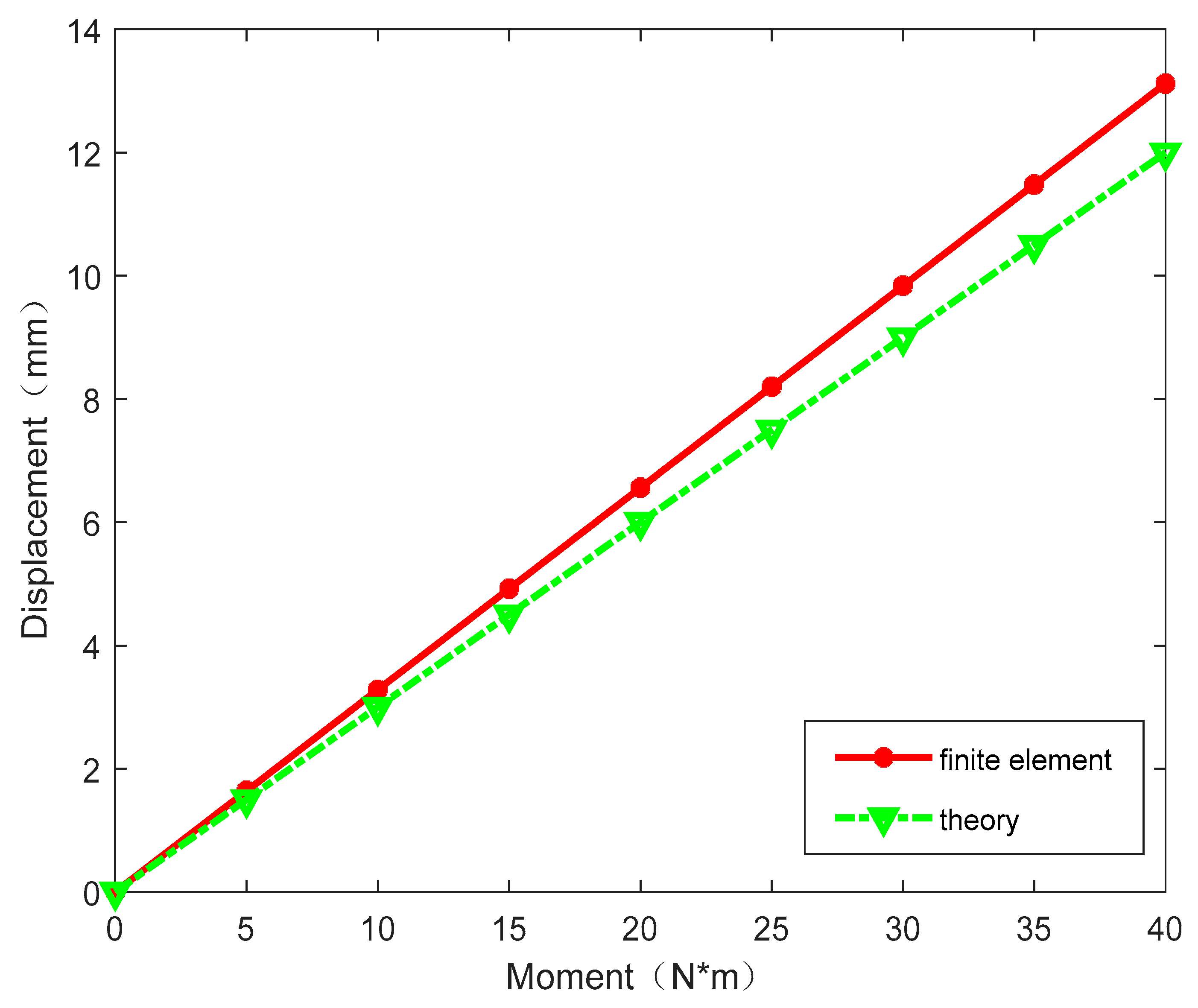
- Structural and aerodynamic models are made to perform the fluid–structure interaction analysis based on the Euler beam theory and the vortex lattice method, and the modeling method is verified by comparing with the results from finite element method.
- The design iteration is applied to find the proper camber change in different working conditions, considering the working process from the water to the air using the fluid–structure interaction analysis.
- A demonstration model is made to verify the camber change, both in the air and in the water, which preliminarily validates the proposed concept.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Feng, J.; Hu, J.; Qi, D. Study on development needs and key technologies of air-water trans-media vehicle. J. Air Force Eng. Univ. 2019, 20, 8–13. [Google Scholar]
- Ji, W.; Qi, X.; Li, D. Operational application and effectiveness evaluation of reentry cross-medium unmanned aerial vehicles. Electron. Opt. Control. 2022, 29, 38–42. [Google Scholar]
- Zeng, Z.; Lyu, C.; Bi, Y.; Jin, Y.; Lu, D.; Lian, L. Review of hybrid aerial underwater vehicle: Cross-domain mobility and transitions control. Ocean Eng. 2022, 248, 110840. [Google Scholar] [CrossRef]
- Yao, G.; Li, Y.; Zhang, H.; Jiang, Y.; Wang, T.; Sun, F.; Yang, X. Review of hybrid aquatic-aerial vehicle (HAAV): Classifications, current status, applications, challenges and technology perspectives. Prog. Aerosp. Sci. 2023, 139, 100902. [Google Scholar] [CrossRef]
- Nicholson, J.W.; Healey, A.J. The Present State of Autonomous Underwater Vehicle (AUV) Applications and Technologies. Mar. Technol. Soc. J. 2008, 42, 44–51. [Google Scholar] [CrossRef]
- Yang, X.; Wang, T.; Liang, J.; Yao, G.; Liu, M. Survey on the novel hybrid aquatic–aerial amphibious aircraft: Aquatic unmanned aerial vehicle (AquaUAV). Prog. Aerosp. Sci. 2015, 74, 131–151. [Google Scholar] [CrossRef]
- Yinggu, Z.; Guoliang, F.; Jianqiang, Y. Modeling longitudinal aerodynamic and hydrodynamic effects of a flying boat in calm water. In Proceedings of the 2011 IEEE International Conference on Mechatronics and Automation, Beijing, China, 7–10 August 2011; pp. 2039–2044. [Google Scholar]
- Stewart, W.; Weisler, W.; MacLeod, M.; Powers, T.; Defreitas, A.; Gritter, R.; Anderson, M.; Peters, K.; Gopalarathnam, A.; Bryant, M. Design and demonstration of a seabird-inspired fixed-wing hybrid UAV-UUV system. Bioinspir. Biomim. 2018, 13, 056013. [Google Scholar] [CrossRef] [PubMed]
- Weisler, W.; Stewart, W.; Anderson, M.B.; Peters, K.J.; Gopalarathnam, A.; Bryant, M. Testing and Characterization of a Fixed Wing Cross-Domain Unmanned Vehicle Operating in Aerial and Underwater Environments. IEEE J. Ocean. Eng. 2017, 43, 969–982. [Google Scholar] [CrossRef]
- Stewart, W.; Weisler, W.; Anderson, M.; Bryant, M.; Peters, K. Dynamic Modeling of Passively Draining Structures for Aerial–Aquatic Unmanned Vehicles. IEEE J. Ocean. Eng. 2020, 45, 840–850. [Google Scholar] [CrossRef]
- Li, H.; Lu, K.; Chen, Y.; Zhu, M.; Lu, P.; Duan, H. Structure design of a novel bionic water-air cross-domain vehicle. J. Unmanned Undersea Syst. 2022, 30, 726–732. [Google Scholar]
- Yang, X.B.; Liang, J.H.; Wen, L.; Wang, T.M. Research status of water-air amphibious trans-media unmanned vehicle. Robot 2018, 40, 102–114. [Google Scholar]
- Siddall, R.; Kennedy, G.; Kovac, M. High-power propulsion strategies for aquatic take-off in robotics. In Proceedings of the 50th International Symposium on Robotics Research, Munich, Germany, 20–21 June 2018; pp. 5–20. [Google Scholar]
- Siddall, R.; Kovac, M. Fast aquatic escape with a jet thruster. IEEE/ASME Trans. Mechatron. 2017, 22, 217–226. [Google Scholar] [CrossRef]
- Siddall, M.; Kovac, M. Launching the AquaMAV: Bioinspired design for aerial-aquatic robotic platforms. Bioinspir. Biomim. 2014, 9, 031001. [Google Scholar] [CrossRef] [PubMed]
- Siddall, R.; Kovac, M. A water jet thruster for an aquatic micro air vehicle. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 3979–3985. [Google Scholar]
- Chen, Y. The Design and Analysis of Fluid Dynamic Characteristics for Submersible Unmanned Aerial Vehicle; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2019. [Google Scholar]
- Ma, Z.; Feng, J.; Yang, J. Research on vertical air–water trans-media control of hybrid unmanned aerial underwater vehicles based on adaptive sliding mode dynamical surface control. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418770531. [Google Scholar] [CrossRef]
- Lu, D.; Xiong, C.; Zeng, Z.; Lian, L. A multimodal aerial underwater vehicle with extended endurance and capabilities. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 4674–4680. [Google Scholar]
- Miller, E.J.; Lokos, W.A.; Cruz, J.; Crampton, G.; Stephens, C.A.; Kota, S.; Ervin, G.; Flick, P. Approach for structurally clearing an adaptive compliant trailing edge flap for flight. In Proceedings of the Society of Flight Test Engineers International Annual Symposium, Lancaster, CA, USA, 14–17 September 2015. [Google Scholar]
- Livne, E.; Precup, N.; Mor, M. Design, construction, and tests of an aeroelastic wind tunnel model of a variable camber continuous trailing edge flap (VCCTEF) concept wing. In Proceedings of the 32nd AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 16–20 June 2014; p. 2442. [Google Scholar]
- Precup, N.; Mor, M.; Livne, E. The design, construction, and tests of a concept aeroelastic wind tunnel model of a high-lift variable camber continuous trailing edge flap (HL-VCCTEF) wing configuration. In Proceedings of the 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 5–9 January 2015; p. 1406. [Google Scholar]
- Woods, B.K.; Friswell, M.I. Preliminary investigation of a fishbone active camber concept. In Proceedings of the ASME Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Stone Mountain, GA, USA, 19–21 September 2012; pp. 555–563. [Google Scholar]
- Woods, B.K.; Friswell, M.I. Fluid-structure interaction analysis of the fish bone active camber mechanism. In Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Boston, MA, USA, 8–11 April 2013; p. 1908. [Google Scholar]
- Lu, J.; Song, W.; Cao, R.; Liang, Y.; Feng, L.; Qi, Y. Airfoil Preference and Adjustable Camber Impact Analysis for Trans-Medium Fixed-Wing Vehicles. J. Unmanned Undersea Syst. 2025, 33, 113–123. [Google Scholar]
- Bousquet, G.; Izraelevitz, J.; Triantafyllou, M. Bioinspired Design of Dual Aerial-Aquatic Vehicles for Ocean Sampling; Research Poster; MIT Towing Tank Lab: Cambridge, MA, USA, 2024. [Google Scholar]
- Lock, R.J.; Vaidyanathan, R.; Burgess, S.C. Development of a biologically inspired multi-modal wing model for aerial-aquatic robotic vehicles. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 3404–3409. [Google Scholar]
- Lock, R.J.; Vaidyanathan, R.; Burgess, S.C.; Loveless, J. Development of a biologically inspired multi-modal wing model for aerial-aquatic robotic vehicles through empirical and numerical modelling of the common guillemot, Uria aalge. Bioinspir. Biomim. 2010, 5, 046001. [Google Scholar] [CrossRef] [PubMed]
- Zyga, L. Seabird’s Morphing Wings Inspire Design for Robots that Can Both Fly and Swim. Available online: https://phys.org/news/2010-11-seabird-morphing-wings-robots.html (accessed on 1 October 2023).
- Carossa, G.M.; Ricci, S.; De Gaspari, A.; Liauzun, C.; Dumont, A.; Steinbuch, M. Adaptive trailing edge: Specifications, aerody-namics, and exploitation. In Smart Intelli-gent Aircraft Structures (SARISTU): Proceedings of the Final Project Conference; Woelcken, P.C., Papadopoulos, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 143–158. [Google Scholar]
- Kuzmina, S.; Ishmuratov, F.; Zichenkov, M.; Chedrik, V.; Amiryants, G.A.; Kulesh, V.; Malyutin, V.; Chedrik, A.; Timokhin, V.; Shalaev, S.; et al. Wind tunnel testing of adaptive wing structures. In Morphing Wing Technologies; Concilio, A., Dimino, I., Lecce, L., Eds.; Butterworth-Heinemann: Oxford, UK, 2017; pp. 713–755. [Google Scholar]
- Concilio, A.; Dimino, I.; Pecora, R. SARISTU: Adaptive Trailing Edge Device (ATED) design process review. Chin. J. Aeronaut. 2021, 34, 187–210. [Google Scholar] [CrossRef]
- Huang, K.; Zhang, J.Y.; Wang, C. Equivalent structure model of fish bone active camber morphing concept and analysis of aeroelastic characteristics. J. Nanjing Univ. Aeronaut. Astronaut. 2024, 56, 516–525. [Google Scholar]
- XFOIL Help Documentation. Available online: https://web.mit.edu/drela/Public/web/xfoil/ (accessed on 1 July 2024).
- Wang, Z.H.; Li, Y.; Wang, A.B.; Wang, X. Flying wing underwater glider: Design, analysis, and performance prediction. In Proceedings of the 2015 International Conference on Control, Automation and Robotics, Singapore, 20–22 May 2015; pp. 74–77. [Google Scholar]




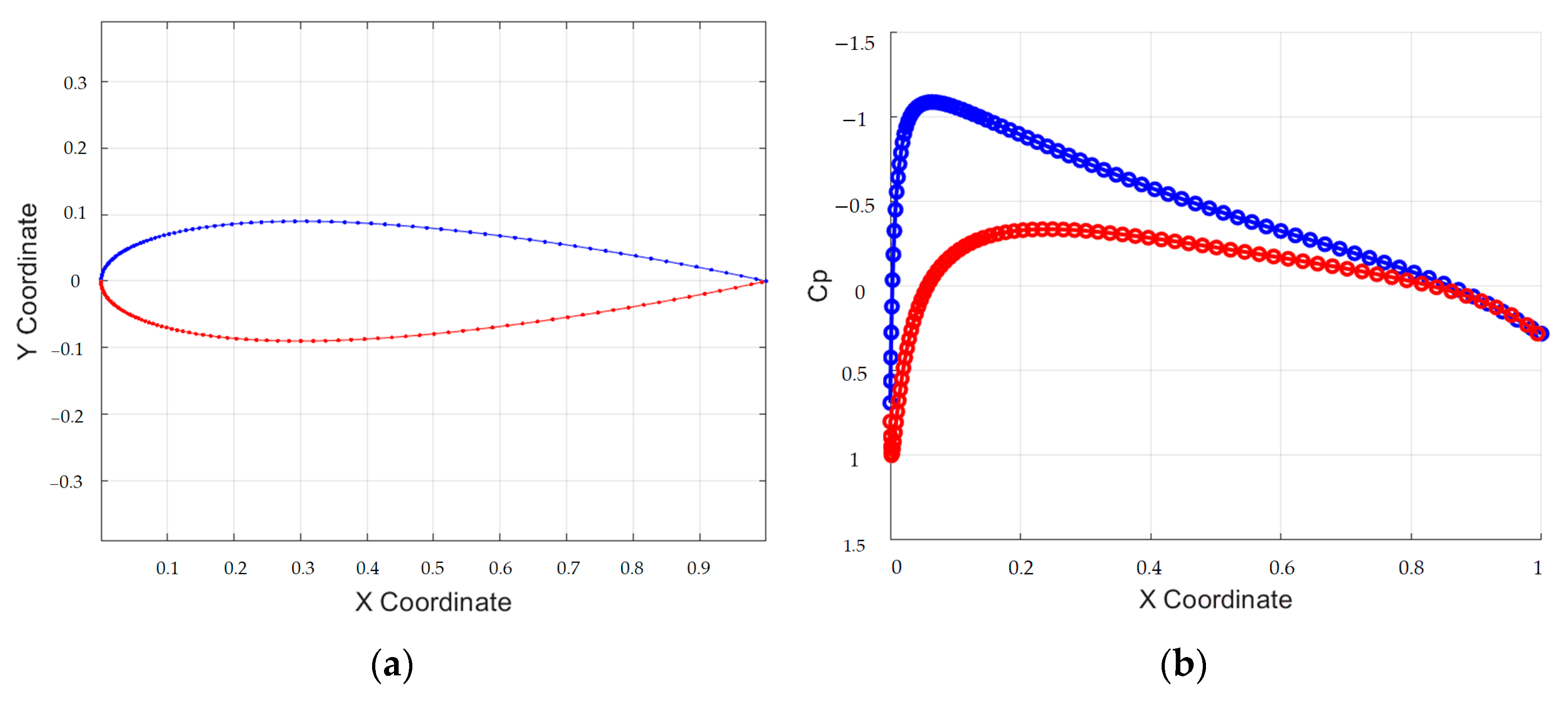
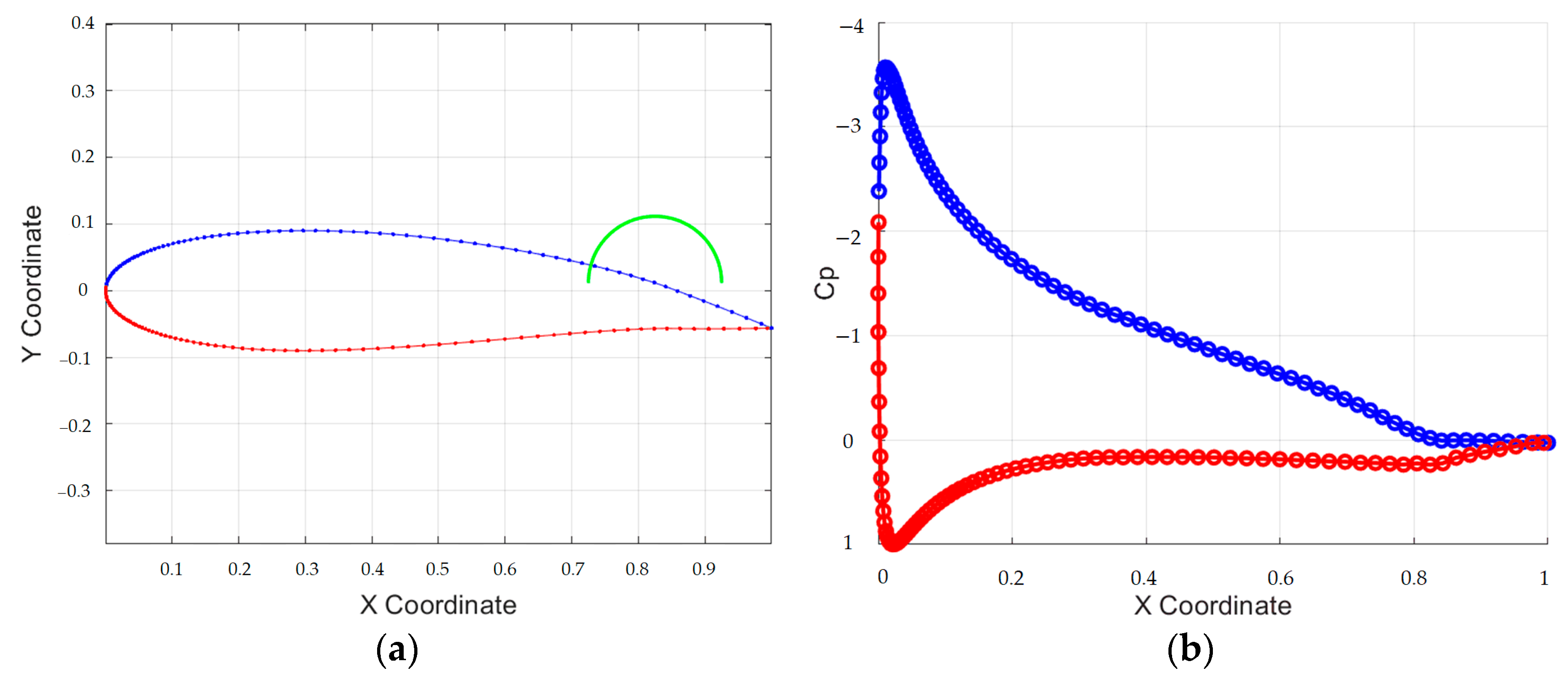

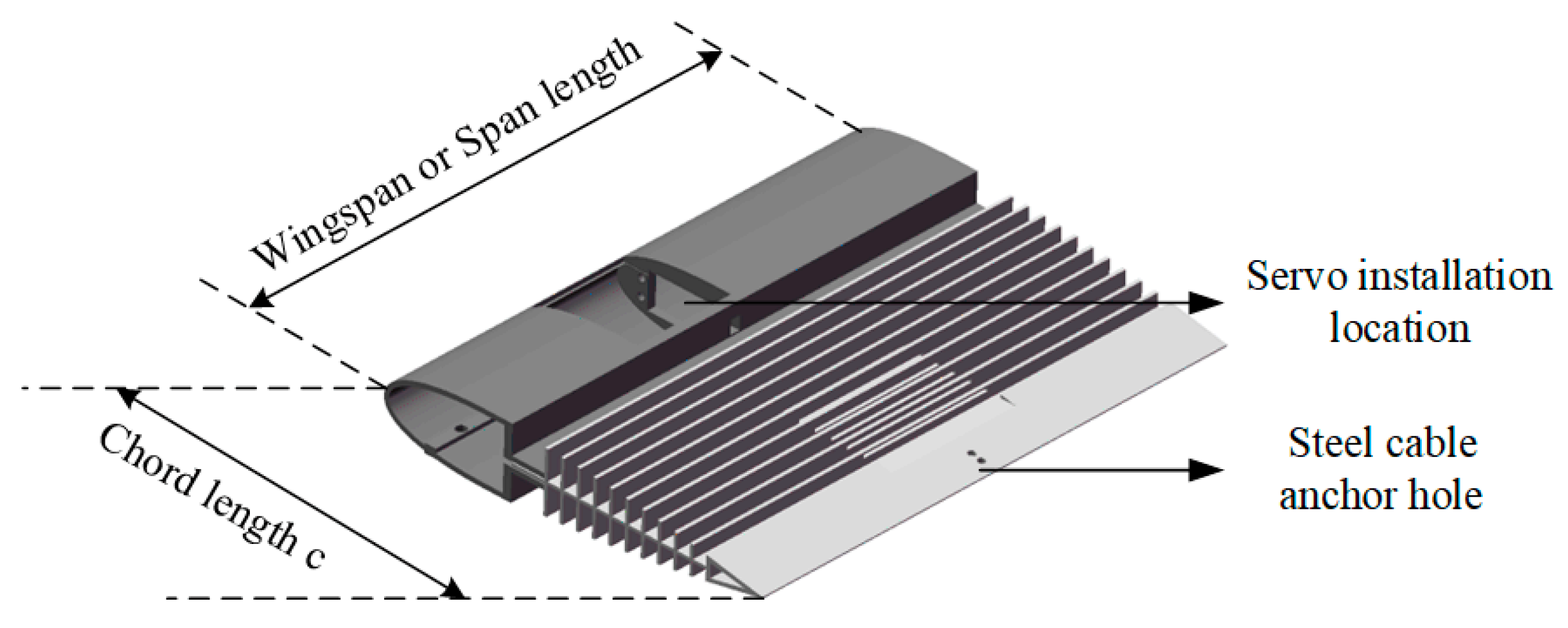




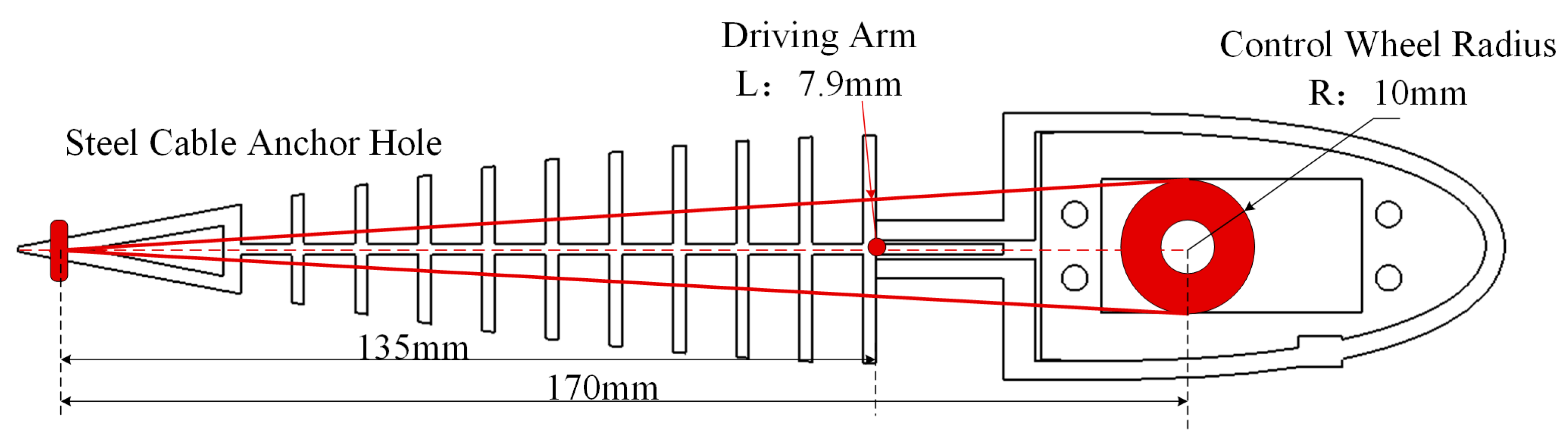
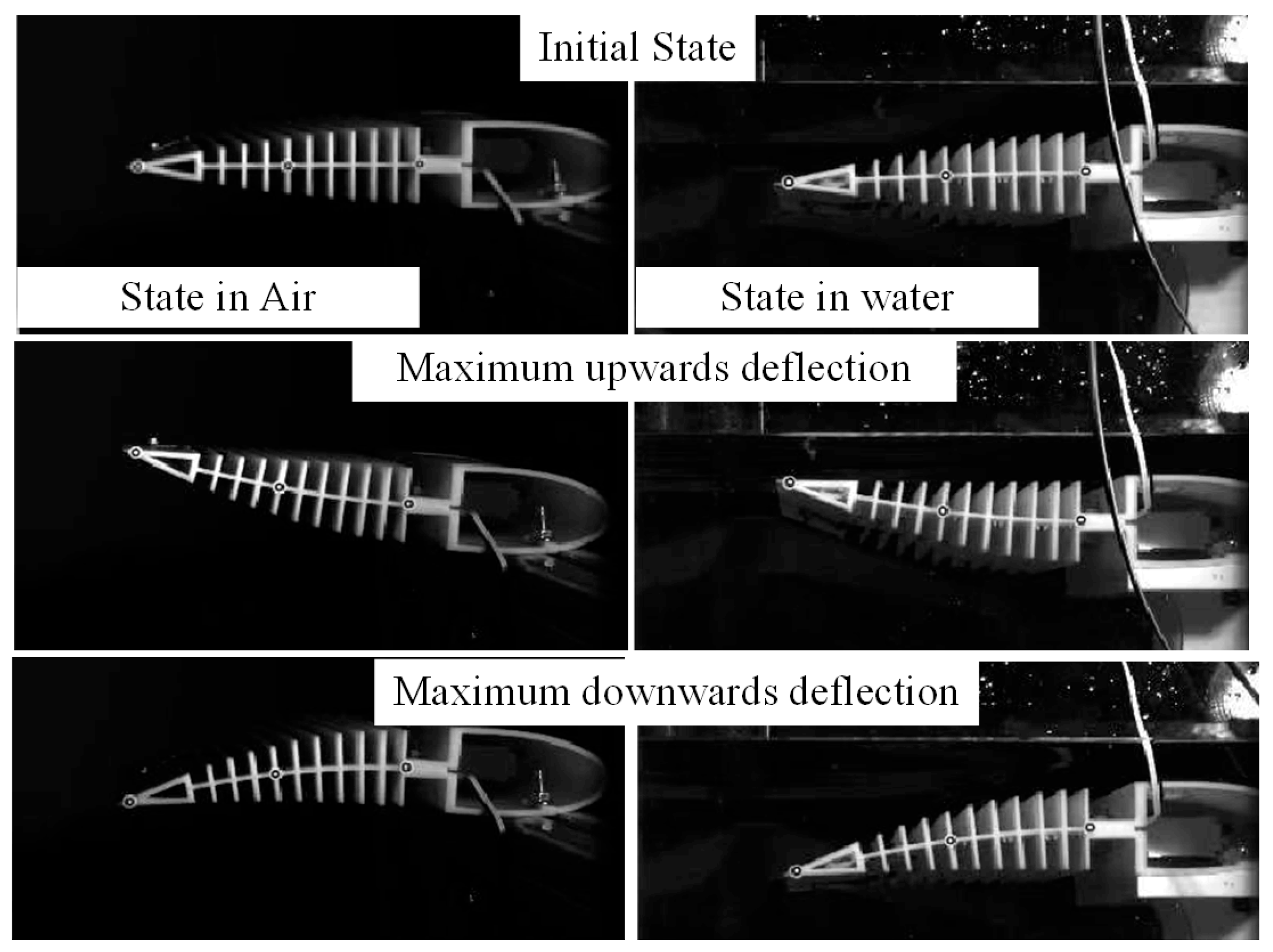
| Working Conditions | Cruising Speed | Angle of Attack Range | Reynolds Number |
|---|---|---|---|
| Underwater Cruise | 0.5 m/s–5 m/s | [−5°,5°] | 1 × 106–2 × 10 |
| Underwater Climbing | 0.5 m/s–5 m/s | [0°,10°] | 1 × 106–2 × 10 |
| Air Cruise | 30 m/s–50 m/s | [0°,10°] | 2 × 107–3.4 × 107 |
| Property | Water (Liquid) | Air (Gas) | Ratio (Water/Air) |
|---|---|---|---|
| Density | 998 kg/m3 | 1.204 kg/m3 | ~829:1 |
| Dynamic Viscosity | 1.002 × 10−3 Pa·s | 1.813 × 10−5 Pa·s | ~55:1 |
| Kinematic Viscosity | 1.004 × 10−6 m2/s | 1.516 × 10−5 m2/s | ~0.066:1 |
| Specific Heat (Cp) | 4182 J/(kg·K) | 1005 J/(kg·K) | ~4.16:1 |
| Compressibility | Incompressible | affected by speed |
| Parameters | Value |
|---|---|
| Airfoil | NACA 0018 |
| Chord length c | 200 mm |
| Spread b | 300 mm |
| Deformation start position | 22.5% |
| Number of vertical walls n | 20 |
| Thickness of longitudinal wall | 2 mm |
| Web thickness | 2 mm |
| Material Parameters | Value |
|---|---|
| Density | 1.14 g·cm−3 |
| Young’s modulus | 2200 MPa |
| Poisson’s ratio | 0.4 |
| Yield stress | 90 MPa |
| Working Conditions | Angle of Attack | Cruising Speed | Media Density | Reynolds Number |
|---|---|---|---|---|
| Underwater Cruise | 3° | 3.4 m/s | 1000 g·cm−3 | 2 × 106 |
| Underwater Climb | 8° | 3.4 m/s | 1000 g·cm−3 | 2 × 106 |
| Air Cruise | 3° | 34 m/s | 1.225 g·cm−3 | 3 × 107 |
| Working Conditions | Variant (Driving Torque) | Target | Value | Trailing Edge Deformation |
|---|---|---|---|---|
| Underwater Cruise | 0 nm | min Cd | 0° | |
| Underwater Climbing | 16 nm | max L/D | 38.46 | 5.08° |
| Air Cruise | 22 nm | max L/D | 33.56 | 8.8° |
| Models | Values |
|---|---|
| Voltage range | DC 5–8.4 v |
| Blocking torque | 60 kg~8.4 v |
| Distance | 270° |
| Size | 23.5 × 8 × 16.8 mm |
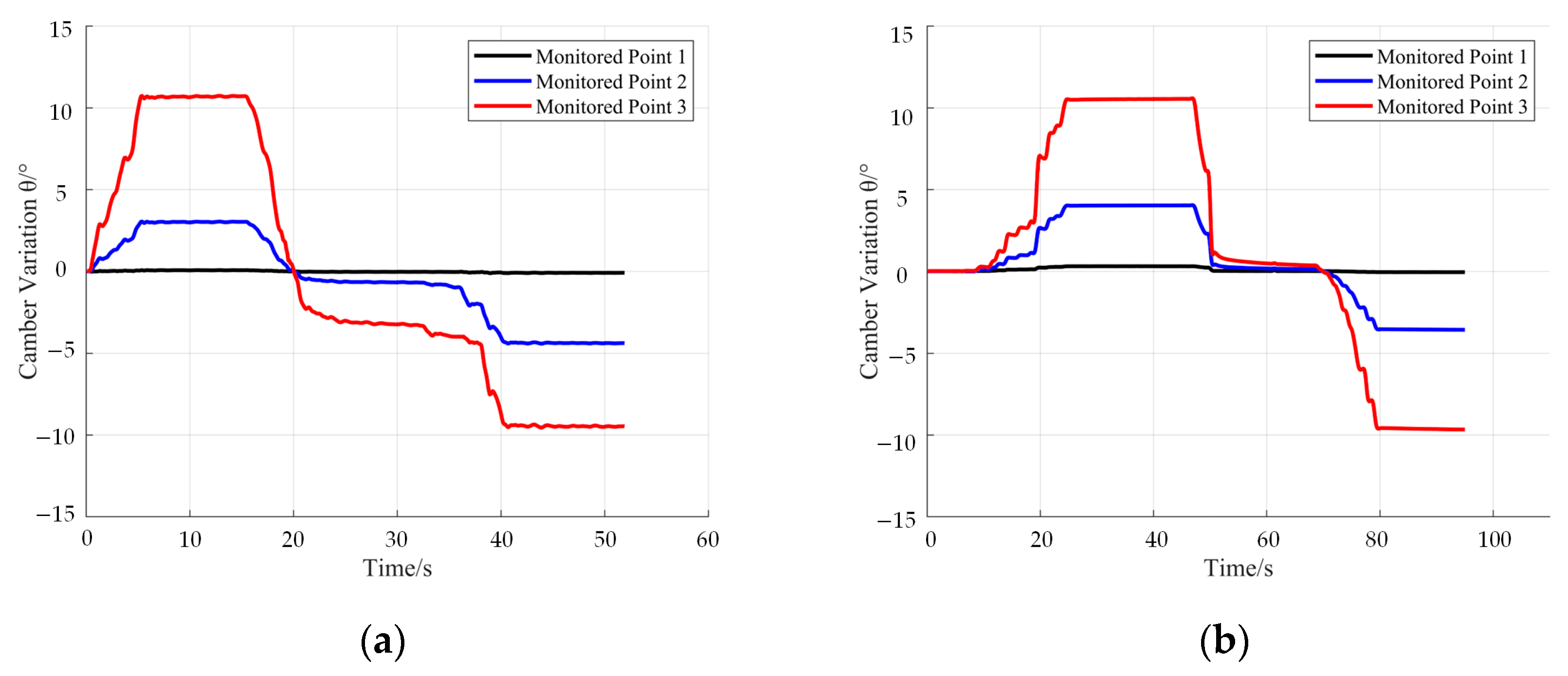
| Working Conditions | Target Angle | Test Angle (Down) | Test Angle (Up) |
|---|---|---|---|
| Underwater cruise | 0° | 0° | 0° |
| Underwater Climbing | 5.08° | 9.49° | 10.81° |
| Air cruise | 8.8° | 9.70° | 10.59° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Xu, M.; Shen, X.; Lai, Z.; Zhao, Y.; Wang, C.; Hu, Q. Conceptual Design and Analysis of a Trans-Domain Aircraft Based on the Camber Morphing Wing. Machines 2025, 13, 428. https://doi.org/10.3390/machines13050428
Wang M, Xu M, Shen X, Lai Z, Zhao Y, Wang C, Hu Q. Conceptual Design and Analysis of a Trans-Domain Aircraft Based on the Camber Morphing Wing. Machines. 2025; 13(5):428. https://doi.org/10.3390/machines13050428
Chicago/Turabian StyleWang, Mingzhen, Mingxuan Xu, Xing Shen, Zhenyang Lai, Yan Zhao, Chen Wang, and Qi Hu. 2025. "Conceptual Design and Analysis of a Trans-Domain Aircraft Based on the Camber Morphing Wing" Machines 13, no. 5: 428. https://doi.org/10.3390/machines13050428
APA StyleWang, M., Xu, M., Shen, X., Lai, Z., Zhao, Y., Wang, C., & Hu, Q. (2025). Conceptual Design and Analysis of a Trans-Domain Aircraft Based on the Camber Morphing Wing. Machines, 13(5), 428. https://doi.org/10.3390/machines13050428








