Modeling and Dynamic Characteristic Analysis of a Rigid–Flexible Coupling Multi-Stage Gear Transmission System for High-Power-Density Diesel Engines
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
1.3. Aims and Methodology
2. Method
2.1. Rigid–Flexible Coupling Multi-Body Dynamics Theory
2.1.1. Dynamic Model of a Nonlinear Decoupled Gear-Bearing System
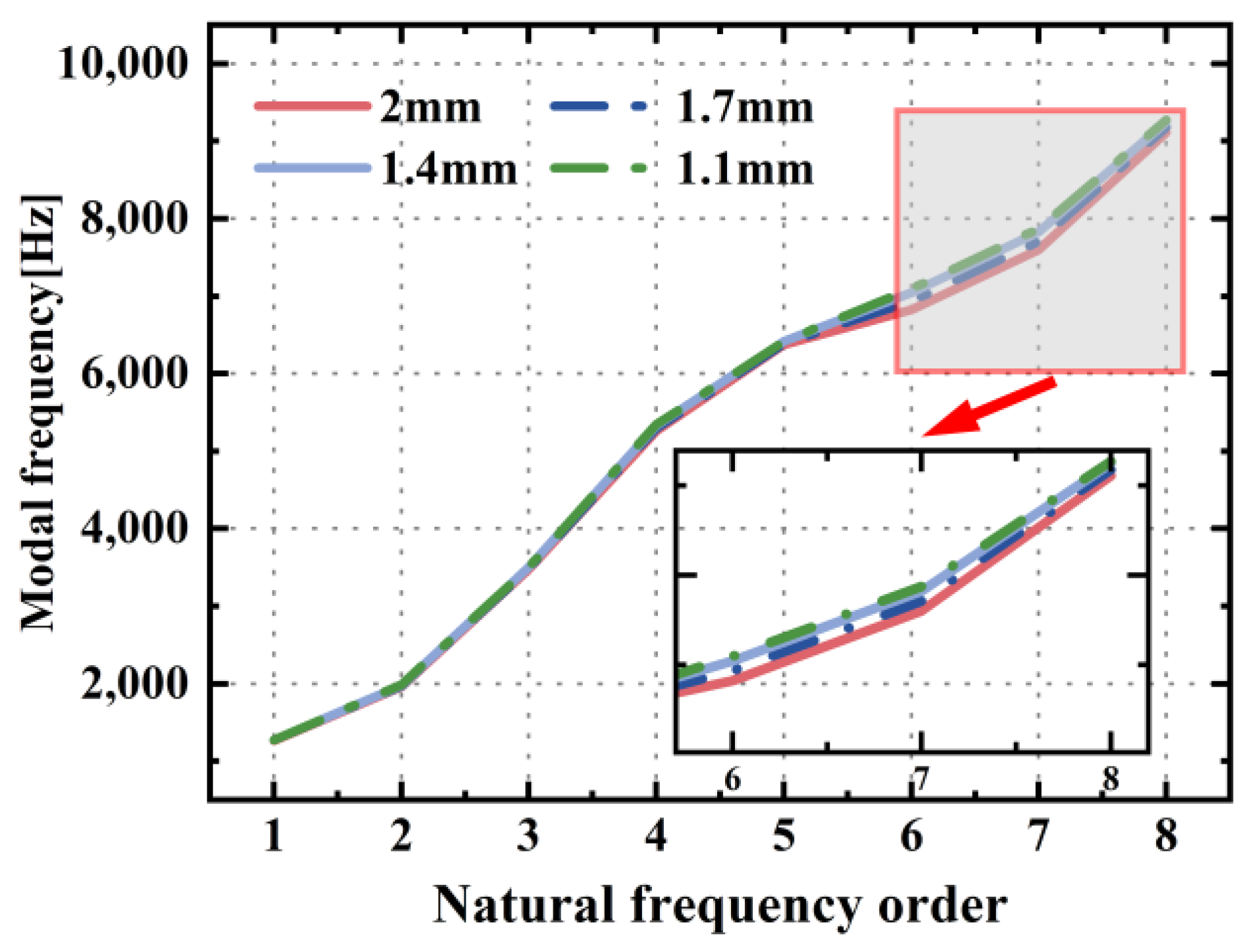
2.1.2. Dynamic Condensation Theory for Model Order Reduction
2.1.3. Rigid–Flexible Coupling Multi-Body Dynamic Model for Geared Gear-Bearing Systems
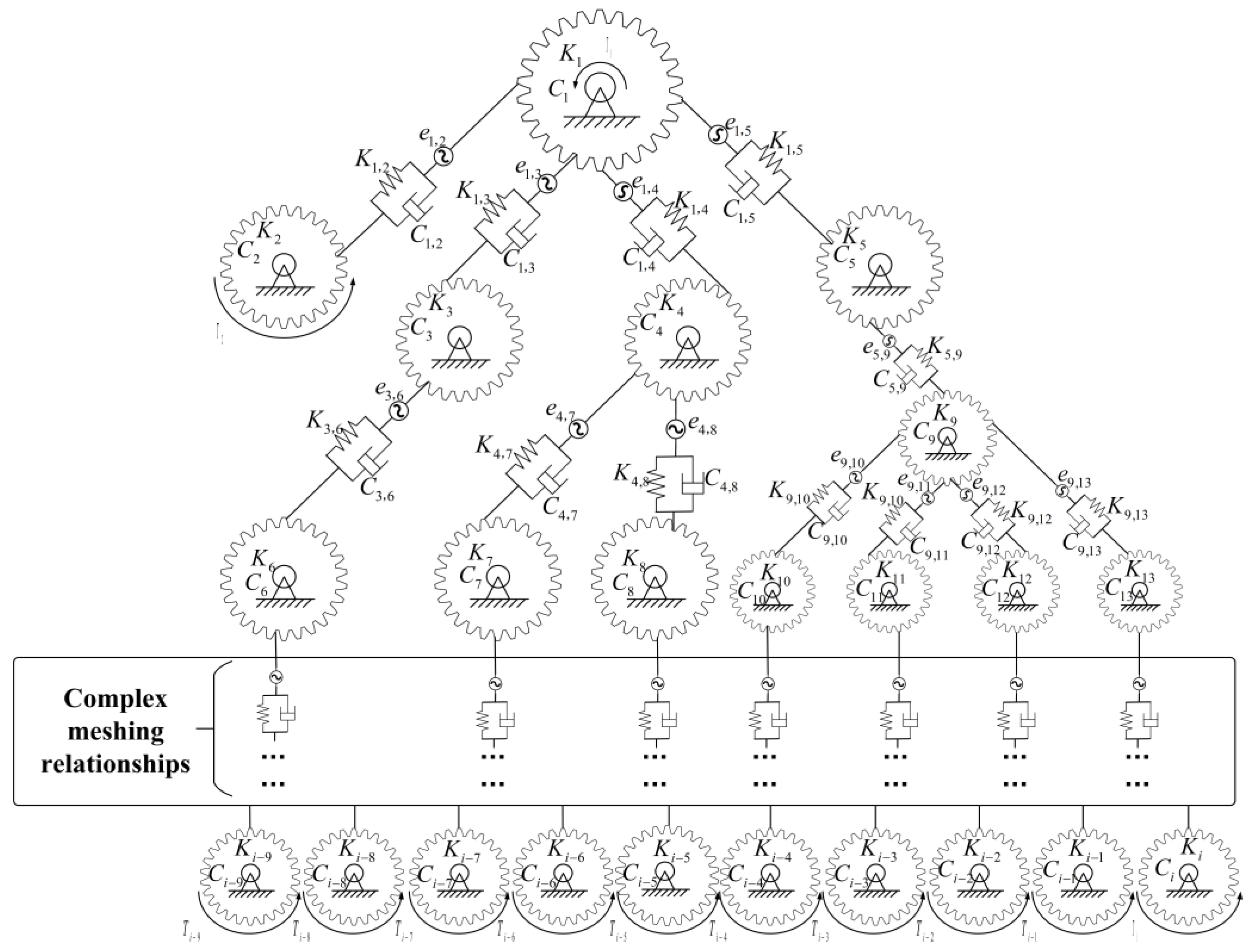
2.2. Construction of a Multi-Stage Rigid–Flexible Coupling Model for a Gear Transmission System
3. Results and Discussion
3.1. Classification of Typical Gears and Gear Pairs
3.2. Angular Acceleration Analysis
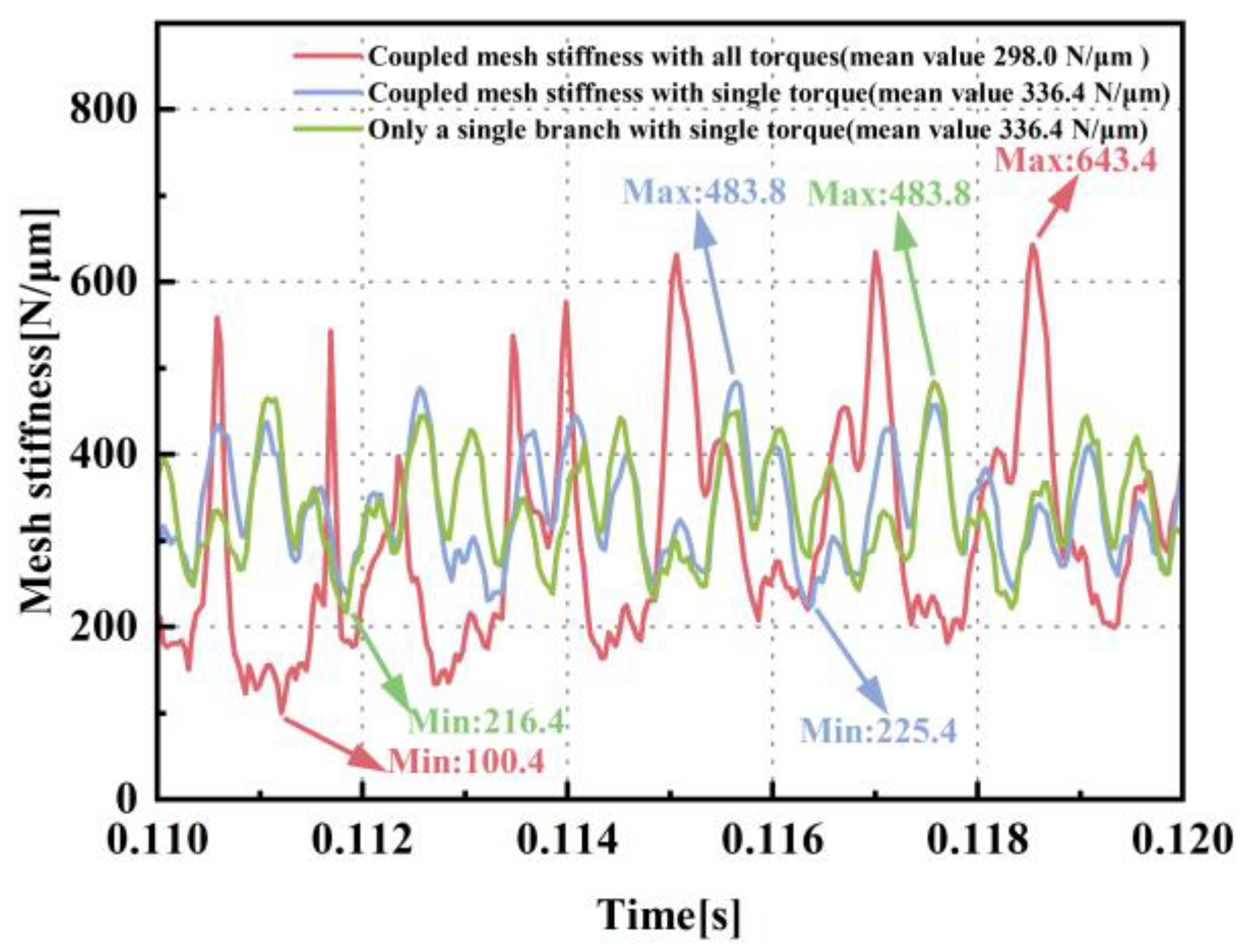
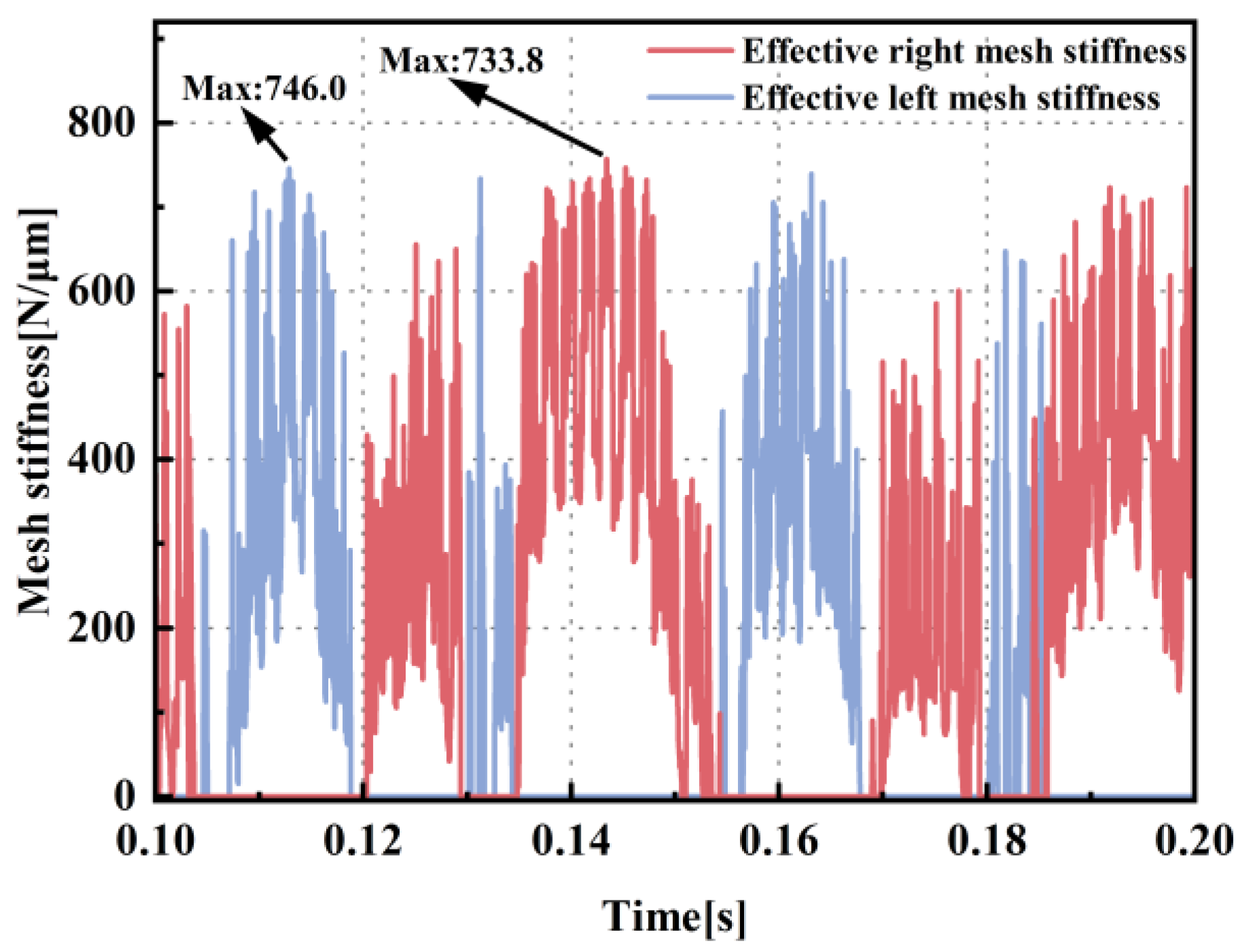
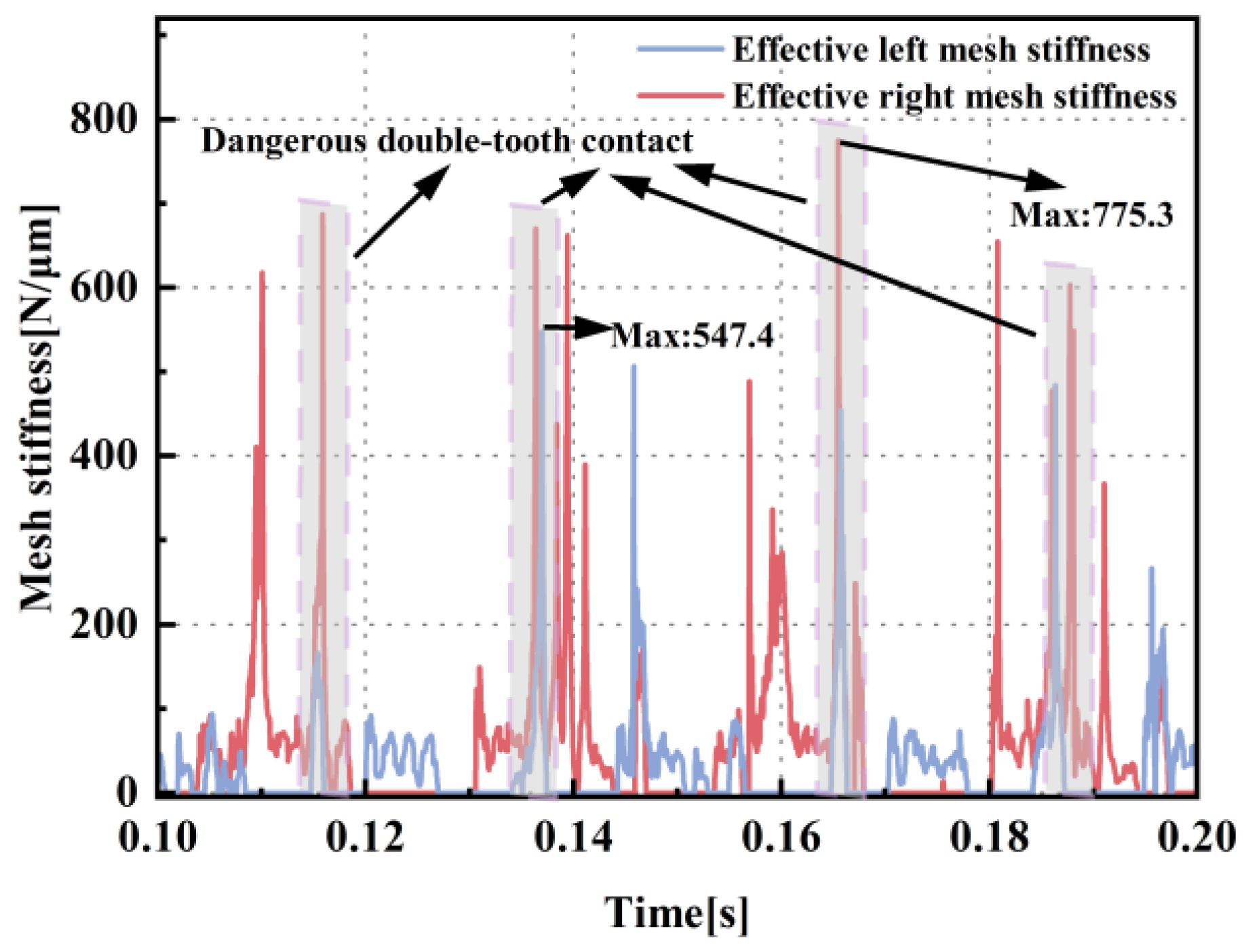
3.3. Mesh Stiffness Analysis
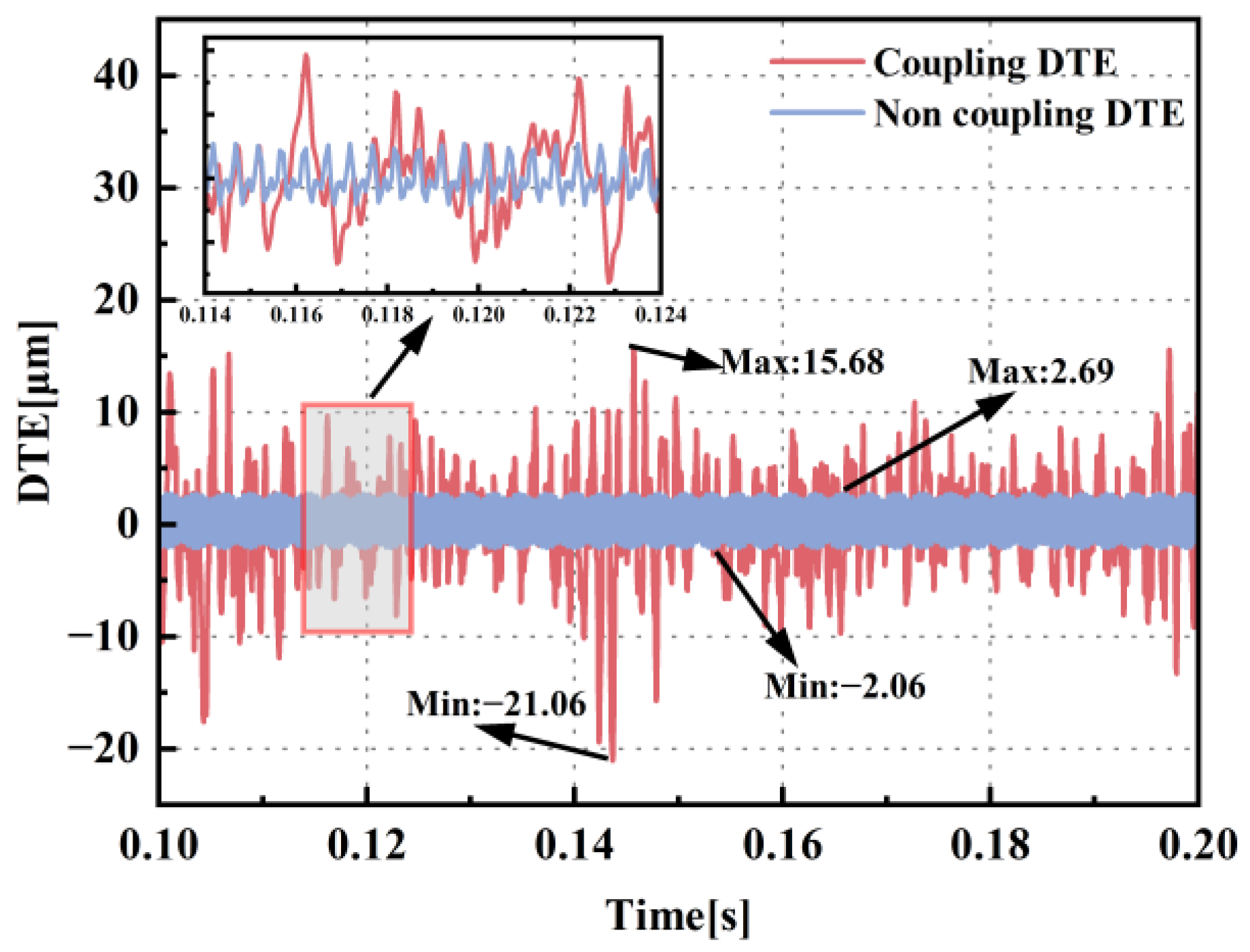
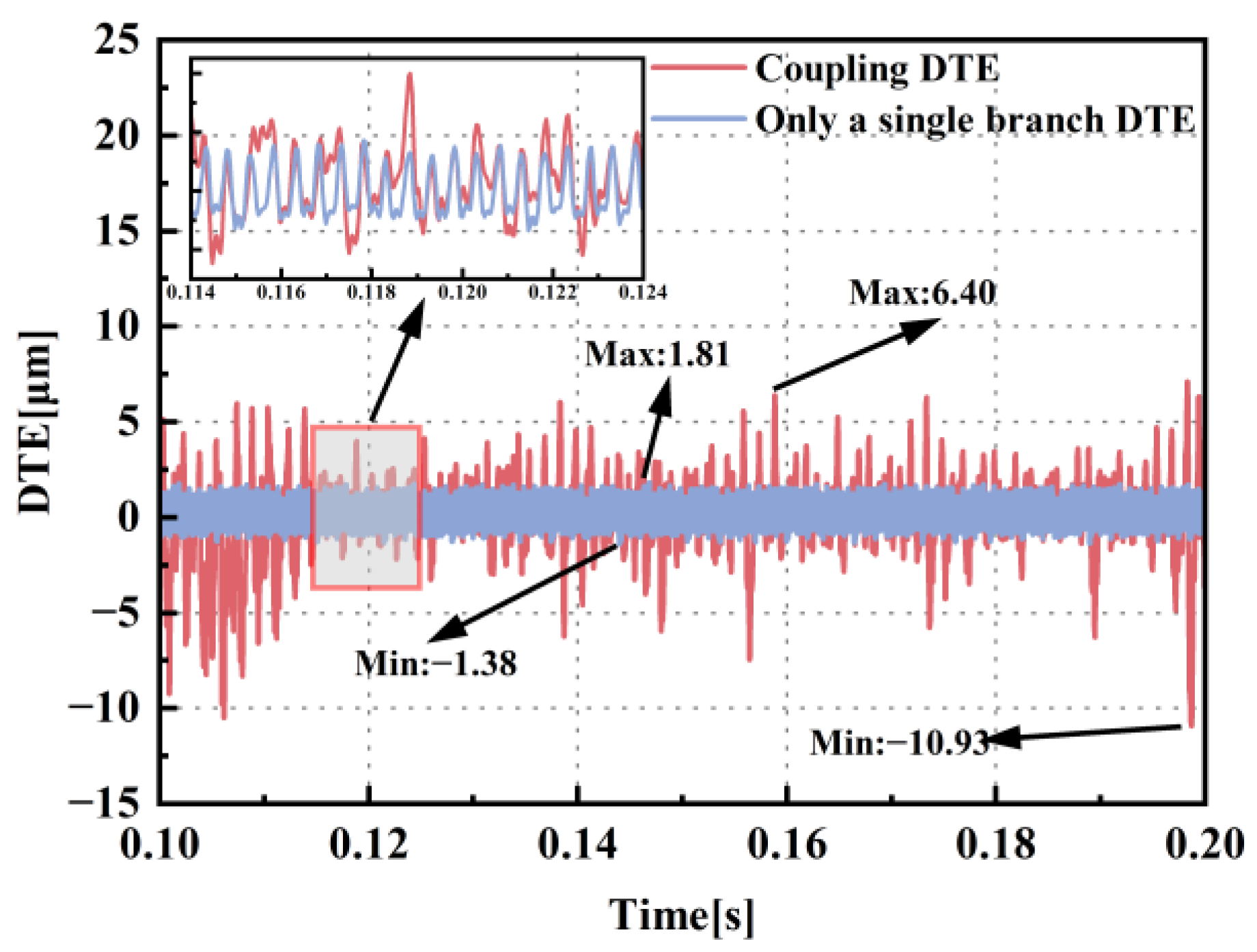
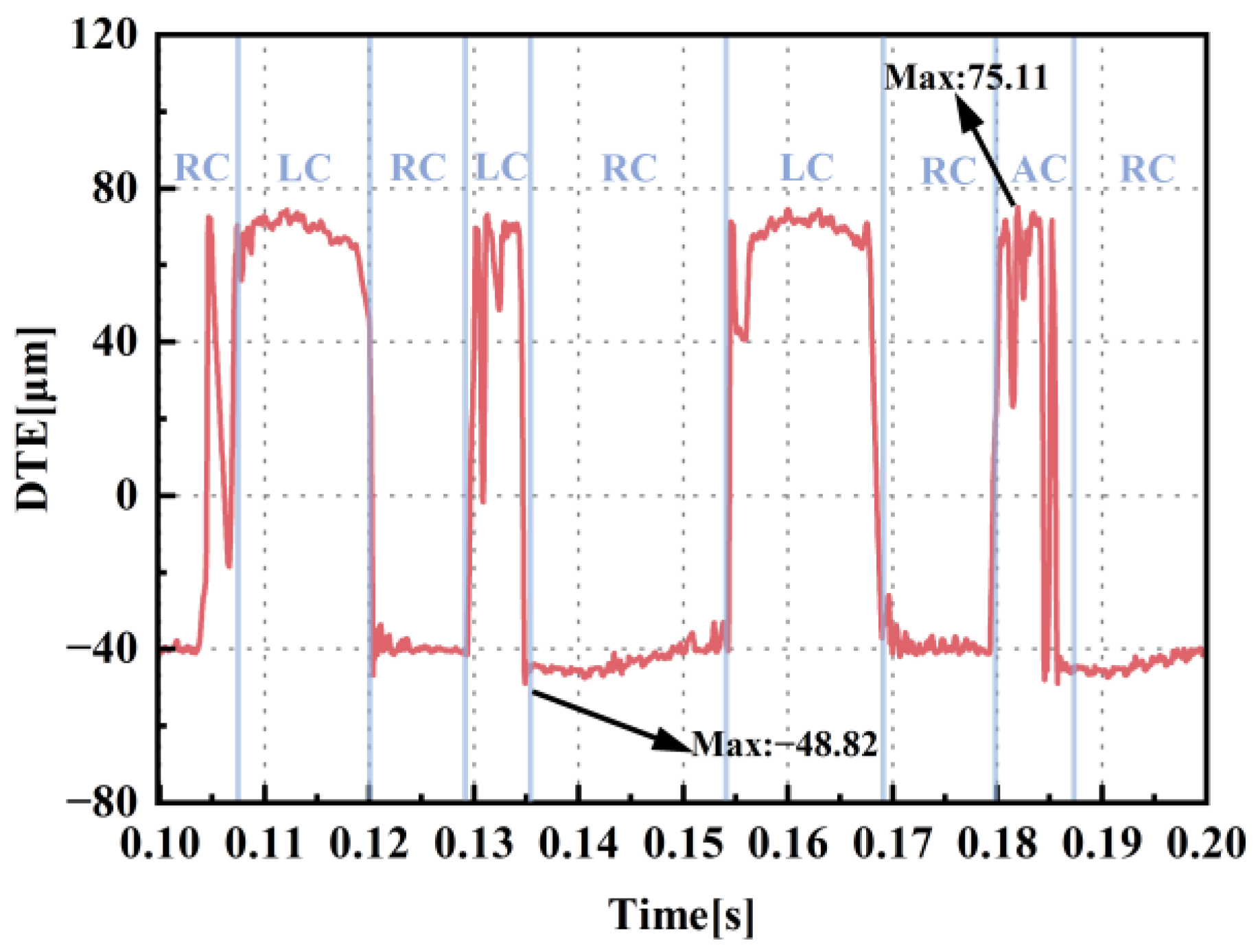
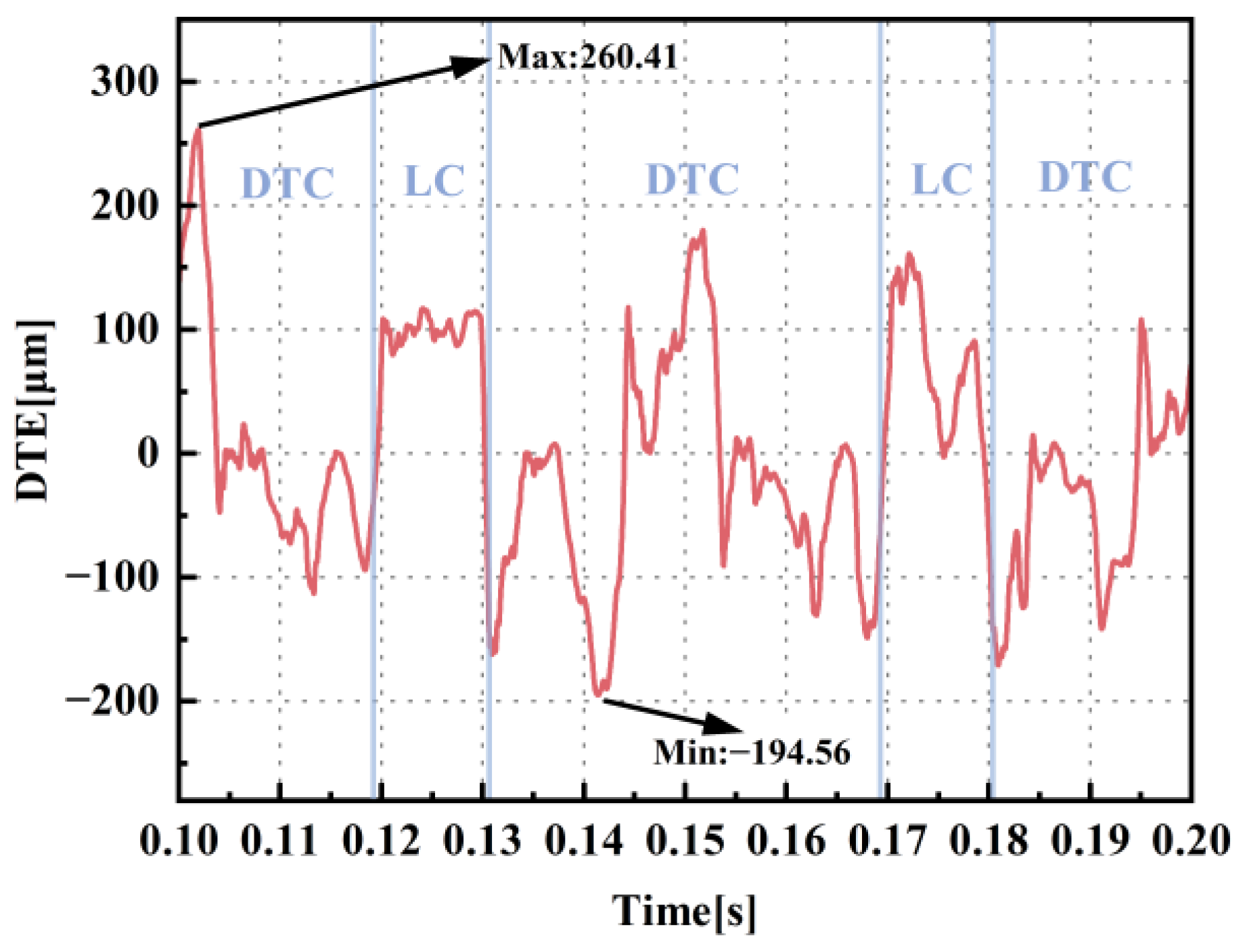
3.4. Dynamic Transmission Error Analysis
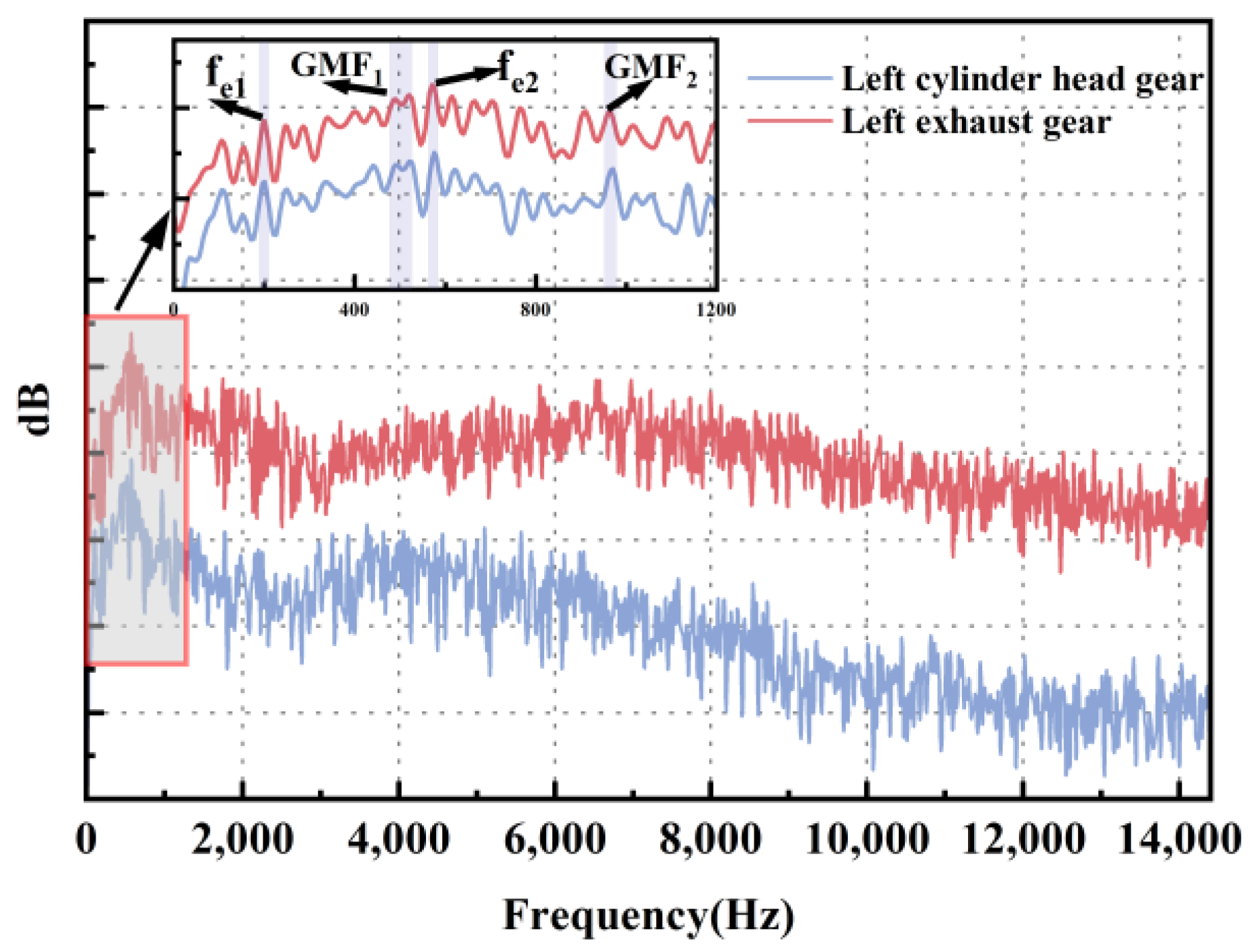
3.5. Vibration Analysis of a Multi-Stage Gear System
4. Conclusions
- (1)
- The spectrum of the gears exhibits prominent low-frequency peaks at 320 Hz and 750 Hz, which is attributed to the nonlinear characteristics of the bearing and gear contact. The spectrum of alternate-load-dominated gears exhibits a shifting phenomenon in low-frequency peaks, which is primarily attributable to variations in the internal contact state of the gears influenced by the alternate torques. The presence of these low-frequency peaks is both counterintuitive and potentially hazardous.
- (2)
- Under the coupled state, the maximum mesh stiffness demonstrates an increase of 69.5%, and the minimum mesh stiffness reaches only 31.5% of its non-coupled state value. The phenomena of marked oscillations in mesh stiffness come from the nonlinear dynamic coupling effects resulting from the propagation of external loads. The changes in the mesh stiffness characteristic can potentially lead to unforeseen failure issues under gear operating conditions.
- (3)
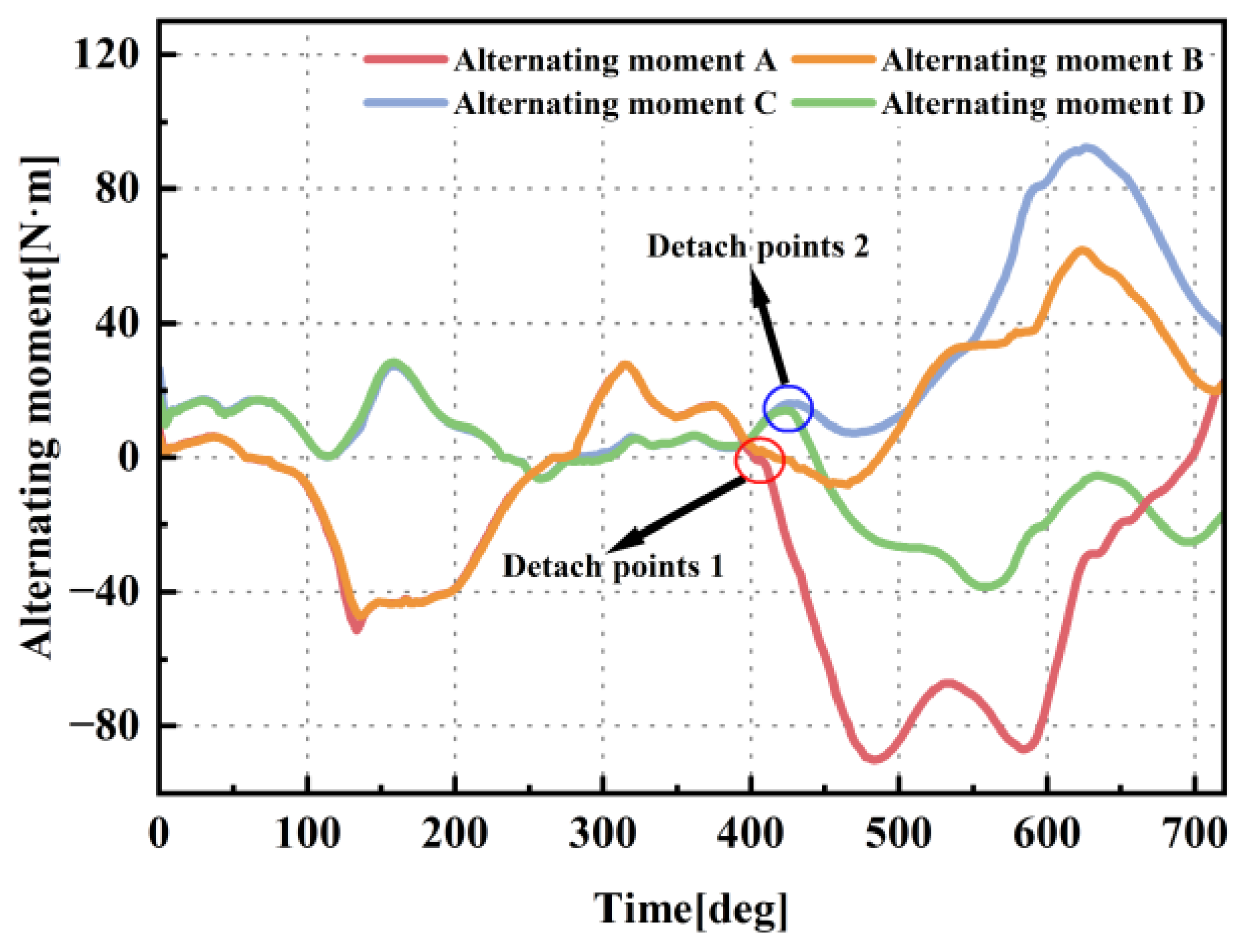
- The intermediate gears are more susceptible to being influenced by counteracting asymmetric torques from adjacent gears, which implies that middle gears are relatively predisposed to developing double-tooth contact and potential failure. The presence of dangerous double-tooth contact regions at 0.115 s, 0.137 s, 0.165 s, and 0.188 s suggests that the failure of the gear transmission system is causally linked to the occurrence of periodic internal impact loads between the gears. The occurrence of internal impact loads is attributed to the delayed transmission effects of alternating loads in the intermediate gears.
- (4)
- Under conditions of alternating torques, the variation in the DTE is strongly correlated with the dynamic behavior of the gear meshing state. When alternating torques cause changes in the gear meshing state, the STE within the gear pair evolves into DTE, leading to high-amplitude fluctuations and the nonlinear dynamic characteristics of DTE. The transmission of external loads through intermediate gear stages induces a propagation delay, which further yields multimodal DTE characteristics in the intermediate gears.
- (5)
- Alternating external loads are the dominant excitation source of vibrations, noise, and failures in the gear transmission system. The load-carrying gears generally exhibit high-amplitude vibration displacements and pronounced oscillatory characteristics compared to load-transmitting gears.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Siyu, C.; Jinyuan, T.; Caiwang, L.; Qibo, W. Nonlinear dynamic characteristics of geared rotor bearing system with dynamic backlash and friction. Mech. Mach. Theory 2011, 46, 466–478. [Google Scholar] [CrossRef]
- Yi, Y.; Huang, K.; Xiong, Y.; Sang, M. Nonlinear dynamic modelling and analysis for a spur gear system with time-varying pressure angle and gear backlash. Mech. Syst. Signal Process. 2019, 132, 18–34. [Google Scholar] [CrossRef]
- Liu, P.; Zhu, L.; Gou, X.; Shi, J.; Jin, G. Dynamics modeling and analyzing of spur gear pair with pitch deviation considering time-varying contact ratio under multi-state meshing. J. Sound Vib. 2021, 513, 116411. [Google Scholar] [CrossRef]
- Zhou, D.; Guo, Y.; Yang, J.; Zhang, Y. Study on the Parameter Influences of Gear Tooth Profile Modification and Transmission Error Analysis. Machines 2024, 12, 316. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, J.; Yao, Z.; Yang, X.; Sun, R.; Zhao, Y. Nonlinear characteristics of a multi-degree-of-freedom spur gear system with bending-torsional coupling vibration. Mech. Syst. Signal Process. 2019, 121, 810–827. [Google Scholar] [CrossRef]
- Bruzzone, F.; Rosso, C. Sources of excitation and models for cylindrical gear dynamics: A review. Machines 2020, 8, 37. [Google Scholar] [CrossRef]
- Li, Z.; Peng, Z. Nonlinear dynamic response of a multi-degree of freedom gear system dynamic model coupled with tooth surface characters: A case study on coal cutters. Nonlinear Dyn. 2016, 84, 271–286. [Google Scholar] [CrossRef]
- Mohammed, O.D.; Rantatalo, M.; Aidanpää, J.-O. Dynamic modelling of a one-stage spur gear system and vibration-based tooth crack detection analysis. Mech. Syst. Signal Process. 2015, 54, 293–305. [Google Scholar] [CrossRef]
- Xu, L.; Luo, Y.; Hu, R. A novel method of modelling contact dynamics for spur gear transmission. Mech. Mach. Theory 2024, 203, 105793. [Google Scholar] [CrossRef]
- Li, Y.; Chen, T.; Wang, X. Non-linear dynamics of gear pair with dynamic backlash subjected to combined internal and external periodic excitations. J. Vib. Control. 2016, 22, 1693–1703. [Google Scholar] [CrossRef]
- Li, H.; Chen, S.; Tang, J.; Sun, Z.; Hu, Y. Nonlinear dynamic modeling and analysis of spur gear based on gear compatibility conditions. Mech. Mach. Theory 2022, 171, 104767. [Google Scholar] [CrossRef]
- Tian, G.; Gao, Z.; Liu, P.; Bian, Y. Dynamic modeling and stability analysis for a spur gear system considering gear backlash and bearing clearance. Machines 2022, 10, 439. [Google Scholar] [CrossRef]
- Lin, T.; Ou, H.; Li, R. A finite element method for 3D static and dynamic contact/impact analysis of gear drives. Comput. Methods Appl. Mech. Eng. 2007, 196, 1716–1728. [Google Scholar] [CrossRef]
- Cirelli, M.; Valentini, P.P.; Pennestrì, E. A study of the non-linear dynamic response of spur gear using a multibody contact based model with flexible teeth. J. Sound Vib. 2019, 445, 148–167. [Google Scholar] [CrossRef]
- Guilbert, B.; Velex, P.; Dureisseix, D.; Cutuli, P. A mortar-based mesh interface for hybrid finite-element/lumped-parameter gear dynamic models—Applications to thin-rimmed geared system. J. Mech. Des. 2016, 138, 123301. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, H.; Zuo, M.J.; Qin, Y. Three new models for evaluation of standard involute spur gear mesh stiffness. Mech. Syst. Signal Process. 2018, 101, 424–434. [Google Scholar] [CrossRef]
- Saxena, A.; Chouksey, M.; Parey, A. Measurement of FRFs of coupled geared rotor system and the development of an accurate finite element model. Mech. Mach. Theory 2018, 123, 66–75. [Google Scholar] [CrossRef]
- Liu, J.P.; Shu, X.B.; Kanazawa, H.; Imaoka, K.; Mikkola, A.; Ren, G.X. A model order reduction method for the simulation of gear contacts based on Arbitrary Lagrangian Eulerian formulation. Comput. Methods Appl. Mech. Eng. 2018, 338, 68–96. [Google Scholar] [CrossRef]
- Huangfu, Y.; Zeng, J.; Ma, H.; Dong, X.; Han, H.; Zhao, Z. A flexible-helical-geared rotor dynamic model based on hybrid beam-shell elements. J. Sound Vib. 2021, 511, 116361. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Pang, R.; Xia, M. Dynamic modeling and vibration analysis of a flexible gear transmission system. Mech. Syst. Signal Process. 2023, 197, 110367. [Google Scholar] [CrossRef]
- Kong, X.; Hu, Z.; Tang, J.; Chen, S.; Wang, Z. Effects of gear flexibility on the dynamic characteristics of spur and helical gear system. Mech. Syst. Signal Process. 2023, 184, 109691. [Google Scholar] [CrossRef]
- Kong, X.; Tang, J.; Hu, Z.; Ding, H.; Wang, Z.; Wang, Q. Dynamic modeling and vibration analysis of spur gear system considering thin-walled gear and hollow shaft. Mech. Mach. Theory 2023, 181, 105197. [Google Scholar] [CrossRef]
- Schurr, D.; Holzwarth, P.; Eberhard, P. Investigation of dynamic stress recovery in elastic gear simulations using different reduction techniques. Comput. Mech. 2018, 62, 439–456. [Google Scholar] [CrossRef]
- Shweiki, S.; Rezayat, A.; Tamarozzi, T.; Mundo, D. Transmission Error and strain analysis of lightweight gears by using a hybrid FE-analytical gear contact model. Mech. Syst. Signal Process. 2019, 123, 573–590. [Google Scholar] [CrossRef]
- Kahraman, A. Dynamic analysis of a multi-mesh helical gear train. J. Mech. Des. 1994, 116, 706–712. [Google Scholar] [CrossRef]
- Li, W.; Li, Z.; Shi, H.; Li, X. Impact of phase configuration of a helical idler gear system on the vibration. Appl. Acoust. 2023, 211, 109467. [Google Scholar] [CrossRef]
- Yao, Z.; Lin, T.; Chen, Q.; Ren, H. Dynamic Response of Electromechanical Coupled Motor Gear System with Gear Tooth Crack. Machines 2024, 12, 918. [Google Scholar] [CrossRef]
- Li, Y.; Yuan, S.; Wu, W.; Song, X.; Liu, K.; Lian, C. Dynamic analysis of the helical gear transmission system in electric vehicles with a large helix angle. Machines 2023, 11, 696. [Google Scholar] [CrossRef]
- Yavuz, S.D.; Saribay, Z.B.; Cigeroglu, E. Nonlinear dynamic analysis of a drivetrain composed of spur, helical and spiral bevel gears. Nonlinear Dyn. 2020, 100, 3145–3170. [Google Scholar] [CrossRef]
- Liu, G.; Parker, R.G. Nonlinear dynamics of idler gear system. Nonlinear Dyn. 2008, 53, 345–367. [Google Scholar] [CrossRef]
- Vinayak, H.; Singh, R. Multi-body dynamics and modal analysis of compliant gear bodies. J. Sound Vib. 1998, 210, 171–214. [Google Scholar] [CrossRef]
- Jiang, S.; Li, W.; Wang, Y.; Yang, X.; Xu, S. Study on electromechanical coupling torsional resonance characteristics of gear system driven by PMSM: A case on shearer semi-direct drive cutting transmission system. Nonlinear Dyn. 2021, 104, 1205–1225. [Google Scholar] [CrossRef]
- Fakhfakh, H.; Bruyère, J.; Velex, P.; Becquerelle, S. A torsional model of multi-stage gears–influence of external excitations and tooth shape modifications. Mech. Ind. 2016, 17, 413. [Google Scholar] [CrossRef]
- Yavuz, S.D.; Saribay, Z.B.; Cigeroglu, E. Nonlinear time-varying dynamic analysis of a multi-mesh spur gear train. In Dynamics of Coupled Structures, Volume 4: Proceedings of the 34th IMAC, a Conference and Exposition on Structural Dynamics 2016; Springer: Cham, Switzerland, 2016; pp. 309–321. [Google Scholar]
- Gao, H.; Zhang, Y. Nonlinear behavior analysis of geared rotor bearing system featuring confluence transmission. Nonlinear Dyn. 2014, 76, 2025–2039. [Google Scholar] [CrossRef]
- Li, W.; Li, Z. Dynamic analysis of a multi-stage gear system considering the coupling between mesh phasing angle and coaxial teeth ratio. Nonlinear Dyn. 2023, 111, 19855–19878. [Google Scholar] [CrossRef]
- Neusser, Z.; Sopouch, M.; Schaffner, T.; Priebsch, H.-H. Multi-Body Dynamics Based Gear Mesh Models for Prediction of Gear Dynamics and Transmission Error; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2010. [Google Scholar]
- Lu, W.; Zhang, Y.; Cheng, H.; Zhou, Y.; Lv, H. Research on dynamic behavior of multistage gears-bearings and box coupling system. Measurement 2020, 150, 107096. [Google Scholar] [CrossRef]
- Hu, Z.; Tang, J.; Wang, Q.; Chen, S.; Qian, L. Investigation of nonlinear dynamics and load sharing characteristics of a two-path split torque transmission system. Mech. Mach. Theory 2020, 152, 103955. [Google Scholar] [CrossRef]
- Yang, Y.; Li, H.; Dai, Y. Nonlinear vibration characteristics of spur gear system subjected to multiple harmonic excitations. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 6026–6050. [Google Scholar] [CrossRef]
- ISO TR 10064-2-1996; Cylindrical Gears—Code of Inspection Practice—Part 2: Inspection Related to Radial Composite Deviations and Runout Verification. ISO: Geneva, Switzerland, 1996.
- Chen, Z.; Zhai, W.; Shao, Y.; Wang, K. Mesh stiffness evaluation of an internal spur gear pair with tooth profile shift. Sci. China Technol. Sci. 2016, 59, 1328–1339. [Google Scholar] [CrossRef]

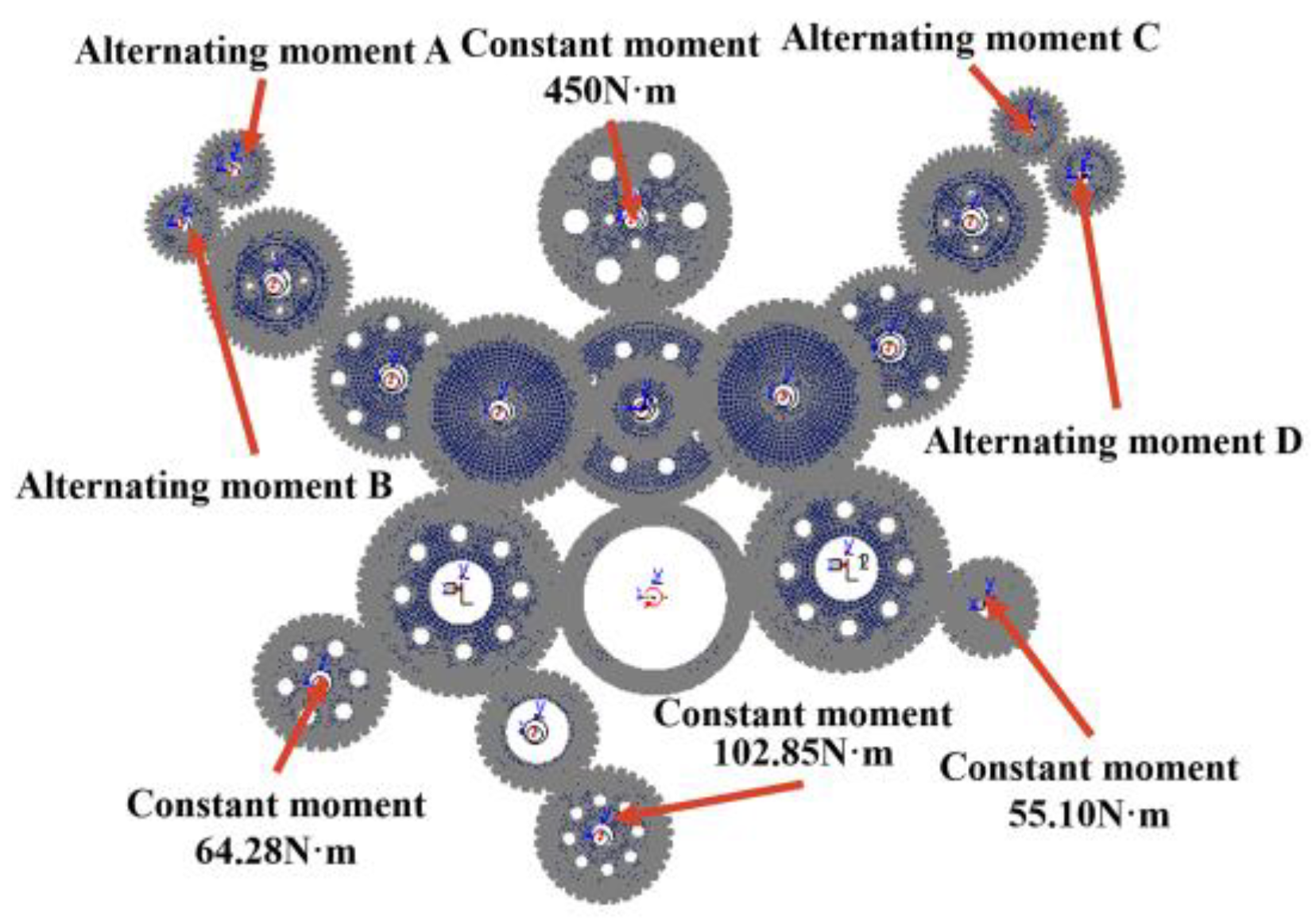







| Gear Model | Gear A | Gear B | Gear C | Gear D | Gear E | Gear F | Gear G | Gear H | Gear I | Gear J |
|---|---|---|---|---|---|---|---|---|---|---|
| Teeth number | 50 | 52 | 26 | 53 | 57 | 27 | 54 | 35 | 31 | 25 |
| Module/(mm) | 4 | 4 | 4 | 3 | 3 | 3 | 4 | 4 | 4 | 4 |
| Pressure angle/(°) | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 |
| Tooth width/(mm) | 44 | 22 | 23 | 39 | 17.5 | 20 | 18 | 16 | 16 | 18 |
| Gear type | helical | helical | helical | Spur | Spur | Spur | helical | helical | helical | helical |
| Circle helix angle/(°) | 12 | 12 | 12 | 0 | 0 | 0 | 12 | 12 | 12 | 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, C.; Feng, H.; Zhu, Z.; Ren, P.; Zhang, Z.; Zhou, Q. Modeling and Dynamic Characteristic Analysis of a Rigid–Flexible Coupling Multi-Stage Gear Transmission System for High-Power-Density Diesel Engines. Machines 2025, 13, 416. https://doi.org/10.3390/machines13050416
Yi C, Feng H, Zhu Z, Ren P, Zhang Z, Zhou Q. Modeling and Dynamic Characteristic Analysis of a Rigid–Flexible Coupling Multi-Stage Gear Transmission System for High-Power-Density Diesel Engines. Machines. 2025; 13(5):416. https://doi.org/10.3390/machines13050416
Chicago/Turabian StyleYi, Chenkun, Huihua Feng, Ziqing Zhu, Peirong Ren, Zhongwei Zhang, and Qidi Zhou. 2025. "Modeling and Dynamic Characteristic Analysis of a Rigid–Flexible Coupling Multi-Stage Gear Transmission System for High-Power-Density Diesel Engines" Machines 13, no. 5: 416. https://doi.org/10.3390/machines13050416
APA StyleYi, C., Feng, H., Zhu, Z., Ren, P., Zhang, Z., & Zhou, Q. (2025). Modeling and Dynamic Characteristic Analysis of a Rigid–Flexible Coupling Multi-Stage Gear Transmission System for High-Power-Density Diesel Engines. Machines, 13(5), 416. https://doi.org/10.3390/machines13050416







