Design and Analysis of a Two-Stage Compliant Amplification Mechanism Based on Bridge-Type and Scott–Russell Structures for Compact Out-of-Plane Actuation
Abstract
1. Introduction
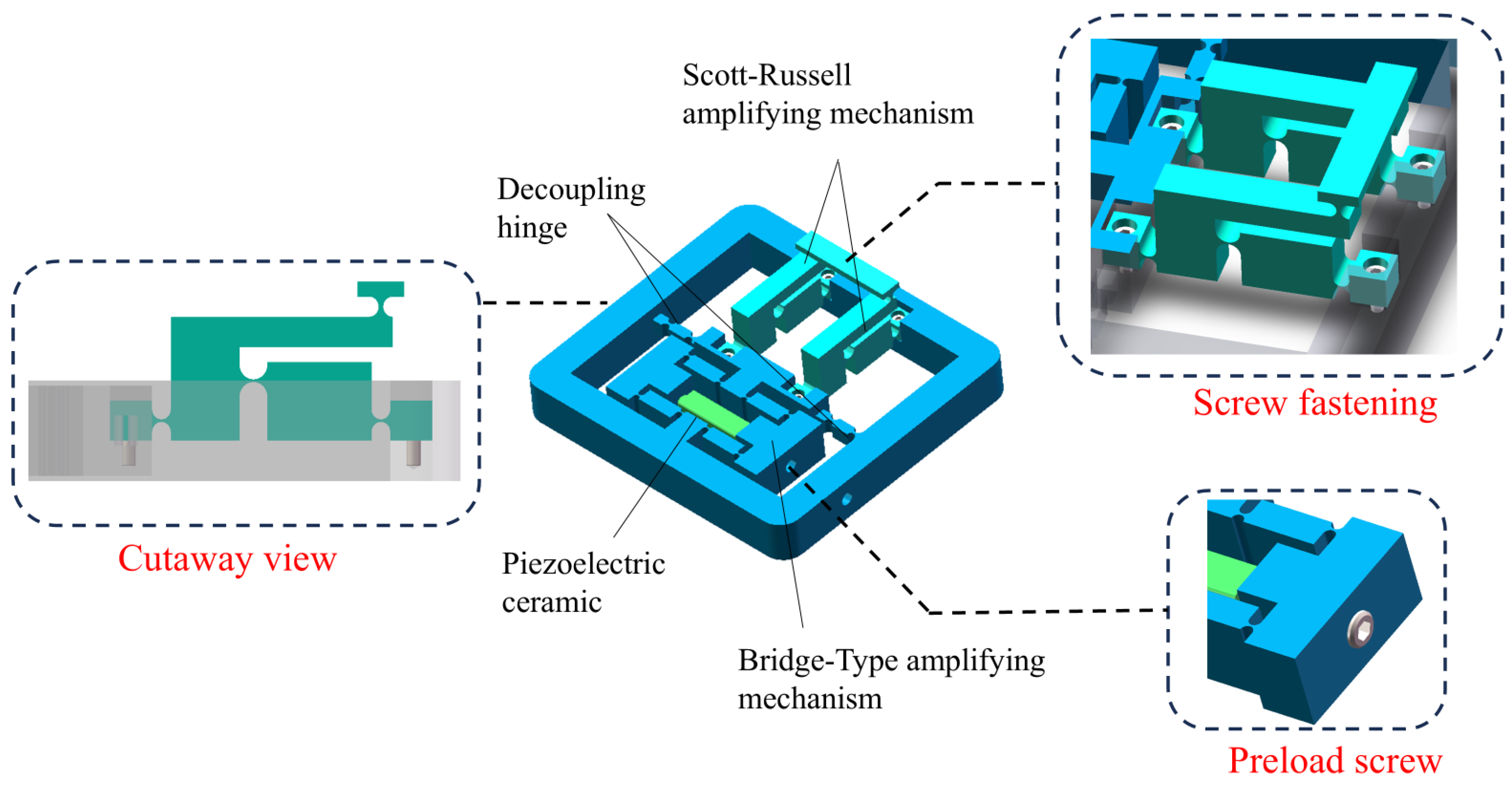
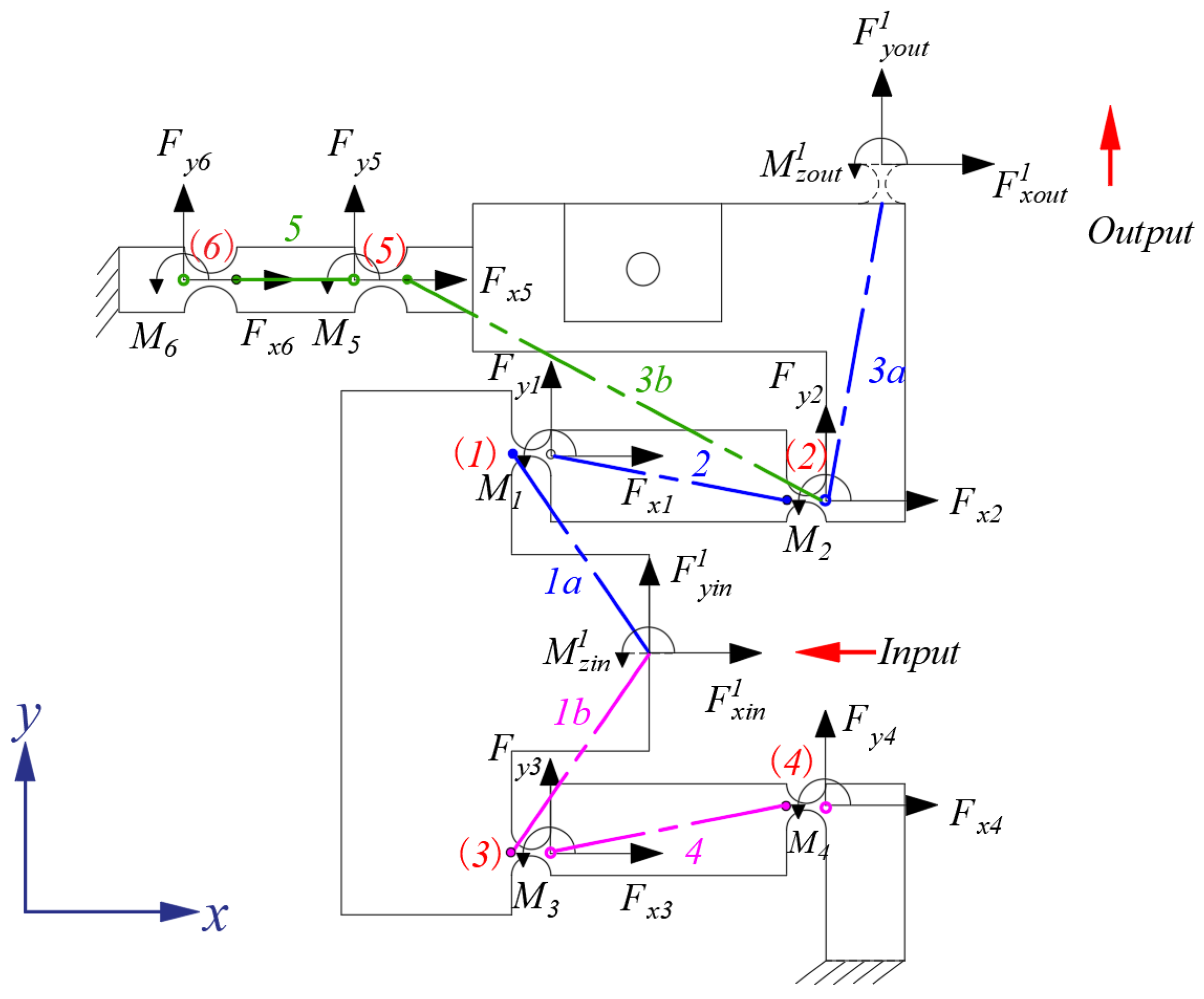
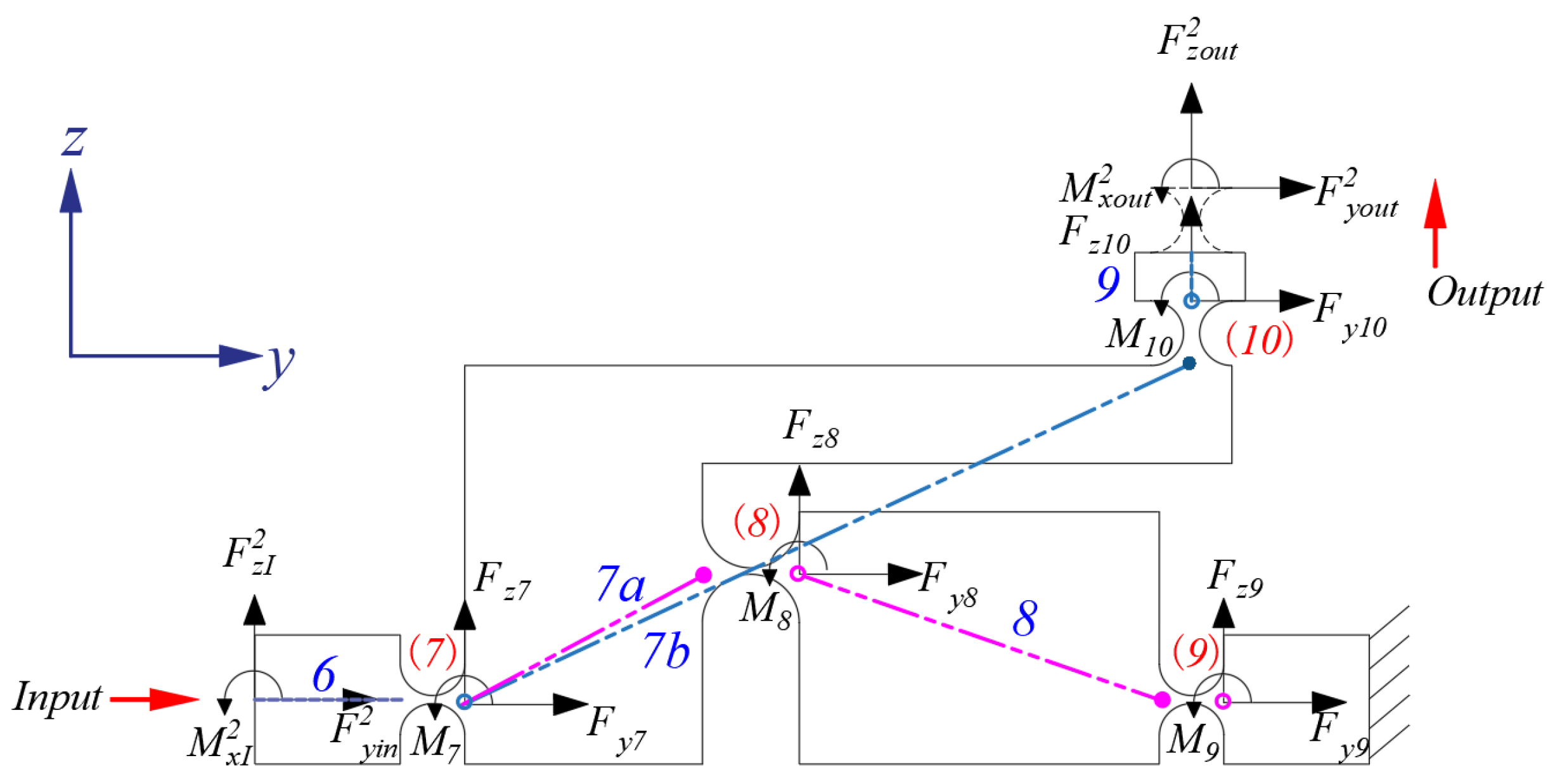
2. Mechanical Design
3. Mathematical Modeling
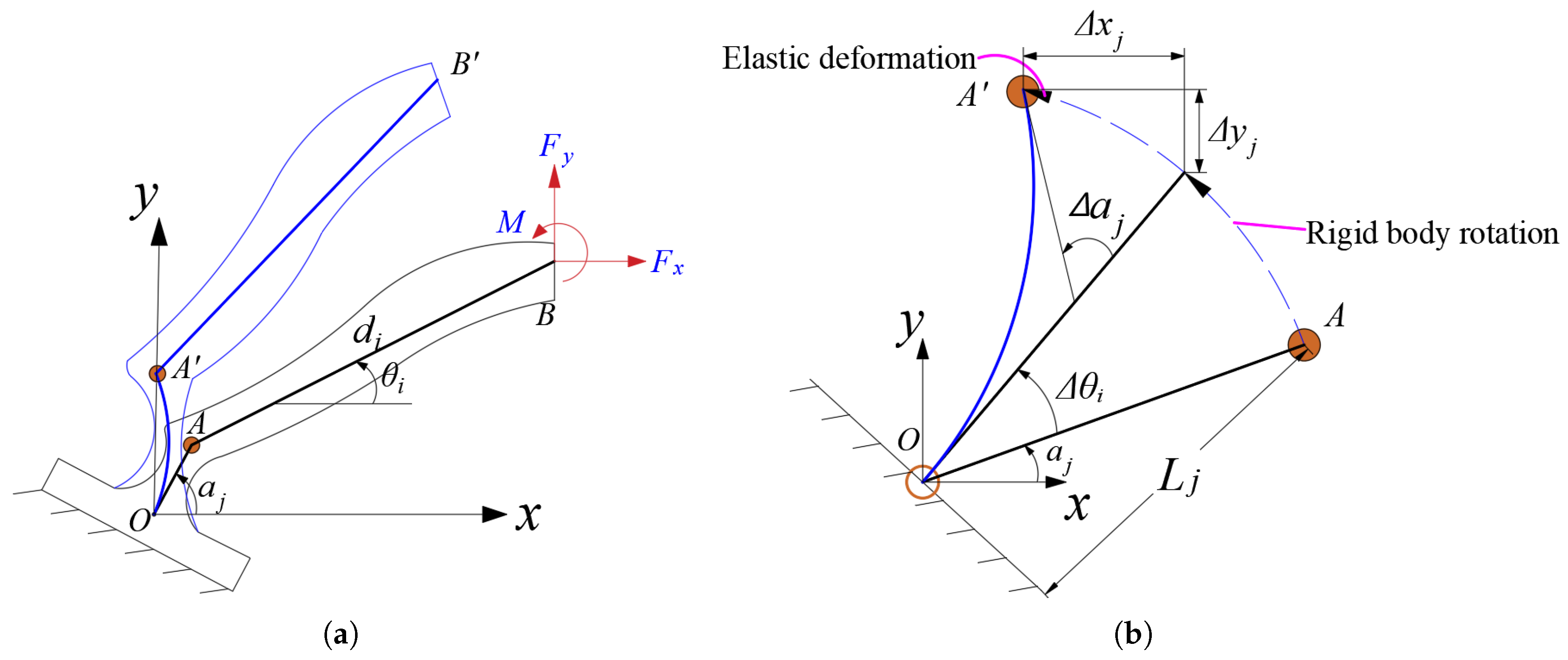
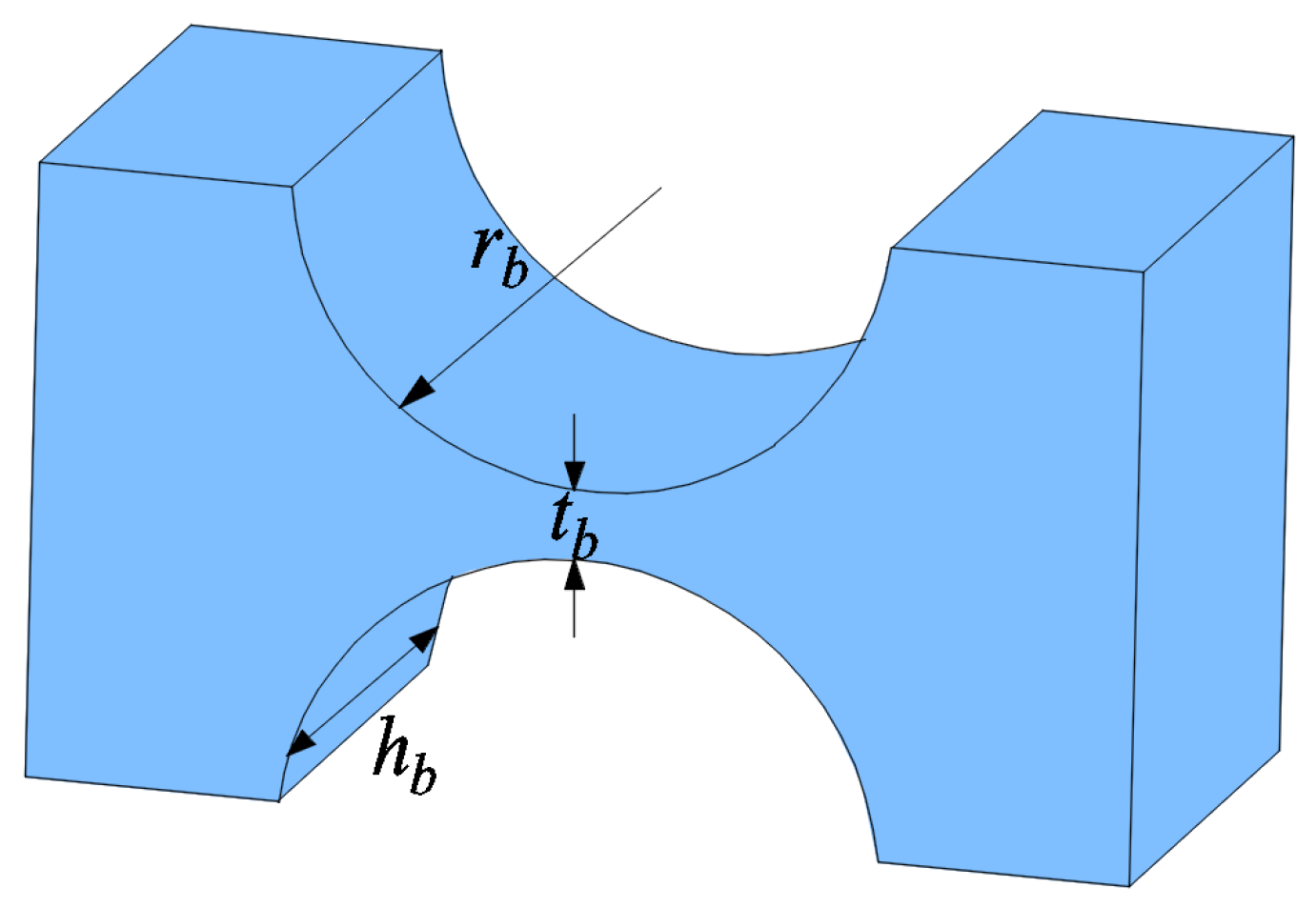
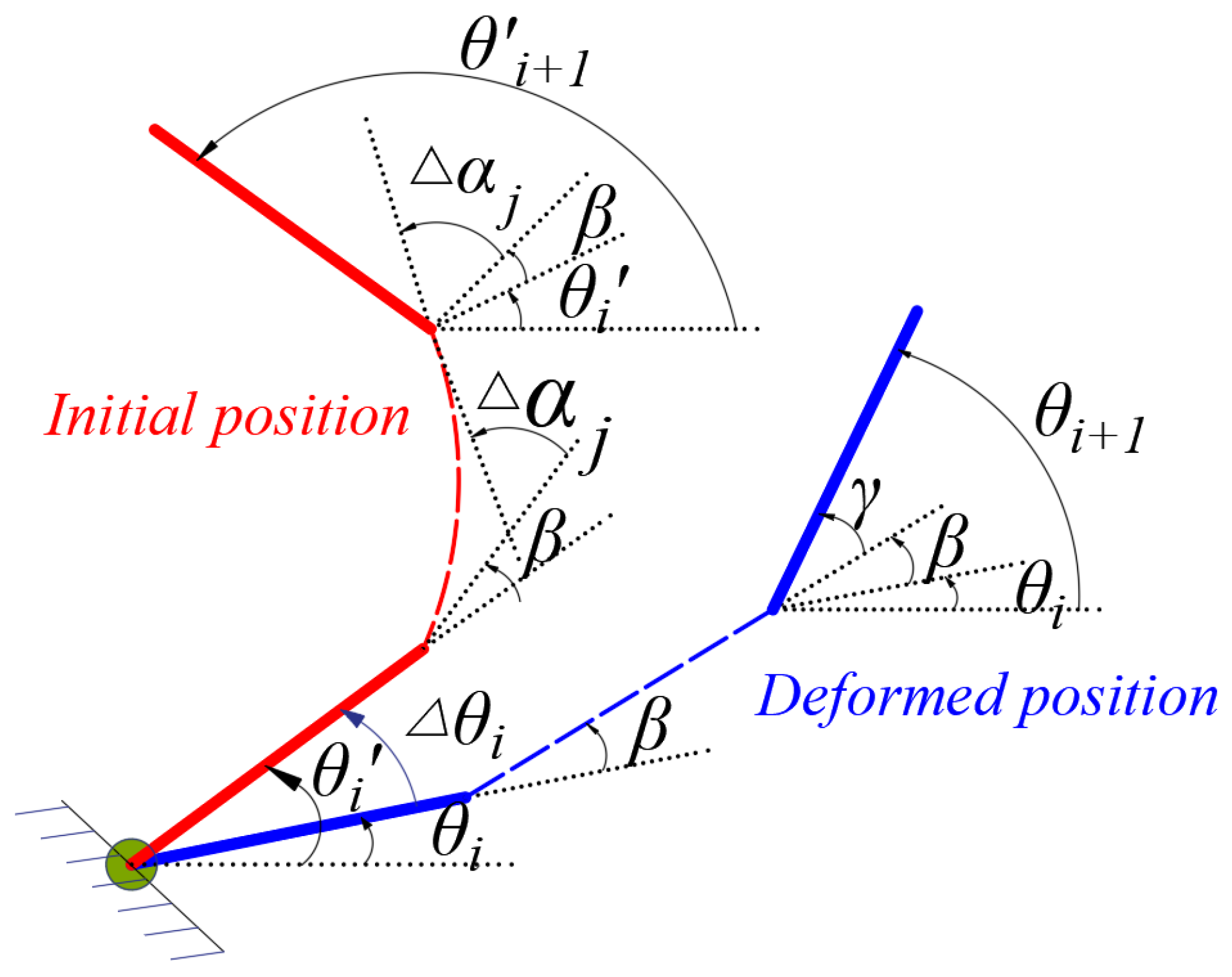
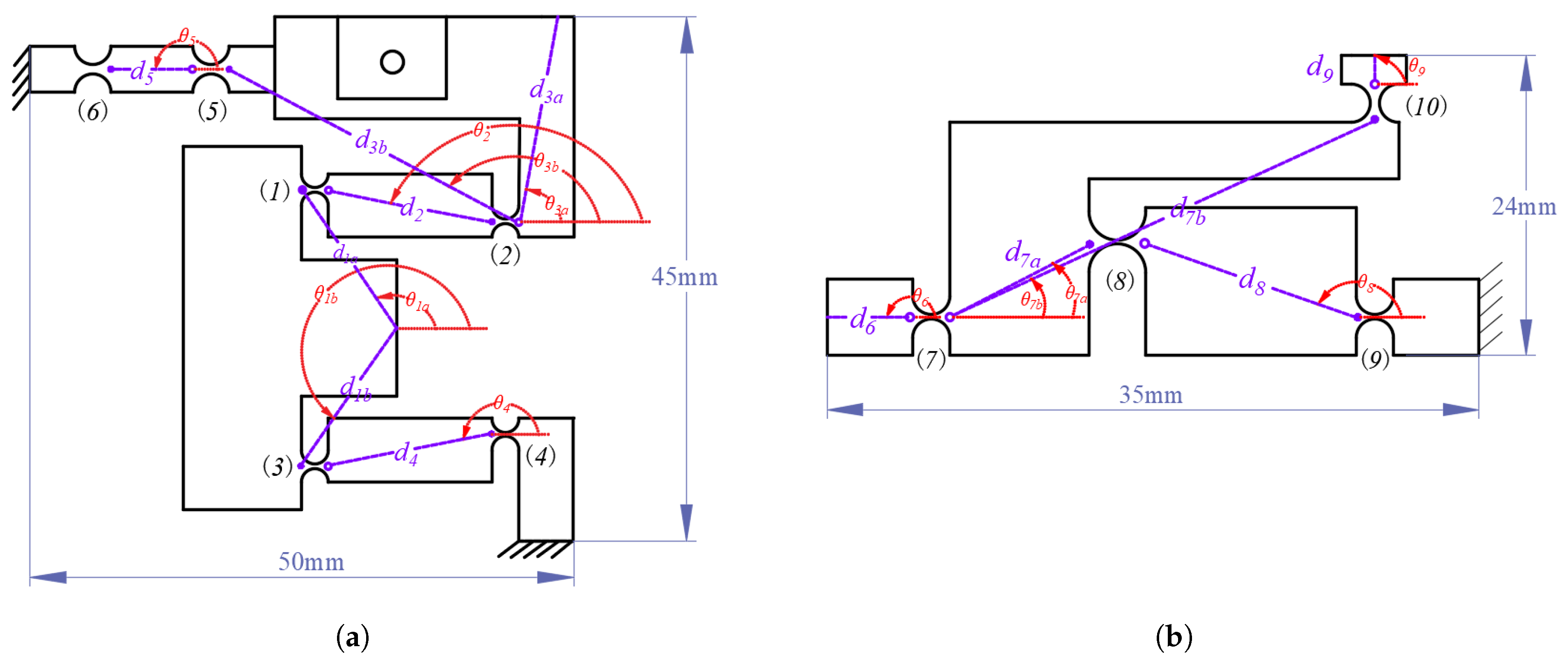
3.1. Constraint Relationship of Rigid Rod-Compliant Hinge
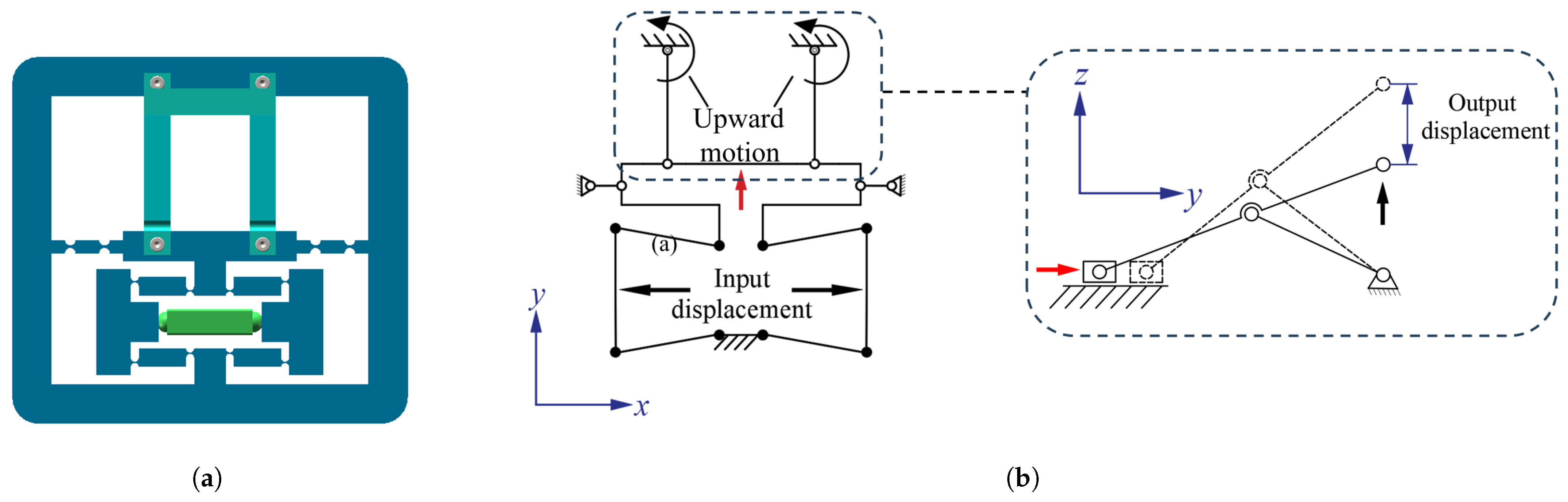
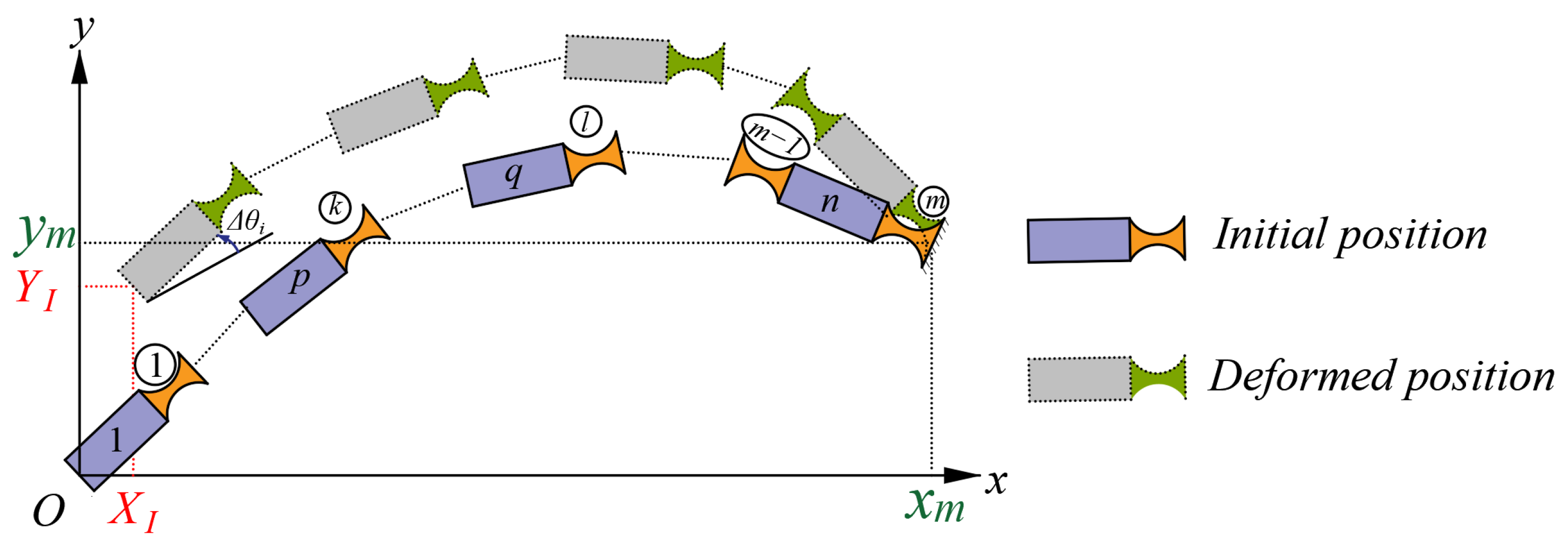
3.2. Bridge-Type Amplification Mechanism
3.3. Scott–Russell Amplification Mechanism
3.4. Two-Stage Displacement Amplification Mechanism
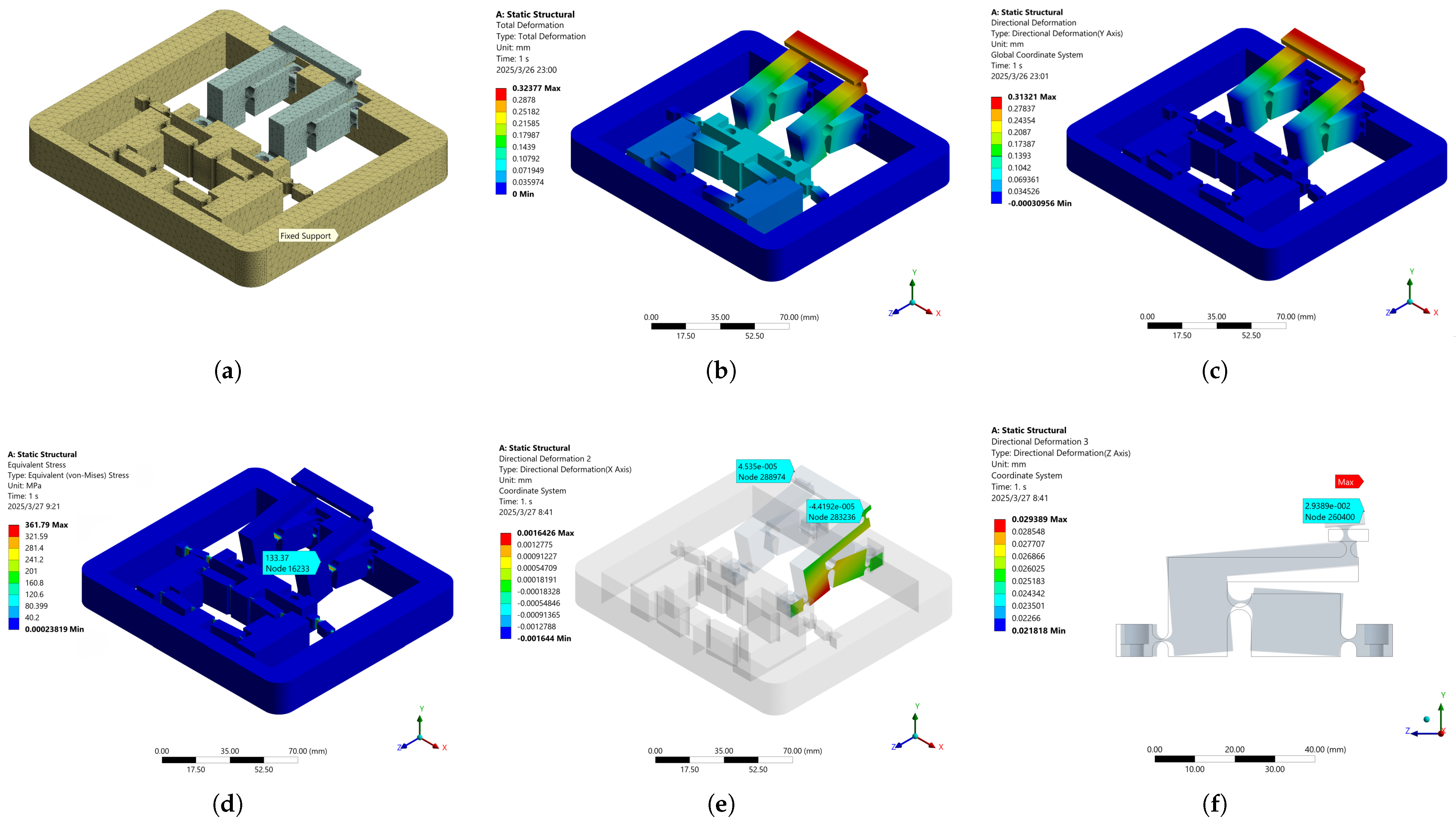
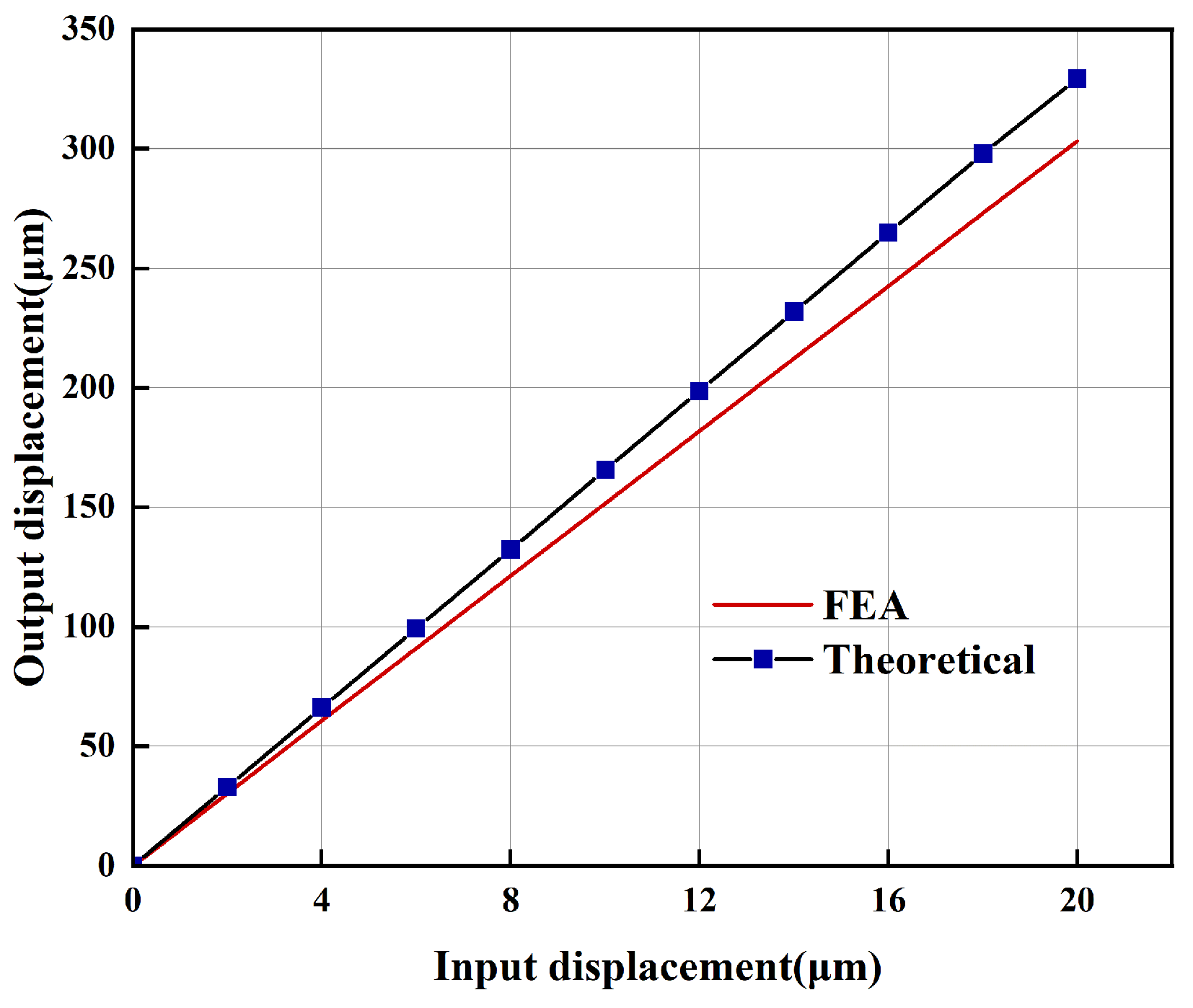
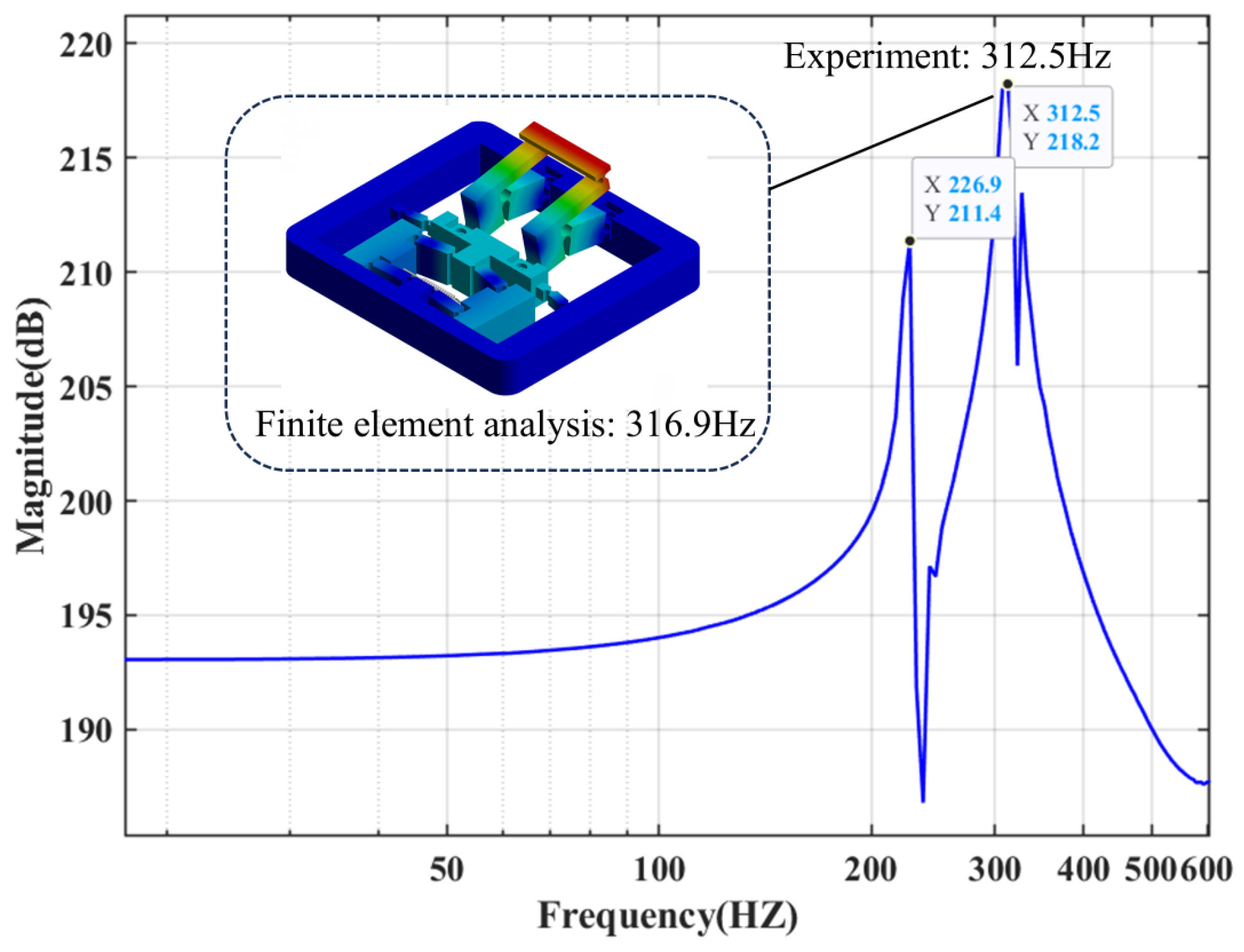
4. Finite Element Simulation and Analysis
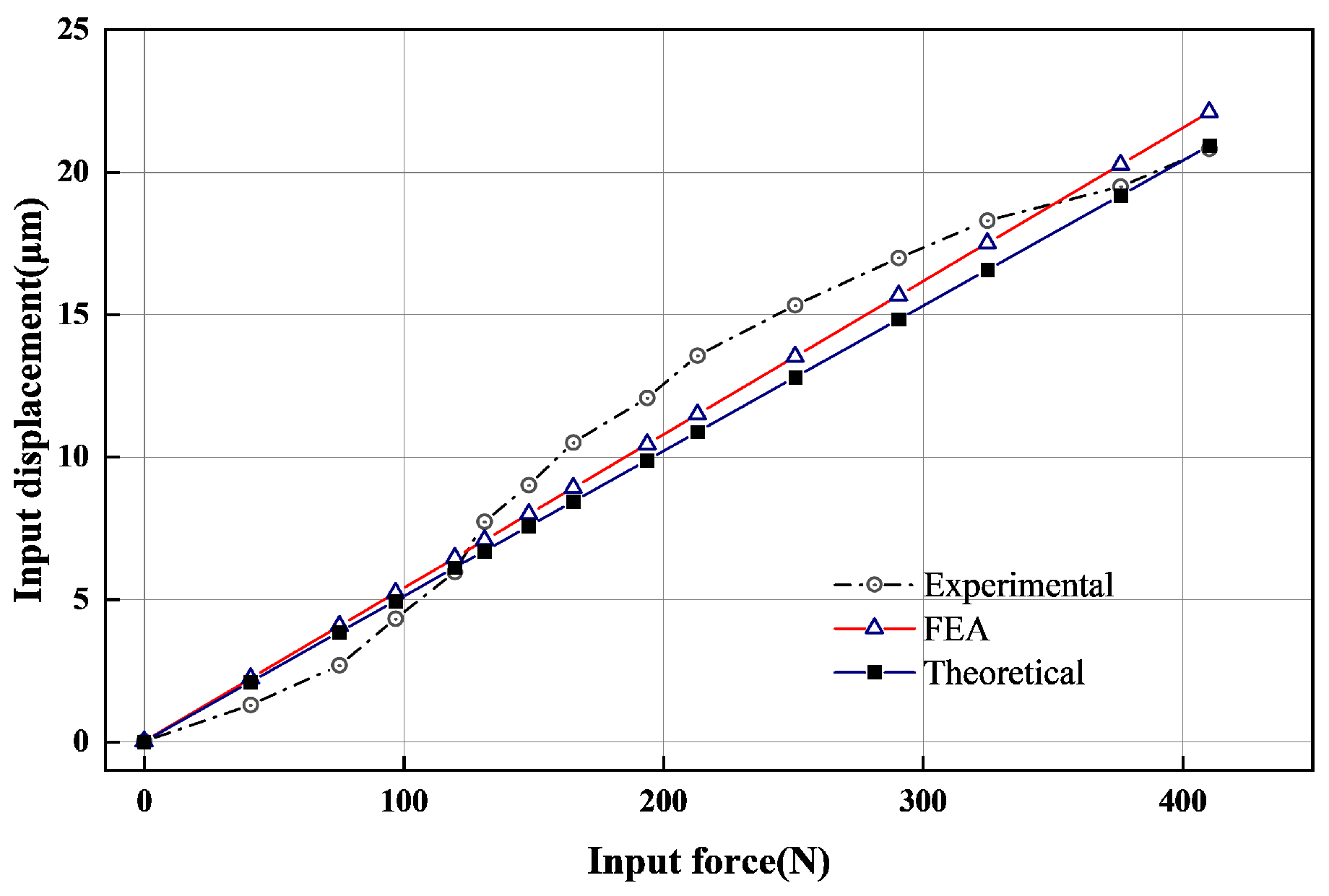
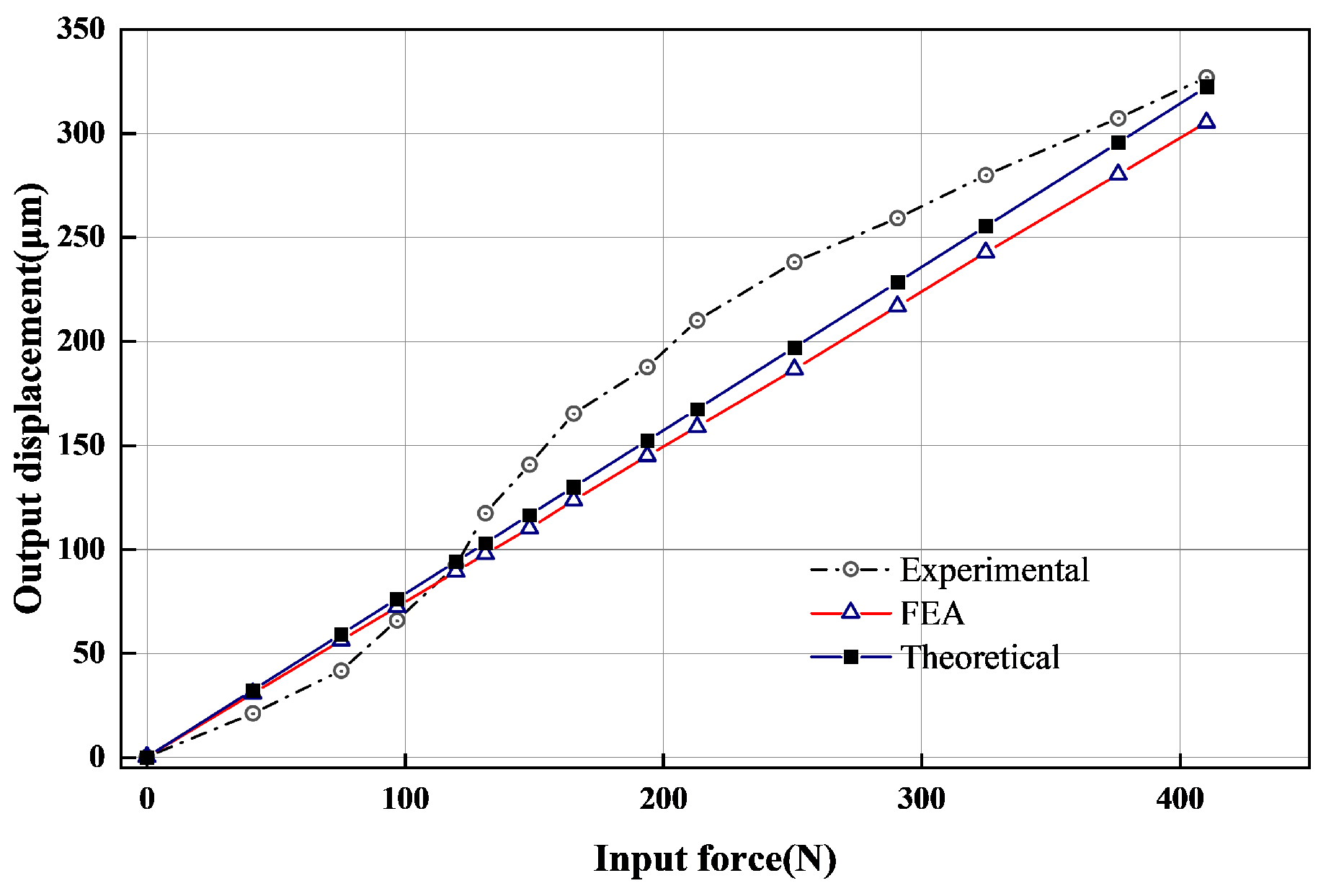
5. Experimental Validation
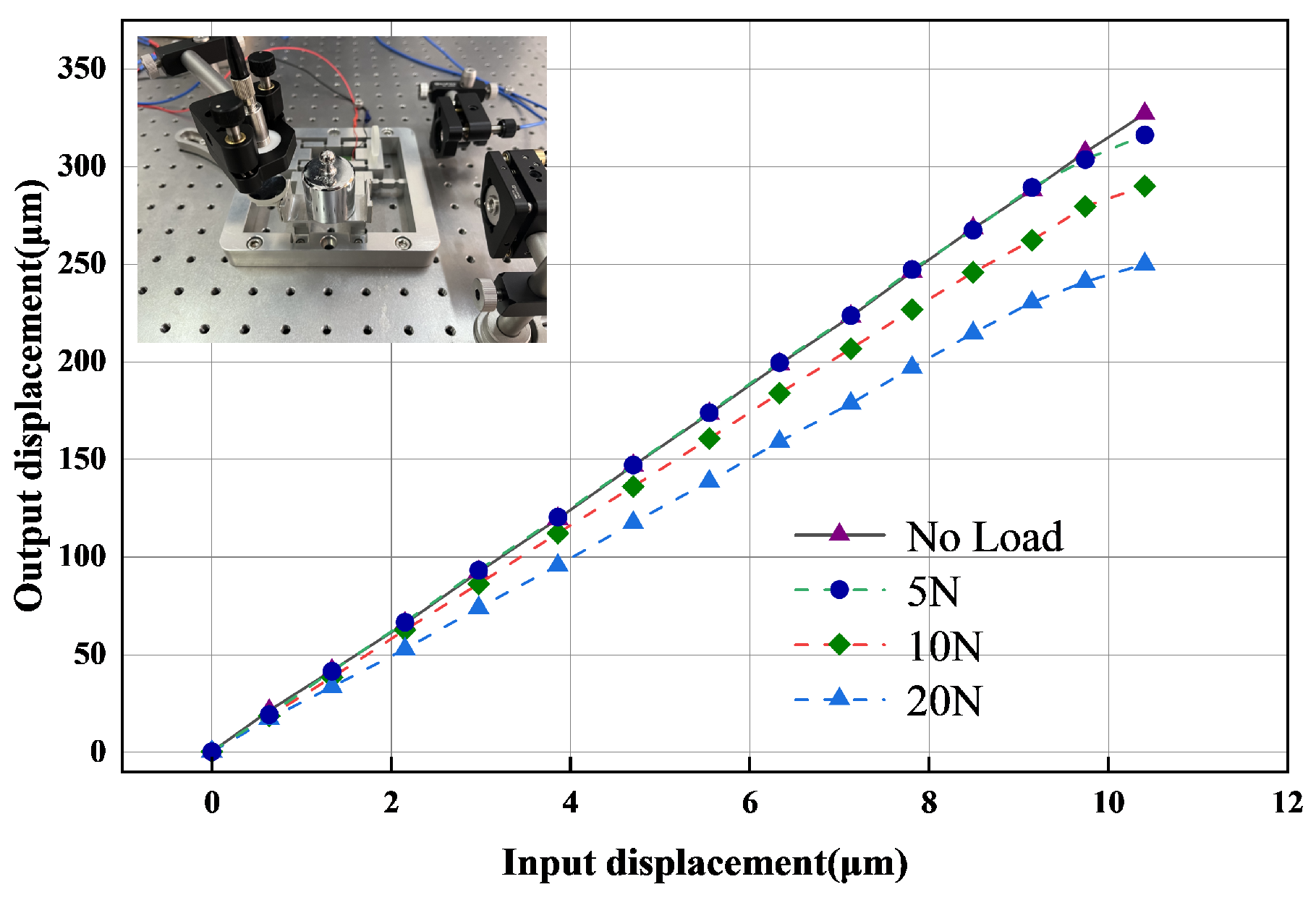
5.1. Prototype Production and Experimental Platform Construction
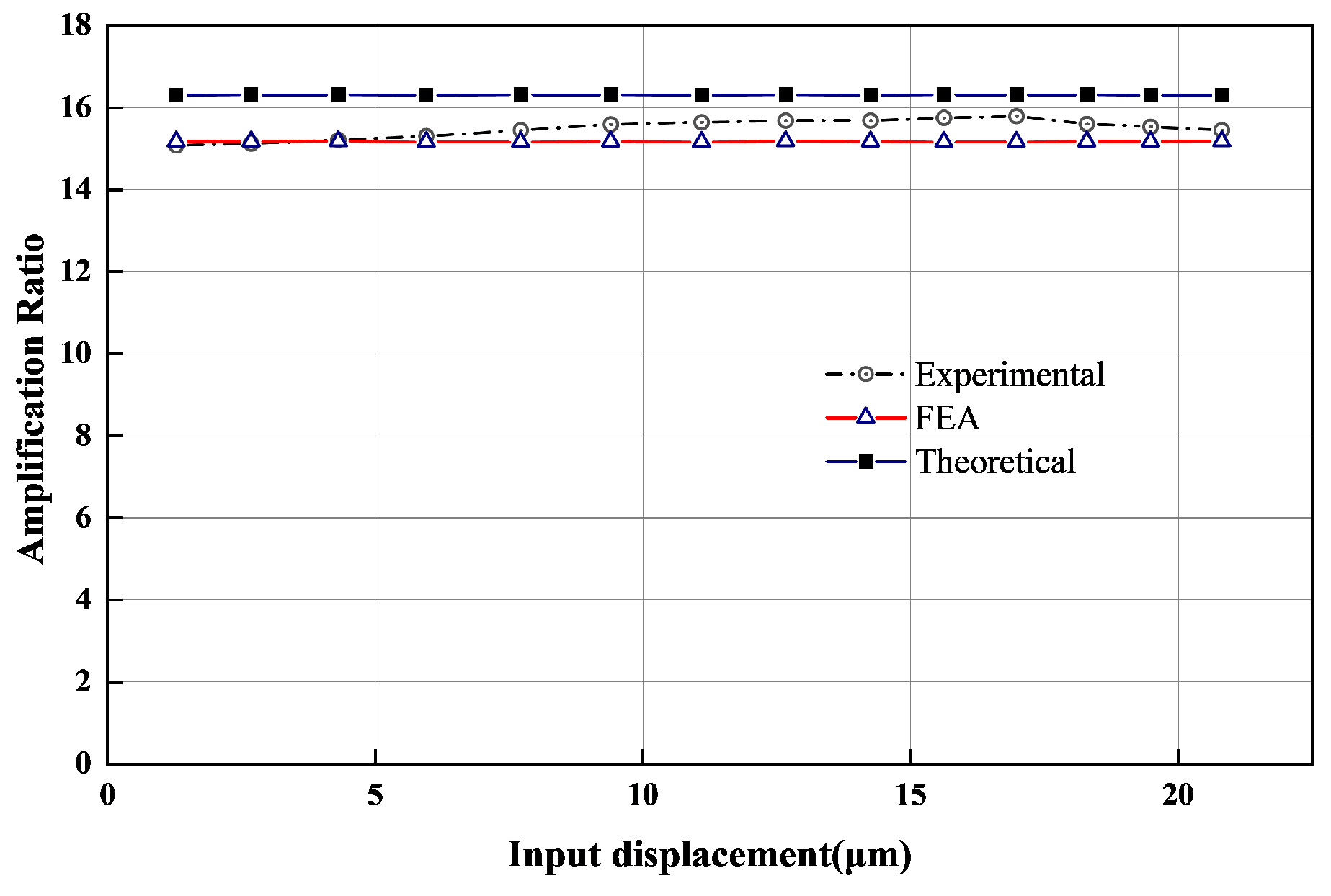
5.2. Mechanical Performance Test
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, K.; Liu, P.; Lu, S.; Yan, P. Design and modeling of a piezo-driven three-dimensional bridge-type amplification mechanism with input/output guiding constraint. Rev. Sci. Instrum. 2022, 93, 025005. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Deng, Z.; Hu, S.; Gao, J.; Gao, X. Designing a novel model of 2-DOF large displacement with a stepwise piezoelectric-actuated microgripper. Microsyst. Technol. 2020, 26, 2809–2816. [Google Scholar] [CrossRef]
- Lyu, Z.; Xu, Q.; Zhu, L. Design and development of a new piezoelectric-actuated biaxial compliant microgripper with long strokes. IEEE Trans. Autom. Sci. Eng. 2022, 20, 206–217. [Google Scholar] [CrossRef]
- Ding, Y.; Lai, L.J. Design and analysis of a displacement amplifier with high load capacity by combining bridge-type and Scott-Russell mechanisms. Rev. Sci. Instrum. 2019, 90, 065102. [Google Scholar] [CrossRef]
- Ling, M.; Cao, J.; Jiang, Z.; Lin, J. Theoretical modeling of attenuated displacement amplification for multistage compliant mechanism and its application. Sens. Actuators A Phys. 2016, 249, 15–22. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, S.; Gu, W.; Zhu, C.; Chen, X. Optimal operation of micro-energy grids considering shared energy storage systems and balanced profit allocations. CSEE J. Power Energy Syst. 2022, 9, 254–271. [Google Scholar]
- Lai, L.J.; Zhu, Z.N. Design, modeling and testing of a novel flexure-based displacement amplification mechanism. Sens. Actuators A Phys. 2017, 266, 122–129. [Google Scholar] [CrossRef]
- Shi, B.; Wang, F.; Han, C.; Huo, Z.; Tian, Y. Design of a precise positioning stage actuated by a double-layer stick-slip actuator used for precise assembly. Mech. Mach. Theory 2023, 185, 105336. [Google Scholar] [CrossRef]
- Chen, W.; Kang, S.; Lu, Q.; Zhang, Q.; Wei, H.; Zhang, Y.; Lin, Z.; Luo, L. A novel bridge-type compliant displacement amplification mechanism under compound loads based on the topology optimisation of flexure hinge and its application in micro-force sensing. Smart Mater. Struct. 2023, 33, 015020. [Google Scholar] [CrossRef]
- Qi, K.q.; Xiang, Y.; Fang, C.; Zhang, Y.; Yu, C.s. Analysis of the displacement amplification ratio of bridge-type mechanism. Mech. Mach. Theory 2015, 87, 45–56. [Google Scholar] [CrossRef]
- Iqbal, S.; Malik, A. A review on MEMS based micro displacement amplification mechanisms. Sens. Actuators A Phys. 2019, 300, 111666. [Google Scholar] [CrossRef]
- Zhu, W.L.; Zhu, Z.; Shi, Y.; Chen, X.; He, Y.; Ehmann, K.F.; Ju, B.F. A novel piezoelectrically actuated 2-DoF compliant micro/nano-positioning stage with multi-level amplification. Rev. Sci. Instrum. 2016, 87, 105006. [Google Scholar] [CrossRef] [PubMed]
- Moon, J.H.; Pahk, H.J.; Lee, B.G. Design, modeling, and testing of a novel 6-DOF micropositioning stage with low profile and low parasitic motion. Int. J. Adv. Manuf. Technol. 2011, 55, 163–176. [Google Scholar] [CrossRef]
- Lee, H.J.; Kim, H.C.; Kim, H.Y.; Gweon, D.G. Optimal design and experiment of a three-axis out-of-plane nano positioning stage using a new compact bridge-type displacement amplifier. Rev. Sci. Instrum. 2013, 84, 115103. [Google Scholar] [CrossRef]
- Yang, R.; Jouaneh, M.; Schweizer, R. Design and characterization of a low-profile micropositioning stage. Precis. Eng. 1996, 18, 20–29. [Google Scholar] [CrossRef]
- Kiziroglou, M.E.; Temelkuran, B.; Yeatman, E.M.; Yang, G.Z. Micro motion amplification—A review. IEEE Access 2020, 8, 64037–64055. [Google Scholar] [CrossRef]
- Zarrabi Ekbatani, R.; Zheng, J.; Chen, X.; Nikzad, M.; Man, Z. Design and Control of a Flexure-Based Dual Stage Piezoelectric Micropositioner. Int. J. Precis. Eng. Manuf. 2024, 25, 1793–1811. [Google Scholar] [CrossRef]
- Zhang, M.; Zhao, Q.; Li, Z.; Wang, S.; He, G.; Zhao, L. Development of a piezoelectric resonator with in-plane displacement-amplification mechanism. Microsyst. Technol. 2024, 31, 231–243. [Google Scholar] [CrossRef]
- Xie, X.; Bigdeli Karimi, M.; Liu, S.; Myanganbayar, B.; Livermore, C. Micro motion amplifiers for compact out-of-plane actuation. Micromachines 2018, 9, 365. [Google Scholar] [CrossRef]
- Zhu, W.L.; Zhu, Z.; Guo, P.; Ju, B.F. A novel hybrid actuation mechanism based XY nanopositioning stage with totally decoupled kinematics. Mech. Syst. Signal Process. 2018, 99, 747–759. [Google Scholar] [CrossRef]
- Gao, H.; Liu, J.; Ling, M.; Chen, T. Geometrically nonlinear design of a rhombus-nested compliant amplification mechanism for use in precision actuators and sensors. Precis. Eng. 2024, 90, 164–175. [Google Scholar] [CrossRef]
- Tian, Y.; Lu, K.; Wang, F.; Zhou, C.; Ma, Y.; Jing, X.; Yang, C.; Zhang, D. A spatial deployable three-DOF compliant nano-positioner with a three-stage motion amplification mechanism. IEEE/ASME Trans. Mechatron. 2020, 25, 1322–1334. [Google Scholar] [CrossRef]




| Elastic Modulus E | Poisson’s Ratio | Yield Strength | Density |
|---|---|---|---|
| 71 | 0.33 | 2.81 | 270 |
| Component | First-Stage Bridge-Type | Second-Stage Scott–Russell | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rigid rod | ||||||||||||
| (mm) | 19.41 | 19.41 | 24.15 | 22.77 | 33.52 | 24.15 | 11 | 10 | 21.4 | 52.45 | 27.18 | 5 |
| (deg) | 126.71 | 226.71 | 151.76 | 75.12 | 152.92 | 188.24 | 180.00 | 180.00 | 48.72 | 32.47 | 135.13 | 90 |
| Component | First-Stage Bridge-Type | Second-Stage Scott–Russell | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Compliant Hinges | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
| (mm) | 1.5 | 1.5 | 1.5 | 1.5 | 2 | 2 | 2 | 3 | 2 | 2 |
| (mm) | 16 | 16 | 16 | 16 | 10 | 10 | 10 | 10 | 10 | 10 |
| (mm) | 0.4 | 0.4 | 0.4 | 0.4 | 1 | 1 | 0.5 | 0.5 | 0.5 | 1 |
| (mm) | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 6 | 4 | 4 |
| Amplification | Input Stiffness | Equivalent Stiffness | |
|---|---|---|---|
| FEA | 15.17 | 18.55 | 1.34 |
| Theoretical | 16.30 | 19.71 | 1.27 |
| Experimental | 15.70 | 17.75 | 1.16 |
| Mechanism | Feature Height (mm) | Footprint Area (cm2) | Compact Index 1 | Amplification Ratio | Output Displacement (μm) | Resonance Frequency (Hz) | Input Stiffness (N/μm) |
|---|---|---|---|---|---|---|---|
Ref. [1] 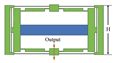 | 40 | 47.50 | 4.30 | 10.19 | 170 | 102.69 | 1.02 |
Ref. [4] 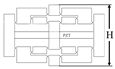 | 52 | 15.98 | 1.30 | 3.51 | 69 | 457 | 4.12 |
Ref. [14]  | 150 | 13.34 | 1.30 | 5.40 | 190 | 151.70 | 1.84 |
Ref. [21] 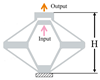 | 60 | 44.40 | 5.10 | 11.00 | 305 | 906 | 1.69 |
Ref. [22] 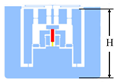 | 100 | 122.60 | 1.80 | 14.70 | 180 | 119.70 | – |
This paper  | 35 | 69.00 | 9.20 | 15.70 | 322 | 312.50 | 17.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, X.; Lu, S.; Wang, F.; Liu, P.; Xiao, G.; Yan, P. Design and Analysis of a Two-Stage Compliant Amplification Mechanism Based on Bridge-Type and Scott–Russell Structures for Compact Out-of-Plane Actuation. Machines 2025, 13, 386. https://doi.org/10.3390/machines13050386
Shi X, Lu S, Wang F, Liu P, Xiao G, Yan P. Design and Analysis of a Two-Stage Compliant Amplification Mechanism Based on Bridge-Type and Scott–Russell Structures for Compact Out-of-Plane Actuation. Machines. 2025; 13(5):386. https://doi.org/10.3390/machines13050386
Chicago/Turabian StyleShi, Xianfeng, Shuaishuai Lu, Fei Wang, Pengbo Liu, Guangchun Xiao, and Peng Yan. 2025. "Design and Analysis of a Two-Stage Compliant Amplification Mechanism Based on Bridge-Type and Scott–Russell Structures for Compact Out-of-Plane Actuation" Machines 13, no. 5: 386. https://doi.org/10.3390/machines13050386
APA StyleShi, X., Lu, S., Wang, F., Liu, P., Xiao, G., & Yan, P. (2025). Design and Analysis of a Two-Stage Compliant Amplification Mechanism Based on Bridge-Type and Scott–Russell Structures for Compact Out-of-Plane Actuation. Machines, 13(5), 386. https://doi.org/10.3390/machines13050386







