Mechanical Fault Diagnosis Method of a Disconnector Based on Improved Dung Beetle Optimizer–Multivariate Variational Mode Decomposition and Convolutional Neural Network–Bidirectional Long Short-Term Memory
Abstract
1. Introduction
- (1)
- After the mechanical failure of disconnectors, the state data cannot be obtained, resulting in insufficient sample size of the fault data.
- (2)
- The actual fault simulation cost of disconnector is high, and the degree and frequency of fault simulation are limited.
- (3)
- There are many joints in the transmission mechanism of the disconnector, there are many types of mechanical faults, and the fault self-evident is weak.
- (1)
- In order to solve the problem of parameters selection of MVMD, an improved dung beetle optimization algorithm is introduced to better decompose the vibration signals collected in the experiment.
- (2)
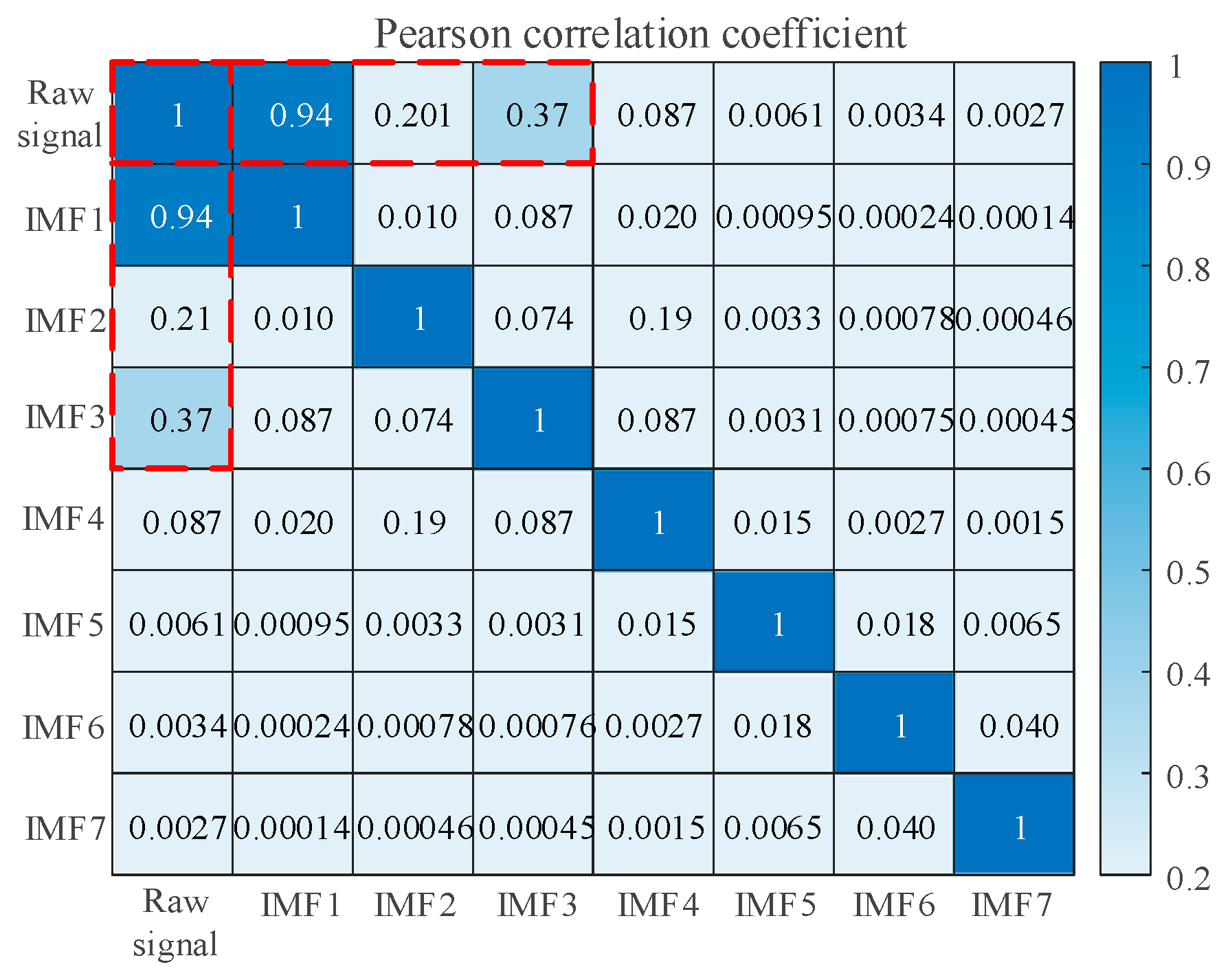
- In order to improve the efficiency of feature extraction, the Pearson correlation coefficient is used to select the intrinsic mode function (IMF) with the highest correlation with the original signal, and the eigenvalues of IMFs are calculated from the energy, entropy, and time–frequency domains to construct the fusion feature as the feature matrix. Extracting fault features from multiple domains can solve the problem of weak self-evident mechanical fault of disconnector to a certain extent.
- (3)
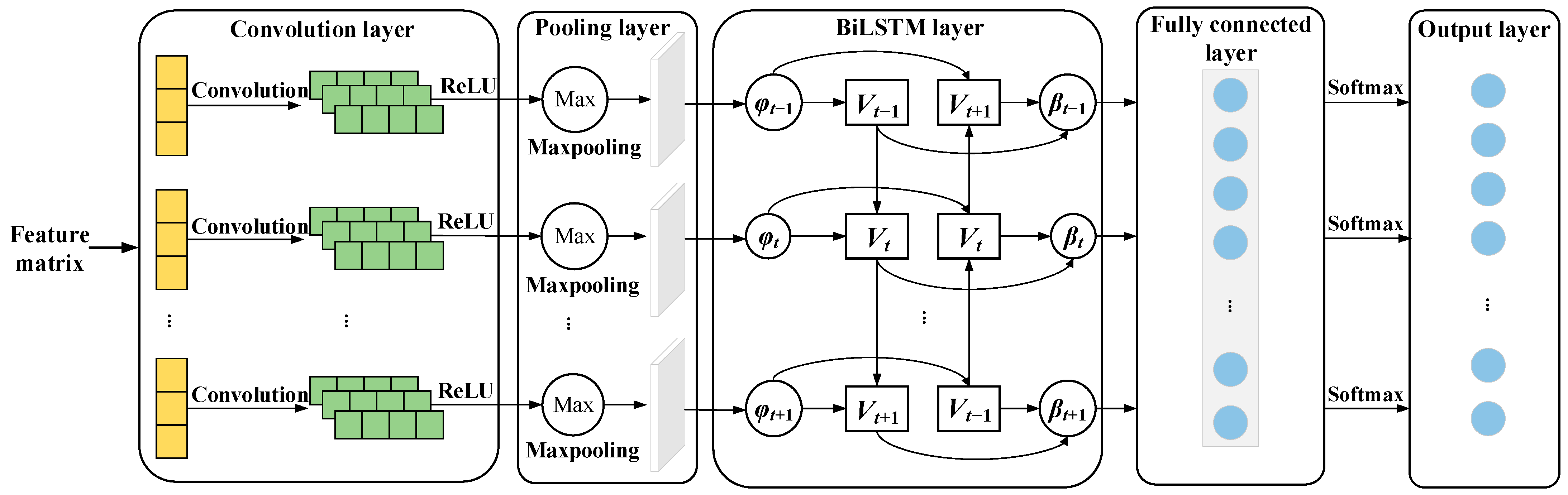
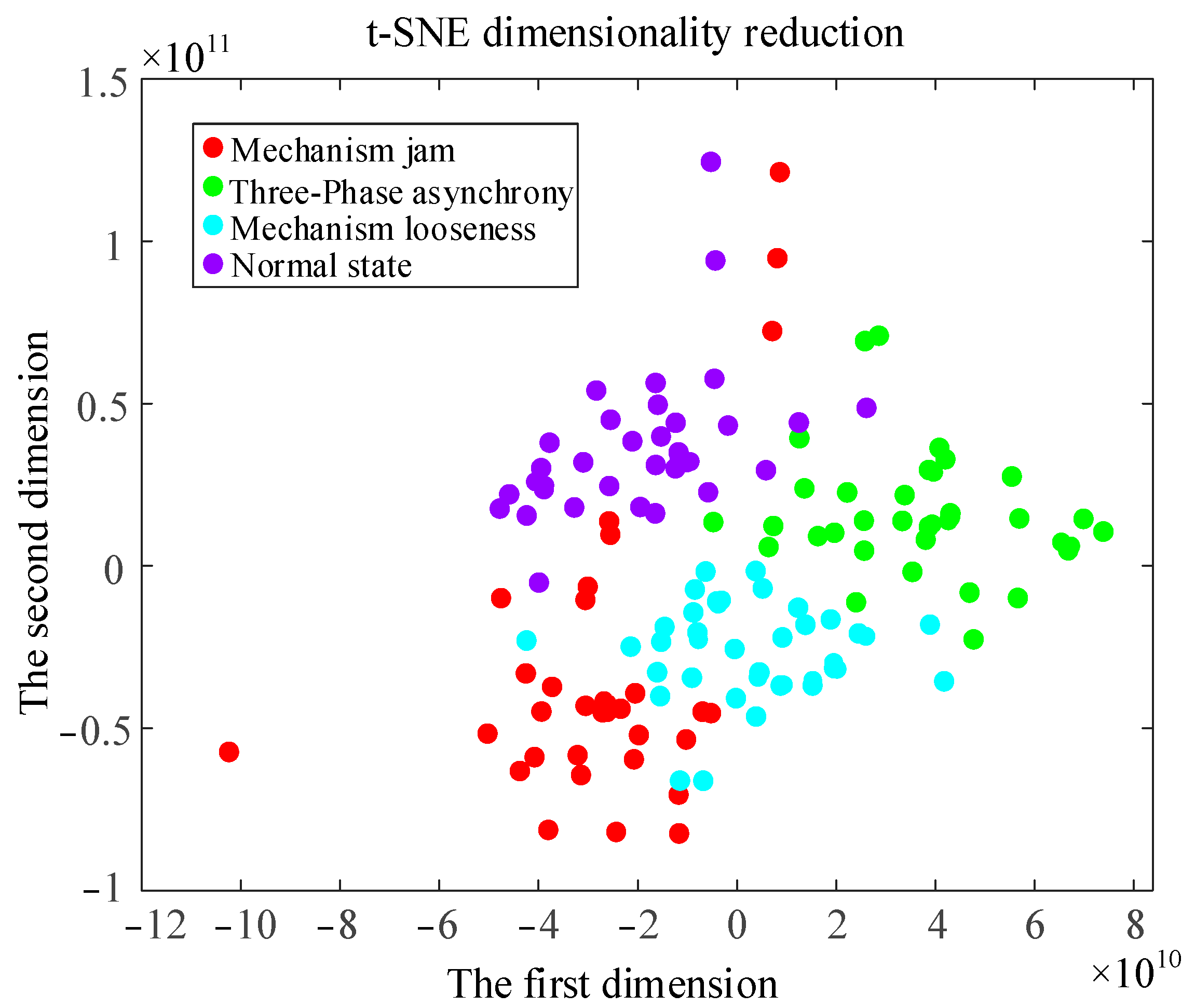
- In order to improve the operation speed and recognition accuracy, the dimensions of the feature matrix are reduced to two dimensions using the t-distributed stochastic neighbor embedding (t-SNE) method, and then the processed matrix is input to CNN-BiLSTM to obtain the fault identification results. The CNN-BiLSTM model can accurately distinguish the four operating conditions of the disconnector, and the fault diagnosis rate is high.
- (4)
- On the premise of controlling the overall cost of the platform, a disconnector fault experimental platform is built. Without destroying the disconnector equipment itself, three typical mechanical faults are innovatively simulated, vibration data under different conditions are collected, and the sample size of fault data is increased. Using the extracted vibration signal data, the usefulness of the constructed model is proved, and the signal variation law under different fault types is discussed.
2. The Proposed Method
2.1. Multivariate Variational Mode Decomposition
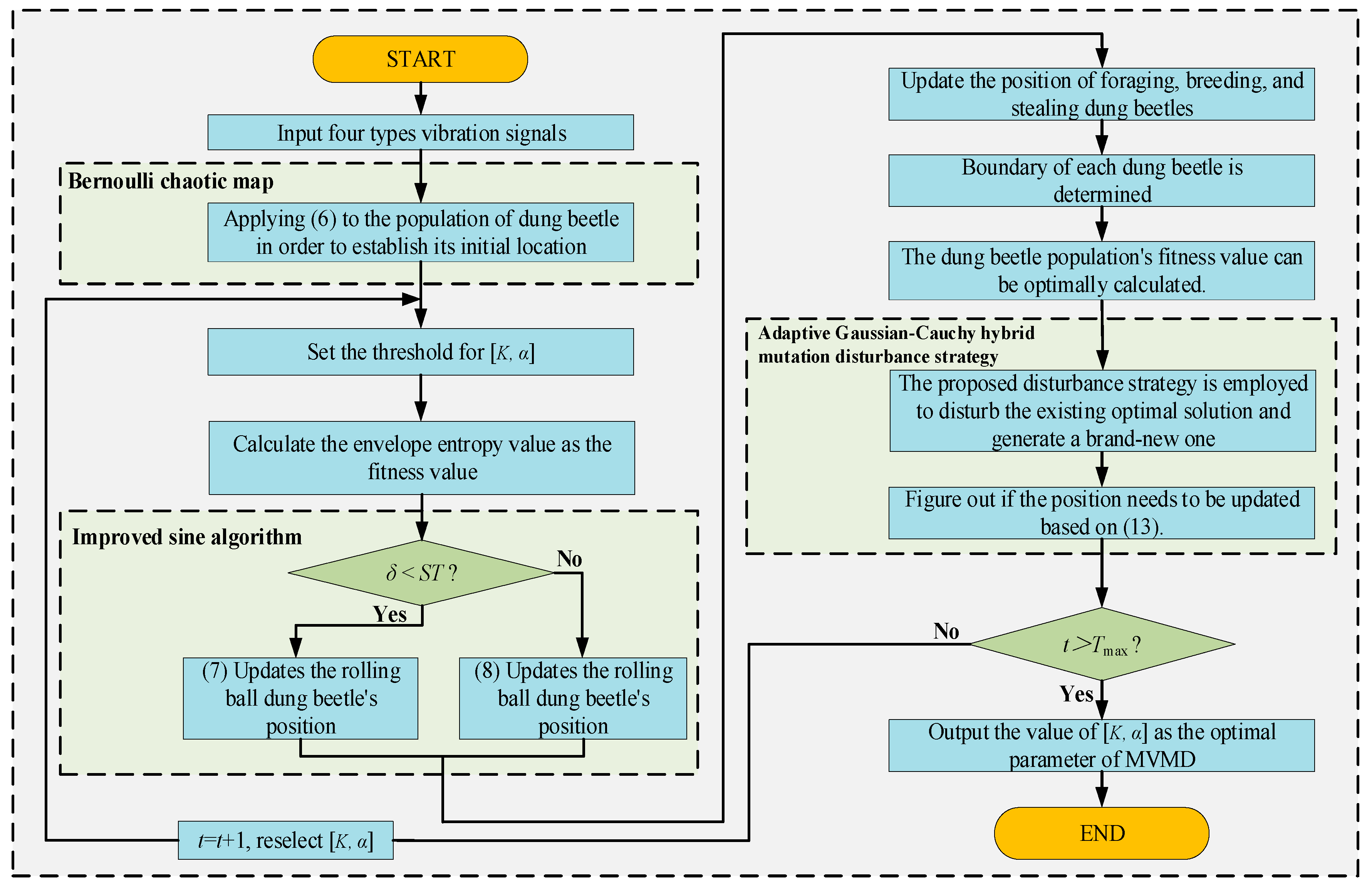
2.2. The Improved DBO Algorithm
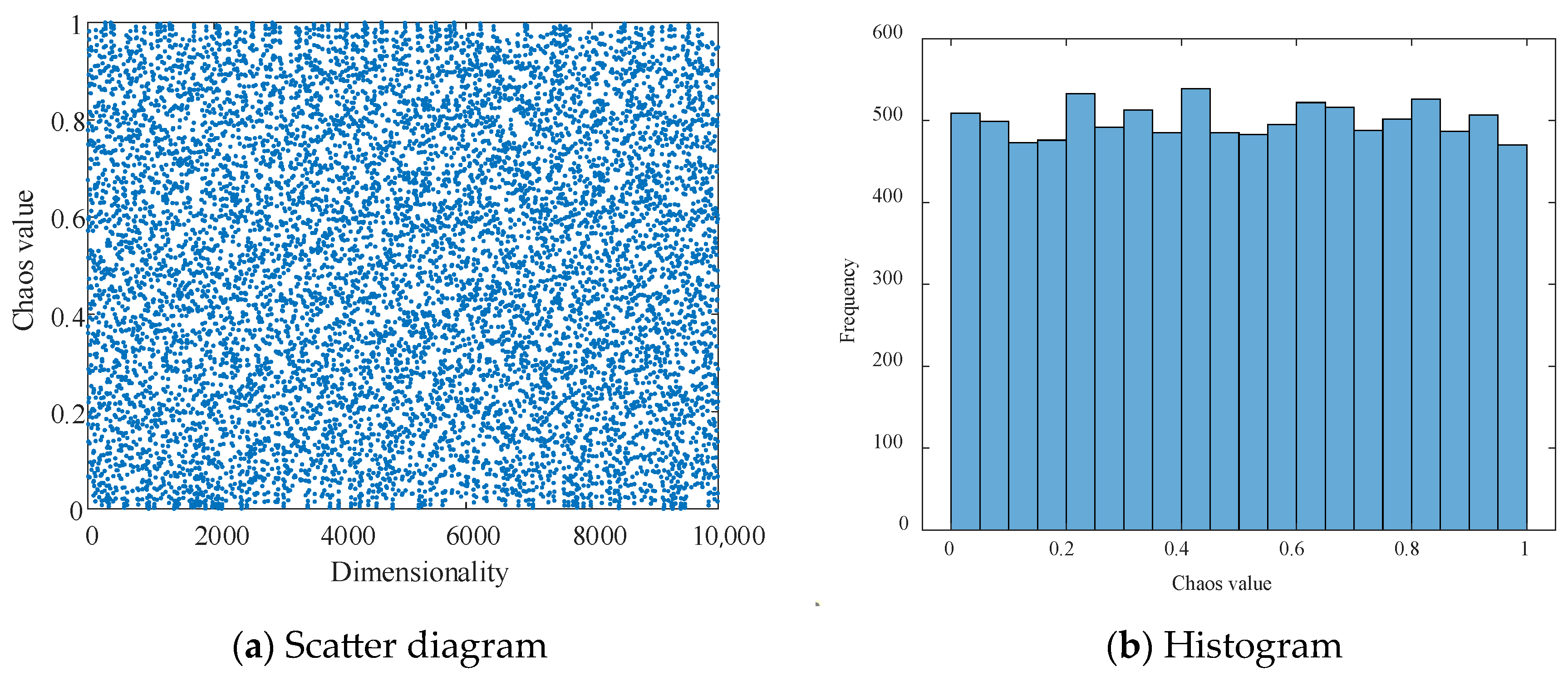
2.2.1. Bernoulli Chaotic Map Strategy
2.2.2. Improved Sine Algorithm (MSA)
2.2.3. Adaptive Gaussian–Cauchy Hybrid Mutation Disturbance Strategy
2.3. Improved Sine Algorithm–Dung Beetle Optimizer (MSADBO)
2.4. The Framework of Disconnector Mechanical Fault Diagnosis
- (1)
- Vibration signal acquisition: Use the dynamic signal acquisition instrument to extract vibration signals including normal state, mechanism jam, mechanism looseness, and three-phase asynchrony, and display and store using the host computer software (Dong-Hua Test: Real Time Data Measurement and Analysis Software System).
- (2)
- Feature selection and extraction: MSADBO is utilized for the optimization of parameters K and α in MVMD. After selecting the optimal parameters, MVMD is used to decompose the signals of different fault types to obtain the IMF components. Calculate the Pearson correlation coefficient between each IMF component and the raw signal and select IMF components whose coefficient value is greater than 0.1 to retain. The energy value, refined composite multiscale diversity entropy (RCMDE), and 13 time–frequency domain eigenvalues are extracted from the energy, entropy, and time–frequency features to form a 34-dimensional initial feature matrix. Afterwards, the 34-dimensional initial feature matrix is reduced to a two-dimensional matrix by the t-SNE algorithm.
- (3)
- Fault classification: Based on a ratio of 3:1, the dataset is partitioned into training and test sets. Fault identification is performed using CNN-BiLSTM and then assessed using the test set. The results of the disconnector mechanical fault diagnosis are output.
3. Disconnector Fault Experiment
3.1. Experimental Platform
3.2. Sensor Arrangement and Fault Setting
3.3. Experimental Process
4. Result Analysis
4.1. Vibration Signal Decomposition Based on MSADBO-MVMD
4.2. Feature Extraction
4.2.1. Selection of IMFS
4.2.2. Construction of Fusion Feature Matrix
- (1)
- Energy feature extraction
- (2)
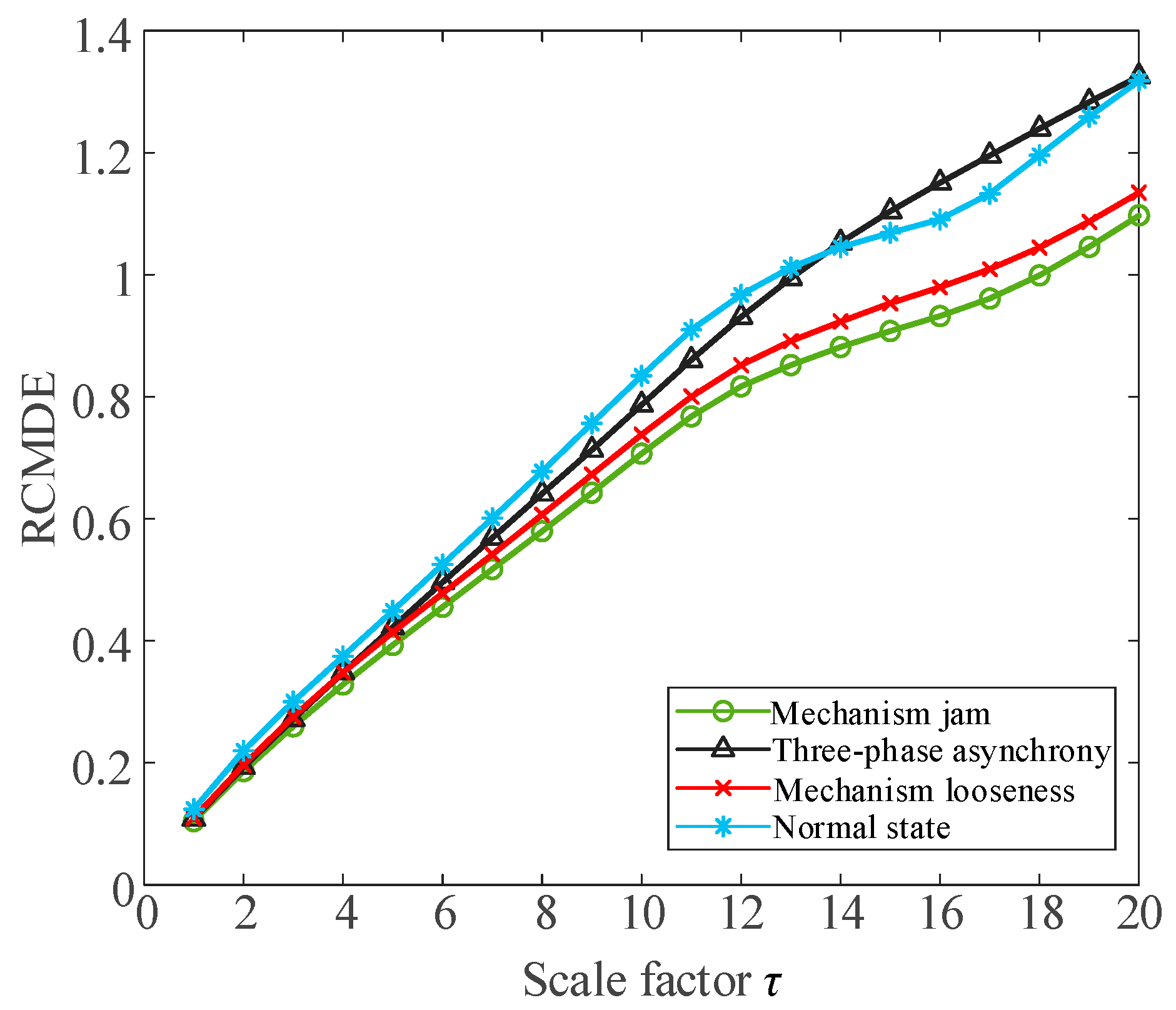
- Entropy feature extraction
- (3)
- Time–frequency feature extraction
4.2.3. Dimensionality Reduction of Fusion Feature Matrix
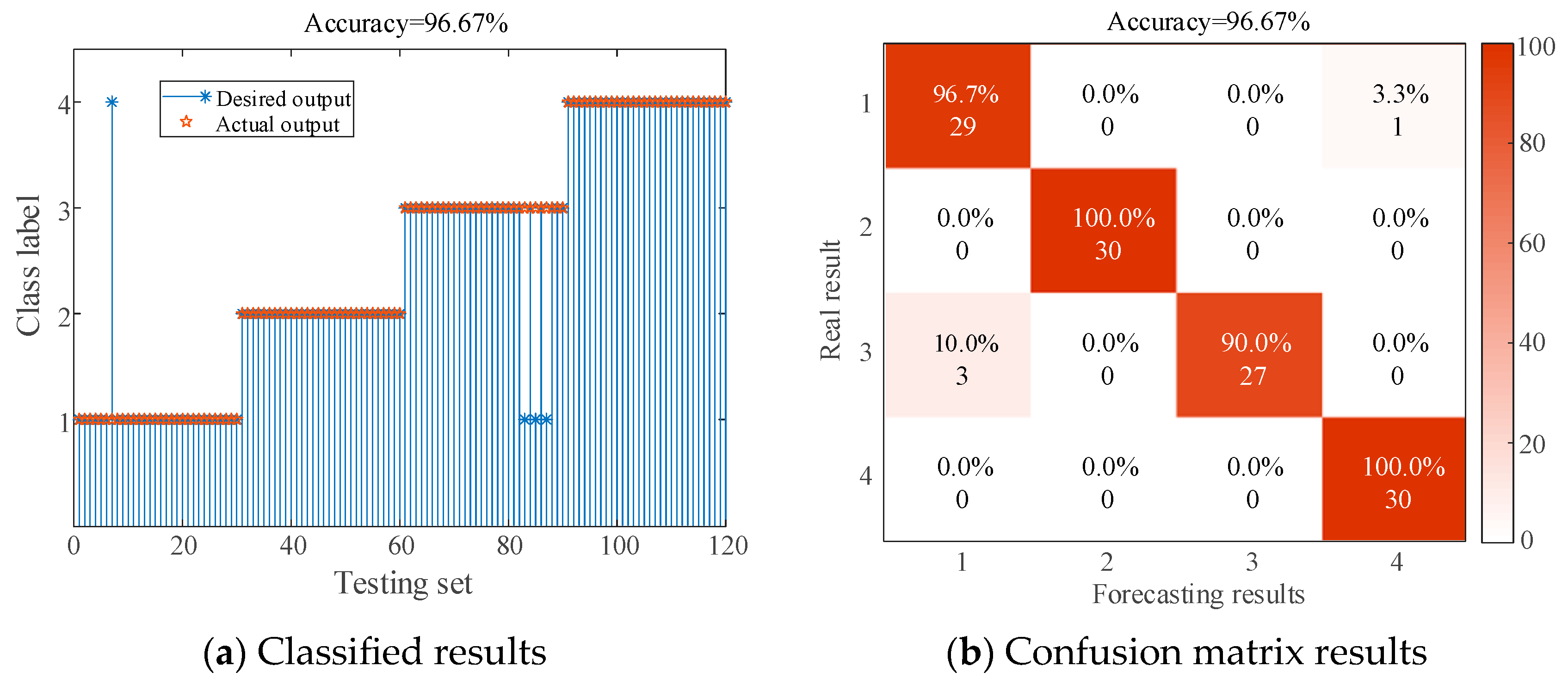
4.2.4. Fault Identification
5. Conclusions
- (1)
- By introducing the MSADBO, significant progress has been made in addressing the issues of slow convergence speed and the tendency to easily slip into the local optimum of the DBO. The parameters K and α of the MVMD can be optimally selected to adaptively decompose the vibration signal.
- (2)
- Selecting effective IMFs based on Pearson correlation coefficient and extracting features from energy, entropy, and time–frequency domains can fully mine potential fault features and improve the accuracy of fault diagnosis.
- (3)
- The dimensions of the feature matrix can be minimized utilizing the t-SNE method, and CNN-BiLSTM is used for fault identification, which significantly reduces the time required for operation and improves the performance of the algorithm model.
- (4)
- Three kinds of disconnector mechanical fault setting methods and the best arrangement of sensors are proposed. The vibration data under four operating conditions are collected to diagnose the mechanical fault of the disconnectors. To a certain extent, the problem of insufficient sample size of disconnectors fault data is solved.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Lin, S.; Zhang, K.; Wang, Q. Fault diagnosis method of disconnector based on operating torque in closing process. In Proceedings of the 2021 IEEE 2nd China International Youth Conference on Electrical Engineering, Chengdu, China, 15–17 December 2021; pp. 1–6. [Google Scholar]
- Jürgensen, J.H.; Brodersson, A.L.; Nordström, L.; Hilber, P. Impact assessment of remote control and preventive maintenance on the failure rate of a disconnector population. IEEE Trans. Power Del. 2018, 33, 1501–1509. [Google Scholar] [CrossRef]
- Mardegan, C.S.; Shipp, D.D. Anatomy of a complex electrical failure and its forensics analysis. IEEE Trans. Ind. Appl. 2014, 50, 2910–2918. [Google Scholar] [CrossRef]
- Cao, S.; Zhao, T.; Wang, G.; Zhang, T.; Liu, C.; Liu, Q.; Zhang, Z.; Wang, X. A Mechanical Defect Localization and Identification Method for High-Voltage Circuit Breakers Based on the Segmentation of Vibration Signals and Extraction of Chaotic Features. Sensors 2023, 23, 7201. [Google Scholar] [CrossRef] [PubMed]
- Runde, M. Failure frequencies for high-voltage circuit breakers, disconnectors, earthing switches, instrument transformers, and gas-insulated switchgear. IEEE Trans. Power Del. 2013, 28, 529–530. [Google Scholar] [CrossRef]
- Peng, T.; Lv, C.; Du, Y.; Lin, F.; Dong, S. Mechanical fault diagnosis of high voltage disconnector based on motor current detection. In Proceedings of the 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference, Chengdu, China, 15–17 March 2019; pp. 1726–1729. [Google Scholar]
- Liu, Q.; Wang, X.; Guo, Z.; Li, J.; Xu, W.; Dai, X.; Liu, C.; Zhao, T. Research on Circuit Breaker Operating Mechanism Fault Diagnosis Method Combining Global-Local Feature Extraction and KELM. Sensors 2024, 24, 124. [Google Scholar] [CrossRef] [PubMed]
- Souza, M.D.; Dhara, R.S.; Bouyer, R.C. Modularization of high voltage gas insulated substations. IEEE Trans. Ind. Appl. 2020, 56, 4662–4669. [Google Scholar] [CrossRef]
- Huang, S.; Shang, B.; Song, Y.; Zhang, N.; Wang, S.; Ning, S. Research on real-time disconnector state evaluation method based on multi-source images. IEEE. Trans. Instrum. Meas. 2022, 71, 1–15. [Google Scholar] [CrossRef]
- Yan, P.; Chang, C.; Hua, D.; Huang, H.; Liu, S.; Cui, P. Adaptive Disconnector States Diagnosis Method Based on Adjusted Relative Position Matrix and Convolutional Neural Networks. Sensors 2025, 25, 1701. [Google Scholar] [CrossRef]
- Qiu, Z.; Ruan, J.; Huang, D.; Huang, Y. Mechanical fault diagnosis of high voltage outdoor disconnector based on motor current signal analysis. In Proceedings of the 2014 International Conference on Power System Technology, Chengdu, China, 20–22 October 2014; pp. 1193–1198. [Google Scholar]
- Zhang, J.; Xu, H.; Wang, X.; Ding, Y.; Dai, X.; Hao, J. Mechanical defect field detection for operational GIS equipment based on vibration signal analysis. In Proceedings of the 2021 6th Asia Conference on Power and Electrical Engineering, Chongqing, China, 8–11 April 2021; pp. 1244–1248. [Google Scholar]
- Sun, S.; Zhang, T.; Li, Q.; Wang, J.; Zhang, W.; Wen, Z.; Tang, Y. Fault diagnosis of conventional circuit breaker contact system based on time-frequency analysis and improved AlexNet. IEEE. Trans. Instrum. Meas. 2021, 70, 1–12. [Google Scholar] [CrossRef]
- Fu, Q.; Jing, B.; He, P.; Si, S.; Wang, Y. Fault feature selection and diagnosis of rolling bearings based on EEMD and optimized elman_adaBoost algorithm. IEEE Sens. J. 2018, 18, 5024–5034. [Google Scholar] [CrossRef]
- Geraei, H.; Rodriguez, E.A.V.; Majma, E.; Habibi, S.; Al-Ani, D. A Noise Invariant Method for Bearing Fault Detection and Diagnosis Using Adapted Local Binary Pattern (ALBP) and Short-Time Fourier Transform (STFT). IEEE Access. 2024, 12, 107247–107260. [Google Scholar] [CrossRef]
- Sun, W.; Ma, H.; Wang, S. A novel fault diagnosis of GIS partial discharge based on improved whale optimization algorithm. IEEE Access. 2024, 12, 3315–3327. [Google Scholar] [CrossRef]
- Song, Q.; Jiang, X.; Wang, S.; Guo, J.; Huang, W.; Zhu, Z. Self-adaptive multivariate variational mode decomposition and its application for bearing fault diagnosis. IEEE. Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Chang, B.; Zhao, X.; Guo, D.; Zhao, S.; Fei, J. Rolling bearing fault diagnosis based on optimized VMD and SSAE. IEEE Access. 2024, 12, 130746–130762. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, C.; Zhang, D.; Li, L.; Yang, S. Improved probabilistic neural network based fault diagnosis of control valve. In Proceedings of the 2023 CAA Symposium on Fault Detection, Supervision and Safety for Technical Processes, Yibin, China, 22–24 September 2023; pp. 1–6. [Google Scholar]
- Zhang, L.; Fu, Z. Harmonic research on fault reconfiguration of active distribution network based on multi-strategy fusion and improved dung beetle optimization algorithm. In Proceedings of the 2024 6th International Conference on Energy Systems and Electrical Power, Wuhan, China, 21–23 June 2024; pp. 843–846. [Google Scholar]
- Yang, C.; Wu, X.; Gong, W.; Wang, Q.; Li, L. An intelligent identification algorithm for obtaining the state of power equipment in SIFT-based environments. Int. J. Performability Eng. 2019, 15, 2382–2391. [Google Scholar]
- Wang, Q.; Zhang, K.; Lin, S. Fault diagnosis method of disconnector based on CNN and D-S evidence theory. IEEE Trans. Ind. Appl. 2023, 59, 5691–5704. [Google Scholar] [CrossRef]
- Sun, M.; Bai, X.; Zhang, W.; Ye, L. Jointed task of multi-scale CNN based power transformer fault diagnosis with vibration and sound signals. In Proceedings of the 2023 Panda Forum on Power and Energy, Chengdu, China, 27–30 April 2023; pp. 1761–1765. [Google Scholar]
- Wang, W.; Zhang, D.; Hu, X.; Han, R.; Guo, Y.; Qiao, Y.; Gao, S.; Wang, Z. Recognition of Complex Abnormal Vibration Voiceprint of Power Transmission and Transformation Equipment in Cold Environment. In Proceedings of the 2024 IEEE 7th Eurasian Conference on Educational Innovation, Bangkok, Thailand, 26–28 January 2024; pp. 394–398. [Google Scholar]
- Ma, W.; Liu, S.; Liang, H.; Zhang, S.; Gao, Y.; Li, D.; Di, X. Fault diagnosis of integrated energy system based on CNN-LSTM. In Proceedings of the 2023 42nd Chinese Control Conference, Tianjin, China, 24–26 July 2023; pp. 5102–5107. [Google Scholar]
- Ma, W.; Ren, X.; Chen, Z. A new signal analysis method after wavelet packet de-noising. In Proceedings of the 2008 International Conference on Wavelet Analysis and Pattern Recognition, Hong Kong, China, 30–31 August 2008; pp. 426–431. [Google Scholar]
- Pan, J.; Li, S.; Zhou, P.; Yang, G.; Lv, D. Dung beetle optimization algorithm guided by improved sine algorithm. Comput. Eng. Appl. 2023, 59, 92–110. [Google Scholar]
- Zhao, S.; Chen, Y.; Rehman, A.U.; Liang, F.; Wang, S.; Zhao, Y.; Deng, W.; Ma, Y.; Cheng, Y. Detection of interturn short-circuit faults in DFIGs based on external leakage flux sensing and the VMD-RCMDE analytical method. IEEE. Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Dhandapani, R.; Mitiche, I.; McMeekin, S.; Morison, G. A novel bearing faults detection method using generalized Gaussian distribution refined composite multiscale dispersion entropy. IEEE. Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Zhai, H.; Wang, X.; Ge, M.; Feng, S.; Cheng, L.; Deng, Y. Improved fault classification method in transmission line based on K-means clustering. In Proceedings of the 2020 5th Asia Conference on Power and Electrical Engineering, Chengdu, China, 4–7 June 2020; pp. 154–158. [Google Scholar]



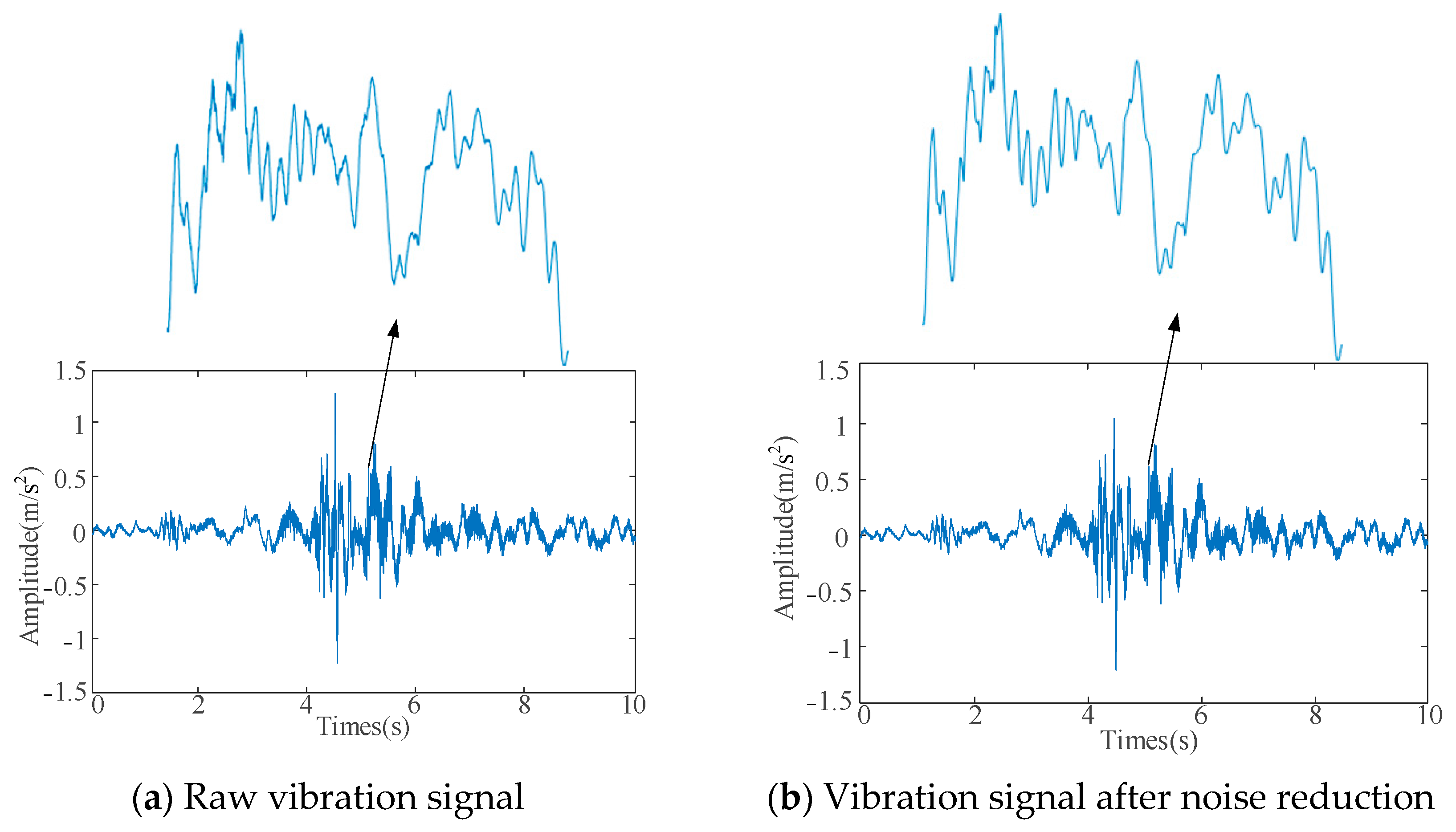
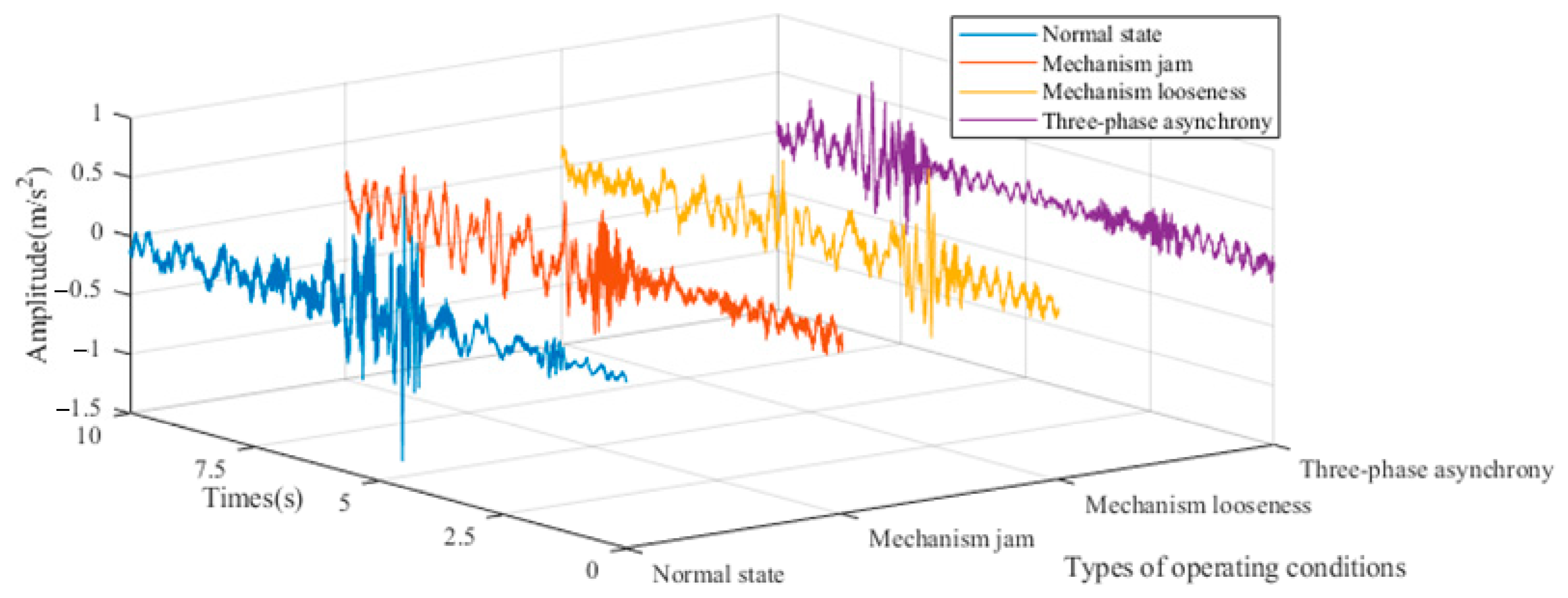
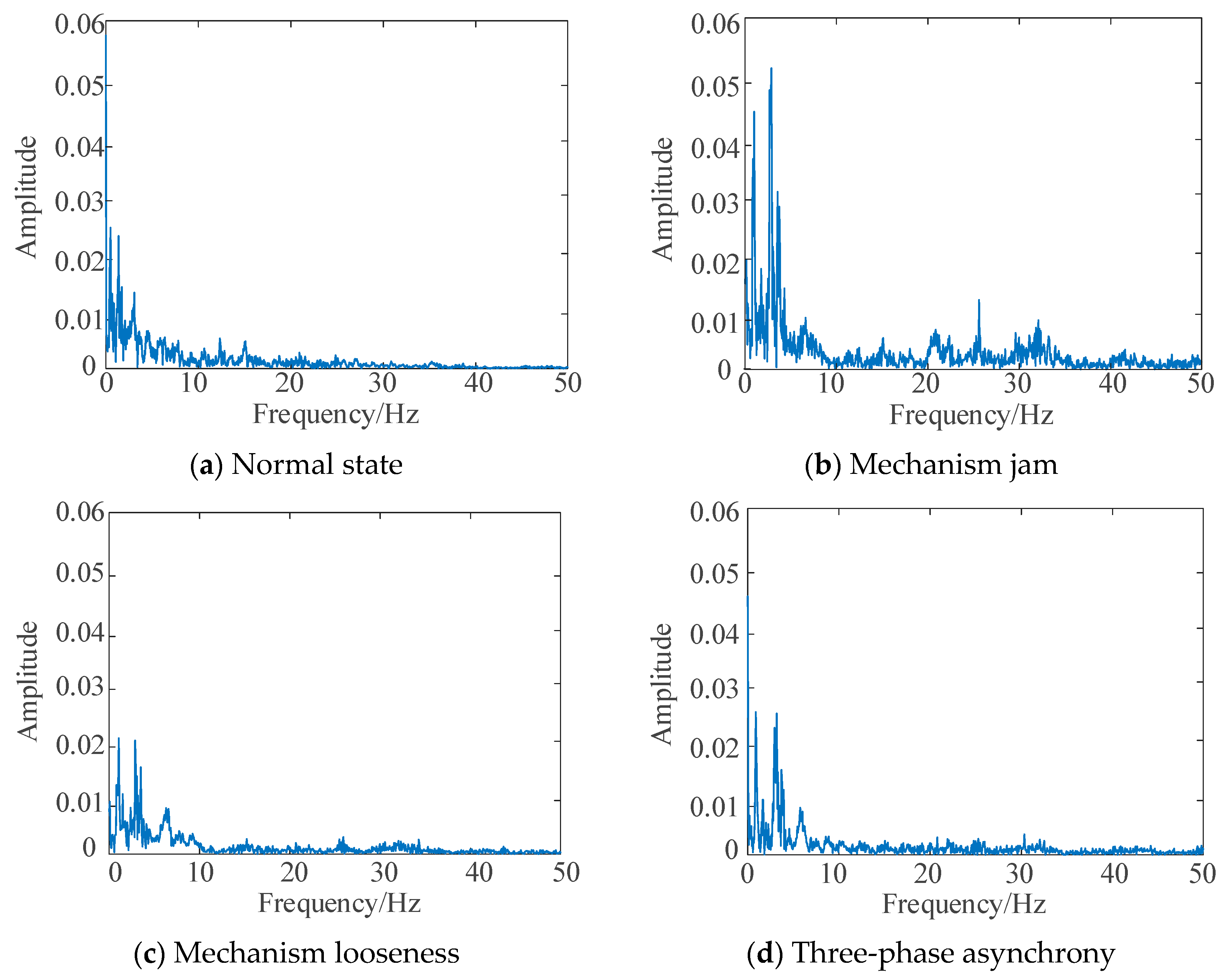


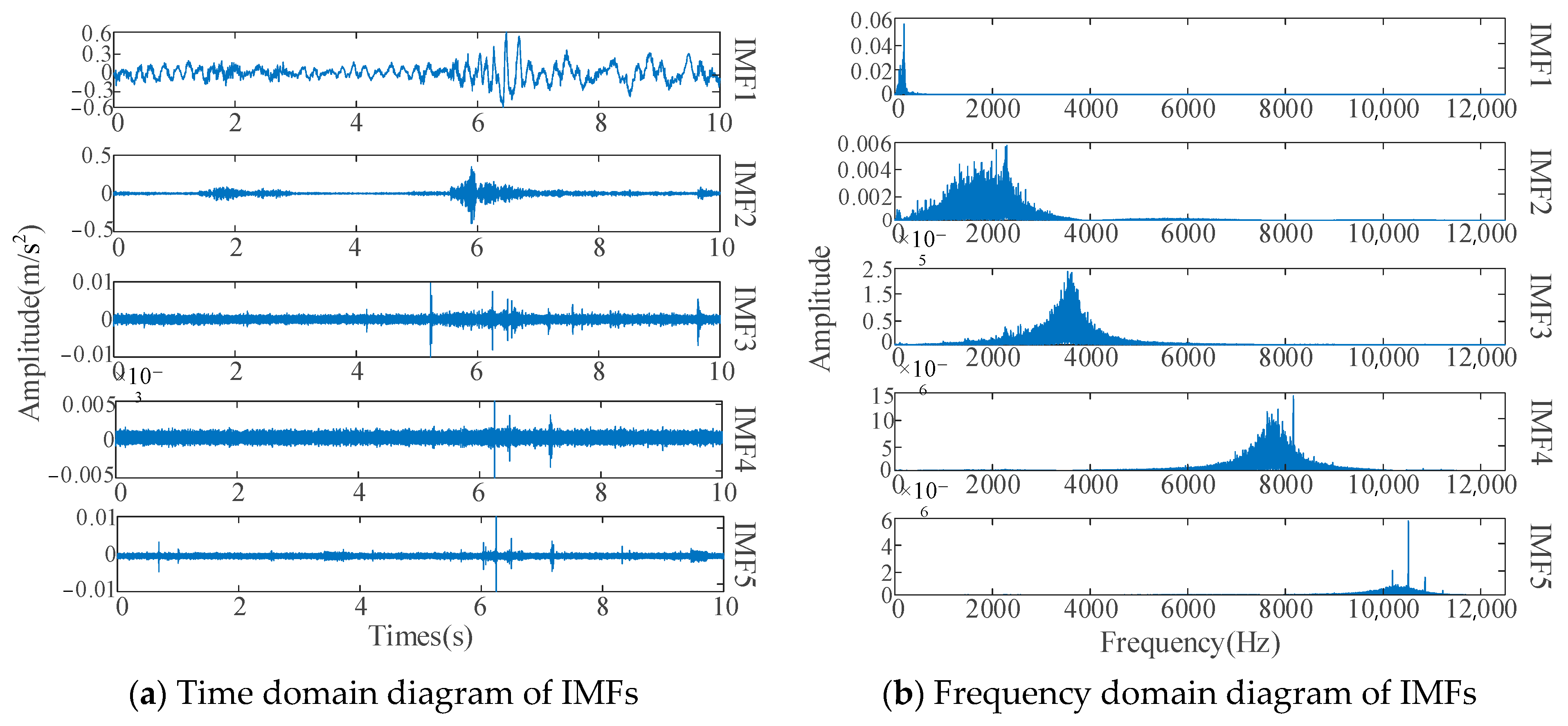
| Population Size | Maximum Number of Iterations | Initial Setting Value of (K, α) | Value Range of K | Value Range of α |
|---|---|---|---|---|
| 20 | 30 | (5,2000) | (1,100) | (10,3000) |
| Type of Operating Conditions | K | α | f |
|---|---|---|---|
| Normal state | 6 | 375 | 6.7197 |
| Mechanism jam | 7 | 268 | 7.4136 |
| Mechanism looseness | 8 | 1245 | 7.8438 |
| Three-phase asynchrony | 5 | 1615 | 6.7453 |
| Pearson Correlation Coefficient | Normal State | Mechanism Jam | Mechanism Looseness | Three-Phase Asynchrony |
|---|---|---|---|---|
| d1 | 0.9600 | 0.9400 | 0.9800 | 0.9600 |
| d2 | 0.3300 | 0.2100 | 0.3200 | 0.3400 |
| d3 | 0.0320 | 0.3700 | 0.1200 | 0.0250 |
| d4 | 0.0067 | 0.0870 | 0.0240 | 0.0099 |
| d5 | 0.0059 | 0.0061 | 0.0053 | 0.0061 |
| d6 | 0.0051 | 0.0034 | 0.0064 | - |
| d7 | - | 0.0027 | 0.0060 | - |
| d8 | - | - | 0.0041 | - |
| Time Domain (Dimensional) | Time Domain (Dimensionless) | Frequency Domain | |||
|---|---|---|---|---|---|
| t1 | t6 | p1 | |||
| t2 | t7 | p2 | |||
| t3 | t8 | p3 | |||
| t4 | t9 | - | - | ||
| t5 | t10 | - | - | ||
| Types | Kernel Size | Step Length | Filling Way |
|---|---|---|---|
| Convolution layer | 2 × 1 × 32 | 1 | same |
| Pooling layer | 2 × 1 | 1 | 0 |
| BiLSTM layer | Number of elements: 50 | - | - |
| No. | Algorithm Type | Identification Accuracy/% |
|---|---|---|
| #1 | MSADBO-MVMD-Fusion features-t-SNE-CNN-BiLSTM | 96.67% (116/120) |
| #2 | MSADBO-VMD-Fusion features-t-SNE-CNN-BiLSTM | 91.67% (110/120) |
| #3 | DBO-MVMD-Fusion features-t-SNE-CNN-BiLSTM | 89.17% (107/120) |
| #4 | SSA-MVMD-Fusion features-t-SNE-CNN-BiLSTM | 90.00% (108/120) |
| #5 | MSADBO-MVMD-Fusion features-t-SNE-CNN-LSTM | 92.50% (111/120) |
| #6 | MSADBO-MVMD-Fusion features-t-SNE-CNN | 93.33% (112/120) |
| #7 | MSADBO-MVMD-Fusion features-t-SNE-ELM | 84.17% (101/120) |
| #8 | MSADBO-MVMD-Energy feature-t-SNE-CNN-BiLSTM | 88.33% (106/120) |
| #9 | MSADBO-MVMD-Entropy feature-t-SNE-CNN-BiLSTM | 90.83% (109/120) |
| #10 | MSADBO-MVMD-Time-frequency feature-t-SNE-CNN-BiLSTM | 89.17% (107/120) |
| #11 | MSADBO-MVMD-Fusion features-PCA-CNN-BiLSTM | 94.17% (113/120) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Ma, H.; Sun, W. Mechanical Fault Diagnosis Method of a Disconnector Based on Improved Dung Beetle Optimizer–Multivariate Variational Mode Decomposition and Convolutional Neural Network–Bidirectional Long Short-Term Memory. Machines 2025, 13, 332. https://doi.org/10.3390/machines13040332
Zhang C, Ma H, Sun W. Mechanical Fault Diagnosis Method of a Disconnector Based on Improved Dung Beetle Optimizer–Multivariate Variational Mode Decomposition and Convolutional Neural Network–Bidirectional Long Short-Term Memory. Machines. 2025; 13(4):332. https://doi.org/10.3390/machines13040332
Chicago/Turabian StyleZhang, Chi, Hongzhong Ma, and Wei Sun. 2025. "Mechanical Fault Diagnosis Method of a Disconnector Based on Improved Dung Beetle Optimizer–Multivariate Variational Mode Decomposition and Convolutional Neural Network–Bidirectional Long Short-Term Memory" Machines 13, no. 4: 332. https://doi.org/10.3390/machines13040332
APA StyleZhang, C., Ma, H., & Sun, W. (2025). Mechanical Fault Diagnosis Method of a Disconnector Based on Improved Dung Beetle Optimizer–Multivariate Variational Mode Decomposition and Convolutional Neural Network–Bidirectional Long Short-Term Memory. Machines, 13(4), 332. https://doi.org/10.3390/machines13040332






