Design and Dimension Optimization of Rigid–Soft Hand Function Rehabilitation Robots
Abstract
1. Introduction
- We combine hierarchical constraint modeling and improved artificial bee colony (IABC) optimization techniques to achieve accurate matching with normal finger motion trajectories.
- In order to balance the requirements of structural compliance and motion coordination, the parameters of the hyperelastic components are optimized by a finite element-driven method.
2. Methods
2.1. Structure Design of the Hand Function Rehabilitation Robot
2.1.1. Overall Scheme Design
- Morphological congruence and kinematic congruence: The adopted configuration must demonstrate anthropomorphic fidelity to human hand architecture, ensuring biomimetic articulation during rehabilitation protocols. Trajectory planning for reference markers requires adherence to the target trajectory of rehabilitation, enabling valid movement replication through coordinated kinematics.
- Actuation precision and adaptive controllability: Drive system selection necessitates high-precision actuation mechanisms for spatially constrained hand-environment interactions. The actuation system requires a modulable force output so that the patient can gradually adapt and participate in rehabilitation training without the need for overly complex sensing systems.
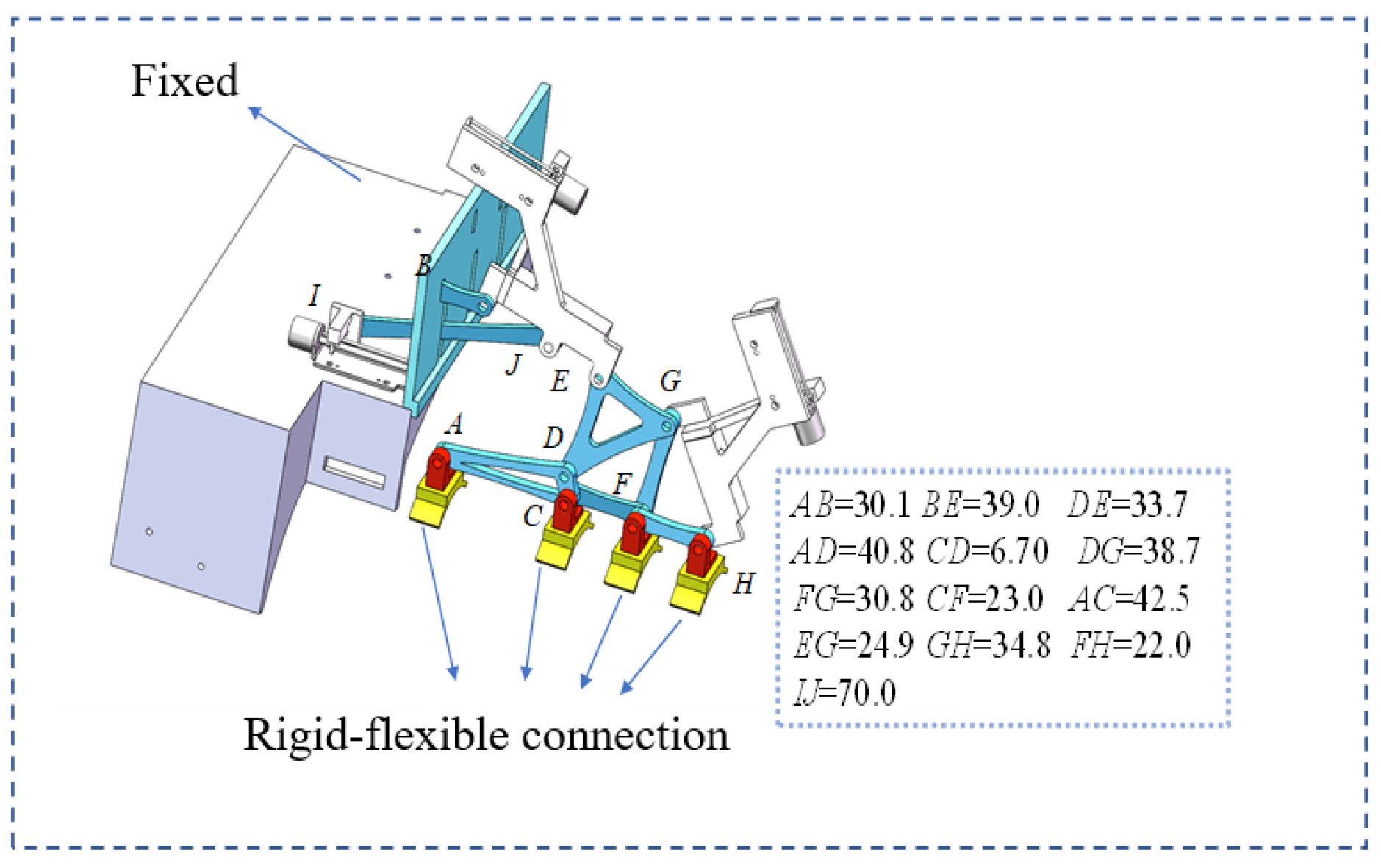
2.1.2. Rigid Mechanism Design
2.1.3. Soft Structure Design
2.2. Dimension Optimization
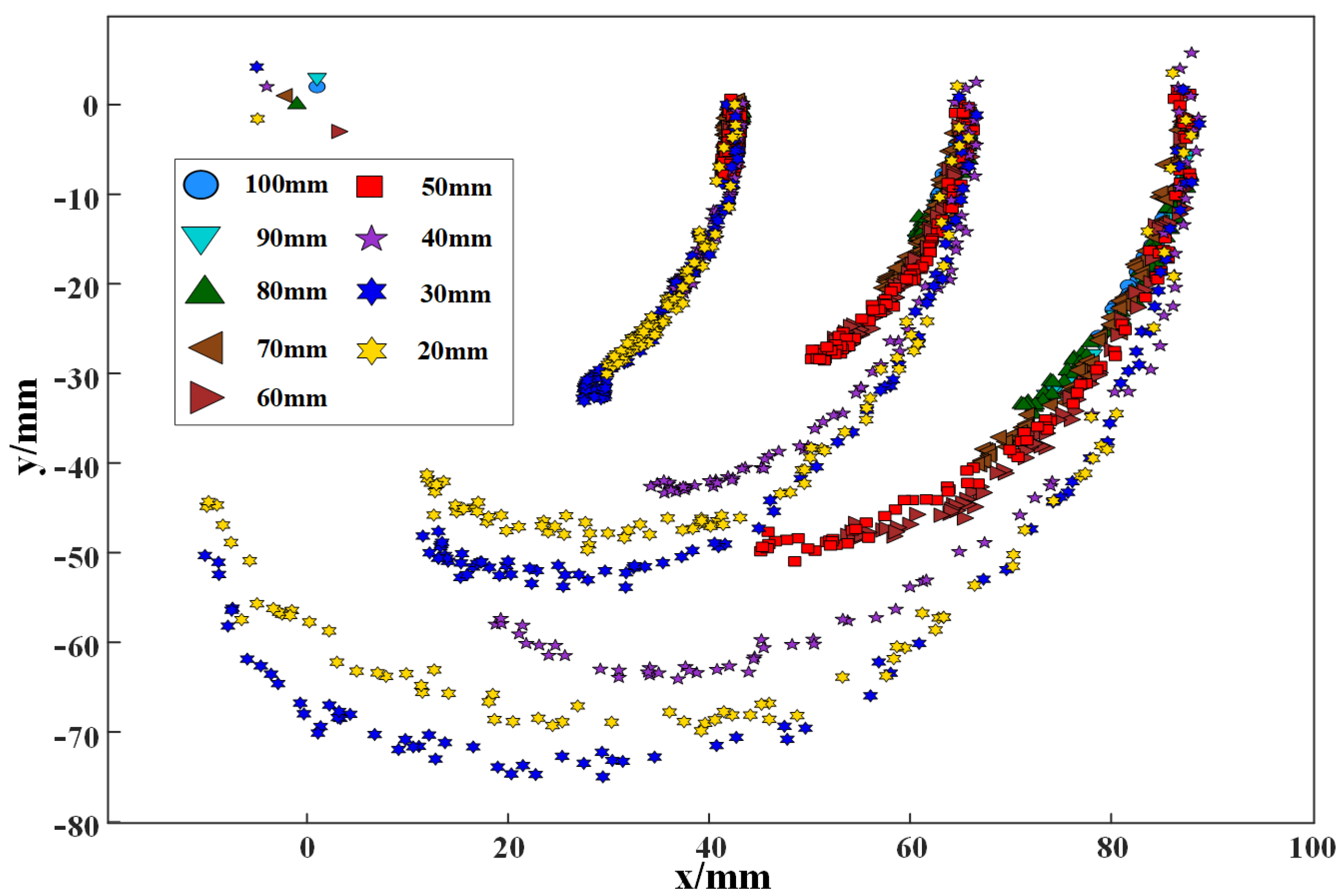
2.2.1. Grasping Motion of Human Hands
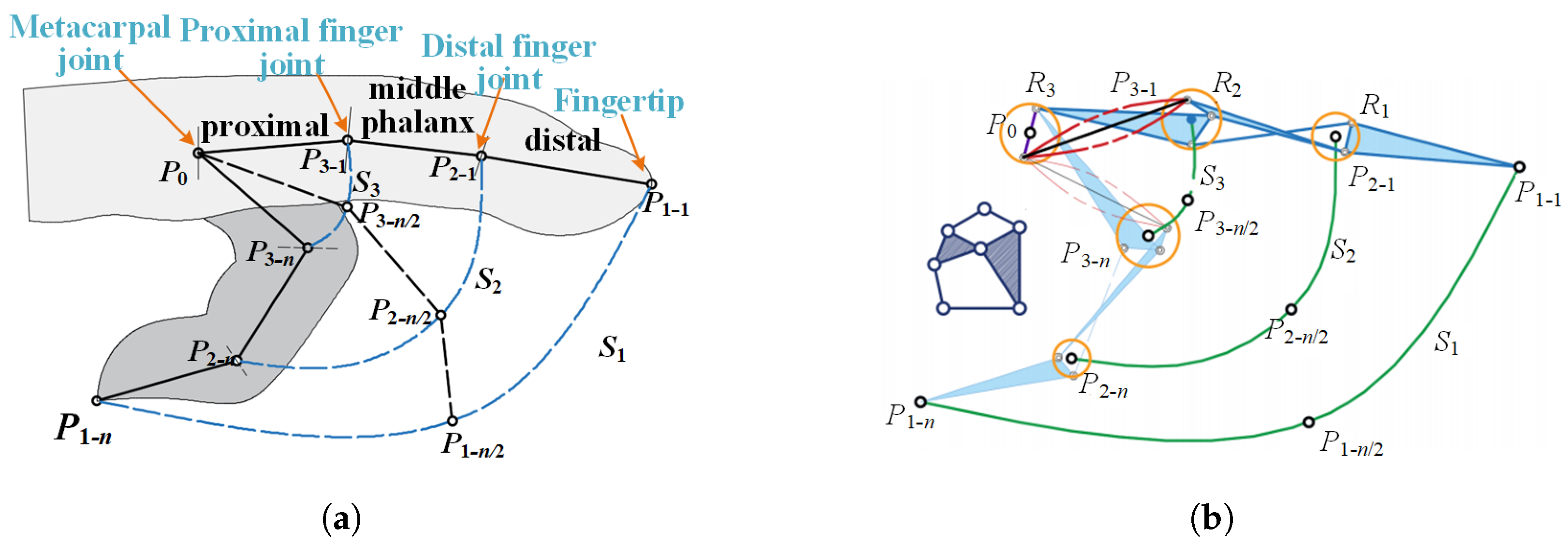
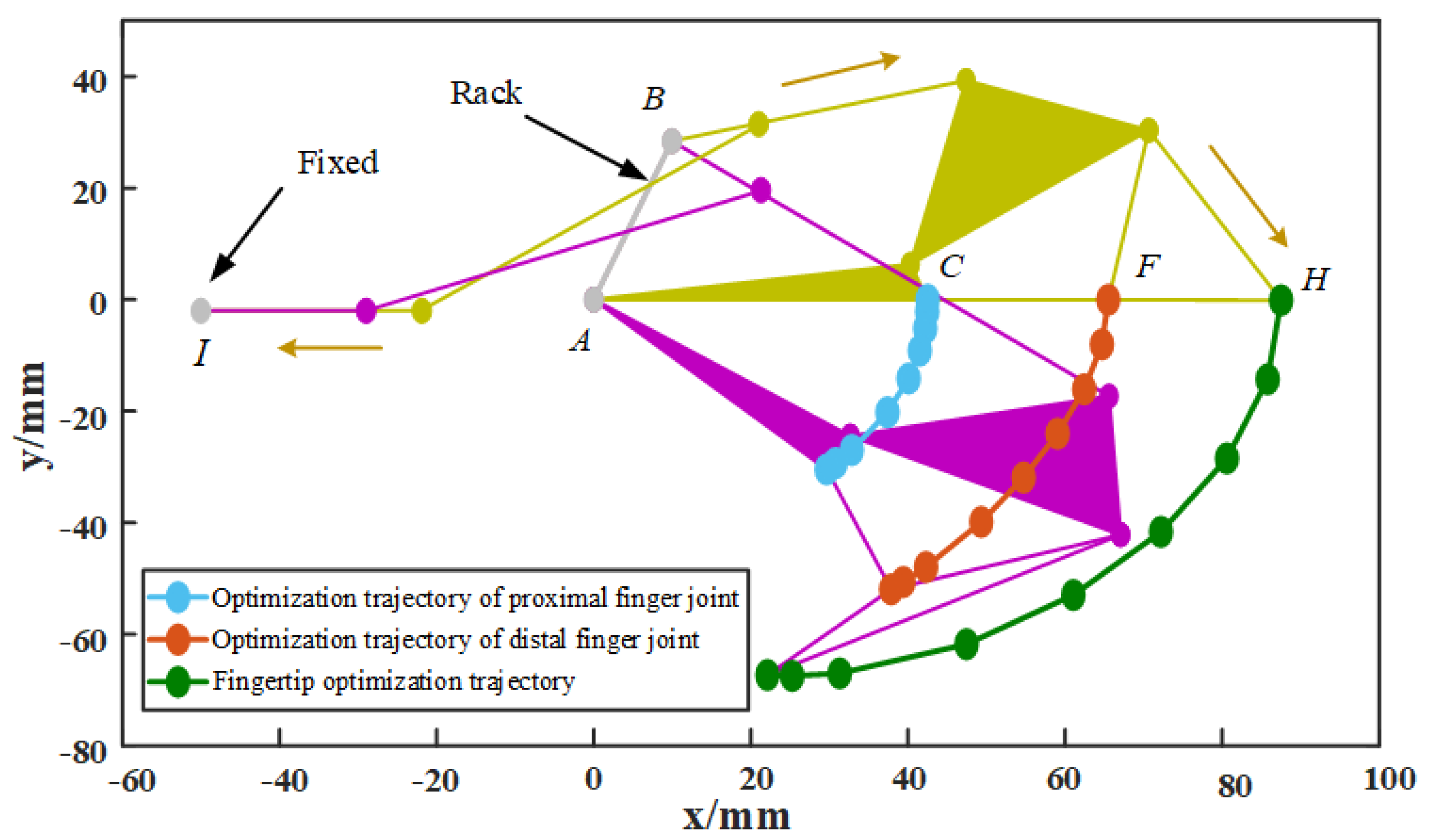
2.2.2. Dimension Optimization of the Rigid Structure Based on MM
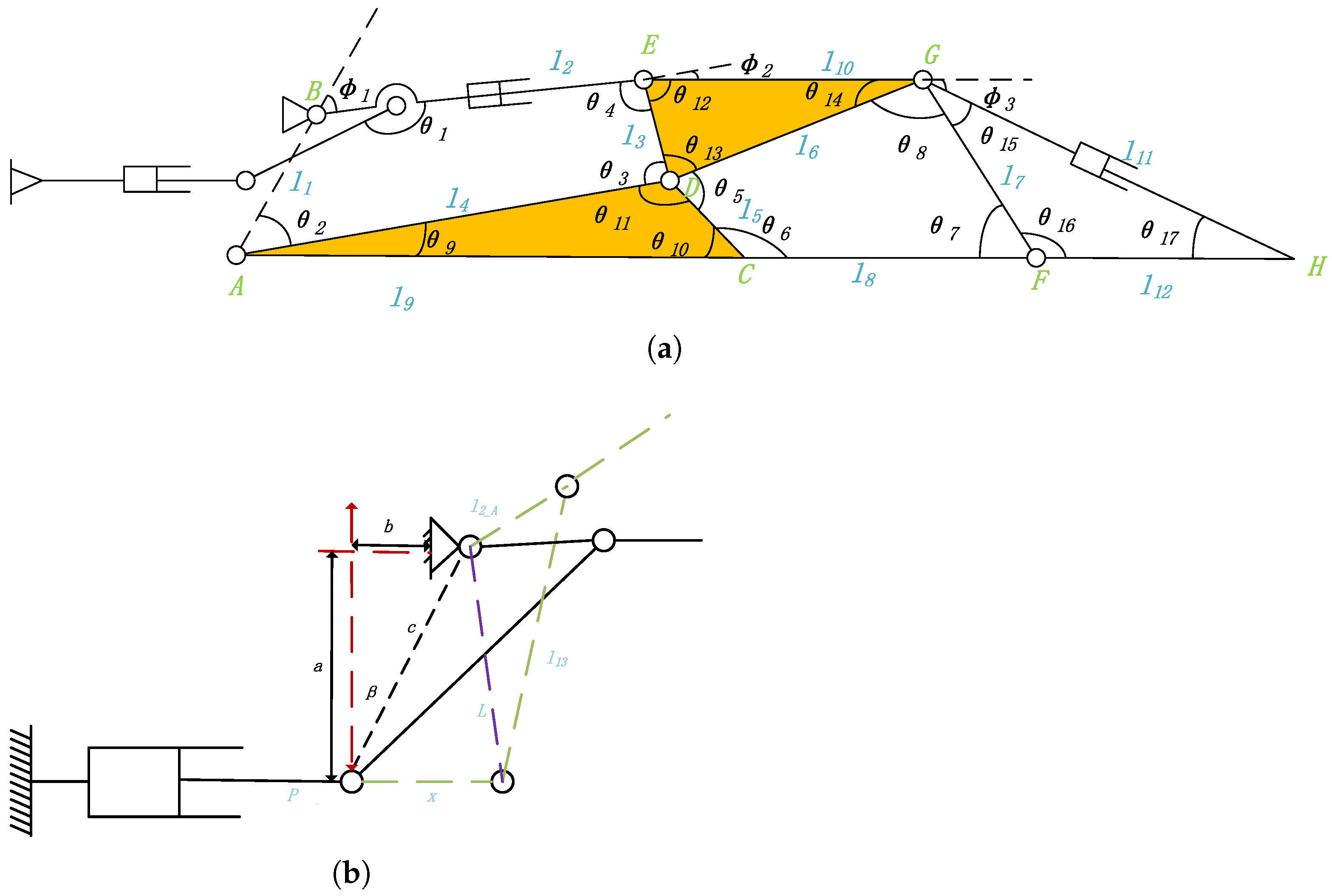
- Selection of initial conditions: Select the basic diagram of the Watt-I six-bar linkage-based mechanism, and on this basis, select the appropriate frame and the reference point matching the finger joint. For the fingertip reference point, if the hinge point is selected as the fingertip point, the number of connecting rods between it and the frame should not be less than 3. If a point on the connecting rod is selected as the fingertip point, the number of connecting rods between it and the frame should not be less than 2. For hinge points corresponding to other finger joints, the number of linkage points located at the proximal knuckle-joint and the middle knuckle-joint are successively reduced from the frame. In particular, the selection of the hinge point is not unique, as it is necessary to establish the initial condition parameter library from which the initial condition is called.
- Determination of the initial parameters for the link length: With the relative position parameters of the hinge points as the initial parameters, the initial coordinate points , , and and the end coordinate points , , and of the proximal knuckle-joint, the middle knuckle-joint, and the distal knuckle-joint were taken as references, the joint constraint range was set, and the hinge coordinate points were obtained by randomly selecting points within the joint range. The initial rod length, driving angle and frame angle of the linkage mechanism are obtained under less constraint conditions, which are used as the initial conditions for subsequent optimization analysis.
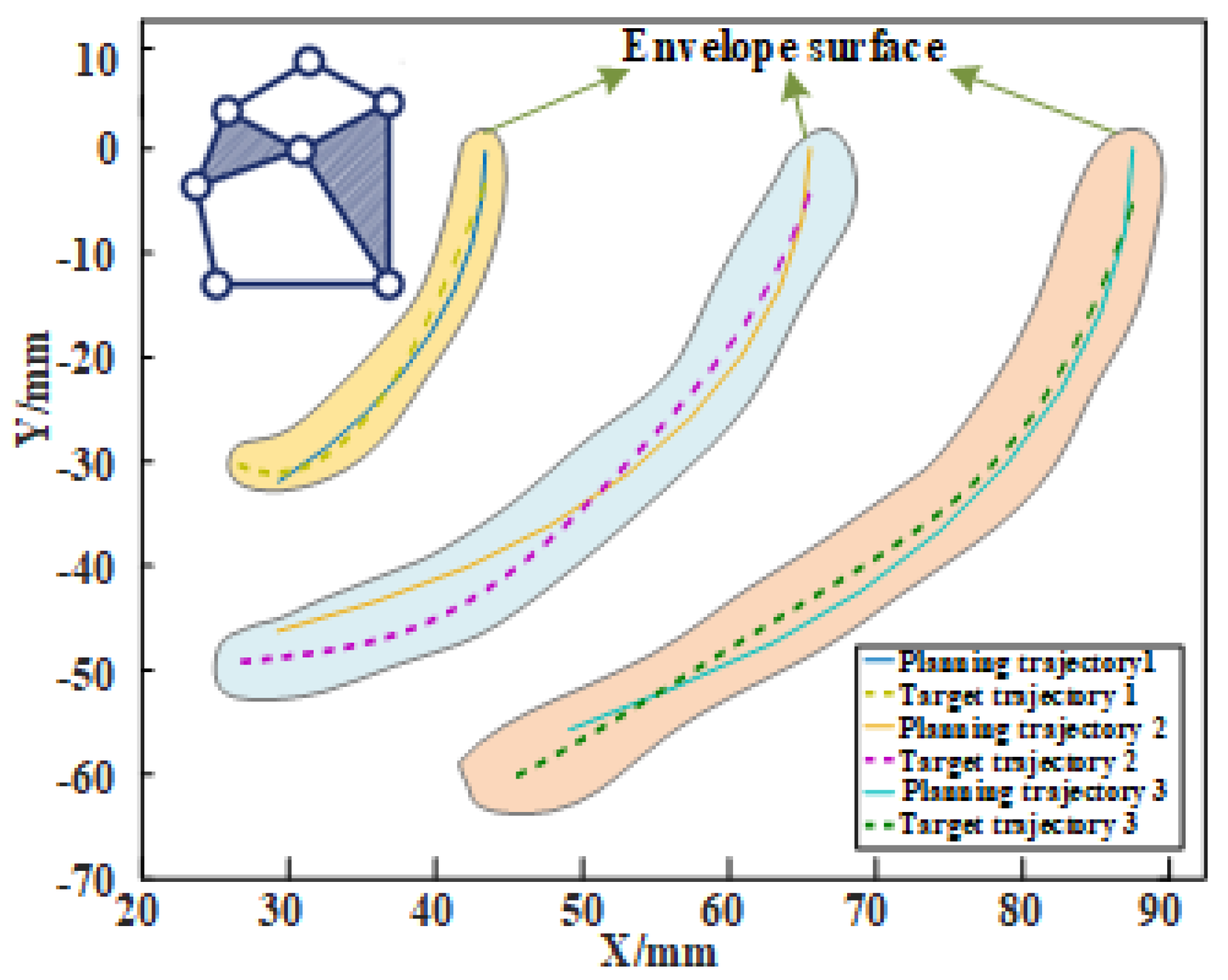
- Optimal design based on hierarchical constraints: The number of constraint points on the three tracks is increased in layers to form a constraint envelope surface. The IABC algorithm is used to further optimize the rod length parameters. Through the gradual increase of constraint points, the center locus of the joint range obtained by the link length parameter is gradually close to the overall fitting locus in Section 3.1. When enough constraints are given and the variation of each rod length is within a small range, the design is completed.
- Continuity analysis of mechanism motion: In the above design process, it is necessary to further judge the continuity of the movement of the mechanism; on the one hand, the movement of the connecting rod mechanism itself is continuous, and on the other hand, the joint range composed of the hinge points can pass the constraint points in order.
- Improved honey source initialization: While ABC’s stochastic initialization fosters population diversity, it compromises convergence efficiency. Our method strategically employs datasets and , where initialization probabilistically allocates 50% of solutions from these datasets. During new source exploration, a parity-check mechanism enforces selection from and , followed by post-selection dataset shuffling with 50% solution redistribution. This mechanism enhances algorithmic convergence while maintaining solution diversity. The initialization procedure is as follows:where is a randomly generated odd-numbered dataset, and is a randomly generated even-numbered dataset.
- Improved employed bee: The conventional ABC algorithm employs randomly selected coefficients () during honey source exploration, introducing stochasticity into the optimization directions. To address this limitation, an inertia weight is integrated into the honey source localization and colony positional update equations as follows:The inertia weight integration enhances algorithmic capabilities by prioritizing global exploration during initial iterations and local exploitation in later phases. To operationalize this dual-phase optimization, we propose a logarithmically decaying nonlinear inertia weight strategy, mathematically expressed as follows:where N is the maximum iterations, is the maximum value of weight, and is the minimum value of weight.
- Improved follower bee: Conventional local search implementations employ stochastic single-dimensional selection during source position updates, utilizing probabilistic field adjustment via -range random numbers. This methodology compromises search efficiency and convergence rates. Our improvement introduces a dual-strategy framework combining equidistant exploration with existing stochastic search rules. As formalized in Equation (20), the enhanced algorithm performs parallel search path generation through randomized interval domains (I and k) while maintaining roulette-based employed bee selection. A greedy selection mechanism compares solutions from equidistant cyclic generation against stochastic search outputs, retaining superior nectar sources.
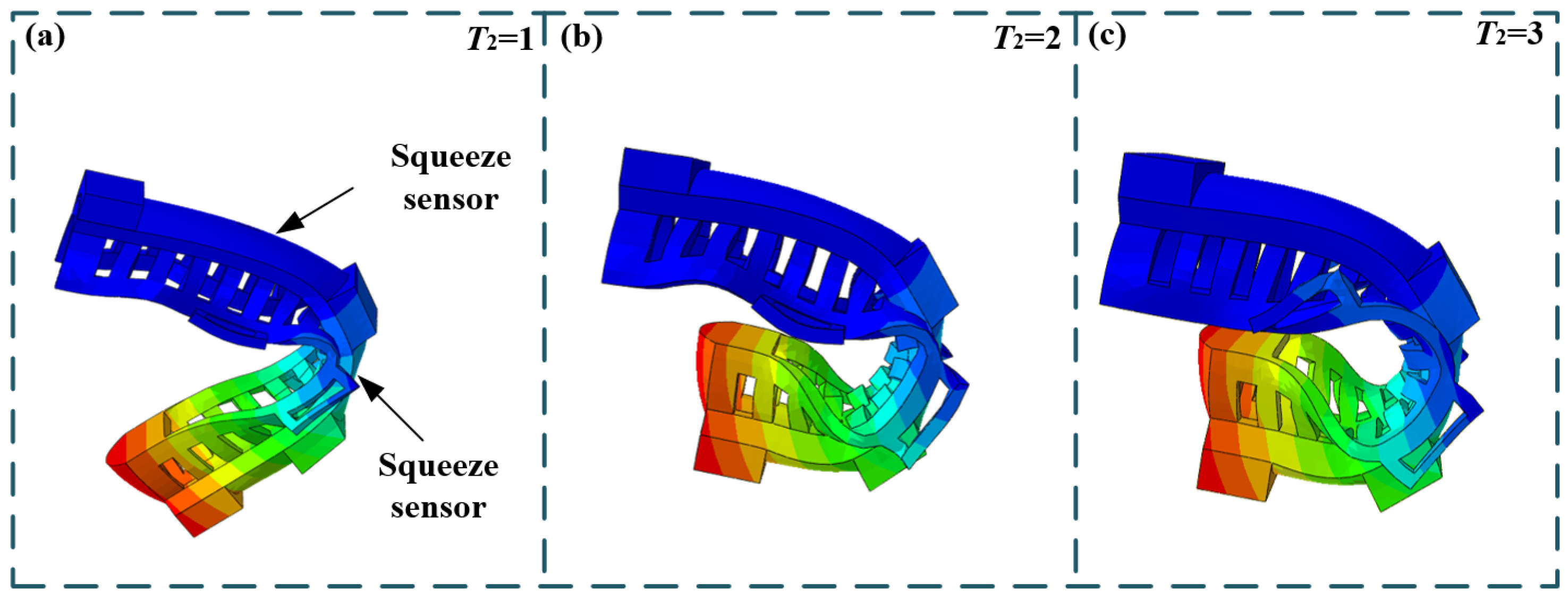
2.2.3. Dimension Optimization of Soft Structure Based on ABAQUS
2.3. Motion Planning and Simulation
2.3.1. Design of Motion Planning
2.3.2. Calculation of the Motion Trajectory
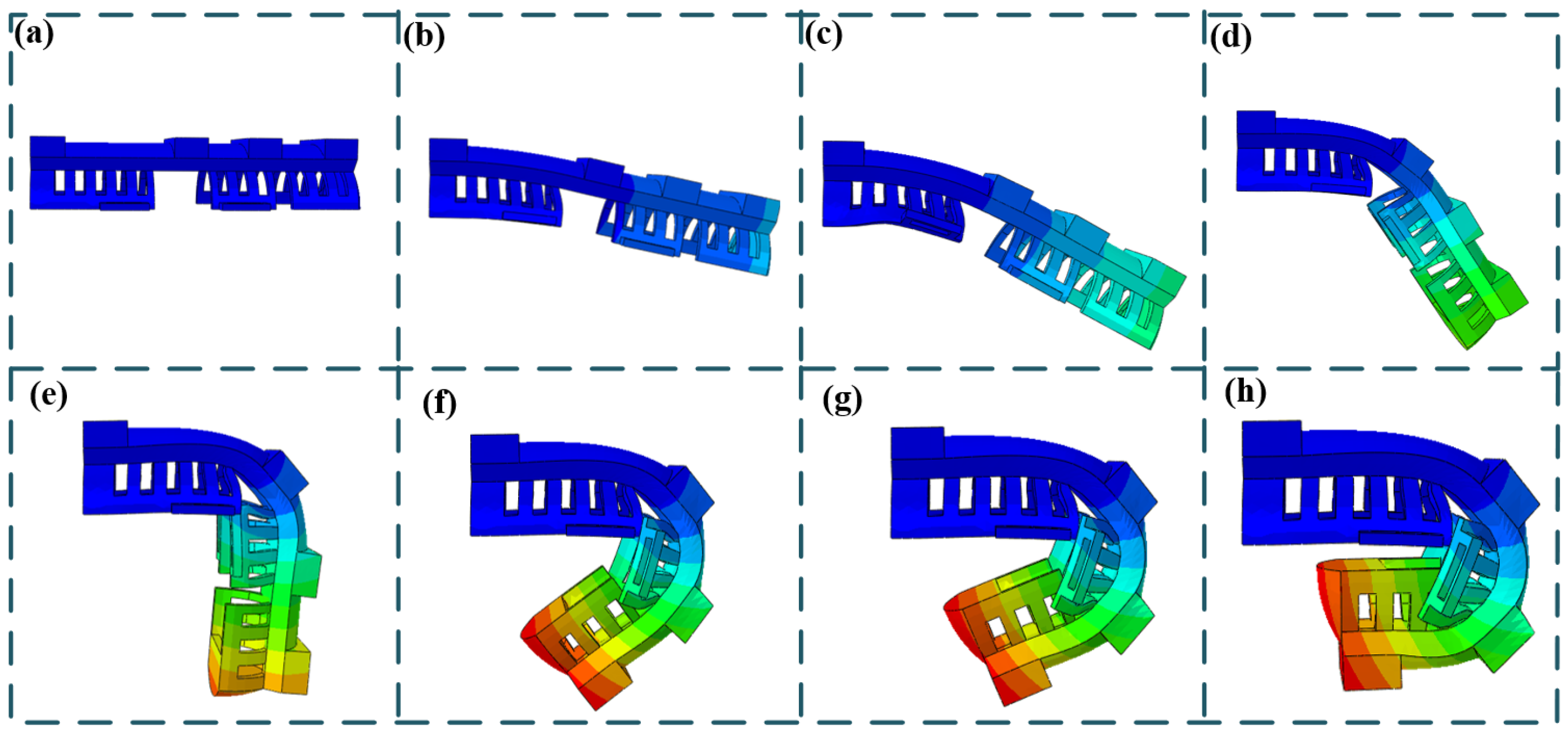
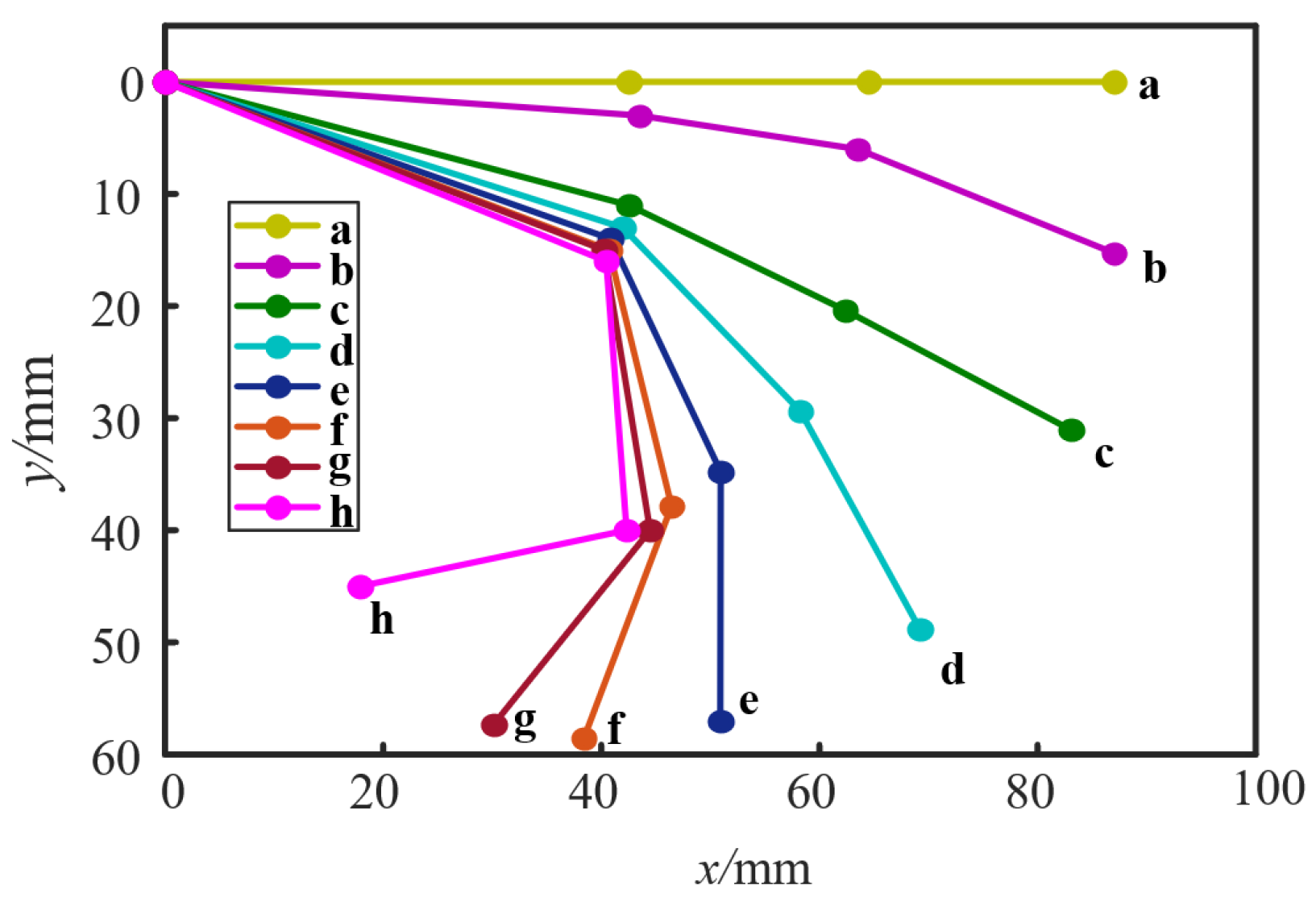
2.3.3. Motion Simulation
3. Experiment Result
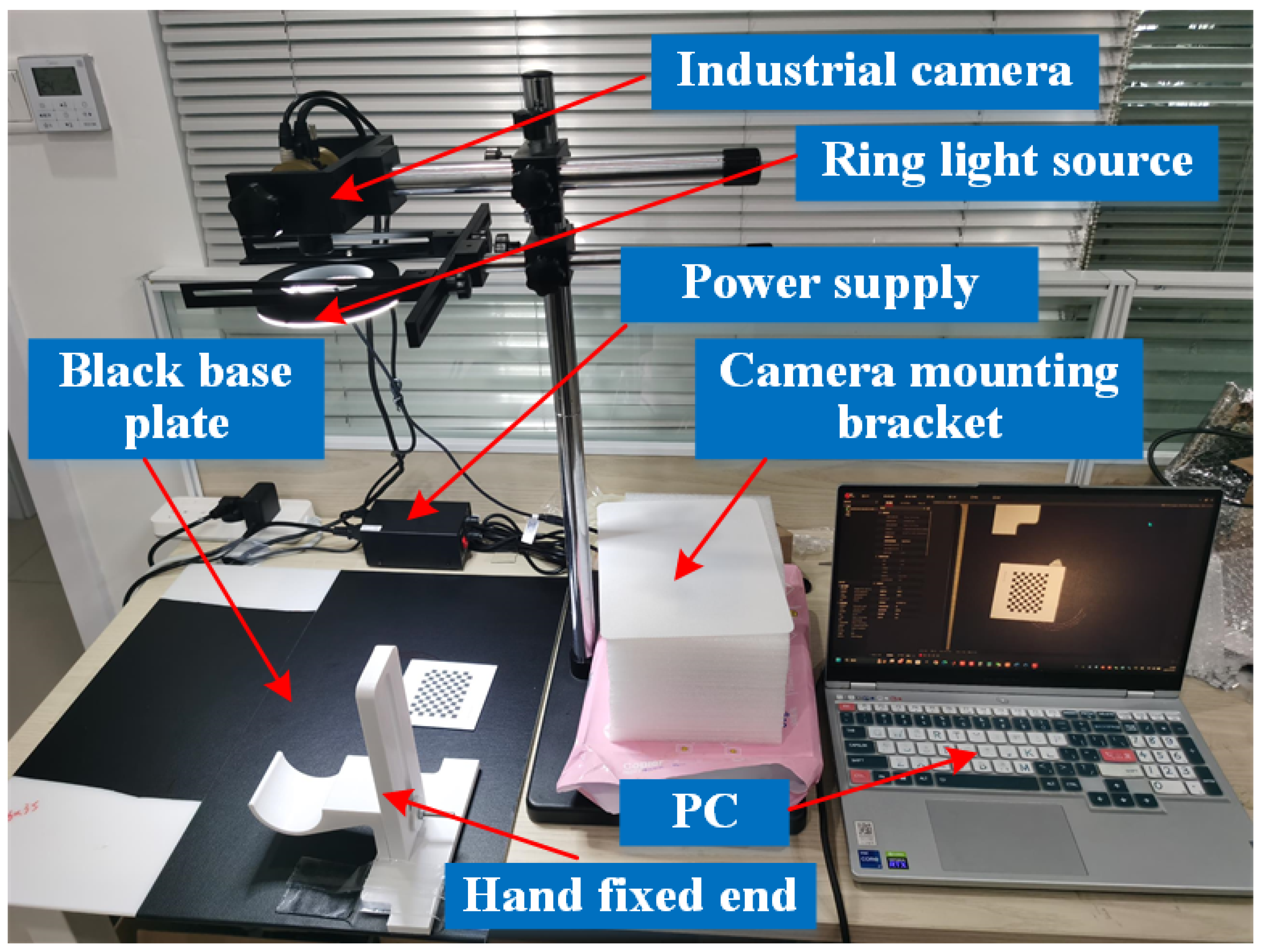
3.1. Prototype Construction
3.2. Performance Test
3.2.1. Rehabilitation Trajectory Matching
3.2.2. Mechanism Stability
4. Discussion
- Manufacturing process optimization: Transition from additive manufacturing and single-cavity injection molding to automated mass production techniques for linkage and soft component fabrication, targeting cycle time reduction.
- Durability enhancement. Durability testing of the robot is required to improve the materials and processes according to the corresponding safety standards. Higher requirements are put forward for soft materials to ensure safety and durability.
- Anthropometric customization: Manufacture products of different sizes for patients to choose from. It is improved to a retractable linkage mechanism, which can be customized and adjusted according to the patient’s hand size. Consider the development of feedback control schemes based on EMG sensing. AI technology is introduced to capture the intention of the patient so that the patient can actively control the actions of the robot.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DoF | Degree of Freedom |
| TPU | Thermoplastic Polyurethane |
| SMP | Shape Memory Polymer |
| IABC | Improved Artificial Bee Colony |
| ABC | Artificial Bee Colony |
| MM | Motion Matching |
| GA | Genetic Algorithm |
| CG | Convergence Generation |
Appendix A
| Function | Dimensionality | Range | Minimum Value |
|---|---|---|---|
| 30 | [−100, 100] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−1.28, 1.28] | 0 | |
| 30 | [−5.12, 5.12] | 0 | |
| 30 | [−600, 600] | 0 | |
| 30 | [−5, 5] | −1 | |
| 30 | [−5, 5] | 0.3 | |
| 30 | [1, 3] | −3 |
References
- Pollock, A.; Farmer, S.E.; Brady, M.C.; Langhorne, P.; Mead, G.E.; Mehrholz, J.; Van Wijck, F. Interventions for improving upper limb function after stroke. Cochrane Database Syst. Rev. 2014, 2014, CD010820. [Google Scholar] [CrossRef]
- Buma, F.; Kwakkel, G.; Ramsey, N. Understanding upper limb recovery after stroke. Restor. Neurol. Neurosci. 2013, 31, 707–722. [Google Scholar] [CrossRef] [PubMed]
- Hunter, S.; Crome, P. Hand function and stroke. Rev. Clin. Gerontol. 2002, 12, 68–81. [Google Scholar] [CrossRef]
- Lum, P.S.; Godfrey, S.B.; Brokaw, E.B.; Holley, R.J.; Nichols, D. Robotic approaches for rehabilitation of hand function after stroke. Am. J. Phys. Med. Rehabil. 2012, 91, S242–S254. [Google Scholar] [CrossRef]
- Park, J.H. Effect of robot-assisted hand rehabilitation on hand function in chronic stroke patients. J. Korea Robot. Soc. 2013, 8, 273–282. [Google Scholar] [CrossRef][Green Version]
- Schabowsky, C.N.; Godfrey, S.B.; Holley, R.J.; Lum, P.S. Development and pilot testing of HEXORR: Hand EXOskeleton rehabilitation robot. J. Neuroeng. Rehabil. 2010, 7, 1–16. [Google Scholar] [CrossRef]
- Hesse, S.; Mehrholz, J.; Werner, C. Robot-assisted upper and lower limb rehabilitation after stroke: Walking and arm/hand function. Dtsch. Ärzteblatt Int. 2008, 105, 330. [Google Scholar]
- Yue, Z.; Zhang, X.; Wang, J. Hand rehabilitation robotics on poststroke motor recovery. Behav. Neurol. 2017, 2017, 3908135. [Google Scholar] [CrossRef]
- Cheng, H.; Huang, R.; Qiu, J. A survey of rehabilitation robot and its clinical applications. Robot 2021, 43, 606–619. [Google Scholar]
- Nelson, C.A.; Nouaille, L.; Poisson, G. A redundant rehabilitation robot with a variable stiffness mechanism. Mech. Mach. Theory 2020, 150, 103862. [Google Scholar] [CrossRef]
- Marconi, D.; Baldoni, A.; McKinney, Z.; Cempini, M.; Crea, S.; Vitiello, N. A novel hand exoskeleton with series elastic actuation for modulated torque transfer. Mechatronics 2019, 61, 69–82. [Google Scholar]
- Chen, Z.; Zhan, F.; Jiang, J.; Wu, D.; Sun, J. A review on soft hand rehabilitation robot. Recent Patents Eng. 2023, 17, 12–36. [Google Scholar] [CrossRef]
- Chu, C.Y.; Patterson, R.M. Soft robotic devices for hand rehabilitation and assistance: A narrative review. J. Neuroeng. Rehabil. 2018, 15, 1–14. [Google Scholar]
- Meng, N.; Kun, W.; Mingxin, L.; Ke, Y.; Zhi, W. Design, analysis and experiment of finger soft actuator with nested structure for rehabilitation training. Adv. Mech. Eng. 2020, 12, 1687814020971538. [Google Scholar] [CrossRef]
- Lin, L.; Zhang, F.; Yang, L.; Fu, Y. Design and modeling of a hybrid soft-rigid hand exoskeleton for poststroke rehabilitation. Int. J. Mech. Sci. 2021, 212, 106831. [Google Scholar] [CrossRef]
- Rose, C.G.; O’Malley, M.K. Hybrid rigid-soft hand exoskeleton to assist functional dexterity. IEEE Robot. Autom. Lett. 2018, 4, 73–80. [Google Scholar] [CrossRef]
- Liu, C.; Lu, J.; Yang, H.; Guo, K. Current state of robotics in hand rehabilitation after stroke: A systematic review. Appl. Sci. 2022, 12, 4540. [Google Scholar] [CrossRef]
- Aggogeri, F.; Mikolajczyk, T.; O’Kane, J. Robotics for rehabilitation of hand movement in stroke survivors. Adv. Mech. Eng. 2019, 11, 1687814019841921. [Google Scholar] [CrossRef]
- Bianchi, M.; Fanelli, F.; Meli, E.; Ridolfi, A.; Vannetti, F.; Bianchini, M.; Allotta, B. Optimization-based scaling procedure for the design of fully portable hand exoskeletons. Meccanica 2018, 53, 3157–3175. [Google Scholar] [CrossRef]
- Lai, J.; Song, A. Design and Characterization of a Novel Compact Hand Exoskeleton Robot for Telerehabilitation and Muscle Spasticity Assessment. IEEE/ASME Trans. Mechatron. 2024, 29, 2416–2427. [Google Scholar] [CrossRef]
- Wang, S.; Dong, M.; Jiao, R.; Sun, S.; Li, J. Design and Analysis of Four-Finger Three-Joint Underactuated Hand Rehabilitation Mechanism. In Intelligent Robotics and Applications; Yang, H., Liu, H., Zou, J., Yin, Z., Liu, L., Yang, G., Ouyang, X., Wang, Z., Eds.; Springer: Singapore, 2023; Volume 14274, pp. 25–37. [Google Scholar]
- Zou, H.; Wu, Q.; Yang, L.; Zhu, Y.; Wu, H. Design and EMG-EEG Fusion-Based Admittance Control of a Hand Exoskeleton With Series Elastic Actuators. IEEE Trans. Med. Robot. Bionics 2025, 7, 347–358. [Google Scholar] [CrossRef]
- Cappello, L.; Meyer, J.T.; Galloway, K.C.; Peisner, J.D.; Granberry, R.; Wagner, D.A.; Engelhardt, S.; Paganoni, S.; Walsh, C.J. Assisting hand function after spinal cord injury with a fabric-based soft robotic glove. J. Neuroeng. Rehabil. 2018, 15, 1–10. [Google Scholar] [CrossRef]
- Duanmu, D.; Li, X.; Huang, W.; Hu, Y. Soft Finger Rehabilitation Exoskeleton of Biomimetic Dragonfly Abdominal Ventral Muscles: Center Tendon Pneumatic Bellows Actuator. Biomimetics 2023, 8, 614. [Google Scholar] [CrossRef]
- Shi, X.; Yang, C.; Lee, P.C.; Xie, D.; Ye, Z.; Li, Z.; Tong, R.K. An interactive soft robotic hand-task training system with wireless task boards and daily objects on post-stroke rehabilitation. Wearable Technol. 2025, 6, e4. [Google Scholar] [CrossRef] [PubMed]
- Rho, E.; Lee, H.; Lee, Y.; Lee, K.D.; Mun, J.; Kim, M.; Kim, D.; Park, H.S.; Jo, S. Multiple Hand Posture Rehabilitation System Using Vision-Based Intention Detection and Soft-Robotic Glove. IEEE Trans. Ind. Inform. 2024, 20, 6499–6509. [Google Scholar] [CrossRef]
- Ying, C.; Qingyun, M.; Hongliu, Y. Research progress on the development of hand rehabilitation robot. Beijing Biomed. Eng. 2018, 37, 650–656. [Google Scholar]
- Yap, H.K.; Lim, J.H.; Nasrallah, F.; Goh, J.C.; Yeow, R.C. A soft exoskeleton for hand assistive and rehabilitation application using pneumatic actuators with variable stiffness. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4967–4972. [Google Scholar]
- Haghshenas-Jaryani, M.; Carrigan, W.; Nothnagle, C.; Wijesundara, M.B. Sensorized soft robotic glove for continuous passive motion therapy. In Proceedings of the 2016 6th IEEE International Conference on Biomedical Robotics and Biomechatronics (BioRob), Singapore, 26–29 June 2016; pp. 815–820. [Google Scholar]
- Liang, R.; Zhang, Q.; He, B.; Li, L. Visual Representation of the Compactness of a Stephenson-II Six-Bar Linkage Exoskeleton Using Solution Region Synthesis Theory. IEEE Robot. Autom. Lett. 2024, 9, 4415–4422. [Google Scholar] [CrossRef]
- Moreno-SanJuan, V.; Cisnal, A.; Fraile, J.C.; Pérez-Turiel, J.; de-la Fuente, E. Design and characterization of a lightweight underactuated RACA hand exoskeleton for neurorehabilitation. Robot. Auton. Syst. 2021, 143, 103828. [Google Scholar] [CrossRef]
- Kim, H.M.; Kim, G.S. Development of a finger-rehabilitation robot for fingers’ flexibility rehabilitation exercise. Int. J. Precis. Eng. Manuf. 2013, 14, 535–541. [Google Scholar] [CrossRef]
- Guo, K.; Lu, J.; Liu, C.; Yang, H. Development, Research, Optimization and Experiment of Exoskeleton Robot for Hand Rehabilitation Training. Appl. Sci. 2022, 12, 10580. [Google Scholar] [CrossRef]
- Zhang, X.; Rong, X.; Luo, H. Optimizing lower limb rehabilitation: The intersection of machine learning and rehabilitative robotics. Front. Rehabil. Sci. 2024, 5, 1246773. [Google Scholar] [CrossRef]
- Jamwal, P.K.; Hussain, S.; Xie, S.Q. Three-stage design analysis and multicriteria optimization of a parallel ankle rehabilitation robot using genetic algorithm. IEEE Trans. Autom. Sci. Eng. 2014, 12, 1433–1446. [Google Scholar] [CrossRef]
- Li, G.; Cheng, L.; Sun, N. Design, manipulability analysis and optimization of an index finger exoskeleton for stroke rehabilitation. Mech. Mach. Theory 2022, 167, 104526. [Google Scholar] [CrossRef]
- Zi, B.; Yin, G.; Zhang, D. Design and optimization of a hybrid-driven waist rehabilitation robot. Sensors 2016, 16, 2121. [Google Scholar] [CrossRef]
- Shen, Q.; Lee, W.T.; Russell, K.; Sodhi, R.S. On motion generation of Watt I mechanisms for mechanical finger design. Trans. Can. Soc. Mech. Eng. 2008, 32, 411–422. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Ning, M.; Zhou, Z.; Wu, Z.; Zhao, J.; Li, X.; Liu, W. One-DOF six-bar space gripper with multiple operation modes and force adaptability. Aerosp. Sci. Technol. 2022, 123, 107485. [Google Scholar] [CrossRef]
- Liang, B.; Tian, Y.; Zhang, W. A Straight Parallel Grasping and Self-Adaptive Gripper with Differential and Watt Linkages. In Proceedings of the 2023 International Conference on Advanced Robotics and Mechatronics (ICARM), Sanya, China, 8–10 July 2023; pp. 624–629. [Google Scholar]
- Rus, D.; Tolley, M.T. Design, fabrication and control of soft robots. Nature 2015, 521, 467–475. [Google Scholar] [CrossRef] [PubMed]
- Cianchetti, M.; Laschi, C.; Menciassi, A.; Dario, P. Biomedical applications of soft robotics. Nat. Rev. Mater. 2018, 3, 143–153. [Google Scholar] [CrossRef]
- Shepherd, R.F.; Ilievski, F.; Choi, W.; Morin, S.A.; Stokes, A.A.; Mazzeo, A.D.; Chen, X.; Wang, M.; Whitesides, G.M. Multigait soft robot. Proc. Natl. Acad. Sci. USA 2011, 108, 20400–20403. [Google Scholar] [CrossRef]




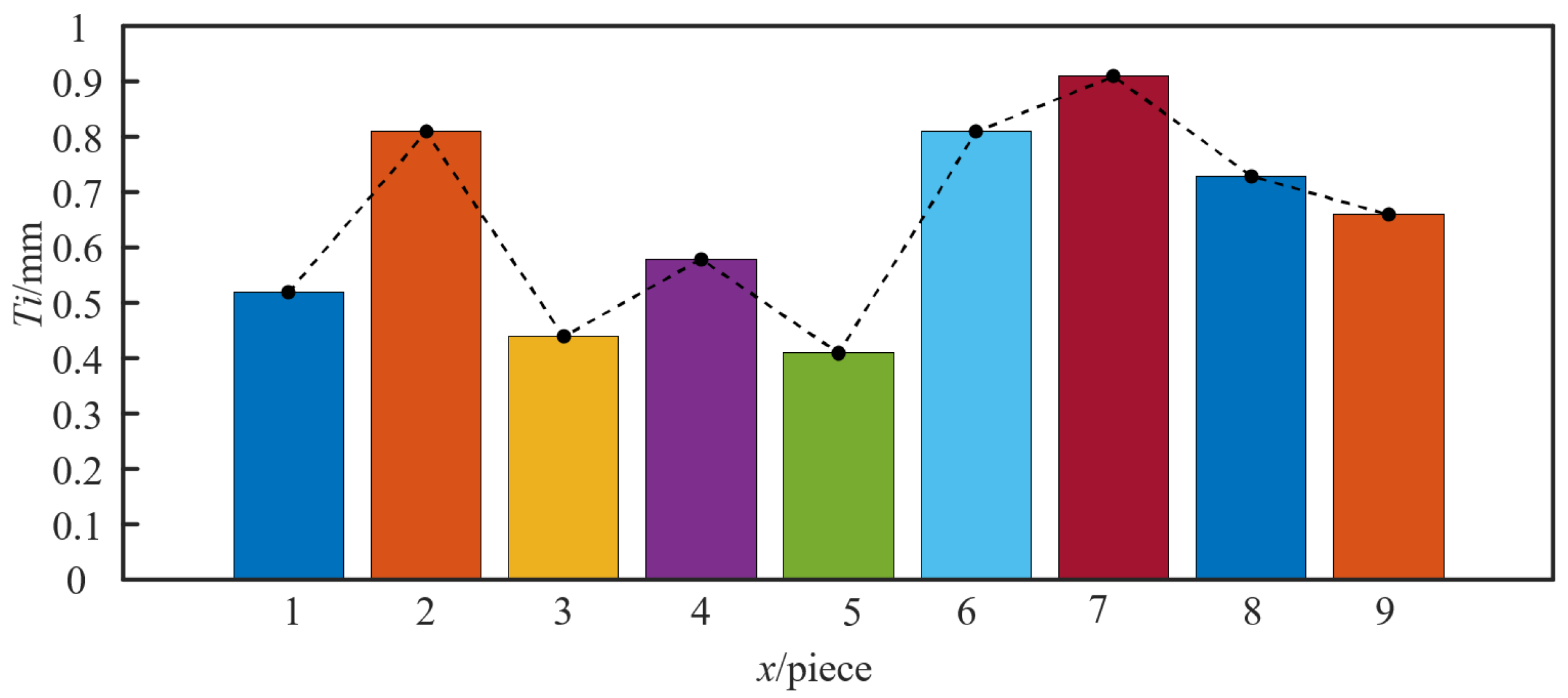
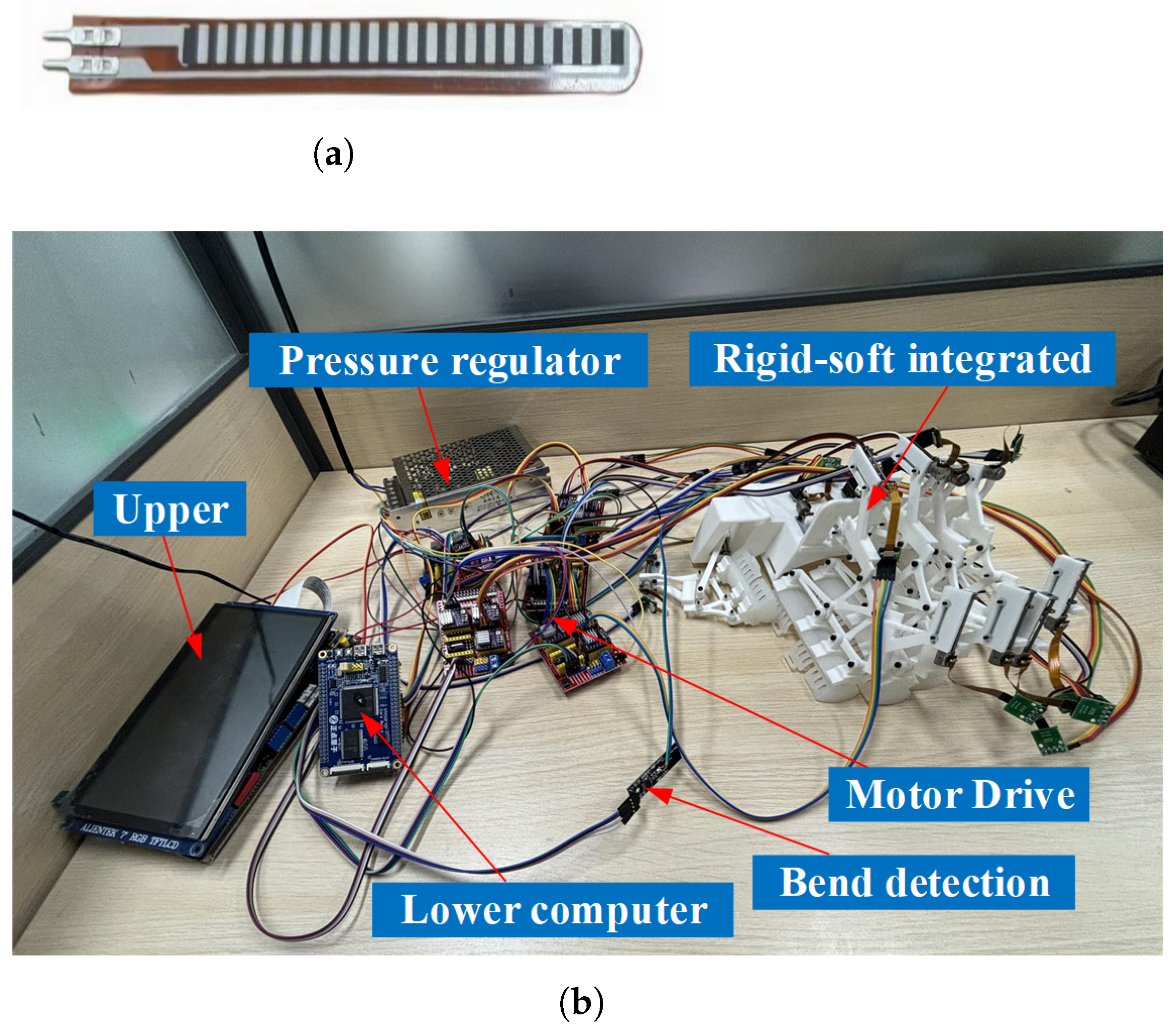

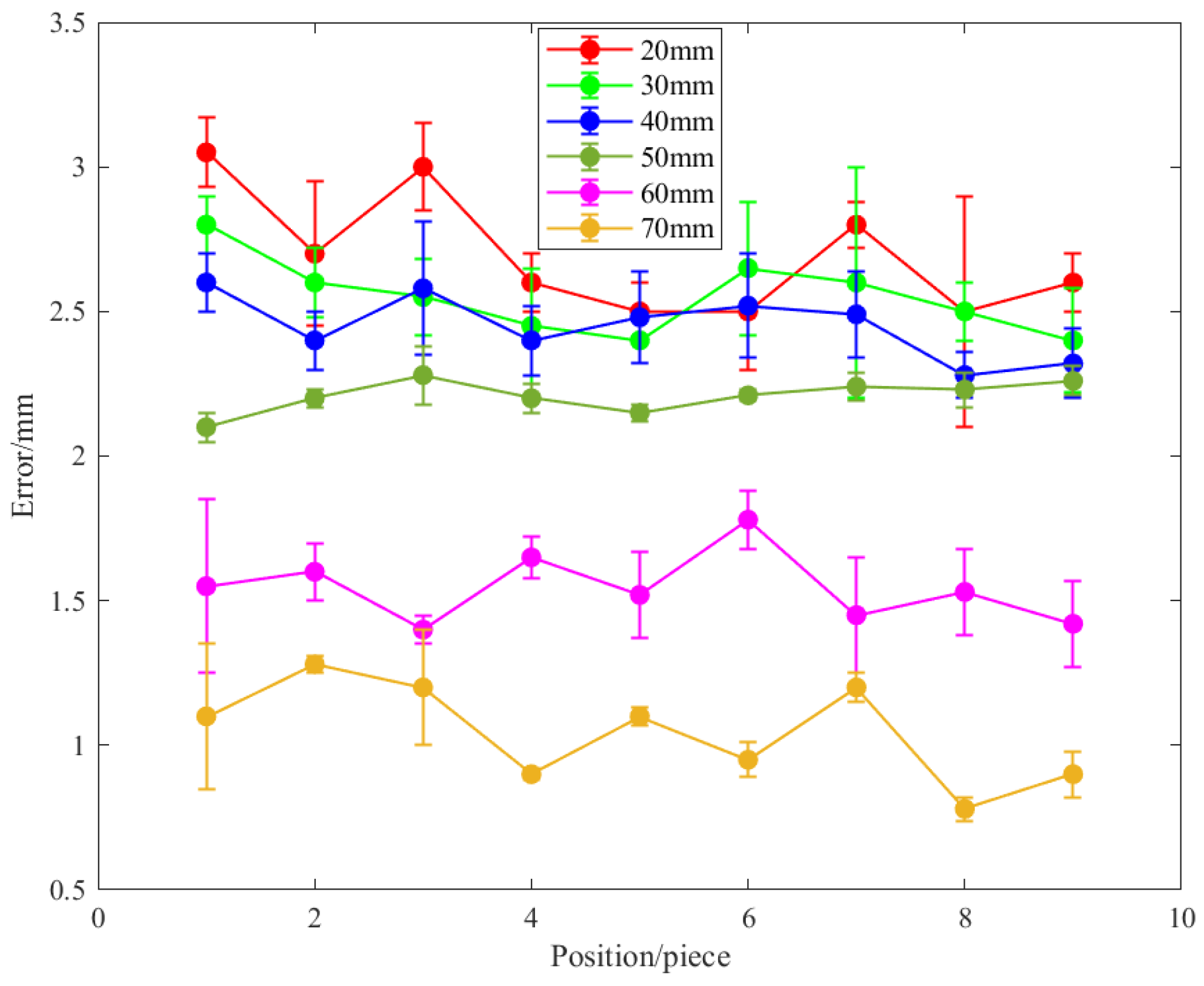


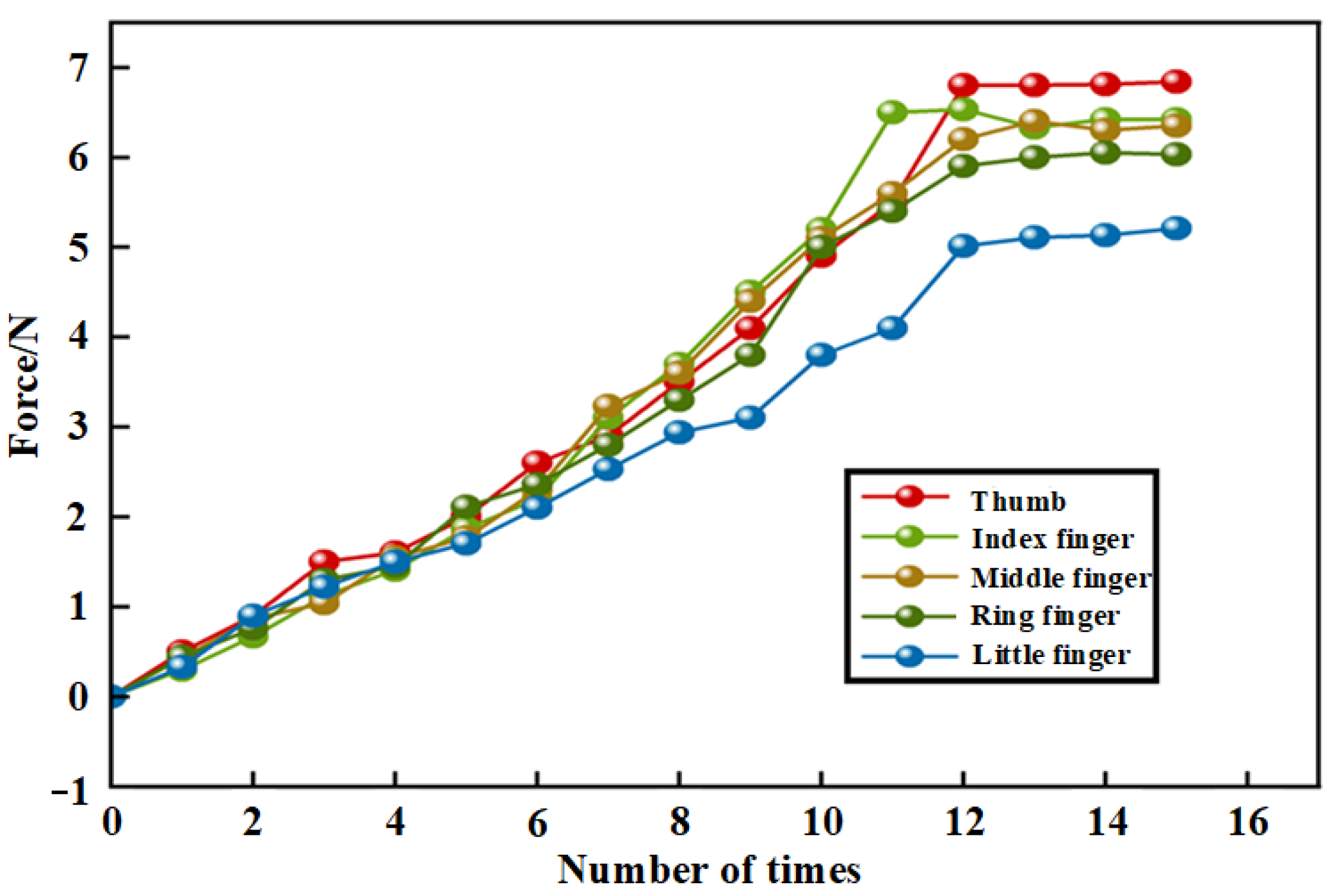

| Comparison Criteria | Silicone Rubber (Ecoflex 10) | Thermoplastic Polyurethane (TPU) | Shape Memory Polymer (SMP) |
|---|---|---|---|
| Biocompatibility | Medical certification | Requires post-processing | Composition-dependent |
| Hardness | Soft | Rigid | Programmable |
| Elongation at Break | >1000% | 300–600% | <200% |
| Fatigue Resistance | >1 million cycles | ∼100k cycles before cracking | Decaying after >100 cycles |
| Manufacturing | Casting | injection molding | Thermal/UV curing |
| Temperature Stability | −50 °C to 200 °C | −40 °C to 120 °C | Environment-sensitive |
| Safety | Optimal | Risk of pressure injuries | Thermal activation may cause discomfort |
| Lifespan | Longest | Moderate | Shortest |
| Applications | Rehabilitation gloves | Exoskeleton frames | Shape-changing tools |
| Ecoflex 5 | Ecoflex 50 | Ecoflex 30 | Ecoflex 33AF | Ecoflex 20 | Ecoflex 10 | |
|---|---|---|---|---|---|---|
| Mixing viscosity (CPS) | 13,000 | 8000 | 3000 | 3000 | 3000 | 14,000 |
| Specific volume | 25.8 | 25.9 | 26.0 | 26.0 | 26.0 | 26.6 |
| Curing time (h) | 0.12 | 3 | 4 | 4 | 4 | 4 |
| Shore hardness | 5 | 50 | 30 | 33 | 20 | 10 |
| Tensile strength (psi) | 350 | 315 | 200 | 200 | 160 | 120 |
| Tear strength (pli) | 75 | 50 | 38 | 38 | 30 | 22 |
| Shrinkage (in./in) | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| Elongation at break (%) | 1000 | 980 | 900 | 900 | 845 | 800 |
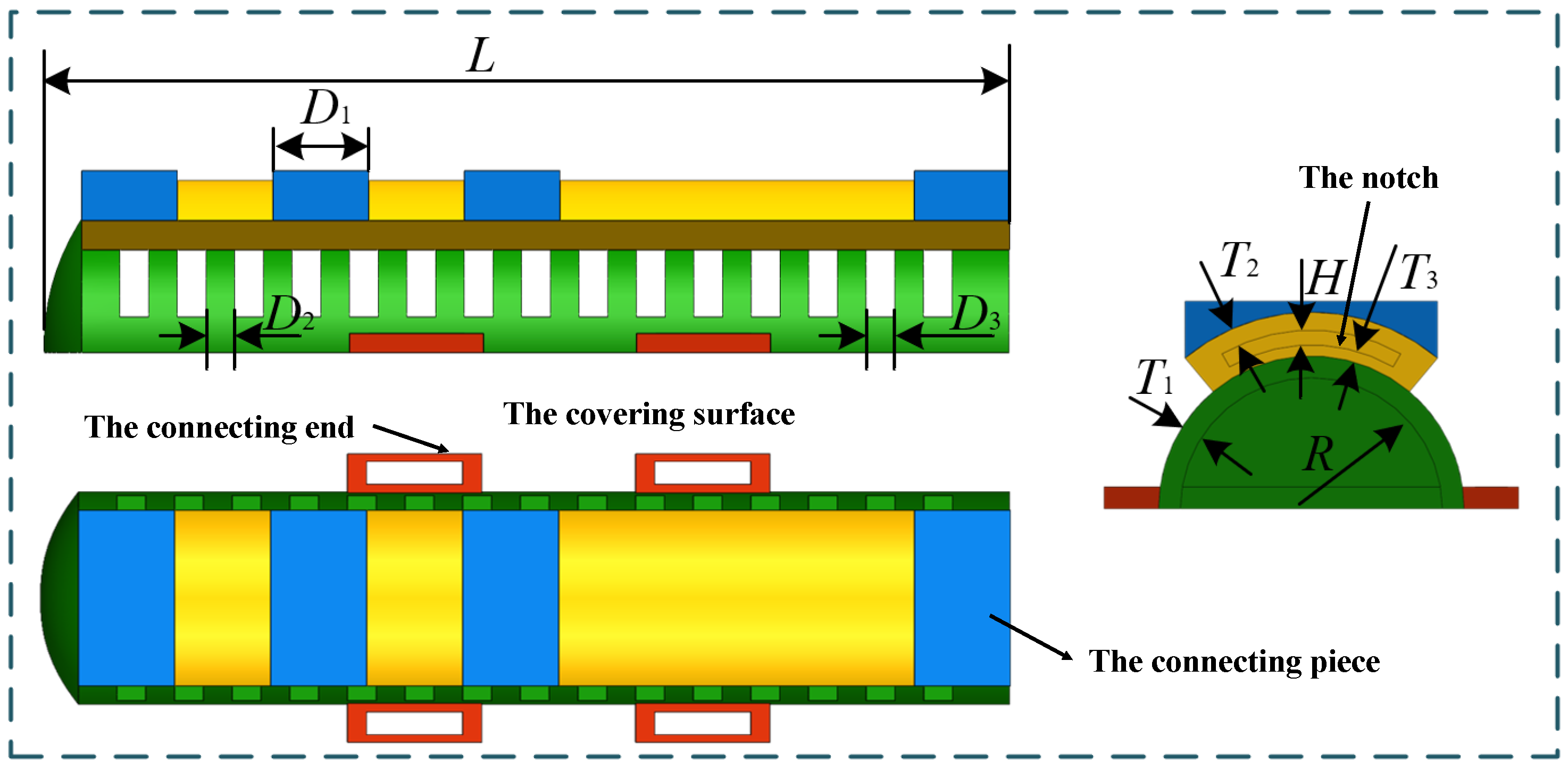
| Parameters | Names |
|---|---|
| L | Total length of soft part |
| Length of soft and rigid joint | |
| Length of seating surface | |
| Length of interval | |
| H | Width of sensor cavity |
| R | Radius of hand cavity |
| Thickness of hand cavity | |
| Thickness of sensor cavity | |
| Thickness of sensor cavity bottom |
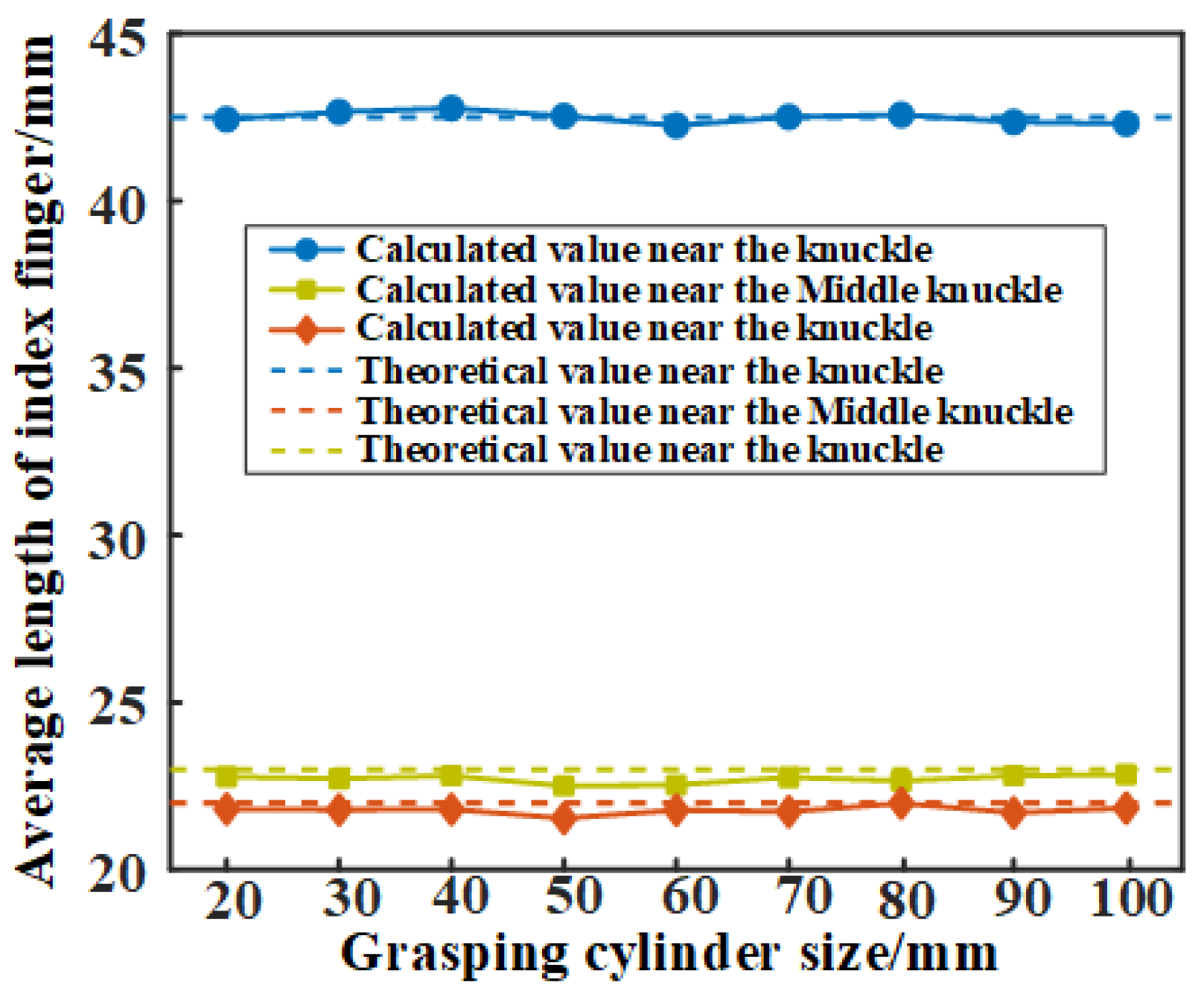
| Proximal Knuckle | Middle Knuckle | Distal Knuckle |
|---|---|---|
| 42.5 mm | 23 mm | 22 mm |
| Diameter | Equation | x | ||||
|---|---|---|---|---|---|---|
| 20 mm | 0 | 0 | 0.1452 | −8.652 | 100.8 | |
| 0 | 0 | 0.0321 | −1.929 | −21.53 | ||
| 0 | 0 | 0.0177 | −1.061 | −56.97 | ||
| 30 mm | 0.0007682 | −0.09985 | 4.4884 | −105.3 | 808.8 | |
| 0.00002659 | −0.003506 | 0.1795 | −3.97 | 21.21 | ||
| 0.0000059 | 00.00081 | 0.04424 | −0.956 | −66.52 | ||
| 40 mm | 0.7206 | 0.1525 | 0.3647 | −5.073 | −15.85 | |
| 2.623 | 4.263 | 3.413 | 9.031 | −35.14 | ||
| 7.256 | 9.744 | 3.113 | 8.953 | −55.86 | ||
| 50 mm | 0.1433 | 0.08951 | −0.3337 | 0.8203 | −4.745 | |
| 0.6242 | 1.992 | 2.965 | 7.08 | −20.19 | ||
| 3.482 | 7.134 | 3.949 | 8.967 | −38.69 | ||
| 60 mm | 0 | 0 | 0.2456 | 1.159 | −5.585 | |
| 0 | 0 | 2.475 | 7.126 | −21.11 | ||
| 0 | 0 | 5.401 | 14.06 | −38.41 | ||
| 70 mm | 0 | 0 | 0.2627 | 0.6765 | −2.654 | |
| 0 | 0 | 1.421 | 6.31 | −13.4 | ||
| 0 | 0 | 3.866 | 13.04 | −25.57 |
| Links | AB | BE | DE | AD | CD | DG | FG |
| Ranges (mm) | 20–40 | 20–45 | 20–40 | 35–45 | 5–12 | 35–45 | 30–45 |
| Links | CF | AC | EG | GH | FH | IJ | |
| Ranges (mm) | 20–35 | 35–45 | 20–35 | 25–35 | 20–35 | 60–75 |
| IABC | ABC | GA | |||||||
|---|---|---|---|---|---|---|---|---|---|
| CG | Time (s) | Values | CG | Time (s) | Values | CG | Time (s) | Values | |
| 51 | 3.243 | 7.41 | 53 | 3.537 | 8.13 | 56 | 4.178 | 8.53 | |
| 43 | 3.564 | 6.33 | 49 | 4.568 | 7.22 | 59 | 5.514 | 6.13 | |
| 41 | 3.745 | 5.41 | 51 | 4.743 | 5.74 | 52 | 5.157 | 6.11 | |
| 57 | 3.413 | 6.12 | 61 | 4.815 | 8.53 | 63 | 5.811 | 7.59 | |
| 44 | 3.348 | 6.13 | 53 | 5.111 | 7.13 | 58 | 6.634 | 6.44 | |
| 51 | 3.411 | −0.99914 | 55 | 5.933 | −0.99564 | 59 | 7.128 | −0.96414 | |
| 48 | 3.875 | 0.30001 | 61 | 6.145 | 0.29996 | 63 | 6.781 | 0.30003 | |
| 36 | 3.136 | −2.9991 | 55 | 6.537 | −2.9975 | 60 | 7.461 | −2.9413 | |
| Parameters | L | H | R | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ranges (mm) | 80–120 | 10 | 3 | 3 | 2 | 13 | 1–3 | 1–3 | 2 |
| Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Ranges (mm) | [−200, 200] | ||||||||
| Results (mm) | 186.96 | 76.62 | −107 | 124.21 | −104.25 | 91.21 | 40.41 | 113.66 | 23.55 |
| Robots | Type | Number of Actuator/Finger | Five Fingers Training | Single Finger Training | Multiple Trajectories | Size Adaptability | Daily Necessities Grasping |
|---|---|---|---|---|---|---|---|
| [22] | Rigid | 1 | - | Yes | - | - | Yes |
| [21] | Rigid | 1 | Yes | - | - | - | - |
| [24] | Soft | 1 | Yes | Yes | - | Yes | Yes |
| [26] | Soft | 1 | Yes | Yes | - | Yes | Yes |
| [31] | Rigid–Soft | 3 | Yes | Yes | Yes | - | Yes |
| [32] | Rigid–Soft | 1 | Yes | Yes | - | Yes | - |
| ours | Rigid–Soft | 3 | Yes | Yes | Yes | Yes | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Ning, M.; Wang, Y.; Yang, J. Design and Dimension Optimization of Rigid–Soft Hand Function Rehabilitation Robots. Machines 2025, 13, 311. https://doi.org/10.3390/machines13040311
Zhang R, Ning M, Wang Y, Yang J. Design and Dimension Optimization of Rigid–Soft Hand Function Rehabilitation Robots. Machines. 2025; 13(4):311. https://doi.org/10.3390/machines13040311
Chicago/Turabian StyleZhang, Rui, Meng Ning, Yuqian Wang, and Jun Yang. 2025. "Design and Dimension Optimization of Rigid–Soft Hand Function Rehabilitation Robots" Machines 13, no. 4: 311. https://doi.org/10.3390/machines13040311
APA StyleZhang, R., Ning, M., Wang, Y., & Yang, J. (2025). Design and Dimension Optimization of Rigid–Soft Hand Function Rehabilitation Robots. Machines, 13(4), 311. https://doi.org/10.3390/machines13040311





