Improving Vehicle Dynamics: A Fractional-Order PIλDμ Control Approach to Active Suspension Systems
Abstract
1. Introduction
2. Modeling
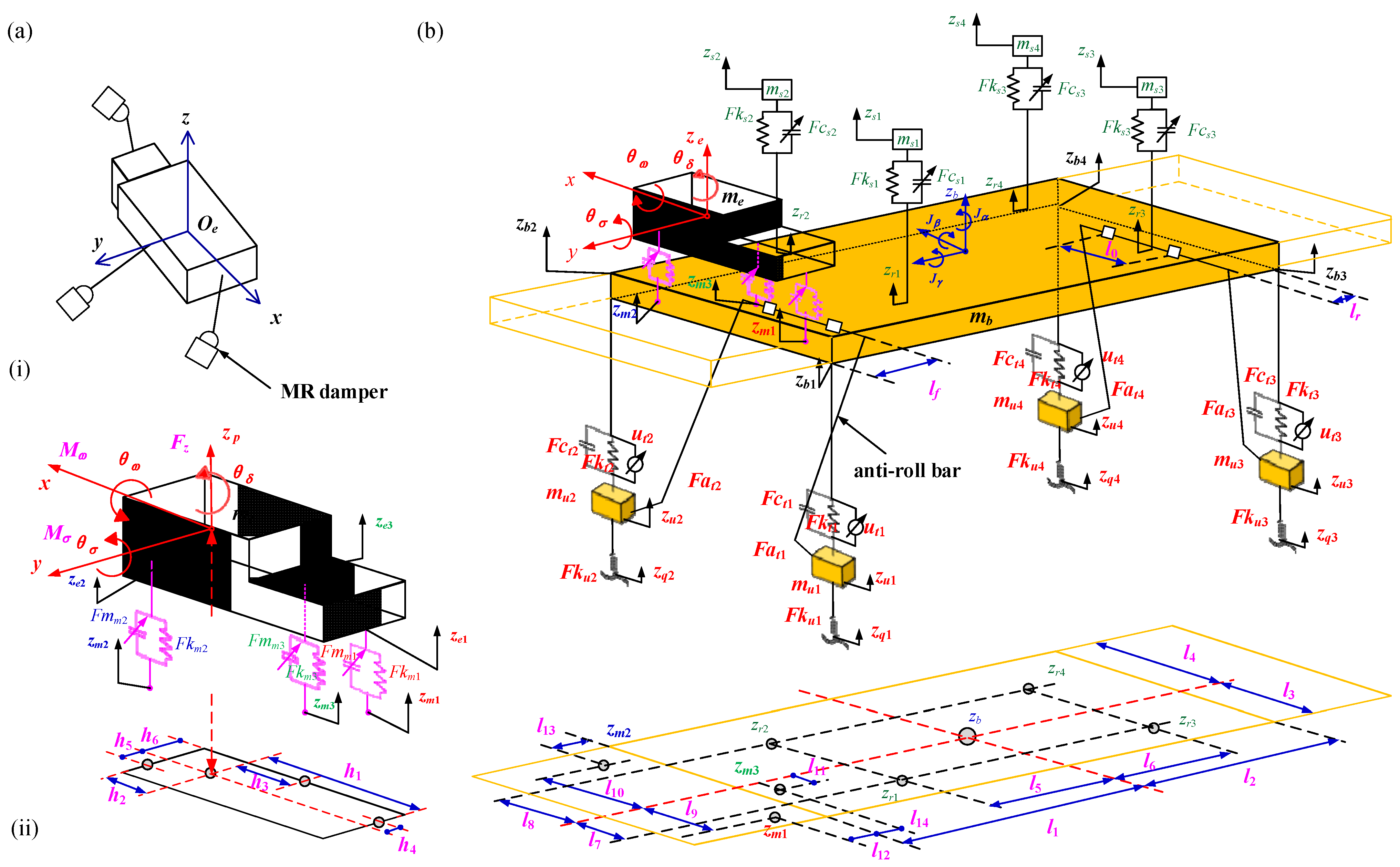
2.1. Active Suspension
- (1)
- The differential equation for the vertical motion of the unsprung mass in each suspension is shown below:
- (2)
- The vertical motion of the vehicle body is related to the change in contact between the wheels and the ground as the vehicle passes over an uneven road surface. The pitching motion of the vehicle body is most pronounced when the vehicle is accelerating and braking. The control of the pitching motion is critical to improving the dynamic stability and comfort of the vehicle. Roll motion occurs mainly when the vehicle is turning, as the vehicle’s center of gravity shifts to the outside, creating roll. Controlling the roll motion is important to maintain vehicle stability and improve cornering performance. The differential equations for the vertical, pitch, and roll motions of a vehicle are as follows [78,79]:
- (3)
- (4)
- The vertical, rolling, and pitching movements of the engine are related to the motion of the pistons. The rapid up-and-down movement of the pistons in the cylinders generates vibrations, which are transmitted to the vehicle body through the engine mounts, potentially causing vertical movement, rolling, and pitching of the engine. The differential equations for the vertical, rolling, and pitching movements of the engine are as follows [89,90]:
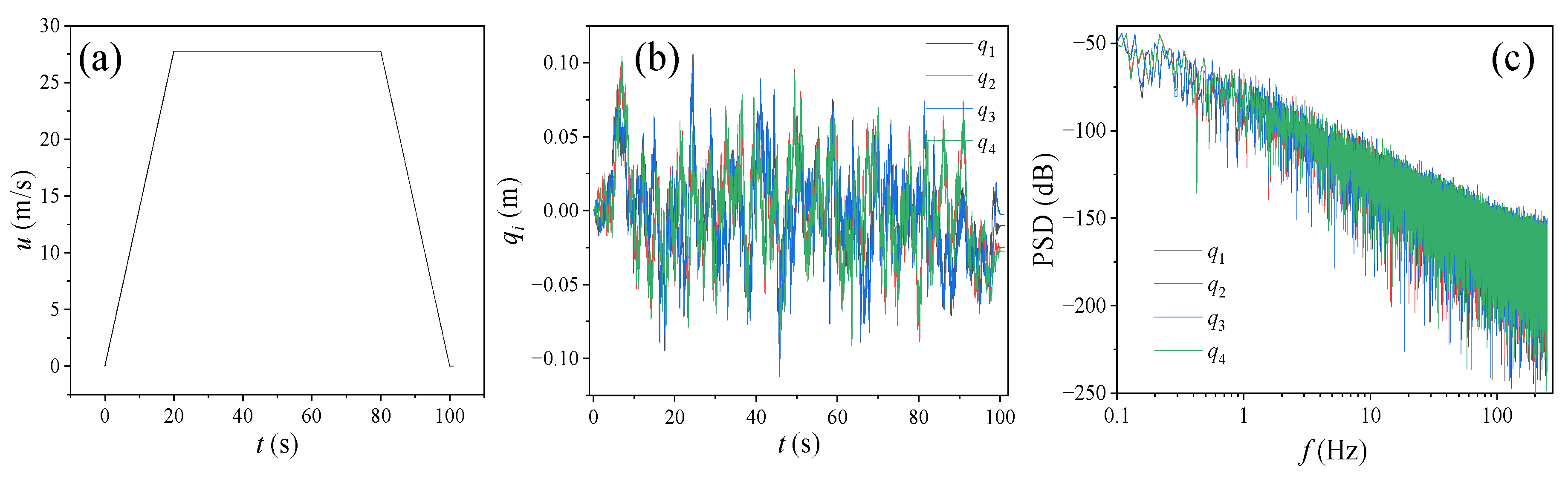
2.2. Road Excitation
2.2.1. Single-Wheel Road Input Analysis
2.2.2. Temporal Displacement of Axle Trajectories During Vehicle Motion
2.2.3. Coherence of Left and Right Wheel Tracks
2.2.4. Four-Wheels Road Excitation Model
3. Methods
3.1. Fractional-Order PIλDμ
3.1.1. Theoretical Framework of Fractional-Order Calculus
3.1.2. Architecture of PIλDμ Controller System
3.2. Optimization Algorithm
3.2.1. Gray Wolf Optimizer
- (1)
- Initialize the population:
- (2)
- Identification of α-wolf, β-wolf, and δ-wolf
- (3)
- Predation process
3.2.2. Penalty Optimization Process
4. Results and Analysis
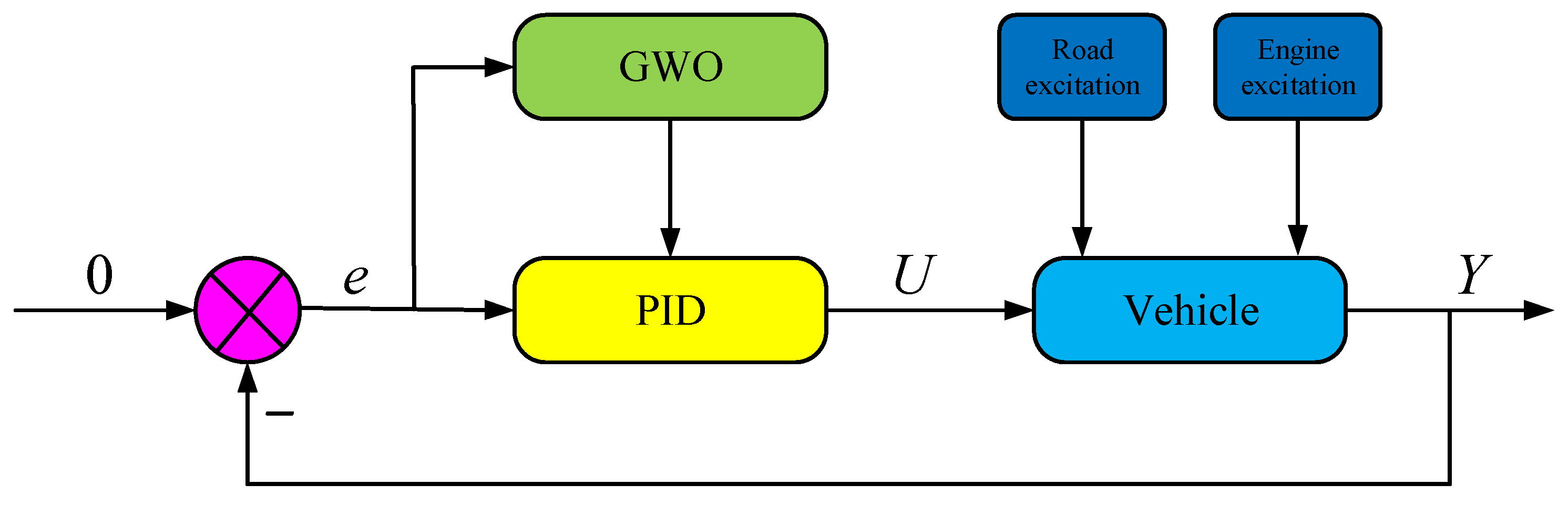
4.1. Logical Architecture
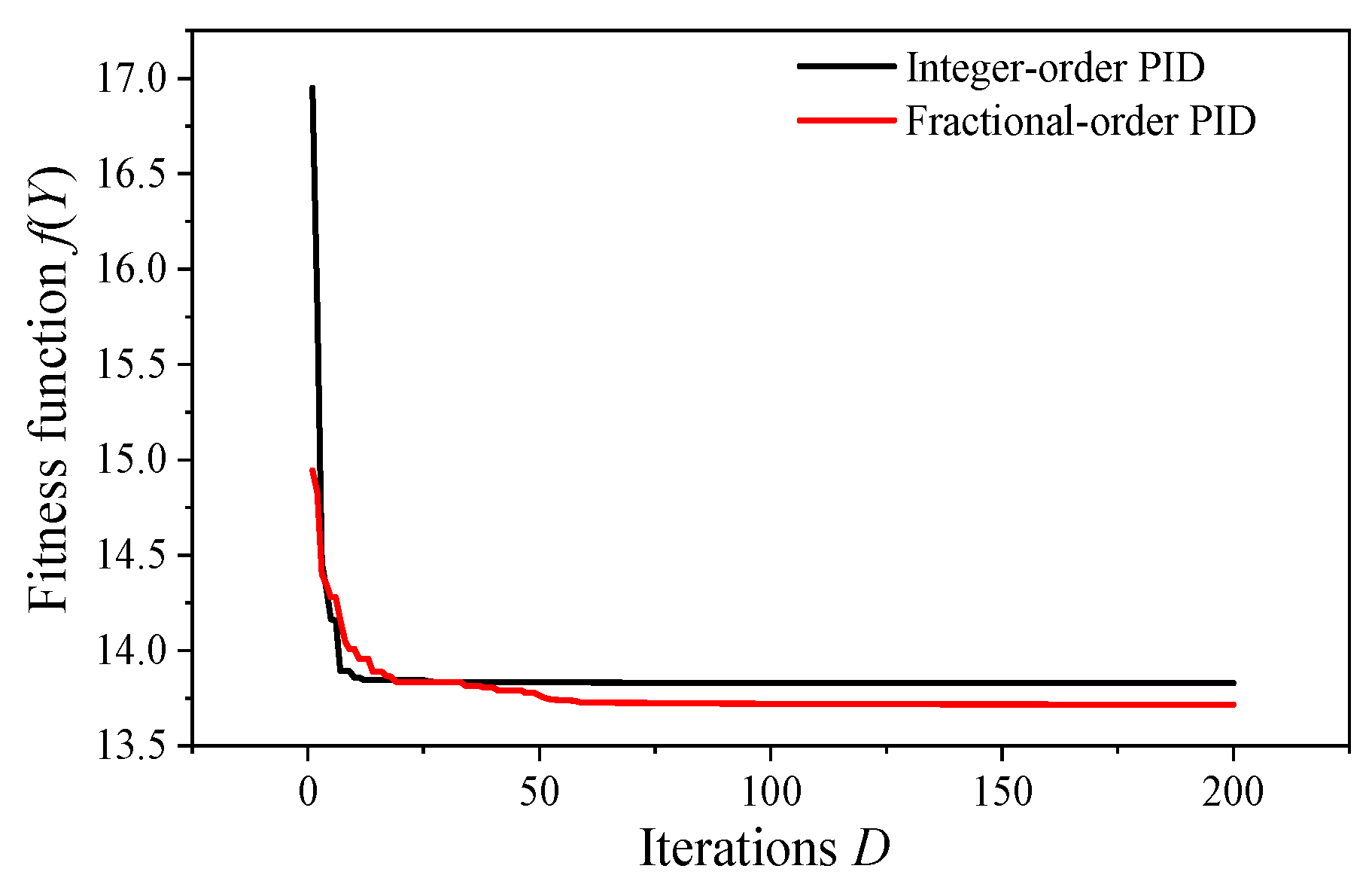
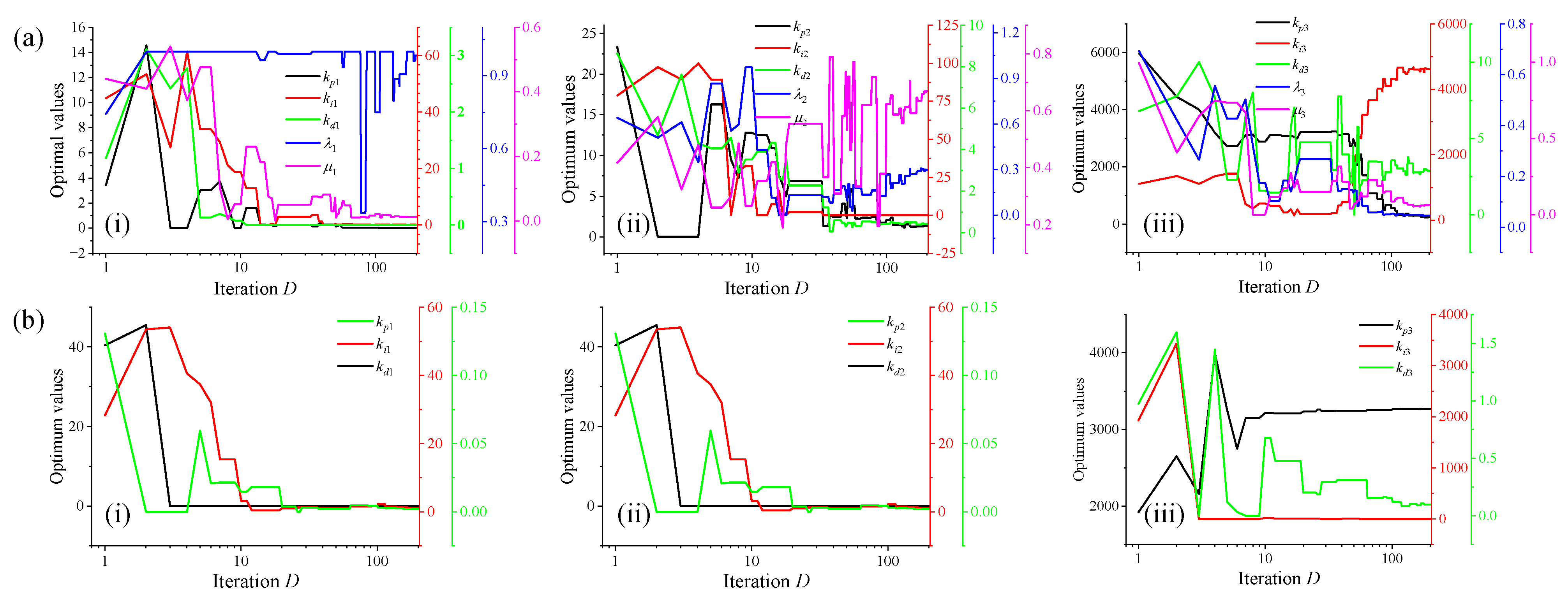
4.2. Parameter Optimization Process
4.3. Dynamic Processes on C-Level Road Surfaces
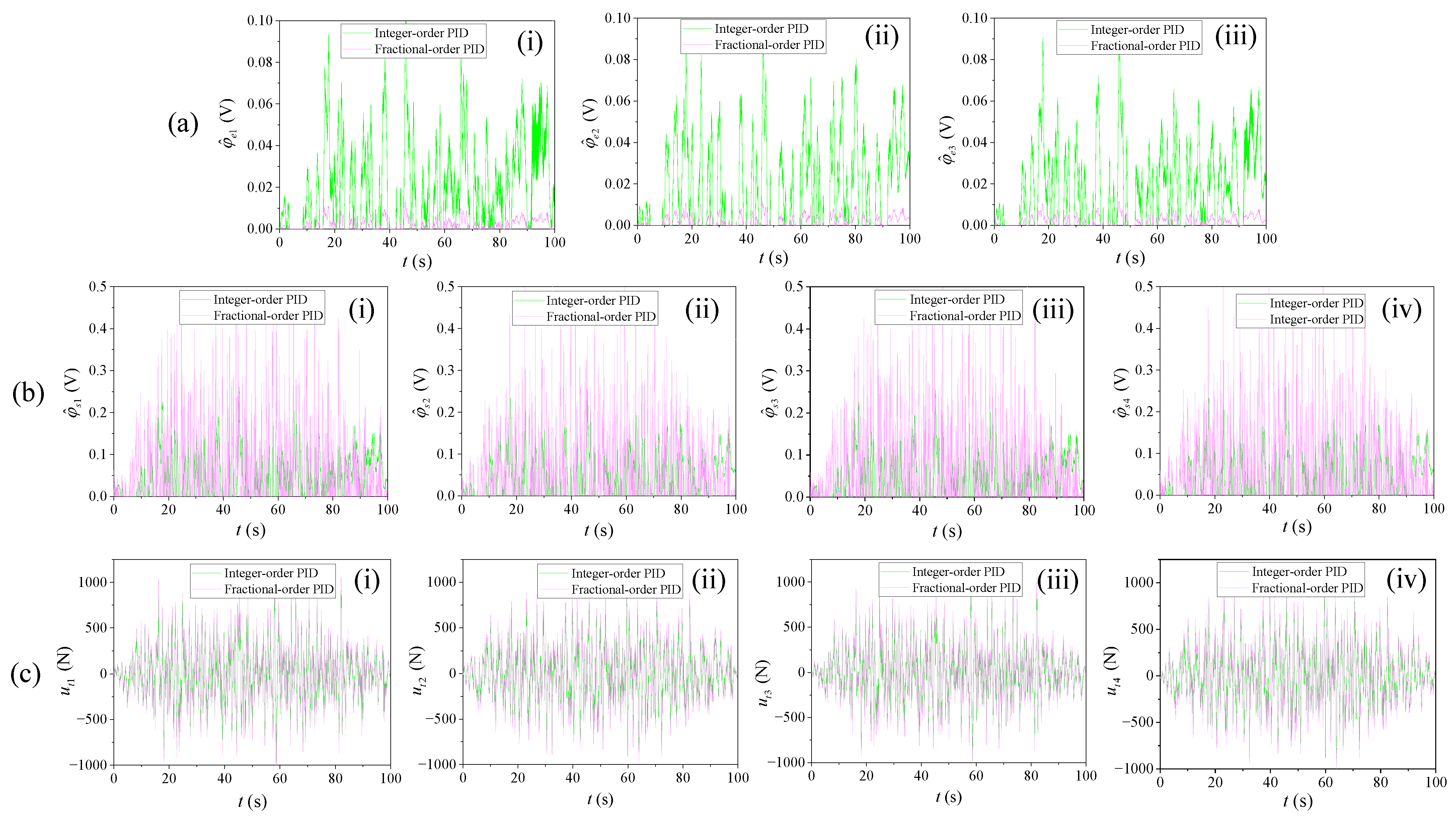
4.3.1. Controller Input
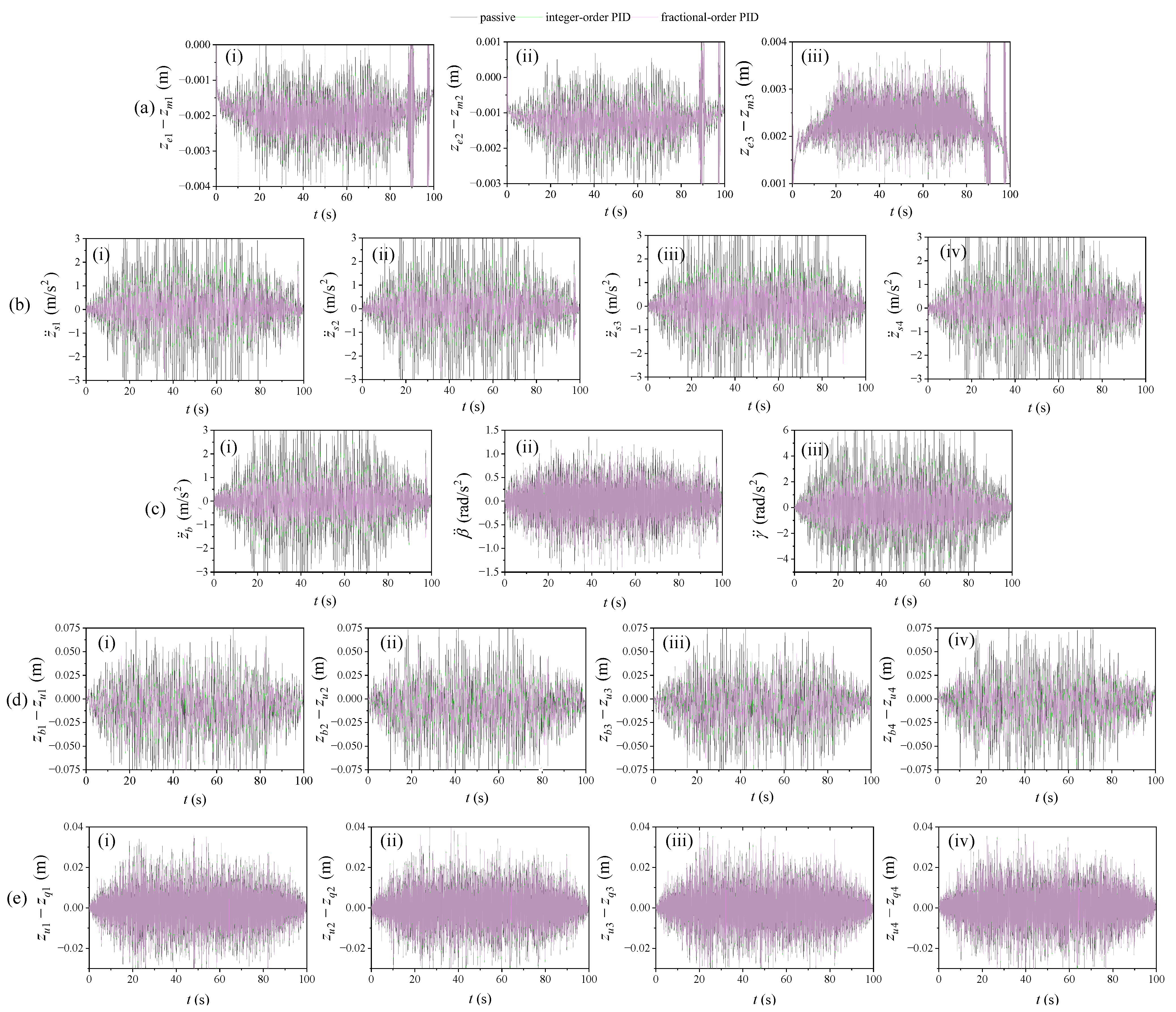
4.3.2. Time-Domain Indicators of Output Response
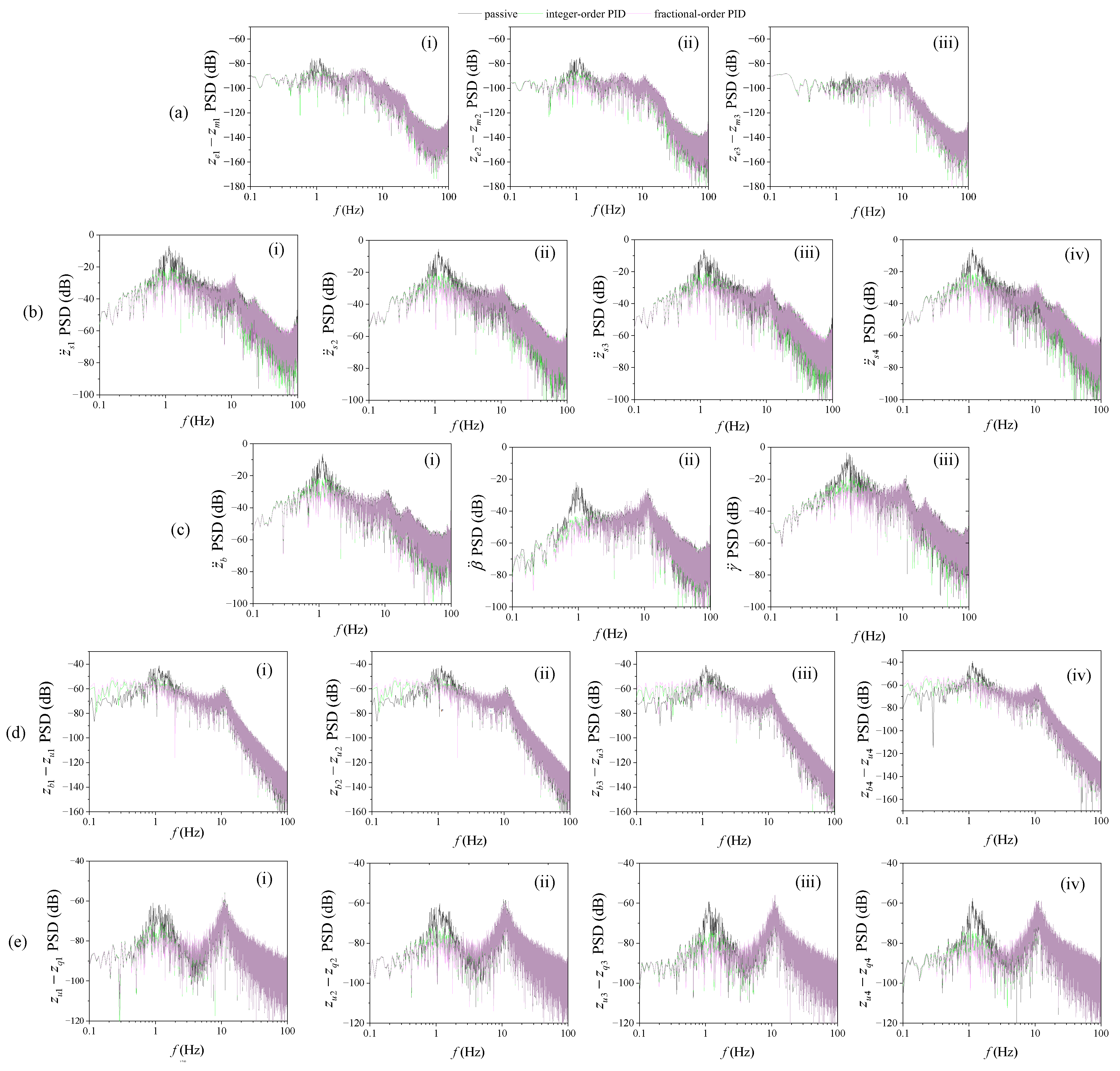
4.3.3. Frequency Domain Comparison of Output Response
4.3.4. RMS Values on Five Different Road Surfaces
5. Comparison and Discussion
5.1. Previous Literature
5.2. Enhancing the Smoothness of Suspension Through the Utilization of Other Technologies
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdelkareem, M.A.A.; Xu, L.; Ali, M.K.A.; Elagouz, A.; Mi, J.; Guo, S.J.; Liu, Y.L.; Zuo, L. Vibration energy harvesting in automotive suspension system: A detailed review. Appl. Energy 2018, 229, 672–699. [Google Scholar]
- Gao, P.; Zhao, C.; Pan, H.; Fang, L. A Model-Free Fractional-Order Composite Control Strategy for High-Precision Positioning of Permanent Magnet Synchronous Motor. Fractal Fract. 2025, 9, 161. [Google Scholar] [CrossRef]
- Li, H.Y.; Jing, X.J.; Karimi, H.R. Output-Feedback-Based H∞ Control for Vehicle Suspension Systems with Control Delay. IEEE Trans. Ind. Electron. 2014, 61, 436–446. [Google Scholar]
- Li, H.Y.; Yu, J.Y.; Hilton, C.; Liu, H.H. Adaptive Sliding-Mode Control for Nonlinear Active Suspension Vehicle Systems Using T-S Fuzzy Approach. IEEE Trans. Ind. Electron. 2013, 60, 3328–3338. [Google Scholar]
- Sun, W.C.; Zhao, Z.L.; Gao, H.J. Saturated Adaptive Robust Control for Active Suspension Systems. IEEE Trans. Ind. Electron. 2013, 60, 3889–3896. [Google Scholar]
- Wang, H.; Jian, H.; Huang, J.; Lan, Y. Fractional-Order MFAC with Application to DC Motor Speed Control System. Mathematics 2025, 13, 610. [Google Scholar] [CrossRef]
- Ferhath, A.A.; Kasi, K. A Review on Various Control Strategies and Algorithms in Vehicle Suspension Systems. Int. J. Automot. Mech. Eng. 2023, 20, 10720–10735. [Google Scholar]
- Ezeta, J.H.; Mandow, A.; Cerezo, A.G. Active and Semi-active Suspension Systems: A Review. Rev. Iberoam. Autom. Inform. 2013, 10, 121–132. [Google Scholar]
- Liu, C.N.; Chen, L.; Lee, H.P.; Yang, Y.; Zhang, X.L. Generalized Skyhook-Groundhook Hybrid Strategy and Control on Vehicle Suspension. IEEE Trans. Veh. Technol. 2023, 72, 1689–1700. [Google Scholar]
- Zhang, J.M.; Liu, J.; Liu, B.L.; Li, M. Fractional Order PID Control Based on Ball Screw Energy Regenerative Active Suspension. Actuators 2022, 11, 189. [Google Scholar] [CrossRef]
- Guan, Q.H.; Du, X.; Wen, Z.F.; Liang, S.L.; Chi, M.R. Vibration characteristics of bogie hunting motion based on root loci curves. Acta Mech. Sin.-PRC 2022, 38, 521447. [Google Scholar]
- Zhu, H.M.; Yang, Z.B.; Sun, X.D.; Wang, D.; Chen, X. Rotor Vibration Control of a Bearingless Induction Motor Based on Unbalanced Force Feed-Forward Compensation and Current Compensation. IEEE Access 2020, 8, 12988–12998. [Google Scholar]
- Hoyle, J.B. Modelling the static stiffness and dynamic frequency response characteristics of a leaf spring truck suspension. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2004, 218, 259–278. [Google Scholar]
- Floreán-Aquino, K.H.; Arias-Montiel, M.; Linares-Flores, J.; Mendoza-Larios, J.G.; Cabrera-Amado, A. Modern Semi-Active Control Schemes for a Suspension with MR Actuator for Vibration Attenuation. Actuators 2021, 10, 22. [Google Scholar] [CrossRef]
- Liu, C.C.; Ren, C.B.; Liu, L. Optimal Control for Cubic Strongly Nonlinear Vibration of Automobile Suspension. J. Low Freq. Noise Vib. Act. Control 2014, 33, 233–243. [Google Scholar]
- Zribi, M.; Karkoub, M. Robust control of a car suspension system using magnetorheological dampers. J. Vib. Control 2004, 10, 507–524. [Google Scholar]
- Koch, G.; Kloiber, T. Driving State Adaptive Control of an Active Vehicle Suspension System. IEEE Trans. Control Syst. Technol. 2014, 22, 44–57. [Google Scholar]
- Dou, G.W.; Yu, W.H.; Li, Z.X.; Khajepour, A.; Tan, S.Q. Sliding Mode Control of Laterally Interconnected Air Suspensions. Appl. Sci. 2020, 10, 4320. [Google Scholar] [CrossRef]
- Li, Y.; Dong, W.; Zheng, T.; Wang, Y.; Li, X. Scene-Adaptive Loader Trajectory Planning and Tracking Control. Sensors 2025, 25, 1135. [Google Scholar] [CrossRef]
- Fan, Y.; Ren, H.B.; Zhao, Y.Z. Observer design based on nonlinear suspension model with unscented Kalman filter. J. Vibroeng. 2015, 17, 3844–3855. [Google Scholar]
- Buckner, G.D.; Schuetze, K.T.; Beno, J.H. Intelligent feedback linearization for active vehicle suspension control. J. Dyn. Syst. Meas. Control 2001, 123, 727–733. [Google Scholar]
- Xie, Z.C.; You, W.; Wong, P.K.; Li, W.F.; Zhao, J. Fuzzy robust non-fragile control for nonlinear active suspension systems with time varying actuator delay. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 238, 46–62. [Google Scholar]
- Su, L.; Mao, Y.Y.; Zhang, Y. Deviation Sequence Neural Network Control for Path Tracking of Autonomous Vehicles. Actuators 2024, 13, 101. [Google Scholar] [CrossRef]
- Lin, X.Y.; Li, K.L.; Wang, L.M. A driving-style-oriented adaptive control strategy based PSO-fuzzy expert algorithm for a plug-in hybrid electric vehicle. Expert Syst. Appl. 2022, 201, 117236. [Google Scholar]
- Tian, Y.T.; Huang, K.; Cao, X.H.; Liu, Y.L.; Ji, X.W. A hierarchical adaptive control framework of path tracking and roll stability for intelligent heavy vehicle with MPC. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 2933–2946. [Google Scholar]
- Liu, H.; Kiumarsi, B.; Kartal, Y.; Koru, A.T.; Modares, H.; Lewis, F.L. Reinforcement Learning Applications in Unmanned Vehicle Control: A Comprehensive Overview. Unmanned Syst. 2023, 11, 17–26. [Google Scholar]
- Sun, X.Q.; Wu, P.C.; Cai, Y.F.; Wang, S.H.; Chen, L. Piecewise affine modeling and hybrid optimal control of intelligent vehicle longitudinal dynamics for velocity regulation. Mech. Syst. Signal Process. 2022, 162, 108089. [Google Scholar]
- Shi, P.C.; Li, L.; Yang, A.X. Intelligent Vehicle Path Tracking Control Based on Improved MPC and Hybrid PID. IEEE Access 2022, 10, 94133–94144. [Google Scholar]
- Sun, X.Q.; Zhang, H.Z.; Cai, Y.F.; Wang, S.H.; Chen, L. Hybrid modeling and predictive control of intelligent vehicle longitudinal velocity considering nonlinear tire dynamics. Nonlinear Dynam. 2019, 97, 1051–1066. [Google Scholar]
- Zhang, R.H.; Wu, N.; Wang, Z.H.; Li, K.N.; Song, Z.M.; Chang, Z.T.; Chen, X.; Yu, F. Constrained hybrid optimal model predictive control for intelligent electric vehicle adaptive cruise using energy storage management strategy. J. Energy Storage 2023, 65, 107383. [Google Scholar]
- Murphey, Y.L.; Park, J.; Chen, Z.H.; Kuang, M.L.; Masrur, M.A.; Phillips, A.M. Intelligent Hybrid Vehicle Power Control-Part I: Machine Learning of Optimal Vehicle Power. IEEE Trans. Veh. Technol. 2012, 61, 3519–3530. [Google Scholar]
- Zhang, L.A.; Wang, Y.Z.; Zhu, H.Z. Theory and Experiment of Cooperative Control at Multi-Intersections in Intelligent Connected Vehicle Environment: Review and Perspectives. Sustainability 2022, 14, 1542. [Google Scholar] [CrossRef]
- Zhang, H.; Xi, Z. New Predefined Time Sliding Mode Control Scheme for Multi-Switch Combination–Combination Synchronization of Fractional-Order Hyperchaotic Systems. Fractal Fract. 2025, 9, 147. [Google Scholar] [CrossRef]
- Nodland, D.; Zargarzadeh, H.; Jagannathan, S. Neural Network-Based Optimal Adaptive Output Feedback Control of a Helicopter UAV. IEEE Trans. Neural Networks Learn. Syst. 2013, 24, 1061–1073. [Google Scholar]
- Tang, X.Z.; Shi, L.F.; Wang, B.; Cheng, A.Q. Weight Adaptive Path Tracking Control for Autonomous Vehicles Based on PSO-BP Neural Network. Sensors 2023, 23, 412. [Google Scholar]
- Liu, B.; Wei, X.D.; Sun, C.; Wang, B.; Huo, W.W. A controllable neural network-based method for optimal energy management of fuel cell hybrid electric vehicles. Int. J. Hydrogen Energy 2024, 55, 1371–1382. [Google Scholar]
- Quintero-Manríquez, E.; Sanchez, E.N.; Antonio-Toledo, M.E.; Muñoz, F. Neural control of an induction motor with regenerative braking as electric vehicle architecture. Eng. Appl. Artif. Intell. 2021, 104, 104275. [Google Scholar]
- Lin, Y.; Tang, P.; Zhang, W.J.; Yu, Q. Artificial neural network modelling of driver handling behaviour in a driver-vehicle-environment system. Int. J. Vehicle Des. 2005, 37, 24–45. [Google Scholar]
- Chen, X.; Zhou, Y. Modelling and Analysis of Automobile Vibration System Based on Fuzzy Theory under Different Road Excitation Information. Complexity 2018, 2018, 2381568. [Google Scholar]
- Ji, G.; Zhang, L.; Shan, M.; Zhang, J. Enhanced variable universe fuzzy PID control of the active suspension based on expansion factor parameters adaption and genetic algorithm. Eng. Res. Express 2023, 5, 035007. [Google Scholar]
- Chiou, J.S.; Tsai, S.H.; Liu, M.T. A PSO-based adaptive fuzzy PID-controllers. Simul. Model. Pract. Theory 2012, 26, 49–59. [Google Scholar] [CrossRef]
- Wang, J.; Lv, K.; Wang, H.; Guo, S.; Wang, J. Research on nonlinear model and fuzzy fractional order PIλDμ control of air suspension system. J. Low Freq. Noise Vib. Act. Control 2022, 41, 712–731. [Google Scholar] [CrossRef]
- Bashir, A.O.; Rui, X.T.; Zhang, J.S. Ride Comfort Improvement of a Semi-active Vehicle Suspension Based on Hybrid Fuzzy and Fuzzy-PID Controller. Stud. Inform. Control 2019, 28, 421–430. [Google Scholar] [CrossRef]
- Shouran, M.; Alenezi, M.; Muftah, M.N.; Almarimi, A.; Abdallah, A.; Massoud, J. A Novel AVR System Utilizing Fuzzy PIDF Enriched by FOPD Controller Optimized via PSO and Sand Cat Swarm Optimization Algorithms. Energies 2025, 18, 1337. [Google Scholar] [CrossRef]
- Soukkou, A.; Soukkou, Y.; Haddad, S.; Benghanem, M.; Rabhi, A. Review, design, stabilization and synchronization of fractional-order energy resources demand-supply hyperchaotic systems using fractional-order PD-based feedback control scheme. Arch. Control Sci. 2023, 33, 539–563. [Google Scholar]
- Fu, M.W.; Shen, D.F.; Zhao, G.; Shang, G.F.; Bai, S.W.; Li, X.F.; Hao, Z.M. Integrated sliding mode intelligent fractional-order backstepping control of warp tension based on fixed-time extended state observer. Text. Res. J. 2023, 93, 3368–3381. [Google Scholar] [CrossRef]
- Muresan, C.I.; Birs, I.R.; Dulf, E.H.; Copot, D.; Miclea, L. A Review of Recent Advances in Fractional-Order Sensing and Filtering Techniques. Sensors 2021, 21, 5920. [Google Scholar] [CrossRef]
- Shao, K.; Xia, W.; Zhu, Y.; Sun, C.; Liu, Y. Research on UAV Trajectory Tracking Control System Based on Feedback Linearization Control–Fractional Order Model Predictive Control. Processes 2025, 13, 801. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, Y.Q.; Pi, Y.G. Tuning fractional order proportional integral controllers for fractional order systems. J. Process Control 2010, 20, 823–831. [Google Scholar] [CrossRef]
- Miao, Y.; Gao, Z.; Yang, C. Adaptive Fractional-order Unscented Kalman Filters for Nonlinear Fractional-order Systems. Int. J. Control Autom. 2022, 20, 283–1293. [Google Scholar] [CrossRef]
- Adhikary, A.; Sen, S.; Biswas, K. Practical Realization of Tunable Fractional Order Parallel Resonator and Fractional Order Filters. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 1142–1151. [Google Scholar] [CrossRef]
- Zhao, C.N.; Jiang, M.R.; Huang, Y.Q. Formal Verification of Fractional-Order PID Control Systems Using Higher-Order Logic. Fractal Fract. 2022, 6, 485. [Google Scholar] [CrossRef]
- Zou, Q.; Jin, Q.B.; Zhang, R.D. Design of fractional order predictive functional control for fractional industrial processes. Chemom. Intell. Lab. 2016, 152, 34–41. [Google Scholar] [CrossRef]
- Vinagre, B.M.; Petrás, I.; Podlubny, I.; Chen, Y.Q. Using fractional order adjustment rules and fractional order reference models in model-reference adaptive control. Nonlinear Dynam. 2002, 29, 269–279. [Google Scholar] [CrossRef]
- Bialic, G.; Stanislawski, R. On the Linear-Quadratic-Gaussian Control Strategy for Fractional-Order Systems. Fractal Fract. 2022, 6, 248. [Google Scholar] [CrossRef]
- Bingi, K.; Prusty, B.R.; Singh, A.P. A Review on Fractional-Order Modelling and Control of Robotic Manipulators. Fractal Fract. 2023, 7, 77. [Google Scholar] [CrossRef]
- Viola, J.; Chen, Y.Q. A Fractional-Order On-Line Self Optimizing Control Framework and a Benchmark Control System Accelerated Using Fractional-Order Stochasticity. Fractal Fract. 2022, 6, 549. [Google Scholar] [CrossRef]
- Kumar, N.; Mehra, M. Generalized fractional-order Legendre wavelet method for two dimensional distributed order fractional optimal control problem. J. Vib. Control 2024, 30, 1690–1705. [Google Scholar] [CrossRef]
- Tavakoli-Kakhki, M.; Haeri, M.; Tavazoei, M.S. Study on Control Input Energy Efficiency of Fractional Order Control Systems. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 475–482. [Google Scholar]
- Ding, Y.X.; Luo, Y.; Chen, Y.Q. Dynamic Feedforward-Based Fractional Order Impedance Control for Robot Manipulator. Fractal Fract. 2023, 7, 52. [Google Scholar] [CrossRef]
- Delavari, H.; Heydarinejad, H. Fractional-Order Backstepping Sliding-Mode Control Based on Fractional-Order Nonlinear Disturbance Observer. J. Comput. Nonlinear Dyn. 2018, 13, 111009. [Google Scholar]
- Pan, H.H.; Sun, W.C. Nonlinear Output Feedback Finite-Time Control for Vehicle Active Suspension Systems. IEEE Trans. Ind. Inform. 2019, 15, 2073–2082. [Google Scholar] [CrossRef]
- Sun, W.C.; Gao, H.J.; Kaynak, O. Vibration Isolation for Active Suspensions with Performance Constraints and Actuator Saturation. IEEE-ASME Trans. Mech. 2015, 20, 675–683. [Google Scholar]
- Wen, S.P.; Chen, M.Z.Q.; Zeng, Z.G.; Yu, X.H.; Huang, T.W. Fuzzy Control for Uncertain Vehicle Active Suspension Systems via Dynamic Sliding-Mode Approach. IEEE Trans. Syst. Man Cybern. Syst. 2018, 47, 24–32. [Google Scholar] [CrossRef]
- Jin, X.J.; Wang, J.D.; He, X.K.; Yan, Z.Y.; Xu, L.W.; Wei, C.F.; Yin, G.D. Improving Vibration Performance of Electric Vehicles Based on In-Wheel Motor-Active Suspension System via Robust Finite Frequency Control. IEEE Trans. Intell. Transp. 2023, 24, 1631–1643. [Google Scholar]
- Gu, Z.; Sun, X.; Lam, H.K.; Yue, D.; Xie, X.P. Event-Based Secure Control of T-S Fuzzy-Based 5-DOF Active Semivehicle Suspension Systems Subject to DoS Attacks. IEEE Trans. Fuzzy Syst. 2022, 30, 2032–2043. [Google Scholar] [CrossRef]
- Liu, L.; Li, X.S.; Liu, Y.J.; Tong, S.C. Neural network based adaptive event trigger control for a class of electromagnetic suspension systems. Control Eng. Pract. 2021, 106, 104675. [Google Scholar]
- Shi, Z.Q.; Cao, R.L.; Zhang, S.S.; Guo, J.; Yu, S.Y.; Chen, H. Active suspension H∞/generalized H2 static output feedback control. J. Vib. Control 2023, 30, 5183–5195. [Google Scholar]
- Zhao, Y.L.; Wang, X. A Review of Low-Frequency Active Vibration Control of Seat Suspension Systems. Appl. Sci. 2019, 9, 3326. [Google Scholar] [CrossRef]
- Go, C.G.; Sui, C.H.; Shih, M.H.; Sung, W.P. A Linearization Model for the Displacement Dependent Semi-active Hydraulic Damper. J. Vib. Control 2010, 16, 2195–2214. [Google Scholar]
- Wang, W.L.; Yu, D.S.; Xu, R. Prediction of the in-service performance of a railway hydraulic damper. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2017, 231, 19–32. [Google Scholar]
- Farjoud, A.; Ahmadian, M.; Craft, M.; Burke, W. Nonlinear modeling and experimental characterization of hydraulic dampers: Effects of shim stack and orifice parameters on damper performance. Nonlinear Dynam. 2012, 67, 1437–1456. [Google Scholar]
- Habib, G.; Detroux, T.; Viguié, R.; Kerschen, G. Nonlinear generalization of Den Hartog’s equal-peak method. Mech. Syst. Signal Process. 2015, 52–53, 17–28. [Google Scholar]
- Habib, G.; Kádár, F.; Papp, B. Impulsive vibration mitigation through a nonlinear tuned vibration absorber. Nonlinear Dynam. 2019, 98, 2115–2130. [Google Scholar]
- Gao, J.; Wu, F.Q.; Li, Z.X. Study on the Effect of Stiffness Matching of Anti-Roll Bar in Front and Rear of Vehicle on the Handling Stability. Int. J. Automot. Technol. 2021, 2, 185–199. [Google Scholar] [CrossRef]
- Nguyen, D.N.; Le, M.P.; Nguyen, T.A.; Hoang, T.B.; Tran, T.T.H.; Dang, N.D. Enhancing the Stability and Safety of Vehicle When Steering by Using the Active Stabilizer Bar. Math. Probl. Eng. 2022, 2022, 5617167. [Google Scholar]
- Adams, S.G.; Bertsch, F.M.; Shaw, K.A.; MacDonald, N.C. Independent tuning of linear and nonlinear stiffness coefficients. J. Microelectromech. Syst. 1998, 7, 172–180. [Google Scholar]
- Aghasizade, S.; Mirzaei, M.; Rafatnia, S. Novel constrained control of active suspension system integrated with anti-lock braking system based on 14-degree of freedom vehicle model. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2018, 232, 501–520. [Google Scholar] [CrossRef]
- Vaddi, P.K.R.; Kumar, C.S. A non-linear vehicle dynamics model for accurate representation of suspension kinematics. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 1002–1014. [Google Scholar]
- Hosen, M.A.; Chowdhury, M.S.H. Accurate approximations of the nonlinear vibration of couple-mass-spring systems with linear and nonlinear stiffnesses. J. Low Freq. Noise Vib. Act. Control 2021, 40, 1072–1090. [Google Scholar]
- Zhang, N.; Zhao, Q. Back-Stepping Sliding Mode Controller Design for Vehicle Seat Vibration Suppression Using Magnetorheological Damper. J. Vib. Eng. Technol. 2021, 9, 1885–1902. [Google Scholar]
- Zhang, L.X.; Zhao, C.M.; Qian, F.; Dhupia, J.S.; Wu, M.L. An Active Control with a Magnetorheological Damper for Ambient Vibration. Machines 2022, 10, 82. [Google Scholar] [CrossRef]
- Woo, S.; Shin, D. A Double Sky-Hook Algorithm for Improving Road-Holding Property in Semi-Active Suspension Systems for Application to In-Wheel Motor. Appl. Sci. 2021, 11, 8912. [Google Scholar] [CrossRef]
- Hui, Y.; Kang, H.J.; Law, S.S.; Hua, X.G. Effect of cut-off order of nonlinear stiffness on the dynamics of a sectional suspension bridge model. Eng. Struct. 2019, 185, 377–391. [Google Scholar]
- Ahamed, R.; Rashid, M.M.; Ferdaus, M.M.; Yusuf, H.B. Modelling and performance evaluation of energy harvesting linear magnetorheological (MR) damper. J. Low Freq. Noise Vib. Act. Control 2017, 36, 177–192. [Google Scholar]
- Yan, Z.Y.; Li, G.; Luo, J.; Zeng, J.S.; Zhang, W.H.; Wang, Y.Y.; Yang, W.J.; Ma, G.T. Vibration control of superconducting electro-dynamic suspension train with electromagnetic and sky-hook damping methods. Vehicle Syst. Dyn. 2022, 60, 3375–3397. [Google Scholar]
- Ning, D.H.; Sun, S.S.; Du, H.P.; Li, W.H.; Zhang, N.; Zheng, M.Y.; Luo, L. An electromagnetic variable inertance device for seat suspension vibration control. Mech. Syst. Signal Process. 2019, 133, 106259. [Google Scholar]
- Shangguan, W.B.; Shui, Y.J.; Rakheja, S. Kineto-dynamic design optimisation for vehicle-specific seat-suspension systems. Vehicle Syst. Dyn. 2017, 55, 1643–1664. [Google Scholar]
- Jeon, J.; Han, Y.M.; Lee, D.Y.; Choi, S.B. Vibration control of the engine body of a vehicle utilizing the magnetorheological roll mount and the piezostack right-hand mount. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2013, 227, 1562–1577. [Google Scholar]
- Choi, S.B.; Song, H.J.; Lee, H.H.; Lim, S.C.; Kim, J.H.; Choi, H.J. Vibration control of a passenger vehicle featuring magnetorheological engine mounts. Int. J. Veh. Des. 2003, 33, 2–16. [Google Scholar]
- Li, R.; Chen, W.M.; Liao, C.R. Hierarchical fuzzy control for engine isolation via magnetorheological fluid mounts. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2010, 224, 175–187. [Google Scholar] [CrossRef]
- Müller, P.C.; Popp, K.; Schiehlen, W.O. Berechnungsverfahren für stochastische Fahrzeugschwingungen. Arch. Appl. Mech. 1980, 49, 235–254. [Google Scholar]
- Si, Z.Y.; Bai, X.X.; Qian, L.J.; Chen, P. Principle and Control of Active Engine Mount Based on Magnetostrictive Actuator. Chin. J. Mech.-Eng. 2022, 35, 146. [Google Scholar] [CrossRef]
- Jin, Y.F.; Luo, X. Stochastic optimal active control of a half-car nonlinear suspension under random road excitation. Nonlinear Dynam. 2013, 72, 185–195. [Google Scholar] [CrossRef]
- Ren, J.P.; Zhang, H.J.; Hao, H.R.; Zhou, D.; Wang, J.W.; Zhao, W.C. Modelling and simulation of suspension system based on topological structure. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 239, 1142–1154. [Google Scholar] [CrossRef]
- Liu, Y.J.; Cui, D.W. Collaborative model analysis on ride comfort and handling stability. J. Vibroeng. 2019, 21, 1724–1737. [Google Scholar] [CrossRef]
- Yuen, K.V.; Guo, H.Z.; Mu, H.Q. Bayesian Vehicle Load Estimation, Vehicle Position Tracking, and Structural Identification for Bridges with Strain Measurement. Struct. Control Health Monit. 2023, 2023, 4752776. [Google Scholar] [CrossRef]
- Liu, D.W.; Jiang, R.C.; Wang, S.; Chen, H.M.; Yang, X. Study on Impact Characteristic of Speed Control Hump on Heavy Vehicle. J. Vib. Eng. Technol. 2015, 3, 601–614. [Google Scholar]
- Wang, X.L.; Cheng, Z.; Ma, N.L. Road Recognition Based on Vehicle Vibration Signal and Comfortable Speed Strategy Formulation Using ISA Algorithm. Sensors 2022, 22, 6682. [Google Scholar] [CrossRef]
- Ma, B.; Li, P.H.; Guo, X.; Zhao, H.X.; Chen, Y. A Novel Online Prediction Method for Vehicle Velocity and Road Gradient Based on a Flexible-Structure Auto-Regressive Integrated Moving Average Model. Sustainability 2023, 15, 15639. [Google Scholar] [CrossRef]
- Cao, Y.; Cao, J.Y.; Yu, F.; Luo, Z. A new vehicle path-following strategy of the steering driver model using general predictive control method. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 232, 4578–4587. [Google Scholar] [CrossRef]
- Attia, T.; Vamvoudakis, K.G.; Kochersberger, K.; Bird, J.; Furukawa, T. Simultaneous dynamic system estimation and optimal control of vehicle active suspension. Vehicle Syst. Dyn. 2019, 57, 1467–1493. [Google Scholar]
- Li, W.; Liang, H.J.; Xia, D.B.; Fu, J.; Yu, M. Explicit model predictive control of magnetorheological suspension for all-terrain vehicles with road preview. Smart Mater. Struct. 2024, 33, 035037. [Google Scholar]
- Ammanagi, S.; Manohar, C.S. Optimal cross-spectrum of road loads on vehicles: Theory and experiments. J. Vib. Control 2016, 22, 4012–4024. [Google Scholar] [CrossRef]
- Bogsjö, K. Coherence of road roughness in left and right wheel-path. Veh. Syst. Dyn. 2008, 46, 599–609. [Google Scholar]
- Colombaroni, C.; Fusco, G.; Isaenko, N. Coherence analysis of road safe speed and driving behaviour from floating car data. IET Intell. Transp. Syst. 2020, 14, 985–992. [Google Scholar]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Duarte-Mermoud, M.A.; Aguila-Camacho, N.; Gallegos, J.A.; Castro-Linares, R. Using general quadratic Lyapunov functions to prove Lyapunov uniform stability for fractional order systems. Commun. Nonlinear Sci. 2015, 22, 650–659. [Google Scholar] [CrossRef]
- Rakkiyappan, R.; Cao, J.D.; Velmurugan, G. Existence and Uniform Stability Analysis of Fractional-Order Complex-Valued Neural Networks With Time Delays. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 84–97. [Google Scholar]
- Yang, Q.; Chen, D.L.; Zhao, T.B.; Chen, Y.Q. Fractional calculus in image processing: A review. Fract. Calc. Appl. Anal. 2016, 19, 1222–1249. [Google Scholar]
- Zhou, P.; Ma, J.; Tang, J. Clarify the physical process for fractional dynamical systems. Nonlinear Dynam. 2020, 100, 2353–2364. [Google Scholar] [CrossRef]
- Bingul, Z.; Gul, K. Intelligent-PID with PD Feedforward Trajectory Tracking Control of an Autonomous Underwater Vehicle. Machines 2023, 11, 300. [Google Scholar] [CrossRef]
- Jamil, A.A.; Tu, W.F.; Ali, S.W.; Terriche, Y.; Guerrero, J.M. Fractional-Order PID Controllers for Temperature Control: A Review. Energies 2022, 15, 3800. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problem. Expert Syst. Appl. 2021, 15, 113917. [Google Scholar]
- Tepljakov, A.; Petlenkov, E.; Belikov, J. FOMCON: A MATLAB toolbox for fractional-order system identification and control. Int. J. Microelectron. Comput. Sci. 2011, 2, 51–62. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2013, 69, 46–61. [Google Scholar] [CrossRef]
- Gupta, S.; Deep, K. A novel random walk grey wolf optimizer. Swarm Evol. Comput. 2019, 44, 101–112. [Google Scholar] [CrossRef]
- Lu, C.; Gao, L.; Yi, J. Grey wolf optimizer with cellular topological structure. Expert Syst. Appl. 2018, 107, 89–114. [Google Scholar]
- Ma, C.; Huang, H.; Fan, Q.; Wei, J.; Du, Y.; Gao, W. Grey wolf optimizer based on Aquila exploration method. Expert Syst. Appl. 2022, 205, 117629. [Google Scholar] [CrossRef]
- Meidani, K.; Hemmasian, A.; Mirjalili, S.; Barati Farimani, A. Adaptive grey wolf optimizer. Neural Comput. Appl. 2022, 34, 7711–7731. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.Z.; Mirjalili, S.M. Evolutionary population dynamics and grey wolf optimizer. Neural Comput. Appl. 2015, 26, 1257–1263. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S.; Zamani, H.; Bahreininejad, A. GGWO: Gaze cues learning-based grey wolf optimizer and its applications for solving engineering problems. J. Comput. Sci. 2022, 61, 101636. [Google Scholar] [CrossRef]
- Dridi, I.; Hamza, A.; Ben Yahia, N. Control of an active suspension system based on long short-term memory (LSTM) learning. Adv. Mech. Eng. 2023, 15, 16878132231156789. [Google Scholar] [CrossRef]
- Nagarkar, M.; Bhalerao, Y.; Bhaskar, D.; Thakur, A.; Hase, V.; Zaware, R. Design of passive suspension system to mimic fuzzy logic control active suspension system. Beni-Suef Univ. J. Basic Appl. Sci. 2022, 11, 109. [Google Scholar] [CrossRef]
- Mrazgua, J.; Chaibi, R.; Tissir, E.; Ouahi, M. Static output feedback stabilization of T-S fuzzy active suspension systems. J. Terramechan. 2021, 97, 19–27. [Google Scholar] [CrossRef]
- Yin, Z.; Su, R.; Ma, X. Dynamic Responses of 8-DoF Vehicle with Active Suspension: Fuzzy-PID Control. World Electr. Veh. J. 2023, 14, 249. [Google Scholar] [CrossRef]
- Lee, G.W.; Hyun, M.; Kang, D.O.; Heo, S.J. High-efficiency Active Suspension based on Continuous Damping Control. Int. J. Automot. Technol. 2022, 23, 31–40. [Google Scholar] [CrossRef]
- Shen, Y.J.; Chen, A.; Du, F.; Yang, X.F.; Liu, Y.L.; Chen, L. Performance enhancements of semi-active vehicle air ISD suspension. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024. [Google Scholar] [CrossRef]
- Nagarkar, M.P.; El-Gohary, M.A.; Bhalerao, Y.J.; Patil, G.J.V.; Patil, R.N.Z. Artificial neural network predication and validation of optimum suspension parameters of a passive suspension system. SN Appl. Sci. 2019, 1, 569. [Google Scholar] [CrossRef]
- Wei, W.; Yu, S.J.; Li, B.Z. Research on Magnetic Characteristics and Fuzzy PID Control of Electromagnetic Suspension. Actuators 2023, 12, 203. [Google Scholar] [CrossRef]
- Shen, Y.J.; Hua, J.; Wu, B.; Chen, Z.; Xiong, X.X.; Chen, L. Optimal design of the vehicle mechatronic ISD suspension system using the structure-immittance approach. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 512–521. [Google Scholar]
- Anandan, A.; Kandavel, A. Investigation and performance comparison of ride comfort on the created human vehicle road integrated model adopting genetic algorithm optimized proportional integral derivative control technique. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2020, 234, 288–305. [Google Scholar]
- Theunissen, J.; Sorniotti, A.; Gruber, P.; Fallah, S.; Ricco, M.; Kvasnica, M.; Dhaens, M. Regionless Explicit Model Predictive Control of Active Suspension Systems with Preview. IEEE Trans. Ind. Electron. 2020, 67, 4877–4888. [Google Scholar]
- Yang, D.D.; Yang, X.F.; Shen, Y.J.; Liu, Y.L.; Bi, S.L.; Liu, X.F. Analysis of ride comfort and road friendliness of heavy vehicle inertial suspension based on the ground-hook control strategy. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 238, 1380–1391. [Google Scholar]
- Zhang, T.Y.; Yang, X.F.; Shen, Y.J.; Liu, X.F.; He, T. Performance Enhancement of Vehicle Mechatronic Inertial Suspension, Employing a Bridge Electrical Network. World Electr. Veh. J. 2022, 13, 12. [Google Scholar] [CrossRef]
- Zeng, Y.H.; Liu, S.J.; E, J.Q. Neuron PI control for semi-active suspension system of tracked vehicle. J. Central South Univ. 2011, 18, 444–450. [Google Scholar]
- Jiang, X.H.; Cheng, T.H. Design of a BP neural network PID controller for an air suspension system by considering the stiffness of rubber bellows. Alex. Eng. J. 2023, 4, 65–78. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, Z.X.; Yu, W.H.; Yu, Y. Cooperative Control of Interconnected Air Suspension Based on Model Predictive Control. Appl. Sci. 2022, 12, 9886. [Google Scholar] [CrossRef]
- Wang, J.S.; Shen, Y.J.; Du, F.; Li, M.; Yang, X.F. Topology Optimization Design and Dynamic Performance Analysis of Inerter-Spring-Damper Suspension Based on Power-Driven-Damper Control Strategy. World Electr. Veh. J. 2024, 15, 8. [Google Scholar] [CrossRef]
- Fossati, G.G.; Miguel, L.F.F.; Casas, W.J.P. Multi-objective optimization of the suspension system parameters of a full vehicle model. Optim. Eng. 2019, 20, 151–177. [Google Scholar] [CrossRef]
- Liu, Y.L.; Shi, D.Y.; Yang, X.F.; Song, H.; Shen, Y.J. The Adverse Effect and Control of Semi-active Inertial Suspension of Hub Motor Driven Vehicles. Int. J. Automot. Technol. 2024, 25, 777–788. [Google Scholar]
- Xu, S.P.; Nguyen, V.; Li, S.M.; Ni, D.K. Performance of the Machine Learning on Controlling the Pneumatic Suspension of Automobiles on the Rigid and Off- Road Surfaces. SAE Int. J. Passeng. Veh. Syst. 2022, 15, 169–182. [Google Scholar]
- Xu, H.; Zhao, Y.Q.; Ye, C.; Lin, F. Integrated optimization for mechanical elastic wheel and suspension based on an improved artificial fish swarm algorithm. Adv. Eng. Softw. 2019, 137, 102722. [Google Scholar]
- Esmaeili, J.S.; Akbari, A.; Farnam, A.; Azad, N.L.; Crevecoeur, G. Adaptive Neuro-Fuzzy Control of Active Vehicle Suspension Based on H2 and H∞ Synthesis. Machines 2023, 11, 1022. [Google Scholar]
- Yang, X.F.; He, T.; Shen, Y.J.; Liu, Y.L.; Yan, L. Research on predictive coordinated control of ride comfort and road friendliness for heavy vehicle ISD suspension based on the hybrid-hook damping strategy. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 238, 443–456. [Google Scholar]
- Ho, C.M.; Tran, D.T.; Ahn, K.K. Adaptive sliding mode control based nonlinear disturbance observer for active suspension with pneumatic spring. J. Sound Vib. 2021, 509, 116241. [Google Scholar]
- Ning, D.H.; Sun, S.S.; Zhang, F.; Du, H.P.; Li, W.H.; Zhang, B.J. Disturbance observer based Takagi-Sugeno fuzzy control for an active seat suspension. Mech. Syst. Signal Process. 2017, 93, 515–530. [Google Scholar]
- Li, Y.; Yang, X.F.; Shen, Y.J.; Liu, Y.L.; Wang, W. Optimal design and dynamic control of the HMDV inertial suspension based on the ground-hook positive real network. Adv. Eng. Softw. 2022, 171, 103171. [Google Scholar]
- Xu, J.A.; Kou, F.R.; Zhang, X.Q.; Chen, C. Multi-mode switching control of electromagnetic hybrid suspension based on human subjective sensation. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 238, 3092–3108. [Google Scholar]
- Liu, W.; Wang, R.C.; Rakheja, S.; Ding, R.K.; Meng, X.P.; Sun, D. Vibration analysis and adaptive model predictive control of active suspension for vehicles equipped with non-pneumatic wheels. J. Vib. Control 2023, 30, 3207–3219. [Google Scholar]
- Wang, B.; Zheng, M.Y.; Zhang, N.; Zhong, W.M.; Yang, S.C. Dynamic Characteristics Analysis of a Novel Displacement-Sensitive Anti-pitch Hydraulically Interconnected Suspension and the Corresponding Full Car. J. Vib. Eng. Technol. 2023, 12, 2759–2774. [Google Scholar]
- Ghorbany, M.; Ebrahimi-Nejad, S.; Mollajafari, M. Global-guidance chaotic multi-objective particle swarm optimization method for pneumatic suspension handling and ride quality enhancement on the basis of a thermodynamic model of a full vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 237, 3334–3352. [Google Scholar]
- Zhang, Y.Y.; Ren, C.L.; Meng, H.D.; Wang, Y. Dynamic Characteristic Analysis of a Half-Vehicle Seat System Integrated with Nonlinear Energy Sink Inerters (NESIs). Appl. Sci. 2023, 13, 12468. [Google Scholar] [CrossRef]
- Alfadhli, A.; Darling, J.; Hillis, A.J. An Active Seat Controller with Vehicle Suspension Feedforward and Feedback States: An Experimental Study. Appl. Sci. 2018, 8, 603. [Google Scholar] [CrossRef]
- Wu, L.P.; Zhou, R.; Bao, J.S.; Yang, G.; Sun, F.; Xu, F.C.; Jin, J.J.; Zhang, Q.; Jiang, W.K.; Zhang, X.Y. Vehicle Stability Analysis under Extreme Operating Conditions Based on LQR Control. Sensors 2022, 22, 9791. [Google Scholar] [CrossRef]
- Zhu, Z.T.; Ge, X.F. Vertical Negative Effect Suppression of In-Wheel Electric Vehicle Based on Hybrid Variable-Universe Fuzzy Control. J. Circuit Syst. Comput. 2022, 31, 15. [Google Scholar]
- Cao, K.; Li, Z.Q.; Gu, Y.L.; Zhang, L.Y.; Chen, L.Q. The control design of transverse interconnected electronic control air suspension based on seeker optimization algorithm. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 2200–2211. [Google Scholar]
- Basargan, H.; Mihály, A.; Gáspár, P.; Sename, O. Adaptive Semi-Active Suspension and Cruise Control through LPV Technique. Appl. Sci. 2021, 11, 290. [Google Scholar]
- Ceballos Benavides, G.E.; Duarte-Mermoud, M.A.; Martell, L.B. Control Error Convergence Using Lyapunov Direct Method Approach for Mixed Fractional Order Model Reference Adaptive Control. Fractal Fract. 2025, 9, 98. [Google Scholar] [CrossRef]
- Ali, D.; Frimpong, S. Artificial intelligence models for predicting the performance of hydro pneumatic suspension struts in large capacity dump trucks. Int. J. Ind. Ergonom. 2018, 67, 283–295. [Google Scholar]
- Gudarzi, M.; Oveisi, A. Robust Control for Ride Comfort Improvement of an Active Suspension System Considering Uncertain Driver’s Biodynamics. J. Low Freq. Noise Vib. Act. Control 2014, 33, 317–339. [Google Scholar] [CrossRef]
- Wu, H.C.; Yang, T.S.; Xiao, W.H.; Wang, X.L.; Wang, W.Y. Online active vibration control for the magnetic suspension rotor using least mean square and polynomial fitting. Nonlinear Dynam. 2024, 112, 7029–7041. [Google Scholar] [CrossRef]
- Song, H.X.; Dong, M.M.; Wang, X. Research on Inertial Force Attenuation Structure and Semi-Active Control of Regenerative Suspension. Appl. Sci. 2024, 14, 2314. [Google Scholar] [CrossRef]
- Li, G.; Ruan, Z.Y.; Gu, R.H.; Hu, G.L. Fuzzy Sliding Mode Control of Vehicle Magnetorheological Semi-Active Air Suspension. Appl. Sci. 2021, 11, 10925. [Google Scholar] [CrossRef]
- Tran, G.Q.B.; Pham, T.P.; Sename, O.; Costa, E.; Gaspar, P. Integrated Comfort-Adaptive Cruise and Semi-Active Suspension Control for an Autonomous Vehicle: An LPV Approach. Electronics 2021, 10, 813. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.; Jeong, H. Key Parameters for Economic Valuation of V2G Applied to Ancillary Service: Data-Driven Approach. Energies 2022, 15, 8815. [Google Scholar] [CrossRef]
- Suganthi, K.; Kumar, M.A.; Harish, N.; HariKrishnan, S.; Rajesh, G.; Reka, S.S. Advanced Driver Assistance System Based on IoT V2V and V2I for Vision Enabled Lane Changing with Futuristic Drivability. Sensors 2023, 23, 3423. [Google Scholar] [CrossRef]
- Zheng, X.Y.; Zhang, H.; Yan, H.C.; Yang, F.W.; Wang, Z.P.; Vlacic, L. Active Full-Vehicle Suspension Control via Cloud-Aided Adaptive Backstepping Approach. IEEE Trans. Cybern. 2020, 50, 3113–3124. [Google Scholar] [CrossRef]
- Elmarakbi, A.; Elkady, M.; El-Hage, H. Development of a new crash/dynamics control integrated mathematical model for crashworthiness enhancement of vehicle structures. Int. J. Crashworthiness 2013, 18, 444–458. [Google Scholar] [CrossRef]
- Li, S.S.; Yuan, Q. Optimization of automotive suspension system using vibration and noise control for intelligent transportation system. Soft Comput. 2023, 27, 8315–8329. [Google Scholar] [CrossRef]
- Yang, X.; Sun, R.; Yang, Y.; Liu, Y.; Hong, J.; Liu, C. Enhanced Seat Suspension Performance Through Positive Real Network Optimization and Skyhook Inertial Control. Machines 2025, 13, 222. [Google Scholar] [CrossRef]
- Fan, X.B.; Chen, M.X.; Huang, Z.P.; Yu, X.L. A review of integrated control technologies for four in-wheel motor drive electric vehicle chassis. J. Braz. Soc. Mech. Sci. 2025, 47, 89. [Google Scholar]
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| mu1 | 50 kg | ku1 | 217,751 N/m |
| mu2 | 50 kg | ku2 | 217,751 N/m |
| mu3 | 68 kg | ku3 | 217,751 N/m |
| mu4 | 68 kg | ku4 | 217,751 N/m |
| l1 | 1.55 m | lf | 0.30 m |
| l2 | 1.45 m | lr | 0.15 m |
| l3 | 0.75 m | l0 | 0.58 m |
| l4 | 0.75 m | kαf | 29.4 N·m/° |
| εu | 0.1 | kαr | 12.8 N·m/° |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Cfb | 1290 N·s/m | βfb | 0.3 |
| ηkb | 1.4 | vkb | 0.3 m/s |
| ηbb | 1.6 | vbb | −0.3 m/s |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| mb | 1350 kg | l11 | 0.05 m |
| Jβ | 5368 kg∙m2 | l12 | 0.15 m |
| Jγ | 529 kg∙m2 | l13 | 0.27 m |
| l5 | 0.15 m | l14 | 0.10 m |
| l6 | 0.53 m | kt1 | 24,606 N/m |
| l7 | 0.35 m | kt2 | 24,606 N/m |
| l8 | 0.35 m | kt3 | 26,115 N/m |
| l9 | 0.50 m | kt4 | 26,115 N/m |
| l10 | 0.50 m | εt | 0.12 |
| ks1 | 22,000 N/m | ks2 | 22,000 N/m |
| ks3 | 17,000 N/m | ks4 | 17,000 N/m |
| εs | 0.11 | km3 | 250,000 N/m |
| km1 | 250,000 N/m | εm | 0.1 |
| km2 | 250,000 N/m |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| kd,2 | −68.2 N/m | fy,2 | −51.7 N |
| kd,1 | −1156.5 N/m | fy,2 | 439.7 N |
| kd,0 | 10,236.7 N/m | fy,2 | 134.8 N |
| cpo,2 | 162.1 N·s/m | λ2,2 | −11.6907 s/m |
| cpo,1 | 711.0 N·s/m | λ2,1 | 11.1987 s/m |
| cpo,0 | 871.9 N·s/m | λ2,0 | 137.7681 s/m |
| mf,2 | −0.207,1 kg | f0 | 80.0 N |
| mf,1 | 0.4785 kg | λ1 | 0.000016 s/m |
| mf,0 | 0.6638 kg |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| ms1 | 80 kg | ms2 | 80 kg |
| ms3 | 85 kg | ms4 | 85 kg |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| me | 230 kg | θσ | 6.54 kg∙m2 |
| θω | 11.84 kg∙m2 | h1 | 0.48 m |
| h2 | 0.45 m | h3 | 0.15 m |
| h4 | 0.06 m | h5 | 0.04 m |
| h6 | 0.35 m |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| mc | 0.82 kg | L | 0.015 m |
| λ | 0.33 | r | 0.06 m |
| Category | Gq(n0)/(10−6 m3) (n0 = 0.1 m−1) | σq/(10−3 m) |
|---|---|---|
| A | 16 | 3.81 |
| B | 64 | 7.61 |
| C | 256 | 15.23 |
| D | 1024 | 30.45 |
| E | 4096 | 60.90 |
| F | 16384 | 121.89 |
| G | 65536 | 243.61 |
| H | 262144 | 487.22 |
| Engine Mountings | Seats | Actuators | ||||||
|---|---|---|---|---|---|---|---|---|
| PID | I | F | PID | I | F | PID | I | F |
| kp1 | 0.0001 | 0.0198 | kp2 | 0.5066 | 1.3749 | kp3 | 3269.5862 | 238.4866 |
| ki1 | 1.1224 | 0.1334 | k2 | 2.4706 | 0.0123 | ki3 | 3.1035 | 4613.0458 |
| kd1 | 0.0020 | 0.0003 | kd2 | 0.0047 | 0.4002 | kd3 | 0.0976 | 2.8533 |
| λ1 | / | 0.9837 | λ2 | / | 0.2986 | λ3 | / | 0.0458 |
| μ1 | / | 0.0126 | μ2 | / | 0.6701 | μ3 | / | 0.0628 |
| PID | ut1 | ut2 | ut3 | ut4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | RMS | 0.0059 | 0.0035 | 0.0036 | 0.0151 | 0.0105 | 0.0146 | 0.0105 | 133.9700 | 144.8095 | 128.7949 | 146.7290 |
| AVE | 0.0033 | 0.0018 | 0.0018 | 0.0085 | 0.0057 | 0.0057 | 0.0055 | 9.8852 | 9.8852 | 7.4277 | 7.42767 | |
| F | RMS | 0.0009 | 0.0005 | 0.0005 | 0.0482 | 0.0484 | 0.0488 | 0.0498 | 163.2996 | 180.5513 | 156.2748 | 185.4619 |
| AVE | 0.0005 | 0.0002 | 0.0003 | 0.0235 | 0.0259 | 0.0242 | 0.0262 | 11.76018 | −5.0096 | 8.3197 | −8.4500 | |
| Road Types | − lg(RMS(Yi)) | |||||||||
| RMS(Y1) | RMS(Y2) | RMS(Y3) | RMS(Y4) | RMS(Y5) | RMS(Y6) | RMS(Y7) | RMS(Y8) | RMS(Y9) | ||
| A | P | 2.6965 | 2.9008 | 2.6405 | 0.4514 | 0.4687 | 0.4656 | 0.4693 | 0.4553 | 0.8725 |
| I | 2.6973 | 2.9026 | 2.6408 | 0.6403 | 0.7358 | 0.6895 | 0.7680 | 0.5948 | 0.9109 | |
| F | 2.6964 | 2.9017 | 2.6405 | 0.6546 | 0.7559 | 0.7074 | 0.7921 | 0.6030 | 0.9112 | |
| B | P | 2.6938 | 2.8937 | 2.6398 | 0.1866 | 0.1751 | 0.1805 | 0.1624 | 0.2271 | 0.6986 |
| I | 2.6964 | 2.9004 | 2.6401 | 0.4560 | 0.5041 | 0.4680 | 0.5100 | 0.4784 | 0.7461 | |
| F | 2.6963 | 2.9003 | 2.6402 | 0.4805 | 0.5334 | 0.4944 | 0.5296 | 0.4995 | 0.7462 | |
| C | P | 2.6821 | 2.8665 | 2.6370 | −0.1211 | −0.1453 | −0.1383 | −0.1667 | −0.5545 | 0.4454 |
| I | 2.6929 | 2.8913 | 2.6380 | 0.2043 | 0.2303 | 0.2006 | 0.2155 | 0.2694 | 0.5074 | |
| F | 2.6927 | 2.8912 | 2.6378 | 0.2360 | 0.2655 | 0.2314 | 0.2485 | 0.3037 | 0.5076 | |
| D | P | 2.6440 | 2.7822 | 2.6268 | −0.4488 | −0.4741 | −0.4714 | −0.5002 | −0.3563 | 0.1561 |
| I | 2.6797 | 2.8601 | 2.6305 | −0.0718 | −0.0536 | −0.0753 | −0.0647 | −0.0031 | 0.2295 | |
| F | 2.6807 | 2.8629 | 2.6306 | −0.0347 | −0.0169 | −0.0422 | −0.0301 | 0.0375 | 0.2296 | |
| E | P | 2.5292 | 2.5894 | 2.5783 | −0.7719 | −0.7964 | −0.7972 | −0.8251 | −0.6648 | −0.1490 |
| I | 2.6317 | 2.7563 | 2.5955 | −0.3597 | −0.3432 | −0.3593 | −0.3487 | −0.2995 | −0.0677 | |
| F | 2.6351 | 2.7607 | 2.5911 | −0.3194 | −0.2998 | −0.3156 | −0.3049 | −0.2579 | −0.0681 | |
| Road Types | − lg(RMS(Yi)) | |||||||||
| RMS(Y10) | RMS(Y11) | RMS(Y12) | RMS(Y13) | RMS(Y14) | RMS(Y15) | RMS(Y16) | RMS(Y17) | RMS(Y18) | ||
| A | P | 0.2128 | 2.1047 | 2.1373 | 2.2162 | 2.1976 | 2.6890 | 2.6950 | 2.6949 | 2.6921 |
| I | 0.3398 | 2.2291 | 2.3219 | 2.3967 | 2.4293 | 2.7150 | 2.7255 | 2.7067 | 2.7099 | |
| F | 0.3446 | 2.3335 | 2.3239 | 2.3898 | 2.4205 | 2.7176 | 2.7283 | 2.7058 | 2.7092 | |
| B | P | 0.0237 | 1.8416 | 1.8458 | 1.9006 | 1.8787 | 2.3777 | 2.3819 | 2.3786 | 2.3787 |
| I | 0.2000 | 1.9828 | 2.0330 | 2.0828 | 2.1181 | 2.4053 | 2.4136 | 2.3908 | 2.3981 | |
| F | 0.2088 | 1.9861 | 2.0336 | 2.0766 | 2.1103 | 2.4090 | 2.4172 | 2.3902 | 2.3976 | |
| C | P | −0.3141 | 1.5464 | −0.3141 | 1.5465 | 1.5371 | 2.0679 | 2.0622 | 2.0574 | 2.0588 |
| I | −0.0290 | 1.7034 | 1.7337 | 1.7720 | 1.7970 | 2.0863 | 2.0945 | 2.0698 | 2.0788 | |
| F | −0.0093 | 1.7068 | 1.7344 | 1.7666 | 1.7905 | 2.0907 | 2.0985 | 2.0696 | 2.0786 | |
| D | P | −0.6168 | 1.2431 | 1.2280 | 1.2689 | 1.2396 | 1.7436 | 1.7480 | 1.7423 | 1.7444 |
| I | −0.3048 | 1.4111 | 1.4326 | 1.4657 | 1.4838 | 1.7724 | 1.7808 | 1.7549 | 1.7646 | |
| F | −0.2816 | 1.4146 | 1.4336 | 1.4606 | 1.4781 | 1.7766 | 1.7849 | 1.7549 | 1.7647 | |
| E | P | −0.9231 | 0.9382 | 0.9210 | 0.9566 | 0.9264 | 1.4349 | 1.4394 | 1.4331 | 1.4353 |
| I | −0.3018 | −0.1141 | 1.1316 | 1.1629 | 1.1765 | 1.4643 | 1.4727 | 1.4460 | 1.4559 | |
| F | −0.5772 | 1.1176 | 1.1328 | 1.1573 | 1.1712 | 1.4687 | 1.4768. | 1.4461 | 1.4561 | |
| Optimization | RMS(Y1) | RMS(Y2) | RMS(Y3) | RMS(Y4) | RMS(Y5) | RMS(Y6) | RMS(Y7) | RMS(Y8) | RMS(Y9) | |
| Ratio (%) | I/P | 0.3 | 0.65 | 1.5 | 35.0 | 46.0 | 40.0 | 50.0 | 27.0 | 8.0 |
| F/P | 0.2 | 0.6 | 0.5 | 36.0 | 48.0 | 42.0 | 52.0 | 30.0 | 9.0 | |
| F/I | −0.03 | 0.1 | −0.03 | 3 | 4.0 | 4.0 | 5.0 | 1.0 | 1.0 | |
| Optimization | RMS(Y10) | RMS(Y11) | RMS(Y12) | RMS(Y13) | RMS(Y14) | RMS(Y15) | RMS(Y16) | RMS(Y17) | RMS(Y18) | |
| Ratio (%) | I/P | 25.0 | 25.0 | 34.0 | 33.2 | 40.0 | 5.0 | 5.0 | 32.0 | 4.5 |
| F/P | 75.0 | 26.0 | 35.0 | 33.6 | 41.0 | 6.0 | 6.0 | 30.0 | 4.4 | |
| F/I | 67.0 | 2.0 | 2.0 | 1.3 | 0.9 | 1.0 | 1.0 | −0.3 | −0.3 | |
| Studies | Control Algorithm | Optimization Amplitude (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| RMS(Y1–3) | RMS(Y4–7) | RMS(Y8) | RMS(Y9) | RMS(Y10) | RMS(Y11–14) | RMS(Y15–18) | ||
| Present | PIλDμ | 0.3% | 46% | 30% | 9% | 75% | 34% | 2.5% |
| Dridi et al. [123] | LSTM | / | / | 27.9% | / | / | / | / |
| Nagarkar et al. [124] | FLC | / | / | 46.0% | / | / | 3.6% | 18.7% |
| Mrazgua et al. [125] FLC | T-S fuzzy | / | / | 57.16% | / | / | / | / |
| Yin et al. [126] | fuzzy PID | / | 21.17% | 22.00% | 21.37% | 24.17% | 15% | 10% |
| Lee et al. [127] | CDC | / | / | 14.53% | / | / | / | / |
| Shen et al. [128] | sky-hook | / | / | 12.8% | / | / | 37.3% | 8.9% |
| Nagarkar et al. [129] | NSGA-II algorithm | / | / | 47% | / | / | 9.2% | 35.8% |
| Wei et al. [130] | fuzzy PID | / | / | 59.08% | 3.06% | 3.54% | 11.98% | 2.09% |
| Shen et al. [131] | tructure-immittance approach | / | / | 18% | 15% | / | / | / |
| Anandan et al. [132] | PID | / | 21% | 35% | 33% | / | 18% | / |
| Theunissen et al. [133] | e-MPC | / | / | 10% | 8–21% | 8–21% | / | / |
| Yang et al. [134] | ground-hook | / | / | 4.87% | / | / | / | 16.19% |
| Zhang et al. [135] | bridge network | / | / | 1.8% | / | / | 21.1% | 6.3% |
| Zeng et al. [136] | Neuron PI | / | / | 37.2% | 45.2% | 38.6% | / | / |
| Jiang et al. [137] | BP-PID | / | / | 27.58% | / | / | 4.48% | 4.17% |
| Zhou et al. [138] | MPC | / | / | 22.38% | / | / | / | / |
| Wang et al. [139] | pigeon-inspired optimization | / | / | 23.1 | / | / | 6.6% | / |
| Fossati et al. [140] | NSGA-II | / | 21.14% | / | / | / | / | / |
| Liu et al. [141] | SH-GH | / | / | 27.45% | / | / | / | 8.53% |
| Xu et al. [142] | fuzzy | / | / | 14.6% | 9.6% | 5.3% | / | / |
| Xu et al. [143] | multi-objective optimization | / | / | 43.88% | / | / | 24.38% | 46.46% |
| Esmaeili et al. [144] | ANFIS | / | / | 62% | / | / | 5.83% | 56.8% |
| Yang et al. [145] | hybrid-hook damping | 26.61% | -6.94% | 22.03% | ||||
| Ho et al. [146] | SMC-NDOB | / | 41.5% | / | / | / | / | / |
| Ning et al. [147] | T-S fuzzy | / | 45.5% | / | / | / | / | / |
| Li et al. [148] | model reference adaptive | / | / | 8.70% | / | / | 28.26% | 18.21% |
| Xu et al. [149] | LQG | / | / | 27.5% | / | / | 6.3% | 17.6% |
| Liu et al. [150] | MPC-H∞ | / | / | 19.4% | / | / | / | 9.3% |
| Wang et al. [151] | DSHIS | / | / | 48.17% | 56% | / | 17.39% | 4.35% |
| Ghorbany et al. [152] | MOPSO | / | / | 71% | 57% | 33% | / | / |
| Zhang et al. [153] | NESI | / | 23.59% | 23.97% | 27.48% | / | / | / |
| Alfadhli et al. [154] | feedforward and feedback | / | 25% | / | / | / | / | / |
| Wu et al. [155] | LQR | / | / | 58.25% | 55.41% | 31.39% | / | / |
| Zhu et al. [156] | VUFC | / | / | 21.0% | / | / | / | / |
| Cao et al. [157] | SOA-PID | / | / | 27.6% | 27.0% | 35.8% | / | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Z.; Cui, C.; Wang, R.; Su, R.; Ma, X. Improving Vehicle Dynamics: A Fractional-Order PIλDμ Control Approach to Active Suspension Systems. Machines 2025, 13, 271. https://doi.org/10.3390/machines13040271
Yin Z, Cui C, Wang R, Su R, Ma X. Improving Vehicle Dynamics: A Fractional-Order PIλDμ Control Approach to Active Suspension Systems. Machines. 2025; 13(4):271. https://doi.org/10.3390/machines13040271
Chicago/Turabian StyleYin, Zongjun, Chenyang Cui, Ru Wang, Rong Su, and Xuegang Ma. 2025. "Improving Vehicle Dynamics: A Fractional-Order PIλDμ Control Approach to Active Suspension Systems" Machines 13, no. 4: 271. https://doi.org/10.3390/machines13040271
APA StyleYin, Z., Cui, C., Wang, R., Su, R., & Ma, X. (2025). Improving Vehicle Dynamics: A Fractional-Order PIλDμ Control Approach to Active Suspension Systems. Machines, 13(4), 271. https://doi.org/10.3390/machines13040271






