Research on the Conditions and Optimization of 3-UPU Parallel Manipulators That Naturally Realize Three Translational Degrees of Freedom
Abstract
1. Introduction
2. The Conditions of 3-UPU PMs Naturally Realize Pure Three Translational DOFs
2.1. The Problem in Tsai 3-UPU PM
2.2. Geometrical Conditions for 3-UPU PM Naturally Realize Pure 3-Translational DOFs
3. Optimization Design of the 3-DOF Translational 3-UPU PMs Based on Motion/Force Transmission Index
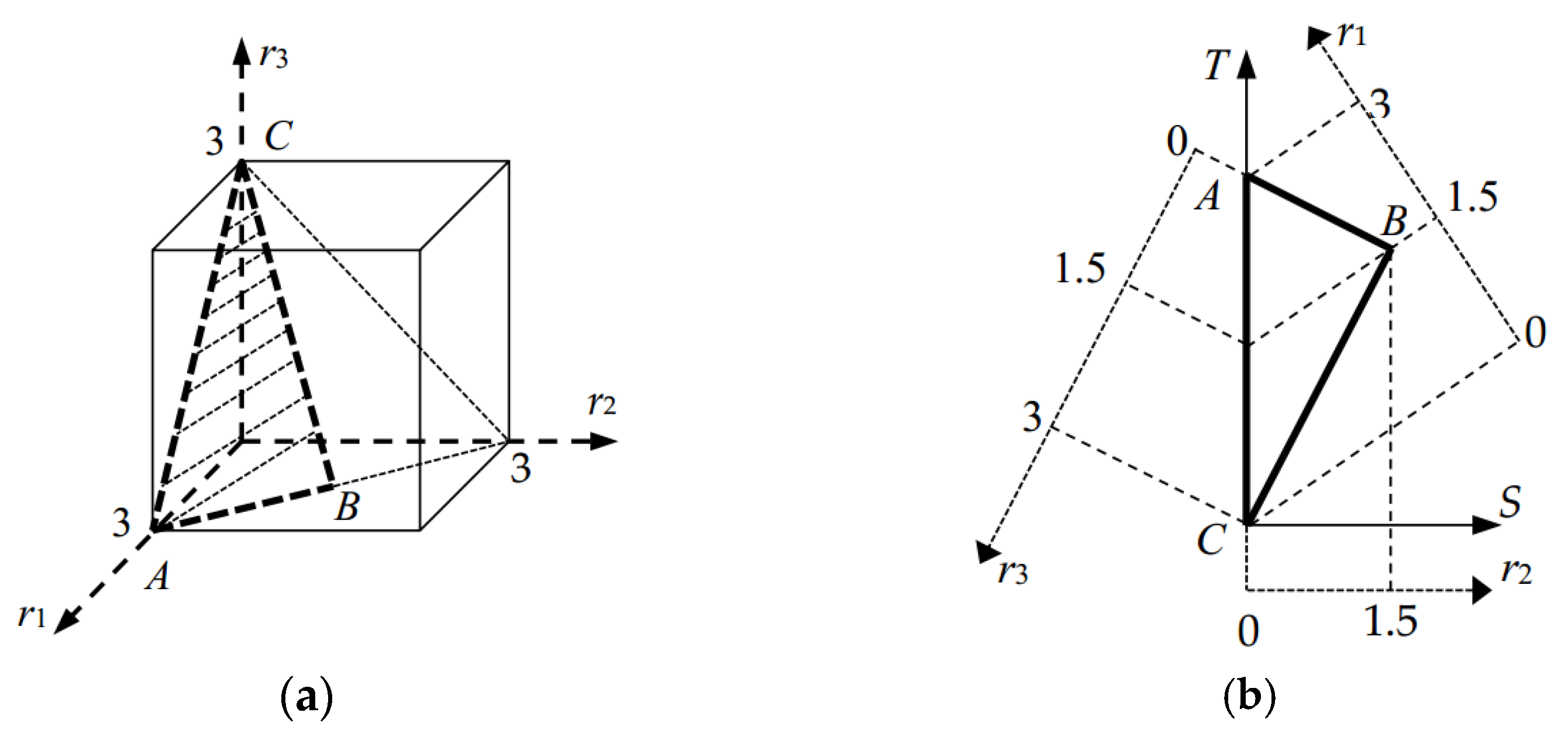
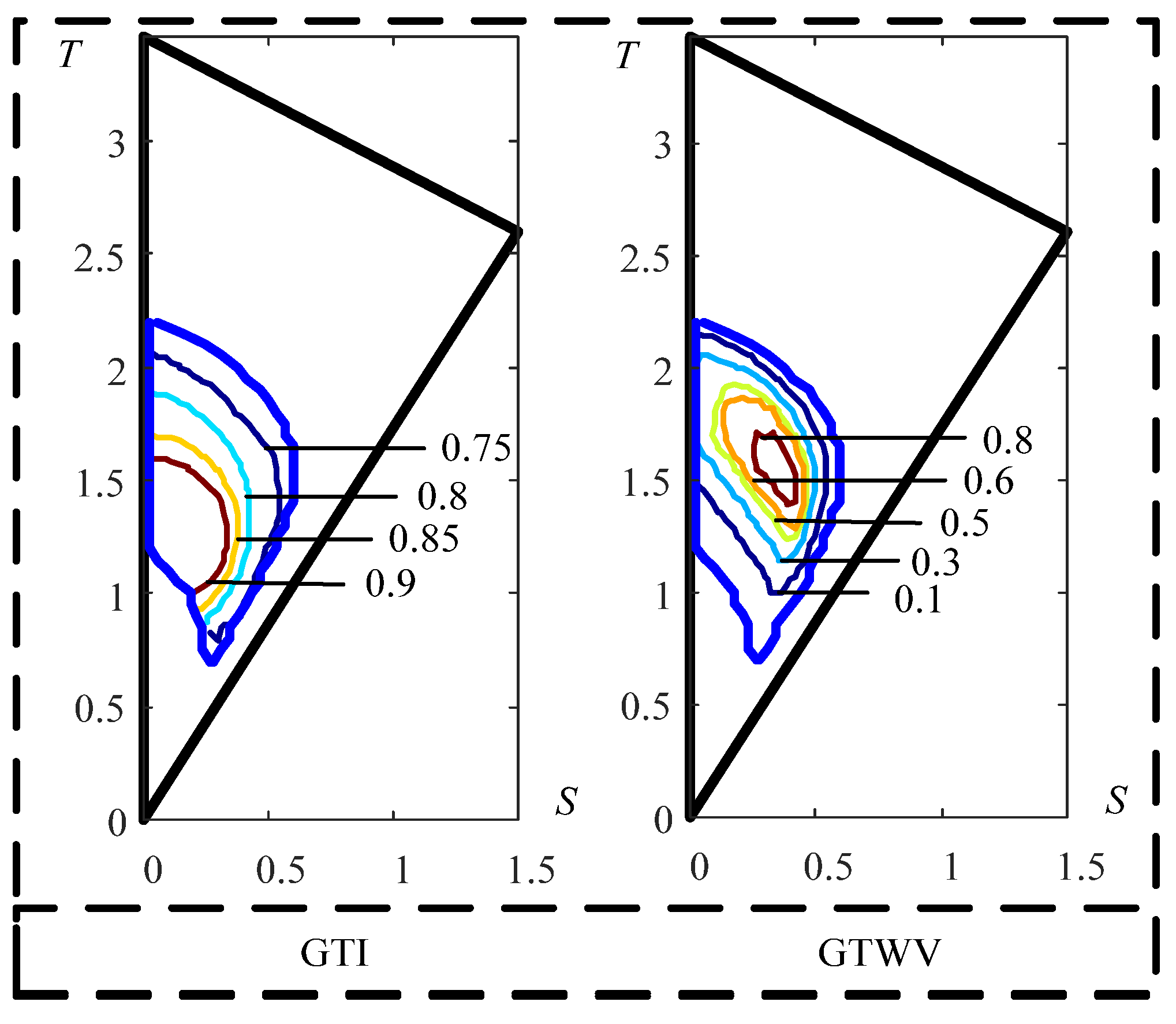
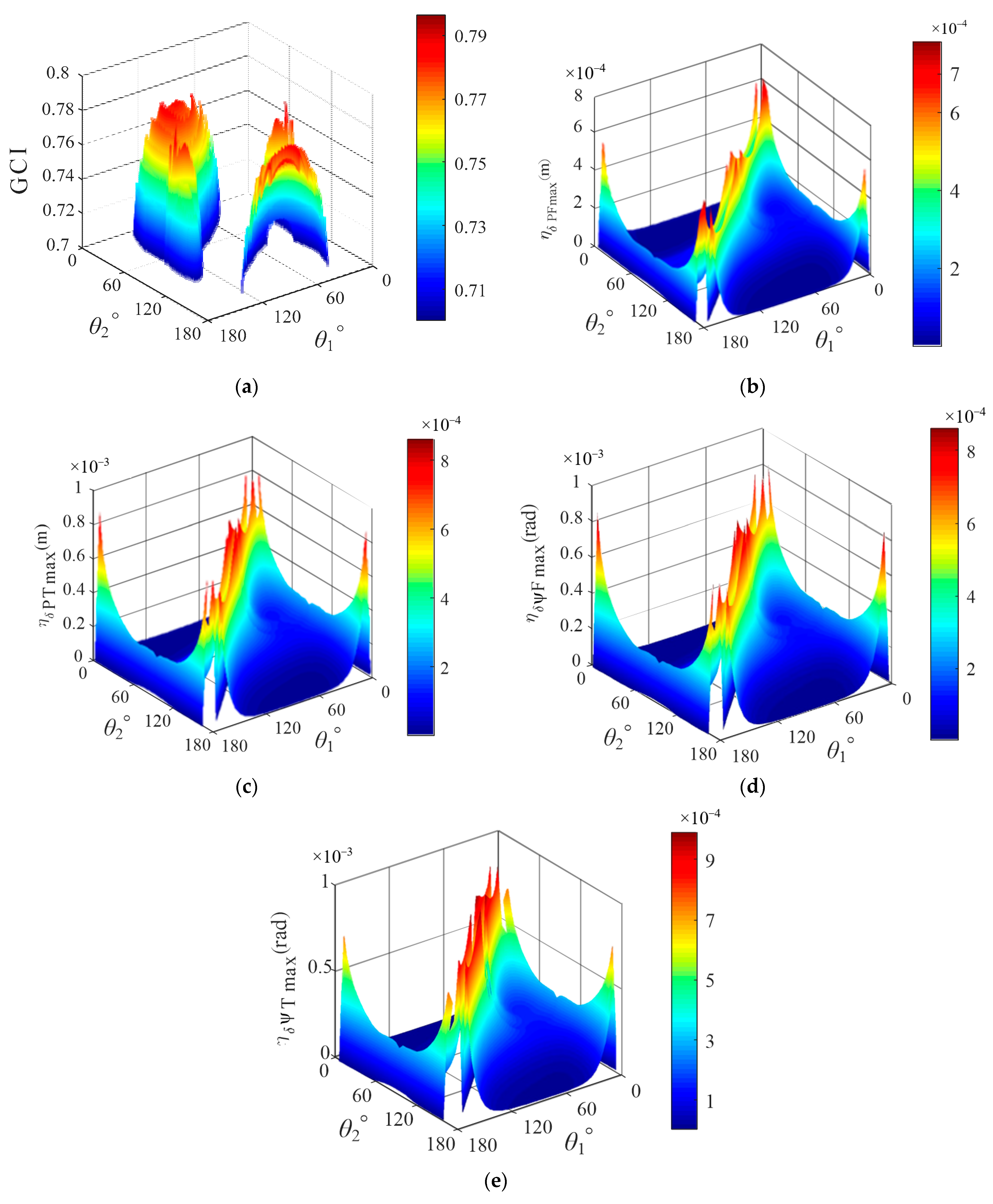
3.1. Motion/Force Transmission Performance Atlases of the 3-UPU Translational PMs
3.2. Dimension Optimization Design Based on Motion/Force Transmission Index
4. Optimization of the Orientations of the Ending R Joints
4.1. Constraint Performance Index
4.2. Stiffness Performance Index
4.3. Multi-Objective Optimization of the 3-UPU PMs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PM | parallel manipulators |
| DOF | degree of freedom |
| MOOGA | multi-objective optimization game algorithm |
| GTW | good transmission workspace |
| GTWV | good transmission workspace volume |
| GTI | The global transmission index |
| OCI | output constraint index |
| GCW | good constraint workspace |
References
- Clavel, R. Delta, A fast robot with parallel geometry. In Proceedings of the International Symposium on Industrial Robots, Lausanne, Switzerland, 26–28 April 1988; pp. 91–100. [Google Scholar]
- Chung-Ching, L.; Hervé, J.M. Translational parallel manipulators with doubly planar limbs. Mech. Mach. Theory 2016, 42, 433–455. [Google Scholar]
- Shen, H.; Chablat, D.; Zeng, B.; Li, J.; Wu, G.; Yang, T. A Translational Three-Degrees-of-Freedom Parallel Mechanism with Partial Motion Decoupling and Analytic Direct Kinematics. J. Mech. Robot. 2020, 12, 021112. [Google Scholar] [CrossRef]
- Niu, Y.Z.; Song, J.W.; Li, F.J.; Li, S.H. Type synthesis method for three translational parallel mechanisms while considering velocity/force anisotropy. J. Mech. Sci. Technol. 2025, 39, 363–374. [Google Scholar] [CrossRef]
- Zhang, G.L.; Yang, G.L.; Deng, Y.M.; Chen, C.Y.; Fang, Z.J.; Li, J.J. Jerk-optimal force and motion synchronous planning for a 3-DOF translational force-controlled end-effector. Robot. Comput.-Integr. Manuf. 2025, 93, 102931. [Google Scholar] [CrossRef]
- Lin, S.T.; Huang, S.Y.; Lan, C.C.; Chidambaram, M.; Sivaramakrishnan, V. Design and experiment of a new translational parallel manipulator with large payload and high repeatability. Mech. Mach. Theory 2023, 180, 105124. [Google Scholar] [CrossRef]
- Tsai, L.W. Kinematics of three-dof platform with three extensible limbs. In Recent Advances in Robot Kinematics; Lenarcic, J., Parenti-Castelli, V., Eds.; Kluwer Academic Publishers: London, UK, 1996; pp. 401–410. [Google Scholar]
- Tsai, L.W.; Joshi, S. Kinematics and optimization of a spatial 3-UPU parallel manipulator. ASME J. Mech. Des. 2000, 122, 439–446. [Google Scholar] [CrossRef]
- Joshi, S.; Tsai, L.W. Jacobian analysis of limited-DOF parallel manipulators. ASME J. Mech. Des. 2002, 124, 254–258. [Google Scholar] [CrossRef]
- Gregorio, R.D.; Parenti-Castelli, V. Mobility analysis of the 3UPU parallel mechanism assembled for a pure translational motion. ASME J. Mech. Des. 2002, 124, 259–264. [Google Scholar] [CrossRef]
- Han, C.; Kim, J.; Kim, J.; Park, F.C. Kinematic Sensitivity Analysis of the 3-UPU Parallel Mechanism. Mech. Mach. Theory 2002, 37, 787–798. [Google Scholar] [CrossRef]
- Lu, Y.; Hu, B. Analysis of kinematics and solution of active/constrained forces of asymmetric 2UPU+X parallel manipulators. Proc IMechE Part C J. Mech. Eng. Sci. 2006, 220, 1819–1830. [Google Scholar] [CrossRef]
- Hu, B.; Yao, Y.; Wu, P. A Comparison Study of Two 3-UPU Translational Parallel Manipulators. Int. J. Adv. Rob. Syst. 2013, 10, 190. [Google Scholar] [CrossRef]
- Bhutani, G.; Dwarakanath, T.A. Novel design solution to high precision 3 axes translational parallel mechanism. Mech. Mach. Theory 2014, 75, 118–130. [Google Scholar] [CrossRef]
- Gan, D.; Dai, J.S.; Dias, J.; Seneviratne, L.D. Variable Motion/Force Transmissibility of a Metamorphic Parallel Mechanism with Reconfigurable 3T and 3R Motion. ASME J. Mech. Rob. 2016, 8, 051001. [Google Scholar] [CrossRef]
- Kong, X. Classification of 3-DOF 3-UPU Translational Parallel Mechanisms Based on Constraint Singularity Loci Using Gröbner Cover. ASME J. Mech. Rob. 2022, 14, 041010. [Google Scholar] [CrossRef]
- Hassani, A.; Khalilpour, S.A.; Bataleblu, A.; Taghirad, H.D. Full dynamic model of 3-UPU translational parallel manipulator for model-based control schemes. Robotica 2022, 40, 2815–2830. [Google Scholar] [CrossRef]
- Tsai, C.Y.; Yu, C.P.; Yeh, P.C.; Lan, C.C. Parametric joint compliance analysis of a 3-UPU parallel robot. Mech. Mach. Theory 2022, 170, 104–721. [Google Scholar] [CrossRef]
- Zhao, J.S.; Wei, S.T.; Sun, H.L. Kinematics and Statics of a 3-UPU Robot in Screw Coordinates. J. Mech. Robot. 2023, 15, 061004. [Google Scholar] [CrossRef]
- Xu, Y.Y.; Zhao, X.W.; Li, G.J.; Tang, X.L. Design and analysis of 3-UPU wave compensation platform based on improved sliding mode control. Ships Offshore Struct. 2024, 19, 2040–2049. [Google Scholar] [CrossRef]
- Wang, J.S.; Wu, C.; Liu, X.J. Performance evaluation of parallel manipulators: Motion/force transmissibility and its index. Mech. Mach. Theory 2010, 45, 1462–1476. [Google Scholar] [CrossRef]
- Wu, C.; Liu, X.J.; Wang, L.P.; Wang, J.S. Optimal design of spherical 5R parallel manipulators considering the motion/force transmissibility. J. Mech. Design. 2010, 132, 031002. [Google Scholar] [CrossRef]
- Meng, Q.Z.; Xie, F.G.; Liu, X.J.; Takeda, Y. An evaluation approach for motion-force interaction performance of parallel manipulators with closed-loop passive limbs. Mech. Mach. Theory 2020, 149, 103844. [Google Scholar] [CrossRef]
- Liu, X.J.; Chen, X.; Nahon, M. Motion/force constrainability analysis of lower-mobility parallel manipulators. ASME J. Mech. Rob. 2014, 6, 031006. [Google Scholar] [CrossRef]
- Marlow, K.; Isaksson, M.; Dai, J.S.; Nahavandi, S. Motion/force transmission analysis of planar parallel mechanisms with closed-loop subchains. ASME J. Mech. Rob. 2016, 138, 062302. [Google Scholar] [CrossRef]
- Hu, B.; Shi, D.S.; Xie, T.F.; Hu, B.B.; Ne, N.J. Kinematically identical manipulators derivation for the 2-RPU+UPR parallel manipulator and their constraint performance comparison. ASME J. Mech. Rob. 2020, 12, 061011. [Google Scholar] [CrossRef]
- Song, J.K.; Zhao, C.; Zhao, K.; Yan, W.J.; Chen, Z.M. Singularity analysis and dimensional synthesis of a 2R1T 3-UPU parallel mechanism based on performance atlas. ASME J. Mech. Rob. 2023, 15, 011001. [Google Scholar] [CrossRef]
- Huang, S.; Schimmels, J.M. The eigenscrew decomposition of spatial stiffness matrix. IEEE Trans. Rob. Autom. 2000, 16, 146–156. [Google Scholar] [CrossRef]
- Raoofian, A.; Taghvaeipour, A.; Kamali, A. On the stiffness analysis of robotic manipulators and calculation of stiffness indices. Mech. Mach. Theory 2018, 130, 382–402. [Google Scholar] [CrossRef]
- Portman, V.T. Robot stiffness evaluability problem: Solution by Schur complements and collinear stiffness values. Mech. Mach. Theory 2021, 161, 104297. [Google Scholar] [CrossRef]
- Wu, G.L.; Zou, P. Stiffness analysis and comparison of a Biglide parallel grinder with alternative spatial modular parallelograms. Robotica 2017, 35, 1310–1326. [Google Scholar] [CrossRef]
- Yan, S.J.; Ong, S.K.; Nee, A.Y.C. Stiffness analysis of parallelogram-type parallel manipulators using a strain energy method. Robot. Comput. Integr. Manuf. 2016, 37, 13–22. [Google Scholar] [CrossRef]
- Zhang, D.; Gao, Z. Forward kinematics, performance analysis, and multi-objective optimization of a bio-inspired parallel manipulator. Robot. Comput. Integr. Manuf. 2012, 28, 484–492. [Google Scholar] [CrossRef]
- Wu, G.; Bai, S.; Hjornet, P. Architecture optimization of a parallel Schönflies-motion robot for pick-and-place applications in a predefined workspace. Mech. Mach. Theory 2016, 106, 148–165. [Google Scholar] [CrossRef]
- Yang, C.; Li, Q.C.; Chen, Q.H. Multi-objective optimization of parallel manipulators using a game algorithm. Appl. Math. Model. 2019, 74, 217–243. [Google Scholar] [CrossRef]
- Huang, Z.; Kong, L.F.; Fang, Y.F. Theory on Parallel Robotics and Control; Machinery Industry Press: Beijing, China, 1997. [Google Scholar]
- Oskar, M.; John, V.N. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1953. [Google Scholar]
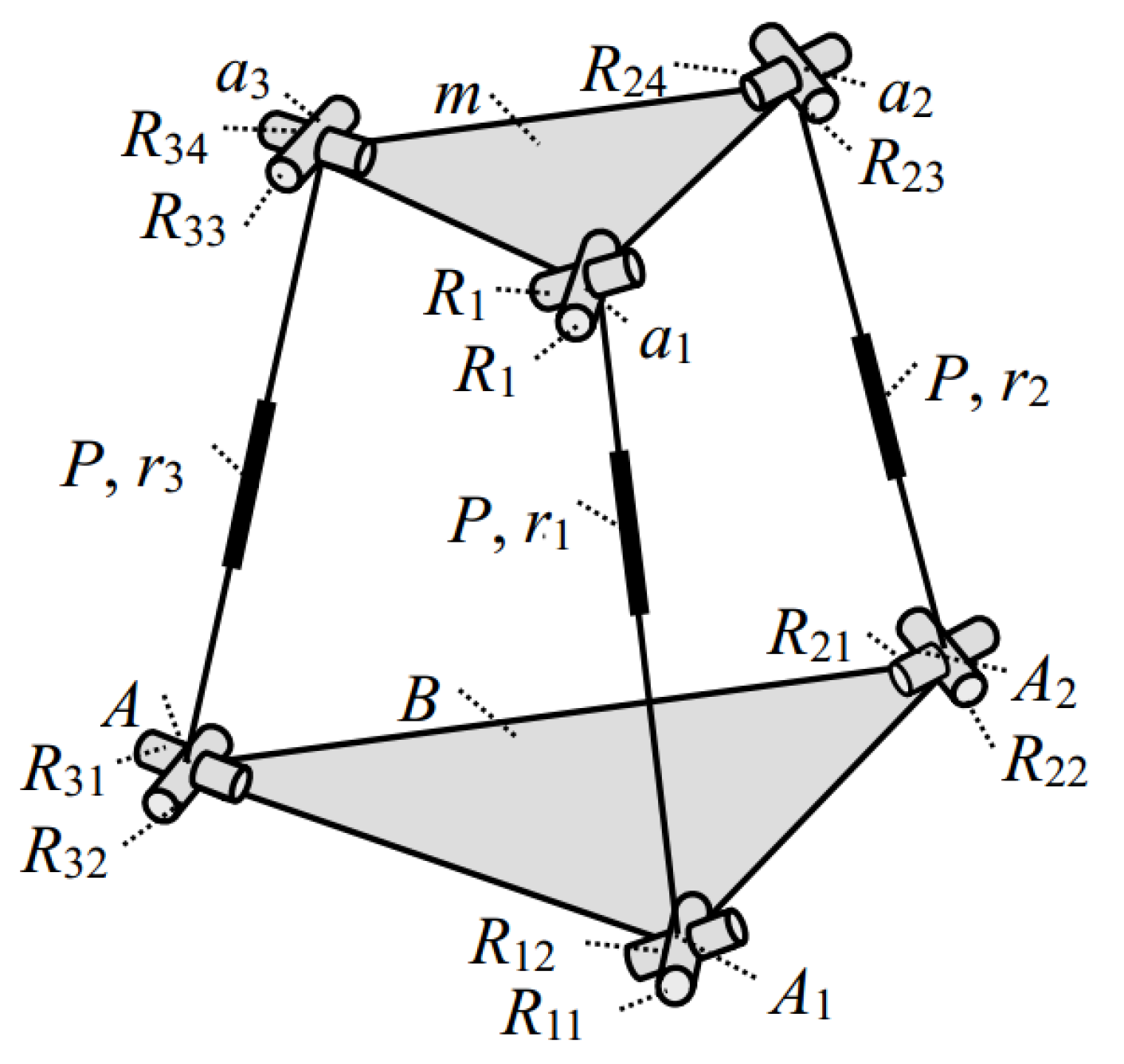
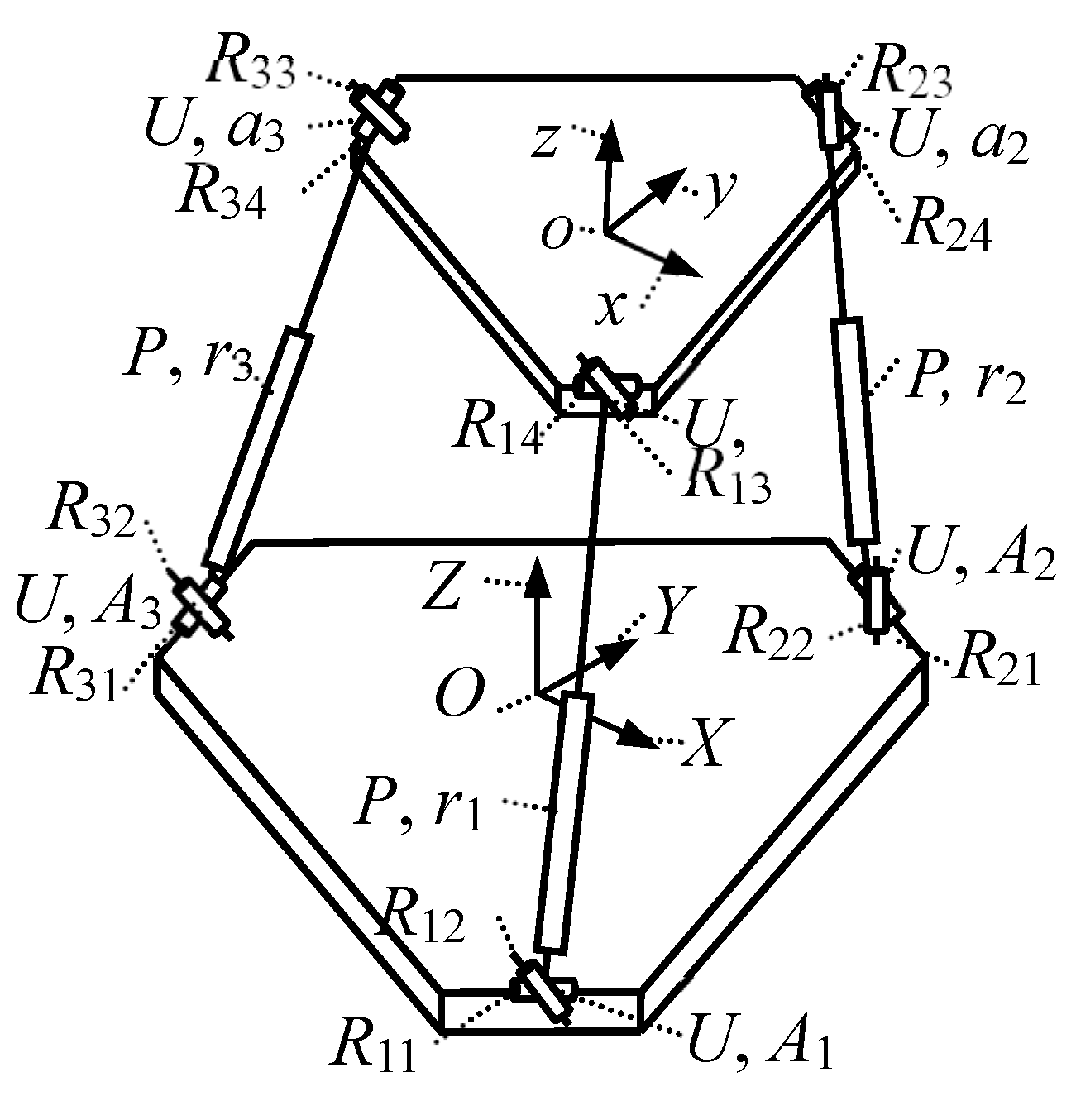
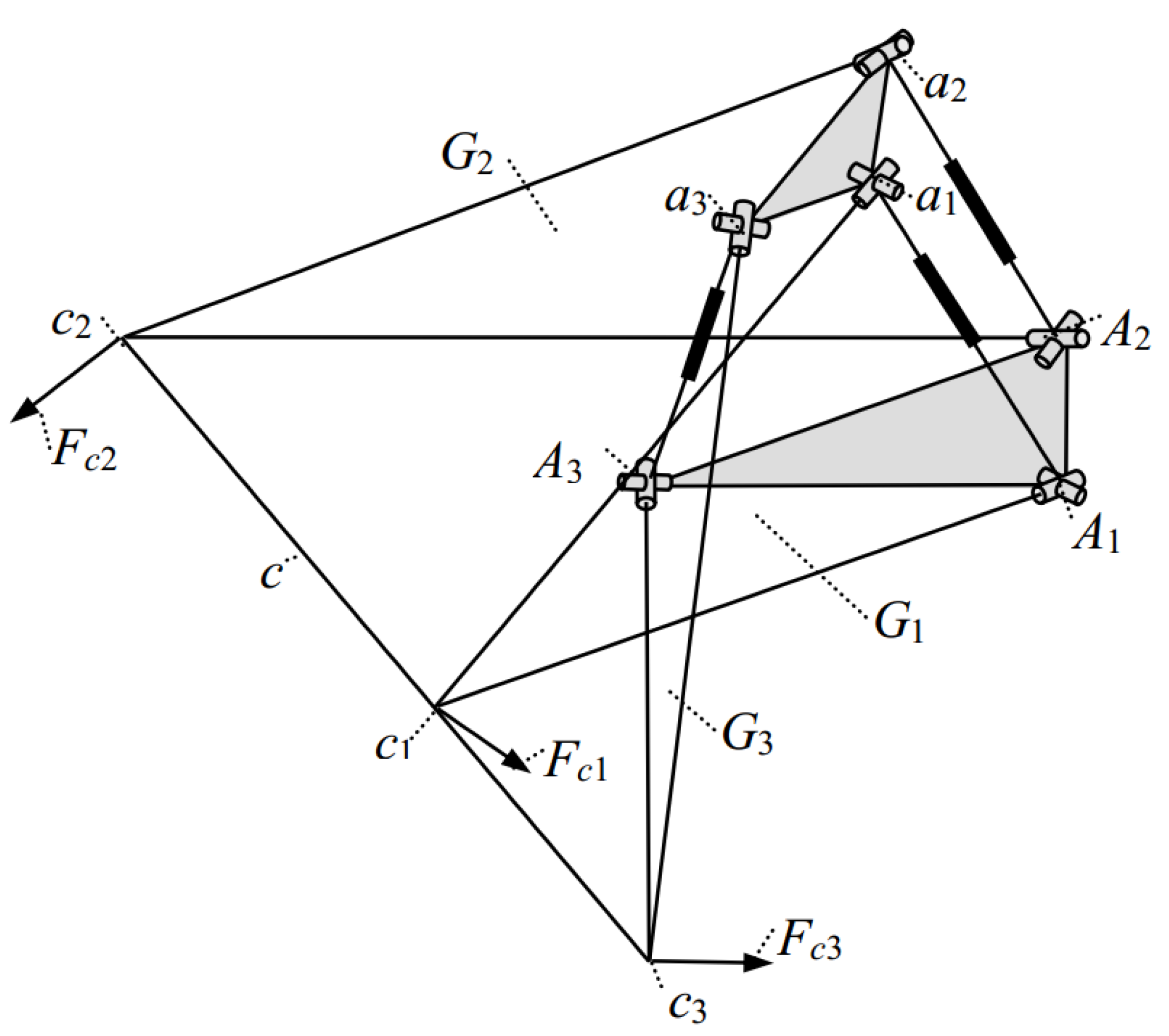
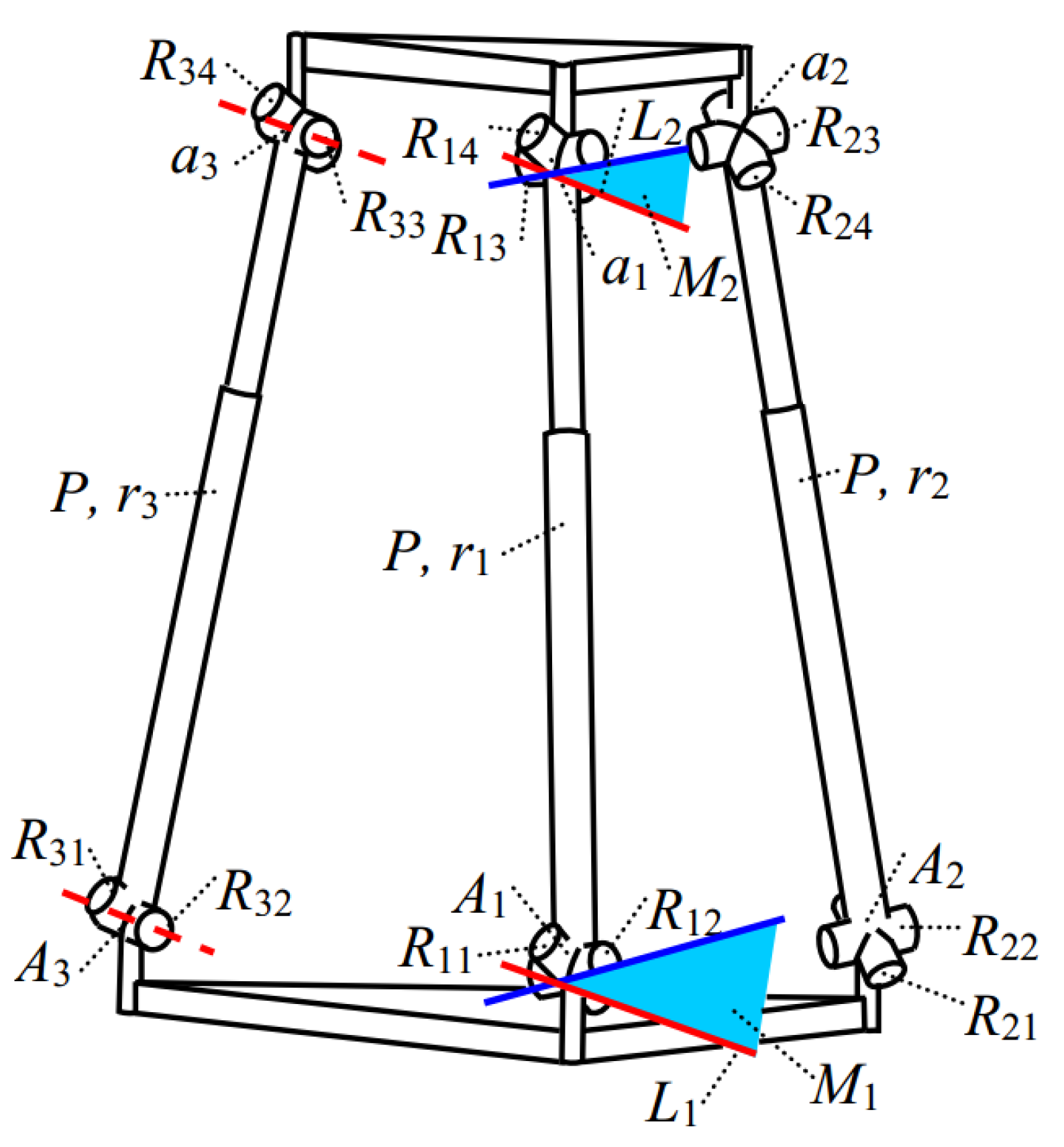

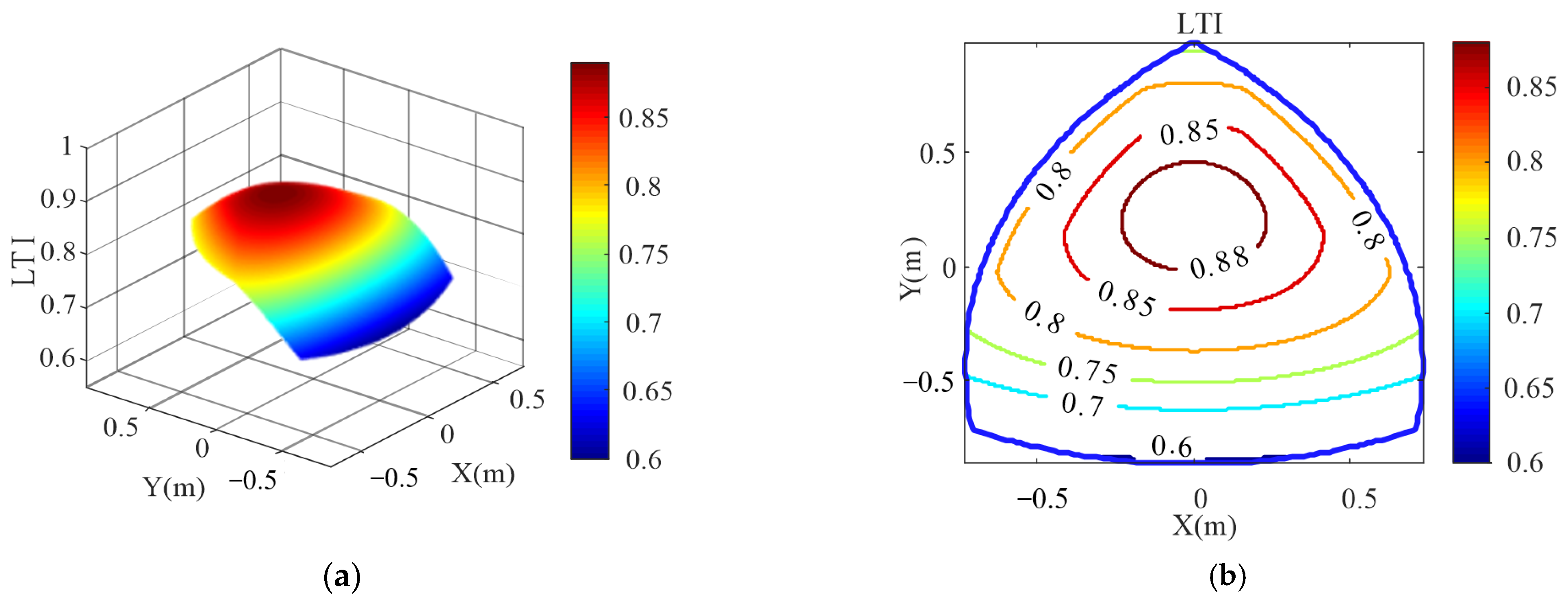

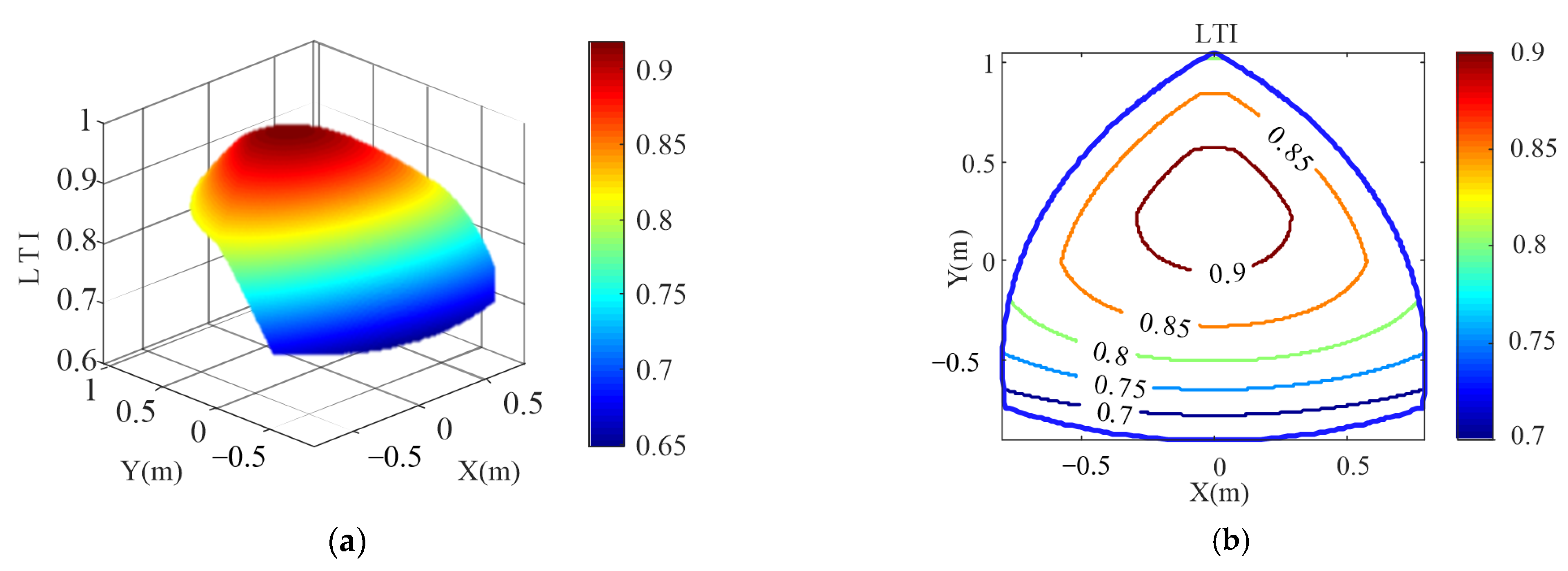
| Index | e(m) | e1(m) | E(m) | E1(m) | GTI | GTWV |
|---|---|---|---|---|---|---|
| Before optimization | 0.5 | 0.7 | 1.5 | 2 | 0.8159 | 0.5599 |
| Optimized | 0.5400 | 0.7340 | 1.6786 | 2.2814 | 0.8334 | 0.8657 |
| Optimum Balance Point (θ1, θ2) | GCI | ηδPFmax | ηδPTmax | ηδψFmax | ηδψTmax |
|---|---|---|---|---|---|
| [97.5°, 3.7°] | 0.7821 | 4.827 × 10−6 | 7.566 × 10−6 | 7.566 × 10−6 | 1.227 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, B.; Bai, P. Research on the Conditions and Optimization of 3-UPU Parallel Manipulators That Naturally Realize Three Translational Degrees of Freedom. Machines 2025, 13, 265. https://doi.org/10.3390/machines13040265
Hu B, Bai P. Research on the Conditions and Optimization of 3-UPU Parallel Manipulators That Naturally Realize Three Translational Degrees of Freedom. Machines. 2025; 13(4):265. https://doi.org/10.3390/machines13040265
Chicago/Turabian StyleHu, Bo, and Peng Bai. 2025. "Research on the Conditions and Optimization of 3-UPU Parallel Manipulators That Naturally Realize Three Translational Degrees of Freedom" Machines 13, no. 4: 265. https://doi.org/10.3390/machines13040265
APA StyleHu, B., & Bai, P. (2025). Research on the Conditions and Optimization of 3-UPU Parallel Manipulators That Naturally Realize Three Translational Degrees of Freedom. Machines, 13(4), 265. https://doi.org/10.3390/machines13040265




