Data Reduction in Proportional Hazards Models Applied to Reliability Prediction of Centrifugal Pumps
Abstract
1. Introduction
2. Brief Overview of MTBF, PHM, and Data Reduction
2.1. Overview of MTBF Concept
2.2. Brief Overview of Cox PHM
2.3. Data Reduction and Variable Selection in PHM
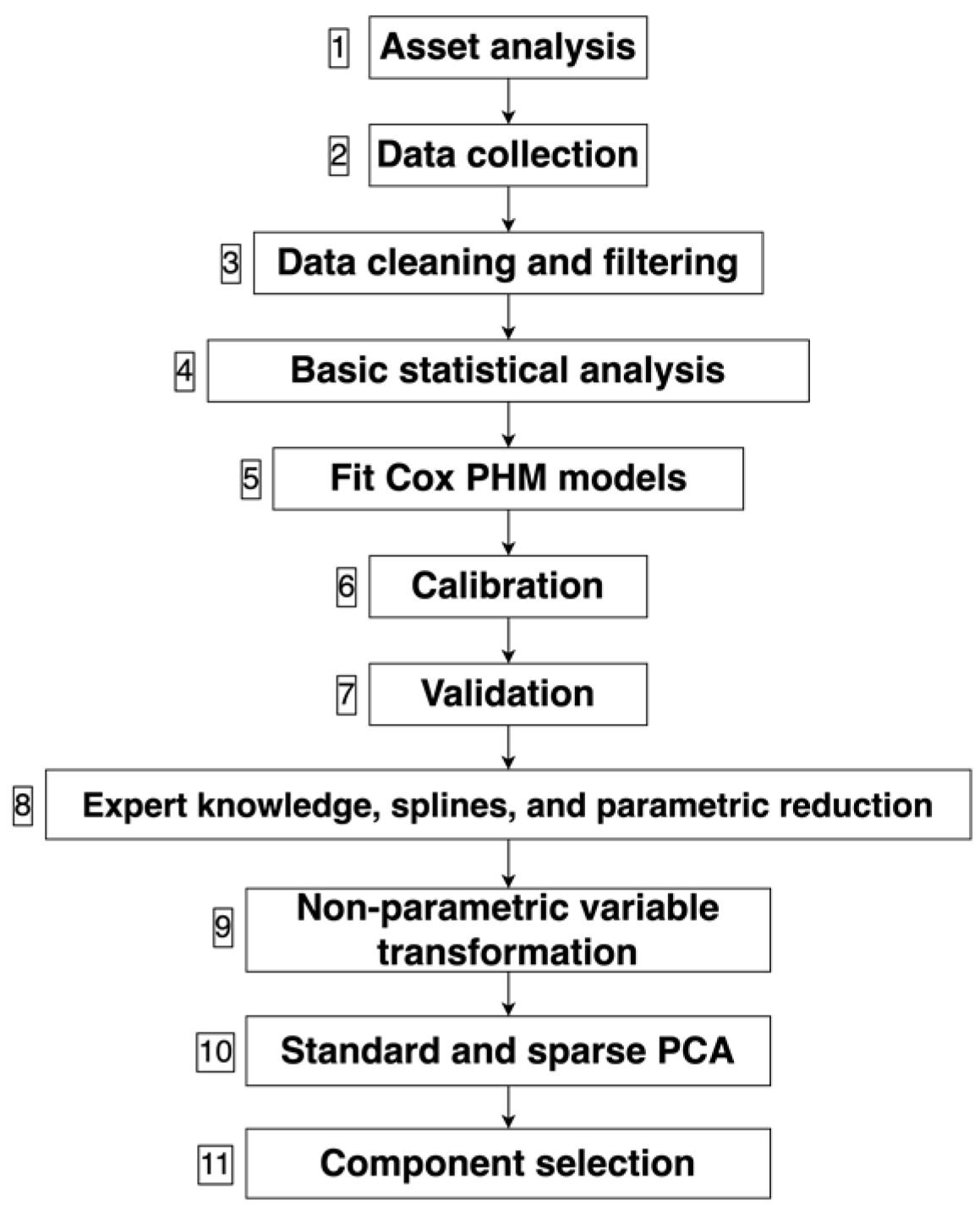
3. Methodology and Analytical Approach
Process Steps
- Asset analysis
- 2.
- Data collection
- 3.
- Data cleaning and filtering
- 4.
- Basic statistical analysis
- 5.
- Fit Cox PHMs
- 6.
- Calibration
- 7.
- Validation
- 8.
- Expert knowledge, RCS, and parametric reduction
- 9.
- Variable transformation
- 10.
- Standard and sparse PCA on raw and transformed variables
- 11.
- Selection of principal components
4. Results
4.1. Full Models and Necessity of Data Reduction
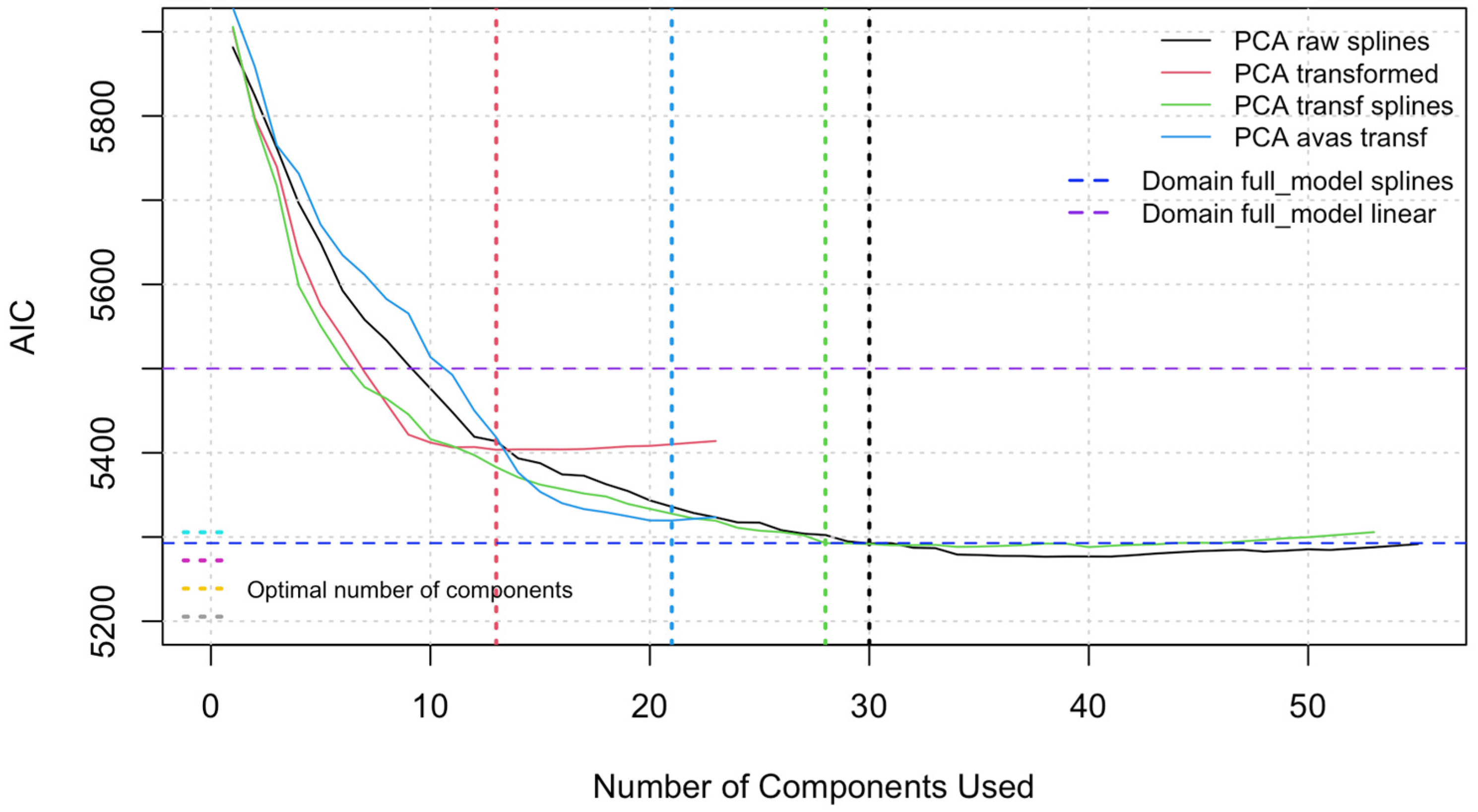
4.2. PCA Reduction
5. Discussion
6. Conclusions and Future Work
- Full linear and spline models showed calibration slopes of 0.830 and 0.722, respectively. Because these slopes are below 0.9, excessive overfitting would be expected, requiring the need for data reduction.
- Strong non-linear components in the full model made it necessary to transform the covariates to relax the linearity assumptions of the regression (which would have resulted in poor model fit).
- The models applying sparse robust PCA obtained results similar to those fitted with the standard PCA method but using fewer d.f.
- The preferred model was fitted using principal components obtained from sparse robust PCA, applied to X variables transformed with the AVAS algorithm. The resulting AIC was 5317.34 with a calibration slope of 0.936 for the prediction of MTBF, indicating a superior result.
- The dimension reduction achieved with the final model was 16 d.f., down from 103 d.f. in the full model with RCS with a corresponding AIC increase of 0.34%.
- Determine the most important variables and check how they impact the predicted MTBF.
- Rank the importance and prediction ability of the raw covariates and principal components of the full and reduced models.
- Examine the assumptions of the Cox PHM to identify potential issues and evaluate their impact on the final models.
- Assess which variables make some pumps behave differently from others, focusing on various groups of covariates: operating conditions, hydraulic design, mechanical design, age, sealing, and maintenance history.
- Repeated failures of the assets were modeled under perfect repair conditions, which implies that the machine has the same lifetime distribution and the same rate function as a new one [71] after repair. This assumption might be challenged.
- Check for variable interactions and their importance in the prediction ability of the model.
- Models were fitted considering that the effect of the covariates remains constant over time. Future work could take a time-dependent approach using the same variables for centrifugal pumps.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. List of Acronyms and Symbols
| Acronym | Explanation |
|---|---|
| ACE | Alternating Conditional Expectation |
| AIC | Akaike information criterion |
| ALS | Alternating Least Squares |
| ANN | Artificial Neural Networks |
| API | American Petroleum Institute |
| AVAS | Additive Variance Stabilizing |
| BIC | Bayesian information criterion |
| CNN | Convolutional Neural Networks |
| CTBN | Continuous Time Bayesian Networks |
| d.f. | Degrees of freedom |
| DCS | Distributed control system |
| DNN | Deep Neural Networks |
| FTA | Failure Tree Analysis |
| GMM | Gaussian Mixed Model |
| ISO | Internation Organization for Standardization |
| k-NN | k-Nearest Neighbours |
| KPI | Key Performance Indicator |
| LARS | Least angle regression |
| LASSO | Least Absolute Shrinkage and Selection Operator |
| LR | Log-Likelihood ratio |
| MGV | Maximum Generalized Variance |
| MTBF | Mean Time Between Failures |
| MTTR | Mean Time To Repair |
| MTV | Maximum Total Variance |
| MWPHM | Mixture Weibull Proportional Hazards Model |
| NHPP | Non-homogeneous Poisson process |
| NPSH | Net Positive Suction Head |
| Ns | Specific speed |
| Nss | Suction specific speed |
| OLS | Ordinary Least Squares |
| OREDA | Offshore and Onshore Reliability Data |
| PbM | Physical-based Models |
| PCA | Principal Component Analysis |
| PF | Particle Filter |
| PHM | Proportional Hazards Model |
| RCS | Restricted cubic splines |
| RMV | Relevance Vector Machine |
| ROC | Receiver-Operating Characteristic Curve |
| rpm | Revolutions per minute |
| RNN | Recurrent Neural Networks |
| RUL | Remaining useful life |
| SAS | Statistical Analysis System |
| SVM | Support Vector Machine |
| TIM | Traditional imperfect maintenance |
| VGP | Variance Gamma Process |
| Symbol | Meaning | Units (if Applicable) |
|---|---|---|
| Λ | Hazard rate | Failures per unit of time |
| R(t) | Reliability function | Dimensionless (0 to 1) |
| Β | Shape parameter (Weibull) | Dimensionless |
| H | Scale parameter (Weibull) | Time units (e.g., days) |
| T | Time | Time units (e.g., days) |
| X | Matrix of predictors | Variable (depends on context) |
| Β | Regression coefficients (Cox model) | Dimensionless |
| R2 | Coefficient of determination | Dimensionless (0 to 1) |
| χ2 | Chi squared | Dimensionless (statistic) |
| Ρ | Spearman’s rank correlation coefficient | Dimensionless (−1 to 1) |
| Dxy | Somers’ rank correlation | Dimensionless (−1 to 1) |
Appendix B. List of RStudio Version 2024.12.1 Packages Used for Computation
| Package/Software | Reference |
|---|---|
| R | R Core Team (2024). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing. https://www.R-project.org/ accessed on 24 February 2025 |
| tidyverse | Wickham et al. (2019). Welcome to the tidyverse. Journal of Open-Source Software, 4(43), 1686. doi: 10.21105/joss.01686. https://cran.r-project.org/web/packages/tidyverse/index.html accessed on 24 February 2025 |
| Matrix | Bates et al. (2023). Matrix: Sparse and Dense Matrix Classes and Methods. https://CRAN.R-project.org/package=Matrix accessed on 24 February 2025 |
| survival | Therneau (2023). A Package for Survival Analysis in R. https://CRAN.R-project.org/package=survival accessed on 24 February 2025 |
| rstatix | Kassambara (2021). rstatix: Pipe-Friendly Framework for Basic Statistical Tests. https://CRAN.R-project.org/package=rstatix accessed on 24 February 2025 |
| survminer | Kassambara & Kosinski (2021). survminer: Drawing Survival Curves using ‘ggplot2’. https://CRAN.R-project.org/package=survminer accessed on 24 February 2025 |
| ggcorrplot | Kassambara (2019). ggcorrplot: Visualization of a Correlation Matrix using ‘ggplot2’. https://CRAN.R-project.org/package=ggcorrplot accessed on 24 February 2025 |
| ggplot2 | Wickham et al. (2023). ggplot2: Create Elegant Data Visualisations Using the Grammar of Graphics. https://CRAN.R-project.org/package=ggplot2 accessed on 24 February 2025 |
| dplyr | Wickham et al. (2023). dplyr: A Grammar of Data Manipulation. https://CRAN.R-project.org/package=dplyr accessed on 24 February 2025 |
| MASS | Venables & Ripley (2002). MASS: Modern Applied Statistics with S (4th ed.). Springer. |
| doBy | Hawthorne & Wesselingh (2016). doBy: Grouping, ordering, and summarizing functions. |
| glmnet | Friedman et al. (2010). Regularization paths for generalized linear models via coordinate descent. J. Stat. Software, 33(1), 1-22. doi: 10.18637/jss.v033.i01. https://www.jstatsoft.org/article/view/v033i01 accessed on 24 February 2025 |
| rms | Harrell (2021). rms: Regression Modeling Strategies. https://CRAN.R-project.org/package=rms accessed on 24 February 2025 |
| Hmisc | Harrell (2021). Hmisc: Harrell Miscellaneous. https://CRAN.R-project.org/package=Hmisc accessed on 24 February 2025 |
| pcaPP | Lê et al. (2008). pcaPP: Principal component methods: A new approach to principal component analysis. https://CRAN.R-project.org/package=pcaPP accessed on 24 February 2025 |
| splines | R Core Team (2021). splines: Regression Spline Functions. https://CRAN.R-project.org/package=splines accessed on 24 February 2025 |
| acepack | Tyler & Wang (2015). acepack: A Package for Fitting the ACE and AVAS Models. https://CRAN.R-project.org/package=acepack accessed on 24 February 2025 |
| BeSS | Friedman & Popescu (2008). BeSS: Best Subset Selection. https://CRAN.R-project.org/package=BeSS accessed on 24 February 2025 |
References
- Nesbitt, B. Handbook of Pumps and Pumping: Pumping Manual International, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2006; ISBN 9781856174763. [Google Scholar]
- Lu, H.; Guo, L.; Azimi, M.; Huang, K. Oil and Gas 4.0 era: A systematic review and outlook. Comput. Ind. 2019, 111, 68–90. [Google Scholar] [CrossRef]
- Vila Forteza, M.; Pascual, D.; Galar, U.; Kumar, A.K.; Verma. Work-in-progress: Reliability prediction of API centrifugal pumps using survival analysis. In Proceedings of the 19th IMEKO TC10 Conference “Measurement for Diagnostics, Optimisation and Control to Support Sustainability and Resilience”, Delft, The Netherlands, 21–22 September 2023. [Google Scholar] [CrossRef]
- Vila Forteza, M.; Jimenez Cortadi, A.; Diez Olivan, A.; Seneviratne, D.; Galar Pascual, D. Advanced Prognostics for a Centrifugal Fan and Multistage Centrifugal Pump Using a Hybrid Model. In Proceedings of the 5th International Conference on Maintenance, Condition Monitoring and Diagnostics 2021, Oulu, Finland, 16–17 February 2021. [Google Scholar] [CrossRef]
- Adraoui, I.E.; Gziri, H.; Mousrij, A. Prognosis of a degradable hydraulic system: Application on a centrifugal pump. Int. J. Progn. Health Manag. 2020, 11, 1–11. [Google Scholar] [CrossRef]
- Cubillo, A.; Perinpanayagam, S.; Esperon Miguez, M. A review of physics-based models in prognostics: Application to gears and bearings of rotating machinery. Adv. Mech. Eng. 2016, 8, 1687814016664660. [Google Scholar] [CrossRef]
- Zhang, S.; Hodkiewicz, M.; Ma, L.; Mathew, J. Machinery Condition Prognosis Using Multivariate Analysis. In Engineering Asset Management; Mathew, J., Kennedy, J., Ma, L., Tan, A., Anderson, D., Eds.; Springer: London, UK, 2006. [Google Scholar] [CrossRef]
- Yu, R.; Li, X.; Tao, M.; Ke, Z. Fault Diagnosis of Feedwater Pump in Nuclear Power Plants Using Parameter-Optimized Support Vector Machine. In Proceedings of the 2016 24th International Conference on Nuclear Engineering, Charlotte, NC, USA, 26–30 June 2016; p. V001T03A013. [Google Scholar] [CrossRef]
- Zurita Millan, D.; Delgado-Prieto, M.; Saucedo-Dorantes, J.; Cariño-Corrales, J.; Osornio-Rios, R.; Ortega, J.; Romero-Troncoso, R. Vibration Signal Forecasting on Rotating Machinery by means of Signal Decomposition and Neurofuzzy Modeling. Shock. Vib. 2016, 2016, 2683269. [Google Scholar] [CrossRef]
- Fouladirad, M.; Belhaj Salem, M.; Deloux, E. Variance Gamma process as degradation model for prognosis and imperfect maintenance of centrifugal pumps. Reliab. Eng. Syst. Saf. 2022, 223, 108417. [Google Scholar] [CrossRef]
- Souza, R.; Sperandio, N.; Erick, G.; Miranda, U.; Silva, W.; Lepikson, H. Deep learning for diagnosis and classification of faults in industrial rotating machinery. Comput. Ind. Eng. 2020, 153, 107060. [Google Scholar] [CrossRef]
- Kumar, A.; Gandhi, C.; Zhou, Y.; Kumar, R.; Xiang, J. Improved deep convolution neural network (CNN) for the identification of defects in the centrifugal pump using acoustic images. Appl. Acoust. 2020, 167, 107399, ISSN 0003-682X. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, X. A Deep Feature Optimization Fusion Method for Extracting Bearing Degradation Features. IEEE Access 2018, 6, 19640–19653. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, T.; Huang, X.; Longchao, C.; Zhou, Q. Fault diagnosis of rotating machinery based on recurrent neural networks. Measurement 2020, 171, 108774. [Google Scholar] [CrossRef]
- Mosallam, A.; Medjaher, K.; Zerhouni, N. Data-driven prognostic method based on Bayesian approaches for direct remaining useful life prediction. J. Intell. Manuf. 2014, 27, 1037–1048. [Google Scholar] [CrossRef]
- Forrester, T.; Harris, M.; Senecal, J.; Sheppard, J. Continuous Time Bayesian Networks in Prognosis and Health Management of Centrifugal Pumps. In Proceedings of the Annual Conference of the PHM Society, Scottsdale, AZ, USA, 23–26 September 2019; p. 11. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Zheng, Y.; Wang, K. Adaptive prognosis of centrifugal pump under variable operating conditions. Mech. Syst. Signal Process. 2019, 131, 576–591. [Google Scholar] [CrossRef]
- Zhang, Q.; Hua, C.; Xu, G. A mixture Weibull proportional hazard model for mechanical system failure prediction utilising lifetime and monitoring data. Mech. Syst. Signal Process. 2014, 43, 103–112. [Google Scholar] [CrossRef]
- Hu, J.; Tse, P. A Relevance Vector Machine-Based Approach with Application to Oil Sand Pump Prognostics. Sensors 2013, 13, 12663–12686. [Google Scholar] [CrossRef]
- Cao, S.; Hu, Z.; Luo, X.; Wang, H. Research on fault diagnosis technology of centrifugal pump blade crack based on PCA and GMM. Measurement 2020, 173, 108558. [Google Scholar] [CrossRef]
- Li, X.; Duan, F.; Mba, D.; Bennett, I. Rotating machine prognostics using system-level models. Lecture Notes in Mechanical Engineering. In Engineering Asset Management 2016: Proceedings of the 11th World Congress on Engineering Asset Management; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; Volume 3, pp. 123–141. [Google Scholar] [CrossRef]
- Kim, S.; Choi, J.H.; Kim, N.H. Challenges and Opportunities of System-Level Prognostics. Sensors 2021, 21, 7655. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Bloch, H.P.; Budris, A.R. Pump User’s Handbook, Life Extension, 4th ed.; The Fairmont Press Inc.: Atlanta, GA, USA, 2014; p. 103. [Google Scholar]
- Bevilacqua, M.; Braglia, M.; Montanari, R. The classification and regression tree approach to pump failure rate analysis. Reliab. Eng. Syst. Saf. 2003, 79, 59–67. [Google Scholar] [CrossRef]
- Braglia, M.; Carmignani, G.; Frosolini, M.; Zammori, F. Data classification and MTBF prediction with a multivariate analysis approach. Reliab. Eng. Syst. Saf. 2012, 97, 27–35. [Google Scholar] [CrossRef]
- Braglia, M.; Castellano, D.; Frosolini, M.; Gabbrielli, R.; Marrazzini, L.; Padellini, L. An ensemble-learning model for failure rate prediction. Procedia Manuf. 2020, 42, 41–48. [Google Scholar] [CrossRef]
- Bevilacqua, M.; Braglia, M.; Frosolini, M.; Montanari, R. Failure rate prediction with artificial neural networks. J. Qual. Maint. Eng. 2005, 11, 279–294. [Google Scholar] [CrossRef]
- Orrù, P.F.; Zoccheddu, A.; Sassu, L.; Mattia, C.; Cozza, R.; Arena, S. Machine learning approach using MLP and SVM algorithms for the fault prediction of a centrifugal pump in the oil and gas industry. Sustainability 2020, 12, 4776. [Google Scholar] [CrossRef]
- Sudadiyo, S. Nonhomogeneous Poisson Process Model for Estimating Mean Time Between Failures of the JE01-AP03 Primary Pump Implemented on the RSG-GAS Reactor. Nucl. Technol. 2024, 1–16. [Google Scholar] [CrossRef]
- Chaoqun, D.; Song, L. A Study of Proportional Hazards Models: Its Applications in Prognostics. In Maintenance Management-Current Challenges, New Developments, and Future Directions; IntechOpen: London, UK, 2023. [Google Scholar] [CrossRef]
- Jardine, A.K.S.; Anderson, P.M.; Mann, D.S. Application of the Weibull proportional hazards model to aircraft and marine engine failure data. Qual. Reliab. Eng. Int. 1987, 3, 77–82. [Google Scholar] [CrossRef]
- Sharma, G.; Sahu, P.K.; Rai, R.N. Imperfect maintenance and proportional hazard models: A literature survey from 1965 to 2020. Life Cycle Reliab. Saf. Eng. 2022, 11, 87–103. [Google Scholar] [CrossRef]
- Gorjian, N.; Sun, Y.; Ma, L.; Yarlagadda, P.; Mittinty, M. Remaining useful life prediction of rotating equipment using covariate-based hazard models–Industry applications. Aust. J. Mech. Eng. 2017, 15, 36–45. [Google Scholar] [CrossRef][Green Version]
- Harrell, F.E., Jr.; Lee, K.L.; Mark, D.B. Multivariable prognostic models: Issues in developing models, evaluating assumptions an adequacy, and measuring and reducing errors. Stat. Med. 1996, 15, 361–387. [Google Scholar] [CrossRef]
- ISO 14224:2016; Petroleum, Petrochemical and Natural Gas Industries—Collection and Exchange of Reliability and Maintenance Data for Equipment. 2016. Available online: https://www.iso.org/standard/64076.html (accessed on 24 February 2025).
- Harrell, F.E., Jr. Regression Modeling Strategies; Springer Series in Statistics; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Lee, E.T. Statistical Methods for Survival Data Analysis; John Wiley & Son: New York, NY, USA, 1982. [Google Scholar]
- Kleinbaum, D.G.; Klein, M. Survival Analysis: A Self-Learning Text, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Jiang, J.; Xiong, Y. Cox models with time-dependent covariates. In Handbook of Survival Analysis; CRC Press: Boca Raton, FL, USA, 2011; pp. 205–226. [Google Scholar]
- Fisher, L.D.; Lin, D.Y. Time-dependent covariates in the Cox proportional-hazards regression model. Annu. Rev. Public Health 1999, 20, 145–157. [Google Scholar] [CrossRef]
- Becker, T. BSc Report Applied Mathematics: Variable Selection; Delft University of Technology: Delft, The Netherlands, 2021. [Google Scholar]
- Petersson, S.; Sehlstedt, K. Variable Selection Techniques for the Cox Proportional Hazards Model: A Comparative Study. 2018. Available online: https://gupea.ub.gu.se/handle/2077/55936 (accessed on 24 February 2025).
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Tibshirani, R. The lasso method for variable selection in the cox model. Stat. Med. 1997, 16, 385–395. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable selection for cox’s proportional hazards model and frailty model. Ann. Stat. 2002, 30, 74–99. [Google Scholar] [CrossRef]
- Zhang, H.H.; Lu, W. Adaptive Lasso for Cox’s proportional hazards model. Biometrika 2007, 94, 691–703. [Google Scholar] [CrossRef]
- Lin, D.; Banjevic, D.; Jardine, A.K.S. Using principal components in a proportional hazards model with applications in condition-based maintenance. Reliab. Eng. Syst. Saf. 2006, 91, 59–69. [Google Scholar] [CrossRef]
- Bankole-Oye, T.; El-Thalji, I.; Zec, J. Combined principal component analysis and proportional hazard model for optimizing condition-based maintenance. Mathematics 2020, 8, 1521. [Google Scholar] [CrossRef]
- de Carvalho Michalski, M.A.; da Silva, R.F.; de Andrade Melani, A.H.; de Souza, G.F.M. Applying Principal Component Analysis for Multi-parameter Failure Prognosis and Determination of Remaining Useful Life. In Proceedings of the 2021 Annual Reliability and Maintainability Symposium (RAMS), Orlando, FL, USA, 24–27 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Liu, W.M.; Chang, C.I. Variants of Principal Components Analysis. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–27 July 2007; pp. 1083–1086. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T.; Tibshirani, R. Sparse principal component analysis. J. Comput. Graph. Stat. 2006, 15, 265–286. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Cox, D.R. Regression Models and Life-Tables. J. R. Stat. Soc. Ser. B 1972, 34, 187–220. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Vrieze, S.I. Model selection and psychological theory: A discussion of the differences between the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). Psychol. Methods 2012, 17, 228–243. [Google Scholar] [CrossRef]
- Harrell, F.E.; Lee, K.L.; Pollock, B.G. Regression models in clinical studies: Determining relationships between predictors and response. JNCI J. Natl. Cancer Inst. 1988, 80, 1198–1202. [Google Scholar] [CrossRef]
- Kooperberg, C.; Stone, C.J.; Truong, Y.K. Hazard regression. J. Am. Stat. Assoc. 1995, 90, 78–94. [Google Scholar] [CrossRef]
- Young, F.W.; Takane, Y.; de Leeuw, J. The principal components of mixed measurement level multivariate data: An alternating least squares method with optimal scaling features. Psychometrika 1978, 43, 279–281. [Google Scholar] [CrossRef]
- Sarle, W.S. SPLIT-CLASS: A Method for Multivariate Categorical Data Analysis; SAS Institute Technical Report; SAS Institute: Cary, NC, USA, 1995. [Google Scholar]
- Kuhfeld, W.F. Marketing Research Methods in SAS: Experimental Design, Choice, Conjoint, and Graphical Techniques; SAS Institute Inc.: Cary, NC, USA, 2009; pp. 1267–1268. [Google Scholar]
- Kuhfeld, W.F. SAS/STAT® 14.1 User’s Guide. The PRINQUAL Procedure. SAS Publishing. 2009. Available online: https://support.sas.com/documentation/onlinedoc/stat/141/prinqual.pdf (accessed on 14 February 2025).
- Breiman, L.; Friedman, J.H. Estimating Optimal Transformations for Multiple Regression and Correlation. J. Am. Stat. Assoc. 1985, 80, 580–598. [Google Scholar] [CrossRef]
- Tibshirani, R. Estimating transformations for regression via additivity and variance stabilization. J. Am. Stat. Assoc. 1988, 83, 394–405. [Google Scholar] [CrossRef]
- Wen, C.; Zhang, A.; Quan, S.; Wang, X. BeSS: An R Package for Best Subset Selection in Linear, Logistic and Cox Proportional Hazards Models. J. Stat. Softw. 2020, 94, 1–24. [Google Scholar] [CrossRef]
- ISO 10816-7:2009; Mechanical Vibration—Evaluation of Machine Vibration by Measurements on Non-Rotating Parts—Part 7: Rotodynamic Pumps for Industrial Applications, Including Measurements on Rotating Shafts. International Organization for Standardization, 2019. Available online: https://www.iso.org/es/contents/data/standard/04/17/41726.html (accessed on 24 February 2025).
- Bradshaw, S.; Liebner, T.; Cowan, D. Influence of impeller suction specific speed on vibration performance. In Proceedings of the Twenty-Ninth International Pump Users Symposium, Houston, TX, USA, 1–3 October 2013. [Google Scholar]
- Pavlou, M.; Ambler, G.; Qu, C.; Seaman, S.R.; White, I.R.; Omar, R.Z. An evaluation of sample size requirements for developing risk prediction models with binary outcomes. BMC Med Res. Methodol. 2024, 24, 146. [Google Scholar] [CrossRef]
- Sauerbrei, W.; Perperoglou, A.; Schmid, M.; Abrahamowicz, M.; Becher, H.; Binder, H.; Dunkler, D.; Harrell, F.E., Jr.; Royston, P.; Georg Heinze for TG2 of the STRATOS initiative. State of the art in selection of variables and functional forms in multivariable analysis—Outstanding issues. Diagn. Progn. Res. 2020, 4, 1–3. [Google Scholar] [CrossRef]
- De Carlo, F.; Arleo, M.A. Imperfect maintenance models, from theory to practice. In Proceedings of the International Conference on Reliability and Maintenance (ICRM), Buenos Aires, Argentina, 15–19 May 2017; pp. 345–356. [Google Scholar]
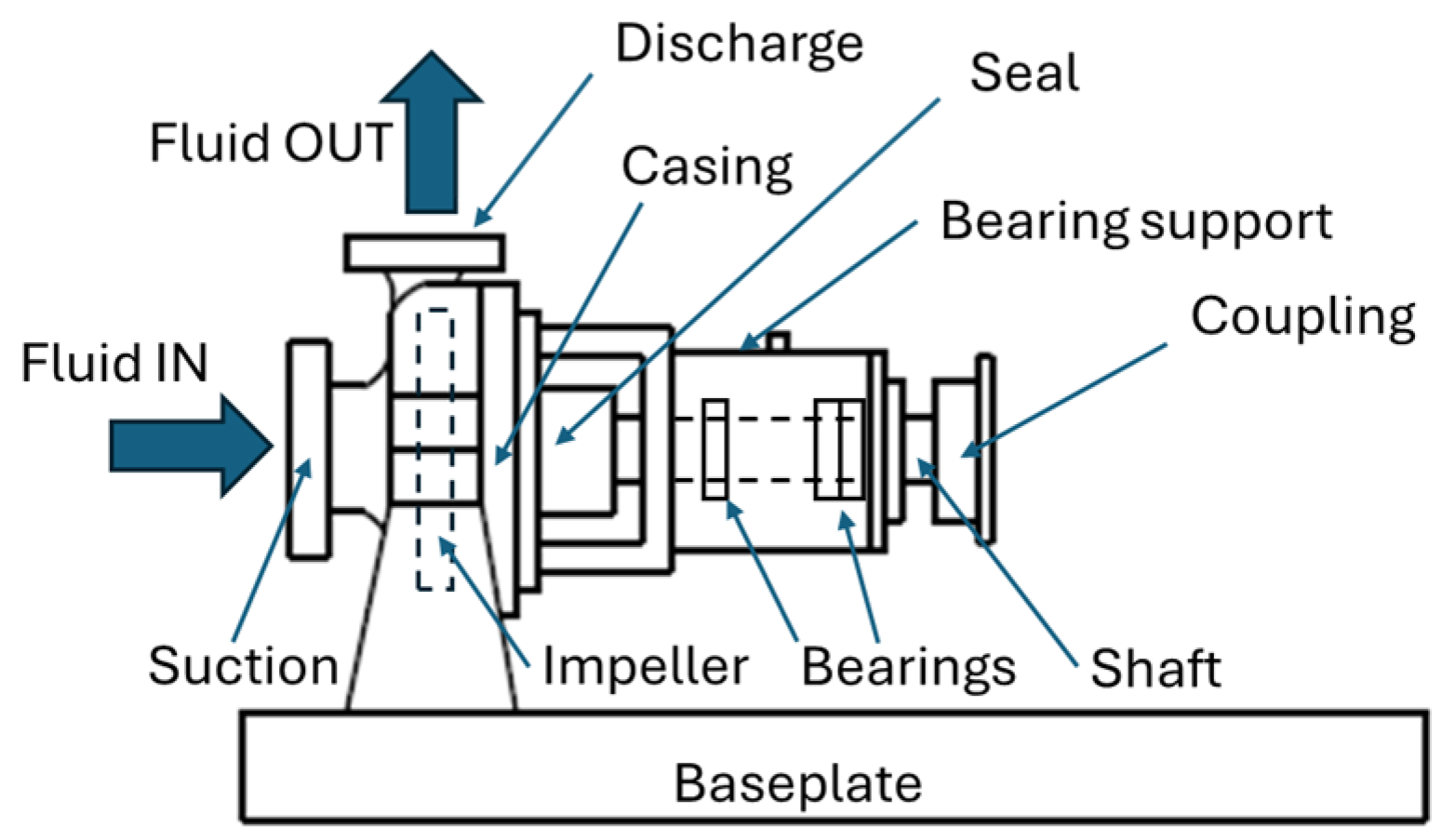

| Pump Code | Pump Type | Orientation |
|---|---|---|
| OH1 | Overhung, flexibly coupled | Horizontal, foot-mounted |
| OH2 | Overhung, flexibly coupled | Horizontal, centerline-supported |
| OH3 | Overhung, flexibly coupled | Vertical in-line, with bearing bracket |
| OH4 | Overhung, rigidly coupled | Vertical in-line, rigid coupling |
| OH5 | Overhung, close-coupled | Vertical in-line, close-coupled |
| OH6 | Overhung, close-coupled | High-speed, integrally geared |
| BB1-A | Between-bearings, single or two stage | Axially split, foot-mounted |
| BB1-B | Between-bearings, single or two stage | Axially split, near-centerline-mounted |
| BB2 | Between-bearings, single or two stage | Radially split, centerline-supported |
| BB3 | Between-bearings, multistage | Axially split, near-centerline-supported |
| BB4 | Between-bearings, multistage | Radially split, single-casing |
| BB5 | Between-bearings, multistage | Radially split, double-casing |
| VS1 | Vertically suspended | Single-casing, discharge through column |
| VS2 | Vertically suspended | Single-casing, discharge through column |
| VS3 | Vertically suspended | Single-casing, discharge through column |
| VS4 | Vertically suspended | Separate discharge pipe, line shaft |
| VS5 | Vertically suspended | Separate discharge pipe, cantilever shaft |
| VS6 | Vertically suspended | Double-casing, radially split |
| VS7 | Vertically suspended | Double-casing, radially split |
| Production Area | Refinery | Dataset | ||
|---|---|---|---|---|
| % Pumps | Qty of Pumps | % Pumps | Qty of Pumps | |
| Atmospheric distillation area | 41.3% | 503 | 44.8% | 303 |
| Conversion area | 26.3% | 320 | 35.8% | 241 |
| Fuel reduction area | 10.8% | 132 | 12.2% | 82 |
| Tanks and dock | 21.6% | 263 | 7.3% | 49 |
| Operating Conditions | Hydraulics | Mechanical | Sealing | Age | Maintenance Historian |
|---|---|---|---|---|---|
| Fluid type | Double suction | rpm | Seal arrgt. | API 610 ed. | Lube workorders |
| ISO 10816-7 [67] vib zone | Tip speed | Power | Seal type | Ordinary workorders | |
| Bottom pump | Diameter ratio | Bearing type | API 682 plan | ||
| Flow ratio | Efficiency | Lube type | Number seals | ||
| NPSH margin | Nss | ||||
| Relative density | Ns | ||||
| Dynamic viscosity | Nss ratio | ||||
| Vapor pressure Discharge pressure Fluid temperature | |||||
| Vibration level |
| Description | Index | Full Model Linear | Full Model RCS | Domain Linear | Domain RCS | Domain Red. RCS and Param. |
|---|---|---|---|---|---|---|
| Model Tests | LR X2 | 623.65 | 873.07 | 542.98 | 623.65 | 792.30 |
| d.f. | 60 | 103 | 35 | 75 | 56 | |
| Discrimination Indices | R2df,666 | 0.608 | 0.731 | 0.558 | 0.697 | 0.696 |
| Dxy | −0.691 | −0.768 | −0.665 | −0.757 | −0.760 | |
| R2df,501 | 0.675 | 0.785 | 0.637 | 0.762 | 0.770 | |
| Predictive Discrimination | Concordance | 0.846 | 0.883 | 0.832 | 0.878 | 0.880 |
| AIC | 5469.44 | 5299.74 | 5500.11 | 5328.58 | 5292.79 | |
| AIC X2 scale | 503.65 | 673.35 | 472.98 | 644.51 | 680.30 | |
| Validation | LR R2 | 0.5355 | 0.6377 | 0.5036 | 0.5987 | 0.6958 |
| Dxy | −0.6552 | −0.7152 | −0.6369 | −0.7071 | −0.7596 | |
| Calibration Slope | 0.8302 | 0.7215 | 0.8701 | 0.7378 | 0.8144 | |
| Calibration | Mean |error| | 0.0768 | 0.1006 | 0.0497 | 0.1031 | 0.1110 |
| 0.9 quantile |error| | 0.1275 | 0.2390 | 0.0732 | 0.2190 | 0.2410 |
| Predictor | Reduction | d.f. Saved | Justification | |
|---|---|---|---|---|
| Linear | Spline | |||
| API edition | Change from categorical to continuous variable (manufacturing year). | 6 | 6 | Reduce d.f. by using a continuous variable instead of a categorical. |
| Pump type | Reduction categories and include lubrication information. | 1 | 1 | Reduce d.f. and group less frequent categories. |
| Fluid type | Group similar categories. | 12 | 12 | Reduce d.f. and modeling issues with less frequent categories. |
| Bearings | Remove covariate. | 1 | 1 | Keep consistency in high-speed pumps. |
| ISO 10816-7 vib. zone | Remove covariate. | 3 | 3 | Redundant with global vibration level. |
| Seal type | Include variable pressurized in seal type cat. Increase 1 d.f. | −1 | −1 | Modeling issues with pressurized covariate. |
| Seals quantity | Remove covariate. | 1 | 1 | Redundant information, explained by pump type covariate. |
| Pressurized | Remove pressurized covariate. | 1 | 1 | Add the covariate information in seal type predictor. Modeling issues with this predictor. |
| Relative density | Remove covariate. | 1 | 4 | It is explained by vapor pressure, viscosity, fluid and temperature. |
| Nss | Remove and change into a different predictor (stable). | 1 | 4 | Change the predictor to stable parameter. |
| Stable | Add a predictor that contains more information than Nss. | −1 | −4 | To include information lost by removing Nss. |
| TOTAL | 25 | 28 | ||
| Predictor | Reduction | d.f. Saved | Change of LR X2 |
|---|---|---|---|
| Number of Workorders | Parametrized log (Workorders + 1). | 3 | +33.00 |
| Fluid temperature | Reduce number of knots. | 1 | +18.42 |
| Discharge pressure | Change from spline to linear. | 3 | −5.78 |
| Speed (rpm) | Parametrized from linear to sqrt (rpm). | 1 | +0.79 |
| Power | Reduce number of knots. | 1 | −1.25 |
| Overall vibration | Reduce number of knots. | 1 | −3.35 |
| Flow ratio | Reduce number of knots. | 2 | +0.70 |
| NPSH margin | Change from spline to linear. | 2 | +2.02 |
| Vapor pressure | Reduce number of knots and convergence issues. | 1 | +1.99 |
| Tip speed | Reduce number of knots. | 1 | +5.00 |
| Ratio diameter | Reduce number of knots. | 1 | −5.93 |
| Suction stability | Reduce number of knots. | 1 | −2.49 |
| Number of Lube Workorders | Reduce number of knots. | 1 | +2.60 |
| TOTAL | 19 | +45.72 |
| Description | Index | PCA Dom Red RCS & Param. | PCA Transf. | PCA Transf. RCS | PCA AVAS | Sparse PCA Raw RCS | Sparse PCA Transf. | Sparse PCA Transf. RCS | Sparse PCA AVAS |
|---|---|---|---|---|---|---|---|---|---|
| Model Tests | LR X2 | 740.76 | 595.51 | 736.40 | 695.50 | 690.35 | 594.28 | 674.62 | 687.74 |
| d.f. | 30 | 13 | 28 | 21 | 22 | 11 | 18 | 16 | |
| Explained Var. | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| Discrimination Indices | R2 | 0.671 | 0.591 | 0.669 | 0.648 | 0.645 | 0.590 | 0.637 | 0.644 |
| Dxy | −0.742 | −0.706 | −0.740 | −0.744 | −0.740 | −0.706 | −0.736 | −0.744 | |
| R2df,501 | 0.758 | 0.687 | 0.757 | 0.740 | 0.737 | 0.688 | 0.730 | 0.738 | |
| Predictive Discrimination | Concordance | 0.871 | 0.853 | 0.870 | 0.872 | 0.870 | 0.853 | 0.867 | 0.872 |
| AIC | 5292.33 | 5403.58 | 5292.70 | 5319.60 | 5326.74 | 5400.8 | 5334.48 | 5317.34 | |
| AIC X2 scale | 680.76 | 569.51 | 704.40 | 653.49 | 646.35 | 572.27 | 638.61 | 655.74 | |
| Validation | LR R2 | 0.633 | 0.568 | 0.633 | 0.618 | 0.617 | 0.566 | 0.613 | 0.620 |
| Dxy | −0.722 | −0.697 | −0.722 | −0.730 | −0.725 | −0.697 | −0.724 | −0.734 | |
| Calibration Slope | 0.886 | 0.937 | 0.898 | 0.920 | 0.923 | 0.934 | 0.933 | 0.936 | |
| Calibration | Mean |err| | 0.1278 | 0.0343 | 0.0740 | 0.0102 | 0.0077 | 0.0325 | 0.0116 | 0.0154 |
| 0.9 quantile |err| | 0.2583 | 0.0647 | 0.1581 | 0.0269 | 0.0182 | 0.0667 | 0.0264 | 0.0339 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vila Forteza, M.; Galar, D.; Kumar, U.; Goebel, K. Data Reduction in Proportional Hazards Models Applied to Reliability Prediction of Centrifugal Pumps. Machines 2025, 13, 215. https://doi.org/10.3390/machines13030215
Vila Forteza M, Galar D, Kumar U, Goebel K. Data Reduction in Proportional Hazards Models Applied to Reliability Prediction of Centrifugal Pumps. Machines. 2025; 13(3):215. https://doi.org/10.3390/machines13030215
Chicago/Turabian StyleVila Forteza, Marc, Diego Galar, Uday Kumar, and Kai Goebel. 2025. "Data Reduction in Proportional Hazards Models Applied to Reliability Prediction of Centrifugal Pumps" Machines 13, no. 3: 215. https://doi.org/10.3390/machines13030215
APA StyleVila Forteza, M., Galar, D., Kumar, U., & Goebel, K. (2025). Data Reduction in Proportional Hazards Models Applied to Reliability Prediction of Centrifugal Pumps. Machines, 13(3), 215. https://doi.org/10.3390/machines13030215









