Speed–Pressure Compound Control of Thrust System Based on the Adaptive Sliding Mode Control Strategy
Abstract
1. Introduction
2. Introduction to the Principle of the Thrust System and Modeling
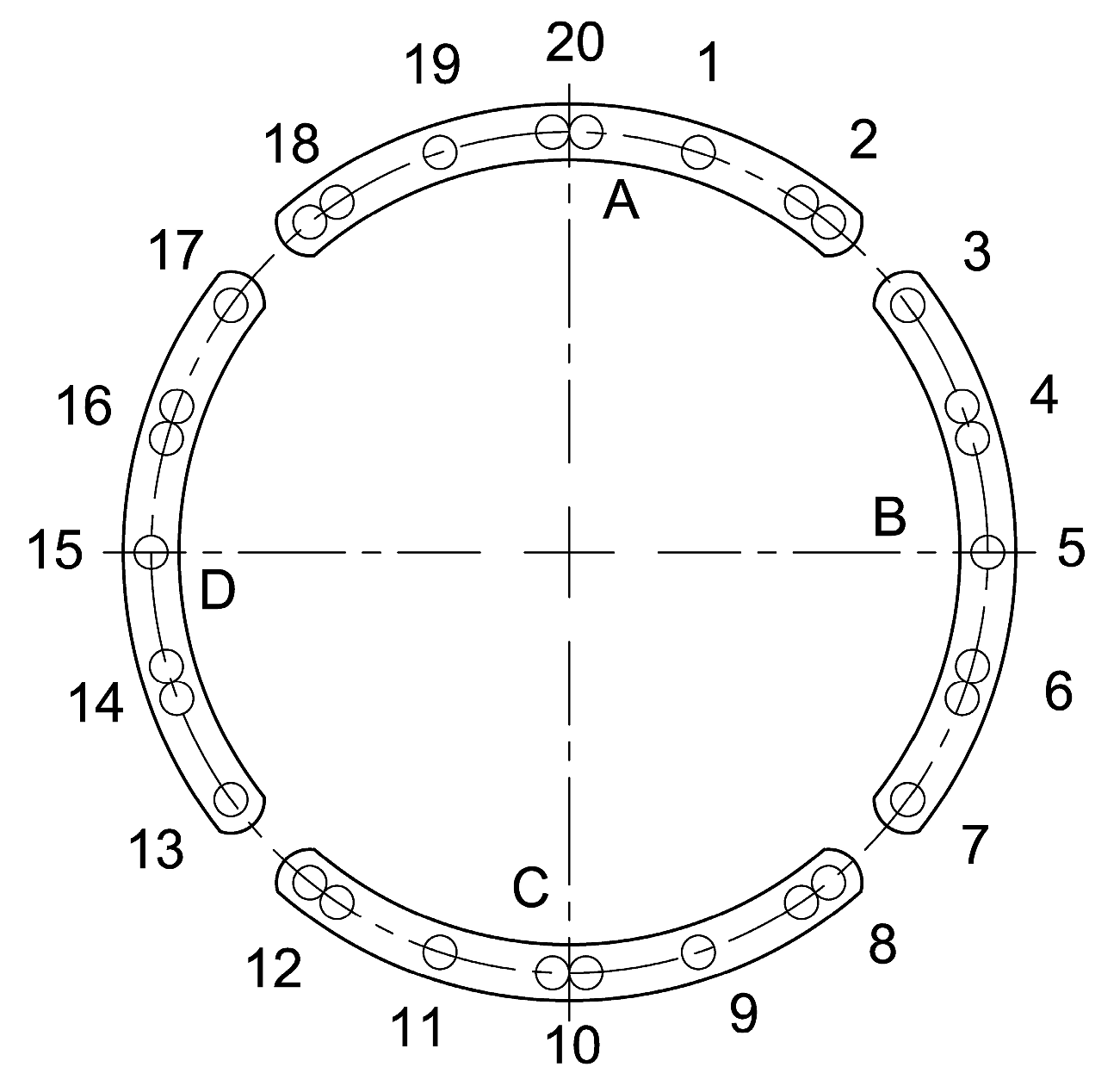
2.1. Principle of the Thrust System
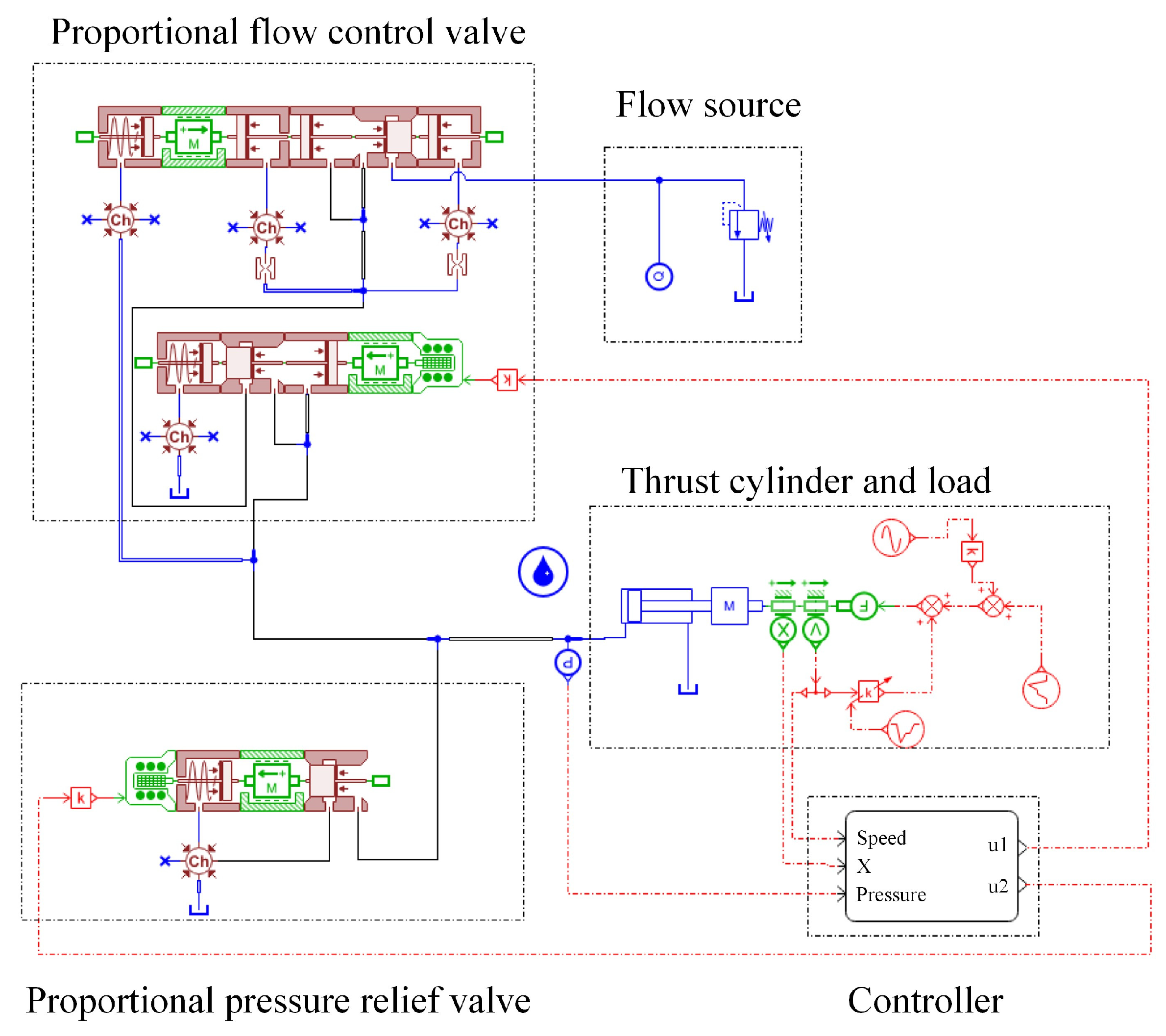
2.2. Thrust System Modeling
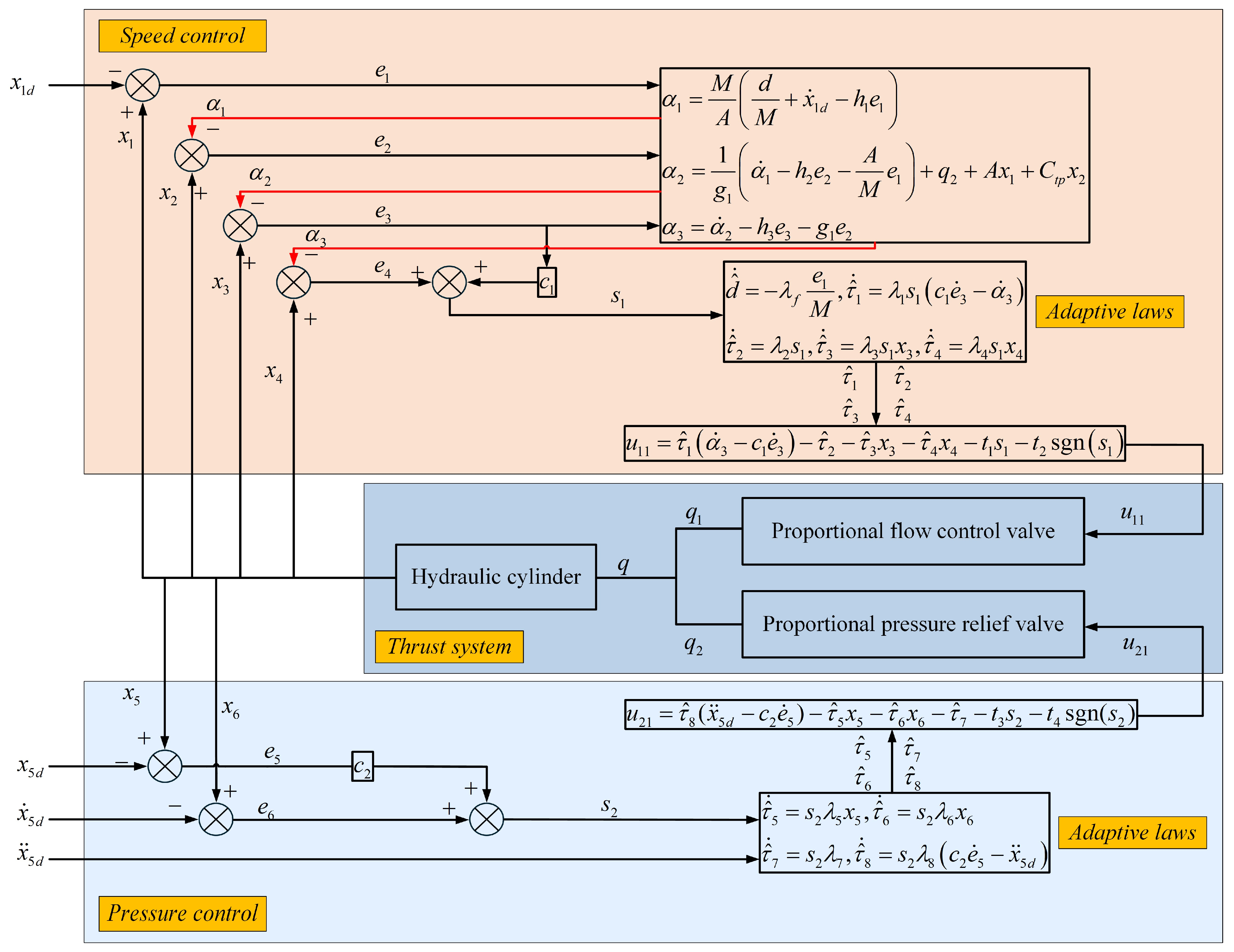
3. Design of the Controller
3.1. Design of the Speed Controller
3.2. Design of the Pressure Controller
4. Simulation Analysis
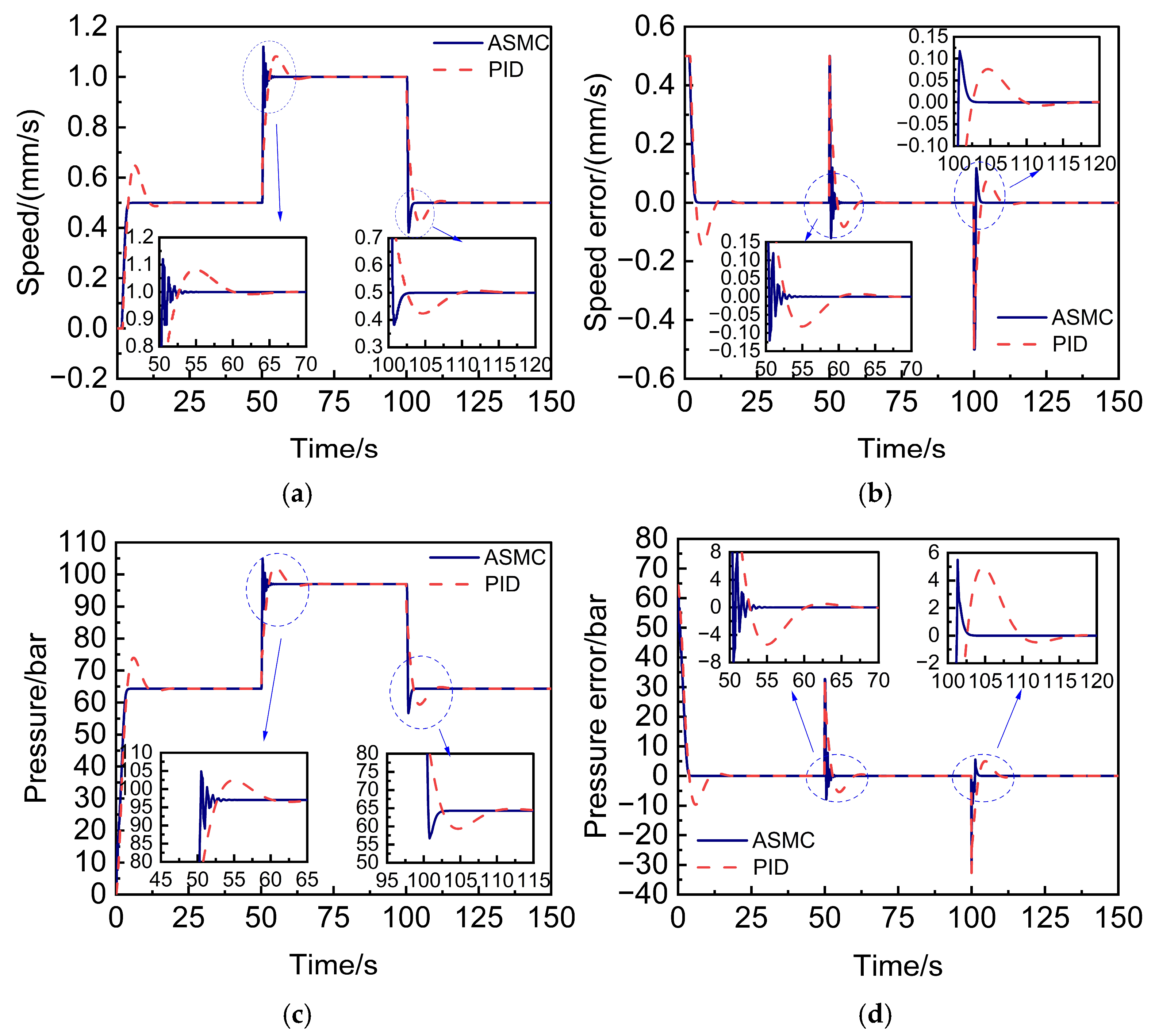
4.1. Simulation and Analysis of Speed Regulation Condition
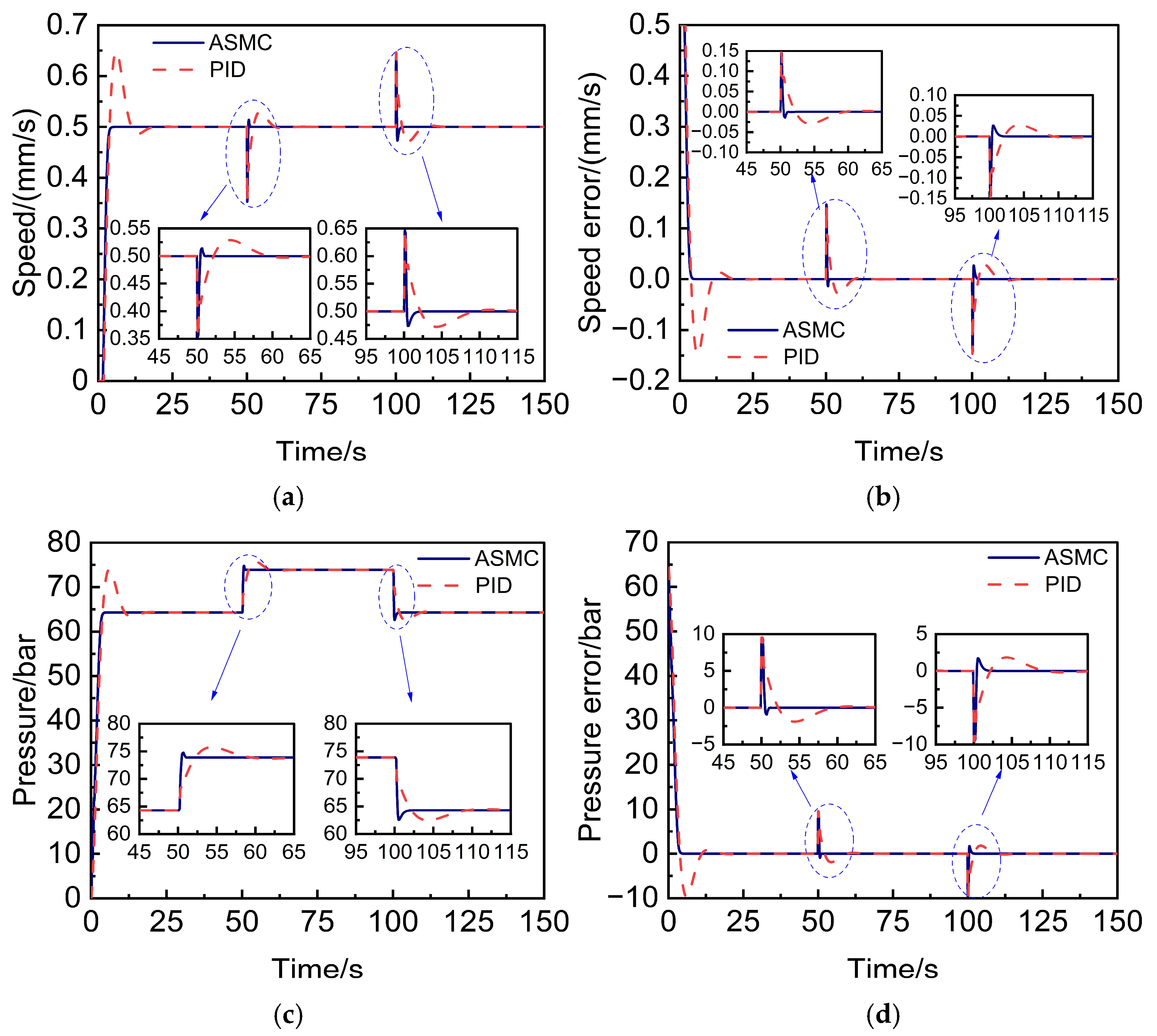
4.2. Simulation and Analysis of a Sudden Changed Load Condition
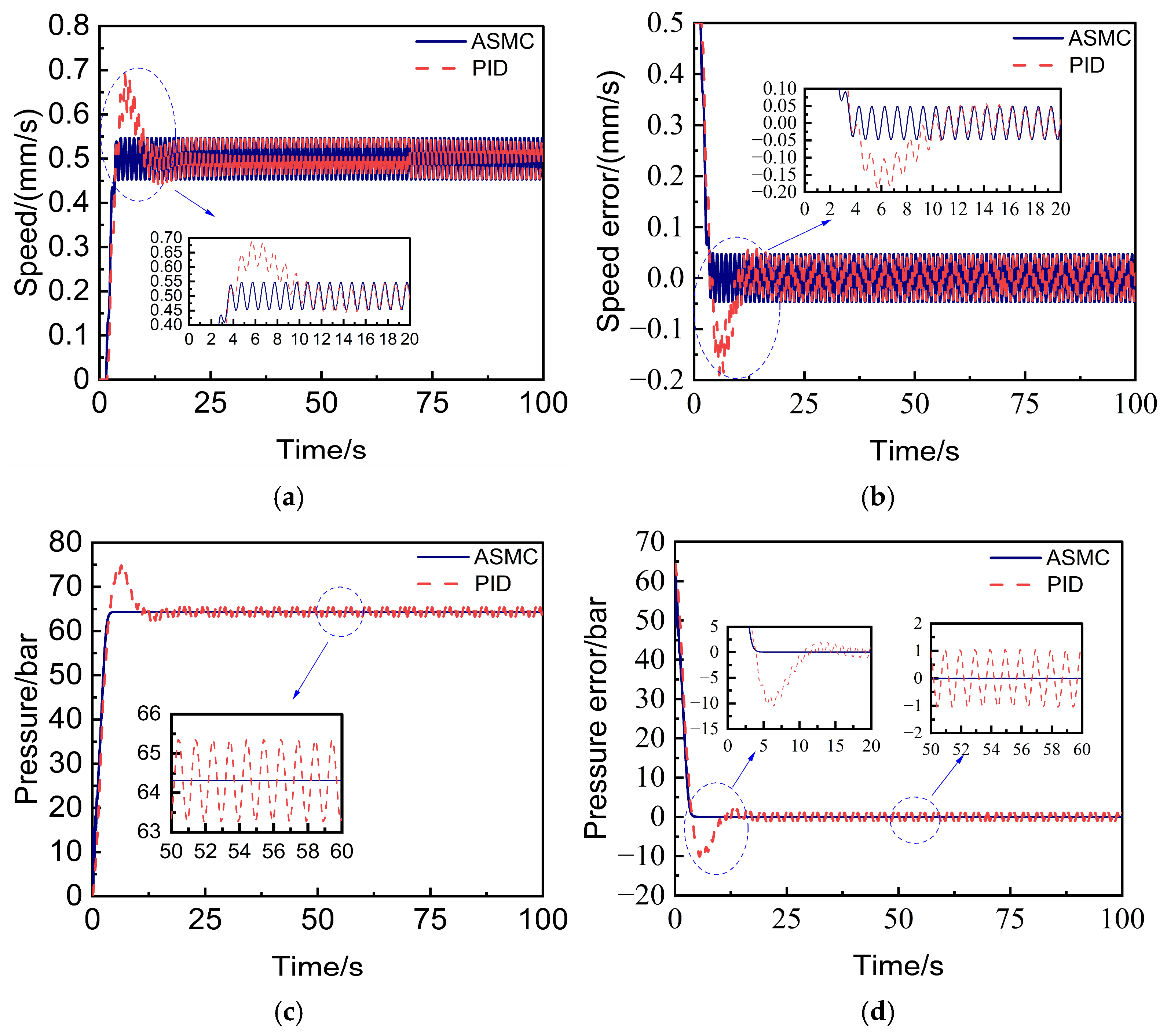
4.3. Simulation and Analysis of the Disturbed Load Condition
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yi, L.G.; Chen, K.; Lu, G.M. Progress in shield tunneling technology for urban underground space in China. Tunn. Constr. 2024, 44, 1. [Google Scholar]
- Bai, Y.; Gao, P.; Ren, R. Research on simulation control of shield machine propulsion hydraulic system. Mod. Manuf. Eng. 2020, 480, 128. [Google Scholar]
- Li, J.K.; Yan, B. The monitoring and analysis of surface subsidence of soft soil rock large section of subway tunnel shield construction. Adv. Mater. Res. 2014, 848, 78–82. [Google Scholar] [CrossRef]
- Meng, F.; Chen, P.; Kang, X. Effects of tunneling induced soil disturbance on the post- construction settlement in structured soft soil. Tunn. Undergr. Space Technol. 2018, 80, 53–63. [Google Scholar] [CrossRef]
- Pourtaghi, A.; Lotfollahi-Yaghin, M. Wavenet ability assessment in comparison to ANN for predicting the maximum surface settlement caused by tunneling. Tunn. Undergr. Space Technol. 2012, 28, 257–271. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, X.; Ji, W.; Simaan, M. Intelligent approach to estimation of tunnel-induced ground settlement using wavelet packet and support vector machines. J. Comput. Civ. Eng. 2017, 31, 04016053. [Google Scholar] [CrossRef]
- Bouayad, D.; Emeriault, F. Modeling the relationship between ground surface settlements induced by shield tunneling and the operational and geological parameters based on the hybrid PCA/ANFIS method. Tunn. Undergr. Space Technol. 2017, 68, 142–152. [Google Scholar] [CrossRef]
- Moeinossadat, S.; Ahangari, K. Estimating maximum surface settlement due to EPBM tunneling by Numerical Intelligent approach: A case study Tehran subway line 7, Tehran, Iran. Transp. Geotech. 2018, 18, 92–102. [Google Scholar] [CrossRef]
- Moghaddasi, R.; Noorian, M. ICA-ANN, ANN and multiple regression models for prediction of surface settlement caused by tunneling. Tunn. Undergr. Space Technol. 2018, 79, 197–209. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Fahimifar, A.; Ghaleini, E. Development of a new hybrid ANN for solving a geotechnical problem related to tunnel boring machine performance. Eng. Comput. 2020, 36, 345–357. [Google Scholar] [CrossRef]
- Libin, T.; SeonHong, N. Comparison of machine learning methods for ground settlement prediction with different tunneling datasets. J. Rock Mech. Geotech. Eng. 2021, 13, 1274–1289. [Google Scholar]
- Hussaine, S.; Linlong, M. Intelligent prediction of maximum ground settlement induced by EPB shield tunneling using automated machine learning techniques. Mathematics 2022, 10, 4637. [Google Scholar] [CrossRef]
- Yazdanparast, M.; Koushkgozar, H.; Hassanpour, J. Predicting maximum settlement induced by EPB shield tunneling through image processing and an intelligent approach. KSCE J. Civ. Eng. 2024, 28, 4076–4087. [Google Scholar] [CrossRef]
- Ren, Y.; Sun, Z.; Chu, C. An Attitude Control Strategy for Shield Thrusting. Tunn. Constr. 2019, 39, 1038–1044. [Google Scholar]
- Li, S.; Cao, X. Synchronous Control Characteristics Analysis of Shield Propulsion Hydraulic System Based on Tracking Differentiator and Self-Adaptive Nonlinear PID. Int. J. Pattern Recognit. Artif. Intell. 2021, 35, 2159053. [Google Scholar] [CrossRef]
- Li, G.; Niu, Y.; Chen, K. Research on hydraulic thrusting control system of shield machine based on BP-PID controller. Tunn. Constr. 2017, 37, 885. [Google Scholar]
- Liu, X.; Ma, L. Study on deviation correction control of shield machine based on PSO-PID. Comput. Meas. Control 2020, 28, 122–126. [Google Scholar]
- Gambhire, S.J.; Kishore, D.R.; Londhe, P.S. Review of sliding mode based control techniques for control system applications. Int. J. Dyn. Control 2021, 9, 363–378. [Google Scholar] [CrossRef]
- Bakhshande, F.; Bach, R.; Söffker, D. Robust control of a hydraulic cylinder using an observer-based sliding mode control: Theoretical development and experimental validation. Control Eng. Pract. 2020, 95, 104272. [Google Scholar] [CrossRef]
- Zhao, Y.; Qiu, C.; Huang, J. Terminal Sliding Mode Force Control Based on Modified Fast Double-Power Reaching Law for Aerospace Electro-Hydraulic Load Simulator of Large Loads. Actuators 2024, 13, 145. [Google Scholar] [CrossRef]
- Lao, L.; Chen, P. Adaptive Sliding Mode Control of an Electro-Hydraulic Actuator with a Kalman Extended State Observer. IEEE Access 2024, 12, 8970–8982. [Google Scholar] [CrossRef]
- Lu, S.; E, D.C.; Dong, X. Hydraulic cylinder displacement tracking control based on improved adaptive high-order sliding mode. Mach. Tool Hydraul. 2023, 51, 144–149. [Google Scholar]
- Zhang, J.; Wang, C.; Zhao, E. Compound sliding mode control of double-pump sub-chamber electro-hydraulic load-simulation system. Mach. Tool Hydraul. 2024, 52, 124–132. [Google Scholar]
- Shi, H.; Gong, G.; Yang, H. Electro-hydraulic proportional control of thrust system for shield tunneling machine. Autom. Constr. 2009, 18, 950–956. [Google Scholar]
- Gong, G.; Hu, G.; Yang, H. Control analysis of thrust hydraulic system for shield tunnelling machine. Zhongguo Jixie Gongcheng/China Mech. Eng. 2007, 18, 1391–1395. [Google Scholar]
- Zhang, W.; Yuan, Q.; Xu, Y. Research on control strategy of electro-hydraulic lifting system based on AMESim and MATLAB. Symmetry 2023, 15, 435. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Q. Adaptive robust tracking control of a proportional pressure-reducing valve with dead zone and hysteresis. Trans. Inst. Meas. Control 2018, 40, 2151–2166. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Liu, Y. Simulated loading experiment of proportional relief valve in the hydraulic system. Mach. Tool Hydraul. 2020, 48, 58–61. [Google Scholar]
- Guo, X.; Wang, C.; Liu, H. Extended-state-observer based sliding mode control for pump-controlled electro-hydraulic servo system. J. Beijing Univ. Aeronaut. Astronaut. 2020, 46, 1159–1168. [Google Scholar]
- Wang, X.; Yuan, D.; Jin, D. Determination of thrusts for different cylinder groups during shield tunneling. Tunn. Undergr. Space Technol. 2022, 127, 104579. [Google Scholar] [CrossRef]
- Sugimoto, M.; Sramoon, A. Theoretical model of shield behavior during excavation. I: Theory. J. Geotech. Geoenvironmental Eng. 2002, 128, 138–155. [Google Scholar] [CrossRef]

| Parameters | Value | Unit |
|---|---|---|
| Stratigraphic coefficient | 2.0 × 108 | N/(m/s) |
| Leakage coefficient | 0.4 | L/min/MPa |
| Density | 850 | kg/m3 |
| Bulk modulus | 1700 | MPa |
| Diameter of rodless chamber | 220 | mm |
| Diameter of piston rod | 160 | mm |
| Desired Speed (mm/s) | Desired Pressure (bar) | Stratigraphic Coefficient (N/(m/s)) | Load (kN) | |
|---|---|---|---|---|
| 0–50 s: | 0.5 | 64 | 2.0 × 108 | 100 |
| 50–100 s: | 1 | 96 | 2.0 × 108 | 100 |
| 100–150 s: | 0.5 | 64 | 2.0 × 108 | 100 |
| Desired Speed (mm/s) | Desired Pressure (bar) | Stratigraphic Coefficient (N/(m/s)) | Load (kN) | |
|---|---|---|---|---|
| 0–50 s: | 0.5 | 64 | 2.0 × 108 | 100 |
| 50–100 s: | 0.5 | 74 | 2.0 × 108 | 130 |
| 100–150 s: | 0.5 | 64 | 2.0 × 108 | 100 |
| Desired Speed (mm/s) | Desired Pressure (bar) | Stratigraphic Coefficient (N/(m/s)) | Load (kN) | Disturbed Load (kN) | |
|---|---|---|---|---|---|
| 0–100 s: | 0.5 | 64 | 2.0 × 108 | 100 | 10sin(2πt) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, T.; Liu, H.; Zheng, Z.; Jia, L.; Jiang, L.; Gong, G.; Yang, H.; Han, D. Speed–Pressure Compound Control of Thrust System Based on the Adaptive Sliding Mode Control Strategy. Machines 2025, 13, 213. https://doi.org/10.3390/machines13030213
Xing T, Liu H, Zheng Z, Jia L, Jiang L, Gong G, Yang H, Han D. Speed–Pressure Compound Control of Thrust System Based on the Adaptive Sliding Mode Control Strategy. Machines. 2025; 13(3):213. https://doi.org/10.3390/machines13030213
Chicago/Turabian StyleXing, Tong, Hong Liu, Zhe Zheng, Lianhui Jia, Lijie Jiang, Guofang Gong, Huayong Yang, and Dong Han. 2025. "Speed–Pressure Compound Control of Thrust System Based on the Adaptive Sliding Mode Control Strategy" Machines 13, no. 3: 213. https://doi.org/10.3390/machines13030213
APA StyleXing, T., Liu, H., Zheng, Z., Jia, L., Jiang, L., Gong, G., Yang, H., & Han, D. (2025). Speed–Pressure Compound Control of Thrust System Based on the Adaptive Sliding Mode Control Strategy. Machines, 13(3), 213. https://doi.org/10.3390/machines13030213






