Performance Analysis and Optimization of a Bio-Inspired Spider-Web-Shaped Energy Absorbing Component for Legged Landers
Abstract
1. Introduction
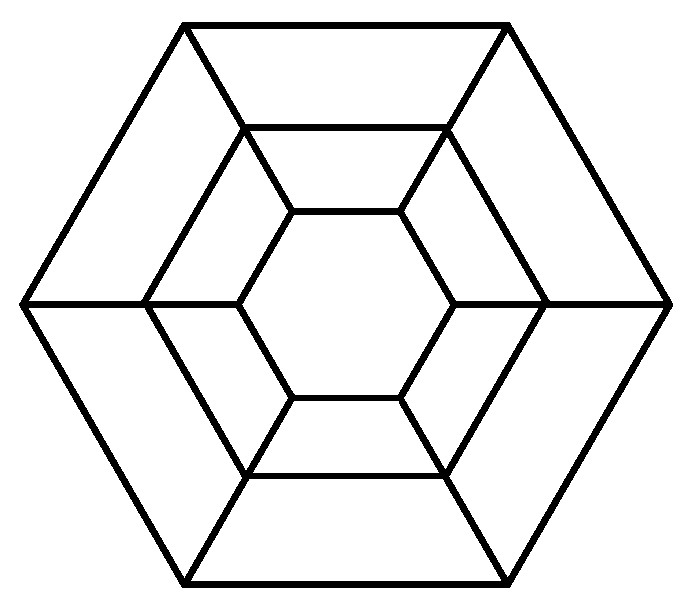
2. Configuration of the Bio-Inspired Spider-Web-Shaped Energy Absorber
- The web is represented by n concentric layers of regular polygons. All polygons have the same number of edges, and the layers are defined sequentially from the innermost (Layer 1) to the outermost (Layer n).
- All polygons lie in the same plane, share a common geometric center, and contain at least one pair of mutually parallel edges between adjacent layers.
- Let the circumcircle radius of the i-th layer polygon be Ri (i ≥ 1), For the adjacent inner and outer layers, the radii are denoted as Ri−1 and Ri+1, respectively. With R0 ≡ 0, the difference in circumcircle radii between two adjacent layers is defined as the layer thickness, expressed as:
- 4.
- The thickness of successive layers increases in a geometric progression, i.e., δi+1 = cδi, where c denotes the thickness ratio. According to this definition and the formula for a geometric sequence, the corresponding relationship among the radii can be derived.
- 5.
- The polygons of adjacent layers are connected by line segments extended through the common geometric center, and all structural members of the web are assigned a uniform width.
3. Performance Analysis of the Bio-Inspired Spider-Web-Shaped Energy Absorber
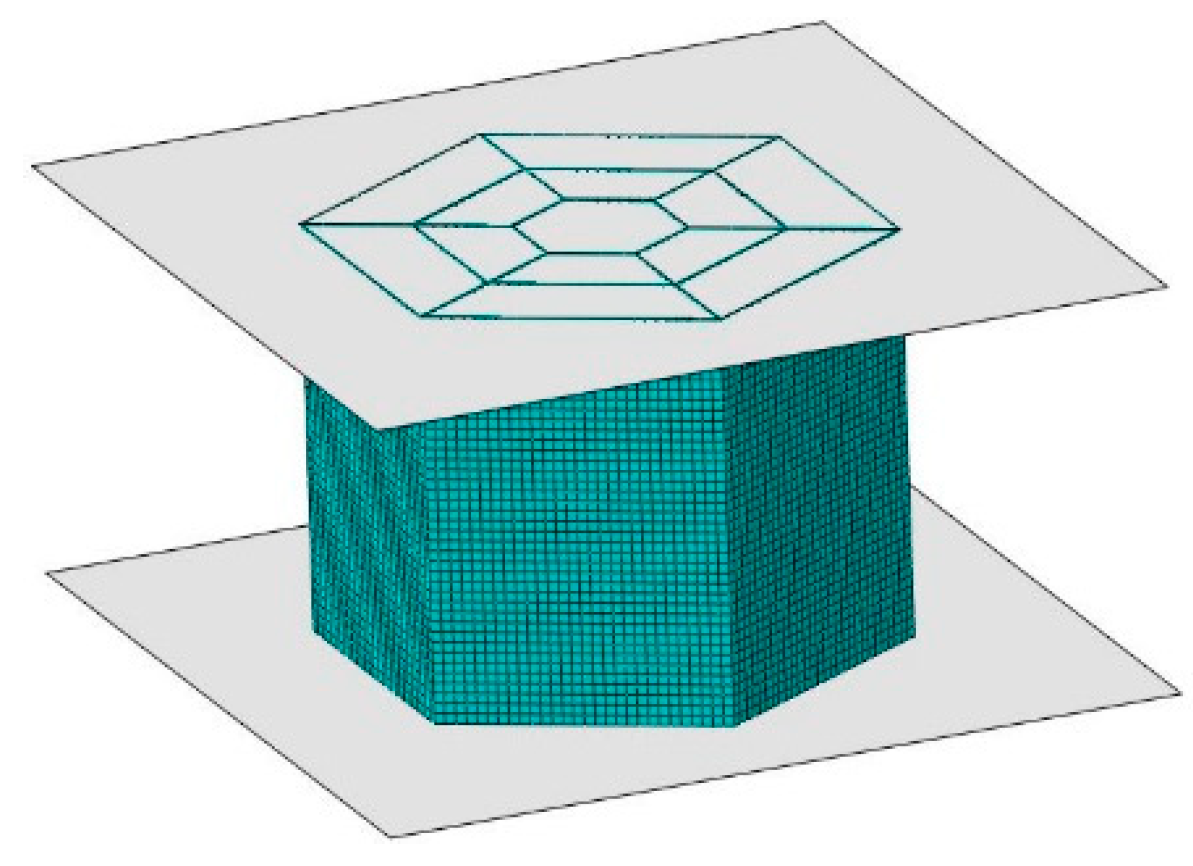
3.1. Parameterized FEM of the Energy Absorber
3.2. FEA of Buffering Performance
4. Optimization of the Cushioning Performance of the Bio-Inspired Spider-Web Energy Absorber
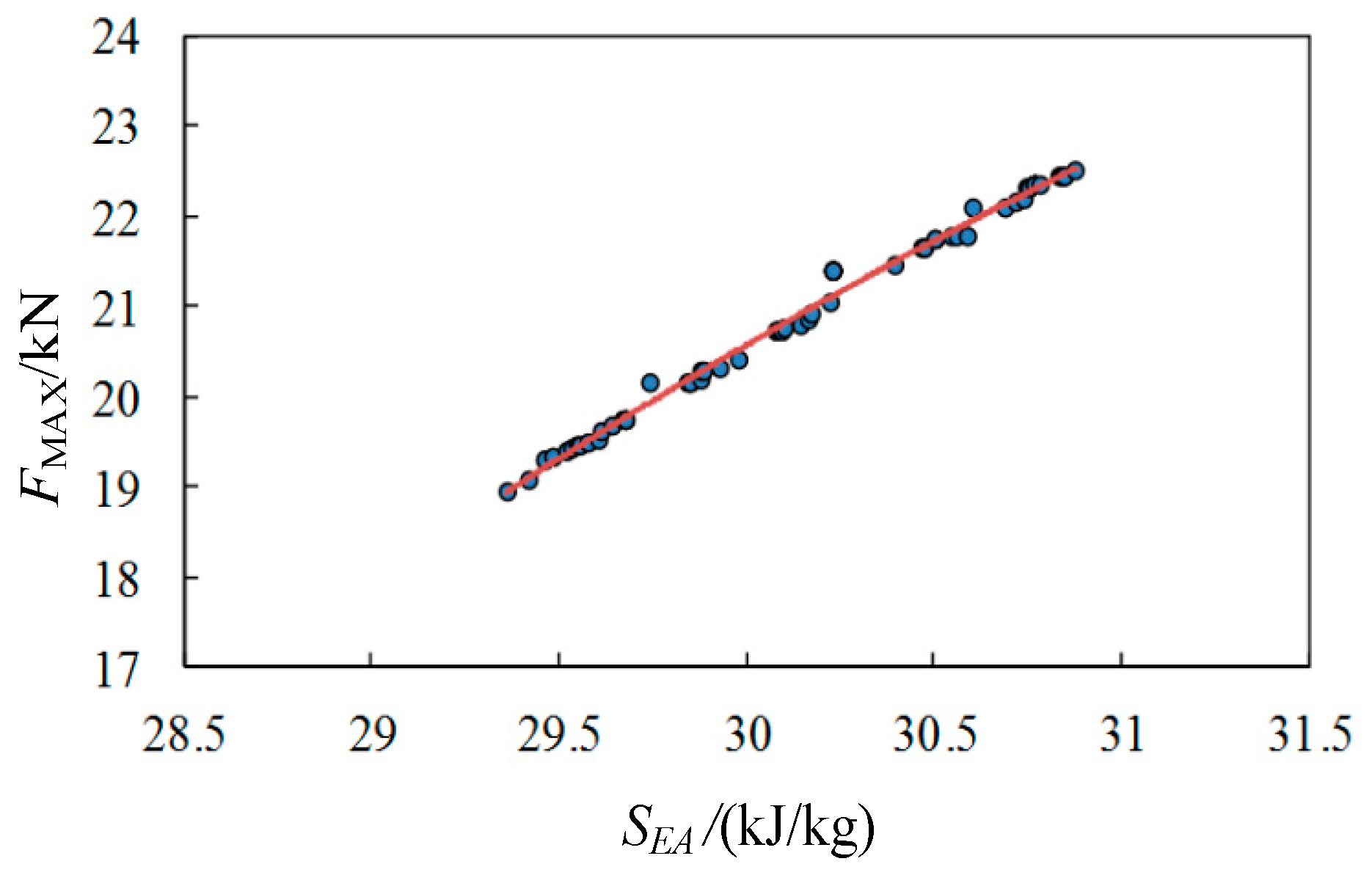
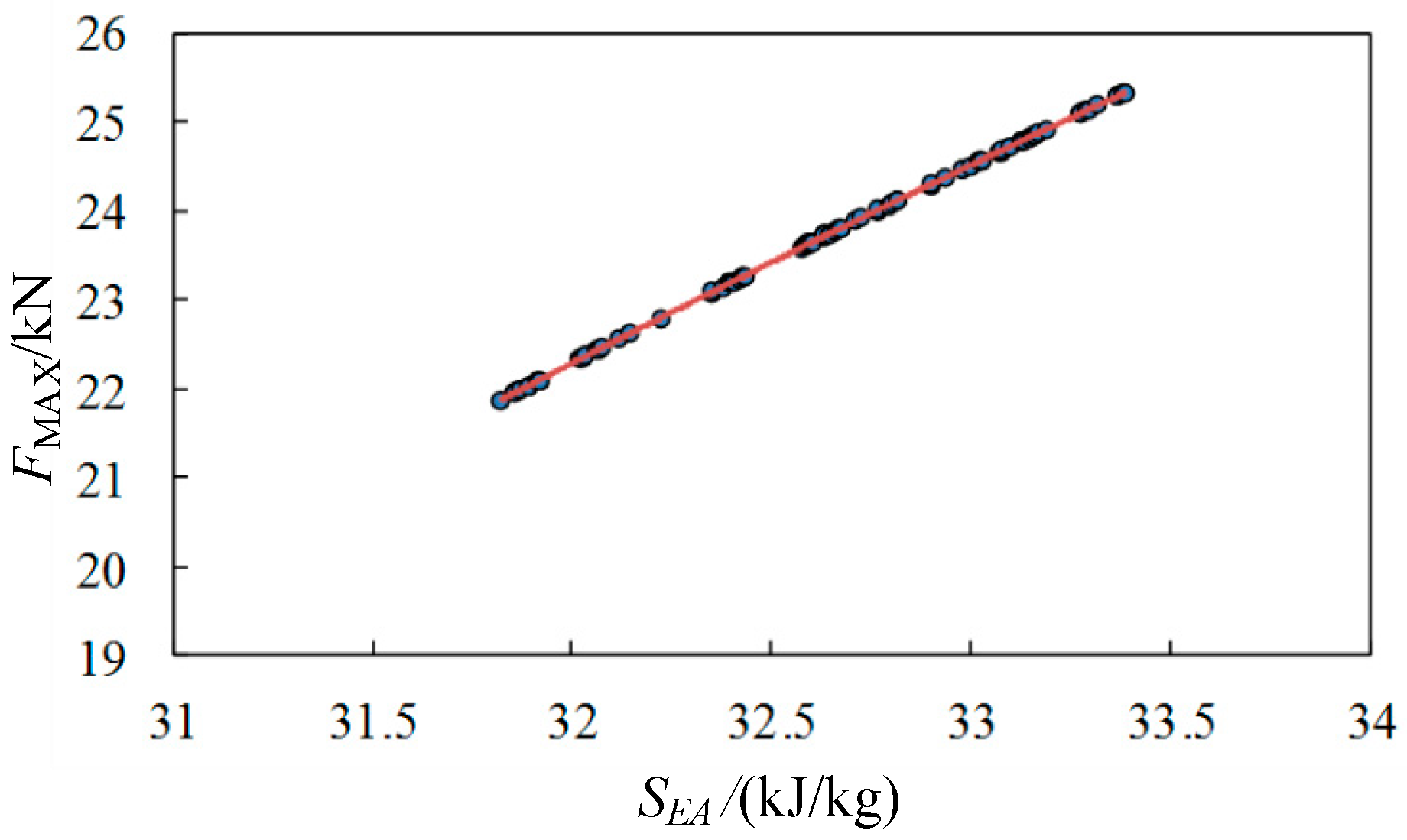
4.1. Response Surface Surrogate Model
4.2. Optimization of Buffering Performance
5. Integrated Energy-Absorption Performance Analysis of the Lander
5.1. Performance Evaluation of Serially Arranged Energy-Absorbing Components
5.2. Dynamic Analysis of the Entire Lander
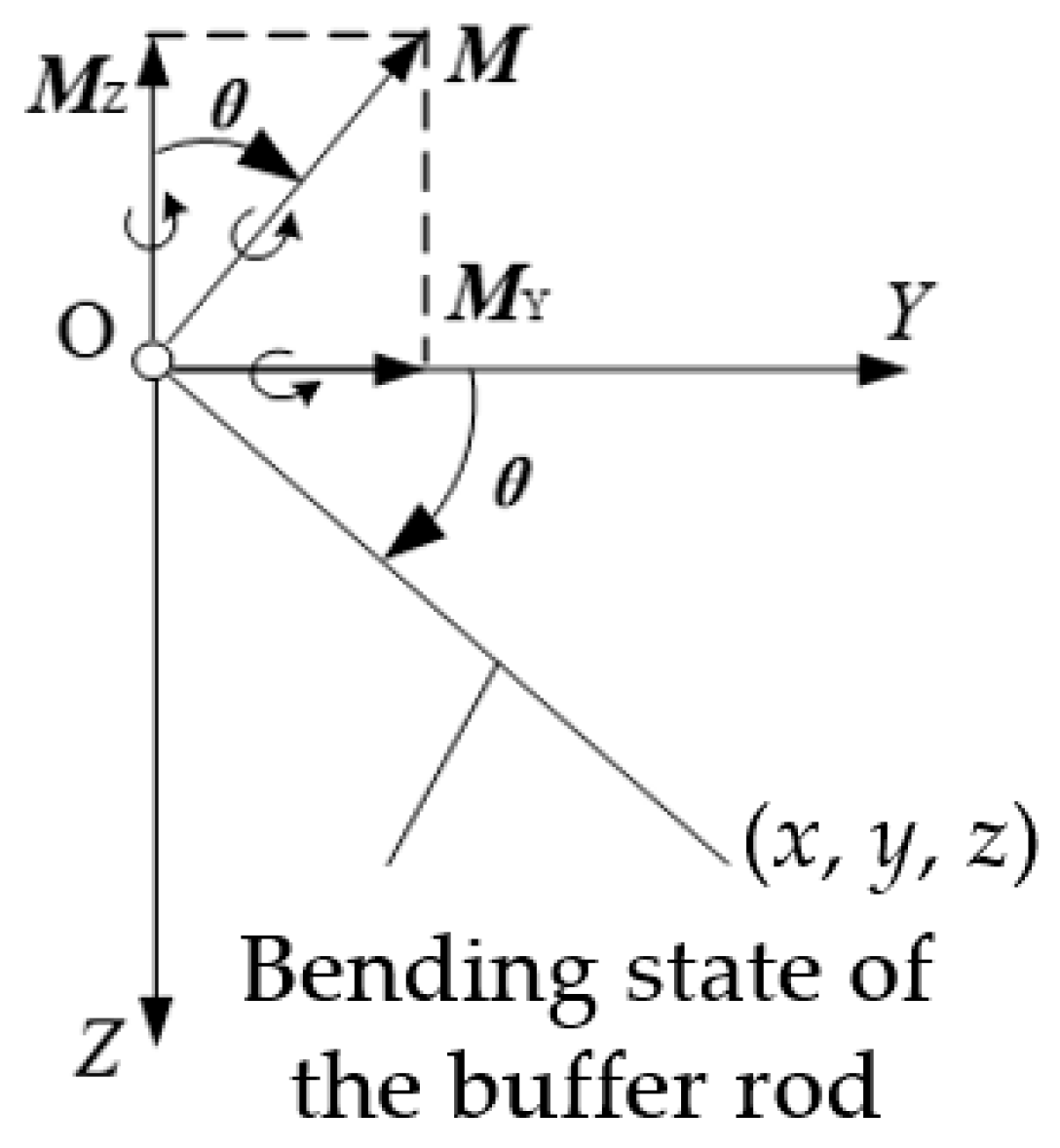
- Anti-overturning capability of the lander. The vertical plane containing the center points of any two adjacent footpads is defined as the overturning plane. During landing, the minimum distance LD between the lander’s center of mass and the overturning plane must remain greater than zero [31]; otherwise, the lander is regarded as overturned.
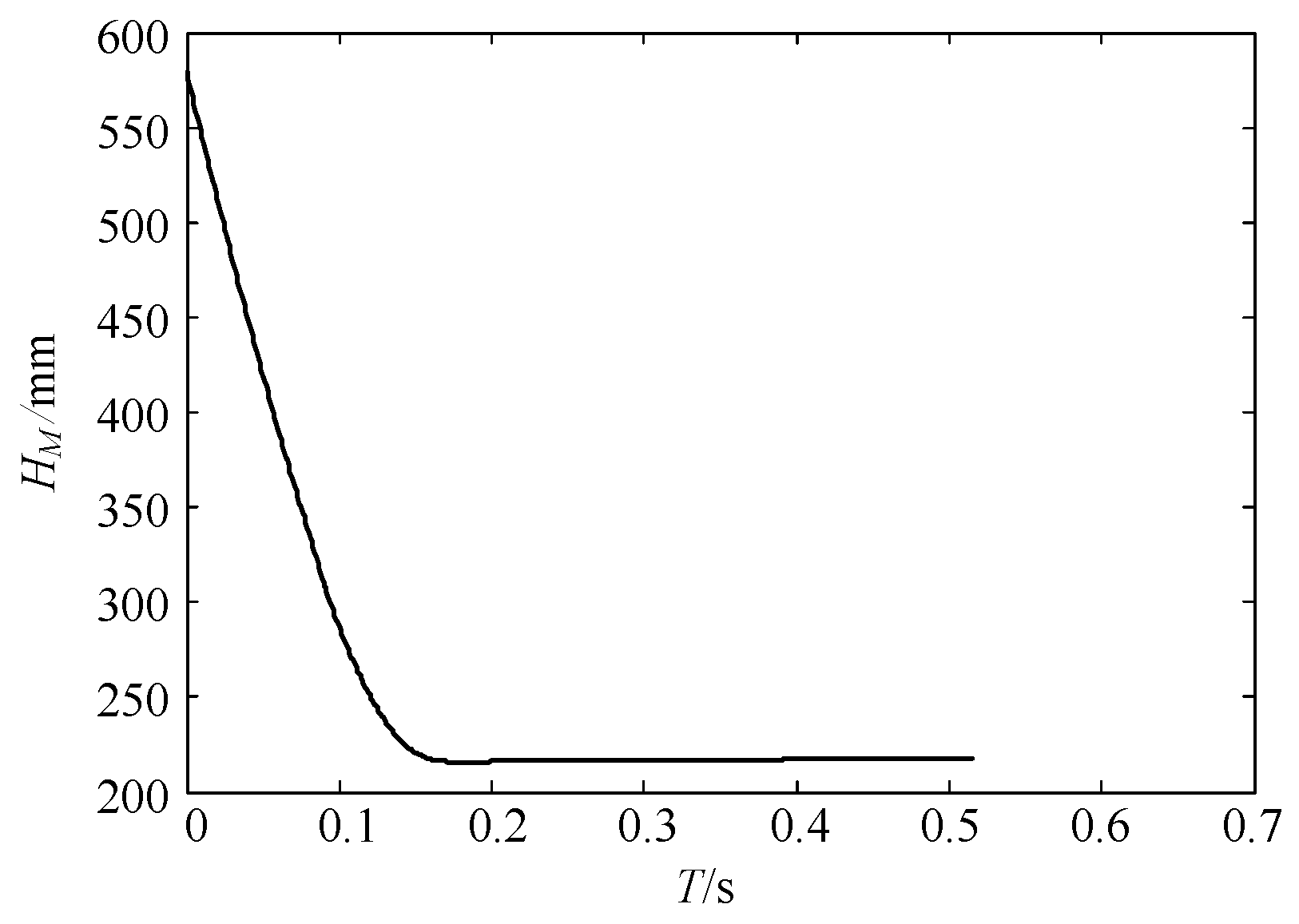
- Anti-damage capability of the main engine nozzle. During touchdown, the minimum vertical distance HM between the center point of the nozzle bottom—located at the base of the lander’s main structure—and the planetary surface must be greater than 200 mm.
- Acceleration overload characteristics. Considering that the payload instruments onboard the lander can only withstand limited overloads, the acceleration overload GL during the soft-landing process should generally not exceed 13 g to ensure the success of the exploration mission.
- Energy absorption performance of the auxiliary struts. As the primary energy-absorbing components of the lander, the auxiliary struts must ensure that their buffer stroke DM remains less than 80 mm under nominal landing conditions.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| m | n | c | d/mm | SAE/(kJ/kg) | Fmax/kN | Fave/kN |
|---|---|---|---|---|---|---|
| 8 | 4 | 1.0564 | 0.1 | 17.54902888 | 10.8827 | 4.183177143 |
| 10 | 3 | 1.1385 | 0.1026 | 16.90981224 | 10.9891 | 3.716534733 |
| 9 | 5 | 1.1538 | 0.1051 | 21.75517072 | 13.0066 | 6.317426602 |
| 7 | 4 | 1.1487 | 0.1077 | 17.18371127 | 11.6465 | 4.135951659 |
| 11 | 4 | 1.0821 | 0.1103 | 21.87818901 | 13.3498 | 6.408761329 |
| 7 | 5 | 1.1333 | 0.1128 | 19.3688417 | 14.02 | 5.601514532 |
| 10 | 3 | 1.0308 | 0.1154 | 17.73160173 | 11.685 | 4.403440465 |
| 7 | 6 | 1.0256 | 0.1179 | 20.34110979 | 17.3044 | 7.256318687 |
| 9 | 6 | 1.0872 | 0.1205 | 24.39294826 | 16.8444 | 9.26953239 |
| 12 | 5 | 1.1538 | 0.1231 | 27.50393461 | 18.594 | 10.39317247 |
| 10 | 5 | 1 | 0.1256 | 23.46560326 | 17.3626 | 8.858411942 |
| 8 | 3 | 1.0769 | 0.1282 | 16.53210892 | 12.707 | 4.193494049 |
| 11 | 4 | 1.1897 | 0.1308 | 23.40011694 | 15.6945 | 8.000165678 |
| 9 | 6 | 1.1795 | 0.1333 | 26.25826307 | 20.0739 | 10.5743346 |
| 12 | 5 | 1.0513 | 0.1359 | 27.57666063 | 19.3898 | 11.81879401 |
| 6 | 4 | 1.0718 | 0.1385 | 17.98435444 | 14.524 | 5.396871558 |
| 8 | 4 | 1.0051 | 0.141 | 20.71502467 | 15.6925 | 7.039913792 |
| 9 | 3 | 1.1744 | 0.1436 | 18.73033967 | 14.723 | 5.520142033 |
| 7 | 5 | 1.1949 | 0.1462 | 21.95592698 | 16.7245 | 8.047709455 |
| 11 | 3 | 1.1026 | 0.1487 | 20.48681212 | 16.5852 | 6.788772706 |
| 11 | 4 | 1.0154 | 0.1513 | 24.85434488 | 18.6526 | 10.08825538 |
| 7 | 6 | 1.0923 | 0.1538 | 23.20862942 | 21.8901 | 10.42033155 |
| 9 | 5 | 1.1077 | 0.1564 | 25.17421387 | 20.2208 | 11.04137353 |
| 6 | 4 | 1.1436 | 0.159 | 19.75357552 | 16.4705 | 6.681771614 |
| 12 | 5 | 1.1231 | 0.1615 | 29.08070728 | 23.181 | 14.53231237 |
| 10 | 6 | 1.1179 | 0.1641 | 29.65395727 | 26.0119 | 15.64965319 |
| 10 | 5 | 1.2 | 0.1667 | 28.24791098 | 21.5655 | 13.31839603 |
| 7 | 5 | 1.0103 | 0.1692 | 21.77857016 | 22.0897 | 9.901310134 |
| 10 | 3 | 1.0205 | 0.1718 | 22.02998303 | 17.5688 | 8.148217814 |
| 6 | 4 | 1.041 | 0.1744 | 19.52189516 | 18.5728 | 7.436543735 |
| 11 | 5 | 1.0359 | 0.1769 | 29.31664866 | 24.8997 | 15.92152359 |
| 8 | 3 | 1.1128 | 0.1769 | 19.79449146 | 16.5892 | 6.909014085 |
| 11 | 4 | 1.1692 | 0.1821 | 27.20002216 | 22.2809 | 12.98523383 |
| 8 | 6 | 1.1641 | 0.1846 | 27.96524234 | 26.5813 | 15.12543305 |
| 6 | 5 | 1.0974 | 0.1872 | 22.30328615 | 21.7682 | 10.35510301 |
| 8 | 4 | 1.1846 | 0.1897 | 24.14628634 | 21.5849 | 10.63247246 |
| 12 | 4 | 1.0615 | 0.1923 | 28.96471035 | 24.6597 | 15.34592751 |
| 9 | 4 | 1.0462 | 0.1949 | 25.60069458 | 23.5611 | 12.39905185 |
| 8 | 6 | 1.0667 | 0.1974 | 27.60146537 | 27.5276 | 16.7534547 |
| 10 | 5 | 1.1282 | 0.2 | 30.31784877 | 28.6609 | 17.51730797 |
References
- Maeda, T.; Otsuki, M.; Hashimoto, T.; Hara, S. Attitude stabilization for lunar and planetary lander with variable damper. J. Guid. Control Dyn. 2016, 39, 1790–1804. [Google Scholar] [CrossRef]
- Lin, Q.; Kang, Z.Y.; Ren, J.; Zhao, Q.; Nie, H. Impact Analysis of lunar lander soft landing performance caused by the body gravity centerline shift. J. Aerosp. Eng. 2015, 28, 04014104. [Google Scholar] [CrossRef]
- Ponnusamy, D.; Maahs, G. Development and testing of leg assemblies for robotic lunar lander. In Proceedings of the 14th European Space Mechanisms and Tribology Symposium, Constance, Germany, 28–30 September 2011. [Google Scholar]
- Doiron, H.H.; Zupp, G.A. Apollo lunar module landing dynamics. In Proceedings of the Structure Dynamics and Materials Conference and Exhibit, Atlanta, GA, USA, 3–6 April 2000. [Google Scholar]
- Yang, J.Z.; Zeng, F.M.; Man, J.F.; Zhu, W. Design and verification of the landing impact attenuation system for Chang’E-3 lander. Sci. China Technol. 2014, 44, 440–449. [Google Scholar] [CrossRef]
- Li, M.; Liu, R.Q.; Luo, C.J.; Guo, H.; Ding, B. Numerical and experimental analyses on series aluminum honeycomb structures under quasi-static load. J. Vib. Shock 2013, 32, 50–56. [Google Scholar]
- Liaghat, G.H.; Alavinia, A. A comment on the axial crush of metallic honeycombs by WU and JIANG. Int. J. Impact Eng. 2003, 28, 1143–1146. [Google Scholar] [CrossRef]
- Hong, S.T.; Pan, J.; Tang, T. Quasi-static crush behavior of aluminum honeycomb specimens under compression dominant com-bined loads. Int. J. Plast. 2006, 22, 73–109. [Google Scholar] [CrossRef]
- Li, M.; Deng, Z.Q.; Guo, H.W.; Liu, R.Q.; Ding, B.C. Optimizing crashworthiness design of square honeycomb structure. J. Cent. South Univ. Technol. 2014, 21, 912–919. [Google Scholar] [CrossRef]
- Deng, L.; Wang, A.W.; Mao, L.W.; Li, K.B. Energy absorption characteristics of a square hole honeycomb sandwich plate under blast loading. J. Vib. Shock 2012, 31, 186–189. [Google Scholar]
- Hu, L.L.; Chen, Y.L. Mechanical properties of triangular honeycombs under in-plane impact loading. J. Vib. Shock 2011, 30, 226–229. [Google Scholar]
- Liu, R.Q.; Guo, H.W. Crashworthiness optimization of different topological structures of metal honeycomb used in a legged-typed lander. J. Vib. Shock 2013, 32, 7–14. [Google Scholar]
- Han, H.L.; Zhang, X.C. In-plane dynamic impact response characteristics of periodic 4-point star-shaped honeycomb struc-tures. J. Vib. Shock 2017, 36, 223–231. [Google Scholar]
- Zhang, G.Q. Energy Absorption and Low Velocity Impact Damage Resistance of Composite Lattice Structures; Harbin Institute of Technology: Harbin, China, 2014. [Google Scholar]
- Luo, C.J.; Liu, R.Q.; Deng, Z.Q.; Wang, C.; Li, M. Experimental studies of energy absorber filled with aluminum foam on the thin-walled met-al tube’s plastic deformation. J. Vib. Shock 2009, 28, 26–30. [Google Scholar]
- Zeng, F.; Pan, Y.; Hu, S.S. Evaluation of cushioning properties and energy-absorption capability of foam aluminium. Explos. Shock 2002, 22, 358–362. [Google Scholar]
- Liang, D.P.; Chai, H.Y.; Zeng, F.M. Nonlinear finite element modeling and simulation for landing leg of lunar lander. J. Beijing Univ. Aeronaut. Astronaut. 2013, 39, 11–15. [Google Scholar]
- Li, M. Research on Energy Absorbers of Legged-Type Lander and Dynamic Simulation on Its Soft Landing Process; Harbin Institute of Technology: Harbin, China, 2013. [Google Scholar]
- Chen, J.B.; Nie, H.; Zhao, J.C.; Bai, H.M.; Bo, W. Research of the factors of buffering performance in lunar lander. J. Astronaut. 2008, 29, 1729–1732. [Google Scholar]
- Tang, S. The Behavior of Aluminum Honeycomb Under Static and Dynamic Compression; Central South University: Changsha, China, 2014. [Google Scholar]
- Liu, R.Q.; Luo, C.J.; Wang, C.; Deng, Z.; Li, M. Research on cushion properties and its evaluation methods of legged-type lander’ s shock absorber. J. Astronaut. 2009, 30, 1180–1188. [Google Scholar]
- Yue, S.; Nie, H.; Zhang, M.; Luo, C. Analysis on performance of a damper used for vertical landing reusable launch vehicle. J. Astronaut. 2016, 37, 646–656. [Google Scholar]
- Kurtaran, H.; Eskandarian, A.; Marzougui, D. Crashworthiness design optimization using successive response surface approximations. Comput. Mech. 2002, 29, 409–421. [Google Scholar] [CrossRef]
- Song, S.G. Research on Design Method of Space Mechanism Based on Digital Design Theory; Beijing University of Aeronautics and Astronautics: Beijing, China, 2013. [Google Scholar]
- Blanchard, U.J. Full-Scale Dynamic Landing-Impact Investigation of a Prototype Lunar Module Landing Gear; National Aeronautics and Space Administration: Washington, DC, USA, 1969.
- Nohmi, M.; Miyahara, A. Modeling for lunar lander by mechanical dynamics software. In Proceedings of the Modeling and Simulation Technologies Conference and Exhibit, San Francisco, CA, USA, 15–18 August 2005. [Google Scholar]
- Wu, H.Y.; Wang, C.J.; Ding, J.Z.; Man, J.; Luo, M. Soft landing performance optimization for novel lander based on multiple working conditions. J. Beijing Univ. Aeronaut. Astronaut. 2017, 43, 776–781. [Google Scholar]
- Wu, H.Y.; Wang, C.J.; Ding, Z.M.; Ding, J.Z.; Liu, X.A. Configuration Optimization of Landing Gear under Two Kinds of Landing Modes. J. Astronaut. 2017, 38, 1032–1040. [Google Scholar]
- Wu, H.Y.; Wang, C.J.; Ding, J.Z.; Wang, J.; Luo, M. Collision parameters updating for single-leg dynamics simulation model of novel lander. J. Vib. Shock 2018, 37, 50–55. [Google Scholar]
- Wu, H.Y.; Wang, C.J.; Ding, J.Z.; Ding, Z. Dynamics simulation analysis for novel lander based on two kinds of landing mode. In Proceedings of the 9th International Conference on Measuring Technology and Mechatronics Automation, Changsha, China, 14–15 January 2017. [Google Scholar]
- Zupp, G.A.; Doiron, H.H. A Mathematical Procedure for Predicting the Touchdown Dynamics of a Soft-Landing Vehicle: NASA-TN-D-7045; NASA: Washington, DC, USA, 1971.


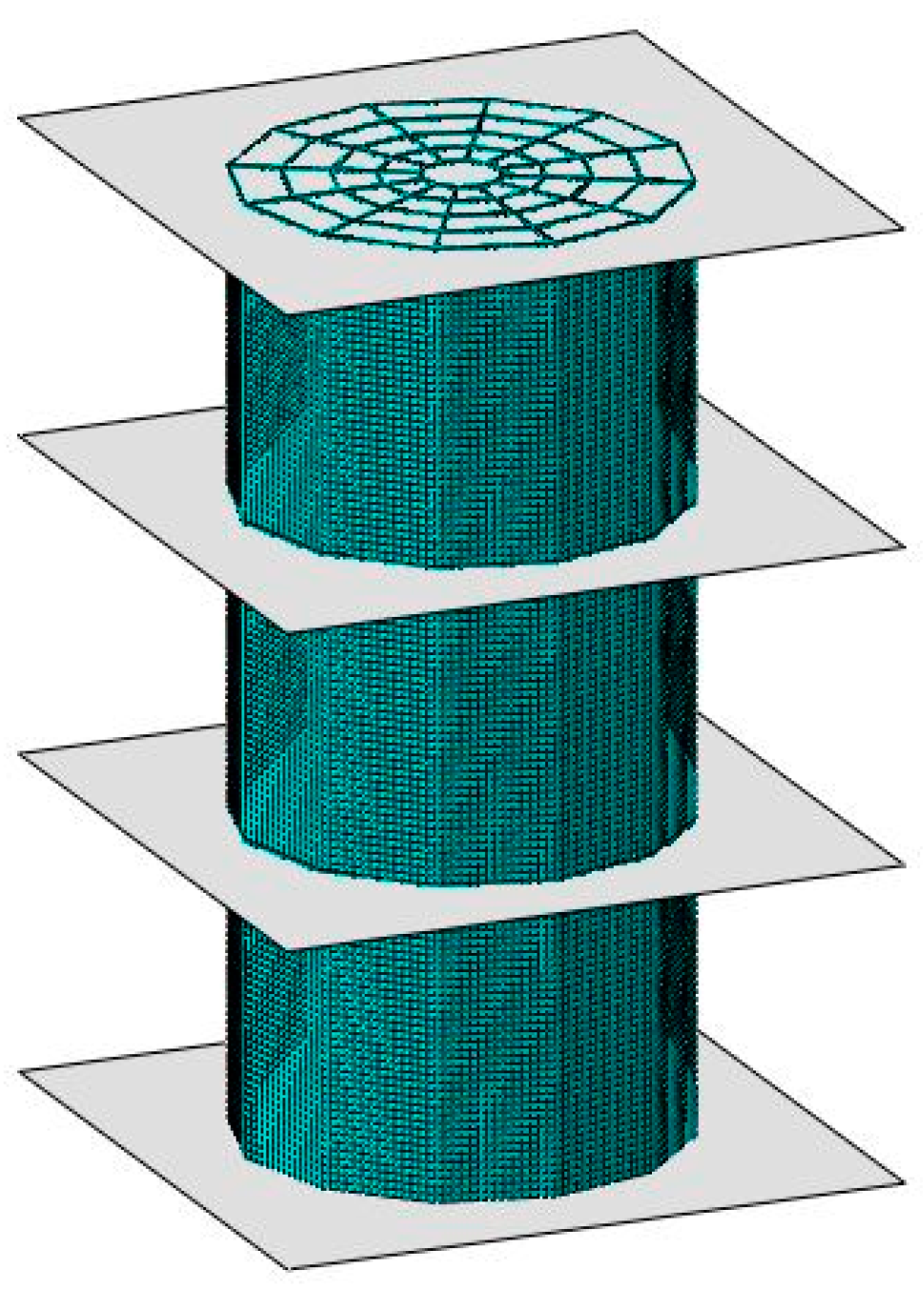
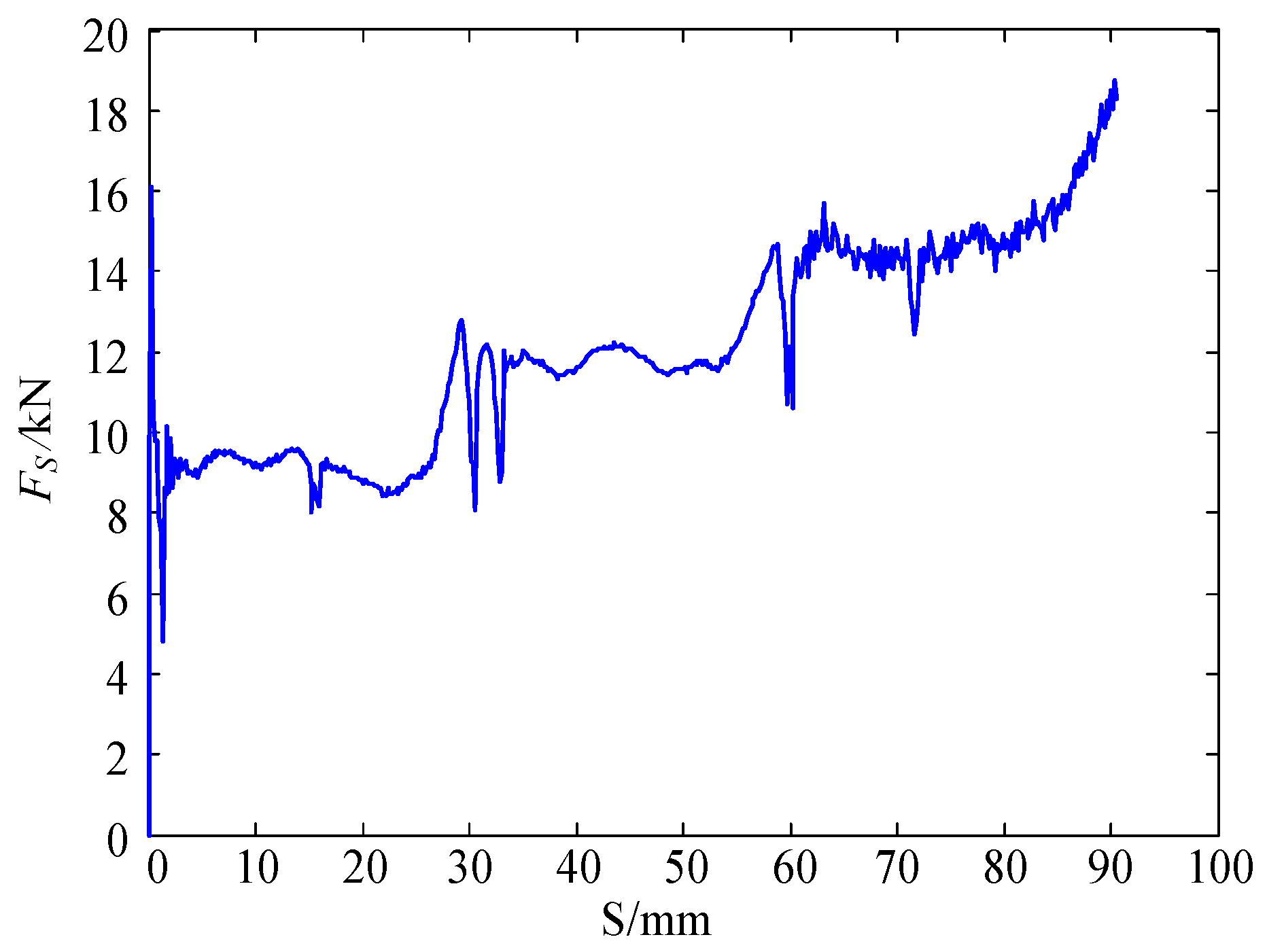
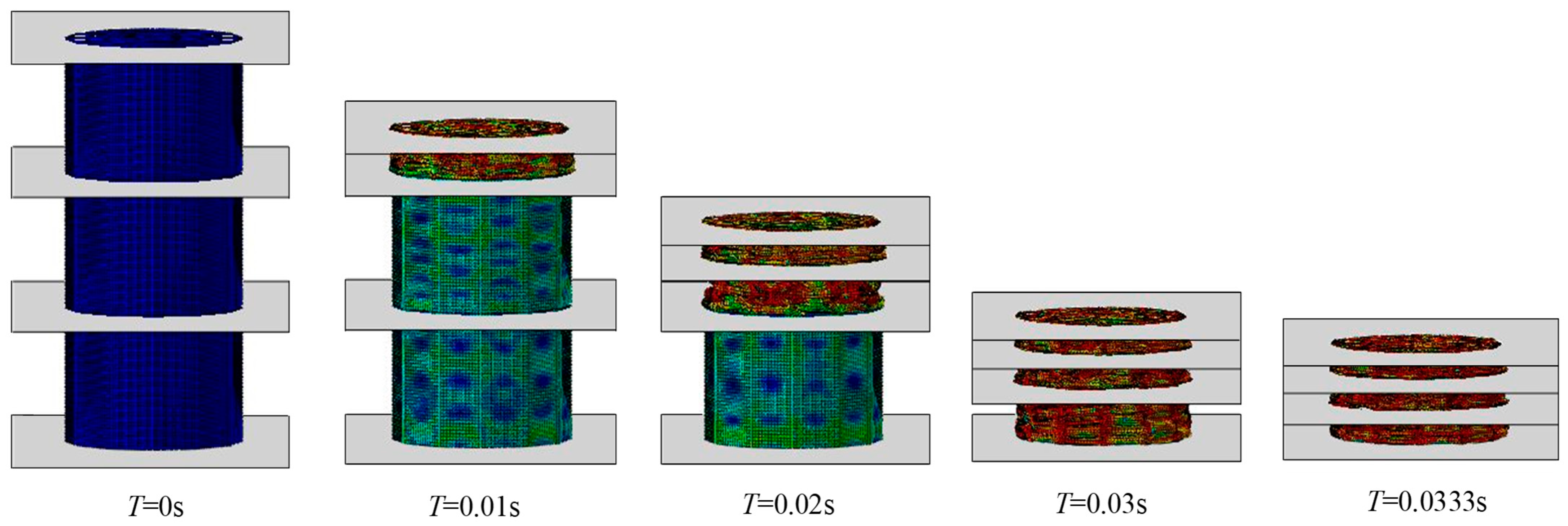


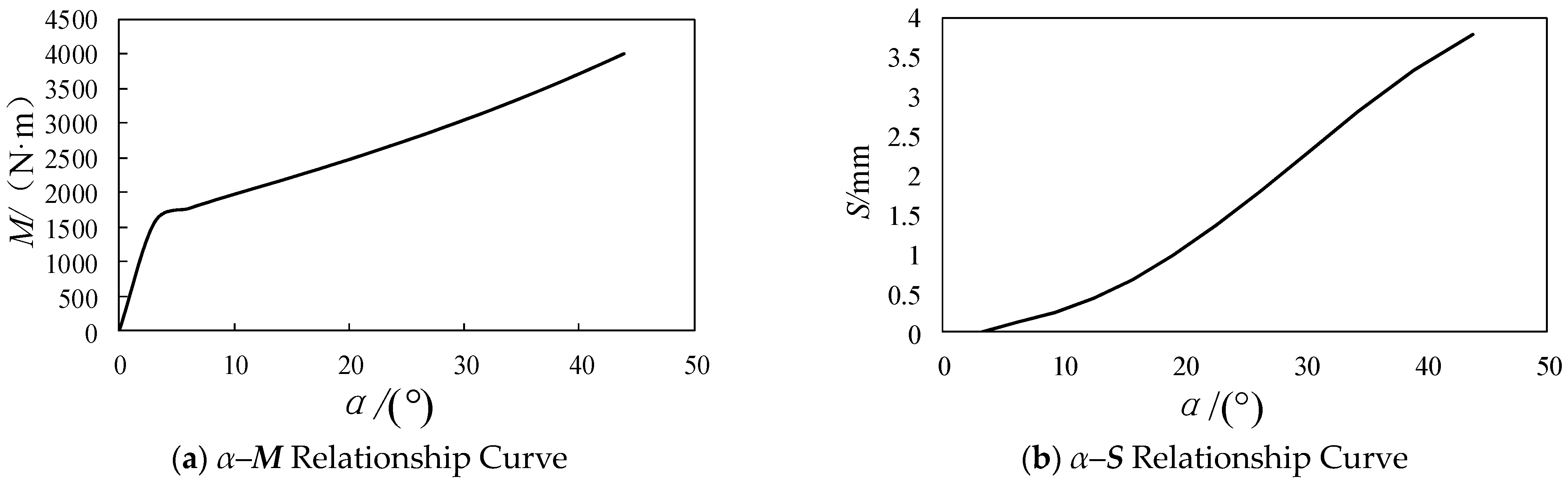



| Density (kg·m−3) | Elastic Modulus (GPa) | Poisson’s Ratio | Yield Strength (MPa) |
|---|---|---|---|
| 12.73 × 103 | 68 | 0.33 | 185 |
| m | n | c | d (mm) |
|---|---|---|---|
| 6~12 | 3~6 | 1~1.2 | 0.1~0.2 |
| Metric | R2 | RMSE |
|---|---|---|
| SAE | 0.995 | 0.00157 |
| Fmax | 0.984 | 0.00410 |
| Fave | 0.999 | 0.00194 |
| Type | Weak Buffering | Moderate Buffering | Strong Buffering |
|---|---|---|---|
| Ranges of Fave (kN) | 9~12 | 12~15 | 15~18 |
| Parameter | Population Size | Number of Generations | Crossover Index | Mutation Index | Crossover Probability |
|---|---|---|---|---|---|
| Value | 12 | 40 | 10 | 20 | 0.9 |
| Type of Energy-Absorbing Component | m | n | c | d (mm) |
|---|---|---|---|---|
| Weak buffering | 12 | 5 | 1.065 | 0.113 |
| Moderate buffering | 12 | 6 | 1.101 | 0.120 |
| Strong buffering | 12 | 6 | 1.200 | 0.141 |
| Parameter | Value |
|---|---|
| α (°) | 1~8 |
| nf | 0, 1, 2, 3 |
| θp (°) | 0~45 |
| Performance Index | Extreme Value | Number of Cases Exceeding Allowable Limit |
|---|---|---|
| Minimum LD | 807.308 mm | 0 |
| Minimum HM | 216.185 mm | 0 |
| Maximum GL | 11.234 g | 0 |
| Maximum DM | 75.366 mm | 0 |
| Performance Index | α (°) | θp (°) | nf |
|---|---|---|---|
| Minimum LD | 8 | 38 | 2 |
| Minimum HM | 5 | 0 | 3 |
| Maximum GL | 1 | 43 | 2 |
| Maximum DM | 8 | 26 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Wang, H.; Yang, K.; Zhang, B.; Wang, X.; Liu, K.; Zhou, S. Performance Analysis and Optimization of a Bio-Inspired Spider-Web-Shaped Energy Absorbing Component for Legged Landers. Machines 2025, 13, 1035. https://doi.org/10.3390/machines13111035
Liu X, Wang H, Yang K, Zhang B, Wang X, Liu K, Zhou S. Performance Analysis and Optimization of a Bio-Inspired Spider-Web-Shaped Energy Absorbing Component for Legged Landers. Machines. 2025; 13(11):1035. https://doi.org/10.3390/machines13111035
Chicago/Turabian StyleLiu, Xueao, Hui Wang, Kai Yang, Bin Zhang, Xuecong Wang, Kaiting Liu, and Shiming Zhou. 2025. "Performance Analysis and Optimization of a Bio-Inspired Spider-Web-Shaped Energy Absorbing Component for Legged Landers" Machines 13, no. 11: 1035. https://doi.org/10.3390/machines13111035
APA StyleLiu, X., Wang, H., Yang, K., Zhang, B., Wang, X., Liu, K., & Zhou, S. (2025). Performance Analysis and Optimization of a Bio-Inspired Spider-Web-Shaped Energy Absorbing Component for Legged Landers. Machines, 13(11), 1035. https://doi.org/10.3390/machines13111035




