Optimization Design of Blade Profile Parameters of Low-Speed and High-Torque Turbodrill Based on GA-LSSVM-MOPSO-TOPSIS Method

Abstract

The exploration and development of deep marine resources are faced with the problems of poor drill ability and serious wellbore instability in high temperature and high-pressure formations. The bottom hole dynamic drilling tool with low vibration characteristics is the best choice for deep well drilling. The output torque of the turbodrill is relatively small, which limits its application potential. In this study, intelligent optimization algorithms are used to improve the blade shape design to improve its output torque. Firstly, based on the moment of momentum theorem, the key blade profile parameters and range affecting the output characteristics of the turbodrill are analyzed and summarized. Subsequently, the five-order polynomial method and UG software (version 10.0) are used to complete the three-dimensional configuration of the bent-twisted blade. Then, based on the GA-LSSVM-MOPSO-TOPSIS intelligent optimization algorithm, the two-dimensional and three-dimensional modeling design parameters under the optimal hydraulic performance are optimized, and the accuracy of the intelligent optimization algorithm and parameters is verified by CFD simulation analysis. The results show that the hydraulic efficiency of only 4.9% is sacrificed, and the output torque is increased by 36.61%, which significantly improves the hydraulic performance of the turbodrill and provides guidance for the design of low-speed and high-torque turbodrills.

1. Introduction

The field of deep-sea resource exploration has important strategic significance and an important role in the context of the current global energy structure transformation and sustainable development [1]. With the gradual depletion of traditional energy resources, the development of deep-sea resources (such as deep oil, natural gas, geothermal energy, and mineral resources) has become the key to meet the growing energy demand [2,3]. Through in-depth exploration and efficient development of deep-sea resources, the effective utilization of underground energy can be realized, carbon emissions can be further reduced, and the transformation and development of clean energy can be promoted. In summary, deep-sea resource exploration is not only an important measure to ensure a future energy supply, but also provides strong support for achieving sustainable development goals [4].

Deep-sea resource exploration is faced with complex and changeable geological structure, poor formation drillability, wellbore instability and other drilling problems, ultra-high temperature, high pressure [5] working conditions, and a harsh environment. The turbodrill has achieved excellent temperature resistance with all-metal material components, making it one of the few downhole power devices that can work reliably in ultra-high temperature downhole environments. When used in conjunction with a diamond bit, its high speed characteristics can effectively improve the crushing and drilling performance under hard rock conditions [6,7]. However, the relatively small output torque limits its application range. Therefore, domestic and foreign scholars have carried out extensive research in order to optimize its hydraulic performance and improve the overall drilling efficiency.

Lin et al. systematically analyzed the flow law of liquid on the blade surface of a turbodrill and clarified the key conditions that need to be met in the design of the blade profile of a high efficiency turbodrill. A new blade profile model is proposed, and the corresponding mathematical model solution method is developed according to the geometric characteristics of the blade, which provides an important reference and guidance for improving the working efficiency of the existing turbodrill [8]. Zhang et al. proposed a complete set of numerical simulation processes covering parametric modeling, performance prediction, and optimization design of turbine blades based on Bezier curve theory and turbo systems. By comparing with the experimental data, the effectiveness and feasibility of the method are verified [9]. Based on the Bessel curve modeling method, Liu designed two blade profiles with different thickness changes. From the top of the blade to the root of the blade, the blade was modeled by equal scale scaling. With the help of numerical simulation technology, it was compared with the traditional turbodrill with curved and twisted blades, and the influence of variable cross-section blades on the performance of the turbodrill was studied in depth [10]. Zhang et al. constructed a set of optimization design methods for turbine blades based on Bezier curve theory, experimental design theory, and response surface method. By comparing results with CFD simulation results, it is found that there is a good agreement between the two. In addition, the performance of the optimized model is significantly improved, which proves the effectiveness and reliability of the method in the blade design [11]. Zhang took the output torque, pressure drop, and efficiency of the turbine as the experimental indexes and selected the parameters of the turbine stator and rotor blade as the experimental factors. The system was studied by orthogonal experimental design. The range analysis and variance analysis of the experimental results were carried out to evaluate the influence of various factors on the experimental indexes, so as to realize the effective optimization of the turbine blade parameters [12]. Huang discussed the influence of key parameters of turbine cascade on turbine torque, pressure drop, and conversion efficiency by orthogonal test combined with multi-index analysis. After systematic research, the cascade parameters with the best comprehensive hydraulic performance were finally determined. This research not only promotes the effective capture of hydraulic energy by the cascade, but also significantly improves the overall performance of the turbine [13].

Dvoynikov et al. proposed a mathematical model of invariants, which is based on pre-set boundary conditions and the main performance characteristics of the turbine being developed to determine the optimal geometric parameters. The hydraulic performance of the turbodrill was successfully optimized by using the finite element method to analyze the design results [14]. Zhang et al. successfully carried out the modeling design of five kinds of turbodrill blades based on the innovative design method combining the Joukowsky conformal transformation method and the classical hydraulic airfoil. Through in-depth study of the flow field performance of these five blades and performance test experiments, the overall performance was significantly improved. This study provides a new idea and method for the efficient design of the turbodrill [15]. Vessaz et al. proposes a novel sub-cycloid tool path planning method with equal radial cutting depth in three-dimensional space, which can significantly improve the surface finish of the blade and optimize its overall performance [16]. Gong et al. analyzed the magnitude and distribution of hydraulic loss in the turbodrill cascade by using the entropy generation method and evaluated a variety of entropy production rates and entropy values. The total flow loss obtained by the entropy generation method was compared with the total flow loss calculated by the differential pressure method. The results show that the two are consistent, which verifies the effectiveness of the entropy generation method in fluid loss analysis [17]. Li et al. proposed a new type of stator and rotor structure to improve the performance output of the turbodrill. The effectiveness of the design structure was confirmed by numerical simulation and experimental verification [18]. He et al. proposed a quasi-three-dimensional blade design method, which assumes that the tangential scale of the blade is proportional to the radius, while maintaining the axial scale unchanged. In addition, a mathematical model for calculating blade torque is established, which can effectively improve the hydraulic performance of the turbodrill [19].

In summary, the turbodrill shows efficient and reliable drilling ability in high temperature, high hardness, and high abrasive formations, which provides important technical support for the exploration and development of deep-sea energy [20]. The hydraulic performance optimization of the turbodrill mainly focuses on the blade design. The optimization process can be divided into two key aspects: one is the optimization of the two-dimensional blade profile, and the other is the improvement of three-dimensional blade space forming. Therefore, comprehensive research and optimization of the two-dimensional and three-dimensional modeling design of the blade is the key to improving the output torque and overall efficiency. The multi-objective optimization algorithm [21] can be used to optimize the structural parameters of the turbodrill blade [22] to achieve the optimal design of the turbodrill. For example, Hu established an optimization model combining BP neural network and non-dominated sorting multi-objective genetic algorithm (NSGA-II), aiming at systematically optimizing the structural size of the turbine and achieving the goal of significantly improving the turbine output torque under high efficiency conditions [23].

The purpose of this paper is to design a low-speed and high-torque turbine blade to improve the hydrodynamic performance of the turbodrill and enhance its applicability in marine energy exploration and development. Firstly, the reasonable range of structural parameters is determined and defined by the design theory of turbine blades. The blade profile is drawn by quintic polynomial method, and the three-dimensional modeling is carried out by UG software. Then, based on the GA-LSSVM-MOPSO-TOPSIS intelligent optimization algorithm, the two-dimensional and three-dimensional modeling design parameters of the turbodrill blades are optimized to achieve the best hydraulic performance. Finally, the computational fluid dynamics (CFD) simulation was carried out by ANSYS Fluent (version 2020 R2). The influence of different modeling parameters on the flow field and performance index was systematically evaluated, and the optimal geometric parameters and their optimization effects were finally determined.

2. Theoretical Model Study

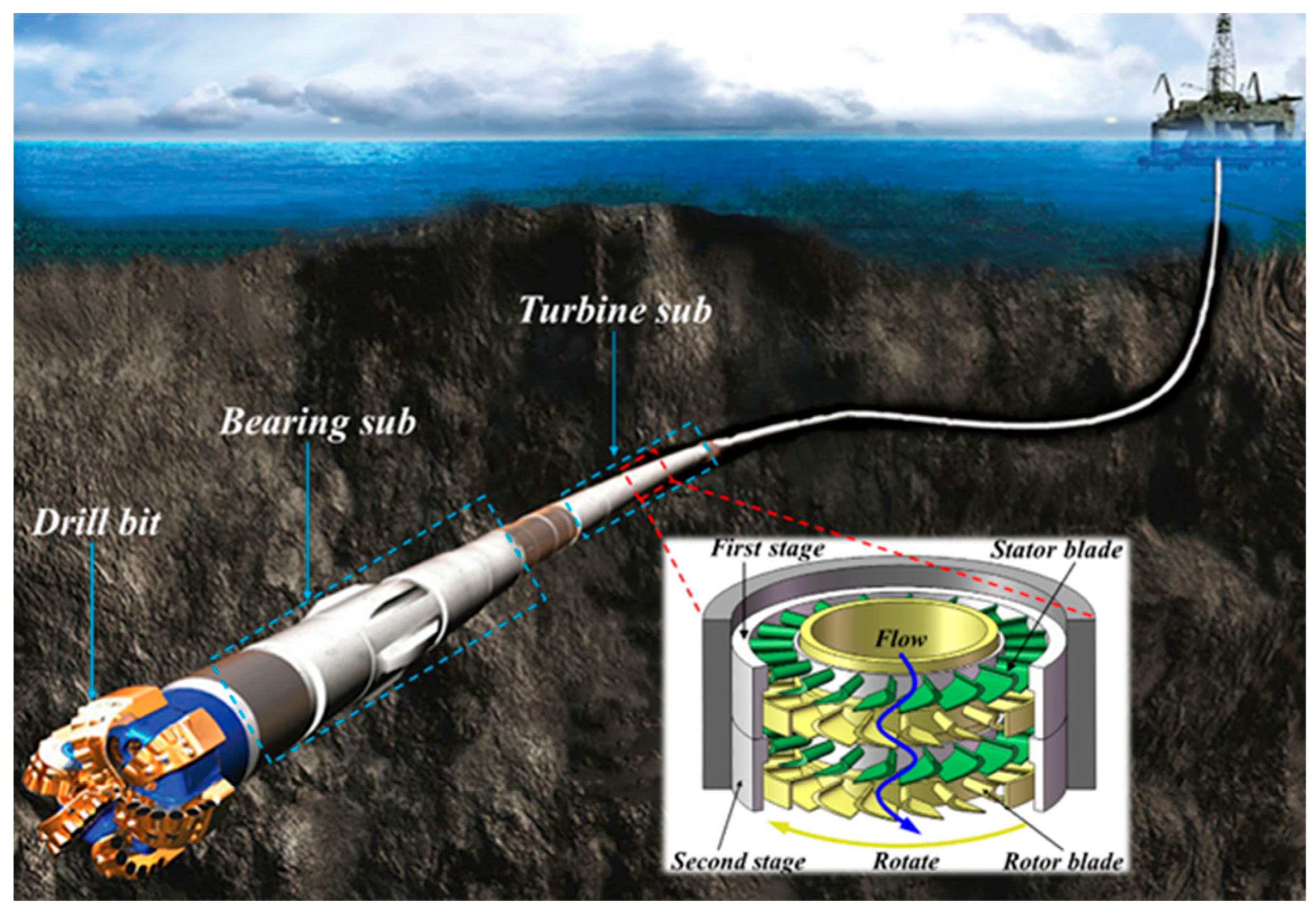
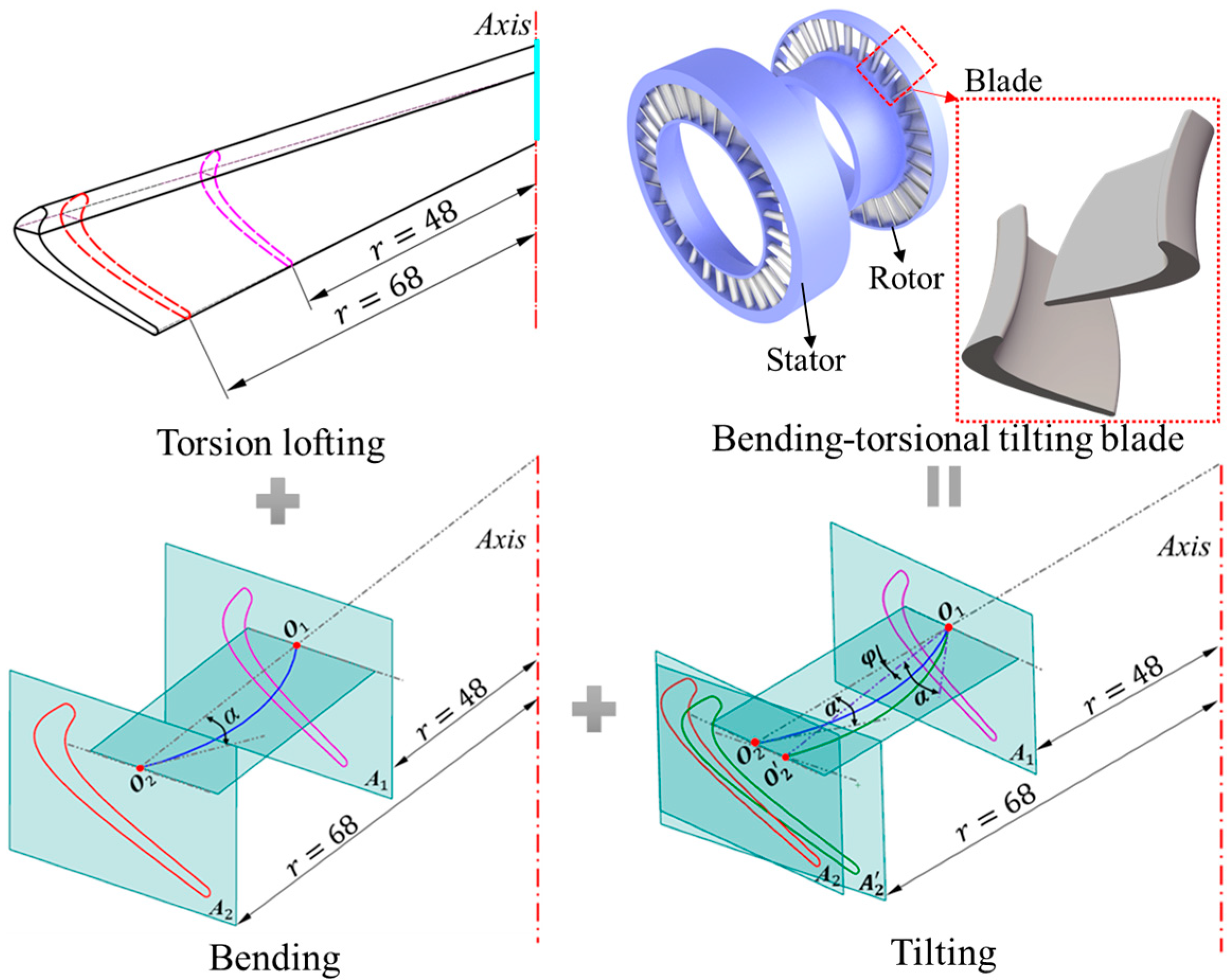
2.1. Working Principle of Turbodrill

The turbodrill is mainly composed of a turbine motor, bearing section and drill bit [24], as shown in Figure 1. The whole turbodrill is a full metal structure, so it has a strong ability to withstand high temperature and high pressure. It is the first drive drilling tool applied in extreme environments. The turbine motor is an axial turbomachinery that is superimposed by a multi-stage stator and rotor to achieve the desired torque and hydraulic efficiency. Its function is to convert the hydraulic energy provided by the drilling fluid pumped from the ground to the downhole into mechanical energy through the diversion of the stator and rotor blades to achieve rotary rock breaking [25]. The bearing section contains a thrust bearing and a radial centralizing bearing. Its function is to provide rotating support, carry load, reduce friction, and maintain alignment, thereby improving the drilling efficiency and stability of the drilling tool.

2.2. Theoretical Model of Turbodrill Output Characteristics

The working flow channel of the turbodrill is located between two coaxial cylindrical surfaces with diameters of $D_1$ and $D_2$, so the flow can be regarded as a series of concentric cylindrical surfaces (see Figure 2a). In order to facilitate the analysis, the central cylindrical surface of the flow channel is often taken, and its diameter is defined as $D=(D_1+D_2)/2$, and the cylindrical surface is flattened into a two-dimensional plane; the intersection line between the flattening plane and the surface of the turbine blade is the blade profile line, which is used to describe the cross-section profile of the blade. The geometric parameters of the blade profile mainly include axial height $H$, front/rear edge radius $R_1$, $R_2$, inlet/outlet structure angle ${\beta }_{1k}$, ${\beta }_{2k}$, blade installation angle ${\beta }_m$, front/rear cone angle ${\gamma }_1$, ${\gamma }_2$, and blade spacing t (see Figure 2b). The changes in these parameters directly affect the hydrodynamic performance and output characteristics of the blade, especially under the condition of low speed and high torque, the sensitivity of torque output and hydraulic efficiency is more significant. During the operation, the rotor rotates at a speed of $n$, and the blades work under the load of drilling fluid. The drilling fluid has two parts: relative motion and circumferential motion caused by the rotor, so its absolute velocity can be decomposed by vector: $\mathit{c}=\mathit{u}+\mathit{w}$, where $u$ represents the circumferential velocity component generated by the rotation of the rotor and $w$ represents the relative velocity component of the fluid relative to the blade. Figure 2c shows the geometric relationship between these velocity components and the blade profile, which is the basis for the calculation of blade parameters, velocity triangle, and hydrodynamic performance.

According to the moment of momentum theorem, the torque $M^{\prime }$ of the turbodrill for drilling fluid can be directly obtained as follows:

$$M^{\prime }=\rho Q_i{R}^{\prime }\left(c_{2}cos{\alpha }_{2k}-c_{1}cos{\alpha }_{1k}\right)$$

(1)

where $\rho$ is the drilling fluid density; $Q_i$ is the flow; $R^{\prime }$ is the radius of the flow channel; ${\alpha }_{2k}$ is the stator inlet angle; ${\alpha }_{1k}$ is the stator outlet angle. From the velocity triangle of Figure 2c, it can be concluded that $c_{1}cos{\alpha }_{1k}=c_{1u}$, $c_{2}cos{\alpha }_{2k}=c_{2u}$. According to the principle of action and reaction, the torque of drilling fluid acting on the turbine rotor is:

$$M_i=-M^{\prime }=\rho Q_i{R}^{\prime }\left(c_{1u}-c_{2u}\right)$$

(2)

In view of the fact that the research object is a turbodrill with a diameter of Φ178 mm, the radial feature size $R^{\prime }$ is fixed in the model for subsequent analysis. When the drilling fluid flow rate $Q_i$ and density $\rho$ flowing through the flow channel of the turbodrill are constant, the output torque $M_i$ of the turbodrill is proportional to ($c_{1u}-c_{2u}$). From the axial velocity $c_{1z}$ of the rotor inlet velocity triangle, it can be seen that:

$$c_{1z}={\displaystyle \frac{Q_i}{\pi Db{\phi }^{\prime }}}$$

(3)

In the formula: $b$ is the width of the vortex flow channel; ${\phi }^{\prime }$ is the section reduction coefficient considering the influence of blade thickness, which is generally taken as 0.9. It can be concluded that:

$$c_{1u}=c_{1z}cot{\alpha }_{1k}={\displaystyle \frac{Q_i}{\pi Db{\phi }^{\prime }}}cot{\alpha }_{1k}$$

(4)

From the rotor outlet velocity triangle, it can be concluded that:

$$c_{2u}=u-c_{2z}cot{\beta }_{2k}={\displaystyle \frac{\pi n{R}^{\prime }}{30}}-{\displaystyle \frac{Q_i}{\pi Db{\phi }^{\prime }}}cot\alpha {\beta }_{2k}$$

(5)

Therefore, the output torque $M_i$ and efficiency $N_i$ of the single-stage blade of the turbodrill can be obtained as follows:

$$\left\{\begin{array}{c}{M}_i=\rho Q_i{R}^{\prime }\left[{\displaystyle \frac{Q_i}{\pi Db{\phi }^{\prime }}}\left(cot{\alpha }_{1k}+cot\alpha {\beta }_{2k}\right)-{\displaystyle \frac{\pi n{R}^{\prime }}{30}}\right]\\ N_i=M_{i}w=\rho Q_i{R}^{\prime }w\left[{\displaystyle \frac{Q_i}{\pi Db{\phi }^{\prime }}}\left(cot{\alpha }_{1k}+cot\alpha {\beta }_{2k}\right)-{\displaystyle \frac{\pi n{R}^{\prime }}{30}}\right]\end{array}\right.$$

(6)

From the above analysis, it can be seen that the conversion torque of the turbodrill mainly depends on the circumferential velocity difference ($c_{1u}-c_{2u}$) at the inlet and outlet of the rotor when the flow rate $Q_i$, size $D$ and drilling fluid properties are fixed. The velocity difference $c_{1u}$ and $c_{2u}$ are closely related to the blade profile parameters of turbine blades. Different blade profile parameters will lead to the change in liquid flow rate in the turbine, which will affect the output torque, hydraulic efficiency, and pressure drop of the turbodrill. Therefore, it is of great practical significance to study the influence of structural parameters of turbodrill blades on their performance characteristics for optimizing the design and application of turbodrill.

According to the operating conditions of the on-site ground pump set, the inlet flow rate of the turbodrill is set to 30 L/s. In the preliminary design, the hydraulic performance requirements of the single stage of the turbodrill include that the output torque should exceed 24 N·m and the pressure drop should be controlled below 140 KPa in the rated speed range of 400~450 rpm. In order to cope with the erosion of drilling fluid and the working environment of high temperature and high pressure, the blade of the turbodrill adopts a shorter and thicker design. In addition, in order to prevent the collision between the stator and the rotor, sufficient axial clearance should be maintained between the blades, so the axial height $H$ of the blade is set to 11 mm. Considering that the high torque design will inevitably affect the hydraulic efficiency, $r_1=0.6\mathrm{m}\mathrm{m}$ is selected for the radius of the front and rear edges, respectively. $r_2=0.4\mathrm{m}\mathrm{m}$, as a certain compensation scheme. The outlet structure angles ${\beta }_{2k}$ and ${\beta }_{1k}$ of the blade profile can be calculated by the following Equation (7).

$$\left\{\begin{array}{c}{\beta }_{2k}=arccot{\displaystyle \frac{M_{max}}{2\rho Q_{i}R{c}_{1z}}}\\ {\beta }_{1k}=\mathrm{arccot}\left(-{\displaystyle \frac{c_z\mathrm{c}\mathrm{o}\mathrm{t}{\beta }_{2k}-u}{c_z}}\right)\end{array}\right.$$

(7)

The blade installation angle refers to the angle formed between the tangent of the leading edge and the trailing edge of the blade and the horizontal line. For turbine blades, the angle should be acute. This parameter has a significant effect on the torque of the turbine, and the empirical formula (8) can be used to quantitatively estimate the range [26]:

$${\beta }_m=38.82-0.2959{\beta }_{1k}+0.914{\beta }_{2k}+0.3718\delta +25.48{\displaystyle \frac{a}{B}}$$

(8)

where $\delta$ is the liquid flow lag angle, and the empirical value range is 5~10°; $a/B$ is the maximum thickness position of the blade, and the empirical value range is 0.3~0.4. The front cone angle ${\gamma }_1$ and the back cone angle ${\gamma }_2$ of the blade determine the sharpness at both ends of the blade. With the increase in these two angles, the thickness of the blade will increase accordingly, resulting in a decrease in sharpness. The design of the front and rear cone angles is very important, which can effectively prevent the separation of the boundary layer in a specific speed range. The corresponding empirical formula is as follows [27]:

$$\left\{\begin{array}{c}{\gamma }_1=3.51arctan\left(({\displaystyle \frac{d_{max}}{2}}-R_1)/({\displaystyle \frac{a}{B}}{L}_n-R_2)\right)\\ {\gamma }_2=2.16arctan\left(\left({\displaystyle \frac{d_{max}}{2}}-R_2\right)/\left(\left(1-{\displaystyle \frac{a}{B}}\right)L_n-R_2\right)\right)\end{array}\right.$$

(9)

where $d_{max}$ is the maximum thickness of the blade; and $L_n$ is the length of the leaf bone line. According to previous studies and empirical formulas, the turbine blade profile parameters are summarized as follows: ${\beta }_{1k}=130°$, γ₁ = 20°, blade number $z=28$, $r_1=0.6\mathrm{m}\mathrm{m}$, $r_2=0.4\mathrm{m}\mathrm{m}$, and blade spacing t = 13 mm. The range of the three parameters that have the greatest influence on the hydraulic performance of the blade profile is: ${\beta }_{2k}=20-30°$, ${\beta }_m=28-45°$, ${\gamma }_2=2-15°$, which needs to be tested and corrected in the subsequent design process.

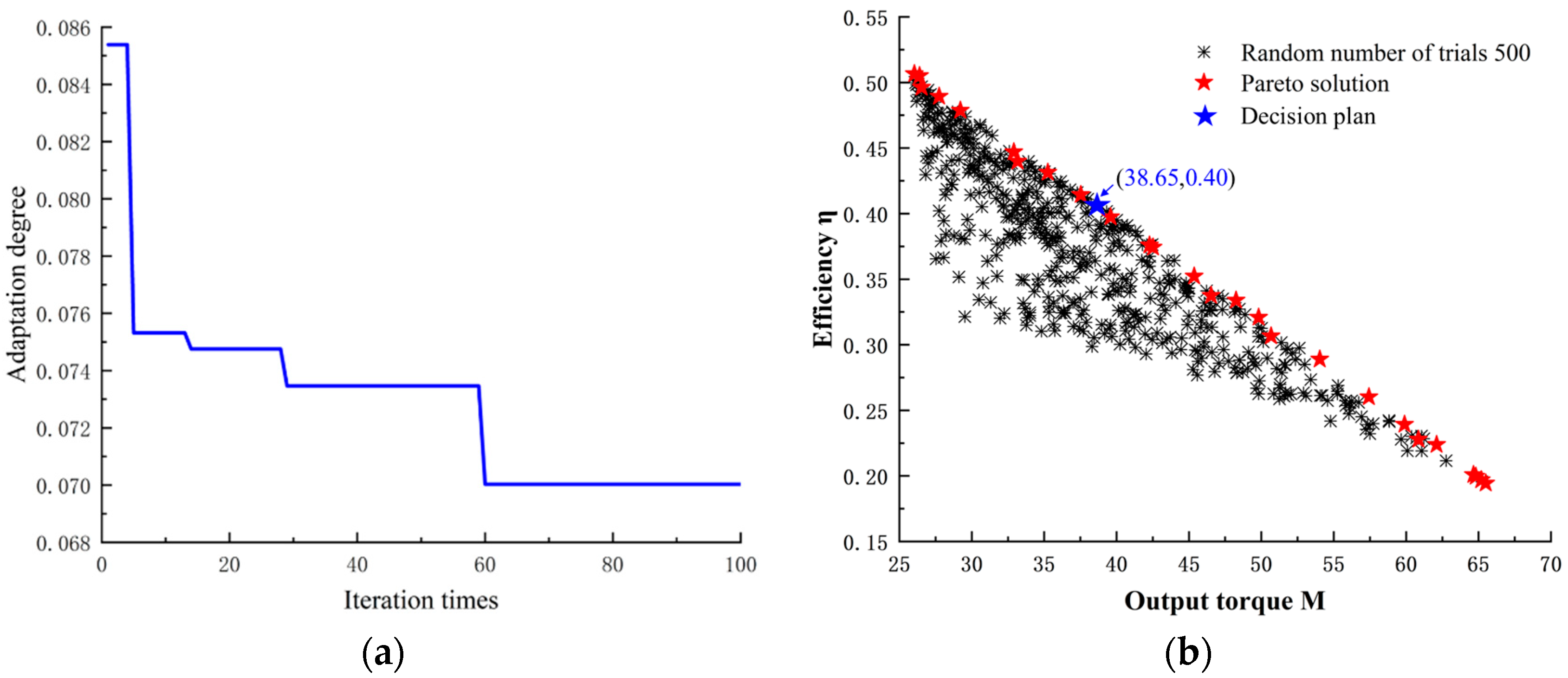
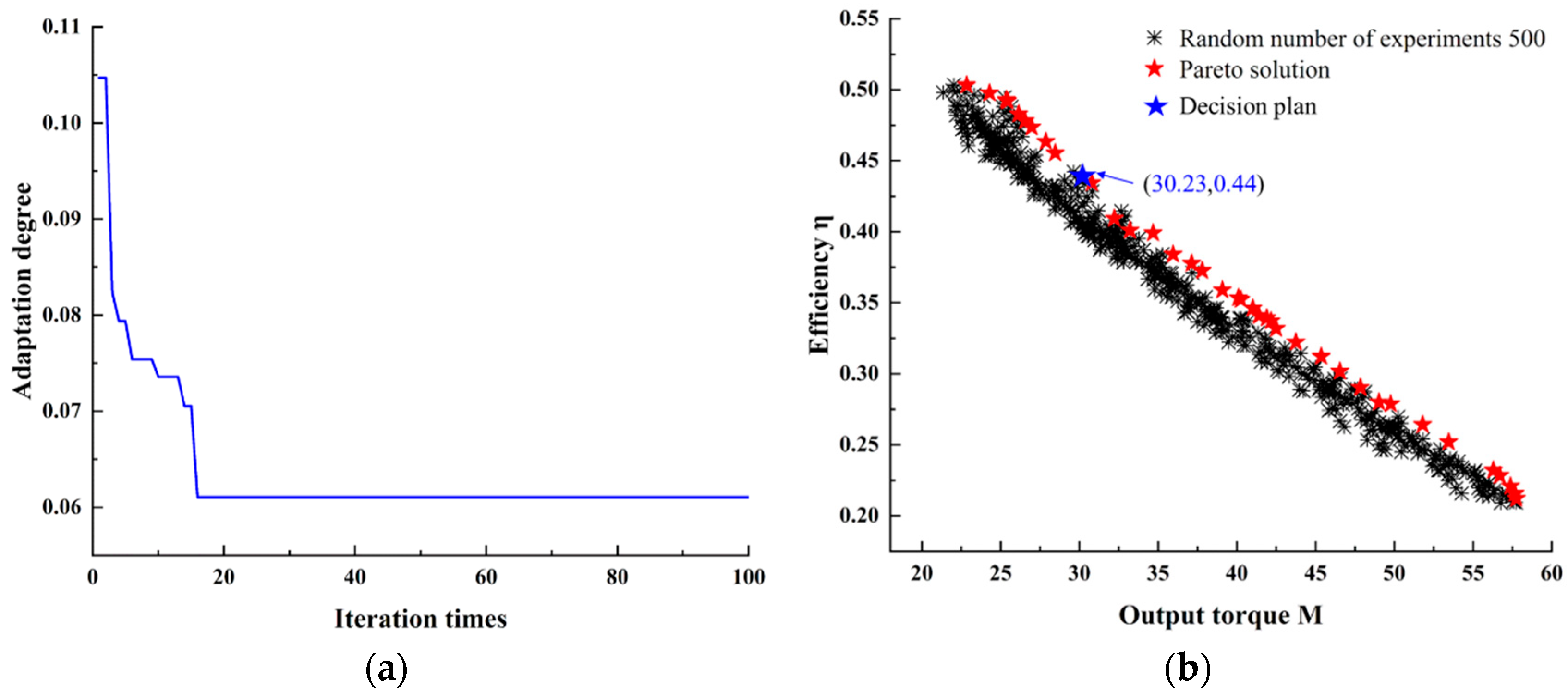
2.3. Intelligent Optimization Algorithm Model

GA-LSSVM-MOPSO-TOPSIS is an innovative multi-objective intelligent optimization algorithm, which combines genetic algorithm (GA), least squares support vector machine (LSSVM), particle swarm optimization (MOPSO) and entropy weight TOPSIS method. The algorithm aims to effectively solve the complex optimization problem of the key performance structural parameters of turbodrills and ensure the best balance between performance and efficiency under the premise of meeting the torque and pressure drop indicators. The key performance structural parameters of the turbodrill mainly include the core parameters of the two-dimensional blade profile (outlet structure angle ${\beta }_{2k}$, blade installation angle ${\beta }_m$, and blade back cone angle ${\gamma }_2$) and the complex modeling parameters of the three-dimensional blade (twist lofting radius $R$, bending angle $\alpha$, and inclination angle $\phi$). The combination of these parameters determines the output characteristics of the turbodrill, as shown in (A) and (B) in Figure 3. Through this optimization algorithm, these parameters can be systematically analyzed and adjusted to improve the overall performance and efficiency of turbodrills.

Firstly, the key performance structural parameters and their preferred ranges of turbodrills were screened by the Box–Behnken design method to generate test data. At the same time, ANSYS Fluent is used for numerical simulation to obtain the prediction results of the target value. These data will be used as sample input of intelligent optimization algorithm. Then, the least squares support vector machine (LSSVM) is used to construct a preliminary prediction model, and the training sample data is learned to reveal the relationship between the objective function between the output torque and the hydraulic efficiency and the influencing factors. The basic formula for the LSSVM model is:

$$\left\{\begin{array}{c}{\displaystyle \frac{min}{w^{\prime },b,\xi }}{\displaystyle \frac{1}{2}}{‖w‖}^2+{\displaystyle \frac{C}{2}}{\displaystyle \sum _{i=1}^N}{\xi }_i^2\\ s.t.y_i-\left({w^{\prime }}^T\Phi \left(x_i\right)+b\right)={\xi }_i,i=\mathrm{1,2},\dots ,N\end{array}\right.$$

(10)

where $w^{\prime }$ is the weight vector; $b$ is bias; ${\xi }_i$ is a relaxation variable; $c$ is the penalty parameter; $\phi (·)$ is the kernel function mapping; $y_i$ is the target output; and $x_i$ is the input feature. The key feature of genetic algorithm (GA) optimization is its excellent global optimization ability, which can effectively deal with a complex search space. This algorithm gradually evolves the optimal solution by simulating the process of biological evolution in nature and using genetic operations such as selection, crossover, and mutation. As shown in Figure 3D, this study applies GA to optimize the penalty parameter $C$ and kernel function parameter $\Phi (·)$ in the least squares support vector machine (LSSVM) model [28]. In this process, GA not only evaluates the fitness of the parameters, but also measures the advantages and disadvantages of individuals in the solution space. The fitness function (Fitness) is defined as the prediction error of the LSSVM model on the training set. Through this method, the prediction performance and generalization ability of the model are further improved.

$$Fitness={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left(y_i-\widehat{y_i}\right)}^2$$

(11)

where $\widehat{y_i}$ is the predicted value of the LSSVM model. After optimizing the penalty parameter $C$ and the kernel function parameter $\Phi (·)$ in the LSSVM model, the multi-objective particle swarm optimization algorithm (MOPSO) is used for further optimization. As shown in Figure 3E, MOPSO aims to identify Pareto front solutions of multiple targets by simulating the behavior of particle swarms. In this process, the velocity and position update rules of particles are very important. The velocity update of particles is not only influenced by their own historical experience but also guided by the experience of other particles in the group. The update formula for its position and speed is as follows:

$$\left\{\begin{array}{c}{v}_{i,j}^{(t+1)}=\omega v_{i,j}^{\left(t\right)}+c_1{r}_1(pbes{t}_{i,j}-x_{i,j}^{\left(t\right)})+c_2{r}_2(gbes{t}_j-x_{i,j}^{\left(t\right)})\\ x_{i,j}^{(t+1)}=x_{i,j}^{\left(t\right)}+v_{i,j}^{(t+1)}\end{array}\right.$$

(12)

where $v_{i,j}^{\left(t\right)}$ is the velocity of particle $i$ in the $j$th dimension; $x_{i,j}^{\left(t\right)}$ is the position; $pbes{t}_{i,j}$ is the best position of particle individual; $gbes{t}_j$ is the global optimal position; $c_1$ and $c_2$ are learning factors; $r_1$ and $r_2$ are random numbers between [0, 1]. Through the multi-objective particle swarm optimization algorithm, we obtain multiple sets of key performance structure parameters of the turbodrill corresponding to the optimal output torque and hydraulic efficiency. Next, the entropy weight method is used to calculate the weight of each parameter, and the decision evaluation is carried out in combination with the analytic hierarchy process (TOPSIS) to identify the optimal solution. In this process, the calculation formula of the weight is as follows:

$${\omega }_j={\displaystyle \frac{-\frac{1}{ln\left(N\right)}{\sum }_{i=1}^N{p}_{ij}ln\left(p_{ij}\right)}{{\sum }_{j=1}^m\left(-\frac{1}{\mathit{ln}\left(N\right)}{\sum }_{i=1}^N{p}_{ij}ln\left(p_{ij}\right)\right)}}$$

(13)

where ${\omega }_j$ is the weight of the target $j$, $p_{ij}=x_{ij}/{\sum }_{i=1}^N{x}_{ij}$ is the element of the normalized decision matrix. The key of TOPSIS is to determine the ideal solution and negative ideal solution and calculate the distance between each scheme and these two solutions, so as to select the optimal scheme. The relative proximity is calculated as:

$$C_i={\displaystyle \frac{D_i^{-}}{D_i^{+}+D_i^{-}}}$$

(14)

where $D_i^{-}$ is the distance from scheme $i$ to the negative ideal solution; $D_i^{+}$ is the distance from scheme $i$ to the positive ideal solution. Based on the above analysis and summary, we can use intelligent optimization algorithms to identify the key performance structural parameters of turbodrills under optimal output torque and hydraulic efficiency conditions. This method not only improves the accuracy of optimization but also provides an important basis for the design and performance improvement of turbodrill.

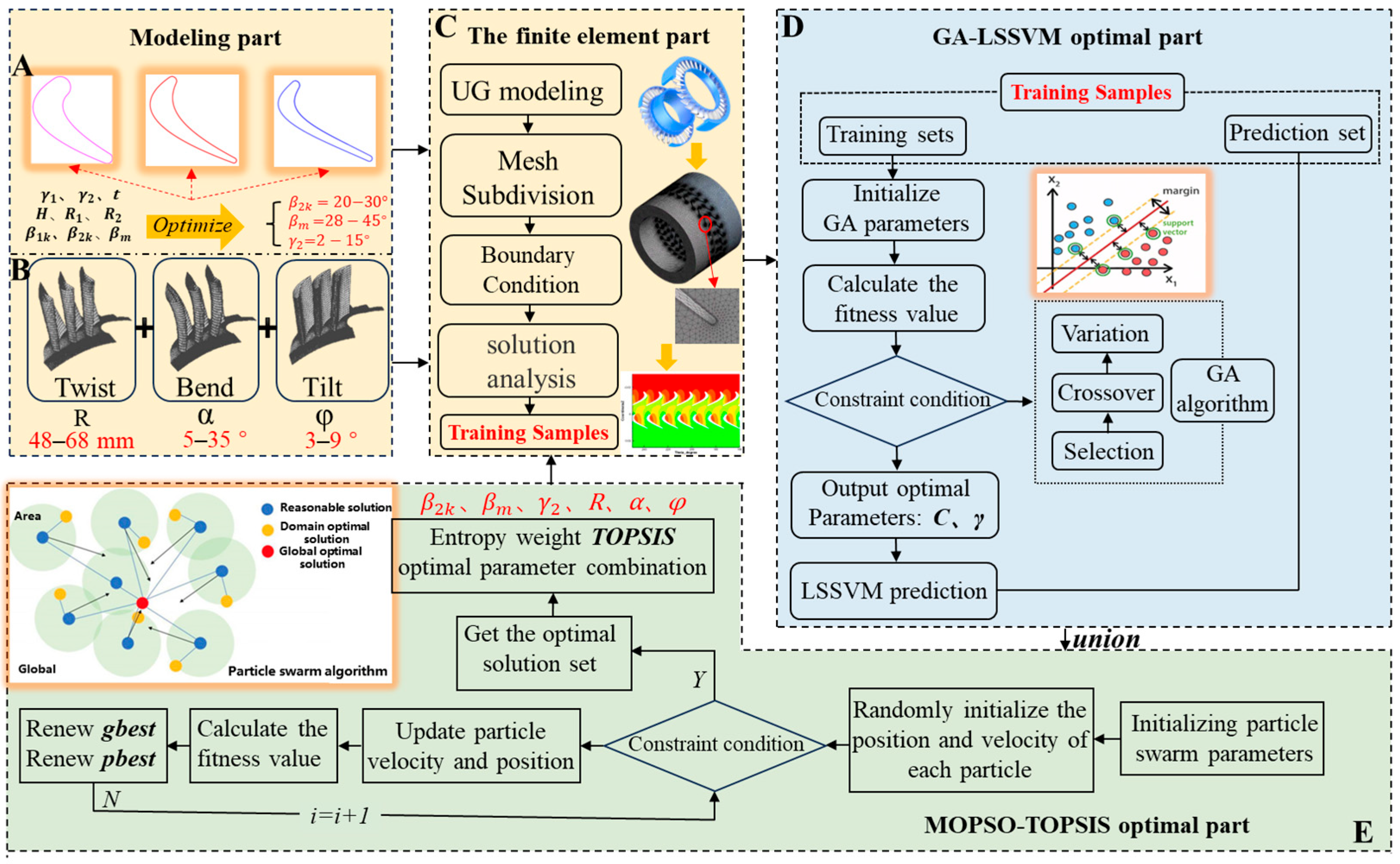
3. Modeling Optimization and Result Analysis

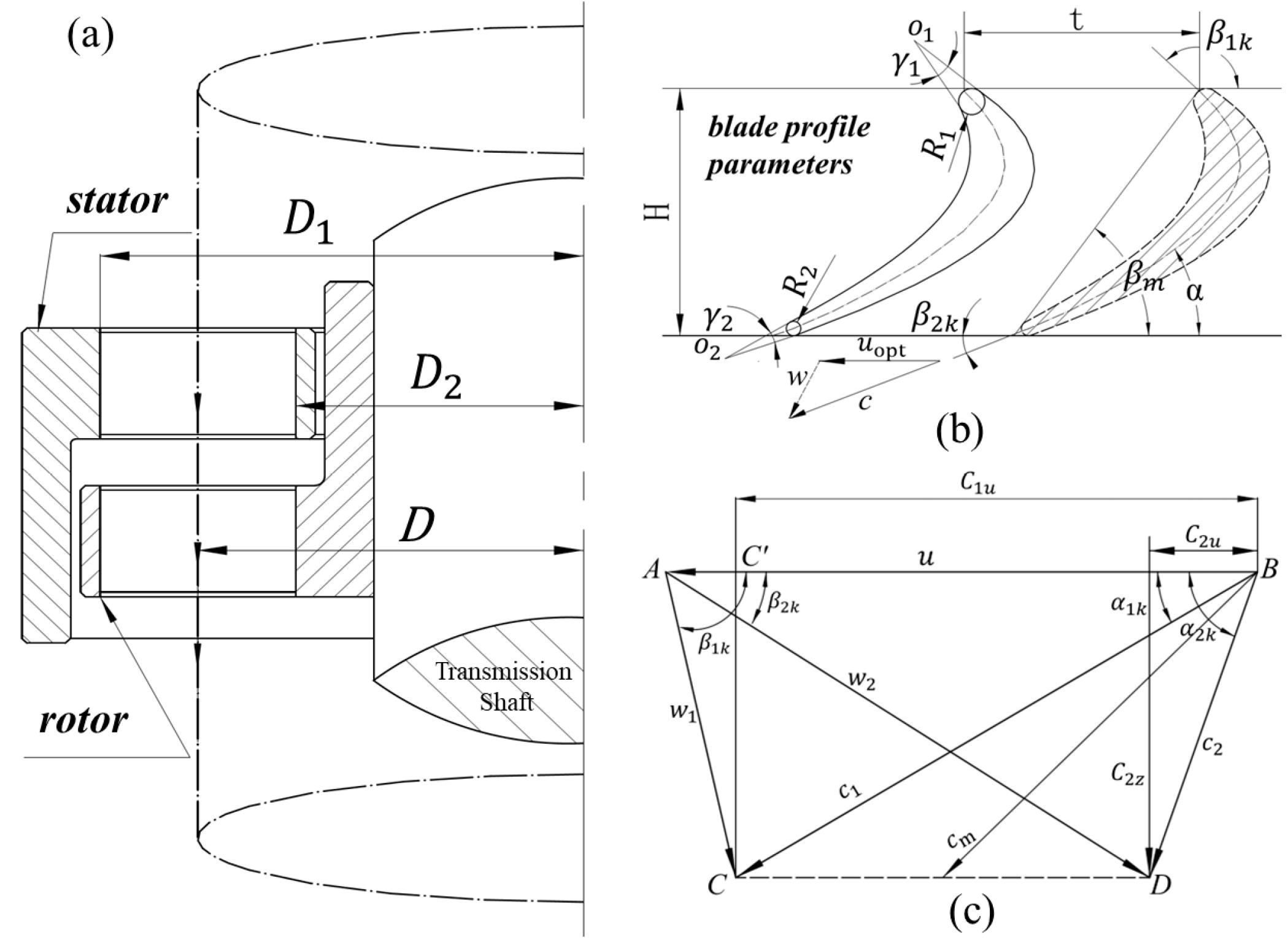
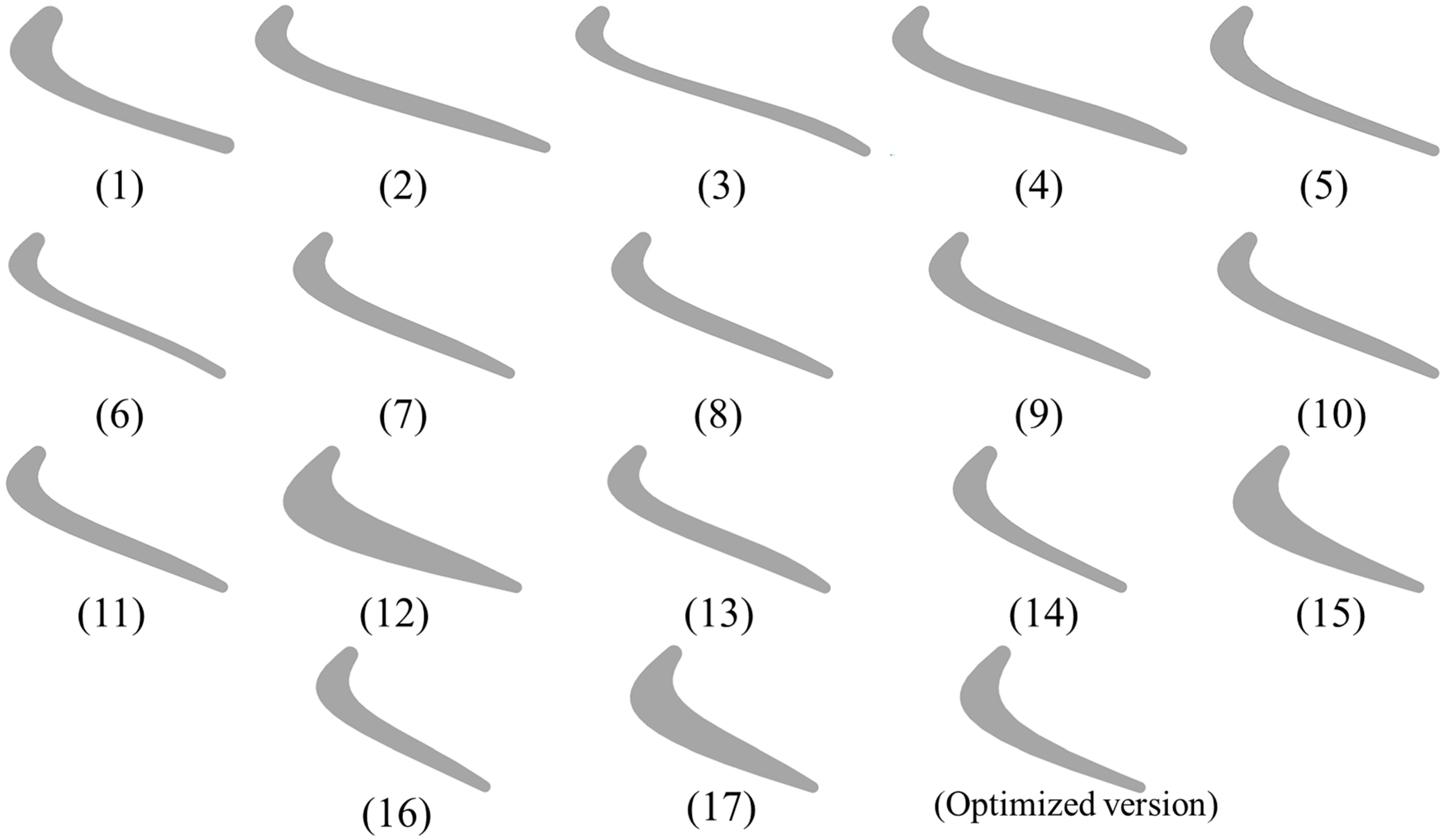
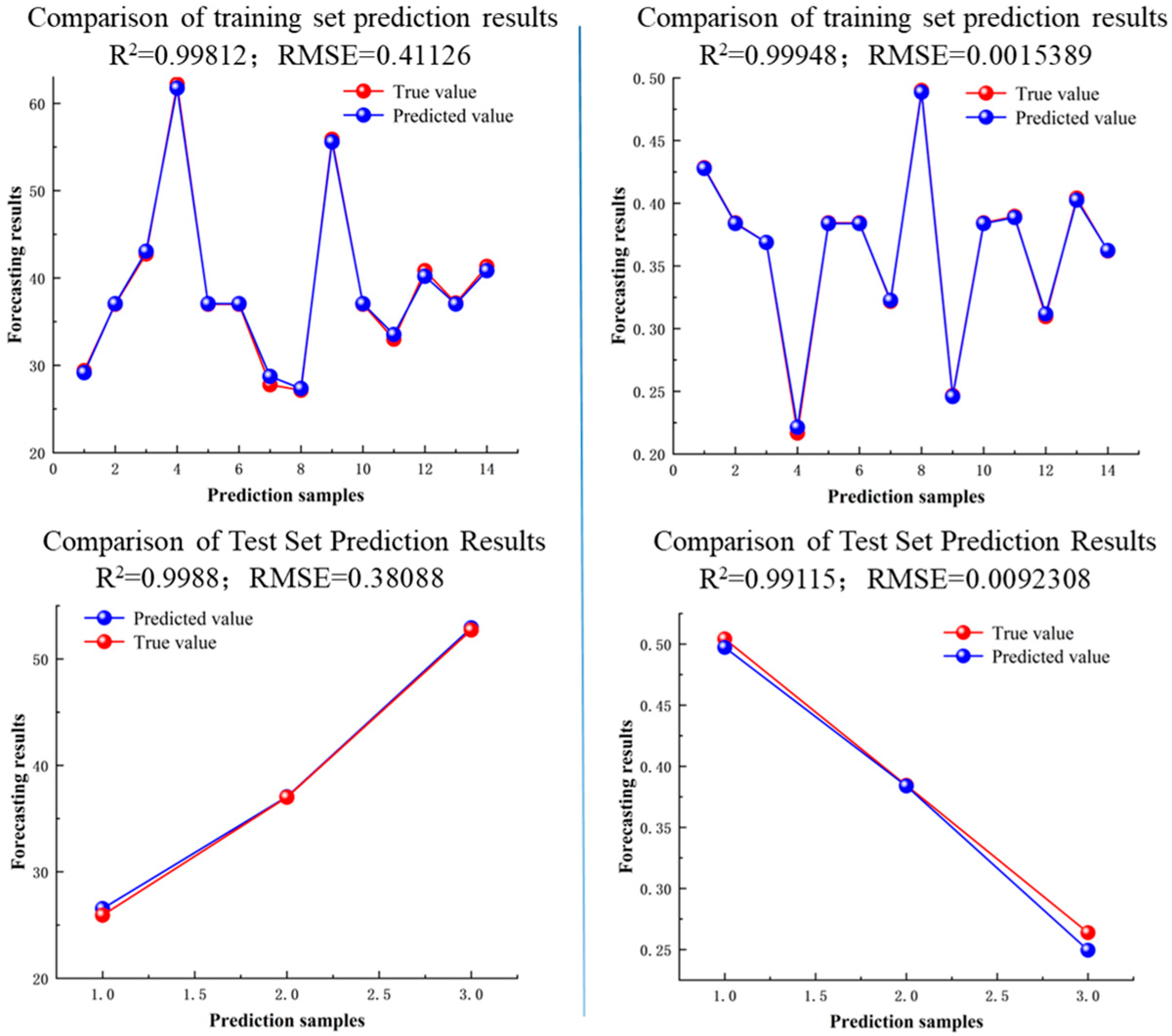
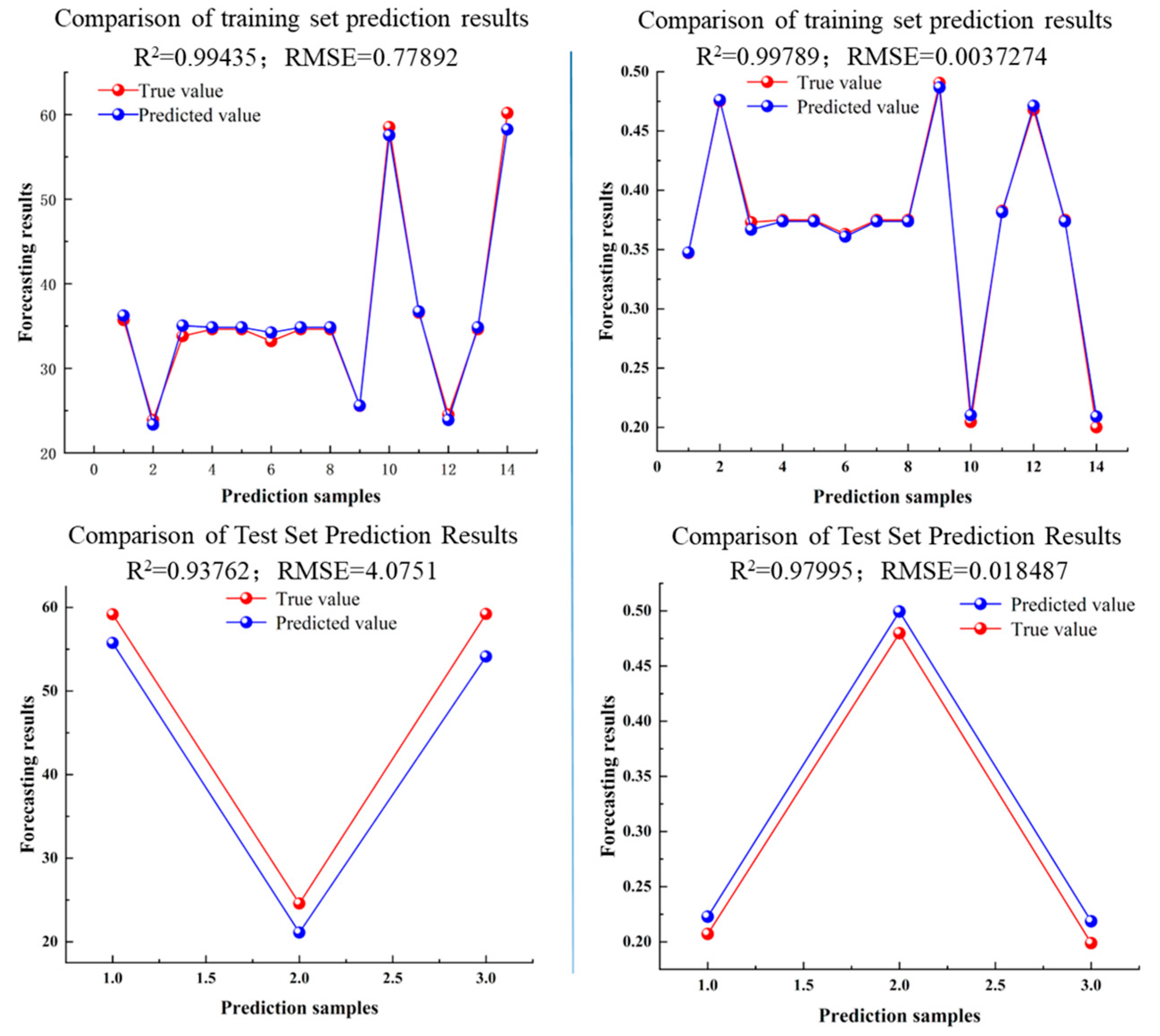
3.1. Intelligent Optimization Analysis of the Core Parameters of the Two-Dimensional Blade Profile Line

The influence of the two-dimensional blade profile of the turbodrill on its hydraulic performance can be quantified by three key parameters. The specific value range is: ${\beta }_{2k}=20-30°$, ${\beta }_m=28-45°$, ${\gamma }_2=2-15°$. In order to screen out the key performance structural parameters of the turbodrill, the experimental data were generated by the Box–Behnken Design (BBD) method. In addition, numerical simulation is carried out with ANSYS Fluent to obtain the numerical solution. These simulation results will be used as input samples of intelligent optimization algorithms to support subsequent analysis.

Table 1. BBD experimental design data of two-dimensional blade profile.

Serial	${\mathit{\beta }}_{2\mathit{k}}$/°	${\mathit{\gamma }}_2$/°	${\mathit{\beta }}_{\mathit{m}}$/°	Torque/N·m	Efficiency/%	Serial	${\mathit{\beta }}_{2\mathit{k}}$/°	${\mathit{\gamma }}_2$/°	${\mathit{\beta }}_{\mathit{m}}$/°	Torque/N·m	Efficiency/%
1	25	2	28	27.77	32.17	10	25	8.5	36.5	37.00	38.44
2	20	8.5	28	55.88	24.66	11	25	8.5	36.5	37.00	38.44
3	30	8.5	28	40.85	30.96	12	20	15	36.5	62.20	21.68
4	25	15	28	52.71	26.38	13	30	15	36.5	32.99	38.96
5	20	2	36.5	41.33	36.20	14	25	2	45	27.16	49.00
6	30	2	36.5	29.39	42.84	15	20	8.5	45	42.76	36.88
7	25	8.5	36.5	37.00	38.44	16	30	8.5	45	25.92	50.42
8	25	8.5	36.5	37.00	38.44	17	25	15	45	37.14	40.41
9	25	8.5	36.5	37.00	38.44

shows the design and results of the BBD experiment. Figure 4 shows the corresponding BBD experimental design data of the two-dimensional blade profile in Table 1.

After importing the data set in Table 1 into Matlab, the training set was first set to account for 80% of the total data set and configure the relevant algorithm parameter range. Subsequently, the genetic algorithm (GA) was used to optimize the model parameters, aiming to identify the best kernel function parameters and penalty parameters. Then, the LSSVM model was initialized, and the training set and the test set were predicted. The results are shown in Figure 5. From the analysis of the diagram, it can be seen that the determination coefficient $R^2$ of the output torque and hydraulic efficiency of the straight blade composed of different blade profile parameters of the turbodrill in the training set and the test set is higher than 0.99, and the root mean square error (RMSE) is also small, which indicates that the results of the training set and the test set are highly consistent. The model has good fitting ability and can effectively predict the output results of the data set that is not included in the training set.

The fitness curve reflects the trend of the best fitness value of each generation with the algebraic change in the GA-LSSVM iterative algorithm, as shown in Figure 6a. It can be observed from the figure that as the number of iterations increases, the slope of the fitness curve decreases rapidly, indicating that the algorithm can quickly find a feasible solution, the fitness value gradually decreases, and the model performance continues to improve, which further reflects the superiority of the algorithm optimization. Next, each individual generated by the GA-LSSVM optimization algorithm is optimized by MOPSO to update the position and speed of the particles, so as to find the Pareto front solution set of the output torque and hydraulic efficiency of the turbodrill. The Pareto optimal solution is verified by 500 random experiments, and the optimal solution is obtained by using the entropy weight Topsis method. It can be seen from Figure 6b that the MOPSO algorithm successfully identifies a series of non-dominated optimal solutions and forms the corresponding Pareto solution set. These non-dominated solutions achieve a good balance between output torque and hydraulic efficiency. The distribution of 500 sets of random test solutions further proves the rationality of the Pareto solution and shows the effectiveness of the algorithm in dealing with complex multi-objective optimization problems. Finally, the optimal solution is determined by the entropy weight Topsis method: M = 38.65 N·m, η = 40%; at this time, the key parameters of the optimized turbine blade profile are: ${\beta }_{2k}=20°$, ${\beta }_m=44.9085°$, ${\gamma }_2=4.2059°$.

3.2. Numerical Simulation Model of Blade Motor Clearance Leakage

The influence of the three-dimensional blades of the turbodrill on its hydraulic performance can be quantified by three key parameters. The specific value range is: $R=48-68\mathrm{m}\mathrm{m}$. $\alpha =5-35°$, $\phi =3-9°$. The same method was used to generate experimental data using the Box–Behnken Design (BBD) method. In combination with ANSYS Fluent, the numerical simulation is carried out to obtain the numerical solution. These simulation results will be used as input samples of intelligent optimization algorithms to support subsequent analysis.

Table 2. Three-dimensional blade forming parameters BBD test design data.

Serial	$\mathit{R}$/mm	$\mathit{\alpha }$/°	$\mathit{\phi }$/°	Torque/N·m	Efficiency/%	Serial	$\mathit{R}$/mm	$\mathit{\alpha }$/°	$\mathit{\phi }$/°	Torque/N·m	Efficiency/%
1	48	20	3	58.52	20.46	10	58	20	6	34.63	37.50
2	68	5	6	24.58	47.98	11	58	5	9	33.21	36.31
3	48	35	6	59.21	19.87	12	58	35	9	33.81	37.31
4	58	20	6	34.63	37.50	13	58	20	6	34.63	37.50
5	48	5	6	59.18	20.71	14	68	20	9	23.88	47.53
6	68	20	3	25.56	49.06	15	68	35	6	24.52	46.78
7	48	20	9	60.19	20.01	16	58	20	6	34.63	37.50
8	58	35	3	35.71	34.71	17	58	20	6	34.63	37.50
9	58	5	3	36.59	38.27

shows the experimental design and results of three-dimensional blade forming parameters BBD. Figure 7 shows the blade profile corresponding to the BBD test design data of the three-dimensional blade forming parameters in Table 2.

The method steps in the previous Section 3.2 are used to optimize the solution, and the results are shown in Figure 8. From the analysis of the figure, it can be seen that the coefficient of determination R² of the output torque and hydraulic efficiency of the spatial complex blades composed of different three-dimensional forming parameters of the turbodrill is higher than 0.93 in the training set and the test set, and the RMSE also meets the requirements. However, the value of the evaluation coefficient R² of the three-dimensional blade is lower than that of the two-dimensional blade. The difference is mainly caused by the more complex flow field flow in the three-dimensional space modeling design of the blade and the sample sparsity caused by the high dimension of the three-dimensional design parameters under the same sample size. Nevertheless, the reported R² still shows that the results of the training set and the test set are highly consistent, and the model has good fitting ability and generalization ability, which can effectively predict the output characteristics of the turbodrill.

It can be observed from Figure 9a that as the number of iterations increases, the slope of the fitness curve decreases significantly. This phenomenon shows that the algorithm performs well in finding feasible solutions, and the model prediction accuracy and performance continue to improve. It can be seen from Figure 9b that the MOPSO algorithm successfully identifies a series of non-dominated optimal solutions and forms the corresponding Pareto solution set. The distribution of 500 sets of random test results further verifies the rationality of the Pareto solution, which achieves a good balance between the output torque and hydraulic efficiency of the turbodrill. Then, the optimal solution is determined by the entropy weight Topsis method: M = 30.23 N·m, η = 44%; at the same time, the key parameters of the optimized turbine space modeling are: $R=62.4962\mathrm{m}\mathrm{m}$, $\alpha =10.2682°$, $\phi =3°$.

3.3. Blade Forming Method and Simulation Setting

The two-dimensional blade profile of the turbodrill consists of two curves of pressure surface and suction surface. Aiming at the design parameter set determined by genetic and multi-objective optimization algorithms, this study uses the quintic polynomial [29] to parametrically express and reconstruct the pressure surface $y_p\left(x\right)$ and the suction surface $y_s\left(x\right)$, that is, the derivative can be realized at the junction. Continuous to the third order, so as to ensure that the second-order derivative (curvature) of the curve is continuous and the curvature change is smooth, which meets the requirements of engineering for the smoothness and manufacturing feasibility of the blade profile.

$$\left\{\begin{array}{c}{y}_p=a_0+a_{1}x+a_2{x}^2+a_3{x}^3+a_4{x}^4+a_5{x}^5\\ y_s=b_0+b_{1}x+b_2{x}^2+b_3{x}^3+b_4{x}^4+b_5{x}^5\end{array}\right.$$

(15)

When the fifth-order polynomial is used to describe the blade profile, the endpoint positions of the suction surface and the pressure surface and their local tangential and curvature information constitute the decisive boundary conditions. Specifically, the spatial coordinates of the starting point and the end point of the two curves, as well as the first derivative (tangent slope) and the second derivative (curvature) at these four points are taken as constraints, which can provide exactly six independent scalar conditions for each quintic polynomial. Substituting these boundary conditions into the general expression of the quintic polynomial (See Equation (15)), a linear system of equations with six unknown coefficients can be obtained. By solving the linear equations, the polynomial coefficients of the pressure surface and the suction surface can be uniquely determined, and then the analytical expressions $y_p\left(x\right)$ and $y_s\left(x\right)$ (See Equation (16)) of the blade profile can be obtained, which provides accurate and smooth geometric description for subsequent geometric reconstruction, flow field calculation and optimization iteration:

$$\left\{\begin{array}{c}{y}_p=1.0006331202-0.4455347316x-0.1535500976x^2+0.0648785697x^3\\ -0.0045958409x^4+0.0000979076x^5\\ y_s=-0.2184893460-1.1894570181x-0.0164378018x^2+0.0395847298x^3\\ -0.0019656988x^4+0.0000101602x^5\end{array}\right.$$

(16)

After inputting the pressure surface and suction surface curve equation into UG software, the two-dimensional blade profile can be generated by using its curve rule command. On this basis, the leading edge and trailing edge curves are drawn to achieve shape closure. Through a series of operations such as subsequent stretching, a three-dimensional model of the straight blade of the stator and rotor of the Φ178 mm turbodrill can be finally constructed.

In order to construct the curved, twisted, and inclined three-dimensional blade of a Φ178 mm turbodrill, the previously determined low-speed and high-torque two-dimensional blade profile was used as the cross-section skeleton, and the parametric modeling and geometric generation were realized in UG (Siemens NX) according to the following processes (see Figure 10): (1) The two-dimensional blade profile was projected onto the radial plane near the center radius of the flow channel $R=(D_1+D_2)/2$ (value range $R$ ∈ [48, 68] mm), and the cross-section was set out along a reference straight line equal to the center axis; if there is a geometric gap in the lofting area, the extension and stitching commands are used to complete the closure curve to ensure the continuity and lofting of the section. (2) The distorted blade is projected on the flow channel according to the inner and outer diameters to construct an approximate three-dimensional torsion geometry. (3) The reference plane is established by taking the axial middle height on the blade profile line, and the curved arc bone line perpendicular to the central axis is drawn. The bending degree of the blade is accurately adjusted by the angle $\alpha$ between the straight line where the control point $O_2$ is located and the tangent line of the bone line (and the connection line $O_1{O}_2$ with point $O_1$), and the parametric control of the bending shape is realized. (4) The new plane $A_2^{\prime }$ and the corresponding blade profile are obtained by rotating the reference plane $A_2$ (and the blade profile on it) around the point $O_1$ with the rotation angle $\phi$, and the blade profile on the internal flow channel is swept with the green curved bone line as the trajectory to generate the final curved, twisted and inclined three-dimensional blade entity. The process realizes the precise control and repeatable parametric modeling of blade geometry through the orderly coupling of cross-section parameterization and distortion-bending-tilt geometric transformation.

In the meshing module of ANSYS software, in order to ensure that the geometric characteristics of complex flow channels are fully analyzed, this study uses tetrahedral unstructured grids to discretize the flow field region. The boundary layer refinement zone is set on the blade surface. The thickness of the first layer grid is 4 × 10⁻⁵ m, and the interlayer growth rate is set to 1.2. A total of five layers of boundary layer grids are generated to accurately capture the near-wall flow characteristics and shear stress distribution. In order to ensure the stability of the numerical calculation and the grid independence of the results, the total number of grids in the subsequent blade schemes is controlled to more than 4 million units, as shown in Figure 11a,b below.

Using the site screw pump design flow of 30 L/s and the flow-path cross-sectional area, the inlet velocity is prescribed as 4.116 m/s while the outlet is set to standard atmospheric pressure. Water is taken as the working fluid, and the rotor is constrained to rotate about the Z-axis. To capture both near-wall behavior and global convergence, the BSL $k\text{-}\omega$ turbulence model is employed. Simulations are performed with a steady-state solver (monitored over 500 time-steps/iterations), and the analysis concentrates on the flow-field topology and hydraulic performance of the designed low-speed, high-torque turbine at 400 rpm to provide numerical evidence for subsequent design optimization.

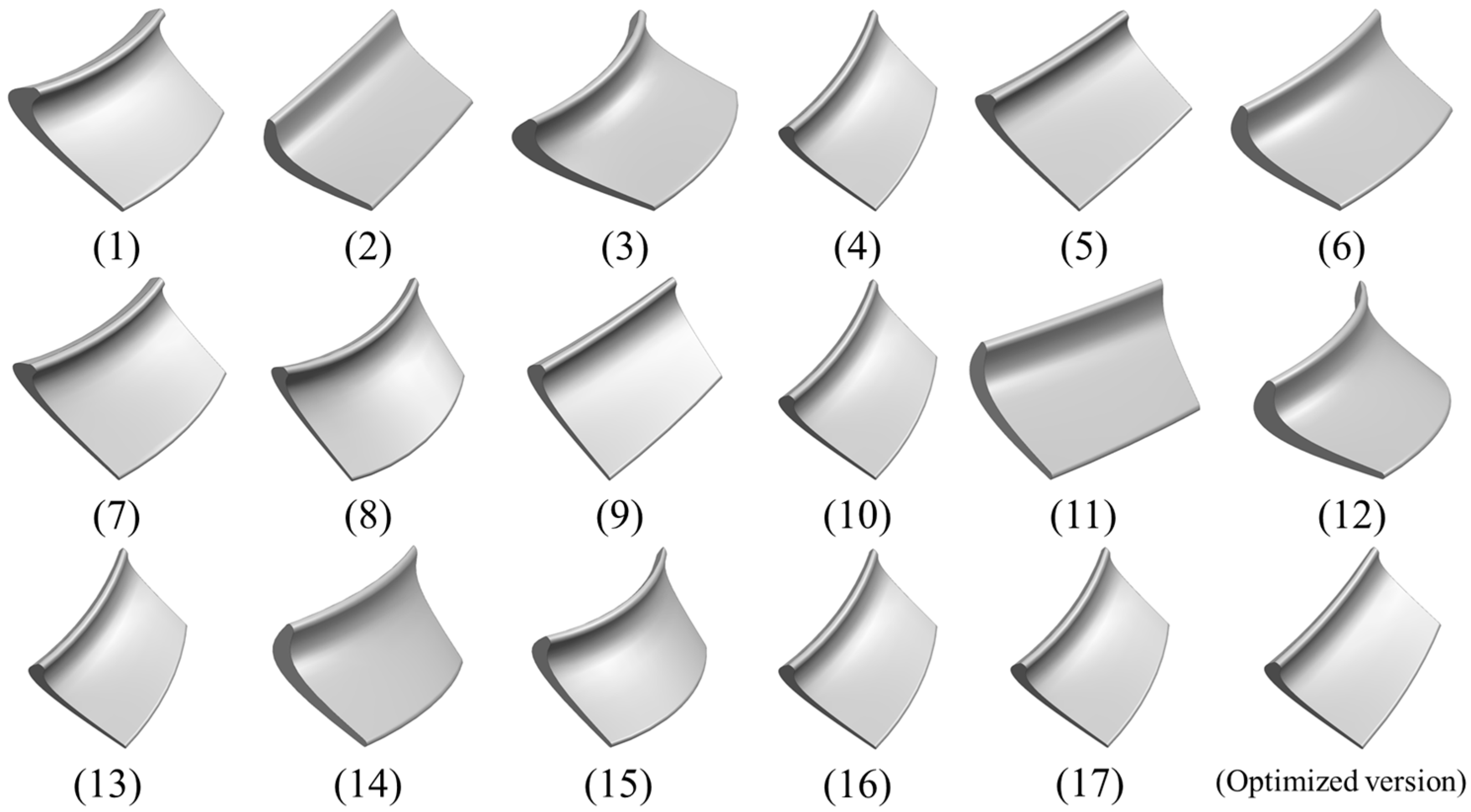
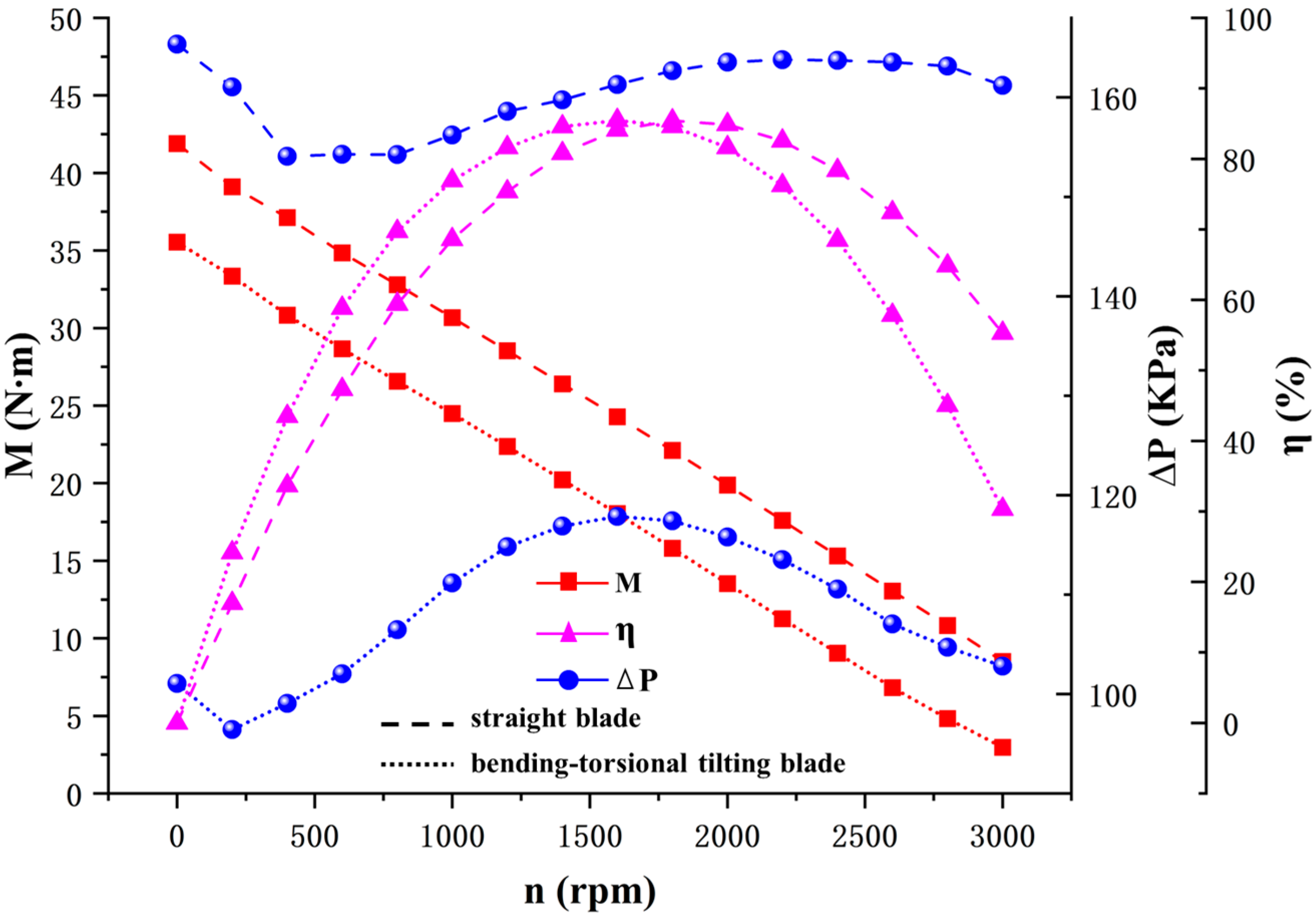
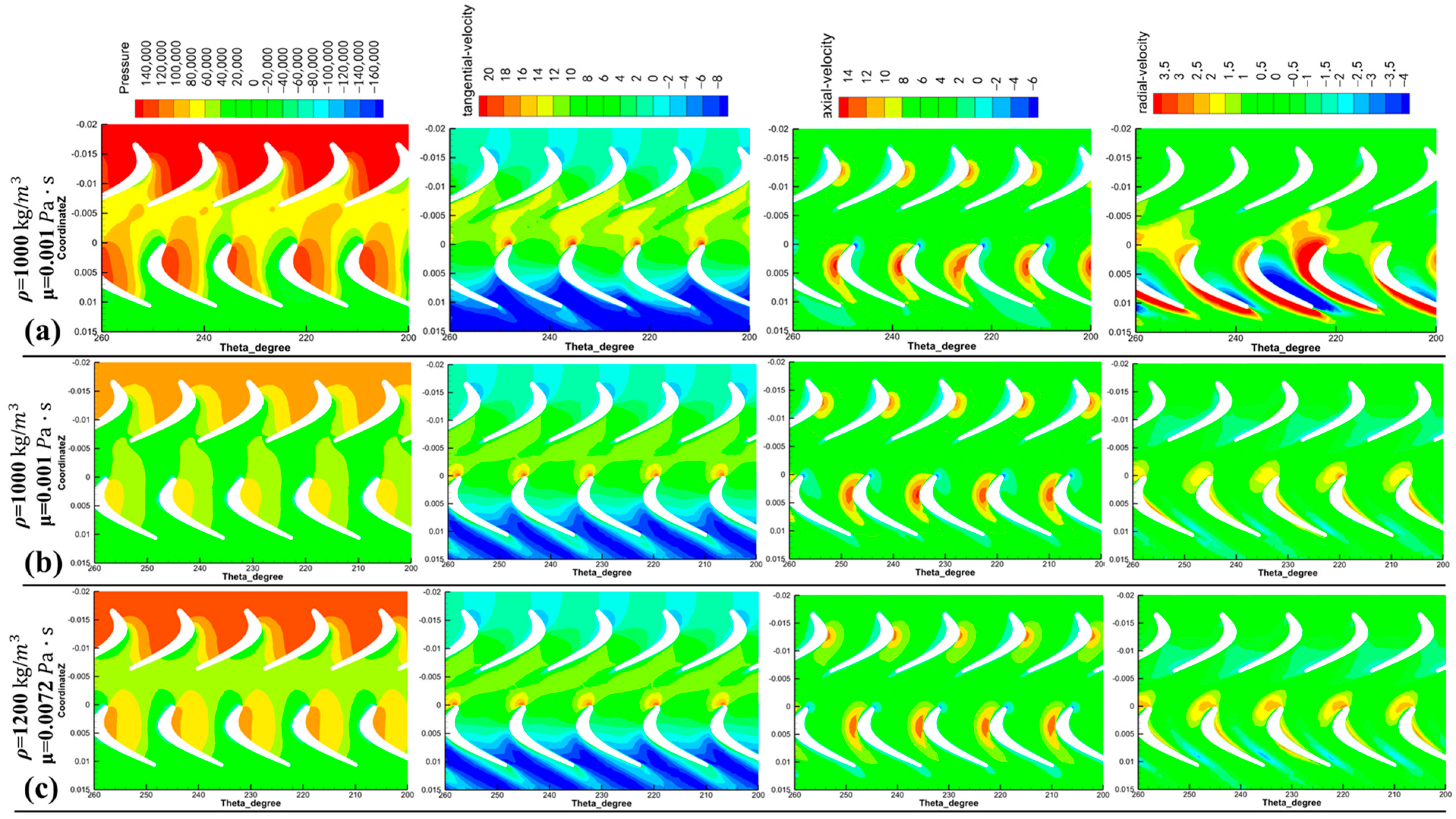
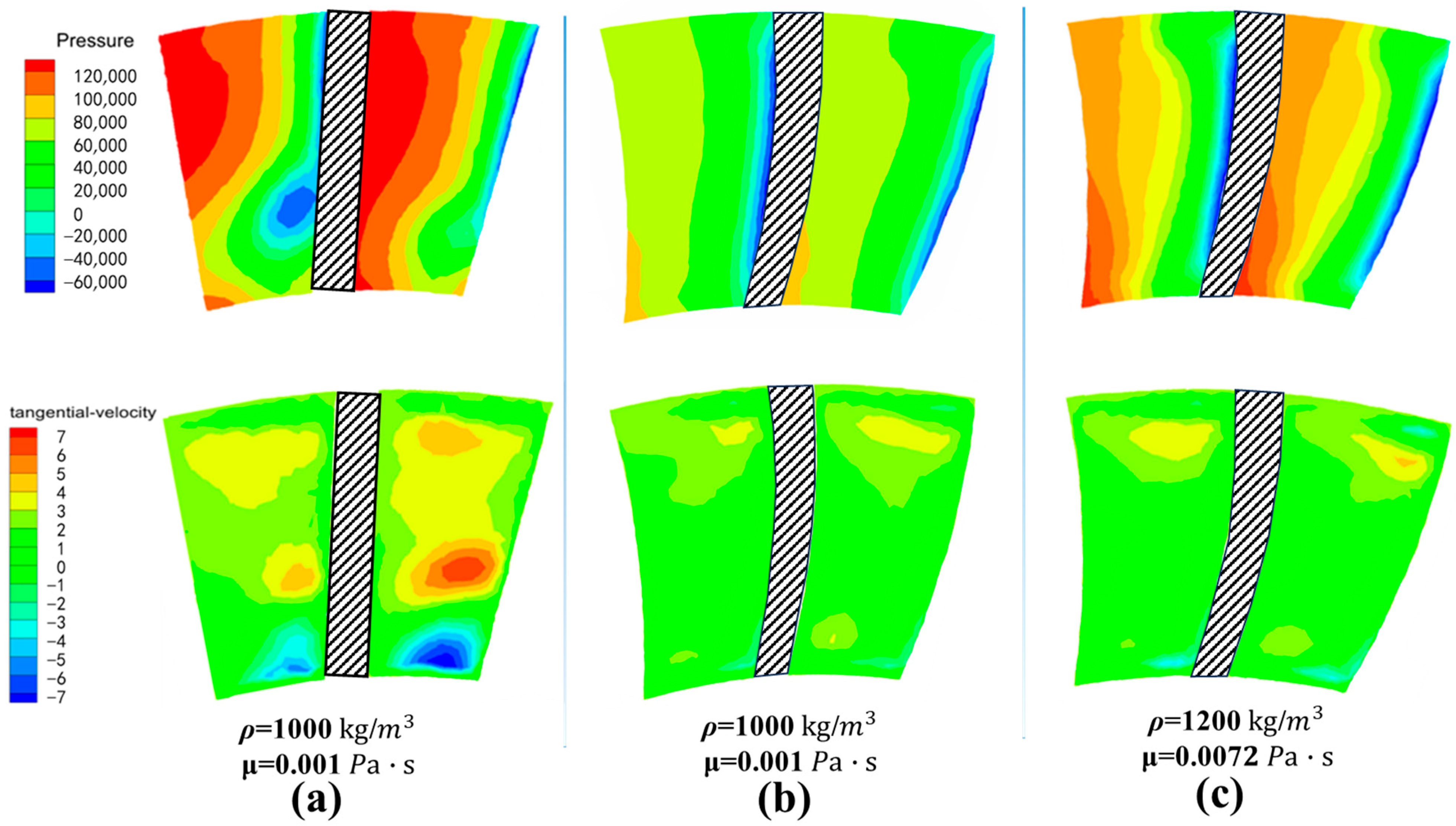
3.4. Research on Simulation Analysis of Turbine Blade

After completing the steps of three-dimensional modeling, flow channel extraction, and meshing the calculation model was imported into Fluent software for simulation analysis to evaluate the output characteristics and hydraulic efficiency of the turbodrill, and to verify the accuracy of the intelligent optimization algorithm. In order to realize the visualization of the key parameters in the flow field, the geometric average cylindrical surface (radius r = 58 mm) of the flow channel of the stator and rotor blades at 400 rpm was selected as the research object. By expanding the cylindrical surface into a plane, the pressure and velocity contours of the flow field can be observed in depth. When analyzing the velocity component, the influence of tangential velocity on fluid kinetic energy and drilling tool performance is very important, so it should be the main concern. In addition, the influence of axial and radial velocity on the overall flow characteristics (such as vortex, etc.) cannot be ignored. Through comprehensive analysis of these factors, it can provide strong guidance for the optimization design and performance improvement of turbodrill.

Analysis of the simulation outputs produced the performance curve for the straight-blade turbodrill (Figure 12). Under a flow rate of 30 L/s the device attains a peak hydraulic efficiency of 85.4% at an optimal speed of 1800 rpm, with an associated pressure drop of 162.69 kPa—substantially greater than that reported for comparable commercial turbodrills, indicating superior energy-conversion behavior. To satisfy the low-speed, high-torque design target, a single-stage turbine is required to deliver at least 25 N·m of torque. The numerical simulation indicates that the proposed blade generates 37.124 N·m at 400 rpm, thus meeting the design criterion. Moreover, the intelligent optimization routine predicted a torque of 38.648 N·m, in close agreement with the simulation result, which supports the validity and applicability of the developed algorithmic model.

By analyzing the pressure and velocity contours of the straight blade shown in Figure 13a and Figure 14a, it can be observed that the straight blade produces a higher pressure drop during the working process. In addition, from the distribution of axial velocity, there is a vortex phenomenon on the suction surface of the blade. The radial velocity cloud diagram further reveals the significant velocity change between the pressure surface and the suction surface of the blade. These phenomena show that although the straight blade meets the design requirements of low speed and high torque, there are still significant hydraulic losses and unstable flow in the flow field, which directly leads to the output energy loss of the turbodrill. In summary, these research results provide an important basis for the design optimization of turbodrills.

Analysis of the simulation outputs yields the performance curve for the turbodrill’s twisted blade (Figure 12). At a flow rate of 30 L/s the configuration attains a peak hydraulic efficiency of 85.5% at an optimal speed of 1600 rpm, with an associated pressure drop of 117.86 kPa—substantially lower than that of the straight-blade counterpart—indicating that the blade’s spatial bending and torsion markedly improve internal flow organization and reduce energy losses. Under the low-speed condition of 400 rpm, the blade produces an output torque of 30.83 N·m, thereby satisfying the design requirement for a low-speed, high-torque turbine. At the same time, the torque value predicted by the intelligent optimization algorithm is 30.23 N·m, which is highly consistent with the simulation results, which further verifies the accuracy and applicability of the optimization algorithm in the optimization of turbodrill parameters. Through the analysis of the pressure and velocity contours of the curved and twisted blade in Figure 13b and Figure 14b, we can clearly see that the pressure drop of the blade type is significantly reduced. The flow velocity between the pressure surface and the suction surface of the blade tends to be stable, the secondary flow phenomenon at the tip and root of the blade is improved, and the flow separation at the tail of the blade is also significantly reduced. In addition, the distribution of the pressure gradient in the flow field becomes more uniform, and the eddy current and hydraulic loss are significantly reduced, thereby optimizing the secondary flow characteristics in the flow channel. These improvements show that the bent-twisted blade has significant advantages in hydrodynamic performance and can effectively improve the overall hydraulic characteristics of the turbodrill.

To further validate the low-speed, high-torque performance of the designed Φ178 mm bend–twist–tilt blade, we conducted comparative simulations against existing blade geometries under identical boundary conditions. For these tests the working fluid was specified with a density of ρ = 1200 kg/m³ and a dynamic viscosity of 0.0072 Pa·s, the k–ε turbulence model was employed, and all other simulation settings were held constant. From the flow field contours of Figure 13c and Figure 14c, it can be seen that with the increase in drilling fluid density and viscosity, the pressure drop of the system increases slightly, but the fluid flow still maintains high stability. Under the working condition of 400 rpm, the output torque of the bent-twisted blade reaches 37.43 N·m, and the hydraulic efficiency is 39.8%. In contrast, the single-stage turbine torque of the existing space-designed blade is 27.4 N·m and the hydraulic efficiency is 44.7% [19], as shown in Figure 15. The results show that the torque output of the designed blade is 36.6% higher than that of the traditional blade. Despite a modest 4.9% reduction in hydraulic efficiency, the substantially improved low-speed, high-torque performance validates the effectiveness and engineering viability of the proposed 2D blade profile and the bending–twist–tilt 3D shaping strategy. These outcomes demonstrate the blade’s strong potential for application in deep-well drilling and other high-load operational scenarios.

4. Conclusions

In this paper, a Φ178 mm turbodrill blade is designed to achieve low-speed and high-torque output. The mathematical model of the output torque of the turbodrill is established by the moment of momentum theorem, and the relationship between the output torque and the parameters of the two-dimensional blade profile is analyzed. At the same time, the GA-LSSVM-MOPSO-TOPSIS intelligent optimization algorithm is used to optimize the two-dimensional and three-dimensional modeling design parameters of turbodrill blades, and the effectiveness of the optimization algorithm and parameters is verified by CFD simulation analysis. The specific conclusions are as follows:

(1)

Based on the theoretical model of the output characteristics of the turbodrill, the key blade profile parameters affecting the output performance are identified. We innovatively propose a three-dimensional modeling method for curved-twisted-tilted blades and summarize six core parameters that have a significant impact on the output characteristics: ${\beta }_{2k}{,\beta }_m,{\gamma }_2;R,\alpha ,\phi$

(2)

Through the GA-LSSVM-MOPSO-TOPSIS intelligent optimization algorithm, we optimized these key two-dimensional and three-dimensional design parameters, and determined the core parameters of the two-dimensional blade profile with the best comprehensive hydraulic performance of the turbodrill: ${\beta }_{2k}=20°$, ${\beta }_m=44.9085°$, ${\gamma }_2=4.2059°$; the optimal spatial parameter combination of bending and twisting blades is: $R=62.4962\mathrm{m}\mathrm{m}$, $\alpha =10.2682°$, $\phi =3°$

(3)

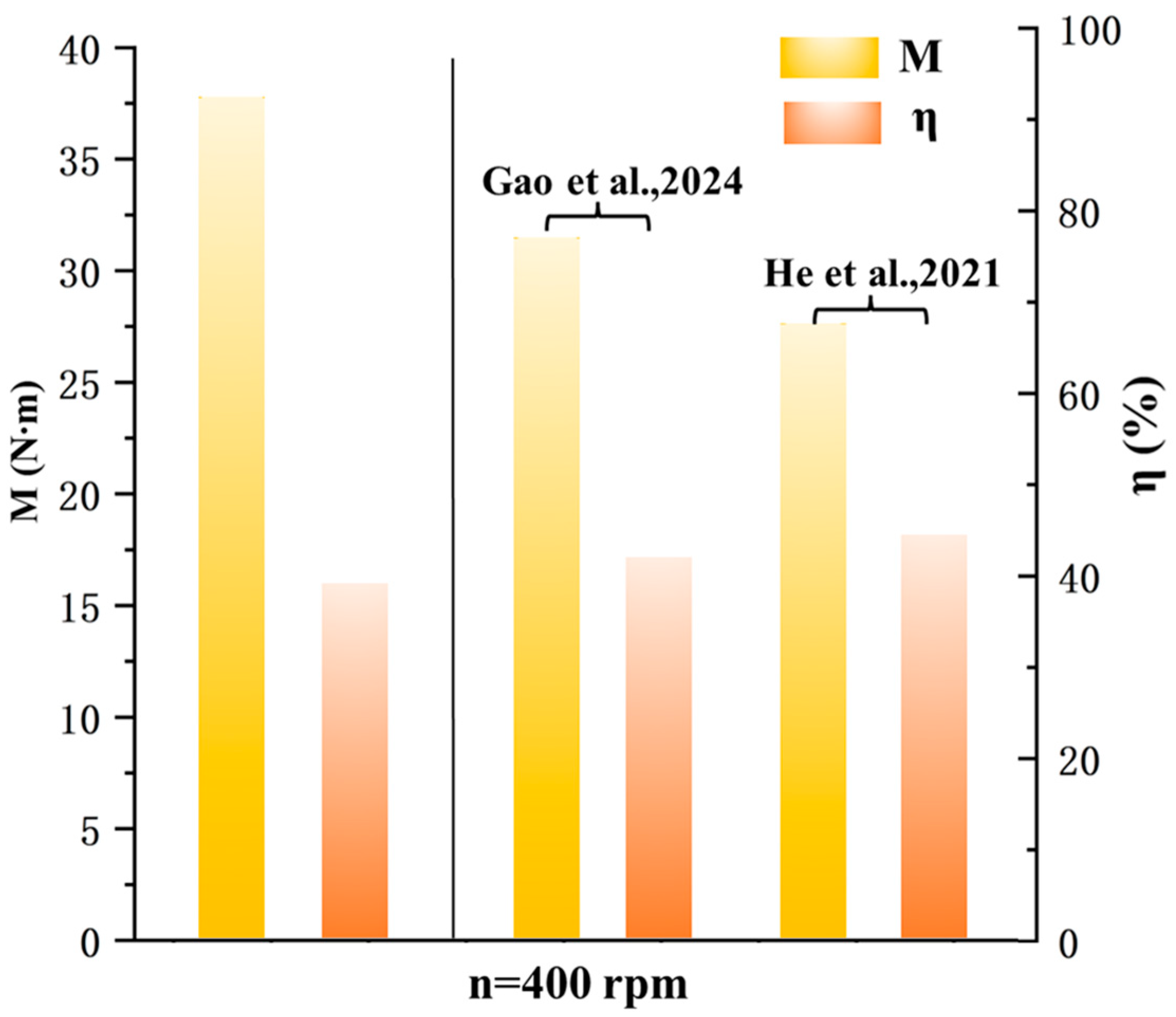
The results of CFD simulation analysis verify the accuracy of the intelligent optimization algorithm and show that the curved-twisted-tilted blade is significantly better than the straight blade in the pressure and velocity distribution of the flow field, and the hydraulic loss is effectively reduced. At 400 rpm, the single-stage turbine output torque of the curved-twisted-tilted blade is 37.4296 N·m, which is 36.61% higher than the existing design, and only 4.9% of the hydraulic efficiency is sacrificed, which lays a certain foundation for the design of low-speed and high-torque turbodrill blades.