Enabling Manual Guidance in High-Payload Industrial Robots for Flexible Manufacturing Applications in Large Workspaces
Abstract
1. Introduction
- Lifting and manipulating heavy objects: In industries such as automotive and aerospace, IRs with hand-guiding capabilities could assist in handling bulky components like engine parts, wings, or fuselage sections, reducing operator strain and increasing throughput [19].
- Sensor integration: Force and torque sensors are essential to detect operator inputs and ensure the robot responds adaptively to manual guidance. Vision systems may also be employed to monitor the workspace for potential collisions.
- Workspace operational zoning: Defining safe zones and implementing virtual barriers can help manage the interaction between humans and robots, particularly in dynamic manufacturing environments.
- Risk assessments and certifications: Comprehensive risk assessments must be conducted to identify potential hazards and implement mitigation strategies. Certification processes ensure that the system meets industry safety standards.
- Extending manual guidance to robotic cells with large workspaces by integrating control of a 6-Degrees-of-Freedom (DoF) serial IR and an additional custom designed linear track positioner (1-DoF).
- Providing an in-depth description of the proposed framework, detailing all experimental practices needed to establish logical connections between different control systems.
- Validation and demonstration on a physical prototype, delivering practical insights and deployment guidelines. The utilized setup includes a high-payload KUKA IR featuring the Robot Sensor Interface (RSI) software package [39] and utilizes the Beckhoff automation technology for the actuation of the additional linear axis.
2. Approach Overview
- (a)
- Linear Track Guidance (1-DoF): The robot remains fixed in its last pose while the linear track moves to reposition the robot along the Y-direction of the robot base frame. The real-time control loop runs on the PLC, which generates and sends position commands to the Beckhoff AX8118 servo drives that operate the servomotors actuating the linear axis. This mode allows the operator to move the robot along the cell and teach positions along the linear track. It should be noted that in this operation mode, the robot controller remains in a passive state, while the PLC receives from the EtherCAT network the orientation data of the end-effector (A, B, C angles) provided by the robot controller, which is required to correctly compute the current rotation matrix and correctly interpret the force data sampled with the F/T sensor.
- (b)
- Robot Guidance (6-DoF): The linear track remains stationary while the robot joints are enabled to move. In this case the pose correction logic is running within the robot controller (KUKA KRC4) and leverages the RSI package to process the real-time force data received via EtherCAT from the PLC, adjusting the robot motion accordingly. In this operation mode, the PLC acts solely as a data streaming unit, transmitting the sensor signals without executing any correction logic.
3. Modeling and Procedure
3.1. Sensor-Based Guidance
3.2. Practical Implementation
- DIGIN: reads values (sensor data) from I/O modules;
- SEN_PREA: reads values stored in the KUKA programming environment (e.g., global variables);
- TRAFO_ROBFRAME: retrieves current transformation matrix between two frames ();
- PT1: applies a low-pass filter;
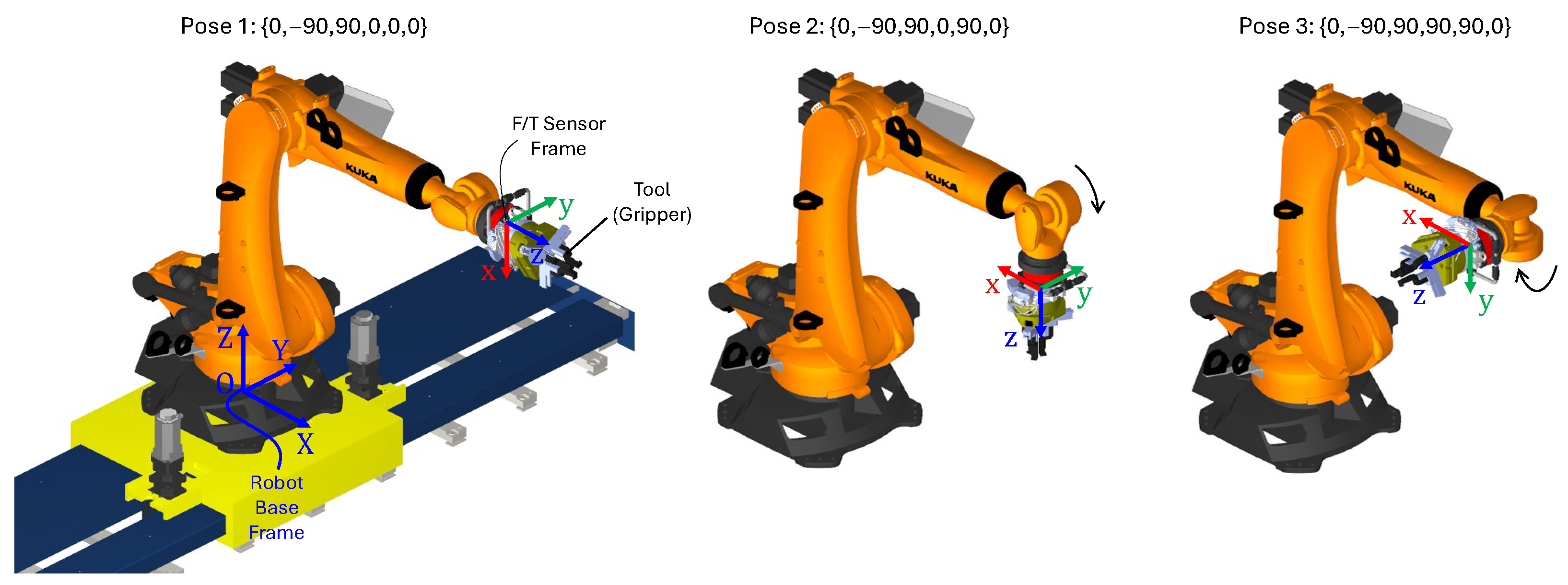
3.3. Load Sensing
- Pose 1
- Pose 2
- Pose 3
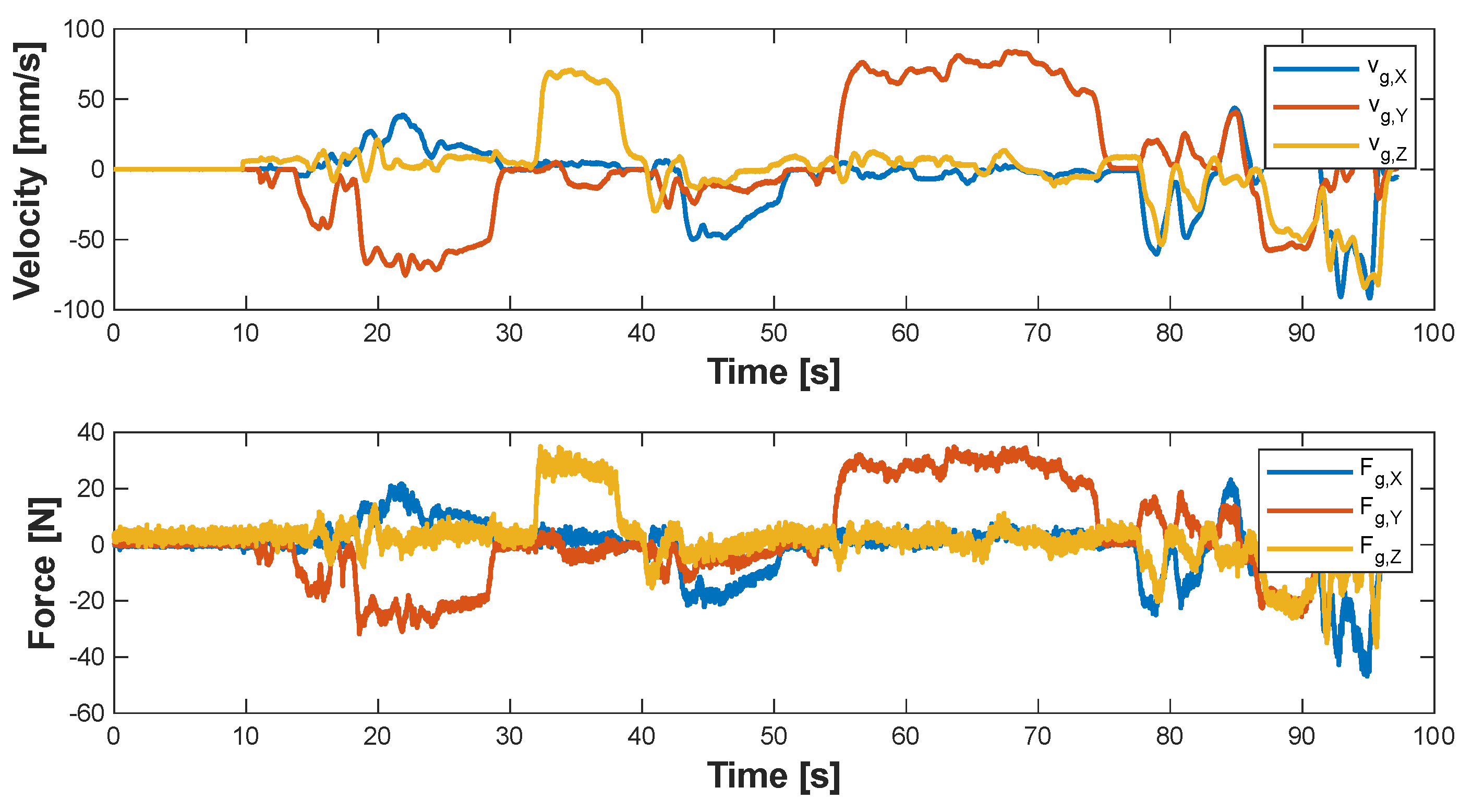
4. Experimental Testing
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhong, R.Y.; Xu, X.; Klotz, E.; Newman, S.T. Intelligent manufacturing in the context of industry 4.0: A review. Engineering 2017, 3, 616–630. [Google Scholar] [CrossRef]
- Oztemel, E.; Gursev, S. Literature review of Industry 4.0 and related technologies. J. Intell. Manuf. 2020, 31, 127–182. [Google Scholar] [CrossRef]
- International Federation of Robotics World Robotics 2025: Industrial Robots. 2025. Available online: https://ifr.org/ifr-press-releases/news/global-robot-demand-in-factories-doubles-over-10-years (accessed on 29 October 2025).
- Bilancia, P.; Schmidt, J.; Raffaeli, R.; Peruzzini, M.; Pellicciari, M. An overview of industrial robots control and programming approaches. Appl. Sci. 2023, 13, 2582. [Google Scholar] [CrossRef]
- Merdan, M.; Hoebert, T.; List, E.; Lepuschitz, W. Knowledge-based cyber-physical systems for assembly automation. Prod. Manuf. Res. 2019, 7, 223–254. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, W.; Zhang, Y.; Han, L.; Li, J.; Lu, Y. Integration and calibration of an in situ robotic manufacturing system for high-precision machining of large-span spacecraft brackets with associated datum. Robot.—Comput.—Integr. Manuf. 2025, 94, 102928. [Google Scholar] [CrossRef]
- Halim, J.; Eichler, P.; Krusche, S.; Bdiwi, M.; Ihlenfeldt, S. No-code robotic programming for agile production: A new markerless-approach for multimodal natural interaction in a human-robot collaboration context. Front. Robot. AI 2022, 9, 1001955. [Google Scholar] [CrossRef]
- Safeea, M.; Neto, P. Precise positioning of collaborative robotic manipulators using hand-guiding. Int. J. Adv. Manuf. Technol. 2022, 120, 5497–5508. [Google Scholar] [CrossRef]
- Dhanda, M.; Rogers, B.A.; Hall, S.; Dekoninck, E.; Dhokia, V. Reviewing human-robot collaboration in manufacturing: Opportunities and challenges in the context of industry 5.0. Robot.—Comput.—Integr. Manuf. 2025, 93, 102937. [Google Scholar] [CrossRef]
- Vicentini, F. Collaborative robotics: A survey. J. Mech. Des. 2021, 143, 040802. [Google Scholar] [CrossRef]
- Bejarano, R.; Ferrer, B.R.; Mohammed, W.M.; Lastra, J.L.M. Implementing a human-robot collaborative assembly workstation. In Proceedings of the 2019 IEEE 17th International Conference on Industrial Informatics (INDIN), Helsinki, Finland, 22–25 July 2019; IEEE: Piscataway, NJ, USA, 2019; Volume 1, pp. 557–564. [Google Scholar]
- Malik, A.A.; Brem, A. Digital twins for collaborative robots: A case study in human-robot interaction. Robot.—Comput.—Integr. Manuf. 2021, 68, 102092. [Google Scholar] [CrossRef]
- Buerkle, A.; Eaton, W.; Al-Yacoub, A.; Zimmer, M.; Kinnell, P.; Henshaw, M.; Coombes, M.; Chen, W.H.; Lohse, N. Towards industrial robots as a service (IRaaS): Flexibility, usability, safety and business models. Robot.—Comput.—Integr. Manuf. 2023, 81, 102484. [Google Scholar] [CrossRef]
- Pan, Z.; Polden, J.; Larkin, N.; Van Duin, S.; Norrish, J. Recent progress on programming methods for industrial robots. Robot.—Comput.—Integr. Manuf. 2012, 28, 87–94. [Google Scholar] [CrossRef]
- Rodriguez-Guerra, D.; Sorrosal, G.; Cabanes, I.; Calleja, C. Human-robot interaction review: Challenges and solutions for modern industrial environments. IEEE Access 2021, 9, 108557–108578. [Google Scholar] [CrossRef]
- Kolbeinsson, A.; Lagerstedt, E.; Lindblom, J. Foundation for a classification of collaboration levels for human-robot cooperation in manufacturing. Prod. Manuf. Res. 2019, 7, 448–471. [Google Scholar] [CrossRef]
- Fujii, M.; Murakami, H.; Sonehara, M. Study on application of a human-robot collaborative system using hand-guiding in a production line. IHI Eng. Rev. 2016, 49, 24–29. [Google Scholar]
- Kim, M.; Zhang, Y.; Jin, S. Control strategy for direct teaching of non-mechanical remote center motion of surgical assistant robot with force/torque sensor. Appl. Sci. 2021, 11, 4279. [Google Scholar] [CrossRef]
- Lee, S.Y.; Lee, Y.S.; Park, B.S.; Lee, S.H.; Han, C.S. MFR (Multipurpose Field Robot) for installing construction materials. Auton. Robot. 2007, 22, 265–280. [Google Scholar] [CrossRef]
- Schraft, R.D.; Meyer, C.; Parlitz, C.; Helms, E. Powermate-a safe and intuitive robot assistant for handling and assembly tasks. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 4074–4079. [Google Scholar]
- Stepputat, M.; Neumann, S.; Wippermann, J.; Heyser, P.; Meschut, G.; Beuss, F.; Sender, J.; Fluegge, W. Flexible Automation through Robot-Assisted Mechanical Joining in Small Batches. Procedia CIRP 2023, 120, 457–462. [Google Scholar] [CrossRef]
- Massa, D.; Callegari, M.; Cristalli, C. Manual guidance for industrial robot programming. Ind. Robot. Int. J. 2015, 42, 457–465. [Google Scholar] [CrossRef]
- Reyes-Uquillas, D.; Hsiao, T. Safe and intuitive manual guidance of a robot manipulator using adaptive admittance control towards robot agility. Robot.—Comput.—Integr. Manuf. 2021, 70, 102127. [Google Scholar] [CrossRef]
- Haninger, K.; Radke, M.; Vick, A.; Krüger, J. Towards high-payload admittance control for manual guidance with environmental contact. IEEE Robot. Autom. Lett. 2022, 7, 4275–4282. [Google Scholar] [CrossRef]
- Comau S.p.A. AURA—Collaborative Robotics for High Payload Applications. 2024. Available online: https://www.comau.com/en/aura-collaborative-robotics-for-high-payload-applications/ (accessed on 18 October 2025).
- FANUC. Hand Guidance Accessory for Standard Robots. 2024. Available online: https://www.fanuc.eu/eu-en/accessory/accessory/hand-guidance (accessed on 18 October 2025).
- Farajtabar, M.; Charbonneau, M. The path towards contact-based physical human—Robot interaction. Robot. Auton. Syst. 2024, 182, 104829. [Google Scholar] [CrossRef]
- Robla-Gómez, S.; Becerra, V.M.; Llata, J.R.; Gonzalez-Sarabia, E.; Torre-Ferrero, C.; Perez-Oria, J. Working together: A review on safe human-robot collaboration in industrial environments. IEEE Access 2017, 5, 26754–26773. [Google Scholar] [CrossRef]
- ISO 10218-1:2011; Robots and Robotic Devices—Safety Requirements for Industrial Robots. ISO: Geneva, Switzerland, 2011. Available online: https://www.iso.org/standard/51330.html (accessed on 15 January 2025).
- ISO/TS 15066:2016; Robots and Robotic Devices—Collaborative Robots. ISO: Geneva, Switzerland, 2016. Available online: https://www.iso.org/standard/62996.html (accessed on 15 January 2025).
- Liu, G.; Li, Q.; Fang, L.; Han, B.; Zhang, H. A new joint friction model for parameter identification and sensor-less hand guiding in industrial robots. Ind. Robot. Int. J. Robot. Res. Appl. 2020, 47, 847–857. [Google Scholar] [CrossRef]
- Yao, B.; Zhou, Z.; Wang, L.; Xu, W.; Liu, Q. Sensor-less external force detection for industrial manipulators to facilitate physical human-robot interaction. J. Mech. Sci. Technol. 2018, 32, 4909–4923. [Google Scholar] [CrossRef]
- Yao, B.; Zhou, Z.; Wang, L.; Xu, W.; Liu, Q.; Liu, A. Sensorless and adaptive admittance control of industrial robot in physical human- robot interaction. Robot.—Comput.—Integr. Manuf. 2018, 51, 158–168. [Google Scholar] [CrossRef]
- de Gea Fernández, J.; Mronga, D.; Günther, M.; Knobloch, T.; Wirkus, M.; Schröer, M.; Trampler, M.; Stiene, S.; Kirchner, E.; Bargsten, V.; et al. Multimodal sensor-based whole-body control for human–robot collaboration in industrial settings. Robot. Auton. Syst. 2017, 94, 102–119. [Google Scholar] [CrossRef]
- Cherubini, A.; Navarro-Alarcon, D. Sensor-based control for collaborative robots: Fundamentals, challenges, and opportunities. Front. Neurorobotics 2021, 14, 576846. [Google Scholar] [CrossRef] [PubMed]
- Bascetta, L.; Ferretti, G.; Magnani, G.; Rocco, P. Walk-through programming for robotic manipulators based on admittance control. Robotica 2013, 31, 1143–1153. [Google Scholar] [CrossRef]
- Xing, X.; Burdet, E.; Si, W.; Yang, C.; Li, Y. Impedance learning for human-guided robots in contact with unknown environments. IEEE Trans. Robot. 2023, 39, 3705–3721. [Google Scholar] [CrossRef]
- Ljasenko, S.; Lohse, N.; Justham, L. Dynamic vs dedicated automation systems-a study in large structure assembly. Prod. Manuf. Res. 2020, 8, 35–58. [Google Scholar] [CrossRef]
- KUKA Robot Sensor Interface. Available online: https://www.kuka.com/en-us/products/robotics-systems/software/application-software/kuka_robotsensorinterface (accessed on 15 January 2025).
- Ferrarini, S.; Bilancia, P.; Raffaeli, R.; Peruzzini, M.; Pellicciari, M. A method for the assessment and compensation of positioning errors in industrial robots. Robot.—Comput.—Integr. Manuf. 2024, 85, 102622. [Google Scholar] [CrossRef]
- Cvitanic, T.; Melkote, S.N. A new method for closed-loop stability prediction in industrial robots. Robot.—Comput.—Integr. Manuf. 2022, 73, 102218. [Google Scholar] [CrossRef]
- Tutarini, A.; Bilancia, P.; León, J.F.R.; Viappiani, D.; Pellicciari, M. Design and implementation of an active load test rig for high-precision evaluation of servomechanisms in industrial applications. J. Ind. Inf. Integr. 2024, 42, 100696. [Google Scholar] [CrossRef]
- Hu, J.; Li, C.; Chen, Z.; Yao, B. Precision motion control of a 6-DoFs industrial robot with accurate payload estimation. IEEE/ASME Trans. Mechatronics 2020, 25, 1821–1829. [Google Scholar] [CrossRef]
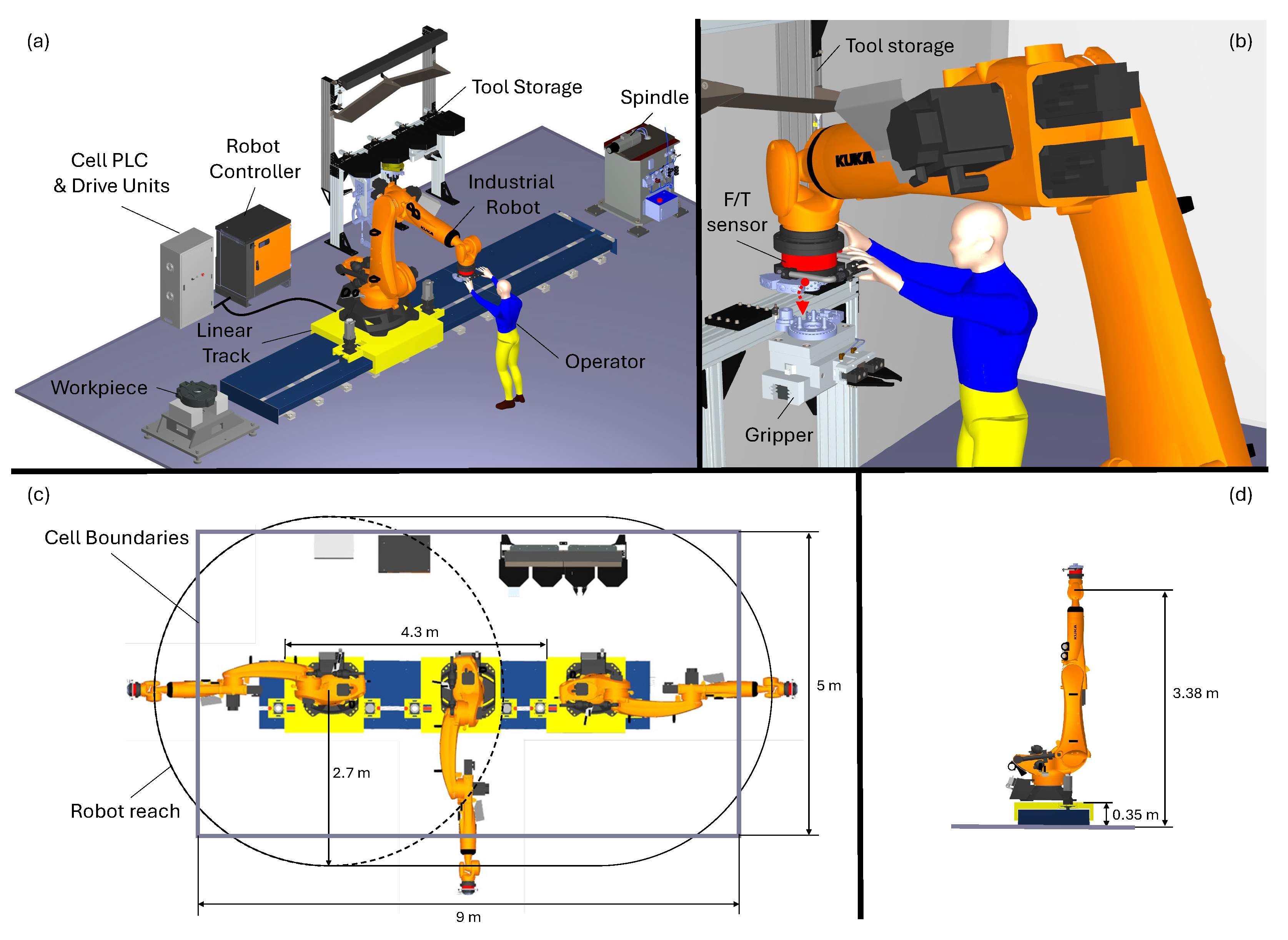

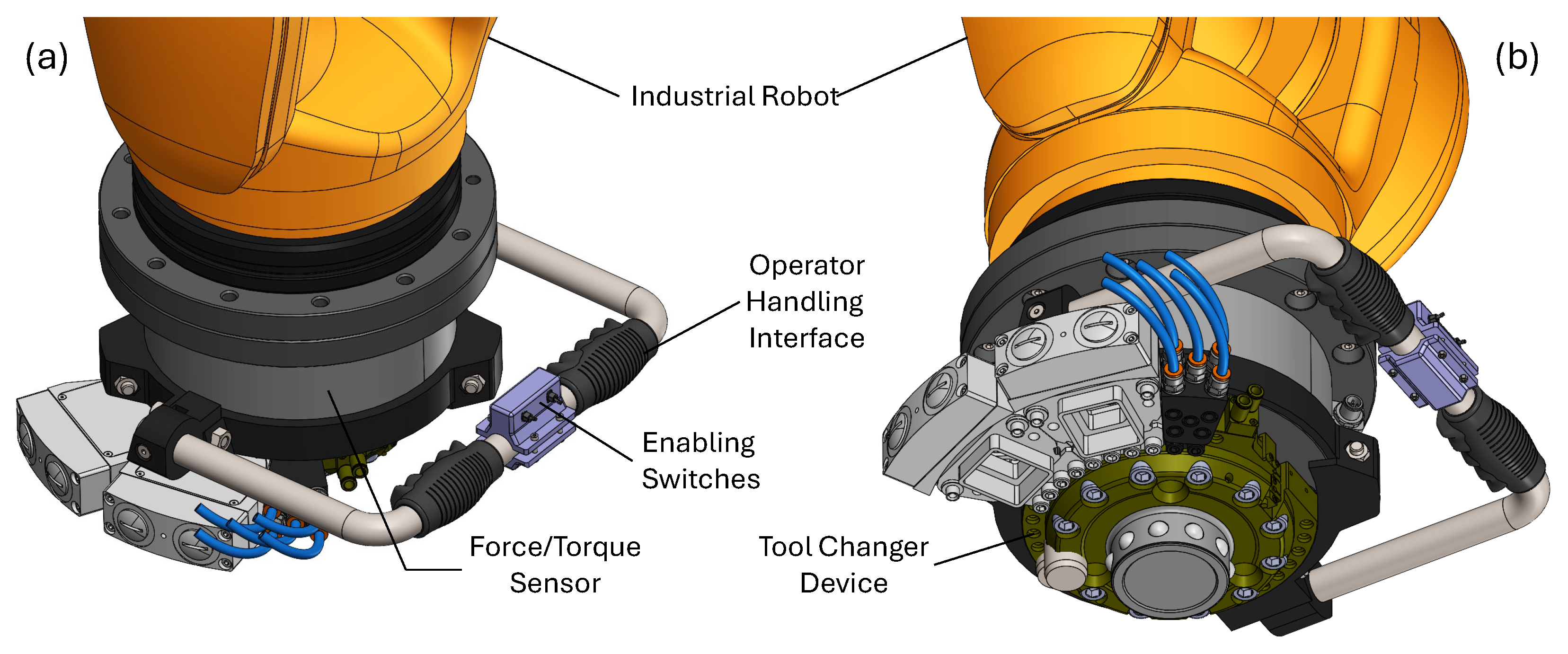



| Device | Model | Characteristics |
|---|---|---|
| Robot | KUKA KR210 R2700 Prime | Reach: 2.7 m Payload: 210 kg Mass (including box and cables): 1190 kg Controller: KRC4 (KSS version 8.3.25) |
| Linear track | Custom solution | Stroke: 4.3 m Platform Mass: 940 kg Servomotors: 2 Beckhoff AM8052 Drive units: 2 Beckhoff AX8118 Reducers: 2 Stoeber PH732 (red. ratio 25) Rack-and-pinion: pinion radius of 53.05 mm Controller: Beckhoff PLC CX5140 |
| Tools | Schunk Tool-1: PZN+240/2 Tool-2: PGN+380/2 & PGN+160/1 | Mass Tool-1: 80 kg Mass Tool-2: 60 kg |
| F/T sensor | Schunk FTN SI-1800-350 | , range: 0–1800 N range: 0–4500 N , , range: 0–350 Nm |
| Spindle | HSD ES 939A 4P | Peak power: 13.5 kW Speed range: 6000–24,000 rpm |
| User | Teach Pendant Time | Manual Guiding Time | Improvement |
|---|---|---|---|
| Expert operator | 7 min 20 s | 3 min 14 s | 55.9% |
| Non-expert operator | 11 min 52 s | 4 min 23 s | 63% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avanzi La Grotta, P.; Salami, M.; Trentadue, A.; Bilancia, P.; Pellicciari, M. Enabling Manual Guidance in High-Payload Industrial Robots for Flexible Manufacturing Applications in Large Workspaces. Machines 2025, 13, 1016. https://doi.org/10.3390/machines13111016
Avanzi La Grotta P, Salami M, Trentadue A, Bilancia P, Pellicciari M. Enabling Manual Guidance in High-Payload Industrial Robots for Flexible Manufacturing Applications in Large Workspaces. Machines. 2025; 13(11):1016. https://doi.org/10.3390/machines13111016
Chicago/Turabian StyleAvanzi La Grotta, Paolo, Martina Salami, Andrea Trentadue, Pietro Bilancia, and Marcello Pellicciari. 2025. "Enabling Manual Guidance in High-Payload Industrial Robots for Flexible Manufacturing Applications in Large Workspaces" Machines 13, no. 11: 1016. https://doi.org/10.3390/machines13111016
APA StyleAvanzi La Grotta, P., Salami, M., Trentadue, A., Bilancia, P., & Pellicciari, M. (2025). Enabling Manual Guidance in High-Payload Industrial Robots for Flexible Manufacturing Applications in Large Workspaces. Machines, 13(11), 1016. https://doi.org/10.3390/machines13111016









